Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of C–H⋯π interactions in modulating the breathing amplitude of a 2D square lattice net: alcohol sorption studies†
Gift
Mehlana
,
Gaëlle
Ramon
and
Susan A
Bourne
*
Centre for Supramolecular Chemistry Research, Department of Chemistry, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa. E-mail: susan.bourne@uct.ac.za; Fax: +27 21 650 5195; Tel: +27 21 650 2563
First published on 30th April 2014
Abstract
A breathing 2D net 1 {[Zn(34pba)2]·DMF}n assembled from mononuclear zinc(II) centres and 3-(4-pyridyl) benzoate (34pba) ditopic linker is presented. 1 undergoes a displacive phase transition to give 1d, [Zn(34pba)2]n on evacuation of DMF. This is accompanied by a 37% decrease in solvent accessible void volume. Exposure of 1d to alcohol vapours shows that the saturation uptake increases with an increase in number of carbon atoms in the alcohol. The enhanced uptake of n-butanol and n-propanol is attributed to the long alkyl chain which enhances C–H⋯π interactions with the hydrophobic pyridyl and phenyl rings of the network. These interactions trigger the breathing motion of the 2D network and allow for the entry of n-propanol and n-butanol into the channels. Methanol and ethanol are unable to initiate the dynamic motion of the framework which increases the channel volume. In consequence, these solvents are absorbed to a lesser extent. Vapour phase competition studies show that the activated material is able to absorb n-butanol in the presence of a high vapour pressure of methanol. The selectivity observed may be based on factors that allow the metal organic framework inclusion compound to assume the most relaxed conformation.
Introduction
The development of microporous metal organic frameworks (MOFs) has received much attention owing to their potential applications such as gas storage, sensing, separation and catalysis.1–6 One major limitation of the majority of MOFs is that the combination of inorganic nodes and organic spacers in crystalline state results in robust materials.7 In contrast, applications such as guest selectivity and separation are better served by guest-responsive dynamic MOFs which can undergo reversible structural transformations between large and small cavities.8 Several kinds of guest-induced structural flexibility have been reported, including “gate-opening”9–11 or “breathing”12,13 behaviour. A considerable number of studies have been devoted to understanding the behaviour of breathing MOFs.14–19 and recent work has highlighted the thermodynamic basis for such breathing behaviour.20 Dynamic breathing motion in MOFs may occur through a displacive phase transition, DPT (without bond breaking) or a reconstructive phase transitions RPT (involving bond breaking).19 The latter is rather rare and involves creation of open metal sites which can enhance the sorption of guest molecules.For many years, attention has focussed on improved methods for achieving selective separation of industrially important liquid and gaseous chemicals.21–24 Current methods are frequently energy intensive and generate large quantities of waste. MOFs offer a cleaner alternative, as their properties (high surface areas, tunable pore size and shape, good thermal stability) are promising for the development of separation technologies. This development is still in the early stages. In the majority of robust metal organic frameworks studied to date the size of the pores of the framework plays a large role in achieving separation of mixed components,25 a process similar to the familiar “molecular sieving.”
Breathing MOFs composed of 2D layers which are interdigited are a special class as the ability of the 2D layers to glide past each other allows for the accommodation of large guest molecules with diameters larger than the pores of framework.26,27 Such movement of the 2D layers is normally triggered by the π⋯π and C–H⋯π interactions of the incoming guest molecules with the host framework. Hence, the surface area of the guest molecule plays a major role in modulating the dynamic motion of the framework. It follows that 2D MOFs should be highly selective to guest molecules with a larger surface area compared to the ones with a smaller surface area.
In this study, we probe and provide insights into the breathing phenomena of a 2D square lattice net on exposure to methanol, ethanol, n-propanol, n-butanol and n-hexanol and water. We also demonstrate that the degree of network breathing depends on the size and hydrophobicity (hence degree of C–H⋯π interactions) of the guest molecule. This effect allows the network to achieve separation of n-butanol from methanol in a mixture. To construct the 2D breathing MOF, we used a ditopic linker 3-(4-pyridyl) benzoate (34pba) and Zn(II) ions. This linker provides some degree of flexibility in the framework, arising from the ability of the ligand to vary its dihedral angles between the pyridyl and phenyl ring as well as the different coordination modes that can be assumed by the carboxylate moiety.
Experimental
Synthesis of 1: {[Zn (34pba)2]·DMF}n
Zn(NO3)2·6H2O (290 mg, 1 mmol) was dissolved in 4 ml DMF. 80 mg (0.4 mmol) of 3-(4-pyridyl) benzoic acid was dissolved in 4 ml DMF. The two solutions were combined in a large vial and heated in an oven at 80 °C. Colourless crystals were formed after 48 hours. Compound 1d, [Zn(34pba)2]n was obtained by desorbing DMF molecules from 1 at 200 °C for 24 hours under vacuum.Hot-stage microscopy (HSM)
The thermal behaviour of compound 1 was monitored using a Nikon SMZ-10 stereoscopic microscope fitted with a Linkan THM hot stage and a Linkam TP92 control unit. The crystals were immersed in paraton oil and heated from 25 to 400 °C. The images of the crystals were captured at different temperatures.Thermogravimetric analysis (TGA)
Thermogravimetric experiments were carried out using a TA Instrument TA-Q500. In a typical run 1–5 mg of the sample was dried on a filter paper, placed in open aluminium pans and heated in a dry air atmosphere of nitrogen (50 ml min−1) at a heating rate of 10 °C min−1 within a temperature range of 25–500 °C.Differential Scanning Calorimetry (DSC)
DSC measurements were performed using a TA Instrument DSC-Q200 under a dry atmosphere of nitrogen gas (50 ml min−1). The samples were dried on a filter paper and a sample mass of 0.5–1.5 mg placed in ventilated aluminium pans with lids and heated at 10 °C min−1 within a temperature range of 25–450 °C.Sorption kinetics of alcohol vapours
Kinetic studies were carried out to analyse the uptake of alcohols by the activated phase 1d. A balance, placed in a thermostatically controlled oven (precision ca. 0.5 °C), is connected to a computer which tracks the experiment. A sample holder is contained within a brass cylinder which has six solvent chambers evenly distributed around the sample. The brass cylinder fits over the sample on the balance and can be sealed. The solvent under study was placed in the solvent chambers, the cylinder was sealed and the vapour pressure allowed to equilibrate for 30 minutes. The scale was zeroed, the seal between sample and solvent vapour removed and the monitoring computer program (PB303S31) started. The increase in mass with time of the sample was recorded and then fitted into standard kinetic models to determine the rate constant for the uptake of each alcohol at 25 °C.PXRD studies
Powder diffraction patterns were measured on a Bruker D8 Advance X-ray diffractometer operating in a DaVinci geometry equipped with a Lynxeye detector using a CuKα-radiation (λ = 1.5406 Å). X-rays were generated by an accelerating voltage of 30 kV and a current of 40 mA. A receiving slit of 0.6 mm and a primary and secondary slits of 2.5 mm were used. Samples were placed on a zero background sample holder and scanned over a range of 4° to 40° in 2θ with a step size of 0.01° per second. Temperature dependant PXRD studies were conducted over a temperature range of 30–320 °C. Samples were scanned from 4° to 40° in 2θ with a step size of 0.02° per second to give a total of 1758 steps. The total time of exposure of the sample to radiation was 7 minutes 52 seconds at a given temperature. A heating rate of 0.5 °C min−1 was used to increase the temperature.Powder pattern decomposition
Powder data for the alcohol inclusion compounds was used for profile fitting. The lattice parameters for compound 1 were used for Pawley fitting and they were allowed to refine. Peak profile fitting was done using PV-TCHZ pseudo-Voight function included in the peak picking routine in TOPAS.28 Profile fitting was performed over a 2θ range of 4–40°. The unit cell parameters were validated by the Pawley fitting method29 by profile matching using the hkl-phase refinement in TOPAS. The background was modelled using the fifth order Chebychev function and a parameter was included to account for sample displacement caused by the zero background sample holder.Single crystal structure determination
Single crystal structure determination was performed using a Bruker ApexII KAPPA CCD diffractometer at 173 K equipped with a graphite monochromated Mo Kα radiation (λ = 0.71073 Å). Unit cell refinement and data reduction were performed using the program SAINT.30 The intensity reflection data was corrected for Lorentz-polarisation and absorption effects using the SADABS program.31 The structure was solved by direct method using the SHELX9732 computer programme package within the X-SEED interface.33 Structure refinement was performed by full-matrix least-squares on F2 using SHELXL. Non-hydrogen atoms were refined with anisotropic thermal parameters where possible. Hydrogen atoms were introduced to calculated positions and refined isotropically. Crystallographic data and refinement parameters are given in Table 1.| Compound | 1 | 1d | 1d-propanol | 1d-butanol |
|---|---|---|---|---|
| Molecular formula | (C24H16N2O4Zn)·(C3H7NO) | C24H16N2O4Zn | (C24H16N2O4Zn)·(C3H8O) | (C24H16N2O4Zn)·(C4H10O) |
| Molecular mass | 534.85 | 461.78 | 503.85 | 539.91 |
| Crystal size/mm | 0.21 × 0.22 × 0.25 | 0.23 × 0.28 × 0.26 | 0.13 × 0.16 × 0.20 | 0.06 × 0.25 × 0.25 |
| Temp./K | 173(2) | 173(2) | 173(2) | 173(2) |
| Crystal symmetry | Tetragonal | Tetragonal | Tetragonal | Tetragonal |
| Space group | P43212 | P43212 | P43212 | P43212 |
| a/Å | 11.5361(3) | 11.5806(3) | 11.6638(4) | 11.728(1) |
| c/Å | 37.317(2) | 34.904(2) | 36.790(3) | 36.977(4) |
| Z | 8 | 8 | 8 | 8 |
| Volume/Å3 | 4966.2(3) | 4681.0(3) | 5005.0(5) | 5086(2) |
| D c/g cm−3 | 1.4306 | 1.310 | 1.385 | 1.3995 |
| 2θ range/° | 1.85–27.89 | 1.85–28.39 | 1.83–27.10 | 2.06–26.53 |
| No. of reflections collected | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798 798 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 511 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248 248 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
| No. unique reflections | 5934 | 5871 | 5524 | 5164 |
| No. reflections with I > 2σI | 5045 | 5200 | 4271 | |
| Data/parameters refined | 5934/329 | 5871/274 | 5524/297 | |
| Goodness of fit, S | 1.059 | 1.053 | 1.043 | |
| R (I > 2σI) | 0.0429 | 0.0404 | 0.0917 | |
| Final wR2 (all data) | 0.1029 | 0.1340 | 0.2739 | |
| Min, max e density/e Å−3 | −0.29, 0.47 | −0.39, 0.61 | −0.46, 0.88 |
Results and discussion
Crystal structure description
Compound 1, {[Zn(34pba)2].DMF}n, is an analogue of our previously reported34 cobalt compound, {[Co(34pba)2].DMF}n, so a full structural description is not given here. 1 crystallises in the tetragonal crystal system and chiral space group P43212. Selected crystallographic parameters for this and subsequent structures are given in Table 1. Each zinc atom is coordinated to the ligands through four oxygen atoms of the carboxylate moieties and two nitrogen atoms of the pyridyl rings as illustrated in Fig. 1.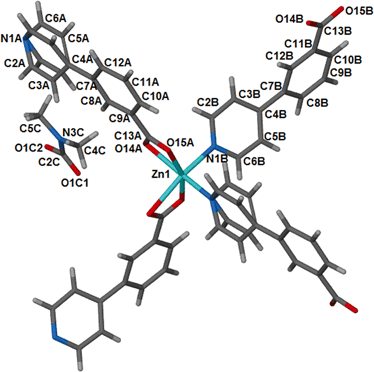 | ||
| Fig. 1 Coordination environment around the metal centre in 1, with atomic labels. This geometry is retained on desolvation of the DMF guest molecules to give 1d. | ||
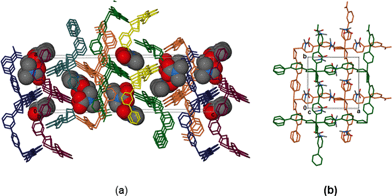
The overall geometry around the zinc centre is a distorted octahedron. As observed in the cobalt analogue, one pyridyl ring (here labelled N1A-C6A) is disordered over two positions with equal site occupancy. The guest DMF is also disordered over two positions. The packing diagram of 1 depicts interdigited 2D layers in which DMF molecules are sandwiched (Fig. 2). Each 2D layer is a simple square grid network, with sql topology. Adjacent 2D-layers are connected via weak intermolecular C–H⋯O hydrogen bonds and by at least one intermolecular interaction between the guest molecule and the network (Table S6†). In addition, there are a number of C–H⋯π contacts between aromatic rings of adjacent networks (distances between 4.2 and 4.6 Å).
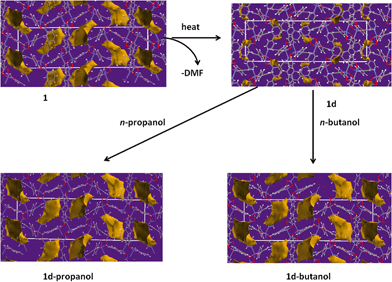
Desorbing the DMF from 1 afforded single crystals of the desolvated network compound [Zn(34pba)2]n, 1d. The crystal structure of 1d reveals that compound 1 undergoes anisotropic shrinkage on desolvation to give 1d. The lattice parameters increase slightly along the a and b-directions and decrease by 2.4 Å along the c-axis during the desolvation process (Table S1†). The net effect is the contraction of the unit cell volume by 5.74%. During this process there is little change in the Zn–O and Zn–N bond lengths (Tables S2–S5†). Further evidence of compression, which could also be called the channel closing behaviour, is seen in the difference of the solvent accessible void volume. In the (virtual) absence of guest DMF molecules, PLATON35 estimates that 1 has a potential void space amounting to 24.8% while 1d has a potential solvent accessible volume of 15.4% of the unit cell. Interestingly, the disorder seen in one pyridyl ring in 1 (and its cobalt analogue) is absent in 1d. Evidence for some dynamic motion of the ligand on the single crystal to single crystal desolvation is provided by a consideration of the torsion angles between the pyridyl and phenyl rings. In 1, the angles between mean planes through the pyridyl and phenyl rings are 40.15° and 7.29°, while in 1d, these angles are 49.00° and 44.30°. The increase in these angles is attributed to the minimisation of steric effects of the rings upon channel closing as the 2D layers move towards one another. Both structures are stabilised by weak hydrogen bonding interactions that prevail in the 2D interdigitated layers (see Tables S6–S7†).
Thermal analysis
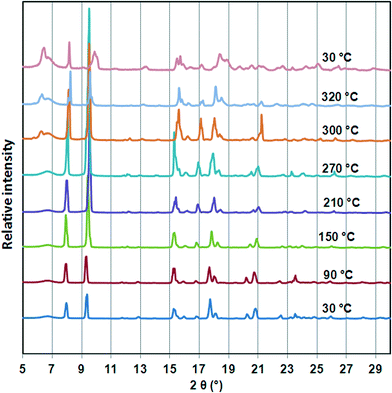
To investigate the thermal stability of 1, TGA, DSC, HSM and temperature dependant PXRD studies were carried out. The TGA (Fig. S1†) profile of 1 shows a 14.94% weight loss over a temperature range of 100–180 °C which corresponds to loss of one DMF molecule per formula unit (calculated 13.65%). The DSC trace of 1 shows a broad endotherm between 150 °C and 200 °C assigned to the loss of DMF molecules from the host network. As previously observed for the cobalt analogue, there is an exotherm at ca. 280 °C before decomposition of the guest free network occurs above 350 °C. HSM confirmed solvent desorption followed by a loss of optical transparency in the crystal on heating from room temperature to 360 °C. Variable temperature PXRD studies (Fig. 3) show that the structure is unchanged (even after DMF is desorbed), but from 210 °C new peaks appear at ca. 6.5 and 17°, indicating a subtle but distinct phase change, corresponding to the exotherm observed in the DSC. The retention of the main structure to above 200 °C agrees well with single crystal data obtained for 1d which shows only minor changes in bond lengths and angles. Furthermore the temperature dependant PXRD studies reveal that all reflections shift to higher 2θ values on heating from 30 °C to 300 °C. This is ascribed to contraction in unit cell volume which is in accordance with single crystal data of 1d. On cooling to room temperature, the pattern observed above 270 °C is maintained, so we conclude that the phase change at that point is irreversible.Alcohol induced dynamic motion of the network
Compound 1 was activated to give 1d as outlined in the experimental section. The activated phase (1d) was exposed to the vapours of dry methanol, ethanol, n-propanol, n-butanol and n-hexanol to give 1d-methanol, 1d-ethanol, 1d-propanol, 1d-butanol and 1d-hexanol respectively. These experiments were carried at room temperature for 24 hours. Thermogravimetry (Fig. S4 and S5†) reveals a positive linear correlation (r2 = 0.988) for the uptake of C1 to C4 alcohols. Details are given in Table 2. The largest alcohol uptake was observed in the presence of n-butanol. Exposure to n-hexanol resulted in very little of the guest being absorbed per formula unit.| Solvent | Kinetic diameter/Å | TGA % weight loss | Network![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solvent ratioa solvent ratioa |
% Volumetric breathing amplitudeb |
|---|---|---|---|---|
| a Based on one Zn(34pba)2 unit. b Calculated as % increase in unit cell volume compared to 1d. | ||||
| Methanol | 3.6 | 2.15 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 0.3 |
1.51 |
| Ethanol | 4.5 | 4.23 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
2.40 |
| n-Propanol | 4.7 | 9.41 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 0.7 |
6.62 |
| n-Butanol | 5.0 | 14.16 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 1.0 |
8.65 |
| n-Hexanol | 4.08 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2 |
— | |
| Water | 2.68 | 14.01 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.2 4.2 |
— |
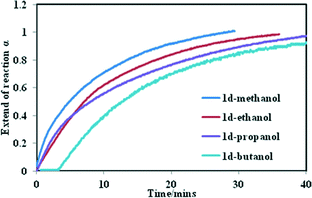
We studied the kinetics of alcohol uptake by the 1d network. Fresh samples of 1d (75 mg with a uniform particle size between 38–45 μm) were exposed to alcohol vapours using the sorption balance described in the experimental section. The amount of alcohol uptake closely matches that obtained from thermogravimetric analysis upon exposing the activated phase to alcohol vapour, except that methanol and ethanol take up slightly more, which we ascribe to surface absorption. Fig. 4 illustrates the α-time curves of the four alcohols as a function of time. When these curves are fitted into the standard kinetic models, the best fit was obtained with standard expanding area (D2) model except for n-butanol which fitted a modified expanding volume diffusion model (D4). Hence, it can be concluded that uptake of alcohols by 1d is governed by a diffusion process.
The rate constant for uptake of methanol to butanol ranged from 3.6 × 10−2 min−1 to 1.6 × 10−2 min−1 at 25 °C respectively. A strong negative correlation was found (R2 = 0.98) when the numbers of carbon atoms in the alcohols were plotted against the rate constant (Fig. S6†). To understand why the rate of reaction decreases with an increase in the number of carbon atoms, four factors have to be taken into account; the vapour pressure of the alcohols at 25 °C, the size of the cavities in the closed form, the size of the alcohols as well as the motion of the 2D network. From the sorption curves it seems as if the methanol, ethanol and propanol are absorbed with ease. For n-butanol a dead time was observed, which may be explained by the larger size of the n-butanol molecule. For it to enter the cavities it has to interact first with the host compound and initiate the movement of the 2D layers before it is absorbed into the channels. This demonstrates that the rate of reaction which governs the sorption of these alcohols is a complex process.
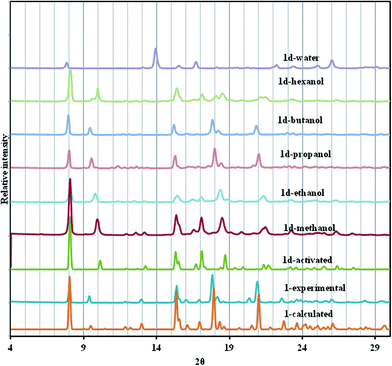
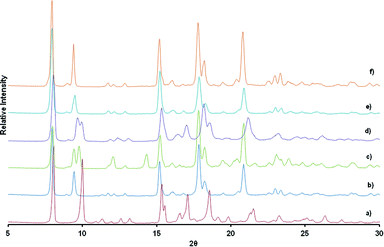
Fig. 5 shows the PXRD of the resultant inclusion compounds. As previously noted from the variable temperature PXRD studies and single crystal structure of 1d, the framework is compressed along the c-axis (Δc = −2.413 Å) on desorption and slightly stretched along the a- and b-axis (Δa and Δb = + 0.116 Å). This behaviour is reversible upon loading the channels with alcohols and diffraction peaks shift to lower 2θ values as the size of the alcohol chain increases. This is consistent with an increase in the unit cell volume and can be described as a breathing motion of the metal organic frameworks. This process allows for the accommodation of large molecules.36,37 In the activated phase 1d, the (0 0 4) reflections are located at 10.10° and correspond to the positions of the cavities/channels in the structure. These reflections evolve towards their original 2θ positions (9.34° in 1) when the number of carbon atoms in the alcohols increases as a result of the expansion of the cavities.
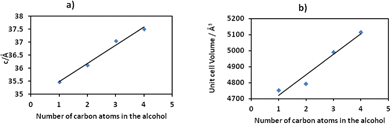
To gain more insight into the motion of the framework, powder pattern decomposition was performed using the Pawley fitting method (Fig. S3†) in TOPAS. This allows for the determination of the unit cell parameters as shown in Table S11† of the different alcohol inclusion compounds as well as calculating the volumetric breathing amplitude (calculated as the difference in unit cell volume between the alcohol inclusion compound and the dry form, 1d expressed as a percentage), Table 2. Plots of the number of carbon atoms in the alcohol vs. the c-axis and vs. the cell volume show a linear relationship as illustrated in Fig. 6. The linear equations defining these curves may be used to estimate the theoretical c-axis values and the corresponding unit cell volumes that one would expect on inclusion of different alcohols. For example the equations that define the plots in Fig. 6 are given as:
| c = 0.669n + 34.79 (for determination of c-axis) | (1) |
| V = 128.16n + 4591.8 (for determination of volume) | (2) |
If we consider absorption of n-pentanol which was not performed in this study, based on the equations defined above, its inclusion in the 2D compound will give a c-axis value of 38.135 Å and a unit cell volume of 5232.6 Å3. The volumetric breathing amplitude was found to follow the order methanol < ethanol < n-propanol < n-butanol. The magnitude of expansion exhibited by this network is very low by comparison to values observed in some three dimensional porous materials, but is still of value in illustrating the effect of changing guest size on the unit cell expansion.38
Single crystals could not be obtained for 1d-methanol or 1d-ethanol, but we were able to carry out single crystal diffraction on 1d-propanol and 1d-butanol (Table 1). These were consistent with the PXRD studies (Table S11†). The structures show that the channels open and the framework breathes in all three crystallographic directions but most notably by expansion of the c-axis to give a unit cell volume of 5005.0(5) Å3 and 5086(2) Å3 for uptake of n-propanol and n-butanol respectively. Although the 1d-butanol structure could not be refined to acceptable levels due to the poor crystal quality induced by sample activation and sorption of n-butanol, it provides useful information on the mechanism of the breathing motion of the 2D framework. The 1d-propanol structure was refined to acceptable levels though the crystal selected for analysis had a network: solvent ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 rather than the 1
0.4 rather than the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 found using TG. One notable difference in this structure compared to 1 or 1d is that one carboxylate group binds in a monodentate rather than bidendate fashion. The Zn1⋯O15B distance in 1d-propanol is 2.683(7) Å, notably longer than any other Zn–O in this or related structures. A similar feature is observed in 1d-butanol. Detailed bond lengths, bond angles and crystallographic parameters are given in the ESI† (Tables S8–S10 and Fig. S2).
0.7 found using TG. One notable difference in this structure compared to 1 or 1d is that one carboxylate group binds in a monodentate rather than bidendate fashion. The Zn1⋯O15B distance in 1d-propanol is 2.683(7) Å, notably longer than any other Zn–O in this or related structures. A similar feature is observed in 1d-butanol. Detailed bond lengths, bond angles and crystallographic parameters are given in the ESI† (Tables S8–S10 and Fig. S2).
To gain a further understanding of the breathing phenomenon, the solvent accessible voids were modelled using Mercury39 with a probe radius of 1.2 Å as illustrated in Fig. 7. Desorption of DMF from 1 results in the shrinking of the cavities while exposure to n-propanol and n-butanol gave rise to expansion of these cavities. The solvent accessible void volumes of the cavities were determined in PLATON30 and were found to be 15.4%, 24.8%, 27.9% and 28.7% in 1d, 1, 1d-propanol and 1d-butanol respectively, confirming the observed expansion of the cavities occupied by guest molecules.
Analysis of the dynamic motion of the network
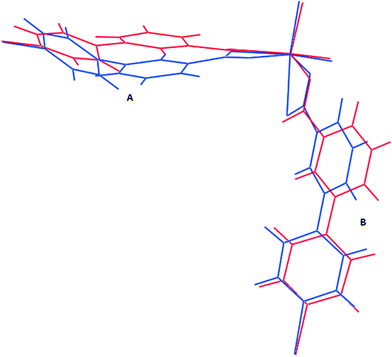
To understand the motion of the ligands on inclusion of alcohols, it is useful to consider the C–C bond which links the two rings in each ligand as a flexible point of rotation. The other potentially flexible point is the orientation of the carboxylate relative to the phenyl ring; however this torsion angle was found to be identical for most cases, differing only in 1d-propanol and 1d-butanol for the carboxylate moiety bound monodentately. An overlay of the structures of the dry form, 1d (blue) and the 1d-propanol (red) (Fig. 8) show clearly that inclusion of n-propanol in 1d results in some conformational changes of the ligands. The rotation of ligand A about the C–C single bond is greater than that in ligand B, which implies that the two ligands in the asymmetric unit exhibit different degrees of breathing. 1d has the highest dihedral angle of 49.00° which may indicate that it has high conformational energy hence is more likely to be unstable. For this reason, its ligands should be more prone to undergo a change in conformation under external stimuli to give a low energy conformation structure. Inclusion of guest molecules in the framework generally reduces the torsion angles between the phenyl and the pyridyl ring as illustrated in Table 3. Thus the factors responsible for the increase in the size of the cavities are: (I) rotation of the ligand at its flexible bond giving rise to cleavage of the Zn–O bond and resulting in lengthening of the bent bridging ligand, (II) the concertina effect this has in increasing the distance of Zn–Zn separation within a 2D layer (along the a- and b-axes) while decreasing the Zn–Zn separation of adjacent 2D layers along the c-axis to accommodate an increase in the size of the guest molecule. These two factors also account for the anisotropic expansion observed in the crystal structures.| Compound | Guest | Dihedral angle (°) ligand A | Dihedral angle (°) ligand B |
|---|---|---|---|
| 1d | None | 49.00 | 44.30 |
| 1 | DMF | 40.15 | 7.29 |
| 1d-propanol | n-Propanol | 38.30 | 15.56 |
| 1d-butanol | n-Butanol | 38.35 | 11.97 |
These results indicate that the size of the guest modulates the extent of the dynamic motion of the rings as explicitly shown by the decrease in the dihedral angles with increase in the size of the guest. The crystal structure of 1 gives more evidence of the dynamic motion of the rings. The modelled DMF molecule has an oxygen atom disordered over two positions which may be due thermal motion guest molecules (Fig. 9). This implies that the molecule may be rotating about the C–N scaffold by 180° which in turn causes rotation of the ligand by 29.6°. The motion of the guest is transmitted to the framework, and accounts for the pyridyl rings disordered over two sites. This is a conformation change which accommodates the two sites occupied by the DMF guest molecule. Similar effects were observed on flexible ultramicroporous frameworks assembled from 34pba ligand and Mn(II). The compound selectively responded to molecular rearrangement of DMF, which lead to conformational reversion of the flexible ligand. These resulted in deformation of the whole crystal lattice.40
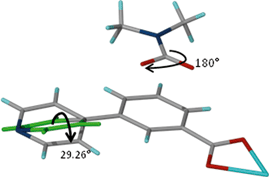 | ||
| Fig. 9 Fragment of compound 1. Rotation of the DMF guest molecule about the N–C bond triggers a conformational change in ligand B of compound 1. | ||
On absorption of n-propanol and n-butanol 1d undergoes a reconstructive phase transition within the same space group P43212 with reversible cleavage of a metal carboxylate bond. The other carboxylate moiety maintains its chelating binding. Reconstructive phase changes are relatively rare and only a few examples have been reported to date, most involving 3D pillared structures.19 In similar alcohol systems reported previously, it has been suggested that the alcohol molecules interact through their hydroxyl groups with the oxygen atoms of the framework while for longer alcohol chains the alkyl groups are expected to bend towards the phenyl rings to enhance hydrophobic van der Waals attractions.41 In our study, we found that the hydroxyl moiety on n-propanol does not interact with the host network, but the propyl chain does indeed “hug” the inside of the network cavity, making a number of weak dispersion contacts with the aromatic rings of the host network (Fig. S2†). The n-butanol structure was not of high enough quality to locate the guest molecule definitively, but it was observed that the unmodelled electron density is also located in close proximity to the host network's aromatic rings.
It seems reasonable that the enhanced uptake of n-butanol is due to the increase in hydrophobicity as the carbon chain increases, hence this molecule interacts more with the hydrophobic framework through CH⋯π and other weak interactions. These interactions trigger the opening of the channels. Methanol and ethanol are less hydrophobic and they interact less with the framework and have low volumetric breathing amplitudes of 1.5% and 2.4% respectively. A similar effect was observed by Serre et al.42 There appears to be a size limit that can be accommodated by these channels, explaining why very little n-hexanol was absorbed. Absorption of alcohols by the framework may be attributed to the presence of the phenyl rings in the framework, providing a hydrophobic effect which attracts the alkyl chains of the alcohols.41 Absorption of water leads to poisoning of the framework as evidenced by the formation of a new phase (Fig. 5). Water molecules are highly polarised in comparison to the alcohols and they have a tendency to attack the open metal sites or disrupt the framework by hydrolysing the carboxylate group moiety coordinated to the metal centres.43 For this reason, recent studies have focussed on strategies to reduce the amount of water that can enter the channels of networks.44 This phenomenon precludes the application of this material as an alcohol–water separator, since favourable alcohol uptakes and unfavourable water uptakes are the prerequisites for effective vapour-phase alcohol separation.45,46
Competition experiments
In order to establish whether one alcohol would be taken up preferentially, we carried out a competition experiment between the two extremes in size, methanol and n-butanol. In the first competition experiment, activated crystals of 1d were soaked in a solvent mixture of n-butanol and methanol with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the second, polycrystalline material was exposed to vapours derived from the same solvent mixture. PXRD studies were performed to see whether the PXRD traces obtained matched those of 1d-methanol or 1d-butanol inclusion compounds. Specific attention was focussed on the position of the (0 0 4) reflections. As previously noted, inclusion of n-butanol gives a peak centred at 9.34° while inclusion of methanol will give Bragg peaks centred at 10°. Results from PXRD studies after soaking the crystals in the solvent mixture for several weeks shows that n-butanol and methanol are absorbed concomitantly as evidenced by the appearance of two reflections peaks between 9.2° and 10.3° attributable to the presence of both 1d-methanol and 1d-butanol phases (Fig. 10). The inclusion of a particular guest in a crystal seems to indicate that under a different condition we may be able to separate the two alcohols. Having this in mind, we exposed polycrystalline material at room temperature to the vapours. PXRD results collected after six hours of exposure to the vapour gave similar results to the ones obtained after soaking the crystals in the solvent mixture in which both alcohols are taken by the network. Although we did not collect the single crystal structure data of 1d-methanol, we believe that the dihedral angles of this structure are very close to those of the activated phase 1d, in which torsion angles are high. This may imply that it is likely to be less stable than the 1d-butanol compound with low torsion angles between the rings. We collected PXRD over a longer period of time to check whether the most stable compound would prevail over the less stable one. The PXRD collected after 24 h and 72 h of exposure shows only one reflection between centred at 9.34°. When compared to the PXRD pattern of 1d-butanol, there is a good match. A 1
1. In the second, polycrystalline material was exposed to vapours derived from the same solvent mixture. PXRD studies were performed to see whether the PXRD traces obtained matched those of 1d-methanol or 1d-butanol inclusion compounds. Specific attention was focussed on the position of the (0 0 4) reflections. As previously noted, inclusion of n-butanol gives a peak centred at 9.34° while inclusion of methanol will give Bragg peaks centred at 10°. Results from PXRD studies after soaking the crystals in the solvent mixture for several weeks shows that n-butanol and methanol are absorbed concomitantly as evidenced by the appearance of two reflections peaks between 9.2° and 10.3° attributable to the presence of both 1d-methanol and 1d-butanol phases (Fig. 10). The inclusion of a particular guest in a crystal seems to indicate that under a different condition we may be able to separate the two alcohols. Having this in mind, we exposed polycrystalline material at room temperature to the vapours. PXRD results collected after six hours of exposure to the vapour gave similar results to the ones obtained after soaking the crystals in the solvent mixture in which both alcohols are taken by the network. Although we did not collect the single crystal structure data of 1d-methanol, we believe that the dihedral angles of this structure are very close to those of the activated phase 1d, in which torsion angles are high. This may imply that it is likely to be less stable than the 1d-butanol compound with low torsion angles between the rings. We collected PXRD over a longer period of time to check whether the most stable compound would prevail over the less stable one. The PXRD collected after 24 h and 72 h of exposure shows only one reflection between centred at 9.34°. When compared to the PXRD pattern of 1d-butanol, there is a good match. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of methanol and n-butanol gives rise to a high vapour pressure of methanol. Despite the high vapour pressure of methanol; the results indicate that the two solvated phases are formed at the beginning of the reaction. As time progresses, n-butanol displaces the absorbed methanol to give the final product 1d-butanol as confirmed by PXRD studies after 72 hours of exposure. In this regard, we conclude that the selectivity of the compound is thermodynamically driven although other factors such as nature of interactions, the packing energy and entropy may also play a role.47
1 molar ratio of methanol and n-butanol gives rise to a high vapour pressure of methanol. Despite the high vapour pressure of methanol; the results indicate that the two solvated phases are formed at the beginning of the reaction. As time progresses, n-butanol displaces the absorbed methanol to give the final product 1d-butanol as confirmed by PXRD studies after 72 hours of exposure. In this regard, we conclude that the selectivity of the compound is thermodynamically driven although other factors such as nature of interactions, the packing energy and entropy may also play a role.47
Conclusions
The 2D coordination network {[Zn(34pba)2].DMF}n, 1, undergoes a single crystal to single crystal transformation on desolvation of the DMF guest molecules accompanied by a displacive phase transition. The desolvated phase [Zn(34pba)2]n, 1d, shows a reconstructive phase transition on inclusion of alcohol vapours as evidenced by cleavage of one the zinc–oxygen bond. This phenomenon was confirmed by single crystal X-ray diffraction. The breathing mechanism of 1d was evaluated from single crystal data and powder data. The unit cell volume was found to increase linearly with an increase in the number of carbon atoms in the alcohol. However absorption of n-hexanol resulted in low volumetric breathing amplitude due to a geometrical threshold above which expansion/opening of the cavities is not possible. The kinetics of breathing was evaluated at 25 °C. Methanol, ethanol and n-propanol were absorbed immediately on exposure to the host compound. A dead time (ca. 2 minutes) was observed before absorption of n-butanol. This was attributed to the small size of the cavities in the closed form of 1d; hence n-butanol has to interact with the host framework to trigger the dynamic motion before it can move into the cavities. The majority of previously reported breathing networks occurs under high guest pressure which is normally referred to as the gate opening pressure. Uncommonly, the system here under study breathes at room temperature and pressure and the magnitude of breathing is controlled by the size and hydrophobicity (hence degree of CH⋯π interactions) of the alcohol guest species.Acknowledgements
Funding for this project was received from the South African National Research Foundation (NRF). Any conclusions expressed in this article are those of the authors and the NRF does not accept liability in this regard. G. M. is grateful for the financial support he received from the University of Cape Town Chemistry Equity Development Programme, the UCT NRF Innovation International Doctoral Scholarship, the UCT 2014 JW Jagger Centenary Gift Scholarship and the International Centre for Diffraction Data (ICDD): 2014 Ludo Frevel Crystallography Scholarship Award.Notes and references
- L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC.
- J. Thian, P. K. Thallapally and B. P. McGrail, in Supramolecular Chemistry: From Molecules to Nanomaterials, ed. P. A. Gale and J. W. Steed, John Wiley & Sons Ltd, Chichester, UK, 2012, vol. 6, pp. 3133–3152 Search PubMed.
- B. Liu, Y. Li, L. Hou, G. Yang, Y.-Y. Wang and Q.-Z. Shi, J. Mater. Chem. A, 2013, 1, 6535 CAS.
- C.-Y. Niu, X.-F. Zheng, Y. He, Z.-Q. Feng and C.-H. Kou, CrystEngComm, 2010, 12, 2847 RSC.
- Y.-Q. Chen, G.-R. Li, Z. Chang, Y.-K. Qu, Y.-H. Zhang and X.-H. Bu, Chem. Sci., 2013, 4, 3678 RSC.
- T. Borjigin, F. Sun, J. Zhang, K. Cai, H. Ren and G. Zhu, Chem. Commun., 2012, 48, 7613 RSC.
- S. Sanda, S. Parshamoni and S. Konar, Inorg. Chem., 2013, 12866 CrossRef CAS PubMed.
- Z. Wang and S. M. Cohen, J. Am. Chem. Soc., 2009, 131, 16675 CrossRef CAS PubMed.
- N. Nijem, H. Wu, P. Canepa, A. Marti, K. J. Balkus, T. Thonhauser, J. Li and Y. J. Chabal, J. Am. Chem. Soc., 2012, 134, 15201 CrossRef CAS PubMed.
- D. Li and K. Kaneko, Chem. Phys. Lett., 2001, 335, 50 CrossRef CAS.
- D. Tanaka, K. Nakagawa, M. Higuchi, S. Horike, Y. Kubota, T. C. Kobayashi, M. Takata and S. Kitagawa, Angew. Chem., Int. Ed., 2008, 47, 3914 CrossRef CAS PubMed.
- K. Barthelet, J. Marrot, D. Riou and G. Férey, Angew. Chem., Int. Ed., 2002, 41, 281 CrossRef CAS.
- K. Davies, S. A. Bourne and C. L. Oliver, Cryst. Growth Des., 2012, 12, 1999 CAS.
- I. Imaz, G. Mouchaham, N. Roques, S. Brandès and J.-P. Sutter, Inorg. Chem., 2013, 52, 11237 CrossRef CAS PubMed.
- F. Millange, N. Guillou, R. I. Walton, J.-M. Grenèche, I. Margiolaki and G. Férey, Chem. Commun., 2008, 4732 RSC.
- P. G. Yot, Q. Ma, J. Haines, Q. Yang, A. Ghoufi, T. Devic, C. Serre, V. Dmitriev, G. Férey, C. Zhong and G. Maurin, Chem. Sci., 2012, 3, 1100 RSC.
- S. Henke, A. Schneemann, A. Wütscher and R. A. Fischer, J. Am. Chem. Soc., 2012, 134, 9464 CrossRef CAS PubMed.
- D. Tanaka, A. Henke, K. Albrecht, M. Moeller, K. Nakagawa, S. Kitagawa and J. Groll, Nat. Chem., 2010, 2, 410 CrossRef CAS PubMed.
- G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380 RSC.
- F.-X. Coudert, C. Mellot-Draznieks, A. H. Fuchs and A. Boutin, J. Am. Chem. Soc., 2009, 131, 3442 CrossRef CAS PubMed.
- E. A. Ukraintseva and D. V. Soldatov, J. Inclusion Phenom. Macrocyclic Chem., 2010, 66, 219 CrossRef CAS.
- S. A. Bourne, K. Corin and L. R. Nassimbeni, Supramol. Chem., 2006, 18, 587 CrossRef CAS.
- L. R. Nassimbeni, S. Marivel, H. Su and E. Weber, RSC Adv., 2013, 3, 25758 RSC.
- N. B. Báthori and L. R. Nassimbeni, Cryst. Growth Des., 2012, 12, 2501 Search PubMed.
- Z. Lin, R. Zou, J. Liang, W. Xia, D. Xia, Y. Wang, J. Lin, T. Hu, Q. Chen, X. Wang, Y. Zhao and A. K. Burrell, J. Mater. Chem., 2012, 22, 7813 RSC.
- S. Sanda, S. Parshamoni and S. Konar, Inorg. Chem., 2013, 52, 12866 CrossRef CAS PubMed.
- S. Wang, L. Li, J. Zhang, X. Yuan and C.-Y. Su, J. Mater. Chem., 2011, 21, 7098 RSC.
- A. A. Coelho, TOPAS-Academic, version 4.1 (Computer software), Coelho Software, Brisbane, 2007 Search PubMed.
- G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357 CrossRef CAS.
- SAINT, version 7.60a, Bruker AXS Inc, Madison, WI, USA, 2006 Search PubMed.
- G. M. Sheldrick, SADABS, version 2.05, 2007 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- L. J. Barbour, J. Supramol. Chem., 2001, 1, 189 CrossRef CAS.
- G. Mehlana, S. A. Bourne, G. Ramon and L. Öhrström, Cryst. Growth Des., 2013, 13, 633 CAS.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148 CrossRef CAS PubMed.
- P. K. Thallapally, J. Tian, M. Radha Kishan, C. A. Fernandez, S. J. Dalgarno, P. B. McGrail, J. E. Warren and J. L. Atwood, J. Am. Chem. Soc., 2008, 130, 16842 CrossRef CAS PubMed.
- X.-H. Zhou, L. Li, H.-H. Li, A. Li, T. Yang and W. Huang, Dalton Trans., 2013, 42, 12403 RSC.
- Y.-S. Wei, K.-J. Chen, P.-Q. Liao, B.-Y. Zhu, R.-B. Lin, H.-L. Zhou, B.-Y. Wang, W. Xue, J.-P. Zhang and X.-M. Chen, Chem. Sci., 2013, 4, 1539 RSC.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466 CrossRef CAS.
- H.-L. Zhou, R.-B. Lin, C.-T. He, Y.-B. Zhang, N. Feng, Q. Wang, F. Deng, J.-P. Zhang and X.-M. Chen, Nat. Commun., 2013, 4, 2534 Search PubMed.
- G. F. de Lima, A. Mavrandonakis, H. A. de Abreu, H. A. Duarte and T. Heine, J. Phys. Chem. C, 2013, 117, 4124 CAS.
- C. Serre, C. Mellot-Draznieks, S. Surblé, N. Audebrand, Y. Filinchuk and G. Férey, Science, 2007, 315, 1828 CrossRef CAS PubMed.
- J. J. Gutiérrez-Sevillano, D. Dubbeldam, L. Bellarosa, N. López, X. Liu, T. J. H. Vlugt and S. Calero, J. Phys. Chem. C, 2013, 117, 20706 Search PubMed.
- L.-H. Xie and M. P. Suh, Chem. - Eur. J., 2011, 17, 13653 CrossRef CAS PubMed.
- K. Zhang, R. P. Lively, M. E. Dose, A. J. Brown, C. Zhang, J. Chung, S. Nair, W. J. Koros and R. R. Chance, Chem. Commun., 2013, 49, 3245 RSC.
- J. Cousinsaintremi, T. Rémy, V. Van Hunskerken, S. van de Perre, T. Duerinck, M. Maes, D. De Vos, E. Gobechiya, C. E. A. Kirschhock, G. V. Baron and J. F. M. Denayer, ChemSusChem, 2011, 4, 1074 CrossRef CAS PubMed.
- M. Lusi and L. J. Barbour, Angew. Chem., Int. Ed., 2012, 51, 3928 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC numbers 980941–980943. For ESI and crystallographic data in CIF and other electronic format see DOI: 10.1039/c4ce00496e |
| This journal is © The Royal Society of Chemistry 2014 |