Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular simulation of oligo-glutamates in a calcium-rich aqueous solution: insights into peptide-induced polymorph selection†
Jens
Kahlen
a,
Christine
Peter
*b and
Davide
Donadio
*acd
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: donadio@mpip-mainz.mpg.de; Tel: +49 6131 379333
bUniversity of Konstanz, Department of Chemistry, 78457 Konstanz, Germany. E-mail: christine.peter@uni-konstanz.de
cDonostia International Physics Center, Paseo Manuel Lardizabal 4, 20018 San Sebastian, Spain
dIkerbasque, Basque Foundation for Science, Bilbao, Spain
First published on 18th May 2015
Abstract
The presence of oligopeptides often has a drastic impact on the nucleation and crystal growth of calcium-containing minerals. Molecular simulation of complexes of peptides with Ca2+ ions can give mechanistic insight into how the pre-alignment of ions from solution by additives may steer the crystallization of calcium rich minerals into different polymorphs. We exploit advanced molecular modeling techniques to sample and analyze the complex multidimensional configurational space of aqueous solutions of oligo-glutamate and Ca2+ ions. We find that glutamate oligomers induce the formation of patterns in the associated Ca2+ ions in solution, which can serve as templates for the growth of different calcium oxalate pseudopolymorphs – depending on the peptide length, in excellent agreement with experimental observations. Glutamate decamers prestructure the Ca2+ ions in remarkable correspondence with typical distances in calcium oxalate dihydrate. These are distinct from those in calcium oxalate trihydrate which typically grows in the absence of peptide or in the presence of shorter glutamate oligomers such as pentamers.
Biomolecules can influence the formation of minerals in solution in multiple ways. Besides interacting directly with existing crystal surfaces, peptides can affect crystal nucleation and growth by binding solvated constituents of the mineral, thus affecting also the early stages of nucleation. Recent studies indicate that in order to understand the mechanisms by which molecular modifiers are able to confer a specific structural pattern to the forming crystal, it is necessary to consider non-classical nucleation pathways, which involve metastable pre-nucleation clusters (PNCs)1–5 or liquid aggregates of the mineral constituents forming by liquid–liquid phase separation.6–10 Biomolecular modifiers have been shown to stabilise both PNCs and liquid mineral droplets.9,11–13 For example, it was observed that peptides of glutamic acid stabilise PNCs of calcium carbonate.12 If biomolecular modifiers were able to not only stabilise but also to tailor the structure of PNCs or liquid mineral droplets, ion–peptide complexes might be viewed as the starting point of a cascade of structural motif encoding.
(Bio)polymer-controlled mineralization of calcium carbonate and calcium phosphate has been extensively investigated, but much less is known about calcium oxalate (CaC2O4). Fischer et al.14 investigated the effect of changing the chain length of poly-L-glutamate on the mineralization of CaC2O4. They found that homopeptidic additives may cause large variations in nucleation rates, pseudopolymorph selection and crystal morphology. At fixed chemical and thermodynamic conditions, adding decamers of glutamate (10Glu) resulted in up to 2 or 3 times longer induction times in the nucleation of CaC2O4 compared to pentamers (5Glu) at the same concentration of 0.1 mmol L−1. More importantly, in the absence of additives, or in the presence of Glu or 5Glu, calcium oxalate trihydrate (COT) was found to be the thermodynamically stable phase. The addition of 10Glu, however induced the crystallization of a di-hydrated pseudopolymorph (COD) in addition to COT. Therefore, solutions of CaC2O4 with poly-glutamate co-solvents are interesting prototypical systems to investigate the effect of polymers on the early stages of crystallization.
In the present paper, we explore peptide–ion complexes formed by oligo-L-glutamates and Ca2+ ions by means of molecular dynamics (MD) simulations. The complexity and the multidimensional nature of the configurational space of these systems and the intrinsically long time scales needed for sufficient statistical sampling made it necessary to exploit state-of-the-art advanced sampling and data analysis techniques, namely Hamiltonian replica exchange (H-REMD)15 and automated projection of the configurational space (sketch-map).16 We show that 10Glu induces characteristic templates of Ca2+ ions that resemble structural features found in COD crystals, thus supporting the hypothesis that a patterning of ions by biopolymers at the nucleation stage affects the phase of the growing mineral.
We have simulated systems consisting of one peptide (5Glu or 10Glu) with and without Ca2+ ions (at a ratio of 10 Ca2+ ions per peptide molecule, in accordance with the experimental conditions14). We used the GROMACS simulation package17,18 (version 4.6.3) and the GROMOS 54A8 FF19 with optimised short-range interactions between Ca2+ ions and the carboxylate groups of the Glu side chains20 and the SPC/E water model.21 All simulations were conducted at 300 K, a detailed account of system composition and of the simulation setup are given in the ESI.† The strong interactions between the deprotonated Glu side chains and the Ca2+ ions20 lead to the formation of stable salt bridges that severely slow down conformational transitions and hinder the exploration of the conformational space. Since the Ca2+-carboxylate ion-pairing in water is mostly dominated by entropy,22 the conformational sampling cannot be enhanced by increasing the temperature. Instead, we have employed H-REMD simulations, where the potential energy of the system is modified to facilitate the sampling of conformational changes. Specifically, we have applied a dihedral angle biasing-potential15 which follows the shape of the potentials of mean force (PMF) corresponding to the rotation around the ϕ and ψ backbone torsion angles and effectively flattens the free energy barriers that hinder conformational transitions. In H-REMD, several replicas of the system are simulated in parallel with the possibility to exchange configurations among the different replicas. In each replica the biasing potential is scaled with a different weight (λ). To obtain the biasing potential, the PMF of rotation around ϕ and ψ were computed for the central monomer-unit of 5Glu in absence of ions via well-tempered metadynamics23 as implemented in PLUMED2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 (for details regarding the biasing potential see the ESI†). The 5Glu systems were simulated with six replicas, at λ = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0. Eight different replicas were used in the H-REMD simulations of the 10Glu systems, at λ = 0.0, 0.21, 0.40, 0.54, 0.68, 0.81, 0.92, and 1.0. Exchange attempts were made every 2 ps. Each replica was equilibrated for 20 ns (5Glu) or 40 ns (10Glu), before 400 ns H-REMD production runs were started. From each of the four H-REMD simulations (5Glu and 10Glu with and without ions) 40
24 (for details regarding the biasing potential see the ESI†). The 5Glu systems were simulated with six replicas, at λ = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0. Eight different replicas were used in the H-REMD simulations of the 10Glu systems, at λ = 0.0, 0.21, 0.40, 0.54, 0.68, 0.81, 0.92, and 1.0. Exchange attempts were made every 2 ps. Each replica was equilibrated for 20 ns (5Glu) or 40 ns (10Glu), before 400 ns H-REMD production runs were started. From each of the four H-REMD simulations (5Glu and 10Glu with and without ions) 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations were analysed.
000 configurations were analysed.
As it is extremely difficult to identify a reduced number of physical parameters that describe the high dimensional conformational space of intrinsically disordered polypeptides in water, we analyzed the simulations with the help of a non-linear dimensional reduction algorithm (sketch-map).16 Dimensionality reduction is performed starting from a high dimensional set of order parameters consisting of all free backbone dihedral angle pairs (ϕ, ψ). The sketch-map algorithm projects the configurations on a two-dimensional map, optimized in such a way that configurations with similar patterns are grouped together and become easily identifiable.
In the following, we present a structural analysis of the 5Glu and 10Glu H-REMD simulations and discuss it in the context of the experimentally observed formation of different CaC2O4 pseudopolymorphs in the presence of these peptides.
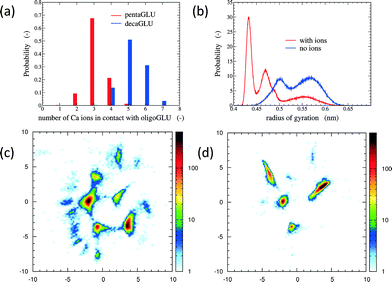
The total number of Ca2+ ions that interact simultaneously with one oligopeptide molecule strongly depends on the chain length (see Fig. 1a). 10Glu interacts on average with five to six Ca2+ ions, while 5Glu interacts on average with three Ca2+ ions. The “sequestration” of free Ca2+ ions from solution by oligoglutamates reduces the effective concentration of Ca2+ in solution, thus lowering supersaturation as a driving force for precipitation. The difference in calcium uptake accounts for the experimentally observed 2-to-3 times longer induction time of the nucleation of CaC2O4 in the presence of 10Glu compared to 5Glu.14
The interaction with Ca2+ ions severely affects the conformational free energy landscape of the oligopeptides. Ca2+ ions induce the formation of salt-bridges between the side chains. These may form between any pair of side chains, stabilizing both extended structures (salt-bridges between neighbouring residues), as well as compact ones (salt-bridges between residues further apart in the sequence). The stabilization of more compact peptide conformations can be seen in the distribution of the radii of gyration (Fig. 1b and ESI†). Fig. 1 shows also the two-dimensional (sketch-)maps of the different conformations of 5Glu in water in the absence (panel c) and the presence (panel d) of Ca2+ ions, colored according to their probability of occurrence (for 10Glu see ESI†). Since we use the same system of “sketch-map” coordinates, it is possible to compare the two probability distributions directly. Most importantly, one sees that the presence of ions significantly reduces the extent of the conformational space visited by the peptides, i.e. the salt bridges severely restrict the sampling.
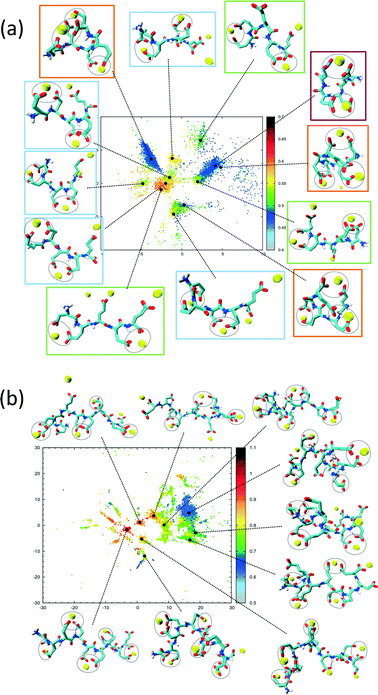
The sketch-map analysis spans the space of structures according to backbone conformations. One can supplement this representation by additional physical parameters. This aids the identification of structural features of the conformational clusters. In Fig. 2 the sketch-map projection of the configurations of 5Glu and 10Glu in the presence of Ca2+ ions is colored according to the radius of gyration; red dots denote extended configurations while blue dots denote compact ones. For 5Glu (panel a) one can recognize 12 major regions of the two-dimensional space (from now on named clusters). Red and yellow regions at the center of the map consist of elongated conformations, while the clusters surrounding it mostly contain more compact conformations. The topology of the sketch map, and the lack of direct connecting paths between different compact (off-center) clusters suggest that conversions of a globular conformation into another occur mostly through elongated structures. The configurations in the clusters can be further characterized via the salt bridges. We have identified four types of clusters, highlighted by the colored frames around the representative snapshots in Fig. 2a. Blue frames indicate relatively elongated structures with two salt-bridges between neighboring side chains and a radius of gyration between 0.52 to 0.57 nm. Further Ca2+ ions frequently interact with either one of the free carboxylate groups or with the deprotonated C-terminus. Green frames group structures with 0.52 < Rgyr< 0.62 nm and two salt-bridges. Globular structures are identified by orange and purple frames. The latter is the most frequently sampled structure: it features only two salt-bridges between the 2nd and 5th and between the 3rd and 4th side chains, and has Rgyr ~ 0.47 nm. In the assignment of these four types of structures to the sketch-map regions we see that they can be realized with different peptide backbone conformations. This grouping of structures according to salt bridges is important to understand the underlying principles that govern the formation of typical distances between Ca2+ ions. As we will see in the following, the characteristic Ca2+–Ca2+ distances found in these complexes can be related to CaC2O4 pseudopolymorphs.
The two-dimensional sketch-map projection of ion–peptide configurations consisting of 10Glu and Ca2+ ions exhibits similar features as the one for the 5Glu–Ca system (Fig. 2b). The conformational space of 10Glu–Ca2+ ion configurations is a lot more complex than the one of the 5Glu system, with a larger number of clusters. In Fig. 2b representative configurations of the most important clusters are shown. As for 5Glu, clusters featuring compact conformations are arranged in the periphery of the map: some are directly connected with one another, while others connect to clusters featuring elongated conformations in the center of the map. Clusters with similar features in terms of the number of salt bridges and the radius of gyration are positioned in different areas of the two-dimensional projection, as they display large differences in the backbone structure. With 10Glu, we can recognize the power of the sketch-map method to project and subsequently characterize typical structural elements in an inherently disordered system. Due to the increased complexity of the conformational space of 10Glu, the sampling is probably not yet comprehensive. Most likely, we see only a subset of the many stable structures that 10Glu forms in the presence of Ca2+ ions. Nevertheless, thanks to the use of H-REMD the sampling is sufficiently representative (see ESI†) so that we can draw conclusions about characteristic conformations and structural elements, in particular regarding the ions relevant for mineralization.
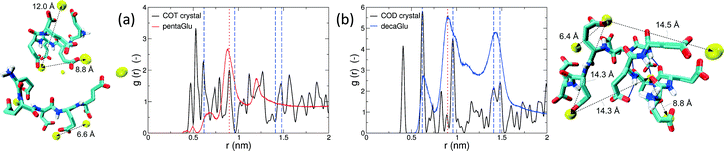
Polymorphism is modulated by highly dynamic nanoscale structures in solution and is likely to be affected by ion–peptide complexes.9,12,13,25 To unravel the molecular mechanisms, by which oligo-glutamates manipulate the nucleation process of CaC2O4, we examine the possibility that the peptides induce specific patterning in the bound Ca2+ ions. Thus, they serve as a template for nucleation of otherwise kinetically or thermodynamically unfavored crystalline polymorphs, as formerly proposed for the crystallization of calcium carbonate in solutions containing poly-acrylate.22 To this end we have compared typical distances between the peptide-bound Ca2+ ions to characteristic pair-wise distances in the two CaC2O4 pseudopolymorphs COT and COD. We have computed the pair correlation functions (PCF) between Ca2+ ions in the H-REMD simulations and compared them to the radial distribution function of calcium in COT and COD (Fig. 3). The PCFs of Ca2+ bound to 5Glu and 10Glu exhibit different features, which are sharper for 10Glu, thus indicating higher ordering. The PCF of Ca2+ in contact with 5Glu displays a single main peak at about 0.9 nm that is found most often in globular conformations, such as the one shown in the upper left snapshot in Fig. 3. Even if this feature corresponds to Ca2+ distances found both in COT and COD, we do not identify a correspondence between the PCF of Ca2+ with 5Glu and a specific crystalline arrangement of CaC2O4 Remarkably, in turn, the main features of the PCF of Ca2+ with 10Glu correspond to three of the four most intense peaks of the PCF of COD at 0.63 nm, 0.9 nm, and 1.43 nm. This coincides with the experimental observation, that COD is formed upon addition of 10Glu to the solution, suggesting that a structural motif encoding is already introduced by 10Glu at the earliest stages of peptide ion-interaction, ultimately affecting the formation of COD instead of COT. Experimentally, it was found that poly-glutamates also affect the shape, i.e. the growth, of CaC2O4 crystals, which indicates that they also interact differently with different mineral surfaces. This mineralization stage will require different simulation methods and setups that will be taken up in the future.
In summary, utilizing molecular dynamics with advanced sampling methods, we have explored the conformational landscape of deprotonated oligoglutamates consisting of 5 and 10 units in aqueous solutions, unraveling the effects of the interaction with Ca2+ ions at the molecular scale. The larger uptake of Ca2+ ions by longer peptides accounts for the longer induction times in the nucleation of calcium oxalate observed experimentally. More importantly, the patterning of the Ca2+ ions bound to 10Glu shows a remarkable correspondence to that of Ca2+ ions in COD, which has been found in experiments to crystallize when this peptide is added in solution. Our results support the hypothesis that structural motifs induced by the interaction with polymers can affect polymorphism in calcium rich minerals already at very early stages prior to nucleation.
Acknowledgements
The authors are grateful to Rafael Munoz-Espi for sharing his insight into the experimental background and Michele Ceriotti for helpful discussions on the sketch-map algorithm. J.K. and C.P. acknowledges funding from the Max Planck Graduate Center and from the German Science Foundation within the Emmy Noether Program, respectively. Computational resources were provided by the Rechenzentrum Garching of the Max Planck Society.References
- F. Betts and A. Posner, Mater. Res. Bull., 1974, 9, 353–360 CrossRef CAS
.
- A. Dey, P. H. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS PubMed
.
- W. J. E. M. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. A. J. M. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef PubMed
.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed
.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed
.
- M. Faatz, F. Gröhn and G. Wegner, Adv. Mater., 2004, 16, 996–1000 CrossRef CAS PubMed
.
- J. Rieger, T. Frechen, G. Cox, W. Heckmann, C. Schmidt and J. Thieme, Faraday Discuss., 2007, 136, 265–277 RSC
.
- S. E. Wolf, L. Müller, R. Barrea, C. J. Kampf, J. Leiterer, U. Panne, T. Hoffmann, F. Emmerling and W. Tremel, Nanoscale, 2011, 3, 1158–1165 RSC
.
- M. A. Bewernitz, D. Gebauer, J. Long, H. Cölfen and L. B. Gower, Faraday Discuss., 2012, 159, 291–312 RSC
.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 341, 885–889 CrossRef CAS PubMed
.
- P. Raiteri, R. Demichelis, J. D. Gale, M. Kellermeier, D. Gebauer, D. Quigley, L. B. Wright and T. R. Walsh, Faraday Discuss., 2012, 159, 161 RSC
.
- A. Picker, M. Kellermeier, J. Seto, D. Gebauer and H. Cölfen, Z. Kristallogr. - Cryst. Mater., 2012, 227, 744–757 CrossRef CAS
.
- A. R. Finney and P. M. Rodger, Faraday Discuss., 2012, 159, 47–60 RSC
.
- V. Fischer, K. Landfester and R. Muñoz Espí, Cryst. Growth Des., 2011, 11, 1880–1890 CAS
.
- K. Ostermeir and M. Zacharias, Biochim. Biophys. Acta, 1834, 2013, 847–853 Search PubMed
.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023–13028 CrossRef CAS PubMed
.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed
.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS
.
- M. M. Reif, P. H. Hünenberger and C. Oostenbrink, J. Chem. Theory Comput., 2012, 8, 3705–3723 CrossRef CAS
.
- J. Kahlen, L. Salimi, M. Sulpizi, C. Peter and D. Donadio, J. Phys. Chem. B, 2014, 118, 3960–3972 CrossRef CAS PubMed
.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem, 1987, 91, 6269–6271 CrossRef CAS
.
- R. E. Bulo, D. Donadio, A. Laio, F. Molnar, J. Rieger and M. Parrinello, Macromolecules, 2007, 40, 3437–3442 CrossRef CAS
.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef
.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS PubMed
.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergstrom and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Setup and parameters of Hamiltonian replica exchange simulations and sketch map analysis; further data on convergence and conformational sampling. See DOI: 10.1039/c5ce00676g |
| This journal is © The Royal Society of Chemistry 2015 |