High-frequency linear rheology of hydrogels probed by ultrasound-driven microbubble dynamics
Akaki
Jamburidze
a,
Marco
De Corato
a,
Axel
Huerre
 a,
Angelo
Pommella
b and
Valeria
Garbin
a,
Angelo
Pommella
b and
Valeria
Garbin
 *a
*a
aDepartment of Chemical Engineering, Imperial College London, London SW7 2AZ, UK. E-mail: v.garbin@imperial.ac.uk
bLaboratoire Charles Coulomb (L2C), UMR 5221 CNRS-Université de Montpellier, Montpellier, France
First published on 3rd May 2017
Abstract
Ultrasound-driven microbubble dynamics are central to biomedical applications, from diagnostic imaging to drug delivery and therapy. In therapeutic applications, the bubbles are typically embedded in tissue, and their dynamics are strongly affected by the viscoelastic properties of the soft solid medium. While the behaviour of bubbles in Newtonian fluids is well characterised, a fundamental understanding of the effect on ultrasound-driven bubble dynamics of a soft viscoelastic medium is still being developed. We characterised the resonant behaviour in ultrasound of isolated microbubbles embedded in agarose gels, commonly used as tissue-mimicking phantoms. Gels with different viscoelastic properties were obtained by tuning agarose concentration, and were characterised by standard rheological tests. Isolated bubbles (100–200 μm) were excited by ultrasound (10–50 kHz) at small pressure amplitudes (<1 kPa), to ensure that the deformation of the material and the bubble dynamics remained in the linear regime. The radial dynamics of the bubbles were recorded by high-speed video microscopy. Resonance curves were measured experimentally and fitted to a model combining the Rayleigh–Plesset equation governing bubble dynamics, with the Kelvin–Voigt model for the viscoelastic medium. The resonance frequency of the bubbles was found to increase with increasing shear modulus of the medium, with implications for optimisation of imaging and therapeutic ultrasound protocols. In addition, the viscoelastic properties inferred from ultrasound-driven bubble dynamics differ significantly from those measured at low frequency with the rheometer. Hence, rheological characterisation of biomaterials for medical ultrasound applications requires particular attention to the strain rate applied.
1 Introduction
Biomedical applications of ultrasound-driven microbubbles include diagnostic imaging1 and drug delivery.2 In these applications, micron-sized gas bubbles are injected intravenously and remain confined in the blood vessels. For therapeutic purposes, microbubbles can be delivered to tissues, for instance by acoustic droplet vaporisation,3,4 or bubbles can be generated directly inside tissues, for instance in high-intensity focused ultrasound and lithotripsy.5–7 The behaviour of bubbles embedded in tissues has been exploited for diagnostic purposes to measure the rheological properties of the tissue, such as in tissue palpation and elastography.8 In these methods, ultrasound with frequency far above the resonance frequency of the bubbles is applied, to avoid bubble oscillations and only cause a displacement due to acoustic radiation force.9–11 The rheological properties extracted from these methods are therefore at a strain rate of 0 Hz. If the ultrasound frequency is close to the bubble resonance frequency, a bubble undergoes oscillatory behaviour, and imposes much larger strain rates on the surrounding medium, up to 106 Hz. The oscillatory deformation could therefore be utilised to measure rheological properties in a regime of deformation that is central to imaging and therapeutic ultrasound. However, while the oscillatory dynamics of bubbles in Newtonian fluids is well characterised,12 our understanding of ultrasound-driven bubble dynamics in viscoelastic media is still limited.Extensive theoretical work has been done on bubble dynamics in viscoelastic media. Most models are based on extensions of the Rayleigh–Plesset equation, taking into account viscosity, elasticity, and compressibility of the surrounding medium, as well as the effects of encapsulation on the bubble dynamics for biomedical applications.13 Bubble oscillations have been investigated inside viscoelastic media with linear viscoelastic models14–17 which are suitable for small deformation of the medium, and nonlinear viscoelastic models,18–22 applicable also for large material deformation. Numerical simulations based on linear constitutive models have shown that in viscoelastic solids the amplitude of the radial oscillations is hindered by elasticity,16 whereas it is increased in viscoelastic liquids.14 The elasticity of the medium can also induce a qualitative change in the bubble dynamics compared to a Newtonian fluid, producing, for example, a modulated radial response.14 Numerical studies based on nonlinear constitutive equations and large-amplitude ultrasound forcing show even more complex bubble dynamics, such as aperiodic oscillations and chaotic behavior.19–22 It is also found that the threshold for inertial cavitation is greatly reduced as the fluid elasticity is increased,18,22 with potential implications for biomedical applications.
These theoretical studies have provided important insights into bubble dynamics in viscoelastic media, but experimental data remain sparse, and careful validation of the applicability of constitutive models has not been performed. A recent study has employed oscillatory bubble dynamics in ultrasound to infer the rheological properties of a soft viscoelastic solid (gelatin).23 Spherical bubbles were created using a pulsed laser inside gels supersaturated with gas. The bubble radius slowly increased over time due to gas transfer into the bubble, and the response as a function of equilibrium bubble radius was measured using a constant excitation frequency of 28 kHz. From a linear analysis of bubble dynamics using the Kelvin–Voigt model, values of shear modulus and shear viscosity were extracted. Because the properties were found to differ depending on the confinement conditions (isolated bubble, bubble near a solid boundary, bubble near a second bubble) the validity of the assumption of linear viscoelasticity should be tested. In ref. 23, the properties were compared with literature values measured at different frequencies24,25 and the samples used in the experiments were not characterised independently using standard rheological methods.
In this paper we examine the ultrasound-driven oscillatory dynamics of spherical bubbles embedded in soft viscoelastic solids. We make agarose gels with different rheological properties by tuning the agarose concentration, and characterise the samples by rotational rheometry. We inject isolated bubbles inside the gels, and record their radial dynamics under ultrasonic forcing using high-speed video microscopy. We develop a test for linear deformation applicable to bubble oscillations, so that strain amplitudes in the linear regime can be used. We then characterise experimentally the resonant behaviour of bubbles, and analyse the data using linear theory based on the Rayleigh–Plesset equation for bubble dynamics, and the Kelvin–Voigt model for the material deformation. The rheological properties extracted from bubble dynamics are compared with those obtained with the rheometer. The validity of the assumption of linear viscoelasticity is carefully tested.
2 Theory
Consider a spherical bubble in an incompressible, homogeneous, viscoelastic medium. We define a spherical coordinate system with origin at the centre of the bubble, with r, θ, and ϕ the radial, azimuthal, and polar coordinates respectively. During acoustic driving, the bubble undergoes volumetric oscillations, expanding and compressing at the frequency of the acoustic pressure oscillations. The motion of the bubble generates in the surrounding medium a velocity field![[u with combining low line]](https://www.rsc.org/images/entities/i_char_0075_0332.gif) = (ur, uθ, uϕ), with ur = Ṙ(R/r)2, and uθ = uϕ = 0.12 The time evolution of the bubble radius, R, is governed by the generalised Rayleigh–Plesset equation:26
= (ur, uθ, uϕ), with ur = Ṙ(R/r)2, and uθ = uϕ = 0.12 The time evolution of the bubble radius, R, is governed by the generalised Rayleigh–Plesset equation:26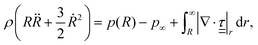 | (1) |
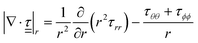 is the radial component of the divergence of the deviatoric stress tensor,
is the radial component of the divergence of the deviatoric stress tensor, 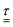 .
.
The pressure in the medium at the interface, p(R), is related to the balance of normal stresses at the interface of the bubble:
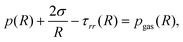 | (2) |
In the linear regime of deformation of a viscoelastic medium,  is traceless, τθθ + τϕϕ = −τrr, and
is traceless, τθθ + τϕϕ = −τrr, and 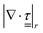 becomes
becomes
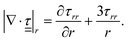 | (3) |
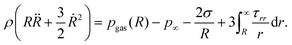 | (4) |
We now specify the constitutive model for the viscoelastic medium, which relates the stress tensor, 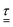 , to the strain tensor,
, to the strain tensor, 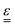 , and the rate of strain tensor,
, and the rate of strain tensor, 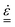 . The Kelvin–Voigt model for the linear deformation of an incompressible viscoelastic solid reads:
. The Kelvin–Voigt model for the linear deformation of an incompressible viscoelastic solid reads:
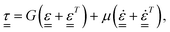 | (5) |
τrr = 2(Gεrr + μ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) rr), rr), | (6) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) rr = ∂ur/∂r = −2R2Ṙ/r3, and εrr = −2(R3 − R03)/3r3. Note that the strain and strain rate are not homogeneous, and decay as r−3. Evaluating the integral in eqn (4) yields:
rr = ∂ur/∂r = −2R2Ṙ/r3, and εrr = −2(R3 − R03)/3r3. Note that the strain and strain rate are not homogeneous, and decay as r−3. Evaluating the integral in eqn (4) yields: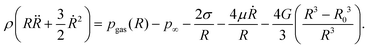 | (7) |
The pressure far from the bubble is p∞ = p0 + pa(t), where p0 is the ambient pressure, and the acoustic pressure pa(t) = Δp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) has amplitude Δp and frequency ω = 2πf. We assume the gas pressure to follow a polytropic relationship,
sin(ωt) has amplitude Δp and frequency ω = 2πf. We assume the gas pressure to follow a polytropic relationship, 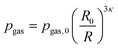 , where R0 is the bubble radius at equilibrium and κ the polytropic exponent.27 The gas pressure at equilibrium is pgas,0 = p0 + 2σ/R0, where p0 is the ambient pressure. In Appendix we calculate the value of κ for the bubble size and frequency range used in our experiments.
, where R0 is the bubble radius at equilibrium and κ the polytropic exponent.27 The gas pressure at equilibrium is pgas,0 = p0 + 2σ/R0, where p0 is the ambient pressure. In Appendix we calculate the value of κ for the bubble size and frequency range used in our experiments.
For sufficiently small forcing amplitude, Δp/p0 ≪ 1, the radial response, R(t) = R0[1 + x(t)], can be assumed to follow the same temporal dependence as the forcing, x(t) = x0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt + φ), where the amplitude of oscillations is small, x0 = ΔR/R0 ≪ 1, and φ is the phase shift between the forcing and the oscillations. Under these assumptions, linearisation of eqn (7) returns the equation for the amplitude x in the form of a damped harmonic oscillator:27
sin(ωt + φ), where the amplitude of oscillations is small, x0 = ΔR/R0 ≪ 1, and φ is the phase shift between the forcing and the oscillations. Under these assumptions, linearisation of eqn (7) returns the equation for the amplitude x in the form of a damped harmonic oscillator:27
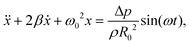 | (8) |
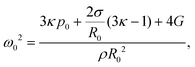 | (9) |
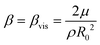 . A comparison of the magnitudes of viscous, thermal, and acoustic contributions to damping shows that this assumption is justified (see Appendix).
. A comparison of the magnitudes of viscous, thermal, and acoustic contributions to damping shows that this assumption is justified (see Appendix).
The amplitude of bubble oscillations as a function of the applied frequency is given by:28
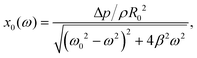 | (10) |
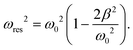 | (11) |
3 Materials and methods
3.1 Gel preparation and characterisation
The viscoelastic solids used in this study are agarose gels. The rheological properties of the gels were tuned through the concentration of agarose. Gels were prepared by mixing desired amounts of agarose powder (Sigma-Aldrich, A9539) with ultra pure water (Milli-Q filtration system, Millipore) and glycerol (Sigma-Aldrich, G9012), with a glycerol to water ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 v/v. The mixture was left to stir and boil at 95 °C until the solution became clear. The mixture was poured into a container and left to set for 4 hours. The gel samples were characterised using a rotational rheometer (MCR 302, Anton Paar) with a parallel plate configuration. The gap between the plates, which were 25 mm in radius, was set to 7 mm, resulting in a minimum strain of 2.8 × 10−6% and a minimum torque of 0.5 nN m. The shear modulus, G, was obtained from a stress relaxation test, while the storage and loss moduli, G′ and G′′ respectively, were measured at a frequency ω = 2π rad s−1. Furthermore, the typical duration of a measurement, of the order of 10−4 s, is much smaller than the poroelastic relaxation time, estimated to be 0.5 s29,30 with the assumption of a mesh size of 500 nm for agarose.29
2 v/v. The mixture was left to stir and boil at 95 °C until the solution became clear. The mixture was poured into a container and left to set for 4 hours. The gel samples were characterised using a rotational rheometer (MCR 302, Anton Paar) with a parallel plate configuration. The gap between the plates, which were 25 mm in radius, was set to 7 mm, resulting in a minimum strain of 2.8 × 10−6% and a minimum torque of 0.5 nN m. The shear modulus, G, was obtained from a stress relaxation test, while the storage and loss moduli, G′ and G′′ respectively, were measured at a frequency ω = 2π rad s−1. Furthermore, the typical duration of a measurement, of the order of 10−4 s, is much smaller than the poroelastic relaxation time, estimated to be 0.5 s29,30 with the assumption of a mesh size of 500 nm for agarose.29
3.2 Injection of isolated bubbles
Isolated bubbles with radii in the range 100–220 μm were injected using a silica capillary with inner diameter of 50 μm and outer diameter of 192 μm (TSP050192, CM Scientific) connected to a compressed nitrogen outlet operating at 0.5 bar. The bubbles were injected in the gel through a hole in the side of the container as the gel was setting. Since the gelation temperature depends on gel concentration, bubble injection temperatures for each concentration were determined by trial and error (24.5 °C, 25.5 °C, and 26.5 °C for 0.5% 1% and 2% respectively). The use of a water–glycerol mixture was found to prevent bubble rise during setting of the gel. It also prevented bubble dissolution, which would lead to the formation of a liquid-filled cavity around the bubble, as observed in ref. 23. The gel samples were 25 × 35 × 15 mm3, and the bubble was always at least 7 mm from any of the surfaces.3.3 Experimental setup
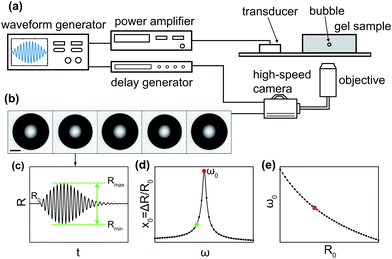
Fig. 1 shows a schematic of the experimental setup. A single-element piezoelectric transducer (P-121.05, Physik Instrumente) was glued to a glass slide, which was positioned on the stage of an inverted microscope (IX71, Olympus) equipped with a 4× objective. The agarose gel sample was positioned on the glass slide in the optical window of the microscope stage. The waveform driving the piezoelectric transducer was generated by an arbitrary waveform generator (33220A, Agilent) and amplified by a linear radio-frequency power amplifier (AG1021, T&C Power Conversion Inc.). The waveform consisted of a single burst of 10 cycles at a frequency in the range 10–50 kHz, with amplitude modulated by a sine envelope to prevent windowing effects. The bubble dynamics were captured using a high-speed camera (Photron, FASTCAM SA5) at 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames per second. Simultaneous triggering of the waveform generator and the high-speed camera was achieved using a pulse-delay generator (9200 Sapphire, Quantum Composer). The pressure generated by the piezoelectric transducer was calibrated using a PVDF hydrophone (RP 33 s, RP Acoustics). The degree of power amplification was adjusted to compensate for the frequency-dependent response of the transducer, so as to maintain a constant pressure for the different frequencies used. A direct measurement of pressure at the location of the bubble could not be performed, because the hydrophone does not provide reliable measurements inside the solid-like gels used for this study. In addition, the repeatability in the position of the bubble is limited, and the sound field inside the gel is not homogeneous. The pressure amplitude Δp will be inferred from the analysis of bubble dynamics using eqn (10).
000 frames per second. Simultaneous triggering of the waveform generator and the high-speed camera was achieved using a pulse-delay generator (9200 Sapphire, Quantum Composer). The pressure generated by the piezoelectric transducer was calibrated using a PVDF hydrophone (RP 33 s, RP Acoustics). The degree of power amplification was adjusted to compensate for the frequency-dependent response of the transducer, so as to maintain a constant pressure for the different frequencies used. A direct measurement of pressure at the location of the bubble could not be performed, because the hydrophone does not provide reliable measurements inside the solid-like gels used for this study. In addition, the repeatability in the position of the bubble is limited, and the sound field inside the gel is not homogeneous. The pressure amplitude Δp will be inferred from the analysis of bubble dynamics using eqn (10).
3.4 Data acquisition and processing
We used an acoustic spectroscopy method31 to experimentally characterise the resonant behaviour of bubbles in an acoustic field, as illustrated in Fig. 1(b–d). Each bubble was repeatedly driven by 10-cycle bursts with increasing frequency in the range f = 10–50 kHz in steps of 1 kHz. An optical recording of the bubble dynamics was taken for each frequency, see Fig. 1(b). The waiting time between subsequent bursts was limited by the download time of the camera sensor to about 10 s. This delay ensured that, if the gel properties were in any way altered by the bubble oscillations, the material had sufficient time to relax back to its equilibrium state before the next recording (see Section 4.1). Each video was analysed frame by frame using built-in edge detection routines in Matlab (MathWorks), to extract the bubble radius as a function of time, R(t), see Fig. 1(c). The amplitude of oscillations was quantified from each video as ΔR = (Rmax − Rmin)/2, where Rmax and Rmin are the maximum and minimum values of the radius. By measuring this quantity for each driving frequency, we reconstruct experimentally the resonance curve, see Fig. 1(d). The uncertainty on the radius is quantified from the standard deviation of a dataset where ultrasound is not applied and the bubble has constant radius. No significant change in the bubble radius due to rectified diffusion32 was observed over the duration of an experiment, to within the experimental uncertainty. Since we characterised the resonant behaviour of bubbles with a range of sizes, we also analysed the bubble natural frequency, ω0, as a function of bubble radius, R0, as shown in Fig. 1(e).4 Results and discussion
4.1 Gel characterisation with rotational rheometer
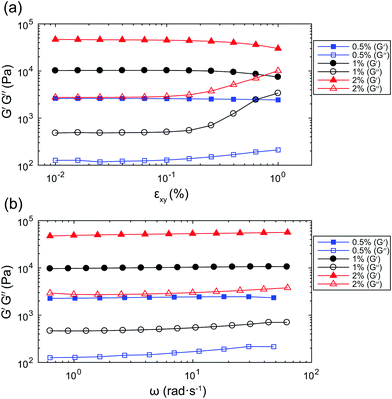
The results of amplitude sweeps and frequency sweeps on gel samples with concentrations 0.5% w/v, 1% w/v, and 2% w/v, are presented in Fig. 2. From the amplitude sweeps in Fig. 2(a), measured at a frequency ω = 2π rad s−1, it can be seen that the storage modulus, G′ (solid symbols), is larger than the loss modulus, G′′ (open symbols), for all three gel concentrations. This observation indicates that the materials behave predominantly like solids. The response of the gels is linear up to a shear strain amplitude εxy ≈ 0.1%. From the frequency sweeps in Fig. 2(b), measured with εxy = 0.06%, it can be seen that the storage modulus, G′, is constant over the range of frequencies accessible with the rheometer, justifying the use of the Kelvin–Voigt model to describe its deformation. For the purpose of comparison with the values that will be obtained from bubble dynamics, we present a summary of the rheological properties for the three gel concentrations in Table 1. The observed ratio of one order of magnitude between G′ and G′′ is similar to that reported for other tissue-mimicking phantoms,33,34 and representative of the behaviour of a range of biological tissues.35,36 The shear viscosity is estimated as μ ≈ G′′/ω. We can estimate the characteristic time for the material to relax after a stress is removed as τ ≈ μ/G. The characteristic times for the three gels are all of the order of τ ∼ 10−2 s. The waiting time between repeat experiments on the same bubble, of the order of seconds, is therefore sufficient for the material to relax to its equilibrium state.| Gel concentration (w/v) | 0.5% | 1% | 2% |
|---|---|---|---|
| G (kPa) | 2.37 ± 0.05 | 9.09 ± 0.28 | 43.53 ± 0.31 |
| G′ at 1 Hz (kPa) | 2.61 ± 0.14 | 10.02 ± 0.76 | 46.67 ± 0.72 |
| G′′ at 1 Hz (kPa) | 0.126 ± 0.017 | 0.482 ± 0.041 | 2.753 ± 0.261 |
| μ ≈ G′′/ω at 1 Hz (Pa s) | 20.1 ± 2.7 | 76.7 ± 6.5 | 438.2 ± 41.5 |
Note that the deformation imparted with the rotational rheometer is pure shear with amplitude εxy, whereas the bubble imparts purely extensional deformation to the material with amplitude εrr(r). If the deformation is in the linear regime, shear and extensional rheological tests return the same properties.37 However, the range of strain amplitudes that corresponds to the linear regime can be different for the two modes of deformation. The maximum strain amplitude for the linear regime of extensional deformation will be determined in the bubble dynamics experiments.
4.2 Gel characterisation from bubble dynamics
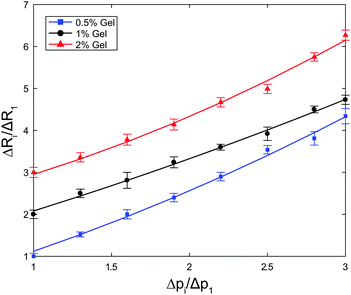
In Fig. 3 we plot the ratio of amplitudes of oscillations ΔRi/ΔR1 as a function of the ratio of forcing amplitudes Δpi/Δp1. The ranges of extensional strain amplitudes applied, evaluated at the bubble interface, εR = εrr(R), were εR ≈ 0.006–0.027, εR ≈ 0.009–0.035, and εR ≈ 0.001–0.003 for the 0.5%, 1% and 2% gels, respectively. For a perfectly linear material response, we expect a linear correlation with coefficient 1. We fit the data to a quadratic relationship, 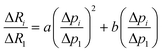 , to quantify the deviation from linearity. The coefficient b is approximately 1 for the 1% gel (b = 0.997), with negligible deviations from linearity (a = 0.083). The 0.5% and 2% gels exhibit slightly non-linear behaviour (b = 0.958 and a = 0.161; b = 0.733 and a = 0.217, respectively) even for the very small strain amplitudes used. Because it is not possible to further reduce the strain amplitude (which is related to ΔR) within the optical resolution of the experiment, we will work in this regime, keeping in mind that small deviations from linear behaviour can be expected.
, to quantify the deviation from linearity. The coefficient b is approximately 1 for the 1% gel (b = 0.997), with negligible deviations from linearity (a = 0.083). The 0.5% and 2% gels exhibit slightly non-linear behaviour (b = 0.958 and a = 0.161; b = 0.733 and a = 0.217, respectively) even for the very small strain amplitudes used. Because it is not possible to further reduce the strain amplitude (which is related to ΔR) within the optical resolution of the experiment, we will work in this regime, keeping in mind that small deviations from linear behaviour can be expected.
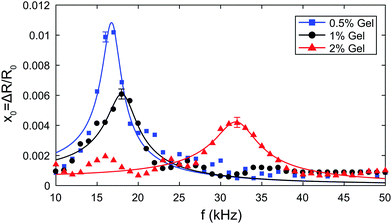 | ||
| Fig. 4 Resonance curves in 0.5%, 1% and 2% gels respectively. The solid line is a fit of eqn (10) to the experimental data. | ||
We can fit eqn (10) to each resonance curve, and extract the values of acoustic pressure amplitude Δp, shear modulus G, and shear viscosity μ from the bubble dynamics data. The results of the fits are summarised in Table 2. The pressure amplitudes are Δp = (642 ± 47) Pa, (624 ± 73) Pa, and (956 ± 71) Pa for the 0.5%, 1% and 2% gels respectively. The values of shear modulus and shear viscosity obtained from the fit of bubble dynamics data are G = (7 ± 3) kPa, (21 ± 6) kPa, and (256 ± 10) kPa, and μ = (144 ± 16) mPa s, (231 ± 29) mPa s, and (280 ± 30) mPa s for the 0.5%, 1% and 2% gels respectively.
| Gel concentration (w/v) | 0.5% | 1% | 2% |
|---|---|---|---|
| Pressure amplitude Δp (Pa) | 642 ± 47 | 624 ± 73 | 956 ± 71 |
| Shear modulus G (kPa) | 7 ± 3 | 21 ± 6 | 256 ± 29 |
| Shear viscosity μ (Pa s) | 0.144 ± 0.016 | 0.231 ± 0.029 | 0.280 ± 0.030 |
To confirm repeatability, resonance curves were measured for over 40 bubbles of different sizes in different gel samples. The results can be summarised by plotting, for each bubble, the value of resonance frequency measured from the resonance curve as a function of the equilibrium bubble radius (Fig. 5). The error bars in Fig. 5 correspond to the width of the resonance curve at 90% of its maximum amplitude. By fitting eqn (9) to the data sets for each gel concentration, we obtain global values for the shear modulus G. The values are consistent with those reported above for a single resonance curve: G = (8 ± 7) kPa, (39 ± 10) kPa, and (239 ± 45) kPa for 0.5%, 1% and 2% gels respectively. Note that the shift in resonance frequency due to viscous damping, given in eqn (11), is negligible and therefore eqn (9) for the natural frequency was used.
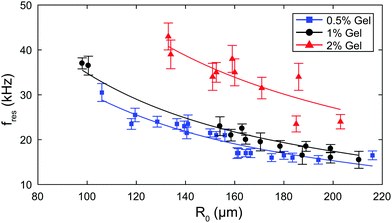 | ||
| Fig. 5 Summary of experimental data for all bubbles: resonance frequency as a function of bubble radius for each gel concentration. The solid line is a fit to eqn (9). | ||
4.3 Comparison of viscoelastic properties measured with rheometer and from bubble dynamics
The values of viscoelastic properties obtained from the fit of bubble dynamics data, which are measured at 10–50 kHz, differ significantly from those obtained with the rheometer at 1 Hz. The values of G are 2–5 times larger, while the values of μ are two orders of magnitude smaller. We checked that fitting the bubble dynamics data to eqn (9) using fixed values of G and μ from the rheometer measurements, and with Δp as the only fitting parameter, is not possible for any value of Δp. In experiments on bubble dynamics near viscoelastic boundaries, Tinguely et al. measured the shear modulus of agarose hydrogels from the propagation velocity of surface elastic waves.39 The resulting values of G corresponded to a frequency of deformation of 17–20 kHz, and were found to be 5–30 times larger than the values obtained from a creep test (0 Hz).We have confirmed experimentally that the bubble dynamics are, to a good approximation, in the linear regime, hence the material response is linear. The difference in the properties measured at high and low frequency therefore suggests that a Kelvin–Voigt model with a single characteristic time is not sufficient to accurately describe the material behaviour over 5 decades in frequency. More complex constitutive linear models will be required to extend the applicability of the modified Rayleigh–Plesset equation over a broad range of frequencies, which can be accessed by probing the dynamics of bubbles of different sizes.
We also found that the bubble dynamics in a viscoelastic medium remain linear only up to a very small amplitude of deformation. The maximum strain rates for the linear regime of extensional deformation [see Fig. 3] correspond to a maximum radial excursion, ΔR/R0, of the order of 1%. Thus, care should be used in employing linear viscoelastic models for large-amplitude bubble oscillations.
5 Conclusions
We have characterised the resonant behaviour of ultrasound-driven microbubbles in a viscoelastic solid, agarose gel, commonly used as a tissue-mimicking phantom for biomedical applications. Gels with different properties were first characterised by standard rheological tests to obtain the zero-frequency shear modulus G, and the storage and loss moduli, G′ and G′′, at a frequency f = 1 Hz. Isolated bubbles embedded in the gels were excited by ultrasound at f = 10–50 kHz, and their response was recorded optically using high-speed video microscopy. We used small forcing amplitudes to ensure that the bubble dynamics, and therefore the deformation of the material, remained in the linear regime. Resonance curves obtained experimentally were analysed in the framework of the Rayleigh–Plesset equation, combined with the Kelvin–Voigt model to account for the rheology of the medium, to extract values of shear modulus, G, and shear viscosity, μ. The resonance frequency of the bubbles was found to increase with increasing shear modulus of the medium. This finding implies that imaging and therapeutic ultrasound protocols need to be optimised depending upon the tissue in which the bubbles are embedded. The values of G and μ obtained from bubble dynamics differ significantly from those measured with the rheometer. This finding clearly shows that, even in the linear regime, material properties measured at high frequency can be completely different to those measured with conventional rheometers. Hence, rheological characterisation of biomaterials for medical ultrasound applications requires particular attention to the strain rate applied. Oscillatory deformation imparted by ultrasound-driven bubble dynamics can be used to measure rheological properties in the frequency range that is used in imaging and therapeutic ultrasound. This method can be extended to non-linear bubble oscillations, so long as the bubble remains spherical, and to materials with highly non-linear response. The experimental validation of non-linear constitutive models combined with the governing equation of bubble dynamics will be the subject of future studies.Appendix
Using the equations given in ref. 27, valid for small amplitudes of the acoustic forcing (Δp ≪ p0), we have calculated the values of the polytropic exponent and of the acoustic and thermal damping coefficients for a bubble of radius R0 = 160 μm, typical of our experiments. The ambient pressure was taken to be p0 = 1 × 105 Pa, and the ratio of specific heats for the gas was approximated with that of an ideal diatomic gas, γ = 1.4. The interfacial tension was taken to be40σ = 67.6 × 10−3 N m−1. The values of the other physical properties used for the calculation are summarised in Table 3. The small amount of agarose polymer used (0.5–2% w/v) can be assumed to have negligible effect on density, speed of sound, and the thermal transport properties of the medium. These properties were calculated for the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 v/v water
3 v/v water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol mixture, without agarose, using data from ref. 40–42. Comparison of the values of thermal conductivity and diffusivity of water and 3% agar gels43 confirms that the difference is negligible. On the other hand, since the agarose forms a gel, it has a dramatic effect on the viscosity of the medium. We therefore used the value of shear viscosity of the agarose gel, rather than that of the 2
glycerol mixture, without agarose, using data from ref. 40–42. Comparison of the values of thermal conductivity and diffusivity of water and 3% agar gels43 confirms that the difference is negligible. On the other hand, since the agarose forms a gel, it has a dramatic effect on the viscosity of the medium. We therefore used the value of shear viscosity of the agarose gel, rather than that of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 v/v water
3 v/v water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol mixture.
glycerol mixture.
| Density of medium: ρ | 1.168 × 103 | kg m−3 |
| Shear viscosity of medium: μ | 0.144 | Pa s |
| Speed of sound in medium: c | 1.8 × 103 | m s−1 |
| Thermal diffusivity in medium: D | 1.031 × 10−7 | m2 s−1 |
| Thermal conductivity of medium: K | 0.364 | W m−1 K−1 |
| Density of air: ρg | 1.163 | kg m−3 |
| Speed of sound in air: cg | 347.36 | m s−1 |
| Thermal diffusivity in air: Dg | 2.257 × 10−5 | m2 s−1 |
| Thermal conductivity of air: Kg | 0.0263 | W m−1 K−1 |
Fig. 6a shows the dependence of the polytropic exponent on frequency. The range of frequencies used in our study is highlighted by the shaded area. Since κ varies slightly over this range, in the model we use its mean value, κ ≈ 1.32.
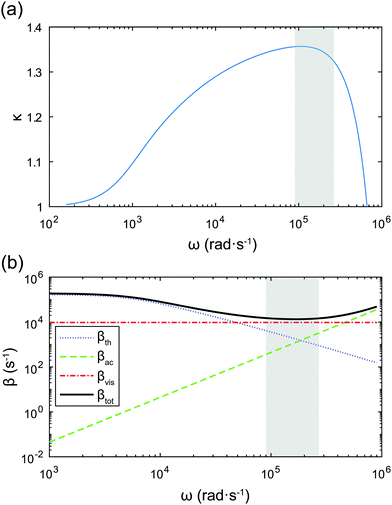 | ||
| Fig. 6 (a) Dependence of the polytropic exponent on the applied frequency. (b) Comparison of thermal, acoustic, and viscous damping coefficients as a function of frequency. The shaded areas mark the frequency range used in our experiments. The bubble radius is R0 = 160 μm and p0 = 1 × 105 Pa, γ = 1.4, σ = 67.6 × 10−3 N m−1. Other physical properties used for the calculation are given in Table 3. | ||
Radiation of sound by the bubble, and therefore acoustic damping, as well as thermal damping, have been neglected in the model. This assumption can be justified by comparing the viscous damping coefficient, βvis, with the acoustic and thermal damping coefficients, βth and βac respectively:
 | (12) |
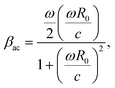 | (13) |
Acknowledgements
The authors thank M. Tinguely for helpful discussions. This work is supported by European Research Council Starting Grant No. 639221.References
-
J. R. B. B. Goldberg and F. Forsberg, Ultrasound Contrast Agents: Basic Principles and Clinical Applications, Dunitz, London, 2nd edn, 2001 Search PubMed
.
- J. J. Choi, K. Selert, F. Vlachos, A. Wong and E. E. Konofagou, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16539–16544 CrossRef CAS PubMed
.
- N. Y. Rapoport, A. M. Kennedy, J. E. Shea, C. L. Scaife and K.-H. Nam, J. Controlled Release, 2009, 138, 268–276 CrossRef CAS PubMed
.
- T. O. Matsunaga, P. S. Sheeran, S. Luois, J. E. Streeter, L. B. Mullin, B. Banerjee and P. A. Dayton, Theranostics, 2012, 2, 1185–1198 CrossRef CAS PubMed
.
- C. Coussios, C. Farny, G. Ter Haar and R. Roy, Int. J. Hyperthermia, 2007, 23, 105–120 CrossRef CAS PubMed
.
- C. C. Coussios and R. A. Roy, Annu. Rev. Fluid Mech., 2008, 40, 395–420 CrossRef
.
- S. Yoshizawa, T. Ikeda, A. Ito, R. Ota, S. Takagi and Y. Matsumoto, Med. Biol. Eng. Comput., 2009, 47, 851–860 Search PubMed
.
- T. Hall, M. Bilgen, M. Insana and T. Krouskop, IEEE Trans. Ultrason. Eng., 1997, 44, 1355–1365 CrossRef
.
- S. R. Aglyamov, A. B. Karpiouk, Y. a. Ilinskii, E. a. Zabolotskaya and S. Y. Emelianov, J. Acoust. Soc. Am., 2007, 122, 1927 CrossRef PubMed
.
- A. Karpiouk, S. Aglyamov, Y. Ilinskii, E. Zabolotskaya and S. Emelianov, IEEE Trans. Ultrason. Eng., 2009, 56, 2380–2387 CrossRef PubMed
.
- E. Shirota and K. Ando, J. Phys.: Conf. Ser., 2015, 656, 012001 CrossRef
.
- M. S. Plesset and A. Prosperetti, Annu. Rev. Fluid Mech., 1977, 9, 145–185 CrossRef CAS
.
- D. B. Khismatullin and A. Nadim, Phys. Fluids, 2002, 14, 3534 CrossRef CAS
.
- J. S. Allen and R. A. Roy, J. Acoust. Soc. Am., 2000, 107, 3167 CrossRef PubMed
.
- C. Hua and E. Johnsen, Phys. Fluids, 2013, 25, 083101 CrossRef
.
- X. Yang and C. C. Church, J. Acoust. Soc. Am., 2005, 118, 3595–3606 CrossRef PubMed
.
- H. Fogler and J. Goddard, Phys. Fluids, 1970, 13, 1135 CrossRef
.
- J. S. Allen and R. A. Roy, J. Acoust. Soc. Am., 2000, 108, 1640–1650 CrossRef CAS PubMed
.
- J. Naude and F. Mendez, J. Non-Newtonian Fluid Mech., 2008, 155, 30–38 CrossRef CAS
.
- H. A. Kafiabad and K. Sadeghy, J. Non-Newtonian Fluid Mech., 2010, 165, 800–811 CrossRef CAS
.
- F. Cunha and D. Albernaz, J. Non-Newtonian Fluid Mech., 2013, 191, 35–44 CrossRef CAS
.
- J. Jimenez-Fernandez and A. Crespo, Ultrasonics, 2005, 43, 643–651 CrossRef CAS PubMed
.
- F. Hamaguchi and K. Ando, Phys. Fluids, 2015, 27, 113103 CrossRef
.
- A. D. Maxwell, C. A. Cain, T. L. Hall, J. B. Fowlkes and Z. Xu, Ultrasound in medicine & biology, 2013, 39, 449–465 Search PubMed
.
- S. Yoon, S. R. Aglyamov, A. B. Karpiouk, S. Kim and S. Y. Emelianov, J. Acoust. Soc. Am., 2011, 130, 2241–2248 CrossRef PubMed
.
- A. Prosperetti, Phys. Fluids, 1982, 25, 409–410 CrossRef
.
- A. Prosperetti, J. Acoust. Soc. Am., 1977, 61, 17 CrossRef
.
-
L. Landau and E. M. Lifshitz, Mechanics, Butterworth-Heinemann, 1976 Search PubMed
.
- J. Narayanan, J.-Y. Xiong and X.-Y. Liu, J. Phys.: Conf. Ser., 2006, 28, 83–86 CrossRef CAS
.
- W.-C. Lin, K. R. Shull, C.-Y. Hui and Y.-Y. Lin, J. Chem. Phys., 2007, 127, 094906 CrossRef PubMed
.
- S. M. van der Meer, B. Dollet, M. M. Voormolen, C. T. Chin, A. Bouakaz, N. de Jong, M. Versluis and D. Lohse, J. Acoust. Soc. Am., 2007, 121, 648–656 CrossRef CAS PubMed
.
- D. Hsieh, J. Acoust. Soc. Am., 1961, 33, 206 CrossRef
.
- K. Manickam, R. R. Machireddy and S. Seshadri, J. Mech. Behav. Biomed. Mater., 2014, 35, 132–143 CrossRef PubMed
.
- C. U. Devi, R. M. Vasu and A. K. Sood, J. Biomed. Opt., 2005, 10, 44020 CrossRef PubMed
.
- T. A. Krouskop, T. M. Wheeler, F. Kallel, B. S. Garra and T. Hall, Ultrasonic imaging, 1998, 20, 260–274 CrossRef CAS PubMed
.
- M. Zhang, B. Castaneda, Z. Wu, P. Nigwekar, J. V. Joseph, D. J. Rubens and K. J. Parker, Ultrasound in Medicine and Biology, 2007, 33, 1617–1631 CrossRef PubMed
.
- C. Macosko, Rheology: principles, measurements, and applications.
- M. Overvelde, V. Garbin, J. Sijl, B. Dollet, N. de Jong, D. Lohse and M. Versluis, Ultrasound in medicine & biology, 2010, 36, 2080–2092 Search PubMed
.
- M. Tinguely, M. G. Hennessy, A. Pommella, O. K. Matar and V. Garbin, Soft Matter, 2016, 12, 4247–4256 RSC
.
-
G. P. Association
et al.
, Physical properties of glycerine and its solutions, Glycerine Producers' Association, 1963 Search PubMed
.
- J. H. Perry, J. Chem. Educ., 1950, 27, 533 CrossRef
.
- N.-S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288 CrossRef CAS
.
- R. G. Holt and R. A. Roy, Ultrasound in Medicine & Biology, 2001, 27, 1399–1412 CAS
.
| This journal is © The Royal Society of Chemistry 2017 |