 Open Access Article
Open Access ArticleMolecular modelling of supramolecular one dimensional polymers
Divya B. Korlepara a and
S. Balasubramanian
a and
S. Balasubramanian *b
*b
aChemistry and Physics of Materials Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, India
bChemistry and Physics of Materials Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, India. E-mail: jncbala@gmail.com; Fax: +91 80 2208 2766; Tel: +91-80 2208 2808
First published on 20th June 2018
Abstract
Supramolecular polymers exemplify the need to employ several computational techniques to study processes and phenomena occuring at varied length and time scales. Electronic processes, conformational and configurational excitations of small aggregates of chromophoric molecules, solvent effects under realistic thermodynamic conditions and mesoscale morphologies are some of the challenges which demand hierarchical modelling approaches. This review focusses on one-dimensional supramolecular polymers, the mechanism of self-assembly of monomers in polar and non-polar solvents and properties they exhibit. Directions for future work are as well outlined.
1 Introduction
The term supramolecule was introduced by Karl Lothar Wolf et al. in 1937.1 Chemistry beyond the molecule, based on non-covalent interactions is known as supramolecular chemistry.2–4 Supramolecular polymers are large-scale (meso, micro) structures arising out of weak non-covalent interactions between molecules in solution. These interactions are directional and are reversible at near-ambient conditions such as hydrogen bonding, π–π, electrostatic, donor–acceptor, hydrophobic attractions and metal-ion coordination. Such polymers form spontaneously from a solution of monomers beyond a critical concentration and below a particular temperature. Commercial exploitation of supramolecular polymers use the advantage of reversibility and responsiveness, specifically in adhesives, printing, cosmetics, personal care, and coatings5–7 and in many bio-medical applications.8–20The mechanism of self-assembly of molecules in solution can be broadly classified into two categories based on the dependence of the association constant K, between species on oligomer size.21 These are isodesmic and cooperative mechanisms.22,23 As the name suggests, in the isodesmic mechanism (or equal-K model) the association constant is independent of the size of the oligomer.24 The degree of polymerisation is found to be broad in an isodesmic process, even under favourable thermodynamic conditions. On the other hand, the cooperative mechanism of self-assembly also known as the nucleation-elongation process, possesses two or more different equilibrium constants with oligomer size. The formation of the nuclei is associated by a nucleation equilibrium constant (Kn), and the elongation process is governed by another equilibrium constant, (Ke). Supramolecular polymers formed via such mechanisms can be topologically 1-dimensional,25–27 2-dimensional28–32 or 3-dimensional structures.33–38 In the current review, we limit ourselves to modelling studies of one-dimensional supramolecular polymers as these constitute the majority of theoretical/computational studies in the literature.
Organic molecules which self-assemble to form 1-d supramolecular polymers, in general, have three components, (see schematic in Fig. 1(a)): an aromatic planar core, a self-assembling moiety and the two connected by a linker which can be used to provide functionality to the molecule. The self-assembling moiety will usually contain an alkyl group or groups bulkier than an alkyl (such as, say, cholesterol). The optimal inter-alkyl distance between neighbouring molecules in a 1-dimensional supramolecular polymer is around 4.2 Å, while the corresponding aromatic cores prefer to be located at distances of around 3.5 Å. In order to meet both these needs, the polymer exhibits a helical twist shown in Fig. 1(b).39–43
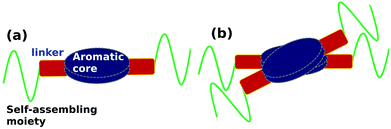 | ||
| Fig. 1 (a) Schematic representation of key moieties of a monomer & its (b) dimer, exhibiting a helical twist. | ||
Chirality is often a central theme in supramolecular polymers, as a preferred helical handedness of the polymer can be used as an experimental probe via circular dichroism spectroscopy.44 While achiral molecules will form 1-d stacks of either handedness in equal proportions, stacks formed out of molecules with a chiral center exhibit a preference of one particular helical sense.44 The position of the chiral center in the self-assembling moiety is seen to determine not only the helical sense of the supramolecular stack,44,45 but also influences its stability. The solvent too plays an important role on the conformation of the molecule in a stack. They can intercalate into the stacks, thereby influencing its conformation.46,47 The orientation of functional groups, primarily in the linker moiety, can give rise to several low-lying geometries of the monomer, the existence of which can be obtained from crystallographic studies.48–50
Superstructures formed by 1-d supramolecular polymers are to a large extent, fibers. These fibers show dynamic self-assembly and dis-assembly in response to change in environment, which are the advantages of supramolecular polymers over the traditional ones. Thus, in this review, we focus on modelling studies of one dimensional polymers,48,51–55 a topic which has been reviewed recently by Bochicchio and Pavan recently.55 The experimental interest in these materials is from optoelectronic applications point of view. UV-Vis absorption and fluorescence spectroscopy are the primary experimental tools employed. These spectra can in turn be calculated for single molecules as well as for very short oligomers in gas phase using quantum chemical calculations. The process of oligomerization can be studied using all-atom molecular dynamics simulations, while nano and meso scale structure and organization can be investigated using coarse grain methods. Formation of fibers from polymers and their morphologies can be studied using continuum methods. The length and time scales associated with these processes and techniques are illustrated in Fig. 2.
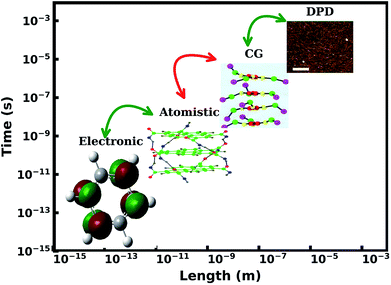 | ||
| Fig. 2 Hierarchy of multiscale modeling of supramolecular polymers. This figure has been reproduced from ref. 56 and 57 with permission from the American Chemical Society. DPD = dissipative particle dynamics, CG = coarse-grained. | ||
2 One dimensional (1D) polymers
2.1 Gas phase calculations
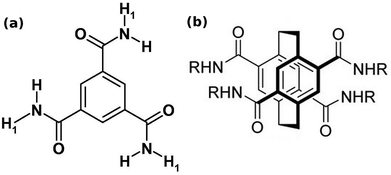 | ||
| Fig. 3 (a) Benzene-1,3,5-tricarboxamide (BTA). This figure has been reproduced from ref. 58 with permission from Elsevier. (b) pCp-4,7,12,15-tetracarboxamide (pCpTA), R = H. This figure has been reproduced from ref. 48 with permission from Wiley-VCH. | ||
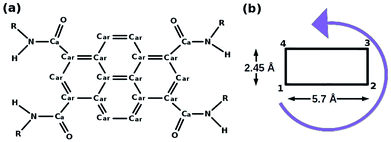 | ||
| Fig. 4 (a) Pyrene derivative (PCA), R = H, (b) its schematic representation. This figure has been reproduced from ref. 50 with permission from the American Chemical Society. | ||
 | ||
| Fig. 5 Two conformations of pCpTA, R = CH3 and the values of dipole moments are also shown. This figure has been reproduced from ref. 48 with permission from Wiley-VCH. | ||
 | ||
| Fig. 6 (a–e) PCA configurations, R = CH3. Symbols ‘U’ & ‘D’ represent the dipole orientation about the aromatic core to be up and down respectively. Use the arrow guide in Fig. 4b. Panel (f) are the energies of the configurations. | ||
| Molecule | Configuration | Dipole moment (D) |
|---|---|---|
| BTA | Planar | 0.491 |
| pCpTA | Anti | 9.60 |
| Syn | 8.90 | |
| PCA | Non-planar/UDUD | 0.27 |
| Non-planar/UUDD | 0.00 | |
| Non-planar/DDUU | 4.75 | |
| Non-planar/DUUD | 0.00 | |
| Non-planar/UUUU | 9.61 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 state) and another in which any one of the dipole vectors is flipped (2
0 state) and another in which any one of the dipole vectors is flipped (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state). The latter is the ground state, as can be rationalized on electrostatic grounds and the same has been observed in quantum chemical calculations as well as force field calculations (Fig. 7). The 2
1 state). The latter is the ground state, as can be rationalized on electrostatic grounds and the same has been observed in quantum chemical calculations as well as force field calculations (Fig. 7). The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state is also thermodynamically stabilized on entropic grounds, as it can be generated in three distinct ways. The longer the oligomer, the greater is the contribution of this entropic stabilization to the 2
1 state is also thermodynamically stabilized on entropic grounds, as it can be generated in three distinct ways. The longer the oligomer, the greater is the contribution of this entropic stabilization to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state. As the net dipole moment of every molecule in a stack is aligned along the same direction, the stack acquires a large electric dipole moment, called the ‘macrodipole’. Futhermore, as the solvent, in general, is non-polar, such macrodipoles of stacks present in solution interact with each other without much dielectric screening. The richness of dipole orientational landscape found in BTA oligomers is further enhanced in oligomers of pCpTA and PCA, as those isolated molecule themselves exhibit many dipole configurations (Fig. 5 and 6).
1 state. As the net dipole moment of every molecule in a stack is aligned along the same direction, the stack acquires a large electric dipole moment, called the ‘macrodipole’. Futhermore, as the solvent, in general, is non-polar, such macrodipoles of stacks present in solution interact with each other without much dielectric screening. The richness of dipole orientational landscape found in BTA oligomers is further enhanced in oligomers of pCpTA and PCA, as those isolated molecule themselves exhibit many dipole configurations (Fig. 5 and 6).
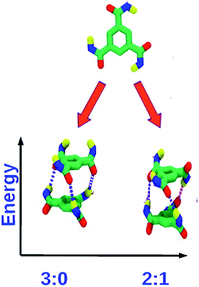 | ||
Fig. 7 Top: monomer of BTA with R = H. Bottom: dimer configurations. The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dipole configuration is the ground state. This figure has been reproduced from ref. 49 with permission from the American Chemical Society. 1 dipole configuration is the ground state. This figure has been reproduced from ref. 49 with permission from the American Chemical Society. | ||
A wide variety of molecules with different functional groups have been synthesized and studied experimentally for their polymerization mechanism.67,68 However, a rationalization of the mechanism exhibited by a given molecule based on its molecular characteristics has eluded researchers for a long time. Based on a careful analysis of molecular functional groups and gas phase quantum chemical calculations of short oligomers, Kulkarni et al. proposed that molecules which possess functional groups that enable the formation of a macrodipole (or in general, one that leads to a long range interaction) along the stacking direction lead to a cooperative mechanism of self-assembly while those which lack such characteristics self-assemble via the isodesmic mechanism.58 Gas phase calculations of binding energies (B.E.) of oligomers for BTA reveal their cooperativity (Fig. 8), where
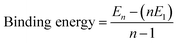 | (1) |
 | ||
| Fig. 8 (a) Binding energy (BE) of BTA obtained from quantum calculations using PBE method with dispersion corrections (b) optimized configuration of a BTA hexamer with electrostatic potential map illustrating the emergence of a macro dipoles. This figure has been reproduced from ref. 58 with permission from Elsevier. | ||
If the system under consideration has electron deficient and electron rich molecules, then they can interact via charge transfer interaction. One of the well known electron deficient molecule is naphthalene diimide (NDI) whose structure is shown in Fig. 9(a). NDI can form ground state charge transfer complexes with electron-rich aromatic solvents such as benzene, o-xylene and mesitylene, one of which is shown in Fig. 9(b).
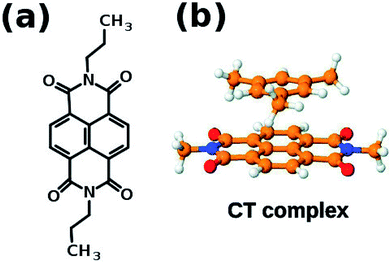 | ||
| Fig. 9 (a) Naphthalene diimide (NDI) derivative 1′ (b) schematic representation of charge transfer complex. This figure has been reproduced from ref. 69 with permission from the PCCP Owner Societies. | ||
With an increase in the ability of the solvent molecule to donate electrons, its interaction with NDI increases as exemplified by the vertical transition wavelengths in Fig. 10 calculated through time dependent DFT (TDDFT) methods on clusters of NDI with different solvent molecules. This work demonstrated that care must be taken in the choice of aromatic solvents for NDI derivatives.69 The energy level diagram and molecular orbitals involved in the CT transition of NDI coordinated by electron rich mesitylene molecules is shown in Fig. 11.
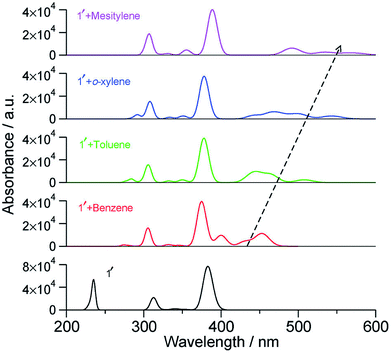 | ||
| Fig. 10 Calculated vertical transitions of NDI derivative-solvent complexes at the BLYP-D3/DZVP//B3LYP/6-31+G(d,p) level of theory (fwhm = 1000 cm−1). The black dashed arrow indicates the changes in the CT transition with increasing electron donating capacity of the solvent molecule. This figure has been reproduced from ref. 69 with permission from the PCCP Owner Societies. | ||
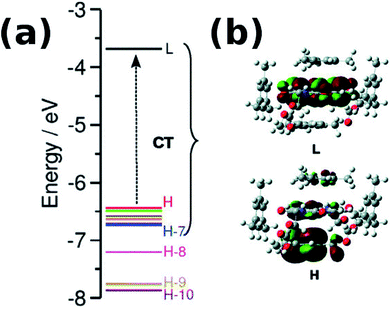 | ||
| Fig. 11 (a) Computed energy level diagram of 1′ with four molecules of mesitylene. (b) Molecular orbitals of 1′ + four molecules of mesitylene. H and L stand for HOMO and LUMO respectively. Reproduced from ref. 69 with permission from the PCCP Owner Societies. | ||
Density functional theory calculations also demonstrated a σ bond formation between Pd metal centres in a oligophenyleneethynylene (OPE) based Pd(II) pyridyl complex which polymerized via both supramolecular and metallophilic interactions.70
While gas phase and cluster calculations can be used to identify intermolecular interactions which contribute to molecular association, the mechanism of self-assembly and larger scale structures can be understood only via calculations carried out including explicit solvent molecules, at finite temperature, under bulk conditions. Due to computational challenges, a full-blown DFT based simulation is not possible and has not been reported in the literature; it is not warranted either. Thus, empirical force field based MD simulations are well suited to answer these questions and these have been carried out with either polar and non-polar solvents.
3 Molecular dynamics simulations
3.1 All atom (AA) simulations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 configuration.49 Using advanced sampling methods, the dimerization free energy of BTA in solution has been calculated to be −12.81 kcal mol−1.49 The free energy change involved in the formation of long oligomers from shorter ones has also been calculated using these simulations which demonstrate the cooperative nature of self-assembly of BTA, consistent with experiments. Both BTA and PCA form long fibers in non-polar solvents.
1 configuration.49 Using advanced sampling methods, the dimerization free energy of BTA in solution has been calculated to be −12.81 kcal mol−1.49 The free energy change involved in the formation of long oligomers from shorter ones has also been calculated using these simulations which demonstrate the cooperative nature of self-assembly of BTA, consistent with experiments. Both BTA and PCA form long fibers in non-polar solvents.With small modifications in the functional groups, it is possible to have molecules to either polymerize or not. This was exemplified in a system eerily similar to BTA. Three molecules of a ester-based BTA family71 are shown in Fig. 12. These molecules have both amide (A) and carboxylate (C) functional groups, thus one can have the possibility of forming either three (AA type) or six (AC type) intermolecular hydrogen bonds between a pair of molecules. Gas phase quantum chemical calculations showed that a AC dimer was more stable than a AA one by 20 kcal mol−1. However the AC dimer cannot elongate to form a polymer as it is left with no ‘free’ hydrogen bonding sites. MD simulations72 rationalized the experimental observations of the capability of BTA-Met and BTA-Phe to form long polymers and that of BTA-Nle to form just dimers. The oligomers of the former two molecules are further stabilized by weak C–H⋯S and C–H⋯π interactions respectively.
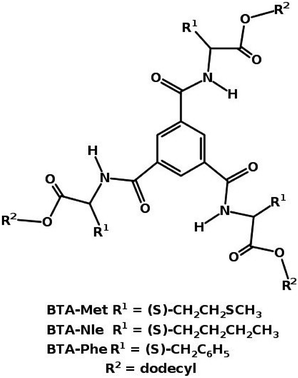 | ||
| Fig. 12 Ester based BTA structures.71 | ||
Supramolecular polymers have a wide range of applications as they can form gels, nano fibers, rod like structures and liquid crystalline (LC) materials.50,52,57,73–75 Both BTA and PCA exhibit a LC phase at room-temperature and have been studied for their ferroelectric behaviour experimentally.52,64,65,76,77 Atomistic MD simulations revealed that BTA in its LC phase displays a reversal of handedness of the hydrogen bond helices upon reversal of electric field applied in a fashion akin to that in ferroelectric experiments.78 However, such a handedness reversal was not observed in the case of PCA;50 an electric field reversal caused the formation of bifurcated intermolecular hydrogen bonds in the latter. The difference in the behavior of these two systems was attributed to the difference in the rotational symmetry of the core of these two molecules. While BTA is C3 symmetric, PCA is C2 symmetric which leads to unequal amide–amide near neighbor distances within a molecule. Thus, we generalize that handedness reversal of hydrogen bond helices in a supramolecular stack in its LC phase upon switching of electric field will happen in systems with either C3 or C4 symmetry in their core.
Atomistic MD simulations50 have also revealed yet another interesting difference between BTA and PCA in their LC phases: their dipolar relaxation mechanisms. At equilibrium (zero external field), the asymmetric dipole configuration is the ground state. The approach to this ground state from a dipole excited state proceeds in a sequential fashion (i.e., the dipole of one molecule flips, followed by its neighbor and so on) in the case of a stack of PCA, while it is found to be random in the case of BTA. The difference in behaviour can be attributed to the difference in dihedral barriers of the two molecules. These intricate details are not directly accessible to experiments, making MD simulations a valuable complementary tool. MD simulations were also able to rationalize results of a beautiful experiment on solvent intercalation within the self-assembling moiety which results in the ability to thermodynamically switch the helical sense of a supramolecular stack. Solvent molecules intercalate into the stack's side chains at low temperature and leave them at higher temperatures leading to a reversal of helical sense of the stack.47
The conjecture that long range interactions (such as dipole–dipole) along the stacking direction leads to cooperative self-assembly was convincingly demonstrated79 in a family of compounds based on Perylene-3,4,5,10-tetracarboxylic acid bisimides (PBIs) which are shown in Fig. 13. The compounds illustrated therein differ either in their linker or in their self-assembling moiety. While molecules 1 and 4 have a carbonate linker (possessing an electric dipole moment), molecule 3 has a polar ether group, devoid of dipole moment. The self-assembling moiety in 1 and 3 are cholesterol, while in 4, it is a chiral swallow tail (CST), branched alkyl group. Molecule 1 followed a cooperative mechanism of self-assembly while both 3 and 4 followed an isodesmic pathway. The cholesteric group provides rigidity while the CST in 4 makes the molecule fluxional and occupy a larger volume, thus destroying the helical order required for self-assembly. The presence of a carbonate group provides the needed dipole–dipole interaction for cooperativity which, along with the order-inducing cholesterol group in 1 leads to a large macrodipole moment along the stack direction. These observations from atomistic MD simulations (see Fig. 14) were corroborated from dielectric spectroscopy experiments as well.
 | ||
| Fig. 13 PBI derivatives and their mechanisms of self-assembly. This figure has been reproduced from ref. 79 with permission from the American Chemical Society. | ||
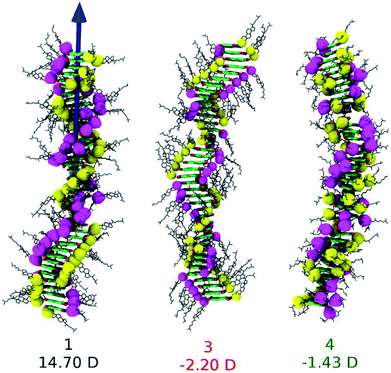 | ||
| Fig. 14 Snapshots from MD simulations of PBI derivatives and their dipole moments. This figure has been reproduced from ref. 79 with permission from the American Chemical Society. | ||
Enhanced sampling methods. While atomistic MD simulations are able to exhibit the aggregation of monomers from solution to form short oligomers, they are unable to capture the elongation of such oligomers to longer stacks due to ‘entropic bottleneck’, i.e., the volume of configuration space spanned by dispersed monomers is so vast (in simulations carried out at experimentally realistic concentrations of the chromophore), that longer oligomers are not formed within the timescales of atomistic MD simulations. Furthermore, even the short oligomers (say, of length 6–10 molecules) exhibit defects (metastable states) which would need a long time to reach the more stable, helically ordered state. If one has to retain atomistic interactions and yet obtain thermodynamically stable structures, one needs to employ enhanced sampling methods.80–86 Replica exchange (or parallel tempering) and replica exchange solute tempering (REST) are some of the methods which have been employed in the area of supramolecular polymer modelling. By utilizing these techniques, one can obtain highly ordered polymer structures with helical H-bonding pattern as shown in Fig. 15. The REST (or REST2)84,86 methods temper just the solute molecules and not the solvent and thus are more efficient in sampling the configuration space of the chromophore molecules than the simpler replica exchange method (T-REMD).87
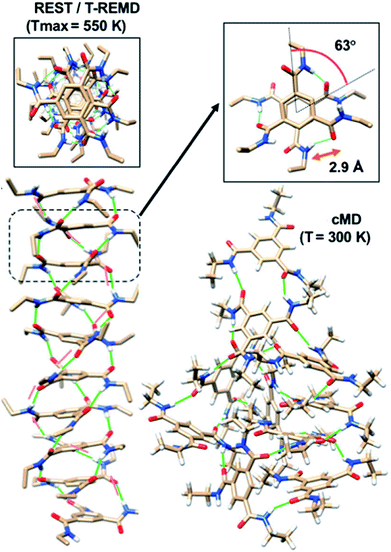 | ||
| Fig. 15 Self-assembled structures from common MD (cMD), T-REMD and REST at different values of Tmax. This figure has been reproduced from ref. 87 with permission from the American Institute of Physics. | ||
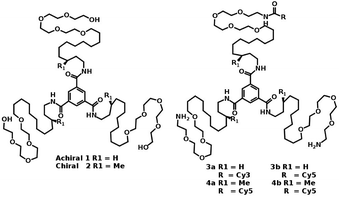 | ||
| Fig. 16 Molecular structures of water soluble chiral and achiral BTA.91 | ||
The cooperative nature of aggregation of BTE in water was studied using atomistic MD simulations.92 Intermolecular hydrogen bonding was identified as a major contributor to the stability of the supramolecular polymer. When the hydrogen bonding ability of the monomer was turned off synthetically (as well as in computation see Fig. 17), the ability to form supramolecular stacks was considerably reduced. Thus, the directional driving force of hydrogen bonding was attributed as the underlying reason for cooperativity.92
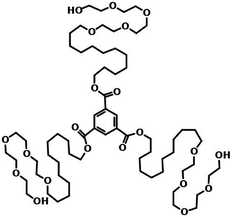 | ||
| Fig. 17 Molecular structures of water soluble BTE. This figure has been reproduced from ref. 92 with permission from the American Chemical Society. | ||
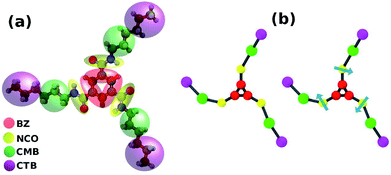 | ||
| Fig. 18 (a) Coarse grain mapping of BTA and (b) the two CG models; the arrow represents a sticky dipole vector. This figure has been reproduced from ref. 56 with permission from the American Chemical Society. | ||
Biomimetic self-assembly driven by an external fuel is one of the long standing problems in supramolecular polymerization. Recently, a oligo(p-phenylenevinylene) derivative (OPV) was found to be selective to ATP over other triphosphates such as UTP, CTP, or GTP. Atomistic MD simulations showed that the ATP-bound OPV oligomers were stabilized by weak hydrogen bonding interactions which were absent in other triphosphates. During the process of self-assembly, the removal of a slip between the OPV core planes with increasing oligomer size was observed and this process explained the experimentally observed lag time in circular dichroism (CD) and UV/Vis spectra.93
The assembly/disassembly of microtubules in biological systems is activated by chemical fuel which triggers conformational transitions in the molecules constituting the tubule. Researchers have worked on synthetic mimics where the conformational transition is triggered photochromically, using the well known system of cis–trans isomerization in azo group based compounds.94,95 Self-assembled microtubule-like structures with hydrophobic regions buried inside the tubule, exposing the hydrophilic part of the molecules to the solvent (water) have been synthesized. The azo group is present within the hydrophobic part of the molecule. Upon shining light, the trans to cis isomerization of the azo group takes place, creating a strain in the tubule which causes its disassembly. Well tempered metadynamics based MD simulations have been able to realistically capture this phenomenon.95
3.2 Coarse grain (CG) modelling
An approach to perform MD simulations at equilibrium to study larger length and longer time scale phenomena than what is accessible via atomistic MD simulations are coarse graining (CG) methods. Herein, individual atoms are done away with and instead a collection of atoms (typically about three non-hydrogen atoms) are ‘glued’ to form a CG bead. Compared to atomistic models, CG models have fewer degrees of freedom, and have softer interactions which enable the use of larger MD timesteps of integration. In the domain of supramolecular polymer modelling, both these characteristics of CG approach enable the computational study of self-assembly at concentrations comparable to that in experiments, and the probing of defect mediated single molecule insertion into pre-organized stacks, without much loss of chemical specificity.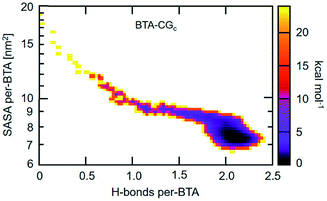 | ||
| Fig. 19 2D self-assembly free energy landscape of BTA-CG model as a function of average number of H-bonds per BTA and average SASA per BTA. This figure has been reproduced from ref. 96 with permission from the American Chemical Society. | ||
CG models have also been used to identify the increase in disorder of the supramolecular polymer formed by a fluorine substituted compound in comparison to its hydrogenated counterpart.98 While the latter is shown experimentally to self-assemble in a cooperative fashion, the former does so in an isodesmic manner.
The monomer exchange of molecule in a BTA stack solvated in linear alkane has been studied using a CG model. The free energy required to remove a molecule from the stack is independent of its position.56 The exact mechanism of monomer insertion into a stack in aqueous solution was demonstrated convincingly by Pavan and coworkers to be via defect locations (hot spots) on the stack. BTA exchange is a stepwise process as shown in Fig. 20(a). While the motion of a monomer from a hot spot on the stack to other regions on the stack itself occurs in the μs timescale, its diffusion into bulk water happens in ms timescale, as seen from well tempered metadynamics based coarse grained MD simulations.97 The free energy profile for this process shown in Fig. 20(b) too exemplifies this step-wise behaviour.
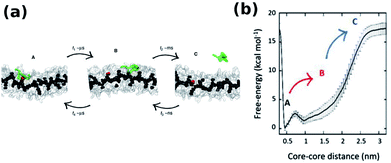 | ||
| Fig. 20 (a) Snapshots of CG-BTA in water from well tempered MD representing state A, B and C, (b) free-energy profile of monomer exchange with water as a solvent.97 | ||
As mentioned earlier, chiral molecules form more stable stacks than achiral ones.91 So, it is very important to understand monomer exchange phenomena on chiral molecules. The exchange rates of chiral monomers in corresponding fibers are slower than achiral ones by 1–2 orders of magnitude. The largest monomer movements occur in proximity of the fiber surface, while the internal core of the fibers appears more static. The rate of dynamic monomer exchange can be influenced by changing the monomer–monomer interaction or the H-bonding between the molecules. The change in interaction energy is proportional to the rate of monomer movements, and the lack of hydrogen bond increases monomer movements.97 These monomer exchange can be used for defect control in materials.
4 Conclusions
While supramolecular polymers have been experimentally studied for nearly two decades or more, their atomistic modelling have been attempted only over the past six to seven years or so. Yet, modelling has contributed several significant original results. Some of these include the identification of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dipole configuration in the classical molecule, BTA, as the ground state, the reversal of helical handedness concomitant with polarization switching in BTA ferroelectrics, and the fine role of defects (hot spots) for monomer insertion into a supramolecular polymer. A variety of molecular modelling techniques, including gas phase quantum chemical methods, atomistic and coarse grained MD simulations have been employed. In view of the long timescales involved in the process of self-assembly, enhanced sampling methods such as adaptive biasing force, well tempered metadynamics, replica exchange solute tempering etc., have been of effectively employed. Yet, mesoscale ordering in terms of fiber formation and their properties have not been modelled. These might require solvent-free models99 and mesoscale methods such as dissipative particle dynamics.100,101
1 dipole configuration in the classical molecule, BTA, as the ground state, the reversal of helical handedness concomitant with polarization switching in BTA ferroelectrics, and the fine role of defects (hot spots) for monomer insertion into a supramolecular polymer. A variety of molecular modelling techniques, including gas phase quantum chemical methods, atomistic and coarse grained MD simulations have been employed. In view of the long timescales involved in the process of self-assembly, enhanced sampling methods such as adaptive biasing force, well tempered metadynamics, replica exchange solute tempering etc., have been of effectively employed. Yet, mesoscale ordering in terms of fiber formation and their properties have not been modelled. These might require solvent-free models99 and mesoscale methods such as dissipative particle dynamics.100,101
It is also vital to derive transferable CG force fields for various moieties and functional groups used in supramolecular polymers, so that the structure and phenomena exhibited by such assemblies can be computed in near real time to interpret new experiments. This will form one of the immediate tasks in our research group.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. B. K. thanks CSIR, India for a Senior Research Fellowship. We thank DST for support.Notes and references
- K. Wolf, H. Frahm and H. Harms, Z. Phys. Chem. (B), 1937, 36, 237–287 Search PubMed
.
- F. Huang and E. V. Anslyn, Chem. Rev., 2015, 115, 6999–7000 CrossRef PubMed
.
- J.-M. Lehn, Angew. Chem., Int. Ed., 1988, 27, 89–112 CrossRef
.
- L. Brunsveld, B. Folmer, E. W. Meijer and R. Sijbesma, Chem. Rev., 2001, 101, 4071–4098 CrossRef PubMed
.
- O. J. Goor, J. E. Brouns and P. Y. Dankers, Polym. Chem., 2017, 8, 5228–5238 RSC
.
- F. Deflorian, S. Rossi and E. Scrinzi, Corros. Eng., Sci. Technol., 2013, 48, 147–154 CrossRef
.
- Q. Wei, C. Schlaich, S. Prévost, A. Schulz, C. Böttcher, M. Gradzielski, Z. Qi, R. Haag and C. A. Schalley, Adv. Mater., 2014, 26, 7358–7364 CrossRef PubMed
.
- S. P. Wijnands, W. Engelen, R. P. Lafleur, E. W. Meijer and M. Merkx, Nat. Commun., 2018, 9, 65 CrossRef PubMed
.
- R. Haag, Angew. Chem., Int. Ed., 2004, 43, 278–282 CrossRef PubMed
.
- Y. Cheng, A. C. Samia, J. D. Meyers, I. Panagopoulos, B. Fei and C. Burda, J. Am. Chem. Soc., 2008, 130, 10643–10647 CrossRef PubMed
.
- H. Gheybi and M. Adeli, Polym. Chem., 2015, 6, 2580–2615 RSC
.
- R. Timpl and J. C. Brown, BioEssays, 1996, 18, 123–132 CrossRef PubMed
.
- R. A. MacDonald, B. F. Laurenzi, G. Viswanathan, P. M. Ajayan and J. P. Stegemann, J. Biomed. Mater. Res., Part A, 2005, 74, 489–496 CrossRef PubMed
.
- P. Carol, S. Sreejith and A. Ajayaghosh, Chem.–Asian J., 2007, 2, 338–348 CrossRef PubMed
.
- C.-Z. Wang, J.-L. Chen, Y. Tang, Y. Zang, G.-R. Chen, T. D. James, J. Li, C. Wu and X.-P. He, ACS Appl. Mater. Interfaces, 2017, 9, 3272–3276 CrossRef PubMed
.
- R. Thirumalai, R. D. Mukhopadhyay, V. K. Praveen and A. Ajayaghosh, Sci. Rep., 2015, 5, 9842 CrossRef PubMed
.
- S. Dong, B. Zheng, F. Wang and F. Huang, Acc. Chem. Res., 2014, 47, 1982–1994 CrossRef PubMed
.
- X. Ji, Y. Yao, J. Li, X. Yan and F. Huang, J. Am. Chem. Soc., 2012, 135, 74–77 CrossRef PubMed
.
- S. Dong, B. Zheng, M. Zhang, X. Yan, X. Ding, Y. Yu and F. Huang, Macromolecules, 2012, 45, 9070–9075 CrossRef
.
- F. Wang, C. Han, C. He, Q. Zhou, J. Zhang, C. Wang, N. Li and F. Huang, J. Am. Chem. Soc., 2008, 130, 11254–11255 CrossRef PubMed
.
- M. M. Smulders, M. M. Nieuwenhuizen, T. F. de Greef, P. van der Schoot, A. P. Schenning and E. W. Meijer, Chem.–Eur. J., 2010, 16, 362–367 CrossRef PubMed
.
- X. Yan, T. R. Cook, J. B. Pollock, P. Wei, Y. Zhang, Y. Yu, F. Huang and P. J. Stang, J. Am. Chem. Soc., 2014, 136, 4460–4463 CrossRef PubMed
.
- Z. Zhang, Y. Luo, J. Chen, S. Dong, Y. Yu, Z. Ma and F. Huang, Angew. Chem., 2011, 123, 1433–1437 CrossRef
.
- R. B. Martin, Chem. Rev., 1996, 96, 3043–3064 CrossRef PubMed
.
- P. Besenius, G. Portale, P. H. Bomans, H. M. Janssen, A. R. Palmans and E. W. Meijer, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17888–17893 CrossRef PubMed
.
- M. M. Smulders, P. J. Stals, T. Mes, T. F. Paffen, A. P. Schenning, A. R. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2009, 132, 620–626 CrossRef PubMed
.
- K. V. Rao, D. Miyajima, A. Nihonyanagi and T. Aida, Nat. Chem., 2017, 9, 1133–1139 CrossRef PubMed
.
- S. Chen, S. M. Polen, L. Wang, M. Yamasaki, C. M. Hadad and J. D. Badjić, J. Am. Chem. Soc., 2016, 138, 11312–11317 CrossRef PubMed
.
- T.-Y. Zhou, Q.-Y. Qi, Q.-L. Zhao, J. Fu, Y. Liu, Z. Ma and X. Zhao, Polym. Chem., 2015, 6, 3018–3023 RSC
.
- W. Seo, K. L. Carpenter, J. A. Gaugler, W. Shao, K. A. Werling, P. M. Fournier, D. S. Lambrecht and A. Star, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1095–1101 CrossRef
.
- J. Adisoejoso, Y. Li, J. Liu, P. N. Liu and N. Lin, J. Am. Chem. Soc., 2012, 134, 18526–18529 CrossRef PubMed
.
- H. Kar, D. W. Gehrig, N. K. Allampally, G. Fernández, F. Laquai and S. Ghosh, Chem. Sci., 2016, 7, 1115–1120 RSC
.
- C. Zhou, J. Tian, J.-L. Wang, D.-W. Zhang, X. Zhao, Y. Liu and Z.-T. Li, Polym. Chem., 2014, 5, 341–345 RSC
.
- L. Chen, S.-C. Zhang, H. Wang, Y.-M. Zhou, Z.-T. Li and D.-W. Zhang, Tetrahedron, 2014, 70, 4778–4783 CrossRef
.
- C.-W. Hu, T. Sato, J. Zhang, S. Moriyama and M. Higuchi, ACS Appl. Mater. Interfaces, 2014, 6, 9118–9125 CrossRef PubMed
.
- J. Tian, T.-Y. Zhou, S.-C. Zhang, S. Aloni, M. V. Altoe, S.-H. Xie, H. Wang, D.-W. Zhang, X. Zhao and Y. Liu, et al., Nat. Commun., 2014, 5, 5574 CrossRef PubMed
.
- K. Jayaramulu, P. Kanoo, S. J. George and T. K. Maji, Chem. Commun., 2010, 46, 7906–7908 RSC
.
- S. Cherumukkil, B. Vedhanarayanan, G. Das, V. K. Praveen and A. Ajayaghosh, Bull. Chem. Soc. Jpn., 2017, 91, 100–120 CrossRef
.
- M. Kumar and S. J. George, Nanoscale, 2011, 3, 2130–2133 RSC
.
- M. Kumar and S. J. George, Chem.–Eur. J., 2011, 17, 11102–11106 CrossRef PubMed
.
- J. Guilleme, M. J. Mayoral, J. Calbo, J. Aragó, P. M. Viruela, E. Ortí, T. Torres and D. González-Rodríguez, Angew. Chem., Int. Ed., 2015, 54, 2543–2547 CrossRef PubMed
.
- P. P. Neelakandan, P. C. Nandajan, B. Subymol and D. Ramaiah, Org. Biomol. Chem., 2011, 9, 1021–1029 RSC
.
- J. Leira-Iglesias, A. Sorrenti, A. Sato, P. A. Dunne and T. M. Hermans, Chem. Commun., 2016, 52, 9009–9012 RSC
.
- P. J. Stals, M. M. Smulders, R. Martín-Rapún, A. R. Palmans and E. W. Meijer, Chem.–Eur. J., 2009, 15, 2071–2080 CrossRef PubMed
.
- R. Marty, R. Nigon, D. Leite and H. Frauenrath, J. Am. Chem. Soc., 2014, 136, 3919–3927 CrossRef PubMed
.
- Y. Nakano, T. Hirose, P. J. Stals, E. W. Meijer and A. R. Palmans, Chem. Sci., 2012, 3, 148–155 RSC
.
- C. Kulkarni, P. A. Korevaar, K. K. Bejagam, A. R. Palmans, E. W. Meijer and S. J. George, J. Am. Chem. Soc., 2017, 139, 13867–13875 CrossRef PubMed
.
- D. E. Fagnani, M. J. Meese, K. A. Abboud and R. K. Castellano, Angew. Chem., Int. Ed., 2016, 55, 10726–10731 CrossRef PubMed
.
- K. K. Bejagam, G. Fiorin, M. L. Klein and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 5218–5228 CrossRef PubMed
.
- D. B. Korlepara, K. K. Bejagam and S. Balasubramanian, J. Phys. Chem. B, 2017, 121, 11492–11503 CrossRef PubMed
.
- T. Metzroth, A. Hoffmann, R. Martín-Rapún, M. M. Smulders, K. Pieterse, A. R. Palmans, J. A. Vekemans, E. W. Meijer, H. W. Spiess and J. Gauss, Chem. Sci., 2011, 2, 69–76 RSC
.
- H. Anetai, Y. Wada, T. Takeda, N. Hoshino, S. Yamamoto, M. Mitsuishi, T. Takenobu and T. Akutagawa, J. Phys. Chem. Lett., 2015, 6, 1813–1818 CrossRef PubMed
.
- M. M. Smulders, A. P. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2008, 130, 606–611 CrossRef PubMed
.
- A. Ajayaghosh, C. Vijayakumar, R. Varghese and S. J. George, Angew. Chem., 2006, 118, 470–474 CrossRef
.
- D. Bochicchio and G. M. Pavan, Adv. Phys.: X, 2018, 3, 1436408 Search PubMed
.
- K. K. Bejagam and S. Balasubramanian, J. Phys. Chem. B, 2015, 119, 5738–5746 CrossRef PubMed
.
- J. Roosma, T. Mes, P. Leclère, A. R. Palmans and E. Meijer, J. Am. Chem. Soc., 2008, 130, 1120–1121 CrossRef PubMed
.
- C. Kulkarni, S. K. Reddy, S. J. George and S. Balasubramanian, Chem. Phys. Lett., 2011, 515, 226–230 CrossRef
.
- T. F. De Greef, M. M. Smulders, M. Wolffs, A. P. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687–5754 CrossRef PubMed
.
- A. R. Palmans and E. W. Meijer, Angew. Chem., Int. Ed., 2007, 46, 8948–8968 CrossRef PubMed
.
- I. Urbanaviciute, X. Meng, T. D. Cornelissen, A. V. Gorbunov, S. Bhattacharjee, R. P. Sijbesma and M. Kemerink, Adv. Electron. Mater., 2017, 3, 1600530 CrossRef
.
- M. A. Veld, D. Haveman, A. R. Palmans and E. W. Meijer, Soft Matter, 2011, 7, 524–531 RSC
.
- X. Caumes, A. Baldi, G. Gontard, P. Brocorens, R. Lazzaroni, N. Vanthuyne, C. Troufflard, M. Raynal and L. Bouteiller, Chem. Commun., 2016, 52, 13369–13372 RSC
.
- A. Gorbunov, T. Putzeys, I. Urbanavičiūtė, R. Janssen, M. Wübbenhorst, R. Sijbesma and M. Kemerink, Phys. Chem. Chem. Phys., 2016, 18, 23663–23672 RSC
.
- A. Gorbunov, X. Meng, I. Urbanaviciute, T. Putzeys, M. Wübbenhorst, R. Sijbesma and M. Kemerink, Phys. Chem. Chem. Phys., 2017, 19, 3192–3200 RSC
.
- J. van Gestel, P. van der Schoot and M. Michels, Macromolecules, 2003, 36, 6668–6673 CrossRef
.
- A. Šarić, A. K. Buell, G. Meisl, T. C. Michaels, C. M. Dobson, S. Linse, T. P. Knowles and D. Frenkel, Nat. Phys., 2016, 12, 874 Search PubMed
.
- T. M. Hermans, Nat. Nanotechnol., 2016, 11, 920 CrossRef PubMed
.
- C. Kulkarni, G. Periyasamy, S. Balasubramanian and S. J. George, Phys. Chem. Chem. Phys., 2014, 16, 14661–14664 RSC
.
- M. J. Mayoral, C. Rest, V. Stepanenko, J. Schellheimer, R. Q. Albuquerque and G. Fernández, J. Am. Chem. Soc., 2013, 135, 2148–2151 CrossRef PubMed
.
- A. Desmarchelier, M. Raynal, P. Brocorens, N. Vanthuyne and L. Bouteiller, Chem. Commun., 2015, 51, 7397–7400 RSC
.
- K. K. Bejagam, R. C. Remsing, M. L. Klein and S. Balasubramanian, Phys. Chem. Chem. Phys., 2017, 19, 258–266 RSC
.
- Y. Liu, Y. Jia, E. Zhu, L. Liu, Y. Qiao, G. Che and B. Yin, New J. Chem., 2017, 41, 11060–11068 RSC
.
- D. Weiss, D. Skrybeck, H. Misslitz, D. Nardini, A. Kern, K. Kreger and H.-W. Schmidt, ACS Appl. Mater. Interfaces, 2016, 8, 14885–14892 CrossRef PubMed
.
- Y. Sun and Z. Li, Polym. Chem., 2017, 8, 4422–4427 RSC
.
- C. F. Fitié, W. C. Roelofs, M. Kemerink and R. P. Sijbesma, J. Am. Chem. Soc., 2010, 132, 6892–6893 CrossRef PubMed
.
- C. F. Fitié, W. C. Roelofs, P. C. Magusin, M. Wübbenhorst, M. Kemerink and R. P. Sijbesma, J. Phys. Chem. B, 2012, 116, 3928–3937 CrossRef PubMed
.
- K. K. Bejagam, C. Kulkarni, S. J. George and S. Balasubramanian, Chem. Commun., 2015, 51, 16049–16052 RSC
.
- C. Kulkarni, K. K. Bejagam, S. P. Senanayak, K. Narayan, S. Balasubramanian and S. J. George, J. Am. Chem. Soc., 2015, 137, 3924–3932 CrossRef PubMed
.
- U. H. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150 CrossRef
.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef
.
- R. C. Bernardi, M. C. Melo and K. Schulten, Biochim. Biophys. Acta, 2015, 1850, 872–877 CrossRef PubMed
.
- C. Abrams and G. Bussi, Entropy, 2013, 16, 163–199 CrossRef
.
- P. Liu, B. Kim, R. A. Friesner and B. Berne, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13749–13754 CrossRef PubMed
.
- X. Huang, M. Hagen, B. Kim, R. A. Friesner, R. Zhou and B. J. Berne, J. Phys. Chem. B, 2007, 111, 5405–5410 CrossRef PubMed
.
- L. Wang, R. A. Friesner and B. Berne, J. Phys. Chem. B, 2011, 115, 9431–9438 CrossRef PubMed
.
- H. H. Arefi and T. Yamamoto, J. Chem. Phys., 2017, 147, 211102 CrossRef PubMed
.
- J. Boekhoven and S. I. Stupp, Adv. Mater., 2014, 26, 1642–1659 CrossRef PubMed
.
- L. Albertazzi, D. van der Zwaag, C. M. Leenders, R. Fitzner, R. W. van der Hofstad and E. W. Meijer, Science, 2014, 344, 491–495 CrossRef PubMed
.
- L. Albertazzi, F. J. Martinez-Veracoechea, C. M. Leenders, I. K. Voets, D. Frenkel and E. W. Meijer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12203–12208 CrossRef PubMed
.
- M. B. Baker, L. Albertazzi, I. K. Voets, C. M. Leenders, A. R. Palmans, G. M. Pavan and E. W. Meijer, Nat. Commun., 2015, 6, 6234 CrossRef PubMed
.
- M. Garzoni, M. B. Baker, C. M. Leenders, I. K. Voets, L. Albertazzi, A. R. Palmans, E. W. Meijer and G. M. Pavan, J. Am. Chem. Soc., 2016, 138, 13985–13995 CrossRef PubMed
.
- A. Mishra, D. B. Korlepara, M. Kumar, A. Jain, N. Jonnalagadda, K. K. Bejagam, S. Balasubramanian and S. J. George, Nat. Commun., 2018, 9, 1295 CrossRef PubMed
.
- C.-S. Chen, X.-D. Xu, S.-Y. Li, R.-X. Zhuo and X.-Z. Zhang, Nanoscale, 2013, 5, 6270–6274 RSC
.
- J. W. Fredy, A. Méndez-Ardoy, S. Kwangmettatam, D. Bochicchio, B. Matt, M. C. Stuart, J. Huskens, N. Katsonis, G. M. Pavan and T. Kudernac, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11850–11855 CrossRef PubMed
.
- D. Bochicchio and G. M. Pavan, ACS Nano, 2017, 11, 1000–1011 CrossRef PubMed
.
- D. Bochicchio, M. Salvalaglio and G. M. Pavan, Nat. Commun., 2017, 8, 147 CrossRef PubMed
.
- N. M. Casellas, S. Pujals, D. Bochicchio, G. M. Pavan, T. Torres, L. Albertazzi and M. García-Iglesias, Chem. Commun., 2018, 54, 4112–4115 RSC
.
- D. Bochicchio and G. M. Pavan, J. Phys. Chem. Lett., 2017, 8, 3813–3819 CrossRef PubMed
.
- Y. Zhou, M. Huang, T. Lu and H. Guo, Macromolecules, 2018, 51, 3135–3148 CrossRef
.
- G. Kacar, Phys. Chem. Chem. Phys., 2018, 20, 12303–12311 RSC
.
| This journal is © The Royal Society of Chemistry 2018 |
