Effects of polymer–nanoparticle interactions on the viscosity of unentangled polymers under extreme nanoconfinement during capillary rise infiltration†
Jyo Lyn
Hor
 a,
Haonan
Wang
b,
Zahra
Fakhraai
a,
Haonan
Wang
b,
Zahra
Fakhraai
 *b and
Daeyeon
Lee
*b and
Daeyeon
Lee
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA. E-mail: daeyeon@seas.upenn.edu
bDepartment of Chemistry, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA. E-mail: fakhraai@sas.upenn.edu
First published on 29th January 2018
Abstract
We explore the effect of confinement and polymer–nanoparticle interactions on the viscosity of unentangled polymers undergoing capillary rise infiltration (CaRI) in dense packings of nanoparticles. In CaRI, a polymer is thermally induced to wick into the dense packings of nanoparticles, leading to the formation of polymer-infiltrated nanoparticle films, a new class of thin film nanocomposites with extremely high concentrations of nanoparticles. To understand the effect of this extreme nanoconfinement, as well as polymer–nanoparticle interactions on the polymer viscosity in CaRI films, we use two polymers that are known to have very different interactions with SiO2 nanoparticles. Using in situ spectroscopic ellipsometry, we monitor the polymer infiltration process, from which we infer the polymer viscosity based on the Lucas–Washburn model. Our results suggest that physical confinement increases the viscosity by approximately two orders of magnitude. Furthermore, confinement also increases the glass transition temperature of both polymers. Thus, under extreme nanoconfinement, the physical confinement has a more significant impact than the polymer–nanoparticle interactions on the viscosity of unentangled polymers, measured through infiltration dynamics, as well as the glass transition temperature. These findings will provide fundamental frameworks for designing processes to enable the fabrication of CaRI nanocomposite films with a wide range of nanoparticles and polymers.
Introduction
Incorporating extremely high concentrations (>50 vol%) of nanoparticles (NPs) into nanocomposite films (NCFs) can drastically enhance their properties and functionalities. For example, protective coatings with ultrahigh strength and toughness can be fabricated by emulating the structure of nacre, a natural NCF with an extremely high loading (>90 vol%) of stiff nanoplatelets.1,2 Perovskite solar cells incorporated with a polymer scaffold supporting high concentrations of perovskite crystals show a high energy conversion efficiency, excellent resistance to humidity and self-healing functionalities.3 Separation membranes based on high concentrations of nanoparticles show enhanced permeability and selectivity, overcoming the traditional trade-off between the two separation properties.4 In addition, thermal energy storage device exhibits increasing thermal conductivity with nanoparticle loading.5 Despite the useful properties and functionalities that can be derived from high concentrations of NPs in NCFs, methods to produce such NCFs require multiple steps and thus tend to be energy-intensive and time-consuming. Solution- or melt-based processes, for example, are challenging to implement for mixtures with high concentrations of NPs because of high viscosity and elasticity, as well as the NPs’ tendency to aggregate during processing.6,7A new class of NCFs that circumvent many of the challenges associated with fabricating highly filled NCFs is polymer-infiltrated nanoparticle films (PINFs). By infiltrating polymers into densely packed NP films, it is possible to create NCFs with extremely high concentrations of NPs.8–11 In previous work, we developed a thermally-induced, capillarity-based approach – capillary rise infiltration (CaRI), to achieve PINFs with >50 vol% NP loading.8,9 This technique involves first generating a bilayer film of NPs and a polymer, followed by thermally annealing the bilayer above the glass transition temperature (Tg) of the polymer to induce polymer wicking into the voids of the dense NP packing via capillarity. PINFs prepared via CaRI have very high modulus and hardness as well as scratch and wear resistance owing to their high filler fractions.8 We have demonstrated that the CaRI process is robust across systems with different polymer–NP interactions as well as polymer molecular weights and morphologies.8,9
In addition to being a powerful and potentially scalable method of producing PINFs, CaRI provides a unique platform to study the viscosity and glass transition of polymers under extreme nanoconfinement. Despite general acceptance that physical confinement leads to a significant deviation of the polymer behavior from its bulk,12,13 a wide range of confinement-induced changes have been reported in the literature, depending on the extent and geometry of confinement, and the polymer–nanoparticle interactions. For instance, some reports have shown that non-attractive nanoparticles significantly slow down the diffusion of polymers in polymer nanocomposites.14–17 In contrast, other studies based on molecular dynamics simulations have reported enhanced chain motion under repulsive polymer–nanoparticle interactions.18 One of the key challenges in deciphering the effect of confinement is that effects of confinement and interfacial effects are often convoluted and thus are difficult to decouple, especially in thin film geometries where free surface effects may play a significant role in glass transition, such that it may mask substrate effects.19–24
In the CaRI system, the characteristic pore size of random close packings of spheres is approximately 20–30% of the NP size.25 It is thus straightforward to confine polymers in extremely small pores (<10 nm) by using disordered packings of NPs. Polymer chains infiltrating the dense NP packings are very close to the NP surface and could be in contact with multiple nanoparticles, with a negligible effect of the free polymer surface.26–28 By analyzing the wicking process of a polymer into a NP packing based on the Lucas–Washburn model, we recently estimated several orders of magnitude increase in the melt viscosity of the unentangled polymer.8 This increased viscosity relative to the bulk value suggests that confinement significantly affects the polymer infiltration dynamics in the tight pore network of the NP packing. Therefore, the CaRI of the polymer into NP packing enables us to systematically explore the effect of polymer–NP interactions under extreme nanoconfinement by varying the type of polymer used in CaRI.16,17
In this work, we study the effect of polymer–NP interactions on the viscosity of unentangled polymers in CaRI. We focus our analyses on unentangled polymer chains to exclude the potential contribution of polymer chain (dis)entanglement, which has been attributed to the enhanced mobility of confined polymer chains of high molecular weights.29,30 We monitor the infiltration process of unentangled poly(styrene) (PS) and poly(2-vinylpyridine) (P2VP) into densely packed silica NP packings. The P2VP-SiO2 NP and PS-SiO2 NP pairs represent strongly and weakly interacting systems, respectively; the nitrogen atom in P2VP interacts strongly with the hydroxyl groups on the SiO2 NP surface via hydrogen bonding,31,32 whereas PS interacts with the SiO2 NP via van der Waals forces. We choose two unentangled polymer molecular weights for each polymer to vary the extent of confinement. This approach enables us to decouple the confinement and interaction effects on the polymer CaRI dynamics. We show that during CaRI, the polymers exhibit higher-than-bulk viscosity, regardless of polymer–NP interactions. We also show that the glass transition temperature (Tg) of these polymers increases significantly in the NP packings, again regardless of polymer–NP interactions. We find that in both systems, the increase in the viscosity is strongly correlated with the increased Tg, and the ratio of viscosity to bulk viscosity does not show a strong dependence on the temperature. These observations suggest that confinement has a more significant impact on the CaRI dynamics than on the extent of polymer–NP interactions.
Experimental
Materials
Poly(styrene) (PS) (PS-8k, Mn = 8000 g mol−1, PDI = 1.10; PS-21k, Mn = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, PDI = 1.04) and poly(2-vinylpyridine) (P2VP) (P2VP-8k, Mn = 7800 g mol−1, PDI = 1.08; P2VP-22k, Mn = 22
000 g mol−1, PDI = 1.04) and poly(2-vinylpyridine) (P2VP) (P2VP-8k, Mn = 7800 g mol−1, PDI = 1.08; P2VP-22k, Mn = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, PDI = 1.06) were purchased from Polymer Source Inc. The silica NP suspension (Ludox TM-50, 25.0 ± 3.5 nm in diameter) was purchased from Sigma Aldrich.
000 g mol−1, PDI = 1.06) were purchased from Polymer Source Inc. The silica NP suspension (Ludox TM-50, 25.0 ± 3.5 nm in diameter) was purchased from Sigma Aldrich.
Preparation and characterization of bilayers
Silicon wafers are cut into approximately 1 cm × 1 cm squares. The wafers are rinsed with acetone, isopropanol, and water, and then dried with nitrogen. The wafers are then further cleaned by oxygen plasma treatment for approximately 5 minutes. 5 wt% PS-8k and 6 wt% PS-21k solutions are prepared by dissolving PS in toluene. 8 wt% P2VP-8k and 8 wt% P2VP-22k are prepared by dissolving P2VP in 1-butanol. SiO2 NP suspension is prepared by diluting the as-purchased suspension in DI water to 10 wt%, and the pH of the suspension is adjusted to ∼11 using 1 M potassium hydroxide (KOH) solution. All solutions are bath-sonicated for at least an hour and filtered prior to use. To generate the bilayer films, the polymer layer is first spin-coated onto the silicon substrate using a WS-400BZ-6NPP/Lite spin-coater from Laurell Technologies Corporation. The polymer film is annealed at 393 K under vacuum conditions for 12 h to remove the residual solvent. Then, the polymer film is oxygen plasma-treated for ∼2 s to render the film surface hydrophilic, on which the SiO2 NP layer is spin-coated. This short plasma treatment facilitates the deposition of uniform nanoparticle layers atop polymer films. Our control experiments show that it is possible to create bilayers without plasma treatment by using isopropanol suspensions of silica nanoparticles and that there is little difference in the properties of CaRI composite films made using the two methods. Details will be reported elsewhere. The thickness of the polymer and NP layer is ∼200 nm to ensure that there is a sufficient amount of polymer to fill the interstices of the NP packing, which has an average porosity of ∼0.35. To generate a polymer film of ∼200 nm, 5 wt% PS-8k and 6 wt% PS-21k solutions are spin-coated at 2000 rpm and 5000 rpm, respectively, whereas 8 wt% P2VP-8k and 8 wt% P2VP-22k are spin-coated at 4000 rpm and 5000 rpm, respectively. The 10 wt% SiO2 NP suspension is spin-coated at 3000 rpm. The bilayer samples are subjected to vacuum for 12 h to remove residual solvents. The vacuum treatment, however, does not significantly change the CaRI behaviour likely indicating that the influence of residual solvent on polymer infiltration dynamics is negligible. Scanning electron microscopy (SEM) images of the bilayer films before and after the polymer infiltration process are taken using a JEOL 7500F HRSEM. Each sample is sputtered with a thin gold/palladium layer using a Cressington Sputter Coater 107 prior to imaging to prevent charging. The samples are imaged at an accelerating voltage of 5 kV, an emission current of 20 μA, and at a working distance of approximately 8 mm.Characterization of the polymer infiltration process
The polymer infiltration process into the voids of the NP packing is monitored in situ using a J.A. Woollam Alpha-SE spectroscopic ellipsometer while the bilayer film sample is annealed above the glass transition temperature (Tg) of the polymer using a Linkam THMS350V heating stage, under constant pressure (ambient conditions). The heating stage has a temperature resolution of ∼1 K. The stage on which the sample is placed is 22 mm in diameter and is open to ambient air. The Linksys software displays the stage temperature and allows the user to input the desired set-point temperature, heating rate, and hold time for the set-point temperature. The ellipsometry data are collected between λ = 380 nm and 900 nm at an incident angle of 70°, and is analyzed using the CompleteEASE software package provided by J.A. Woollam. The psi (Ψ) and delta (Δ) data are fitted using a three-layer (nanoparticle/composite/polymer) Cauchy model on a Si substrate with a native oxide layer.8,9 The Cauchy model is expressed as: n(λ) = A + B/λ2 + C/λ4; k(λ) = 0, where A, B and C are optical constants, λ is the wavelength, n and k are the real and imaginary components of the index of refraction. The model fitting interprets the raw data into physical parameters describing each layer in the sample, namely the thickness and the refractive index.33Glass transition temperature measurements
The glass transition temperatures (Tg) of bulk polymer samples are determined using the TA Instruments Q2000 differential scanning calorimetry (DSC). PS samples are measured in a hermetically sealed pan, whereas P2VP samples are measured in a non-hermetically sealed pan. Each polymer sample (∼6 mg) is initially cooled to 293 K, before subjecting it to two heating and cooling cycles in the range of 293–423 K at 10 K min−1. Tg is defined as the midpoint of the step transition of the heat flow/capacity and expressed as the average from the two cooling cycle measurements. The Tg values measured using DSC are in good agreement with those reported previously.34,35 The Tg values of the confined polymers in the CaRI nanocomposite films are measured using a J.A. Woollam M-2000V spectroscopic ellipsometer. The PINF is mounted onto a Linkam THMS 600 temperature-controlled stage attached to the ellipsometer. The in situ ellipsometry sampling rate is 1 s with high accuracy zone-averaging. Three heating and cooling cycles between 303 K and 423 K under dry nitrogen flow are performed for each sample, with a heating rate of 30 K min−1 and a cooling rate of 10 K min−1, respectively. The Tg data are reported upon cooling. The thickness and refractive index of the sample are determined by fitting the cooling ramp raw data to the Cauchy model, as described earlier. Tg of the residual polymer layer and confined polymer for each film is determined via the intersection of the linear fits to the supercooled and glassy regimes in the plots of nanocomposite and polymer layer refractive indices versus temperature (see ESI,† Fig. S6). The thickness of the composite layer is held constant for the dynamic data fits.Results and discussion
Polymer infiltration dynamics
To study polymer capillary rise infiltration (CaRI) under confinement, we generate a bilayer composed of a dense disordered packing of 25 nm SiO2 nanoparticles (NPs) atop a polymer layer. We use poly(styrene) (PS) and poly(2-vinylpyridine) (P2VP) as the weakly and strongly interacting polymers. P2VP is known to interact with SiO2 NP via hydrogen bonding interactions, whereas PS interacts with SiO2 NPs primarily through van der Waals interactions. We also use PS and P2VP with two different molecular weights: ∼8000 (8k) and ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (21k) g mol−1. The radii of gyrations of 8k and 21k PS and P2VP, calculated based on the Kuhn segment length of each polymer,36 are approximately ∼2.5 nm and ∼4 nm, respectively, which are comparable to or slightly larger than the characteristic pore radius of the SiO2 NP packing (∼3.5 nm). The bilayer film is annealed above the glass transition temperature (Tg) of the polymer to induce the infiltration of the polymer into the interstices of the NP packing. The changes that take place in the film during the CaRI process are schematically illustrated in Fig. 1.
000 (21k) g mol−1. The radii of gyrations of 8k and 21k PS and P2VP, calculated based on the Kuhn segment length of each polymer,36 are approximately ∼2.5 nm and ∼4 nm, respectively, which are comparable to or slightly larger than the characteristic pore radius of the SiO2 NP packing (∼3.5 nm). The bilayer film is annealed above the glass transition temperature (Tg) of the polymer to induce the infiltration of the polymer into the interstices of the NP packing. The changes that take place in the film during the CaRI process are schematically illustrated in Fig. 1.
We perform in situ spectroscopic ellipsometry to monitor polymer infiltration into the disordered SiO2 NP packing. The infiltration of polymers in CaRI has been shown to follow the Lucas–Washburn model, which has been successfully used in prior experimental and computational studies to describe polymer wicking under confinement:8,29,37–41
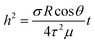 | (1) |
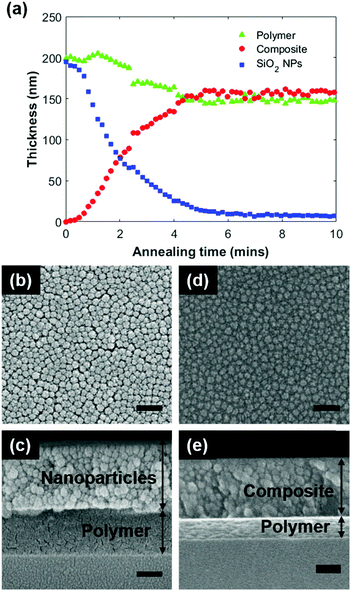
Fig. 2(a) shows the thickness profile changes of the neat SiO2 NP layer, the composite layer, and the polymer layer with annealing time for the PS8k/SiO2 NP film at 403 K. During CaRI, the polymer wicking into the SiO2 NP causes a decrease in both the NP and polymer layer thicknesses, while the thickness of the composite layer – the portion of SiO2 NP layer which has been filled with polymer –increases. This is also evident in Fig. 2(b–e) which shows the polymer filling of the interstices of the SiO2 NP packing and the decrease in polymer layer thickness after CaRI. The presence of the polymer in the interstices of the NP packing following CaRI is also evident from the atomic force microscopy (AFM) topography and phase images (see ESI,† Fig. S7). The interparticle distance between nanoparticles before (25.7 ± 2.9 nm) and after (26.1 ± 2.7 nm) CaRI, estimated from Fig. 2(b and d), shows a negligible change, strongly indicating that the packing density of the nanoparticle layer does not change upon CaRI. Albeit having different infiltration rates, we observe that all polymers follow a similar infiltration behaviour (see the ESI,† Fig. S2 and S3). At early times, the formation of the meniscus before the capillary rise and higher initial resistance causes the movement of the polymer melt to be in an unsteady state.42 Gradually, the infiltration stabilizes and approaches a steady state, where the slope of the composite growth remains uniform over the course of infiltration. We consider the steady state infiltration process in our analyses to infer the viscosity of the polymer melt based on eqn (1).
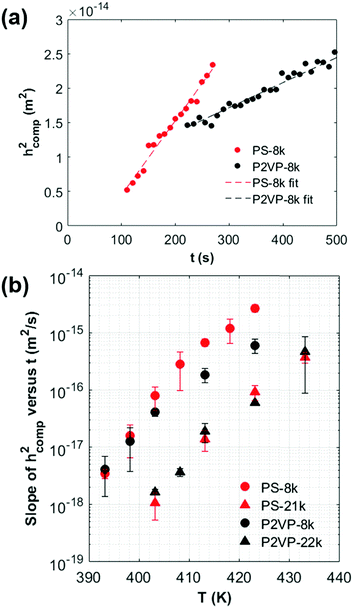
From the thickness profiles, we plot the composite layer thickness squared (hcomp2) as a function of time (t) to confirm the Lucas–Washburn model. Fig. 3(a) shows the linear dependencies of hcomp2versus t for the PS-8k and P2VP-8k systems, consistent with the Lucas–Washburn model. We anneal each polymer–NP system in a range of temperature. For each run, we verify the validity of the Lucas–Washburn model as in Fig. 3(a), then extract the slope from each hcomp2versus t plot, which represents the prefactor in the Lucas–Washburn model σR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/4τ2μ. For each polymer system, the value of the slope, as shown in Fig. 3(b), increases with temperature, indicating a more rapid infiltration process. This observation is consistent with the decreasing polymer melt viscosity as the temperature is increased.
θ/4τ2μ. For each polymer system, the value of the slope, as shown in Fig. 3(b), increases with temperature, indicating a more rapid infiltration process. This observation is consistent with the decreasing polymer melt viscosity as the temperature is increased.
Based on each slope, we infer the viscosity μ of the confined polymer by estimating the remaining parameters in the Lucas–Washburn prefactor, σR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/4τ2μ, from literature values.42–44Table 1 summarizes the parameters that are used to determine the viscosity μ. The pore radius R and tortuosity τ values are intrinsic to the SiO2 NP packing and are estimated based on the size of the NP and the porosity of the packing.25,45 The surface tension of PS and P2VP are estimated based on the molecular weight and the temperature of the melt.46,47 There are varying reports of PS contact angles on silicon oxide surfaces ranging from 7°–23°;29,48 we choose θ = 20° for this purpose, but the temperature-dependence of viscosity is independent of this choice. P2VP is reported to form a strongly bound layer on the SiO2 NP surface due to favourable hydrogen bonding,31,49–51 thus we estimate θ ∼ 0° in the case of P2VP. We perform a sensitivity analysis by testing a range of contact angle values θ and considering other empirical relations in calculating the polymer surface tension, σ(T) (see the ESI,† Fig. S4). This analysis confirms that the magnitude of the estimated viscosity of the confined polymer is robust across a range of estimated θ and σ(T) parameters. To assess the effect of confinement and polymer–NP interactions, we compare the measured confined polymer viscosity with bulk values which are obtained from literature values.52,53
θ/4τ2μ, from literature values.42–44Table 1 summarizes the parameters that are used to determine the viscosity μ. The pore radius R and tortuosity τ values are intrinsic to the SiO2 NP packing and are estimated based on the size of the NP and the porosity of the packing.25,45 The surface tension of PS and P2VP are estimated based on the molecular weight and the temperature of the melt.46,47 There are varying reports of PS contact angles on silicon oxide surfaces ranging from 7°–23°;29,48 we choose θ = 20° for this purpose, but the temperature-dependence of viscosity is independent of this choice. P2VP is reported to form a strongly bound layer on the SiO2 NP surface due to favourable hydrogen bonding,31,49–51 thus we estimate θ ∼ 0° in the case of P2VP. We perform a sensitivity analysis by testing a range of contact angle values θ and considering other empirical relations in calculating the polymer surface tension, σ(T) (see the ESI,† Fig. S4). This analysis confirms that the magnitude of the estimated viscosity of the confined polymer is robust across a range of estimated θ and σ(T) parameters. To assess the effect of confinement and polymer–NP interactions, we compare the measured confined polymer viscosity with bulk values which are obtained from literature values.52,53
| Polymer/nanoparticle | Average pore radius, R (nm) | Tortuosity, τ | Surface tension as function of temperature, σ(T [°C]) (mN m−1) | Polymer contact angle on SiO2 NP, θ |
|---|---|---|---|---|
| PS-8k/SiO2 NP | 3.5 | 1.95 | 40.5–0.068T | 20° |
| PS-21k/SiO2 NP | 3.5 | 1.95 | 42.1–0.068T | 20° |
| P2VP-8k/SiO2 NP | 3.5 | 1.95 | 46.7–0.063T | 0° |
| P2VP-22k/SiO2 NP | 3.5 | 1.95 | 46.7–0.063T | 0° |
Role of confinement and polymer–NP interactions
To assess the role of confinement and polymer–NP interactions, we compare the confined and bulk polymer viscosity as a function of temperature, as shown in Fig. 4. For both polymers, we note a significant increase in the viscosity of the confined polymer relative to the bulk values reported in the literature,52,53 regardless of the polymer–NP interaction strength. The two graphs show remarkable similarities in the absolute values of viscosities for the confined PS and P2VP, and the extents of viscosity increases are also very similar.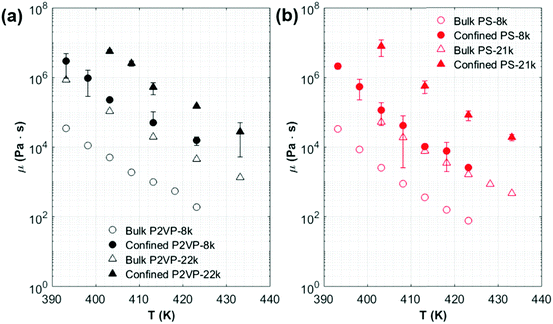 | ||
| Fig. 4 Bulk and confined polymer viscosity of (a) P2VP-8k and P2VP-22k, and (b) PS-8k and PS-21k as a function of temperature. Each data point for the confined polymer viscosities is an average of at least 2 runs, and the error bar represents 1 standard deviation. The bulk viscosity values are obtained from the literature (see the ESI†). | ||
The relative increase in the viscosity due to confinement (μconfined/μbulk) also does not strongly depend on temperature, as shown in Fig. 5. This is the opposite of what one would expect if the polymer–NP interactions significantly slowed the chain motion. In particular, the strength of hydrogen bonding is known to be strongly temperature dependent;54 thus one may have expected a strong temperature dependence of the normalized viscosity in the case of P2VP, which we do not observe. Furthermore, for a given polymer, there is no significant difference in μconfined/μbulk for the two molecular weights (Fig. 5). These observations imply that the increase in viscosity is not strongly influenced by the polymer–NP interactions.
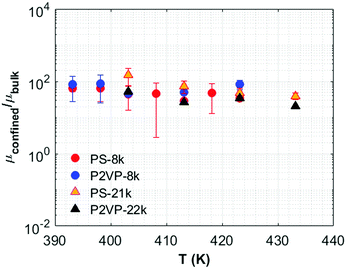 | ||
| Fig. 5 The confined polymer viscosity normalized by the bulk viscosity (μconfined/μbulk) for all polymer systems, as a function of temperature. | ||
The significant increase in the polymer viscosity is reminiscent of an abrupt increase reported for the viscosity of simple liquids such as siloxane confined in a very narrow slit, although the phenomenon was attributed to a liquid-to-solid-like (i.e., first-order-like) transition in packing of the molecule.55 More relevant to our observation is the slowdown of chain diffusion observed in polymer nanocomposites, which was attributed to entropic barriers that are associated with chains passing through small constrictions between NPs. These studies showed that stronger interactions between NPs and polymers do not necessarily lead to more significant reduction in diffusivity,17,54 consistent with our observations. Other measures of polymer dynamics have also described slowing down of chain relaxation14,56 and diffusion16,57 near strongly and weakly interacting solid surfaces. Another mechanism that could lead to the observed slowdown is the tortuous path and the high curvature in the NP packings which can increase the interchain packing proximity.58 Such a change could in turn significantly strengthen polymer–NP interactions even in the case of the weak polymer–NP interacting system and lead to increased viscosity.
Interestingly, reports on the viscosity of polymers in thin films provide some conflicting trends. The viscosity of polymers in thin films decrease for a weakly interacting polymer-substrate system, which has been attributed to the enhanced free surface dynamics.58 The polymer viscosity in thin films has been reported to increase for a strongly interacting polymer-substrate system above a threshold temperature.59 Increases in the viscosity of unentangled polymers during CaRI in dense nanoparticle packings (Fig. 4 and 5) are in stark contrast to the enhanced mobility observed in the capillary rise of highly entangled polymers in cylindrical pores of anodized aluminium oxide (AAO) membranes.29 We attribute this discrepancy to the difference in confinement geometry and disentanglement effects. When infiltrating a dense nanoparticle packing, polymer chains transport through tortuous pathways with variable pore sizes (narrow necks and wide gaps), instead of straight, uniform, cylindrical nanochannels in AAO membranes. The narrow regions may act as entropic barriers, where polymer chains have to sample multiple conformations to squeeze through the narrow pores for infiltration to occur. The enhanced mobility of high molecular weight polymers under confinement was attributed to a disentanglement effect,29,30 whereby increased confinement leads to decreased entanglement density. In our case, we do not expect such a phenomenon to play a role as both molecular weights studied here are below the entanglement limit.
Monitoring the infiltration dynamics in CaRI provides insights into the effects of confinement on translational (i.e., centre-of-mass) mobility of the polymers, whereas the determination of glass transition temperature of the polymers provides indirect information regarding their segmental relaxation under extreme confinement, as Tg is typically attributed to the arresting of segmental modes of motion in bulk polymers.60–62 We determine the Tg values of the fully annealed films, consisting of a composite layer atop a residual polymer layer, via spectroscopic ellipsometry, which is a well-established method for the accurate determination of Tg values of polymers under confined geometries.22,23,63–66 We use a 2-layer composite/polymer model to fit the spectroscopic ellipsometry data (see the ESI,† Fig. S6). We also measure the Tg values of the bulk polymer samples independently via differential scanning calorimetry (DSC) to validate our spectroscopic ellipsometry Tg measurements (see the ESI,† Table T1).
Fig. 6 shows the confined and bulk Tg values for each polymer–NP system. In all systems, we observe increased Tg in the confined systems relative to the bulk, which is highly correlated with the increased viscosity we observe, even in the case of the weakly interacting system (PS-SiO2). Previous studies have shown that while strong interfacial interactions between SiO2 and P2VP do not necessarily lead to increased Tg in nanocomposites, confinement has shown to increase Tg.22,67 Although most studies involving PS films on SiO2 show decrease in Tg due to the free surface effect,63,65 one study has shown that the Tg value of PS confined in AAO membranes with 55 nm pores, in the absence of free surface, increases, consistent with our results.58
Surprisingly, in our current study, the increase in Tg for the two polymers of similar molecular weights are approximately the same. Also, a similar increase in ΔTg values is observed for the two polymers when the molecular weight of the polymers is increased. These observations point to the fact that physical confinement has a stronger impact on the glass transition of polymers than polymer–NP interactions under these extreme nanoconfinement conditions. This is in contrast to measurements in thin films where free surface (polymer–air interface) effects always dominate, resulting in a decrease in average Tg for PS as opposed to increased Tg in P2VP.22,23 Overall, observed increases in Tg values are consistent with the increased viscosity for PS and P2VP, suggesting that the increased viscosity in CaRI under extreme nanoconfinement is likely correlated with the impact of confinement on segmental motion of the chains as deduced from their Tg values.
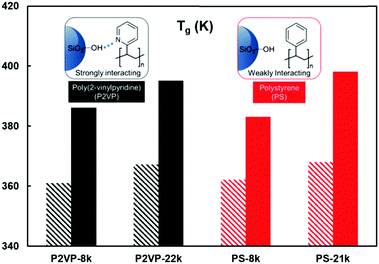 | ||
| Fig. 6 The glass transition temperature Tg of P2VP (black) and PS (red) in the bulk (striped bar) and the confined state (filled bar). | ||
Conclusions
In this work, we perform capillary rise infiltration (CaRI) of unentangled polymers into a disordered, dense nanoparticle packing of SiO2 to study the viscosity and glass transition of the polymers with different polymer–nanoparticle interactions under extreme nanoconfinement, where the polymer chain size is comparable or smaller than the average pore size. Using the Lucas–Washburn model, we measure the viscosity of the polymer during infiltration in disordered nanoparticle packings, and observe increased viscosity of unentangled polymers under such extreme nanoconfinement conditions relative to their respective bulk values, significantly different from the results obtained based on highly entangled polymers undergoing capillary rise in well-defined cylindrical pores. Surprisingly and somewhat unexpectedly, the extent of the viscosity increase is not strongly dependent upon the polymer–NP interactions. We also observe a comparable increase in Tg for both the strongly and the weakly interacting polymer–NP systems, which is different from prior studies on Tg changes observed in supported polymer thin films.Overall, our results demonstrate that confinement, rather than polymer–NP interactions, has a more significant impact on the viscosity and glass transition of polymers in CaRI systems. The increases in Tg are strongly correlated with the viscosity changes observed for the two polymers, suggesting that extreme nanoconfinement affects the transport phenomena of polymers by influencing the segmental motion. Our results provide fundamental frameworks for the optimization of process parameters such as temperature and annealing time to enable scalable manufacturing of polymer-infiltrated NP films using CaRI.
There are several outstanding questions that warrant future investigation. Our ongoing work, for instance, focuses on the infiltration dynamics of highly entangled polymers to test the validity of the Lucas–Washburn model. The effect of molecular weight and polymer–nanoparticle interactions of polymers on the mechanical properties of CaRI composites is potentially of significant importance as high molecular weight polymers can lead to bridging of multiple NPs and in turn a significant enhancement of the toughness of the composite.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was primarily supported by Penn MRSEC NSF-1720530 and partially by NSF-1449337, NSF DMR-1350044 and NSF-1662695. We thank T. Liu for her assistance with the M-2000V spectroscopic ellipsometer and the TA Instruments Q2000 DSC. We thank J. A. Lefever for his assistance with AFM. We also thank R. A. Riggleman and P. J. Griffin for helpful discussions.Notes and references
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2014, 14, 23–36 CrossRef PubMed
.
- M. A. Meyers, J. McKittrick and P. Y. Chen, Science, 2013, 339, 773–779 CrossRef CAS PubMed
.
- Y. Zhao, J. Wei, H. Li, Y. Yan, W. Zhou, D. Yu and Q. Zhao, Nat. Commun., 2016, 7, 10228 CrossRef CAS PubMed
.
- T. C. Merkel, B. D. Freeman, R. J. Spontak, Z. He, I. Pinnau, P. Meakin and A. J. Hill, Science, 2002, 296, 519–522 CrossRef CAS PubMed
.
- A. Tessema, D. Zhao, J. Moll, S. Xu, R. Yang, C. Li, S. K. Kumar and A. Kidane, Polym. Test., 2017, 57, 101–106 CrossRef CAS
.
- W. Caseri, Macromol. Rapid Commun., 2000, 21, 705–722 CrossRef CAS
.
- Y. Li, P. Tao, A. Viswanath, B. C. Benicewicz and L. S. Schadler, Langmuir, 2013, 29, 1211–1220 CrossRef CAS PubMed
.
- Y.-R. Huang, Y. Jiang, J. L. Hor, R. Gupta, L. Zhang, K. J. Stebe, G. Feng, K. T. Turner and D. Lee, Nanoscale, 2015, 7, 798–805 RSC
.
- J. L. Hor, Y. Jiang, D. J. Ring, R. A. Riggleman, K. T. Turner and D. Lee, ACS Nano, 2017, 11, 3229–3236 CrossRef CAS PubMed
.
- Y. Qiang, N. Manohar, K. J. Stebe and D. Lee, Mol. Syst. Des. Eng. 10.1039/C7ME00099E
.
- N. Manohar, K. J. Stebe and D. Lee, ACS Macro Lett., 2017, 1104–1108 CrossRef CAS
.
- K. I. Winey and R. A. Vaia, MRS Bull., 2007, 32, 314–319 CrossRef CAS
.
- K. Chrissopoulou and S. H. Anastasiadis, Soft Matter, 2015, 11, 3746–3766 RSC
.
- Y. Li, M. Kröger and W. K. Liu, Soft Matter, 2014, 10, 1723–1737 RSC
.
- G. J. Schneider, K. Nusser, S. Neueder, M. Brodeck, L. Willner, B. Farago, O. Holderer, W. J. Briels and D. Richter, Soft Matter, 2013, 9, 4336 RSC
.
- S. Gam, J. S. Meth, S. G. Zane, C. Chi, B. A. Wood, M. E. Seitz, K. I. Winey, N. Clarke and R. J. Composto, Macromolecules, 2011, 44, 3494–3501 CrossRef CAS
.
- C. C. Lin, S. Gam, J. S. Meth, N. Clarke, K. I. Winey and R. J. Composto, Macromolecules, 2013, 46, 4502–4509 CrossRef CAS
.
- T. Desai, P. Keblinski and S. K. Kumar, J. Chem. Phys., 2005, 122, 134910 CrossRef PubMed
.
-
H. Peng, R. Nieuwendaal and C. L. Soles, Polymer Science: A Comprehensive Reference, 10 Volume Set, 2012, pp. 345–376 Search PubMed
.
- A. Saiter, D. Prevosto, E. Passaglia, H. Couderc, L. Delbreilh and J. M. Saiter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 1–7 CrossRef PubMed
.
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Faraday Discuss., 1994, 98, 219–230 RSC
.
- E. C. Glor, G. V. Angrand and Z. Fakhraai, J. Chem. Phys., 2017, 146, 203330 CrossRef PubMed
.
- E. C. Glor and Z. Fakhraai, J. Chem. Phys., 2014, 141, 194505 CrossRef PubMed
.
- K. Paeng, S. F. Swallen and M. D. Ediger, J. Am. Chem. Soc., 2011, 133, 8444–8447 CrossRef CAS PubMed
.
- A. Bertei, B. Nucci and C. Nicolella, Chem. Eng. Trans., 2013, 32, 1531–1536 Search PubMed
.
- C. Franz, F. Lange, Y. Golitsyn, B. Hartmann-Azanza, M. Steinhart, M. Krutyeva and K. Saalwächter, Macromolecules, 2016, 49, 244–256 CrossRef CAS
.
- S. Ok, M. Steinhart, A. Şerbescu, C. Franz, F. Vaca Chávez and K. Saalwächter, Macromolecules, 2010, 43, 4429–4434 CrossRef CAS PubMed
.
- F. Lange, P. Judeinstein, C. Franz, B. Hartmann-Azanza, S. Ok, M. Steinhart and K. Saalwächter, ACS Macro Lett., 2015, 4, 561–565 CrossRef CAS
.
- K. Shin, S. Obukhov, J.-T. Chen, J. Huh, Y. Hwang, S. Mok, P. Dobriyal, P. Thiyagarajan and T. P. Russell, Nat. Mater., 2007, 6, 961–965 CrossRef CAS PubMed
.
- D. M. Sussman, W. Tung, K. I. Winey, K. S. Schweizer and R. A. Riggleman, Macromolecules, 2014, 47, 6462–6472 CrossRef CAS
.
- A. P. Holt, P. J. Griffin, V. Bocharova, A. L. Agapov, A. E. Imel, M. D. Dadmun, J. R. Sangoro and A. P. Sokolov, Macromolecules, 2014, 47, 1837–1843 CrossRef CAS
.
- A. P. Holt, V. Bocharova, S. Cheng, A. M. Kisliuk, B. T. White, T. Saito, D. Uhrig, J. P. Mahalik, R. Kumar, A. E. Imel, T. Etampawala, H. Martin, N. Sikes, B. G. Sumpter, M. D. Dadmun and A. P. Sokolov, ACS Nano, 2016, 10, 6843–6852 CrossRef CAS PubMed
.
- W. Ogieglo, H. Wormeester, M. Wessling and N. E. Benes, ACS Appl. Mater. Interfaces, 2012, 4, 935–943 CAS
.
- L. An, D. He, J. Jing, Z. Wang, D. Yu, B. Jiang, Z. Jiang and R. Ma, Eur. Polym. J., 1997, 33, 1523–1528 CrossRef CAS
.
- P. Papadopoulos, D. Peristeraki, G. Floudas, G. Koutalas and N. Hadjichristidis, Macromolecules, 2004, 37, 8116–8122 CrossRef CAS
.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed
.
- D. I. Dimitrov, a Milchev and K. Binder, Ann. N. Y. Acad. Sci., 2009, 1161, 537–548 CrossRef CAS PubMed
.
- M. Engel and B. Stühn, J. Chem. Phys., 2010, 132, 224502 CrossRef CAS PubMed
.
- A. Shavit and R. A. Riggleman, Soft Matter, 2015, 11, 8285–8295 RSC
.
- P. E. De Jongh and T. M. Eggenhuisen, Adv. Mater., 2013, 25, 6672–6690 CrossRef CAS PubMed
.
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed
.
- K. Y. Suh, P. Kim, H. Eui Jeong and J. Kwan Kim, Nanoscale Microscale Thermophys. Eng., 2006, 10, 263–274 CrossRef CAS
.
- S. Gruener, T. Hofmann, D. Wallacher, A. V. Kityk and P. Huber, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 6–9 CrossRef PubMed
.
- D. Hołownia, I. Kwiatkowska and J. Hupka, Physicochem. Probl. Miner. Process., 2008, 42, 251–262 Search PubMed
.
- S. Rémond, J. L. Gallias and A. Mizrahi, Granular Matter, 2008, 10, 329–334 CrossRef
.
- G. T. Dee and B. B. Sauer, J. Colloid Interface Sci., 1992, 152, 85–103 CrossRef CAS
.
- B. B. Sauer and G. T. Dee, Macromolecules, 2002, 35, 7024–7030 CrossRef CAS
.
- R. Seemann, K. Jacobs and R. Blossey, J. Phys.: Condens. Matter, 2001, 13, 4915–4923 CrossRef CAS
.
- P. J. Griffin, V. Bocharova, L. R. Middleton, R. J. Composto, N. Clarke, K. S. Schweizer and K. I. Winey, ACS Macro Lett., 2016, 5, 1141–1145 CrossRef CAS
.
- J. Moll and S. K. Kumar, Macromolecules, 2012, 45, 1131–1135 CrossRef CAS
.
- G. P. Baeza, C. Dessi, S. Costanzo, D. Zhao, S. Gong, A. Alegria, R. H. Colby, M. Rubinstein, D. Vlassopoulos and S. K. Kumar, Nat. Commun., 2016, 7, 1–6 Search PubMed
.
- P. J. Fox and T. G. Flory, J. Am. Chem. Soc., 1948, 70, 2384–2395 CrossRef
.
- Y. Takahashi, N. Ochiai, Y. Matshushita and I. Noda, Polym. J., 1996, 28, 1065–1070 CrossRef CAS
.
- W. S. Tung, P. J. Griffin, J. S. Meth, N. Clarke, R. J. Composto and K. I. Winey, ACS Macro Lett., 2016, 5, 735–739 CrossRef CAS
.
- J. Klein and E. Kumacheva, Science, 2016, 269, 816 CrossRef PubMed
.
- C. Batistakis, A. V. Lyulin and M. A. J. Michels, Macromolecules, 2012, 45, 7282–7292 CrossRef CAS
.
- J. Choi, N. Clarke, K. I. Winey and R. J. Composto, Macromolecules, 2017, 50, 3038–3042 CrossRef CAS
.
- J. Chen, L. Li, D. Zhou, X. Wang and G. Xue, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 1–8 Search PubMed
.
- R. N. Li, F. Chen, C. H. Lam and O. K. C. Tsui, Macromolecules, 2013, 46, 7889–7893 CrossRef CAS
.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707 CrossRef CAS
.
- E. Donth, J. Non-Cryst. Solids, 1982, 53, 325–330 CrossRef CAS
.
- K. Kunal, C. G. Robertson, S. Pawlus, S. F. Hahn and A. P. Sokolov, Macromolecules, 2008, 41, 7232–7238 CrossRef CAS
.
- J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens and J. R. Dutcher, Phys. Rev. Lett., 1996, 77, 2002–2005 CrossRef CAS PubMed
.
- G. Beaucage, R. Composto and R. S. Stein, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 319–326 CrossRef CAS
.
- J. L. I. Keddie, R. A. L. Jones and R. A. Cory, Europhys. Lett., 1994, 27, 59–64 CrossRef CAS
.
- S. Kim, S. A. Hewlett, C. B. Roth and J. M. Torkelson, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 30, 83–92 CrossRef CAS PubMed
.
- A. Holt, J. Sangoro, Y. Wang, A. L. Agapov and A. P. Sokolov, Macromolecules, 2013, 46, 4168–4173 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Amplitude (Ψ) and phase change (Δ) data and model fit from in situ spectroscopic ellipsometry; thickness changes of NPs, composites, and polymer layers during CaRI; linear dependence of h2versus t for PS-21k/SiO2 NP and P2VP/SiO2 NP annealed at 423 K; sensitivity analysis on the viscosity calculation of the PS-8k/SiO2 NP based on polymer melt surface tension models and contact angle values; determination of bulk polymer viscosity values from the literature; determination of confined and bulk polymer glass transition temperature (Tg) using spectroscopic ellipsometry; atomic force microscopy (AFM) topography and phase images of the PS-8k/SiO2 NP bilayer film surface before and after CaRI; glass transition temperature (Tg) measured using spectroscopic ellipsometry and differential scanning calorimetry. See DOI: 10.1039/c7sm02465g |
| This journal is © The Royal Society of Chemistry 2018 |