Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reduced dimensionality hyphenated NMR experiments for the structure determination of compounds in mixtures†
Justinas
Sakas
 and
Nicholle G. A.
Bell
and
Nicholle G. A.
Bell
 *
*
EaStCHEM School of Chemistry, University of Edinburgh, King’s Buildings, Joseph Black Building, David Brewster Road, Edinburgh EH9 3FJ, UK. E-mail: Nicholle.Bell@ed.ac.uk
First published on 23rd January 2019
Abstract
For the structure determination of molecules in mixtures using NMR spectroscopy, the dispersion of 13C chemical shifts provides much needed separation of resonances in the indirectly detected dimension of 2D heterocorrelated NMR experiments. This separation is crucial for establishing networks of coupled spins by hyphenated techniques that combine hetero- and homonuclear polarisation transfers. However, as the sample complexity increases, 13C chemical shifts stop being unique, hindering spectral interpretation. The resulting ambiguities can be removed by adding another dimension to these experiments. However, the spectra obtained from complex samples are riddled with overlapped signals, meaning that another dimension will only reduce the spectral resolution and prevent structure determination. A promising solution is to stay in two dimensions and use the combined 13C and 1H chemical shifts to separate signals. We have developed a suite of (3,2)D reduced dimensionality hyphenated NMR experiments that preserve the information content of 3D spectra but offer all of the advantages of 2D spectra – high resolution and ease of manipulation with only a mild sensitivity penalty. The proposed experiments complement the existing (3,2)D HSQC-TOCSY and include a (3,2)D HSQC-NOESY/ROESY, (3,2)D HSQC-CLIP-COSY and (3,2)D HSQC-HSQMBC. The new experiments represent a set of NMR techniques typically employed in the structure determination of complex compounds and have been adopted here for use on mixtures. The resolving power of these experiments is illustrated on the analysis of hot water extracts of green tea.
Introduction
NMR structure determination of compounds without their purification from mixtures of varying complexity is a challenging task. First of all, the compounds have to reach a concentration threshold to yield sufficient signal intensities to become observable, and secondly, the signals of individual molecules must be tractable in order to identify the investigated molecule or its fragments. This paper contributes to addressing the second issue by tapping into a large arsenal of NMR techniques developed for the analysis of single molecules. Our aim, similar to others in this field, is to enhance the resolving power of NMR experiments. Different approaches can be employed to achieve this, such as spreading the signals into multiple dimensions,1 exciting only a fraction of the nuclei,2 utilising nuclei with larger chemical shift dispersion (usually 13C), reducing the footprint of individual signals by collapsing their multiplets,3,4 or “separating” the molecules by their size in an NMR tube through molecular diffusion.5–7 For very complex mixtures, chemical modification in the form of molecular tagging with fully enriched NMR active isotopes seems to be the only option to unambiguously determine structures, although here the main limitation is the potential reach from a given tag and therefore only parts of the molecules can be studied at one time.8–10In this contribution we exploit the possibility of combining 1H and 13C chemical shifts to achieve much needed separation of resonances in the indirectly detected dimension of 2D heterocorrelated NMR experiments. This separation is crucial for establishing networks of coupled spins via hyphenated techniques. These techniques combine heteronuclear polarisation transfers, usually in the form of 1H–13C HSQC, with through bond (COSY and TOCSY) or through-space (NOESY or ROESY) homonuclear polarisation transfer steps. We also use this approach in a long-range 1H, 13C correlated experiment.
The basic premise of these techniques is, that as the sample complexity increases, 13C chemical shifts stop being unique at some point, hindering the interpretation of hyphenated heterocorrelated spectra. This ambiguity can, in principle, be tackled by adding another dimension to these experiments, e.g. in a form of a 3D HSQC-TOCSY.11 However, the spectra of complex mixtures are riddled with so many overlapping signals that another dimension, even with non-uniform sampling, will not aid the structure determination process and instead will lower the spectral resolution. A better method is to use the fact that the combined 13C and 1H chemical shifts of a given CH pair are more unique, and use them to distinguish overlapped 13C chemical shifts. Experiments that utilise this approach are commonly referred to as reduced dimensionality NMR experiments.12 The (3,2)D reduced dimensionality hyphenated NMR experiments preserve the information content of the corresponding 3D spectra but offer all of the advantages of 2D spectroscopy – high resolution and ease of manipulation with only a mild sensitivity penalty.
The described approach has so far been applied to produce (3,2)D HSQC-TOCSY experiments.13–15 In the work presented here, we have extended it to a suite of complementary experiments, including (3,2)D HSQC-CLIP-COSY, (3,2)D HSQC-NOESY/ROESY and (3,2)D HSQC-HSQMBC. The new experiments, derived from a set of NMR techniques typically employed in the structure determination of pure, but complicated molecules, were adopted here for use on mixtures. The results are illustrated on the analysis of carbohydrates obtained through the hot water extraction of green tea.
Results
Reduced-dimensionality experiments provide equivalent information to that of the corresponding higher dimensionality techniques, i.e. they correlate n chemical shifts, but they achieve this in a n − x chemical shift space by simultaneous sampling of several chemical shifts during each or some of the incrementable periods of (n, n − x)D experiments. In the case of (3,2)D 1H, 13C correlated, hyphenated experiments, the 13C and 1H chemical shifts of directly bonded 13CHn pairs are sampled simultaneously to record Ω13C ± κΩ1H offset frequencies in a (3,2)D 1H, 13C HSQC part of the experiment. Here, Ω13C (Ω1H) represents the difference between an individual 13C (1H) chemical shift and the respective r.f. carrier frequency; κ is a scaling factor between two frequencies. Such an experiment samples proton chemical shifts twice; the first time during the indirectly-detected period, and the second time during the directly detected period. In between these periods, a polarisation transfer occurs, which can either be homonuclear or, in the case of 1H, 13C long-range correlation, heteronuclear. The displacement of cross peaks by ±κΩ1H relative to their position in standard 1H, 13C correlated, hyphenated spectra separates signals with identical 13C chemical shifts, but also allows the determination of the 1H chemical shift of the initial proton in the F1 dimension, when the direct correlation cross peak is absent.As a consequence of modulating 13C chemical shifts by 1H frequencies, the number of cross peaks doubles, increasing signal overlap. This issue can however be dealt with easily by recording two data sets while changing the phase of the first 90° 1H pulse in the pulse sequence by 90°. This treatment produces cos(2πΩ1Hκt1) or sin(2πΩ1Hκt1) modulated signals in F1. Consequently, cross peaks in the (3,2)D spectra appear as in phase or antiphase doublets, centred around 13C chemical shifts and separated by 2κΩ1H in F1, i.e. displaced by ±κΩ1H relative to the original HSQC cross peak. The cosine and sine modulated datasets are acquired in an interleaved manner and processed to produce two simplified spectra by the addition or subtraction of the original spectra. The simplified spectra thus contain only one part of the F1 doublets, each as positive signals with increased intensity. They are referred to here as the Ω13C + κΩ1H and the Ω13C − κΩ1H spectrum.
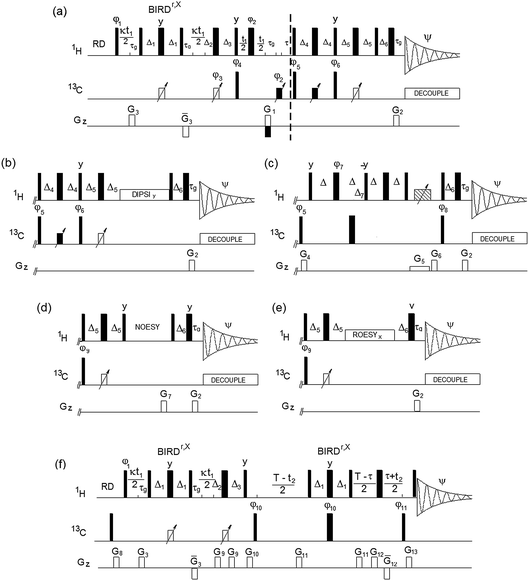
Inherent to 2D 1H, 13C HSQC spectra and the spectra of all hyphenated extensions, is the singlet character of cross peaks in F1. It is crucial that this feature is preserved in the (3,2)D 1H, 13C experiments, as failure to do so would lead to undesirable splitting of signals, increased overlap and reduced sensitivity. In all experiments presented here, the evolution of proton–proton couplings during 1H chemical shift labelling is therefore suppressed by a BIRDr,X pulse16,17 placed in the middle of this period. The BIRD pulse, in addition to 13C spins, also inverts protons attached to 12C, thus allowing Ω1H labelling of 13C-attached protons, while refocusing the coupling evolution with 12C-attached protons and the directly bonded 13C atom.
The Bruker pulse programs, hsqcedetgpsisp2.3,18 hsqcdietgpsisp.2,19 hsqcetgpnosp and hsqcetgprosp20 were used as the basis for the (3,2)D-based TOCSY, NOESY and ROESY experiments. The DIPSI-2 pulse sequence21 was applied for the TOCSY transfer, while a low power CW pulse was used for the ROESY spin lock. The (3,2)D BIRDr,X-HSQC-HSQMBC experiment is a modification of the corresponding 3D pulse sequence.22 The resulting pulse sequences of (3,2)D BIRDr,X-HSQC-(HH/CH-transfer) experiments are shown in Fig. 1.
The proposed experiments are illustrated on the analysis of hot water extracts of green tea. We have recently embarked on a project that uses green tea to assess degradation of organic matter in different soil types. This simple organic mixture acts as a proxy to the degradation of soil organic matter and is used in a citizen science experiment,23 where members of the public and researchers record the weight loss of buried tea bags after 3 months. Our aim is to provide a molecular signature of the tea degradation process in different soil types as monitored by MS and NMR. Green tea is a well-studied mixture and its hot water extracts contain a number of NMR detectable compounds such as catechins, flavonoids, caffeine, amino acids and carbohydrates.24 Carbohydrates are the most abundant compound type producing crowded signals in the 1H NMR spectra of green tea (Fig. 2) and as such will be used here to illustrate the resolving power of the proposed experiments.
To illustrate a redistribution of cross peaks, as a result of combined 1H and 13C chemical shift sampling, a 2D 1H, 13C HSQC spectrum of a green tea sample is shown in Fig. 1S,† together with two (3,2)D BIRDr,X-HSQC spectra. Partial (3,2)D BIRDr,X-HSQC-TOCSY spectra of the carbohydrate region are shown in Fig. 3, including the equivalent standard sensitivity-enhanced 2D 1H, 13C HSQC spectrum (Fig. 3a). Fig. 3c and d show separated Ω13C + κΩ1H and Ω13C − κΩ1H (3,2)D BIRDr,X-HSQC-TOCSY spectra, while Fig. 3b shows an overlay of all three spectra.
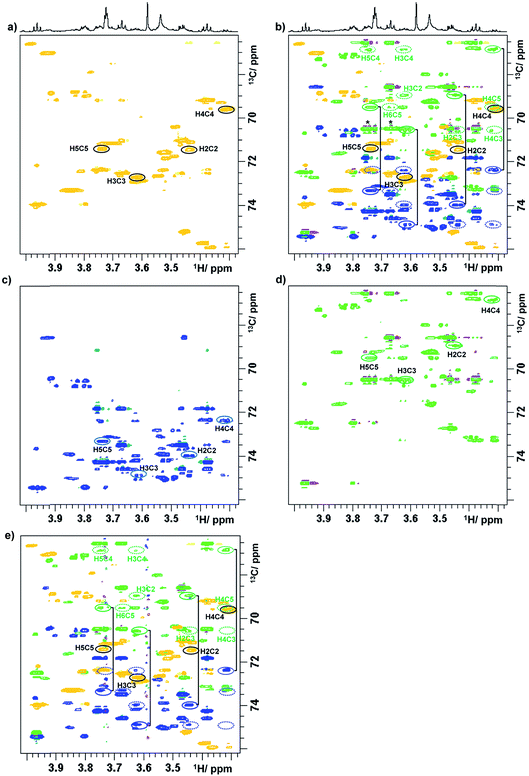 | ||
| Fig. 3 Partial (3,2)D spectra of green tea. (a) Regular sensitivity-enhanced 2D HSQC spectrum; (b) overlay of spectra (a), (c) and (d); (c) Ω13C + κΩ1H (3,2)D BIRDr,X-HSQC-TOCSY spectrum; (d) Ω13C − κΩ1H (3,2)D BIRDr,X-HSQC-TOCSY spectrum; (e) (3,2)D BIRDr,X-HSQC-CLIP-COSY spectrum. As a demonstration, the resonances of C2–C5 carbons of α-D-glucopyranose are identified. 1D traces are shown in Fig. 2S.† Intense signals of sucrose that accidentally appear on the same F1 frequency as those of C3α in the Ω13C − κΩ1H spectrum are labelled with an asterisk in (b). Full line ellipsoids represent the displaced cross peaks, while dashed ellipsoids represent the relay cross peaks. | ||
The process of identification and assignment of signals from the same molecule is illustrated here on α-D-glucopyranose, a minor component of this mixture. While the chemical shifts of C2α and C5α of α-D-glucopyranose differ by only 8 Hz (and in a lower resolution spectrum would be undistinguishable), the difference in the chemical shifts of H2α and H5α protons leads to a clear separation of their TOCSY traces (Fig. 3b). As discussed previously,15 the separation of signals in the Ω13C + κΩ1H and the Ω13C − κΩ1H spectra is different. While an accidental overlap can occur in one of the spectra, separation is usually achieved in the other. This can be seen on the C3α trace of the Ω13C − κΩ1H spectrum, where strong sucrose signals interfere, but this is not the case for the Ω13C + κΩ1H spectrum, where the signals are well separated. 1D traces through the C1–C5 carbons of α-D-glucopyranose taken from the Ω13C − κΩ1H (3,2)D BIRDr,X-HSQC-TOCSY spectra are shown in Fig. 2S.†
The next experiment to be presented is a (3,2)D BIRDr,X-HSQC-CLIP-COSY, which is a modification of a recently published 2D HSQC-CLIP-COSY25,26 method. Here, the perfect-echo based mixing sequence for in-phase coherence transfer between directly coupled protons is employed in place of an isotropic mixing of a TOCSY. An overlay of the Ω13C ± κΩ1H (3,2)D BIRDr,X-HSQC-CLIP-COSY spectra and a regular HSQC spectrum is presented in Fig. 3e. A comparison with an equivalent presentation of the TOCSY-based experiment (Fig. 3b) indicates that both experiments provide similar information, although the sensitivity of the CLIP-COSY based experiment is lower, as discussed later.
The reduced dimensionality approach was also applied to two through-space proton–proton correlation experiments, HSQC-NOESY and HSQC-ROESY (pulse sequences shown in Fig. 1d and e, respectively). The obtained spectra contain only a few NOESY/ROESY cross peaks. This is to be expected, as the efficiency of NOE-based transfer for small molecules in particular is low on high field instruments, even reaching zero. For carbohydrate structure determination, the most important though-space correlations are those across glycosidic linkages. These have been detected by the (3,2)D BIRDr,X-HSQC-NOESY/ROESY experiments and are presented in Fig. 3S.†
The last experiment discussed is a (3,2)D BIRDr,X-HSQC-HSQMBC technique, which can be viewed as a modification of a 3D HSQC-HSQMBC technique.22 An expansion identical to that of Fig. 3 shows an overlay of the Ω13C + κΩ1H and the Ω13C − κΩ1H (3,2)D BIRDr,X-HSQC-HSQMBC spectra together with a regular 2D HSQC spectrum (Fig. 4).
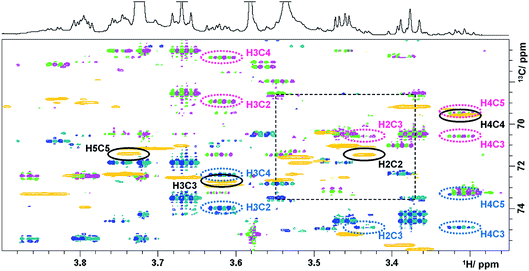 | ||
| Fig. 4 Overlay of HSQC (gold) and the Ω13C ± κΩ1H (3,2)D BIRDr,X-HSQC-HSQMBC spectra (pink/green and blue/green) of green tea. Resonances of C2–C5 carbons of α-D-glucopyranose are identified. 1D traces are shown in Fig. 4S.† | ||
A number of long-range cross peaks are visible in this region, as recognised by their antiphase appearance of a proton–carbon long-range coupling. One-bond correlations are strongly suppressed in the (3,2)D BIRDr,X-HSQC-HSQMBC spectra, nevertheless can appear as four weak cross peaks positioned in the corners of a rectangle separated by 2κΩ1H and 1JCH in F1 and F2, respectively. The long-range cross peaks of carbons C2–C5 of α-D-glucopyranose were identified in this spectrum. The F2 traces through the corresponding cross peaks taken from the Ω13C + κΩ1H spectrum are shown in Fig. 4S.† These include correlations of C3 and C5 with H1, which are outside of the spectral region shown in Fig. 4. All expected correlations for C2–C5 carbons were detected by this experiment with good sensitivity.
Discussion
The sensitivity of NMR experiments is always a concern, hence the following discussion focuses on this aspect of the proposed experiments. The overall theoretical sensitivity of a (3,2)D BIRDr,X-HSQC experiment is half of that of a regular 2D HSQC experiment acquired in the same overall time. In practice, additional signal-to-noise reduction occurs, which can be attributed to the 1JCH mismatch and the evolution of proton–proton couplings during the BIRDr,X pulse; signal-to-noise of 30–45% was observed in individual Ω13C ± κΩ1H (3,2)D BIRDr,X-HSQC spectra relative that of a 2D HSQC spectrum, i.e. roughly comparable to 3D HSQC-based hyphenated extensions. The spectra are clean and without t1 noise, with the exception of the CLIP-COSY extension, where strong signals left minor traces, likely due to the use of the gradient z-filter.27 In all experiments the coherence selection gradient was applied at 20% of the maximum strength (unlike the standard 80%) to minimise diffusion related losses during the long mixing times used in the NOESY, ROESY and also CLIP-COSY experiments. This is not a concern in the (3,2)D BIRDr,X-HSQC-HSQMBC, where gradient coherence selection is not used. Nevertheless, high quality spectra are obtained here as well, mainly due to two G-BIRD blocks28 that dephase the magnetization of remote protons.As can be seen from the comparison of corresponding TOCSY and CLIP-COSY Ω13C + κΩ1H spectra (Fig. 2d and e), their appearance is very similar. Nevertheless, the sensitivity of the TOCSY transfer is greater, as seen from the comparison of the 1D traces through the Ω13C + κΩ1H (3,2)D BIRDr,X-HSQC-TOCSY and CLIP-COSY spectra in Fig. 2S.† We have tested different settings using Δ between 8.33 and 16.7 ms, however the obtained signal-to-noise was between 30 and 50% of that obtained for a 20 ms mixing time TOCSY. This drop of sensitivity has been discussed previously26 and is caused by the presence of passive proton–proton couplings.
As stated above, the efficiency of the through-space correlation was low, with the ROESY transfer being more efficient than the NOESY transfer. The reduced dimensionality through-space correlation experiments will therefore be most useful for heterogeneous samples with large NOEs such as organic polymers or polysaccharides.
On the other hand, the (3,2)D BIRDr,X-HSQC-HSQMBC designed for establishing long-range correlations of protonated carbons showed a good sensitivity. In this experiment, the active and passive proton–carbon couplings compete for the available magnetisation during the long-range evolution interval T. Even very small couplings, e.g. between C1 and H3 and H5 of α-D-glucopyranose show correlations (see Fig. 4S†). The experiment was repeated twice by optimising the refocusing interval τ for 13CH or 13CH2 pairs. For the CH optimised experiment, low intensity one-bond correlation cross peaks appear in the spectra due to a mismatch of 1JCH couplings with those used to set the τ interval (0.5/1JCH). These cross peaks are characteristically positioned in the four corners of a rectangle separated by 1JCH in F2 and by 2κΩ1H in F1, as seen in Fig. 4. For CH2 optimised experiments (τ = 0.25/1JCH), the intensity of CH one-bond cross peaks increases. It is interesting to note that for CH optimised experiments, very intense one-bond CH2 cross peaks appear in the spectra (the long-range correlation cross peaks are at the same time weak), while for CH2 optimised experiments the intensity of the one-bond CH2 cross peaks drops close to zero (and the long-range correlation cross peaks are more intense). This behaviour is explained in the ESI† using product spin operators. The analysis presented there indicates that refocusing of one-bond couplings before the long-range evolution interval, T, should be considered as a way of removing one-bond correlation cross peaks.
Experimental
The sample was prepared via hot water extraction. 150 mg of Lipton green tea (EAN 87 22700 05552 5) in 40 mL of Milli-Q® water was heated to 80 °C for 30 minutes. The extractant was separated using centrifugation at 8000 rpm and freeze dried. The freeze dried powder (20 mg) was dissolved in D2O (600 μL, 100% deuterated, Sigma Aldrich®) spun down in a centrifuge. All spectra were acquired on a 4-channel NEO 800 MHz Bruker spectrometer equipped with a 5 mm TCI CryoProbe™ with automated tuning and matching at 300 K. The following parameters were used: 2048 and 2048 complex points in t2 and t1, respectively, spectral widths of 9.8 and 160 ppm in F2 and F1, yielding t2 and t1 acquisition times of 131 and 31.8 ms, respectively. Eight scans were acquired for each t1 increment using a relaxation time of 1.5 s. The polarisation transfer was optimised for 1JCH = 150 Hz. Forward linear prediction to 4096 points was applied in F1. A zero filling to 4096 was applied in F2. A cosine square window function was used for apodization prior to Fourier transformation in both dimensions.The following parameters are associated with the pulse sequences shown in Fig. 1. Narrow and wide filled rectangles represent 90° and 180° pulses, respectively. Open rectangles with inclined arrows represent 180° 13C CHIRP pulses (p14, 500 μs), while filled rectangles with inclined arrows are 180° composite 13C CHIRP pulses (p24, 2 ms). The following delays were used: Δ1 = 0.5/1JCH − p14/2; τg = 1.2 ms (1 ms PFG + 200 μs gradient recovery delay); Δ2 = 0.25/1JCH − τg − p14/2; Δ3 = 0.25/1JCH + τg − p14/2 + κt1(0); τ = τg + p180 × 2t1(0); Δ4 = 0.125/1JCH + p14/4; Δ5 = 0.25/1JCH − p14/2; Δ6 = τg − 0.78p90 + DE, where p90 and p180 are 90° and 180° 1H pulses, κ is the scaling factor for Ω1H frequencies, t1(0) is the initial t1 increment (3 μs) and DE is a pre scan delay (10 μs).
Unless specified otherwise, the pulses were applied from the x axis; φ1 = x or y for cosine and sine modulated signals, respectively; φ2 = 2x, 2(−x); φ3 = x; φ4 = x, −x; φ5 = 2x, 2(−x); φ6 = 2y, 2(−y); Ψ = x, 2(−x), x. Phases φ3, φ4 and Ψ were increased by 180° simultaneously with t1 incrementation; the real and imaginary points were acquired by changing the polarity of the G1 gradient and increasing by 180° the phase φ5. The gradient G3 was 600 μs long, while all other gradients were applied for 1 ms. The following relative gradient strengths was used: G1 = 20%, G2 = 5.025%, and G3 = 70%, where 100% represents 53 Gauss per cm.
The (3,2)D BIRDr,X-HSQC-TOCSY spectrum was acquired using identical parameters, a 20 ms mixing time for the TOCSY transfer used a DIPSI-2 pulse sequence21 (γB1/2π = 5 kHz). The (3,2)D BIRDr,X-HSQC-ROESY spectrum was acquired using a 200 ms CW ROESY spin lock at γB1/2π = 3570 Hz. The (3,2)D BIRDr,X-HSQC-NOESY spectrum was acquired using a 250 ms NOESY mixing time, G7 = 15%. The phase φ9 = 4x, 4(−x) in the NOESY and ROESY. Phases φ3, φ4 and Ψ were increased by 180° simultaneously with t1 incrementation; the real and imaginary points were acquired by changing the polarity of the G1 gradient.
For the (3,2)D BIRDr,X-HSQC-CLIP-COSY, Δ = 11.4 ms and Δ7 = 0.25/1JCH. A 20 ms CHIRP pulse was applied simultaneously with a G5 (−5%) PFG followed by a G6 = −19.4%; G4 = 11%. Phases were as follows: φ7 = 2y, 2(−y); φ8 = x, −x; Ψ = 2(x, −x), 2(−x, x). Phases φ3, φ4 and Ψ were increased by 180° simultaneously with t1 incrementation; the real and imaginary points were acquired by changing the polarity of the G1 gradient.
For the (3,2)D BIRDr,X-HSQC-HSQMBC spectrum, T represents the long-range evolution interval that was set to 62.5 ms and τ = n × 0.5/1JCH, n = 1 for CH and n = 0.5 for all multiplicities. φ10 = x, −x; φ10 = 2x, 2(−x); Ψ = x, 2(−x), x. Phase φ10 was incremented in a TPPI manner by 90°, phase Ψ was increased by 180° simultaneously with t1 incrementation. G8 = 10%, G9 = 11.6%, G10 = 26%, G11 = 16%, G12 = 50%, G13 = 22%.
The number of scans (NS) was 8, except for the ROESY and the HSQC-HSQMBC, where NS = 12. The overall acquisition time was 7 hours 40 minutes (standard sensitivity-enhance HSQC), 15 hours 38 minutes ((3,2)D HSQC), 15 hours 48 minutes (TOCSY), 17 hours 52 minutes (NOESY), 25 hours 41 minutes (ROESY), 16 hours 5 minutes (CLIP-COSY) and 25 hours 16 minutes (HSQC-HSQMBC).
Conclusions
In conclusion, we have presented a series of reduced dimensionality 2D hyphenated HSQC-based experiments designed to deal with the overlap of carbon resonances encountered in mixtures. In combination with high digital resolution, achievable by non-linear sampling, these experiments are suitable for tracing out individual spin systems of small to medium size molecules embedded in mixtures of considerable complexity.Conflicts of interest
The authors declare no conflicts of interests.Acknowledgements
The authors would like to thank Juraj Bella and Dr Lorna Murray for maintenance of the NMR spectrometers. J. Sakas would like to acknowledge the financial support received from an EPSRC Undergraduate Vacation Scholarship. N. G. A. Bell would like to acknowledge the financial support received from a NERC Soil Security Programme Fellowship.Notes and references
- C. Griesinger, O. W. Sorensen and R. R. Ernst, J. Magn. Reson., 1987, 73, 574–579 CAS
.
- H. Kessler, H. Oschkinat and C. Griesinger, J. Magn. Reson., 1986, 70, 106–133 CAS
.
- K. Zangger, Prog. Nucl. Magn. Reson. Spectrosc., 2015, 86–87, 1–20 CrossRef CAS PubMed
.
- J. A. Aguilar, S. Faulkner, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2010, 49, 3901–3903 CrossRef CAS PubMed
.
- W. S. Price, Concepts Magn. Reson., 1997, 9, 299–336 CrossRef CAS
.
- W. S. Price, Concepts Magn. Reson., 1998, 10, 197–237 CrossRef CAS
.
- H. Barjat, G. A. Morris, S. Smart, A. G. Swanson and S. C. R. Williams, J. Magn. Reson., Ser. B, 1995, 108, 170–172 CrossRef CAS
.
- N. G. A. Bell, M. C. Graham and D. Uhrin, Analyst, 2016, 141, 4614–4624 RSC
.
- N. G. A. Bell, L. Murray, M. C. Graham and D. Uhrin, Chem. Commun., 2014, 50, 1694–1697 RSC
.
- G. A. Bell, A. A. L. Michalchuk, J. W. T. Blackburn, M. C. Graham and D. Uhrin, Angew. Chem., Int. Ed., 2015, 54, 8382–8385 CrossRef PubMed
.
- V. V. Krishnamurthy, J. Magn. Reson., Ser. B, 1995, 106, 170–177 CrossRef CAS
.
- S. Kim and T. Szyperski, J. Am. Chem. Soc., 2003, 125, 1385–1393 CrossRef CAS PubMed
.
- S. M. Pudakalakatti, A. Dubey, G. Jaipuria, U. Shubhashree, S. K. Adiga, D. Moskau and H. S. Atreya, J. Biomol. NMR, 2014, 58, 165–173 CrossRef CAS PubMed
.
- A. Singh, A. Dubey, S. K. Adiga and H. S. Atreya, J. Magn. Reson., 2018, 286, 10–16 CrossRef CAS PubMed
.
- N. Brodaczewska, Z. Kostalova and D. Uhrin, J. Biomol. NMR, 2018, 70, 115–122 CrossRef CAS PubMed
.
- J. R. Garbow, D. P. Weitekamp and A. Pines, Chem. Phys. Lett., 1982, 93, 504–509 CrossRef CAS
.
- D. Uhrin, T. Liptaj and K. E. Kover, J. Magn. Reson., Ser. A, 1993, 101, 41–46 CrossRef CAS
.
- L. E. Kay, P. Keifer and T. Saarinen, J. Am. Chem. Soc., 1992, 114, 10663–10665 CrossRef CAS
.
- J. Schleucher, M. Schwendinger, M. Sattler, P. Schmidt, O. Schedletzky, S. J. Glaser, O. W. Sorensen and C. Griesinger, J. Biomol. NMR, 1994, 4, 301–306 CrossRef CAS PubMed
.
- A. Bax and D. G. Davis, J. Magn. Reson., 1985, 63, 207–213 CAS
.
- S. P. Rucker and A. J. Shaka, Mol. Phys., 1989, 68, 509–517 CrossRef CAS
.
- D. Uhrin, J. Magn. Reson., 2002, 159, 145–150 CrossRef CAS PubMed
.
- J. A. Keuskamp, B. J. J. Dingemans, T. Lehtinen, J. M. Sarneel and M. M. Hefting, Methods Ecol. Evol., 2013, 4, 1070–1075 CrossRef
.
- Y. F. Yuan, Y. L. Song, W. H. Jing, Y. T. Wang, X. Y. Yang and D. Y. Liu, Anal. Methods, 2014, 6, 907–914 RSC
.
- T. Gyongyosi, I. Timari, J. Haller, M. R. M. Koos, B. Luy and K. E. Kover, ChemPlusChem, 2018, 83, 53–60 CrossRef
.
- M. R. M. Koos, G. Kummerlowe, L. Kaltschnee, C. M. Thiele and B. Luy, Angew. Chem., Int. Ed., 2016, 55, 7655–7659 CrossRef CAS PubMed
.
- M. J. Thrippleton and J. Keeler, Angew. Chem., Int. Ed., 2003, 42, 3938–3941 CrossRef CAS PubMed
.
- C. Emetarom, T. L. Hwang, G. Mackin and A. J. Shaka, J. Magn. Reson., Ser. A, 1995, 115, 137–140 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9fd00008a |
| This journal is © The Royal Society of Chemistry 2019 |