Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-invasive depth determination of inclusion in biological tissues using spatially offset Raman spectroscopy with external calibration†
Sara
Mosca
 a,
Priyanka
Dey
a,
Priyanka
Dey
 b,
Marzieh
Salimi
b,
Marzieh
Salimi
 b,
Francesca
Palombo
b,
Francesca
Palombo
 b,
Nick
Stone
b,
Nick
Stone
 *b and
Pavel
Matousek
*b and
Pavel
Matousek
 *a
*a
aCentral Laser Facility, Research Complex at Harwell, STFC Rutherford Appleton Laboratory, UK Research and Innovation, Harwell Campus OX11 0QX, UK. E-mail: pavel.matousek@stfc.ac.uk
bSchool of Physics and Astronomy, University of Exeter, Exeter EX4 4QL, UK. E-mail: N.Stone@exeter.ac.uk
First published on 22nd September 2020
Abstract
Spatially offset Raman spectroscopy (SORS) allows chemical characterisation of biological tissues at depths of up to two orders of magnitude greater than conventional Raman spectroscopy. In this study, we demonstrate the use of SORS for the non-invasive prediction of depth of an inclusion within turbid media (e.g. biological tissues) using only external calibration data sets, thus extending our previous approach that required internal calibration. As with the previous methodology, the concept is based on relative changes in Raman band intensities of the inclusion that are directly related to the path length of Raman photons travelling through the medium thereby encoding the information of depth of the inclusion. However, here the calibration model is created using data only from external measurements performed at the tissue surface. This new approach facilitates a fully non-invasive methodology applicable potentially to in vivo medical diagnosis without any a priori knowledge. Monte Carlo simulations of photon propagation have been used to provide insight into the relationship between the spatial offset and the photon path lengths inside the tissues enabling one to derive a general scaling factor permitting the use of spatial offset measurements for the depth prediction. The approach was validated by predicting the depth of surface-enhanced Raman scattering (SERS) labelled nanoparticles (NPs) acting as inclusions inside a slab of ex vivo porcine tissue yielding an average root mean square error of prediction of 7.3% with respect to the overall tissue thickness. Our results pave the way for future non-invasive deep Raman spectroscopy in vivo by enabling, for example, the localisation of cancer lesions or cancer biomarkers in early disease diagnosis and targeted treatments.
Introduction
Recent developments in deep Raman spectroscopy such as spatially offset Raman spectroscopy (SORS) and transmission Raman spectroscopy (TRS)1,2 have opened a number of new application areas including non-invasive disease diagnosis with its ability to characterise deep layers inside biological tissues.3,4–6 SORS takes advantage of characteristic light propagation in diffusely scattering (turbid) media,7 being capable of retrieving information about deep layers by introducing a spatial separation between the illumination zone and the Raman collection area.8 Recent medically-oriented research has also demonstrated the use of SORS and TRS for monitoring physical information such as pH9 and temperature10 and localising and predicting the depth of an inclusion (target) within turbid media.11–13 Moreover, surface-enhanced Raman spectroscopy (SERS) nanoparticles (NPs) can be used to target specific biomarkers of interest at depth by combining SERS and SORS techniques (i.e. SESORS) permitting, for example, effective in vivo imaging of cancer lesions14–16 or neurotransmitters through skull.17 Specifically, in the clinical environment, the in vivo determination of the depth of subsurface target (e.g. lesion) within body could potentially improve the effectiveness of diagnosis and subsequent treatments. Recent research has proposed and demonstrated the use of SORS to retrieve the depth information of a single inclusion buried within a diffusively scattering synthetic phantom12 and ex vivo tissues.13 The method relies on there being a difference in the optical properties (e.g. absorption coefficient μa and scattering coefficient μ′s) of the diffusive medium as a function of wavelength over the acquired Raman spectral range.11 This condition is satisfied readily by biologically relevant samples (e.g. tissues and organs) where μa and μ′s change significantly over the NIR range.18 When Raman photons of different Raman bands, positioned at different wavelengths, travel through this type of matrix, they undergo a different intensity attenuation by the matrix.19 Due to this effect, the difference in the relative intensities of two, or more, Raman bands of the inclusion can be used to monitoring its depth inside a matrix. In such an application, the prediction of the depth is achieved by evaluating relative Raman intensities of inclusion following a calibration procedure that relates these spectral intensity distortions to the depth based on prior internal calibration measurements.12 However, such procedures are inherently invasive and as such not readily transferable to in vivo diagnosis.To date the fully non-invasive calibration has only been demonstrated in transmission geometries. In this work, for the first time, we propose a calibration method for depth prediction that relies exclusively on SORS data collected at the sample surface and therefore constituting a fully non-invasive concept applicable in non-invasive fashion, potentially also for use in in vivo applications. Monte Carlo modelling (i.e. MC) of photon propagation20 was used to derive the relationship between propagation path length, depth and spatial offset.21 The proposed method was tested and compared with previous approaches in terms of accuracy of depth prediction of a single inclusion buried up to tens of millimetres deep inside synthetic phantom and ex vivo porcine tissue. The concepts constitutes a major step towards realizing the potential of SORS for non-invasive in vivo localisation of abnormal regions of tissue, such as in disease diagnosis.
Proposed concept – external SORS calibration
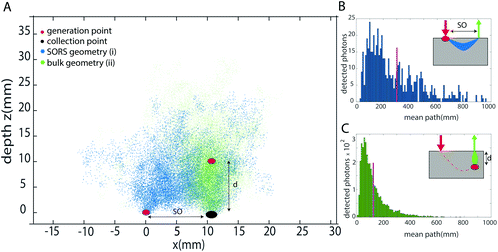
As previously introduced, the prediction of the depth is obtained by modelling the intensity distortion due to diffuse scattering and absorption events inside a turbid matrix of at least two different Raman bands of the inclusion. This distortion is related to the photon path length inside the medium. The concept of external calibration resides in finding the correspondence between the intensity distortion and the depth. In the TRS concept, for example, fully non-invasive calibration is readily achievable by placing the inclusion on both sides of the sample, i.e. into the laser illumination and collection zones in turn and obtaining a TRS spectrum for each. The relative intensity distortion of the inclusion observed can be directly related to sample thickness. Any smaller distortion observed for this inclusion when located inside the matrix a specific depth can then be assigned to it based on the above calibration measurement using a proportionality relationship. In contrast to TRS,10,13,22 placing the inclusion into the laser illumination and Raman collection cannot be assigned straightforwardly any specific depth in SORS as the spatial offset does not equate directly to depth – although it is related to it by some scaling factor. To find this relationship and specifically the scaling factor, we have carried out Monte Carlo (MC) simulations for medically relevant scenarios. Our MC analysis compared two principal SORS scenarios:I. With an inclusion placed at the surface of the matrix (within the illumination zone only) and with Raman signal collected at a fixed spatial offset SO = d (Fig. 1a – blue dots).
II. With the inclusion buried deep inside a matrix at depth d0 right below the Raman collection zone (Fig. 1a – cyan dots). (Note that in this case, the only critical parameter is the depth of inclusion below the Raman collection zone – the location of the illumination zone is irrelevant in the first approximation of negligible dimensions of the inclusion as the laser illumination-to-target section of the photon path is traversed by laser photons that themselves do not contribute to the relative Raman intensity distortion.)
From each of the above scenarios, it is possible to reconstruct the statistical distribution of photon path lengths and extrapolate a mean photon path length (Fig. 1b and c). This can then be related to a certain degree of intensity distortion observed. It is anticipated that the imprinting of the same distortion on the spectrum in the two geometries requires the spatial offset to be smaller than the depth of the inclusion by a given scaling factor SF. This is because the spatial offset geometry (with the inclusion at the surface) involves photon trajectories that on average are statistically bent somewhat into the medium, away from the inclusion-Raman collection zone axis, due to the presence of the air-sample interface.
Conversely, in the situation where the inclusion is fully buried inside the medium, the photon trajectories are more direct between the inclusion and the Raman collection zone. A scaling factor SF was derived from the Monte Carlo simulations translating a given spatial offset, SO, into a particular depth of inclusion inside the matrix dSO, such that it would induce the same distortion. To create a calibration model, one needs to divide the spatial offset by the scaling factor in order to derive an equivalent depth (dSO = SO/SF) that can then be used to predict an unknown depth of the inclusion inside the same matrix.
Experimental
Calibration procedure and measurement protocol
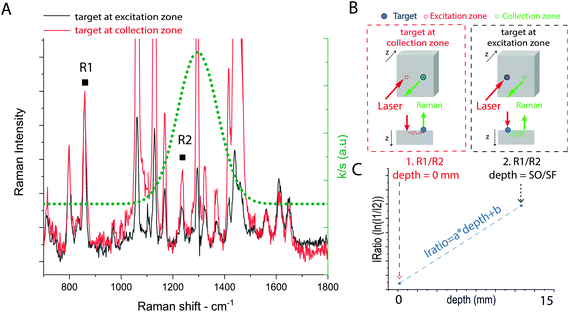
The external calibration procedure is summarized in Fig. 2. It consists of the sequential acquisition of Raman spectra, at a fixed spatial offset SO, of a target placed at the surface in two positions as illustrated in Fig. 2b:(i) At the Raman collection zone on the sample surface (minimum intensity distortion d = 0 mm).
(ii) At the laser illumination zone on the sample surface (maximum intensity distortion d = SO/SF mm).
For both the calibration measurements (Fig. 2a), a Gaussian-shape curve fit was performed on two Raman bands R1 and R2 of the target to evaluate the effect of differential absorption. The natural logarithm of the intensity ratio of the two bands (i.e. IRatio = ln(R1/R2)) for the measurement (i) corresponds to the minimum intensity distortion for a depth of the target d = 0, while the same parameter for measurement (ii) corresponds to the maximum intensity distortion for a depth of the target equal to the spatial offset divided by the scaling factor extrapolated from MC simulation (d = d(SO) = SO/SF). A linear trend was used to create a model between the intensity distortion, evaluated as above, and the depth (Fig. 2c). The prediction of the depth was obtained by reading an unknown intensity distortion (IRatio) and solving the equation for the depth resulting from the calibration procedure (depth = (IRatio − b)/a). The measurement protocol consisted of the sequential acquisition of Raman spectra from the model phantom with a fixed spatial offset (SO = 15 mm). The first step of the protocol consists in the alignment of the inclusion under the optical axis (z-axis, collection zone). This is carried out by setting a zero spatial offset (SO = 0 mm) and maximising the signal of the inclusion by moving the sample along the (x,y) axes. This preliminary step ensures the presence of the inclusion under the collection path. After that, the experiments start with the inclusion (e.g. paracetamol or NPs) at the surface (z = 0) and subsequently being moved deeper along the z-axis.
Monte Carlo modelling
The numerical simulation of photon propagation was performed using the Monte Carlo method where photons were individually followed within a three-dimensional space in a random walk-like propagation as in previous work.19–21 The model considers the samples to be a semi-infinite turbid medium (with specific absorption and scattering properties, μa and μ′s, respectively) with an air-medium interface at the surface (z = 0, Cartesian coordinate); with photons propagating in a straight line over a distance ls and thereafter its direction is fully randomized at the next scattering event. The propagation distance over which the photon direction is randomized can be approximated as the photon transport length of the scattering medium (lS = 1/μ′s).23 After each interaction, the weight of the photon is reduced by a factor equal to the albedo (W′ = Wμ′s/(μ′s + μa) according to the Albedo-weight method24). After a boundary-interaction check, a roulette algorithm for photon termination is implemented, leading to photons eventually terminating in an unbiased manner by conserving energy.20 The simulation parameters were chosen to mimic the experimental condition to enable the comparison between experimental and theoretical data. Point-like excitation and collection geometry were used with excitation and collection radius of rex = 0.5 mm and rcoll = 1 mm, respectively. The following two configurations, mimicking the calibration measurements, were studied:I. Photon generated at the surface (0,0,0) and collected at the surface with a spatial offset SO = 10 mm.
II. Photon generated at a depth d = 10 mm inside the turbid media and collected at the surface.
Different pairs of values of μa = (0, 0.005, 0.01, 0.05, 0.1) mm−1 and μ′s = (0.5, 1, 1.5, 2) mm−1 were simulated to represent the typical optical properties of tissues and organs in the NIR region of interest.18 The numerical code was written in Matlab (2018b, the MathWorks). For each geometry and the pair of optical properties, one million (106) photons were propagated for a maximum number of steps of 5 × 103.
Model samples
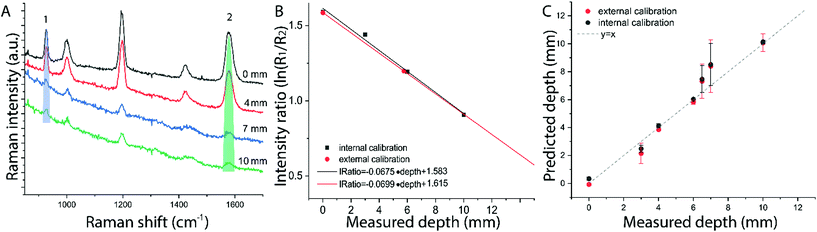
Firstly, a heterogeneous synthetic phantom made of polyethylene stacks (PE) with dimensions of 50 mm × 50 mm × 3 mm per layer and a paracetamol tablet (2 mm radius, 3 mm thickness) embedded at the centre of one of the PE layers were used to mimic the presence of an inclusion (paracetamol) at depth in a turbid medium (PE). The multi-layer phantom12 was an assembly with an overall thickness of 24 mm and the mass of the inclusion was ∼125 mg. The inclusion layer was moved through the turbid medium along the z-axis by varying its depth from the surface (d = 3, 6, 9, 12 mm).The second type of multi-layer phantom was made of ex vivo animal tissue (turbid matrix) and SERS nanoparticles (NPs) (inclusion).13 The ex vivo tissue consisted of a stack of sliced back bacon from pork loin (45 × 45 × 2 mm or 45 × 45 × 3 mm per slice) purchased fresh from a local store and frozen until used. The SERS NPs used as an inclusion consisted of gold NPs (approximately 100 nm diameter) labelled with Raman reporters (d8-4,40-dipyridyl-d8DIPY) and coated with a silica shell (acquired from Oxonica25) already characterised and used previously.13,16 The SERS NPs were transferred into a quartz cuvette (2 mm optical path length; H × W × D = 2 × 10 × 2 mm3) and then multiple layers of porcine tissue were added either side of the cuvette. The sample used for the study consisted of approximately 2.8 × 1014 NPs ml−1. The total thickness of the bilayer sample was kept constant, around 36 mm, while the depth of the cuvette containing the NPs was varied (d = 0, 4, 7, 10 mm) by adding tissue layers or moving the quartz cuvette along the optical axis (z-axis) within the stratified tissue slab.
SORS setup
Raman measurements were carried out using a custom-built Raman system for conventional point-like spatial offset Raman spectroscopy (SORS) measurements.12,13 A schematic of the set-up is shown in ESI (see Fig. SI-1†). Briefly, the laser light (from a 830 nm diode laser, IPS, Monmouth Junction, NJ) is delivered to the sample through an optical imaging system to a spot size of ∼500 μm at the sample surface. The scattered light is collected from a zone of approximately 1.5 mm diameter on the sample surface at a 30° angle relative to the laser beam and coupled through an optical fibre to a Raman spectrometer (Kaiser HoloSpec f/1.8i) and a deep-depletion CCD camera (Andor iDus-420A-BR-DD). The spatial offset is achieved by moving the entire excitation path assembly along the plane parallel to the sample surface. Raman spectra were recorded at a spatial offset of 15 mm with 200 mW laser power at the sample for the synthetic phantom and 300 mW for the ex vivo porcine tissue, with 30 s × 10 accumulations in the spectral range ∼100 to 1900 cm−1 at a spectral resolution of ∼8 cm−1.Results and discussion
Firstly, we studied the photon propagation in terms of mean path length (ESI, Fig. SI-2†) for the two geometries introduced in the MC section, for a range of μa and μ′s relevant to biological tissues in the NIR spectral range.18Fig. 3 shows the scaling factor SF calculated as the ratio between the mean paths of the two geometries (i.e. (i) and (ii) in the section Proposed Concept – External calibration in SORS) resulting from the MC modelling. The results of MC modelling indicate that the mean path length of photons generated when at the surface and collected with a spatial offset SO (mpSORS) is 2–3 times larger than the mean path of photons generated from an inclusion deep inside the medium at depth equal to the spatial offset SO (mpDEPTH). The same mean photon path length is expected to lead to similar distortion of Raman signals. This implies that, to imprint the same distortion in the two geometries (i.e. (i) and (ii) in Fig. 2), the spatial offset needs to be scaled down (by using a proper scaling factor) to create a model that links the depth of the inclusion with the intensity distortion.To validate the proposed concept, different sets of SORS measurements at 15 mm offset were performed on a multi-layer system based on a turbid medium (PE or ex vivo tissue) with an inclusion (paracetamol or NPs) buried at different depths.
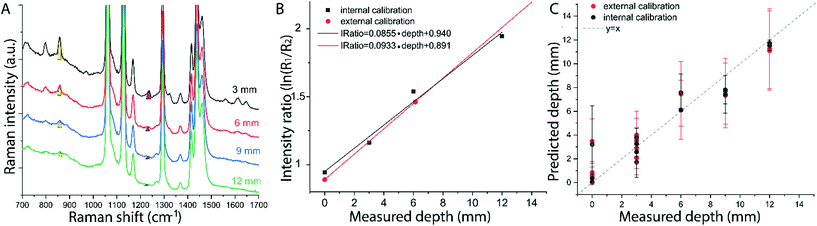
The results on the synthetic stratified phantom are shown in Fig. 4. The Raman spectra collected at various depths (d = 3, 6, 9, 12 mm) for paracetamol buried inside the PE matrix (Fig. 4a) show the differential absorption behaviour of the two paracetamol Raman bands at 857 and 1235 cm−1 (the band at 1235 cm−1 falls under the PE absorption peak at 930 nm). A scaling factor SF = 2.45, derived from MC modelling for μ′s = 0.5 mm−1 and μa = 0 (ESI-2†), was used to create the calibration model for depth prediction based on the intensity distortion defined as the natural logarithm of the ratio of the intensities (857 to 1235 cm−1) for a depth equal to the SO/SF = 6.12 mm as in our previous work12 (red circles in Fig. 4b). Fig. 4c shows the predicted depths of the inclusion resulting from the measured intensity ratio. Similarly, the results on the ex vivo tissue-based bilayer phantom are shown in Fig. 5. The Raman signal of SERS NPs at various depths (0, 4, 7, 10 mm) was retrieved with a spatial offset of 15 mm through 36 mm thick porcine tissue (Fig. 5a). Likewise, as observed in previous studies,13 the intensity of the Raman component at 1580 cm−1 (which falls under an absorption band of water, a significant component of the ex vivo tissue) is dramatically reduced relative to the 930 cm−1 band as a result of increasing depth. A scaling factor SF = 2.61, obtained from MC modelling for μ′s = 0.5 mm−1 and μa = 0.05 mm−1 (similar value for porcine muscle at 950 nm was reported in ref. 18), was used to relate the intensity distortion (defined as the natural logarithm of the ratio of the intensities at 930 and 1580 cm−1) measured with the target placed on the surface above the excitation area and the depth (SO/SF = 5.75 mm) for creating the calibration model for depth prediction (Fig. 5b).
The predicted depths of the NPs resulting from the measured intensity ratio of R1 and R2 (i.e. I1/I2) are shown in Fig. 5c. The effectiveness of the new calibration approach based on SORS measurements at the surface (i.e. external calibration, red symbols in Fig. 4b–c and 5b–c), is compared with the previous approach (Table 1) that used a calibration model for the distortion based on internal measurements12 (i.e. internal calibration, black symbols in Fig. 4b–c and 5b–c). Taking into account all the depths for the inclusion, with only the measurement at 15 mm spatial offset, it was possible to predict the depth of paracetamol and NPs in their respective matrices with a root-mean-square error of prediction (RMSEP) of 10.7% and 7.3% respectively (i.e. ±1.28 mm and ±0.73 mm, respectively). As expected, the calibration model based on internal measurement resulted in a more accurate prediction with an RMSEP of 9.5% for the synthetic phantom and 7.2% for the ex vivo tissue sample. Nevertheless, the proposed methodology based on SORS at a fixed offset with a calibration procedure that relies only on surface measurements proved to be still very effective with the added benefit of being entirely applied in a non-invasive manner (as opposed to the internal calibration procedure).
| RMSEP | External mm (%) | Internal mm (%) |
|---|---|---|
| Synthetic phantom | 1.28 (10.7%) | 1.15 (9.5%) |
| PE – paracetamol (n = 14) | ||
| Ex vivo tissue phantom | 0.73 (7.3%) | 0.72 (7.2%) |
| Porcine tissue – NPS (n = 7) |
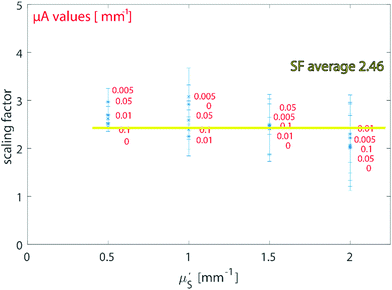
It should be noted that specific values of SF were used to analyse the samples according to the a priori knowledge of the optical properties. When the values of μ′s and μa are unknown but expected to be within the above-studied range, a rough approximation can be made by considering the average SF resulting from the above MC carried out for typical optical properties of tissue in the NIR region (average value SFav = 2.46 in Fig. 2). To test and exemplify this, the average value SFav was used to create a calibration model for the ex vivo tissue dataset (see ESI-3†). Since the variation of the scaling factor is moderate-low within the calculated scenario, the alteration on the calibration model resulted in a modified RMSEP of only around 2% (new RMSEP = 9.24% with SFav = 2.46 – see ESI-3†).
The above results are applicable to semi-homogeneous samples and for turbid media, with large scale spatial heterogeneities (e.g. multi-layer systems) but cannot be applied directly if the photon path length varies through more complex dependencies and the relation between intensity distortion and depth of inclusion is not readily scalable with a single scaling factor. Overall, the presented results pave the way towards the use of SORS for non-invasive in vivo identification and depth prediction of lesions within biological tissues.
Conclusions
We have proposed and demonstrated the use of SORS for non-invasive prediction of the depth of inclusions within a homogenous turbid medium without recourse to internal calibration models as required by previous methodologies. The depth of paracetamol tablet and SERS-active NPs buried as single entities inside either a polyethylene matrix or porcine tissue, respectively, have been determined with the non-invasive measurement using only externally acquired calibration measurements. The performance of the method was compared with that of our previous approach based on internal calibration measurements. Although the internal calibration model yielded somewhat more accurate depths, with a lower RMSEP, the external measurement concept proved to be still highly effective (RMSEP 7.3% and 10.7%, instead of 7.2% and 9.5% yielded by the internal calibration method) with a critical advantage of being completely non-invasive and as such highly suitable for in vivo uses. Similar results were reported with the use of TRS measurements.13 Here, by applying Monte Carlo modelling of photon propagation, it was possible to extend the concept to the SORS geometry creating a model that can be used in situations where TRS cannot be applied. This leads to a wider range of applications where depth determination of a single inclusion is required. In particular, the external calibration concept was validated with ex vivo porcine tissue to model typical situations that can be present in in vivo scenarios in terms of tissue components (e.g. water, lipid and blood) and geometrical factors. Within this context, the capability of the detection and depth prediction of SERS labelled NPs in biological tissues opens the way for future applications for non-invasive in vivo disease diagnostics in clinical settings.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by EPSRC Programme Grant Raman Nanotheranostics ‘RaNT’ (EP/R020965/1). The authors would like to acknowledge the support of Michael Natan and Cabot in providing the NPs used in this study.References
- P. Matousek, I. P. Clark, E. R. C. Draper, M. D. Morris, A. E. Goodship, N. Everall, M. Towrie, W. F. Finney and A. W. Parker, Appl. Spectrosc., 2005, 59, 393–400 CrossRef CAS
.
- P. Matousek, Appl. Spectrosc., 2006, 60, 185–187 Search PubMed
.
- M. D. Keller, S. K. Majumder and A. Mahadevan-Jansen, Opt. Lett., 2009, 34, 926–928 CrossRef
.
- P. Matousek and N. Stone, Analyst, 2009, 134, 1058–1066 RSC
.
- P. Matousek and N. Stone, J. Biophotonics, 2013, 6, 7–19 CrossRef CAS
.
- P. Matousek and N. Stone, Chem. Soc. Rev., 2016, 45, 1794–1802 RSC
.
- F. Martelli, T. Binzoni, A. Pifferi, L. Spinelli, A. Farina and A. Torricelli, Sci. Rep., 2016, 6, 1–14 CrossRef
.
- P. Matousek, M. D. Morris, N. Everall, I. P. Clark, M. Towrie, E. Draper, A. Goodship and A. W. Parker, Appl. Spectrosc., 2005, 59, 1485–1492 CrossRef CAS
.
- B. Gardner, N. Stone and P. Matousek, J. Raman Spectrosc., 2020, 1–5 CAS
.
- B. Gardner, N. Stone and P. Matousek, Faraday Discuss., 2016, 187, 329–339 RSC
.
- B. Gardner, N. Stone and P. Matousek, Anal. Chem., 2017, 89, 9730–9733 CrossRef CAS
.
- S. Mosca, P. Dey, T. A. Tabish, F. Palombo, N. Stone and P. Matousek, Anal. Chem., 2019, 91, 8994–9000 CrossRef CAS
.
- S. Mosca, P. Dey, T. A. Tabish, F. Palombo, N. Stone and P. Matousek, J. Biophotonics, 2020, 13, 1–7 CrossRef
.
- F. Nicolson, B. Andreiuk, C. Andreou, H.-T. Hsu, S. Rudder and M. F. Kircher, Theranostics, 2019, 9, 5899–5913 CrossRef CAS
.
- A. I. Henry, B. Sharma, M. F. Cardinal, D. Kurouski and R. P. Van Duyne, Anal. Chem., 2016, 88, 6638–6647 CrossRef CAS
.
- N. Stone, M. Kerssens, G. R. Lloyd, K. Faulds, D. Graham and P. Matousek, Chem. Sci., 2011, 2, 776 RSC
.
- A. S. Moody, P. C. Baghernejad, K. R. Webb and B. Sharma, Anal. Chem., 2017, 89, 5688–5692 CrossRef CAS
.
- S. Mosca, P. Lanka, N. Stone, G. Valentini, S. Konugolu Venkata Sekar, P. Matousek and A. Pifferi, Biomed. Opt. Express, 2020, 11, 1697–1706 CrossRef
.
- K. L. Bechtel, W. Shih and M. S. Feld, Opt. Express, 2008, 16, 12737–12745 CrossRef CAS
.
-
S. L. Jacques and L. Wang, in Optical-Thermal Response of Laser-Irradiated Tissue. Lasers, Photonics, and Electro-Optics, Springer, Boston, MA, 1995, pp. 73–100 Search PubMed
.
- P. Matousek, M. D. Morris, N. Everall, I. P. Clark, M. Towrie, E. R. C. Draper, A. E. Goodship and A. W. Parker, Appl. Spectrosc., 2005, 59, 1485 CrossRef CAS
.
- M. Z. Vardaki, H. Sheridan, N. Stone and P. Matousek, Appl. Spectrosc., 2017, 71, 1849–1855 CrossRef CAS
.
- B. B. Das, F. Liu and R. R. Alfano, Rep. Prog. Phys., 1997, 60, 227–292 CrossRef
.
- A. Sassaroli and F. Martelli, J. Opt. Soc. Am. A, 2012, 29, 2110 CrossRef
.
- W. E. Doering, M. E. Piotti, M. J. Natan and R. G. Freeman, Adv. Mater., 2007, 19, 3100–3108 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Schematic of the experimental set-up, results of Monte Carlo modelling, Calibration model based on different SF. See DOI: 10.1039/d0an01292k |
| This journal is © The Royal Society of Chemistry 2020 |