Evaluating medical device and material thrombosis under flow: current and emerging technologies
Jun Ki
Hong
 abcde,
Lingzi
Gao
abcde,
Lingzi
Gao
 cdef,
Jasneil
Singh
cdef,
Jasneil
Singh
 ceg,
Tiffany
Goh
ceg,
Tiffany
Goh
 ceg,
Alexander M.
Ruhoff
ceg,
Alexander M.
Ruhoff
 cef,
Chiara
Neto
cef,
Chiara
Neto
 ad and
Anna
Waterhouse
ad and
Anna
Waterhouse
 *bcdef
*bcdef
aSchool of Chemistry, The University of Sydney, NSW 2006, Australia
bSchool of Medical Sciences, Faculty of Medicine and Health, The University of Sydney, NSW 2006, Australia. E-mail: anna.waterhouse@sydney.edu.au
cHeart Research Institute, Newtown, NSW 2042, Australia
dThe University of Sydney Nano Institute, The University of Sydney, NSW 2006, Australia
eThe Charles Perkins Centre, The University of Sydney, NSW 2006, Australia
fCentral Clinical School, Faculty of Medicine and Health, The University of Sydney, NSW 2006, Australia
gSchool of Biomedical Engineering, Faculty of Engineering, The University of Sydney, NSW 2006, Australia
First published on 12th October 2020
Abstract
Although blood-contacting medical devices are used widely, blood clot formation (thrombosis) leads to device failure and potentially catastrophic adverse thrombotic events for patients, such as stroke or pulomonary embolism. Systemic anti-thrombotic drugs aimed at reducing these complications do not always prevent device thrombosis and can cause increased bleeding risks. Therefore, our understanding of material thrombosis mechanisms needs to be improved in order to develop next generation blood-contacting medical devices and materials. Medical device development requires material thrombogenicity evaluation according to the International Standards 10993-4 Biological evaluation of medical devices–Selection of tests for interactions with blood, which highlights that one of the key aspects for testing is a clinically relevant flow system. In this review, we first provide an overview of the current knowledge regarding material thrombosis and important physical and biological aspects of blood flow in relation to thrombus formation. We then examine commonly used in vitro flow systems to evaluate material and medical device thrombosis, focusing on their capabilities, advantages and disadvantages. Finally, we explore recent advances in technology that will aid in improving the design and fabrication of flow systems, mechanistic analysis and computational modelling.
1. Introduction
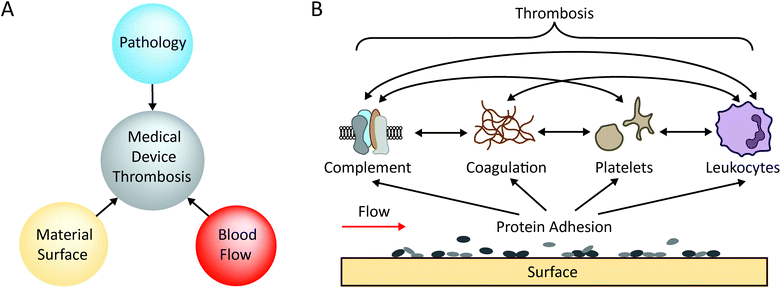
Blood-contacting medical devices are often used to treat a wide range of diseases. Devices range in size, function, material composition, anatomical placement and duration of contact with the blood. Examples of blood-contacting medical devices include stents,1–3 catheters,4–6 ventricular assist devices (VADs), artificial heart valves and vascular grafts.7–9 Despite the many advantages provided by such devices, synthetic biomaterials are affected by biological fouling (biofouling).10–13 Biofouling of medical devices is the non-specific adsorption of proteins onto material surfaces which then allows cell adhesion. In the presence of microbes this can lead to infection and sepsis,14,15 and in contact with blood, this can lead to blood clots (thrombosis) and subsequent complications such as occlusive thrombus formation, stroke via thrombus embolisation, as well as device failure through ‘clogging’.16,17Medical-device induced thrombosis is one of the major complications of implantable medical devices that are exposed to blood.16,18,19 Virchow's triad describes the 3 key conditions necessary for thrombosis to occur.20 In relation to material-induced thrombosis, these are the hypercoagulability of the blood (pathology), haemodynamic factors (low flow/stasis or high flow), and medical device materials, shown in Fig. 1A. The typical process by which biomaterial thrombosis occurs is illustrated in Fig. 1B. Due to their high plasma concentrations and high diffusion coefficients, plasma protein adsorption to the material surface is followed by synergistic adhesion and activation of coagulation factors,21 platelets, leukocytes11 and/or complement cascade proteins,21 resulting in thrombosis.19 A vast number of different types of proteins can adsorb to the surface to initiate thrombosis, including; fibrinogen, high molecular weight kininogen (HMWK), pre-kallikrein (PK), factor XII (FXII), complement proteins, von Willebrand Factor (vWF), and immunoglobulins, leading to complex protein–biomaterial and protein–protein interactions.22 For example, activation of surface-bound FXII not only triggers thrombin generation via the intrinsic pathway of coagulation, but also induces complement activation.14 In the case of fibrinogen, conformational change after adsorption is the key parameter for platelet adhesion and activation rather than adsorbed quantity.23 On the surface of materials, the adsorbed amount and conformation of these plasma proteins is dependent on material surface properties such as wettability,24 surface charge,25 chemistry, and topography.26–28 The adsorbed protein layer subsequently dictates the activation of coagulation, platelets, and leukocytes. For a detailed review of the thrombogenicity of biomaterials, we direct readers to a recently published review series.10–12,14 Variations in medical device type, implant location and geometry can induce disturbed flow conditions (both low and high flow, see section 2), making the interplay of biological pathways complex. Ultimately, our understanding of the mechanisms which underpin material-induced thrombosis is still incomplete.14,29,30
Current clinical solutions to medical-device thrombosis involves the administration of anticoagulants such as heparin, warfarin and/or antiplatelet therapies.17 However, they have the continued risk of bleeding complications and do not always prevent medical-device thrombosis.14 Despite the development of many new medical devices, materials and surface coatings in recent decades, we have generally failed to decrease medical device thrombosis clinically or reduce the need for anti-thrombotic therapies.7,22,31–33 As such, there remains an unmet clinical need for low and anti-thrombogenic materials for blood-contacting medical devices.19,31,34
There are a number of reasons for the lack of understanding of blood–material interactions,35 one in particular is due to a lack of standardised, predictive in vitro and in vivo haemocompatibility tests.35–38 The International Standard Medical Device Testing – ISO 10993-4 (Biological evaluation of medical devices – Selection of tests for interactions with blood) describes the recommended methods of testing for medical devices that interact with blood for regulatory purposes.3,30,38,39 According to these Standards, the characterisation of blood interactions with medical devices and materials should mimic the clinical conditions as closely as possible and analysis should be performed to assess activation of the major pathways and key factors involved in medical device thrombosis (depending on the device type): thrombosis, coagulation, platelets, haematology, and complement.40 Given these criteria, and that the majority of blood-contacting medical devices used clinically are exposed to flowing blood, the ISO10993-4 suggests model systems should include clinically relevant blood flow conditions and use whole blood.41,42 A number of different in vivo and in vitro models and systems have been developed for this purpose, each with specific advantages and disadvantages.29,43In vivo animal models allow evaluation of medical devices or materials with whole blood under physiological flow conditions; however, they can be cost prohibitive and time consuming.40 More importantly, animal model data may not be an accurate representation of clinical device performance due to the considerable variations in blood composition, anatomy and physiology between species.44,45
In vitro blood flow models for testing the thrombogenicity of device materials typically use human whole blood or separated blood components from volunteer donations, and are generally less costly.36 Small sample volumes allow for replicate testing of multiple materials and controls simultaneously using the same batch of blood. In combination with controlled flow conditions, temperature and anticoagulation, in vitro methods can provide further insights into thrombotic processes that may occur on medical device materials.36 Nonetheless, they are not without their own set of limitations. The lack of activation-inhibiting functions of endothelial cells and blood recirculation in model systems can result in accumulation of activated cells and proteins and cause the material-induced thrombotic reactions to occur more quickly which prevents studies longer than a few hours being carried out with in vitro methods.36,40 As such, a combination of methods are required to effectively assess the potential translation of materials to clinical applications. Utilising and further developing in vitro systems to their fullest potential will aid in the development of future anti-thrombogenic medical devices and materials.
1.1 Overview
This review highlights and summarises some of the commonly used in vitro methods for analysing blood–biomaterial interactions dynamically. The focus is particularly on methods that include the effect of blood flow, which has a key role in governing thrombus formation (see section 2). We first describe the flow and biological parameters relevant to medical device thrombosis. Second, we describe some common systems used to evaluate and study material haemocompatibility, highlighting their applications, distinct advantages, as well as their limitations. We conclude by providing an outlook into the development of new techniques to assess and understand the dynamic interplay of events at the blood–material interface. Such strategies include the utilisation of cutting-edge bioengineering tools and advances in microscopy techniques as well as computational fluid dynamic modelling.Understanding the complex interactions of medical device materials with blood, proteins, and cells is essential for the development of more sophisticated materials for the next generation of blood-contacting medical devices such as those used in the treatment of cardiovascular disease. Some proposed materials in development include the immobilisation of anti-thrombogenic or thrombolytic proteins and biomolecules or the fabrication of anti-fouling coatings.11,12,46 However, this is beyond the scope of the current review and instead, we direct interested readers to numerous recent reviews on novel anti-thrombogenic and thrombolytic surface coatings and materials.47–53
2. Blood flow-induced medical device thrombosis
Blood flow in the body is driven by the physiological action of the heart or is imparted by the mechanical movement of the medical device. The interplay between blood flow and thrombus formation is complex and several reviews have summarised important flow features of blood.54,55 In order to describe blood flow in vessels and constrained geometries typical of medical devices, it is useful to define first, in simple terms, a few concepts used in fluid dynamics.2.1 Physical basis of blood flow and fluid dynamic properties
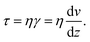 | (1) |
Wall shear stress τ increases with increasing velocity gradient near the vessel wall and increasing fluid viscosity. It is important to quantify wall shear stress in blood vessels because the flow interacts with the vessels endothelium.58 For example, in arteries at regions with lower wall shear stress, blood components have longer residence times near the wall, and this has been associated with higher risk of atherosclerosis.59
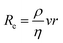 | (2) |
2.2 Implications of blood flow for medical device thrombosis
Physiologically, shear stress in blood vessels of differing sizes usually ranges between 2 and 36 dyne per cm2 (Table 1). There are well-established associations between fluid dynamic parameters such as stagnation, high shear stress and turbulence, and thrombotic processes such as coagulation and platelet activation and aggregation.20,67 Low blood flow increases transport and diffusion of proteins and cells to surfaces, increasing the residence time of prothrombotic components on a surface and causing leukocyte adhesion.20,21 Additionally, high shear rate and stress induced by blood flow can affect mechanosensitive proteins and cells and cause thrombus formation.29,68 These are discussed further in sections 2.3.1 and 2.3.2.| Flow rate (mL min−1) | Wall shear stress (dyne per cm2) | Maximum shear strain rate (s−1) | Ref. | |
|---|---|---|---|---|
| Left ventricular assist device (LVAD); extracorporeal membrane oxygenator (ECMO).a Calculated from eqn (1), assuming dynamic viscosity of human whole blood to be 3.5 mPa s at 37 °C.120 Medical device values are maximum with references representing ranges from different device types. Catheter dimensions are outer diameter. | ||||
| Anatomical locations | ||||
| Aortic valve | 5000 | 4–11 | 20 | 94–98 |
| Large arteries | 250–500 | 14–36 | 300–800 | 83, 99 and 100 |
| Coronary artery | 120–300 | 5–15 | 800–2500 | 101–103 |
| Stenotic vessels | 120–180 | 36–450 | 800–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
83, 99 and 103 |
| Large veins | 200–700 | 2–3.4 | 10–500 | 84, 104–106 |
| Medical devices | ||||
| LVAD pump | 5400 | 6000 | 171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429a 429a |
99 and 107 |
| ECMO pump | 4000 | 1750 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000a 000a |
108 |
| Peripheral intravenous catheter 2.1 mm | 28 (blood flow rate) 240 (infusion rate) | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429a 429a |
69 and 109 |
| Peripheral intravenous catheter 1.1 mm | 28 (blood flow rate) 60 (infusion rate) | 1000 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571a 571a |
69 and 109 |
| Coronary stent | 120 | 40 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
74, 103 and 110–113 |
| Prosthetic heart valve | 5000 | 2400 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 571 |
114–119 |
The shear forces in medical devices are typically far greater than those found in the body as shown in Table 1 (40–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 dyne per cm2). Considerable variation in shear stress can occur within the one device, such as catheters and ventricular assist devices, which introduce both low and high shear stress conditions depending on their size, placement and geometric configuration.69,70 Of note, the highest shear rate in peripherally inserted catheters is caused by the mixing of the infusion solution with the blood at the catheter tip/endothelium/blood interface.69 Turbulent blood flow can occur in medical devices at regions of expansion, bifurcations, and joints/connections.71 Variations in device design can also affect haemodynamics, for example, the different pump mechanisms in left ventricular assist devices (axial and centrifugal flow pumps), have differing blood residence times and shear rates.72,73 Additionally, it is worth noting that shear and turbulence can increase drastically during exercise, for example, in coronary stents.74
000 dyne per cm2). Considerable variation in shear stress can occur within the one device, such as catheters and ventricular assist devices, which introduce both low and high shear stress conditions depending on their size, placement and geometric configuration.69,70 Of note, the highest shear rate in peripherally inserted catheters is caused by the mixing of the infusion solution with the blood at the catheter tip/endothelium/blood interface.69 Turbulent blood flow can occur in medical devices at regions of expansion, bifurcations, and joints/connections.71 Variations in device design can also affect haemodynamics, for example, the different pump mechanisms in left ventricular assist devices (axial and centrifugal flow pumps), have differing blood residence times and shear rates.72,73 Additionally, it is worth noting that shear and turbulence can increase drastically during exercise, for example, in coronary stents.74
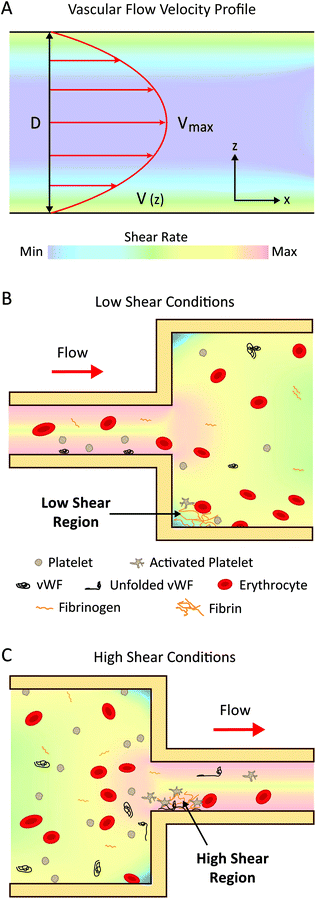
2.3 Haemodynamic implications for thrombus formation
In the following sections, we will elaborate on the biological mechanisms affected by variations in flow described in section 2.2. For the purposes of this review, we will classify shear rates as ‘low’ and ‘high’. ‘Low’ shear rates refer to a range between 0–1000 s−1, which are shear rates generally found in the veins, most arteries, and many medical devices. ‘High’ shear rates refer to values greater than 1000 s−1, which occur in specific arteries, pathological conditions, (such as atherosclerosis), and also found in number of medical devices (Table 1).As well as coagulation factor accumulation, cell adhesion can occur at low shear rates. Leukocyte adhesion is initiated above a shear stress threshold of ∼0.5 dyne per cm2 and rolling occurs optimally between ∼0.5–1.5 dyne per cm2. This process is regulated by the mechanical behaviour of specific classes of adhesion receptors on the leukocytes and endothelial cells on blood vessel walls.77 Additionally, erythrocytes, originally thought to only play a passive role in thrombosis, are now appreciated to be actively involved. At low shear rates, erythrocyte rouleaux increases blood viscosity and leads to increased local concentrations of coagulation factors.20 Furthermore, there is increasing evidence for the role of erythrocyte adhesion to the vessel wall and adhesion to growing thrombi, both indirectly and directly via fibrin and von Willebrand Factor (vWF).78
Although platelets can bind to fibrinogen at low shear (100–300 s−1)79 they are not activated at low shear rates and therefore are not thought to contribute significantly to thrombosis under low blood flow conditions.
In relation to medical devices, changes in device geometry such as expansions and connections can cause regions of low flow, recirculation and stagnation (Fig. 2B). These regions have a higher propensity for coagulation and subsequent thrombotic complications, observed from computational modelling and clinical data,69,80,81 such as in catheters, extracorporeal device connection points, and haemodialysis access sites.29 The introduction of catheters to veins can impede blood flow and cause occlusion of the vessel, leading to regions of low velocity and recirculation.69 These effects are increased with larger sized catheters with flow rates being reduced by up to 93% in some cases.80 Indeed, clinical meta-studies of peripherally-inserted central catheters revealed an increased risk of venous thromboembolism with the use of larger-diameter catheters81 and a decreased risk with the use of smaller-diameter catheters.82
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1 which greatly enhances vWF-platelet binding.84
000 s−1 which greatly enhances vWF-platelet binding.84
In addition to the shear-induced activation of platelets and vWF, erythrocytes are also sensitive to high shear stress and turbulence, which can cause membrane rupture and release of haemoglobin.17,89 Subsequent free haemoglobin can cause a number of thrombotic complications such as hypercoagulation,90,91 thromboembolism,78 and platelet activation induced by a reduction in nitric oxide bioavailability.78,91–93
These mechanosensitive properties of blood have major consequences for the thrombogenicity of medical devices. For instance, stents implanted in coronary arteries are exposed to high shear stress which causes platelet activation, requiring patients to receive dual anti-platelet therapies to prevent stent thrombosis.121,122 In VADs, the extremely high shear stress induces vWF conformational changes which exposes degradation sites for the protease ADAMTS-13, resulting in rapid depletion of large vWF multimers, leading to poor vWF-platelet adhesion and a bleeding condition known as acquired von Willebrand Syndrome.99 Furthermore, haemolysis and associated complications can be caused by artificial heart valves,123 haemodialysis circuits,124 and VADs.16
3. Methods to assess thrombosis on medical device materials under flow
In this section, we will highlight some of the most common in vitro analysis methods which incorporate flow that are used to assess the interaction of biomaterials with blood and blood components, summarised in Table 2. We briefly describe the operating principle of each method along with some examples of their utility and application for studying the thrombogenicity of various materials under blood flow. Given its importance in designing and interpreting experimental model systems, we will first give a brief overview of computational fluid dynamic (CFD) simulation of blood flow in relation to medical devices and in vitro model systems.| Method | Shear strain rate (s−1) | Advantages | Disadvantages | Ref. |
|---|---|---|---|---|
| Chandler loops | 50–428 | • Whole blood | • Narrow shear range | 134, 146, 152 and 153 |
| • Simple | • Only mimics low shear medical devices | |||
| • Low cost | • Recirculation | |||
| • Material inside tubing or tubing itself | • End-point assay | |||
| • Medium blood volume (∼3–20 mL per sample) | ||||
| Flow loops | 50–82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 143 143 |
• Whole blood | • Medical device flow/shear difficult to replicate unless medical device is used to drive flow | 134, 144 and 152 |
| • Medically relevant pumps/devices can be incorporated or material inside tubing or tubing itself | • Recirculation (generally) | |||
| • Time point sampling possible | • Large blood volume (∼50–100 mL per sample) | |||
| • Single pass flow possible | • Haemolysis (unless evaluating haemolysis) | |||
| TEG/ROTEM | 0.1–0.5 | • Whole blood or plasma | • Only low shear | 154–161 |
| • Low blood volume (<1 mL per sample) | • Non-physiological flow pattern | |||
| • No effects of stasis (Virchow's Triad) | • Baseline variability across individuals | |||
| • Fast results and real-time outputs | • Choice of material limited to cup material or coating thereof | |||
| Cone-and-plate rheometry | 0.1–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
• Whole blood or platelets | • Complicated flow regimes at higher shear rates | 158 and 162 |
| • Wide range of shear rates | • Cone material is usually not modifiable | |||
| • Easily interchangeable sample material | • Possibility of fluid evaporation over time | |||
| • Physical clot properties at known time-point | ||||
| • Low blood volume (<1 mL per sample) | ||||
| • Potential for real-time measurements | ||||
| Parallel plates and microfluidic devices | 50–1000 | • Whole blood or platelets | • Replicating turbulence is difficult at the microscale | 148, 163–170 |
| • Wide range of shear rates | • Impact of viscosity effects is greater | |||
| • Low blood volume (<1 mL per sample) | ||||
| • Real-time measurements | ||||
| • Desired geometry possible to replicate wide range of flow conditions | ||||
| • Materials/coatings can be incorporated | ||||
3.1 Computational fluid dynamic modelling of blood flow in medical devices and in vitro models
As medical device thrombus formation is material16 and flow dependent,67 numerical characterisation of the haemodynamic conditions within medical devices, including, but not limited to velocity, pressure and wall shear stress, is critical. The flow changes due to blood-contacting medical devices such as catheters (Fig. 3A),69 stents,110,111 and mechanical valves (Fig. 3B)115,125 have been widely modelled using CFD simulations, as have ex vivo devices and tubing systems.126 CFD simulations of more geometrically complex medical devices such as ECMO108 and LVADs (Fig. 3C)107,127 require more advanced, specialised knowledge and are more computationally expensive to accurately model. However, this is particularly important due to the widely varying geometries of components such as centrifugal pumps, roller pumps, and oxygenators. These contain dramatic expansion and contraction of flow at inlets, outlets, and in pump regions, which lead to turbulent flow, fluctuating viscosity, fluctuating velocity, and zones of stagnation.128 For example, previous CFD models from multiple groups have identified the shear stress range in LVAD impellors to range between 0–6000 dyne per cm2,99,107,129,130 however from the simulations it can be noted that 99% of the blood volume does not experience shear stress greater than 500 dyne per cm2 (Table 1). However, this is similar for most devices. Additionally, dedicated simulations can be conducted that specifically investigate thrombus formation, for example, the positioning of an LVAD outflow cannula in the aorta significantly affect thrombus distribution throughout the aorta due to the altered aortic flow conditions.131 CFD models of in vitro experimental systems are useful for rigorous design of the model, to characterise the model set up and flow conditions, and to interpret results.132 They are referred to in subsequent parts of section 3.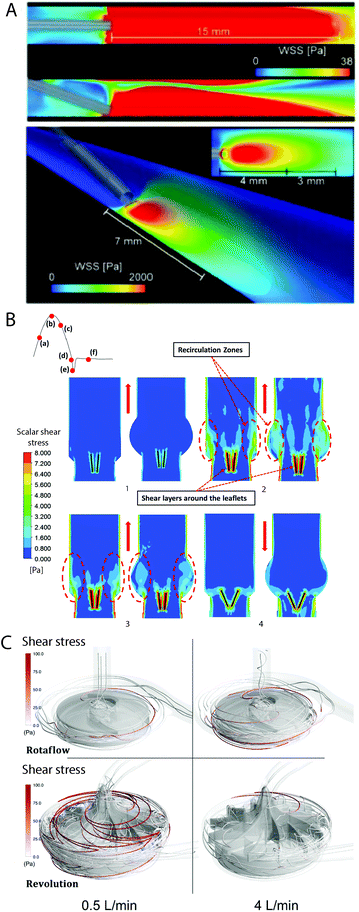 | ||
| Fig. 3 Computational fluid dynamic (CFD) modelling is commonly used to model medical devices. (A) Wall shear stress (WSS) of catheter placement in a blood vessel.69 Reproduced from ref. 69 with permission from Springer Nature, copyright 2018. (B) CFD model showing high shear stress, stagnation and recirculation near the leaflets of a bileaflet mechanical heart valve (at 0 degree tilt) in straight or anatomic aortas, during different phases of the cardiac cycle (1–4).125 Reproduced from ref. 125 with permission from John Wiley and Sons, copyright 2020. (C) Shear stress on a particle streamline of a centrifugal pump used in extracorporeal oxygenation machines (ECMO).108 Reproduced from ref. 108 with permission from Springer Nature, copyright 2019. | ||
3.2 Test flow loops
Flow loops vary widely in their design and method of imparting fluid flow.29,30 Flow loops allow the evaluation of thrombus formation directly via thrombus weight, as well as surface thrombosis using microscopy such as scanning electron microscopy (SEM).133 In blood sampled from these loops, cell number and activation state, and protein levels and activation state, can be measured via flow cytometry, enzyme-linked immunosorbent assays respectively, and desired specific assays can be carried out, for example, for haemolysis.133,134Importantly, blood flow measurements allow comparison of results to clinical or medical device flow parameters. Laser Doppler and laser speckle are useful techniques for measuring flow rates in vessels in vivo,135–137 however, these generally provide relative flow measurements and laser speckle is limited by its poor depth specificity.138 Therefore, they are not generally used for investigating biomaterial thrombogenicity, although laser speckle or laser Doppler have been used to compare or calibrate flow rates in tubing or capillary tubes in vitro, prior to in vivo use.139–141 In contrast, Doppler ultrasound provides quantitative flow rate measurements and has been used to measure blood flow in in vivo models of device thrombogenicity, for example, vascular grafts,142 as well as to measure blood flow in in vitro models of circuits containing medical devices143 or tubing systems.136,137,144
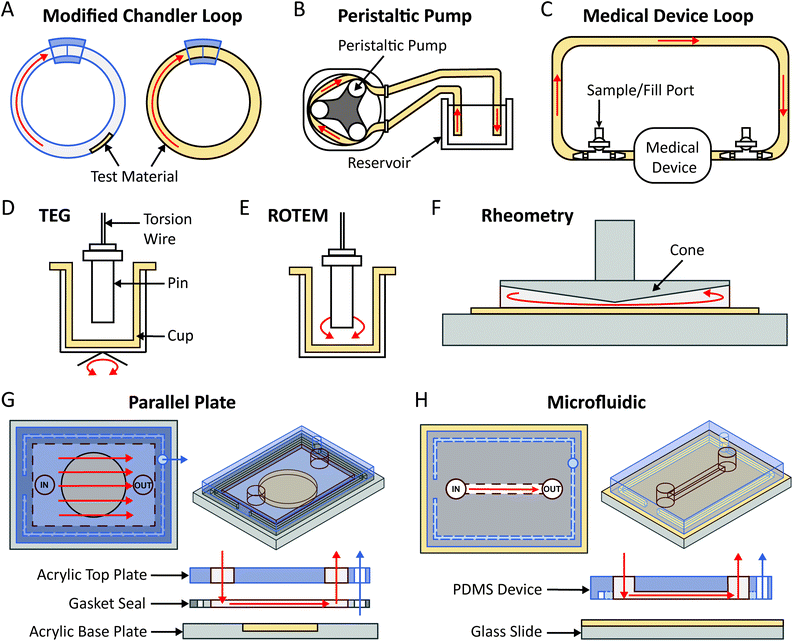
The simplest flow loop system is the modified Chandler loop which uses a rotating wheel to drive blood flow in tubing loops and is an established method for investigations into material thrombosis under flow.145 Materials can either be placed inside or used as the tubing (Fig. 4A), allowing blood contact under flow rates of 25–200 mL min−1, replicating venous and coronary artery flow rates (Table 1). Modified Chandler loops have been used to measure a variety of materials, with specific tests driven by the aims of each investigation (Table 2). For example, to investigate the haemocompatibility of alternative materials for prosthetic heart valves, Brubert et al. placed various block co-polymers in a modified Chandler loop, exposing materials to blood flow at shear rates up to 300 s−1. Platelet and coagulation cascade activation on these materials was reduced relative to polystyrene and while more thrombogenic than clinically used alternatives including bovine pericardium, inflammation was reduced.146
A key advantage of modified Chandler loops is the ability to incorporate whole blood into a simple, relatively low-cost setup to study material thrombogenicity under flow. However, these loops have several limitations. They require a large blood volume to test multiple materials and controls and the assays are usually end point. Modified Chandler loops are closed systems which recirculate the same, small blood volume over the material surface, which can overestimate the thrombogenicity of materials due to accumulation of activated blood components. While suitable for replicating low shear strain rates, to our knowledge, modified Chandler loops have not replicated shear rates above 500 s−1 (Table 2). Additionally, the paucity of CFD simulations of modified Chandler loops has impaired our understanding of flow conditions within these systems, with some studies indicating that, due to the tubing curvature, traditional straight tube approximations of flow are inaccurate at higher rotation rates.147
To overcome the flow limitations of Chandler loops for testing medical grade tubing, components and devices, large flow loops powered by peristaltic pumps,133,134,148 and flow loops linked directly to medical device circuits (e.g. LVAD,133,149 ECMO148) have been used (Fig. 4B and C). The peristaltic pump flow loop pumps blood from a reservoir, through a tubing loop and back to the reservoir (Fig. 4B). The peristaltic pump generates pulsatile flow more characteristically similar to that observed in vivo, as flow velocity and thus the resulting rheological conditions may be controlled by varying the pump power and frequency.127,134 Furthermore, these pumps are used in clinical haemodialysis and cardiopulmonary bypass circuits. Previously van Oeveren et al. mimicked coronary blood circulation in peristaltic flow loops using a flow rate of 40 mL min−1 to generate a shear stress of 12 dyne per cm2.134 Similar to the modified Chandler loop, the material being tested may be placed inside or used as the tubing of the loop. Meanwhile for medical device flow loops, a loop is formed by tubing connected between the inlet and outlet of the medical device, in which part of the tube contains a fill port and outlet port from which the circulating blood is filled and removed (Fig. 4C). As the medical device being tested is part of the loop, flow and shear rate conditions such as those of the LVAD and ECMO are more easily replicated, and the material surface being tested is contained within the medical device component.133,148,149
Key advantages of large flow loops compared to modified Chandler loops include the ability to achieve and control a wider range of flow and shear rate conditions and to recirculate larger volumes of blood, allowing evaluation of actual clinical devices. However, they require acquisition of large volumes of fresh blood and haemolysis can occur due to blood recirculation (although this is not a disadvantage if evaluating rates of haemolysis).134 Furthermore, generating CFD models of peristaltic flow to ascertain the precise flow and shear conditions within the large flow loop experimental setup is much more difficult than producing CFD models for fully-developed, ‘smooth’ flow experimental systems.127,150,151 Previous attempts to computationally model peristaltic pump systems revealed that flow and shear conditions are significantly affected by the wall geometry (highlighting the gap between CFD assumptions and experimental models).127
Arising from the need for a flow loop system which produces higher shear rate ranges while minimising haemolysis, the Haemobile ball valve model was recently designed to generate flow waves most similar to that of in vivo physiological conditions, compared to modified Chandler loops and large flow loops.134 The pulsatile flow within the loop is controlled by a ball valve in the cylindrical chamber of the flow loop, which also ensures uni-directional flow of blood within the loop.144 A Doppler ultrasound flow probe was used to determine flow rates and subsequently calculate the wall shear stress and confirm pulsatile flow patterns.144 The only drawback is that it is still a closed loop system. So far, the Haemobile has been used successfully to evaluate the thrombogenicity of polymer tubing and vascular graft materials.134,144
3.3 Thromboelastrography (TEG)/rotational thromboelastometry (ROTEM)
TEG/ROTEM are viscoelastic methods of monitoring clot formation. These tests consist of a plastic cup and a pin attached to a torsion wire (Fig. 4D and E). In TEG, the cup oscillates 4.75° every 5 seconds (Fig. 4D), while in ROTEM the pin oscillates 5.25° every 6 seconds, inducing low shear rates analogous to venous blood flow (Fig. 4E).161 In response to recalcification, fibrin fibre formation increases torsion on the wire, which is detected as clot firmness.156 These assays provide several useful indicators of material thrombogenicity, including: time to fibrin formation or clotting time, rate of clot formation, maximum clot strength and clot susceptibility to fibrinolysis.156,161 Shear stress in TEG/ROTEM is low (0.1–0.5 dyne per cm2) however, limited CFD information is available for how these numbers were derived.155,157 TEG/ROTEM systems are predominantly used clinically to diagnose a range of coagulopathies including trauma induced coagulopathy and to assess bleeding risks during cardiac surgery.161TEG/ROTEM is an easy and effective technique which shows promise for assessing the effects of low shear on biomaterial coagulation. Recently, TEG has been utilised to study the thrombogenicity of material surface coatings applied to the base cup under low flow. The anti-adhesive, omniphobic tethered-liquid perfluorocarbon (TLP) surface coating applied to TEG cups displayed increased clotting time, reduced rate of clot formation and reduced clot strength relative to untreated Cryolite® (acrylic polymer) cups. Furthermore, TLP displayed faster fibrinolysis compared to control cups.160 Similarly, a poly(carbonate-urea)urethane polymer coating incorporating polyhedral oligomeric silsesquioxanes displayed reduced maximum clot strength and increased clot lysis at 60 minutes post-thrombus formation.154,171
TEG/ROTEM have several limitations. TEG/ROTEM recycles the same volume of blood throughout the assay in a non-physiological flow pattern. Furthermore, the cup material is currently limited to polymethylmethyacrylate (PMMA, acrylic) in ROTEM and Cryolite® in TEG.161 Thus, material thrombosis studies are currently restricted to surface modifications which can be applied to the cups supplied with the TEG/ROTEM analysers. In TEG®6s and ROTEM® Sigma devices, the test cup comes integrated into microfluidic channels which contain reservoirs with lyophilised activator or inhibitor reagents (e.g. tissue factor).122,123 While this modification has allowed even faster thrombogenicity/haemostasis monitoring clinically, utilisation of older models to study biomaterial thrombosis might be most appropriate due to detachable cups allowing facile material modifications (e.g. with surface coatings). Finally, it is worth noting that there is high variability between individual blood donors necessitating the use of baseline measurements if comparison to clinical data is desired.172
3.4 Cone-and-plate rheometry
Cone-and-plate (CP) rheometry has been used for decades to study haemorheology and blood coagulation processes.63,173,174 The cone-and-plate set-up typically consists of a rotating cone on top of a flat baseplate, with the fluid of interest between the conical surface and the baseplate as illustrated in Fig. 4F. The angular separation between the cone surface and the base-plate usually varies between 0.5°–5°,175 which allows it to maintain uniform shear stress on the fluid of interest (independent of the radial location and the gap clearance).176,177 The rotation of the cone can be varied to impart different shear rates while the cone geometry can confer varying shear stresses as well as producing turbulent flow at high shear rates.176,178 Some applications of the CP rheometer in the context of blood rheology and coagulation have included measurement of platelet activation,83 blood viscosity,65 erythrocyte aggregation, haemolysis,64,179 effect of shear stress on whole blood coagulation,158,159 and thrombus contraction.180,181To assure that the desired fluid shear stress and shear rate are reflected in the experimental setup, CFD simulations have been used to model cone and plate apparatuses. Important parameters influencing thrombus formation that should be considered in CFD modelling include the cone surface and base-plate angle, the rotation and the heat transfer occurring between the cone and fluid.182 The accuracy of cone and plate CFD models is limited by the temperature and diffusion profile of the cone to disk gap, assumptions for the Nusselt and Sherwood numbers for heat transfer,182 whether a non-slip (zero velocity) assumption applies at fluid-surface boundary,183 whether flow may be assumed to be unidirectional,184 and accurately modelling the non-Newtonian properties of blood.
The cone-and-plate rheometer has also found applications in the testing of materials thrombogenicity and propensity for protein and cellular adsorption to artificial surfaces.185–187 These studies include the interaction between platelets and erythrocytes on synthetic surfaces such as stainless steel, PMMA and PEO-modified PMMA where the number of platelets in an aggregate were dependent on the material and shear rate (more platelets per aggregate for hydrophilic surfaces and at higher shear rates).188 Conversely, increased shear rates led to the decrease in the number of platelet-erythrocyte aggregates.188 Another study of platelet adhesion to tetrafluoroethylene-propylene copolymer surfaces suggested that shear-induced platelet ADP release determines the deposition, following the activation of thrombin.189,190 Interestingly, this is not the case for artery subendothelium.191 Recently, the study of platelet aggregation on carbon-based ceramic coatings under blood flow revealed interesting insights into the different mechanisms of aggregate formation.192 Platelet aggregation on hydrophobic carbon-coated surfaces at shear rates of 1800 s−1 was found to be dependent upon platelet activation. Under the same shear conditions, platelet aggregation on the more hydrophilic carbon-coatings were not shown to be reliant on the platelet activation state.192
Some of the advantages provided by the cone-and-plate method includes the ability to impart uniform shear stress across the sample and over a wide range of shear conditions (up to order of 105 s−1),162 and the ability to test different materials, with relatively small blood volumes with the potential for real-time outputs.174,177 A similar set-up with parallel plate geometries exists, (not to be confused with parallel plate flow chambers as discussed in section 3.5) which utilises a flat, rotating plate instead of a cone geometry. However, the parallel plate geometry imparts non-uniform shear stress due to the varying radial velocity of the flat plate.193
The limitations of the cone-and-plate system are that the technique does not reproduce the exact conditions of the blood flow such as in the case where eddy currents and regions of disturbed flow arise upon cellular adsorption causing undulations in the topography of the sample surface.64,176 Importantly, the testing of modified materials is limited to the sample placed on the baseplate since the cone is left unmodified which may influence the adhesion of blood components, depending on the cone material.194 Additionally, the rheological data are influenced heavily by the utilised geometries and are susceptible to user errors caused by incorrect blood sample loading such as underfilling or overfilling and the inclusion of trapped air and air bubbles.64,195–197
3.5 Parallel plate & microfluidics
Parallel plate and microfluidic flow devices are miniaturised flow models which have been used extensively in the field of haematology ranging from early straight channel glass capillary flow chambers to more recent custom devices.86,148,198 Studies using these devices have included the impact of surface adsorbed coagulation proteins on platelet adhesion,199 shear strain rates on vWF elongation,200 and shear gradient dependent platelet activation.67 The same techniques have been explored for clinical use in diagnostic applications.201,202There are no strict criteria differentiating parallel plate and microfluidic flow systems, and in some cases these terms are used interchangeably.203–205 Broadly, parallel plate flow chambers have channel cross sections with smaller height to width ratios and simpler flow paths (Fig. 4G and H). Velocity distribution through the channel cross section changes depending on the height to width ratios of the channel, from square (1.0) to parallel plate (0.0).206 Theoretical shear stress profiles for commonly used rectangular channels of finite width are highest at channel faces and drops to zero at the corners.207 Shear stress profiles in devices with complex geometries can be characterised with CFD to ensure the desired flow characteristics are replicated in vitro.148
Miniature flow models with channel geometries closer to parallel plate flow are commonly constructed by sandwiching a gasket (which defines the height) between two plates on which the surface of interest is mounted (Fig. 4G). A vacuum can be applied through the gasket to seal the flow channel and prevent device separation. In comparison, microfluidic devices can vary widely in channel complexity to generate complex flow paths. Devices can be formed using a variety of fabrication methods, most commonly by casting channels in elastomeric polymers, e.g. polydimethylsiloxane (PDMS) (Fig. 4H), termed soft lithography, from moulds fabricated utilising photolithography techniques. This result in channels with an open rectangular cross section, which are sealed by adhesion to a base containing the material of interest, to create an enclosed device (Fig. 4H). For both systems, precise flow control can be achieved using syringe or peristaltic pumps.
These systems have been applied to the study of thrombosis on medically relevant materials through the incorporation of a broad range of relevant polymers, metals and coatings in parallel plate and microfluidic devices. For example, platelet adhesion to various polymers and metals was investigated under flow, without165–169,208 or with pre-adsorption from protein solutions or plasma163,209 at shear strain rates of 43–1000 s−1. Notably, Jamiolkowski et al. measured dynamic adsorption of platelets over time to a range of medically relevant opaque materials using a suspension of platelets and cleared erythrocytes to minimise light scattering enabling surface visualisation by epifluorescence microscopy. The medical grade titanium alloy, Ti6Al4V, supported high levels of platelet adhesion, which was more pronounced at the highest shear strain rate (1000 s−1), compared to silicon carbide, alumina, coated titanium alloy (MPC-Ti6Al4V), yittria partially stabilised zirconia, and zirconia toughened alumina.165 Unique flow effects such as stagnation caused by crevice geometries,164 or due to sudden expansion of a flow path can also be modelled at this scale.166 Kragh et al. showed decreased platelet embolisation on carbothane compared to pelethane, with increasing embolic events at lower flow rates (<100 s−1 compared to ∼500 s−1), using a stagnation point flow chamber, where whole blood flow originated from a single point and spread radially across the surface.166 Additionally, the thrombogenicity of surface coatings has been evaluated using parallel plates or microfluidics. A tetraglyme coating reduced platelet adhesion compared to control, observed by real-time microscopy,210 and pressure measurements in a microfluidic channel showed a prolonged thrombus formation time on the anti-adhesive, TLP coating compared to control.211
Advantages of parallel plate and microfluidic devices include the replication of key aspects of fluid flow in vitro such as wall shear stress, shear strain rates, and fluidic effects resulting from channel geometry.148 Due to their small scale and low perfusion volumes these models allow the conservation of donor blood and reagents while maintaining physiologically relevant single pass flow where blood or individual blood components are passed over a test surface without recirculation. Dynamic changes in surface platelet adhesion and thrombotic events can be monitored through microscopy revealing aspects of thrombosis not seen on end-point or fixed samples.164–166,208 This technology has become more accessible over time as many commercial miniature flow systems have become available.
There are, however, limitations to these models as miniaturisation can also be a weakness. Flow at this scale is laminar, therefore, it is not possible to induce turbulent flow unless the smallest channel dimension is greater than 500 μm.148 Additionally, aspects of microscale blood flow should be considered when designing microfluidic models. Flow in small vessels (<1 mm) and therefore microfluidic channels, is non-Newtonian, meaning, the cell free layer at the vessel wall occupies a larger portion of the vessel, which decreases the viscosity of the blood, known as the Fahraeus-Lindqvist Effect.212,213 Channel dimensions also influence shear stress distribution in rectangular cross sections, therefore, lower height to width ratios should be used when even shear stress distributions are desired across the width of the channel.214,215
3.6 Remarks on current blood flow-material evaluation methods
A wide variety of flow systems are utilised to evaluate medical device thrombogenicity under flow, each providing numerous and varied data outputs. Here we described the advantages and disadvantages of the most commonly used techniques including peristaltic pump driven flow systems, modified Chandler loops, TEG/ROTEM, cone and plate rheometry, parallel plates and microfluidics. Flow loops and Chandler loops require larger volumes of blood but can measure multiple soluble markers from the blood. They can also evaluate medical devices directly, making them useful for translational studies. TEG/ROTEM allow evaluation of clotting parameters that are comparable to clinical measurements using low blood volumes, however, they can only operate under low flow conditions. Shear-induced adhesion and activation of blood proteins and cells has been made possible with cone-and-plate rheometry, and parallel plate or microfluidic systems. These systems require lower volumes of blood and can operate under a wider range of shear stress conditions. Furthermore, the parallel plates and microfluidic systems can provide real-time outputs such as pressure and microscopic visualisation, and are single pass flow systems compared to the flow loops and cone-and-plate rheometers which continuously expose materials to the same blood sample over the duration of the experiment.Medical device thrombosis is a complex, multi-phase process involving protein/cellular adhesion, clot growth and thrombolysis. Therefore, a single method cannot provide accurate assessment of all aspects of material thrombosis. It is clear that a combination of different methods should be employed in order to thoroughly evaluate the thrombogenicity of materials for applications in medical devices. Naturally, this could include the development of new and improved methods (both experimental and computational) that can offer an enhanced understanding of the processes underlying materials thrombosis. The following section (section 4) will explore some emerging bioengineering and characterisation techniques that could be employed for future investigations that aim to study the dynamic interaction of blood and materials. Of note, the examination of material thrombogencitiy should always be closely aligned to those outlined in the ISO 10993-4 standards and will also require effective pre-clinical, animal models in order to complement the understanding of the safety and efficacy of blood-contacting materials for potential future applications.
4. Emerging bioengineering and characterisation techniques
Recent progress in microfabrication, microscopy, and other multidisciplinary fields have enabled greater understanding of numerous physiological and pathological processes. Application of these novel techniques and adaptation of older techniques to the field of biomaterial thrombosis presents an opportunity to advance testing systems, knowledge and ultimately improve medical devices. We will highlight some exciting advances that could be used to develop model systems to address specific gaps in the field, improve analysis methods to obtain greater insight into dynamic events in material thrombosis, and advances in computational modelling that could improve accuracy of models and better predict outcomes of newly developed anti-thrombotic materials.4.1 Microfabrication for advanced experimental system design
Fabrication techniques on the milli- to nanometre scale have improved dramatically in recent decades. This has enabled more complex geometries to be incorporated into flow systems that replicate physiological and pathological conditions.148 Traditional soft lithography limits these channel shapes to rectangular structures and thus, they do not mimic the geometries of medical devices. Mannino et al. produced cylindrical channels using thin optical fibres as moulds (Fig. 5A). Changes in the optical fibre shape created complex channel geometries, with these used to develop vascular models of aneurysms, bifurcations, and stenoses (Fig. 5B).216 This low-cost and simple fabrication process could be adopted to replicate specific desired geometries of medical devices on a small scale.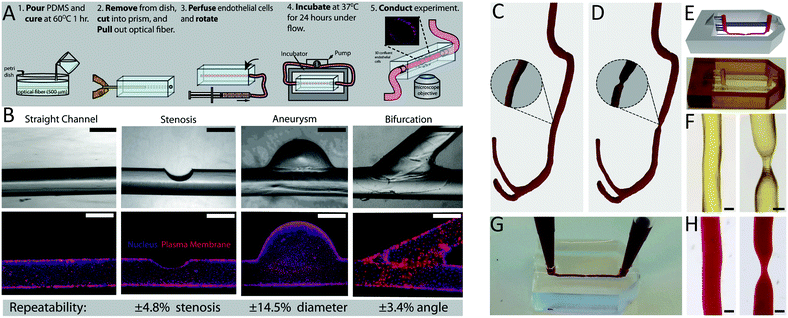 | ||
| Fig. 5 Novel fabrication techniques for microfluidic models. (A) Casting PDMS around optical fibres generated perfusable models of (B) straight vessels, stenoses, aneurysms and bifurcations.216 Complex, patient-specific geometries were obtained from computed tomography scans, modelling (C) healthy and (D) stenotic vessels. (E) Higher resolution 3D-printing technologies including stereolithography were used to develop microfluidic moulds of those geometries. (F) Geometric features were accurately reproduced with high resolution. (G and H) Microchannels were perfusable, enabling experiments with whole blood.219 (A and B) Reproduced from ref. 216 with permission from Springer Nature, copyright 2015. (C–H) Reproduced from ref. 219 with permission from the Royal Society of Chemistry, copyright 2017. | ||
Stereolithography (SLA), a more advanced additive manufacturing technique, has enabled the reproducible fabrication of microfluidics with complex geometries, cross-sectional channel resolution down to 18 μm × 20 μm (ref. 217) and low surface roughness.218 Using SLA, Costa et al. 3D-printed microfluidic replicas of healthy and stenotic blood vessels from patient computerised tomography scans (Fig. 5C–H).219 The ability to combine patient- and device-specific geometries with rapid prototyping techniques could allow personalised evaluation of medical device complications.
Another emerging fabrication technique is Two-Photon Polymerisation (2PP) lithography.220 This enables fabrication of fluidic systems with complex 3D architectures and nanoscale resolution. By combining standard photolithography with 2PP, channel widths of 420 nm have been fabricated in a non-cleanroom environment.220 However, the high cost and long print times have so far restricted use to specialised applications requiring significant precision.221 Recent attempts at customising the printing setup have significantly reduced print times.220,222 With a wider adoption of such systems, further advances in medical device mimetic models will be likely.
In addition to developing model systems with more sophisticated geometries, incorporation of more medically relevant materials could improve model systems. Traditionally, microfluidic systems are fabricated from glass and PDMS. However, glass is not generally used in medical devices and silicone is only used in a subset of medical devices. Recently, microfluidics have been fabricated out of a wide range of medically relevant polymers including polyurethane,223 polycarbonate, polyvinylchloride, and polytetrafluoroethylene,224 although the specific properties of these materials used for research differ from their clinically used counterparts, partly due to differences in the manufacturing and finishing processes.224 Furthermore, with advances in blood-contacting tissue engineered constructs for medical applications such as vascular grafts225 and heart valves,226 these tissue engineered materials could also be incorporated into experimental systems to evaluate their thrombogenicity.227,228 It should be noted that many of these techniques are for use to generate micron scale flow channels and if studies on turbulence are desired, larger channel dimensions are necessary as discussed in section 3.5.
4.2 Microscopic analysis for medical device thrombosis
Recent microscopy advances which overcome the technical limitations of conventional microscopes present the opportunity to capture material thrombosis events under flow with improved spatiotemporal resolution. Super resolution microscopy (SRM) techniques have recently pushed the boundaries of resolution to the tens of nanometre scale and offer the opportunity to study material–protein and material–cell interactions in greater detail to understand the cellular and molecular mechanisms involved in material thrombosis. The optimal choice of the SRM method depends on the in vitro experimental set-up. Generally, structured illumination microscopy (SIM) is better suited for live 3D-imaging due to reduced light intensity allowing longer imaging with less phototoxicity. For example, SIM has recently been used to observe dynamic cell rolling in a microfluidic flow model.229,230 However, the reduced light intensity comes at the expense of spatiotemporal resolution relative to other SRM methods.231To capture highly dynamic material thrombosis events in flowing blood, it is important to be able to acquire volumetric data at high speed with sufficient axial resolution. Suitable methods include, spinning disk confocal microscopy and lattice light sheet microscopy (LLSM). For example, LLSM was recently utilised to image leukocyte interactions with the vascular endothelium under flow in 3D, in an in vivo zebrafish model.232 New advances combining LLSM with adaptive optics (AO-LLSM) has helped to enhance spatial resolution.233 Of note, AO-LLSM was used to image the in vivo interactions of human breast cancer cells with zebrafish vascular endothelial cells.233 To our knowledge, LLSM is yet to be applied to in vitro biomaterial thrombosis flow models. The requirement for open working space above the sample and immersion into media for imaging in LLSM means spinning disk confocal microscopy is currently better suited for imaging enclosed in vitro blood flow experiments.
Live imaging deep within whole blood biomaterial thrombi is limited currently due to increased light scattering with increased tissue penetration, particularly due to the large number of opaque erythrocytes in whole blood. Combining two-photon imaging or spinning disk confocal microscopy with tissue clearing has enabling imaging up to a millimetre into fixed and cleared whole blood thrombi.234 This technique enables assessment of differences in thrombus formation at the biomaterial surface and in bulk solution. However, drawbacks include the necessity for end point analysis, long tissue processing time, and possible sample shrinkage.234
In addition to advances in microscopy techniques themselves, integrating microscopy with traditional flow techniques can provide more detailed information. For example, placing an inverted microscope under the baseplate of a custom cone-and-plate rheometer has previously been employed to observe the differential responses of cells under shear stress.179,235–237 This method could potentially allow the simultaneous acquisition of rheological information, as well as real-time visualisation of changes to the thrombotic behaviour of blood on various materials under applied shear. The main drawback of this method to study the thrombogenicity of materials is that the materials need to be optically transparent to allow for the acquisition of microscopy data, however, this is also the case for many of the microscopy techniques discussed here.
Finally, developments in approaches to data analysis is another area which could further complement and enhance the capability of microscopy techniques. Image processing techniques utilising machine learning have been used recently to rapidly classify platelet morphology in large data sets.238 Similar techniques could potentially be employed to monitor platelet response to material surfaces, for instance. This type of automation saves time and reduces human error and bias.
4.3 Computational modelling for medical device thrombosis
As previously discussed, CFD modelling is a valuable tool in the study of haemodynamic flow conditions in vivo, in vitro, and in situ. However, remaining challenges are associated with replicating aspects of flow dynamics, device material properties, and incorporating biological pathways when modelling medical devices and experimental systems.Flow dynamics in medical devices and in vitro often involve pulsatile, low shear and turbulent regimes. As previously discussed, (section 2) blood behaves as a non-Newtonian fluid under low shear conditions.62,65 Studies comparing different approaches to modelling both pulsatile150,151,239 and non-Newtonian blood flow,240,241 revealed variability in the results of fluid flow parameter numerical maps. Therefore, to improve accuracy of models in these flow regimes, further studies could validate computational models with experimental data using methods such as particle tracking velocimetry (PTV),242 and laser Doppler velocimetry (LDV).97 These techniques are valuable to determine blood flow patterns in models of medical devices (Fig. 6),97,243,244 however, their use to correlate flow parameters with material thrombogenicity in experimental in vitro flow systems is lacking. With advances in microscopy discussed in section 4.2, future improvements in this area are possible. For example, spinning-disc confocal microscopy allowed velocity profiles to be generated at desired depths throughout the microfluidic channel using an RBC suspension (20% haematocrit),245 and high-speed confocal microscopy revealed temperature-dependent changes in blood cell dispersion (using 12% haematocrit).246 Furthermore, turbulence can be a challenge to model and study experimentally,71,247 and the accuracy of the CFD turbulence models are limited by the accuracy of the chosen computational equations. Micro particle image velocimetry (microPIV),248–251 LDV249–251 and 3D PTV252 have been useful tools to study turbulence. However, the accuracy of microPIV, LDV and PTV are limited by data acquisition speed, because microturbulence is challenging to capture and track.249
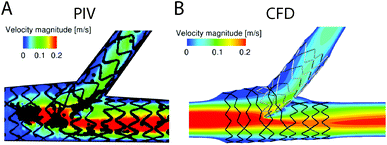 | ||
| Fig. 6 (A) Particle image velocimetry (PIV) and (B) computational fluid dynamic (CFD) comparisons of the fluid velocity profiles modelled in stented artery.243 For devices where fluid dynamic conditions may be difficult to computationally model, PIV may be used to gain experimental data. Alternatively, experimental PIV models may be used to verify CFD models. Figure reproduced from ref. 243 with permission from SAGE Publishing, copyright 2015. | ||
In addition to flow, the accurate modelling of material surface properties in a CFD model is important as material surface properties significantly influence protein adhesion and subsequent thrombus formation.10,11 The exact surface properties which result in such phenomena (e.g. wettability,24 surface charge,25 chemistry and topography26–28) are not easily converted into parameters for use in CFD models. For example, surface roughness, is often introduced into CFD simulations by altering the surface friction coefficient.253,254 While useful for characterising the bulk fluid dynamics at surfaces, this approach does not account for the complex protein and cellular interactions with the surface material, which contribute to material thrombosis.
Mathematically modelling biological pathways has also been applied to the field of thrombosis to predict overall thrombus growth,255 coagulation,20 platelet activation,256 and platelet adhesion and aggregation.257,258 A future direction for assessing thrombosis in vitro and in medical devices is through CFD modelling combined with mathematical models of the biomechanical and biochemical pathways involved in thrombus formation. Ultimately, all mathematical and computational models need to be supported by experimental validation and improved in vitro experimental flow systems to understand material interactions with biological systems.
5. Conclusions
Methods to test the performance of blood-contacting medical devices should account for the multitude of factors which reflect their end-use and carefully weigh up their benefits against the potential risks. Such factors for consideration include materials, medical device design and the clinical conditions under which the medical devices are handled, implemented, and operate. Haemodynamics is a key parameter of medical device thrombosis due to its crucial role in governing thrombus formation as well as the potential for the devices to be exposed to disturbed blood flow (or the lack thereof), during clinical applications, and should be appropriately reflected in the testing of material and device thrombosis.This review explored the advantages and disadvantages of the range of available in vitro methods that are commonly used to assess the interaction of medical devices and materials with blood under flow conditions. While many models exist, there is no single method which allows accurate assessment of all aspects of material thrombosis. Multiple methods should be used to evaluate the thrombogenicity of materials, surface coatings, or medical devices, in alignment with ISO 10993-4 Standards. Furthermore, while traditional material development and medical device evaluation has used blood flow loop systems such as the modified Chandler loop and peristaltic pump driven flow, a more mechanistic understanding of material thrombosis is possible with cone-and-plate rheometry, and parallel plate or microfluidic systems, because these systems require lower volumes of blood, can operate under a wider range of shear stress conditions and can provide real-time outputs.
As the field reaches maturity, we can hope to see studies that are able to include higher levels of complexity to more closely mimic relevant clinical scenarios. Improvements in engineering systems, design and production capabilities have enabled researchers to fabricate more advanced testing models on smaller scales with geometries to replicate clinically relevant flow conditions, increased resolution, and to incorporate device-specific materials. Continuing progress in other closely aligned areas of research such as high speed and high-resolution microscopy and computational fluid dynamics modelling can be utilised for biomaterial thrombosis studies to gain more in-depth knowledge of material thrombogenicity. Improved methods for assessing biological interactions with materials under blood flow, and for evaluating their potential for clinical applications will enable the development of safer blood-contacting medical devices.
Abbreviations
| μ | Kinematic viscosity (SI unit: m2 s−1) (c.g.s unit: Stokes, St) |
| γ | Wall shear rate (SI unit: s−1) |
| η | Dynamic viscosity (SI Unit: Pa s) |
| 2PP | Two-photon polymerisation |
| CFD | Computational fluid dynamics |
| CP | Cone and plate (in the context of cone and plate rheometry) |
| D | Diameter |
| ECMO | Extracorporeal membrane oxygenation |
| FXII | Factor XII |
| GPIIb | Platelet glycoprotein receptor Ib |
| HMWK | High-molecular weight kininogen |
| ISO | International organisation for standardisation |
| LDV | Laser Doppler velocimetry |
| LLSM | Lattice light-sheet microscopy |
| AO-LLSM | Adaptive optics lattice light-sheet microscopy |
| PDMS | Polydimethylsiloxane |
| PMMA | Polymethylmethacrylate |
| PK | Pre-Kallikrein |
| PRP | Platelet-rich plasma |
| PTV | Particle tracking velocimetry |
| PIV | Particle image velocimetry |
| R e | Reynolds number |
| ROTEM | Rotational thromboelastometry |
| SEM | Scanning electron microscopy |
| SIM | Structured illumination microscopy |
| SLA | Stereolithography |
| SRM | Super-resolution microscopy |
| TEG | Thromboelastography |
| TLP | Tethered-liquid perfluorocarbon |
| ν | Velocity (SI unit: m s−1) |
| VAD/LVAD | Ventricular assist device/left ventricular assist device |
| vWF | Von Willebrand factor |
| τ | Wall shear stress (SI unit: Pa)(c.g.s. unit: dyne per cm2, conversion 1 dyne per cm2 = 0.1 Pa) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
JKH acknowledges the Australian Government Research Training Program (RTP) Scholarship, The University of Sydney RTP Supplementary Scholarship and The Heart Research Institute for support. CN acknowledges funding from the Australian Research Council (ARC) under the Future Fellowship scheme. JS and TG acknowledge support from the School of Biomedical Engineering, University of Sydney. AW acknowledges funding from the ARC DECRA (DE160101308), The University of Sydney, Heart Research Institute, The University of Sydney Nano Institute, Clive and Vera Ramaciotti Foundations Health Investment Grant and Vanguard Grant (103004) from the National Heart Foundation of Australia.References
- J. Aoki, A. J. Lansky, R. Mehran, J. Moses, M. E. Bertrand, B. T. McLaurin, D. A. Cox, A. M. Lincoff, E. M. Ohman, H. D. White, H. Parise, M. B. Leon and G. W. Stone, Circulation, 2009, 119, 687–698 CrossRef CAS
.
- A. B. Lumsden, M. G. Davies and E. K. Peden, J. Endovasc. Ther., 2009, 16, II31–II62 CrossRef
.
- F. Jung, C. Wischke and A. Lendlein, MRS Bull., 2011, 35, 607–613 CrossRef
.
- J. Hou, J. Zhang, M. Ma, Z. Gong, B. Xu and Z. Shi, Thromb. Res., 2019, 184, 38–43 CrossRef CAS
.
- L. J. Walshe, S. F. Malak, J. Eagan and K. A. Sepkowitz, J. Clin. Oncol., 2002, 20, 3276–3281 CrossRef
.
- W. Geerts, Hematology Am. Soc. Hematol. Educ. Prog., 2014, 2014, 306–311 CrossRef
.
- G. D. Dangas, J. I. Weitz, G. Giustino, R. Makkar and R. Mehran, J. Am. Coll. Cardiol., 2016, 68, 2670–2689 CrossRef
.
- S. P. Pinney, A. C. Anyanwu, A. Lala, J. J. Teuteberg, N. Uriel and M. R. Mehra, J. Am. Coll. Cardiol., 2017, 69, 2845–2861 CrossRef
.
- M. R. Mehra, Eur. Heart J., 2019, 40, 673–677 CrossRef
.
- J. L. Brash, T. A. Horbett, R. A. Latour and P. Tengvall, Acta Biomater., 2019, 94, 11–24 CrossRef CAS
.
- M. Gorbet, C. Sperling, M. F. Maitz, C. A. Siedlecki, C. Werner and M. V. Sefton, Acta Biomater., 2019, 94, 25–32 CrossRef CAS
.
- M. F. Maitz, M. C. L. Martins, N. Grabow, C. Matschegewski, N. Huang, E. L. Chaikof, M. A. Barbosa, C. Werner and C. Sperling, Acta Biomater., 2019, 94, 33–43 CrossRef CAS
.
- Y. Wo, E. J. Brisbois, R. H. Bartlett and M. E. Meyerhoff, Biomater. Sci., 2016, 4, 1161–1183 RSC
.
- I. H. Jaffer and J. I. Weitz, Acta Biomater., 2019, 94, 2–10 CrossRef CAS
.
- L. Liu, H. Shi, H. Yu, S. Yan and S. Luan, Biomater. Sci., 2020, 8, 4095–4108 RSC
.
- T. Hilal, J. Mudd and T. G. DeLoughery, Res. Pract. Thromb. Haemostasis, 2019, 3, 589–598 CrossRef
.
- I. H. Jaffer, J. C. Fredenburgh, J. Hirsh and J. I. Weitz, J. Thromb. Haemostasis, 2015, 13(Suppl 1), S72–S81 CrossRef
.
- A. V. Finn, M. Joner, G. Nakazawa, F. Kolodgie, J. Newell, M. C. John, H. K. Gold and R. Virmani, Circulation, 2007, 115, 2435–2441 CrossRef
.
- P. K. Qi, M. F. Maitz and N. Huang, Surf. Coat. Technol., 2013, 233, 80–90 CrossRef CAS
.
- K. Rana and K. B. Neeves, Blood Rev., 2016, 30, 357–368 CrossRef CAS
.
- M. B. Gorbet and M. V. Sefton, Biomaterials, 2004, 25, 5681–5703 CrossRef CAS
.
- C. A. Labarrere, A. E. Dabiri and G. S. Kassab, Front. Bioeng. Biotechnol., 2020, 8, 123 CrossRef
.
- B. Sivaraman and R. A. Latour, Biomaterials, 2010, 31, 832–839 CrossRef CAS
.
- H. T. Spijker, R. Graaff, P. W. Boonstra, H. J. Busscher and W. van Oeveren, Biomaterials, 2003, 24, 4717–4727 CrossRef CAS
.
- C. Sperling, M. Fischer, M. F. Maitz and C. Werner, Biomaterials, 2009, 30, 4447–4456 CrossRef CAS
.
- L. Zhang, B. Casey, D. K. Galanakis, C. Marmorat, S. Skoog, K. Vorvolakos, M. Simon and M. H. Rafailovich, Acta Biomater., 2017, 54, 164–174 CrossRef CAS
.
- A. Toscano and M. M. Santore, Langmuir, 2006, 22, 2588–2597 CrossRef CAS
.
- C. Blaszykowski, S. Sheikh and M. Thompson, Biomater. Sci., 2015, 3, 1335–1370 RSC
.
- S. Sukavaneshvar, Adv. Drug Delivery Rev., 2017, 112, 24–34 CrossRef CAS
.
- S. Braune, M. Grunze, A. Straub and F. Jung, Biointerphases, 2013, 8, 33 CrossRef
.
- M. Hedayati, M. J. Neufeld, M. M. Reynolds and M. J. Kipper, Mater. Sci. Eng., R, 2019, 138, 118–152 CrossRef
.
- R. Puri, V. Auffret and J. Rodes-Cabau, J. Am. Coll. Cardiol., 2017, 69, 2193–2211 CrossRef
.
- V. J. Nijenhuis, J. Brouwer, R. Delewi, R. S. Hermanides, W. Holvoet, C. L. F. Dubois, P. Frambach, B. De Bruyne, G. K. van Houwelingen, J. A. S. Van Der Heyden, P. Tousek, F. van der Kley, I. Buysschaert, C. E. Schotborgh, B. Ferdinande, P. van der Harst, J. Roosen, J. Peper, F. W. F. Thielen, L. Veenstra, D. R. P. P. Chan Pin Yin, M. J. Swaans, B. Rensing, A. W. J. van ‘t Hof, L. Timmers, J. C. Kelder, P. R. Stella, J. Baan and J. M. ten Berg, N. Engl. J. Med., 2020, 382, 1696–1707 CrossRef CAS
.
- A. J. Ullman, A. C. Bulmer, T. R. Dargaville, C. M. Rickard and V. Chopra, Expert Rev. Med. Devices, 2019, 16, 25–33 CrossRef CAS
.
- I. Reviakine, F. Jung, S. Braune, J. L. Brash, R. Latour, M. Gorbet and W. van Oeveren, Blood Rev., 2017, 31, 11–21 CrossRef CAS
.
- M. Bernard, E. Jubeli, M. D. Pungente and N. Yagoubi, Biomater. Sci., 2018, 6, 2025–2053 RSC
.
- I. Sotiri, M. Robichaud, D. Lee, S. Braune, M. Gorbet, B. D. Ratner, J. L. Brash, R. A. Latour and I. Reviakine, Acta Biomater., 2019, 87, 55–60 CrossRef CAS
.
- L. Reeve and P. Baldrick, Expert Rev. Med. Devices, 2017, 14, 161–167 CrossRef CAS
.
- U. T. Seyfert, V. Biehl and J. Schenk, Biomol. Eng., 2002, 19, 91–96 CrossRef CAS
.
- W. van Oeveren, Scientifica, 2013, 2013, 392584 CrossRef CAS
.
- A. Podias, T. Groth and Y. Missirlis, J. Biomater. Sci., Polym. Ed., 1994, 6, 399–410 CrossRef CAS
.
- H. Fu, Y. Jiang, D. Yang, F. Scheiflinger, W. P. Wong and T. A. Springer, Nat. Commun., 2017, 8, 324 CrossRef
.
- M. Weber, H. Steinle, S. Golombek, L. Hann, C. Schlensak, H. P. Wendel and M. Avci-Adali, Front. Bioeng. Biotechnol., 2018, 6, 99 CrossRef
.
- R. P. Gallegos, P. J. Nockel, A. L. Rivard and R. W. Bianco, J. Heart Valve Dis., 2005, 14, 423–432 Search PubMed
.
- B. L. Zhang, R. W. Bianco and F. J. Schoen, Front. Cardiovasc. Med., 2019, 6, 72 CrossRef CAS
.
- H. Du, C. Li, Y. F. Luan, Q. Liu, W. K. Yang, Q. Yu, D. Li, J. L. Brash and H. Chen, Mater. Horiz., 2016, 3, 556–562 RSC
.
- V. Jokinen, E. Kankuri, S. Hoshian, S. Franssila and R. H. A. Ras, Adv. Mater., 2018, 30, e1705104 CrossRef
.
- B. D. Ippel and P. Y. W. Dankers, Adv. Healthcare Mater., 2018, 7, 1700505 CrossRef
.
- S. Peppou-Chapman, J. K. Hong, A. Waterhouse and C. Neto, Chem. Soc. Rev., 2020, 49, 3688–3715 RSC
.
- G. Mackie, L. Gao, S. Yau, D. C. Leslie and A. Waterhouse, Trends Biotechnol., 2019, 37, 268–280 CrossRef CAS
.
- C. Howell, A. Grinthal, S. Sunny, M. Aizenberg and J. Aizenberg, Adv. Mater., 2018, 30, e1802724 CrossRef
.
- K. S. Lavery, C. Rhodes, A. McGraw and M. J. Eppihimer, Adv. Drug Delivery Rev., 2017, 112, 2–11 CrossRef CAS
.
- X. Liu, L. Yuan, D. Li, Z. Tang, Y. Wang, G. Chen, H. Chen and J. L. Brash, J. Mater. Chem. B, 2014, 2, 5718–5738 RSC
.
- H. H. Lipowsky, Microcirculation, 2005, 12, 5–15 CrossRef
.
- A. Marossy, P. Svorc, I. Kron and S. Gresova, Clin. Hemorheol. Microcirc., 2009, 42, 239–258 CAS
.
-
R. J. Hunter, Foundations of Colloid Science, Oxford University Press, Oxford, 1993 Search PubMed
.
-
D. F. Evans and H. Wennerstrom, The Colloidal Domain, Wiley-VCH, New York, 1999 Search PubMed
.
- B. J. Ballermann, A. Dardik, E. Eng and A. Liu, Kidney Int. Suppl., 1998, 67, S100–S108 CrossRef CAS
.
- D. Katritsis, L. Kaiktsis, A. Chaniotis, J. Pantos, E. P. Efstathopoulos and V. Marmarelis, Prog. Cardiovasc. Dis., 2007, 49, 307–329 CrossRef
.
- L. F. Brass and S. L. Diamond, J. Thromb. Haemostasis, 2016, 14, 906–917 CrossRef CAS
.
-
F. M. White, Fluid Mechanics, McGraw Hill, 2011 Search PubMed
.
- G. A. Pop, D. J. Duncker, M. Gardien, P. Vranckx, S. Versluis, D. Hasan and C. J. Slager, Neth. Heart J., 2002, 10, 512–516 CAS
.
- R. E. Wells, Jr., R. Denton and E. W. Merrill, J. Lab. Clin. Med., 1961, 57, 646–656 Search PubMed
.
- M. M. Alves, C. Rocha and M. P. Goncalves, Clin. Hemorheol. Microcirc., 2013, 53, 369–386 Search PubMed
.
- R. E. Wells, Jr. and E. W. Merrill, Science, 1961, 133, 763–764 CrossRef
.
- J. T. Brundage, Am. J. Physiol., 1934, 110, 659–665 CrossRef
.
- W. S. Nesbitt, E. Westein, F. J. Tovar-Lopez, E. Tolouei, A. Mitchell, J. Fu, J. Carberry, A. Fouras and S. P. Jackson, Nat. Med., 2009, 15, 665–673 CrossRef CAS
.
- Y. Qiu, D. R. Myers and W. A. Lam, Nat. Rev. Mater., 2019, 4, 294–311 CrossRef
.
- R. Piper, P. J. Carr, L. J. Kelsey, A. C. Bulmer, S. Keogh and B. J. Doyle, Sci. Rep., 2018, 8, 3441 CrossRef
.
- K. Bourque, C. Cotter, C. Dague, D. Harjes, O. Dur, J. Duhamel, K. Spink, K. Walsh and E. Burke, ASAIO J., 2016, 62, 375–383 CrossRef CAS
.
- K. H. Fraser, M. E. Taskin, B. P. Griffith and Z. J. Wu, Med. Eng. Phys., 2011, 33, 263–280 CrossRef
.
- I. Birschmann, M. Dittrich, T. Eller, B. Wiegmann, A. J. Reininger, U. Budde and M. Struber, J. Heart Lung Transplant., 2014, 33, 80–87 CrossRef
.
- N. Moazami, K. Fukamachi, M. Kobayashi, N. G. Smedira, K. J. Hoercher, A. Massiello, S. Lee, D. J. Horvath and R. C. Starling, J. Heart Lung Transplant., 2013, 32, 1–11 CrossRef
.
- J. Charonko, S. Karri, J. Schmieg, S. Prabhu and P. Vlachos, Ann. Biomed. Eng., 2009, 37, 1310–1321 CrossRef
.
- Y. Cadroy, T. A. Horbett and S. R. Hanson, J. Lab. Clin. Med., 1989, 113, 436–448 CAS
.
- M. Koupenova, B. E. Kehrel, H. A. Corkrey and J. E. Freedman, Eur. Heart J., 2017, 38, 785–791 CAS
.
- R. P. McEver and C. Zhu, Annu. Rev. Cell. Dev. Biol., 2010, 26, 363–396 CrossRef CAS
.
- J. W. Weisel and R. I. Litvinov, J. Thromb. Haemostasis, 2019, 17, 271–282 CrossRef CAS
.
- A. Bonnefoy, Q. D. Liu, C. Legrand and M. M. Frojmovic, Biophys. J., 2000, 78, 2834–2843 CrossRef CAS
.
- T. P. Nifong and T. J. McDevitt, Chest, 2011, 140, 48–53 CrossRef
.
- T. K. Liem, K. E. Yanit, S. E. Moseley, G. J. Landry, T. G. Deloughery, C. A. Rumwell, E. L. Mitchell and G. L. Moneta, J. Vasc. Surg., 2012, 55, 761–767 CrossRef
.
- R. S. Evans, J. H. Sharp, L. H. Linford, J. F. Lloyd, S. C. Woller, S. M. Stevens, C. G. Elliott, J. S. Tripp, S. S. Jones and L. K. Weaver, Chest, 2013, 143, 627–633 CrossRef
.
- M. H. Kroll, J. D. Hellums, L. V. McIntire, A. I. Schafer and J. L. Moake, Blood, 1996, 88, 1525–1541 CrossRef CAS
.
- L. D. Casa, D. H. Deaton and D. N. Ku, J. Vasc. Surg., 2015, 61, 1068–1080 CrossRef
.
- J. R. O'Brien, Lancet, 1990, 335, 711–713 CrossRef
.
- B. Sebastian and P. S. Dittrich, Annu. Rev. Fluid Mech., 2018, 50, 483–504 CrossRef
.
- C. A. Siedlecki, B. J. Lestini, K. K. Kottke-Marchant, S. J. Eppell, D. L. Wilson and R. E. Marchant, Blood, 1996, 88, 2939–2950 CrossRef CAS
.
- S. W. Schneider, S. Nuschele, A. Wixforth, C. Gorzelanny, A. Alexander-Katz, R. R. Netz and M. F. Schneider, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7899–7903 CrossRef CAS
.
- M. V. Kameneva, G. W. Burgreen, K. Kono, B. Repko, J. F. Antaki and M. Umezu, ASAIO J., 2004, 50, 418–423 CrossRef
.
- S. E. Olia, T. M. Maul, J. F. Antaki and M. V. Kameneva, Int. J. Artif. Organs, 2016, 39, 150–159 CrossRef CAS
.
- C. C. Helms, M. Marvel, W. Zhao, M. Stahle, R. Vest, G. J. Kato, J. S. Lee, G. Christ, M. T. Gladwin, R. R. Hantgan and D. B. Kim-Shapiro, J. Thromb. Haemostasis, 2013, 11, 2148–2154 CrossRef CAS
.
- P. C. Minneci, K. J. Deans, H. Zhi, P. S. Yuen, R. A. Star, S. M. Banks, A. N. Schechter, C. Natanson, M. T. Gladwin and S. B. Solomon, J. Clin. Invest., 2005, 115, 3409–3417 CrossRef CAS
.
- J. T. Horobin, S. Sabapathy and M. J. Simmonds, Artif. Organs, 2017, 41, 1017–1025 CrossRef
.
- C. Meierhofer, E. P. Schneider, C. Lyko, A. Hutter, S. Martinoff, M. Markl, A. Hager, J. Hess, H. Stern and S. Fratz, Eur. Heart J. Cardiovasc. Imaging, 2013, 14, 797–804 CrossRef
.
- P. van Ooij, M. Markl, J. D. Collins, J. C. Carr, C. Rigsby, R. O. Bonow, S. C. Malaisrie, P. M. McCarthy, P. W. M. Fedak and A. J. Barker, J Am Heart Assoc, 2017, 6, e005959 Search PubMed
.
- E. Bollache, P. W. M. Fedak, P. van Ooij, O. Rahman, S. C. Malaisrie, P. M. McCarthy, J. C. Carr, A. Powell, J. D. Collins, M. Markl and A. J. Barker, J. Thorac. Cardiovasc. Surg., 2018, 155, 2277–2286 CrossRef
.
- C. H. Yap, N. Saikrishnan and A. P. Yoganathan, Biomech. Model. Mechanobiol., 2012, 11, 231–244 CrossRef
.
- R. Torii, I. El-Hamamsy, M. Donya, S. V. Babu-Narayan, M. Ibrahim, P. J. Kilner, R. H. Mohiaddin, X. Y. Xu and M. H. Yacoub, J. Thorac. Cardiovasc. Surg., 2012, 143, 1422–1428 CrossRef
.
- A. Nascimbene, S. Neelamegham, O. H. Frazier, J. L. Moake and J. F. Dong, Blood, 2016, 127, 3133–3141 CrossRef CAS
.
- C. K. Holland, J. M. Brown, L. M. Scoutt and K. J. Taylor, Ultrasound Med. Biol., 1998, 24, 1079–1086 CrossRef CAS
.
- J. J. Wentzel, Y. S. Chatzizisis, F. J. Gijsen, G. D. Giannoglou, C. L. Feldman and P. H. Stone, Cardiovasc. Res., 2012, 96, 234–243 CrossRef CAS
.
- E. S. Weydahl and J. E. Moore, J. Biomech., 2001, 34, 1189–1196 CrossRef CAS
.
- H. Zafar, F. Sharif and M. J. Leahy, Int. J. Cardiol. Heart Vasc., 2014, 5, 68–71 Search PubMed
.
- C. P. Cheng, R. J. Herfkens and C. A. Taylor, Am. J. Physiol.: Heart Circ. Physiol., 2003, 284, H1161–H1167 CrossRef CAS
.
- G. Ciuti, D. Righi, L. Forzoni, A. Fabbri and A. M. Pignone, Am. J. Neuroradiol., 2013, 34, 2000–2004 CrossRef CAS
.
- S. P. Jackson, Blood, 2007, 109, 5087–5095 CrossRef CAS
.
- B. P. Selgrade and G. A. Truskey, Artif. Organs, 2012, 36, E89–E96 CrossRef
.
- S. Gross-Hardt, F. Hesselmann, J. Arens, U. Steinseifer, L. Vercaemst, W. Windisch, D. Brodie and C. Karagiannidis, Crit. Care, 2019, 23, 348 CrossRef
.
- D. McPherson, O. Adekanye, A. R. Wilkes and J. E. Hall, Anesth. Analg., 2009, 108, 1198–1202 CrossRef
.
- F. Rikhtegar, F. Pacheco, C. Wyss, K. S. Stok, H. Ge, R. J. Choo, A. Ferrari, D. Poulikakos, R. Muller and V. Kurtcuoglu, PLoS One, 2013, 8, e58147 CrossRef CAS
.
- M. Sanmartin, J. Goicolea, C. Garcia, J. Garcia, A. Crespo, J. Rodriguez and J. M. Goicolea, Rev. Esp. Cardiol., 2006, 59, 20–27 CrossRef
.
- J. J. Wentzel, D. M. Whelan, W. J. van der Giessen, H. M. M. van Beusekom, I. Andhyiswara, P. W. Serruys, C. J. Slager and R. Krams, J. Biomech., 2000, 33, 1287–1295 CrossRef CAS
.
- M. I. Papafaklis, C. V. Bourantas, P. E. Theodorakis, C. S. Katsouras, K. K. Naka, D. I. Fotiadis and L. K. Michalis, JACC Cardiovasc Interv, 2010, 3, 1181–1189 CrossRef
.
- V. Raghav, I. Okafor, M. Quach, L. Dang, S. Marquez and A. P. Yoganathan, Ann. Thorac. Surg., 2016, 101, 1759–1765 CrossRef
.
- F. Khalili, P. P. T. Gamage and H. A. Mansy, J. Appl. Biotechnol. Bioeng., 2017, 2, 187–191 Search PubMed
.
- H. A. Dwyer, P. B. Matthews, A. Azadani, L. Ge, T. S. Guy and E. E. Tseng, J. Thorac. Cardiovasc. Surg., 2009, 138, 1227–1233 CrossRef
.
- D. Hasler and D. Obrist, PLoS One, 2018, 13, e0194384 CrossRef
.
- Q. Li, F. Hegner and C. H. Bruecker, J. Biomech. Eng., 2020, 142, 011006 CrossRef
.
- S. Baratchi, M. T. K. Zaldivia, M. Wallert, J. Loseff-Silver, S. Al-Aryahi, J. Zamani, P. Thurgood, A. Salim, N. M. Htun, D. Stub, P. Vahidi, S. J. Duffy, A. Walton, T. H. Nguyen, A. Jaworowski, K. Khoshmanesh and K. Peter, Circulation, 2020, 142, 1092–1105 CrossRef CAS
.
- J. J. Hathcock, Arterioscler., Thromb., Vasc. Biol., 2006, 26, 1729–1737 CrossRef CAS
.
- D. H. Lee and J. M. de la Torre Hernandez, Eur. Cardiol., 2018, 13, 54–59 CrossRef
.
- S. J. Wilson, D. E. Newby, D. Dawson, J. Irving and C. Berry, Heart, 2017, 103, 573–580 CrossRef CAS
.
- M. Alkhouli, A. Farooq, R. S. Go, S. Balla and C. Berzingi, Clin. Cardiol., 2019, 42, 692–700 CrossRef
.
- H. D. Polaschegg, Semin. Dial., 2009, 22, 524–531 CrossRef
.
- S. S. Abbas, M. S. Nasif, R. Al-Waked and M. A. Meor Said, Artif. Organs, 2020, 44, E20–E39 CrossRef CAS
.
- G. Fuchs, N. Berg, L. M. Broman and L. Prahl Wittberg, Sci. Rep., 2018, 8, 13985 CrossRef
.
- M. B. Farag, C. Karmonik, F. Rengier, M. Loebe, M. Karck, H. von Tengg-Kobligk, A. Ruhparwar and S. Partovi, Methodist Debakey Cardiovasc. J., 2014, 10, 185–189 CrossRef
.
- S. S. Najjar, M. S. Slaughter, F. D. Pagani, R. C. Starling, E. C. McGee, P. Eckman, A. J. Tatooles, N. Moazami, R. L. Kormos, D. R. Hathaway, K. B. Najarian, G. Bhat, K. D. Aaronson, S. W. Boyce and H. B. t. T. A. T. Investigators, J. Heart Lung Transplant., 2014, 33, 23–34 CrossRef
.
- K. Bourque, C. Cotter, C. Dague, D. Harjes, O. Dur, J. Duhamel, K. Spink, K. Walsh and E. Burke, ASAIO J., 2016, 62, 375–383 CrossRef CAS
.
- A. R. Curtas, H. G. Wood, P. E. Allaire, J. C. McDaniel, S. W. Day and D. B. Olsen, ASAIO J., 2002, 48, 552–561 CrossRef
.
- Y. Zhang, B. Gao and C. Yu, Comput. Methods Programs Biomed., 2016, 133, 217–227 CrossRef
.
- M. Huang, S. Fan, W. Xing and C. Liu, Math. Comput. Model., 2010, 52, 2036–2042 CrossRef
.
- J. Linneweber, P. M. Dohmen, U. Kertzscher, K. Affeld, Y. Nose and W. Konertz, Artif. Organs, 2007, 31, 345–351 CrossRef
.
- W. van Oeveren, I. F. Tielliu and J. de Hart, Int. J. Biomater., 2012, 2012, 673163 Search PubMed
.
- K. R. Forrester, C. Stewart, J. Tulip, C. Leonard and R. C. Bray, Med. Biol. Eng. Comput., 2002, 40, 687–697 CrossRef CAS
.
- J. Shang, Z. Chen, M. Wang, Q. Li, W. Feng, Y. Wu, W. Wu, M. P. Graziano and M. Chintala, Thromb. Res., 2014, 134, 433–439 CrossRef CAS
.
- D. M. Mizurini, I. M. Francischetti, J. F. Andersen and R. Q. Monteiro, Thromb. Haemostasis, 2010, 104, 1116–1123 CrossRef CAS
.
- A. K. Dunn, H. Bolay, M. A. Moskowitz and D. A. Boas, J. Cereb. Blood Flow Metab., 2001, 21, 195–201 CrossRef CAS
.
- M. Linden, H. Golster, S. Bertuglia, A. Colantuoni, F. Sjoberg and G. Nilsson, Microvasc. Res., 1998, 56, 261–270 CrossRef CAS
.
- R. J. Roman and C. Smits, Am. J. Physiol., 1986, 251, F115–F124 CrossRef CAS
.
- G. Smedley, K. P. Yip, A. Wagner, S. Dubovitsky and D. J. Marsh, IEEE Trans. Biomed. Eng., 1993, 40, 290–297 CrossRef CAS
.
- S. W. Jordan, C. A. Haller, R. E. Sallach, R. P. Apkarian, S. R. Hanson and E. L. Chaikof, Biomaterials, 2007, 28, 1191–1197 CrossRef CAS
.
- L. G. Durand, D. Garcia, F. Sakr, H. Sava, R. Cimon, P. Pibarot, A. Fenster and J. G. Dumesnil, J. Heart Valve Dis., 1999, 8, 85–95 CAS
.
- G. E. Engels, S. L. Blok and W. van Oeveren, Biointerphases, 2016, 11, 031004 CrossRef
.
- C. L. Haycox and B. D. Ratner, J. Biomed. Mater. Res., 1993, 27, 1181–1193 CrossRef CAS
.
- J. Brubert, S. Krajewski, H. P. Wendel, S. Nair, J. Stasiak and G. D. Moggridge, J. Mater. Sci.: Mater. Med., 2016, 27, 32 CrossRef
.
- H. Touma, I. Sahin, T. Gaamangwe, M. B. Gorbet and S. D. Peterson, J. Biomech. Eng., 2014, 136, 071004 CrossRef
.
- S. M. Hastings, M. T. Griffin and D. N. Ku, Platelets, 2017, 28, 427–433 CrossRef CAS
.
- S. Jahanmir, A. Z. Hunsberger, H. Heshmat, M. J. Tomaszewski, J. F. Walton, W. J. Weiss, B. Lukic, W. E. Pae, C. M. Zapanta and T. Z. Khalapyan, Artif. Organs, 2008, 32, 366–375 CrossRef
.
- A. Redaelli, F. Boschetti and F. Inzoli, Comput. Biol. Med., 1997, 27, 233–247 CrossRef CAS
.
- M. G. Al-Azawy, A. Turan and A. Revell, Comput. Methods Biomech. Biomed. Eng., 2016, 19, 271–285 CrossRef
.
- D. N. Sarode and S. Roy, Expert Rev. Med. Devices, 2019, 16, 603–616 CrossRef CAS
.
- R. A. Gardner, J. Lab. Clin. Med., 1974, 84, 494–508 CAS
.
- R. Y. Kannan, H. J. Salacinski, J. De Groot, I. Clatworthy, L. Bozec, M. Horton, P. E. Butler and A. M. Seifalian, Biomacromolecules, 2006, 7, 215–223 CrossRef CAS
.
- S. A. Mousa, S. Khurana and M. S. Forsythe, Arterioscler., Thromb., Vasc. Biol., 2000, 20, 1162–1167 CrossRef CAS
.
-
M. Othman and H. Kaur, in Hemostasis and Thrombosis: Methods and Protocols, ed. E. J. Favaloro and G. Lippi, Springer New York, New York, NY, 2017, pp. 533–543, DOI:10.1007/978-1-4939-7196-1_39
.
-
M. Pressly, M. D. Neal, G. Clermont and R. S. Parker, presented in part at the Foundations of Computer Aided Process Operations/Chemical Process Control, Tuscan, AZ, 2016
.
- M. Ranucci, T. Laddomada, M. Ranucci and E. Baryshnikova, Physiol. Rep., 2014, 2, e12065 CrossRef
.
- M. Ranucci, M. Ranucci and E. Baryshnikova, Blood Coagulation Fibrinolysis, 2018, 29, 172–177 CrossRef CAS
.
- T. R. Roberts, D. C. Leslie, A. P. Cap, L. C. Cancio and A. I. Batchinsky, J. Biomed. Mater. Res., Part B, 2020, 108, 496–502 CrossRef CAS
.
- D. Whiting and J. A. DiNardo, Am. J. Hematol., 2014, 89, 228–232 CrossRef CAS
.
- H. Shankaran and S. Neelamegham, Biorheology, 2001, 38, 275–304 CAS
.
- V. Balasubramanian and S. M. Slack, J. Biomater. Sci., Polym. Ed., 2002, 13, 543–561 CrossRef CAS
.
- M. A. Jamiolkowski, D. D. Pedersen, W. T. Wu, J. F. Antaki and W. R. Wagner, Biomaterials, 2016, 96, 72–83 CrossRef CAS
.
- M. A. Jamiolkowski, J. R. Woolley, M. V. Kameneva, J. F. Antaki and W. R. Wagner, J. Biomed. Mater. Res., Part A, 2015, 103, 1303–1311 CrossRef
.
- T. Kragh, J. Schaller, U. Kertzscher, K. Affeld, A. Reininger and M. Spannagl, Microfluid. Nanofluid., 2015, 19, 155–167 CrossRef CAS
.
- L. Krishnan, N. Varghese, C. Muraleedharan, G. Bhuvaneshwar, F. Derangere, Y. Sampeur and R. Suryanarayanan, Biomol. Eng., 2002, 19, 251–253 CrossRef CAS
.
- L. M. Liu, Y. Koo, B. Collins, Z. G. Xu, J. Sankar and Y. Yun, PLoS One, 2017, 12, e0182914 CrossRef
.
- R. D. Schaub, M. V. Kameneva, H. S. Borovetz and W. R. Wagner, J. Biomed. Mater. Res., 2000, 49, 460–468 CrossRef CAS
.
- Y. Wu, M. Zhang, K. D. Hauch and T. A. Horbett, J. Biomed. Mater. Res., Part A, 2008, 85, 829–839 CrossRef
.
- A. de Mel, K. Chaloupka, Y. Malam, A. Darbyshire, B. Cousins and A. M. Seifalian, J. Biomed. Mater. Res., Part A, 2012, 100, 2348–2357 Search PubMed
.
- B. Korpallova, M. Samos, T. Bolek, I. Skornova, F. Kovar, P. Kubisz, J. Stasko and M. Mokan, Clin. Appl. Thromb./Hemostasis, 2018, 24, 1199–1207 CrossRef
.
- F. Skovborg, A. V. Nielsen and J. Schlichtkrull, Scand. J. Clin. Lab. Invest., 1968, 21, 83–88 CrossRef CAS
.
- C. J. Glover, L. V. McIntire, L. B. Leverett, J. D. Hellums, C. H. Brown and E. A. Natelson, Trans. - Am. Soc. Artif. Intern. Organs, 1974, 20B, 463–468 Search PubMed
.
- I. V. Shevchuk, J. Heat Transfer-Trans. ASME, 2011, 133, 024502 CrossRef
.
- G. Girdhar and D. Bluestein, Expert Rev. Med. Devices, 2008, 5, 167–181 CrossRef
.
- R. Tran, D. R. Myers, J. Ciciliano, E. L. Trybus Hardy, Y. Sakurai, B. Ahn, Y. Qiu, R. G. Mannino, M. E. Fay and W. A. Lam, J. Cell. Mol. Med., 2013, 17, 579–596 CrossRef CAS
.
- J. N. Topper, J. Cai, Y. Qiu, K. R. Anderson, Y. Y. Xu, J. D. Deeds, R. Feeley, C. J. Gimeno, E. A. Woolf, O. Tayber, G. G. Mays, B. A. Sampson, F. J. Schoen, M. A. Gimbrone, Jr. and D. Falb, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 9314–9319 CrossRef CAS
.
- N. Watanabe, T. Shimada, M. Hakozaki and R. Hara, Int. J. Artif. Organs, 2018, 41, 838–844 CrossRef CAS
.
- A. L. Samson, I. Alwis, J. A. A. Maclean, P. Priyananda, B. Hawkett, S. M. Schoenwaelder and S. P. Jackson, Blood, 2017, 130, 2453–2462 CrossRef CAS
.
- V. Tutwiler, H. Wang, R. I. Litvinov, J. W. Weisel and V. B. Shenoy, Biophys. J., 2017, 112, 714–723 CrossRef CAS
.
- I. V. Shevchuk, J. Heat Transfer, 2011, 133, 024502 CrossRef
.
- K. Bataineh, J. Fluids Eng.-Trans. ASME, 2014, 136, 101201 CrossRef
.
- K. M. Bataineh, Comput. Fluids, 2014, 101, 105–113 CrossRef
.
- M. Sanak, B. Jakiela and W. Wegrzyn, Bull. Pol. Acad. Sci.: Tech. Sci., 2010, 58, 317–322 CAS
.
- B. Shenkman, N. Savion, R. Dardik, I. Tamarin and D. Varon, Thromb. Res., 2000, 99, 353–361 CrossRef CAS
.
- J. M. Lackner, W. Waldhauser, P. Hartmann, F. Bruckert, M. Weidenhaupt, R. Major, M. Sanak, M. Wiesinger and D. Heim, J. Funct. Biomater., 2012, 3, 283–297 CrossRef CAS
.
- N. P. Rhodes, A. P. Shortland, A. Rattray and D. F. Williams, J. Mater. Sci. Mater. Med., 1998, 9, 767–772 CrossRef CAS
.
- T. M. Alkhamis, R. L. Beissinger and J. R. Chediak, Blood, 1990, 75, 1568–1575 CrossRef CAS
.
- T. M. Alkhamis, R. L. Beissinger and J. R. Chediak, Biomaterials, 1993, 14, 865–870 CrossRef CAS
.
- T. B. Tschopp and H. R. Baumgartner, Thromb. Haemostasis, 1976, 35, 334–341 CrossRef CAS
.
- A. Mzyk, G. Imbir, K. Trembecka-Wojciga, J. M. Lackner, H. Plutecka, E. Jasek-Gajda, J. Kawalko and R. Major, ACS Biomater. Sci. Eng., 2020, 6, 898–911 CrossRef CAS
.
- J. J. Chiu and S. Chien, Physiol. Rev., 2011, 91, 327–387 CrossRef
.
-
C. Sperling, M. F. Maitz and C. Werner, in Hemocompatibility of Biomaterials for Clinical Applications, 2018, pp. 77–104, DOI:10.1016/b978-0-08-100497-5.00005-7
.
- A. J. Davies, Meas. Sci. Technol., 2015, 26, 127001 CrossRef
.
- L. H. O. Hellström, M. A. Samaha, K. M. Wang, A. J. Smits and M. Hultmark, Meas. Sci. Technol., 2015, 26, 015301 CrossRef
.
- R. Cardinaels, N. K. Reddy and C. Clasen, Rheol. Acta, 2019, 58, 525–538 CrossRef CAS
.
- R. Van Kruchten, J. M. Cosemans and J. W. Heemskerk, Platelets, 2012, 23, 229–242 CrossRef CAS
.
- M. Zhang, Y. Wu, K. Hauch and T. A. Horbett, J. Biomater. Sci., Polym. Ed., 2008, 19, 1383–1410 CrossRef CAS
.
- T. V. Colace and S. L. Diamond, Arterioscler. Thromb. Vasc. Biol., 2013, 33, 105–113 CrossRef CAS
.
- H. Lee, W. Na, B. K. Lee, C. S. Lim and S. Shin, Clin. Hemorheol. Microcirc., 2019, 71, 249–266 Search PubMed
.
-
A. Burklund, A. Tadimety, Y. Nie, N. Hao and J. X. Zhang, in Adv. Clin. Chem, Elsevier, 2020, vol. 95, pp. 1–72 Search PubMed
.
- A. Brown, G. Burke and B. J. Meenan, Biotechnol. Bioeng., 2011, 108, 1148–1158 CrossRef CAS
.
- F. J. Tovar-Lopez, G. Rosengarten, E. Westein, K. Khoshmanesh, S. P. Jackson, A. Mitchell and W. S. Nesbitt, Lab Chip, 2010, 10, 291–302 RSC
.
- N. J. Kent, L. Basabe-Desmonts, G. Meade, B. D. MacCraith, B. G. Corcoran, D. Kenny and A. J. Ricco, Biomed. Microdevices, 2010, 12, 987–1000 CrossRef CAS
.
- J. M. Koo and C. Kleinstreuer, J. Micromech. Microeng., 2003, 13, 568–579 CrossRef
.
- R. G. Bacabac, T. H. Smit, S. C. Cowin, J. J. Van Loon, F. T. Nieuwstadt, R. Heethaar and J. Klein-Nulend, J. Biomech., 2005, 38, 159–167 CrossRef
.
- N. Kawagoishi, C. Nojiri, K. Senshu, T. Kido, H. Nagai, T. Kanamori, K. Sakai, H. Koyanagi and T. Akutsu, Artif. Organs, 1994, 18, 588–595 CrossRef CAS
.
- Y. Wu, M. Zhang, K. D. Hauch and T. A. Horbett, J. Biomed. Mater. Res., Part A, 2008, 85, 829–839 CrossRef
.
- M. Zhang and T. A. Horbett, J. Biomed. Mater. Res., Part A, 2009, 89, 791–803 CrossRef
.
- D. C. Leslie, A. Waterhouse, J. B. Berthet, T. M. Valentin, A. L. Watters, A. Jain, P. Kim, B. D. Hatton, A. Nedder, K. Donovan, E. H. Super, C. Howell, C. P. Johnson, T. L. Vu, D. E. Bolgen, S. Rifai, A. R. Hansen, M. Aizenberg, M. Super, J. Aizenberg and D. E. Ingber, Nat. Biotechnol., 2014, 32, 1134–1140 CrossRef CAS
.
-
L. Waite, Applied biofluid mechanics, McGraw-Hill, New York, 2007 Search PubMed
.
- K. Vahidkhah, S. L. Diamond and P. Bagchi, Biophys. J., 2014, 106, 2529–2540 CrossRef CAS
.
- L. D. Casa and D. N. Ku, Biomed. Microdevices, 2014, 16, 115–126 CrossRef
.
- D. P. Sarvepalli, D. W. Schmidtke and M. U. Nollert, Ann. Biomed. Eng., 2009, 37, 1331–1341 CrossRef
.
- R. G. Mannino, D. R. Myers, B. Ahn, Y. Wang, R. Margo, H. Gole, A. S. Lin, R. E. Guldberg, D. P. Giddens, L. H. Timmins and W. A. Lam, Sci. Rep., 2015, 5, 12401 CrossRef
.
- H. Gong, B. P. Bickham, A. T. Woolley and G. P. Nordin, Lab Chip, 2017, 17, 2899–2909 RSC
.
- N. P. Macdonald, J. M. Cabot, P. Smejkal, R. M. Guijt, B. Paull and M. C. Breadmore, Anal. Chem., 2017, 89, 3858–3866 CrossRef CAS
.
- P. F. Costa, H. J. Albers, J. E. A. Linssen, H. H. T. Middelkamp, L. van der Hout, R. Passier, A. van den Berg, J. Malda and A. D. van der Meer, Lab Chip, 2017, 17, 2785–2792 RSC
.
- O. Vanderpoorten, Q. Peter, P. K. Challa, U. F. Keyser, J. Baumberg, C. F. Kaminski and T. P. J. Knowles, Microsyst. Nanoeng., 2019, 5, 40 CrossRef
.
- S. Waheed, J. M. Cabot, N. P. Macdonald, T. Lewis, R. M. Guijt, B. Paull and M. C. Breadmore, Lab Chip, 2016, 16, 1993–2013 RSC
.
- B. W. Pearre, C. Michas, J. M. Tsang, T. J. Gardner and T. M. Otchy, Addit. Manuf., 2019, 30, 100887 CAS
.
- W.-I. Wu, K. N. Sask, J. L. Brash and P. R. Selvaganapathy, Lab Chip, 2012, 12, 960–970 RSC
.
- X. Hou, Y. S. Zhang, G. T.-d. Santiago, M. M. Alvarez, J. Ribas, S. J. Jonas, P. S. Weiss, A. M. Andrews, J. Aizenberg and A. Khademhosseini, Nat. Rev. Mater., 2017, 2, 17016 CrossRef CAS
.
- E. C. Filipe, M. Santos, J. Hung, B. S. L. Lee, N. Yang, A. H. P. Chan, M. K. C. Ng, J. Rnjak-Kovacina and S. G. Wise, JACC Basic Transl. Sci., 2018, 3, 38–53 CrossRef
.
- A. Kheradvar, E. M. Groves, L. P. Dasi, S. H. Alavi, R. Tranquillo, K. J. Grande-Allen, C. A. Simmons, B. Griffith, A. Falahatpisheh, C. J. Goergen, M. R. Mofrad, F. Baaijens, S. H. Little and S. Canic, Ann. Biomed. Eng., 2015, 43, 833–843 CrossRef
.
- C. J. Bettinger, K. M. Cyr, A. Matsumoto, R. Langer, J. T. Borenstein and D. L. Kaplan, Adv. Mater., 2007, 19, 2847–2850 CrossRef CAS
.
- K. Ren, W. Dai, J. Zhou, J. Su and H. Wu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8162–8166 CrossRef CAS
.
- K. AbuZineh, L. I. Joudeh, B. Al Alwan, S. M. Hamdan, J. S. Merzaban and S. Habuchi, Sci. Adv., 2018, 4, eaat5304 CrossRef CAS
.
- S. B. Cheepala, A. Pitre, Y. Fukuda, K. Takenaka, Y. Zhang, Y. Wang, S. Frase, T. Pestina, T. K. Gartner, C. Jackson and J. D. Schuetz, Blood, 2015, 126, 2307–2319 CrossRef CAS
.
- C. S. Hansel, M. N. Holme, S. Gopal and M. M. Stevens, Biomaterials, 2020, 226, 119406 CrossRef CAS
.
- H. R. Manley, D. L. Potter, J. M. Heddleston, T. L. Chew, M. C. Keightley and G. J. Lieschke, J. Leukocyte Biol., 2020, 108, 455–468 CrossRef CAS
.
- T. L. Liu, S. Upadhyayula, D. E. Milkie, V. Singh, K. Wang, I. A. Swinburne, K. R. Mosaliganti, Z. M. Collins, T. W. Hiscock, J. Shea, A. Q. Kohrman, T. N. Medwig, D. Dambournet, R. Forster, B. Cunniff, Y. Ruan, H. Yashiro, S. Scholpp, E. M. Meyerowitz, D. Hockemeyer, D. G. Drubin, B. L. Martin, D. Q. Matus, M. Koyama, S. G. Megason, T. Kirchhausen and E. Betzig, Science, 2018, 360, eaaq1392 CrossRef
.
- P. Hook, T. Brito-Robinson, O. Kim, C. Narciso, H. V. Goodson, J. W. Weisel, M. S. Alber and J. J. Zartman, Biomed. Opt. Express, 2017, 8, 3671–3686 CrossRef
.
- B. R. Blackman, K. A. Barbee and L. E. Thibault, Ann. Biomed. Eng., 2000, 28, 363–372 CrossRef CAS
.
- B. R. Blackman, G. Garcia-Cardena and M. A. Gimbrone, Jr., J. Biomech. Eng., 2002, 124, 397–407 CrossRef
.
- N. E. Hastings, M. B. Simmers, O. G. McDonald, B. R. Wamhoff and B. R. Blackman, Am. J. Physiol.: Cell Physiol., 2007, 293, C1824–C1833 CrossRef CAS
.
- J. A. Pike, V. A. Simms, C. W. Smith, N. V. Morgan, A. O. Khan, N. S. Poulter, I. B. Styles and S. G. Thomas, Platelets, 2020, 1–5, DOI:10.1080/09537104.2020.1748588
.
- S. U. Siddiqui, N. K. Verma, S. Mishra and R. S. Gupta, Appl. Math. Comput., 2009, 210, 1–10 CrossRef
.
- J. V. Soulis, G. D. Giannoglou, Y. S. Chatzizisis, K. V. Seralidou, G. E. Parcharidis and G. E. Louridas, Med. Eng. Phys., 2008, 30, 9–19 CrossRef
.
- M. Ashrafizaadeh and H. Bakhshaei, Comput. Math. Appl., 2009, 58, 1045–1054 CrossRef
.
- G. Silva, N. Leal and V. Semiao, Int. J. Heat Fluid Flow, 2008, 29, 1211–1220 CrossRef
.
- J. S. Raben, S. Morlacchi, F. Burzotta, F. Migliavacca and P. P. Vlachos, J. Appl. Biomater. Funct. Mater., 2015, 13, e116–e126 CAS
.
- R. A. Malinauskas, P. Hariharan, S. W. Day, L. H. Herbertson, M. Buesen, U. Steinseifer, K. I. Aycock, B. C. Good, S. Deutsch, K. B. Manning and B. A. Craven, ASAIO J., 2017, 63, 150–160 CrossRef
.
- R. Lima, S. Wada, S. Tanaka, M. Takeda, T. Ishikawa, K. Tsubota, Y. Imai and T. Yamaguchi, Biomed. Microdevices, 2008, 10, 153–167 CrossRef
.
- D. Pinho, R. O. Rodrigues, V. Faustino, T. Yaginuma, J. Exposto and R. Lima, J. Biomech., 2016, 49, 2293–2298 CrossRef
.
- F. Ghalichi, X. Deng, A. De Champlain, Y. Douville, M. King and R. Guidoin, Biorheology, 1998, 35, 281–294 CrossRef CAS
.
- K. Shinohara, Y. Sugii, A. Aota, A. Hibara, M. Tokeshi, T. Kitamori and K. Okamoto, Meas. Sci. Technol., 2004, 15, 1965–1970 CrossRef CAS
.
- P. Browne, A. Ramuzat, R. Saxena and A. P. Yoganathan, Ann. Biomed. Eng., 2000, 28, 39–47 CrossRef CAS
.
- J. O. Taylor, B. C. Good, A. V. Paterno, P. Hariharan, S. Deutsch, R. A. Malinauskas and K. B. Manning, Cardiovasc. Eng. Technol., 2016, 7, 191–209 CrossRef
.
- C. Y. Schule, K. Affeld, M. Kossatz, C. O. Paschereit and U. Kertzscher, Int. J. Artif. Organs, 2017, 40, 109–117 CrossRef
.
- U. Gülan, B. Lüthi, M. Holzner, A. Liberzon, A. Tsinober and W. Kinzelbach, Exp. Fluids, 2012, 53, 1469–1485 CrossRef
.
- K. Takashima, R. Shimomura, T. Kitou, H. Terada, K. Yoshinaka and K. Ikeuchi, Tribol. Int., 2007, 40, 319–328 CrossRef CAS
.
- N. Amor, L. Geris, J. Vander Sloten and H. Van Oosterwyck, Acta Biomater., 2011, 7, 779–790 CrossRef CAS
.
- P. D. Goodman, E. T. Barlow, P. M. Crapo, S. F. Mohammad and K. A. Solen, Ann. Biomed. Eng., 2005, 33, 780–797 CrossRef
.
- J. S. Soares, J. Sheriff and D. Bluestein, Biomech. Model. Mechanobiol., 2013, 12, 1127–1141 CrossRef
.
- B. Chopard, D. R. de Sousa, J. Latt, L. Mountrakis, F. Dubois, C. Yourassowsky, P. Van Antwerpen, O. Eker, L. Vanhamme, D. Perez-Morga, G. Courbebaisse, E. Lorenz, A. G. Hoekstra and K. Z. Boudjeltia, R. Soc. Open Sci., 2017, 4, 170219 CrossRef
.
- H. Hosseinzadegan and D. K. Tafti, Cardiovasc. Eng. Technol., 2017, 8, 164–181 CrossRef
.
| This journal is © The Royal Society of Chemistry 2020 |