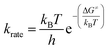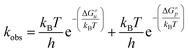DOI:
10.1039/D0RA02713H
(Paper)
RSC Adv., 2020,
10, 16650-16658
Cyclization step of noradrenaline and adrenaline autoxidation: a quantum chemical study
Received
24th March 2020
, Accepted 17th April 2020
First published on 28th April 2020
Abstract
Catecholamine autoxidation has been recognized as one of the potential trigger factors for catecholaminergic neuron loss characteristics of neurodegenerative diseases. The cyclization step with intramolecular Michael addition of catecholamine o-quinones has been shown to be the irreversible and rate limiting step of the autoxidation reaction across a broad pH range and has a complex pH dependence that has not yet been fully understood. Using quantum chemical calculations, we demonstrated that in the case of noradrenaline and adrenaline two catecholamine o-quinone species, one with an unprotonated and one with a protonated quinone group can participate in the cyclization reaction and that the mechanisms of these reactions significantly differ, emphasizing the importance of quinone group protonation states in the reaction mechanism. With a thorough exploration of the reaction kinetics, we further showed that at acidic pH the cyclization reaction rate is pH independent, while at alkaline pH the pH dependence is marked, explaining the experimentally observed complex pH dependence.
Introduction
The monoaminergic neurotransmitters adrenaline and noradrenaline are two major biologically important catecholamines in the nervous system. The former is primarily produced by the adrenal medulla and a few foci in the central nervous system,1 while the latter is produced by the sympathetic postganglionic neurons and neurons within the locus coeruleus. In addition to being an integral regulator of multiple physiological processes such as the spectrum of cardiovascular functions, adrenaline also has clinical application in the management of cardiorespiratory emergencies like anaphylaxis, cardiac arrest, angioedema and severe acute asthmatic exacerbations.2,3 On the other hand, noradrenaline mediates a range of neurocognitive and motor functions, as well as brain neural differentiation, plasticity and survival, compensatory response mechanisms in acute brain injuries and the progression of neurodegenerative mechanisms in chronic brain disorders.4,5
In aqueous solution catecholamines undergo a spontaneous non-enzymatic autoxidation. This autoxidation reaction has become a focus of interest in the search for the trigger factor for the catecholaminergic neuron loss characteristic for neurodegenerative diseases, especially Alzheimer's and Parkinson's disease.6 The reaction chain begins with an oxidation step that yields the catecholamine quinone form and superoxide anion. The superoxide anion further decomposes to various reactive oxygen species (ROS), while the quinone form undergoes cyclization with intramolecular Michael addition to yield aminochrome, a precursor of neuromelanin.7 Besides catecholamine autoxidation, other biochemical processes such as the electron transfer chain, various biogenic amine degradation by monoamine oxidase (MAO) and chronic inflammatory processes, are also sources of ROS in the central nervous system, which damage biological macromolecules such as lipids, proteins and nucleic acids and cause cell dysfunction and neuron loss.8–10 Other potential mechanisms of neurodegeneration include amyloid plaque formation and direct aminochrome toxicity. Aminochrome is etiologically important in a number of pathophysiological mechanisms such as neuroinflammation, mitochondrial dysfunction, dysfunction of protein degradation, α-synuclein aggregation, and oxidative stress, which are all implicated in neurodegenerative disorders.11,12
In catecholaminergic neurons, the synthesis of catecholamines occurs in different cell compartments with varying pH. Dopamine is synthesized in the cytosol with pH of ∼7.1 and readily transported into secretory vesicles with an acidic environment (pH of ∼5.3) by vesicular monoamine transporter 2 (VMAT-2).13–15 Inside the acidic secretory vesicle, dopamine is enzymatically converted to noradrenaline. In cells that produce adrenaline, noradrenaline is transported back from the vesicle to the cytosol where it is enzymatically converted to adrenaline which is again transported into secretory vesicles by the vesicular monoamine transporter 1 (VMAT-1) present in adrenergic neuroendocrine cells.16 Catecholaminergic signaling occurs via classic synaptic transmission across a few nm wide synaptic gap that is acidified during signal transmission,15,17 as well as via extrasynaptic volume transmission in the range of a few μm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 and endocrine signaling,2 with both of the latter mechanisms occurring in the extracellular fluid/blood with a pH ∼ 7.4.
18 and endocrine signaling,2 with both of the latter mechanisms occurring in the extracellular fluid/blood with a pH ∼ 7.4.
Several studies of catecholamine autoxidation have consistently reported complex pH dependence of the catecholamine autoxidation rate, and identified the cyclization step with intramolecular Michael addition as the irreversible and rate limiting step of the autoxidation reaction across a broad pH range.19–29 However, the exact reaction mechanism remains unclear,30 and the existing attempts to delineate it fail to explain the complex pH dependence. Recently, using computational methods, we proposed a reaction mechanism of dopamine autoxidation that accounted for the pH dependence at a narrow physiological pH range, which was in agreement with experimental data.31 Since catecholamines are present in various biological compartments with varying pH, understanding the cyclization step at different pH is critical to a full appreciation of catecholamine autoxidation in physiological conditions.
Accordingly, the present study aimed to further our understanding of the cyclization step of the catecholamines – noradrenaline and adrenaline autoxidation reaction in aqueous solution by considering two reaction pathways at a broad pH range using quantum chemical methods and critical comparison with the available experimental data.
Computational details
Computational reaction kinetics determination
Using the Gaussian 16 software package, quantum chemical calculations were employed to study the autoxidation reaction mechanism of catecholamine o-quinones.32 The initial structural geometries of the catecholamine o-quinones complexed with various species were built with Molden v5.9 software package33 and optimized at the M06-2X/6-31+G(d,p) theory level, which represents a reasonable balance of computational integrity and cost; and is recommended for kinetic calculations.34 The integral equation formalism variant polarizable continuum solvation model (PCM) of Tomasi and coworkers which describes the solute as a composite of interlocking spheres and the solvent as a dielectric continuum, was applied to account for the effect of solvation.35 Accordingly, with a dielectric constant of 78.3 applied to represent the aqueous solution, the solvent reaction field was included to re-optimize the structural geometries. The same protocol was also used for the products' minima. Transition state search started from the manually-set initial geometries. A vibrational analysis was performed in the harmonic approximation for all stationary points. Calculated frequencies were used for thermodynamic corrections of relative reaction and activation free energies at 298.15 K. In contrast to the reactants' and products' minima which bear all real frequencies, the transition states have one imaginary frequency, with the reactive motion being delineated by the corresponding eigenvector. Atomic charges were calculated using the Merz–Singh–Kollman scheme.
Equations ΔG = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa − pH) and ΔG = kBT
ln(10)(pKa − pH) and ΔG = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa) were applied to calculate the free energy change associated with proton transfer from and to an ionizable group with a certain pKa value, to and from bulk water in an aqueous solution with a certain pH value, respectively.
ln(10)(pH − pKa) were applied to calculate the free energy change associated with proton transfer from and to an ionizable group with a certain pKa value, to and from bulk water in an aqueous solution with a certain pH value, respectively.
Computational pKa determination
In the Brønsted–Lowry acid base theory, acids are species that are able to donate proton to a proton acceptor. If the acceptor is bulk water then there are analytical relations between the free energy for the process, acid dissociation constant and pH value. For the deprotonation reaction,and| |
pKa = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka Ka
| (2) |
| |
ΔGaq = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka Ka
| (3) |
the pKa is given by| |
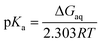 | (4) |
where ΔGaq is the Gibbs energy of deprotonation in aqueous solution, R is the gas constant, and T is the absolute temperature.
For pKa calculations, the thermodynamic cycle shown in Fig. 1 was followed. For gas-phase reaction energies (ΔGgas) a high level ab initio method using CBS-QB3 theory was used.36 The absence of imaginary frequencies in the optimized structure verified that the stationary point represented a local minimum. To calculate solvation free energies (ΔGs) the MP2 theory with 6-31++G (2d,2p) basis set37 and various solvent reaction field models including universal solvation model, based on density (SMD),38 PCM,35 conductor-like polarizable continuum model (CPCM)39 and isodensity polarizable continuum model (IPCM)40 were used. Furthermore, a cluster-continuum model with SMD was employed to take into account specific hydrogen bonding that could be important for pKa calculations. As suggested by Vianello and coworkers a reaction set (Fig. 2) consistent with the concept of homodesmotic reactions, with matching number of hydrogen bonds on both sides of the equation, was constructed to calculate the solvation free energy.41 Since calculations of solvation free energies of charged species are highly demanding and subject to error up to 4 kcal mol−1,38 the Langevin Dipole (LD) model that can more accurately model solvation effects for molecules with a high charge was also employed.42 The Merz–Kollman atomic charges which served as an input for the LD model constructed in the ChemSol 2.1 software, were derived with Guassian 16 using PCM/MP2/6-31++G (2d,2p).
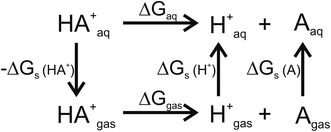 |
| | Fig. 1 Thermodynamic cycle used for pKa calculations. ΔGgas free energy of deprotonation in gas-phase; ΔGs solvation free energy; ΔGaq free energy of deprotonation in aqueous solution. | |
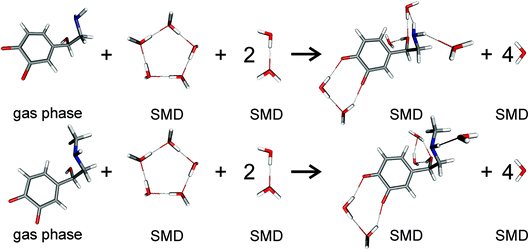 |
| | Fig. 2 Scheme of noradrenaline o-quinone (top) and adrenaline o-quinone (bottom) interacting with water molecules to calculate the solvation free energy. Analogous schemes were used to calculate the solvation free energies for all protonation states. | |
For the thermodynamic cycle used
| | |
ΔGaq = ΔGgas + ΔΔGsol
| (5) |
| | |
ΔΔGsol = ΔGs(H+) + ΔGs(A) − ΔGs(AH+)
| (6) |
The solvation free energy of a proton ΔGs(H+) = −264.0 kcal mol−1 was adopted from the literature.43 The value includes the formation of hydronium ion and its free energy of hydration. The gas phase standard free energy of a proton Ggas(H+) = −6.287 kcal mol−1 at 298.15 K was derived from the Sacku–Tetrode equation.36 For conversion of ΔGgas, for which the 1 atm reference state is used for calculation, to 1 M reference state, which is used for ΔGs calculation, the following equation was used:
| |
ΔGgas(1 M) = ΔGgas(1 atm) + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) ln(24.46)
| (7) |
Therefore, the pKa values reported were calculated using:
| |
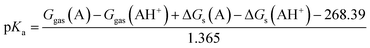 | (8) |
The eqn (8) was derived following the procedure suggested by Liptak and coworkers by combining eqn (4)–(7) and values for ΔGs(H+) and Ggas(H+) from the literature.36
Results and discussion
Two catecholamine o-quinone species, one with unprotonated and one with protonated quinone group, were considered to participate in the cyclization reaction (Fig. 3).19 After the plausible mechanisms for cyclization were identified, the activation free energies for the reactions were calculated. Furthermore, the effect of pH on activation free energies and reaction kinetics was investigated.
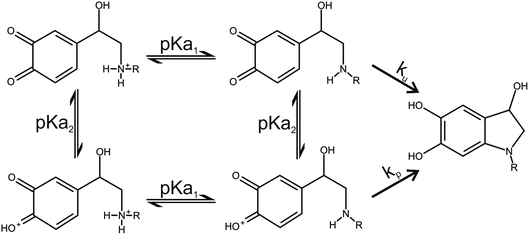 |
| | Fig. 3 Noradrenaline (R = H) and adrenaline (R = CH3) o-quinone cyclization reaction pathways. | |
Cyclization of catecholamine o-quinones with unprotonated quinone group
For species with unprotonated quinone group, several reaction scenarios have been considered (Table 1). The reaction mechanisms that were predicted to be strongly endergonic were ruled out as feasible; accordingly, the transition state search and activation free energy calculations were not employed. The reaction mechanism where a proton was extracted from the sessile C–H by one hydroxide ion was slightly endergonic and cyclization did not occur, suggesting that this is also not the preferred mechanism.
Table 1 Reaction free energies for different cyclization reaction scenarios for noradrenaline and adrenaline o-quinone with unprotonated quinone group
| Cyclization reaction scenario |
Reaction free energy (kcal mol−1) |
| Noradrenaline o-quinone |
Adrenaline o-quinone |
| Spontaneous with protonated amino group |
148.35 |
138.99 |
| Spontaneous with unprotonated amino group |
11.10 |
8.20 |
| H2O extracts a proton from unprotonated amino group |
28.72 |
27.13 |
| H2O extracts a proton from sessile C–H |
53.42 |
47.87 |
| Two H2O extract a proton from unprotonated amino group and sessile C–H simultaneously |
57.08 |
54.31 |
| OH− extracts a proton from unprotonated amino group |
−24.85 |
−27.72 |
| OH− extracts a proton from sessile C–H |
6.03 |
6.56 |
| Two OH− extract a proton from unprotonated amino group and sessile C–H simultaneously |
−58.95 |
−62.28 |
The reaction mechanism where a proton was extracted from the unprotonated amino group by one hydroxide ion was strongly exergonic, hence, transition state search was employed. The corresponding intrinsic activation free energies (ΔG≠i,u) were 8.37 kcal mol−1 and 4.18 kcal mol−1 for noradrenalin and adrenalin o-quinone respectively (Fig. 4). Comparing these values and the intrinsic activation free energy for dopamine o-quinone cyclization reaction (6.78 kcal mol−1)31 shows that intrinsic activation free energies are very small, almost barrier-less, and reaffirms that methylation of amino group decreases the intrinsic activation free energy.44 Please note, that the rearrangement of protons after cyclization step was not investigated further since bulk water is a proton rich environment where proton diffusion rate is very fast (1.6 × 1011 s−1) and does not represent a rate limiting step.31
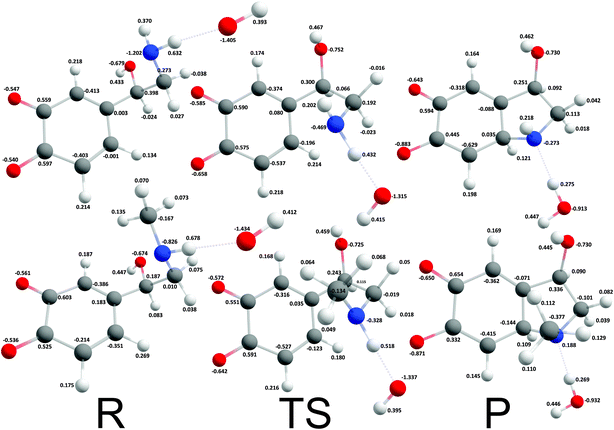 |
| | Fig. 4 Optimized geometries and atomic charges of the reactants (R), transition state (TS) and products (P) of noradrenaline (top) and adrenaline (bottom) o-quinone with unprotonated quinone group cyclization reaction. Reactants are complexes between catecholamine o-quinone and a hydroxide ion (OH−). Products are cyclized single charged catecholamine o-quinone and a molecule of water. Carbon atoms are represented with gray, oxygen atoms red, hydrogen atoms white and nitrogen atoms with blue color. | |
Despite being strongly exergonic, the scenario where protons were extracted by two hydroxide ions from the unprotonated amino group and the sessile C–H simultaneously was not further investigated, since the free energy of formation of two hydroxide ions (22.4 kcal mol−1 at pH 7.4) is too high, making this reaction pathway less favorable.31
Cyclization of catecholamine o-quinones with protonated quinone group
For catecholamine o-quinones with protonated quinone group, a spontaneous cyclization with protonated amino group was predicted to be strongly endergonic with reaction free energies of 130.56 kcal mol−1 and 111.81 kcal mol−1 for noradrenaline and adrenaline o-quinone respectively, and was accordingly ruled out as feasible, reaffirming that even at very acidic pH the amino group must be first deprotonated before intramolecular Michael addition can take place.19,25,45
Cyclization reactions of catecholamine o-quinone with protonated quinone and unprotonated amino group were strongly exergonic with reaction free energies of −32.28 kcal mol−1 and -37.97 kcal mol−1 for noradrenaline and adrenaline o-quinone respectively. In this scenario the cyclization occurred spontaneously without extraction of the proton from unprotonated amino group, with virtually barrier-less intrinsic activation free energy (ΔG≠i,p) of 1.21 kcal mol−1 and 1.11 kcal mol−1 respectively (Fig. 5).
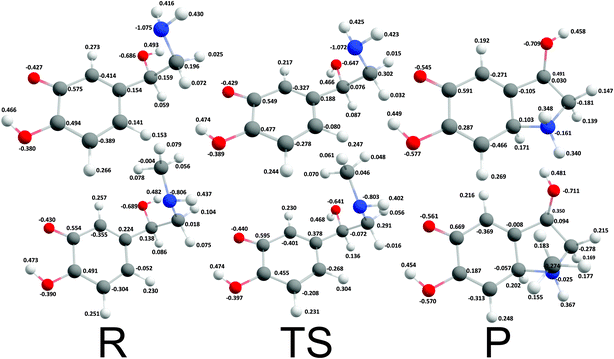 |
| | Fig. 5 Optimized geometries and atomic charges of the reactants (R), transition state (TS) and products (P) of noradrenaline (top) and adrenaline (bottom) o-quinone with protonated quinone group cyclization reaction. Reactants are catecholamine o-quinone with protonated quinone group and unprotonated amino group. Products are cyclized single charged catecholamine o-quinone. Carbon atoms are represented with gray, oxygen atoms red, hydrogen atoms white and nitrogen atoms with blue color. | |
pH dependence of catecholamine o-quinone cyclization activation free energy
Complete activation-free energy for cyclization of catecholamine o-quinones with unprotonated quinone group (ΔG≠u) that would be comparable to the experimental values include also the free energy of hydroxide ion formation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH), where experimental pKa of water (pKa,w) 15.7 is taken into account; the free energy of amino group deprotonation kBT
ln(10)(pKa,w − pH), where experimental pKa of water (pKa,w) 15.7 is taken into account; the free energy of amino group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH); and the free energy of quinone group deprotonation kBT
ln(10)(pKa,1 − pH); and the free energy of quinone group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,2 − pH).46 Therefore, at:
ln(10)(pKa,2 − pH).46 Therefore, at:
pH > pKa,1,
| |
ΔG≠u = ΔG≠i,u + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH) ln(10)(pKa,w − pH)
| (9) |
at p
Ka,2 < pH < p
Ka,1,
| |
ΔG≠u = ΔG≠i,u + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH) + kBT ln(10)(pKa,w − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) ln(10)(pKa,1 − pH)
| (10) |
| |
ΔG≠u = ΔG≠i,u + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w + pKa,1 − 2pH) ln(10)(pKa,w + pKa,1 − 2pH)
| (11) |
and at pH < p
Ka,2,
| |
ΔG≠u = ΔG≠i,u + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH) + kBT ln(10)(pKa,w − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) + kBT ln(10)(pKa,1 − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,2 − pH) ln(10)(pKa,2 − pH)
| (12) |
| |
ΔG≠u = ΔG≠i,u + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w + pKa,1 + pKa,2 − 3pH) ln(10)(pKa,w + pKa,1 + pKa,2 − 3pH)
| (13) |
Complete activation-free energy for cyclization of catecholamine o-quinones with protonated quinone group (ΔG≠p) include also the free energy of quinone group protonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2); and the free energy of amino group deprotonation kBT
ln(10)(pH − pKa,2); and the free energy of amino group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH). Therefore, at:
ln(10)(pKa,1 − pH). Therefore, at:
pH > pKa,1,
| |
ΔG≠p = ΔG≠i,p + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2) ln(10)(pH − pKa,2)
| (14) |
p
Ka,2 < pH < p
Ka,1,
| |
ΔG≠p = ΔG≠i,p + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) + kBT ln(10)(pKa,1 − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2) ln(10)(pH − pKa,2)
| (15) |
| |
ΔG≠p = ΔG≠i,p + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pKa,2) ln(10)(pKa,1 − pKa,2)
| (16) |
pH < p
Ka,2,
| |
ΔG≠p = ΔG≠i,p + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) ln(10)(pKa,1 − pH)
| (17) |
Please note that the activation free energy of cyclization of catecholamine o-quinones with unprotonated quinone group is pH dependent across all pH range. Cyclization of catecholamine o-quinones with protonated quinone group is on the other hand pH dependent only at pH higher and lower than pKa,1 and pKa,2 respectively, while at pH between pKa,1 and pKa,2 it is pH independent.
Noradrenaline and adrenaline o-quinone pKa values
Since the activation free energies are markedly influenced by pKa, pKa values for noradrenaline and adrenaline o-quinone were determined using several methods of solvation free energy calculations (Table 2). Exact experimental pKa values for catecholamine o-quinones are not available. Amino group pKa,1 is experimentally not accessible because at alkaline pH the cyclization rate is too fast and catecholamine o-quinones are not stable. In this respect, the experimental pKa,1 values of adrenaline and noradrenaline were applied. Approximation is plausible since the closest carbonyl group is topologically six bonds away from the amino group. Quinone group pKa,2 is experimentally inaccessible due to highly acidic conditions, but is estimated to be −6 or lower;47 however, our results suggest that pKa,2 is significantly lower than −6.
Table 2 Calculated pKa values for noradrenaline and adrenaline o-quinone using MP2/6-31++G (2d,2p) and several methods to calculate solvation free energya
| |
PCM |
CPCM |
IPCM |
SMD |
CC |
LD |
EXP |
| The experimental values of pKa,1 are for noradrenaline and adrenaline, since the values for their o-quinones are not available. PCM – isodensity polarizable continuum model; CPCM – conductor-like polarizable continuum model; PCM – integral equation formalism variant polarizable continuum model; SMD – universal solvation model, based on density; CC – cluster-continuum model with SMD; LD – Langevin dipoles; EXP – experimental values. |
| Noradrenaline o-quinone |
pKa,1 |
1.4 |
1.4 |
5.4 |
8.7 |
14.2 |
11.9 |
8.6 (ref. 3) |
| pKa,2 |
−21.4 |
−21.4 |
−16.3 |
−14.6 |
−15.2 |
−25.3 |
≤−6 (ref. 47) |
| Adrenaline o-quinone |
pKa,1 |
2.1 |
2.1 |
5.8 |
9.1 |
13.2 |
11.9 |
8.7 (ref. 3) |
| pKa,2 |
−22.4 |
−22.4 |
−14.5 |
−15.2 |
−15.5 |
−19.2 |
≤−6 (ref. 47) |
Calculations of pKa values are extremely demanding and represent one of the strictest tests for the quality of solvation models.48,49 Comparing the calculated and experimental pKa values, the SMD solvent reaction field model predicted the most accurate values.38 Cluster-continuum model with SMD did not substantially improve the calculations, suggesting that specific hydrogen bonding is not very important for calculations of catecholamine o-quinones pKa values.
Reaction kinetics of noradrenaline and adrenaline o-quinone cyclization
The reaction rate constant (krate) and activation free energy bear the following relation:| |
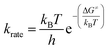 | (18) |
Considering that two major parallel pathways of catecholamine o-quinone cyclization reaction proceed simultaneously, the predicted observed reaction rate constant (kobs) is the sum of reaction rate constants for cyclization of catecholamine o-quinones with unprotonated (ku) and protonated (kp) quinone group.
| |
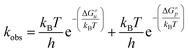 | (20) |
Taking into account the complete activation free energies at different pH intervals, the following pH dependence of the predicted observed reaction rate constant can be derived:
| |
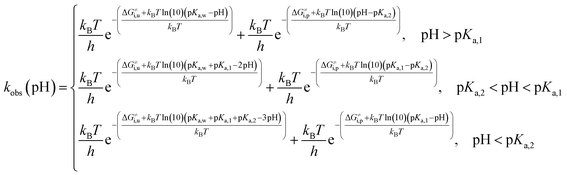 | (21) |
The pH-dependence of predicted observed reaction rate constant for noradrenaline and adrenaline o-quinone cyclization applying the experimental pKa values from Table 2 is featured in Fig. 6. At alkaline pH, the predominant pathway is the cyclization of catecholamine o-quinone with unprotonated quinone group where a proton is extracted by hydroxide ion from unprotonated amino group.50 Please note that at highly alkaline pH, the cyclization step is not the rate limiting step of catecholamine autoxidation, indicated by a plateau and loss of pH dependence of experimentally observed catecholamine autoxidation reaction rate constant at highly alkaline pH.19,22,25 At acidic pH, the cyclization of catecholamine o-quinone with protonated quinone group becomes predominant, indicated by a plateau that is independent of pH and becomes again pH dependent at extremely low pH. The pH dependence of proposed cyclization reaction mechanism is in qualitative agreement with experimental data, proving the validity of our model.19,50,51 Moreover, at physiological pH, the cyclization reaction is faster for adrenaline than noradrenaline o-quinone, which is also consistent with experimental data.22,29 Since noradrenaline o-quinone is more stable at physiological pH than adrenaline o-quinone, it is more susceptible to enter competing oxidative pathways like tautomerization leading to chain breakdown.52
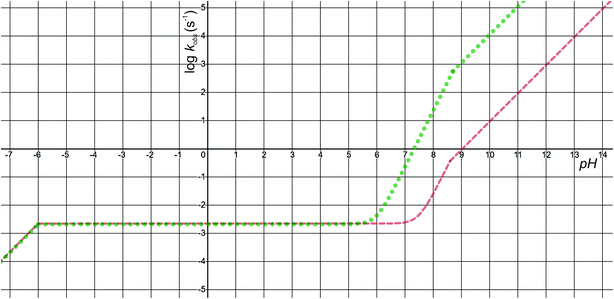 |
| | Fig. 6 The pH-dependence of predicted observed reaction rate constant for noradrenaline (red interrupted line) and adrenaline (green dotted line) o-quinone cyclization reaction applying the experimental pKa values from Table 2. | |
Quantitatively, the proposed model is reasonably close to experimental data. The predicted observed reaction rate constants are dependent on calculated intrinsic activation free energies where error up to 3 kcal mol−1 is expected due to the error of hydration free energy calculations for charged species.53 Furthermore, experimental pKa values are not available, while the calculated pKa values of monoamines are expected to have error of 3 or even more units.37 El-Ayaan et al. predicted the noradrenaline o-quinone pKa values of pKa,1 = 9.53 and pKa,2 = 1.55 from experimental cyclization reaction kinetic data.19 However, they performed the experiments in the presence of different salts and iron(III) or periodate that might significantly influence the kinetics of the reaction.25 Moreover, the catecholamine autoxidation reaction rate is also influenced by the electrostatic properties of immediate surroundings influencing the dispersion and localization of charges on the reactants,50 which could significantly alter the local pKa values of reactants and the intrinsic activation free energy of the cyclization reaction, consequently changing the observed autoxidation reaction rate constants.54 This could be biologically relevant since catecholamines are stored in secretory vesicles with numerous other charged molecules55 and since catecholaminergic signaling occurs in a complex environment of a synapse and extracellular space.56 Therefore, further studies investigating the effects of various charged molecules on catecholamine o-quinone cyclization reaction are warranted.
Conclusions
Using quantum chemical methods, the present study investigated the cyclization step of the catecholamines- noradrenaline and adrenaline autoxidation reaction in aqueous solution by considering two reaction pathways across a broad pH range. The result showed that two catecholamine o-quinone species, one with unprotonated and one with protonated quinone group, can participate in the cyclization reaction. At acidic pH, spontaneous cyclization of catecholamine o-quinone with protonated quinone and unprotonated amino group is predominant and its kinetics is pH independent; while at alkaline pH, the cyclization of catecholamine o-quinone with unprotonated quinone group where a proton is extracted from the unprotonated amino group by hydroxide ion prevails and is highly pH dependent. Furthermore, analytical solution for describing the complex pH dependence of the observed cyclization reaction rate constant and predicted pKa values for noradrenaline and adrenaline o-quinone are also provided. The proposed model is consistent with experimental data and provides deeper understanding of the catecholamine o-quinone cyclization mechanism. It remains a challenge for the future to address these reactions on multiscale QM/MM level and to build a macroscopic model of catecholaminergic neurodegeneration.57
Conflicts of interest
The author has no conflicts of interest.
Acknowledgements
The author would like to thank Janez Mavri for many stimulating discussions, the National Institute of Chemistry for CPU time, Dr Chiedozie K. Ugwoke for manuscript proofreading and Enej Bacic for technical support. This work was supported by the Slovenian Research Agency (grant number P3-0043).
References
- K. Kitahama, J. Pearson, L. Denoroy, N. Kopp, J. Ulrich, T. Maeda and M. Jouvet, Neurosci. Lett., 1985, 53, 303–308 CrossRef CAS PubMed.
- J. Wu, M. H. Ji, Z. Y. Wang, W. Zhu, J. J. Yang and Y. G. Peng, J. Cardiovasc. Pharmacol., 2013, 62, 325–328 CrossRef CAS PubMed.
- R. Álvarez-Diduk and A. Galano, J. Phys. Chem. B, 2015, 119, 3479–3491 CrossRef PubMed.
- G. Šimić, M. Babić Leko, S. Wray, C. R. Harrington, I. Delalle, N. Jovanov-Milošević, D. Bažadona, L. Buée, R. de Silva, G. Di Giovanni, C. M. Wischik and P. R. Hof, Prog. Neurobiol., 2017, 151, 101–138 CrossRef PubMed.
- G. Leanza, R. Gulino and R. Zorec, Front. Mol. Neurosci., 2018, 11, 254 CrossRef PubMed.
- J. Segura-Aguilar, D. Metodiewa and C. J. Welch, Biochim. Biophys. Acta, 1998, 1381, 1–6 CrossRef CAS.
- S. Baez, Y. Linderson and J. Segura-Aguilar, Chem.-Biol. Interact., 1994, 93, 103–116 CrossRef CAS PubMed.
- M. Pavlin, M. Repič, R. Vianello and J. Mavri, Mol. Neurobiol., 2016, 53, 3400–3415 CrossRef CAS PubMed.
- D. G. Graham, Mol. Pharmacol., 1978, 14, 633–643 CAS.
- L. E. Cassagnes, M. Chhour, P. Pério, J. Sudor, R. Gayon, G. Ferry, J. A. Boutin, F. Nepveu and K. Reybier, Free Radicals Biol. Med., 2018, 120, 56–61 CrossRef CAS PubMed.
- I. Paris, C. Perez-Pastene, S. Cardenas, P. Iturriaga-Vasquez, P. Iturra, P. Muñoz, E. Couve, P. Caviedes and J. Segura-Aguilar, Neurotoxic. Res., 2010, 18, 82–92 CrossRef PubMed.
- J. Segura-Aguilar, Front. Neurosci., 2019, 13, 271 CrossRef PubMed.
- F. A. Chaudhry, R. H. Edwards and F. Fonnum, Annu. Rev. Pharmacol. Toxicol., 2008, 48, 277–301 CrossRef CAS PubMed.
- M. Mani and T. A. Ryan, Front. Neural Circuits, 2009, 3, 3 Search PubMed.
- J. Du, L. R. Reznikov, M. P. Price, X. M. Zha, Y. Lu, T. O. Moninger, J. A. Wemmie and M. J. Welsha, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8961–8966 CrossRef CAS PubMed.
- J. D. Erickson, M. K. H. Schäfer, T. I. Bonner, L. E. Eiden and E. Weihe, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 5166–5171 CrossRef CAS PubMed.
- S. Nikolaus, C. Antke, K. Kley, T. D. Poeppel, H. Hautzel, D. Schmidt and H.-W. Müller, Rev. Neurosci., 2007, 18, 439–472 CAS.
- M. Uchigashima, T. Ohtsuka, K. Kobayashi and M. Watanabe, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4206–4211 CrossRef CAS PubMed.
- U. El-Ayaan, R. F. Jameson and W. Linert, J. Chem. Soc., Dalton Trans., 1998, 1315–1319 RSC.
- A. Bindoli, G. Scutari and M. P. Rigobello, Neurotoxic. Res., 1999, 1, 71–80 CrossRef CAS PubMed.
- D. C. Tse, R. L. McCreery and R. N. Adams, J. Med. Chem., 1976, 19, 37–40 CrossRef CAS PubMed.
- M. D. Hawley, S. V. Tatawawadi, S. Piekarski and R. N. Adams, J. Am. Chem. Soc., 1967, 89, 447–450 CrossRef CAS PubMed.
- W. H. Harrison, W. W. Whisler and B. J. Hill, Biochemistry, 1968, 7, 3089–3094 CrossRef CAS PubMed.
- M. Z. A. Rafiquee, M. R. Siddiqui, M. S. Ali and H. A. Al-Lohedan, Spectrochim. Acta, Part A, 2014, 126, 21–27 CrossRef CAS PubMed.
- E. Pelizzetti, E. Mentasti and E. Pramauro, J. Chem. Soc., Perkin Trans. 2, 1976, 14, 1651–1655 RSC.
- R. P. Bacil, L. Chen, S. H. P. Serrano and R. G. Compton, Phys. Chem. Chem. Phys., 2020, 22, 607–614 RSC.
- C. Lin, L. Chen, E. E. L. Tanner and R. G. Compton, Phys. Chem. Chem. Phys., 2017, 20, 148–157 RSC.
- S. Schindler and T. Bechtold, J. Electroanal. Chem., 2019, 836, 94–101 CrossRef CAS.
- M. Rafiee, L. Khalafi, F. Mousavi, F. Babaloii and F. Kalhori, Electroanalysis, 2017, 29, 2004–2007 CrossRef CAS.
- R. Kishida and H. Kasai, J. Phys. Soc. Jpn., 2018, 87, 084802 CrossRef.
- N. Umek, B. Gersak, N. Vintar, M. Sostaric and J. Mavri, Front. Mol. Neurosci., 2018, 11, 467 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- M. D. Liptak, K. C. Gross, P. G. Seybold, S. Feldgus and G. C. Shields, J. Am. Chem. Soc., 2002, 124, 6421–6427 CrossRef CAS PubMed.
- K. Perdan-Pirkmajer, J. Mavri and M. Krẑan, J. Mol. Model., 2010, 16, 1151–1158 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098–16104 CrossRef CAS.
- M. Kržan, J. Keuschler, J. Mavri and R. Vianello, Biomolecules, 2020, 10, 2 CrossRef PubMed.
- J. Florián and A. Warshel, J. Phys. Chem. B, 1997, 101, 5583–5595 CrossRef.
- J. Ho and M. L. Coote, Theor. Chem. Acc., 2009, 125, 3–21 Search PubMed.
- R. Kishida, A. G. Saputro, R. L. Arevalo and H. Kasai, Int. J. Quantum Chem., 2017, 117, e25445 CrossRef.
- M. O. Salomäki, L. Marttila, H. Kivelä, T. Ouvinen and J. O. Lukkari, J. Phys. Chem. B, 2018, 122, 6314–6327 CrossRef PubMed.
- J. N. Bronsted, Chem. Rev., 1928, 5, 231–338 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1984, 164, 213–227 CrossRef CAS.
- M. Repič, M. Purg, R. Vianello and J. Mavri, J. Phys. Chem. B, 2014, 118, 4326–4332 CrossRef PubMed.
- A. Warshel, Biochemistry, 1981, 20, 3167–3177 CrossRef CAS PubMed.
- A. S. Al-Ayed, H. A. Al-Lohedan, M. Z. A. Rafiquee, M. S. Ali and Z. A. Issa, Transition Met. Chem., 2013, 38, 173–181 CrossRef CAS.
- R. V. Lloyd, Chem. Res. Toxicol., 1995, 8, 111–116 Search PubMed.
- P. Manini, L. Panzella, A. Napolitano and M. D'Ischia, Chem. Res. Toxicol., 2007, 20, 1549–1555 Search PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
- Y. Y. Sham, Z. T. Chu and A. Warshel, J. Phys. Chem. B, 1997, 101, 4458–4472 CrossRef CAS.
- E. Crivellato, B. Nico and D. Ribatti, Anat. Rec., 2008, 291, 1587–1602 CrossRef PubMed.
- J. J. E. Chua, S. Kindler, J. Boyken and R. Jahn, J. Cell Sci., 2010, 123, 819–823 CrossRef CAS PubMed.
- D. Pregeljc, D. Teodorescu-Perijoc, R. Vianello, N. Umek and J. Mavri, Neurotoxic. Res., 2020, 37, 724–731 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 and endocrine signaling,2 with both of the latter mechanisms occurring in the extracellular fluid/blood with a pH ∼ 7.4.
18 and endocrine signaling,2 with both of the latter mechanisms occurring in the extracellular fluid/blood with a pH ∼ 7.4.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa − pH) and ΔG = kBT
ln(10)(pKa − pH) and ΔG = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa) were applied to calculate the free energy change associated with proton transfer from and to an ionizable group with a certain pKa value, to and from bulk water in an aqueous solution with a certain pH value, respectively.
ln(10)(pH − pKa) were applied to calculate the free energy change associated with proton transfer from and to an ionizable group with a certain pKa value, to and from bulk water in an aqueous solution with a certain pH value, respectively.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka
Ka
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka
Ka
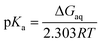

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46)
ln(24.46)
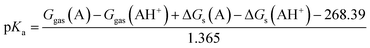
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH), where experimental pKa of water (pKa,w) 15.7 is taken into account; the free energy of amino group deprotonation kBT
ln(10)(pKa,w − pH), where experimental pKa of water (pKa,w) 15.7 is taken into account; the free energy of amino group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH); and the free energy of quinone group deprotonation kBT
ln(10)(pKa,1 − pH); and the free energy of quinone group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,2 − pH).46 Therefore, at:
ln(10)(pKa,2 − pH).46 Therefore, at:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH)
ln(10)(pKa,w − pH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH) + kBT
ln(10)(pKa,w − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH)
ln(10)(pKa,1 − pH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w + pKa,1 − 2pH)
ln(10)(pKa,w + pKa,1 − 2pH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w − pH) + kBT
ln(10)(pKa,w − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) + kBT
ln(10)(pKa,1 − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,2 − pH)
ln(10)(pKa,2 − pH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,w + pKa,1 + pKa,2 − 3pH)
ln(10)(pKa,w + pKa,1 + pKa,2 − 3pH)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2); and the free energy of amino group deprotonation kBT
ln(10)(pH − pKa,2); and the free energy of amino group deprotonation kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH). Therefore, at:
ln(10)(pKa,1 − pH). Therefore, at:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2)
ln(10)(pH − pKa,2)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH) + kBT
ln(10)(pKa,1 − pH) + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pH − pKa,2)
ln(10)(pH − pKa,2)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pKa,2)
ln(10)(pKa,1 − pKa,2)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)(pKa,1 − pH)
ln(10)(pKa,1 − pH)