Collective dynamics in lipid membranes containing transmembrane peptides
Elizabeth G.
Kelley
 *a,
Paul D.
Butler
*a,
Paul D.
Butler
 abc and
Michihiro
Nagao
abc and
Michihiro
Nagao
 ade
ade
aNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD, USA. E-mail: egk@nist.gov
bDepartment of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA
cDepartment of Chemistry, The University of Tennessee Knoxville, TN 37996, USA
dDepartment of Materials Science and Engineering, University of Maryland, College Park, MD 20742, USA
eDepartment of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA
First published on 4th May 2021
Abstract
Biological membranes are composed of complex mixtures of lipids and proteins that influence each other's structure and function. The biological activities of many channel-forming peptides and proteins are known to depend on the material properties of the surrounding lipid bilayer. However, less is known about how membrane-spanning channels affect the lipid bilayer properties, and in particular, their collective fluctuation dynamics. Here we use neutron spin echo spectroscopy (NSE) to measure the collective bending and thickness fluctuation dynamics in dimyristoylphosphatidylcholine (di 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC, DMPC) lipid membranes containing two different antimicrobial peptides, alamethicin (Ala) and gramicidin (gD). Ala and gD are both well-studied antimicrobial peptides that form oligomeric membrane-spanning channels with different structures. At low concentrations, the peptides did not have a measurable effect on the average bilayer structure, yet significantly changed the collective membrane dynamics. Despite both peptides forming transmembrane channels, they had opposite effects on the relaxation time of the collective bending fluctuations and associated effective bending modulus, where gD addition stiffened the membrane while Ala addition softened the membrane. Meanwhile, the lowest gD concentrations enhanced the collective thickness fluctuation dynamics, while the higher gD concentrations and all studied Ala concentrations dampened these dynamics. The results highlight the synergy between lipids and proteins in determining the collective membrane dynamics and that not all peptides can be universally treated as rigid bodies when considering their effects on the lipid bilayer fluctuations.
0 PC, DMPC) lipid membranes containing two different antimicrobial peptides, alamethicin (Ala) and gramicidin (gD). Ala and gD are both well-studied antimicrobial peptides that form oligomeric membrane-spanning channels with different structures. At low concentrations, the peptides did not have a measurable effect on the average bilayer structure, yet significantly changed the collective membrane dynamics. Despite both peptides forming transmembrane channels, they had opposite effects on the relaxation time of the collective bending fluctuations and associated effective bending modulus, where gD addition stiffened the membrane while Ala addition softened the membrane. Meanwhile, the lowest gD concentrations enhanced the collective thickness fluctuation dynamics, while the higher gD concentrations and all studied Ala concentrations dampened these dynamics. The results highlight the synergy between lipids and proteins in determining the collective membrane dynamics and that not all peptides can be universally treated as rigid bodies when considering their effects on the lipid bilayer fluctuations.
1 Introduction
Lipid bilayers were once thought to be a passive matrix for membrane proteins that performed the wide variety of functions essential to life. However, it has become increasing apparent over the past 40 years or so that the activity of many membrane-embedded proteins critically depends on physical properties of the surrounding lipid matrix. A lipid membrane has a thickness, elasticity, and viscosity that influence processes from protein conformational changes and folding,1,2 to the energetic penalty for protein-induced membrane curvature,3–5 and the time required for protein diffusion through the two dimensional membrane.6–8From the lipid membrane perspective, the absorption and insertion of large rigid proteins can have a significant effect on the structure and dynamics of the soft lipid bilayer. Proteins are anywhere from 100 to 1000 times more rigid than the surrounding lipid matrix, meaning the soft lipid bilayer will locally deform to accommodate the protein.9–11 Depending on the relative hydrophobic thicknesses of the protein versus the lipid bilayer as well as the protein concentration in the membrane, reports have shown that the lipid bilayer can deform by as much as 0.3 nm to 0.4 nm, upwards of 10% of its unperturbed equilibrium thickness.9,10,12 Proteins and peptides also have been shown to induce membrane curvature13–15 as well as change the membrane stiffness, often quantified as the bending modulus κ.16–25
Fewer studies have looked at the effects of peptides on the membrane dynamic fluctuations, despite growing evidence that these dynamics are also essential to protein conformational changes, protein–protein interactions, and membrane adhesion.26–29 Lipid bilayers undergo dynamic conformational changes over many orders of magnitude in length scale and time scale. The mesoscale collective dynamics on the length scale of the membrane itself are arguably the most biologically relevant for local processes.30 These collective lipid dynamics on the nanometer length scale and nanosecond time scale are synergistic with the thermal motions of the individual atoms and domains in proteins that drive larger scale conformational changes between kinetically distinct protein states.31,32 Helfrich and Jackobsson also suggested that collective membrane dynamics, and in particular, the peristaltic-like thickness fluctuations would help peptide monomers in each leaflet find each other to form membrane spanning channels.33 But on the other hand, one can also imagine that the formation of a rigid membrane-spanning channel could inhibit these dynamics and effectively pin the two membrane leaflets together.
Here we measured the effects of two well-studied membrane-spanning peptides, gramicidin (gD) and alamethicin (Ala), on the collective dynamics of model dimyristoylphophatidylcholine (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
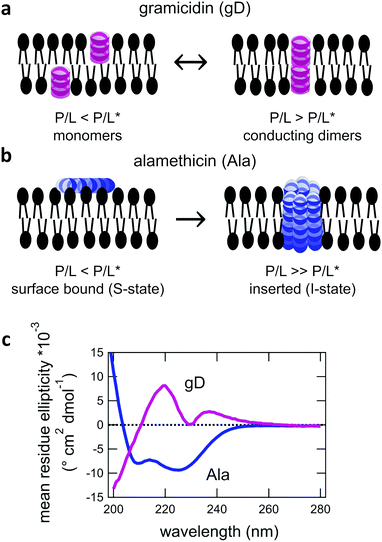
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 PC, DMPC) phospholipid membranes. Both gD and Ala are prototypical model peptides known to form membrane-spanning channels with different structures. gD is a hydrophobic 15 amino acid peptide that forms ion channels specific to monovalent cations. At low concentrations, gD monomers are incorporated in each membrane leaflet and adopt a β6.3 helical structure (Fig. 1a).10,34 At higher peptide concentrations, the gD monomers are in equilibrium with antiparallel dimers that are stabilized by 6 intermolecular hydrogen bonds and form the active membrane-spanning channel.35,36 Meanwhile, Ala is a hydrophobic 20 amino acid peptide that forms α-helices on the surface of lipid membranes at low concentrations, often referred to as the S-state in literature.37–39 Above its critical concentration threshold, Ala inserts into the membrane (the so-called I-state). At even higher concentrations, Ala forms oligomeric peptide-lined pores containing between 6 and 8 peptide monomers that are referred to as barrel-stave pores in literature (Fig. 1b).40–42
0 PC, DMPC) phospholipid membranes. Both gD and Ala are prototypical model peptides known to form membrane-spanning channels with different structures. gD is a hydrophobic 15 amino acid peptide that forms ion channels specific to monovalent cations. At low concentrations, gD monomers are incorporated in each membrane leaflet and adopt a β6.3 helical structure (Fig. 1a).10,34 At higher peptide concentrations, the gD monomers are in equilibrium with antiparallel dimers that are stabilized by 6 intermolecular hydrogen bonds and form the active membrane-spanning channel.35,36 Meanwhile, Ala is a hydrophobic 20 amino acid peptide that forms α-helices on the surface of lipid membranes at low concentrations, often referred to as the S-state in literature.37–39 Above its critical concentration threshold, Ala inserts into the membrane (the so-called I-state). At even higher concentrations, Ala forms oligomeric peptide-lined pores containing between 6 and 8 peptide monomers that are referred to as barrel-stave pores in literature (Fig. 1b).40–42
We focus on low concentrations where the peptides are expected to form membrane-spanning channels, but not so high in concentration that the peptides perturb the average membrane structure. Even at these low concentrations, we see that the membrane spanning channels have a significant effect on the collective bending and thickness fluctuation dynamics measured with neutron spin echo (NSE) spectroscopy. Gramidicin incorporation significantly slowed the bending fluctuations, suggesting an approximate 2× increase in the effective bending modulus at concentrations as low as a mole fraction of 1.2% (mol%). Meanwhile, Ala increased the relaxation rate of the same dynamics and lead to almost a 2× decrease in the effective bending modulus over the same concentration range. Quite interestingly, low concentrations of gD enhanced the collective thickness fluctuation dynamics. Yet higher gD concentrations and all studied Ala concentrations dampened the out of plane thickness fluctuation dynamics. Together, the NSE data show that even low concentrations of a transmembrane peptide can have a significant effect on the collective lipid membrane dynamics that will also depend on the peptide structure and local interactions with the surrounding lipids.
2 Materials and methods
2.1 Materials
1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1,2-dimyristoyl-d54-sn-glycero-3-phosphocholine (DMPC-d54) were purchased from Avanti Polar Lipids. Deuterium oxide (99.5%D) was purchased from Cambridge Isotopes. All other chemicals, including gramicidin from Bacilius brevis and alamethicin from Trichoderma virde, were obtained from Sigma Aldrich. All materials were used without further purification.2.2 Sample preparation
A unique advantage of neutron scattering is that neutrons interact differently with hydrogen (H) and deuterium (D), allowing for specific structural and/or dynamical features to be highlighted by tuning the H/D ratio in the samples. As such, unilamellar vesicles containing the desired H/D contrast and amount of peptide were prepared using established protocols. The desired amount of gD and DMPC or DMPC-d54 were mixed gravimetrically and then dissolved in trifluoroethanol (TFE) at 35 °C. For DMPC–Ala mixtures, the desired amount of DMPC was added to a vial gravimetrically, and then the corresponding amount of an Ala in methanol stock solution was added to the lipid powder. The DMPC–Ala mixtures were then codissolved in a TFE/methanol mixture at 35 °C. Once all the lipid-peptide mixtures were dissolved and the solutions were homogeneous by eye, the organic solvents were removed under a stream of nitrogen at ≈50 °C and then under vacuum at a temperature ≥30 °C overnight. The dry films were hydrated with D2O to a concentration of 100 mg of lipid to 1 mL of solvent above the main transition temperature (Tm) of DMPC to form a multilamellar vesicle (MLV) suspension. Subsequently, the MLV suspension was sequentially extruded though 400 nm (21×), 200 nm (21×), and finally 100 nm (41×) filters at temperatures ≥35 °C to produce homogeneous solutions of relatively monodisperse unilamllaer vesicles. Small angle neutron scattering (SANS) data were collected on all solutions to ensure that the samples contained ≥90% unilamellar vesicles (ULVs) prior to additional characterization.432.3 UV-Vis spectroscopy
UV-Vis measurements were performed using a Thermo Scientific Evolution 201 UV Vis Spectrophotometer. All lipid vesicle solutions were diluted 5× with a solution containing a mass fraction of 6% sodium dodecyl sulfate (SDS) in D2O to break apart the vesicles. The solutions were briefly vortex mixed until transparent by eye and then loaded into a 1 mm quartz cuvette. UV Vis spectra were recorded between 200 nm and 400 nm. The background signal from the pure vesicle solution was subtracted and the measured absorbance at 280 nm was used to calculate the concentration of gD in solution using a molar extinction coefficient of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 (mol L)−1 cm−1.44
700 (mol L)−1 cm−1.44
2.4 Circular dichroism spectroscopy
Circular Dichroism (CD) measurements were performed using a Chira-Scan CD spectrometer. Samples were loaded into a 1 mm quartz cuvette and equilibrated at 35 °C for at least 15 minutes prior to starting the data collection. Data were collected between 195 nm and 280 nm with a 1 nm step size with 5 s averaging per point. The samples were diluted with D2O such that the peptide concentration was between 0.02 mmol L−1 and 0.6 mmol L−1. The background signal from the corresponding lipid vesicle solution was subtracted from the peptide-containing samples in the software provided with the instrument.2.5 Small-angle X-Ray scattering
Small-angle X-ray scattering (SAXS) experiments were performed on the 12-ID-B beamline at the Advanced Photon Source at Argonne National Laboratory. Samples were run using a flow cell and the temperature was maintained within ±2 °C. Data were collected using a X-ray wavelength (λ) of 0.09 nm and a sample to detector to distance of 2 m to measure a scattering vector (q) range of 0.04 nm−1 ≤ q ≤ 10 nm−1. q is defined as q = (4π/λ)sin(θ/2) in which θ is the scattering angle. Data were collected using 2 s acquisition times and averaged over 30 acquisitions. The data were reduced and the background scattering from D2O was subtracted using the software packages provided by the beamline.2.6 Small-angle neutron scattering
Small-angle neutron scattering (SANS) data were collected on the NGB30 SANS and NG3 VSANS instruments at the NIST Center for Neutron Research (NCNR, Gaithersburg, MD). Scattering data on the NGB30 SANS instrument were collected with a neutron wavelength (λ) of 0.6 nm and a nominal wavelength distribution (Δλ/λ) of 0.12. Sample to detector distances (SDD) of 1 m, 4 m, and 13 m were used to provide access to a q-range of 0.04 nm−1 ≤ q ≤ 4 nm−1. Scattering data on the NG3 VSANS instrument were collected with λ = 0.6 nm and Δλ/λ = 0.12 with the two movable carriages positioned at either 1 m and 5 m or 4.5 m and 18 m to provide access to a combined q range of 0.04 nm−1 ≤ q ≤ 5 nm−1. All SANS data were collected at 35 °C and reduced to absolute intensity using the macros provided by NIST.452.7 Neutron spin echo spectroscopy (NSE)
Neutron spin echo spectroscopy (NSE) measurements were performed on the NG5 and NGA NSE spectrometers at the NCNR.46 The experiments on the NG5-NSE used incident neutron wavelengths, λ, of 0.6 nm and 0.8 nm to access timescales of 0.05 ns to 15 ns for λ = 0.6 nm and 0.1 ns to 40 ns for λ = 0.8 nm. The measured q-range was from 0.4 nm−1 to 2 nm−1 for the thickness fluctuation measurements. The NGA-NSE was utilized to measure bending fluctuations using λ = 0.8 nm and 1.1 nm to access q-range from 0.4 nm−1 to 1 nm−1 and Fourier times from 0.1 ns to 100 ns.46Data were collected on both the NG5 and NGA-NSE spectrometers at a constant temperature of T = 35 °C. The data for the lipid samples were corrected for the instrument resolution and solvent background using the DAVE software package to give the intermediate scattering function, I(q,t)/I(q,0).47 The NSE data for the peptide-containing membranes are compared to previously published data for pure DMPC that were collected on the IN15 NSE spectrometer at the Institut Laue-Langevin (ILL, Grenoble, France).48
The NSE data for all temperatures were fit with a stretched exponential function for single membrane fluctuation dynamics as described by Zilman and Granek,
| I(q,t)/I(q,0) = exp[−(Γ(q)t)2/3] | (1) |
For protiated lipids in D2O, the neutron scattering length density contrast between the lipid membrane and the surrounding solvent makes NSE sensitive to the local height (i.e. predominantly bending) fluctuations normal to the plane of the membrane. The relaxation rate corresponding to these fluctuations is determined by a balance between the membrane stiffness and the viscosity of the surrounding solvent. The work by Zilman and Granek predicted that the Γ scales with q3 and is inversely related membrane bending modulus, κ. However, subsequent work by Watson and Brown showed that the membrane dynamics measured on the nanoscale with NSE are governed by an effective bending modulus, 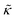 ,50 as originally proposed in theoretical work by Seifert and Langer.51 In the Watson-Brown refinement to the NSE data analysis framework for lipid membranes, the relaxation rate still scales with q3, but is inversely related to the effective bending modulus,
,50 as originally proposed in theoretical work by Seifert and Langer.51 In the Watson-Brown refinement to the NSE data analysis framework for lipid membranes, the relaxation rate still scales with q3, but is inversely related to the effective bending modulus, 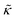 ,
,
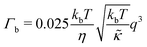 | (2) |
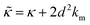 .50,51 The first term in the
.50,51 The first term in the 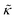 expression describes the contributions from the bending modulus, κ, and the second term accounts for the dissipation within the bilayer from the redistribution of the individual lipids where d is the height of the neutral surface above the bilayer midplane and km is the monolayer compressibility modulus. The added term in the
expression describes the contributions from the bending modulus, κ, and the second term accounts for the dissipation within the bilayer from the redistribution of the individual lipids where d is the height of the neutral surface above the bilayer midplane and km is the monolayer compressibility modulus. The added term in the 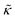 expression accounts for the source of dissipation within the bilayer that comes into play on the nanoscale because the local changes in lipid density caused by the membrane deformation cannot fully relax in the finite time scale, effectively leading to an increased energy penalty for deforming the membrane on the nanoscale.
expression accounts for the source of dissipation within the bilayer that comes into play on the nanoscale because the local changes in lipid density caused by the membrane deformation cannot fully relax in the finite time scale, effectively leading to an increased energy penalty for deforming the membrane on the nanoscale.
In the present work, it is not clear if and how adding the membrane-spanning peptides affects the bending modulus or the dissipation within the bilayer given by 2d2km in the expression above. As such, we will focus on relative changes in the effective stiffness compared to a pure lipid membrane containing no peptide, 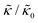 . The reported changes reflect the peptide-induced effects on the measured relaxation rate and the effective membrane stiffness on the nanoscale.
. The reported changes reflect the peptide-induced effects on the measured relaxation rate and the effective membrane stiffness on the nanoscale.
Contrast matching the lipid tails to the surrounding aqueous solvent using tail-deuterated lipids emphasizes the coherent dynamics of the headgroup regions of the inner and outer leaflets of the bilayer. The NSE data collected using this contrast scheme show an excess in dynamics at q-values corresponding to the bilayer thickness, and these dynamics are attributed to the collective thickness fluctuations.48,52–55 The dynamics were characterized using two additive decay constants,
| Γ = Γb + Γt | (3) |
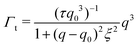 | (4) |
The Γt expression fits the measured peak due to the thickness fluctuation dynamics to a Lorentzian function where the peak height is related to τ, the relaxation time of the thickness fluctuations, q0 is the peak position, and ξ−1 is the half-width at half maximum (HWHM) of the peak and is related to the fluctuation amplitude.48,55 We present the fractional amplitude, σd, as σd = 2(ξq0)−1, or the peak full width half max (FWHM) normalized by the peak position. Both the amplitude and relaxation time for the peptide-containing membranes are normalized by the pure lipid membrane to emphasize the relative changes.
3 Results
The secondary structure of both the gD and Ala peptides34–37,39–42 as well as their effects on the structure and elasticity of model lipid membranes are well studied in literature.9,12,56–60 Circular dichroism (CD) spectra were collected to confirm that the gD and Ala peptides were incorporated into the membranes with their characteristic β6.3- and α- helical structures, respectively, that can form transmembrane pores (Fig. 1c) The membrane structure and dynamics measurements were performed at low peptide concentrations where gD is expected to predominately form dimers and Ala is thought to be inserted into the membrane. While the local lipid membrane structure is likely affected by the peptides, the peptide concentration range is low enough that these effects have not propagated over the entire membrane surface and changed the global membrane structure. At these concentrations, we are able to study the effects of the membrane-spanning channels on the collective bending and thickness fluctuations without competing effects from long-range structural deformations of the membranes.3.1 Average membrane structure
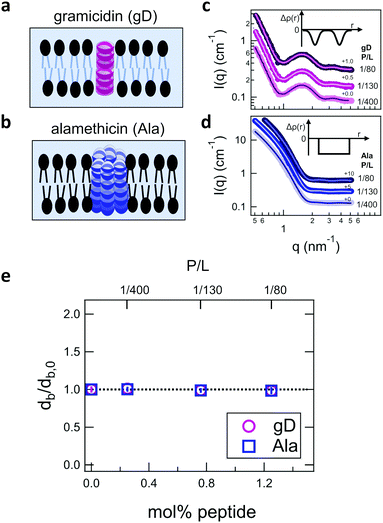
Shown in Fig. 2 are representative SANS data and fits to the appropriate form factor models for DMPC lipid membranes containing gD or Ala. The different contrast conditions in the SANS data for DMPC + gD (Fig. 2c) and DMPC + Ala (Fig. 2d) also illustrate the different contrast conditions used in the NSE experiments. The data in Fig. 2c are for gD in lipid membranes composed of a mixture of tail-deuterated DMPC-d54 and protiated DMPC to match the lipid tail region to the surrounding D2O solvent as schematically shown in Fig. 2a, the same contrast conditions used for NSE measurements of thickness fluctuations. The solid lines through the points are fits to a form factor model that describes the membrane scattering length density (Δρ) as three layers: one layer each for the inner and outer headgroup regions and one layer for the hydrophobic tail region (inset in Fig. 2c). The data in Fig. 2d are for Ala in protiated DMPC in D2O, where the lipid headgroups and hydrographic tails both have contrast with the surrounding solvent as illustrated in Fig. 2b, and are the same contrast conditions used to measure the collective bending fluctuations with NSE. The similar scattering length densities of the head and tail regions of the bilayer gives a simpler scattering pattern without minima and maxima at high q. The SANS data were fit with a simpler form factor model that treats the membrane as a single layer (inset in Fig. 2d). The different lipid scattering length density contrasts and their respective form factor models both gave values for the bilayer thickness (db) for pure DMPC at 35 °C that were consistent with other reports in literature, db ≈ 3.6 nm.61,62Comparing the SANS data for the different peptides showed no measurable changes with increasing concentration, which was further supported by the data modeling. As seen in Fig. 2e, the relative changes in bilayer thickness, db/db,0 ≈ 1 were within the uncertainty of the measurements up to 1.1 mol% peptide, which corresponds to a peptide to lipid molar ratio (P/L) of ≈1/80.
3.2 Collective height fluctuation dynamics
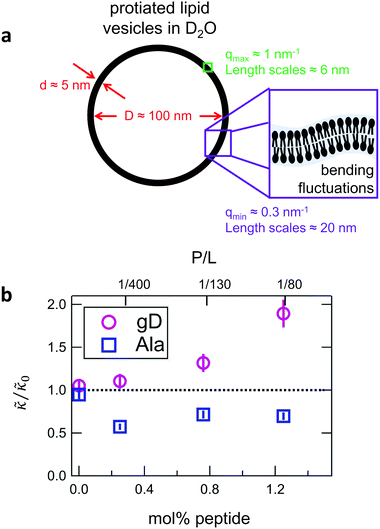
While the SANS data showed no measurable change in the average membrane thickness, the NSE measurements revealed an almost two-fold change in the relaxation rates of the collective bending fluctuations over the same peptide concentration range. NSE measurements were made on protiated lipid vesicles in D2O over a q-range of 0.3 nm−1 ≤ q ≤ 1 nm−1 and Fourier times up to 100 ns. These experimental conditions were selected to be sensitive to the membrane height fluctuations at length scales of ≈6 nm to 20 nm, which corresponds to length scales that are greater than the bilayer thickness, but less than the vesicle radius as illustrated in the cartoon in Fig. 3a. The relaxation rates of the membrane bending fluctuations on the nanoscale measured with NSE are inversely related to the effective bending modulus,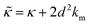 , meaning a larger value of
, meaning a larger value of 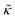 for a stiffer membrane results in a slower measured decay in NSE.
for a stiffer membrane results in a slower measured decay in NSE.
Here we focus on relative changes in the effective bending modulus with added peptide compared the pure lipid membrane, 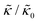 . These changes reflect the measured change in the relaxation rate of the bending dynamics independent of any assumptions of how
. These changes reflect the measured change in the relaxation rate of the bending dynamics independent of any assumptions of how 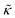 and κ are quantitatively related. Quite interestingly, while both peptides led to an approximately two fold change in
and κ are quantitatively related. Quite interestingly, while both peptides led to an approximately two fold change in 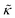 , they had the opposite effect (Fig. 3b). The effective bending modulus monotonically increased with increasing gD concentration, indicating that the membrane became stiffer with increasing peptide concentration and
, they had the opposite effect (Fig. 3b). The effective bending modulus monotonically increased with increasing gD concentration, indicating that the membrane became stiffer with increasing peptide concentration and 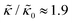 at 1.2 mol% gD (P/L ≈ 1/80). Meanwhile, Ala incorporation reduced the effective bending modulus to
at 1.2 mol% gD (P/L ≈ 1/80). Meanwhile, Ala incorporation reduced the effective bending modulus to 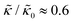 at concentrations as low as 0.25 mol% (P/L ≈ 1/400) and only varied slightly with a further increase in peptide concentration.
at concentrations as low as 0.25 mol% (P/L ≈ 1/400) and only varied slightly with a further increase in peptide concentration.
3.3 Collective thickness fluctuation dynamics
In addition to collective bending fluctuations, lipid membranes also undergo collective thickness fluctuations out of the membrane plane on the nanoscale. While thickness fluctuations have been considered theoretically for more than 30 years,12,63,64 they have only become experimentally accessible over the past decade or so by taking advantage of contrast variation in neutron scattering and the unique dynamic range accessible with NSE.30,48,53,55 Here we extend the use of NSE to measure the effects of peptide addition on the lipid membrane thickness fluctuations.Shown in Fig. 4(a) is a cartoon illustration of the neutron scattering length density contrast needed to measure the thickness fluctuations with NSE. Contrast matching the lipid tail region to the surrounding solvent using tail-deuterated lipids both reduced the incoherent background signal in the sample and emphasized the dynamics of the headgroups regions relative to one another. NSE data measured at these contrast conditions show excess dynamics in addition to what is expected for pure bending fluctuations discussed above.30,48,53,55 The excess in dynamics is at the length scale of the bilayer thickness (i.e. the dip in the form factor in Fig. 2c) and is most clearly seen in a plot of Γ/q3versus q where Γ is the relaxation rate measured with NSE. The q3 normalization accounts for the contributions from the bending fluctuations. In other words, data for pure bending fluctuations would appear as a constant, flat line in a plot of Γ/q3versus q. The data in Fig. 4(b) and (c) show a peak at q ≈ 1 nm−1 that we attribute to the collective thickness fluctuations.
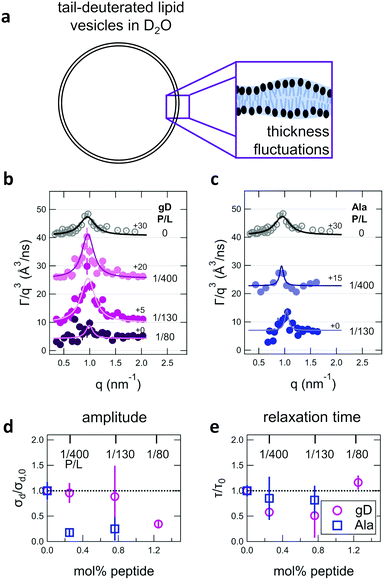 | ||
| Fig. 4 (a) Cartoon illustration of a lipid vesicle with the hydrophobic tails contrast-matched to the surrounding solvent, the contrast condition used to measure the collective thickness fluctuations with NSE. Plots of the relaxation rates fit to the NSE data, Γ, normalized by the scattering vector, q, cubed (Γ/q3) versus q measured for DMPC lipid membranes containing (b) gramidicin and (c) alamethicin at the indicated P/L ratios. The q3 normalization accounts for the contribution from the pure bending fluctuations and emphasizes the excess in dynamics that are attribute to the collective thickness fluctuations, seen as the peak at q ≈ 1.0 nm−1. The solid lines are fits to the data with the empirical expression given by eqn (3). Corresponding normalized amplitude (d) and relaxation times (e) determined from the fits to the thickness fluctuation data. The amplitude and relaxation time are normalized by the values for the pure DMPC lipid membrane, σd,0 and τ0, respectively, to emphasize the changes in the dynamics upon peptide incorporation. | ||
The NSE data indicated that there are noticeable effects of the added peptides that depend on the peptide chemistry and concentration within the membranes. Most notably, the data for the low gD concentrations with P/L of 1/400 and 1/130 (corresponding to mol% values of 0.25% and 0.76%, respectively), showed clear peaks that were more pronounced and the peak maxima were at greater Γ/q3 values than in the pure DMPC membrane, suggesting that the thickness fluctuation dynamics were faster at low gD concentrations. In contrast, the peaks in the NSE data for Ala at the same peptide concentrations were comparable in height, but appeared to be narrower in width compared to pure DMPC, suggesting that Ala reduced the thickness fluctuation amplitude and suppressed the out-of-plane dynamics. What is more, the data measured for the highest gD concentrations (gD P/L = 1/80) suggested that the dynamics were almost completely suppressed.
Fitting the NSE data with the empirical model given by eqn (4) quantified the relative changes in the thickness fluctuation amplitude and relaxation time given in Fig. 4(d) and (e), respectively. Only the peak half width at half maximum (ξ−1) and relaxation time (τ) in eqn (4) were fit during the analysis. The thickness fluctuation amplitude was calculated as σd = 2(ξq0)−1, and all other parameters were determined from either the corresponding SANS data or the NSE results for the collective bending fluctuations. The fits in Fig. 4b and c were constrained to the q-range of 0.5 nm−1 ≤ q ≤ 1.5 nm−1, the q-range where there was a clear peak in the NSE data for the pure DMPC membranes. Parameters from fits to the data in which there were clear peaks for pure DMPC or for the low gD concentrations (P/L = 1/400 and 1/80) were the same regardless of whether or not the q-range was constrained to the peak region during the fit. However, the thickness fluctuation data without clear peaks for the highest gD concentration (gD 1/80) and both studied Ala concentrations (Ala 1/400 and 1/130) were equally well fit by a narrow peak over the constrained q-range as shown in Fig. 4b and c, or by a broad, shorter peak over the entire q-range.
The fits to the clear peaks in the thickness fluctuation data for gD at P/L ratios of 1/400 and 1/130 supported that gD addition had little effect on the thickness fluctuation amplitude but decreased the relaxation time almost two fold compared to pure DMPC lipid membranes at these low concentrations. Meanwhile, the fit results in Fig. 4c and d for gD 1/80 and Ala 1/400 and 1/130 over the constrained q-range suggested that the thickness fluctuation amplitude decreased without significantly affecting the relaxation rate (i.e. a narrow peak with a similar height), what we might naively expect to see if the presence of membrane-spanning peptides effectively pinned the two leaflets together. Though as discussed above, the experimental data could also be fit assuming that the fluctuations had a larger thickness fluctuation amplitude and were much slower (i.e. a very broad and shorter peak).
4 Discussion
The wealth of literature on both gD and Ala provides a solid foundation for the present studies on the effects of transmembrane peptides on the collective membrane dynamics. The CD data in Fig. 1 show the characteristic helical structures of gD and Ala interacting with a lipid membranes. While the CD spectra show that the peptides are incorporated in the membrane, the data cannot confirm whether or not the peptides are in their transmembrane states. The secondary structure of the monomeric and conducting dimeric form of gD (Fig. 1a) as well as the absorbed and inserted states of Ala (Fig. 1b) are the same. As such, we cannot say anything about pore formation from the CD data alone, though comparing the conditions studied here with results in literature suggests that both gD and Ala predominantly form transmembrane pores at the studied conditions.Previous studies of the gD dimerization equilibrium in diphytanoylphosphatidylcholine (DPhPC) lipid membranes give association (kA) and dissociation (kD) rate constants of kA = 4.6 × 1013 cm2 s−1 mol−1 and kD = 0.48 s−1, respectively.56 Accordingly, the dimer concentration [D] can be estimated as [D] = kA/kD[M]2 > 95%, where [M] is the peptide monomer concentration added to the lipid membranes. Moreover, DMPC is thinner than DPhPC membranes, which should increase kA and further favor dimer formation. A number of studies have shown that P/L* for Ala to transition from the bound state to the inserted state is quite low in dioleoylphosphatidylcholine (DOPC), <1/200.12,39 The fully saturated DMPC lipid membranes studied here have a smaller area per headgroup (AL) than unsaturated DOPC membranes and even less room in their headgroups to accommodate a bound peptide, which should favor peptide insertion at even lower P/L*.12 As such, we expect that Ala is inserted into the membrane at the studied P/L of 1/130 and 1/80. The thinner DMPC membranes with a smaller AL should further reduce P/L* compare to pure DMPC, suggesting P/L* ≪ 1/200; however, it is not clear how much it would be reduced and Ala at P/L = 1/400 may be below the transition.
Quite interestingly, incorporation of these low peptide concentrations significantly affected the collective membrane dynamics despite not changing the overall membrane structure. The collective dynamics measured with NSE are thermally-driven, equilibrium processes, a direct consequence of the membrane being soft. As such, the timescales of these dynamics are governed by a balance of the membrane elastic and transport properties, such as the membrane bending modulus (κ) and viscosity (ηm). Typically changes in the membrane elastic and viscous properties are directly linked to changes in the membrane structure. For example, the well-known polymer brush model shows that κ scales with the membrane thickness squared, i.e. a thicker membrane is more rigid.19 Several works have shown that an increase or decrease in κ due to a change in the membrane composition, environment changes, or incorporating other small molecules such as small molecule drugs or peptide can be directly correlated to the corresponding changes in the bilayer structure. We also recently showed that both the membrane elastic and viscous properties scale with the area per lipid in mixed lipid membranes, directly linking the membrane structure and dynamics.65 In the context of these previous results, we would not expect to see any changes in the membrane dynamics based on the lack in overall structural changes in Fig. 2, especially not to the extent measured for the bending and thickness fluctuations with added gD and Ala. Together the results seem to suggest that the peptides are influencing the membrane dynamics through some other mechanism.
Perhaps even more surprisingly, gD and Ala had opposite effects on the effective membrane rigidity 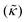 despite both peptides forming membrane-spanning pores. The slowed dynamics and increase in
despite both peptides forming membrane-spanning pores. The slowed dynamics and increase in 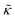 with increasing gD concentration follows the trend one might expect upon adding rigid peptide inclusions to a soft lipid membrane. In fact, a number of theoretical works predict that the membrane rigidity will directly scale with the area fraction of rigid phase (ϕ) in inhomogeneous membranes.66–68 We showed that these theories worked well in describing the measured dynamics and associated order of magnitude increase in effective membrane stiffness in phase separated lipid membranes, where ϕ ranged from ≈0.1 to ≈0.8.69 However, considering the relative molecular sizes of the DMPC lipids61 and gramacidin channels34 suggests that here ϕ for gD is <0.05, even at the highest peptide concentration studied. These small area fractions are much lower than expected for the measured 2× increase in
with increasing gD concentration follows the trend one might expect upon adding rigid peptide inclusions to a soft lipid membrane. In fact, a number of theoretical works predict that the membrane rigidity will directly scale with the area fraction of rigid phase (ϕ) in inhomogeneous membranes.66–68 We showed that these theories worked well in describing the measured dynamics and associated order of magnitude increase in effective membrane stiffness in phase separated lipid membranes, where ϕ ranged from ≈0.1 to ≈0.8.69 However, considering the relative molecular sizes of the DMPC lipids61 and gramacidin channels34 suggests that here ϕ for gD is <0.05, even at the highest peptide concentration studied. These small area fractions are much lower than expected for the measured 2× increase in 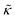 , even assuming that the peptides are 100× to 1000× more rigid than the surrounding lipid membrane.9,10
, even assuming that the peptides are 100× to 1000× more rigid than the surrounding lipid membrane.9,10
A number of experimental and computational studies suggest that several lipids are bound to each gD monomer.70–74 Interestingly, simulation results by Kim et al. showed that the lipids bound to the gD peptide were harder to compress (i.e. more rigid) than the bulk lipid membrane.73 If we instead assume that the rigid phase is made up of the gD dimers and a layer of bound lipids, then the effective rigid area fraction (ϕ) would increase by a factor of 3 and the theoretically predicted value of 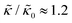 at the highest gD concentration. Estimating ϕ from the measured increase in
at the highest gD concentration. Estimating ϕ from the measured increase in 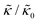 would require that the rigid clusters were made of gD + 2 to 3 layers of bound lipids. While this estimate is larger than results in literature that suggest there is only one layer of DMPC lipids bound to gD,70,71,73 the NSE data do seem to indicate that treating the peptide and the bound lipids as rigid clusters may be important for understanding the collective dynamics in lipid membranes.
would require that the rigid clusters were made of gD + 2 to 3 layers of bound lipids. While this estimate is larger than results in literature that suggest there is only one layer of DMPC lipids bound to gD,70,71,73 the NSE data do seem to indicate that treating the peptide and the bound lipids as rigid clusters may be important for understanding the collective dynamics in lipid membranes.
Meanwhile, the scaling theories discussed above do not allow for the decrease in 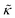 measured with added Ala, yet several other studies have reported peptide-induced softening in lipid membranes.16–18,22,39,75–78 In many of these reports, the softening was at least in part attributed to local thinning of the membrane.22,77,78 However, Ala is actually slightly longer than the hydrophobic thickness of the DMPC bilayer, which is likely compensated for by a slight thickening in the membrane around the inserted peptide, not a local membrane thinning.58,59 Other studies also suggest that Ala is slightly tilted in DMPC membranes to compensate for the slight hydrophobic mismatch.57,60 In either case, the present results suggest that the measured changes in
measured with added Ala, yet several other studies have reported peptide-induced softening in lipid membranes.16–18,22,39,75–78 In many of these reports, the softening was at least in part attributed to local thinning of the membrane.22,77,78 However, Ala is actually slightly longer than the hydrophobic thickness of the DMPC bilayer, which is likely compensated for by a slight thickening in the membrane around the inserted peptide, not a local membrane thinning.58,59 Other studies also suggest that Ala is slightly tilted in DMPC membranes to compensate for the slight hydrophobic mismatch.57,60 In either case, the present results suggest that the measured changes in 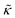 would be due to a local disruption of the bilayer structure that did not propagate over the entire vesicle surface. Similarly, simulations by Argawal suggested that Ala-induced membrane softening reported for dioleoylphosphatidylcholine (DOPC) membranes,17,39 was due to local rearrangements of the lipid molecules immediately surrounding the peptide and depended on the protein-lipid interactions.24
would be due to a local disruption of the bilayer structure that did not propagate over the entire vesicle surface. Similarly, simulations by Argawal suggested that Ala-induced membrane softening reported for dioleoylphosphatidylcholine (DOPC) membranes,17,39 was due to local rearrangements of the lipid molecules immediately surrounding the peptide and depended on the protein-lipid interactions.24
An alternative explanation may be that the asymmetric shape of Ala affects the nanoscale membrane dynamics. The simple scaling theories discussed above in the context of the gD results assume that the rigid inclusions are symmetric and embedded in equal numbers on each side of the bilayer.66–68 However, Ala is actually better represented as a kinked cylinder due to the kink in the helix at the proline residue,79 and as a result, the oligomeric barrel-stave pores are also asymmetric in shape.42 In fact, theoretical work by Dan and Safran80 suggested that the aysmmetric Ala pore shape couples to the local membrane curvature and results in the experimentally measured dependence of the Ala conduction state on the spontaneous curvatures of the surrounding lipid membrane.41 There are also several experimental and theoretical works that suggest that the addition of asymmetrically shaped proteins and peptides, such as magainin18 or Ca2 +-ATPase,16 could lead to a softening in the membrane because the protein can couple to local curvature changes in the bilayer. Likewise, coupling of the non-cylindrical alamethicin channel shape with the membrane curvature may lead to the enhanced dynamics seen here.
Addition of low gD and Ala concentrations also had opposite effects on the collective thickness fluctuations. As seen in Fig. 4, the NSE data for the pure DMPC membranes show a clear peak near q ≈ 1 nm−1, where the peak width is associated with the fluctuation amplitude and the peak height is associated with the fluctuation relaxation time. A pronounced peak is also seen in the data for the two lowest gD concentrations (gD 1/400 and 1/130) that is similar in width but taller than seen in the pure DMPC lipid membrane. The quantitative fit results in Fig. 4d and e show that the thickness fluctuation amplitude was comparable to the pure lipid membrane at low gD concentrations, but the relaxation time decreased ≈2×. In other words, the thickness fluctuations dynamics were faster at low gramicidin concentration, with a characteristic timescale on the order of 80 ns to 90 ns. The timescale of the nanoscale thickness fluctuation dynamics is orders of magnitude faster than the gD channel lifetimes (≈10 ms),81 suggesting that the enhanced dynamics at low peptide concentrations may help facilitate gramidicin dimer formation by bringing the monomers in each leaflet in close contact as originally suggested in theoretical work by Helfrich and Jakobsson.33
In contrast, Ala at the two concentrations studied and the highest gD concentration studied (P/L = 1/80) lessened the collective thickness fluctuations. The diminished peaks in the NSE data suggest that the collective fluctuation dynamics for gD 1/80 and Ala 1/400 and 1/130 were either smaller in amplitude and beyond the spatial resolution of the measurements, or much slower and beyond the temporal resolution of the measurement. Either way, the thickness fluctuations are clearly damped.
The thickness fluctuation data alone cannot rule out one possibility or the other. In fact, considering both the height and thickness fluctuation data may even suggest that gD and Ala also have opposite effects on the thickness fluctuations despite both peptides damping the dynamics. In pure lipid membranes, the thickness fluctuation amplitude (σd) is inversely related to the membrane combressibility modulus (KA ∼ σd−2) while the time scale is related to the membrane viscosity (τ ∼ ηm). Both membrane elastic properties, κ and KA, are related according to the expression κ = βKAdm2 where β is a numerical value that describes the degree of coupling between the leaflets and dm is the effective mechanical thickness of the membrane.
The opposite trends in 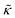 in Fig. 3 may suggest that the peptides also have opposite effects on KA and therefore σd, with gD decreasing the thickness fluctuation amplitude and Ala increasing the amplitude. However, it is also unclear as to how the presence of a transmembrane peptide would affect the values of β or dm. Work by Shchelokovskyy et al. suggested that the FP23 HIV fusion peptide reduced the interactions between leaflets and shifted β closer to the value expected for freely sliding leaflets.77 Meanwhile, studies of cholesterol-containing membranes have suggested that rigid inclusions affect the mechanical thickness of the membrane. (i.e. dm in the expression above).82,83 While it is clear that the presence of transmembrane peptides can have a significant effect on the collective thickness fluctuations, further studies are needed to better understand the mechanism of these effects and the synergy between lipid and peptides in determining biomembrane dynamics. The present results may suggest that β or dm are changing upon incorporation of gD and Ala, and the changes are opposite for the two peptides. Studies aimed at better understanding these effects are on going and will be discussed in a future publication.
in Fig. 3 may suggest that the peptides also have opposite effects on KA and therefore σd, with gD decreasing the thickness fluctuation amplitude and Ala increasing the amplitude. However, it is also unclear as to how the presence of a transmembrane peptide would affect the values of β or dm. Work by Shchelokovskyy et al. suggested that the FP23 HIV fusion peptide reduced the interactions between leaflets and shifted β closer to the value expected for freely sliding leaflets.77 Meanwhile, studies of cholesterol-containing membranes have suggested that rigid inclusions affect the mechanical thickness of the membrane. (i.e. dm in the expression above).82,83 While it is clear that the presence of transmembrane peptides can have a significant effect on the collective thickness fluctuations, further studies are needed to better understand the mechanism of these effects and the synergy between lipid and peptides in determining biomembrane dynamics. The present results may suggest that β or dm are changing upon incorporation of gD and Ala, and the changes are opposite for the two peptides. Studies aimed at better understanding these effects are on going and will be discussed in a future publication.
The present results highlight that peptides can affect the collective membrane dynamics even when there are no measurable changes in the average structure. Moreover, the present results suggest transmembrane proteins can not be treated universally as rigid bodies when considering the collective fluctuations, and that the effects of embedded proteins on the surrounding membrane dynamics can be much more complicated than predicted by simple scaling theories. The results also emphasize that it is important to take a more holistic view of both the structure and dynamics of complex membrane systems. For example, recent work had also started to reveal that antimicrobial peptides can significantly alter lipid exchange and flip-flop kinetics at lower concentrations than needed to form oligomeric pores and without causing significant changes in the overall membrane structure.83–86 Similarly, the sub-micromolar (<10−6 mol L−1) Ala concentrations studied here have been shown to kill several strains of bacteria despite not affecting the overall membrane structure.87,88 The present studies suggest that low antimicrobial peptide concentrations can significantly impact the collective membrane dynamics in model membranes and thus the corresponding elastic properties that influence membrane-related cell processes such as cell budding or endocytosis. Given the highly dynamic and non-equilibrium nature of many biological processes, it is perhaps unsurprising that the motions of biomolecules are intimately linked to their structure and function.
The present experiments were designed specifically to look at the effects of well-studied transmembrane peptides on collective membrane dynamics; nevertheless, we hope that the results from these simple models can inform investigations into more complex membrane systems. Biological membranes are far more complex than the systems studied here. Transmembrane protein domains can account for upwards of 20% to 30% of the area of cell membrane.89–91 These different proteins likely have coupled and compound effects on the membrane properties. Moreover, proteins and peptides are highly dynamic entities on their own.31,32,38,73 Future experimental and computational studies of the protein dynamics may provide insights into how they couple with the lipid membrane dynamics as well. Given that the function of many membrane-embedded proteins is sensitive to the properties of the surrounding lipid matrix, it is likely that the reverse is also true, where the structure and dynamics of the surrounding lipid membrane are influenced by the properties of the embedded proteins as seen in the simple model systems studied here.
5 Conclusions
Here we measured the effects of two well-studied transmembrane peptides, gD and Ala, on the structure and dynamics of model lipid membranes. While there were no measurable changes in the average membrane structure, the collective fluctuations on the nanometer length scale and nanosecond timescale were significantly affected. Added peptide concentrations as low as 1.25 mol% (P/L ≈ 1/80) led to an almost two fold change in the effective bending modulus,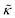 , with gD stiffening and Ala softening the membrane. Meanwhile, low gD concentrations enhanced the collective thickness fluctuations, while the same Ala concentrations dampened the out of plane thickness fluctuations measured with NSE. The present results underscore how synergies between membrane structure and dynamics as well as between protein structure and local protein-lipid interactions may help determine the physical properties of biomembranes.
, with gD stiffening and Ala softening the membrane. Meanwhile, low gD concentrations enhanced the collective thickness fluctuations, while the same Ala concentrations dampened the out of plane thickness fluctuations measured with NSE. The present results underscore how synergies between membrane structure and dynamics as well as between protein structure and local protein-lipid interactions may help determine the physical properties of biomembranes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Andrea Woodka for assistance with the SANS and NSE experiments and Xiaobing Zuo for assistance with SAXS data collection at APS. Access to the NGA NSE and VSANS instruments was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-2010792. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operating for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The identification of any commercial products does not imply endorsement or recommendation by the National Institute of Standards and Technology.Notes and references
- S. D. Shoemaker and T. K. Vanderlick, Biophys. J., 2003, 84, 998–1009 CrossRef CAS PubMed.
- J. L. Robertson, J. Gen. Physiol., 2018, 150, 1472–1483 CrossRef CAS PubMed.
- M. G. J. Ford, I. G. Mills, B. J. Peter, Y. Vallis, G. J. K. Praefcke, P. R. Evans and H. T. McMahon, Nature, 2002, 419, 361–366 CrossRef CAS PubMed.
- J. Zimmerberg and S. McLaughlin, Curr. Biol., 2004, 14, R250–R252 CrossRef CAS PubMed.
- J. C. Stachowiak, F. M. Brodsky and E. A. Miller, Nat. Cell Biol., 2013, 15, 1019–1027 CrossRef CAS PubMed.
- W. L. C. Vaz, F. Goodsaid-Zalduondo and K. Jacobson, FEBS Lett., 1984, 174, 199–207 CrossRef CAS.
- S. Ramadurai, A. Holt, V. Krasnikov, G. van den Bogaart, J. A. Killian and B. Poolman, J. Am. Chem. Soc., 2009, 131, 12650–12656 CrossRef CAS PubMed.
- J. Lippincott-Schwartz, E. Snapp and A. Kenworthy, Nat. Rev. Mol. Cell Biol., 2001, 2, 444–456 CrossRef CAS PubMed.
- T. A. Harroun, W. T. Heller, T. M. Weiss, L. Yang and H. W. Huang, Biophys. J., 1999, 76, 937–945 CrossRef CAS PubMed.
- O. S. Andersen, I. Roger and E. Koeppe, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 107–130 CrossRef CAS PubMed.
- H. J. Lessen, P. J. Fleming, K. G. Fleming and A. J. Sodt, J. Chem. Theory Comput., 2018, 14, 4487–4497 CrossRef CAS PubMed.
- H. W. Huang, Biophys. J., 1986, 50, 1061–1070 CrossRef CAS.
- J. C. Stachowiak, C. C. Hayden and D. Y. Sasaki, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7781–7786 CrossRef CAS PubMed.
- S. Pujals, H. Miyamae, S. Afonin, T. Murayama, H. Hirose, I. Nakase, K. Taniuchi, M. Umeda, K. Sakamoto, A. S. Ulrich and S. Futaki, ACS Chem. Biol., 2013, 8, 1894–1899 CrossRef CAS PubMed.
- N. W. Schmidt and G. C. Wong, Curr. Opin. Solid State Mater. Sci., 2013, 17, 151–163 CrossRef CAS PubMed.
- P. Girard, J. Prost and P. Bassereau, Phys. Rev. Lett., 2005, 94, 088102 CrossRef CAS PubMed.
- G. Pabst, S. Danner, R. Podgornik and J. Katsaras, Langmuir, 2007, 23, 11705–11711 CrossRef CAS PubMed.
- H. Bouvrais, P. Meleard, T. Pott, K. J. Jensen, J. Braks and J. H. Ipsen, Biophys. Chem., 2008, 137, 7–12 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- J.-H. Lee, S.-M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101 CrossRef PubMed.
- R. S. Gracia, N. Bezlyepkina, R. L. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- S. Tristram-Nagle, R. Chan, E. Kooijman, P. Uppamoochikkal, W. Qiang, D. P. Weliky and J. F. Nagle, J. Mol. Biol., 2010, 402, 139–153 CrossRef CAS PubMed.
- P. W. Fowler, J. Helie, A. Duncan, M. Chavent, H. Koldso and M. S. P. Sansom, Soft Matter, 2016, 12, 7792–7803 RSC.
- H. Agrawal, M. Zelisko, L. Liu and P. Sharma, Sci. Rep., 2016, 6, 25412 CrossRef CAS PubMed.
- A. Kumagai, F. Dupuy, Z. Arzov, Y. Elhady, D. Moody, R. Ernst, B. Deslouches, R. Monterlaro, Y. Di and S. Tristram-Nagle, Soft Matter, 2019, 15, 1860–1868 RSC.
- T. Weikl, D. Andelman, S. Komura and R. Lipowsky, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 59–66 CrossRef CAS PubMed.
- S. F. Fenz, T. Bihr, D. Schmidt, R. Merkel, U. Seifert, K. Sengupta and A.-S. Smith, Nat. Phys., 2017, 13, 906–913 Search PubMed.
- J. Steinkuehler, B. Rozycki, C. Alvey, R. Lipowsky, T. Weikl, R. Dimova and D. Discher, J. Cell Sci., 2019, 132, jcs216770 Search PubMed.
- L. Li, J. Hu, B. Różycki and F. Song, Nano Lett., 2020, 20, 722–728 CrossRef CAS PubMed.
- E. G. Kelley, P. D. Butler and M. Nagao, Characterization of Biological Membranes-Structure and Dynamics, de Gruyter, 2019, ch. 4, pp. 131–176 Search PubMed.
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS PubMed.
- K. A. Henzler-Wildman, M. Lei, V. Thai, S. J. Kerns, M. Karplus and D. Kern, Nature, 2007, 450, 913–916 CrossRef CAS PubMed.
- P. Helfrich and E. Jakobsson, Biophys. J., 1990, 57, 1075–1084 CrossRef CAS PubMed.
- B. Wallace, Biophys. J., 1986, 49, 295–306 CrossRef CAS PubMed.
- R. Ketchem, B. Roux and T. Cross, Structure, 1997, 5, 1655–1669 CrossRef CAS PubMed.
- T. W. Allen, O. S. Andersen and B. Roux, J. Am. Chem. Soc., 2003, 125, 9868–9877 CrossRef CAS PubMed.
- V. Vitkova, P. Meleard, T. Pott and I. Bivas, Eur. Biophys. J., 2006, 35, 281–286 CrossRef CAS PubMed.
- L. Thøgersen, B. Schiøtt, T. Vosegaard, N. C. Nielsen and E. Tajkhorshid, Biophys. J., 2008, 95, 4337–4347 CrossRef PubMed.
- J. Pan, D. P. Tieleman, J. F. Nagle, N. Kučerka and S. Tristram-Nagle, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 1387–1397 CrossRef CAS PubMed.
- V. Rizzo, S. Stankowski and G. Schwarz, Biochemistry, 1987, 26, 2751–2759 CrossRef CAS PubMed.
- S. Keller, S. Bezrukov, S. Gruner, M. Tate, I. Vodyanoy and V. Parsegian, Biophys. J., 1993, 65, 23–27 CrossRef CAS PubMed.
- R. S. Cantor, Biophys. J., 2002, 82, 2520–2525 CrossRef CAS PubMed.
- H. L. Scott, A. Skinkle, E. G. Kelley, M. N. Waxham, I. Levental and F. A. Heberle, Biophys. J., 2019, 117, 1381–1386 CrossRef CAS PubMed.
- J. A. Killian, K. U. Prasad, D. Hains and D. W. Urry, Biochemistry, 1988, 27, 4848–4855 CrossRef CAS PubMed.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- N. Rosov, S. Rathgeber and M. Monkenbusch, Neutron Spin Echo Spectroscopy at the NIST Center for Neutron Research, American Chemical Society, 1999, vol. 739, book section 7, pp. 103–116 Search PubMed.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- A. C. Woodka, P. D. Butler, L. Porcar, B. Farago and M. Nagao, Phys. Rev. Lett., 2012, 109, 058102 CrossRef PubMed.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS PubMed.
- M. C. Watson and F. L. H. Brown, Biophys. J., 2010, 98, L9–L11 CrossRef CAS PubMed.
- U. Seifert and S. Langer, Europhys. Lett., 1993, 23, 71 CrossRef.
- M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031606 CrossRef PubMed.
- M. Nagao, S. Chawang and T. Hawa, Soft Matter, 2011, 7, 6598–6605 RSC.
- R. Ashkar, M. Nagao, P. D. Butler, A. C. Woodka, M. K. Sen and T. Koga, Biophys. J., 2015, 109, 106–112 CrossRef CAS PubMed.
- M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler, J. Phys. Chem. Lett., 2017, 8, 4679–4684 CrossRef CAS PubMed.
- T. I. Rokitskaya, Y. N. Antonenko and E. A. Kotova, Biochim. Biophys. Acta, Bioenerg., 1996, 1275, 221–226 CrossRef.
- M. Bak, R. P. Bywater, M. Hohwy, J. K. Thomsen, K. Adelhorst, H. J. Jakobsen, O. W. Sørensen and N. C. Nielsen, Biophys. J., 2001, 81, 1684–1698 CrossRef CAS.
- M. Venturoli, B. Smit and M. M. Sperotto, Biophys. J., 2005, 88, 1778–1798 CrossRef CAS PubMed.
- D. Constantin, G. Brotons, A. Jarre, C. Li and T. Salditt, Biophys. J., 2007, 92, 3978–3987 CrossRef CAS PubMed.
- S. Ye, K. T. Nguyen and Z. Chen, J. Phys. Chem. B, 2010, 114, 3334–3340 CrossRef CAS PubMed.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef PubMed.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS.
- S. Hladky and D. Gruen, Biophys. J., 1982, 38, 251–258 CrossRef CAS.
- I. Miller, Biophys. J., 1984, 45, 643–644 CrossRef CAS.
- E. G. Kelley, P. D. Butler, R. Ashkar, R. Bradbury and M. Nagao, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 23365–23373 CrossRef CAS PubMed.
- V. S. Markin, Biophys. J., 1981, 36, 1–19 CrossRef CAS PubMed.
- W. Helfrich and M. M. Kozlov, J. Phys. II, 1994, 4, 1427–1438 CrossRef CAS.
- R. R. Netz and P. Pincus, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 4114–4128 CrossRef CAS PubMed.
- E. Kelley, P. Butler and M. Nagao, Soft Matter, 2019, 15, 2762–2767 RSC.
- S.-W. Chiu, S. Subramaniam and E. Jakobsson, Biophys. J., 1999, 76, 1929–1938 CrossRef CAS PubMed.
- G. Orädd and G. Lindblom, Biophys. J., 2004, 87, 980–987 CrossRef PubMed.
- Z. Kóta, T. Páli and D. Marsh, Biophys. J., 2004, 86, 1521–1531 CrossRef.
- T. Kim, K. Lee, P. Morris, R. Pastor, O. Andersen and W. Im, Biophys. J., 2012, 102, 1551–1560 CrossRef CAS PubMed.
- I. Sugar, A. Bonanno and P.-G. Chong, Int. J. Mol. Sci., 2018, 19, 3690 CrossRef PubMed.
- E. Bivas and P. Méléard, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2003, 67, 012901 CrossRef PubMed.
- S. Tristram-Nagle and J. F. Nagle, Biophys. J., 2007, 93, 2048–2055 CrossRef CAS PubMed.
- P. Shchelokovskyy, S. Tristram-Nagle and R. Dimova, New J. Phys., 2011, 13, 25004 CrossRef CAS PubMed.
- T. Pott, C. Gerbeaud, N. Barbier and P. Méléard, Chem. Phys. Lipids, 2015, 185, 99–108 CrossRef CAS PubMed.
- R. Fox and F. Richards, Nature, 1982, 300, 325–330 CrossRef CAS PubMed.
- N. Dan, P. Pincus and S. A. Safran, Langmuir, 1993, 9, 2768–2771 CrossRef CAS.
- E. Bamberg and P. Lauger, J. Membr. Biol., 1973, 11, 177–194 CrossRef CAS PubMed.
- J. Pan, S. Tristram-Nagle and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021931 CrossRef PubMed.
- M. Doktorova, F. A. Heberle, D. Marquardt, R. Rusinova, R. L. Sanford, T. A. Peyear, J. Katsaras, G. W. Feigenson, H. Weinstein and O. S. Andersen, Biophys. J., 2019, 116, 860–873 CrossRef CAS PubMed.
- M. H. L. Nguyen, M. DiPasquale, B. W. Rickeard, M. Doktorova, F. A. Heberle, H. L. Scott, F. N. Barrera, G. Taylor, C. P. Collier, C. B. Stanley, J. Katsaras and D. Marquardt, Langmuir, 2019, 35, 11735–11744 CrossRef CAS PubMed.
- M. H. L. Nguyen, M. DiPasquale, B. W. Rickeard, C. G. Yip, K. N. Greco, E. G. Kelley and D. Marquardt, New J. Chem., 2021, 45, 447–456 RSC.
- J. E. Nielsen, V. A. Bjørnestad, V. Pipich, H. Jenssen and R. Lund, J. Colloid Interface Sci., 2021, 582, 793–802 CrossRef CAS PubMed.
- N. O'Brien-Simpson, N. Pantarat, T. Attard, K. Walsh and E. Reynolds, PLoS One, 2016, 11, e0151694 CrossRef.
- K. J. Barns and J. C. Weisshaar, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 725–732 CrossRef CAS PubMed.
- S. Takamori, M. Holt, K. Stenius, E. A. Lemke, M. Grønborg, D. Riedel, H. Urlaub, S. Schenck, B. Brügger, P. Ringler, S. A. Müller, B. Rammner, F. Gräter, J. S. Hub, B. L. De Groot, G. Mieskes, Y. Moriyama, J. Klingauf, H. Grubmüller, J. Heuser, F. Wieland and R. Jahn, Cell, 2006, 127, 831–846 CrossRef CAS PubMed.
- A. D. Dupuy and D. M. Engelman, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2848–2852 CrossRef CAS PubMed.
- U. Coskun and K. Simons, FEBS Lett., 2010, 584, 1685–1693 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |