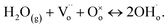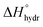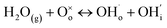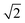Solid oxide proton conductors beyond perovskites
Sacha
Fop
 *ab
*ab
aISIS Facility, Rutherford Appleton Laboratory, Harwell, OX11 0QX, UK. E-mail: sacha.fop@stfc.ac.uk
bThe Chemistry Department, University of Aberdeen, Meston Walk, Aberdeen AB24 3UE, UK
First published on 4th August 2021
Abstract
Solid oxide proton conductors are crucially emerging as key materials for enabling hydrogen-based energy conversion, storage, and electrochemical technologies. Oxides crystallising in the ideal ABO3 perovskite structure, such as barium cerates and zirconates, are widely investigated thanks to their excellent proton conducting properties. Nevertheless, alternative structure-type solid oxide systems (hexagonal perovskite derivatives, brownmillerite, scheelite, etc.) can efficiently incorporate and enable the transport of protonic defects, with recent reports of materials exhibiting high ionic conductivity comparable to the conventional perovskite conductors. This perspective provides an overview of these alternative and less established proton conducting materials, with particular attention to the relationship between the structural and ionic conduction features and the mechanistic aspects. The goals are to highlight the differences between these materials and the traditional perovskites and to point out new potential crystal routes for the discovery of innovative solid oxide proton conductors.
1. Introduction
Carbon emissions must be reduced to mitigate the effects of climate change and keep the global average temperature increase below 2 °C above pre-industrial levels. To achieve this target, it is essential to transition away from fossil fuels and progress towards cleaner and renewable means of energy generation. Low carbon solutions provided by hydrogen-based energy conversion, storage and electrochemical technologies will have a fundamental role in contributing to broad decarbonisation.1,2 Conventional solid-state hydrogen-based electrochemical devices such as ceramic fuel cells and electrolysers employ oxide ion conducting materials. These systems however generally show adequate ionic conductivities only at high working temperatures (>700 °C), thus posing technical challenges in terms of materials selection and durability and limiting the widespread application of these technologies.3–7 Systems based on solid oxide proton conductors offer promise of operations at reduced temperatures, thanks to the generally lower activation energy for proton diffusion (∼0.3–0.6 eV) compared to oxide ion conduction in oxides (∼0.6–1.2 eV).8,9 Iwahara et al. were the first to demonstrate the potential of perovskite-type solid oxide proton conductors in energy-related applications in the early 1980s and 1990s.10–15 Since then, the most intensively studied solid oxide proton conductors became doped barium cerate- and zirconate-based perovskite-type oxides, due to their high proton conductivities. The properties of Ba(Ce,Zr)O3 perovskite proton conductors are well established and have been extensively reviewed.8,9,15–22The crystal structure of BaCeO3 and BaZrO3 materials is based on the perovskite ABO3 structure, which is composed by a network of corner-sharing BO6 octahedra in which the larger A cations occupy the interstitial voids (Fig. 1a). Depending on the composition and the level of hydration, the ideal cubic perovskite structure (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) is usually stable at high temperatures, with rhombohedral, orthorhombic, and monoclinic distortions at lower temperatures due to tilting of the octahedral units.23–26 Proton conduction in these systems is enabled by the introduction of protonic defects via the dissociative absorption of water according to the hydration reaction,
m) is usually stable at high temperatures, with rhombohedral, orthorhombic, and monoclinic distortions at lower temperatures due to tilting of the octahedral units.23–26 Proton conduction in these systems is enabled by the introduction of protonic defects via the dissociative absorption of water according to the hydration reaction,
Water dissociates into a proton and a hydroxide ion by filling of an oxygen vacancy.8,27 Pure BaCeO3 and BaZrO3 show limited proton incorporation due to the absence of available oxygen vacancies. Water absorption, and hence the creation of protonic species, is promoted by the introduction of oxygen vacancies via trivalent acceptor doping on the Ce/Zr-site. Y is the most commonly used acceptor dopant for effective proton conduction,16,20 although numerous dopants have been tested.28–32 The highest ionic conductivities are reported for barium cerate–zirconate solid solutions co-doped with Y and Yb.33,34 The dissociative absorption of water results in the incorporation of a hydroxyl ion and in the formation of a covalent bond between a proton and a lattice oxygen atom. Protons are generally located in proximity of the O–O octahedron edge (Fig. 1b)24,25,35,36 and have the tendency of forming hydrogen bonds with neighbouring oxygen atoms.37 Proton transport follows a Grotthuss mechanism characterised by the fast rotational diffusion of the protonic defect around an oxygen atom (with activation energy of ∼0.08–0.2 eV), followed by intra-octahedral hopping of a single proton towards a neighbouring oxide ion (∼0.4–0.5 eV) and successive migration to an oxygen of an adjacent octahedron (Fig. 1c).38–42 Under humid reducing atmospheres these systems show pure proton conduction, with a proton transport number tH (which is the ratio of proton conductivity to total conductivity) close to unity.13,43–45 However, at high temperatures and under higher partial pressure of oxygen, both barium cerates and zirconate present mixed oxide ion and electronic p-type conductivity, with tH generally reducing to ∼0.6–0.7 at 500 °C, due to an increase in the mobility of the oxygen vacancies and of the concentration of hole defects.43,46,47
Cerate and zirconate perovskites represent one of the most promising group of solid oxide proton conductors, as demonstrated by reports of excellent performances at low temperatures (300–600 °C) in proton ceramic fuel cells (PCFCs), electrolysis cells (PCECs), and reactor cells.33,34,48–54 For example, a peak power density of 548 mW cm−2 at 500 °C has been reported for a PCFC with an optimized BaZr0.4Ce0.4Y0.1Yb0.1O3 electrolyte,34 a value that greatly exceeds the performance of commercially available solid oxide fuel cells with yttria stabilized zirconia electrolytes.5,48 However, barium cerate- and zirconate-based electrolytes also have some distinct disadvantages. BaCeO3-based compounds are chemically unstable under CO2 and H2O, usually decomposing into BaCO3 or Ba(OH)2 and the corresponding oxide.55–57 BaZrO3-based materials show greater stability,58,59 but their refractory nature makes grain growth difficult and results in a large grain boundary resistance which is detrimental for the overall conductivity.16,20,60,61
In the last two decades, research into alternative solid proton conductors possessing good ionic conductivity and stability has led to the discovery of proton conduction in several structural families. These include perovskite derivative oxides, systems containing tetrahedral moieties and fluorite-related oxides, with recent reports of materials exhibiting proton conductivities comparable to benchmark Y-doped BaCeO3 and BaZrO3 perovskite conductors (Fig. 2). These systems have promising properties, and in some cases show structural and proton conducting characteristics which are considerably different from the ones of conventional perovskite proton conductors (Table 1). Although citing numerous and state-of-the-art studies, it is beyond the scope of this perspective to give an exhaustive summary of all the properties of these alternative proton conducting oxide systems. Rather, this perspective provides an overview of the most relevant alternative and less established proton conducting materials, with a concise and up-to-date account of the structure–property relationships and the mechanistic aspects of hydration and ionic conduction. The aims are to highlight crucial and diverse structural features enabling proton incorporation and transport, and to invite further fundamental research into the proton conducting properties of other promising and unexplored oxide systems for the discovery of novel solid proton conductors.
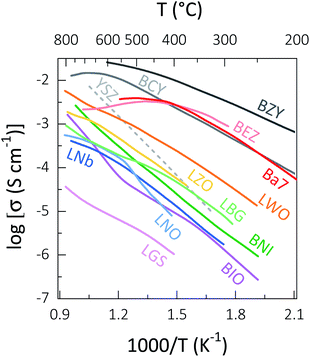 | ||
| Fig. 2 Conductivities of selected solid oxide proton conductors: Ba7Nb4MoO20 (Ba7, bulk);68 Ba5Er2Al2ZrO13 (BEZ, total);72 BaNd0.8Ca0.2InO3.90 (BNI, bulk);106 Ba2In2O5 (BIO, total);114 La0.99Ca0.01NbO4−δ (LNO, total);138 La0.8Ba1.2GaO3.9 (LBG, total);167 La3Ga5.06Si0.94O14−δ (LGS, bulk);179 La1.95Ca0.05Zr2O7−δ (LZO, total);216 La2.85Sr0.15NbO7−δ (LNb, total);231 La27W5O55.5 or “La6WO12” (LWO, total).248 The bulk conductivity of BaCe0.9Y0.1O3−δ (BCY),8 the extrapolated bulk conductivity data of BaZr0.8Y0.2O3−δ (BZY)8 and the conductivity of the solid oxide ion electrolyte Zr0.92Y0.08O1.96 (YSZ)4 are shown for comparison. | ||
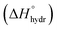 and experimental activation energy values of proton conductivity (EHa) are also reported
and experimental activation energy values of proton conductivity (EHa) are also reported
| Compound | σ, 300 °C (S cm−1) | σ, 500 °C (S cm−1) | tH, 300 °C | t H, 500 °C | nH2O | (kJ mol−1) | E Ha (eV) | Ref. |
|---|---|---|---|---|---|---|---|---|
| BaCe0.9Y0.1O3−δ | 5.8 × 10−4 | 7.1 × 10−3 | ∼1 | 0.8–0.9 | ∼0.09 (0.1) | −163 | 0.53 | 8 and 46 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BaZr0.8Y0.2O3−δ | 3.5 × 10−3 | 1.8 × 10−2 | ∼1 | 0.98 | 0.178 (0.2) | −22 (T < 500 °C) | 0.47 | 8, 47 and 60 |
| −93 (T > 500 °C) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Ba7Nb4MoO20 | 7.0 × 10−4 | 4.0 × 10−3 | 0.35 | ∼0.80 | ∼0.80 (1) | −18 (T < 300 °C) | 0.57 | 68 and 69 |
| −76 (T > 300 °C) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Ba5Er2Al2ZrO13 | 9.8 × 10−4 | 3.0 × 10−3 | ∼1 | ∼1 | ∼0.27 (2) | −13 (T < 400 °C) | 0.40 | 72 |
| −192 (T > 400 °C) | ||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Ba4Nb2O9 | — | 6.0 × 10−6 | ∼0.2 (at 700 °C) | 0.333 (0.333) | — | — | 73 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Ba4Ta2O9 | — | 7.8 × 10−7 | ∼0.15 (at 700 °C) | ∼0.375 (1) | — | — | 74 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BaLaInO4 | 4.0 × 10−8 | 9.5 × 10−7 | ∼0.9 | ∼0.6 | 0.62 | — | 0.87 | 82 and 83 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BaLa0.9A0.1InO3.95; A = Ca, Sr, Ba | 0.6–1.8 × 10−6 | 3.1–5.1 × 10−5 | ∼0.95 | 0.65–0.75 | 0.70–1.05 | — | ∼0.80 | 73, 82 and 83 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2NiO4+δ | 4.0 × 101 | 3.6 × 101 | — | — | 0.03 | — | — | 89 |
| Pr2NiO4+δ | 1.0 × 102 | 1.0 × 102 | — | — | ∼0.03 | — | — | 89 and 90 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BaNd0.8Ca0.2InO3.90 | 3.3 × 10−6 | 1.3 × 10−4 | 0.47 | 0.53 | 0.011 | — | 0.67 | 106 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| BaNd0.8Ca0.2ScO3.90 | 8.3 × 10−5 (at 600 °C) | 0.62 (at 700 °C) | 0.316 | — | 0.23–0.37 | 107 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Ba2In2O5 | 1.3 × 10−6 | 3.2 × 10−5 | 0.84 | 0.35 | 1 (1) | −74 to −63 | ∼0.60 | 114–117 and 124 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| RE0.99Ca0.01NbO4−δ; RE = La, Nd, Tb, Er | — | 2.4–6.3 × 10−5 | — | ∼1 | — | −165 to −115 | 0.52–0.59 | 138 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| RE0.99Ca0.01TaO4−δ; RE = La, Nd, Gd, Er | — | 2.8–4.7 × 10−5 | — | ∼1 | — | −170 to −100 | 0.52–0.67 | 140 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La0.8Ba1.2GaO3.9 | 7.4 × 10−6 | 1.4 × 10−4 | ∼0.90* | ∼0.80* | ∼0.08 (0.1) | — | 0.44–0.75 | 167, 169 and 172 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La3Ga5.06M0.94O14−δ, M = Si, Ti, Sn | — | 1.8–7.3 × 10−6 | — | ∼0.93* | — | −120 to −97 | 0.63–0.83 | 179 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La3Ga5.6Ta0.4O14 | — | 3.0 × 10−6 | — | ∼0.92* | — | −85 | 0.72 | 180 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2Zr2O7 | 5.0 × 10−7 (at 600 °C) | — | — | ∼0 | — | — | 200 and 201 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La1.95Ca0.05Zr2O7−δ | — | 2.4 × 10−4 | — | ∼1 | ∼0.03 | −190 | 0.68 | 216–219 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Sm1.92Ca0.08Ti2O7−δ | 1.6 × 10−5 | 5.0 × 10−4 | ∼0.77* | — | ∼0.04 (0.08) | — | 0.52–0.59 | 202 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Sm1.92Ca0.08Sn2O7−δ | 2.7 × 10−6 | 5.8 × 10−5 | ∼0.98* | — | ∼0.05 (0.08) | −100 | 0.83 | 203 and 204 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2Ce2O7 | 2.1 × 10−6 | 2.4 × 10−4 | ∼1 | ∼0.20 | ∼0.20 (1) | −90 to −77 | 0.44–0.84 | 205–207 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La1.95Ca0.05Ce2O7−δ | — | 1.0 × 10−3 | — | ∼0.70* | — | — | — | 222 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Nd2Ce2O7 | 1.6 × 10−7 | 2.7 × 10−5 | ∼0.40* | — | ∼0.03 | −72 | — | 207 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La3NbO7 | — | 4.3 × 10−9 | — | ∼0.18* | 2.5 × 10−3 (1) | — | — | 233 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2.97Ca0.03NbO7 | 5.4 × 10−7 | 2.0 × 10−5 | ∼0.54* | ∼0.40* | — | −117 | 0.77 | 231 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2.85Sr0.15NbO7 | 1.7 × 10−6 | 6.6 × 10−5 | ∼0.50* | ∼0.42* | — | −116 | 0.77 | 231 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2.60Sr0.40NbO7 | 1.2 × 10−3 (at 600 °C) | ∼0.40 (at 600 °C) | — | — | — | 230 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La3TaO7 | — | 1.3 × 10−7 | — | — | — | — | 1.44 | 232 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2.97Ca0.03TaO7 | 1.7 × 10−7 | 5.4 × 10−6 | ∼0.49* | ∼0.35* | — | −122 | 0.74 | 231 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La2.85Ca0.15TaO7 | 4.7 × 10−7 | 2.4 × 10−5 | ∼0.42* | ∼0.57* | — | −133 | 0.71 | 231 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| La27W5O55.5 (La6WO12) | 1.0 × 10−4 | 1.0 × 10−3 | ∼1 | ∼1 | ∼0.40 (0.5) | −90 to −87 | 0.65 | 242, 244 and 247 |
2. Perovskite derivatives
The intrinsic flexibility and versatility of the perovskite structure allows the formation of a large number of derivatives via the introduction of defects and structural disorder. In addition, layered or intergrowth derivatives can be formed when the ABO3 layers are separated by different structural motifs. Some of these derivative systems are able to incorporate and enable fast diffusion of protonic defects thanks to the presence of intrinsic structural oxygen vacancies and flexible metal frameworks.2.1 Hexagonal perovskites
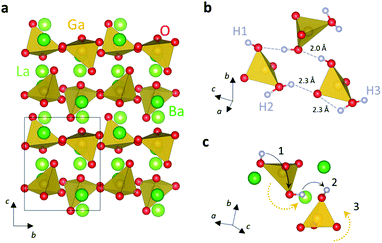
Hexagonal perovskites form from mixed stacking sequences of hexagonal (h) and cubic (c) close-packing of [AO3] layers, which result in the formation of face-sharing and corner-sharing BO6 octahedra.62 Mixed combinations of corner-sharing and face-sharing octahedra can give rise to a variety of hexagonal perovskite derivatives.63 Different hexagonal polytypic structures are usually designated by specifying the total number of layers contained in the unit cell followed by a letter denoting the lattice type (H for hexagonal, C for cubic and R for rhombohedral).64 These hexagonal structures are highly versatile and able to accommodate intrinsic cationic and anionic vacancies, with the formation of mixed metal coordination environments and different stacking arrangements.63,65–67High proton conductivity in a hexagonal perovskite was first discovered in the cation deficient 7H derivative Ba7Nb4MoO20 by Fop et al.68 In dry conditions, the conductivity of Ba7Nb4MoO20 is purely oxide ionic, with an oxide ion transport number of >0.99. Proton conduction is enabled under a humidified atmosphere, with a proton transport number of ∼0.8 at 500 °C. The proton conductivity is 4.0 × 10−3 S cm−1 at 500 °C, comparable to doped barium cerate and zirconate perovskites. This system also presents good stability in reducing and CO2-rich environments and chemical compatibility with typical electrode materials such as NiO and Ba0.5Sr0.5Co0.8Fe0.2O3−δ (BSCF).68
In dry Ba7Nb4MoO20 the cation vacancies are ordered, and the average structure is composed by an intergrowth of 12R hexagonal perovskite units and oxygen deficient ([BaO2]) palmierite-like layers formed by MOx polyhedra with mixed local 4-, 5-, and 6-fold coordination due to partial occupation of two different average crystallographic tetrahedral and octahedral oxygen sites (Otet and Ooct) (Fig. 3a).69 Water is absorbed on the intrinsic oxygen vacancies present on the palmierite-like layer and predominantly distributed on the average Ooct sites.68,69 The water absorption leads to disordering of the metal-stacking vacancy distribution due to a shift of the cation in the palmierite layer towards an adjacent mutually exclusive vacant site, as result of the repulsion between a proton pointing towards the nearest MOx unit and a metal cation (Fig. 3b). Partial occupation of the two metal sites results in the formation of disordered local stacking configurations creating a complex average network of isolated, face-sharing and corner-sharing polyhedral units in the hydrated material (Fig. 3c).
The significant structural flexibility of Ba7Nb4MoO20 allows the accommodation of the local cation and anion disorder introduced by hydration and enables a high concentration of water uptake, ≥0.8 molecules of H2O per formula unit.68,69
Neutron diffraction experiments and atomistic calculations demonstrate that protons are in proximity of the average Otet and Ooct sites.69 The positional oxide ion disorder generated by the close proximity of available oxygen sites due to the particular topology of the palmierite-like layers leads to delocalisation of the protonic defects over a variety of low energy configurations around their equilibrium site. Such delocalisation results in the creation of two-dimensional low energy transport pathways along the palmierite-like layers, where the proton defects can migrate via rotation and hopping motion with calculated migration energies in the range 0.18–0.61 eV depending on the local configuration (Fig. 3d). Importantly, the proton diffusion is assisted by the high flexibility and rotational mobility of the isolated variable coordination MOx units. Proton diffusion is usually slower in lower symmetry perovskite oxides such as orthorhombic SrCeO3 and CaZrO3, due to an additional enthalpy contribution needed for tilting of adjacent octahedra closer enough to allow proton hopping.8,70 Localisation of the protonic defects also generally leads to reduced proton conductivity, as in the case of the hexagonal 6H phase of Sc-doped BaTiO3−δ.71 In hydrated Ba7Nb4MoO20, frustration of the proton sub-lattice and the high dynamic flexibility of the variable coordination MOx moieties enable fast proton transport.
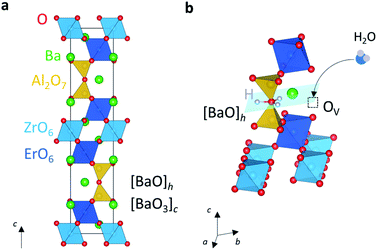
Another member of the hexagonal perovskite family displaying high proton conductivity is Ba5Er2Al2ZrO13.72 This system is a 10H hexagonal perovskite derivative with a structure composed by the stacking of cubic [BaO3] and oxygen deficient hexagonal [BaO] layers. The intrinsic oxygen deficient layers result in the creation of tetrahedral sites which are occupied by the aluminium atoms to form Al2O7 units (Fig. 4a).
While in dry air the conductivity is electronic p-type, Ba5Er2Al2ZrO13 presents a large protonic component in humidified air, showing a proton transport number of ∼1 from 300 to 600 °C and conductivity of 3.0 × 10−3 S cm−1 at 500 °C.72 Water is absorbed on the intrinsic oxygen vacancies of the hexagonal [BaO] layer, with the proton sites located on the apical oxygen atoms of the Al2O7 units (Fig. 4b).72 Both Ba7Nb4MoO20 and Ba5Er2Al2ZrO13 share the existence of oxygen deficient Ba–O layers with intrinsic oxygen vacancies enabling water absorption and fast proton transport.
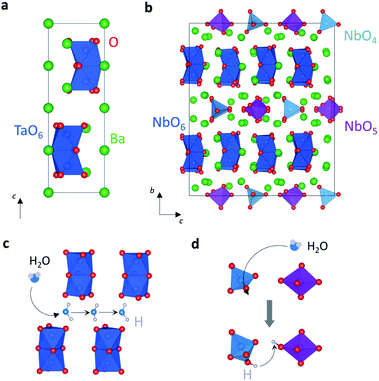
Compounds of the series Ba4M2O9 (M = Nb, Sb, Ta) are hexagonal derivatives exhibiting mixed oxide ion, proton and electronic conduction.73–75 While the ionic conductivities are far below those of representative proton conductors (<10−5 S cm−1 at 400 °C), these systems present complex polymorphic behaviour and interesting hydration and conduction mechanisms. The Nb and Ta compounds have the same low temperature α polymorph, which is composed by partially disordered isolated face-sharing octahedral (Nb/Ta)2O9 dimers separated by large voids. The high temperature phases of Ba4Ta2O9 and Ba4Sb2O9 both exhibit a 6H structure formed by face sharing octahedral units connected to BaO6 octahedra through corner-sharing (Fig. 5a).74,76 On the other hand, the niobate presents a high temperature orthorhombic γ-phase composed by layers of isolated face-sharing Nb2O9 dimers separated by ordered rows of isolated NbO4 and NbO5 units (Fig. 5b).77
The high temperature 6H–Ba4Ta2O9 and γ-Ba4Nb2O9 phases can be quenched to room temperature and are able to incorporate a substantial amount of water. In 6H–Ba4Ta2O9, discrete water molecules are intercalated in the void between the Ta2O9 dimers. Ab initio molecular dynamics (AIMD) simulations show that the H2O molecule unusually does not dissociate into H+ and OH−, migrating intact through the voids (Fig. 5c).78 In the γ-Ba4Nb2O9 phase, water is absorbed via hydroxylation of the NbO4 tetrahedra and hydrogenation of the NbO5 trigonal bipyramids to give two NbO4OH4 units. AIMD simulations evidence that proton conduction mainly occurs within the ab plane of the NbO5 polyhedra by hopping between oxygen atoms of adjacent NbO4OH units (Fig. 5d).78
Other hexagonal perovskite derivatives which exhibit proton conductivity are cation deficient 12R Sr3RENb3O12 (RE = La, Nd) and 5H Ba5Nb4O15.79–81 The structures of both compounds are composed by trimers (12R) or tetramers (5H) of corner-sharing NbO6 octahedra spaced by cationic vacancies. These systems present mixed ionic and electronic conduction, with proton transport dominating under wet oxidising conditions. The ionic conductivities are modest (∼10−6 S cm−1 at 550 °C), but their values can be substantially increased by acceptor doping on the Nb-site.79,80
These accounts highlight the inherent structural versatility of hexagonal perovskite derivatives of accommodating cation and anion defects/disorder and their ability in incorporating and enabling transport of protonic defects through different mechanisms. Even though reports of proton conduction in these systems are quite scarce, the most recent results on Ba7Nb4MoO20 and Ba5Er2Al2ZrO13 are particularly promising and encourage further exploration of proton conduction in the vast family of hexagonal perovskite derivatives.
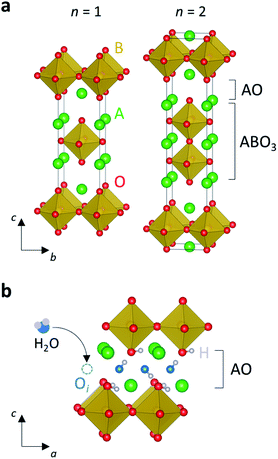
2.2 Ruddlesden–Popper structures
Layered perovskite derivatives form when perovskite-like slabs are spaced by some different structural motif. Ruddlesden–Popper (RP) phases are a particular class of layered perovskites with general formula An+1BnO3n+1. The structures of RP phases are composed by n perovskite layers alternated with rock-salt slabs, thus forming a framework in which n layers of corner-sharing BO6 octahedra are separated by AO layers (Fig. 6a). BaLaInO4-based oxides have K2NiF4-type structures (n = 1) and exhibit mixed oxide ion and proton conduction.82–85 These systems have generally large protonic components with proton transport numbers >0.80 under wet conditions at temperatures below 450 °C, although their conductivities are rather low (10−6 to 10−5 S cm−1). Several ferrite and nickelate RP oxides with general compositions A2BO4 (n = 1) or A3B2O7 (n = 2) (A = Sr, La, Nd, Pr; B = Fe, Ni) show triple mixed conductivity (i.e. protonic, oxide ion and electronic). These systems present good chemical compatibility with barium cerate and zirconate conductors86–88 and are currently investigated for application as electrodes in hydrogen-based electrochemical devices.89–97 For example, measurements on symmetrical cells based on a Y-doped BaCeO3 electrolyte with Pr2NiO4+δ and La2NiO4+δ cathodes demonstrated high oxygen reduction reaction (ORR) activity and area specific resistance (ASR) similar to BSCF (≤1 Ω cm2 at 600 °C).89,90,98 High power outputs (1070 mW cm−2 at 700 °C) have also been reported for a PCFC with a BaZr0.1Ce0.7Y0.1Yb0.1O3−δ electrolyte and the RP n = 2 cathode material Pr2BaNiMnO7−δ, with no degradation at 0.7 V at 600 °C for 100 h.99RP structures are notoriously able to accommodate excess interstitial oxygen.100 In contrast with acceptor doped perovskites, the dissociative absorption of water in these RP systems occurs via hydration of the available interstitial oxygen sites along the rock-salt layers,90,93,101,102 following the relationship:
OH occupies an interstitial site, while a hydrogen atom is bonded to an apical oxygen of the metal octahedra (Fig. 6b). Preliminary calculations (without the consideration of the interstitial oxygen defects) on La2NiO4/La3Ni2O7 have evidenced two possible proton migration pathways, inter-layers, i.e. across two adjacent AO layers, and inner-layer.102 The inter-layers pathway has a very large energy barrier (>3.5 eV) and probably does not contribute to the proton diffusion. The inner-layer pathway presents considerably lower energy barrier (1.29–1.66 eV) and involves a Grotthuss mechanism with rotation and hopping of the protons between the apical and equatorial oxygen positions of the metal octahedra (similarly to the case of cubic perovskites).102,103
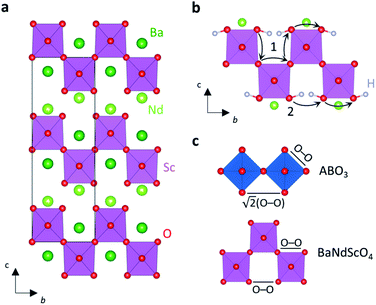
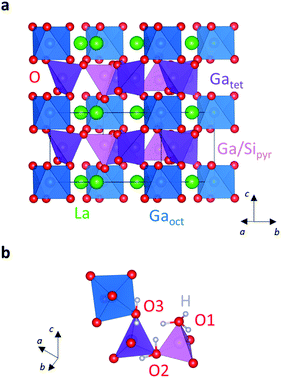
Compounds of the series BaNdMO4 (M = In, Sc) are RP derivatives.104,105 Their structures are composed by (Ba3/4Nd1/4MO3)2 perovskite layers alternated with NdO rock-salt blocks. They differentiate from the common RP structure because the edge of the MO6 octahedron faces the rock-salt unit (Fig. 7a). These systems are mixed oxide ionic and electronic conductors and recent reports have revealed significant proton conductivity in acceptor-doped materials of composition BaNd1−xCaxMO4−x/2.106,107 The doped indate exhibits higher conductivity than the Sc compound. At 500 °C, BaNd0.8Ca0.2InO3.90 exhibits conductivity of 1.3 × 10−4 S cm−1 under humidified air and a proton transport number of ∼0.53, although this system presents poor chemical stability in a humid atmosphere.106
Water is absorbed onto the oxygen deficient layer at the interface between the perovskite and the rock-salt layers, with the protons located on the equatorial oxygen atoms of the MO6 octahedra.107 Protons diffuse via rotational and hopping motions along the lowest energy intra- and inter-octahedral pathways, which have similar migration barriers of 0.63 eV and 0.69 eV respectively (Fig. 7b). Inter-octahedral proton hopping is generally unfavoured in cubic perovskite structures due to the large inter-octahedral O–O distance (Fig. 7c). Inter-octahedral diffusion predominantly occurs in lower symmetry perovskite-type structures, where the hopping distance is shortened by octahedral tilting.8,70 However, in the BaNdMO4 structure the inter-octahedral O–O separation is comparable to the intra-octahedral O–O distance, thus enabling both pathways (Fig. 7c).107
The results on RP materials suggest that similar layered perovskite structures could potentially support analogous mechanisms of proton incorporation and transport. Dion-Jacobson phases with general formula MAn−1BnO3n+1 (M = alkali metal) are closely related to the RP structure, having a layer of alkali metal as the separating motif between the perovskite blocks.108 Aurivillius phases are constituted by perovskite layers spaced by rock-salt BiO sheets in which Bi is in a square-based pyramidal coordination.109 Both these structure systems support oxide ion conduction,108,109 with signatures of proton conductivity in some Dion–Jacobson materials,110,111 and could therefore constitute an interesting avenue of research into novel layered perovskite proton conductors.
2.3 Brownmillerite materials
Another class of layered perovskite derivatives is the brownmillerite family. The brownmillerite structure, with general formula A2B2O5, can be described as an oxygen deficient perovskite structure, having 1/6 of oxygen sites empty. The intrinsic oxygen vacancies are fully ordered in rows along the [110]p direction (where the subscript p denotes the perovskite subcell) and form corner-sharing octahedral perovskite layers alternated with tetrahedral layers (Fig. 8a). The most studied brownmillerite material is the oxide ion conductor Ba2In2O5.112 At high temperature (T > 900 °C), disordering of the oxygen vacancies leads to a transition to a highly conductive cubic phase.112,113Under humidified atmosphere, Ba2In2O5 exhibits significant proton conductivity, with a proton transport number >0.70 below 400 °C.114,115 The large number of intrinsic oxygen vacancies enables the water absorption. Ba2In2O5 can uptake a considerable concentration of water, forming the fully hydrated phase Ba2In2O5(H2O), or BaInO3H.116–118 Upon hydration, the dry brownmillerite structure transforms from orthorhombic to a tetragonal perovskite-like phase (at T < 300 °C), where the intrinsic oxygen vacancies in the tetrahedral layer are fully occupied by the water oxygen atoms (Fig. 8b).118,119 Protons are located on two different sites; H1 is on a partially occupied position bonded to an apical octahedral oxygen, while H2 is on a fully occupied site lying between two equatorial oxygen atoms corresponding with the tetrahedral layer in the dehydrated structure.120–122 Protons are ordered according to a defined local configuration, in which H1 is hydrogen bonded towards the equatorial oxygen of the octahedral layer of the dry structure (Fig. 8c).123 The hydrogen bond configuration affects the mobility of the protonic defects and restricts the number of sites available for hopping, thus resulting in anisotropic proton conduction.122,124
The conductivity of Ba2In2O5 under humidified conditions is ∼10−5 S cm−1 at 400 °C.114 Doping on the In-site generally leads to stabilisation of the perovskite-like structure and to increased proton conductivity.118,125 Interestingly, the cubic phase can be stabilised also by oxyanion doping via the introduction of silicate, phosphate or sulfate groups, with the conductivity increasing to 2.4 × 10−3 S cm−1 at 400 °C in Ba2In1.8Si0.2O5.1.126,127 Ba2In2O5 decomposes in hydrogen-containing atmospheres above 500 °C, with the formation of In metal and BaCO3 and a considerable reduction of the ionic conductivity over time.115 Due to the presence of electronic conductivity and the generally poor stability under reducing conditions, fuel cells with Ba2In2O5-based electrolytes exhibit generally low power densities (<10 mW cm−2 at 600 °C).128
Other brownmillerite compounds exhibiting proton conductivity are Ba2InGaO5 and Sr2ScGaO5.129,130 The ionic conductivity of Ba2InGaO5 is quite modest due to ordering of the In and Ga cations along the stacking axis, which further stabilises the orthorhombic brownmillerite structure.129 Sr2ScGaO5 also exhibits a moderate protonic component.130 However, heavily Zn-doped Sr2ScGaO5 (Sr2Sc1−xZnxGaO5−0.5x, 0.4 ≤ x ≤ 0.6) presents a highly disordered and highly oxygen deficient perovskite structure with a peculiar one-coordinate oxygen site and shows significant proton conductivity, with three orders of magnitude increase in the conductivity in comparison with the parent compound.130
A recent study has demonstrated that the brownmillerite Sr2Co2O5 can absorb one H per formula unit, forming hydronated HSrCoO2.5 (although this phase is stable only up to 160 °C).131,132 Atomistic calculations show that protons are distributed among apical and equatorial octahedral oxygen sites and that they adopt a wide range of configurations with similar energies.133 The cooperative transition between the different configurations creates a frustrated proton sub-lattice enabling high proton mobility. Measurements on a thin film of HSrCoO2.5 showed conductivity of 0.33 S cm−1 at 140 °C.132 However, further measurements on a bulk dense sample are required to confirm such high conductivity and rule out any effects from proton transport along physisorbed water at the inner surface of the porous film.134
Brownmillerite-based materials with intrinsic oxygen vacancies offer potential of high proton conductivity, thanks to the ability of the structure of incorporating large concentrations of water. Other brownmillerite compounds showing oxygen intercalation ability may be able to incorporate water and enable proton transport,135–137 thus constituting further candidate proton conductors.
3. Oxides with tetrahedral moieties
Proton conduction has been reported in various systems possessing tetrahedral moieties as their principal structural feature. These tetrahedral units are present in isolated or corner-sharing motifs and generally assist the protonic transport thanks to their high flexibility and rotational mobility.3.1 REMO4 phases
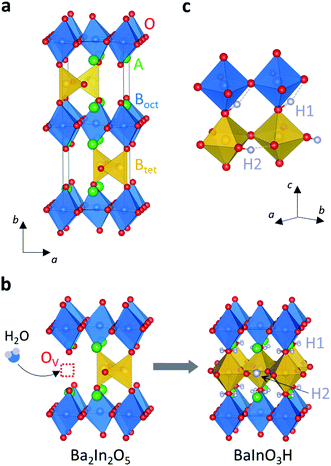
Haugsrud and Norby were the first to demonstrate high proton conductivity in REMO4-based materials, namely in several acceptor doped ortho-niobates and ortho-tantalates with general formula RE1−xAxMO4 (RE = La, Gd, Nd, Tb, Er, Y; A = Ca, Sr, Ba; M = Nb, Ta).138 Compared to acceptor doped perovskite conductors, proton conductivity in these ortho-niobates and ortho-tantalates is attained for relatively low doping levels (x = 0.01–0.05). Proton conduction is dominant (proton transport number ∼1.0) under humidified and reducing atmospheres below 800 °C, while the conductivity is p-type electronic under oxidizing conditions at high temperatures.138–140These rare earth ortho-niobates and ortho-tantalates are isostructural, crystalising in the monoclinic fergusonite-type structure at low temperatures and in the tetragonal scheelite phase at high temperatures (Fig. 9a). Both structure types are composed by isolated tetrahedral units sharing corners with REO12 dodecahedral units; the low temperature fergusonite structure can be considered as a slight monoclinic distortion of the tetragonal high temperature phase.141 The transition temperature depends on the composition and for LaNbO4 is in the range 500–530 °C.139,142 The fergusonite–scheelite transition in LaNbO4 has originally been described as a second order transition between the ferroelastic monoclinic phase and the paraelastic tetragonal phase.143 However, recent reports suggest a reconstructive first order transition induced by displacement of the Nb cation from the centre of the tetrahedron and change in NbO coordination from 4 in the scheelite phase to a 6-coordinated distorted octahedral arrangement in the fergusonite phase, with two long and four short Nb–O distances.144,145 The fergusonite–scheelite transition is relevant to the proton conductivity, since it coincides with a reduction in the activation energy for proton transport (from 0.78 eV to 0.55 eV in La0.99Ca0.01NbO4−δ), which is associated to an increase in the mobility of the proton defects in the scheelite phase.138,142 However, the presence of this transition may be detrimental for practical electrolyte applications due to the different thermal expansion coefficients of the two phases (around 15 × 10−6 °C−1 for the low temperature monoclinic phase and 8.6 × 10−6 C−1 for the high temperature polymorph) and the tendency to microcracking.146 The scheelite phase can be stabilised at room temperature via substitution of Nb with isovalent cations such as V, As, and Sb, generally resulting in an increase of the conductivity at lower temperatures.147–150
Acceptor doping of LaNbO4 introduces extrinsic oxygen vacancies, enabling water absorption. Atomistic calculations on the scheelite LaNbO4 structure have demonstrated that oxygen vacancies are stabilized by local relaxation and condensation of the NbO4 tetrahedra around a vacant oxygen site to form Nb2O7 or Nb3O11 polyhedral linkages (Fig. 9b).151,152
The thermodynamics of hydration and the proton mobility depend on the size of the rare-earth element. Hydration is more exothermic (i.e. more favourable) as the rare-earth cation becomes smaller, with the enthalpy of the water absorption reaction reducing from −115 kJ mol−1 in the La niobate, to −165 kJ mol−1 for the Er-containing composition.138 This trend is in contrast with REPO4 phosphates, of which crystal structures are composed by similar isolated tetrahedral units.153 On the other hand, the proton mobility is lower when the RE cation is smaller due to lattice size effects and to the decreasing lattice polarizability of the smaller unit cell.138 The LaNbO4-based materials exhibit the highest conductivity, with a value of ∼10−3 S cm−1 at 800 °C in La0.99Ca0.01NbO4−δ.138,139
Structural optimization calculations on scheelite LaNbO4 have demonstrated that protons are located on two stable positions in proximity of the only crystallographic oxygen site: along the edge of the NbO4 tetrahedron (H1, lowest energy) and on a site between two lanthanum ions (H2) (Fig. 9c).152,154 Long-range proton migration occurs along the pathway connecting the H1 and H2 sites, through rapid rotation of the proton around the oxide ion (with an energy barrier of 0.04–0.06 eV) followed by hopping between two adjacent tetrahedra (with a barrier of 0.41 eV) (Fig. 9d).154
Despite exhibiting lower conductivities than perovskite cerate oxides, doped LaNbO4-based materials shows greater stability in CO2-containing atmospheres,155 which together with a proton transport number close to unity make these materials highly interesting for fuel cell applications. Tests on different proton-conducting electrode materials have demonstrated generally good chemical compatibility of LaNbO4 materials with LaMO3 (M = Mn, Fe, Co) perovskite type cathodes and NiO,155–157 while they show poor compatibility with proton-conducting ceramic anodes because of undesirable reactions at high temperatures.158 Anode supported fuel cell with La0.99Ca0.01NbO4−δ electrolytes have shown modest peak power densities (24 mW cm−2 at 750 °C) due to the large polarization resistance between the electrodes and the electrolyte (20–40 Ω cm2 at 800 °C).155,157,158
Acceptor doped monazite-type systems LaVO4, LaAsO4, and LaSbO4 also present significant proton conductivity under humidified atmosphere.159–161 The monoclinic monazite structure is similar to the scheelite structure and is composed by isolated distorted MO4 tetrahedra sharing their edges with LaO9 polyhedra.162 Doped LaVO4 and LaAsO4 exhibit the highest conductivities; the proton conductivity of La0.99Ca0.01VO4−δ is ∼3 × 10−4 S cm−1 at 800 °C, although the ortho-vanadate is unstable under reducing conditions.159
Atomistic calculations on LaAsO4 have revealed that extrinsic oxygen vacancies are introduced via condensation of two adjacent tetrahedra to form a pyro-arsenate As2O7 unit, similar to the case of LaNbO4.160 Protons are statistically distributed on two lowest energy positions located on two non-equivalent oxygen sites within the same tetrahedron. Interestingly, while incorporated protons in oxides generally reside around oxide ions forming OH groups, in LaAsO4 the protonic defects are stabilised as covalent hydrogen arsenate ions, HAsO42−.159 During the inter-tetrahedral proton migration, the host lattice mainly exhibits rotational and translational relaxation with little distortion of the AsO4 polyhedra, a feature that is common in proton conducting oxides with isolated tetrahedral moieties and in contrast with ABO3 perovskites where proton transport is generally accompanied by large distortion of the corner-sharing BO6 octahedra.163
A variety of compositions crystallize with the scheelite, monazite or in closely related structures162,164–166 and could offer an interesting crystal chemistry space for the investigation of proton conduction in systems with isolated tetrahedral moieties.
3.2 Gallium-based oxides
High proton conductivity has been reported in lanthanum–barium gallates of general formula La1−xBa1+xGaO4−x/2.167,168 The parent compound LaBaGaO4 possesses an orthorhombic β-K2SO4-type structure composed by isolated distorted GaO4 tetrahedra and ordered alternating layers of Ba and La atoms (Fig. 10a). LaBaGaO4 shows high resistivity with limited proton conduction. Variation of the La/Ba ratio to produce the solid solution La1−xBa1+xGaO4−x/2 results in the introduction of oxygen vacancies enabling high ionic conduction. The member with x = 0.2, La0.8Ba1.2GaO3.9, shows proton conductivity of ∼10−4 S cm−1 at 500 °C under humidified O2.167,168The oxygen vacancies in La0.8Ba1.2GaO3.9 are accommodated through the condensation of two adjacent GaO4 units to form a Ga2O7 group (in a way analogous to acceptor doped LaNbO4).169 On the local scale, the oxygen vacancies are pinned to the nearest-neighbour cation site by the 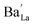 defects and there is no ordering of the Ga2O7 units.170 Water incorporation induces the break-up of the Ga2O7 units,169 according to the reaction
defects and there is no ordering of the Ga2O7 units.170 Water incorporation induces the break-up of the Ga2O7 units,169 according to the reaction
| Ga2O7 + H2O → 2GaO4H. |
Protons in La0.8Ba1.2GaO3.9 are located on three different sites, pointing almost perpendicular to the Ga–O bond direction (Fig. 10b).171 Protons migrate following a curved path between two intra-tetrahedral oxide ions due to the repulsive interactions with nearby large Ba/La cations, followed by jump onto an oxygen of an adjacent GaO4 unit (Fig. 10c).169
The rate-determining step for proton diffusion is the intra-tetrahedra migration, which has a considerably higher energy barrier (∼0.4–0.7 eV) than the inter-tetrahedral hopping (∼0.07 eV).169,172 The latter is favoured by the inter-tetrahedral hydrogen bond O⋯H interactions, which are shorter (∼2.0 Å) than the intra-tetrahedral ones (∼2.3 Å),171,173 thus highlighting the significance of the H bonding configuration (Fig. 10b) in defining the mechanism of proton transport in La0.8Ba1.2GaO3.9. Importantly, the inter-tetrahedral proton migration is also facilitated by the rotational mobility of the GaO4 units,174,175 a mechanism that is similar to the rapid phosphate group reorientation in the solid-acid protonic conductor CsH2PO4.176 It is worth noticing that while intra-polyhedral hoppings are common in perovskite systems with corner-sharing octahedral units, intra-tetrahedral proton hopping is particularly unfavoured in La0.8Ba1.2GaO3.9 and in other oxide structures with isolated tetrahedral units such as LaNbO4 and LaAsO4.163,177
Proton conductivity has been reported in gallium-based oxides having general composition RE3Ga5MO14 (RE = La, Nd; M = Si, Ti, Sn, Ta).178–180 These compounds belong to the langasite family and their structure is composed by alternated layers of Ga in a mixed 6-fold (octahedral) and 4-fold (tetrahedral/planar trigonal pyramidal) coordination, with the pyramidal site being partially occupied by the Ga/M cations (Fig. 11a).
Extrinsic oxygen vacancies are introduced by variation of the Ga/M ratio to form RE3Ga5+xM1−xO14−δ and enable water absorption. The hydration thermodynamics is affected by the size of the M ions, generally becoming more favourable with increasing the size of the cationic radius (enthalpy of hydration reducing from −97 kJ mol−1 for M = Si, to −120 kJ mol−1 for M = Sn).179 Calculations demonstrated that protons can adopt different configurations on the three non-equivalent oxygen positions O1, O2, and O3 (Fig. 11b). The lowest energy proton positions are bound to the O3 site, which is shared by the GaO4 tetrahedra and GaO6 octahedra.178 Proton conductivity appears to be anisotropic, with a lower enthalpy of diffusion along the c-axis in the Si langasite, while the ionic migration is easier along the ab plane for the Ta langasite (langatate). The different anisotropy of proton conductivity is due to the different cation ordering for the two compositions.180
All the RE3Ga5MO14 compositions are mixed p-type electronic and ionic conductors at high temperatures due to a minority of electron holes, and pure oxide ion and proton conductors at lower temperatures. The conductivity of these materials is predominantly protonic below 800 °C and in the range ∼10−6 to 10−4 S cm−1 between 400 and 800 °C.178–180 While the proton conductivities of these compounds are lower than conventional perovskite conductors, the langasite structure allows for large compositional variations,181 thus providing a wide range of langasite-type oxides of which proton conducting properties are mostly unexplored.
The conductivities of gallium-based oxides are among the highest exhibited by oxides containing tetrahedral moieties. Further examples are constituted by reports of proton conductivity in acceptor doped Gd3−xAxGaO6 (A = Ca, Sr), of which structure is composed by distorted isolated GaO4 tetrahedra,182 and in cuspidines of composition La4Ga2−xTixO9+x/2, which present corner-sharing Ga2O7 polyhedral units.183 The Ga3+ cation has a strong preference for tetrahedral coordination,184 with the structures of several gallates containing either isolated tetrahedra or different types of corner-sharing GaO4 polyhedral units linkages.185–188 Given the structural variety of these systems, investigation of further gallium-based oxides potentially able to support substantial proton conductivity is warranted.
3.3 Apatite-type oxides
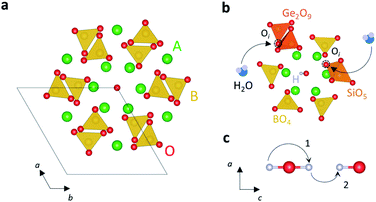
Apatite oxides have general formula A10−xB6O26±δ, where A is a rare-earth metal such as La or an alkaline earth metal such as Sr or Ba, and B is a p-block element such as P, Si or Ge. The apatite structure possesses hexagonal symmetry and is formed by a framework of isolated BO4 tetrahedra constituting two channels running parallel to the c-axis; the inner channel contains rows of A cations in a ring formation with a row of oxide ions at the centre (Fig. 12a).Si- and Ge-based lanthanum apatites are known oxide ion conductors thanks to the presence of interstitial oxygen defects which mediate the oxide ion transport.189,190 These systems are able to absorb significant concentrations of water;191,192 for example, ∼0.75H2O molecules per formula unit in La9.6Si6O26.4 and ∼0.55H2O molecules in La9.67Ge6O26.5.193,194 Similarly to the case of Ruddlesden–Popper oxides, water is incorporated on the interstitial oxygen sites.191,193
The interstitial sites are close to the centre of the La channel in Si-apatites, forming distorted SiO5 units,193 while they are in proximity of the GeO4 tetrahedra forming Ge2O9 units in Ge-apatites (Fig. 12b).194,195 Water absorption leads to the introduction of protonic defects which are located on the oxide ions at the centre of the La ring, in an arrangement which agrees with the one of isostructural hydroxyapatite (Ca10(PO4)6(OH)2) (Fig. 12b).195
Despite the large levels of water absorption, the presence of proton conductivity in these apatite oxides is unclear. León-Reina et al. reported an increase in the conductivity of La9.75Ge6O26.62 under humidified atmosphere suggesting proton conduction below 400 °C.196 However, Orera et al. argued that the increase in ionic conductivity may be associated with an enhancement of the oxide ion conduction due to the larger concentration of interstitial oxide ions.191 Preliminary calculations demonstrated that protons are most stable when pointing towards a neighbouring oxide ion in the channel, thus implying that long-range diffusion requires OH rotation before proton transfer (Fig. 12c). However, such rotational motion has a high energy barrier (∼1.5 eV), suggesting that proton diffusion through rotation and hopping within the channel is unfavourable.195 Further electrical characterisation (i.e., determination of the proton transport number and investigation of the presence of any isotope effect) is required to unambiguously determine whether Si- and Ge-based apatite oxides can support proton conduction.
Isostructural hydroxyapatite materials can support proton conduction, with reports of membrane electrolytes with high proton conductivity (∼10−2 S cm−1 at 700 °C) and efficient fuel cell applications.197,198 Moreover, it has been demonstrated that it possible to prepare apatite oxide systems with d1 cations (Cr5+) showing mixed protonic and electronic conductivity for potential electrode utilisation.199 Thanks to its large flexibility, the apatite structure allows the accommodation of a wide range of cations and defects which can enable different types of ionic transports, thus motivating further investigation of oxides crystallising in this structural family.
4. Fluorite-related oxides
Fluorite-based oxides are usually known for their oxide ion conducting properties. Fluorite materials such as yttria stabilised zirconia (YSZ) and doped ceria constitute the most conventional oxide ion conductors thanks to ability of the structure of supporting oxide ion conduction. Some oxide materials having fluorite or fluorite-related superstructures however exhibit significant proton conductivity.4.1 A2B2O7 compounds
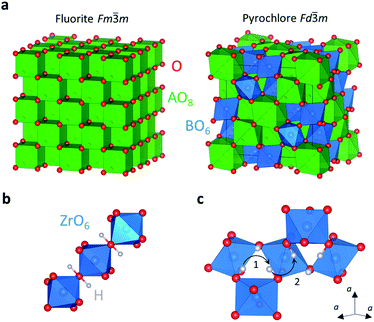
Rare-earth oxides with general formula A2B2O7 (A = La, Nd, Sm, Er; B = Ti, Zr, Sn, Ce) exhibit proton conductivity.200–208 These compounds are typically classified as having fully ordered pyrochlore structures or oxygen deficient disordered fluorite-type structures. The pyrochlore structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) is composed by chains of distorted BO6 octahedra, with the A cations in a distorted 8-fold cubic coordination, while the fluorite structure (space group Fm
m) is composed by chains of distorted BO6 octahedra, with the A cations in a distorted 8-fold cubic coordination, while the fluorite structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) can be described by a face-centred cubic arrangement of A cations in a cubic 8-fold coordination (Fig. 13a). The pyrochlore structure is considered as a superstructure of the ideal cubic fluorite, having twice the unit cell parameter and 1/8 of the oxygen sites unoccupied.209
m) can be described by a face-centred cubic arrangement of A cations in a cubic 8-fold coordination (Fig. 13a). The pyrochlore structure is considered as a superstructure of the ideal cubic fluorite, having twice the unit cell parameter and 1/8 of the oxygen sites unoccupied.209
The formation of the A2B2O7 pyrochlore phase is driven by the tendency for ordering of the cations on the A and B sites. This tendency depends on the relative sizes of the cations: as the difference in cationic sizes increases (i.e. the radius of the A-site cation becomes larger), stabilisation of the ordered pyrochlore unit cell is favoured.204,210,211 The ratio between the ionic radii of the A and B cations (rA/rB) can be used as a tolerance factor for describing the formation of one structure over the other.212 For example, La2Zr2O7 adopts the pyrochlore structure,211 while La2Ce2O7 is most often reported as a disordered fluorite.205 The oxygen vacancies can exhibit short-range ordering or disordering, thus leading to the formation of either pyrochlore-like (in fluorite systems) or fluorite-like (in pyrochlore structures) domains on the local scale.211,213,214
Acceptor doping on the A site with alkaline earth cations promotes water incorporation through the introduction of oxygen vacancies.201,204,208 The hydration is almost independent on the nature of the B site cation but correlates with the size of the rare-earth element, becoming more favourable (enthalpy of hydration more exothermic) on increasing the ionic radius of the RE cation, displaying a trend opposite to RE1−xAxMO4 materials. For example, the enthalpy of hydration in Ca-doped A2Sn2O7 reduces to −44 kJ mol−1 for A = Er to −76 kJ mol−1 for A = Sm and −103 kJ mol−1 for A = La.215
The most studied compositions are doped La2Zr2O7 and La2Ce2O7 thanks to their higher conductivities and larger protonic components. Ca-doped La2Zr2O7 has a conductivity of ∼10−4 S cm−1 at 600 °C and a proton transport number of ∼1 under wet reducing atmosphere,201,216–219 while doped La2Ce2O7 compounds have conductivity of ∼10−3 S cm−1 at the same temperature, albeit with a lower protonic component.205,220 Contrary to BaCeO3-based perovskites, doped-A2Ce2O7 materials exhibit excellent chemical stability in H2O- and CO2-containing atmospheres, showing no signs of reaction after exposure at 700 °C for 100 h.221 These systems are investigated for ammonia synthesis, hydrogen separation membranes and fuel cell applications,221–223 with peak power densities >700 mW cm−2 at 700 °C reported for PCFCs with doped A2Ce2O7 electrolytes.224–226
Atomistic calculations on pyrochlore La2Zr2O7 demonstrated that protons are located on a lowest energy site on the shared apical oxygen of the corner-sharing ZrO6 octahedral units (Fig. 13b).227,228 Long-range proton diffusion occurs along the ZrO6 octahedral network, through an intra-polyhedral migration pathway composed by two separated hopping paths.228 A proton hops on the edges of the equilateral triangle formed by three adjacent equivalent proton sites and can then migrate towards the next closed region (Fig. 13c). The two paths have very similar migration energies of 0.32 eV and 0.39 eV respectively. A third path corresponding to partial rotation around the oxygen atom has little contribution to the long-range conduction due to its considerable higher energy (0.54 eV).228 This is in contrast with conventional perovskite conductors, where migration occurs via a rotation and hopping mechanism with the rotational step having the lowest energy barrier.8,229
4.2 RE3BO7 oxides
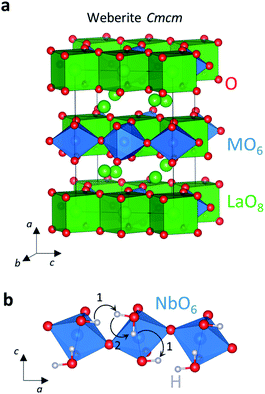
Niobates and tantalates of composition RE3MO7 (RE = Y, La–Lu; M = Nb, Ta) present mixed electronic, oxide ion and proton conductivity, with a significant protonic component under wet oxidising conditions.230–234 The compounds containing the larger lanthanides (RE = La, Gd) generally crystallise with a weberite structure, while the compositions with the smaller lanthanide cations have fluorite, distorted fluorite or pyrochlore structures.234,235 The weberite structure is an anion deficient fluorite-related superstructure exhibiting different polytype forms.236 The La3MO7 weberite structure (space group Cmcm or Pnma) can be described as composed by chains of corner-sharing MO6 octahedra perpendicular to the b-axis and edge-sharing distorted LaO8 cubes (Fig. 14a).237,238 Similarly to the case of A2B2O7 oxides, the Ln3MO7 compositions having the fluorite structure exhibit shot-range ordering of the anion vacancies and contain pyrochlore microdomains on the local scale.239In the niobates, the enthalpy of hydration regularly decreases with the radius of the rare-earth cation. The water absorption is favoured for the compounds containing smaller RE3+ ions: the water concentration is 2–3% water per formula unit for the compounds with RE = Y, Yb, Lu, while it is considerably lower for La3NbO7.233 Extrinsic oxygen vacancies can be introduced in the weberite lanthanum niobate/tantalate structures via acceptor doping. The doped La3−xAxMO7−x/2 (A = Ca, Sr) compositions are stable under oxidising and reducing conditions and exhibit mixed ionic–electronic conductivity with a wide electrolytic domain (∼10−20 to 10−5 atm in pO2) and a proton transport number of 0.4 at 600 °C.230,231 The enthalpies of hydration are in the range −133 kJ mol−1 to −117 kJ mol−1 and their conductivities are ∼10−4 to 10−3 S cm−1 at 600 °C.230,231
Calculations on weberite La3NbO7 showed that the most stable proton sites are on the non-shared equatorial oxygen atom of the NbO6 octahedra (Fig. 14), in contrast with La2Zr2O7 where protons are located on the shared apical oxygen.240 Protons migrate via rotational and hopping motion through a long-range lowest energy percolation pathway along the non-shared equatorial oxygen atoms and parallel to the a-axis (Fig. 14b). The rotational paths around the non-shared equatorial oxygen atoms have energy barrier of 0.34–0.43 eV, while the intra- and inter-octahedral hoppings have barriers of 0.41–0.54 eV.240
The anisotropicity of migration is related to the configuration of the octahedral chains and the preference of protons of residing on the non-shared equatorial oxide ions.241 The rate-determining step for diffusion is the inter-octahedral hopping between two adjacent non-shared oxygen atoms, which presents the highest energy barrier.241
4.3 Lanthanum tungstate oxides
Several lanthanide tungstate oxides with a ∼3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Ln2O3–WO3 molar ratio (Ln = La, Nd, Gd and Er) have been reported to show predominant proton conduction under humidified atmosphere below 900 °C.242–247 Lanthanum tungstate oxides in the compositional region 25–30 mol% La2O3 have general formula La28−xW4+xO54+3x/2v2−3x/2 (v denotes the number of oxygen vacancies) and are also known as La27W5O55.5−δ, La5.5WO11.25−δ or La6WO12. They exhibit proton transport number of ∼1 and conductivities of ∼10−3 S cm−1 at 600 °C.242,244,248 These systems present good stability under CO2 atmosphere, with no signs of degradation after annealing at 700 °C and 800 °C.249 La6WO12 is also chemically and mechanically compatible with conventional cathode materials such as La0.7Sr0.3MnO3−δ (LSM) and La0.75Sr0.25Cr0.5Mn0.5O3−δ (LSCM) and chromite anode perovskites such as La0.85Sr0.15Cr0.9Ni0.1O3−δ (LSCN) and La0.75Ce0.1Sr0.15CrO3−δ (LSCCe), while it reacts with BSCF.250–253 Fuel cells with La6WO12-based electrolytes display open circuit voltage (OCV) values close to the theoretical Nernst voltage, although delivering only modest power densities (∼50 mW cm−2 at 700 °C).244,251,254 Due to the presence of mixed protonic and electronic conduction at T > 700 °C, La6WO12-based materials have also been investigated for application as high temperature hydrogen separation membranes, which constitute an interesting solution for the recovering of H2 from low-quality gases.255 High hydrogen permeability rates >10−2 mL min−1 cm−2 have been obtained for Mo- and Re-substituted La6WO12-based membranes due to a substantial increase in the electronic conductivity,256,257 while permeation rates of 0.15 mL min−1 cm−2 have been reported for dual-phase composite membranes.258 These values are significantly higher than the typical hydrogen rates of state-of-the-art doped SrCeO3 perovskite membranes (∼10−3 mL min−1 cm−2).259,260
1 Ln2O3–WO3 molar ratio (Ln = La, Nd, Gd and Er) have been reported to show predominant proton conduction under humidified atmosphere below 900 °C.242–247 Lanthanum tungstate oxides in the compositional region 25–30 mol% La2O3 have general formula La28−xW4+xO54+3x/2v2−3x/2 (v denotes the number of oxygen vacancies) and are also known as La27W5O55.5−δ, La5.5WO11.25−δ or La6WO12. They exhibit proton transport number of ∼1 and conductivities of ∼10−3 S cm−1 at 600 °C.242,244,248 These systems present good stability under CO2 atmosphere, with no signs of degradation after annealing at 700 °C and 800 °C.249 La6WO12 is also chemically and mechanically compatible with conventional cathode materials such as La0.7Sr0.3MnO3−δ (LSM) and La0.75Sr0.25Cr0.5Mn0.5O3−δ (LSCM) and chromite anode perovskites such as La0.85Sr0.15Cr0.9Ni0.1O3−δ (LSCN) and La0.75Ce0.1Sr0.15CrO3−δ (LSCCe), while it reacts with BSCF.250–253 Fuel cells with La6WO12-based electrolytes display open circuit voltage (OCV) values close to the theoretical Nernst voltage, although delivering only modest power densities (∼50 mW cm−2 at 700 °C).244,251,254 Due to the presence of mixed protonic and electronic conduction at T > 700 °C, La6WO12-based materials have also been investigated for application as high temperature hydrogen separation membranes, which constitute an interesting solution for the recovering of H2 from low-quality gases.255 High hydrogen permeability rates >10−2 mL min−1 cm−2 have been obtained for Mo- and Re-substituted La6WO12-based membranes due to a substantial increase in the electronic conductivity,256,257 while permeation rates of 0.15 mL min−1 cm−2 have been reported for dual-phase composite membranes.258 These values are significantly higher than the typical hydrogen rates of state-of-the-art doped SrCeO3 perovskite membranes (∼10−3 mL min−1 cm−2).259,260
La28−xW4+xO54+3x/2v2−3x/2 compounds crystallise in an oxygen deficient fluorite-related tetragonal superstructure composed by WO6 octahedra oriented in alternating directions and with the lanthanum cations in a regular 8-fold cubic coordination (La1) or having a highly distorted 7-fold coordination (La2).261 Some of the La2 sites are partially occupied by the excess tungsten present in the structure (x), which effectively act a self-dopant creating intrinsic WLa substitutional defects.261,262 The cation disorder is accompanied by large static disorder in the oxygen sub-lattice.261–265 Characterisation of the hydration and proton conduction mechanisms of these systems is still lacking, probably due to challenges associated in modelling the large anion and cation disorder present in the structure.
Overall, the presence of substantial proton conductivity in oxides having fluorite-related superstructures motivates the investigation of the proton conducting properties of similar structural systems. For example, several bismuth-based oxides having complex fluorite-related superstructures exhibit very high oxide ion conductivities.266–269 The high ionic conduction is due to the presence of anion disorder and of flexible metal polyhedral units with variable coordination; these structural features could potentially also allow for significant proton transport in these systems.
5. Concluding remarks
This perspective has presented an overview of the most significant types of solid oxide proton conductors beyond cerate and zirconate perovskite oxides. Such compounds belong to different structural families and exhibit a variety of distinct water absorption and proton transport mechanisms. The structural and mechanistic features of hydration and proton conduction were discussed, highlighting the salient differences between these alternative materials and the traditional perovskite oxide conductors. The diverse characteristics of these less established conductors point to new potential crystal routes and can be used to inform the discovery of novel solid oxide proton conductors.A fundamental prerequisite for proton conduction is the incorporation of protonic defects, which in perovskite oxides (and several other proton conductors) usually occurs via water absorption on the extrinsic oxygen vacancies introduced by acceptor doping. However, the solubility and nature of the dopants limit the oxygen vacancy concentration and influence the degree of hydration.8,138,270 In this respect, systems with inherently defective lattices such as hexagonal perovskite derivatives with oxygen deficient layers and brownmillerite oxides are particularly interesting, as they can absorb large concentrations of water on the intrinsic oxygen vacancies already present in their structures. This also theoretically eliminates any proton trapping effects caused by donor doping, which are usually detrimental for the overall conductivity of conventional perovskite conductors.8,42,271
Proton transport in perovskites and other oxides having extended octahedral networks usually occurs via rotation and hopping of protons along intra-polyhedral pathways. Intra-polyhedral hopping is instead unfavoured in systems containing tetrahedral units, where inter-tetrahedral migration is the common diffusion route. Notably, flexible isolated tetrahedral and variable coordination moieties with high dynamic and rotational mobility enable proton transport. An important aspect that emerges is that the mechanisms of proton transport strongly depend on the coordination environments and the particular topology of the crystal structure. This is in analogy with oxide ion conducting materials,169,268,272–274 and encourages the exploration of structure types with disordered sub-lattices and/or able to support variable coordination environments. Structure-type oxides with extended tetrahedral networks could also constitute an interesting avenue of research.
Recent reports demonstrating significant proton conductivity in semiconducting oxides,275 Li-intercalation materials276,277 and high entropy oxides278 further expand the explorable chemical and structural space and inspire innovative strategies for the design of novel proton conducting systems. Highly hydrated metastable oxide phases potentially showing high proton conductivity could also be stabilised via high temperature synthesis under humidified atmospheres or with low temperature fabrication processes.279 As in the case of Li-ion and oxide ion conducting materials,280,281 computational screening methods could be implemented for selecting candidate solid oxide proton conductors and guide the experimental discovery process.282 The latter should go hand in hand with a thorough determination of the crystal structure characteristics enabling the desired proton transport properties. Neutron and X-ray diffraction techniques will still have a central role in the characterisation of the average crystal structures and identification of the proton sites, essential pieces of information in order to understand the properties of proton conducting oxides.283–285 Analysis of the local structural details with total scattering (pair distribution function, PDF) methods,286 X-ray absorption spectroscopy287 and solid-state NMR121,176 will be important for the investigation of increasingly complex systems or disordered oxides and to characterise the effects of local order/disorder on the functional properties. The employment of neutron spectroscopy techniques such as inelastic and quasi elastic neutron scattering (INS and QENS), which make use of the contrast given by the large incoherent neutron scattering cross section of the hydrogen atom, will allow to complement the structural studies with the characterisation of the proton dynamics and the diffusional phenomena.284,288 Further opportunities will arise with the development of advanced sample environments enabling in situ studies of materials under operating conditions and with multiple probes. In addition, it is clear how computational techniques and atomistic modelling methods will be complementary to the experimental approach for the comprehensive characterisation of the mechanisms and energetics of protonation and conduction.
Discovery of the next-generation solid oxide proton conductors crucially depends on exploring novel materials and structure types, and on the fundamental understanding of the structure and mechanistic relationships. The latter is of paramount importance for the development of solid proton conducting materials equating or having superior performances to perovskite-based oxides.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Leverhulme Trust (RPG-2017-351) is gratefully acknowledged.References
- I. Staffell, D. Scamman, A. Velazquez Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491 RSC
.
- S. van Renssen, Nat. Clim. Change, 2020, 10, 799–801 CrossRef
.
- B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352 CrossRef CAS
.
- A. J. Jacobson, Chem. Mater., 2010, 22, 660–674 CrossRef CAS
.
- E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935–939 CrossRef CAS PubMed
.
- M. A. Laguna-Bercero, J. Power Sources, 2012, 203, 4–16 CrossRef CAS
.
- J. B. Hansen, Faraday Discuss., 2015, 182, 9–48 RSC
.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS
.
- E. C. C. De Souza and R. Muccillo, Mater. Res., 2010, 13, 385–394 CrossRef
.
- H. Iwahara, T. Esaka, H. Uchida and N. Maeda, Solid State Ionics, 1981, 3–4, 359–363 CrossRef CAS
.
- H. Iwahara, H. Uchida and N. Maeda, J. Power Sources, 1982, 7, 293–301 CrossRef CAS
.
- H. Iwahara, H. Uchida and S. Tanaka, Solid State Ionics, 1983, 9–10, 1021–1025 CrossRef CAS
.
- H. Iwahara, T. Yajima and H. Ushida, Solid State Ionics, 1994, 70–71, 267–271 CrossRef CAS
.
- H. Iwahara, T. Yajima, T. Hibino, K. Ozaki and H. Suzuki, Solid State Ionics, 1993, 61, 65–69 CrossRef CAS
.
- H. Iwahara, Solid State Ionics, 1996, 86–88, 9–15 CrossRef CAS
.
- E. Fabbri, D. Pergolesi and E. Traversa, Chem. Soc. Rev., 2010, 39, 4355–4369 RSC
.
- L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387 RSC
.
- E. Fabbri, L. Bi, D. Pergolesi and E. Traversa, Adv. Mater., 2012, 24, 195–208 CrossRef CAS
.
- L. Bi, S. Boulfrad and E. Traversa, Chem. Soc. Rev., 2014, 43, 8255–8270 RSC
.
- N. Kochetova, I. Animitsa, D. Medvedev, A. Demin and P. Tsiakaras, RSC Adv., 2016, 6, 73222–73268 RSC
.
- N. L. R. M. Rashid, A. A. Samat, A. A. Jais, M. R. Somalu, A. Muchtar, N. A. Baharuddin and W. N. R. Wan Isahak, Ceram. Int., 2019, 45, 6605–6615 CrossRef CAS
.
- C. Duan, J. Huang, N. Sullivan and R. O'Hayre, Appl. Phys. Rev., 2020, 7, 011314 CAS
.
- L. Malavasi, C. Ritter and G. Chiodelli, Chem. Mater., 2008, 20, 2343–2351 CrossRef CAS
.
- A. K. Eriksson Andersson, S. M. Selbach, T. Grande and C. S. Knee, Dalton Trans., 2015, 44, 10834–10846 RSC
.
- G. C. Mather, G. Heras-Juaristi, C. Ritter, R. O. Fuentes, A. L. Chinelatto, D. Pérez-Coll and U. Amador, Chem. Mater., 2016, 28, 4292–4299 CrossRef CAS
.
- J. F. Basbus, M. D. Arce, F. R. Napolitano, H. E. Troiani, J. A. Alonso, M. E. Saleta, M. A. González, G. J. Cuello, M. T. Fernández-Díaz, M. P. Sainz, N. Bonanos, C. E. Jimenez, L. Giebeler, S. J. A. Figueroa, A. Caneiro, A. C. Serquis and L. V. Mogni, ACS Appl. Energy Mater., 2020, 3, 2881–2892 CrossRef CAS
.
- T. Norby, M. Widerøe, R. Glöckner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC
.
- H. Iwahara, T. Yajima and H. Ushida, Solid State Ionics, 1994, 70–71, 267–271 CrossRef CAS
.
- H. Matsumoto, Y. Kawasaki, N. Ito, M. Enoki and T. Ishihara, Electrochem. Solid-State Lett., 2007, 10, B77–B80 CrossRef CAS
.
- S. Imashuku, T. Uda, Y. Nose, G. Taniguchi, Y. Ito and Y. Awakura, J. Electrochem. Soc., 2009, 156, B1–B8 CrossRef CAS
.
- D. Han, K. Shinoda, S. Sato, M. Majima and T. Uda, J. Mater. Chem. A, 2015, 3, 1243–1250 RSC
.
- E. Gilardi, E. Fabbri, L. Bi, J. L. M. Rupp, T. Lippert, D. Pergolesi and E. Traversa, J. Phys. Chem. C, 2017, 121, 9739–9747 CrossRef CAS
.
- L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu, Z. Cheng and M. Liu, Science, 2009, 326, 126–129 CrossRef CAS PubMed
.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210 CrossRef CAS
.
- K. S. Knight, Solid State Ionics, 2000, 127, 43–48 CrossRef CAS
.
- I. Ahmed, C. S. Knee, M. Karlsson, S. -. Eriksson, P. F. Henry, A. Matic, D. Engberg and L. Börjesson, J. Alloys Compd., 2008, 450, 103–110 CrossRef CAS
.
- L. Mazzei, A. Perrichon, A. Mancini, G. Wahnström, L. Malavasi, S. F. Parker, L. Börjesson and M. Karlsson, J. Mater. Chem. A, 2019, 7, 7360–7372 RSC
.
- K. D. Kreuer, T. Dippel, Y. M. Baikov and J. Maier, Solid State Ionics, 1996, 86–88, 613–620 CrossRef CAS
.
- W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1996, 86–88, 647–652 CrossRef
.
- W. Münch, G. Seifert, K. D. Kreuer and J. Maier, Solid State Ionics, 1997, 97, 39–44 CrossRef
.
- W. Münch, K. D. Kreuer, G. Seifert and J. Maier, Solid State Ionics, 2000, 136–137, 183–189 CrossRef
.
- J. A. Dawson, J. A. Miller and I. Tanaka, Chem. Mater., 2015, 27, 901–908 CrossRef CAS
.
- W. Suksamai and I. S. Metcalfe, Solid State Ionics, 2007, 178, 627–634 CrossRef CAS
.
- T. Schober and H. G. Bohn, Solid State Ionics, 2000, 127, 351–360 CrossRef CAS
.
- K. Nomura and H. Kageyama, Solid State Ionics, 2007, 178, 661–665 CrossRef CAS
.
- M. Oishi, S. Akoshima, K. Yashiro, K. Sato, J. Mizusaki and T. Kawada, Solid State Ionics, 2008, 179, 2240–2247 CrossRef CAS
.
- D. Han, Y. Noda, T. Onishi, N. Hatada, M. Majima and T. Uda, Int. J. Hydrogen Energy, 2016, 41, 14897–14908 CrossRef CAS
.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS
.
- C. Duan, R. J. Kee, H. Zhu, C. Karakaya, Y. Chen, S. Ricote, A. Jarry, E. J. Crumlin, D. Hook, R. Braun, N. P. Sullivan and R. O'Hayre, Nature, 2018, 557, 217–222 CrossRef CAS
.
- H. An, H. Lee, B. Kim, J. Son, K. J. Yoon, H. Kim, D. Shin, H. Ji and J. Lee, Nat. Energy, 2018, 3, 870–875 CrossRef CAS
.
- C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O'Hayre, Nat. Energy, 2019, 4, 230–240 CrossRef CAS
.
- S. Choi, T. C. Davenport and S. M. Haile, Energy Environ. Sci., 2019, 12, 206–215 RSC
.
- E. Vøllestad, R. Strandbakke, M. Tarach, D. Catalán-Martínez, M. Fontaine, D. Beeaff, D. R. Clark, J. M. Serra and T. Norby, Nat. Mater., 2019, 18, 752–759 CrossRef
.
- G. Marnellos and M. Stoukides, Science, 1998, 282, 98–100 CrossRef CAS PubMed
.
- K. H. Ryu and S. M. Haile, Solid State Ionics, 1999, 125, 355–367 CrossRef CAS
.
- S. V. Bhide and A. V. Virkar, J. Electrochem. Soc., 1999, 146, 2038–2044 CrossRef CAS
.
- N. Zakowsky, S. Williamson and J. T. S. Irvine, Solid State Ionics, 2005, 176, 3019–3026 CrossRef CAS
.
- R. Sažinas, C. Bernuy-López, M. Einarsrud and T. Grande, J. Am. Ceram. Soc., 2016, 99, 3685–3695 CrossRef
.
- R. Sažinas, M. F. Sunding, A. Thøgersen, I. Sakaguchi, T. Norby, T. Grande and J. M. Polfus, J. Mater. Chem. A, 2019, 7, 3848–3856 RSC
.
- Y. Yamazaki, R. Hernandez-Sanchez and S. M. Haile, Chem. Mater., 2009, 21, 2755–2762 CrossRef CAS
.
- D. Pergolesi, E. Fabbri, A. D'Epifanio, E. Di Bartolomeo, A. Tebano, S. Sanna, S. Licoccia, G. Balestrino and E. Traversa, Nat. Mater., 2010, 9, 846–852 CrossRef CAS
.
- L. Katz and R. Ward, Inorg. Chem., 1964, 3, 205–211 CrossRef CAS
.
- J. Darriet and M. A. Subramanian, J. Mater. Chem., 1995, 5, 543–552 RSC
.
- L. S. Ramsdell, Am. Mineral., 1947, 32, 64–82 CAS
.
- S. Fop, J. M. S. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769 CrossRef CAS
.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55, 2127–2137 RSC
.
- A. Gilane, S. Fop, F. Sher, R. I. Smith and A. C. Mclaughlin, J. Mater. Chem. A, 2020, 8, 16506–16514 RSC
.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752–757 CrossRef CAS PubMed
.
- S. Fop, J. A. Dawson, A. D. Fortes, C. Ritter and A. C. McLaughlin, Chem. Mater., 2021, 33, 4651–4660 CrossRef CAS
.
- M. S. Islam, Solid State Ionics, 2002, 154–155, 75–85 CrossRef CAS
.
- N. Torino, P. F. Henry, C. S. Knee, T. S. Bjørheim, S. M. H. Rahman, E. Suard, C. Giacobbe and S. G. Eriksson, Dalton Trans., 2017, 46, 8387–8398 RSC
.
- T. Murakami, J. R. Hester and M. Yashima, J. Am. Chem. Soc., 2020, 142, 11653–11657 CrossRef CAS PubMed
.
- C. D. Ling, M. Avdeev, R. Kutteh, V. V. Kharton, A. A. Yaremchenko, S. Fialkova, N. Sharma, R. B. Macquart, M. Hoelzel and M. Gutmann, Chem. Mater., 2009, 21, 3853–3864 CrossRef CAS
.
- C. D. Ling, M. Avdeev, V. V. Kharton, A. A. Yaremchenko, R. B. Macquart and M. Hoelzel, Chem. Mater., 2010, 22, 532–540 CrossRef CAS
.
- M. T. Dunstan, A. F. Pavan, V. V. Kharton, M. Avdeev, J. A. Kimpton, V. A. Kolotygin, E. V. Tsipis and C. D. Ling, Solid State Ionics, 2013, 235, 1–7 CrossRef CAS
.
- M. T. Dunstan, W. Liu, A. F. Pavan, J. A. Kimpton, C. D. Ling, S. A. Scott, J. S. Dennis and C. P. Grey, Chem. Mater., 2013, 25, 4881–4891 CrossRef CAS
.
- M. T. Dunstan, F. Blanc, M. Avdeev, G. J. McIntyre, C. P. Grey and C. D. Ling, Chem. Mater., 2013, 25, 3154–3161 CrossRef CAS
.
- J. Wind, R. A. Mole, D. Yu, M. Avdeev and C. D. Ling, Chem. Mater., 2018, 30, 4949–4958 CrossRef CAS
.
- C. Tabacaru, A. Aguadero, J. Sanz, A. L. Chinelatto, A. Thursfield, D. Pérez-Coll, I. S. Metcalfe, M. T. Fernandez-Díaz and G. C. Mather, Solid State Ionics, 2013, 253, 239–246 CrossRef CAS
.
- A. L. Chinelatto, K. Boulahya, D. Pérez-Coll, U. Amador, C. Tabacaru, S. Nicholls, M. Hoelzel, D. C. Sinclair and G. C. Mather, Dalton Trans., 2015, 44, 7643–7653 RSC
.
- L. F. K. Unti, E. C. Grzebielucka, A. S. Antonio Chinelatto, G. C. Mather and A. L. Chinelatto, Ceram. Int., 2019, 45, 5087–5092 CrossRef
.
- N. Tarasova, I. Animitsa, A. Galisheva and D. Korona, Materials, 2019, 12, 1668 CrossRef CAS
.
- N. Tarasova, I. Animitsa and A. Galisheva, J. Solid State Electrochem., 2020, 24, 1497–1508 CrossRef CAS
.
- N. Tarasova, I. Animitsa, A. Galisheva and V. Pryakhina, Solid State Sci., 2020, 101, 106121 CrossRef CAS
.
- N. Tarasova, A. Galisheva and I. Animitsa, Int. J. Hydrogen Energy, 2021, 46, 16868–16877 CrossRef CAS
.
- J. R. Tolchard and T. Grande, Solid State Ionics, 2007, 178, 593–599 CrossRef CAS
.
- C. Yang, X. Zhang, H. Zhao, Y. Shen, Z. Du and C. Zhang, Int. J. Hydrogen Energy, 2015, 40, 2800–2807 CrossRef CAS
.
- J. Lyagaeva, D. Medvedev, E. Pikalova, S. Plaksin, A. Brouzgou, A. Demin and P. Tsiakaras, Int. J. Hydrogen Energy, 2017, 42, 1715–1723 CrossRef CAS
.
- J. Dailly, S. Fourcade, A. Largeteau, F. Mauvy, J. C. Grenier and M. Marrony, Electrochim. Acta, 2010, 55, 5847–5853 CrossRef CAS
.
- A. Grimaud, F. Mauvy, J. Marc Bassat, S. Fourcade, M. Marrony and J. Claude Grenier, J. Mater. Chem., 2012, 22, 16017–16025 RSC
.
- Z. Chen, J. Wang, D. Huan, S. Sun, G. Wang, Z. Fu, W. Zhang, X. Zheng, H. Pan, R. Peng and Y. Lu, J. Power Sources, 2017, 371, 41–47 CrossRef CAS
.
- L. Miao, J. Hou, Z. Gong, Z. Jin and W. Liu, Int. J. Hydrogen Energy, 2019, 44, 7531–7537 CrossRef CAS
.
- W. Li, B. Guan, L. Ma, S. Hu, N. Zhang and X. Liu, J. Mater. Chem. A, 2018, 6, 18057–18066 RSC
.
- H. Tian, W. Li, L. Ma, T. Yang, B. Guan, W. Shi, T. L. Kalapos and X. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 49574–49585 CrossRef CAS
.
- Z. Wang, W. Yang, S. P. Shafi, L. Bi, Z. Wang, R. Peng, C. Xia, W. Liu and Y. Lu, J. Mater. Chem. A, 2015, 3, 8405–8412 RSC
.
- C. Gu, X. Wu, J. Cao, J. Hou, L. Miao, Y. Xia, C. Fu and W. Liu, Int. J. Hydrogen Energy, 2020, 45, 23422–23432 CrossRef CAS
.
- A. P. Tarutin, J. G. Lyagaeva, D. A. Medvedev, L. Bi and A. A. Yaremchenko, J. Mater. Chem. A, 2021, 9, 154–195 RSC
.
- A. P. Tarutin, J. G. Lyagaeva, A. S. Farlenkov, A. I. Vylkov and D. M. Medvedev, Ceram. Int., 2019, 45, 16105–16112 CrossRef CAS
.
- Q. Wang, J. Hou, Y. Fan, X. Xi, J. Li, Y. Lu, G. Huo, L. Shao, X. Fu and J. Luo, J. Mater. Chem. A, 2020, 8, 7704–7712 RSC
.
- M. Yashima, M. Enoki, T. Wakita, R. Ali, Y. Matsushita, F. Izumi and T. Ishihara, J. Am. Chem. Soc., 2008, 130, 2762–2763 CrossRef CAS PubMed
.
- L. Troncoso, M. D. Arce, M. T. Fernández-Díaz, L. V. Mogni and J. A. Alonso, New J. Chem., 2019, 43, 6087–6094 RSC
.
- L. Zhang, F. Yao, J. Meng, W. Zhang, H. Wang, X. Liu, J. Meng and H. Zhang, J. Mater. Chem. A, 2019, 7, 18558–18567 RSC
.
- M. Chen, Y. Xuan, F. Zhang, L. He, X. Wang, H. Pan, J. Ren and Z. Lin, Int. J. Hydrogen Energy, 2020, 45, 14964–14971 CrossRef CAS
.
- K. Fujii, Y. Esaki, K. Omoto, M. Yashima, A. Hoshikawa, T. Ishigaki and J. R. Hester, Chem. Mater., 2014, 26, 2488–2491 CrossRef CAS
.
- A. K. Cochrane, M. Telfer, C. A. L. Dixon, W. Zhang, P. S. Halasyamani, E. Bousquet and P. Lightfoot, Chem. Commun., 2016, 52, 10980–10983 RSC
.
- Y. Zhou, M. Shiraiwa, M. Nagao, K. Fujii, I. Tanaka, M. Yashima, L. Baque, J. F. Basbus, L. V. Mogni and S. J. Skinner, Chem. Mater., 2021, 33, 2139–2146 CrossRef CAS PubMed
.
- M. Shiraiwa, T. Kido, K. Fujii and M. Yashima, J. Mater. Chem. A, 2021, 9, 8607–8619 RSC
.
- W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Nat. Commun., 2020, 11, 1224 CrossRef CAS PubMed
.
- K. R. Kendall, C. Navas, J. K. Thomas and H. zur Loye, Chem. Mater., 1996, 8, 642–649 CrossRef CAS
.
- R. J. Goff, D. Keeble, P. A. Thomas, C. Ritter, F. D. Morrison and P. Lightfoot, Chem. Mater., 2009, 21, 1296–1302 CrossRef CAS
.
- V. Thangadurai and W. Weppner, Solid State Ionics, 2004, 174, 175–183 CrossRef CAS
.
- J. B. Goodenough, J. E. Ruiz-Diaz and Y. S. Zhen, Solid State Ionics, 1990, 44, 21–31 CrossRef CAS
.
- S. B. Adler, J. A. Reimer, J. Baltisberger and U. Werner, J. Am. Chem. Soc., 1994, 116, 675–681 CrossRef CAS
.
- G. B. Zhang and D. M. Smyth, Solid State Ionics, 1995, 82, 153–160 CrossRef CAS
.
- J. Jankovic, D. P. Wilkinson and R. Hui, J. Electrochem. Soc., 2011, 158, B61–B68 CrossRef CAS
.
- T. Schober, J. Friedrich and F. Krug, Solid State Ionics, 1997, 99, 9–13 CrossRef CAS
.
- T. Schober and J. Friedrich, Solid State Ionics, 1998, 113–115, 369–375 CrossRef CAS
.
- V. Jayaraman, A. Magrez, M. Caldes, O. Joubert, F. Taulelle, J. Rodriguez-Carvajal, Y. Piffard and L. Brohan, Solid State Ionics, 2004, 170, 25–32 CrossRef CAS
.
- W. Fischer, G. Reck and T. Schober, Solid State Ionics, 1999, 116, 211–215 CrossRef
.
- J. Martinez, C. E. Mohn, S. Stølen and N. L. Allan, J. Solid State Chem., 2007, 180, 3388–3392 CrossRef CAS
.
- R. Dervişoğlu, D. S. Middlemiss, F. Blanc, Y. Lee, D. Morgan and C. P. Grey, Chem. Mater., 2015, 27, 3861–3873 CrossRef PubMed
.
- J. Bielecki, S. F. Parker, L. Mazzei, L. Börjesson and M. Karlsson, J. Mater. Chem. A, 2016, 4, 1224–1232 RSC
.
- J. Bielecki, S. F. Parker, D. Ekanayake, S. M. H. Rahman, L. Börjesson and M. Karlsson, J. Mater. Chem. A, 2014, 2, 16915–16924 RSC
.
- A. Fluri, E. Gilardi, M. Karlsson, V. Roddatis, M. Bettinelli, I. E. Castelli, T. Lippert and D. Pergolesi, J. Phys. Chem. C, 2017, 121, 21797–21805 CrossRef CAS
.
- E. Quarez, S. Noirault, M. T. Caldes and O. Joubert, J. Power Sources, 2010, 195, 1136–1141 CrossRef CAS
.
- J. F. Shin, A. Orera, D. C. Apperley and P. R. Slater, J. Mater. Chem., 2011, 21, 874–879 RSC
.
- J. F. Shin, D. C. Apperley and P. R. Slater, Chem. Mater., 2010, 22, 5945–5948 CrossRef CAS
.
- X. Li and M. Ihara, J. Electrochem. Soc., 2015, 162, F927–F938 CrossRef CAS
.
- C. Didier, J. Claridge and M. Rosseinsky, J. Solid State Chem., 2014, 218, 38–43 CrossRef CAS
.
- C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Chem. Mater., 2020, 32, 4347–4357 CrossRef CAS
.
- N. Lu, P. Zhang, Q. Zhang, R. Qiao, Q. He, H. Li, Y. Wang, J. Guo, D. Zhang, Z. Duan, Z. Li, M. Wang, S. Yang, M. Yan, E. Arenholz, S. Zhou, W. Yang, L. Gu, C. Nan, J. Wu, Y. Tokura and P. Yu, Nature, 2017, 546, 124–128 CrossRef CAS
.
- N. Lu, Y. Wang, S. Qiao, H.-B. Li, Q. He, Z. Li, M. Wang, J. Zhang, S. C. Tsang, J. Guo, S. Yang, J. Zhang, K. Deng, D. Zhang, J. Ma, Y. Wu, J. Zhu, Y. Tokura, C.-W. Nan, J. Wu and P. Yu, e-print arXiv:1811.10802, 2018.
- M. S. Islam, A. M. Nolan, S. Wang, Q. Bai and Y. Mo, Chem. Mater., 2020, 32, 5028–5035 CrossRef CAS
.
- B. Scherrer, M. V. F. Schlupp, D. Stender, J. Martynczuk, J. G. Grolig, H. Ma, P. Kocher, T. Lippert, M. Prestat and L. J. Gauckler, Adv. Funct. Mater., 2013, 23, 1957–1964 CrossRef CAS
.
- W. Paulus, H. Schober, S. Eibl, M. Johnson, T. Berthier, O. Hernandez, M. Ceretti, M. Plazanet, K. Conder and C. Lamberti, J. Am. Chem. Soc., 2008, 130, 16080–16085 CrossRef CAS PubMed
.
- A. Nemudry, M. Weiss, I. Gainutdinov, V. Boldyrev and R. Schöllhorn, Chem. Mater., 1998, 10, 2403–2411 CrossRef CAS
.
- T. Motohashi, Y. Hirano, Y. Masubuchi, K. Oshima, T. Setoyama and S. Kikkawa, Chem. Mater., 2013, 25, 372–377 CrossRef CAS
.
- R. Haugsrud and T. Norby, Nat. Mater., 2006, 5, 193–196 CrossRef CAS
.
- R. Haugsrud and T. Norby, Solid State Ionics, 2006, 177, 1129–1135 CrossRef CAS
.
- R. Haugsrud and T. Norby, J. Am. Ceram. Soc., 2007, 90, 1116–1121 CrossRef CAS
.
- C. Ferrara, A. Mancini, C. Ritter, L. Malavasi and C. Tealdi, J. Mater. Chem. A, 2015, 3, 22258–22265 RSC
.
- M. Huse, A. W. B. Skilbred, M. Karlsson, S. G. Eriksson, T. Norby, R. Haugsrud and C. S. Knee, J. Solid State Chem., 2012, 187, 27–34 CrossRef CAS
.
- L. Jian and C. M. Wayman, J. Am. Ceram. Soc., 1997, 80, 803–806 CrossRef CAS
.
- S. W. Arulnesan, P. Kayser, J. A. Kimpton and B. J. Kennedy, J. Solid State Chem., 2019, 277, 229–239 CrossRef CAS
.
- J. E. Auckett, L. Lopez-Odriozola, S. J. Clark and I. R. Evans, J. Mater. Chem. A, 2021, 9, 4091–4102 RSC
.
- T. Mokkelbost, H. L. Lein, P. E. Vullum, R. Holmestad, T. Grande and M. Einarsrud, Ceram. Int., 2009, 35, 2877–2883 CrossRef CAS
.
- A. D. Brandão, I. Antunes, J. R. Frade, J. Torre, V. V. Kharton and D. P. Fagg, Chem. Mater., 2010, 22, 6673–6683 CrossRef
.
- S. Wachowski, A. Mielewczyk-Gryń, K. Zagórski, C. Li, P. Jasiński, S. J. Skinner, R. Haugsrud and M. Gazda, J. Mater. Chem. A, 2016, 4, 11696–11707 RSC
.
- S. Wachowski, B. Kamecki, P. Winiarz, K. Dzierzgowski, A. Mielewczyk-Gryń and M. Gazda, Inorg. Chem. Front., 2018, 5, 2157–2166 RSC
.
- A. Mielewczyk-Gryń, S. Wachowski, A. Witkowska, K. Dzierzgowski, W. Skubida, K. Świerczek, A. Regoutz, D. J. Payne, S. Hull, H. Zhang, I. Abrahams and M. Gazda, J. Am. Ceram. Soc., 2020, 103, 6575–6585 CrossRef
.
- A. Kuwabara, R. Haugsrud, S. Stølen and T. Norby, Phys. Chem. Chem. Phys., 2009, 11, 5550–5553 RSC
.
- G. C. Mather, C. A. J. Fisher and M. S. Islam, Chem. Mater., 2010, 22, 5912–5917 CrossRef CAS
.
- N. Kitamura, K. Amezawa, Y. Tomii, N. Yamamoto and T. Hanada, Solid State Ionics, 2004, 175, 563–567 CrossRef CAS
.
- H. Fjeld, K. Toyoura, R. Haugsrud and T. Norby, Phys. Chem. Chem. Phys., 2010, 12, 10313–10319 RSC
.
- A. Magrasó, M. Fontaine, R. Bredesen, R. Haugsrud and T. Norby, Solid State Ionics, 2014, 262, 382–387 CrossRef
.
- J. R. Tolchard, H. L. Lein and T. Grande, J. Eur. Ceram. Soc., 2009, 29, 2823–2830 CrossRef CAS
.
- T. Norby and A. Magrasó, J. Power Sources, 2015, 282, 28–33 CrossRef CAS
.
- L. Bi, E. Fabbri and E. Traversa, Electrochim. Acta, 2018, 260, 748–754 CrossRef CAS
.
- M. Huse, T. Norby and R. Haugsrud, J. Electrochem. Soc., 2011, 158, B857 CrossRef CAS
.
- T. S. Bjørheim, T. Norby and R. Haugsrud, J. Mater. Chem., 2012, 22, 1652–1661 RSC
.
- P. Winiarz, K. Dzierzgowski, A. Mielewczyk-Gryń, M. Gazda and S. Wachowski, Chem.–Eur. J., 2021, 27, 5393–5398 CrossRef CAS
.
- N. Clavier, R. Podor and N. Dacheux, J. Eur. Ceram. Soc., 2011, 31, 941–976 CrossRef CAS
.
- K. Toyoura and K. Matsunaga, J. Phys. Chem. C, 2013, 117, 18006–18012 CrossRef CAS
.
- J. Wang, L. Zhou, Y. Wang, J. Xu, X. Yang and X. Kuang, J. Solid State Chem., 2018, 268, 16–21 CrossRef CAS
.
- X. Yang, A. J. Fernández-Carrión, J. Wang, F. Porcher, F. Fayon, M. Allix and X. Kuang, Nat. Commun., 2018, 9, 4484 CrossRef
.
- J. Li, F. Pan, S. Geng, C. Lin, L. Palatinus, M. Allix, X. Kuang, J. Lin and J. Sun, Nat. Commun., 2020, 11, 4751 CrossRef CAS PubMed
.
- S. Li, F. Schönberger and P. Slater, Chem. Commun., 2003, 2694–2695 RSC
.
- F. Schönberger, E. Kendrick, M. S. Islam and P. R. Slater, Solid State Ionics, 2005, 176, 2951–2953 CrossRef
.
- E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871–875 CrossRef CAS PubMed
.
- M. Coduri, S. Casolo, N. Jalarvo and M. Scavini, J. Appl. Crystallogr., 2019, 52, 712–721 CrossRef CAS
.
- E. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, J. Mater. Chem., 2010, 20, 10412–10416 RSC
.
- N. Jalarvo, O. Gourdon, Z. Bi, D. Gout, M. Ohl and M. P. Paranthaman, Chem. Mater., 2013, 25, 2741–2748 CrossRef CAS
.
- F. Giannici, D. Messana, A. Longo and A. Martorana, J. Phys. Chem. C, 2011, 115, 298–304 CrossRef CAS
.
- E. Kendrick, J. Kendrick, A. Orera, P. Panchmatia, M. S. Islam and P. R. Slater, Fuel Cells, 2011, 11, 38–43 CrossRef CAS
.
- Y. Cheng, J. Balachandran, Z. Bi, C. A. Bridges, M. P. Paranthaman, L. L. Daemen, P. Ganesh and N. Jalarvo, J. Mater. Chem. A, 2017, 5, 15507–15511 RSC
.
- G. Kim, J. M. Griffin, F. Blanc, S. M. Haile and C. P. Grey, J. Am. Chem. Soc., 2015, 137, 3867–3876 CrossRef CAS
.
- K. Toyoura, N. Hatada, Y. Nose, I. Tanaka, K. Matsunaga and T. Uda, J. Phys. Chem. C, 2012, 116, 19117–19124 CrossRef CAS
.
- T. S. Bjørheim, R. Haugsrud and T. Norby, Solid State Ionics, 2014, 264, 76–84 CrossRef
.
- T. S. Bjørheim and R. Haugsrud, Solid State Ionics, 2015, 275, 29–34 CrossRef
.
- T. S. Bjørheim, V. Shanmugappirabu, R. Haugsrud and T. E. Norby, Solid State Ionics, 2015, 278, 275–280 CrossRef
.
-
B. V. Mill and Y. V. Pisarevsky, Langasite-type materials: from discovery to present state, Proceedings of the 2000 IEEE/EIA International Frequency Control Symposium and Exhibition (Cat. No. 00CH37052), 2000 Search PubMed
.
- A. Iakovleva, A. Chesnaud, I. Animitsa and G. Dezanneau, Int. J. Hydrogen Energy, 2016, 41, 14941–14951 CrossRef CAS
.
- M. C. Martín-Sedeño, D. Marrero-López, E. R. Losilla, L. León-Reina, S. Bruque, P. Núñez and M. A. G. Aranda, Chem. Mater., 2005, 17, 5989–5998 CrossRef
.
- D. Waroquiers, X. Gonze, G. Rignanese, C. Welker-Nieuwoudt, F. Rosowski, M. Göbel, S. Schenk, P. Degelmann, R. André, R. Glaum and G. Hautier, Chem. Mater., 2017, 29, 8346–8360 CrossRef CAS
.
- P. Jiang, W. Gao, R. Cong and T. Yang, Dalton Trans., 2015, 44, 6069–6074 RSC
.
- F. Jiang, P. Jiang, M. Yue, W. Gao, R. Cong and T. Yang, J. Solid State Chem., 2017, 254, 195–199 CrossRef CAS
.
- J. Yang, P. Jiang, M. Yue, D. Yang, R. Cong, W. Gao and T. Yang, J. Catal., 2017, 345, 236–244 CrossRef CAS
.
- P. Jiang, F. Jiang, M. Yue, J. Ju, C. Xu, R. Cong and T. Yang, Angew. Chem., Int. Ed., 2019, 58, 5978–5982 CrossRef CAS
.
- E. Kendrick, M. S. Islam and P. R. Slater, J. Mater. Chem., 2007, 17, 3104–3111 RSC
.
- P. M. Panchmatia, O. Alodia, G. J. Rees, M. E. Smith, J. V. Hanna, P. R. Slater and I. M. Saiful, Angew. Chem., Int. Ed., 2011, 50, 9328–9333 CrossRef CAS PubMed
.
- A. Orera and P. R. Slater, Solid State Ionics, 2010, 181, 110–114 CrossRef CAS
.
- A. Pons, E. Béchade, J. Jouin, M. Colas, P. Geffroy, O. Masson, P. Thomas, I. Kagomiya, T. Asaka, K. Fukuda, A. Slodczyk and P. Colomban, J. Eur. Ceram. Soc., 2017, 37, 2149–2158 CrossRef CAS
.
- B. J. Corrie, J. F. Shin, S. Hull, K. S. Knight, M. C. Vlachou, J. V. Hanna and P. R. Slater, Dalton Trans., 2016, 45, 121–133 RSC
.
- L. Malavasi, A. Orera, P. R. Slater, P. M. Panchmatia, M. S. Islam and J. Siewenie, Chem. Commun., 2011, 47, 250–252 RSC
.
- P. M. Panchmatia, A. Orera, E. Kendrick, J. V. Hanna, M. E. Smith, P. R. Slater and M. S. Islam, J. Mater. Chem., 2010, 20, 2766–2772 RSC
.
- L. León-Reina, J. M. Porras-Vázquez, E. R. Losilla and M. A. G. Aranda, J. Solid State Chem., 2007, 180, 1250–1258 CrossRef
.
- K. Yamashita, H. Owada, T. Umegaki, T. Kanazawa and K. Katayama, Solid State Ionics, 1990, 40–41, 918–921 CrossRef CAS
.
- X. Wei and M. Z. Yates, Chem. Mater., 2012, 24, 1738–1743 CrossRef CAS
.
- Y. Aoki, K. Kikutani, E. Tsuji and H. Habazaki, ECS Electrochem. Lett., 2014, 3, F61–F64 CrossRef CAS
.
- T. Shimura, M. Komori and H. Iwahara, Solid State Ionics, 1996, 86–88, 685–689 CrossRef CAS
.
- T. Omata, K. Okuda, S. Tsugimoto and S. Otsuka-Matsuo-Yao, Solid State Ionics, 1997, 104, 249–258 CrossRef CAS
.
- K. E. J. Eurenius, E. Ahlberg, I. Ahmed, S. G. Eriksson and C. S. Knee, Solid State Ionics, 2010, 181, 148–153 CrossRef CAS
.
- K. E. J. Eurenius, E. Ahlberg and C. S. Knee, Solid State Ionics, 2010, 181, 1577–1585 CrossRef CAS
.
- K. E. J. Eurenius, E. Ahlberg and C. S. Knee, Dalton Trans., 2011, 40, 3946–3954 RSC
.
- V. Besikiotis, C. S. Knee, I. Ahmed, R. Haugsrud and T. Norby, Solid State Ionics, 2012, 228, 1–7 CrossRef CAS
.
- W. Sun, S. Fang, L. Yan and W. Liu, Fuel Cells, 2012, 12, 457–463 CrossRef CAS
.
- L. Kalland, A. Løken, T. S. Bjørheim, R. Haugsrud and T. Norby, Solid State Ionics, 2020, 354, 115401 CrossRef CAS
.
- Z. Zhong, Y. Jiang, Z. Lian, X. Song and K. Peng, Ceram. Int., 2020, 46, 12675–12685 CrossRef CAS
.
- M. A. Subramanian, G. Aravamudan and G. V. Subba Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef CAS
.
- V. Besikiotis, S. Ricote, M. H. Jensen, T. Norby and R. Haugsrud, Solid State Ionics, 2012, 229, 26–32 CrossRef CAS
.
- P. E. R. Blanchard, R. Clements, B. J. Kennedy, C. D. Ling, E. Reynolds, M. Avdeev, A. P. J. Stampfl, Z. Zhang and L. Jang, Inorg. Chem., 2012, 51, 13237–13244 CrossRef CAS PubMed
.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873–1878 CrossRef CAS
.
- L. Kalland and C. E. Mohn, Phys. Chem. Chem. Phys., 2020, 22, 13930–13941 RSC
.
- L. Kalland, S. T. Norberg, J. Kyrklund, S. Hull, S. G. Eriksson, T. Norby, C. E. Mohn and C. S. Knee, Phys. Chem. Chem. Phys., 2016, 18, 24070–24080 RSC
.
- T. S. Bjørheim, V. Besikiotis and R. Haugsrud, Dalton Trans., 2012, 41, 13343–13351 RSC
.
- T. Omata and S. Otsuka-Matsuo-Yao, J. Electrochem. Soc., 2001, 148, E252–E261 CrossRef CAS
.
- Q. A. Islam, S. Nag and R. N. Basu, Mater. Res. Bull., 2013, 48, 3103–3107 CrossRef CAS
.
- E. P. Antonova, M. V. Ananyev, A. S. Farlenkov, E. S. Tropin, A. V. Khodimchuk and N. M. Porotnikova, Russ. J. Electrochem., 2017, 53, 651–657 CrossRef CAS
.
- E. P. Antonova, A. S. Farlenkov, E. S. Tropin, V. A. Eremin, A. V. Khodimchuk and M. V. Ananyev, Solid State Ionics, 2017, 306, 112–117 CrossRef CAS
.
- J. Zamudio-García, L. d. Santos-Gómez, J. M. Porras-Vázquez, E. R. Losilla and D. Marrero-López, J. Alloys Compd., 2020, 816, 152600 CrossRef
.
- Z. Tao, L. Bi, S. Fang and W. Liu, J. Power Sources, 2011, 196, 5840–5843 CrossRef CAS
.
- J. Wang, Y. Xie, Z. Zhang, R. Liu and Z. Li, Mater. Res. Bull., 2005, 40, 1294–1302 CrossRef CAS
.
- L. Yan, W. Sun, L. Bi, S. Fang, Z. Tao and W. Liu, Int. J. Hydrogen Energy, 2010, 35, 4508–4511 CrossRef CAS
.
- B. Zhang, K. Wu and K. Peng, J. Power Sources, 2018, 399, 157–165 CrossRef CAS
.
- B. Zhang, Z. Zhong, T. Tu, K. Wu and K. Peng, J. Power Sources, 2019, 412, 631–639 CrossRef CAS
.
- M. Zhang, D. Wang, L. Miao, Z. Jin, K. Dong and W. Liu, Electrochem. Commun., 2021, 126, 107026 CrossRef CAS
.
- M. E. Björketun, C. S. Knee, B. J. Nyman and G. Wahnström, Solid State Ionics, 2008, 178, 1642–1647 CrossRef
.
- K. Toyoura, A. Nakamura and K. Matsunaga, J. Phys. Chem. C, 2015, 119, 8480–8487 CrossRef CAS
.
- M. A. Gomez, M. A. Griffin, S. Jindal, K. D. Rule and V. R. Cooper, J. Chem. Phys., 2005, 123, 094703 CrossRef
.
- T. Shimura, Y. Tokiwa and H. Iwahara, Solid State Ionics, 2002, 154–155, 653–658 CrossRef CAS
.
- R. Haugsrud and T. Risberg, J. Electrochem. Soc., 2009, 156, B425 CrossRef CAS
.
- N. Preux, A. Rolle, C. Merlin, M. Benamira, M. Malys, C. Estournes, A. Rubbens and R. Vannier, C. R. Chim., 2010, 13, 1351–1358 CrossRef CAS
.
- A. Chesnaud, M. -. Braida, S. Estradé, F. Peiró, A. Tarancón, A. Morata and G. Dezanneau, J. Eur. Ceram. Soc., 2015, 35, 3051–3061 CrossRef CAS
.
- A. V. Shlyakhtina, K. S. Pigalskiy, D. A. Belov, N. V. Lyskov, E. P. Kharitonova, I. V. Kolbanev, A. B. Borunova, O. K. Karyagina, E. M. Sadovskaya, V. A. Sadykov and N. F. Eremeev, Dalton Trans., 2018, 47, 2376–2392 RSC
.
- T. Subramani and A. Navrotsky, Inorg. Chem., 2019, 58, 16126–16133 CrossRef CAS
.
- L. Cai and J. C. Nino, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 269–290 CrossRef CAS
.
- H. J. Rossell, J. Solid State Chem., 1979, 27, 115–122 CrossRef CAS
.
- A. Kahn-Harari, L. Mazerolles, D. Michel and F. Robert, J. Solid State Chem., 1995, 116, 103–106 CrossRef CAS
.
- L. López-Conesa, J. M. Rebled, M. H. Chambrier, K. Boulahya, J. M. González-Calbet, M. D. Braida, G. Dezanneau, S. Estradé and F. Peiró, Fuel Cells, 2013, 13, 29–33 CrossRef
.
- K. Kato, K. Toyoura, A. Nakamura and K. Matsunaga, Solid State Ionics, 2014, 262, 472–475 CrossRef CAS
.
- K. Kato, K. Toyoura, A. Nakamura and K. Matsunaga, J. Phys. Chem. C, 2014, 118, 9377–9384 CrossRef CAS
.
- R. Haugsrud, Solid State Ionics, 2007, 178, 555–560 CrossRef CAS
.
- T. Shimura, S. Fujimoto and H. Iwahara, Solid State Ionics, 2001, 143, 117–123 CrossRef CAS
.
- A. Magrasó, J. Power Sources, 2013, 240, 583–588 CrossRef
.
- R. Hancke, A. Magrasó, T. Norby and R. Haugsrud, Solid State Ionics, 2013, 231, 25–29 CrossRef CAS
.
- G. S. Partin, D. V. Korona, A. Y. Neiman and K. G. Belova, Russ. J. Electrochem., 2015, 51, 381–390 CrossRef CAS
.
- Y. Cao, N. Duan, L. Jian, A. Evans and R. Haugsrud, J. Am. Ceram. Soc., 2016, 99, 3309–3316 CrossRef CAS
.
- M. Zayas-Rey, L. dos Santos-Gómez, D. Marrero-López, L. León-Reina, J. Canales-Vázquez, M. A. G. Aranda and E. R. Losilla, Chem. Mater., 2013, 25, 448–456 CrossRef CAS
.
- S. Escolástico, C. Solís and J. M. Serra, Int. J. Hydrogen Energy, 2011, 36, 11946–11954 CrossRef
.
- E. Quarez, K. V. Kravchyk and O. Joubert, Solid State Ionics, 2012, 216, 19–24 CrossRef CAS
.
- C. Solís, L. Navarrete, S. Roitsch and J. M. Serra, J. Mater. Chem., 2012, 22, 16051–16059 RSC
.
- C. Solís, V. B. Vert, M. Balaguer, S. Escolástico, S. Roitsch and J. M. Serra, ChemSusChem, 2012, 5, 2155–2158 CrossRef
.
- M. Balaguer, C. Solís, F. Bozza, N. Bonanos and J. M. Serra, J. Mater. Chem. A, 2013, 1, 3004–3007 RSC
.
- M. J. Zayas-Rey, L. dos Santos-Gómez, J. M. Porras-Vázquez, E. R. Losilla and D. Marrero-López, J. Power Sources, 2015, 294, 483–493 CrossRef CAS
.
- S. Escolástico, C. Solís, T. Scherb, G. Schumacher and J. M. Serra, J. Membr. Sci., 2013, 444, 276–284 CrossRef
.
- M. Amsif, A. Magrasó, D. Marrero-López, J. Ruiz-Morales, J. Canales-Vázquez and P. Núñez, Chem. Mater., 2012, 24, 3868–3877 CrossRef CAS
.
- S. Escolastico, J. Seeger, S. Roitsch, M. Ivanova, W. A. Meulenberg and J. M. Serra, ChemSusChem, 2013, 6, 1523–1532 CrossRef CAS
.
- S. Escolástico, C. Solís, C. Kjølseth and J. M. Serra, Energy Environ. Sci., 2014, 7, 3736–3746 RSC
.
- X. Qi and Y. S. Lin, Solid State Ionics, 2000, 130, 149–156 CrossRef CAS
.
- S. -. Song, E. D. Wachsman, J. Rhodes, S. E. Dorris and U. Balachandran, Solid State Ionics, 2004, 167, 99–105 CrossRef CAS
.
- A. Magrasó, J. M. Polfus, C. Frontera, J. Canales-Vázquez, L. Kalland, C. H. Hervoches, S. Erdal, R. Hancke, M. S. Islam, T. Norby and R. Haugsrud, J. Mater. Chem., 2012, 22, 1762–1764 RSC
.
- L. Kalland, A. Magrasó, A. Mancini, C. Tealdi and L. Malavasi, Chem. Mater., 2013, 25, 2378–2384 CrossRef CAS
.
- A. Magrasó, C. H. Hervoches, I. Ahmed, S. Hull, J. Nordström, A. W. B. Skilbred and R. Haugsrud, J. Mater. Chem. A, 2013, 1, 3774–3782 RSC
.
- T. Scherb, S. A. J. Kimber, C. Stephan, P. F. Henry, G. Schumacher, S. Escolástico, J. M. Serra, J. Seeger, J. Just, A. H. Hill and J. Banhart, J. Appl. Crystallogr., 2016, 49, 997–1008 CrossRef CAS
.
- A. Magrasó and C. Frontera, Dalton Trans., 2016, 45, 3791–3797 RSC
.
- R. Punn, A. M. Feteira, D. C. Sinclair and C. Greaves, J. Am. Chem. Soc., 2006, 128, 15386–15387 CrossRef CAS PubMed
.
- C. H. Hervoches and C. Greaves, J. Mater. Chem., 2010, 20, 6759–6763 RSC
.
- X. Kuang, J. L. Payne, M. R. Johnson and I. Radosavljevic Evans, Angew. Chem., Int. Ed., 2012, 51, 690–694 CrossRef CAS
.
- C. D. Ling, S. Schmid, P. E. R. Blanchard, V. Petříček, G. J. McIntyre, N. Sharma, A. Maljuk, A. A. Yaremchenko, V. V. Kharton, M. Gutmann and R. L. Withers, J. Am. Chem. Soc., 2013, 135, 6477–6484 CrossRef CAS PubMed
.
- A. Kruth and J. T. S. Irvine, Solid State Ionics, 2003, 162–163, 83–91 CrossRef CAS
.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647–651 CrossRef CAS PubMed
.
- X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498–504 CrossRef CAS
.
- X. Yang, A. J. Fernández-Carrión, J. Wang, F. Porcher, F. Fayon, M. Allix and X. Kuang, Nat. Commun., 2018, 9, 4484 CrossRef PubMed
.
- J. R. Peet, C. A. Fuller, B. Frick, M. Zbiri, A. Piovano, M. R. Johnson and I. R. Evans, Chem. Mater., 2017, 29, 3020–3028 CrossRef CAS
.
- Y. Zhou, X. Guan, H. Zhou, K. Ramadoss, S. Adam, H. Liu, S. Lee, J. Shi, M. Tsuchiya, D. D. Fong and S. Ramanathan, Nature, 2016, 534, 231–234 CrossRef CAS
.
- R. Lan and S. Tao, Adv. Energy Mater., 2014, 4, 1301683 CrossRef
.
- T. Wei, L. A. Zhang, Y. Chen, P. Yang and M. Liu, Chem. Mater., 2017, 29, 1490–1495 CrossRef CAS
.
- M. Gazda, T. Miruszewski, D. Jaworski, A. Mielewczyk-Gryń, W. Skubida, S. Wachowski, P. Winiarz, K. Dzierzgowski, M. Łapiński, I. Szpunar and E. Dzik, ACS Mater. Lett., 2020, 2, 1315–1321 CrossRef CAS
.
- R. B. Cervera, S. Miyoshi, Y. Oyama, Y. E. Elammari, T. Yagi and S. Yamaguchi, Chem.
Mater., 2013, 25, 1483–1489 CrossRef CAS
.
- L. Kahle, A. Marcolongo and N. Marzari, Energy Environ. Sci., 2020, 13, 928–948 RSC
.
- J. Lee, N. Ohba and R. Asahi, Chem. Mater., 2020, 32, 1358–1370 CrossRef CAS
.
- P. Wisesa, C. Li, C. Wang and T. Mueller, RSC Adv., 2019, 9, 31999–32009 RSC
.
- F. G. Kinyanjui, S. T. Norberg, I. Ahmed, S. G. Eriksson and S. Hull, Solid State Ionics, 2012, 225, 312–316 CrossRef CAS
.
- M. Karlsson, Dalton Trans., 2013, 42, 317–329 RSC
.
- P. Colomban, Fuel Cells, 2013, 13, 6–18 CrossRef CAS
.
- L. Malavasi, H. Kim and T. Proffen, J. Appl. Phys., 2009, 105, 123519 CrossRef
.
- K. Amezawa, Curr. Opin. Electrochem., 2020, 21, 250–256 CrossRef CAS
.
- M. Karlsson, Phys. Chem. Chem. Phys., 2015, 17, 26–38 RSC
.
| This journal is © The Royal Society of Chemistry 2021 |