Cation binding of Li(I), Na(I) and Zn(II) to cobalt and iron sulphide clusters – electronic structure study†
Ellie L.
Uzunova

Institute of General and Inorganic Chemistry, Bulgarian Academy of Sciences, Acad. G.Bonchev Str., block 11, Sofia 1113, Bulgaria. E-mail: ellie@svr.igic.bas.bg
First published on 15th August 2022
Abstract
The binding of alkaline (Li+ and Na+) and zinc (Zn2+) cations to mononuclear disulphides MS2 and to persulphides, containing an S–S bond, M(S2), to binuclear disulphides M2S2 and persulphides M2(S2) and to cubic tetranuclear sulphides M4S4 where M = Fe, Co, is examined by density functional theory with the B3LYP functional, and dispersion corrections were applied. For the small-sized clusters (up to two transition metal centres), the energy gaps between different configurations were verified by CCSD(T) calculations. Persulphides M(S2) are more stable than disulphides MS2 as bare clusters, upon carbonyl and chloride ligand coordination and upon cation binding (Li+, Na+, Zn2+). The one-electron reduction of alkali cations and two-electron reduction of Zn2+ reverses order of stability and the planar disulphides (MS2-reduced cation) become more stable; the energy gap disulphide to persulphide increases. In all reduced clusters, zinc ions form bonds with sulphur and with the transition metal centre (Co or Fe). Lithium cations also form bonds to cobalt or iron, but only in the M2S2 clusters, upon reduction. Energy barriers were calculated for the disulphide to persulphide reaction in the Zn–Co–S2 system in the isolated clusters (gas-phase), in water, acetonitrile and 1-Cl-hexane solution. Most significant decrease in the energy barriers were obtained with less-polar solvents, acetonitrile, and particularly, 1-Cl-hexane. In M4S4 clusters, the cations do not reach optimal coordination to the sulphur centres. The global minima of M2S2 clusters are antiferromagnetic; in the reduced Zn–M2S2 clusters, magnetic moment is induced at zinc centres as a result of charge transfer between Zn and Co or Zn and Fe.
1. Introduction
Transition metal sulphides have the ability to accept, efficiently redistribute and store electrons, which they can selectively transfer to a substrate. Their potential applications range from catalysts in redox reactions and photosynthesis to materials for electrodes.1–13 Disulphides of cobalt and iron were considered promising as anode materials in sodium-ion batteries.1 Zink-ion batteries are another alternative to the lithium-ion or sodium-ion batteries and they can operate in either aqueous or non-aqueous media.10–12 Cobalt disulphide outperforms iron disulphide as redox electrode for non-aqueous Zn batteries and an intercalation mechanism involving sulphide S2− to persulphide (SS)2− interconversion was proposed.10 Theoretical studies expand our knowledge for the unique properties of transition metal sulphides.14 Cubic [Fe4S4] or dimeric [Fe2S2] centres compose the active sites in various proteins (rubredoxin, ferredoxin, hydrogenase enzymes), where the active sites are coordinated by inorganic ligands, CN− and CO.15 Depending on their local protein and ligand coordination these clusters are able to catalyse redox reactions, including CO2 reduction, or to be applied for nitrogen fixation and photosynthesis.2,8,9 Iron sulphides are among the most widely studied as either solid state materials,16–18 or clusters.7–9,13,19–26 As far as clusters and molecular systems are considered, the sulphides are found to be structural analogues of oxides: the clusters with M/S ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (M = Fe, Zn) have nearly identical structure as the corresponding oxide clusters, the smaller clusters being planar and the larger ones forming hollow polyhedra, where all atoms become three-coordinated.13,14,22,23,27–30 At M/S ratio 1
1 (M = Fe, Zn) have nearly identical structure as the corresponding oxide clusters, the smaller clusters being planar and the larger ones forming hollow polyhedra, where all atoms become three-coordinated.13,14,22,23,27–30 At M/S ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (M = Mo, W) the disulphides can crystallize in two-dimensional (2D) structures, consisting of sandwich-type monolayers S–M–S with six-fold coordination of the central M atom within the monolayer.31 The monolayers are kept together by van der Waals forces. Other members of the chalcogen group (Se, Te) also form layered 2D structures: MSe2, MTe2, (M = Mo, W).32,33 These materials are thin semiconductors and they can be optimized for application as photodetectors, LED materials or photocatalysts. The chalcogens allow more flexible geometry in their compounds and higher coordination numbers than oxygen, due to their lower electronegativity and the presence of d-orbitals, which allow s–d and s–p–d hybridization. At the molecular level, the members of the chalcogen group, sulphur, selenium and tellurium form diatomic molecules with triplet ground state, similar to oxygen, and hydrides H2M (M = S, Se, Te). The bond strength decreases with increasing the element number.34 The importance of H2S and sulphides in the origin of life35,36 prompted reinvestigation of the H2S Auger spectra and the photoionization fragmentation paths resulting from double and triple ionization were elucidated.37–39 Experimental and theoretical studies on the diatomic molecular sulphides of the 3d elements MS (M = Sc–Cu) proved that they have identical electronic ground states as the corresponding oxides, and the M–S bond strength follows a similar trend to the M–O bond strength, except for CoS.40–43 The CoS molecule forms the strongest bond among all monosulphides of the 3d elements, which was attributed to possible 3d–4p orbital mixing, so as to form a stronger π-bonding orbital with sulphur.41,42 It can be expected that even in the lack of stabilizing ligands, bare cobalt sulphide clusters would be as stable as the iron sulphides and indeed, cobalt analogues of the iron–sulphur dimers, trimers and tetramers have been synthesized.44,45 Despite of the fact that cobalt sulphides proved active in electrochemistry and electrocatalysis,3–6,46 they remain much less studied.
2 (M = Mo, W) the disulphides can crystallize in two-dimensional (2D) structures, consisting of sandwich-type monolayers S–M–S with six-fold coordination of the central M atom within the monolayer.31 The monolayers are kept together by van der Waals forces. Other members of the chalcogen group (Se, Te) also form layered 2D structures: MSe2, MTe2, (M = Mo, W).32,33 These materials are thin semiconductors and they can be optimized for application as photodetectors, LED materials or photocatalysts. The chalcogens allow more flexible geometry in their compounds and higher coordination numbers than oxygen, due to their lower electronegativity and the presence of d-orbitals, which allow s–d and s–p–d hybridization. At the molecular level, the members of the chalcogen group, sulphur, selenium and tellurium form diatomic molecules with triplet ground state, similar to oxygen, and hydrides H2M (M = S, Se, Te). The bond strength decreases with increasing the element number.34 The importance of H2S and sulphides in the origin of life35,36 prompted reinvestigation of the H2S Auger spectra and the photoionization fragmentation paths resulting from double and triple ionization were elucidated.37–39 Experimental and theoretical studies on the diatomic molecular sulphides of the 3d elements MS (M = Sc–Cu) proved that they have identical electronic ground states as the corresponding oxides, and the M–S bond strength follows a similar trend to the M–O bond strength, except for CoS.40–43 The CoS molecule forms the strongest bond among all monosulphides of the 3d elements, which was attributed to possible 3d–4p orbital mixing, so as to form a stronger π-bonding orbital with sulphur.41,42 It can be expected that even in the lack of stabilizing ligands, bare cobalt sulphide clusters would be as stable as the iron sulphides and indeed, cobalt analogues of the iron–sulphur dimers, trimers and tetramers have been synthesized.44,45 Despite of the fact that cobalt sulphides proved active in electrochemistry and electrocatalysis,3–6,46 they remain much less studied.
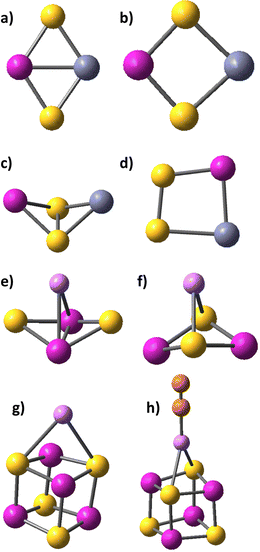
The diverse applications of transition metal sulphides rely on their ability to reversibly accept and donate electrons. The cobalt and iron disulphides MS2, M2S2, with M = Fe, Co, their persulphide isomers, containing an S–S bond, and the cubic M4S4 cage-shaped sulphides are examined in the present study by density functional theory with respect to stability of different isomeric structures, bonding and magnetic properties. Persulphides are structural analogues of peroxides and they are denoted as M(S2) or M2(S2), as the disulphur molecule is not dissociated upon binding to the cobalt or iron centres. The formal oxidation state of the transition metal cation is M(IV)S2 in sulphides and M(II)(S2) in persulfides. In binuclear persulphide clusters, M2(S2), disulphur may bind to the metal cations side-on, or bridging and the main bonding patterns are shown on Fig. 1.
The effect of carbonyl and chloride ligands on the electron distribution is assessed. Li+, Na+ and Zn2+ cations bind at sulphur centres in the cobalt and iron–sulphide clusters, as they bear partial negative charge and the energy minimum configuration is sought. Two schemes of cluster reduction are examined: (i) the isomerisation sulphide → persulphide with reduction of the transition metal cation formal oxidation state; (ii) alkaline cation reduction and electron delocalization within the cluster: Li+ + e− + (MxSn) → Li(MxSn); Na+ + e− + (MxSn) → Na(MxSn), where MxSn denote sulphide and persulphide clusters MS2, M(S2), M2S2, M2(S2), M4S4. The reduction process was studied as a two-step reaction in which cations were allowed to bind to the clusters, relaxed, and then electrons were attached to the cation-cluster structure and re-optimized. The degree to which bonded alkali cations retain Lewis acid properties is evaluated by nitrogen and oxygen adsorption. The reaction mechanism of sulphide-persulphide isomerisation upon Zn2+ cation binding and the reduction Zn2+ + 2e− + M(S2) → Zn(MS2) in different solvents (water, acetonitrile and 1-chlorohexane) is traced.
2. Computational details
The B3LYP functional47–50 was selected for DFT calculations among several density functionals tested for the FeS and CoS molecules, for which experimental data are available, see Table S1 in ESI.† For the smaller-sized clusters MS2 and M2S2, also including carbonyl and halogen ligands, the coupled-cluster method singles and doubles, including non-iterative triples, CCSD(T), was applied to the B3LYP optimized geometries in order to verify their B3LYP calculated relative stability.51–53 The 6-311+G(2df) basis set with diffuse and polarization functions was employed, which consists of the McLean–Chandler (12s, 9p) → (621111, 52111) basis sets for second-row atoms54,55 and the Wachters–Hay all electron basis set for the first transition row, using the scaling factors of Raghavachari and Trucks.56–58 All calculations were performed with the Gaussian 16 software.59 The spin-unrestricted formalism was applied to clusters containing two or more transition metal cations and anti-ferromagnetic states were determined in the broken-symmetry approach by taking into account spin-polarization on ligands, cations, and bridging sulphur atoms.60,61 Transition states in studying the Zn(II) coordination reaction mechanism were identified by the presence of a single imaginary frequency. Intrinsic reaction coordinate (IRC) calculations were performed to confirm the transition states structure and for evaluating activation energies.62 Reaction studies in solution were performed using the Polarizable Continuum Model63 (PCM) and by explicitly taking into account water molecule and acetonitrile coordination to Zn(II) cations and to the sulphide cluster. Dispersion effects were taken into account for cation binding to the sulphide clusters by using the formula of Grimme with Becke–Johnson damping.64 Magnetic moments at the atoms (μ) were calculated as a difference between α and β natural populations. The bond populations and charge distributions were examined by using natural orbitals and natural bond orbital (NBO) analysis.65,66 The electrostatic potential (ESP) of the clusters was calculated from the B3LYP density and molecular electrostatic potential (MEP) maps were derived; they denote electropositive and electronegative regions in the clusters.3. Results and discussion
3.1. Sulphides MS, disulfides MS2 and persulphides M(S2)
Experimental bond lengths, dissociation energies, vibrational frequencies, electron affinities are available for the diatomic molecules FeS and S2, Table 1, while for CoS only the bond length and the ground electron state were reported.42,43,67–69 The B3LYP density functional provides accurate description of FeS, CoS and S2 in terms of bond length; the dissociation energies and electron affinities of FeS and S2 also match well with experiment, see Table 1. B3LYP outperforms other hybrid functionals (B3PW91 and M06), pure functionals (BLYP and TPSS) in predicting dissociation energies and electron affinities, see section Method validation and Table S1 in ESI.† The Fe–S bond bears higher ionic character as compared to the Co–S bond, evidenced by the calculated natural charge, Fe(+0.71q) vs. Co(+0.55q). NBO analysis indicates that the Co 4s orbital is lower in energy than the Fe 4s orbital and the local orbital occupancy reads as Co 4s0.67 3d7.65 4p0.10; Fe 4s0.45 3d6.66 4p0.15. The stronger Co–S bond is due to 4s–3dxzdyz orbital mixing, which lowers the energy of the π-bonding orbitals. The Co4s orbital also contributes to the σ-bond.| Cluster/method | R M–O, Å | D zpe, kJ mol−1 | ω, cm−1 | EA, eV |
|---|---|---|---|---|
| Experimental data are from references:a Ref. 43.b Ref. 67.c Ref. 68.d Ref. 13.e Ref. 42.f Ref. 69. | ||||
| FeS; 5Δ | ||||
| B3LYP | 2.029 | 327.7 | 515.6 | 1.717 |
| Exp. | 2.017a | 328.9 ± 14.6b | 523.2c | 1.725 ± 0.010d |
| CoS; 4Δ | ||||
| B3LYP | 1.989 | 323.4 | 520.6 | 1.293 |
| Exp. | 1.978e | |||
| S2; 3Σg− | ||||
| B3LYP | 1.909 | 423.2 | 712.4 | 1.682 |
| Exp. | 1.889b | 421.6b | 725.7b | 1.670 ± 0.015f |
The disulphide CoS2 also forms shorter Co–S bonds than FeS2, but the persulphides with lengthened Co–S and Fe–S bonds are more stable: Co(S2) is separated from CoS2 by 0.57 eV, while FeS2 and Fe(S2) lie close by energy, 0.13 eV. The possible co-existence of cyclic and opened structure for Fe:S ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, namely disulphide/persulphide, was suggested in previous studies.13,24,70 The S–S bond is lengthened, as compared to the S2 molecule, to 2.15–2.19 Å in Fe(S2) and Co(S2), see Table 2 and Table S3 in ESI.† The electron affinity of FeS2 was experimentally determined from PES spectra of the anion, FeS2− at 3.222 ± 0.009 eV.13 The electron attachment breaks the S–S bond, the ground state monoanion adopts opened structure with a broader angle ∠S–Fe–S of 168.4°, and our B3LYP calculated adiabatic electron affinity (AEA) for this isomer is 3.240 eV, in excellent agreement with the experiment. The calculated vertical detachment energy of 3.692 eV, however, is higher than the experimental value of 3.306 eV.13 A signal from isomer was detected with lower accuracy, 2.05 ± 0.09 eV, which corresponds to our calculated AEA value of 1.89 eV for iron persulfide Fe(S2). The neutral CoS2 has a local minimum in linear 4Σg configuration at 1.90 eV above the global minimum, with lengthened Co–S bonds as compared to other cobalt disulphides, including carbonyl and chloride coordinated CoS2. The linear FeS2 however, is not a local minimum, but a second-order saddle point, which bends in either the xy or xz plane to form the 5A1 stable disulphide. The cobalt disulphide monoanion is linear, in a 5Δg ground state. The B3LYP calculated EA is 3.453 eV, and the vertical detachment energy is 3.822 eV. A persulphide monoanion in 5A1 state, with lengthened Co–S bonds of 2.258 and angle ∠S–Fe–S of 56.8° is found by 1.23 eV above the linear monoanion. The AEA value, calculated for this persulphide isomer is 1.733 eV.
2, namely disulphide/persulphide, was suggested in previous studies.13,24,70 The S–S bond is lengthened, as compared to the S2 molecule, to 2.15–2.19 Å in Fe(S2) and Co(S2), see Table 2 and Table S3 in ESI.† The electron affinity of FeS2 was experimentally determined from PES spectra of the anion, FeS2− at 3.222 ± 0.009 eV.13 The electron attachment breaks the S–S bond, the ground state monoanion adopts opened structure with a broader angle ∠S–Fe–S of 168.4°, and our B3LYP calculated adiabatic electron affinity (AEA) for this isomer is 3.240 eV, in excellent agreement with the experiment. The calculated vertical detachment energy of 3.692 eV, however, is higher than the experimental value of 3.306 eV.13 A signal from isomer was detected with lower accuracy, 2.05 ± 0.09 eV, which corresponds to our calculated AEA value of 1.89 eV for iron persulfide Fe(S2). The neutral CoS2 has a local minimum in linear 4Σg configuration at 1.90 eV above the global minimum, with lengthened Co–S bonds as compared to other cobalt disulphides, including carbonyl and chloride coordinated CoS2. The linear FeS2 however, is not a local minimum, but a second-order saddle point, which bends in either the xy or xz plane to form the 5A1 stable disulphide. The cobalt disulphide monoanion is linear, in a 5Δg ground state. The B3LYP calculated EA is 3.453 eV, and the vertical detachment energy is 3.822 eV. A persulphide monoanion in 5A1 state, with lengthened Co–S bonds of 2.258 and angle ∠S–Fe–S of 56.8° is found by 1.23 eV above the linear monoanion. The AEA value, calculated for this persulphide isomer is 1.733 eV.
| Cluster model | State | R M–S, Å | R S–S, Å | ∠SCoS, deg | R X–M, Å | μ M | μ S | ΔEtot, eV B3LYP | ΔEtot, eV CCSD(T) |
|---|---|---|---|---|---|---|---|---|---|
| a ΔEtot: total energy difference relative to the ground state energy for a given composition; for Co(S2) Etot = −2179.226190 Hartree (B3LYP); for Fe(S2) Etot = −2060.174869 Hartree (B3LYP); zero-point and dispersion correction included. CCSD(T) Etot = −2177.080007 for Co(S2) and −2058.068628 for Fe(S2). | |||||||||
| Co(S2) | 4A1 | 2.141 | 2.155 | 60.4 | 2.17 | 0.41 | 0 | 0 | |
| CoS2 | 4B2 | 1.980 | 110.7 | 2.02 | 0.49 | 0.50 | 0.38 | ||
| 4Σg | 2.103 | 180.0 | 2.24 | 0.38 | 1.90 | 1.81 | |||
| (CO)Co(S2) | 4B1 | 2.196 | 2.085 | 56.7 | 1.888 | 2.14 | 0.40 | 0 | 0 |
| (CO)CoS2 | 4A1 | 2.037 | 154.8 | 1.795 | 1.49 | 0.80 | 0.96 | 1.33 | |
| Cl–Co(S2) | 3B2 | 2.173 | 2.024 | 55.5 | 2.108 | 2.00 | −0.04 | 0 | 0 |
| Cl–CoS2 | 3B2 | 1.983 | 113.6 | 2.094 | 1.77 | 0.05 | 1.72 | 1.89 | |
| Fe(S2) | 5A1 | 2.166 | 2.186 | 60.6 | 3.33 | 0.33 | 0 | 0 | |
| FeS2 | 5B2 | 2.015 | 113.5 | 3.34 | 0.33 | 0.13 | 0.14 | ||
| (CO)Fe(S2) | 5A | 2.238 | 2.074 | 55.2 | 1.884 | 3.10 | 0.48 | 0 | 0 |
| (CO)FeS2 | 5A | 2.044 | 107.6 | 2.053 | 3.09 | 0.54 | 0.97 | 0.93 | |
| Cl–Fe(S2) | 4B2 | 2.239 | 2.053 | 54.5 | 2.138 | 3.27 | −0.18 | 0 | 0 |
| Cl–FeS2 | 4A1 | 2.040 | 113.8 | 2.134 | 3.17 | −0.12 | 1.25 | 1.40 | |
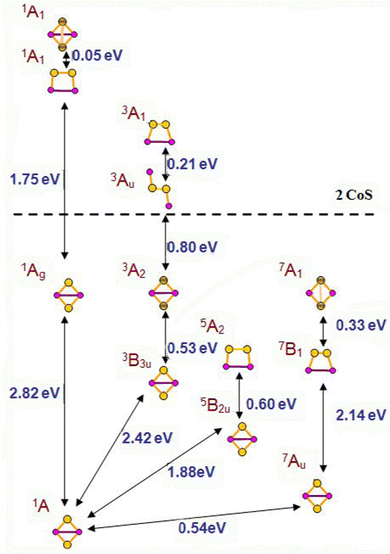
Invariably, persulphides are more stable than disulphides. The dissociation limit to Co(4F, 3d74s2) + S2 lies at 2.51 eV above the global minimum and similarly, the dissociation limit to Fe(5D, 3d74s2) + S2 lies at 2.57 eV above the global minimum of Fe(S2), therefore all computed geometries are thermodynamically stable. The global minimum and the ground states of cobalt disulphide isomers are quartet states, and those of iron disulphide isomers are quintet states, as they are in the diatomic molecular sulphides. The CCSD(T) calculated energies confirm the ordering by stability, predicted by B3LYP. It is worth noting that sulphur atoms bear certain magnetic moment and in the lower spin multiplicity clusters, antiferromagnetic ordering is observed. In persulphides, the angle ∠S–M–S varies in a narrow range, 54.5° to 60.4°, while in the disulphides the range is wider, 107.6° to 120.7° for most structures, but with even larger variations for (CO)CoS2, 154.8° and for CoS2 in 6A1 state, 155.9°. Natural population analysis reveals increased 4p orbital occupancy in CoS2, Co 4s0.49 3d7.62 4p0.33, and the 4s orbital occupancy is also higher than in FeS2, Fe 4s0.41 3d6.58 4p0.35, see also Table S2 in ESI.† In Co(S2) the 4p orbital occupancy further increases, Co 4s0.47 3d7.90 4p0.41, but this is not the case for Fe(S2), with Fe 4s0.40 3d6.85 4p0.22. The cobalt and sulphur centres in cobalt persulphide, Co(S2) bear minor charges of +0.22 at Co and −0.11 at S. In iron persulphide the Fe–S bonds tolerate certain ionic character as found in the disulphide, with natural charge of +0.50 at Fe and −0.25 at S. The moderate difference in cation local orbital occupancy between FeS2 and Fe(S2) and the high local charge on sulphur atoms in the persulphide explain the small energy gap between the persulphide and the disulphide of iron.
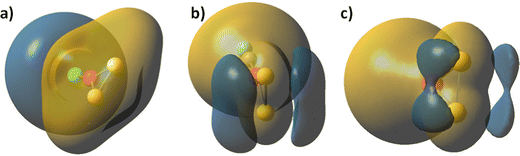
When carbonyl and chloride ligands are coordinated to the metal cation in the plane of the MS2 bonds, they increase significantly the energy gap between persulphides and sulphides. The metal–sulphur bonds are lengthened upon carbonyl and chloride ligand coordination in disulphides and persulphides, while the S–S bond in persulphides XM(S2) is strengthened. The Co–S bonds are weakened more significantly by carbonyl ligands for Co(S2) and CoS2 (lengthening of 0.05–0.06 Å) while chloride anion coordination causes minor change of Co–S bonds in ClCo(S2) (0.003 Å), but more significant strengthening of the S–S bond, Table 2. For XFe(S2) and XFeS2 the trends are similar, with the exception that both carbonyl and chloride coordination weaken significantly the Fe–S bond in XFe(S2), as it is lengthened by 0.07 Å. Carbonyl coordination is stronger, as evidenced by the Co–CO and Fe–CO bonds, which are by up to 0.3 Å shorter as compared to the Co–Cl and Fe–Cl bonds. Both ligands, CO and Cl− can be used for fine tuning of electrophilic/nucleophilic properties in the clusters, see Fig. 2.
The chloride and carbonyl ligands act in favour of electron density delocalization in a different way. In the chloride coordinated Co(S2), the electronegativity at the ligand dominates. Carbonyl ligands are a strong electron donor and therefore the charge on sulphur centres becomes more negative. The two symmetric clouds of increased electron density above and below the molecular plane at the sulphur atoms, which are already present in Co(S2), Fig. 2c, become larger. The charge distribution confirms that carbonyl groups increase the polarity of Co–S and Fe–S bonds, see Table S2 in ESI.† Chloride coordination decreases the probability of a nucleophilic attack at the sulphur centres.
3.2. Clusters with M/S = 1 ratio: Co2S2, Co4S4, Fe4S4, Co2Fe2S4
A number of isomers, containing persulfo-groups exist for Co2S2: side-on binding, or bridging two separated cobalt centres in non-planar cyclic clusters, Fig. 3. They all lie at more than 2 eV above the global minimum, which is a rhombic disulphide in antiferromagnetic 1A state. All disulphides and persulphides contain a Co–Co bond, Table 3. Chloride ligands weaken the Co–Co bond, the Co–S bonds become slightly strengthened, but the bond angles undergo minor change and the antiferromagnetic ordering is nearly identical with that of Co2S2 in the global minimum. In the non-planar cyclic clusters with C2v symmetry the Co–Co bonds are lengthened and they allow two configurations: (i) disulphide with separated sulphur atoms and bonding pattern denoted as Co2(μ-S)2 (ii) persulphide with midway positioned S–S bond (Co2-μ-η2:η2-S2), though this S–S bond is weaker as compared to the planar side-on bonded disulphur, Co2-η2-S2. The configurations lying close to the global minimum all have very similar geometry: rhombic planar disulphides in variable high-spin state (triplet, quintet and septet multiplicity) with even stronger Co–Co bond and ferromagnetic ordering. The next closely lying clusters are those with side-on bonded disulphur, in quintet and septet state. The non-planar clusters lie at higher energy, by 2.95 eV for the triplet 3A2 state (with Co–Co bond) and by 3.01 eV in the septet 7A1 state (with S–S bond, persulphide). There is no significant difference in bond population between planar and non-planar disulphide clusters with separated S-atoms and a Co–Co bond present. The persulphide cluster in 7A1 state with separated cobalt atoms and an S–S bond, is more covalent and the local AO occupancies deviate from that of the global minimum. The natural charge on cobalt is +0.61 in the antiferromagnetic ground state cluster (−0.61 on S) and the Co 4s occupancy is lower than in the mononuclear sulphides, Co 4s0.373d7.714p0.26, while in the non-planar persulphide the natural charge on Co is +0.43 and the Co 4s occupancy is higher, Co 4s0.513d7.844p0.20, see also Table S2 in ESI.† The same trend is observed in diiron disulphides, Fe2S2 and persulphides, Fe2(S2). The binding of disulphur never occurs end-on, in distinction to the binding of dioxygen, which forms stable super-oxide compounds. A single persulphide in which disulphur connects two separated cobalt centres in trans-orientation, and in 3Au electronic state, lies above the dissociation limit to CoS, see Fig. 3.| Cluster model | State | R Co–S, Å | R S–S, Å | R Co–Co, Å | ∠SCoS, ∠CoSSb, deg | Dihedral ∠SCoSCo, deg | μ Co | μ S | ΔEtot, eV B3LYP | ΔEtot, eV CCSD(T) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Negative signs in magnetic ordering denotes antiferromagnetic ordering. b ∠SCoS for sulfide clusters with separated sulfur atoms and for non-planar disulfide clusters; ∠CoSS for planar clusters with bridging or side-on bonded S2. ΔEtot – total energy difference relative to the ground state energy of neutral Co2S2: Etot = −3562.050919 Hartree for B3LYP, zero-point and dispersion correction included; −3558.797034 Hartree for CCSD(T). | ||||||||||
| Co2S2, D2h, Co2(μ-S)2 | 1A | 2.183 | 3.655 | 2.388 | 113.7 | 2.46, −2.46 | 0.00 0.00 | 0 | 0 | |
| Co2S2, C2v, Co2(μ-S)2 | 3A2 | 2.105 | 3.153 | 2.496 | 97.0 | 33.7 | 0.86 | 0.14 | 2.95 | 2.81 |
| Co2S2, C2v, Co2-μ-η2:η2-S2 | 7A1 | 2.260 | 2.302 | 3.508 | 61.2 | 43.2 | 2.80 | 0.20 | 3.01 | 2.88 |
| Co2(S2), C2v, Co2-η2-S2 | 5A2 | 2.130 | 2.169 | 2.330 | 92.2 | 1.87 | 0.13 | 2.48 | 2.57 | |
| Co2S2Cl2, C2v, Co2(μ-S)2 | 1A | 2.133 | 3.462 | 2.494 | 108.5 | 2.47, −2.47 | 0.00 | |||
The Co4S4 and Fe4S4 clusters are stable in cubic configuration, with antiferromagnetic ordering at the Co or Fe centres. The bridging sulphur atoms bear small magnetic moment and in most clusters, it is close to zero, Table S5, ESI.† The coordination of carbonyl ligands at the four metal cation centres brings minor lengthening of Co–S and Fe–S bonds; the local magnetic moment on Co and Fe increases, and respectively, the antiferomagnetic coupling is stronger. Chloride ligands stabilize the cubic clusters as the M–S bonds are considerably shortened, particularly for the mixed Co2Fe2S4Cl4 cluster. The position of alkali cations upon coordination is above the plane of a four-member ring, Fig. 1g. The Li+ cations form weak bonds to the M4S4 clusters and electrostatic interactions play dominant role in binding to the negatively charged sulphur centres, as they retain a natural charge of +0.94, which, upon one-electron reduction remains almost unchanged, to +0.91. The charges on sulphur atoms become consequently more negative, from −0.22 to −0.79, (Table 2 in ESI†). The Li+–S internuclear distances of 2.647 Å and Li+–Co distance of 2.778 Å are shortened upon one-electron reduction, to 2.348 Å and 2.662 Å. The clusters also undergo deformation and the S–S inter-nuclear distances in the down non-bonding ring are broadened: from 3.147 Å for Li+ binding to 3.440 Å for Li+,e− binding. It can be concluded, that cation binding to M4S4 clusters is sub-optimal, as compared to mononuclear MS2 and dinuclear M2S2 clusters. The MEP maps indicate that Li+ cation binding creates a dominant positive electrostatic potential, overwhelming the whole M4S4 cluster, irrespective of ligand coordination, Fig. 4. In the reduced cluster, nucleophilic areas appear at the sulphur centres and they are much smaller at the ring, where Li+,e− binding occurs.
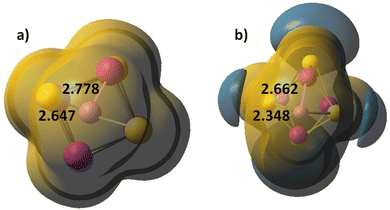 | ||
| Fig. 4 Molecular electrostatic potential (MEP) map of (a) Co4S4–Li+ and (b) Co4S4–Li+,e−. Li–S bond lengths are denoted. Atom colors as in Fig. 1. Electropositive area is golden yellow, electronegative areas – blue. Contour lines are at 0.015 a.u. | ||
3.3. Binding of Li and Na cations to mononuclear and dinuclear disulphides and persulphides
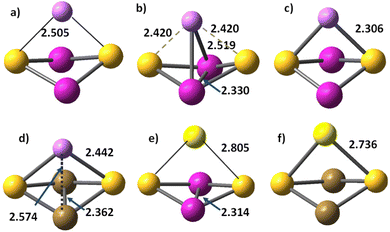
The alkali cations bind to the mononuclear disulphides by forming rhombic planar or rhomboid non-planar clusters with minor deviation from planarity, Scheme 1. The cation binding to persulphides results in boat-shaped rhomboid clusters. The energy gap between cobalt persulphide and disulphide increases from 0.38 eV for the bare disulphide to 0.66 eV upon Li+ binding, Table 4 (0.64 eV for Na+, see Table S7 in ESI†) and the trend is very similar for iron persulphide/disulphide. Upon one-electron reduction the ordering by stability is reversed and disulphides become more stable than persulphides, as shown in Scheme 1, with a much larger disulphide-to-persulphide energy gap: 1.26 eV for Li+,e−, 1.32 eV for Na+,e− in CoS2; the values for iron are even higher. Neither lithium, nor sodium cations are able to form bonds with the transition metal center (Fe, Co) in the reduced mononuclear clusters. The cation charge does not experience significant change upon reduction and remains close to +0.9 in the disulphides, while in persulphides it is lowered to +0.75 (Li+,e−) and to +0.86 (Na+,e−). The local natural charge at Co and Fe centers is strongly diminished, particularly in persulphides: from close to +1.0 before reduction, to +0.3 after reduction.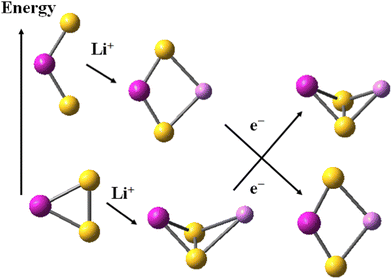 | ||
| Scheme 1 Relative stability of disulphide and persulphide clusters upon Li+ cation binding and subsequent one-electron reduction. Atom colors as in Fig. 1. | ||
| Cluster nodel | State | R M–S, Å | R S–Cat, Å | ∠S–M–S, deg | μ M | μ S | ΔEtota eV B3LYP |
|---|---|---|---|---|---|---|---|
| a ΔEtot – total energy difference relative to the ground state energy, zero-point and dispersion corrections included. | |||||||
| Co(S2)–Li+ | 4A′ | 2.198 | 2.377 | 59.4 | 2.33 | 0.33 | 0.0 |
| CoS2–Li+ | 4B2 | 2.029 | 2.421 | 97.4 | 2.13 | 0.41 | 0.66 |
| CoS2–Li+,e− | 5A1 | 2.081 | 2.360 | 120.3 | 2.50 | 0.75 | 0.0 |
| Co(S2)–Li+,e− | 5A′ | 2.349 | 2.253 | 54.6 | 3.57 | 0.19 | 1.26 |
| Co2S2–Li+ | 7A | 2.223 | 2.505 | 98.1 | 2.53 | 0.43 | |
| Co2S2–Li+,e− (Li–S; Li–Co2) bonds | 6A | 2.245 | 2.420 (S), 2.519 (Co) | 107.7 | 2.27 | 0.23 | 0.0 |
| Co2S2–Li+,e− (Li–S) bond | 6B1 | 2.239 | 2.306 | 86.6 | 2.71 | −0.23 | 2.20 |
| Fe(S2)–Li+ | 5A′ | 2.228 | 2.369 | 54.3 | 3.47 | 0.26 | 0.0 |
| FeS2–Li+ | 5B2 | 2.043 | 2.426 | 102.3 | 3.33 | 0.31 | 0.35 |
| FeS2–Li+,e− | 6A1 | 2.110 | 2.357 | 118.8 | 3.72 | 0.64 | 0.0 |
| Fe(S2)–Li+,e− | 6A′ | 2.368 | 2.257 | 57.5 | 4.62 | 0.17 | 1.34 |
| Fe2S2–Li+ | 7A | 2.197 | 2.502 | 100.4 | 3.12 | −0.12 | |
| Fe2S2–Li+,e (Li–S; Li–Fe2) bonds | 8A | 2.271 | 2.442 (S), 2.574 (Fe) | 106.8 | 3.30 | 0.20 | 0.0 |
| Fe2S2–Li+,e (Li–S) bond | 6A | 2.207 | 2.390 | 100.5 | 2.69 | −0.16 | 0.91 |
The cobalt–sulphur and iron–sulphur bonds are lengthened upon Li+ and Na+ cation binding by 0.03–0.06 Å, more significantly upon Li+ binding, Table 4 and Table S7 in ESI.† Upon 1e− reduction, Li+–S and Na+–S bonds are strengthened, while Co–S and Fe–S bonds are lengthened, most notably in persulphides, with bond length changes of 0.12–0.14 Å. The magnetic moment on transition metal and sulphur centers increases upon reduction in the disulphides; in persulphides the magnetic moment increases predominantly at the transition metal centre. Though chloride ligands diminish the nucleophilic strength at S atoms, Li+ binding is possible, because sulphur centres still bear a small negative charge. In these clusters Cl–MS2Li+ and Cl–M(S2)–Li+ the Co–S and Fe–S bonds undergo minor lengthening, while the Li+–S bonds become significantly stronger, see Table 6 in ESI.†
Cation binding to the dinuclear Co2S2 and Fe2S2 clusters is weaker as compared to mononuclear clusters, evidenced by the lengthened Li+–S and Na+–S bonds, Table 4 and Table S7 in ESI.† For Co2S2–Li+,e− two sextet states are found: (i) the ground state 6A (Fig. 5b) with Li+–Co, Co–Co and Li+–S bonds, and (ii) a less-stable configuration in 6B1 state at much higher energy of 2.20 eV, with shorter Li–S bonds, but lack of Li–Co interaction and without a Co–Co bond (Fig. 5c). In diiron disulphide Fe2S2, the Li+,e− binding to sulphur is weaker than in Co2S2, and all bonds, including Fe–Fe, are lengthened. The octet ground state 8A has a similar structure to the Co2S2–Li+,e− ground state, with Li+–Fe, Fe–Fe, and Li+–S bonds (Fig. 5d). The lowest energy state in the sextet multiplicity channel Fe2S2Li 6A, contains only Li+–S bonds, Table 4. The monovalent cation (Li+, Na+) to sulphur bonds are always strengthened upon reduction, more significantly the Li–S bonds. Sodium binding is generally weaker, and even in the reduced clusters, Na–Co and Na–Fe bonds do not form.
Upon one-electron reduction of M2S2–Li+ or M2S2–Na+, (M = Fe,Co) the extra charge is delocalized at S, Co or Fe centers, with the transition metal cation 4s and 4p orbitals involved, while the 3d occupancies undergo minor changes. The S 3p orbital occupancy varies in the range from 4.2 to 5.0 and the molecular electrostatic potential (MEP) maps indicate strong increase in negative charge density at S atoms in reduced clusters, see Fig. S1 and Table S2 in ESI.† Cation binding changes the magnetic ordering in dinuclear clusters and they become more stable in high-spin state, Table 4. Antiferromagnetic coupling does not have an impact on the cluster stability after alkali cation coordination and upon reduction.
Though local charges and MEP maps indicate the strength of Lewis acidity and electrophillic properties of cations, the adsorption of nitrogen and oxygen allows discerning their reactivity towards different nucleophillic reactants. Lithium clusters are known for their ability to bind nitrogen and they have been proposed as material for Li–N2 batteries.71,72 The highest adsorption capacity is found in mononuclear disulphides, and though the positively charged CoS2–Li+ cluster has higher N2 adsorption energy of 40.7 kJ mol−1, the reduced cluster with N2 adsorption energy of 23.1 kJ mol−1 has a more favourable N2/O2 ratio, 1.58 vs. 2.10, as shown in Table 5. Still, Li3+ clusters have the highest N2/O2 adsorption ratio of 2.51.
| Cluster | E (N2) | E (O2) |
|---|---|---|
| a For iron disulphide clusters see Table S8 in ESI. | ||
| Co2S2–Li+ | 14.4 | 8.6 |
| Co2S2–Li+,e− | 11.3 | 5.6 |
| CoS2–Li+ | 40.7 | 25.8 |
| CoS2–Li+,e− | 23.1 | 11.0 |
| CoS2–Na+ | 27.6 | 18.0 |
| CoS2–Na+,e− | 15.7 | 11.2 |
| Li3+ | 23.1 | 9.2 |
3.4. Binding of Zn cations to mononuclear and dinuclear disulphides and persulphides
The coordination of zinc cations follows a similar trend as the coordination of lithium cations, the persulphides being more stable than the disulphides of Zn2+, and reversal of the stability upon reduction in favor of disulphides, Table 6. The non-planar rhomboid persulphides Co(S2)–Zn2+ and Fe(S2)–Zn2+ are the global minima, Fig. 1c, and they are separated by small energy gaps from the planar disulphides CoS2–Zn2+ and FeS2–Zn2+, Fig. 1b: 0.42 eV for CoS2–Zn2+ and 0.22 eV for FeS2–Zn2+. These energy gaps are much smaller than in the alkali–ion coordinated clusters and closer to the gaps in the bare clusters. The rhombic planar disulphides become the global minima upon 2e− reduction, and Zn–Co and Zn–Fe bonds contribute to the cluster stability, Fig. 1a. The energy gap to persulphides increases, though not as much as in Li- and Na-clusters. The structure of persulphides upon reduction is not the boat shaped typical for alkali cations, but disulphur becomes side-on bonded to Co–Zn and Fe–Zn, see Fig. 1d. The binding of zinc in cation state is largely covalent and the positive charge is efficiently redistributed, as Zn centres bear a charge not higher than +1.35. The cobalt or iron centres acquire a higher positive charge and the charge on sulphur becomes less negative, Table S2, ESI.† The persulphide and disulphide clusters efficiently donate electrons to zinc cations and the AO occupancy is in the range Zn 4s0.46–0.52 4p0.18–0.21. Upon two-electron reduction, the negative charges are again redistributed throughout the cluster: the zinc local charge is reduced from +1.35 to +0.8 in mononuclear disulphides, the sulphur charge changes from −0.15 to −0.75 and the charge at Co or Fe change from +1.0 to +0.60, + 0.70. The 4p orbitals at the transition metal centers (Co, Fe, Zn) experience the largest increase in population. The local AO occupancy at sulphur centers varies in the range 3s1.80–1.95 3p4.2–5.0, the lower 3p orbital occupancy of 4.2–4.3 being typical for persulphides, mid-range occupancy of 3p4.5–4.7 for disulphides, and higher occupancy of 3p4.9–5.0 for Li+,e−, Na+,e− or Zn2+,2e− binding to the clusters. The Zn(II) cations have close crystal and ionic radii to Co(II) in high-spin state73 and in all of the reduced clusters Zn–Co bonds are formed. The ground-state Zn–Co disulphide clusters have their analogues as Co2S2 clusters – rhombic planar, with Co–Zn bond. Fe(II) in high spin state also forms Fe–Zn bond, slightly lengthened than the Co–Zn bond, Table 6. In the reduced persulphide clusters, the S–S bond is retained and Zn–Co bonds are formed. Two forms were found, one with S–S side bonding to Co only and Zn binding end-on to Co (or Fe), with bonding pattern Zn–(Co-η2-S2) – this configuration does not have an iron analogue. The side-on bonded disulphur to a Zn–Co bond (or Zn–Fe bond) is more stable, (Zn–Co)-η2-S2.| Cluster model | State | R M–S Å | R S–Cat Å | ∠S–M–S, deg | μ M | μ S | ΔEtot, eV B3LYP |
|---|---|---|---|---|---|---|---|
| a ΔEtot – total energy difference relative to the ground state energy, zero-point and dispersion corrections included. | |||||||
| Co(S2)–Zn2+ | 4A′ | 2.308 | 2.318 | 59.1 | 2.50 | 0.26 | 0.0 |
| CoS2–Zn2+ | 4B2 | 2.146 | 2.313 | 95.2 | 2.39 | 0.29 | 0.42 |
| CoS2–Zn2+,2e− | 4B1 | 2.202 | 2.235, 2.441 (Co–Zn) | 114.5 | 2.38 | 0.29 | 0.0 |
| Co(S2)–Zn2+,2e− (ZnCo)-η2-S2 | 4A′′ | 2.213 | 2.543, 2.437, (Co–Zn) | 102.7, ∠CoSS | 2.16 | 0.44 | 0.90 |
| Co(S2)–Zn2+,2e− Zn–(Co-η2-S2) | 4A′ | 2.134 | 2.169, 2.510 (Co–Zn) | 58.6 | 2.18 | 0.41 | 1.08 |
| Co2S2–Zn2+ | 7A | 2.322 | 2.339 | 93.1 | 2.62 | 0.38 | |
| Co2S2–Zn2+,2e− | 7A | 2.247 | 2.624 2.691 (Co–Zn) | 109.2 | 2.30/0.70 (Zn) | 0.35 | 0.00 |
| Co2S2–Zn2+,2e− | 5A | 2.256 | 2.560 2.703 (Co–Zn) | 106.9 | 2.27/−0.74 (Zn) | 0.10 | 0.29 |
| Fe(S2)–Zn2+ | 5A′ | 2.337 | 2.312 | 59.0 | 3.59 | 0.20 | 0.0 |
| FeS2–Zn2+ | 5B2 | 2.148 | 2.307 | 97.4 | 3.52 | 0.21 | 0.22 |
| FeS2–Zn2+,2e− | 5A1 | 2.255 | 2.232, 2.499 Zn–Fe | 111.5 | 3.56 | 0.21 | 0.0 |
| Fe(S2)–Zn2+,2e− (ZnFe)-η2-S2 | 5A′′ | 2.232 | 2.343, 2.448 Zn–Fe | 97.03, ∠Fe–SS | 3.66 | 0.20 | 1.29 |
| Fe2S2–Zn2+ | 7A | 2.327 | 2.341 | 89.0 | 3.17 | 0.18 | |
| Fe2S2–Zn2+,2e− | 7A | 2.279 | 2.500 2.728 (Fe–Zn) | 104.6 | 3.24/−0.76 (Zn) | 0.14 | 0.00 |
The dinuclear disulphides bind Zn cations in a similar way to Li cations and upon reduction Co–Co and Fe–Fe bonds emerge. In the reduced state, Zn always forms bonds to the transition metal cation centers in addition to the Zn–S bonds, Table 6. Magnetic moment of 0.7–0.8 MB is induced at Zn, as a result from the difference between α and β 4s orbital populations. In Fe2S2–Zn clusters and in the quintet state of Co2S2–Zn, the unpaired spin moment at Zn is antiferromagnetically coupled to that at Fe, Co centers. Nevertheless, the binding of Zn to the dinuclear clusters Co2S2 and Fe2S2 is not as strong as in the mononuclear clusters. The bonds to sulphur centers and to the Co and Fe centers are significantly lengthened, particularly in the reduced forms. The septet and quintet state of Co2S2–Zn2+,2e− have very similar geometry and their magnetic structure differs by spin ordering, which places them closely spaced by energy (0.29 eV).
The potential energy surfaces of mononuclear disulphides and persulphides MS2 and M(S2) are rather flat, indicating small energy barriers for the conversion reaction between the two isomers. Zinc binding to the mononuclear clusters increases the energy gap between the two isomers and the energy barrier for the isomerisation reaction also increases.
The barrier is smaller for the cation form in CoS2Zn2+ to Co(S2)Zn2+ (0.18 eV), but more significant for FeS2Zn2+ to Fe(S2)Zn2+ (0.46 eV), see Fig. 6a. The isomerisation reaction of the reduced clusters to disulphides, in which again Co–Zn bonds are present, has a higher energy barrier of 1.16 eV for the isolated clusters (gas-phase) at standard temperature and pressure, Fig. 6b. The transition state, identified by a single imaginary frequency in the vibrational spectrum, contains neither S–S bonds, nor Co–Zn bonds, but only Co–S and Zn–S bonds. Water and acetonitrile solvents do not lower as much as expected the energy barrier of the cationic form, though up to two water and acetonitrile molecules participate in direct coordination of each cation in the clusters. The coordination of solvent to the reduced clusters is weaker and one water or acetonitrile molecules forms bond per Zn and a second one per Co cation centres. The Zn(II)–OH2 bond length in the cation form equals 1.997 Å and the Zn(II)–N bond length is 2.001 Å; upon reduction the coordination of a single water molecule is at a Zn–OH2 distance of 2.124 Å and the acetonitrile molecule also drifts away at a distance of 2.148 Å. The solvent 1-chlorohexane is much less polar, with dielectric constant ε = 5.9491 and while it does not coordinate directly to the clusters, it reduces more significantly the energy barriers for both the cationic (to 0.11 eV) and for the reduced zinc–cobalt–sulphur clusters. Water reduces the energy barrier of the Co(S2)Zn(0) to CoS2Zn(0) isomerisation from 1.16 to 0.90 eV, acetonitrile – to 0.72 eV and 1-chlorohexane – to 0.38 eV.
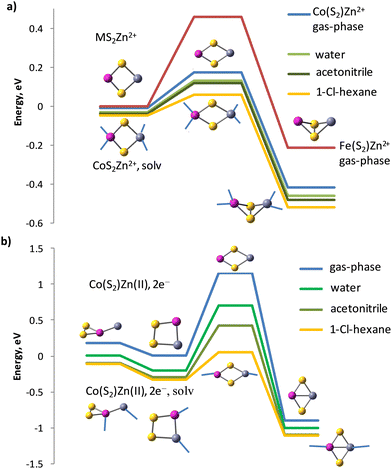 | ||
| Fig. 6 IRC reaction path following of (a) disulphide to persulphide isomerisation of cationic clusters CoS2–Zn2+, FeS2–Zn2+ in gas-phase and in solution, and (b) persulphide to disulphide isomerisation in reduced clusters Co(S2)–Zn(II),2e−. Zinc-cobalt persulphide forms two isomers with bonding patterns: (ZnCo)-η2-S2 in 4A” state and Zn–(Co-η2-S2) in 4A’ state, see Table 6. Acetonitrile and water molecule coordination to the clusters is denoted by blue lines. | ||
Iron persulphide Fe(S2) has a very small endothermic effect (0.14 eV) for the isomerisation to FeS2 as a bare cluster and the calculated activation barrier for gas-phase isomerisation FeS2 → Fe(S2) is 0.55 eV, higher than in the CoS2 → Co(S2) reaction (0.31 eV). Zn2+ cation binding does not increase this gap measurably (0.22 eV), but the activation barrier for the disulphide to persulphide isomerisation is again higher (0.46 eV) than in CoS2Zn2+ (0.18 eV). Upon 2e− reduction, the reaction persulphide Fe(S2)Zn(0) to disulphide FeS2Zn(0) turns exothermic by 1.29 eV and with an activation barrier of 1.55 eV, the Zn cations would strongly prefer binding to FeS2 in the reduced cluster, see Fig. S2 in ESI.† Though solvents lower the energy barrier of the zinc–iron persulphide to disulphide isomerisation, it remains still high in 1-chlorohexane (0.79 eV) as compared to the cobalt analogue (0.38 eV) and the heat effect in solution is not significantly changed, with minor decrease to 1.15 eV. While the isomerisation reaction is reversible for the cobalt disulphide, for iron disulphide much higher energy is needed to convert the stable disulphide FeS2Zn(0) back to a persulphide configuration.
4. Conclusions
The mononuclear disulphide and persulphide clusters of iron and cobalt are separated by small energy gaps and the two isomeric forms are inter-convertible, the persulphides being more stable. The binding of a carbonyl or chloride electron–donor ligand to the transition metal centre or cations (Li+, Na+, Zn2+) to sulphur increases the energy gap between persulphides and sulphides, and persulphides remain more stable than disulphides. The joint addition of cation and electron–donor ligand does not increase further the energy gaps. Upon one-electron reduction of Li+ and Na+ bonded clusters, or two-electron reduction of Zn2+ bonded clusters, the persulphide/sulphide stability is reversed and disulphides become more stable. Though disulphides and persulphides of Zn–Co and Zn–Fe are separated by smaller energy gaps as compared to the lithium and sodium bonded clusters, the isomerization reaction has an energy barrier, which is higher for the reduced clusters. Polar solvents, such as water and acetonitrile lower the energy barriers of the isomerisation reaction disulphide to persulphide and vice versa, but despite the direct coordination of water and acetonitrile molecules to the transition metal centres, their impact is much smaller as compared to the non-binding, less polar solvent 1-chlorohexne. The results reveal that upon reduction or electron transfer and delocalization, metal–metal bonds are formed, more easily Co–Co, Fe–Fe, Co–Zn, Fe–Zn, but also Co–Li and Fe–Li. In a reversible isomerization reaction sulphide-to-persulphide, S–S and Co–Zn bonds undergo break-up and re-form again. These effects can be expected also in adsorbed clusters and in layered materials.Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
The author acknowledges the provided access to the e-infrastructure of the NCHDC – part of the Bulgarian National Roadmap on RIs with the financial support by the grant No. D01-387/18.12.2020 and also thanks Projects CoE “National Center of Mechatronics and Clean Technologies” (BG05M2OP001-1.001-0008) and “Molecular design of photoactive metal-containing systems with advanced applications (PhotoMetalMod)” κП-06-H59/6 by the Bulgarian National Science Fund.References
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Chem. Soc. Rev., 2017, 46, 3529 RSC
.
- T. Nann, S. K. Ibrahim, P.-M. Woi, S. Xu, J. Ziegler and C. J. Pickett, Angew. Chem., Int. Ed., 2010, 49, 1574 CrossRef CAS PubMed
.
- H. Yu, X. Guo, X. Liu, S. Lu, Y. Lu, Q. Liu, Z. Li and Z. He, Energy Technol., 2019, 7, 1900015 CrossRef CAS
.
- F. Xiao, X. Yang, D. Wang, H. Wang, D. Y. W. Yu and A. L. Rogach, ACS Appl. Mater. Interfaces, 2020, 12, 12809 CrossRef CAS PubMed
.
- Y. Ma, Y. Ma, D. Bresser, Y. Ji, D. Geiger, U. Kaiser, C. Streb, A. Varzi and S. Passerini, ACS Nano, 2018, 12, 7220 CrossRef CAS PubMed
.
- S. Peng, X. Han, L. Li, Z. Zhu, F. Cheng, M. Srinivansan, S. Adams and S. Ramakrishna, Small, 2016, 12, 1359 CrossRef CAS PubMed
.
- H. Beinert, R. H. Holm and E. Münck, Science, 1997, 277, 653 CrossRef CAS PubMed
.
- H. Ogino, S. Inomata and H. Tobita, Chem. Rev., 1998, 98, 2093 CrossRef CAS PubMed
.
- R. B. King and Th. E. Bitterwolf, Coord. Chem. Rev., 2000, 206-207, 563 CrossRef CAS
.
- R. Zhang, Ch Pan, R. G. Nuzzo and A. A. Gewirth, J. Phys. Chem. C, 2019, 123, 8740 CrossRef CAS
.
- N. Borchers, S. Clark, B. Horstmann, K. Jayasayee, M. Juel and P. Stevens, J. Power Sources, 2021, 484, 229309 CrossRef CAS
.
- L. E. Blanc, D. Kundu and L. F. Nazar, Joule, 2020, 4, 771–799 CrossRef CAS
.
- H.-J. Zhai, B. Kiran and L.-S. Wang, J. Phys. Chem. A, 2003, 107, 2821 CrossRef CAS
.
- C. R. A. Catlow, Z. X. Guo, M. Miskufova, S. A. Shevlin, A. G. H. Smith, A. A. Sokol, A. Walsh, D. J. Wilson and S. M. Woodley, Philos. Trans. R. Soc., A, 2010, 368, 3379–3456 CrossRef CAS PubMed
.
- A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Chem. Rev., 2013, 113, 6621 CrossRef CAS PubMed
.
- U. Terranova and N. H. de Leeuw, J. Phys. Chem. Solids, 2017, 317-323, 111 Search PubMed
.
- C. Mitchell, U. Terranova, A. M. Beale, W. Jones, D. J. Morgan, M. Sankar and N. H. De Leeuw, Catal. Sci. Technol., 2021, 11, 779–784 RSC
.
- A. Roldan and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2017, 19, 12045–12055 RSC
.
- X.-B. Wang, Sh Niu, X. Yang, S. K. Ibrahim, Ch. J. Pickett, T. Ichiye and L.-S. Wang, J. Am. Chem. Soc., 2003, 125, 14072 CrossRef CAS PubMed
.
- N. Zhang, T. Hayase, H. Kawamata, K. Nakao, A. Nakajima and K. Kaya, J. Chem. Phys., 1996, 104, 3413 CrossRef CAS
.
- A. Nakajima, T. Hayase, F. Hayakawa and K. Kaya, Chem. Phys. Lett., 1997, 280, 381 CrossRef CAS
.
- S. Haider, D. Di Tommaso and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2013, 15, 4310 RSC
.
- U. Terranova and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 13426 RSC
.
- S. Clima and M. F. A. Hendrickx, J. Phys. Chem. A, 2007, 111, 10988 CrossRef CAS PubMed
.
- V. T. Tran and M. F. A. Hendrickx, J. Phys. Chem. A, 2011, 115, 13956 CrossRef CAS PubMed
.
- O. Hübner and J. Sauer, J. Chem. Phys., 2002, 116, 617 CrossRef
.
- S. Hamad, C. Richard, A. Catlow, E. Spano, J. M. Matxain and J. M. Ugalde, J. Phys. Chem. B, 2005, 109, 2703–2709 CrossRef CAS PubMed
.
- A. A. Al-Sunaidi, A. A. Sokol, C. Richard, A. Catlow and S. M. Woodley, J. Phys. Chem. C, 2008, 112(18), 860 Search PubMed
.
- G. L. Gutsev, K. G. Belay, K. V. Bozhenko, L. G. Gutsev and B. R. Ramachandran, Phys. Chem. Chem. Phys., 2016, 18, 27858–27867 RSC
.
- G. L. Gutsev, C. A. Weatherford, P. Jena, E. Johnson and B. R. Ramachandran, Chem. Phys. Lett., 2013, 556, 211 CrossRef CAS
.
-
M. M. Khan, Nanostructured Materials for Visible Light Photocatalysis, Micro and Nano Technologies, 2022, pp. 185–195 Search PubMed
.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nature Rev. Mat., 2017, 2, 17033 CrossRef CAS
; C. N. R. Rao and U. Maitra, Ann. Rev. Mater. Res., 2015, 45, 29 CrossRef
.
- H. S. Lee, Nano Lett., 2012, 12, 3695 CrossRef CAS PubMed
.
- J. Berkowitz, J. Chem. Phys., 1975, 62, 4074 CrossRef CAS
; D. G. Streets and J. Berkowitz, J. Electron Spectrosc. Relat. Phenom., 1976, 9, 269 CrossRef
; T. Balkis, A. F. Gaines, G. Ozgen, I. T. Ozgen and M. C. Flowers, J. Chem. Soc. Faraday Trans. II, 1976, 72, 524 RSC
; L. D. Pettit, Quart. Rev., 1971, 25, 1 RSC
.
- M. J. Filtness, I. B. Butler and D. Rickard, Appl. Earth Sci., 2003, 112, B171 Search PubMed
.
- K. R. Olson and K. D. Straub, Physiology, 2016, 31, 60–72 CrossRef CAS PubMed
.
- Y. Hikosaka, P. Lablanquie, F. Penent, J. G. Lambourne, R. I. Hall, T. Aoto and K. Ito, J. Electron Spectrosc. Relat. Phenom., 2004, 137–140, 287 CrossRef CAS
.
- K. Le Guen, C. Miron, D. Céolin, R. Guillemin, N. Leclercq, M. Simon, P. Morin, A. Mocellin, O. Björneholm, A. N. de Brito and S. L. Sorensen, J. Chem. Phys., 2007, 127, 114315 CrossRef CAS PubMed
.
- J. H. D. Eland, R. F. Fink, P. Linusson, L. Hedin, S. Plogmaker and R. Feifel, Phys. Chem. Chem. Phys., 2011, 13, 18428–18435 RSC
.
- A. J. Merer, Annu. Rev. Phys. Chem., 1989, 40, 407 CrossRef CAS
.
- A. J. Bridgeman and J. Rothery, J. Chem. Soc., Dalton Trans., 2000, 211 RSC
.
- M. A. Flory, S. K. McLamarrah and L. M. Ziurys, J. Chem. Phys., 2005, 123, 164312 CrossRef CAS PubMed
.
- S. Takano, S. Yamamoto and S. Saito, J. Mol. Spectrosc., 2004, 224, 137 CrossRef CAS
.
- L. Deng, E. Bill, K. Wieghardt and R. H. Holm, J. Am. Chem. Soc., 2009, 131, 11213 CrossRef CAS PubMed
.
- T. E. Bitterwolf and P. Pal, Inorg. Chim. Acta, 2006, 359, 1501 CrossRef CAS
.
- P. Ganesan, M. Prabu, J. Sanetuntikul and S. Shanmugam, ACS Catal., 2015, 5, 3625 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed
.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200 CrossRef CAS
.
- J. Cizek, Adv. Chem. Phys., 1969, 14, 35 CAS
.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910 CrossRef CAS
.
- J. A. Pople, R. Krishnan, H. B. Schlegel and J. S. Binkley, Int. J. Quant. Chem., 1978, XIV, 545 CrossRef
.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef CAS
.
- K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef
.
- A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033 CrossRef CAS
.
- P. J. Hay, J. Chem. Phys., 1977, 66, 4377 CrossRef CAS
.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062 CrossRef
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- T. Lovell, F. Himo, W.-G. Han and L. Noodleman, Coord. Chem. Rev., 2003, 238-239, 211 CrossRef CAS
.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131 CrossRef CAS
; R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052 CrossRef
.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS
; H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918 CrossRef PubMed
.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comp. Chem., 2011, 32, 1456 CrossRef CAS PubMed
.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS
.
-
F. Weinhold and J. E. Carpenter, The Structure of Small Molecules and Ions, Plenum, 1988 Search PubMed
.
-
Handbook of Chemistry and Physics, ed. D. R. Lide, T. J. Bruno and W. M. Haynes (Editor in Chief), CRC Press, Boca Raton, FL, 97th edn, 2016–2017 Search PubMed
.
- B. Liang, X. Wang and L. Andrews, J. Phys. Chem. A, 2009, 113, 5375 CrossRef CAS PubMed
.
- S. Moran and G. B. Ellison, J. Phys. Chem., 1988, 92, 1794 CrossRef CAS
.
- D. Schröder, N. Kretzschmar, H. Schwarz, C. Rue and P. B. Armentrout, Inorg. Chem., 1999, 38, 3474 CrossRef PubMed
.
- Z. Zhang, S. Wu, C. Yang, L. Zheng, D. Xu, R. Zha, L. Tang, K. Cao, X.-G. Wang and Z. Zhou, Angew. Chem., Int. Ed., 2019, 58, 17782 CrossRef CAS PubMed
.
- D. Yu, D. Wu, J.-Y. Liu, Y. Li and W.-M. Sun, Phys. Chem. Chem. Phys., 2020, 22, 26536 RSC
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary material for method validation, Table S1, Natural orbital population, Table S2, extended version of Tables 2 and 3 on CoS2, FeS2 and Co2S2 cluster isomers, as Tables S3 and S4. Data on M4S4 clusters and full-length data on Li- and Na-cation binding, as well as N2/O2 adsorption are in Tables S5–S8. Molecular electrostatic potential (MEP) maps of Li cation-bonded clusters and the persulphide/disulphide isomerisation in the Fe–S–Zn system are presented in Fig. S1 and S2. See DOI: https://doi.org/10.1039/d2cp02415b |
| This journal is © the Owner Societies 2022 |