Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory investigation of Ru(II) and Os(II) asymmetric transfer hydrogenation catalysts†
Elizabeth M.
Bolitho
 a,
James P. C.
Coverdale
a,
James P. C.
Coverdale
 b,
Juliusz A.
Wolny
b,
Juliusz A.
Wolny
 *c,
Volker
Schünemann
*c,
Volker
Schünemann
 c and
Peter J.
Sadler
c and
Peter J.
Sadler
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK. E-mail: p.j.sadler@warwick.ac.uk
bSchool of Pharmacy, Institute of Clinical Sciences, University of Birmingham, Edgbaston, B15 2TT, UK
cFachbereich Physik, Technische Universität Kaiserslautern, Kaiserslautern, Germany. E-mail: wolny@physik.uni-kl.de
First published on 14th February 2022
Abstract
Transition metal ions have a unique ability to organise and control the steric and electronic effects around a substrate in the active site of a catalyst. We consider half-sandwich Ru(II) (Noyori-type) and Os(II) sulfonyldiamine 16-electron active catalysts [Ru/Os(η6-p-cymene)(TsDPEN-H2)], where TsDPEN is N-tosyl-1,2-diphenylethylenediamine containing S,S or R,R chiral centres, which catalyse the highly efficient asymmetric transfer hydrogenation of aromatic ketones to chiral alcohols using formic acid as a hydride source. We discuss the recognition of the prochiral ketone acetophenone by the catalyst, the protonation of a ligand NH and transfer of hydride from formate to the metal, subsequent transfer of hydride to one enantiotopic face of the ketone, followed by proton transfer from metal-bound NH2, and regeneration of the catalyst. Our DFT calculations illustrate the role of the two chiral carbons on the N,N-chelated sulfonyldiamine ligand, the axial chirality of the π-bonded p-cymene arene, and the chirality of the metal centre. We discuss new features of the mechanism, including how a change in metal chirality of the hydride intermediate dramatically switches p-cymene coordination from η6 to η2. Moreover, the calculations suggest a step-wise mechanism involving substrate docking to the bound amine NH2 followed by hydride transfer prior to protonation of the O-atom of acetophenone and release of the enantio-pure alcohol. This implies that formation and stability of the M–H hydride intermediate is highly dependent on the presence of the protonated amine ligand. The Os(II) catalyst is more stable than the Ru(II) analogue, and these studies illustrate the subtle differences in mechanistic behaviour between these 4d6 and 5d6 second-row and third-row transition metal congeners in group 8 of the periodic table.
Introduction
Catalysts for transfer hydrogenation reactions are important in natural biological systems and in synthetic chemistry. In both cases, the common source of reducing equivalents is hydride, in biology originating from nicotinamide adenine dinucleotide (phosphate), NAD(P)H, or flavin mono- or di-nucleotides, FMNH2/FADH2, and in chemical transformations from formic acid or propanol. Examples are in Table 1. A range of boron, nitrogen, and silicon-based hydride donors are also used in organic transfer hydrogenations.1 Typically substrates are aldehydes, ketones or imines. When the catalyst is chiral (natural or synthetic), transfer hydrogenation is often enantioselective (asymmetric transfer hydrogenation, ATH).| Catalyst | Substrate | Hydride | Conditions | Ref. |
|---|---|---|---|---|
| [RuII(diphosphine)(diamine)Cl2] | Ketones and imines | Formic acid | Acidic | 3 and 4 |
| [RuII(η6-arene)(TsDPEN)Cl] | Ketones and imines | Formic acid | Acidic | 5–11 |
| [(η6-p-cym)Ru(N,N′)Cl] | NAD+ | Formate | Aqueous | 12 |
| [RuII(η6-C6H5(CH2)3NH-DPEN-R)Cl] | Ketones | Formic acid | Aqueous | 13 |
| [RuII(η6-Ph(CH2)3-(en)-N-R)Cl] | NAD+ | Formate | Aqueous | 14 |
| [RuII(phenylpropylamino-TsDPEN)Cl] | Ketones and imines | Formic acid | Cancer cells | 15 |
| [OsII(η6-arene)(TsDPEN)] | Acetophenone | Formic acid | Acidic | 16 and 17 |
| [OsII(η6-arene)(TsDPEN)] | Pyruvate | Formate | Cancer cells | 18 |
| [OsII(η6-arene)(TsDPEN)] | Quinones | Formic acid | Acidic | 19 |
| [Os(η6:κ1-C6H5(CH2)3OH/O)(XY)]+ | Pyruvate | Formate | Cancer cells | 20 |
| [IrIII(Cp*)(N,N)(OH2)] | Quinones | NADH | Aqueous | 21 |
| [(CpXRhIII(N,N′)Cl)]n+ | NAD+ | Formate | Aqueous | 22 |
| [(CpXRhIII(N,N′)Cl)]n+ | Pyruvate | Formate | Aqueous | 22 |
| Lactate dehydrogenase (LDH) | Pyruvate | NADH | Cells | 23 |
| NAD(P)H oxidoreductases | NAD+ | Substrate | Cells | 24 |
Although in some bacteria and archaea. Hydrogenases contain metals (Fe, Ni), in mammals hydrogenases appear to be only non-metalloenzymes. In synthetic chemistry, transition metal catalysts, especially complexes containing Ru(II), Os(II), Rh(III), or Ir(III), are often very efficient and offer a wide range of transformations. Here we concentrate on organometallic half-sandwich Ru(II) and Os(II) ATH catalysts for the asymmetric reduction of the ketone acetophenone, which is often used as a reference substrate. Such complexes are of interest not only for in vitro chemical transformations, but also for their possible activity in living biological cells and potential role in metal-based therapies.2
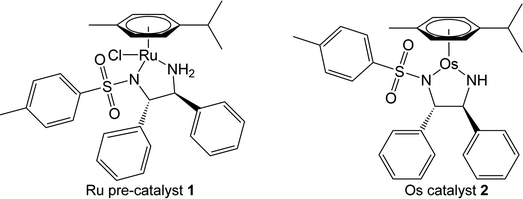
Ruthenium-catalysed ATH of ketones to afford optically pure alcohols was first described by Noyori et al. in the 1990s. The Noyori complex [Ru(p-cymene)(TsDPEN-H)Cl] 1 (where TsDPEN = N-tosyl-diphenylethylenediamine) is a pre-catalyst, which first requires treatment with a base, eliminating HCl to form a coordinatively-unsaturated 16-electron amido active catalyst [Ru(p-cymene)(TsDPEN-H2)], a neutral complex deprotonated at each N of the chelate ring. The role of the sulfonyl substituent in stabilising the doubly-deprotonated chelated diamine ligand is notable.
The commonly accepted catalytic cycle (Fig. 1) requires hydride and proton sources, which facilitate the in situ generation of a neutral 18-electron hydride complex [Ru(p-cymene)(TsDPEN-H)H]. Once formed, the hydride complex can transfer hydride to ketones or imines enantioselectively via an outer-sphere ligand-assisted process.5,25,26 The stereoselectivity of reduction is governed by the chirality of the phenylated carbon atoms of the diamine ligand, (S,S)-TsDPEN-H2 typically yielding the S-alcohol reduction product, while (R,R)-TsDPEN-H2 typically yields the R-alcohol.27 The process regenerates the 16-electron active catalyst, which can re-accept hydride from the donor source, thus completing the catalytic cycle.
 | ||
| Fig. 1 The classical TH mechanism for ruthenium arene catalysts. The hydride catalyst is generated from a hydride source (formic acid, blue) which may involve carboxylate O-coordination to the metal centre. Reduction of the prochiral substrate (acetophenone, red) is thought to involve a 6-membered concerted transition state. A CH/π interaction is shown between the η6-arene of the catalyst hydride complex, and the arene substituent of the substrate. Based on ref. 10. | ||
The classical transfer hydrogenation (TH) mechanism involves a 6-membered cyclic transition state (Fig. 1).27 Such a mechanism allows simultaneous hydrogenation of O and C of the substrate carbonyl group by the concerted transfer of catalyst hydridic Ru–H and protic N–H hydrogens. Theoretical calculations have suggested that an alternative β-elimination/insertion mechanism is unlikely, as it requires unfavourable partial de-coordination of the η6-arene ligand from the metal centre.27 A mechanistic study of ATH in DMF/water using [Ru(p-cymene)(TsDPEN-H)Cl] showed that water can hydrogen bond with the substrate during the transition state for hydride transfer, and that hydride transfer becomes more step-wise in nature, as opposed to being truly concerted.28
It is well accepted that observed enantioselectivities in ATH reductions are the result of various steric and electronic factors.29 Interestingly, experiments have indicated that the hydride catalyst interacts with the sterically-congested face of the substrate, rather than the uncrowded face. It has been suggested that a favourable CH/π interaction occurs between the η6-arene ligand (p-cymene) and the aromatic substituent of the carbonyl substrate (Fig. 1) stabilising the more sterically-crowded over the less-crowded transition state.10,27 While the catalyst amine group directs the stereochemistry during the reduction, it is thought that the CH/π interaction stabilizes one of the diastereomeric transition states over the other. This theory has been supported by observations that electron-donating substituents on the substrate increase enantioselectivity, while those bearing electron-withdrawing substituents decrease enantioselectivity. These substituents modulate the ability of the substrate to partake in CH/π interactions,27 thus influencing the stability of the transition state.
However, the theoretical calculations reported to date mostly use simplified models, lacking the pendant phenyl groups of the diamine ligand, as well as the tosylate functional group.10 Similar CH/π interactions have been described between the substrate and the p-cymene ring in other ruthenium ATH catalysts, but again were not sterically hindered around the Ru–NH2 active catalytic site, and did not bear pendant phenyl groups on the diamine ligand.30,31 More recently, a DFT study of the asymmetric transfer hydrogenation of acetophenone N-benzylimine by [Ru(p-cymene)(TsDPEN-H)Cl] identified not only a CH/π interaction between one of the substrate arenes and the p-cymene ligand, but also a second interaction between the other arene ring on the substrate and the proximal pendant phenyl group of the diamine.32
The Os(II) analogues of Ru(II) ATH catalysts have been little studied.33 Though typically considered more inert than Ru(II), and exhibiting slower ligand exchange kinetics, Os(II) complexes have been shown to catalyse TH reactions at comparable, or sometimes greater, rates than their Ru(II) analogues.16 Osmium complexes bearing the chiral ligand (1R,2S)-(+)-cis-1-amino-2-indanol have been shown to catalyse TH reactions to afford chiral alcohols with enantiomeric excesses (ee) > 89%.34 Separately, the conversion and enantioselectivities of base-assisted TH of ketones by osmium catalysts bearing amino acid ligands were found to be highly dependent on the nature of the substrate and the reaction temperature.35
We have reported a series of osmium complexes [Os(η6-arene)(diamine)], analogous to the Noyori ruthenium complex. However, unlike their ruthenium counterparts, the active 16-electron Os(II) catalyst [Os(p-cymene)(TsDPEN-H2)] 2 is highly stable in air, and can be isolated directly, while maintaining catalytic enantioselectivity and exceeding the turnover frequency of the analogous Ru(II) complex (Fig. 2).16 Interestingly, both Ru and Os catalysts maintain catalytic activity in cancer cells, providing the first examples of in-cell TH catalysis (Ru) and in-cell ATH catalysis (Os) using synthetic catalysts, a new potential strategy for the treatment of resistant cancers using low dose metal therapy with a novel mechanism of action.18,36
The exploration of [Os(arene)(TsDPEN-H2)] catalysts has so far been centred on reduction of ketones and subcellular targets for reduction.17,19,37 The chemical mechanism of Os(II)-catalysed hydride transfer has generally been assumed to be similar to the accepted mechanism for Ru(II) analogues. The mechanism of the Os(II)-catalysed TH of pyruvic acid investigated using density functional theory (DFT) at the hybrid meta-GGA level M06 functional in conjugation with 6-31G(d) basis set for small atoms, and Stuttgart relativistic effective core potential basis set for Os (ECP60MDF), recently identified a proton-coupled hydride transfer mechanism, involving interaction between the catalyst η6-arene and substrate carboxyl group, which influences the resulting enantioselectivity.38
In this work, we use full modelling of the Ru(II) and Os(II) [Ru/Os(p-cymene)(TsDPEN-H2)] catalysts to investigate the mechanisms of their catalytic activity in ATH of the ketone acetophenone. Our calculations provide new insight into the transfer of hydride from formic acid to the metal, the recognition of acetophenone by the active hydride complex, and stereoselective hydride transfer along with a proton to the ketone. The roles of the four types of chiral centres present in the catalyst are discussed: axial chirality of the π-bonded p-cymene arene ligand, the two chiral C centres on the TsDPEN-H2 backbone, chirality at the metal centre, and chirality of the 5-membered chelate ring. Such modelling provides unprecedented insights into the mechanism for catalysis of these metal-assisted transfer hydrogenation reactions, and in this case the subtle difference between Ru(II) and Os(II) catalysts.
Results
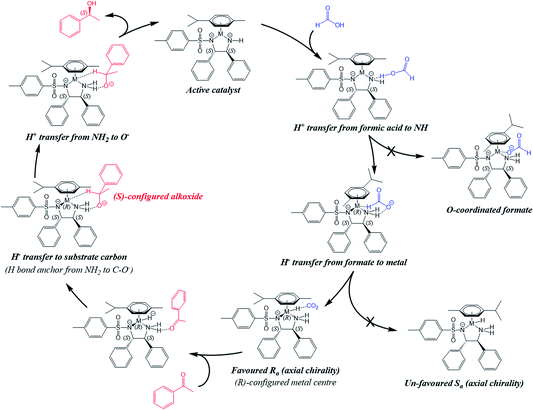
A possible catalytic cycle for the reduction of acetophenone by Ru(II) pre-catalyst 1 [Ru(p-cymene)(TsDPEN-H)Cl] and the Os(II) analogue of the active catalytic species [Os(p-cymene)(TsDPEN-H2)] 2 in the presence of formic acid as a hydride donor was modelled using DFT calculations. First, we describe features of the chiral centres in the models we have constructed by DFT calculations.Stereochemistry of the hydride intermediates
The two phenylated carbons of the diamine backbone of the chelated DPEN ligand are chiral, as is the 5-membered M–N–C–C–N′ chelate ring, which can adopt δ or λ configurations. In our modelling, this chelate ring conformation was found to be always λ for the S,S-chiral ligand; the opposite δ conformation appears to bring about more steric congestion due to closer approach of ligand phenyls and the N–SO2–tolyl group.In the case of Ru complex 1, the pre-catalyst must first eliminate HCl to form the active (less stable) catalytic species. This step is not required for Os complex 2, because it is isolable as a stable species and can be prepared directly by synthesis. For catalysis to proceed, a metal–hydride bond (Ru–H or Os–H) is formed. The hydride complex has a chiral metal centre (Fig. 3, Fig. S4, PDB1 and Fig. S5, PDB2).† Additionally, axial chirality arises from the orientation of the p-cymene ligand with respect to the N,N′-chelate (Fig. 3). The structure of the transition state for inversion of axial chirality of [M(p-cymene)(TsDPEN-H)H] is shown in the ESI (Fig. S1 and Fig. S6, PDB3),† the energy barrier for p-cymene rotation has been estimated to be 18 kJ mol−1 on going from Sa to Ra for the R-absolute configuration of the metal.
 | ||
| Fig. 3 Structures of the R-configured hydride complex [R-M(p-cymene)(S,S-TsDPEN-H)H], where M = Ru or Os showing the axial chirality involving rotation of the π-bonded p-cymene ligand: (a) Sa axial chirality (0 kJ mol−1) and (b) Ra axial chirality (5 kJ mol−1). Note that the chelated ligand contains a protonated NH group (as NH2 in TsDPEN-H), which facilitates hydride transfer to the metal (Fig. S4 and S5, PDB1 and PDB2).† | ||
Metal chirality
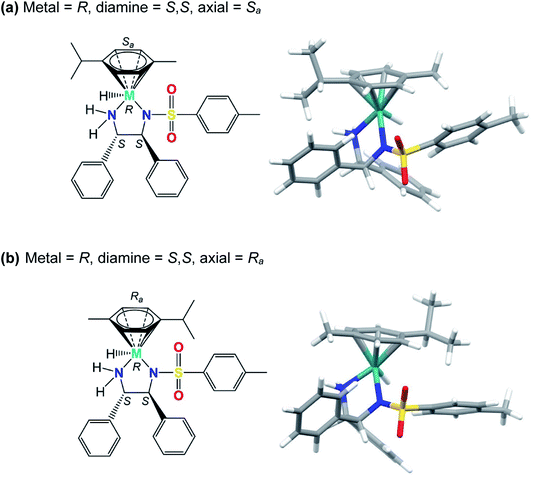
Our modelling shows that the absolute configuration of the metal centre plays a crucial role in determining the electronic energy of the diastereoisomers of complexes containing the (S,S)-ligand. The hydride diastereomers with S chirality (and consequent η2 coordination) are of much higher energy for Ru and Os than for R chirality (η6 coordination). The differences were slightly dependent on the axial chirality, being 111 and 112 kJ mol−1 for the Ra and Sa rotamers of Ru, respectively. The η2 coordination for the Os complexes brings about even more significant energetic destabilisation, yielding values of 146 and 148 kJ mol−1, for the Ra and Sa rotamers, respectively. This suggests that for complexes bearing the (S,S)-configured diamine, diastereomers bearing an S-configured metal centre, S(M), are less stable than their counterparts bearing R-configured metal centres, R(M). They are shown in Fig. 4 and the corresponding PDB files (Fig. S7, PDB4 and Fig. S8, PDB5) are in the ESI.†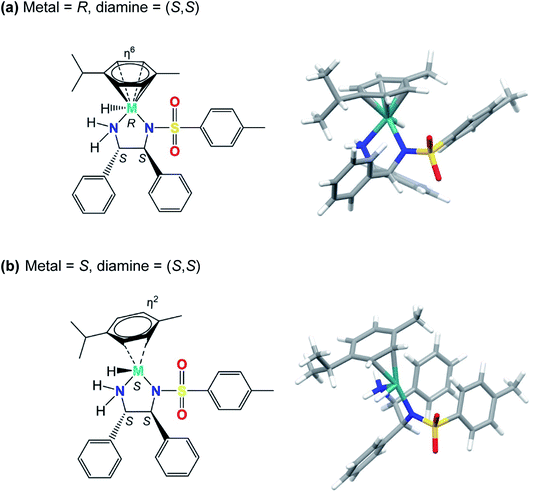 | ||
| Fig. 4 Structures of the [M(η6-p-cymene)(TsDPEN-H)H] diastereomers (where M = Ru/Os) with (a) R or (b) S chirality at the metal centre (M), and (S,S) chiral centres on the sulfonyldiamine ligand. No significant differences could be found between Os and Ru corresponding diastereoisomers. With diamine chirality fixed as (S,S), the isomer with R metal chirality (containing the (S,S) diamine) has p-cymene bound via η6 coordination, and the isomer with S metal chirality (containing the (S,S) diamine) has η2 arene coordination. The energies of the diastereomers with S metal chirality are 145 kJ mol−1 (Os) and 110 kJ mol−1 (Ru) relative to the corresponding diastereomers with R metal chirality. A possible reason for this dramatic change seems to be the higher steric clashes between p-cymene and the sulfonyldiamine ligand phenyl rings. In the case of the R metal chirality diastereoisomer (containing the (S,S) diamine), the p-cymene substituent is further from the phenyl group bound to the TsN-CH carbon than it is from the phenyl group bound to the NH2-CH carbon. For S metal chirality, this congestion is reduced by p-cymene ring slippage (to η2 coordination) with a concomitant shortening of M–N and M–hydride bonds (compare Fig. S7 and S8, PDB4 and PDB5).† | ||
Inspection of the calculated structures reveals a ring slippage on going from the R(M) to the S(M) diastereoisomer with a concomitant change of the cymene coordination mode from η6 to η2. Additionally, on changing from R(M) to the S(M) metal chirality, the Ru–H bond (for Ra axial chirality) shortens from 1.607 to 1.566 Å for Ru complex 1 and from 1.64 to 1.592 Å for Os complex 2. On the other hand, the M–Ntosylate bond shortens from 2.115 to 2.035 Å for the Ru complex and from 2.128 to 2.046 Å for the Os complex. Comparing R(M) and S(M) configurations, the Os–NH2 bond shortens from 2.162 to 2.069 Å, while the Ru–NH2 bond shortens from 2.136 to 2.052 Å, respectively. Apparently, the interchange of the hydride and arene ligands in the S-(S,S) diastereoisomer to give the R-(S,S)-diastereoisomer brings about very extensive steric clashes that are avoided by changing from pseudo-octahedral to strongly-distorted penta-coordination.
Axial chirality
Previous 1H NMR studies revealed the formation of two Os–H singlets (−5.85 and −6.05 ppm) which changed from a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1.2
1 to 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio over time,16 suggesting that a diastereomeric mixture of hydrides was present. However, our calculations reveal ΔG > 100 kJ mol−1 (K < 3 × 10−18) between these diastereomers, which suggests that the two 1H NMR resonances cannot be attributed to the above mixture of diastereomers, and instead are related to further chirality in the molecule. This is most likely the axial chirality (Ra and Sa) with a preference for Sa (0 kJ mol−1) vs. Ra (5 kJ mol−1). This difference of 5 kJ mol−1 between these axial isomers would give a 1
1 ratio over time,16 suggesting that a diastereomeric mixture of hydrides was present. However, our calculations reveal ΔG > 100 kJ mol−1 (K < 3 × 10−18) between these diastereomers, which suggests that the two 1H NMR resonances cannot be attributed to the above mixture of diastereomers, and instead are related to further chirality in the molecule. This is most likely the axial chirality (Ra and Sa) with a preference for Sa (0 kJ mol−1) vs. Ra (5 kJ mol−1). This difference of 5 kJ mol−1 between these axial isomers would give a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 ratio of 1H NMR Os–H peaks, with 20% Sa and 80% Ra.
4 ratio of 1H NMR Os–H peaks, with 20% Sa and 80% Ra.
The transition state for the axial chirality and energy barrier for rotation of the p-cymene is ca. 18 kJ mol−1, implying that rotation may be partially hindered. Hence, in the DFT modelling, both possible axial chiralities were considered (Fig. 3). In future work, the stereochemical relationship between the hydride and p-cymene substituents could be investigated by NOESY NMR.
The reaction profile of the reduction of acetophenone
The reaction profile for the reduction of acetophenone catalysed using the ruthenium pre-catalyst [Ru(p-cymene)(S,S-TsDPEN-H2)Cl] was modelled with formic acid as the solvent. The species with minimal energy was found to be the hydride complex with the acetophenone bound via π–π stacking to the tosylate phenyl ring. The following species were identified (Fig. 5).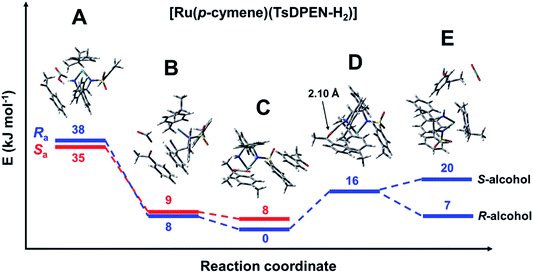 | ||
| Fig. 5 Energy profile for the reduction of acetophenone catalysed by [Ru(p-cymene)(S,S-TsDPEN-H2)], with formic acid as the hydride donor. Note the axial chirality was taken into account only for the first three steps. Species A: [Ru(p-cymene)(S,S-TsDPEN-H2)] + formic acid + acetophenone (Fig. S10 and S11, PDB7 and PDB8†). Species B: [Ru(p-cymene)(S,S-TsDPEN-H)]+ + formate + acetophenone (the white dot in the middle is showing the transfer of H+), Fig. S12 and S13, PDB9 and PDB10.† Species C: [R-Ru(p-cymene)(S,S-TsDPEN-H)H] + CO2 + acetophenone (Fig. S2 and S9: PDB6, Fig. S14 and S15: PDB11 and PDB12†). Species D: [R-Ru(p-cymene)(S,S-TsDPEN-H-acetophenone)H] + CO2 (Fig. S16, PDB13†) Species E: [Ru(p-cymene)(S,S-TsDPEN-H2)] + CO2 + phenylethanol (Fig. S17 and S18, PDB14 and PDB15†). Note, bonds between Ru and p-cymene are omitted for clarity. | ||
Species A [Ru(p-cymene)(S,S-TsDPEN-H2)] + formic acid + acetophenone: The initial complex corresponds to the product formed after HCl abstraction from the pre-catalyst. The NH2 group of the TsDPEN ligand is deprotonated (Ru–NH) and with a ca. 2.4 Å contact with H–C hydrogen of a HCO2H molecule. Acetophenone is weakly bound to the complex, lying approximately parallel to formic acid and one of the phenyl rings of the nitrogen ligands (Fig. S10 and S11, PDB7 and PDB8† for both rotamers differing in axial chirality). These species lie 35–38 kJ mol−1 higher in energy than the hydride species, with Ra axial chirality being of slightly higher energy than Sa.
Species B [Ru(p-cymene)(S,S-TsDPEN-H)]+ + formate + acetophenone: This species results from protonation of the NH group of the ligand (Fig. S12 and S13, PDB9 and PDB10†). The transferred proton has ca. 1.69 Å contact with a formate oxygen. The protonation leads to a significant lowering of the electronic energy, which is now only approximately 8 kJ mol−1 higher than that of the reference Ru–H hydride.
Remarkably, the next step (B to C) does not correspond to carboxylate O-coordination of formate to the metal, as previously proposed.39 Our modelling revealed that imposing such a coordination in the starting structure leads to a movement of formate onto the rim of the catalyst (Ru–O distance > 3 Å) due to a stronger interaction between the formate oxygen and the diamine ligand NH2, leading to a significant increase in energy of the species (due to the poor acidity of the amine). The same effect was established for the osmium analogue.
Species C [Ru(p-cymene)(S,S-TsDPEN-H)H] + CO2 + acetophenone: The next structure in the catalytic cycle is the M–H hydride complex. As stated above, for the (S,S) chirality of the chelated ligand, only the η6-p-cymene M(R)-enantiomers of the hydride complex are stable. Due to axial chirality, two diastereoisomers are possible, of which Ra chirality is the most stable species in the catalytic cycle, the Sa diastereoisomer being 8 kJ mol−1 higher in energy (note that with bound acetophenone this is contrary to the isolated hydride system discussed above). The PDB structures of both diastereoisomers differing in axial chirality are given in the ESI† (Fig. S14 and S15, PDB11 and PDB12) and are shown in Fig. 6. Two noteworthy features of these structures are that acetophenone is bound via π–π stacking to the tosylate phenyl, and there is a significant interaction of the formed CO2 molecule with the M–H hydride, with a H–C distance of ca. 2.6 Å (Fig. 5 and 6).
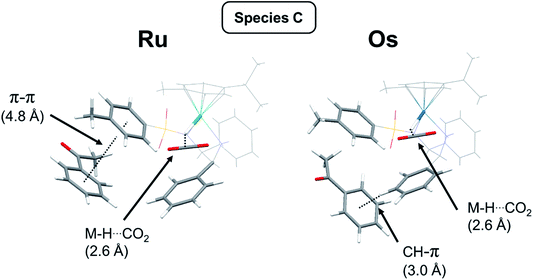 | ||
| Fig. 6 Structures of species C (M = Ru or Os) showing the interaction of [M(η6-p-cymene)](TsDPEN-H)H (with R metal chirality, (S,S) ligand chirality, and Ra chirality) with acetophenone (substrate). The relevant molecular fragments are highlighted for clarity. For the Ru system, π–π interaction between acetophenone and the tosylate ring is seen, whereas for the Os complex, both rings are shifted, and a pendant phenyl ring (from the diamine ligand) points towards the ketone phenyl ring (dashed line, CH⋯C(ring) distance of 3.04 Å). Both Ru and Os show interaction (2.6 Å) between the metal hydride and CO2 (Ru: Fig. S15, PDB12; and Os: Fig. S24, PDB21†). | ||
Species D [Ru(p-cymene)(S,S-TsDPEN-H-acetophenone)H] + CO2: The next structure in the catalytic cycle that we were able to identify by DFT modelling is the hydride complex with acetophenone anchored to the catalyst via a carbonyl-O⋯HNH hydrogen bond (2.127 Å). The structure of its axial Ra-diastereomer can be found in Fig. S16, PDB13.†
Other possibilities for substrate docking were explored, such as hydride–carbonyl contact, and the previously proposed simultaneous proximity of the substrate carbonyl group and the amine hydrogen/hydride pair (with two possible arrangements, i.e. hydride–carbon and hydride oxygen proximity).16 All of these models led to movement of the ketone molecule onto the rim of the complex. It appears that these arrangements are energetically unfavourable due to both electronic and steric reasons.
Species E [Ru(p-cymene)(S,S-TsDPEN-H2)] + CO2 + phenylethanol: This final species corresponds to the reduced ketone (the alcohol) with S- or R-chirality and the initial catalyst described for species A. Interestingly, interactions between both molecules lead to a lower energy in the case of the [Ru(p-cymene)(S,S-TsDPEN-H2)]/R-alcohol pair (8 kJ mol−1) compared to that with the S-alcohol pair (20 kJ mol−1). This is in contrast with the previously reported high enantioselectivity for formation of the S-alcohol with the (S,S)-ligand, and R-alcohol from the (R,R)-ligand. The most likely explanation is that the observed enantioselectivity arises from kinetic factors rather than the thermodynamic energies revealed by the DFT calculations (vide infra). Structures can be found in Fig. S17 and S18 (PDB14 and PDB15).†
The reaction profile for [Os(p-cymene)(S,S-TsDPEN-H2)] is shown in Fig. 7. The energy profile for the osmium complex is similar to that of ruthenium. The first difference is that the energy of species B, corresponding to the second stage, i.e. protonation of the chelated sulfonyldiamine ligand by formic acid, is ca. 8 kJ mol−1 higher for the osmium complex. On the other hand, the energy of the structure with the N–H bound ketone (D) relative to the hydride structure C is 8 kJ mol−1 higher than for the ruthenium analogue. Apart from that, there are subtle differences in the way acetophenone interacts with the Ru and Os complexes. The corresponding structures are compared in Fig. 6. While for the Ru system, clear π–π interaction involving the acetophenone and tosylate ring is seen, for the Os complex, both rings are shifted and a chelated ligand phenyl ring points towards the ketone phenyl ring, revealing a C–H⋯aromatic ring interaction with C–H⋯C(ring) distance of 3.04 Å (dashed line in Fig. 6).
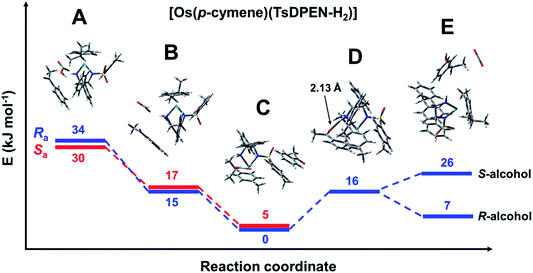 | ||
| Fig. 7 Energy profile for the reduction of acetophenone catalysed by [Os(p-cymene)(S,S-TsDPEN-H2)]. Note the axial chirality was taken into account only for the first three steps. Species A: [Os(p-cymene)(S,S-TsDPEN-H2)] + formic acid + acetophenone (Fig. S19 and S20, PDB16 and PDB17†). Species B: [Os(p-cymene)(S,S-TsDPEN-H)]+ + formate anion + acetophenone (Fig. S21 and S22, PDB18 and PDB19†). Species C: [Os(p-cymene)(S,S-TsDPEN-H)H] + CO2 + acetophenone (Fig. S23 and S24, PDB20 and PDB21†). Note the different mode of interactions of acetophenone compared to the corresponding Ru–hydride. Species D: [Os(p-cymene)(S,S-TsDPEN-H-acetophenone)H] + CO2 (Fig. S25, PDB22†). Species E: [Os(p-cymene)(S,S-TsDPEN-H2)] + CO2 + phenylethanol (Fig. S26 and S27, PDB23 and PDB24†). | ||
Mechanistic considerations
The structure identified for the ruthenium hydride complex with acetophenone bound to an NH2 hydrogen of the ligand is a plausible starting point for the reduction. As shown in Fig. 8, the ketone and catalyst molecules are pre-organised so that the vector defined by the hydride and carbonyl carbon atom points towards one of the enantiotopic faces of the ketone. We have modelled several variants of the reduction starting from this assembly; the only one with a reasonably low-energy structure involves a starting geometry in which only the hydride was set closer to the carbonyl carbon, while the amine proton is still bound to nitrogen, i.e. there is no concerted transfer of hydride and proton. Geometry optimisation led first to formation of the S-alkoxide bound to the NH2 group of the ligand, and then a gradual transfer of the amino proton to form the alcohol. The final product corresponds to the recovered catalyst with S-phenylethanol (α-methylbenzyl alcohol) forming a contact to the NH group of the ligand via a hydrogen bond (OH⋯N distance of 2.41 Å) (see Fig. 8). The estimated transition state between this and the ketone bound to the hydride complex via NH⋯O hydrogen-bonding (structure D in Fig. 7) is shown in Fig. 9. It corresponds to the above-mentioned S-alkoxide bound to the NH2 group of the ligand.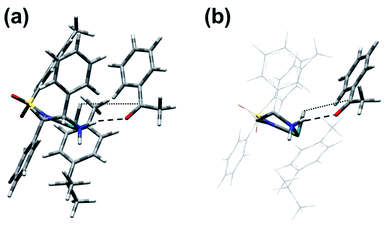 | ||
| Fig. 8 (a) Pre-organisation of the [Ru(p-cymene)(S,S-TsDPEN-H)]/acetophenone assembly with CO⋯H2N H-bonding (denoted by the dashed line), the initial stage of the catalytic cycle. Note that the vector defined by hydride H and carbonyl C atoms points towards one of the enantiotopic faces of the ketone. (b) Simplified scheme to highlight bonding interactions between catalyst diamine and substrate carbonyl (Fig. S16, PDB13†). | ||
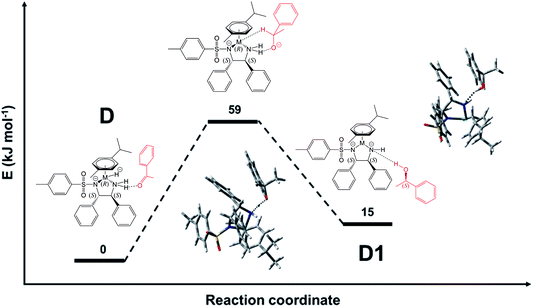 | ||
| Fig. 9 QST-estimated structure for the transition state from species D, in which the acetophenone keto group is bound to the catalyst NH2, to the recovered Ru-catalyst D1, in which the product alcohol is still bound via HN⋯HO bond. The transition state is estimated to lie 59 kJ mol−1 above the structure with minimal energy (D). The contacts indicated by dashed lines in the transition state are 1.32 Å for NH⋯OC (see Fig. S28, PDB25†) and 1.20 Å (O–H⋯N). For species D, the N–H⋯OC distance is 2.13 Å (Fig. S16, PDB13†), while O–H⋯N for species D1 is 2.41 Å (Fig. S29, PDB26†). | ||
Within this model, the chirality of the reduced acetophenone is S (for the S,S absolute configuration of the chelated ligand) in line with experimental findings.16 This agreement suggests that the poor acidity of the NH2 group plays an important role in the mechanism, as was also seen above in the destabilisation of the Ru–O(formate) bond. It seems that this is even more pronounced for a hydride complex, while the dissociation of a proton from the NH2 group would lead to an effective combined charge of −3 from the hydride and sulfonyldiamine N ligands. Thus, it is the initial transfer of hydride that then allows the transfer of the NH2 proton to regenerate the active catalyst.
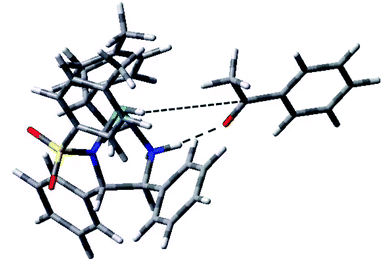
We checked the possibility of the exchange of the phenyl and methyl groups shown in Fig. 8 that might lead to the possibility of attack of hydride on the alternative enantiotopic face. We optimised the geometry of such a structure, as shown in Fig. 10. It is ca. 9 kJ mol−1 higher in energy than the molecule shown in Fig. 8. Significantly, it does not appear to be pre-organised in favour of a particular enantiomer of the reduction product.
 | ||
| Fig. 10 Another conformer of the [Ru(p-cymene)(S,S-TsDPEN-H)H]/acetophenone assembly with the CO⋯HN hydrogen bonding (dashed line). The second dashed line is the vector defined by hydride H and carbonyl C atoms which lies nearly perfectly in the ketone plane, so there is no preference for either diastereotopic face, unlike the conformation shown in Fig. 8 (Fig. S28, PDB25†). | ||
This structure corresponds to another stereoisomer regarding the orientation of the ketone O⋯HN contact. The hydride ligand lies nearly perfectly in the plane of the ketone fragment of acetophenone, i.e. in the plane defining the enantiotopic faces. Considering the possibilities for different orientations of the p-cymene ring, leading to different axial chirality, at least four different stereoisomers of the complex with hydrogen-bonding from the catalyst amine to the bound ketone oxygen, would be expected. Each of them may reveal different energies and pre-organisation, leading to a given enantiomer of the product and corresponding to a different transition state.
Overall, our calculations suggest that the reduction of acetophenone using such catalysts proceeds first by docking of the ketone substrate onto an amine NH2 proton of the chelated sulfonyldiamine ligand, followed by enantioselective hydride transfer onto a particular face of the ketone carbonyl carbon. Then, protonation occurs by transfer of a proton from the amine NH2 to the ketone oxygen to release the enantiopure alcohol. Moreover, the hydride complex is highly dependent for stability on the presence of the amine NH2 protons. The proposed sequence of steps and cycle for the reduction of acetophenone by the Ru(II) and Os(II) catalysts, and the stereoisomer preference with hydrogen-bonded ketone, corresponding to the molecule in Fig. 8, are shown in Fig. 11 and 12, respectively.
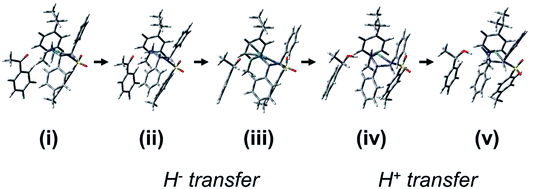 | ||
| Fig. 11 The sequence of processes for the reduction of acetophenone by the Ru(II) catalyst starting from the H-bonded ketone. (i) Species C (Fig. S15, PDB12†). (ii) Possible transition state for hydride transfer towards the carbonyl group with preference for one enantiotopic face of the substrate ketone (cf.Fig. 8). (iii) The alkoxide is formed, with catalyst NH2 group still retained (Fig. S29, PDB26†). (iv) Transition state for the amino proton transfer (Fig. S28, PDB25†). (v) Catalyst NH− adopts trigonal planar geometry (Fig. S31, PDB28†). | ||
Discussion of experimental evidence
In the absence of experimental evidence, DFT calculations may lead to spurious possibilities. These DFT calculations serve to stimulate our thinking about the detailed mechanism of asymmetric transfer hydrogenation of ketones by half-sandwich Ru(II) and Os(II) arene complexes, especially for Os(II) catalysts, which have only recently been explored, and the design of experiments to provide evidence for the proposed pathways. In this section, we briefly discuss our calculations in the context of existing experimental data.We have reported that reduction of acetophenone using the 16-electron Os(II) catalyst 2 yields the S-configured alcohol (S-phenylethanol) in the presence of the Os catalyst bearing an S,S-diamine ligand.16 Similarly, the R-configured alcohol was obtained by reduction in the presence of the catalyst bearing an R,R-diamine ligand. Alcohol chirality was determined after workup and extraction, using chiral chromatography (GC-MS using a chrompac cyclodextrin-β-236M-19 column). DFT calculations for the S,S-catalyst initially indicated that the energy of the S-alcohol and the 16-electron catalyst is higher than the corresponding assembly with the R-alcohol, thus if the reaction outcome was purely governed by thermodynamics, the predicted enantioselectivity of the reduction would be opposite to experimental observations. It seems likely therefore that experimental enantioselectivity is driven by the kinetics of the hydride transfer.
Three possible orientations of substrate and catalyst were considered: (1) the structure with the minimum energy, in which the acetophenone ketone substrate is π–π stacked with the diamine pendant phenyl groups far away from the catalyst hydride and NH2 (for Ru but not Os, Fig. 6), (2) O–HN bound ketone where the hydride is oriented towards one of the enantiotopic faces of the ketone (Fig. 8 for Ru), and (3) O–HN bound ketone with hydride oriented towards the plane of the ketone with no preference for either enantiotopic face of the ketone (Fig. 10 for Ru). The stereoisomers for orientations (2) and (3) are +16 and +25 kJ mol−1, respectively, higher in energy than the π–π structure. In fact, the kinetically-favoured formation of the alcohol involves hydride transfer to the carbonyl with preference for one of the enantiotopic faces. In the case of orientation (2), this corresponds to the observed experimental enantioselectivity. Thus, the calculated stereochemical model for the TH of acetophenone agrees with the experimental data. Further DFT modelling will explore the transition states for all stereoisomers (i.e. two orientations of bound ketone, with two different axial chiralities, for both Ru and Os).
As a result of the present DFT calculations, we can now suggest that the two Os–H 1H NMR resonances observed in spectra of the active hydride species (with chemical shifts of −5.89 and −6.04 ppm, and 187Os satellites, 1J(1H, 187Os) = 44 Hz), can be assigned to the two possible axial conformers (Ra and Sa), and not to a mixture of Os–H diastereomers as originally proposed.16 Calculated energies of the axial species suggest that they would be present in an 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, in agreement with experimental observations.
1 ratio, in agreement with experimental observations.
Future experimental studies of these Os(II) catalysts might involve the use of deuterium-labelled formate to probe kinetic isotope effects and the stereospecificity for H/D transfer. Such reported studies for Ru(II) have indicated that H transfer from formate to the ketone is rate-limiting, and (in agreement with the DFT calculations above) that H transfer is sequential rather than concerted.
Conclusions
Catalytic delivery of hydrogen to a substrate to carry out chemical reduction can be achieved by different systems (metal or organic) in a variety of ways. For metal-catalysed reactions, this could involve redox change at the metal centre, however in the case of transfer hydrogenation, the reduction occurs via an outer-sphere process, with no apparent direct interaction between the substrate and the catalyst metal centre. For Ru/TsDPEN systems, the TH mechanism is generally well understood: experiments have demonstrated transfer of deuterium (2H) from formate to the substrate,28 and many reports have explored the breadth of compatible substrates, including how particular substituents impact conversion and enantioselectivity. Various sources of hydride have been explored, including 2-propanol and formic acid in chemical systems,5,25 as well as organic hydride donors, such as NADH, in biological systems.36 More recently, computational studies have provided detailed insight into the subtler aspects of the ATH mechanism.30,32We have modelled the catalytic reduction of acetophenone using the Noyori ruthenium TsDPEN catalyst, and its analogous osmium complex, in the presence of formic acid, revealing a novel interaction between the substrate and the chiral diamine ligand. We find the electronic energies of the diastereomers of the chiral diamine ligand to be dependent on the absolute configuration at the Ru/Os centre: The S diastereomer is less stable than the R diastereomer due to extensive steric clashes, resulting in ring slippage (from η6 to η2) for the latter. Previous 1H NMR studies revealed the formation of two Os–H singlets which changed from a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1.2
1 to 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio over time, suggesting a mixture of these diastereomers. However, our calculations suggest that this not the case, and this observation arises instead as a consequence of axial chirality (p-cymene orientation).
1 ratio over time, suggesting a mixture of these diastereomers. However, our calculations suggest that this not the case, and this observation arises instead as a consequence of axial chirality (p-cymene orientation).
Modelling of the reaction profile for the reduction of [Ru(p-cymene)(S,S-TsDPEN-H)Cl] and [Os(p-cymene)(S,S-TsDPEN-H2)] with formic acid revealed acetophenone preferentially bound via π–π stacking to the tosylate phenyl ring, followed by protonation of the amino group of the ligand. Remarkably, our calculations suggest that the formation of Ru/Os–H does not occur via O-coordinated formate as proposed previously, instead involving a significant interaction between CO2 product and the metal-hydride. In the final DFT structure in the catalytic cycle, acetophenone is anchored to the catalyst via a H-bond between the substrate carbonyl-O⋯HNH group. Further geometry optimisation revealed the formation of alkoxide bound to the NH2 group, leading to gradual amino proton transfer, suggesting that hydride transfer itself allows the dissociation of the NH2 to form the initial pre-catalyst. Moreover, our calculations suggest that substrate docking to the amine followed by hydride transfer occurs prior to substrate protonation. Thus, the presence of the amine proton is crucial for the stability of the hydride.
In future work, efforts will be made to identify the transition states for all possible (minimum four) diastereoisomers involving the H-bonded ketone, with calculation of the pathways along the identified internal reaction coordinate for both Ru and Os analogues, following the approach outlined previously.29 It is envisaged that a detailed understanding of the reaction coordinates for both metals will provide mechanistic insights into why the osmium complexes can achieve higher rates of catalysis for ATH reduction compared to their well-established ruthenium analogues, even after accounting for dissociation of HCl from the pre-catalyst.
It will also be interesting to discuss and compare the mechanisms for transfer hydrogenation catalysed by the organometallic complexes described here, with those for purely organic catalysts, including natural enzymes. The effective (stereospecific) addition of H2 to substrates may involve reductants ranging from H2 itself, to sequential addition of H˙ (H atoms), electrons, and protons. For both types of catalyst, there are likely to be key roles for neighbouring groups in recognising and orienting the substrate, and transferring the reducing equivalents. The versatile ability of metal ions in transition metal coordination complexes to organise the structures and electronic properties of their ligands in the first and second coordination spheres, to generate ‘H2’, as well as control the dynamics of substrate recognition and product release, through changes in coordination numbers and coordination geometries and oxidation states, is notable.
Materials and methods
DFT calculations
The calculations were performed with the Gaussian 16 packet.40 The relevant structures were optimised using the TPSS functional,41 and QZVP basis set.42 Grimme’s D3 dispersion correction was applied.43 Gaussian’s IEFPCM option was used to model the formic acid as solvent. Typically, the optimization of the geometry for each energy minima shown takes two to three months using the parallel computations with 24 Intel XEON SP 6126 (http://ark.intel.com/products/120483/) processors (cf.https://elwe.rhrk.uni-kl.de/elwetritsch/hardware.shtml). No imaginary frequencies were found for the optimized geometries. The data for the transition states of the cymene rotation and hydride transfer are estimated only as corresponding to not yet fully optimized geometries. All computational data are available from JAW on request.Author contributions
The research was conceptualized by EMB, JPCC, JAW, VS and PJS. Formal analysis was carried out by JAW with methodology and investigation supported by EMB, JPCC and PJS. Writing of the original draft, review and editing was carried out by EMB, JPCC, JAW and PJS.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
We thank Diamond Light Source and Warwick Collaborative Postgraduate Research Scholarship (WCPRS, PhD award for E. M. B.), the Engineering and Physical Sciences Research Council (EPSRC grant no. EP/P030572/1), and Anglo American Platinum (for P. J. S.), for funding. V. S. and J. A. W. acknowledge support by the research initiative NANOKAT, as well as Allianz für Hochleistungsrechnen Rheinland–Pfalz (AHRP) for providing CPU-time within the project TUK-SPINPLUSVIB.Notes and references
- S. Ilic, A. Alherz, C. B. Musgrave and K. D. Glusac, Chem. Soc. Rev., 2018, 47, 2809–2836 RSC
.
- S. Banerjee and P. J. Sadler, RSC Chem. Biol., 2021, 2, 12–29 RSC
.
- T. Ohkuma, Proc. Jpn. Acad., Ser. B, 2010, 86, 202–219 CrossRef CAS PubMed
.
- C. A. Sandoval, T. Ohkuma, K. Muñiz and R. Noyori, J. Am. Chem. Soc., 2003, 125, 13490–13503 CrossRef CAS PubMed
.
- R. Noyori and S. Hashiguchi, Acc. Chem. Res., 1997, 30, 97–102 CrossRef CAS
.
- J. Václavík, P. Sot, B. Vilhanová, J. Pecháček, M. Kuzma and P. Kačer, Molecules, 2013, 18, 6804–6828 CrossRef PubMed
.
- T. Ikariya and A. J. Blacker, Acc. Chem. Res., 2007, 40, 1300–1308 CrossRef CAS PubMed
.
- T. Ikariya, K. Murata and R. Noyori, Org. Biomol. Chem., 2006, 4, 393–406 RSC
.
- M. Yamakawa, H. Ito and R. Noyori, J. Am. Chem. Soc., 2000, 122, 1466–1478 CrossRef CAS
.
- M. Yamakawa, I. Yamada and R. Noyori, Angew. Chem., Int. Ed., 2001, 40, 2818–2821 CrossRef CAS PubMed
.
- T. Ohkuma, N. Utsumi, K. Tsutsumi, K. Murata, C. Sandoval and R. Noyori, J. Am. Chem. Soc., 2006, 128, 8724–8725 CrossRef CAS PubMed
.
- F. Chen, J. J. Soldevila-Barreda, I. Romero-Canelón, J. P. C. Coverdale, J.-I. Song, G. J. Clarkson, J. Kasparkova, A. Habtemariam, V. Brabec, J. A. Wolny, V. Schünemann and P. J. Sadler, Dalton Trans., 2018, 47, 7178–7189 RSC
.
- R. Soni, T. H. Hall, B. P. Mitchell, M. R. Owen and M. Wills, J. Org. Chem., 2015, 80, 6784–6793 CrossRef CAS PubMed
.
- F. Chen, I. Romero-Canelón, J. J. Soldevila-Barreda, J. I. Song, J. P. C. Coverdale, G. J. Clarkson, J. Kasparkova, A. Habtemariam, M. Wills, V. Brabec and P. J. Sadler, Organometallics, 2018, 37, 1555–1566 CrossRef CAS PubMed
.
- Y. Fu, C. Sanchez-Cano, R. Soni, I. Romero-Canelon, J. M. Hearn, Z. Liu, M. Wills and P. J. Sadler, Dalton Trans., 2016, 45, 8367–8378 RSC
.
- J. P. C. Coverdale, C. Sanchez-Cano, G. J. Clarkson, R. Soni, M. Wills and P. J. Sadler, Chem.–Eur. J., 2015, 21, 8043–8046 CrossRef CAS PubMed
.
- E. M. Bolitho, J. P. C. Coverdale, H. E. Bridgewater, G. J. Clarkson, P. D. Quinn, C. Sanchez-Cano and P. J. Sadler, Angew. Chem., Int. Ed., 2021, 60, 6462–6472 CrossRef CAS PubMed
.
- J. P. C. Coverdale, I. Romero-Canelón, C. Sanchez-Cano, G. J. Clarkson, A. Habtemariam, M. Wills and P. J. Sadler, Nat. Chem., 2018, 10, 347–354 CrossRef CAS PubMed
.
- E. M. Bolitho, N. G. Worby, J. P. C. Coverdale, J. A. Wolny, V. Schünemann and P. J. Sadler, Organometallics, 2021, 40, 3012–3023 CrossRef CAS
.
- S. Infante-Tadeo, V. Rodríguez-Fanjul, A. Habtemariam and A. M. Pizarro, Chem. Sci., 2021, 12, 9287–9297 RSC
.
- S. Betanzos-Lara, Z. Liu, A. Habtemariam, A. M. Pizarro, B. Qamar and P. J. Sadler, Angew. Chem., Int. Ed., 2012, 51, 3897–3900 CrossRef CAS PubMed
.
- J. J. Soldevila-Barreda, A. Habtemariam, I. Romero-Canelón and P. J. Sadler, J. Inorg. Biochem., 2015, 153, 322–333 CrossRef CAS PubMed
.
- M. J. Rogatzki, B. S. Ferguson, M. L. Goodwin and L. B. Gladden, Front. Neurosci., 2015, 9, 22 Search PubMed
.
- L. Sellés Vidal, C. L. Kelly, P. M. Mordaka and J. T. Heap, Biochim. Biophys. Acta, Proteins Proteomics, 2018, 1866, 327–347 CrossRef PubMed
.
- A. Fujii, S. Hashiguchi, N. Uematsu, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1996, 118, 2521–2522 CrossRef CAS
.
- K.-J. Haack, S. Hashiguchi, A. Fujii, T. Ikariya and R. Noyori, Angew. Chem., Int. Ed. Engl., 1997, 36, 285–288 CrossRef CAS
.
- R. Noyori, M. Yamakawa and S. Hashiguchi, J. Org. Chem., 2001, 66, 7931–7944 CrossRef CAS PubMed
.
- X. Wu, J. Liu, D. Di Tommaso, J. A. Iggo, C. R. Catlow, J. Bacsa and J. Xiao, Chem.–Eur. J., 2008, 14, 7699–7715 CrossRef CAS PubMed
.
- P. A. Dub and J. C. Gordon, Dalton Trans., 2016, 45, 6756–6781 RSC
.
- Y. Meftah, Y. Boumedjane, P. Fleurat-Lessard, F. Delbecq and C. Michel, J. Organomet. Chem., 2021, 939, 121765 CrossRef CAS
.
- J.-W. Handgraaf and E. J. Meijer, J. Am. Chem. Soc., 2007, 129, 3099–3103 CrossRef CAS PubMed
.
- P. Šot, M. Kuzma, J. Václavík, J. Pecháček, J. Přech, J. Januščák and P. Kačer, Organometallics, 2012, 31, 6496–6499 CrossRef
.
- P. Crochet and V. Cadierno, Inorganics, 2021, 9, 55 CrossRef CAS
.
- J. W. Faller and A. R. Lavoie, Org. Lett., 2001, 3, 3703–3706 CrossRef CAS PubMed
.
- R. A. Sarfraz, T. G. Kazi, S. Iqbal, H. I. Afridi, M. K. Jamali, N. Jalbani and M. B. Arain, Appl. Organomet. Chem., 2008, 22, 187–192 CrossRef CAS
.
- J. J. Soldevila-Barreda, I. Romero-Canelón, A. Habtemariam and P. J. Sadler, Nat. Commun., 2015, 6, 6582 CrossRef CAS PubMed
.
- J. P. C. Coverdale, H. E. Bridgewater, J.-I. Song, N. A. Smith, N. P. E. Barry, I. Bagley, P. J. Sadler and I. Romero-Canelón, J. Med. Chem., 2018, 61, 9246–9255 CrossRef CAS PubMed
.
- W. Wang and X. Yang, Chem. Commun., 2019, 55, 9633–9636 RSC
.
- J. J. Soldevila-Barreda, P. C. A. Bruijnincx, A. Habtemariam, G. J. Clarkson, R. J. Deeth and P. J. Sadler, Organometallics, 2012, 31, 5958–5967 CrossRef CAS
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146404 CrossRef PubMed
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154118 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1fd00075f |
| This journal is © The Royal Society of Chemistry 2022 |