Open Access Article
Open Access ArticleFlowmetering for microfluidics
C. Cavaniol *ab,
W. Cesarb,
S. Descroix
*ab,
W. Cesarb,
S. Descroix a and
J.-L. Viovy
a and
J.-L. Viovy *a
*a
aInstitut Curie and Institut Pierre Gilles de Gennes, PSL Research University, CNRS UMR 168, Paris, France. E-mail: charles.cavaniol@curie.fr
bFluigent SAS, Kremlin-Bicêtre, France
First published on 23rd June 2022
Abstract
Originally designed for chromatography, electrophoresis, and printing technologies, microfluidics has since found applications in a variety of domains such as engineering, chemistry, environmental, and life sciences. The fundamental reason for this expansion has been the development of miniature components, allowing the handling of liquids at the microscale. For the maturation of microfluidic technologies, the need for affordable, reliable, and quantitative techniques to measure flow rates from 1 nL min−1 to 1 mL min−1 appears as a strong challenge. We review herein the different technologies available and those under development, and discuss their sensing principles and industrial maturity. Given the need of traceability of these measurements, we then focus on the developments of primary standards to measure microfluidic flow rates by metrological institutes. We conclude this review with some perspectives and pending challenges for microfluidic flowmeters.
1 Introduction
The field of microfluidics emerged in the 70's, and has since grown in a quasi-exponential way, becoming one of the main empowering technologies in biology and medicine (see ref. 1–3 for reviews). Microfluidics was defined by Stone et al. as the “devices and methods for controlling and manipulating fluid flows with length scales less than a millimeter”.4 Practical achievements, however, had already been proposed earlier. In 1965, Richard Sweet at Standford University developed an inkjet printer using a vibrating nozzle with a 35 μm hole,5 which is regarded as the first microfluidic device.3,6 This work was continued by Bassous et al. at IBM.7 Inkjet printing is now a multibillion US$ market, and is still based on microfluidics, making it, volume-wise, a major field of application. The next step in microfluidics history was initiated at Standford University by Terry et al., who developed the first miniaturized gas chromatograph using a silicon wafer.8,9 Microfluidics has since then raised interest in a constantly increasing range of applications, taking advantage of several unique features: i/in direct inspiration from microelectronics, microfluidics allows to achieve high integration, automation, and parallelization of multiple steps (leading to the concept of “microfluidic processor” and “Micro-Total Analysis System”, a term first coined by Widmer and Manz10); ii/microfluidics allows the reliable manipulation of sub-microliter quantities of fluids, and thus a dramatic reduction in this device's sizes and the required sample and reagent quantities; iii/finally, microfluidics has also opened the route to intrinsically new concepts, such as “digital PCR”11,12 or “organs on chip”.13–15 These intrinsic advantages have resonated with biological and medical markets, in which reagents and samples can be extremely limited and expensive, and the development of systems in biology and molecular medicine has called for massively parallel analyses. In 2013, the microfluidic market was valued at US$ 1.6 billion,16 and is expected to reach US$ 44.0 billion by 2025.17 This high growth rate is largely due to recent applications in genomics, point-of-care diagnostics, and drug delivery systems.18–20 However, such an expansion could only be achieved thanks to the development of functional components, allowing the handling of liquids at the microscale and, in particular, in actuators and sensors.21,22 According to the market survey Results survey on microfluidics flow control performed in 2015 with industrial and academic players in microfluidics by enabling MNT,23 the properties of fluids used vary significantly depending on the application, from gas to liquid, aqueous to organic, monophasic or a multi phasic, Newtonian or not, with a viscosity ranging from 1 to 1000 mPa s. Moreover, flow conditions may also vary widely with commonly applied flow rates ranging from 1 nL min−1 to 1 mL min−1 in continuous or pulsating mode. Lastly, temperature and pressure ranges can vary from 0 to 100 °C and from 0 to 30 bar, respectively. Considering these disparities, an ideal flowmeter must be able to measure the flow rate over a very wide range and independent of the nature of the liquid, irrespective of the ambient conditions. Covering all these conditions with a single device is probably an unattainable challenge, while providing the community with a set of technologies suitable for different ranges of applications would certainly be an acceptable situation. As measurement tools, these flowmeters belong to the large field of metrology, the scientific domain related to measurement. To compare and discuss the accuracy and reliability of different flowmeters, it appears fundamental to be able to trace these measurements to a common reference material. The International Vocabulary of Metrology (VIM) defines the traceability as “the property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty”.24 A reference can be considered as a measurement unit through its practical realization, or a measurement procedure including the measurement unit for a non-ordinal quantity, or a measurement standard. Such standards, called as primary standards, are provided by metrological institutes to allow measurement traceability to the International System of Units. Herein, we review the current technologies and devices dedicated to flow measurement in microfluidics. To do so, we will first describe the main operating principles of the existing flow measurement methods, focusing on their strengths and weaknesses, and discuss their respective level of maturity. To cover a large number of applications, herein, we have focused on sensors capable of measuring Newtonian's liquid flow rates ranging from 1 nL min−1 to 1 mL min−1. Indeed, except the early state-of-the-art done by Gravesen et al., the other reviews in the field are fully or partially dedicated to microfluidic flowmeters for gases.22 Given the importance of microfabrication techniques in the development of microfluidics, since the 90s, most reviews have focused on MEMS-based flowmeters21,22,25–27 and classified them according to their working principle based on the theoretical framework, e.g., thermal and non-thermal. These works also depict the fabrication process including the materials used, their transducing principle, and performances. More recently, different approaches to review microfluidic flowmeters have been found, either focusing on cantilever-based flowmeters28,29 or on flowmeters for biomedical applications.30 In comparison with other reviews, herein, we also propose to the reader a new perspective on the field by discussing the recent developments of primary standards for microfluidic flows by metrological institutes.2 Flow rate measurements at the microscale
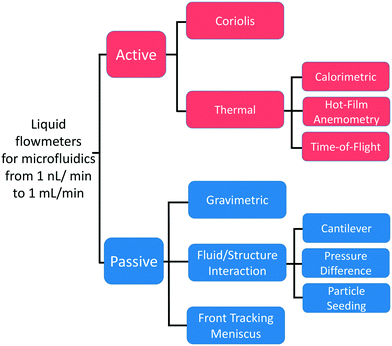
First manufactured using MEMS techniques, flow sensors have accompanied and enabled the development of microfluidics. The need for liquid flows measurements of small value initially arose with the development of liquid chromatography. In 1974, Van Putten et al. manufactured a miniature sensor able to measure microfluidic gas flows based on a technique called hot-wire anemometry (HWA).31 The first liquid flow sensor for microfluidics, based on a time-of-flight (TOF) technology, was developed by Miller et al. in 1982.32 In the 1990s, the rapid growth of microfluidics led to a diversification of flow rate measurement methods. Some of these technologies reached the industrialization stage and are now available in the market. With the benefits of PDMS-based microdevices and the emergence of new applications, other methods have been developed but remain at the proof-of-concept stage to date. To describe the different flow sensors technologies, we divided the measuring principles into two categories active and passive sensors (Fig. 1):• We define an active sensor as a system that supplies energy to the liquid to measure its disturbance. Active sensors are divided into thermal and Coriolis flowmeters. Thermal sensors heat the liquid and measure the heat transport to obtain the flow rate. In Coriolis sensors, the channel through which the liquid flows is excited to generate a force called the Coriolis force. This force results in a second motion of the channel whose amplitude is used to measure the flow rate. Together, both technologies represent more than two-thirds of the flow sensors used in microfluidics.33
• We define a passive sensor as a system that does not supply any energy to disturb the fluid. Here, the liquid dissipates energy in the sensor body. We identify them according to their transducing principle. First, the flow rate is determined through the measurement of the sensor body movement or deformation (fluid–structure interaction). Second, the traditional gravimetric method measures the mass of the flowing liquid over time, while more recently, the advance of the meniscus front tracked in a capillary at the exit of the microfluidic circuit has been used to measure the flow rate, similar to a macroscopic bubble flowmeter. The last two principles will be further discussed in the section related to the development of primary standards by metrological institutes.
2.1 Active flowmeters
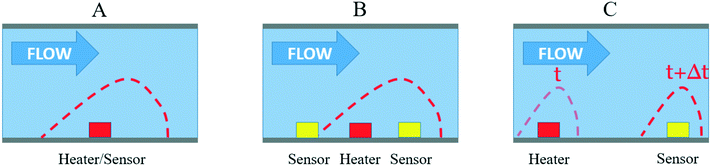
First, the hot-wire and hot-film anemometry (HFA) measure the heat transfer from a hot body to the flowing fluid (Fig. 2A). The heating element is also used as a heat dissipation sensor. With HWA, a resistive wire sensor is set within the fluid flow, whereas for HFA, a thin film resistive sensor is placed adjacent to the flow. According to King's law,34 the heat loss Qh can be related to the fluid velocity v as
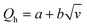 | (1) |
| R(T) = R(T0)[1 + α(T − T0)] | (2) |
| Q ∝ P = R(T)I2 |
Another thermal principle measurement has been developed that partly overcomes the problems encountered by HWA sensors: the calorimetric principle (Fig. 2B). Here, two or more thermal sensors are placed around the heater.25,36 Calorimetric sensors measure the temperature asymmetry caused by the passing fluid using a constant current applied to the heater.37 They consume less power than HWA sensors, and the two sensors on both sides of the heater allow to determine the flow direction. However, calorimetric sensors have two main limitations: non-linearity and sensitivity. The measurement saturates over a certain flow rate, which is assumed to be related to the limited heat transfer between the liquid and both the sensor and heater filament surfaces.38,39 For instance, Dijkstra et al. were able to measure water flow rates down to 40 nL min−1, but the sensor was saturated over 400 nL min−1.40 Generally, only a flow rate range over one order of magnitude could be measured.27 Secondly, to increase the calorimetric sensor sensitivity, it is necessary either to bring the temperature sensors closer to the heater, which can increase the manufacturing cost, or to increase the temperature range, which can be problematic when flowing thermosensitive liquids (such as biological samples). Increasing the heater temperature can also lead to strong changes in the liquid density and viscosity.41 For instance, Dijkstra et al. used a temperature range larger than 40 °C.40 As a third alternative to increase the sensitivity, the channel diameter can also be reduced, which increases the liquid velocity and thus the heat convection. However, the risk of clogging also increases. Finally, the less commonly used technology is time-of-flight sensors (see Fig. 2C).42 With TOF, a heat pulse is emitted from the heater and measured downstream by a temperature sensor. At least one heater and one thermal sensor are required to measure the flow rates. The same sensitivity problems as that in calorimetric sensors are encountered. In addition, the temperature diffusion along the channel is a major limitation of the TOF sensors. Indeed, the diffusion smoothes its temperature profile as a heat pulse is driven by the liquid, thus decreasing the measurement precision. However, Berthet et al. were able to reduce the signal-to-noise ratio using pseudostochastic temperature pulses and a cross correlation method between the detected and the injected signals.43 They were also able to reduce the impact of the diffusion with several downstream sensors to obtain a linear flow rate measurement over two orders of magnitude with only a few degree Celsius operating range.
MEMS thermal flow sensors are usually regarded as the most mature flow sensor technology.27 Since the 70s, MEMS technology has offered the ability to develop low-cost, scalable, and small device footprint thermal flow sensors with high sensitivity. Despite many drawbacks, the calorimetric principle is usually the sensing method used in commercially available flowmeters for microfluidic applications. The measurement depends strongly on the thermal properties of the liquid (thermal conductivity and diffusivity), thus requiring a calibration step for each liquid. Moreover, the measuring range of a sensor varies according to the liquid thermal properties. For instance, the M-flow unit sensor commercialized by Fluigent can measure flow rates from 1 to 80 μL min−1 when flowing water, but 20 to 500 μL min−1 for other liquids.44 In addition, the measurement saturation drastically limits the sensor's dynamic range. Finally, to reduce the temperature differences used, the temperature sensors can be set closer to the heater. However, this complicates the manufacturing protocol, and therefore increases the sensor cost. To maintain a competitive price, the manufacturers have reduced the internal diameter of the channel to increase the sensitivity. As the measurement saturates, for each flow rate range, there is a corresponding internal diameter. For the lowest flow rates, the sensor diameter can be a limitation. Indeed, for water flows in the μL min−1 range or less, commercial sensors are 25 μm in diameter. Because their hydrodynamic resistance increases, their integration in a fluidic circuit may be compromised. Practically, they can be clogged very easily. Other thermal sensors can be found in the literature based on surface plasmon resonance temperature imaging, which is used to measure the heat dissipation similar to HFA sensors,45 or thermal lens microscopy, which is used to generate a heat pulse similar to TOF sensors.46 However, these principles will not be introduced in depth in this review as they do not represent credible technologies to measure microfluidic flow rates due to their very low maturity (only one scientific publication each), size, and complexity.
As shown in Fig. 3, the operation principle of the Coriolis flowmeter is based on the periodic rotation of the U-shape channel with an angular velocity ωact.50 This vibration is allowed due to the deposition of a conducting layer on top of the channel. By running an alternating current in the conductor while subjecting it to a constant magnetic field B, a periodical Lorentz force FL is applied to the channel, which allows an oscillatory motion. As the mass flow Φm flows through the channel, the vibrations induce a perpendicular Coriolis force Fc. This force is proportional to the mass flow Φm and the angular velocity ωact.
| Fc = −2Lx(ωact ∧ Φm) | (3) |
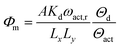 | (4) |
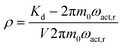 | (5) |
 | ||
| Fig. 3 Representation of the Coriolis flowmeter principle: the channel rotates periodically around the y axis with an angular velocity ωact. When a mass flow Φm flows through the channel, a Coriolis force Fc will cause a secondary vertical motion.118 | ||
| Flowmeter | Range (μL min−1) | Relative uncertainty (%) | Response time (s) | Estimated price (€) | Estimated compacity (cm3) | Ref. |
|---|---|---|---|---|---|---|
| a These data correspond to industrial sensors (prices can vary depending on the packaging, hardware, software, and purchase volume). | ||||||
| Active sensors | ||||||
| Calorimetrica | 0.07–1.5 | 10 | 0.04 | 100–1000 | 50 | 57 |
| 1–80 | 5 | 0.04 | 100–1000 | 50 | 58 | |
| 40–1000 | 5 | 0.04 | 100–1000 | 50 | 58 | |
| HFA | 3–167 | 5 | 0.01 | 100–1000 | 50 | 59 |
| 0.02–0.16 | 20–2.5 | 0.02 | 100–1000 | 50 | 35 | |
| 0.04–0.3 | NA | NA | 100–1000 | 50 | 40 | |
| TOF | 10–1000 | 6 | 0.012 | 100–1000 | 50 | 43 |
| Coriolisa | 0.84–3300 | 0.2 | 0.2 | 2000–4000 | 400 | 60 |
| Passive sensors | ||||||
| Cantilever | 2–35 | 0.1 | NA | 1000–5000 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
61 |
| 5–500 | 0.1 | 0.01 | 400–2000 | 400 | 62 | |
| Pressure difference | 1.1–1100 | 10 | 0.1 | 250–1000 | 1000 | 54 |
| 1.7–1700 | NA | NA | 400–1000 | 50 | 56 | |
| Particle seeding | 0.001–54 | 2–5 | 1 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
63 |
| FTM | 5–100 | 2 | 300 | 4000–8000 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
64 |
| Gravimetric | 0.1–1000 | 0.6–0.1 | 2 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
65, 66 |
| 17–1.6 105 | 6–0.15 | 3 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
65–67 | |
| 0.017–1000 | 4–0.05 | 2 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
65, 66 | |
0.05–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.6–0.15 | 20 | >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
>100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
65, 66 | |
| 17–3300 | 0.62–0.06 | 10 | 5000 | >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
65, 66 | |
| 2–100 | 6–100 | 2.5 | 3000 | 5000 | 63, 68 | |
The Coriolis flowmeter represents a very promising alternative to the thermal sensors usually used in microfluidic applications. It does not require any calibration step, allows flow rate measurements over 3 orders of magnitude, and also allows the measurement of the liquid density. Although its price and internal diameter remain limitations in its use, it seems feasible to find a compromise between resolution, price, flow rate range, and internal diameter.
2.2 Passive flowmeters
As explained previously, passive sensors are identified according to their transducing principle: fluid/structure interaction, gravimetric, and front tracking meniscus. In this section, we will focus on fluid/structure interaction sensors; the other two will be introduced in the section on the development of primary standards by metrological institutes. The sensors based on fluid/structure interaction can be divided in subcategories depending on their measurement principle: (i) pressure difference measurement, (ii) cantilever bending, and (iii) motion of seeded particles. All these methods use the dissipation of energy from the liquid into a test body to either induce its motion or its deformation.| Δp = Rh(η)Q | (6) |
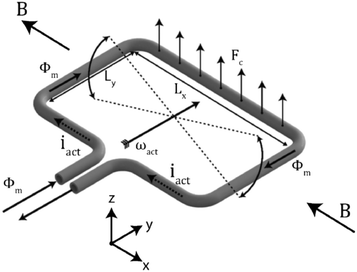
 | ||
| Fig. 4 Differential pressure flow rate sensor with capacitive readouts.55 | ||
Although much progress has been made to increase the flow rate measurement ranges (up to 3 orders of magnitude54,56), this technology remains, to our knowledge, a proof-of-concept. Its limitations seem to have so far prevented attempts for its industrialization and commercialization. Indeed, flow rate measurement is based on prior knowledge of the liquid viscosity. As viscosity is temperature-dependent, the optimization of the experimental conditions is highly recommended.53 In addition, sensor contaminations can be major sources of error. First, it can change the geometry of the channel, resulting in a hydrodynamic resistance variation. As shown by Oosterbroek et al., a poor prediction of the channel hydrodynamic resistance can lead to a 20% error in the flow rate measurement.55 This problem can be transitory due to the presence of dust during the experiment, but it can also persist because of clogging. Second, the pressure sensors can be contaminated by fouling, affecting the mechanical properties of the membrane, which would in turn result in a measurement bias.
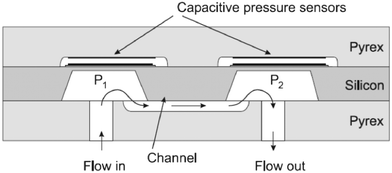
 | ||
| Fig. 5 On the top: Bending of a cantilever under flow with seeded particles, adapted from Wexler et al.69 At the bottom: The different confinement degrees of the cantilever-based flowmeters: A-the cantilever is fully confined, B-the cantilever is only confined along one direction, C-the cantilever is not confined. | ||
In the second geometry, the beam is confined in one direction, leaving most of the fluid flowing at its tip. Proposed by Gass et al., this configuration was used in the first cantilever-based flowmeter for microfluidics.62 They were able to measure flow rates up to two orders of magnitude. As shown by Wexler et al., this configuration allows the use of a depth-averaged model to predict the flow surrounding the cantilever.69 In the regimes of small deflections and high confinement degrees, an analytical solution to the movement of the beam could be found. These authors showed analytically, experimentally, and by means of simulations that the beam follows two deformation regimes: below a certain flow rate the deformation is linear, then the deflection of the beam increases more slowly. However, these regimes will depend on the system parameters mentioned above such as the Young's modulus, degree of confinement, beam size, and the liquid's viscosity. As a variant of this strategy, Attia et al. proposed a system in which a drag-inducing element is immersed in the flow and retained by a spring-like deformable feature attached at the other side.72 This approach is a direct transposition in microfluidics of the spring dynamometer. Stop-flow lithography73,74 can be used to prepare springs with non-uniform properties, and thus extend the range of measurable flow rates. However, this approach raises problems of calibration, is difficult to model with quantitative theories, and shares with the previous one the disadvantage of mobile structures immersed in the liquid (risk of clogging or contamination, hydrodynamic resistance). Finally, the beam is neither confined in its length nor its height. In this geometry, the cantilever is located in the boundary layer thickness of the flow. Recently, great interest has been shown for this geometry of cantilever-based sensors as it mimicks hair-cells or cilia.28,29,75,76 These mechanoreceptors are used by living systems as transducers for flow sensing and chemical sensing. Liu's group has been a pioneer in developing artificial hair-cell flow sensors, fabricated in either polymer or silicon material.77,78 This sensor consists of an array of high aspect ratio cantilevers, each of them coupled to a strain gauge. The torque induced by the flow introduces a longitudinal strain that can be detected by the piezoresistors at the base. Using an array of cantilevers with different geometries, the authors were able to extend the range of measurable flow rates. It would also allow to adapt to the viscosity of the liquid. Among these 3 different configurations of cantilevers, it seems that this approach represents the most viable solution to meet the specifications of a flowmeter for microfluidics. Due to the low confinement of the beam, the hydrodynamic resistance of the sensor is only moderately increased. Moreover, the lesser the confinement of the beam, the lesser is the risk of clogging or deterioration. Finally, this configuration is more suitable toward a flowmeter, allowing to measure a wider range of flow rates for liquids of different viscosities.
Manufactured using MEMS techniques, cantilever-based flowmeters share some advantages with thermal flowmeters as they are compact and in the same price range. Contrary to thermal sensors, this technology can be adapted to liquids by manufacturing cantilever arrays. However, this technology has major shortcomings, which limit its transition to commercial use. As the deflection of the cantilever depends on the liquid's viscosity, a calibration step is necessary. Due to its transducing principle, the test body is set within the liquid flow so that it is exposed to contamination risks (liquid with seeded particles/cells, bubbles, or biochemical compounds such as proteins). The mechanical properties of a beam covered by chemical compounds would be affected, for e.g., its thickness, overall elastic modulus, and moment of inertia, which will lead to a less deformable beam, and thus a measurement bias. Over a certain threshold force (torque) on the beam that could be exerted by either a pulse in the flow rate or by objects transported by the flow, bending can occur as plastic deformation, resulting in permanent bending. Worse, the cantilever could break, potentially reducing its lifetime.
On the other hand, laser Doppler velocimetry relies on an interference fringe system with nearly parallel spacing d, which is formed by two intersecting coherent laser beams. When the particles seeded in the flow pass through the interference fringe system, they are alternately light and dark. The scattered light signal shows amplitude modulation with a Doppler frequency fDoppler = U/d corresponding to the particle velocity U orthogonal to the fringe spacing. However, as shown with the μ-PIV, scanning the channel height is required to measure the full velocity profile to obtain the flow rate.85,86 A great improvement was made by Czarske et al. with the laser Doppler velocity profile sensor, which does not require the scanning of the channel height.87 The position as well as the velocity of individual tracer particles are determined due to two superposed fan-like fringe systems, one being converging and the other one being diverging along the optical axis.
Although many advances have been made whether in μ-PIV to increase the scanning speed, or in laser Doppler with the addition of the laser Doppler flow profile sensor, these techniques were not turned into commercial end-user products due to two main limitations: its compacity and the particles themselves. The optical devices necessary to carry out measurements with seeded particles are far too voluminous (microscope, fast camera, objective, data processing) to be integrated in a fluidic circuit and are additionally expensive. However, this technique seems particularly suitable for sensor calibration. Thus, a holographic PIV system has been recently implemented at NIST to develop primary standards.63 An original method has also been proposed using a rotating wheel asymmetrically positioned in a microfluidic channel.88–90 The rotation arises from the dissipation of the liquid viscous stress at the surface of the wheel so that the flow measurement does not theoretically depend on the liquid viscosity. Thus, the rotation rate is linear to the flow rate. Even if such a sensor seems to be a promising solution as a disposable sensor, it gathers most of the limitations previously listed.
Flow sensors in microfluidics rely on a wide range of measurement principles. The technologies presented above have all been developed in academic laboratories, but their degree of maturity significantly varies and most of them have not yet led to routine end-user products. In this respect, two technologies stand out: thermal and Coriolis flowmeters. Commercial flowmeters dedicated to microfluidic applications and based on these two technologies are already on the market. However, the increasing part of life science applications in microfluidics has led to new needs, particularly for disposable sensors capable of measuring flow rates over wide ranges without prior calibration steps. This justifies further efforts to develop products based on principles not exploited yet commercially. Also, the diversification of microfluidic applications has increased the variety of needs regarding flow measurements. Among others, the nature of the liquids used and the range of flow rates varies significantly depending on the research field. This progressive complexification of the field, combined with the maturation of microfluidics into widely spread tools in industrial research, production, and diagnosis, call for increased normalization and standardization, and raise the need for methods and tools, allowing reliable comparison of these different technologies and traceability to primary existing standards. This is the role of metrology. Recent efforts have been made to adapt this field to low and very low flow rates to compare the performance of different flowmeters and provide standards and calibrations necessary for regulatory processes.
3 Metrology and primary standards for microfluidic flows
Until the 17th century, no global agreement or entities existed to define measurement ref. 91. The definition of units was extremely diverse regarding geographic dispersion. This was an obvious hurdle in equitable and efficient transactions. With the creation of the decimal unit system in 1799 and the development of experimental sciences, it appeared necessary to establish an independent international organization to coordinate the worldwide measurement system. The Meter Convention was ratified in Paris on May the 20th of 1875 by representatives of seventeen nations.92 It settled the creation of the International Bureau of Weights and Measures (BIPM), an intergovernmental organization under the authority of the General Conference on Weights and Measures (CGPM), and the supervision of the International Committee for Weights and Measures (CIPM) to handle the demand for measurement standards. The National Metrology Institutes (NMIs) constitute the local relays of the international institutions. The global organization is completed by Regional Metrology Organizations (RMOs). Their main responsibilities are to facilitate traceability to primary standards, coordinate comparisons of national measurement standards, and update and share their facilities and knowledge. Over the years, the metrology system has evolved and other international organizations have been created to meet the needs of different aspects of metrology such as the International Organization of Standardization (ISO) and International Organization of Legal Metrology (OIML). Together, they closely cooperate and form the global metrology system. We review below the current achievements and progresses within the field of metrology for microfluidic flow measurements.3.1 Development of primary standards for microfluidic flows
The development of primary standards relies on an international project organized within or between the RMOs by the NMIs. This development must follow a well-defined procedure to allow traceability of the measurements. Each NMI first develops its own flow sensor calibration system composed of a flow generator, a device under test (DUT), and a reference flowmeter, as shown in Fig. 6. To achieve a proper validation of the facilities, calibration systems must vary among NMIs to avoid systematic bias.66 Once the system is implemented, a characterization is performed. Then each NMI claims its specifications and declares the nature of the liquids used, the flow rate measurements achieved, and their combined standard uncertainty (see the GUM for more information on uncertainty93). To validate the measurements and uncertainties claimed by each NMI for the whole flow range, results are submitted for intercomparisons. These intercomparisons are performed through at least two DUTs called transfer standards. The use of many transfer standards is required to prevent any systematic errors. It can either be a flowmeter or a flow actuator. The project pilot must calibrate the DUTs at the beginning and at the end of the intercomparisons. Each NMI is required to estimate the uncertainty due to drift. The measurements and their combined uncertainties obtained from the intercomparisons are then statistically analyzed and characterized by a consistency value (a detailed procedure of this statistical analysis can be found in ref. 94). These intercomparisons allow to support mutual confidence in calibration and measurement capabilities (CMCs).95 The claimed CMCs, containing the flow range, uncertainties, and liquids used, are submitted to the belonging RMOs for validation. If validated, CMCs are then published in the BIPM key comparison database (KCDB).96 Such projects allow the implementation of new calibration capacities. Academic labs, international flowmeter manufacturers, or other NMIs can thus use these facilities to validate and get accreditation for the performance of their technology or calibration services.3.2 The metrology for drug delivery (MEDD) project
The development of primary standards for microfluidic flows was deemed necessary for scientific, economic, and public health reasons. Metrology institutes have seen a growing demand from flowmeter manufacturers to certify their technologies. Furthermore, the lack of facilities able to measure these flows has had a detrimental impact on clinical applications, in which its consequences can be particularly dramatic. Indeed, dosing errors in drug delivery have been shown to be one of the main causes of adverse patient incidents.97–101 Precisely, numerous accidents (especially in neonatal care100–102) have been listed in the past years related to dosing errors in drug delivery by infusion.In order to meet these needs, the European Metrology for Drug Delivery project (EMDD),103 funded by the Euramet European Metrology Research Programme (EMRP), was started in 2012. So far, some metrological infrastructures have been developed for flow rates between 1.6 mL min−1 and 8.3 μL min−1 but neither characterized nor validated. To remedy this obvious lack of infrastructure capable of measuring microfluidic flows, the objectives of the MEDD project were to develop and characterize primary standards for liquid flow at atmospheric conditions for flow rates from 10 mL min−1 down to 1 nL min−1 with a target uncertainty better than 0.5% in steady state flows, to test commercially available flowmeters in various operation conditions, and finally to test drug delivery systems.
This project involves National Metrology Institutions (CETIAT (FR), DTI (DK), IPQ (P), METAS (SZ), VSL (NL), and MIKES VTT (FIN)), as well as industrial and academic partners (Bronkhorst High-Tech (NL) and FH Lubeck University (DE)).65,66,94,98,104–109 Toward primary standards for microfluidic flows two methods have been investigated–the gravimetric principle and the front tracking meniscus in a capillary; only the first one was submitted for intercomparisons.†
3.3 Gravimetric flow rate measurement
The principle of gravimetric calibration systems is based on the measurement of the fluid mass over time. Knowing the liquid density ρl, the measurement of the mass increment Δm per unit time Δt allows the flow rate measurement.
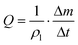 | (7) |
The development of a primary standard allowing the traceability of microfluidic flow rate measurements can only be achieved with a high level of control of the flow stability, the quantities that define the liquid, and the mass measurement system. Liquid monitoring was performed either by a pressure controller or by syringe pumps. Flow stability is the most important parameter to control. The precision of the pressure control is based on a constant hydrodynamic resistance Rh of the fluidic system. Rh can be altered during the calibration by deformable tubing or by impurities in the liquid. Thus, in most cases, stainless steel tubings were used. Syringe pump actuation can be problematic when studying very low flow rates. Indeed, the fluctuations of the order of 10% have been observed in the flow rate ranges of the order of nL min−1.110 Water was used as the test liquid for the calibration of all systems. Special attention was paid to the water treatment. In most cases, ultrapure and degassed water was used as dust and bubbles can modify the resistance of the channel or even add a bias in the mass increment. The density of the liquid is taken to be a constant ρl = 103 kg m−3. However, the lack of temperature control during the experiments can alter this parameter and thus increase the measurement error. The measurement precision is given by the resolution of the scale and its acquisition frequency. The measurements are obtained on a sampling period that allows to adapt to the mass increment, and to smooth the experimental noise by an average. However, the very low acquisition frequency of the scales used can be observed. Coupled with time averaging, these measurement systems represent a major limitation to observe flow rate fluctuations. With the aim of developing primary standards for dynamic flows, this technique seems inappropriate.
Two major sources of error emerged during flow rate calibration: the liquid evaporation and the interaction between the outlet of the fluidic system and the liquid in the beaker. These phenomena become much more significant as the studied flow rate decreases. To limit liquid evaporation that takes place in ambient air (a few μL min−1), better results were achieved by covering the liquid with an oil layer (down to a tenth of a nL min−1) than with air saturation in humidity (order of one μL min−1). Second, the outlet needle is immersed in the liquid to prevent the flow from being dripped, causing a discontinuous measurement of the added mass. However, new sources of uncertainty arise from the interaction between the needle and the liquid. Firstly, the immersion of the needle in the liquid causes an addition of mass due to buoyancy. Indeed, the buoyancy increases as the beaker fills up. Increasing the surface area of the beaker would reduce this effect but would also result in greater evaporation. Secondly, the contact between the needle and the liquid results in capillary forces that should be taken into account with pressure actuation. The characterization of the error becomes significantly more difficult when using an oil layer to prevent evaporation. Attempts were made to calibrate these effects and account for them in the flow measurement. However, these results are preliminary and are subject to caution. Indeed, evaporation, buoyancy, and surface tension forces are correlated. The calculation of uncertainties becomes significantly more complex according to the GUM.93 In addition, no mention was made of the hysteresis effect of the contact angle between the liquid and the needle, although this effect has been widely described in the microfluidic literature.111,112 In order to take into account these sources of error in the flow measurement, eqn (7) was corrected. Depending on the setup and calibrations carried out, each NMI used its own working equation for flow. For instance, at NIST, eqn (7) becomes
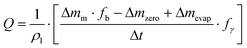 | (8) |
3.4 Front tracking meniscus (FTM)
In response to the limitations of the gravimetric principle previously mentioned, investigations on the front tracking meniscus method were carried on by Lubeck University.110,113 First investigated for low flow rate by Richter et al.,114 this method relies on tracking the meniscus displacement of a flowing liquid in a capillary of known dimensions set at the outlet of the calibration system, as described in Fig. 7. The flow rate is measured according to
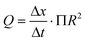 | (9) |
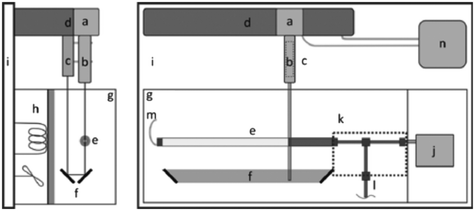 | ||
| Fig. 7 Representation of the experimental setup for front tracking meniscus method. On the right: Top view. a) CCD camera, b) lens, c) LED, d) linear stage, e) capillary, f) mirrors, g) regulated chamber, h) heating element, i) vibration-free table, j) DUT, k) thermally-insulated fittings and tubing, l) valve, m) polymer tubing, n) PC. On the left: Side view.113 | ||
Experiments were carried out with distilled, demineralized, and degassed water. The calibration system was used to evaluate a precision syringe pump and a commercial thermal flow sensor from 5 nL min−1 to 100 nL min−1. To fully characterize the calibration system, numerous sources of uncertainty have been characterized on different variables such as Δt, Δx, and R through the law of propagation of uncertainties. For smaller flow rates or shorter sampling periods, the precision of the image process is the largest source of uncertainty. These effects are all the more important as the radius of the capillary increases. Moreover, as the curvature of the interface increases, the measurement of the meniscus position is affected. Conversely, when increasing the flow rate or for long sampling periods, the radius uncertainty is predominant.
Contrary to the gravimetric principle that could only measure flows in the μL min−1 range, FTM is able to probe flows down to nL min−1; consequently, it is a calibration system much more adapted to microfluidic flow. Thus, CETIAT has recently started to develop a primary standard based on the FTM principle to decrease the minimum measurable flow.115 However, it remains a metrological tool and cannot be used in an industrial or academic setting as a sensor. Indeed, the portability of the system does not meet the dimensioning of a microfluidic experiment, but above all, it can only be set at the outlet of the microfluidic circuit. This greatly restricts the fields of application of such a sensor.
4 Perspectives
Herein, we have reviewed the current strategies for microfluidic flow measurement, from their physical principles to their metrological aspects. We distinguished two main families, namely, active systems, in which energy is provided to the fluid and the measure is associated with the coupling of the flow with this energy transfer, and passive systems, measuring directly or indirectly the effect of the flow on a sensor. Currently, active systems cover the essentials of commercial products, the most widely used being the thermal sensors. Coriolis-based sensors have been proposed more recently and have gained interest in spite of their higher complexity and cost. This can be explained by their higher accuracy at very low flow and more “universal” character, notably due to their relative independence to the thermal and mechanical properties of the fluid. However, these commercial flowmeters are probably too expensive for many microfluidic applications; thus, we believe that the future needs will call for a renewal of interest in passive flow sensors and stimulate the maturation of at least some of the concepts recalled above (or new ones yet to be invented) into commercial products. Sensors based on pressure-differences may, in particular, be good candidates for not very demanding applications. They have the disadvantage of being dependant on the fluid's viscosity, but for numerous point-of-use or disposable applications, the gain in cost and simplicity may be worth the loss in the accuracy. This could be the case, for e.g., for water monitoring (in which the fluid's viscosity does not vary much), cell culture, or organs-on-chip (in which only the orders of magnitude of flow rates may be sufficient, for e.g., to ensure sufficient perfusion of nutriments or reagents).On the application side, microfluidics expand toward more and more diverse research fields and markets, and we anticipate that this expansion will require further developments in flow measurement strategies. First, the development of instruments, notably for clinical use, requires very accurate and reliable measurements and standardization. This is addressed by metrology, but there is still a delay and a performance gap between the development of flowmeters by academic and industrial players, and the development of primary standards within metrological institutes. Indeed, the first began in the 1970s and can reach tens of nL min−1, while the second, developed since the 2010s, can only measure flow rates down to 2 μL min−1. This partially explains the standardization problems encountered by microfluidics. As an obvious reason, metrology has the highest standards in terms of reliability and naturally tends to be more conservative (a trend to be paralleled with the also long delay between the discovery of new analytical technologies and their acceptance by health regulation authorities). Furthermore, establishing and maintaining comparability of measurement results can only be achieved through an international system that allows traceability from the measurement standard level (NMIs) down to routine field measurements. This is a multi-stakeholders process, which may also induce delays. To bridge the performance gap stated above, we suggest that a good compromise could be to accept that the idea that the sensors used for calibration are not “ultimate” versions of the commercial ones they check but based on different principles limited to calibration purposes (e.g., front meniscus or gravimetric measurements), and restrict calibration to long steady-state measurements. This would have the disadvantage of not ensuring the full certification of the stability of the sensors but could still constitute a first useful step for the certification of low flow rate sensors.
Conflicts of interest
Jean-Louis Viovy is a cofounder/shareholder of Fluigent.References
- D. Qin, Y. Xia, J. A. Rogers, R. J. Jackman, X.-M. Zhao and G. M. Whitesides, Microfabrication, Microstructures and Microsystems, 1998, pp. 1–20 Search PubMed
.
- G. M. Whitesides, The origins and the future of microfluidics, Nature, 2006, 442(7101), 368–373 CrossRef CAS PubMed
.
- N. Convery and N. Gadegaard, 30 Years of Microfluidics, Micro Nano Eng., 2019, 2, 76–91 CrossRef
.
- H. A. Stone, A. D. Stroock and A. Ajdari, Engineering Flows in Small Devices, Annu. Rev. Fluid Mech., 2004, 36(1), 381–411 CrossRef
.
- R. G. Sweet, High frequency recording with electrostatically deflected ink jets, Rev. Sci. Instrum., 1965, 36(2), 131–136 CrossRef
.
- F. C. M. van de Pol and J. Branebjerg, Micro fluid-handling systems: state of the art and opportunities, in Fifth International Conference on Advanced Robotics'Robots in Unstructured Environments, IEEE, 1991, vol. 1, pp. 283–290, Available from: https://ieeexplore.ieee.org/document/240639/ Search PubMed.
- E. Bassous, H. H. Taub and L. Kuhn, Ink jet printing nozzle arrays etched in silicon, Appl. Phys. Lett., 1977, 31(2), 135–137 CrossRef CAS
.
- S. C. Terry, A gas chromatography system fabricated on a silicon wafer using integrated circuit technology, Stanford University, 1975 Search PubMed.
- S. C. Terry, J. H. Herman and J. B. Angell, A Gas Chromatographic Air Analyzer Fabricated on a Silicon Wafer, IEEE Trans. Electron Devices, 1979, 26(12), 1880–1886 Search PubMed
.
- A. Manz, N. Graber and H. M. Widmer, Miniaturized total chemical analysis systems: A novel concept for chemical sensing, Sens. Actuators, B, 1990, 1(1–6), 244–248 CrossRef CAS
.
- C. M. Hindson, J. R. Chevillet, H. A. Briggs, E. N. Gallichotte, I. K. Ruf and B. J. Hindson, et al. Absolute quantification by droplet digital PCR versus analog real-time PCR, Nat. Methods, 2013, 10(10), 1003–1005 CrossRef CAS PubMed
, Available from: https://www.nature.com/articles/nmeth.2633.
- A. A. Morley, Digital PCR: A brief history, Biomol. Detect. Quantif., 2014, 1(1), 1–2 CrossRef
, Available from: https://linkinghub.elsevier.com/retrieve/pii/S2214753514000023.
- M. Verhulsel, M. Vignes, S. Descroix, L. Malaquin, D. M. Vignjevic and J.-L. Viovy, A review of microfabrication and hydrogel engineering for micro-organs on chips, Biomaterials, 2014, 35(6), 1816–1832 CrossRef CAS PubMed
, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0142961213013744.
- L. A. Low, C. Mummery, B. R. Berridge, C. P. Austin and D. A. Tagle, Organs-on-chips: into the next decade, Nat. Rev. Drug Discovery, 2021, 20(5), 345–361 CrossRef CAS PubMed
, https://www.nature.com/articles/s41573-020-0079-3.
- D. E. Ingber, Human organs-on-chips for disease modelling, drug development and personalized medicine, Nat. Rev. Genet., 2022 DOI:10.1038/s41576-022-00466-9
.
- Markets and Markets (2013) Microfluidics market by materials (polymers, silicon, glass), pharmaceuticals (microreactors, toxicity screening, lab on chip, proteomic & genomic analysis) drug delivery devices(microneedles, micropumps), IVD (POC)–global tr.
- Microfluidics Market by Product (Devices, Components (Chips, Sensors, Pump, Valves, and Needles)), Application (IVD [POC, Clinical, Veterinary], Research, Manufacturing, Therapeutics), End User and Region – Global Forecast to 2025.
- C. D. Chin, V. Linder and S. K. Sia, Commercialization of microfluidic point-of-care diagnostic devices, Lab Chip, 2012, 12(12), 2118–2134 RSC
.
- P. S. Dittrich and A. Manz, Lab-on-a-chip: Microfluidics in drug discovery, Nat. Rev. Drug Discovery, 2006, 5(3), 210–218 CrossRef CAS PubMed
.
- S. Yadav, Analysis of value creation and value capture in microfluidics market, Massachusetts Institute of Technology, Engineering Systems Division, 2010, Available from: https://dspace.mit.edu/handle/1721.1/59276 Search PubMed.
- Micro System Technologies 90, Micro Liquid-Handling Devices – A Review, in Intergovernmental Panel on Climate Change, ed. F. C. M. Van De Pol and J. Branebjerg, Springer Berlin, Heidelberg, Berlin, Heidelberg, 1990, pp. 799–805, Available from: https://www.cambridge.org/core/product/identifier/CBO9781107415324A009/type/book_part Search PubMed
.
- P. Gravesen, J. Branebjerg and O. S. Jensen, Microfluidics - A review, J. Micromech. Microeng., 1993, 3(4), 168–182 CrossRef CAS
, Available from: https://iopscience.iop.org/0960-1317/3/4/002.
- H. Van Heeren, Results survey on microfluidics & sensors, 2016, July Search PubMed.
- International vocabulary of metrology–Basic and general concepts and associated terms, in International vocabulary of metrology(VIM), 2012, https://www.nist.gov/system/files/documents/pml/div688/grp40/International-Vocabulary-of-Metrology.pdf Search PubMed
.
- N. Nguyen, Micromachined flow sensors—a review, Flow Meas. Instrum., 1997, 8(1), 7–16 CrossRef
, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0955598697000198.
- J. T. W. Kuo, L. Yu and E. Meng, Micromachined thermal flow sensors-A review, Micromachines, 2012, 3(3), 550–573 CrossRef
.
- F. Ejeian, S. Azadi, A. Razmjou, Y. Orooji, A. Kottapalli and M. Ebrahimi Warkiani, et al., Design and applications of MEMS flow sensors: A review. Sensors Actuators, Sens. Actuators, A, 2019, 295, 483–502, DOI:10.1016/j.sna.2019.06.020
.
- C. Liu, Micromachined biomimetic artificial haircell sensors, Bioinspiration Biomimetics, 2007, 2(4), S162–S169 CrossRef PubMed
.
- F. Rizzi, A. Qualtieri, T. Dattoma, G. Epifani and M. De Vittorio, Biomimetics of underwater hair cell sensing, Microelectron. Eng., 2015, 132, 90–97 CrossRef CAS
.
- S. Silvestri and E. Schena, Micromachined flow sensors in biomedical applications, Micromachines, 2012, 3(2), 225–243 CrossRef
.
- A. F. P. Van Putten and S. Middelhoek, Integrated silicon anemometer, Electron. Lett., 1974, 10(21), 425–426 CrossRef CAS
.
- T. E. Miller and H. Small, Thermal Pulse Time-of-Flight Liquid Flow Meter, Anal. Chem., 1982, 54(6), 907–910 CrossRef CAS
.
- H. Heeren, Results survey on microfluidics flow control, 2016 Search PubMed.
- L. V. King, XII. On the convection of heat from small cylinders in a stream of fluid: Determination of the convection constants of small platinum wires with applications to hot-wire anemometry, Philos. Trans. R. Soc., A, 1914, 214(509–522), 373–432, DOI:10.1098/rsta.1914.0023
.
- S. Wu, Q. Lin, Y. Yuen and Y. C. Tai, MEMS flow sensors for nano-fluidic applications, Sens. Actuators, A, 2001, 89(1–2), 152–158 CrossRef CAS
.
- E. Meng and Y. C. Tai, A parylene MEMS flow sensing array, Transducers 2003 – 12th Int Conf Solid-State Sensors, Actuators Microsystems, Dig Tech Pap., 2003, vol. 1, pp. 686–689 Search PubMed.
- B. Mimoun, A. van der Horst, R. Dekker, D. van der Voort, A. van der Horst and M. Rutten, et al., Thermal flow sensors on flexible substrates for minimally invasive medical instruments, in 2012 IEEE Sensors, IEEE, 2012, pp. 1–4, Available from: https://ieeexplore.ieee.org/document/6411429/ Search PubMed
.
- T. S. J. Lammerink, N. R. Tas, M. Elwenspoek and J. H. J. Fluitman, Micro-liquid flow sensor, Sens. Actuators, A, 1993, 37–38, 45–50 CrossRef CAS
, Available from: https://linkinghub.elsevier.com/retrieve/pii/092442479380010E.
- P. Fürjes, G. Légrádi, C. Dücső, A. Aszódi and I. Bársony, Thermal characterisation of a direction dependent flow sensor, Sens. Actuators, A, 2004, 115(2–3), 417–423 CrossRef
, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0924424704003401.
- M. Dijkstra, M. J. de Boer, J. W. Berenschot, T. S. J. Lammerink, R. J. Wiegerink and M. Elwenspoek, Miniaturized flow sensor with planar integrated sensor structures on semicircular surface channels, in 2007 IEEE 20th International Conference on Micro Electro Mechanical Systems(MEMS), IEEE, 2007, pp. 123–126, Available from: https://ieeexplore.ieee.org/document/<?ccdc_no 4433031?>4433031<?ccdc END?>/ Search PubMed.
- N. T. Nguyen, X. Y. Huang and K. C. Toh, Thermal flow sensor for ultra-low velocities based on printed circuit board technology, Meas. Sci. Technol., 2001, 12(12), 2131–2136 CrossRef CAS
.
- R. Antony, M. S. Giri Nandagopal, N. Sreekumar and N. Selvaraju, Detection principles and development of microfluidic sensors in the last decade, Microsyst. Technol., 2014, 20(6), 1051–1061, DOI:10.1007/s00542-014-2165-0
.
- H. Berthet, J. Jundt, J. Durivault, B. Mercier and D. Angelescu, Time-of-flight thermal flowrate sensor for lab-on-chip applications, Lab Chip, 2011, 11(2), 215–223 RSC
.
- https://www.fluigent.com/product/microfluidic-components/frp-flow-rate-platform/
.
- S. Deng, P. Wang, S. Liu, T. Zhao, S. Xu and M. Guo, et al., A Novel Microfluidic Flow Rate Detection Method Based on Surface Plasmon Resonance Temperature Imaging, Sensors, 2016, 16(7), 964 CrossRef PubMed
, Available from: https://www.mdpi.com/1424-8220/16/7/964.
- Y. Kikutani, K. Mawatari, K. Katayama, M. Tokeshi, T. Fukuzawa and M. Kitaoka, et al., Flowing thermal lens micro-flow velocimeter, Sens. Actuators, B, 2008, 133(1), 91–96 CrossRef CAS
.
- G. G. Coriolis, Mémoire sur les équations du mouvement relatifs des systèmes de corps, Journal de l'École polytechnique, 1835, 142–154 Search PubMed
.
- P. Enoksson, G. Stemme and E. Stemme, A silicon resonant sensor structure for coriolis mass-flow measurements, J. Microelectromech. Syst., 1997, 6(2), 119–125 CrossRef
.
- https://www.bronkhorst.com/int/products/liquid-flow/mini-cori-flow/
.
- J. Groenesteijn, Microfluidic platform for Coriolis-based sensor and actuator systems, PhD, University of Twente, 2016, DOI:10.3990/1.9789036540117
.
- J. Haneveld, T. S. J. Lammerink, M. J. De Boer, R. G. P. Sanders, A. Mehendale and J. C. Lötters, Modeling, design, fabrication and characterization of a micro Coriolis mass flow sensor, J. Micromech. Microeng., 2010, 20(12), 125001 CrossRef
.
- T. V. P. Schut, D. Alveringh, W. Sparreboom, J. Groenesteijn, R. J. Wiegerink and J. C. Lotters, Fully integrated mass flow, pressure, density and viscosity sensor for both liquids and gases, in 2018 IEEE Micro Electro Mechanical Systems(MEMS). IEEE, 2018, pp. 218–221, Available from: https://ieeexplore.ieee.org/document/8346523/ Search PubMed.
- M. A. Boillat, A. J. van der Wiel, A. C. Hoorgerwerf and N. F. de Rooij, Differential pressure liquid flow sensor for flow regulation and dosing systems, Proc. - IEEE Micro Electro Mech. Syst., 8th, 1995, 350–352 Search PubMed
.
- T. Rodrigues, F. J. Galindo-Rosales and L. Campo-Deaño, Towards an optimal pressure tap design for fluid-flow characterisation at microscales, Materials, 2019, 12(7), 8–10 Search PubMed
.
- R. E. Oosterbroek, T. S. J. Lammerink, J. W. Berenschot, G. J. M. Krijnen, M. C. Elwenspoek and A. van den Berg, A micromachined pressure/flow-sensor, Sens. Actuators, A, 1999, 77(3), 167–177 CrossRef CAS
, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0924424799001880.
- A. Shakir, K. Srihari, B. Murcko, C. Yun and B. Sulouff, Flow sensor using micromachined pressure sensor, Proc IEEE Sensors, 2008, pp. 62–65 Search PubMed.
- SLG Liquid Flow Meter Series, 2020, Available from: https://sensirion.com/media/documents/69EBDF62/61658A36/Sensirion_Liquid_Flow_Meters_SLG_Datasheet_1.pdf Search PubMed
.
- SLI Liquid Flow Meter Series, 2020, Available from: https://sensirion.com/media/documents/9D0BBC1B/616588DA/Sensirion_Liquid_Flow_Meters_SLI_Datasheet.pdf Search PubMed
.
- R. Ahrens and K. Schlote-Holubek, A micro flow sensor from a polymer for gases and liquids, J. Micromech. Microeng., 2009, 19(7), 074006 CrossRef
.
- mini Cori-Flow Series ML120, Available from: https://www.bronkhorst.com/getmedia/9dc94505-0494-43fc-ac6a-de18019932ce/mini-cori-flow-ml120.pdf Search PubMed
.
- N. Noeth, S. S. Keller and A. Boisen, Integrated cantilever-based flow sensors with tunable sensitivity for in-line monitoring of flow fluctuations in microfluidic systems, Sensors, 2013, 14(1), 229–244 CrossRef PubMed
.
- V. Gass, B. H. van der Schoot and N. F. de Rooij, Nanofluid handling by micro-flow-sensor based on drag force measurements, Proc. - IEEE Micro Electro Mech. Syst., 8th, 1993, 167–172 CrossRef
.
- P. Salipante, S. D. Hudson, J. W. Schmidt and J. D. Wright, Microparticle tracking velocimetry as a tool for microfluidic flow measurements, Exp. Fluids, 2017, 58(7), 1–10 CrossRef CAS
.
- M. Ahrens, S. Klein, B. Nestler and C. Damiani, Design and uncertainty assessment of a setup for calibration of microfluidic devices down to 5 nL min-1, Meas. Sci. Technol., 2014, 25(1), 015301 CrossRef CAS
.
- H. Bissig, H. T. Petter, P. Lucas, E. Batista, E. Filipe and N. Almeida, et al., Primary standards for measuring flow rates from 100 nl/min to 1 ml/min-gravimetric principle, Biomed. Tech., 2015, 60(4), 301–316 Search PubMed
.
- EURAMET, Final Publishable JRP Report MetroNORM: IND57, Eur Metrol Res Program, 2017, (July), p. 28, Available from: https://metronorm-emrp.eu/wp-content/uploads/2017/08/IND57-MetroNORM-Final-publishable-JRP-report-approved.pdf Search PubMed
.
- O. Florestan, M. Sandy and S. Julien, Recent improvements of the French liquid micro-flow reference facility, Meas. Sci. Technol., 2018, 29(2), aa97ef, DOI:10.1088/1361-6501/aa97ef
.
- J. W. Schmidt and J. D. Wright, Micro-flow calibration facility at NIST, in 9th ISFFM, 2015 Search PubMed.
- J. S. Wexler, P. H. Trinh, H. Berthet, N. Quennouz, O. Du Roure and H. E. Huppert, et al. Bending of elastic fibres in viscous flows: The influence of confinement, J. Fluid Mech., 2013, 720, 517–544 CrossRef
.
- B. Semin, J. P. Hullin and H. Auradou, Influence of flow confinement on the drag force on a static cylinder, Phys. Fluids, 2009, 21(10), 1–9 Search PubMed
.
- N. Noeth, S. S. Keller and A. Boisen, Fabrication of a cantilever-based microfluidic flow meter with nL min −1 resolution, J. Micromech. Microeng., 2011, 21(1), 015007 CrossRef
.
- R. Attia, D. C. Pregibon, P. S. Doyle, J. L. Viovy and D. Bartolo, Soft microflow sensors, Lab Chip, 2009, 9(9), 1213–1218 RSC
.
- D. Dendukuri, D. C. Pregibon, J. Collins, T. A. Hatton and P. S. Doyle, Continuous-flow lithography for high-throughput microparticle synthesis, Nat. Mater., 2006, 5(5), 365–369 CrossRef CAS PubMed
.
- D. Dendukuri, S. S. Gu, D. C. Pregibon, T. A. Hatton and P. S. Doyle, Stop-flow lithography in a microfluidic device, Lab Chip, 2007, 7(7), 818–828 RSC
.
- J. Tao and X. Yu, Hair flow sensors: From bio-inspiration to bio-mimicking - A review, Smart Mater. Struct., 2012, 21(11), 113001 CrossRef
.
- L. Zhang, X. Yu, S. You, H. Liu, C. Zhang and B. Cai, Highly sensitive microfluidic flow sensor based on aligned piezoelectric poly(vinylidene fluoride-trifluoroethylene) nanofibers, Appl. Phys. Lett., 2015, 107(24), 242901 CrossRef
.
- J. M. Engel, J. Chen, C. Liu and D. Bullen, Polyurethane rubber all-polymer artificial hair cell sensor, J. Microelectromech. Syst., 2006, 15(4), 729–736 CrossRef CAS
.
- N. Chen, C. Tucker, J. M. Engel, Y. Yang, S. Pandya and C. Liu, Design and Characterization of Artificial Haircell Sensor for Flow Sensing With Ultrahigh Velocity and Angular Sensitivity, J. Microelectromech. Syst., 2007, 16(5), 999–1014, DOI:10.1109/JMEMS.2007.902436
.
- S. T. Wereley and C. D. Meinhart, Recent Advances in Micro-Particle Image Velocimetry, Annu. Rev. Fluid Mech., 2010, 42(1), 557–576 CrossRef
.
- G. J. Santiago, T. S. Wereley, D. C. Meinhart, J. D. Beebe and J. R. Adrian, A particle image velocimetry system for microfluidics, Exp. Fluids, 1998, 25(4), 316–319, DOI:10.1007/s003480050235
.
- C. D. Meinhart, S. Wereley and M. Gray, Volume illumination for two-dimensional particle image velocimetry, Meas. Sci. Technol., 2000, 11(6), 809–814 CrossRef CAS
.
- J. S. Park, C. K. Choi and K. D. Kihm, Optically sliced micro-PIV using confocal laser scanning microscopy(CLSM), Exp. Fluids, 2004, 37(1), 105–119 CrossRef
.
- J. S. Park and K. D. Kihm, Three-dimensional micro-PTV using deconvolution microscopy, Exp. Fluids, 2006, 40(3), 491–499 CrossRef
.
- S. Kim and S. J. Lee, Measurement of 3D laminar flow inside a micro tube using micro digital holographic particle tracking velocimetry, J. Micromech. Microeng., 2007, 17(10), 2157–2162, DOI:10.1088/0960-1317/17/10/030
.
- L. Buettner and J. Czarske, A multimode-fibre laser-Doppler anemometer for highly spatially resolved velocity measurements using low-coherence light, Meas. Sci. Technol., 2001, 12(11), 1891–1903 CrossRef CAS
.
- A. K. Tieu, M. R. Mackenzie and E. B. Li, Measurements in microscopic flow with a solid-state LDA, Exp. Fluids, 1995, 19(4), 293–294 CrossRef
.
- J. Czarske, L. Büttner, T. Razik and H. Müller, Boundary layer velocity measurements by a laser Doppler profile sensor with micrometre spatial resolution, Meas. Sci. Technol., 2002, 13(12), 1979–1989 CrossRef CAS
.
- B. U. Moon, S. S. H. Tsai and D. K. Hwang, Rotary polymer micromachines: in situ fabrication of microgear components in microchannels, Microfluid. Nanofluid., 2015, 19(1), 67–74 CrossRef CAS
.
- R. Attia, Modifications de surfaces et integration de MEMS pour les laboratoires sur puce, 2010 Search PubMed.
- C. Cavaniol, Towards a universal flow sensor for Microfluidics, 2020 Search PubMed.
- J.-P. Fanton, A brief history of metrology: past, present, and future, Int. J. Metrol. Qual. Eng., 2019, 10(8), 5, DOI:10.1051/ijmqe/2019005
.
- CGPM, La conférence du mètre, Documents Diplomatiques, 1875 Search PubMed.
- Guide to the expression of uncertainty of measurement, in ISO/IEC GUIDE 98-3:2008(E) Contents, 2008, Available from: https://isotc.iso.org/livelink/livelink/fetch/2000/2122/4230450/8389141/ISO_IEC_Guide_98-3_2008%28E%29_-_Uncertainty_of_measurement_--_Part_3%2C_Guide_to_the_expression_of_uncertainty_in_measurement_%28GUM%2C1995%29.pdf?nodeid=8389142&vernum=-2 Search PubMed.
- P. Lucas, Comparison of standards for low liquid flow rates, 2017, EURAMET pr Search PubMed.
- Calibration and Measurement Capabilities(CMCs): A paper by the joint BIPM/ILAC WG(2007), 2007, pp. 1–6 Search PubMed.
- https://www.bipm.org/kcdb/
.
- A. F. Al-Assaf, L. J. Bumpus, D. Carter and S. B. Dixon, Preventing errors in healthcare: a call for action, Hosp. Top., 2003, 81(3), 5–13 CrossRef PubMed
.
- A. M. Timmerman, R. A. Snijder, P. Lucas, M. C. Lagerweij, J. H. Radermacher and M. K. Konings, How physical infusion system parameters cause clinically relevant dose deviations after setpoint changes, Biomed. Tech., 2015, 60(4), 365–376 Search PubMed
.
- S. Klein and P. Lucas, Low liquid flows-an important aspect in medical technology, Biomed. Tech., 2015, 60(4), 269–270 Search PubMed
.
- P. T. Lee, F. Thompson and H. Thimbleby, Analysis of infusion pump error logs and their significance for health care, Br. J. Nurs., 2012, 21(Sup 8), S12–S20, DOI:10.12968/bjon.2012.21.Sup8.S12
.
- R. A. Snijder, M. K. Konings, P. Lucas, T. C. Egberts and A. D. Timmerman, Flow variability and
its physical causes in infusion technology: a systematic review of in vitro measurement and modeling studies, Biomed. Tech., 2015, 60(4), 277–300 Search PubMed
, Available from: https://www.degruyter.com/view/j/bmte.2015.60.issue-4/bmt-2014-0148/bmt-2014-0148.xml.
- A. C. Van Der Eijk, R. M. F. P. T. Van Rens, J. Dankelman and B. J. Smit, A literature review on flow-rate variability in neonatal IV therapy, Paediatr. Anaesth., 2013, 23(1), 9–21 CrossRef PubMed
.
- https://www.drugmetrology.com/
.
- E. Batista, N. Almeida, A. Furtado, E. Filipe, L. Sousa and R. F. Martins, et al., Assessment of drug delivery devices, Biomed. Tech., 2015, 60(4), 347–357 Search PubMed
.
- F. Ogheard, A. K. Niemann, E. Batista, H. Bissig, A. M. Timmerman and R. A. Snijder, et al., Assessment of drug delivery devices and accessories A few show cases Flow rate error, compliance and impact of operating conditions, 2015 Search PubMed.
- F. Ogheard, S. Margot and J. Savary, Experimental study of buoyancy and surface tension effects of an immersed capillary gravimetric micro-flow facility, 2016 Search PubMed.
- H. Bissig, M. Tschannen and M. de Huu, Micro-flow facility for traceability in steady and pulsating flow, Flow Meas. Instrum., 2015, 44, 34–42, DOI:10.1016/j.flowmeasinst.2014.11.008
.
- P. Lucas, M. Ahrens, J. Geršl, W. Sparreboom and J. Lötters, Primary standard for liquid flow rates between 30 and 1500 nl/min based on volume expansion, Biomed. Tech., 2015, 60(4), 317–335 Search PubMed
.
- P. Lucas, Primary standard nanoflow rates Overview of this presentation Low to ultra-low flow rates Presenting the results of MeDD Today' s program Part I and II, 2014, (September 2013) Search PubMed.
- M. Ahrens, S. Klein, B. Nestler and C. Damiani, Design and uncertainty assessment of a setup for calibration of microfluidic devices down to 5 nL min-1, Meas. Sci. Technol., 2014, 25(1), 015301 CrossRef CAS
, Available from: https://stacks.iop.org/0957-0233/25/i=1/a=015301?key=crossref.2ea028aba7915d5352938678fb9bd1b9.
- L. Leger and J. F. Joanny, Liquid spreading, Rep. Prog. Phys., 1992, 55(4), 431–486 CrossRef CAS
, Available from: https://stacks.iop.org/0034-4885/55/i=4/a=001?key=crossref.e2191f33f9e732f5779fece847bdb224.
- J. F. Joanny and P. G. de Gennes, A new model for contact angle hysteresis, J. Chem. Phys., 1984, 2(2), 211–225 Search PubMed
.
- M. Ahrens, B. Nestler, S. Klein, P. Lucas, H. T. Petter and C. Damiani, An experimental setup for traceable measurement and calibration of liquid flow rates down to 5 nl/min, Biomed. Tech., 2015, 60(4), 337–345 Search PubMed
.
- M. Richter, P. Woias and D. Weiss, Microchannels for applications in liquid dosing and flow-rate measurement, Sens. Actuators, A, 1997, 62(1–3 pt 3), 480–483 CrossRef CAS
.
- F. Ogheard, P. Cassette and A. W. Boudaoud, Development of an optical measurement method for “sampled” micro-volumes and nano-flow rates, Flow Meas. Instrum., 2020, 73, 101746, DOI:10.1016/j.flowmeasinst.2020.101746
.
- H. Bissig, M. Tschannen and M. De Huu, Improving process quality by means of accurate and traceable calibration of flow devices with process-oriented liquids, Chimia, 2018, 72(3), 124–129 CrossRef CAS PubMed
.
- H. Bissig and A. K. Niemann, Cross check of the pulsating flow tester at DTI and METAS, 2014, pp. 1–37, http://www.drugmetrology.com/wp-content/uploads/2016/09/<?pdb_no 2014?>2014<?pdb END?>_10_14_D_2_1_5_Report_Puls_Cross_Check_METAS.pdf Search PubMed.
- R. Monge, J. Groenesteijn, D. Alveringh, R. J. Wiegerink, J. Lötters and L. J. Fernandez, SU–8 micro coriolis mass flow sensor, Sens. Actuators, B, 2017, 241 DOI:10.1016/j.snb.2016.10.133
.
Footnote |
| † We also included recent development of primary standards at NIST based on the recent work of Schmidt et al., though intercomparisons were made but not validated yet.68 Moreover, we know some recent advances in calibration facilities could have been made in the different NMIs63,67,116 but few characterizations were available and they weren't validated by means of intercomparisons. Consequently, changes in the calibration setup will just be mentioned. In addition, although CMCs claims concerned steady state flows calibration, facilities to measure pulsating flows were also investigated at METAS and DTI117 but they won't be discuss in the scope of this review. |
| This journal is © The Royal Society of Chemistry 2022 |