Open Access Article
Open Access ArticleA reactivity model for oxidative addition to palladium enables quantitative predictions for catalytic cross-coupling reactions†
Jingru
Lu
,
Sofia
Donnecke
,
Irina
Paci
 * and
David C.
Leitch
* and
David C.
Leitch
 *
*
Department of Chemistry, University of Victoria, 3800 Finnerty Rd, Victoria BC, V8P 5C2, Canada. E-mail: ipaci@uvic.ca; dcleitch@uvic.ca
First published on 28th February 2022
Abstract
Making accurate, quantitative predictions of chemical reactivity based on molecular structure is an unsolved problem in chemical synthesis, particularly for complex molecules. We report an approach to reactivity prediction for catalytic reactions based on quantitative structure-reactivity models for a key step common to many catalytic mechanisms. We demonstrate this approach with a mechanistically based model for the oxidative addition of (hetero)aryl electrophiles to palladium(0), which is a key step in myriad catalytic processes. This model links simple molecular descriptors to relative rates of oxidative addition for 79 substrates, including chloride, bromide and triflate leaving groups. Because oxidative addition often controls the rate and/or selectivity of palladium-catalyzed reactions, this model can be used to make quantitative predictions about catalytic reaction outcomes. Demonstrated applications include a multivariate linear model for the initial rate of Sonogashira coupling reactions, and successful site-selectivity predictions for Suzuki, Buchwald-Hartwig, and Stille reactions of multihalogenated substrates relevant to the synthesis of pharmaceuticals and natural products.
Introduction
The synthesis of structurally complex organic molecules relies on forging new chemical bonds between diverse molecular building blocks. Catalytic cross-coupling is one of the most versatile and widely-used methods to link these molecular fragments,1 with applications ranging from the manufacture of active pharmaceutical ingredients,2 to the selective modification of biomolecules,3 to the creation of new functional materials.4 While much has been done to develop and understand new cross-coupling reactions and catalysts, less is known about how the specific molecular structures of complex building blocks affect the likelihood of successful coupling.5–7 As a result, time- and resource–intensive reaction screening and optimization campaigns are often required for each new synthetic target. These involve many iterations and can still result in failure to find appropriate conditions for a given transformation, impeding access to potentially promising new medicines and materials.Emerging approaches in reactivity prediction that combine high-throughput experimentation8–14 with molecular descriptor sets15–24 and multivariate statistical analysis including machine learning25–34 can accelerate the screening/optimization process and increase success rates; however, predictions generated by these approaches are often limited to the specific reaction under investigation. Developing and refining the next generation of organic chemistry tools, including computer-aided synthesis design, automated reaction optimization, and predictive algorithms,35 requires the development of general and quantitative frameworks that rapidly link molecular structure to reactivity for many different reactants and catalysts.
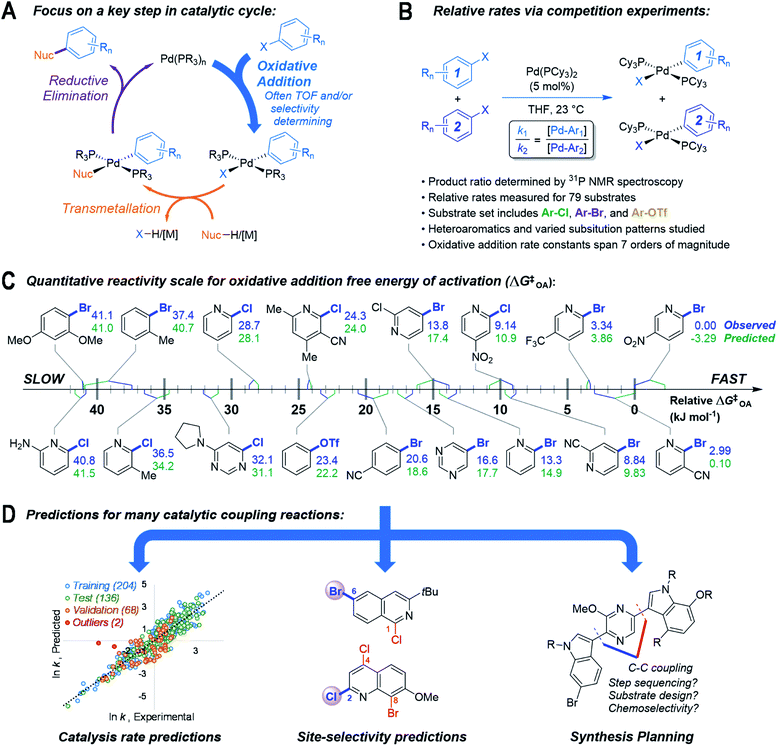
Here, we describe an approach to predict outcomes for multiple catalytic cross-coupling reactions by focusing on the structure–reactivity relationships for one key mechanistic step (Fig. 1). Specifically, we targeted oxidative addition, a fundamental organometallic transformation common to many catalytic reactions.36 Oxidative addition is particularly relevant to palladium-catalyzed cross-coupling, where it is often the rate and/or selectivity determining step37 (Fig. 1A). We hypothesized that a quantitative structure-reactivity model for the oxidative addition38–40 of aryl electrophiles to a catalytically-relevant Pd(0) complex would enable predictions for palladium-catalyzed cross-coupling reactions under a variety of conditions. We assembled this model by correlating experimental relative rate data (Fig. 1B) with easily-obtained molecular descriptors for a diverse set of substrates, with an emphasis on incorporating pharmaceutically-relevant heterocycles (Fig. 1C).
As hypothesized, the resulting model can be applied to many different cross-coupling reactions. It can predict catalytic rate constants as a function of substrate structure even when different catalysts/solvents are used, can correctly identify the most reactive position(s) when multiple reaction sites are available, and can also help to guide synthetic route planning (Fig. 1D). Importantly from both a fundamental and practical perspective, the predictive ability of this reactivity model extends well beyond the specific molecular structures and reaction conditions included in the initial data set. By revealing how subtle changes to the reacting molecules affect a key step in a catalytic mechanism, this model serves as a powerful predictive tool for cross-coupling, and will enable more sophisticated and accurate computer-aided retrosynthetic design. Finally, this work demonstrates the potential of focusing reaction prediction efforts on fundamental mechanistic steps in catalytic mechanisms.41
Results and discussion
Development of the oxidative addition reactivity model
As the basis for a quantitative structure/reactivity model for cross-coupling catalysis, we conducted a series of oxidative addition competition experiments in THF using a library of 79 (hetero)aryl chlorides, bromides, and triflates, reacting with Pd(PCy3)2 (Fig. 1B). Measuring the Pd(II) product ratio by 31P NMR spectroscopy gives relative observed rate constants, and the corresponding relative free energies of activation (ΔG‡OA), with 2-bromo-5-nitropyridine set to ΔG‡OA = 0.As a check on these kinetic data, we constructed Hammett plots for five sets of substrates, obtaining reaction constants consistent with previous reports (Fig. S31–S37†). From these data, we have constructed a unified reactivity scale that spans more than 7 orders of magnitude in rate (Fig. 1D), containing substrates with a wide variety of steric and electronic parameters, as well as the three aforementioned leaving groups. We also ruled out the possibility of reversible oxidative addition leading to thermodynamic product ratios by mixing equimolar amounts of six separate pairs of oxidative addition products, all of which retained their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio even after extended time (Table S3†). Finally, we isolated and characterized six new representative Pd(II) oxidative addition complexes to confirm their structures as trans-Pd(PCy3)2(Ar)(X) (compounds S1–S6, Fig. S7–S30†).
1 mole ratio even after extended time (Table S3†). Finally, we isolated and characterized six new representative Pd(II) oxidative addition complexes to confirm their structures as trans-Pd(PCy3)2(Ar)(X) (compounds S1–S6, Fig. S7–S30†).
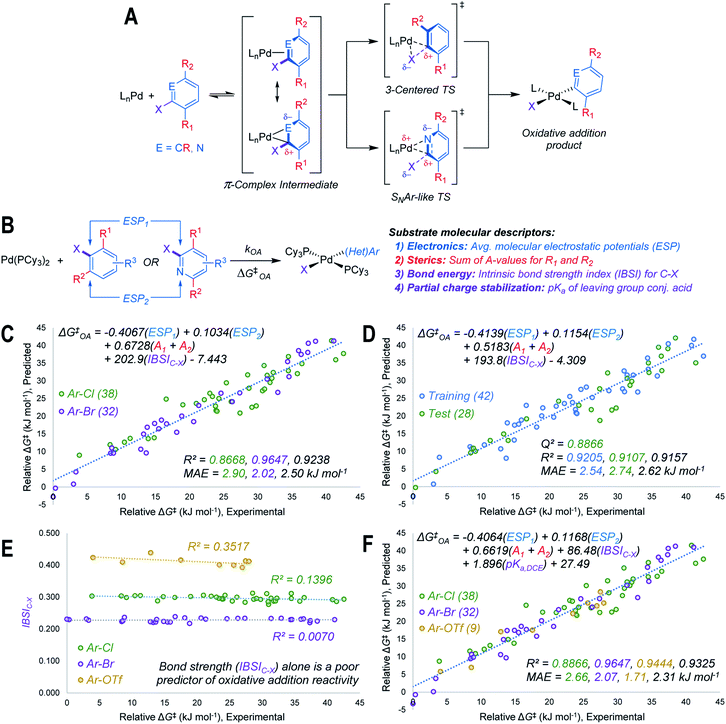
Using the mechanistic features of oxidative addition to Pd(0) as a guide, we considered molecular descriptors that would provide mechanistically meaningful correlations between substrate structures and oxidative addition reactivity (Fig. 2A).39 Mechanisms for aryl halide oxidative addition to Pd(0) have been extensively studied both computationally40,42–44 and experimentally,45–49 and are generally proposed to proceed via initial coordination of the aromatic π-system to Pd. Two bonding extremes can be envisioned for the π-complex intermediate, where the degree of polarization of the coordinated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or C
C or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond in the substrate influences partial charge distribution in the π-complex. From this intermediate, two types of oxidative addition transition state have been proposed: a 3-centered, relatively non-polar transition state involving simultaneous Pd–C and Pd–X bond formation, and a polarized transition state with C–X heterolytic bond cleavage occurring alongside Pd–C bond formation; this latter pathway resembles the proposed mechanism for nucleophilic aromatic substitution (SNAr).46,49 While other coordination modes between the (hetero)aryl substrate and Pd are possible, we restricted our analysis to the π-complex intermediates that would immediately precede oxidative addition.
N bond in the substrate influences partial charge distribution in the π-complex. From this intermediate, two types of oxidative addition transition state have been proposed: a 3-centered, relatively non-polar transition state involving simultaneous Pd–C and Pd–X bond formation, and a polarized transition state with C–X heterolytic bond cleavage occurring alongside Pd–C bond formation; this latter pathway resembles the proposed mechanism for nucleophilic aromatic substitution (SNAr).46,49 While other coordination modes between the (hetero)aryl substrate and Pd are possible, we restricted our analysis to the π-complex intermediates that would immediately precede oxidative addition.
Based on the structural and electronic features of these transition states, we built our reactivity model for oxidative addition from a combination of average molecular electrostatic potentials (ESP) as electronic descriptors for specific atoms in the substrate,38,50–54 A-values as steric descriptors,55 and the intrinsic bond strength index (IBSI) as a bond energy descriptor (Fig. 2B).56 Importantly, all of these descriptors are directly calculated from electronic wavefunctions (obtained from density functional theory calculations), or are tabulated in the literature. An initial multivariate linear regression analysis27,57 of the descriptor sets for the Ar–Cl and Ar–Br substrates versus relative ΔG‡OA (kJ mol−1) reveals a strong correlation across the halide substrate library (Fig. 2C).
This model incorporates two ESP values: one for the carbon undergoing substitution (ESP1), and a second for an atom adjacent to the reactive site (ESP2). For 2-halopyridines, ESP2 corresponds to the nitrogen atom. For substrates where the adjacent atoms are inequivalent carbons, which would lead to two possible π-coordination sites prior to oxidative addition, ESP2 is the value that leads to the smaller predicted ΔG‡OA (i.e. the faster oxidative addition); either the smaller positive value, or the larger negative value. The model also incorporates two substituent A-values for groups R1 and R2 to account for steric effects on the oxidative addition rate. While the steric effect of groups ortho to the reactive C–X bond is intuitive, the effect of R2 for 2-halopyridine substrates is not initially obvious; however, our experimental results reveal the steric influence of R2 is approximately equal to that of R1 throughout the 2-halopyridine substrate set. As these two terms have very similar coefficients when treated separately during linear regression (Table S8†), we opted to use the sum (A1 + A2) as a single descriptor. Finally, including the IBSI is necessary to create a model applicable to both (hetero)aryl chlorides and bromides.
We evaluated the robustness of this linear model by regression analysis of five random training (60%) and test (40%) sets, and comparing the mean absolute errors (MAE) and predictive squared correlation coefficients (Q2);58 one example is shown in Fig. 2D (remainder in Fig. S60–S63†). All of these analyses give similar linear equations, and excellent agreement between predicted and experimental values in the test sets. We also evaluated alternative models (Table S9†), and partitioned the data into targeted training and test sets to evaluate out-of-sample prediction accuracy (Fig. S64–S67†). The out-of-sample predictions are in excellent agreement with the observed ΔG‡OA.
Our initial attempts to incorporate aryl triflate electrophiles into this model using the aforementioned descriptor set were unsuccessful, leading to poor correlations and inaccurate predictions. We attribute this to C–X bond strength being an insufficient descriptor to differentiate between the reactivity of various leaving groups. Bond strength arguments, often using calculated BDEs, are used to rationalize relative oxidative addition reactivity for different substrates, such as for site selectivity in multihalogenated systems.59–61 In our initial model (Fig. 2C and D), the IBSI term is essentially a step function: there are relatively narrow value distributions within the Ar–Br or Ar–Cl data sets, but a large gap between those data sets that reflects the weaker C–Br bond. Plotting a univariate correlation between IBSIC–X and ΔG‡OA for all three electrophile classes reveals a similarly tiered structure (Fig. 2E). Strikingly, there is zero correlation between IBSI and ΔG‡OA, either within each electrophile class or across the entire data set. Furthermore, the relative ordering of bond strength (C–O > C–Cl > C–Br) is inconsistent with the fact that aryl triflates react faster than identically-substituted aryl bromides with Pd(PCy3)2 (kPhOTf/kPhBr ∼100). Clearly, bond strength on its own is a poor predictor of oxidative addition reactivity when comparing two substrates with either the same62 or different leaving groups.
To account for additional transition state stabilization by the leaving group itself, which builds up negative charge as the C–X bond is broken (Fig. 2A), we used a simple descriptor of anion stability: the pKa of the leaving group's conjugate acid. Adding the pKa values for HOTf, HBr, and HCl (−11.3, −4.4, and 0.2 respectively, previously measured in DCE as a non-polar solvent63) results in a unified predictive model (Fig. 2F). Both IBSIC–X and pKa are required as descriptors, with the unified model re-weighting the IBSI term down by a factor of 2. Notably, the relative contributions of the ESP and A-value terms remain essentially constant.
This model provides, for the first time, a reliable method to quantitatively evaluate the relative reactivity of a hypothetical multisubstituted (hetero)aryl triflate, bromide, or chloride toward oxidative addition with a Pd(0) complex without the need to calculate transition state energies. We again performed cross-validation with a set of five random 60/40 training/test data partitions, which give excellent agreement between experimental and predicted values (Fig. S69–S73†). Of the 79 substrates, there are only four examples identified as prediction outliers (standardized residual ≥2, Table 1). There are no obvious features of these outliers that would point to systematic prediction errors for a particular substructure; there are several similar examples (bromobenzenes, fluoropyridines, and pyrimidines) that are predicted accurately.
Finally, to examine the relative contribution of each descriptor to the predicted ΔG‡OA of the two models (Fig. 2C and F), we applied a min/max scaling to the descriptor values prior to multivariate regression. The coefficients of the normalized models and their relative contributions are shown in Table 2. In both models, ESP1 is the most consequential descriptor, followed by ESP2 at roughly half the weighting. In contrast, steric effects account for <10% of the predicted ΔG‡OA. The C–X bond strength as reported by the IBSI descriptor is also a relatively small contributor (16–20%), consistent with the observation of its poor correlation to ΔG‡OA when X remains constant (Fig. 2E). In fact, the pKa of HX is just as consequential for predicting ΔG‡OA as the IBSI in the model from Fig. 2F (X = Cl, Br, OTf).
Mechanistic aspects of oxidative addition linked to molecular descriptors.
The predictive power of this reactivity model is a direct result of its mechanistic foundation. ESP1 is related to the electrophilicity of the carbon undergoing oxidative addition, reflecting the degree of partial positive charge in the π-complex intermediate and transition state: a larger positive ESP1 leads to a smaller ΔG‡OA and thus faster oxidative addition. In contrast, ESP2 reflects the degree of negative charge on the adjacent atom (C or N), where a larger negative ESP2 leads to a faster oxidative addition. Considered together, these ESP terms indicate that a more polarized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or C
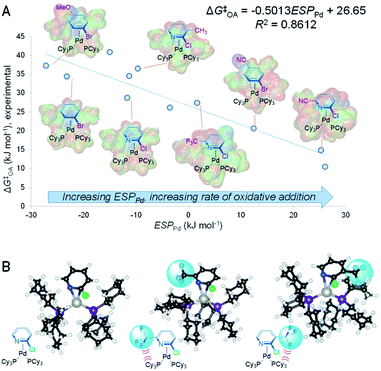
C or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond in the substrate leads to faster oxidative addition. It follows from this analysis that the ESP at Pd in the intermediate and/or transition state should also affect the oxidative addition rate, with a larger positive ESPPd correlating with faster oxidative addition. We have confirmed this by determining ESPPd for a set of 11 calculated π-complex intermediates and 6 transition states (Fig. S40–S56†). Remarkably, there is a linear correlation between ESPPd for the π-complexes and ΔG‡OA (Fig. 3A and S57†), revealing the significant effect that substrate–catalyst bonding has on the electronic structure, and therefore reactivity, of Pd.
N bond in the substrate leads to faster oxidative addition. It follows from this analysis that the ESP at Pd in the intermediate and/or transition state should also affect the oxidative addition rate, with a larger positive ESPPd correlating with faster oxidative addition. We have confirmed this by determining ESPPd for a set of 11 calculated π-complex intermediates and 6 transition states (Fig. S40–S56†). Remarkably, there is a linear correlation between ESPPd for the π-complexes and ΔG‡OA (Fig. 3A and S57†), revealing the significant effect that substrate–catalyst bonding has on the electronic structure, and therefore reactivity, of Pd.
Analyzing how the substrate binds to the catalyst also sheds light on the observed equal weights of the steric A-values for R1 and R2 in affecting ΔG‡OA for the 2-halopyridine substrate series. Larger substituents in these positions destabilize the π-complex intermediate and oxidative addition transition state through steric repulsion between the bound substrate and the ancillary phosphine ligands. Because the Pd center coordinates to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, substituents adjacent to either C or N will occupy roughly equivalent positions with respect to the phosphines. Comparing the calculated structures of the π-complex intermediates for 2-chloropyridine to its 3- and 6-trifluoromethyl substituted analogues illustrates this feature of the substrate–catalyst interaction (Fig. 3B). Importantly, this mechanistic insight into equal steric effects for R1 and R2 flows directly from our quantitative reactivity model.
N bond, substituents adjacent to either C or N will occupy roughly equivalent positions with respect to the phosphines. Comparing the calculated structures of the π-complex intermediates for 2-chloropyridine to its 3- and 6-trifluoromethyl substituted analogues illustrates this feature of the substrate–catalyst interaction (Fig. 3B). Importantly, this mechanistic insight into equal steric effects for R1 and R2 flows directly from our quantitative reactivity model.
Case study #1: predicting reaction rates
To test our hypothesis that the oxidative addition model is applicable to predicting outcomes for cross-coupling catalysis, we applied ΔG‡OA predictions in three case studies. The first test case involves modeling the initial rates of Sonogashira coupling reactions, drawn from published data sets containing 410 individual rates (29 substrates and 17 catalysts, Fig. 4A).64,65 We first predicted ΔG‡OA for each of the 29 aryl bromides in the data sets, using the equation from Fig. 2C (the simpler model when considering only halide-based electrophiles); while 9 of these substrates are included in our experimental oxidative addition data set, the other 20 are out-of-sample predictions.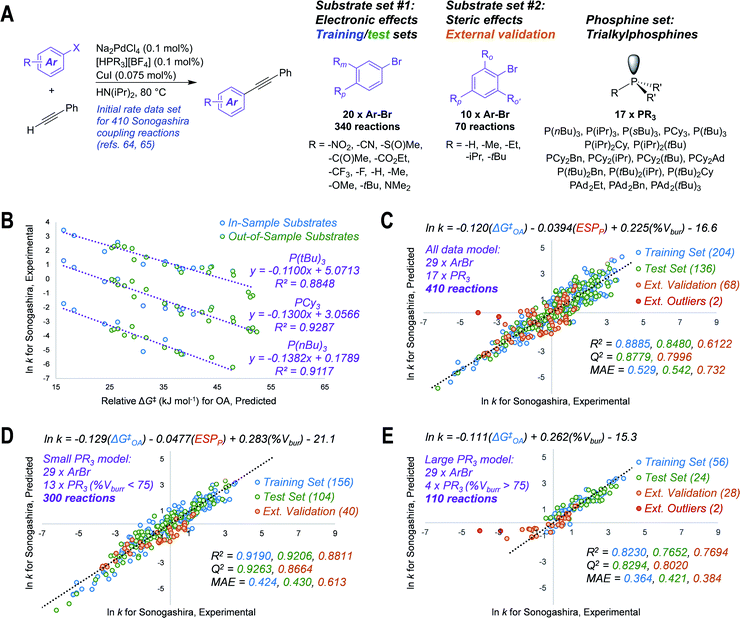 | ||
Fig. 4 Translating oxidative addition predictions to quantitative models of catalytic reactivity. (A) General reaction scheme and chemical space explored for 410 Sonogashira reactions, with two distinct substrate sets; initial rates determined previously.64,65 (B) Univariate linear correlations between predicted ΔG‡OA for oxidative addition to Pd(PCy3)2 and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for Sonogashira coupling with three phosphines; out-of-model substrates are Ar–Br molecules not included in ΔG‡OA training set. (C) Unified three-descriptor model for predicting ln k for Sonogashira coupling with three phosphines; out-of-model substrates are Ar–Br molecules not included in ΔG‡OA training set. (C) Unified three-descriptor model for predicting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for the entire set of 410 reactions (29 substrates, 17 ligands), with data partitioned into training (60% of set #1), test (40% of set #1), and external validation (set #2); two external outlier points (red) are not included in the external validation statistics. (D) Subset of the model with 13 “small” phosphines (% Vbur <75). (E) Subset of the model with 4 “large” phosphines (% Vbur >75); two external outlier points (red) are not included in the external validation statistics. MAE = mean absolute error. Colour-coding on R2, Q2, and MAE values corresponds to the matching data subset. k for the entire set of 410 reactions (29 substrates, 17 ligands), with data partitioned into training (60% of set #1), test (40% of set #1), and external validation (set #2); two external outlier points (red) are not included in the external validation statistics. (D) Subset of the model with 13 “small” phosphines (% Vbur <75). (E) Subset of the model with 4 “large” phosphines (% Vbur >75); two external outlier points (red) are not included in the external validation statistics. MAE = mean absolute error. Colour-coding on R2, Q2, and MAE values corresponds to the matching data subset. | ||
Remarkably, the predicted ΔG‡OA values are linearly-correlated with the corresponding ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k values for all 17 investigated phosphine ligands (Fig. S74 and S75†). Correlations for three of these ligands – P(nBu)3, PCy3, and P(tBu)3 – are shown in Fig. 4B. These correlations hold despite the fact that the Sonogashira reactions are conducted under different conditions (higher temperature, different solvent) than our oxidative addition experiments, and the fact that our predicted ΔG‡OA is derived from a model using only PCy3. We suspect that this aspect of the model's usefulness stems from a consistency in the relative reactivity of the aryl halide substrates under different conditions, even if the absolute reaction rates differ. Thus, ΔG‡OA can be applied to quantitatively predict the outcome of catalytic reactions for out-of-sample substrates, out-of-sample reaction conditions, and even out-of-sample catalysts.
k values for all 17 investigated phosphine ligands (Fig. S74 and S75†). Correlations for three of these ligands – P(nBu)3, PCy3, and P(tBu)3 – are shown in Fig. 4B. These correlations hold despite the fact that the Sonogashira reactions are conducted under different conditions (higher temperature, different solvent) than our oxidative addition experiments, and the fact that our predicted ΔG‡OA is derived from a model using only PCy3. We suspect that this aspect of the model's usefulness stems from a consistency in the relative reactivity of the aryl halide substrates under different conditions, even if the absolute reaction rates differ. Thus, ΔG‡OA can be applied to quantitatively predict the outcome of catalytic reactions for out-of-sample substrates, out-of-sample reaction conditions, and even out-of-sample catalysts.
We then expanded the application of ΔG‡OA by combining it with descriptors for the 17 free phosphines to assemble a single and unified linear model to accurately predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for the entire 410 Sonogashira reaction data set. Two descriptors were calculated for the free phosphines – the average ESP at phosphorus, and the percent buried volume (% Vbur) at phosphorus66 – which were combined with ΔG‡OA in a multivariate regression analysis. As shown in Fig. 4C, we obtain excellent linear fit and predictive power with initial rates spanning 10 orders of magnitude. These phosphine descriptors outperform the analogous descriptors calculated for the corresponding mono or bis(phosphine) Pd(0) complexes (Fig. S79 and S80†). The training and test sets used to build this model are from a random 60/40 split of substrate set #1, which focuses on electronic effects (Fig. 4A).
k for the entire 410 Sonogashira reaction data set. Two descriptors were calculated for the free phosphines – the average ESP at phosphorus, and the percent buried volume (% Vbur) at phosphorus66 – which were combined with ΔG‡OA in a multivariate regression analysis. As shown in Fig. 4C, we obtain excellent linear fit and predictive power with initial rates spanning 10 orders of magnitude. These phosphine descriptors outperform the analogous descriptors calculated for the corresponding mono or bis(phosphine) Pd(0) complexes (Fig. S79 and S80†). The training and test sets used to build this model are from a random 60/40 split of substrate set #1, which focuses on electronic effects (Fig. 4A).
To challenge the model, we reserved substrate set #2, which focuses on steric effects, as an external validation set. Despite the fact that the Sonogashira rate prediction model training set (substrate set #1, blue and green points in Fig. 4C) contains no substrates with ortho-substituents, and therefore no information about steric effects on reaction rate, the model is still able to predict ln k for substrate set #2 with a mean absolute error of 0.732 (Q2 = 0.7996). Only two reactions are identified as significant outliers: 2,4,6-triisopropylphenylbromide with P(tBu)3 and PAd2(tBu) (the most sterically-hindered substrate with the two largest ligands), which are much slower than the model predicts.
The ability to predict ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k for Sonogashira reactions of an out-of-sample substrate class stems directly from the generality of the predicted ΔG‡OA from our oxidative addition reactivity model. The substrate molecular properties – electronics, sterics, and C–X bond strengths – are all encoded within the predicted ΔG‡OA values by virtue of the structurally diverse oxidative addition training set. Thus, applying ΔG‡OA as a single descriptor takes all of these molecular features into account, enabling accurate catalytic reactivity predictions even if the available training data is not as comprehensive.
k for Sonogashira reactions of an out-of-sample substrate class stems directly from the generality of the predicted ΔG‡OA from our oxidative addition reactivity model. The substrate molecular properties – electronics, sterics, and C–X bond strengths – are all encoded within the predicted ΔG‡OA values by virtue of the structurally diverse oxidative addition training set. Thus, applying ΔG‡OA as a single descriptor takes all of these molecular features into account, enabling accurate catalytic reactivity predictions even if the available training data is not as comprehensive.
Improved prediction accuracy can be achieved by separating the 410-member data set into two subsets based on phosphine ligand size. One set includes reactions using 13 phosphines with a % Vbur <75, and the other includes the 4 largest phosphines (% Vbur >75). For the small phosphine set, a slight reweighting of the three descriptors leads to smaller MAEs for training, test, and external data sets (Fig. 4D). For the large phosphines, we used a 70/30 training/test split due to the smaller number of data points. We also found that a simpler, two-descriptor model is superior for this subset, with only ΔG‡OA and %Vbur needed to make accurate predictions (Fig. 4E). This partition into small and large phosphine sets is consistent with prior studies that describe a change in mechanism, where oxidative addition occurs from either bis(phosphine) or mono(phosphine) Pd(0) intermediates.17,33,67 Notably, our predicted ΔG‡OA is effective in both cases. This case study not only demonstrates how ΔG‡OA can be used to predict how substitution patterns on the electrophile will affect the kinetic behavior of a coupling reaction, but also how ΔG‡OA can be used in concert with catalyst-based descriptors to develop models that account for both substrate and catalyst effects on rate.
Case study #2: predicting site selectivity
The second case study tests the use of ΔG‡OA in predicting site selectivity for cross-coupling when multiple reactive positions are present (Fig. 5). Previous approaches to this problem have involved spectroscopic descriptors,68 the distortion–interaction transition state model,62 and qualitative arguments based on empirical observations.37,60 This latter method is most suitable for synthetic planning efforts, but it is largely applied “by analogy” to known systems, and it is not quantitative. Thus, formulating rapid but accurate predictions for the likely coupling site of structurally-complex multihalogenated substrates would be greatly beneficial for synthetic planning.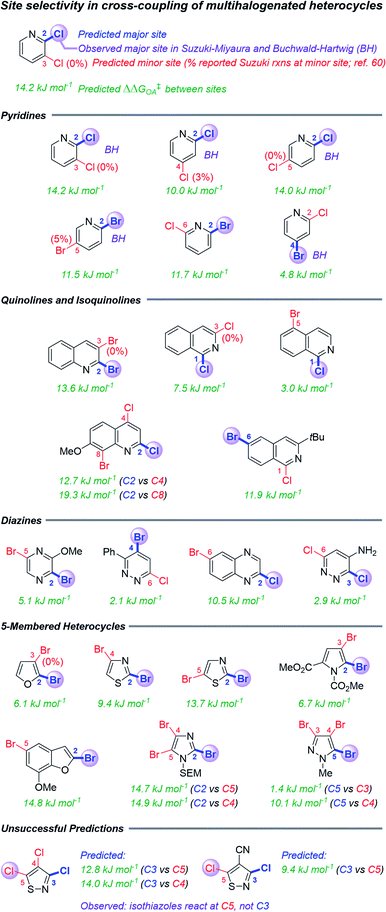 | ||
| Fig. 5 Predicted and reported selectivities for multihalogenated heterocycles in Suzuki–Miyaura and Buchwald–Hartwig cross-coupling reactions (examples of Buchwald–Hartwig substrates denoted with “BH”). Coloured labels on the heterocycles correspond to predicted major site (blue), predicted minor site (red, along with percentage of exceptions as reported in ref. 60), and observed site (purple sphere). The magnitude of ΔΔG‡OA between the two sites is given in green. | ||
Because all of the descriptors in the ΔG‡OA prediction model are local rather than global, one can calculate distinct ΔG‡OA values for each reactive site in a molecule, with the predicted major site corresponding to the lowest ΔG‡OA. Assessing a series of multihalogenated heterocycles with reported experimental selectivities for Suzuki–Miyaura60 and Buchwald–Hartwig69–73 coupling reveals that these ΔG‡OA predictions correctly identify the major site of reactivity across a diverse range of substrates, including many heterocycle classes (isoquinolines, diazines, and several 5-membered heterocycles) not included in our initial training set (Fig. 5). These predictions also correctly identify when a C–Cl position is more reactive than a C–Br position in the same molecule, and vice versa. The model is, of course, not without limitations: predictions for two isothiazole substrates are not accurate, pointing to C3 as the preferred site over the correct C5 position.
In addition to identifying the major site of reactivity, the predictions are also quantitative (Fig. 6). A large difference between the ΔG‡OA for each site (ΔΔG‡OA) indicates very high predicted selectivity for one site over another, while a small ΔΔG‡OA indicates likely poor selectivity. Two specific examples of this are given in Fig. 6A. For Suzuki–Miyaura coupling of methyl 2,6-dichloronicotinate, our model predicts ΔΔG‡OA = 5.4 kJ mol−1, favoring C6 by ∼7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 65 °C. The observed selectivity using Pd(PPh3)4 as a catalyst at 65 °C is 5
1 at 65 °C. The observed selectivity using Pd(PPh3)4 as a catalyst at 65 °C is 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6 to C3 (ΔΔG‡ = 4.5 kJ mol−1).74 For 3,6-dichloro-4-methoxypyridazine, our model predicts ΔΔG‡OA = 0.7 kJ mol−1, favoring C6 by ∼1.3
1 C6 to C3 (ΔΔG‡ = 4.5 kJ mol−1).74 For 3,6-dichloro-4-methoxypyridazine, our model predicts ΔΔG‡OA = 0.7 kJ mol−1, favoring C6 by ∼1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 100 °C (though this difference is smaller than the model MAE). The observed selectivity using Pd(PPh 3)4 as a catalyst at 100 °C is 3
1 at 100 °C (though this difference is smaller than the model MAE). The observed selectivity using Pd(PPh 3)4 as a catalyst at 100 °C is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C6 to C3, (ΔΔG‡ = 3.4 kJ mol−1).75 These predictions are also amenable to Buchwald–Hartwig coupling reactions: the predicted selectivity for 2,4-dichloropyridine is ΔΔG‡OA = 10.0 kJ mol−1, favoring C2 by 25
1 C6 to C3, (ΔΔG‡ = 3.4 kJ mol−1).75 These predictions are also amenable to Buchwald–Hartwig coupling reactions: the predicted selectivity for 2,4-dichloropyridine is ΔΔG‡OA = 10.0 kJ mol−1, favoring C2 by 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 100 °C; a set of Buchwald–Hartwig aminations using a Xantphos-based catalyst proceed with C2
1 at 100 °C; a set of Buchwald–Hartwig aminations using a Xantphos-based catalyst proceed with C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C4 selectivity of 20
C4 selectivity of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 50
1 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (ΔΔG‡ = 9.3–12.1 kJ mol−1 at 100 °C).73
1 (ΔΔG‡ = 9.3–12.1 kJ mol−1 at 100 °C).73
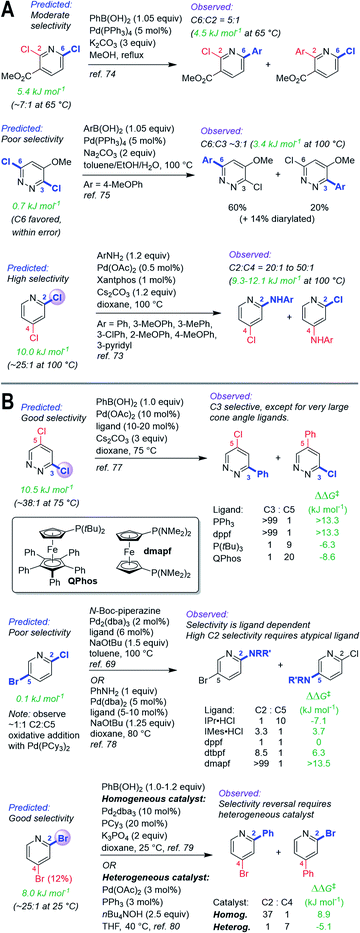 | ||
| Fig. 6 (A) Quantitative selectivity predictions for dihalogenated heterocycles with small-to-medium ΔΔG‡OA between two sites, and observed product ratios. (B) Predictions for substrates with observed tunable selectivity, demonstrating that “simple” catalysts are quantitatively consistent with predicted selectivities; overriding predicted reactivity requires targeted screening and/or catalyst design. Coloured labels on the heterocycles correspond to predicted major site (blue), predicted minor site (red, along with percentage of exceptions as reported in ref. 60), and observed site (purple sphere). The magnitude of ΔΔG‡OA between the two sites is given in green. | ||
Site selectivity is known to be influenced by reaction conditions, such as catalyst and solvent.37,60,76 Our prediction model is based on a simple monodentate phosphine using non-polar reaction solvents, which represents a standard combination used in synthetic applications. To illustrate how our model could guide the development of chemo/regiodivergent coupling reactions, we have applied predictions to substrates known to have tunable selectivity (Fig. 6B). First, 3,5-dichloropyridazine is predicted to have good selectivity for C3 over C5 (ΔΔG‡OA = 10.6 kJ mol−1), consistent with the observed selectivity using simple ligands (PPh3, dppf); therefore, inverting this selectivity should require extensive catalyst/solvent screening. Researchers at Merck took this exact approach, discovering that the large QPhos ligand gives high C5 selectivity.77
Second, the predicted ΔΔG‡OA for 2-chloro-5-bromopyridine is 0.2 kJ mol−1, indicating effectively no selectivity; we confirmed this by oxidative addition of this substrate with Pd(PCy3)2, which gives a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of C2 and C5 products. Thus, our prediction indicates achieving selectivity one way or the other will require more complex systems. Consistent with this, two previous studies reveal ligand-controlled reactivity at either C2 or C5, with high C2 selectivity requiring extensive screening and catalyst parameterization, and use of an unconventional diaminophosphine (dmapf).69,78
1 mixture of C2 and C5 products. Thus, our prediction indicates achieving selectivity one way or the other will require more complex systems. Consistent with this, two previous studies reveal ligand-controlled reactivity at either C2 or C5, with high C2 selectivity requiring extensive screening and catalyst parameterization, and use of an unconventional diaminophosphine (dmapf).69,78
Finally, we predict that 2,4-dibromopyridine should be selective for C2 (ΔΔG‡OA = 8.0 kJ mol−1, C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C4 ∼25
C4 ∼25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 25 °C), which is exactly what is observed experimentally using homogeneous Pd catalysis.79 A recent report revealed that heterogeneous, nanoparticle-based Pd catalysis is capable of inverting the selectivity to ∼1
1 at 25 °C), which is exactly what is observed experimentally using homogeneous Pd catalysis.79 A recent report revealed that heterogeneous, nanoparticle-based Pd catalysis is capable of inverting the selectivity to ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 C2
7 C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C4.80 As for the examples above, overriding the predicted selectivity requires a dramatically different catalyst system.
C4.80 As for the examples above, overriding the predicted selectivity requires a dramatically different catalyst system.
Case study #3: retrospective synthesis planning
As a final case study, we have retrospectively applied ΔG‡OA predictions to two reported synthesis toward dragmacidin D (Fig. 7).81–83 The general sequence relies on two regioselective cross-coupling reactions to a dihalogenated pyrazine core (Fig. 7A). Among the key design questions are how to achieve selective, sequential couplings, and how to ensure compatibility with the existing Ar–Br in indole 1 (which is present in the natural product).83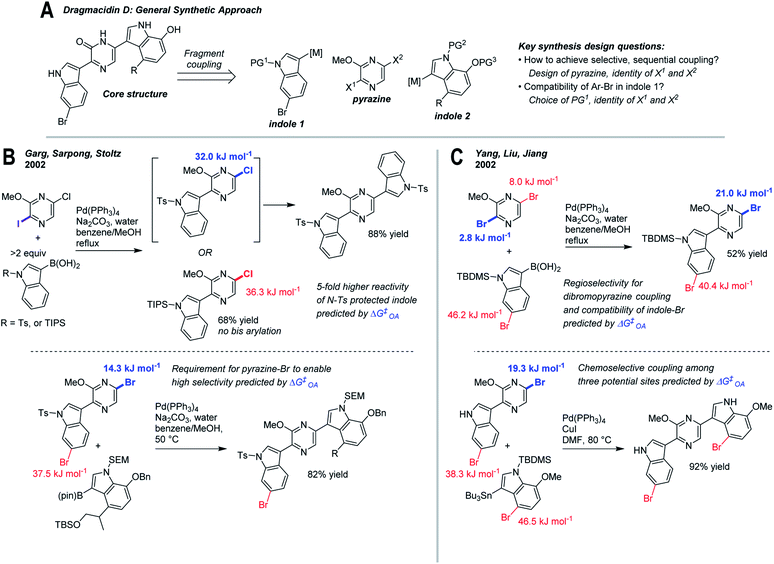 | ||
| Fig. 7 Retrospective analysis of applying ΔG‡OA predictions to synthesis design: dragmacidin D. (A) Retrosynthesis of core structure, involving selective fragment coupling to a dihalogenated pyrazine. (B) Approach involving differential halogenation, tosylate protecting group on indole 1, and switch from 5-chloro to 5-bromopyrazine intermediates for selective coupling.81 (C) Approach involving regioselective coupling to dibromopyrazine, TBS protecting group on indole 1, and regioselective Stille coupling.82 | ||
Two approaches to this problem have been reported. En route to the first completed synthesis of dragmacidin D, Garg, Sarpong, and Stoltz (Fig. 7B)81 conducted model studies using 2-iodo-5-chloro-3-methoxypyrazine to maximize site-selectivity, though they observed that the nature of the protecting group on the indole also has a significant effect on reactivity. With an N-Ts protecting group, bis(arylation) is readily achieved at elevated temperature, whereas with N-TIPS, the intermediate pyrazine is deactivated, preventing a second coupling. The remote electronic effect of the N-Ts group, which activates the C5 pyrazine position, is described as a fortuitous discovery. Applying our ΔG‡OA predictions to these intermediates clearly reveals not only the existence but the magnitude of this effect, leading to ∼5-fold higher predicted reactivity between N-Ts and N-TIPS substrates. Thus, a subtle but important reactivity difference could be anticipated based on predicted ΔG‡OA prior to experimental work, and help guide protecting group selection.
The second coupling required a switch to the 2-iodo-5-bromo-3-methoxypyrazine to maximize site-selectivity, which again could be predicted based on our model. The ΔΔG‡OA for the two Ar–Br positions in the pyrazine-indole intermediate used in the synthesis is 23.2 kJ mol−1, consistent with the observed high selectivity. Hypothetical use of the corresponding 5-chloropyrazine intermediate gives a predicted ΔΔG‡OA of <5 kJ mol−1 (∼6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 50 °C), which while still selective for the desired position, would likely lead to overreaction and yield loss. Again, this type of prediction could help to guide synthetic design and subsequent experimental investigations.
1 at 50 °C), which while still selective for the desired position, would likely lead to overreaction and yield loss. Again, this type of prediction could help to guide synthetic design and subsequent experimental investigations.
Yang, Liu, and Jiang reported a similar approach (Fig. 7C)82 that employed 2,5-dibromo-3-methoxypyrazine as the pyrazine building block; a series of model studies established that regioselective C2-coupling is possible. Despite the fact that both sites appear very similar, our model predicts that C2 is the major site, albeit with moderate selectivity (ΔΔG‡OA = 5.1 kJ mol−1, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 80 °C); this lower selectivity may be reflected in the lower isolated yield relative to the differential halogenation strategy of Garg et al. In the subsequent Stille coupling, Yang et al. use the unprotected indole derivative, which we predict is ∼10-fold less reactive than the corresponding N-Ts substrate; nevertheless, the desired reaction site is heavily favored relative to the other two Ar–Br positions, consistent with the observed regioselectivity.
1 at 80 °C); this lower selectivity may be reflected in the lower isolated yield relative to the differential halogenation strategy of Garg et al. In the subsequent Stille coupling, Yang et al. use the unprotected indole derivative, which we predict is ∼10-fold less reactive than the corresponding N-Ts substrate; nevertheless, the desired reaction site is heavily favored relative to the other two Ar–Br positions, consistent with the observed regioselectivity.
Conclusions
We have demonstrated that a quantitative structure–reactivity model for oxidative addition, a key step in many catalytic mechanisms, enables accurate predictions for the outcome of various cross-coupling reactions. By correlating relative reaction rates with easily-obtained molecular descriptors, we can predict the reactivity of diverse (hetero)aryl electrophiles toward oxidative addition to Pd(0). This reactivity model links molecular structure to predicted ΔG‡OA for any hypothetical substrate, with applicability well beyond the oxidative addition training set. We used these ΔG‡OA values to predict rates and selectivities for many different catalytic reactions under various conditions, including Sonogashira, Suzuki, Buchwald–Hartwig, and Stille couplings.Given the importance of palladium-catalyzed reactions in the synthesis of complex organic molecules, we anticipate that quantitative reactivity predictions could be used during synthetic planning to design substrates with high intrinsic selectivity, and/or to identify where achieving the desired selectivity is likely to be more challenging/resource intensive. Applying ΔG‡OA predictions to hypothetical synthetic sequences and potential intermediates could therefore be used to design more selective routes and/or prioritize different potential routes prior to commencing experimental investigations. It could also be used to identify where extensive reaction development is necessary (e.g. overriding predicted selectivity), or where “simple” systems are likely to be successful. As we expand this oxidative addition reactivity model to incorporate additional sets of reaction conditions and catalysts, we expect it will not only shed new light on the mechanistic aspects of cross-coupling, but also find widespread use in refining and augmenting computer-aided synthesis design and automated reaction discovery/optimization. Finally, we are exploring quantitative reactivity models based on key steps in other catalytic mechanisms to generate accurate and general predictions across the synthesis landscape.
Data availability
Additional data files are available as part of the ESI,† including machine readable tables of descriptors (xlsx and csv formats) and coordinate files for calculated structures (xyz format).Author contributions
J. Lu: conceptualization, methodology, investigation, validation, formal analysis, writing. S. Donnecke: investigation, formal analysis, writing. I. Paci: conceptualization, methodology, formal analysis, supervision, writing. D. C. Leitch: conceptualization, methodology, formal analysis, supervision, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge with respect the Lekwungen peoples on whose traditional territory the University of Victoria (UVic) stands, and the Songhees, Esquimalt and WSÁNEĆ peoples whose historical relationships with the land continue to this day. We also acknowledge funding from the New Frontiers in Research Fund – Exploration (DCL) and NSERC Discovery Grant program (IP and DCL). Supercomputing resources at Westgrid and Compute Canada were integral to this work.References
- L.-C. Campeau and N. Hazari, Organometallics, 2019, 38, 3–35 CrossRef CAS PubMed
.
- J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177–2250 CrossRef CAS
.
- E. V. Vinogradova, C. Zhang, A. M. Spokoyny, B. L. Pentelute and S. L. Buchwald, Nature, 2015, 526, 687–691 CrossRef CAS
.
- K. Wang, A. Osuka and J. Song, ACS Cent. Sci., 2020, 6, 2159–2178 CrossRef CAS PubMed
.
- P. S. Kutchukian, J. F. Dropinski, K. D. Dykstra, B. Li, D. A. DiRocco, E. C. Streckfuss, L.-C. Campeau, T. Cernak, P. Vachal, I. W. Davies, S. W. Krska and S. D. Dreher, Chem. Sci., 2016, 7, 2604–2613 RSC
.
- B. Mahjour, Y. Shen, W. Liu and T. Cernak, Nature, 2020, 580, 71–75 CrossRef CAS PubMed
.
- S. K. Kariofillis, S. Jiang, A. M. Żurański, S. S. Gandhi, J. I. M. Alvarado and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 1045–1055 CrossRef CAS PubMed
.
- A. B. Santanilla, E. L. Regalado, T. Pereira, M. Shevlin, K. Bateman, L.-C. Campeau, J. Schneeweis, S. Berritt, Z.-C. Shi, P. Nantermet, Y. Liu, R. Helmy, C. J. Welch, P. Vachal, I. W. Davies, T. Cernak and S. D. Dreher, Science, 2015, 347, 49–53 CrossRef PubMed
.
- M. Shevlin, ACS Med. Chem. Lett., 2017, 8, 601–607 CrossRef CAS PubMed
.
- S. W. Krska, D. A. DiRocco, S. D. Dreher and M. Shevlin, Acc. Chem. Res., 2017, 50, 2976–2985 CrossRef CAS PubMed
.
- S. M. Mennen, C. Alhambra, C. L. Allen, M. Barberis, S. Berritt, T. A. Brandt, A. D. Campbell, J. Castañón, A. H. Cherney, M. Christensen, D. B. Damon, J. Eugenio de Diego, S. García-Cerrada, P. García-Losada, R. Haro, J. Janey, D. C. Leitch, L. Li, F. Liu, P. C. Lobben, D. W. C. MacMillan, J. Magano, E. McInturff, S. Monfette, R. J. Post, D. Schultz, B. J. Sitter, J. M. Stevens, I. I. Strambeanu, J. Twilton, K. Wang and M. A. Zajac, Org. Process Res. Dev., 2019, 23, 1213–1242 CrossRef CAS
.
- C. L. Allen, D. C. Leitch, M. S. Anson and M. A. Zajac, Nat. Catal., 2019, 2, 2–4 CrossRef
.
- E. S. Isbrandt, R. J. Sullivan and S. G. Newman, Angew. Chem., Int. Ed., 2019, 58, 7180–7191 CrossRef CAS PubMed
.
- B. Mahjour, Y. Shen and T. Cernak, Acc. Chem. Res., 2021, 54, 2337–2346 CrossRef CAS
.
- N. Fey, A. C. Tsipis, S. E. Harris, J. N. Harvey, A. G. Orpen and R. A. Mansson, Chem.-Eur., 2006, 12, 291–302 CrossRef CAS PubMed
.
- J. Jover, N. Fey, J. N. Harvey, G. C. Lloyd-Jones, A. G. Orpen, G. J. J. Owen-Smith, P. Murray, D. R. J. Hose, R. Osborne and M. Purdie, Organometallics, 2010, 29, 6245–6258 CrossRef CAS
.
- Z. L. Niemeyer, A. Milo, D. P. Hickey and M. S. Sigman, Nat. Chem., 2016, 8, 610–617 CrossRef CAS PubMed
.
- K. Wu and A. G. Doyle, Nat. Chem., 2017, 9, 779–784 CrossRef CAS PubMed
.
- D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594 CrossRef CAS PubMed
.
- N. Fey, A. Koumi, A. V. Malkov, J. D. Moseley, B. N. Nguyen, S. N. G. Tyler and C. E. Willans, Dalton Trans., 2020, 49, 8169–8178 RSC
.
- L. C. Gallegos, G. Luchini, P. C. St. John, S. Kim and R. S. Paton, Acc. Chem. Res., 2021, 54, 827–836 CrossRef CAS PubMed
.
- T. Gensch, G. d P. Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. L. D'Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed
.
- A. W. McFord, C. P. Butts, N. Fey and R. W. Alder, J. Am. Chem. Soc., 2021, 143, 13573–13578 CrossRef CAS PubMed
.
- D. J. Durand and N. Fey, Acc. Chem. Res., 2021, 54, 837–848 CrossRef CAS PubMed
.
- B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld and C. Corminboeuf, Chem. Sci., 2018, 9, 7069–7077 RSC
.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS PubMed
.
- C. B. Santiago, J.-Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398–2412 RSC
.
- B. Maryasin, P. Marquetand and N. Maulide, Angew. Chem., Int. Ed., 2018, 57, 6978–6980 CrossRef CAS PubMed
.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631 CrossRef CAS PubMed
.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K. Shimizu, ACS Catal., 2020, 10, 2260–2297 CrossRef CAS
.
- F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS
.
- M. D. Wodrich, A. Fabrizio, B. Meyer and C. Corminboeuf, Chem. Sci., 2020, 11, 12070–12080 RSC
.
- S. H. Newman-Stonebraker, S. R. Smith, J. E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 374, 301–308 CrossRef CAS PubMed
.
- J. A. Hueffel, T. Sperger, I. Funes-Ardoiz, J. S. Ward, K. Rissanen and F. Schoenebeck, Science, 2021, 374, 1134–1140 CrossRef CAS PubMed
.
- Y. Shen, J. E. Borowski, M. A. Hardy, R. Sarpong, A. G. Doyle and T. Cernak, Nat. Rev. Methods Primers, 2021, 1, 1–23 CrossRef
.
- J. A. Labinger, Organometallics, 2015, 34, 4784–4795 CrossRef CAS
.
- E. K. Reeves, E. D. Entz and S. R. Neufeldt, Chem.-Eur., 2021, 27, 6161–6177 CrossRef PubMed
.
- B. A. Anjali and C. H. Suresh, ACS Omega, 2017, 2, 4196–4206 CrossRef CAS PubMed
.
- C. Sandford, L. R. Fries, T. E. Ball, S. D. Minteer and M. S. Sigman, J. Am. Chem. Soc., 2019, 141, 18877–18889 CrossRef CAS PubMed
.
- M. Kashihara, C. P. Gordon and C. Copéret, Org. Lett., 2020, 22, 8910–8915 CrossRef CAS PubMed
.
- M. Busch, M. D. Wodrich and C. Corminboeuf, ACS Catal., 2017, 7, 5643–5653 CrossRef CAS
.
- H. M. Senn and T. Ziegler, Organometallics, 2004, 23, 2980–2988 CrossRef CAS
.
- M. Ahlquist and P.-O. Norrby, Organometallics, 2007, 26, 550–553 CrossRef CAS
.
- C. L. McMullin, J. Jover, J. N. Harvey and N. Fey, Dalton Trans., 2010, 39, 10833–10836 RSC
.
- C. Amatore, A. Jutand, F. Khalil, M. A. M'Barki and L. Mottier, Organometallics, 1993, 12, 3168–3178 CrossRef CAS
.
- M. Portnoy and D. Milstein, Organometallics, 1993, 12, 1665–1673 CrossRef CAS
.
- F. Barrios-Landeros, B. P. Carrow and J. F. Hartwig, J. Am. Chem. Soc., 2009, 131, 8141–8154 CrossRef CAS PubMed
.
- E. A. Mitchell, P. G. Jessop and M. C. Baird, Organometallics, 2009, 28, 6732–6738 CrossRef CAS
.
- B. U. W. Maes, S. Verbeeck, T. Verhelst, A. Ekomié, N. von Wolff, G. Lefèvre, E. A. Mitchell and A. Jutand, Chem.-Eur., 2015, 21, 7858–7865 CrossRef CAS PubMed
.
- C. H. Suresh, P. Alexander, K. P. Vijayalakshmi, P. K. Sajith and S. R. Gadre, Phys. Chem. Chem. Phys., 2008, 10, 6492–6499 RSC
.
- F. B. Sayyed and C. H. Suresh, New J. Chem., 2009, 33, 2465–2471 RSC
.
- G. S. Remya and C. H. Suresh, Phys. Chem. Chem. Phys., 2016, 18, 20615–20626 RSC
.
- S. A. Grimmel and M. Reiher, Faraday Discuss., 2019, 220, 443–463 RSC
.
- S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289 CrossRef CAS PubMed
.
-
J. A. Hirsch, in Topics in Stereochemistry, John Wiley & Sons, Ltd, 1967, pp. 199–222 Search PubMed
.
- J. Klein, H. Khartabil, J.-C. Boisson, J. Contreras-García, J.-P. Piquemal and E. Hénon, J. Phys. Chem. A, 2020, 124, 1850–1860 CrossRef CAS PubMed
.
- M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301 CrossRef CAS PubMed
.
- V. Consonni, D. Ballabio and R. Todeschini, J. Chem. Inf. Model., 2009, 49, 1669–1678 CrossRef CAS PubMed
.
- Y. Garcia, F. Schoenebeck, C. Y. Legault, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 6632–6639 CrossRef CAS PubMed
.
- J. Almond-Thynne, D. C. Blakemore, D. C. Pryde and A. C. Spivey, Chem. Sci., 2017, 8, 40–62 RSC
.
- V. Palani, M. A. Perea and R. Sarpong, Chem. Rev., 2022 DOI:10.1021/acs.chemrev.1c00513
.
- C. Y. Legault, Y. Garcia, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 12664–12665 CrossRef CAS PubMed
.
- E. Paenurk, K. Kaupmees, D. Himmel, A. Kütt, I. Kaljurand, I. A. Koppel, I. Krossing and I. Leito, Chem. Sci., 2017, 8, 6964–6973 RSC
.
- M. an der Heiden and H. Plenio, Chem. Commun., 2007, 972–974 RSC
.
- M. R. an der Heiden, H. Plenio, S. Immel, E. Burello, G. Rothenberg and H. C. J. Hoefsloot, Chem.-Eur., 2008, 14, 2857–2866 CrossRef CAS PubMed
.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC
.
- F. Schoenebeck and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 2496–2497 CrossRef CAS PubMed
.
- S. T. Handy and Y. Zhang, Chem. Commun., 2006, 299–301 RSC
.
- J. Ji, T. Li and W. H. Bunnelle, Org. Lett., 2003, 5, 4611–4614 CrossRef CAS PubMed
.
- R. Jiang, D. Duckett, W. Chen, J. Habel, Y. Y. Ling, P. LoGrasso and T. M. Kamenecka, Bioorg. Med. Chem. Lett., 2007, 17, 6378–6382 CrossRef CAS PubMed
.
- J. K. Laha, P. Petrou and G. D. Cuny, J. Org. Chem., 2009, 74, 3152–3155 CrossRef CAS PubMed
.
- L. Qin, H. Cui, D. Zou, J. Li, Y. Wu, Z. Zhu and Y. Wu, Tet. Lett., 2010, 51, 4445–4448 CrossRef CAS
.
- R. J. Burton, M. L. Crowther, N. J. Fazakerley, S. M. Fillery, B. M. Hayter, J. G. Kettle, C. A. McMillan, P. Perkins, P. Robins, P. M. Smith, E. J. Williams and G. L. Wrigley, Tet. Lett., 2013, 54, 6900–6904 CrossRef CAS
.
- W. Yang, Y. Wang and J. R. Corte, Org. Lett., 2003, 5, 3131–3134 CrossRef CAS PubMed
.
- E. Blaise, A. E. Kümmerle, H. Hammoud, J. X. de Araújo-Júnior, F. Bihel, J.-J. Bourguignon and M. Schmitt, J. Org. Chem., 2014, 79, 10311–10322 CrossRef CAS PubMed
.
- E. K. Reeves, O. R. Bauman, G. B. Mitchem and S. R. Neufeldt, Isr. J. Chem., 2020, 60, 406–409 CrossRef CAS PubMed
.
- X. Dai, Y. Chen, S. Garrell, H. Liu, L.-K. Zhang, A. Palani, G. Hughes and R. Nargund, J. Org. Chem., 2013, 78, 7758–7763 CrossRef CAS PubMed
.
- M. H. Keylor, Z. L. Niemeyer, M. S. Sigman and K. L. Tan, J. Am. Chem. Soc., 2017, 139, 10613–10616 CrossRef CAS PubMed
.
- C. Sicre, J.-L. Alonso-Gómez and M. M. Cid, Tetrahedron, 2006, 62, 11063–11072 CrossRef CAS
.
- N. W. J. Scott, M. J. Ford, N. Jeddi, A. Eyles, L. Simon, A. C. Whitwood, T. Tanner, C. E. Willans and I. J. S. Fairlamb, J. Am. Chem. Soc., 2021, 143, 9682–9693 CrossRef CAS PubMed
.
- N. K. Garg, R. Sarpong and B. M. Stoltz, J. Am. Chem. Soc., 2002, 124, 13179–13184 CrossRef CAS PubMed
.
- C.-G. Yang, G. Liu and B. Jiang, J. Org. Chem., 2002, 67, 9392–9396 CrossRef CAS PubMed
.
- N. K. Garg and B. M. Stoltz, Chem. Commun., 2006, 3769–3779 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental and computational procedures, statistical modeling information, supplementary figures, tables of molecular descriptors, and coordinate files for calculated structures. See DOI: 10.1039/d2sc00174h |
| This journal is © The Royal Society of Chemistry 2022 |