Open Access Article
Open Access ArticleDirectly measuring Fe(III)-catalyzed SO2 oxidation rate in single optically levitated droplets†
Xue
Cao
,
Zhe
Chen
,
Yu-Xin
Liu
,
Xin-Bo
Jing
,
Lin-Fang
Li
,
Pai
Liu
* and
Yun-Hong
Zhang
 *
*
Institute of Chemical Physics, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, 100081, Beijing, China. E-mail: pliu@bit.edu.cn; yhz@bit.edu.cn
First published on 12th December 2022
Abstract
Sulfate aerosols are produced in China's winter haze at an unresolved rapid rate. Such fast kinetics may arise from a heterogeneous SO2 conversion in urban aerosols, which differs significantly from the aqueous S(IV) oxidation in bulk solutions. Given the uniqueness of aerosols as a multiphase reactor, it is preferable to measure the heterogeneous SO2 conversion rate in situ, ideally in levitated microdroplets. Here, we directly measure the Fe(III)-catalyzed SO2 conversion in single microdroplets trapped and levitated with a gradient-force aerosol optical tweezer. The sulfate formation rate was inferred from the droplet's growth rate driven by the heterogeneous reaction. Our results show that the Fe(III)-catalyzed SO2 conversion in aerosols is 2 to 3 decades faster than that determined in bulk solutions. The SO2 reactive uptake coefficient at pH ∼5.0 and 298 K is on the order of 10−4 to 10−3. The reaction rate scales with droplet surface area, indicating that the major reaction location is the air–water interface. This interfacial reaction is further corroborated by a positive kinetic salt effect, a trait of the interaction between ions and the neutral molecules, such as Fe(III) ions and SO2 molecules. The reaction rate decreases by up to a decade, as the Fe(III)/S(VI) coexisting time increases, possibly owing to a complexation between Fe(III) and S(VI) ions.
Environmental significanceSulfate is a major secondary inorganic component of atmospheric particulate matter, and its production is closely related to urban haze formation. Sulfate can be produced rapidly via a heterogeneous process, in which SO2 molecules are directly converted at the aerosol surface, catalyzed by the transition metal ions. In this study, we directly measure the kinetics of Fe(III)-catalyzed SO2 oxidation at the aerosol surface. The kinetic effects of SO2 concentration, total Fe(III) molar fraction, ambient humidity, and hours of S(VI)/Fe(III) coexistence are investigated. We emphasize that the SO2 conversion rate in incipient aerosols and in aged ones can differ by nearly a decade, which should be incorporated in the air-quality models. |
1 Introduction
The rapid formation of sulfate aerosols is the chemical driver of the severe winter haze events in China, exerting tremendous negative impacts on social economy and public health.1–4 During the past decade, SO2 emission in China's urban area has been effectively controlled: The annual average SO2 concentration decreased from 9.1 ppb in 2013 to 1.7 ppb in 2018.5 Yet, during the same period, sulfate aerosol concentration in polluted air only decreased moderately, from 19.2 to 12.1 μg m−3.6 And severe air pollution events still occurred in winter seasons.4,7,8 To further contain secondary sulfate pollutants, we need to thoroughly understand the mechanisms and kinetics of SO2 conversion in polluted air.Per the traditional view, SO2 in the gas phase is oxidized by OH radicals9 and stable Criegee intermediates.10 Aqueous reaction pathways include the oxidation of S(IV) by O3, O2 (catalyzed by transition metal ions, TMI), and H2O2 dissolved in cloud and fog droplets.11,12 But these mechanisms cannot explain the rapid sulfate PM2.5 formation in the north China plain (NCP). The sulfate PM2.5 concentration simulated with air quality models13 were 3–4 times lower than that measured in the atmosphere. This gap has motivated many research efforts to discover the hitherto unidentified sulfate sources in polluted environments:11,14–22 New aqueous SO2 conversion mechanisms have been identified, and the kinetics of existing mechanisms have been updated.
The significance of aqueous SO2 conversion, however, was questioned in recent kinetic studies.1,23 The concern partly arises from a reaction space constraint.1,23 The volume of aerosol water in polluted air is several decades smaller than that of clouds, and such small aerosol water volume precludes large-scale sulfate formation via aqueous routes.1 Instead, interfacial reactions – a direct conversion of SO2 molecules at the aerosol surface – can exploit the large surface area of microdroplets and thereby produce sulfate rapidly. Wang et al.1 reported that the Mn(II)-catalyzed SO2 oxidation at the aerosol surface is two decades faster than that in bulk solutions. A subsequent air-quality model simulation23 showed that this Mn(II)-catalyzed interfacial reaction accounts for 92.5% of the sulfate in the NCP haze events. These lab studies and model simulations indicate that the dominating sulfate formation mechanism in polluted air is interfacial SO2 oxidation catalyzed by TMI, primarily by Mn(II) ions.1,23
The recent studies emphasized the significance of TMI-catalyzed SO2 oxidation at aerosol surface,1,23 but some knowledge gaps still exist in our understanding of this reaction route. For example, the reaction kinetics of Fe(III)-catalyzed SO2 oxidation remain unconstrained. In traditional solution chemistry, both Fe(III) and Mn(II) ions were known for their catalytic effects expediting the aqueous S(IV) oxidation.24 And when Fe(III) and Mn(II) coexist, a synergistic effect25 leads to a reaction rate faster than the summation of the rates of the reactions catalyzed by individual Fe(III) or Mn(II). But recent chamber studies1,16 showed that the Fe(III)-catalyzed reaction did not produce sulfate aerosols at a rate as rapid as the Mn(II)-catalyzed one. Zhang et al.16 reported that the Fe(III)-catalyzed reaction is immeasurably slow; When both Fe(III) and Mn(II) were added, very limited synergist effects were observed. Wang et al.1 also reported that adding Fe(III) ions did not accelerate sulfate formation; When Fe(III) and Mn(II) coexist, an increase in Fe(III) mixing fraction did not cause any increase in reaction rate. Another recent study by Angle et al.17 showed that the TMI-catalyzed oxidation of aqueous S(IV) is faster in microdroplets than in bulk solution, possibly owing to a rate-enhancing effect of the air–water interface. Such a rate enhancement was observed for both the Mn(II)-catalyzed reactions and the Fe(III)-catalyzed ones.17 It remains unclear why the Fe(III) ions lose their capability when the reaction occurs at the aerosol surface.
These knowledge gaps have motivated the present study. Here, we directly measured the rate of Fe(III)-catalyzed SO2 oxidation in single (NH4)2SO4 droplets levitated by an aerosol optical tweezer (AOT).17,26 The AOT utilizes optical gradient force to steadily trap a single droplet,27,28 allowing us to measure the reaction rate in it with Raman spectroscopy.17,26 Measuring kinetics in a single levitated droplet has the following advantages. First, when the target being measured is a single droplet, it is much easier to manipulate the droplet properties (size, composition, and ionic strength) and ambient conditions (gas concentration, humidity).11,17,26 Second, when a droplet is levitated at the optical trap, the backscattered Raman light can be exploited for an in situ kinetic measurement17,26 during reactions. Third, a single droplet is an optical resonant cavity, and the cavity-enhanced Raman spectra (CERS) reveal the reaction-induced hygroscopic growth of the droplets with a nanometer precision.27,28 This one-nanometer droplet growth can then be used to infer the sulfate production at a 10−14 mol precision.26
In the following, we first describe the experimental setup of AOT that facilitated measuring reaction kinetics in levitated droplets. This is followed by a recap on how to infer reaction rate from droplets' hygroscopic growth. Next, we discuss the reaction rate as a function of SO2 concentration, droplet size, Fe(III) concentration, ionic strength, and aging time. We conclude with the atmospheric implication of our findings.
2 Methods
2.1 Aerosol optical tweezer
The AOT system is the same one used in our previous study,26 and one may refer to the ESI† of that paper for details of AOT schematics and gas-flow arrangements. Here, we only provide a brief recap on the key specifications of the apparatus. The optical trap was constructed with a 532 nm Gaussian beam tightly focused inside a 6 mL sample cell. Specifically, this beam was focused with a 100× oil immersion objective scope (Olympus UIS2 PlanCN) with a numerical aperture of 1.25. Similar to the design by Reid and coworkers,27 our system uses the 532 nm beam, which constructs the optical trap, to serve as the incident light for Raman scattering. When a single aerosol droplet was trapped and levitated, the backscattered Raman signal was captured with a spectrometer (Zolix Ominc λ-500, 1200 grooves per mm grating) with a time resolution of one frame per second.2.2 Aerosol generation
Aerosols were generated by nebulizing standard solutes comprising a mixture of ammonium sulfate (AS, (NH4)2SO4), ammonium bisulfate (ABS, NH4HSO4), and iron sulfate (IS, Fe2(SO4)3). These chemicals were purchased from Sinopharm Chemical Reagent Co. (analytical reagents, purity ≥ 99.0%) without further purification. The molar ratio of AS and ABS was either 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0; the molar fraction of IS was fixed at 0.001, 0.01, or 0.1%. One may refer to Table S1 in ESI† for the initial droplet compositions. Ultrapure water (18.2 MΩ cm, Barnstead Easypure II) was used to prepare the solution. The ultrasonic nebulizer was produced by Yuyue (402AI model).
0; the molar fraction of IS was fixed at 0.001, 0.01, or 0.1%. One may refer to Table S1 in ESI† for the initial droplet compositions. Ultrapure water (18.2 MΩ cm, Barnstead Easypure II) was used to prepare the solution. The ultrasonic nebulizer was produced by Yuyue (402AI model).
2.3 Aerosol pH and ionic strength
Droplet pH was maintained at ∼5.0 by dissolving 8.00 ppm NH3 gas into the droplet water comprising a mixture of AS and IS (or AS/ABS and IS). The ionic strength (I) was adjusted between ca. 15 and 36 mol kg−1 by changing the ambient relative humidity (RH) condition between 80% and 60%. The variation of RH during an experiment was maintained within ±1%. The values of droplet initial pH and I were computed with E-AIM model III,29 per:| pH = −log(γH+mH+) | (1) |
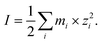 | (2) |
2.4 Measuring reaction rate
When RH is fixed, the sulfate solute molarity, [S(VI)], is also a constant, owing to an equilibrium of water partition. At such an equilibrium condition, an increasing sulfate mass inside the droplet will cause an increasing droplet volume. In other words, converting SO2 to sulfate inside a droplet will induce a hygroscopic growth of the droplet. Such reaction-induced droplet growth facilitates us to measure the reaction rate precisely, if we can measure the droplet size precisely, for example: | (3) |
3 Results and discussion
3.1 Influence of SO2 concentration
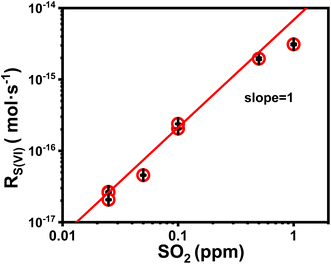
We first discuss the kinetic effect of SO2 concentration. In these experiments, the droplet pH was maintained at ∼5.0; the ambient RH, at ∼60%; Fe(III) molar fraction, 0.01%. SO2 concentration varied between 25 and 103 ppb. Fig. 1 plots the reaction rate RS(IV) as a function of SO2 concentration. Note that the unit of RS(IV) here is mole of sulfate produced in a unit time per a single droplet. The trends in Fig. 1 show that the sulfate formation rate correlates positively with SO2 concentration. Quantitatively, we show that a linear fitting (red line in Fig. 1) describes the data best, indicating that the reaction rate is first order in SO2. This observation agrees with our knowledge of the Fe(III)-catalyzed SO2 conversion.303.2 The location of heterogeneous reaction
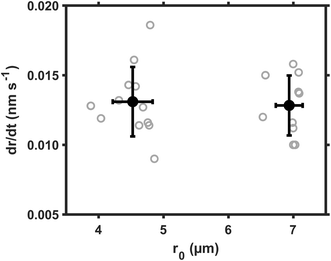
The size dependence of reaction rate provides us insight on the location of heterogeneous reactions.26 For example, if SO2 are first dissolved in aerosol water and the S(IV) are oxidized homogeneously therein, the reaction rate will be proportional to droplet volume, RS(VI) ∝ r03; if the SO2 are directly converted at the droplet surface, the reaction rate will be proportional to droplet surface area, RS(VI) ∝ r02. We evaluated these scaling laws by using the droplet growth rate, dr/dt, which was measured directly during reactions. Eqn (3) indicates that dr/dt ∝ RS(VI) × r0−2 holds for short-range droplet growth driven by sulfate formation. Then, the kinetic scaling laws can be reduced to dr/dt ∝ r0 for aqueous reaction, and to dr/dt = constant for the interfacial reaction.Fig. 2 shows the dr/dt of droplets within two size bins: the smaller droplets around 4.5 μm radii, and the larger ones around 7.0 μm radii. The pH of these droplets was maintained at ∼5.0; the SO2 concentration, at 25 ppb; Fe(III) molar fraction, at 0.01%; RH, at ∼60%. Inside these two size bins, we repeatedly measured dr/dt more than ten times (see the gray circles). Then we calculated the mean values for dr/dt and r0, as well as their one standard deviation (black circles and error bars). Despite the fluctuation, the mean dr/dt values for droplets inside each size bin are clearly independent of the corresponding mean r0 values. (The mean dr/dt was 0.0131 ± 0.002 nm s−1 and 0.0128 ± 0.002 nm s−1, respectively, when the mean r0 was 4.525 ± 0.308 μm and 6.936 ± 0.207 μm.) With this constant dr/dt, we infer that the reaction occurs primarily at the droplet surface. Were aqueous reactions the case, dr/dt would increase linearly with r0, and the dr/dt data at ∼7 μm would instead be clustered around 0.02 nm s−1.
In the following, we normalize the sulfate formation rate with SO2 concentration and droplet surface area, per the expression of reactive uptake coefficient ΓSO2:26
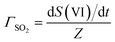 | (4.1) |
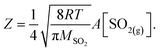 | (4.2) |
3.3 Influence of metal concentration
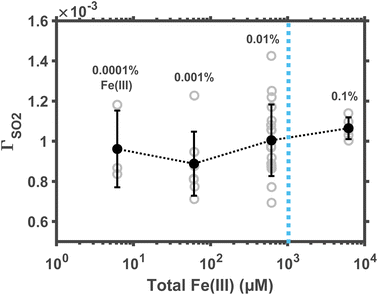
Not all Fe(III) in aerosol water are soluble. The soluble Fe(III) ions include FeOH2+, Fe(OH)2+, and Fe2(OH)24+; their concentration in dilute solution might be estimated per the precipitation equilibrium relationship. But it remains unclear whether such a relationship still provides accurate predictions in aerosol water at the non-ideal, high-ionic-strength condition. Here, we empirically measured the reaction rate at changing concentrations of total Fe(III), including both soluble and insoluble Fe(III). In these experiments, droplet pH was maintained at ∼5; ambient RH, at ∼60%. The molar fraction of total Fe(III) in droplet solute varied between 0.0001% and 0.1% (correspondingly, the total Fe(III) concentration varied between ∼6.2 μM and ∼6.2 mM.)The results are shown in Fig. 3. Although the total Fe(III) varied across three orders of magnitude, the reaction rate at pH ≈ 5 remains a constant. This constant reaction rate indicates that most of the Fe(III) in droplets was insoluble. Such an observation of excessive total Fe(III) agrees with traditional kinetic studies. For example, Martin et al.31 found that, at pH ≈ 5, the first-order rate coefficient of Fe(III)-catalyzed oxidation of aqueous S(IV) is also independent of Fe(III) concentration. In polluted air, the Fe(III) concentration is about 18 ng mair−3, and the aerosol water content is about 300 μg mair−3.20 These conditions suggest that the total Fe(III) molarity in aerosol water is ∼1 mM (dotted line in Fig. 3), far beyond the solubility limit. Therefore, one may assume that the reaction kinetics at fixed pH conditions is zeroth order in the total airborne Fe(III).
3.4 Influences of ambient humidity
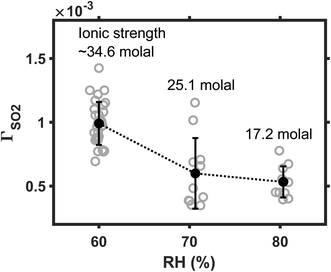
We next investigate the influence of ambient humidity on reaction rate. In these experiments, the SO2 was maintained at 25 ppb; Fe(III) molar fraction, at 0.01%. Ambient RH varied among 60, 70, and 80%. The results are plotted in Fig. 4. As RH decreases from 80 to 60%, the mean reaction rate increases by a factor of ∼2. The faster reaction at lower RH conditions may arise from the kinetic salt effect. When RH decreases, droplet water becomes more concentrated, and droplet ionic strength I increases. (For example, ESI Fig. S2† shows that the I of ammonium sulfate droplet increases from ∼17 to 35 mol, as the ambient RH decreases from 80 to 60%.) Reactions are accelerated at the high I condition if the rate-limiting step of the reaction involves an interaction between charge neutral molecules and ions1,26,32 here, the neutral SO2 molecules and the Fe(III) ions. This positive kinetic salt effect also indicates that SO2 is directly converted at the droplet surface, without an a priori dissolution and dissociation.1 For example, SO2 and O2 may react with Fe(III) at droplet surface, producing Fe(II) and SO5− radicals. Instead, if the SO2 were first dissolved and dissociated into S(IV) ions, then the rate-limiting step would involve an interaction between S(IV) ions and Fe(III) ions. Such ion–ion reaction would be inhibited when I is large.17 One may refer to Angle et al.'s recent kinetic study17 for such a slower TMI-catalyzed S(IV) oxidation at higher I conditions.The faster reaction rate at lower RH conditions is unlikely due to the enrichment effect (i.e., droplet solvent evaporates, the aqueous reactant is concentrated, and the reaction is accelerated.) We find that this explanation is not very compelling, because when the SO2 molecules are directly converted at the aerosol surface, their availability is unaffected by the enrichment of the aqueous phase. The Fe(III) catalysts do exist in the aqueous phase. But, when the total Fe(III) concentration is much greater than the solubility limit, the actual concentration of soluble Fe(III) is unlikely to be affected by the enrichment of droplet water either.
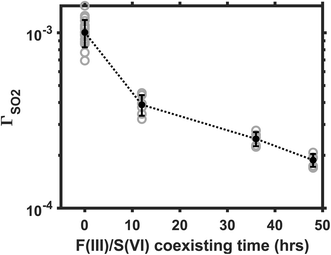
3.5 Influence of Fe(III)/S(VI) coexisting time
The aqueous Fe(III)-catalyzed S(IV) conversion is self-inhibiting because the reaction product S(VI) is an effective complexation agent to the Fe(III) catalysts.17,24 Martin and Hill24 reported that the Fe(III)-catalyzed reaction in bulk solution decelerates significantly when the S(VI) concentration increases from a μM to a mM level. Here, we investigate the influence of Fe(III)/S(VI) coexisting time on the heterogeneous reaction rate. In this part of experiment, we aged the AS/IS mixture solutions for 12, 36, or 48 hours before nebulizing them into aerosols. The reaction rate in the droplets made from aged solutions was then compared with that in the droplets made from the fresh solution. The SO2 was maintained at 25 ppb; Fe(III) molar fraction, at 0.01%. Ambient RH, at 60%. Fig. 5 plots the ΓSO2 as a function of the Fe(III)/S(VI) coexisting time. The reaction rate decelerates by almost a decade, as the Fe(III)/S(VI) coexisting time increased from 0 to 48 hours. This observation indicates that the Fe(III)/S(VI) complexation is also a significant factor affecting the heterogeneous SO2 conversion. The Fe(III)-catalyzed reaction may be a decade slower in real-world sulfate aerosols that have gone through an elongated aging process.3.6 Comparing with other reaction mechanisms
Table 1 compares the kinetic data obtained in the present study with those reported in ref. 1, 26 and 31. Per our present study, the Fe(III)-catalyzed SO2 oxidation occurs primarily at aerosol surface. At room temperature and a pH ∼5 condition, such a reaction exhibits ΓSO2 on the order of 10−4. This reaction rate is 2–3 decades faster than what the solution chemistry predicts. For example, Martin et al.31 reported that the Fe(III)-catalyzed S(IV) oxidation in bulk solution at pH 5.0 has a first-order rate coefficient of ∼10−3 s−1. This rate coefficient corresponds to a ΓSO2 of ∼1.7 × 10−6 for the heterogeneous reaction inside the droplets with a ∼10 μm radius (refer to Table 1 footnotes for details of calculation).| References | Catalysts | Reaction location | Conditions | Uptake coef. |
|---|---|---|---|---|
| a Martin et al.31 measured the rate of Fe(III)-catalyzed S(IV) oxidation in bulk solutions. They found that the first order rate coefficient k of this reaction is ca. 10−3 s−1 at pH 5.0 condition. One may estimate the corresponding uptake coefficient ΓSO2 by using the eqn (4.1) in this paper. Specifically, rate per droplet is dS(IV)/dt = (4/3)πr3k[S(IV)]; the sulfite molarity [S(IV)] = HSO2PSO2(1 + K1s[H+]−1 + K1sK2s[H+]−2), where HSO2 and PSO2 respectively denote the Henry's law constant of SO2 and SO2 gas partial pressure. The K1s, and K2s respectively denote the first and second dissociation equilibrium constants of sulfite hydrate. Droplet radius r was assumed to be 10 μm matching our experimental condition. The PSO2 is trivial and can take any arbitrary value. b Chen et al.26 measured the uncatalyzed SO2 oxidation rate in levitated aerosol microdroplets. The ΓSO2 was calculated with eqn (5) and (8) in their paper. c Wang et al.1 measured the Mn(II)-catalyzed SO2 oxidation rate by using a smoke chamber. The ΓSO2 was calculated with the dataset shown in the Fig. 1b in their paper. | ||||
| The present study | Fe(III) | Aerosol surface | pH 5; 60% RH; incipient aerosols | 9.9(±1.7) × 10−4 |
| pH 5; 80% RH; incipient aerosols | 5.3(±1.2) × 10−4 | |||
| pH 5; 60% RH; aged aerosols | 1.4(±0.2) × 10−4 | |||
| Martin et al. (1991) | Fe(III) | Bulk solutiona | pH 5; r = 10 μm (assumed) | ∼1.7 × 10−6 |
| Chen et al. (2022) | Uncatalyzed | Aerosol surfaceb | pH 3.5–5.5; 60% RH | ∼4.9 × 10−7 |
| pH 3.5–5.5; 80% RH | ∼8.1 × 10−8 | |||
| Aerosol interior | pH 5; 60% RH; r = 10 μm (assumed) | ∼6.6 × 10−6 | ||
| pH 5; 80% RH; r = 10 μm (assumed) | ∼5.5 × 10−7 | |||
| Wang et al. (2021) | Mn(II) | Aerosol surfacec | pH 4–5; >80% RH; 0.81% Mn(II) | ∼1.6 × 10−4 |
| pH 4–5; >80% RH; 5.54% Mn(II) | ∼7.1 × 10−4 | |||
The much faster reaction rate observed in our present study is not an experimental artefact. Previously, Chen et al.26 used the AOT to measure the uncatalyzed SO2 oxidation rate in levitated droplets. In that study, we conducted the experiment by using the same AOT apparatus and the same ammonium sulfate chemicals, but we did not intentionally add any Fe(III) to the droplets. At such conditions, the reaction at pH ∼5.0 exhibited a ΓSO2 on the orders of 10−7 to 10−6. This comparison indicates that the 2-to-3-decade faster reaction observed here is due to our intentional addition of Fe(III) to droplet water. In other words, if such faster kinetics were a systematic artefact of the AOT apparatus, Chen et al. would also observe a ΓSO2 on the order of 10−4 for the uncatalyzed reactions.
One should also note that the ΓSO2 on the order of 10−4 to 10−3 is even greater than what is needed to explain the missing sulfate in haze events. Such an observation indicates that the Fe(III)-catalyzed heterogeneous SO2 oxidation in the atmosphere is not as fast as that in the laboratory aerosols, particularly those freshly-made ones. As we discussed earlier, the catalytic capability of Fe(III) is impaired if Fe(III) and S(VI) coexists for a long time. On the other hand, recent studies proposed that a strong electric field exists at the air–water interface, triggering a spontaneous conversion of some OH− ions at droplet surface into OH radicals and free electron.33,34 Such unique environment at air–water interface may also alter the kinetics of redox reactions.
4 Conclusion
In this work, we directly measured Fe(III)-catalyzed SO2 conversion inside optically levitated microdroplets. We show that aerosol optical tweezers – coupled with cavity-enhanced Raman spectroscopy – can be utilized to determine the rate of heterogeneous reactions between SO2 gas and microdroplets. Our findings show that the rate of Fe(III)-catalyzed SO2 oxidation is first order in SO2 concentration. During the heterogeneous reaction, the droplet growth rate is independent of the droplet initial radius, indicating that the sulfate production rate (per droplet) is proportional to the droplet surface area. Such a surface scaling law in turn suggests that the heterogeneous reaction occurs primarily at the air–water interface. The reaction rate is faster at lower RH conditions, possibly owing to a positive kinetic salt effect for ion–molecule reactions. The reaction rate at pH ∼ 5 remains constant despite the total Fe(III) molar fraction varies across three decades, indicating that most Fe(III) is insoluble. This excessive Fe(III) condition also holds valid for real-world aerosols in polluted air. The reaction rate decelerates nearly one decade as the Fe(III)/S(VI) coexists for two days, indicating that the contribution of the Fe(III)-catalyzed reaction to sulfate may significantly diminish in aged aerosols.Author contributions
P. L. and Y. Z. designed the research; X. C. and Z. C. performed the experiments; P. L. performed the theoretical calculations; P. L. and X. C. wrote the first draft of the manuscript; and all of the authors analyzed the data and contributed to revising the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Prof. Dr Jonathan P. Reid at the University of Bristol for helping us set up the aerosol optical tweezer and for sharing the spectra inversion algorithm. This study was supported by the National Natural Science Foundation of China (No. 42205113, 42127806, 91544223, 91844301, and 21806169), and Beijing Institute of Technology Research Fund Program for Young Scholars.References
- W. Wang, M. Liu, Y. Song and M. Ge, Sulfate formation is dominated by manganese-catalyzed oxidation of SO2 on aerosol surfaces during haze events, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed
.
- J. P. D. Abbatt and O. Mohler, Solid ammonium sulfate aerosols as ice nuclei: A pathway for cirrus cloud formation, Science, 2006, 313, 1770–1773 CrossRef CAS PubMed
.
- C. A. Pope and G. D. Thurston, Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution, JAMA, 2002, 287, 1132–1141 CrossRef CAS PubMed
.
- H. He and J. Hao, Mineral dust and NOx promote the conversion of SO2 to sulfate in heavy pollution days, Sci. Rep., 2014, 4, 4172 CrossRef PubMed
.
- F. Yan, W. Chen and X. Wang, Stabilization for the secondary species contribution to PM2.5 in the Pearl River Delta (PRD) over the past decade, China: A meta-analysis, Atmos. Environ., 2020, 242, 117817 CrossRef CAS
.
- D. Shang, J. Peng, S. Guo, Z. Wu and M. Hu, Secondary aerosol formation in winter haze over the Beijing-Tianjin-Hebei Region, China, Front. Environ. Sci. Eng., 2021, 15, 1–13 CrossRef
.
- X. Li, B. Zhao, W. Zhou and J. Jiang, Responses of gaseous sulfuric acid and particulate sulfate to reduced SO2 concentration: a perspective from long-term measurements in Beijing, Sci. Total Environ., 2020, 721, 137700 CrossRef CAS PubMed
.
- P. Kasibhatla, W. L. Chameides and J. S. John, A three-dimensional global model investigation of seasonal variations in the atmospheric burden of anthropogenic sulfate aerosols, J. Geophys. Res.: Atmos., 1997, 102, 3737–3759 CrossRef CAS
.
- W. R. Stockwell and J. G. Calvert, The mechanism of the HO-SO2 reaction, Atmos. Environ., 1983, 17, 2231–2235 CrossRef CAS
.
- R. L. Mauldin, T. Berndt and M. Kulmala, A new atmospherically relevant oxidant of sulphur dioxide, Nature, 2012, 488, 193–196 CrossRef CAS PubMed
.
- T. Liu, A. W. H. Chan and J. P. D. Abbatt, Multiphase oxidation of sulfur dioxide in aerosol particles: Implications for sulfate formation in polluted environments, Environ. Sci. Technol., 2021, 55, 4227–4242 CrossRef CAS PubMed
.
-
J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, 3rd edn, 2016 Search PubMed
.
- Y. Wang, Q. Zhang and Y. Xie, Enhanced sulfate formation during China's severe winter haze episode in January 2013 missing from current models, J. Geophys. Res.: Atmos., 2014, 119, 10425–10440 CrossRef
.
- G. Li, H. Su and Y. Cheng, Multiphase chemistry experiment in fogs and aerosols in the North China Plain (McFAN): integrated analysis and intensive winter campaign 2018, Faraday Discuss., 2021, 226, 207–222 RSC
.
- X. Wang, Y. Lei, T. Liu and K. He, A unit-based emission inventory of SO2, NOx and PM for the Chinese iron and steel industry from 2010 to 2015, Sci. Total Environ., 2019, 676, 18–30 CrossRef CAS PubMed
.
- H. Zhang, Y. Xu and L. Jia, A chamber study of catalytic oxidation of SO2 by Mn2+/Fe3+ in aerosol water, Atmos. Environ., 2021, 245, 118019 CrossRef CAS
.
- K. J. Angle, E. E. Neal and V. H. Grassian, Enhanced rates of transition-metal-ion-catalyzed oxidation of S(IV) in aqueous aerosols: Insights into sulfate aerosol formation in the atmosphere, Environ. Sci. Technol., 2021, 55, 10291–10299 CrossRef CAS PubMed
.
- M. Gen, R. Zhang, D. D. Huang, Y. Li and C. K. Chan, Heterogeneous oxidation of SO2 in sulfate production during nitrate photolysis at 300 nm: Effect of pH, relative humidity, irradiation intensity, and the presence of organic compounds, Environ. Sci. Technol., 2019, 53, 8757–8766 CrossRef CAS PubMed
.
- Y. W. Chen and J. P. Burrows, Contribution of the gas-phase reaction between hydroxyl radical and sulfur dioxide to the sulfate aerosol over West Pacific, Atmos. Chem. Phys., 2021, 2021, 1–29 Search PubMed
.
- Y. Cheng, Z. Wang and H. Su, Reactive nitrogen chemistry in aerosol water as a source of sulfate during haze events in China, Sci. Adv., 2016, 2, e1601530 CrossRef PubMed
.
- T. Liu, S. L. Clegg and J. P. D. Abbatt, Fast oxidation of sulfur dioxide by hydrogen peroxide in deliquesced aerosol particles, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 1354–1359 CrossRef CAS PubMed
.
- J. Gao, G. Shi and A. Nenes, Targeting atmospheric oxidants can better reduce sulfate aerosol in China: H2O2 aqueous oxidation pathway dominates sulfate formation in haze, Environ. Sci. Technol., 2022, 56, 10608–10618 CrossRef CAS PubMed
.
- T. Wang, M. Liu, Y. Song, M. Hu and T. Zhu, Sulfate formation apportionment during winter haze events in North China, Environ. Sci. Technol., 2022, 56, 7771–7778 CrossRef CAS PubMed
.
- L. R. Martin and M. W. Hill, The iron catalyzed oxidation of sulfur: reconciliation of the literature rates, Atmos. Environ., 1967, 21, 1487–1490 CrossRef
.
- L. R. Martin and T. W. Good, Catalyzed oxidation of sulfur dioxide in solution: the iron-manganese synergism, Atmos. Environ., Part A, 1991, 25, 2395–2399 CrossRef
.
- Z. Chen, P. Liu, W. Wang, X. Cao, Y. Zhang and M. Ge, Rapid sulfate formation via uncatalyzed autoxidation of sulfur dioxide in aerosol microdroplets, Environ. Sci. Technol., 2022, 56, 7637–7646 CrossRef CAS PubMed
.
- R. Symes, R. M. Sayer and J. P. Reid, Cavity enhanced droplet spectroscopy: principles, perspectives and prospects, Phys. Chem. Chem. Phys., 2004, 6, 474–487 RSC
.
- T. C. Preston and J. P. Reid, Accurate and efficient determination of the radius, refractive index, and dispersion of weakly absorbing spherical particle using whispering gallery modes, J. Opt. Soc. Am. B, 2013, 30, 2113–2122 CrossRef CAS
.
- A. S. Wexler and S. L. Clegg, Atmospheric aerosol models for systems including the ions H+, NH4+, Na+, SO42−, NO3−, Cl−, Br−, and H2O, J. Geophys. Res.: Atmos., 2002, 107, 4207 CrossRef
.
-
J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Atmospheric Chemistry and Physics of Air Pollution, 3rd edn, 2016 Search PubMed
.
- L. R. Martin, M. W. Hill, A. F. Tai and T. W. Good, The iron catalyzed oxidation of sulfur(IV) in aqueous solution: differing effects of organics at high and low pH, J. Geophys. Res.: Atmos., 1991, 96, 3085–3097 CrossRef CAS
.
- H. Herrmann, Kinetics of aqueous phase reactions relevant for atmospheric chemistry, Chem. Rev., 2003, 103, 4691–4716 CrossRef CAS PubMed
.
- J. P. Heindel, H. Hao, R. A. LaCour and T. Head-Gordon, Spontaneous formation of hydrogen peroxide in water microdroplets, J. Phys. Chem. Lett., 2022, 13, 10035–10041 CrossRef CAS PubMed
.
- D. Xing and X. Zhang, Capture of hydroxyl radicals by hydronium cations in water microdroplets, Angew. Chem., 2022, 61, e202207587 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00125j |
| This journal is © The Royal Society of Chemistry 2023 |