Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling polymorphism in molecular cocrystals by variable temperature ball milling†
Kevin
Linberg
 ab,
Bettina
Röder
a,
Dominik
Al-Sabbagh
ab,
Bettina
Röder
a,
Dominik
Al-Sabbagh
 a,
Franziska
Emmerling
a,
Franziska
Emmerling
 *ab and
Adam A. L.
Michalchuk
*ab and
Adam A. L.
Michalchuk
 *a
*a
aBundesanstalt für Materialforschung und -prüfung (BAM), Richard-Willstätter-Strasse 11, 12489 Berlin, Germany. E-mail: franziska.emmerling@bam.de; adam.michalchuk@bam.de
bDepartment of Chemistry, Humboldt-Universität zu Berlin, Brook-Taylor-Strasse 2, 12489 Berlin, Germany
First published on 24th June 2022
Abstract
Mechanochemistry offers a unique opportunity to modify and manipulate crystal forms, often providing new products as compared with conventional solution methods. While promising, there is little known about how to control the solid form through mechanochemical means, demanding dedicated investigations. Using a model organic cocrystal system (isonicotinamide:glutaric acid), we here demonstrate that with mechanochemistry, polymorphism can be induced in molecular solids under conditions seemingly different to their conventional thermodynamic (thermal) transition point. Whereas Form II converts to Form I upon heating to 363 K, the same transition can be initiated under ball milling conditions at markedly lower temperatures (348 K). Our results indicate that mechanochemical techniques can help to reduce the energy barriers to solid form transitions, offering new insights into controlling polymorphic forms. Moreover, our results suggest that the nature of mechanochemical transformations could make it difficult to interpret mechanochemical solid form landscapes using conventional equilibrium-based tools.
Introduction
Mechanochemistry offers an environmentally benign alternative to solvent-based processes and opens the door towards sustainable chemical and material manufacturing. Following from decades of research focused on inorganic materials processing, mechanochemistry is now being widely explored for its applications across metal–organic1,2 and organic3,4 materials. Despite considerable efforts,5 the mechanisms that underpin mechanochemical reactions remain far from being understood. This lack of understanding greatly limits our ability to exploit the full potential of mechanochemistry and maximise the impact of this game-changing technology.Mechanochemical reactions occur under non-equilibrium conditions. For example, the mass transport between the solid particles is kinetically hindered, while conditions of elevated temperature and pressure are transient and spatially localized. Such conditions can often lead to the formation of kinetically ‘trapped’, metastable polymorphic phases.6,7 In this respect, mechanochemistry offers a new dimension for preparing solid forms that are difficult – or even impossible – to obtain through solution chemistry.6 Many factors can influence the outcome of a mechanochemical transformation, including the material of the milling jar,8,9 the presence of additives (liquid or solid),7,10 and the type or intensity of mechanical treatment.11–14 While reaction temperature has been routinely applied to control solution chemistry, its use as a control parameter for mechanochemical transformations remains less common15–20 and poorly understood. Early evidence suggests that equilibrium milling temperatures can be used in combination with milling intensity to enhance mechanochemical reactivity and increase reaction yields.19 In this direction, mechanochemistry seemingly allows the separate control of temperature and mechanical effects, thereby offering potential for greater selectivity compared to that of classical solvent syntheses.
To gauge the intricate ability of temperature to influence mechanochemical reactions, one needs to investigate transformations that are highly sensitive to experimental conditions. In this light, solid state polymorphism offers an excellent probe to assess how temperature affects mechanochemical outcomes. Polymorphs are crystalline solids whose molecules are arranged in different ways.21 Different organic polymorphs typically have very similar lattice energies, often differing by <2 kJ mol−1.22 Controlling polymorphism therefore requires the ability to manipulate both the kinetics and thermodynamic landscape of a solid. Polymorphic control during mechanochemical processing has been studied in some detail, but has focused on control through liquid or solid additives (e.g. liquid assisted grinding, LAG,23,24 seeding,10 or the addition of polymers25). These strategies target the selective stabilisation of the nuclei and their surfaces in the early stages of crystal formation. However, there has not yet been a thorough investigation into the control over polymorphism through changes in the equilibrium milling temperature.
We here explore how temperature can be used to control the mechanochemically driven polymorphism of molecular organic solids. As the polymorphic behaviour of cocrystal systems of isonicotinamide and dicarboxylic acids is rich and has been thoroughly investigated,26 materials in this class offer good candidates for polymorphic systems. We use as a model system the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystals of glutaric acid (GLU) and isonicotinamide (INA), where one polymorph is known in the literature27 and a second polymorph was newly discovered. Importantly, both polymorphic forms can be prepared under ambient conditions, therefore making the GLU:INA cocrystal polymorphs excellent candidates with which to study control over mechanochemical polymorphism.
1 cocrystals of glutaric acid (GLU) and isonicotinamide (INA), where one polymorph is known in the literature27 and a second polymorph was newly discovered. Importantly, both polymorphic forms can be prepared under ambient conditions, therefore making the GLU:INA cocrystal polymorphs excellent candidates with which to study control over mechanochemical polymorphism.
Experimental details
Materials
All chemicals were purchased commercially and used without further purification: glutaric acid (ACROS, 99%, GLU) and isonicotinamide (ACROS, 99%, INA).Ball milling
For all milling experiments, custom-designed three-part milling jars were used.28 These jars comprise a central cylinder made of polymethylmethacrylate (PMMA) with a wall thickness of 0.7 mm hemispherical caps made from V2A stainless steel. To control the bulk temperature of the ball mill, we developed a temperature-controlled jacket jar holder (see Fig. SI1 and more details in S1 of the ESI†). The ball-milling experiments were performed with a Pulverisette 23 (Frisch, Germany) vibratory ball mill at 50 Hz, 35 Hz, or 20 Hz with one 10 mm stainless steel milling ball (4.04 ± 0.02 g) for 15 min to 10 h. The cocrystal (INA:GA) was produced by co-grinding stoichiometric mixtures of isonicotinamide (48 mg, 0.197 mmol) and glutaric acid (52 mg, 0.197 mmol). The resulting cocrystal was obtained as a white crystalline solid. The powder was characterized immediately after the end of the ball-milling reaction. During experiments, the ambient relative humidity was ca. 22%.In situ temperature measurements
The temperature in the grinding jar was monitored using a PT 100 sensor placed in the stainless-steel cap of the three-part grinding jar. A hole was drilled in the milling jar cap to within 6 mm of the internal surface to allow the thermocouple to approach the internal atmosphere of the jar without breaching its seal. Time-resolved temperature measurements were recorded every second for 10 h at 50 Hz, 35 Hz, and 20 Hz using a RDXL6SD data logger (Omega, Germany).Ex situ powder X-ray diffraction
All samples were characterized by powder X-ray diffraction (PXRD) immediately after the end of the milling process. Diffraction patterns were collected at room temperature using a D8 Advance diffractometer (Bruker, AXS, Germany) with Cu Kα1 (λ = 0.154060 nm) and Cu Kα2 (λ = 0.154440 nm) radiation over a 2θ range from 5 to 50° using a step size of 0.02° and a step time of 0.8 s. Diffraction patterns of the samples were additionally measured after an ageing period of 2 and 4 days to check for changes in phase composition and crystallinity.Variable temperature PXRD was collected using the same D8 Advance diffractometer and a corundum heating plate. The samples were heated from 298 K to 393 K in 5 K steps with a heating rate of 10 K min−1 and an equilibration time of 2 min for each data point. Diffraction patterns were collected over a 2θ range from 5 to 50° using a step size of 0.02° and a step time of 0.4 s.
Rietveld refinement was performed using the Topas V6 suite.29 Phase analysis was done by refining data against literature crystallographic structures, as deposited in the Cambridge Crystallographic Database (CCDC): Form I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27(ULAXAG), and isonicotinamide (EHOWIH01
27(ULAXAG), and isonicotinamide (EHOWIH01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 and EHOWIH02
30 and EHOWIH02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30), glutaric acid (GLURAC09).31
30), glutaric acid (GLURAC09).31
Time-resolved in situ (TRIS) powder X-ray diffraction and temperature
Time-resolved in situ (TRIS)32 X-ray diffraction measurements were performed at the μ-spot beamline at BESSY II (Helmholtz-Zentrum Berlin für Material and Energie) using monochromatic radiation of λ = 0.7314 nm. Each PXRD profile was obtained by accumulating scattering intensities for 5 s. The mill was positioned to ensure that the X-ray beam passed through the shortest chord length of the jar to minimize artificial peak broadening.28 The resulting diffraction patterns were processed using DPDAK33 v150 and the background corrections were done in python with the arPLS method.34 The relative humidity at the beamline during the experiments was ca. 48%.Solving the solution by X-ray powder diffraction
For solving the structure, XRPD data collected on a D8 Discover (Bruker, AXS, Germany) with Cu Kα1(λ = 0.154060 nm) radiation was used. Form II was loaded into a borosilicate capillary with an internal diameter of 1.0 mm. Diffraction data were collected at room temperature over a 2θ range from 5 to 50° with a step size of 0.009° and a step time of 16.5 s. PXRD data were indexed and solved using the simulated annealing routine in Expo2014.35 The Rietveld refinement was done using the Topas V6 suite.29 Initial parameters for the molecular structure were taken from the crystallographic data of Form I.Computational details
Simulations were performed on experimentally determined crystal structures, as available from the Cambridge Crystallographic Data Centre (CCDC): Form I (ULAXAG) and Form II (2170487). DFT calculations were done within the framework of plane wave density functional theory, as implemented in CASTEP v19.11.36 The exchange–correlation function of Perdew–Burke–Ernzerhof revised for solids (PBEsol)37 was used, along with the dispersion correction of Tkatchenko–Scheffler (TS).38 The core–valence interaction was modelled with a norm-conversing pseudopotential, generated on-the-fly with CASTEP. The wavefunction was expanded in plane waves to a maximum kinetic energy of 900 eV. The electronic structure was sampled on a Γ-centred Monkhorst–Pack k-point grid with a maximum spacing of 0.08 Å−2. Convergence was accepted when the residual atomic forces reached <1.0−3 eV Å−1, with SCF convergence accepted at <10−13 eV. The simulation geometries agree well with the experimental values, as shown in Table 1. The systematic underestimation of the experimental unit cell volumes is to be expected as the experiments were recorded at elevated temperatures (Form I: 154 K; Form II: 298 K), while DFT simulations inherently model geometry at 0 K.| SG | a/Å | b/Å | c/Å | β/° | V/Å3 | ΔV/% | |
|---|---|---|---|---|---|---|---|
| Form I (Exp) | P21/c | 9.90 | 16.75 | 7.32 | 95.48 | 1207.37 | −3.22 |
| Form I (sim) | P21/c | 9.67 | 16.51 | 7.36 | 97.60 | 1168.52 | |
| Form II (Exp) | P21/a | 26.39 | 5.21 | 8.89 | 99.44 | 1204.81 | −4.94 |
| Form II (sim) | P21/a | 25.96 | 5.20 | 8.59 | 98.87 | 1145.21 |
Lattice energies (Ef) were calculated as,
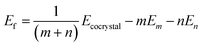 | (1) |
Results and discussion
Following on from our previous work,13 we investigate here whether mechanochemically driven polymorphism can be controlled through changes in the equilibrium milling temperature. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
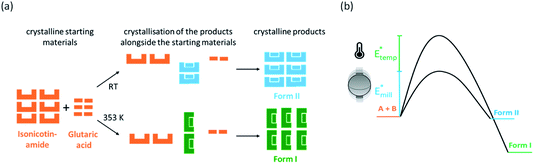
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal of isonicotinamide (INA) and glutaric acid (GLU) was selected as a model system, as shown in Fig. 1, which has one known polymorphic form (Form I)27 that can be obtained by liquid assisted grinding (LAG).40 Our early ball milling studies demonstrated that neat grinding (NG) the stoichiometric mixture of INA and GLU instead yields a previously unreported polymorph of the INA:GLU cocrystal (Form II), as shown in Fig. 1. The presence of a second polymorphic form, readily accessible by ball milling under ambient conditions, therefore rendered the INA:GLU system an excellent model system for studies on polymorphism by ball milling.
1 cocrystal of isonicotinamide (INA) and glutaric acid (GLU) was selected as a model system, as shown in Fig. 1, which has one known polymorphic form (Form I)27 that can be obtained by liquid assisted grinding (LAG).40 Our early ball milling studies demonstrated that neat grinding (NG) the stoichiometric mixture of INA and GLU instead yields a previously unreported polymorph of the INA:GLU cocrystal (Form II), as shown in Fig. 1. The presence of a second polymorphic form, readily accessible by ball milling under ambient conditions, therefore rendered the INA:GLU system an excellent model system for studies on polymorphism by ball milling.
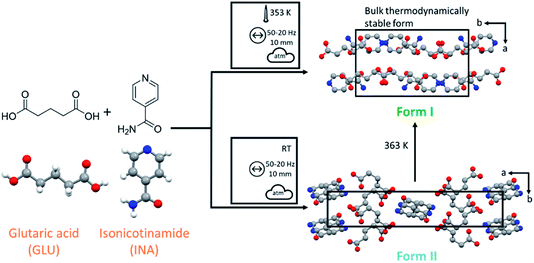 | ||
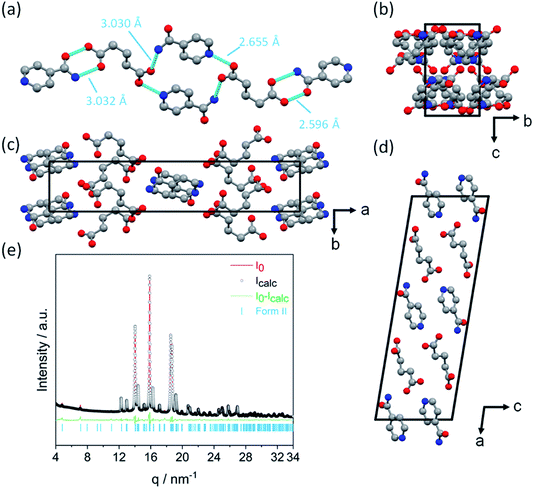
| Fig. 1 Reaction scheme for the cocrystal mechanosynthesis of GLU and INA. Form I (ref. 27) and Form II viewed along the crystallographic c-axis. Mechanochemical nomenclature is taken from ref. 39. Atoms are coloured as follows: carbon (grey), oxygen (red) and nitrogen (blue). | ||
The crystal structure of Form II was determined by XRPD, as shown in Fig. 2. Form II crystallizes in the monoclinic space group P21/a with one INA and one GLU molecule in the asymmetric unit. Each glutaric acid molecule interacts with three isonicotinamide molecules through four unique hydrogen bonds (Fig. 2a). The first carboxyl group of GLU forms an O–H⋯N hydrogen bond with the aromatic nitrogen atom of the first INA molecule and an N–H⋯O hydrogen bond with the amide group of the second INA molecule. The second carboxyl group of the GLU molecule forms an R22(8)-hetero-synthon with the amide group of the third INA molecule via O–H⋯O and N–H⋯O interactions. The crystallographic data and the refinement parameters are summarized in Table 2.
| Polymorph | Form II |
| Molecular formula | C11H14N2O5 |
| Formula weight/g mol−1 | 254.24 |
| Crystal system | Monoclinic |
| Space group | P21/a |
| Z | 4 |
| a/Å | 26.371(7) |
| b/Å | 5.209(13) |
| c/Å | 8.904(2) |
| β/° | 99.335(3) |
| Volume/Å3 | 1205.6(5) |
| d/g cm−3 | 1.402 |
| Diffractometer/radiation type | Bruker D8 Discover/Cu Kα1 (λ = 0.154060 nm) |
| 2θ range | 5–50° |
| R p | 4.28 |
| R exp, Rwp | 0.717, 6.15 |
| GOF | 8.58 |
Mechanochemically prepared Form II converted to Form I when aged at room temperature (Fig. S2.2).† Complete conversion to Form I was detected after four days of aging. This result suggests that Form I is thermodynamically stable under ambient conditions. To further understand the thermodynamic relationship of the two polymorphs, we investigated their relative stability. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Form I and Form II was slurried for three days in a range of solvents, which all led to the formation of Form I (Fig. S2.3†). Although our DFT simulations suggest that Form II should be more stable at 0 K, the relative stability inverts at around 130 K. Form I is therefore favoured under ambient conditions also in our simulations (see Fig. S2.4 of the ESI†).
1 mixture of Form I and Form II was slurried for three days in a range of solvents, which all led to the formation of Form I (Fig. S2.3†). Although our DFT simulations suggest that Form II should be more stable at 0 K, the relative stability inverts at around 130 K. Form I is therefore favoured under ambient conditions also in our simulations (see Fig. S2.4 of the ESI†).
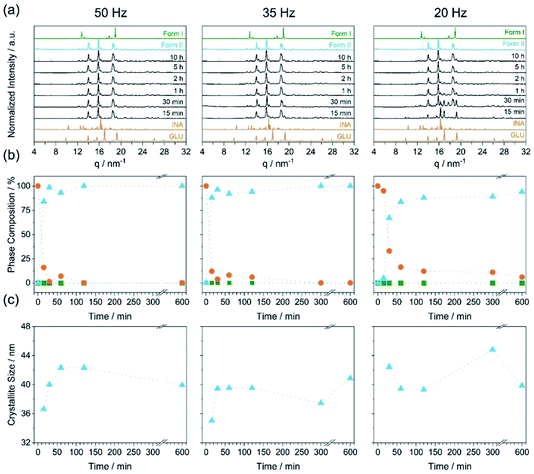
For a polymorphic transformation to occur, a given crystal form must be driven over an energy barrier. This can be done, for example, by introducing defects into the crystal structure13 or by increasing the equilibrium system temperature. To indirectly assess the effects of material activation (defect formation) on the polymorphism of INA:GLU, we explored neat grinding with one stainless steel ball (10 mm, 4.04 ± 0.02 g) at three milling frequencies (input energies), namely 50 Hz, 35 Hz, and 20 Hz (Fig. 3a). For all conditions investigated, neat grinding a stoichiometric mixture of INA and GLU (Fig. 3b, orange) led to the formation of Form II (Fig. 3b, blue). In most experiments, Form II was obtained in a pure form, with a few (low energy) milling conditions yielding a mixture of Form II and residual reactant material. For example, our highest energy milling experiments (50 Hz, 10 mm, ca. 2.03 mJ per impact) led to the crystallization of pure Form II, whereas our lowest energy milling (20 Hz, 10 mm, ca. 0.32 mJ per impact) led to a mixture of Form II and the starting material, even after 10 h of milling. Under no ambient temperature milling conditions were traces of Form I detected. We note that the crystallite size of Form II did not change significantly upon ball milling, remaining within the range of ca. 35–44 nm regardless of the milling time or intensity (Fig. 3c). This suggests that Form II crystallises at its comminution limit, or is very rapidly comminuted to this size.
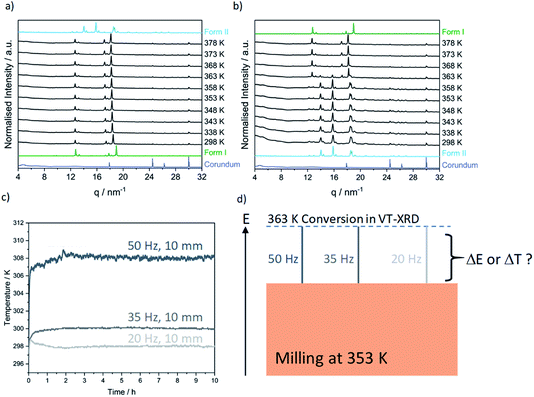
Contrary to our recent work on the polymorphism of the INA:CBZ cocrystal,13 polymorphism in the INA:GLU cocrystal system seemingly cannot be driven towards the thermodynamically stable form simply by increasing the degree of material activation (i.e. increasing the milling energy). To this end, we instead explored the potential of temperature to drive the polymorphic transformation during ball milling. The natural evolution of the equilibrium temperature during ball milling was first characterised by inserting a thermocouple into the cap of the milling jar (see S1 in the ESI† for details). At the highest intensity milling conditions (50 Hz, 10 mm), the maximum equilibrium temperature achieved in the milling jar after 2 h of milling was 308 K (see Fig. 4c). We subsequently performed a series of variable temperature PXRD (VT-PXRD) measurements to assess whether such temperatures could affect the polymorphic behaviour of INA:GLU (Fig. 4). No signs of polymorphic transformations were observed when Form I was heated to 378 K (Fig. 4a). However, when a powder of Form II was heated, it converted to Form I at 363 K (Fig. 4b). In the absence of lengthy aging (see Fig. S2.2†), our VT-PXRD results therefore do suggest that the thermodynamically stable form of INA:GLU can be obtained from Form II when the activation (kinetic) barrier is overcome. We note that the onset temperature for the polymorphic transformation is well above the maximum equilibrium temperature (308 K) that can be reached in our ball milling experiments.
A polymorphic transformation from Form II to Form I clearly occurred upon heating the powder to 363 K. We became curious whether the ball milling energy could be combined with equilibrium temperature to achieve this transition point. Noting the maximum equilibrium heating of ΔT = 10 K which could be achieved in our experiments (Fig. 4c), we made a significant (and highly simplified) assumption that a milling temperature of 353 K, accompanied by this 10 K temperature accumulation, should drive the system over the temperature threshold to polymorphic transition, Fig. 4d. We do stress that our temperature controlled milling vessel ensures that equilibrium temperatures in the milling jar do not significantly exceed the target temperature ±1.5 K. Moreover, the ΔT that occurs during milling results from equilibration between the jar and the atmosphere and can therefore be expected to differ significantly at 298 and 353 K (see Fig. 3c). While crude, however, this assumption provided a good starting point for temperature-controlled milling.
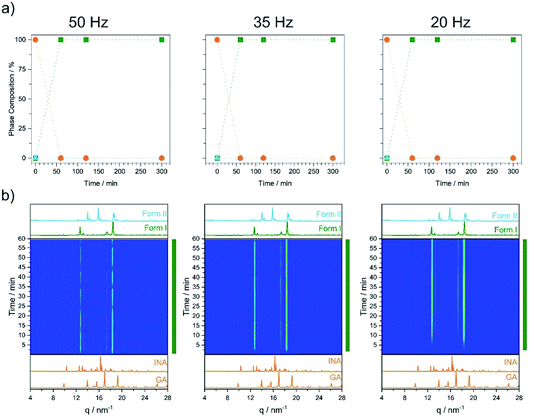
As a first test, we investigated cocrystal formation at 353 K, ball milling at 50 Hz where ΔT = 10 K was expected to occur within minutes of grinding. Under these conditions, milling the stoichiometric mixture of INA + GLU (Fig. S5.6†) led directly to the formation of Form I without any signs of Form II (Fig. 5a). No further transformation of Form I occurred when milling was extended for up to 5 h. Remarkably, milling stoichiometric mixtures of INA + GLU at lower frequencies (35 Hz and 20 Hz) led to the same outcome: the formation of Form I without any signs of Form II for up to 5 h of ball milling. As Form II can be easily interconverted to Form I by milling at 353 K, and Form I converts to Form II when milled at room temperature (see Fig. S4.2a and b†), our sparse ex situ investigations could not unambiguously rule out the potential formation of Form II as an intermediate.
Using time-resolved in situ (TRIS) powder X-ray diffraction we therefore considered more closely the time evolution of cocrystallisation, Fig. S4.1† and 5b. When a stoichiometric mixture of INA + GLU was ball milled at ambient temperatures and at 50 Hz, the first reflections of Form II were observed within ca. 2 min of milling, (see Bragg reflections at q = 14, 15.8, 18.5 nm−1, Fig. S4.1†). With continued ball milling, the amount of Form II increased, with consumption of starting materials. A pure phase of Form II was achieved under these conditions in ca. 12 min, with no further changes observed over prolonged grinding. Importantly, no reflections of Form I were observed during the ball milling process. A similar behaviour was observed for mechanochemical cocrystallisations performed at 35 Hz and 20 Hz, albeit at significantly slower rates. When the same cocrystallisations were performed at 353 K, milling at all three frequencies (50 Hz, 35 Hz, and 20 Hz) led directly to crystallisation of Form I, Fig. 5. No traces of Form II could be detected in any cases, although the rate of Form I growth slowed with decreasing milling frequency (see Fig. 5b). It follows that ball milling allows us to drive formation of Form I at markedly lower temperatures than are necessary under equilibrium conditions (i.e. during VT-PXRD).
It appears from the above results that combinations of equilibrium temperature and milling intensity can be used to influence the polymorphic outcome of cocrystal nucleation. By making slight adjustments to the equilibrium milling temperature, we therefore tried to determine to what extent such combinations are possible. When the equilibrium milling temperature was reduced from 353 K to 348 K, Form I resulted from all milling conditions (50 Hz, 35 Hz, and 20 Hz; Table 3). The ability to crystallise Form I at lower temperatures suggests that the true thermodynamic transition point differs slightly from that observed during VT-XRPD (363 K), presumably owing to large kinetic barriers to nucleation and phase transition. It therefore may be possible that the additional milling energy and dynamic stress helps to overcome kinetic barriers to the nucleation of Form I at lower temperatures (see Fig. 6b).
| Temperature/K | Frequency/Hz |
|---|---|
| 50 (2.03 mJ per impact) | |
| RT | Form II |
| 313 | Form II (15 min) |
| Form II (120 min) | |
| 323 | Form II (15 min) |
| Form II (120 min) | |
| 333 | Form I or Form II (15 min) |
| Form I or Form II (120 min) | |
| 337 | From I and traces of Form II (15 min) |
| Form I (120 min) | |
| 343 | Form I (30 min) |
| Form I (80 min) | |
| Form I (85 min) | |
| Form II (95%) + Form I (5%) 90 min | |
| Form I or Form II 120 min | |
| 345 | Form I (120 min) |
| 348 | Form I (120 min) |
| 353 | Form I (120 min) |
As we continued to reduce the milling temperature below 348 K, the polymorphic outcome became increasingly stochastic. At equilibrium temperatures within ca. 333–345 K, most reactions led to the formation of Form I, regardless of the milling frequency. However, we note that repeating experiments under identical milling conditions within this temperature range could occasionally lead to the formation of Form II. Yet, as the temperatures were decreased further to <333 K, all milling experiments led to the crystallisation of Form II (i.e. the room temperature result). While we certainly cannot discount the potential influence of seeds in the stochastic outcome of these milling experiments, we note that Form I can be readily transformed to Form II (and vice versa) when milled at the appropriate temperature (see Fig. S4.2†). It therefore does not seem likely that seeding (even if occurring in the early stages of crystallisation) could sustain a bulk polymorphic outcome under incorrect temperature conditions. Instead, we believe that this stochastic behaviour at intermediate equilibrium temperatures reflects the highly inhomogeneous conditions of mechanochemical reactions and likely exists as a general feature in temperature-controlled polymorphism in mechanochemistry. Moreover, we note that transition from the ‘stable’ thermal regime to the stochastic regime occurs over a small temperature range (15 K) on the order of seasonal variations. In addition to humidity,41 small changes in temperature presumably lead to irreproducibility between laboratories. Further detailed work on the subtle control over the solid form with variable temperature ball milling is certainly required and promises to offer a new dimension of control in mechanochemical solid form screening.
Conclusions
Using a new temperature-controlled milling set-up, we investigated the polymorphism in the stoichiometric organic cocrystal model system isonicotinamide:glutaric acid. Both polymorphs of the cocrystal could be obtained by neat ball milling, albeit at different temperatures. At ambient temperature, neat grinding consistently led to Form II. VT-XRPD experiments showed that Form II converts to Form I at 363 K. Remarkably, Form I could instead be reproducibly generated by ball milling at temperatures as low as only 348 K, i.e. 15 K below the apparent transition temperature from VT-XRPD. Importantly, time-resolved in situ XRD data showed that at elevated temperatures, Form I crystallises directly from the reactants without any traces of Form II. Moreover, the frequency only has an influence on the kinetics of the mechanochemical process but does not affect the polymorph formation. Ball milling at temperatures below 333 K always led to Form II in our experiments, consistent with the ambient temperature result. This does suggest that there is an upper and lower boundary temperature that dictates the milling conditions that unambiguously yield each polymorphic form. Yet, ball milling at intermediate temperatures between ca. 333 K and 345 K proved remarkably complex. There appeared to be no consistency in which polymorph was produced when co-grinding 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of isonicotinamide and glutaric acid. In some cases, ball milling led to the formation of Form I, while other experiments under the same apparent milling conditions led to the formation of Form II. We believe that this region represents a ‘transition point’ wherein the stochasticity of the mechanochemical conditions yields a non-uniform outcome.
1 mixtures of isonicotinamide and glutaric acid. In some cases, ball milling led to the formation of Form I, while other experiments under the same apparent milling conditions led to the formation of Form II. We believe that this region represents a ‘transition point’ wherein the stochasticity of the mechanochemical conditions yields a non-uniform outcome.
Our experiments demonstrate that a high degree of control over mechanochemical polymorphism can be obtained by combining temperature and milling energy to overcome activation barriers. In doing so, it becomes possible to drive solid state transformations at equilibrium temperatures apparently lower than those required by heating alone (e.g. VT-PXRD). This result provides an important indication that a fine degree of control over mechanochemical reactions can be obtained by carefully selecting both the equilibrium temperature and ball milling energy, thereby opening the door towards new dimensions in the design of mechanochemical experiments. Better understanding of this remarkable tunability promises further developments towards greener and more sustainable chemistry.
Author contributions
Experimental and computational investigations were carried out by KL and DA. The heating stage for the mechanochemical experiments was designed and built by RB. AALM and FE conceived, designed, and supervised the project. KL, AALM, and FE prepared the manuscript, which was discussed and agreed by KL, BR, DA, FE, and AALM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank BESSY II (Helmholtz Zentrum Berlin) for beam time and BAM IT for computational resources. Torvid Feiler is acknowledged for his help with the synchrotron experiments.Notes and references
- T. Stolar and K. Užarević, Mechanochemistry: An Efficient and Versatile Toolbox for Synthesis, Transformation, and Functionalization of Porous Metal–Organic Frameworks, CrystEngComm, 2020, 22(27), 4511–4525, 10.1039/D0CE00091D
.
- G. Ayoub, B. Karadeniz, A. J. Howarth, O. K. Farha, I. Đilović, L. S. Germann, R. E. Dinnebier, K. Užarević and T. Friščić, Rational Synthesis of Mixed-Metal Microporous Metal–Organic Frameworks with Controlled Composition Using Mechanochemistry, Chem. Mater., 2019, 31(15), 5494–5501, DOI:10.1021/acs.chemmater.9b01068
.
- G.-W. Wang, Mechanochemical Organic Synthesis, Chem. Soc. Rev., 2013, 42(18), 7668–7700, 10.1039/C3CS35526H
.
- J. Andersen and J. Mack, Mechanochemistry and Organic Synthesis: From Mystical to Practical, Green Chem., 2018, 20(7), 1435–1443, 10.1039/C7GC03797J
.
- A. A. L. Michalchuk and F. Emmerling, Time-Resolved In Situ Monitoring of Mechanochemical Reactions, Angew. Chem., Int. Ed., 2022, 61(21), e202117270, DOI:10.1002/anie.202117270
.
- A. M. Belenguer, T. Friščić, G. M. Day and J. K. M. Sanders, Solid-State Dynamic Combinatorial Chemistry: Reversibility and Thermodynamic Product Selection in Covalent Mechanosynthesis, Chem. Sci., 2011, 2(4), 696–700, 10.1039/C0SC00533A
.
- A. M. Belenguer, G. I. Lampronti, A. A. L. Michalchuk, F. Emmerling and J. K. M. Sanders, Quantitative Reversible One Pot Interconversion of Three Crystalline Polymorphs by Ball Mill Grinding, CrystEngComm, 2022, 24, 4256, 10.1039/D2CE00393G
.
- E. Losev, S. Arkhipov, D. Kolybalov, A. Mineev, A. Ogienko, E. Boldyreva and V. Boldyrev, Substituting Steel for a Polymer in a Jar for Ball Milling Does Matter, CrystEngComm, 2022, 24(9), 1700–1703, 10.1039/D1CE01703A
.
- L. S. Germann, M. Arhangelskis, M. Etter, R. E. Dinnebier and T. Friščić, Challenging the Ostwald Rule of Stages in Mechanochemical Cocrystallisation, Chem. Sci., 2020, 11(37), 10092–10100, 10.1039/D0SC03629C
.
- F. Fischer, S. Greiser, D. Pfeifer, C. Jäger, K. Rademann and F. Emmerling, Mechanochemically Induced Conversion of Crystalline Benzamide Polymorphs by Seeding, Angew. Chem., Int. Ed., 2016, 55(46), 14281–14285, DOI:10.1002/anie.201607358
.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, Complexities of Mechanochemistry: Elucidation of Processes Occurring in Mechanical Activators via Implementation of a Simple Organic System, CrystEngComm, 2013, 15(32), 6403–6412, 10.1039/C3CE40907D
.
- V. V. Boldyrev, S. V. Pavlov and E. L. Goldberg, Interrelation between Fine Grinding and Mechanical Activation, Int. J. Miner. Process., 1996, 44–45, 181–185, DOI:10.1016/0301-7516(95)00028-3
.
- K. Linberg, P. Szymoniak, A. Schönhals, F. Emmerling and A. A. L. Michalchuk, The Origin of Delayed Polymorphism in Molecular Crystals under Mechanochemical Conditions, ChemRxiv, 2022, 10, DOI:10.26434/chemrxiv-2022-04jdf.
- N. Bouvart, R.-M. Palix, S. G. Arkhipov, I. A. Tumanov, A. A. L. Michalchuk and E. V. Boldyreva, Polymorphism of Chlorpropamide on Liquid-Assisted Mechanical Treatment: Choice of Liquid and Type of Mechanical Treatment Matter, CrystEngComm, 2018, 20(13), 1797–1803, 10.1039/C7CE02221B
.
- H. Kulla, C. Becker, A. A. L. Michalchuk, K. Linberg, B. Paulus and F. Emmerling, Tuning the Apparent Stability of Polymorphic Cocrystals through Mechanochemistry, Cryst. Growth Des., 2019, 19(12), 7271–7279, DOI:10.1021/acs.cgd.9b01158
.
- H. Kulla, S. Haferkamp, I. Akhmetova, M. Röllig, C. Maierhofer, K. Rademann and F. Emmerling, In Situ Investigations of Mechanochemical One-Pot Syntheses, Angew. Chem., Int. Ed., 2018, 57(20), 5930–5933, DOI:10.1002/anie.201800147
.
- K. Užarević, V. Štrukil, C. Mottillo, P. A. Julien, A. Puškarić, T. Friščić and I. Halasz, Exploring the Effect of Temperature on a Mechanochemical Reaction by In Situ Synchrotron Powder X-Ray Diffraction, Cryst. Growth Des., 2016, 16(4), 2342–2347, DOI:10.1021/acs.cgd.6b00137
.
- K. Užarević, N. Ferdelji, T. Mrla, P. A. Julien, B. Halasz, T. Friščić and I. Halasz, Enthalpy vs. Friction: Heat Flow Modelling of Unexpected Temperature Profiles in Mechanochemistry of Metal–Organic Frameworks, Chem. Sci., 2018, 9(9), 2525–2532 RSC
.
- J. M. Andersen and J. Mack, Decoupling the Arrhenius Equation via Mechanochemistry, Chem. Sci., 2017, 8(8), 5447–5453, 10.1039/C7SC00538E
.
- M. Descamps, J. F. Willart, E. Dudognon and V. Caron, Transformation of Pharmaceutical Compounds upon Milling and Comilling: The Role of Tg, J. Pharm. Sci., 2007, 96(5), 1398–1407, DOI:10.1002/jps.20939
.
- J. Bernstein, Polymorphism – A Perspective, Cryst. Growth Des., 2011, 11(3), 632–650 CrossRef
.
- J. Nyman and G. M. Day, Static and Lattice Vibrational Energy Differences between Polymorphs, CrystEngComm, 2015, 17(28), 5154–5165, 10.1039/C5CE00045A
.
- P. Ying, J. Yu and W. Su, Liquid-Assisted Grinding Mechanochemistry in the Synthesis of Pharmaceuticals, Adv. Synth. Catal., 2021, 363(5), 1246–1271, DOI:10.1002/adsc.202001245
.
- A. M. Belenguer, G. I. Lampronti, A. J. Cruz-Cabeza, C. A. Hunter and J. K. M. Sanders, Solvation and Surface Effects on Polymorph Stabilities at the Nanoscale, Chem. Sci., 2016, 7(11), 6617–6627, 10.1039/C6SC03457H
.
- D. Hasa, E. Carlino and W. Jones, Polymer-Assisted Grinding, a Versatile Method for Polymorph Control of Cocrystallization, Cryst. Growth Des., 2016, 16(3), 1772–1779, DOI:10.1021/acs.cgd.6b00084
.
- P. Vishweshwar, A. Nangia and V. M. Lynch, Supramolecular Synthons in Phenol–Isonicotinamide Adducts, CrystEngComm, 2003, 5(31), 164–168, 10.1039/B304078J
.
- P. Vishweshwar, A. Nangia and V. M. Lynch, Molecular Complexes of Homologous Alkanedicarboxylic Acids with Isonicotinamide: X-Ray Crystal Structures, Hydrogen Bond Synthons, and Melting Point Alternation, Cryst. Growth Des., 2003, 3(5), 783–790, DOI:10.1021/cg034037h
.
- G. I. Lampronti, A. A. L. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. M. Sanders, A. Bacchi and F. Emmerling, Changing the Game of Time Resolved X-Ray Diffraction on the Mechanochemistry Playground by Downsizing, Nat. Commun., 2021, 12(1), 6134, DOI:10.1038/s41467-021-26264-1
.
-
A. Bruker, Topas V4. 2: General Profile and Structure Analysis Software for Powder Diffraction Data, Bruker AXS Karlsr. Ger., 2009 Search PubMed
.
- C. B. Aakeröy, A. M. Beatty, B. A. Helfrich and M. Nieuwenhuyzen, Do Polymorphic Compounds Make Good Cocrystallizing Agents? A Structural Case Study That Demonstrates the Importance of Synthon Flexibility, Cryst. Growth Des., 2003, 3(2), 159–165 CrossRef
.
- S. Bhattacharya, V. G. Saraswatula and B. K. Saha, Thermal Expansion in Alkane Diacids—Another Property Showing Alternation in an Odd–Even Series, Cryst. Growth Des., 2013, 13(8), 3651–3656, DOI:10.1021/cg400668w
.
- A. A. L. Michalchuk and F. Emmerling, Time-Resolved In Situ Monitoring of Mechanochemical Reactions, Angew. Chem., Int. Ed., 2022, e202117270, DOI:10.1002/anie.202117270
.
- G. Benecke, W. Wagermaier, C. Li, M. Schwartzkopf, G. Flucke, R. Hoerth, I. Zizak, M. Burghammer, E. Metwalli, P. Muller-Buschbaum, M. Trebbin, S. Forster, O. Paris, S. V. Roth and P. Fratzl, A Customizable Software for Fast Reduction and Analysis of Large X-Ray Scattering Data Sets: Applications of the New DPDAK Package to Small-Angle X-Ray Scattering and Grazing-Incidence Small-Angle X-Ray Scattering, J. Appl. Crystallogr., 2014, 47, 1797–1803, DOI:10.1107/S1600576714019773
.
- S.-J. Baek, A. Park, Y.-J. Ahn and J. Choo, Baseline Correction Using Asymmetrically Reweighted Penalized Least Squares Smoothing, Analyst, 2015, 140(1), 250–257, 10.1039/C4AN01061B
.
- A. Altomare, N. Corriero, C. Cuocci, A. Falcicchio, A. Moliterni and R. Rizzi, EXPO Software for Solving Crystal Structures by Powder Diffraction Data: Methods and Application, Cryst. Res. Technol., 2015, 50(9–10), 737–742, DOI:10.1002/crat.201500024
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100(13), 136406 CrossRef
.
- A. Tkatchenko and M. Scheffler, Accurate Molecular van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102(7), 073005 CrossRef PubMed
.
- A. A. L. Michalchuk, E. V. Boldyreva, A. M. Belenguer, F. Emmerling and V. V. Boldyrev, Tribochemistry, Mechanical Alloying, Mechanochemistry: What Is in a Name?, Front. Chem., 2021, 9, 359, DOI:10.3389/fchem.2021.685789
.
- H. Kulla, A. A. L. Michalchuk and F. Emmerling, Manipulating the Dynamics of Mechanochemical Ternary Cocrystal Formation, Chem. Commun., 2019, 55(66), 9793–9796, 10.1039/C9CC03034D
.
- I. A. Tumanov, A. Michalchuk, A. Politov, E. Boldyreva and V. V. Boldyrev, Inadvertent Liquid Assisted Grinding: A Key to “Dry” Organic Mechano-Co-Crystallisation?, CrystEngComm, 2017, 19(21), 2830–2835 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2170487. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2fd00115b |
| This journal is © The Royal Society of Chemistry 2023 |