Open Access Article
Open Access ArticleA systematic mechanistic survey on the reactions between OH radical and CH3OH on ice†
W. M. C.
Sameera
 *ab,
Avon P.
Jayaweera
*ab,
Avon P.
Jayaweera
 b,
Atsuki
Ishibashi
b,
Atsuki
Ishibashi
 a,
Hiroshi
Hidaka
a,
Hiroshi
Hidaka
 a,
Yasuhiro
Oba
a,
Yasuhiro
Oba
 a and
Naoki
Watanabe
a and
Naoki
Watanabe
 a
a
aInstitute of Low Temperature Science, Hokkaido University, Sapporo, Hokkaido 060-0819, Japan. E-mail: wmcsameera@lowtem.hokudai.ac.jp
bDepartment of Chemistry, University of Colombo, Colombo 00300, Sri Lanka
First published on 18th March 2023
Abstract
A systematic mechanistic survey was performed for the CH3OH + OH reaction on ice. ONIOM(ωB97X-D/Def2-TZVP:AMOEBA09) calculations suggested a range of binding energies for the CH2OH radical (0.29–0.69 eV) and CH3OH (0.15–0.72 eV) molecule on hexagonal water ice (Ih) and amorphous solid water (ASW). Computed average binding energies of CH2OH radical (0.49 eV) and CH3OH (0.41 eV) are relatively stronger compared to the CH3O radical binding energies (0.32 eV, Sameera et al., J. Phy. Chem. A, 2021, 125, 387–393). Thus, the CH3OH molecule, CH2OH and CH3O radicals can adsorb on ice, where the binding energies follow the order CH2OH > CH3OH > CH3O. The multi-component artificial force-induced reaction (MC-AFIR) method systematically determined the reaction mechanisms for the CH3OH + OH reaction on ice, where two reaction paths, giving rise to CH2OH and CH3O radicals, were confirmed. A range of reaction barriers, employing the ωB97X-D/Def2-TZVP level of theory, was found for each reaction (0.03–0.11 eV for CH2OH radical formation, and 0.03–0.44 eV for CH3O radical formation). Based on the lowest energy reaction paths, we suspect that both reactions operate on ice. The computed data in this study evidence that the nature of the binding site or the reaction site has a significant effect on the computed binding energies or reaction barriers. Thus, the outcomes of the present study will be very useful for the computational astrochemistry community to determine reliable binding energies and reaction barriers on ice.
Introduction
Radical species in the interstellar medium (ISM) play a key role in forming complex organic molecules (COMs).1–8 The radicals in the ISM, such as the primary radicals (H, OH, CO, HCO, CH3O, CH2OH, CH3, NH, and NH2)9,10 can be formed through surface reactions and the photodissociation of small molecules in interstellar ice. At very low temperatures (e.g., 10 K), radical species adsorb on ice grain surfaces. Among the primary radicals, only H can diffuse on the ice at 10 K. The other primary radicals may start migrating on the ice at relatively high temperatures, the so-called warming-up stage. When a radical species encounters another radical or a molecule on ice, relatively large radicals or molecules can be formed. Therefore, quantitative details of the radical adsorption, radical diffusion, and radical reactions on ice are essential to understand the mechanisms of COMs formation. The radical processes on ice are challenging to characterize from experimental methods. Thus, computational studies are indispensable.11Quantum mechanics (QM) and quantum mechanics/molecular mechanics (QM/MM) methods, typically employing density functional theory (DFT), allow fast and accurate determination of potential energy surfaces (PES) of complex molecular systems.11–13 Then, the properties of the molecular systems, radical binding energy, reaction barriers, diffusion barriers, and reaction mechanisms can be calculated. We have used QM and QM/MM methods to calculate the binding energy of radical species on ice. The radical species interact with the dangling hydrogen (d-H) or dangling oxygen (d-O) on ice. Depending on the combination of dangling atoms at the binding site on ice, a range of binding energies was found for OH (0.06–0.74 eV),14 HCO (0.12–0.42 eV),14 CH3 (0.11–0.26 eV),14 CH3O (0.10–0.50 eV),15 PH2 (0.16–0.21 eV),16 PH (0.12–0.16 eV),16 P (0.07–0.15 eV),16 OCSH (0.19–0.46 eV).17 We have also calculated radical reactions on ices; PH3 + D,16 and OCS + H,17 and CH3SH + H,18 where the computed reaction mechanisms explained the experimental results.
CH3OH is one of the molecules in the ISM that plays a crucial role in COMs formation. Thus, the formation of CH3OH in the ISM and the reactions between CH3OH and the primary radicals are very important. The successive hydrogenation of CO, an abundant molecule in the ISM, gives rise to CH3OH (Scheme 1).19,20 The first hydrogenation yields the HCO radical, and the second hydrogenation gives rise to the H2CO molecule. CH3O or CH2OH radicals are the products of the third hydrogenation. Final hydrogenation gives CH3OH. Among the three intermediate radicals in the mechanism, only the CHO and CH3O radicals were found in the ISM.21–23
Reactions between the CH3OH and OH radical, an abundant primary radical in the ISM, is a major interest to the astrochemistry field. Two reaction mechanisms have been proposed for the CH3OH + OH reaction in the gas phase or on ice (Scheme 2). When CH3OH and an OH radical come closer, OH⋯CH3OH complex, a spectroscopically characterized complex,24 is formed. According to ab initio computations on the gas phase reaction, CH2OH radical formation [i.e., reaction (i)] has a relatively low energy barrier, where quantum tunnelling plays a key role.25–29 Another theoretical survey suggested that the cross-section yielding the CH3O radical is higher than that for the CH2OH radical.27 The computed branching ratios at low temperatures and low pressure suggested that the CH2OH radical remains,28 while below 40 K, the computed branching ratio was uncertain and sensitive to the computational methodology. Thus, outcomes of the reaction (i.e., CH2OH or CH3O) at low temperatures are currently under active discussion. Recently, the importance of this reaction on ice dust was also proposed.30
In the present study, we calculated the binding energy of the CH2OH radical and CH2OH molecule on ice, employing a number of binding sites, and compared it with the binding energy of the CH3O radical on ice.15 Then, reaction mechanisms between CH3OH and an OH radical on the ice were systematically determined.
Computational methods and models
Binding energy
Ice cluster models were taken from our previous study15 to replicate amorphous solid water (ASW) and crystalline water ice (Ih) (Fig. 1). The ASW model has 162 H2O molecules, where 50 H2O molecules are in the QM region, and 112 H2O molecules are in the MM region. The Ih models B and C, have 162 and 168 H2O molecules, respectively. The QM region of model B has 48 H2O molecules, and the MM region has 114 H2O molecules. In model C, the QM and MM regions have 156 and 112 H2O molecules, respectively.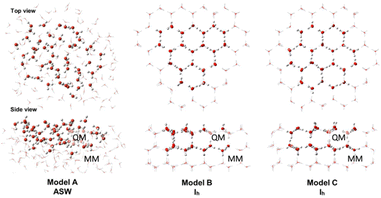 | ||
| Fig. 1 Top and side views of the ice cluster models. The QM region is shown with “ball and stick” illustration, and the MM region is shown in “wireframe” illustration. | ||
Geometry optimizations were performed using the two-layer ONIOM method as implemented in the PyQM/MM interface.31 The ωB97X-D,32 functional and def2-TZVP,33 basis sets were used for the ONIOM,34,35 high-layer. The AMOEB09 36–38 polarizable force field was used for the ONIOM low-layer. To avoid structure deformations, atoms in the ONIOM-low layer were frozen during the structure optimization. Vibrational frequency calculations were performed for the optimized structures to calculate the zero-point energy and to confirm the local minima (i.e., no imaginary frequencies). Binding energies were calculated using the following formula;
| Binding energy = |E(ice-molecule/radical) − Eice − Emolecule/radical| |
Reaction mechanisms
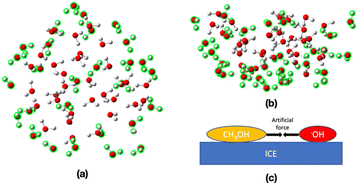
Reaction mechanisms between a CH3OH molecule and an OH radical on ASW were determined by using the multi-component artificial force-induced reaction (MC-AFIR)13,39 method as implemented in the GRRM17 program.40 For this purpose, an ice cluster model, consisting of 76 H2O molecules, was employed. In this model, 28 H2O molecules on the side and bottom walls were frozen during the structure optimization, as highlighted in green in Fig. 2a and b, and the remaining 48 H2O molecules were left flexible. The ωB97X-D method and the 6-31G* basis sets,41–44 were used for the AFIR calculations. The CH3OH molecule and OH radical were placed randomly on the ice surface. Then, an artificial force parameter of 100 kJ mol−1 was added between the CH3OH and OH radical (Fig. 2c). After that, the resulting reaction paths (i.e., AFIR paths), were inspected and approximate transition states (TSs) were identified, and fully optimized using the ωB97X-D/6-31G* level of theory, as implemented in the Gaussian16 program.45Starting from the TS optimized structures, Pseudo intrinsic reaction coordinate calculations (IRC)46,47 were performed for 20 steps forward and 20 steps backward from the optimized TS structures. Then, the local minima (LM) connecting the TSs (i.e., the reactant complex and product) were calculated. Vibrational frequency calculations were performed to confirm that the optimized LM have no imaginary frequency and the optimized TSs have one imaginary frequency; and to calculate zero-point energies. Potential energies of the optimized LM or TSs were calculated as the single-point energy using the ωB97X-D/def2-TZVP level of theory.
Results and discussion
Binding energy of CH2OH and CH3OH on ice
We have chosen 16 binding sites, eight from Ih (A–H) and eight from ASW (I–P) ice cluster models, to calculate binding energies. The computed binding energies are shown in Fig. 3. The molecular structures of the optimized structures are shown in Fig. S1 and S2.† The computed binding energies of the CH2OH radical are in the range 0.29–0.69 eV, and the average binding energy is 0.49 eV (Fig. 3a). In the case of CH3OH, the computed binding energies are in the range 0.15–0.72 eV, and the computed average binding energy is 0.41 eV (Fig. 3b).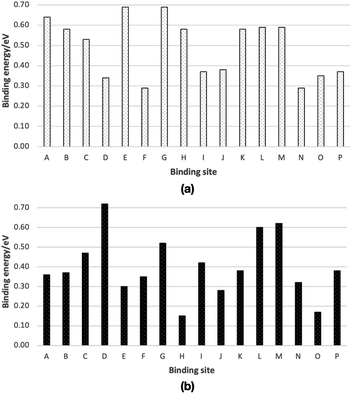 | ||
| Fig. 3 Calculated binding energies of (a) a CH2OH radical and (b) a CH3OH on ice, from ONIOM(ωB97X-D/Def2-TZVP:AMOEBA09) calculations. Optimized molecular structures are shown in Fig. S1 and S2.† Binding energies are summarized in Table S1.† | ||
Based on the average binding energies, we concluded that CH2OH radical binding energy on ice is larger than that of the CH3OH radical. From our previous study, using the same computational methods, we found that the average binding energy of the CH3O radical is 0.32 eV.15 Thus, the binding energy of the CH3OH molecule, CH2OH radical, and CH3O radical follows the order CH3O (0.32 eV) < CH3OH (0.41 eV) < CH2OH (0.49 eV). Therefore, if CH3OH, CH2OH, and CH3O are formed on ice, the thermal desorption probability of these species would follow the opposite order, CH3O < CH3OH < CH2OH.
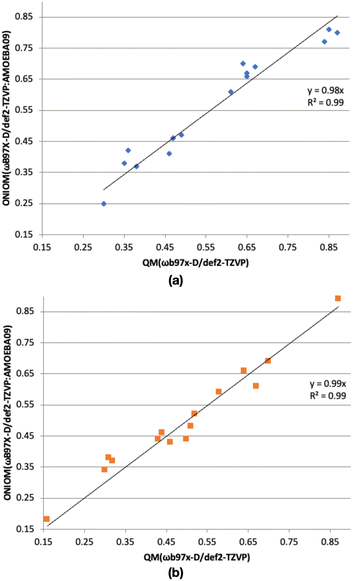
In our ice models, a relatively large MM region is chosen. To check whether the MM region has a significant effect on the computed binding energies, we have compared binding energies (without ZPE) from ONIOM(ωB97X-D/Def2-TZVP:AMOEBA09) and ωB97X-D/Def2-TZVP methods (Fig. 4). In the case of the CH2OH radical, the R2 value of the plot is 0.99, indicating good agreement between the ONIOM(QM:MM) and QM binding energies. Similarly, the R2 value of the plot of CH3OH of 0.99, shows the good agreement between the computed binding energies from the ONIOM(ωB97X-D/Def2-TZVP:AMOEBA09) and ωB97X-D/Def2-TZVP methods.
The maximum discrepancy of the CH2OH radical binding energies (without ZPE, Table S2†) of 0.07 eV of binding site A, is very small compared the computed binding energy of A, 0.77 eV. When we consider the lowest binding energy (0.25 eV), the discrepancy between the computed binding energy from ONIOM(ωB97X-D/Def2-TZVP:AMOEBA09) and ωB97X-D/Def2-TZVP methods is also small (0.05 eV). Thus, in general, binding energies from ONIOM(QM:MM) and QM methods are in agreement. Similarly, the maximum discrepancy of the CH3OH radical binding energies (without ZPE, Table S2†) is 0.06 eV, belonging to binding sites E and N with the computed binding energy of 0.38 and 0.37 eV, respectively. If we consider the lowest binding energy of CH3OH (0.18 eV, binding site H), the discrepancy between the computed binding energy from ONIOM(QM:MM) and QM methods is very small (0.02 eV). Therefore, the ONIOM(QM:MM) method gave reliable binding energies.
In the present study, it is important to note that we have chosen 16 binding sites to calculate binding energies. Thus, we were able to cover a number of arrangements of the dangling atoms at the binding sites, where the interactions between the radical and the binding site are diverse, allowing us to collect a range of binding energies.
CH3OH + OH reaction on ice
This section focuses on the mechanisms for the reaction between CH3OH and an OH radical on ice. An MC-AFIR search was performed to determine reaction paths systematically, and two reaction paths were found on ice; (a) CH3OH + OH → CH2OH + H2O and (b) CH3OH + OH → CH3O + H2O. We have chosen four AFIR paths for each reaction mechanism and potential energy surfaces were calculated (Fig. 5). The lowest and highest computed potential energy barrier for the CH2OH radical formation is 0.03 eV and 0.11 eV, respectively (Fig. 5a), and therefore the computed reaction barrier is in a range. Similarly, the computed potential energy barrier for the CH3O radical formation is also in a range (Fig. 5b), where the lowest energy barrier is 0.03 eV, while the highest barrier is 0.44 eV. If the lowest energy reaction path is taken into account (i.e., 0.03 eV for the formation of the CH2OH radical and 0.03 eV for the formation of the CH3O radical), both reaction mechanisms may operate on ice. In the case of the products of the reactions, the CH2OH radical is thermodynamically more stable compared to the CH3O radical in all cases. Further, if we take the lowest energy paths of the two mechanisms, the HO–H⋯CH2OH complex is −1.08 eV more stable compared to the entry point of the potential energy profile, while the HO⋯CH3O complex is −0.85 eV more stable compared to its entry point.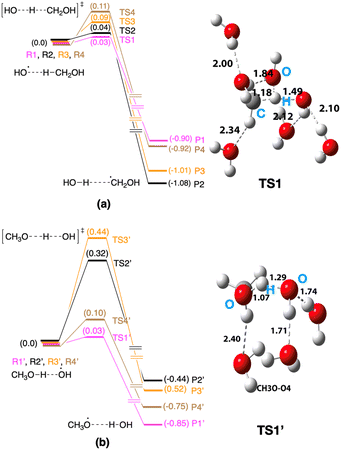 | ||
| Fig. 5 Computed potential energy surfaces for (a) CH3OH + OH → CH2OH + H2O and (b) CH3OH + OH → CH3O + H2O reactions. Optimized transition state structures are shown in Fig. S3 and S4†). | ||
In this reaction path survey, we restricted the analysis to four reaction paths for each reaction (eight reaction paths in total). Even with these data, we can see a range of reaction barriers for each reaction. If we extend the analysis for collecting more reaction paths, we suspect that the reaction barrier range will be broadened. The lowest barrier limit is the key to the rate of the reaction. In this present case, both reactions operate at a very low reaction barrier of 0.03 eV. Therefore, both reaction mechanisms would operate on interstellar ice.
Conclusions
We have used the ONIOM(ωB97X-D/def2-TZVP:AMOEBA09) method to calculate CH2OH and CH3OH radical binding on ASW and Ih. A range of binding energies were found for each species; CH3OH: 0.15–0.72 eV; CH2OH: 0.29–0.69 eV. Thus, both CH2OH and CH3OH radicals would adsorb on interstellar ice. The calculated average binding energies, 0.41 eV of CH3OH and 0.49 eV of CH2OH, indicate the strong binding preference of CH2OH, and are relatively stronger compared to the CH3O radical binding energies (0.32 eV).15 Reaction paths for the CH3OH + OH were searched using the MC-AFIR method. Two reaction mechanisms were determined, giving rise to CH2OH and CH3O products. A range of reaction barriers was found for each reaction mechanism; 0.03–0.11 eV for the CH2OH radical formation and 0.02–0.44 eV for the CH3O radical formation. Both radicals can be formed on ice if the lowest energy paths are taken into account. As radical binding on ice and radical reactions on ice cover a range of numbers, a systematic sampling of binding energies or reaction barriers becomes critical, which is the key lesson we have learned from this study.Author contributions
WMCS designed the project, performed calculations, and wrote the original manuscript with help from APJ. AI, HH, YO and NW performed the experiments relevant to this study. All co-authors have revised the manuscript and given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by the JSPS KAKENHI grant numbers JP19K03940 (to WMCS), JP21H05416 (to WMCS), JP17H06087 (to NW), and JSPS grant number JPJSBP 120229901 (to WMCS). Supercomputing resources at the Institute for Information Management and Communication at Kyoto University in Japan and the Institute for Molecular Science (IMS) in Japan are also acknowledged.References
- E. Herbst and E. F. Van Dishoeck, Annu. Rev. Astron. Astrophys., 2009, 47, 427–480 CrossRef CAS.
- S. Bottinelli, C. Ceccarelli, J. P. Williams and B. Lefloch, Astron. Astrophys., 2007, 463, 601–610 CrossRef CAS.
- E. Herbst and R. T. Garrod, Front. Astron. Space Sci., 2022, 8, 1–6 Search PubMed.
- A. Bacmann, V. Taquet, A. Faure, C. Kahane and C. Ceccarelli, Astron. Astrophys., 2012, 541, L12–5 CrossRef.
- C. Vastel, C. Ceccarelli, B. Lefloch and R. Bachiller, Astrophys. J., 2014, 795, L2–11 CrossRef.
- R. T. Garrod, S. L. W. Weaver and E. Herbst, Astrophys. J., 2008, 682, 283–302 CrossRef CAS.
- K. I. Öberg, E. F. Van Dishoeck, H. Linnartz and S. Andersson, Astrophys. J., 2010, 718, 832–840 CrossRef.
- K. J. Chuang, G. Fedoseev, S. Ioppolo, E. F. van Dishoeck and H. Linnartz, Mon. Not. R. Astron. Soc., 2016, 455, 1702–1712 CrossRef CAS.
- R. T. Garrod, S. L. W. Weaver and E. Herbst, Astrophys. J., 2008, 682, 283–302 CrossRef CAS.
- K. Öberg, E. F. van Dishoeck, H. Linnartz and S. Andersson, Astrophys. J., 2010, 718, 832–840 CrossRef.
- W. M. C. Sameera, B. Senevirathne, T. Nguyen, Y. Oba, A. Ishibashi, M. Tsuge, H. Hidaka and N. Watanabe, Front. Astron. Space Sci., 2022, 9, 890161 CrossRef.
- W. M. C. Sameera and F. Maseras, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 375–385 CAS.
- W. M. C. Sameera, S. Maeda and K. Morokuma, Acc. Chem. Res., 2016, 49, 763–773 CrossRef CAS PubMed.
- W. M. C. Sameera, B. Senevirathne, S. Andersson, F. Maseras and G. Nyman, J. Phys. Chem. C, 2017, 121, 15223–15232 CrossRef CAS.
- W. M. C. Sameera, B. Senevirathne, S. Andersson, M. Al-Lbadi, H. Hidaka, A. Kouchi, G. Nyman and N. Watanabe, J. Phys. Chem. A, 2021, 125, 387–393 CrossRef CAS PubMed.
- T. Nguyen, Y. Oba, W. M. C. Sameera, A. Kouchi and N. Watanabe, Astrophys. J., 2021, 918, 73 CrossRef CAS.
- T. Nguyen, Y. Oba, W. M. C. Sameera, A. Kouchi and N. Watanabe, Astrophys. J., 2021, 922, 146 CrossRef CAS.
- T. Nguyen, Y. Oba, W. M. C. Sameera, A. Kouchi and N. Watanabe, Astrophys. J., 2023, 944, 219 CrossRef.
- A. G. G. M. Tielens and W. Hagen, Astron. Astrophys., 1982, 114, 245–260 CAS.
- N. Watanabe and A. Kouchi, Astrophys. J., 2002, 571, L173–L176 CrossRef CAS.
- J. Cernicharo, N. Marcelino, E. Roueff, M. Gerin, A. Jiménez-Escobar and G. M. Caro, Astrophys. J., 2012, 759, L43 CrossRef.
- L. E. Snyder, J. M. Hollis and B. L. Ulich, Astrophys. J., 1976, 208, L91–L94 CrossRef CAS.
- V. M. Rivilla, M. T. Beltrán, A. Vasyunin, P. Caselli, S. Viti, F. Fontani and R. Cesaroni, Mon. Not. R. Astron. Soc., 2019, 483, 806–823 CrossRef CAS.
- F. J. Hernandez, J. T. Brice, C. M. Leavitt, G. A. Pino and G. E. Douberly, J. Phys. Chem. A, 2015, 119, 8125–8132 CrossRef CAS PubMed.
- S. Blázquez, D. González, A. García-Sáez, M. Antiñolo, A. Bergeat, F. Caralp, R. Mereau, A. Canosa and B. Ballesteros, ACS Earth Space Chem., 2019, 3, 1873–1883 CrossRef PubMed.
- R. J. Shannon, M. A. Blitz, A. Goddard and D. E. Heard, Nat. Chem., 2013, 5, 745–749 CrossRef CAS PubMed.
- O. Roncero, A. Zanche and A. Aguado, Phys. Chem. Chem. Phys., 2018, 20, 25951–25958 RSC.
- A. J. Ocaña, S. Blázquez, A. Potapov, B. Ballesteros, A. Canosa, M. Antiñolo, L. Vereecken, J. Albaladejo and E. Jiménez, Phys. Chem. Chem. Phys., 2019, 21, 6942–6957 RSC.
- L. G. Gao, J. Zheng, A. Fernández-Ramo, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918 CrossRef CAS PubMed.
- A. Ishibashi, H. Hidaka, Y. Oba, A. Kouchi and N. Watanabe, Astrophys. J., 2021, 921, L13 CrossRef CAS.
- M. Rathnayake, W. M. C. Sameera and N. Watanabe, ChemRxiv, 2022, preprint, DOI:10.26434/chemrxiv-2022-2c8mz.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- W. M. C. Sameera and F. Maseras, J. Chem. Inf. Model., 2018, 58, 1828–1835 CrossRef CAS PubMed.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- J. W. Ponder and D. A. Case, Force Fields for Protein Simulations, Adv. Protein Chem., 2003, 66, 27–85 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Comput. Chem., 2002, 23, 1497–1506 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- W. M. C. Sameera, A. K. Sharma, S. Maeda and K. Morokuma, Chem. Rec., 2016, 16, 2349–2363 CrossRef CAS PubMed.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki, T. Ichino, Y. Sumiya, K. Sugiyama and Y. Ono, J. Comput. Chem., 2018, 39, 233–251 CrossRef CAS PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, GAUSSIAN 16 (Revision C.01), Gaussian, Inc., Wallingford, CT, 2016.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- H. P. Hratchian and H. B. Schlegel, Theory and Applications of Computational Chemistry, The First Forty Years, 2005, pp. 195–249 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00033h |
| This journal is © The Royal Society of Chemistry 2023 |