Self-healing bottlebrush polymer networks enabled via a side-chain interlocking design

Abstract

Exploring novel healing mechanisms is a constant impetus for the development of self-healing materials. Herein, we find that side-chain interlocking of bottlebrush polymers can form a dynamic network and thereby serve as a driving force for the self-healing process of the materials. Molecular dynamics simulation indicates that the interlocking is formed by the interpenetration between the long side chains of adjacent molecules and stabilized by van der Waals interactions and molecular entanglements of side chains. The interlocking can be tailored by changing the length and density of the side chains through atom transfer radical polymerization. As a result, the optimized bottlebrush polymer shows a healing efficiency of up to 100%. Unlike chemical interactions, side-chain interlocking eliminates the introduction of specific chemical groups. Therefore, bottlebrush polymers can even self-heal under harsh aqueous conditions, including acid and alkali solutions. Moreover, the highly dynamic side-chain interlocking enables bottlebrush polymers to efficiently dissipate vibration energy, and thus they can be used as damping materials. Collectively, side-chain interlocking expands the scope of physical interactions in self-healing materials and hews out a versatile way for polymers to accomplish self-healing capability in various environments.

---

New concepts

A bottle brush is an ordinary scrubbing tool in our daily life. When we put bottle brushes together, they usually stick together due to the mutual insertion of side bristles. However, such an interaction is usually neglected in synthetic polymers. This article reveals that the side-chain interlocking of bottlebrush polymers can form a dynamic network, thereby imparting the materials with excellent self-healing performance even under harsh aqueous conditions. The core concept is to construct side-chain interlocking by the interpenetration between long side chains of bottlebrush molecules, and such interlocking is stabilized by van der Waals interactions and molecular entanglements of side chains. Since interlocking is physical in nature, it is insensitive to the external environment. Therefore, bottlebrush polymers can readily self-heal even in water, acid and alkali solutions. These findings will expand the scope of physical interactions in self-healing materials and open a novel avenue for the molecular design of materials healing in various environments.

1. Introduction

Most polymeric materials end up with physical damage during practical applications. Such physically damaged materials are usually discarded, leading to serious plastic pollution. To address this dilemma, intrinsic self-healing polymers capable of restoring their structural integrity, physical properties or special functions have been developed and they have become a rising star in industry.^1–3 Due to their intrinsic self-healing ability, such polymers can be used longer, possess high reliability and even be recycled, which will reduce their negative impact on the environment. Currently, intrinsic self-healing polymers often rely on reversible chemical interactions, including dynamic non-covalent bonds (such as hydrogen bonds,^4–8 ionic interactions,^9,10 coordination bonds¹¹ and so on) and dynamic covalent bonds (such as Diels–Alder bonds,^12,13 disulfide bonds,^14–16 boronate ester bonds^17–19 and so on). Nevertheless, construction of these chemical mechanisms requires particular functional groups, which will increase the difficulty in scale-up production and practical application of the polymers. Moreover, most of the chemical interactions are vulnerable to environmental factors (high humidity, acid, alkali, etc.), which can deteriorate the mechanical properties and self-healing efficiency.^20–23 Therefore, there is a constant desire for exploring brand-new healing mechanisms to enable the further advance of self-healing polymers.

Recently, physical interactions, such as van der Waals forces,^24–26 microphase separation²⁷ and microcrystal interactions,^20,22 have attracted increasing interest to fabricate self-healing polymers due to their less sensitivity to the chemical environment. For instance, dipole–dipole interaction is adopted to fabricate self-healing materials based on commercial poly(vinylidene fluoride), which can heal even in alkaline water with pH = 13.^26,28 Nano-scale microphase separation can be engineered to endow polymers based on the available commodity olefin with excellent mechanical properties and self-healability.^20,22,27 Key-and-lock interchain junctions in the copolymer of methyl methacrylate (MMA) and butyl acrylate (BA) even can accelerate the under-water repairability, as the hydrophobic van der Waals force makes the side groups present more compact conformation.^24,25 Importantly, these physical-interaction-based mechanisms are versatile for constructing polymers with either simple or elaborately designed structures.

Exploring new healing mechanisms is especially valuable for polymers with elaborately designed structures, which usually possess unique properties. However, it is more challenging to engineer supramolecular interactions or dynamic covalent bonds in these polymers. For example, bottlebrush polymers, featured by dense side chains and a worm-like conformation with stretched backbones and few entanglements,^29–35 engender many distinctive physical properties such as super softness, high flexibility, strain-stiffening behavior and biological lubricity.^{33,34,36–40} They hold many potential applications as single-molecule nanowires, biolubricants, super sensitive stimuli-responsive materials and drug carriers.^36–38,41 Nevertheless, ultra-softness makes bottlebrush materials easy to flow. Therefore, bottlebrush elastomers are usually crosslinked by permanent covalent bonds, which are unable to self-heal mechanical damages. There are several investigations on constructing healing mechanisms for bottlebrush polymers based on the chemical interactions, including disulfide bonds,^42,43 Diels–Alder bonds,⁴⁴ transesterification,⁴⁵ hydrogen bonds,⁴⁶ coordination⁴⁷ and so on, which make the synthetic routes much more complicated. In fact, the special conformation and multiple tunable side chains provide great possibilities for bottlebrush polymers to introduce dynamic physical interactions.

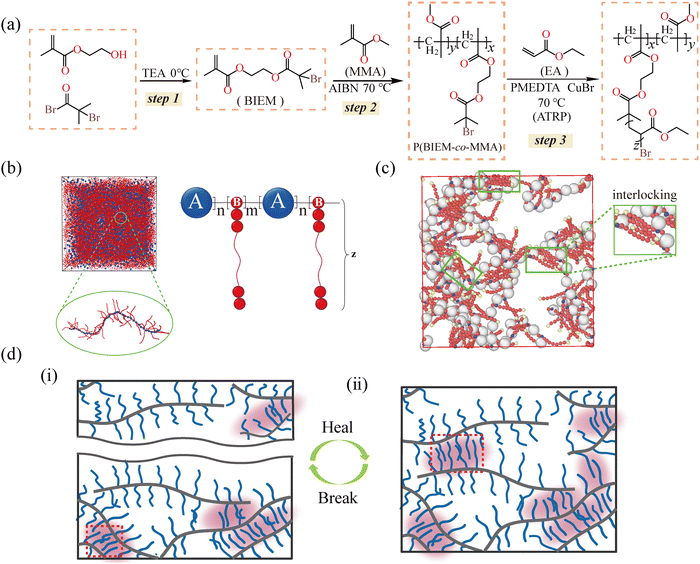
Herein, we explore a novel physical mechanism, the interlocking of long side chains, to fabricate a class of self-healing bottlebrush polymers (Fig. 1(a)). By tailoring the length and density of the side chains through atom transfer radical polymerization (ATRP), the bottlebrush polymers are endowed with excellent healing efficiency up to 100%. Molecular dynamics (MD) simulation reveals that the long side chains of adjacent molecules interpenetrate each other to form side-chain interlocking interactions, and such interlocking is stabilized by van der Waals interactions and molecular entanglements of side chains (Fig. 1(b) and (c)). Upon mechanical damage, the side-chain interlocking de-locks or disengages. During repair, the side chains of adjacent bottlebrushes re-interpenetrate driven by molecular motion to re-form the interlocking interaction, leading to the reconstruction of the network on the wound (Fig. 1(d)). Unlike chemical interactions, the side-chain interlocking interaction is insensitive to the external environment. Therefore, bottlebrush polymers can readily self-heal even in water, acid and alkali solutions. Additionally, the highly dynamic side-chain interlocking enables the bottlebrush polymers to efficiently dissipate the vibration energy, and the energy dissipation efficiency is up to 83%. The dynamic side-chain interlocks open a novel dimension for the molecular design of self-healing materials without chemical dynamic interactions.

Fig. 1 (a) Synthesis steps of the bottlebrush polymers. Step 1: Synthesis of the initiator monomer (BIEM). Step 2: MMA and BIEM are copolymerized by free-radical copolymerization with AIBN as the initiator. Step 3: EA is grafted to the copolymerization backbone of MMA and BIEM by ATRP to form the bottlebrush polymers. (b) The coarse-grained model of bottlebrush polymer designs according to the experiment. Type A beads represent the PMMA backbone, type B beads represent the PEA side chains, m and n determine the grafting density of the side chain, and z is the length of the side chains. The diagram on the right shows the equilibrium snapshot of the system n = m = 1, z = 20. (c) The equilibrium snapshot of the granularity analysis model. (d) Schematic diagram of the destructive and self-healing process: (i) under the external force, the interlocking interaction unlocks and (ii) during the healing process, the mobility of the molecules makes the neighboring side chains re-interpenetrate to form the interlocking interaction.

2. Results and discussion

2.1 Molecular design of bottlebrush polymers based on side-chain interlocking interactions

Based on our previous work⁴⁸ and the research of pioneers,^24,25,49 polyacrylate (PEA) with appropriate rigidity is selected as the side chain of the bottlebrush polymer. The “grafting from” strategy is adopted for synthesizing the bottlebrush polymer,⁵⁰ as displayed in Fig. 1(a). At first, an ATRP initiator monomer, 2-(2-bromoisobutyryloxy)ethyl methacrylate (BIEM), is synthesized and confirmed by ¹H NMR (Fig. S1, ESI†). BIEM is then randomly copolymerized with methylmethacrylate (MMA) to procure the macromolecular ATRP initiator P(BIEM-co-MMA), which also serves as the backbone of the bottlebrush polymer. The grafting density is regulated by adjusting the feed ratio of BIEM to MMA (Table S2, ESI†) and quantified by ¹H NMR (Fig. S2, ESI†). Afterward, the side chains of PEA are grafted to P(BIEM-co-MMA) by ATRP. The side-chain length is controlled by the feed ratio of ethyl acrylate (EA). The detailed synthesis process is shown in the ESI.†

Six groups of samples, named x-y-EA-z, are synthesized to investigate the influence of grafting density and side-chain length on the self-healing and mechanical properties, where x and y respectively stand for the contents of BIEM and MMA in the backbone, which is also the embodiment of grafting density, and z represents the length of the side chains. The higher the value of x : y, the higher the grafting density; the higher the value of z, the longer the side chains, see Table S3 (ESI†) for details. After eliminating thermal history, the differential scanning calorimetry (DSC) results reveal that the glass transition temperature (T_g) of all samples is lower than room temperature (25 °C), as shown in Fig. S4 and S5 (ESI†). Therefore, these bottlebrush polymers are elastomers at room temperature. Simultaneously, the T_g decreases with increasing grafting density and side-chain length, indicating that a higher grafting density and a longer side-chain length can improve segmental mobility.

Interestingly, although the prepared bottlebrush polymers are not crosslinked, they possess elasticity, as the deformed sample can recover its original shape after deformation (Fig. S6, S7 and Movie S1, ESI†). This phenomenon indicates that there is a stable network in the bottlebrush polymers. To confirm the stable network, rheological measurements are performed. Indeed, the temperature-dependent storage modulus (G′) demonstrates a rubbery plateau, proving the existence of the network (Fig. S8, ESI†).

To reveal how the network forms, we perform MD simulations based on granularity analysis for the bottlebrush polymers. The detailed parameters and simulation methods are described in the ESI.† In the granularity analysis model, the backbone, side chain and side-chain terminal are marked by white, red and blue beads, respectively (Fig. 1(b)). The equilibrium snapshots can be used to track the permeation, interpenetration and entanglement behaviors between the side chains. Clearly, the equilibrium snapshots exhibit the amount of side-chain interlocking structures (Fig. 1(c)), and the long side chains interpenetrate with each other to form tight interlocks. Such interlocks act as physical cross-linking points to form a stable network, which results in a rubbery plateau in a certain temperature range.^51,52 To exclude the contribution of covalent crosslinks, sample 1-4-EA-50 is dissolved with tetrahydrofuran (THF) (Fig. S9, ESI†). Indeed, the complete dissolution reveals that there are no covalent crosslinks between molecular chains.

2.2 Mechanical properties of bottlebrush polymers

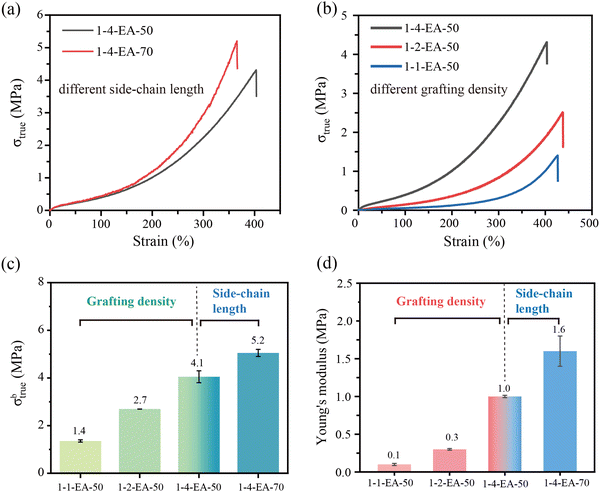
To optimize the mechanical properties of the bottlebrush polymers, the influences of grafting density and side-chain length are systematically explored (Fig. 2 and Fig. S10, ESI†). Unlike un-crosslinked but entangled polymer melts whose stress decreases with increasing strain after a yielding point,²⁰ bottlebrush polymers with high grafting density and long side-chain length show typical strain-adaptation behavior. They show a low initial elastic modulus at small deformations, while becoming stiff at large deformations to endure large force, as shown in Fig. 2(a) and (b). This behavior is a common feature of covalently crosslinked bottlebrush polymers.^32,36,38 For 1-4-EA-20 with short side chains and 1-8-EA-50 with a small grafting density, the content of the flexible PEA side chains is not enough, and the rigid backbone (P(BIEM-co-MMA)) dominates the mechanical properties, leading to a high Young's modulus and the absence of the strain-adaptation behavior (Fig. S10 and Table S6, ESI†). Therefore, 1-4-EA-20 and 1-8-EA-50 do not have the mechanical properties of typical bottlebrush polymers.

Fig. 2 Effects of the side chain length and grafting density on the mechanical properties. Representative stress–strain curves of (a) samples 1-4-EA-50 and 1-4-EA-70 with different side-chain lengths and (b) samples 1-4-EA-50, 1-2-EA-50, and 1-1-EA-50 with different grafting densities at a tensile rate of 100 mm min⁻¹. (c) σ^b_true comparison of samples with different grafting densities and side-chain lengths. (d) Young's modulus comparison of samples with different grafting densities and side chain lengths.

We first investigate the impacts of grafting density on the mechanical properties. For 1-4-EA-50, its true stress at break (σ^b_true) is as high as 4.1 MPa, despite the absence of covalent crosslinking. With increasing grafting density, the σ^b_true of the bottlebrush polymers decreases gradually (Fig. 2(c)). For 1-4-EA-50, 1-2-EA-50 and 1-1-EA-50, as the grafting density gradually increases, the σ^b_true of samples decreases from 4.1 MPa to 1.4 MPa. In addition, the same trend is observed for Young's modulus (Fig. 2(d) and Table S6, ESI†). For 1-4-EA-50, 1-2-EA-50 and 1-1-EA-50, as the grafting density gradually increases, the Young's modulus reduces from 1.0 MPa to 0.1 MPa (Fig. 2(d)). These phenomena can be related to steric repulsion: tighter grafting causes greater steric repulsion, which is unfavorable for the formation of interlocking and entanglement between side chains.^37,52,53

Next, the impacts of side-chain lengths are examined. For 1-4-EA-20, 1-4-EA-50 and 1-4-EA-70, as the side-chain length increases, the fracture stress declines first but then increases (Fig. S11, ESI† and Fig. 2(c)). It is easy to understand that with the increase in the side-chain length, the rigidity of the backbone is gradually diluted, leading to higher flexibility but a lower mechanical strength. Nevertheless, the further increase in the side-chain length results in side-chain entanglement. The increased side-chain entanglement can be confirmed by Young's modulus (Fig. 2(d)). The initial decrease in Young's modulus from 1-4-EA-20 to 1-4-EA-50 is attributed to the plasticizing effect of the flexible long side chain (Table S6, ESI†). But from 1-4-EA-50 to 1-4-EA-70 (Fig. 2(d)), the abnormally increased Young's modulus (from 1.0 MPa to 1.6 MPa) implies the increase in side-chain entanglement. The side-chain entanglement makes the σ^b_true of 1-4-EA-70 reach 5.2 MPa which is greater than that of 1-4-EA-50 (4.1 MPa).

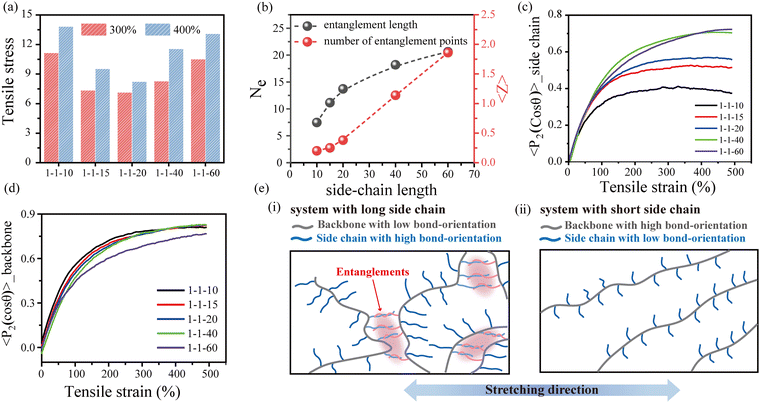
To explore the underlying mechanism of the effect of the side-chain architecture on the mechanical properties of the bottlebrush polymers, we conducted uniaxial stretching mode of MD simulations to characterize the tensile behavior of bottlebrush polymers with various grafting densities and side-chain lengths. The simulation results indicate that the tensile stress decreases with increasing grafting density (Fig. S12, ESI†), which is consistent with the experimental results. As the grafting density decreases, the rigid backbone becomes the dominant composition, so the bottlebrush polymer gradually changes from soft-tough to hard-brittle. However, the effect of side-chain length on the mechanical properties is relatively complicated. With the growth of side-chain length, the tensile strength first decreases and then increases, as shown in Fig. 3(a). As analyzed earlier, we believe that the topological entanglements derived from the interpenetration of longer side chains are the underlying factor for the elevated mechanical properties. By implementing the same primitive path analysis (PPA) proposed by Everaers et al.,⁵⁴ we calculate the entanglement length (N_e) of the side chains and the average number of entanglement points (〈Z〉) per side chain (Fig. 3(b)). Obviously, when the side-chain length is less than 20, almost no topological entanglement occurs between the side chains. As the side-chain length increases, N_e increases and gradually attains plateaus, accompanied by a rapid increase in 〈Z〉. More details about PPA can be found in the ESI.†

Fig. 3 Molecular mechanism of the effects of side chain length and grafting density on the mechanical properties. (a) Samples with different side-chain lengths are compared at 300% and 400% constant tensile stress. (b) The average entanglement length and the number of entanglement nodes of the side chain are calculated based on the PPA method. Bond orientation behavior of (c) the side chain and (d) the backbone during stretching. (e) Schematic diagram of the microstructural evolution of the system with (i) a long side chain and (ii) a short side chain during stretching. The blue and red lines represent the main chain and the side chain respectively.

Similar to chemical cross-linking, entanglement points increase the tensile stress by inhibiting the motility of the molecular chains, which is accompanied by an increase in chain segment orientation. Second-order Legendre polynomials are typically used to describe bond orientation:

〈P₂(cos θ)〉 = (3 〈cos² θ〉 − 1)/2 (1)

This function describes the average value of the angle θ between a given bond vector and the reference direction, which refers to the stretching direction in this work. The possible values of 〈P₂(cos θ)〉 range from −0.5 to 1. 〈P₂(cos θ)〉 = −0.5 and 〈P₂(cos θ)〉 = 1 indicate the perfect orientation perpendicular and parallel to the stretching direction, respectively.

Fig. 3(c) shows the bond orientation of the side chains during the stretching process. As expected, when the side-chain length is greater than 20, the elevated entanglement points increase the orientation of the side chains along the stretching direction, which leads to a rapid increase in the tensile stress. When the side-chain length is less than 20, the decreasing side-chain length leads to increased content of the rigid backbone, which also contributes to an increase in tensile stress. Fig. 3(d) presents the bond orientation behavior of the backbone during the stretching process. It can be found that the backbone of the long-side-chain systems shows low orientation, which is opposite to the tendency of the side chains. In addition, the backbone size (ΔR_eed²), obtained by calculating the difference between the mean square end-to-end distances in the stretched and equilibrium states, supports similar conclusions (Fig. S13, ESI†). Therefore, the mechanical properties of the system with short side chains depend mainly on the contribution of the backbone, and the stress contribution gradually shifts to the side-chain entanglements as the side-chain length increases, as schematically shown in Fig. 3(e). Overall, the entanglement between the long side chains leads to an increasing orientation of the side chains during stretching, which enhances the mechanical properties of long side-chain bottlebrushes. Meanwhile, the irregular entanglement between side chains weakens the orientation of the backbone during stretching. By contrast, for short side-chain bottlebrushes, there is almost no topological entanglement between the side chains, and the tensile stress is mainly contributed by the backbone orientation along the stretching direction.

2.3 Self-healing properties of bottlebrush polymers

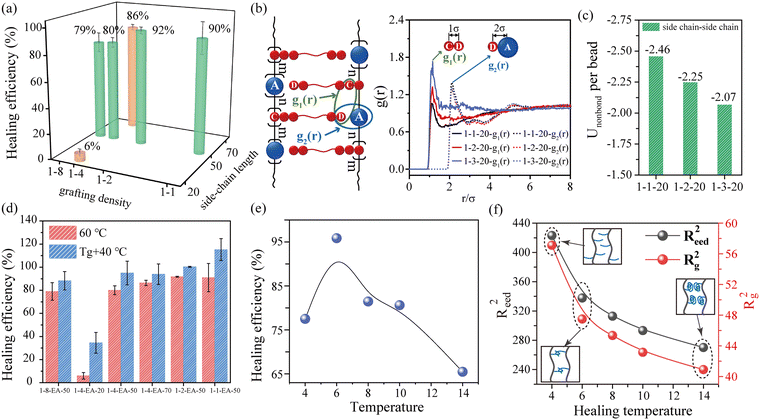
Since the side-chain interlocking is a dynamic physical interaction in nature, the bottlebrush polymers exhibit self-healing performance. The scratches vanish after healing at 40 °C for 12 h (Fig. S14, ESI†). To quantify the self-healing performance of the bottlebrush polymers, dumbbell samples are entirely sliced into halves and then reconnected at 60 °C for different times. Tensile tests on the healed samples are conducted to evaluate their healing efficiency (Fig. S15, ESI† and Fig. 4(a)), which is represented by the recovery of fracture toughness (integrated area under the stress–strain curve). As expected, the longer the time, the better the repair. Except for 1-4-EA-20, other bottlebrush polymers all possess a magnificent healing efficiency higher than 80% after healing at 60 °C for 24 h.

Fig. 4 (a) Self-healing efficiency after 24 h at 60 °C of the experimental samples. (b) The radial distribution function g(r) of different side-chain densities, including the g₁(r) of side chain ends (C–D) and g₂(r) of side chain ends and the backbone (D–A). (c) The non-bonding energy of each homogenized side chain bead. (d) The self-healing efficiency of the samples is compared at 60 °C and T_g + 40 °C (T_g + 40 °C: T_1-8-EA-50 = 47 °C, T_1-4-EA-20 = 40 °C, T_1-4-EA-50 = 35 °C, T_1-4-EA-70 = 26 °C, T_1-2-EA-50 = 30 °C, and T_1-1-EA-50 = 25 °C) for 24 h, respectively. (e) Healing efficiency of the 1–1–40 system at different temperatures. (f) Mean square radius of gyration and mean square end-to-end distance of a self-healed side chain in the 1–1–40 system.

Due to the low grafting density and shortest side-chain length of 1-4-EA-20, it is laborious for the adjacent side chains to closely re-interpenetrate and re-create side-chain interlocking interactions. Therefore, even if the healing temperature is above T_g, the cut halves of 1-4-EA-20 only reconnect together through surface adhesion rather than the formation of the interlocking interaction (Fig. S15(b), ESI†). As a result, the healing efficiency of 1-4-EA-20 is quite low (6%) (Fig. 4(a)). For the remaining samples with appropriate grafting density and side-chain length, the side chains can re-interpenetrate and recombine across the cut sections to generate the interlocking interaction at 60 °C, enabling efficient repairment. Furthermore, the 24 h-healing efficiency monotonically increases with the increasing side-chain length, but it increases first and then decreases slightly with the increment of grafting density (Fig. 4(a)).

To understand the healing mechanism, MD simulation is conducted to correlate the healing performance of bottlebrush polymers with different grafting densities and side-chain lengths (Fig. S16, ESI†). Consistent with the experimental results, the simulations also indicate that a longer side chain is more conducive to improving healing efficiency (Fig. S16(h), ESI†). The interaction energy between side chains is quantitatively characterized by calculating the average non-bond energy of the side chain beads before and after healing for the bottlebrush polymers with different side-chain lengths, as shown in Fig. S16(i) (ESI†). It is revealed that the non-bonding interaction energy between side chains increases with the increase in side chain length. Since higher non-bonding energy is conducive to the mutual attraction of the side chains and the formation of stable side-chain interlocking interactions, samples with longer side chains hold better repairing performance.

Unlike side-chain length, the grafting density exhibits a non-monotonic effect on the self-healing performance. In particular, a moderate grafting density could enable achieving a high healing efficiency, which agrees well with the experimental results (Fig. S16(h), ESI† and Fig. 4(a)). We believe that the degree of interpenetration and interaction between the side chains jointly determine the self-healing properties of the bottlebrush polymers. Therefore, for the bottlebrush polymers with different grafting densities, we calculate the radial distribution function (g(r)) (Fig. 4(b)) and the average non-bond interaction energy of the side-chain beads (Fig. 4(c)), which represent the degree of interpenetration and the binding strength between the side chains, respectively. g(r), describing the particle density as a function of the distance from the referred atom, is generally used to characterize the aggregation between particles, which includes the g₁(r) of side chain ends (C–D) and g₂(r) of side chain ends and the backbone (D–A) (Fig. 4(b)). As shown in Fig. 4(b), the smaller the peak value of g₁(r), the harder it is for the side to interpenetrate. The simulation results show that, on the one hand, the dense grafting leads to insufficient space for the side chains to interpenetrate, which makes it difficult to form the side-chain interlocking interaction. But on the other hand, once the mutual penetration is reformed, the samples with closer side chains will possess a higher non-bond energy, which makes the recombined side-chain interlocks more stable (Fig. 4(c)). This is the primary reason for the nonlinear variation of the healing efficiency with the grafting density.

Taking into account the different T_g values between samples, the segmental mobility at 60 °C is quite unidentical for different samples, which will impact the self-healing behavior to a certain extent. To eliminate this interference, we choose T_g + 40 °C as the healing temperature. The self-healing behavior at T_g + 40 °C (T_g + 40 °C < 60 °C) is examined for all the bottlebrush polymers. This condition leads to the identical temperature interval above T_g, basically ensuring that the segment motion is as close as possible for different bottlebrush polymers. The self-healing results under this condition are shown in Fig. 4(d) and Fig. S17 (ESI†). Except for 1-4-EA-20, the healing efficiency of all the samples is greater than 90%, and for 1-2-EA-50 and 1-1-EA-50, the healing efficiency even reaches 100%. At T_g + 40 °C, the effect of side-chain length on the healing performance is consistent with that at 60 °C. However, the effect of grafting density on the healing efficiency at T_g + 40 °C becomes monotonic, which is inconsistent with that at 60 °C. For 1-8-EA-50, 1-4-EA-50, 1-2-EA-50 and 1-1-EA-50, the healing efficiency increases with the increase in grafting density. The probable reason is that when the segmental mobility is identical, the degree of side-chain re-penetration is also the same. Under this circumstance, the interaction energy of the side chains dominates the self-healing performance. A higher grafting density leads to a higher interaction energy, thereby increasing the healing efficiency. This also indirectly proves that the degree of interpenetration and interaction energy between the side chains jointly determine the self-healing performance.

In general, with the increase in temperature, the faster the molecular chain moves, the higher the healing efficiency.⁵⁵ However, in our system, the healing efficiency at 60 °C is inferior to that at T_g + 40 °C (Fig. 4(d)). In other words, when the repairing temperature is sufficient to drive the segmental motion, an excessively high temperature is detrimental to the improvement of healing efficiency. The reason for this abnormal phenomenon may be that the molecular motion at high temperatures will lead to the dissociation of the side-chain interlocking interaction. The released side chains will spontaneously curl under high temperatures, which increases the difficulty in the formation of the interpenetrating side-chain interlocking.

To confirm this molecular mechanism, we investigate the effect of temperature on the healing efficiency by MD simulations (here the 1–1–40 system is chosen), and the simulative results are consistent with the experimental results (Fig. 4(e) and Fig. S18(a), ESI†). The healing efficiency increases and then decreases with an increase in the healing temperature (T*), and the maximum healing efficiency appears at T* = 6.0. Subsequently, the side-chain size after healing is calculated, including the mean-square end distance (R_eed²) and the mean-square radius of gyration (R_g²), as shown in Fig. 4(f). Interestingly, as T* increases, the side chains gradually curl up driven by entropy. This indicates that there is a suitable T* for the side chains to assume a semi-curled state, which provides a possibility for the reformation of entanglement between the interlocked side chains. When the T* is low, the segmental motion is too slow to accomplish the healing process. Meanwhile, at low T*, the side chains are rather extended so that the side-chain interlocking interaction is weak, which is unfavorable for the bottlebrushes to heal the mechanical properties (Fig. 4(f)). At excessively high temperatures, side chains will curl up into clumps, and the rebinding possibility between side chains also decreases, causing decreased healing efficiency (Fig. 4(f)). However, mechanical interlocking structures with higher strength can be formed between the semi-curled side chains. The stronger interlocking allows the repaired bottlebrush polymers to exhibit a higher degree of bond orientation during stretching (Fig. S18(b), ESI†), thereby leading to a higher healing efficiency at a moderate healing temperature.

Due to its physical nature, the interlocking structure is insensitive to external environments. A thin protective 1-4-EA-50 membrane (400 μm) is coated on the test paper to verify the corrosion resistance under harsh conditions. The color of the pH test paper coated with 1-4-EA-50 does not change after treatment in acidic and basic solutions for 9 days at room temperature (Fig. 5(a)). This result demonstrates the high stability and reliability of the bottlebrushes under acidic and alkaline conditions, thanks to the physical side-chain interlocks. As such, the bottlebrush polymers can repair the mechanical damage even in water, aqueous acid (pH = 3, HCl aqueous) and alkali (pH = 13 NaOH aqueous) (Fig. 5(b) and Movie S2, Fig. S19, ESI†). Interestingly, self-healing can be accelerated by water and aqueous acid. The 6 h-healing efficiencies in water and aqueous acid are higher than the 12 h-healing efficiencies in air Fig. 5(c), further implying the chemical-environment insensitivity of the physical dynamic side-chain interlocking interaction.

Fig. 5 (a) The pH test paper coated with the protective 1-4-EA-50 film was immersed in acidic and basic solutions. The thickness of the film is around 400 μm. (b) The cut bottlebrush polymers can be stretched after healing in basic solutions (pH = 13) for 90 min. The movie can be seen in the ESI.† (c) Healing efficiency of 1-4-EA-50 at T_g + 40 °C (35 °C) under various harsh conditions.

2.4 Demonstration of shock absorption and vibration damping

The highly dynamic nature of the side-chain interlocking interaction enables the bottlebrush polymers to dissipate mechanical energy. 1-4-EA-50 with optimum comprehensive performance is selected and tested by dynamic mechanical analysis (DMA). On the temperature-dependent loss factor (tan δ) curve (Fig. S20, ESI†), the peak value of tan δ reaches 1.6. At room temperature, the tan δ is about 0.85, which is far more than 0.3 (rubbers with tan δ > 0.3 can be considered as satisfying damping materials).⁵⁶ Besides, the temperature span of tan δ > 0.3 is about 80 °C, located in the high-temperature range of 8–88 °C (Fig. S20, ESI†), which is much broader than that of the commercial elastomers, including natural rubber (NR), bromobutyl rubber (BIIR) and polyurethane (PU).^57–60 This result indicates that the bottlebrush polymers possess excellent damping performance.

To verify the energy absorption ability of the bottlebrush polymers, a drop-weight impact test is adopted (Fig. 6(a)). An impulse force of 30 N is applied to a 1-4-EA-50 sheet of 1 mm thickness, the force and acceleration transmitted across the sheet are recorded, and the results are compared with those of BIIR and PU (Fig. 6(b)). The comparison indicates that 1-4-EA-50 can obviously reduce the impact energy, and the detected acceleration of 1-4-EA-50 is smaller than those of BIIR and PU (Fig. 6(c)). Moreover, the vibration absorption capacity is measured by shaking table demonstrative experiments (Fig. 6(d)). The sinusoidal longitudinal vibration signal is applied to 1-4-EA-50, BIIR and PU. The acceleration amplitude of 1-4-EA-50 is much lower than those of BIIR and PU (Fig. 6(e)). The amplitude-dissipation efficiency is defined as the value of the amplitude reduction as a percentage of the shaking table amplitude.⁶¹ The amplitude-dissipation efficiency of 1-4-EA-50 is about 83%, which is much higher than those of BIIR (57%) and PU (40%) (Fig. 6(f)). Meanwhile, the signal phase of 1-4-EA-50 lags significantly (Fig. S21, ESI†). These results indicate that the bottlebrush polymer exhibits a great damping effect because the dynamic side-chain interlocking interaction can absorb the energy during vibration.

Fig. 6 Aseismic experiments (a) drop hammer impact tests: impulse signals (the impulse force) of the materials with 1 mm are produced using an impact hammer and the impulse force is in the range of 30–35 N. The response signals are collected using the acceleration sensor. (b) The result signals of drop weight impact tests on selected damping materials (1-4-EA-50, BIIR and PU). The black curve represents the impulse force of the drop-weight impact, and the other curves represent the acceleration. (c) The peak value of the acceleration signals for 1-4-EA-50, BIIR and PU. The acceleration signal peak of 1-4-EA-50 is much smaller than those of BIIR and PU. (d) Shaking table demonstrative experiments: the acceleration sensors are placed on the shaking table and materials, respectively. They are all submitted to a sinusoidal longitudinal vibration of 670 kHz frequency and the response signals are collected. (e) The resulting signals of the shaker table demonstrative experiments. The amplitude of the vibration signal on 1-4-EA-50 is dissipated significantly and is much smaller than those of BIIR and PU. (f) The dissipation efficiencies of 1-4-EA-50, BIIR and PU.

3. Conclusions

To summarize, we exploit a new and versatile mechanism, the dynamic side-chain interlocking, to endow the bottlebrush polymers with elasticity, excellent self-healing performance (100% healing of toughness) and high-energy dissipation (83% of dissipation efficiency). The side-chain interlocking is formed by the interpenetration between the long side chains of adjacent molecules and can be tailored by adjusting the grafting density and side-chain length. Simultaneously, the side chains can form molecular entanglements at appropriate chain lengths, which are beneficial for the mechanical properties and healing process. Impressively, the construction of side-chain interlocking does not rely on chemical interactions. Therefore, side-chain interlocking is insensitive to the chemical environments, and thus the bottlebrushes can heal under harsh aqueous conditions, including acid and alkali solutions. Moreover, the highly dynamic side-chain interlocking enables the bottlebrush polymers to efficiently dissipate the vibration energy, which is critical for damping materials. These findings will expand the scope of physical interactions in self-healing materials and open a brand-new avenue for the molecular design of self-healing polymers.

4. Experimental section

Materials

The materials and agents are obtained from the indicated commercial suppliers and were used without further purification unless otherwise specified: 2-hydroxyethyl methacrylate (HEMA, Adamas, 99%, safe dry), 2-bromoisobutyryl bromide (BIB) (Adamas, 99%), triethylamine (TEA, Adamas, 99%), anhydrous dichloromethane (DCM, Adamas, 99%, safe dry), methyl methacrylate (MMA, Adamas, 99%), 2,2-azobis(isobutyronitrile) (AIBN, TCI, 98.0%), ethyl acrylate (EA, TCI, 99.0% (GC)), N,N,N′,N′′,N′′-pentamethyldiethylenetriamine (PMEDTA, TCI, 99.0% (GC)), and copper(I) bromide (CuBr) purified by stirring overnight in glacial acetic acid. More details about the raw materials are provided in Table S1 (ESI†).

Synthesis

Synthesis of 2-(2-bromoisobutyryloxy)ethyl methacrylate (BIEM). HEMA (80 mmol), TEA (80 mmol), and anhydrous dichloromethane (60 mL) were added to a dry round-bottom flask, the mixture was cooled in an ice bath while stirring, and a solution of 2-BIB (88.0 mmol) in anhydrous dichloromethane (10 mL) was added dropwise using a constant pressure funnel over 30 min under an argon atmosphere. The mixed solution was kept cold and stirred overnight to complete the reaction. After at least 24 h, the white precipitate was filtered out and washed with DCM twice, and the obtained organic phase was washed three times with 15 wt% HCl solution, 15 wt% NaHCO₃ solution and deionized water respectively and then dried under anhydrous MgSO₄, and the solvent was removed using a rotary evaporator to obtain a pale yellow liquid, which was defined by ¹H NMR (Fig. S1, ESI†).

Synthesis of macroinitiators P(BIEM-co-MMA). The macroinitiators were synthesized by free-radical copolymerization of MMA and BIEM. MMA, BIEM and AIBN were dissolved in toluene in the specified proportion, and the solution was bubbled with argon for 30 min and then heated at 70 °C for at least 12 h under an argon atmosphere. The resulting solution was precipitated in methanol at least three times, and finally the precipitate was dried at 45 °C in a vacuum oven for at least 48 h. The actual ratio of MMA and BIEM in the copolymer was determined by ¹H NMR, and then the number of MMA (n) and BIEM (m) in the copolymer chain was calculated by combining the results of ¹H NMR (Fig. S2, ESI†) and GPC. The details of the macroinitiators are shown in Table S2 (ESI†).

Synthesis of bottlebrushes. Bottlebrushes were prepared by atom transfer radical polymerization (ATRP) making use of a macroinitiator as the initiator. Typically for 4-1-EA-50, the Shrek reaction bottle was used as the reaction vessel, macroinitiator-4-1(1 g, 1.05 mmol Br) was dissolved in 10 mL of toluene first, then EA (5.2553 g, 0.0525 mol) and PMEDTA (0.3639 g, 2.10 mmol) were dissolved in another 10 mL of toluene, and the mixture was cooled in an ice bath and bubbled with argon for 2 h to remove oxygen from the solution as much as possible; afterwards, CuBr (0.1506 g, 1.05 mmol) was added to the reaction solution quickly and the reaction vessel was sealed, thereafter the mixture was heated 70 °C for 4 h under an argon atmosphere. After the reaction, THF was added to the reaction solution to cool it down to room temperature rapidly, the product was filtered through a plug of neutral alumina oxide to remove most of Cu²⁺ and Cu⁺, and THF was used as the eluent. After filtering, THF was removed through a rotary evaporator at 35 °C, and then the resulting solution was precipitated in a mixed solvent of methanol and deionized water (3 : 1) at least three times. The precipitate was dried at 35 °C in a vacuum oven for at least 48 h finally. The details of the bottlebrushes are shown in Table S3 (ESI†).

A detailed description of the synthetic procedures can be found in the ESI.†

Simulation method

In order to establish the relationship between the microstructure and macroscopic properties of the bottlebrush polymer more profoundly, we constructed a coarse-grained model including the backbone and side chain according to the experiment by using molecular dynamics (MD) simulations. A detailed description can be found in the ESI.†

Characterization

The ¹H NMR spectra are recorded on a Bruker AV III HD spectrometer operating at 400 MHz. The molecular weight is measured using a Tosoh HIC-8320GPC with tetrahydrofuran (THF) as the eluent. The heat flow curves of bottlebrush polymers are acquired on the Q2000 (TA instruments). The rheological measurements are carried out using the HAAKE MARS (Mars III). Tensile experiments are performed on an Instron 5967 tensile tester. The primitive path analysis (PPA) proposed by Everaers et al.,⁵⁴ which is based on the concept of Edwards’ tube model,⁶² is employed to identify the primitive path of each strand. A detailed description of the characterization methods can be found in the ESI.†

Author contributions

J. R. W., J. L. and L. Q. Z. conceived and supervised the project. H. X. designed the experiments, carried out the experiments and wrote the paper. T. K. Y. performed the molecular simulation and assisted with the writing work. Q. W., L. J. Z. and Z. T. X. assisted with the characterization.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the Science and Technology Department of Sichuan Province (Grant no. 2021YFS0402 and 2021JDJQ0018), the National Natural Science Foundation of China (Grant no. 51873110) and the State Key Laboratory of Polymer Materials Engineering, Sichuan University. Jun Liu wants to thank the financial support of the National Science Fund for Excellent Young Scholars (Grant no. 52122311). The authors thank prof. Guangwu Zhou and Miss Luole Du for the help with the damping and shock absorption demonstration.

References

1. M. W. Urban, Nat. Chem., 2012, 4, 80–82.
2. T. P. Huynh, P. Sonar and H. Haick, Adv. Mater., 2017, 29, 1604973.
3. M. D. Hager, P. Greil, C. Leyens, S. van der Zwaag and U. S. Schubert, Adv. Mater., 2010, 22, 5424–5430.
4. J. Cao, C. Lu, J. Zhuang, M. Liu, X. Zhang, Y. Yu and Q. Tao, Angew. Chem., Int. Ed., 2017, 56, 8795–8800.
5. X. Zhang and J. He, Sci. Rep., 2015, 5, 9227.
6. Y. Eom, S. M. Kim, M. Lee, H. Jeon, J. Park, E. S. Lee, S. Y. Hwang, J. Park and D. X. Oh, Nat. Commun., 2021, 12, 621.
7. H. Wang, H. Liu, Z. Cao, W. Li, X. Huang, Y. Zhu, F. Ling, H. Xu, Q. Wu, Y. Peng, B. Yang, R. Zhang, O. Kessler, G. Huang and J. Wu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11299–11305.
8. R. Guo, Q. Zhang, Y. Wu, H. Chen, Y. Liu, J. Wang, X. Duan, Q. Chen, Z. Ge and Y. Zhang, Adv. Mater., 2023, e2212130,  DOI:10.1002/adma.202212130.
9. L. Zhang, H. Xiong, Q. Wu, Y. Peng, Y. Zhu, H. Wang, Y. Yang, X. Liu, G. Huang and J. Wu, Sci. Chin. Mater., 2021, 64, 1780–1790.
10. Y. Deng, Q. Zhang, B. L. Feringa, H. Tian and D. H. Qu, Angew. Chem., 2020, 132, 5316–5321.
11. C. H. Li and J. L. Zuo, Adv. Mater., 2020, 32, e1903762.
12. W. Pu, D. Fu, Z. Wang, X. Gan, X. Lu, L. Yang and H. Xia, Adv. Sci., 2018, 5, 1800101.
13. G. Du, A. Mao, J. Yu, J. Hou, N. Zhao, J. Han, Q. Zhao, W. Gao, T. Xie and H. Bai, Nat. Commun., 2019, 10, 800.
14. Y. Lai, X. Kuang, P. Zhu, M. Huang, X. Dong and D. Wang, Adv. Mater., 2018, 30, e1802556.
15. J. Canadell, H. Goossens and B. Klumperman, Macromolecules, 2011, 44, 2536–2541.
16. C. Zhang, H. Liang, D. Liang, Z. Lin, Q. Chen, P. Feng and Q. Wang, Angew. Chem., Int. Ed., 2021, 60, 4289–4299.
17. J. J. Cash, T. Kubo, A. P. Bapat and B. S. Sumerlin, Macromolecules, 2015, 48, 2098–2106.
18. Q. Wu, H. Xiong, Y. Zhu, X. Ren, L.-L. Chu, Y.-F. Yao, G. Huang and J. Wu, ACS Appl. Polym. Mater., 2019, 2, 699–705.
19. Q. Wu, H. Xiong, Y. Peng, Y. Yang, J. Kang, G. Huang, X. Ren and J. Wu, ACS Appl. Mater. Interfaces, 2019, 11, 19534–19540.
20. Y. Yang, H. Wang, L. Huang, M. Nishiura, Y. Higaki and Z. Hou, Angew. Chem., Int. Ed., 2021, 60, 26192–26198.
21. H. Wang, Y. Yang, M. Nishiura, Y. L. Hong, Y. Nishiyama, Y. Higaki and Z. Hou, Angew. Chem., Int. Ed., 2022, 61, e202210023.
22. H. Wang, Y. Yang, M. Nishiura, Y. Higaki, A. Takahara and Z. Hou, J. Am. Chem. Soc., 2019, 141, 3249–3257.
23. H. Lei, S. Wang, D. J. Liaw, Y. Cheng, X. Yang, J. Tan, X. Chen, J. Gu and Y. Zhang, ACS Macro Lett., 2019, 8, 582–587.
24. M. W. Urban, D. Davydovich, Y. Yang, T. Demir, Y. Zhang and L. Casabianca, Science, 2018, 362, 220–225.
25. D. Davydovich and M. W. Urban, Nat. Commun., 2020, 11, 5743.
26. Y. Liu, T. Chen, Z. Jin, M. Li, D. Zhang, L. Duan, Z. Zhao and C. Wang, Nat. Commun., 2022, 13, 1338.
27. W. Haobing, Y. Yang, M. Nishiura, Y.-L. Hong, Y. Nishiyama, Y. Higaki and Z. Hou, Angew. Chem., Int. Ed., 2022, 134, e202210023.
28. Y. Cao, H. Wu, S. I. Allec, B. M. Wong, D. S. Nguyen and C. Wang, Adv. Mater., 2018, 30, e1804602.
29. R. Verduzco, X. Li, S. L. Pesek and G. E. Stein, Chem. Soc. Rev., 2015, 44, 2405–2420.
30. S. S. Sheiko, B. S. Sumerlin and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 759–785.
31. T. Pelras, C. S. Mahon and M. Mullner, Angew. Chem., Int. Ed., 2018, 57, 6982–6994.
32. G. Xie, M. R. Martinez, M. Olszewski, S. S. Sheiko and K. Matyjaszewski, Biomacromolecules, 2019, 20, 27–54.
33. H. V. Nguyen, Y. Jiang, S. Mohapatra, W. Wang, J. C. Barnes, N. J. Oldenhuis, K. K. Chen, S. Axelrod, Z. Huang, Q. Chen, M. R. Golder, K. Young, D. Suvlu, Y. Shen, A. P. Willard, M. J. A. Hore, R. Gomez-Bombarelli and J. A. Johnson, Nat. Chem., 2022, 14, 85–93.
34. M. Abbasi, L. Faust and M. Wilhelm, Adv. Mater., 2019, 31, e1806484.
35. L. H. Cai, T. E. Kodger, R. E. Guerra, A. F. Pegoraro, M. Rubinstein and D. A. Weitz, Adv. Mater., 2015, 27, 5132–5140.
36. M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501.
37. W. F. Daniel, J. Burdynska, M. Vatankhah-Varnoosfaderani, K. Matyjaszewski, J. Paturej, M. Rubinstein, A. V. Dobrynin and S. S. Sheiko, Nat. Mater., 2016, 15, 183–189.
38. M. Vatankhah-Varnosfaderani, A. N. Keith, Y. Cong, H. Liang, M. Rosenthal, M. Sztucki, C. Clair, S. Magonov, D. A. Ivanov, A. V. Dobrynin and S. S. Sheiko, Science, 2018, 359, 1509–1513.
39. J. Bolton, T. S. Bailey and J. Rzayev, Nano Lett., 2011, 11, 998–1001.
40. X. Shi, Y. Zhang, Y. Tian, S. Xu, E. Ren, S. Bai, X. Chen, C. Chu, Z. Xu and G. Liu, Small Methods, 2021, 5, e2000416.
41. E. Dashtimoghadam, F. Fahimipour, A. N. Keith, F. Vashahi, P. Popryadukhin, M. Vatankhah-Varnosfaderani and S. S. Sheiko, Nat. Commun., 2021, 12, 3961.
42. K. J. Arrington, S. C. Radzinski, K. J. Drummey, T. E. Long and J. B. Matson, ACS Appl. Mater. Interfaces, 2018, 10, 26662–26668.
43. C. Choi, J. L. Self, Y. Okayama, A. E. Levi, M. Gerst, J. C. Speros, C. J. Hawker, J. Read de Alaniz and C. M. Bates, J. Am. Chem. Soc., 2021, 143, 9866–9871.
44. M. Vatankhah Varnosfaderani, S. Sheiko, K. Matyjaszewski, W. F. Daniel, Q. Li, B. Morgan and R. J. Spontak, presented in part at the Proc. SPIE 10163, Portland, Oregon, United States, 2017.
45. J. L. Self, C. S. Sample, A. E. Levi, K. Li, R. Xie, J. R. de Alaniz and C. M. Bates, J. Am. Chem. Soc., 2020, 142, 7567–7573.
46. Y. Chen, A. M. Kushner, G. A. Williams and Z. Guan, Nat. Chem., 2012, 4, 467–472.
47. D. Mozhdehi, S. Ayala, O. R. Cromwell and Z. Guan, J. Am. Chem. Soc., 2014, 136, 16128–16131.
48. H. Xiong, L. Zhang, Q. Wu, H. Zhang, Y. Peng, L. Zhao, G. Huang and J. Wu, J. Mater. Chem. A, 2020, 8, 24645–24654.
49. Y. Fang, T. Yue, S. Li, Z. Zhang, J. Liu and L. Zhang, Macromolecules, 2021, 54, 1095–1105.
50. Y. Cong, M. Vatankhah-Varnosfaderani, V. Karimkhani, A. N. Keith, F. A. Leibfarth, M. R. Martinez, K. Matyjaszewski and S. S. Sheiko, Macromolecules, 2020, 53, 8324–8332.
51. H. Liang, B. J. Morgan, G. Xie, M. R. Martinez, E. B. Zhulina, K. Matyjaszewski, S. S. Sheiko and A. V. Dobrynin, Macromolecules, 2018, 51, 10028–10039.
52. H. Liang, Z. Wang, S. S. Sheiko and A. V. Dobrynin, Macromolecules, 2019, 52, 3942–3950.
53. M. Vatankhah-Varnoosfaderani, W. F. Daniel, A. P. Zhushma, Q. Li, B. J. Morgan, K. Matyjaszewski, D. P. Armstrong, R. J. Spontak, A. V. Dobrynin and S. S. Sheiko, Adv. Mater., 2017, 29, 1604209.
54. R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823–826.
55. J. Chen, Y. Gao, L. Shi, W. Yu, Z. Sun, Y. Zhou, S. Liu, H. Mao, D. Zhang, T. Lu, Q. Chen, D. Yu and S. Ding, Nat. Commun., 2022, 13, 4868.
56. D. J. Hourston and F.-U. Schäfer, Polym. Adv. Technol., 1996, 7, 273–280.
57. L. Zhang, H. Wang, Y. Zhu, H. Xiong, Q. Wu, S. Gu, X. Liu, G. Huang and J. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 53239–53246.
58. A. V. Kaliyathan, A. V. Rane, M. Huskic, M. Kunaver, N. Kalarikkal, D. Rouxel and S. Thomas, Compos. Sci. Technol., 2020, 200, 108484.
59. S. Shan, X. Wu, Y. Lin and A. Zhang, ACS Appl. Polym. Mater., 2022, 4, 7554–7563.
60. W. Zhao, M. Li and H.-X. Peng, Macromol. Mater. Eng., 2010, 295, 838–845.
61. J. Huang, Y. Xu, S. Qi, J. Zhou, W. Shi, T. Zhao and M. Liu, Nat. Commun., 2021, 12, 3610.
62. S. F. Edwards, Proc. Phys. Soc., London, 1967, 91, 513–519.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00274h

‡ These authors contributed equally to this work and should be considered as co-first authors.

---