A role of intermolecular interaction modulating thermal diffusivity in organosuperelastic and organoferroelastic cocrystals

Abstract

Although the finding of superelasticity and ferroelasticity in organic crystals has been serendipitous, an increasing number of organic crystals with such deformation properties have been witnessed. Understanding the structure–property relationship can aid in the rational selection of intermolecular interactions to design organic crystals with desired superelastic or ferroelastic properties. In this study, we investigated the mechanical deformation in two cocrystals, prepared with the parent compound, 1,4-diiodotetrafluorobenzene with two coformers, 1,2-bis(4-pyridyl)ethane and pyrene. The parent compound and coformers were chosen to introduce distinct weak interactions such as halogen bonds and C–H⋯F, and π⋯π interactions in the crystal structure. The two cocrystals exhibited different mechanical deformations, superelasticity, and ferroelasticity, respectively. The single-crystal X-ray diffraction and energy framework analysis of the crystal structure of the cocrystals revealed that both deformations were caused by mechanical twinning. Interestingly, a difference in the extent of deformation was observed, modulated by a combination of strong and weak intermolecular interactions in the superelastic cocrystal, and only weak interaction in the ferroelastic one. In this comparison, the superelastic cocrystal exhibited higher thermal diffusivity than the ferroelastic cocrystal, indicating the presence of symmetrical and relatively robust intermolecular interactions in the superelastic cocrystal.

---

Introduction

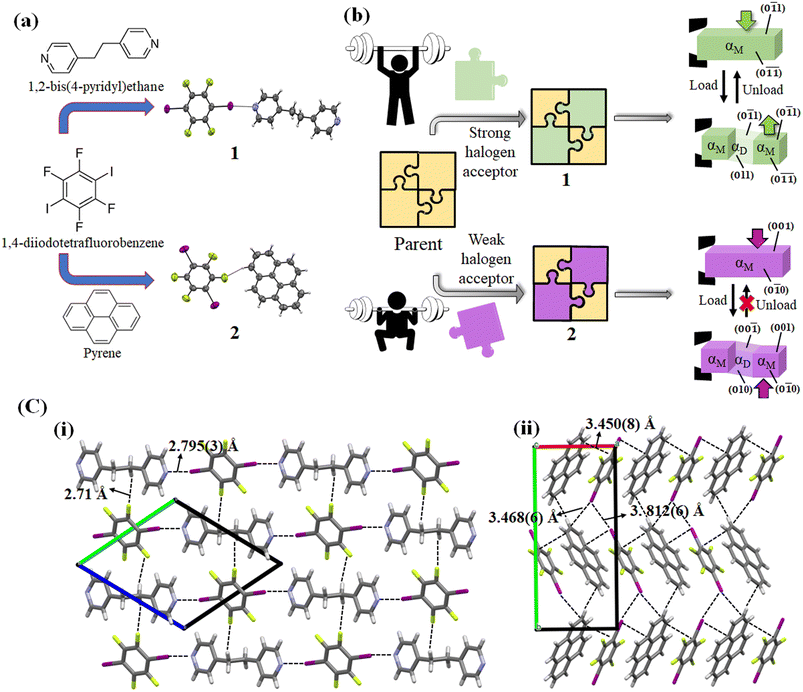
Over the last decade, distinct mechanical deformation behavior in organic molecular crystals has been reported, thereby making them a prospective candidate as next-generation structural materials for actuators,¹ multi-stimuli responsive sensors,² optical waveguides,³ and soft robotics.⁴ Organic molecular crystals have been found to exhibit several mechanical deformation behaviors such as elastic and plastic bending,^5–7 light-induced bending,^8,9 superelasticity,^10–12 ferroelasticity,^13,14 superplasticity,¹⁵ shape memory effect,^16,17 and many more. Superelastic and ferroelastic organic molecular crystals stand out as excellent and superior candidates in materials science due to their reversibility and diffusionless transformation behavior. Although both superelastic and ferroelastic deformations exhibit diffusionless transformation, the reversibility manner of the shape restoration differs. In superelastic deformation, the shape recovery is simply attained by removal of the applied force,¹⁰ whereas in ferroelastic deformation, the shape change due to spontaneous strain is regained by application of force in the opposite direction to that of the deformation direction.¹³ Digging into the mechanism, superelastic deformation is enabled by martensitic transformation,¹⁰ whereas ferroelastic deformation is manifested by twinning deformation.¹⁸ Recently, twinning has been found to be the common cause for both superelastic and ferroelastic deformation in organic crystals.^11,19

While many organic molecular crystals exhibiting superelastic and ferroelastic deformation have been reported in recent years, a rational approach for designing and obtaining the desired superelastic and ferroelastic deformation is lacking.^10–13,20 For crystal structure designing with novel properties, a detailed understanding of various strong and weak molecular interactions is essential to modify the strength and geometry of intermolecular interactions. A thorough analysis showed that different crystal structures with polar space groups and weak intermolecular interactions such as weak hydrogen bonding, halogen bonding, and van der Waals interactions contribute to superelastic or ferroelastic deformation.^20–22 The influence of weak intermolecular interactions involving halogen groups such as an aromatic C–F group,^23–26 and halogen–halogen^27,28 and π stacking interactions^29–31 on directing the crystal packing in the presence or absence of strong hydrogen bonds has been extensively studied, and can serve as an excellent tool for crystal designing. Li et al. suggested that such crystals could be designed by considering the orientational change of molecules caused by twinning in superelastic and ferroelastic deformation.³² They prepared a cocrystal composed of 3,5-dimethylbenzoic acid and 4,4′-bipyridine bonded by an acid-pyridine hetero-synthon and resembling an organic trimer, which demonstrated a bidirectional superelastic deformation through a 90° rotation of the aromatic plane of 4,4′-bipyridine.³² In our previous report about the shape memory effect of 1,2-bis(4pyridyl)ethane dodecafluorosuberate,¹⁷ we realized that the introduction of weak dispersive interactions like C–F⋯π, and C–H⋯F in the crystal structure changed the deformation behavior from biased ferroelastic³³ to the shape memory effect (interconversion of superelastic to ferroelastic). In this case, this weak dispersion interaction combined with strong hydrogen bonding N⁺–H⋯O⁻ contributed to the shape memory effect with an increased critical forward stress value. Thalladi et al. mentioned that C–H⋯F interactions could be exploited to construct desirable organic crystals as compared to well-known C–H⋯O and C–H⋯N interactions owing to their ability to stabilize the crystal structures.³⁴ Additionally, Jain et al. demonstrated the role of halogen bonds in synthesizing higher-order cocrystals and further established that halogen bonds can exhibit analogous behavior to hydrogen bonds.³⁵ Mukherjee and Desiraju previously indicated that the strength of halogen bonds can manifest in elastic or plastic bending in organic crystals.³⁶ Thus, halogen bond-mediated/directed synthesis of a supramolecular assembly could be a possible way to design organic molecular crystals with desired superelastic and ferroelastic deformation. Variations in the strength of halogen bonds with excellent directionality³⁷ and other weak dispersive interactions³⁸ can manipulate the spontaneous strain generation required for ferroelastic deformation and spontaneous shape recovery in a superelastic deformation.

In addition to developing the designing principles for superelastic and ferroelastic deformation, studying the anisotropic thermal transport properties of these materials such as thermal diffusivity would be insightful owing to the range of thermal management applications of these crystals.^39,40 Previous studies have reported that the anisotropic mechanical properties of soft materials in response to high frequency can be correlated with thermal diffusivity.^41,42 Studying the anisotropic thermal properties in ferroelastic and superelastic organic crystals would be beneficial to understand the manner of heat transport with respect to their structural order. Furthermore, the reversible phase transition properties of these crystals in response to mechanical stress can be utilized as thermal switches.^43,44 The micro-level miniaturization of the integrated devices demands efficient flexibility and thermal management, which can be fulfilled by the controlled deformation behavior of these crystals and used as wearable devices.^45–47 It has been demonstrated that inorganic ferroelastic materials can be utilized for thermal management applications.^44,48–50 Sieradzki et al. studied the changes in the thermal conductivity of Li₂TiGeO₅ ceramics in the ferroelastic phase transition or domain formation.⁵⁰ Wang et al. reported the difference in thermal conductivity values of layered PdSe₂ before and after ferroelastic phase transition by uniaxial compression and demonstrated that the high ratio of the switchable thermal conductivity value between the two phases could be utilized for flexibility and thermal management.⁴⁴ However, there is only one study concerning the measurement of anisotropic heat transport properties in a superelastic organic crystal due to the limited approaches/techniques to measure the thermal diffusivity of organic crystals.⁴⁰

Keeping these considerations in mind, we attempted to prepare single crystals of two cocrystals consisting of a weak halogen bond donor and acceptor, where 1,4-diiodotetrafluorobenzene served as the halogen donor. It produced cocrystals with the halogen acceptor 1,2-bis(4-pyridyl)ethane (cocrystal 1) and pyrene (cocrystal 2), respectively. Different deformation behaviors, i.e., superelastic and ferroelastic deformation, were observed in 1 and 2, respectively. The anisotropic thermal diffusivity values of the two cocrystals were measured by typical microscale temperature-wave analysis (μ-TWA). A difference in the combination of relatively strong halogen interactions (C–I⋯N) and weak interactions (C–H⋯F and π⋯π) in the crystal structure of the two cocrystals could be responsible for the different mechanical deformations and thermal diffusivity behaviors.

Results and discussion

Single crystal synthesis and characterization

For cocrystal preparation, a halogen bond donor, 1,4-diiodotetrafluorobenzene was selected as the parent compound. In previous studies, 1,4-diiodotetrafluorobenzene has been utilized to prepare supramolecular structures owing to its ability to form a range of interactions, including C–I⋯N, C–H⋯F, and π⋯π.⁵¹ Such weak C–H⋯F, C–F⋯π interactions can form crystal packing even in the absence of strong hydrogen bonds.⁵² Furthermore, the C–I⋯N interactions have been demonstrated to be strong and directional to facilitate the self-assembly of a 1D infinite network, and other interactions such as C–H⋯F and π⋯π enable the formation of a 3D network.⁵³ In addition, Corradi et al. noted that the halogen bonding of 1,4-diiodotetrafluorobenzene was significantly accountable for the supramolecular structure formation with 1,2-bis(4-pyridyl)ethane and hydroquinone compared to hydrogen bonding.⁵¹ In order to manipulate the weak interactions in the crystal structure, two coformers of 1,2-bis(4-pyridyl)ethane and pyrene were selected on the basis of halogen bond acceptor strength. 1,2-Bis(4-pyridyl)ethane acts as a strong halogen acceptor due to the electron rich nitrogen atom, while pyrene acts as a weak halogen acceptor due to the absence of an electron rich group in its structure.

The colorless block shape single crystals of cocrystal 1 were obtained by slow evaporation of a dichloromethane solution of 1,4-diiodotetrafluorobenzene and 1,2-bis(4-pyridyl)ethane mixed at a molar ratio of 1 : 1.⁵⁴ The single crystal of cocrystal 1 crystallizes in a triclinic crystal system with space group P1̄. The molecules formed an infinite 1D chain via the C–I⋯N (4.898(4) Å, 175.6°) halogen bonds with d(I1⋯N1) = 2.795(3) Å in an ABAB manner along the a axis. Furthermore, weak C–H⋯F hydrogen bonds connect the nearby 1D chains to create a three-dimensional crystal structure along the bc plane (Fig. 1 and Table S1, ESI†).

Fig. 1 (a) Molecular structures and formation of cocrystals 1 and 2, (b) illustration of the difference in the mechanical deformation of interest, and (c) crystal structures of (i) cocrystal 1 along the bc plane and (ii) cocrystal 2 along the a axis.

On the other hand, the colorless block-shaped single crystals of cocrystal 2 were obtained by slow evaporation of an ethanolic solution of 1,4-diiodotetrafluorobenzene and pyrene mixed in a molar ratio of 1 : 1.⁵⁵ The single crystals of 2 crystallize in a monoclinic crystal system with space group P2₁/c. The single crystal of cocrystal 2 formed a column-like structure via π–π stacking in an A⋯B⋯A⋯B⋯ face-to-face manner along the a axis with an interplanar distance of 3.450 Å. Furthermore, the adjacent columns are linked together by C–I⋯I–C (3.812(6) Å) interactions along the b axis (Fig. 1 and Table S1, ESI†). The shortest C–H⋯F interactions (2.56 Å, 145.05°) were found along the c axis, stabilizing the crystal structure of 2. The structures of cocrystals 1 and 2 along with their deformation behaviors are illustrated in Fig. 1.

Microscopic observation

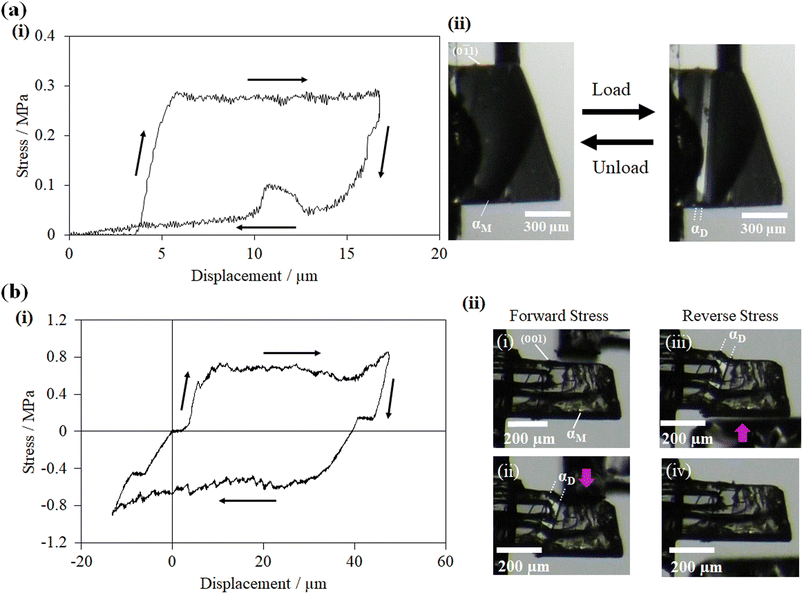
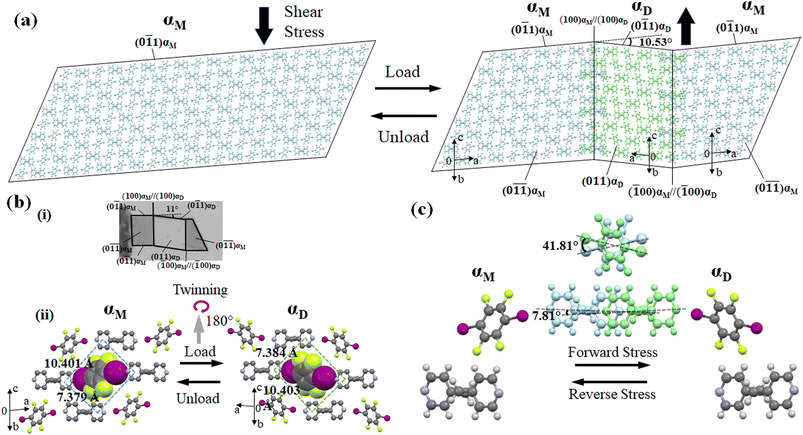
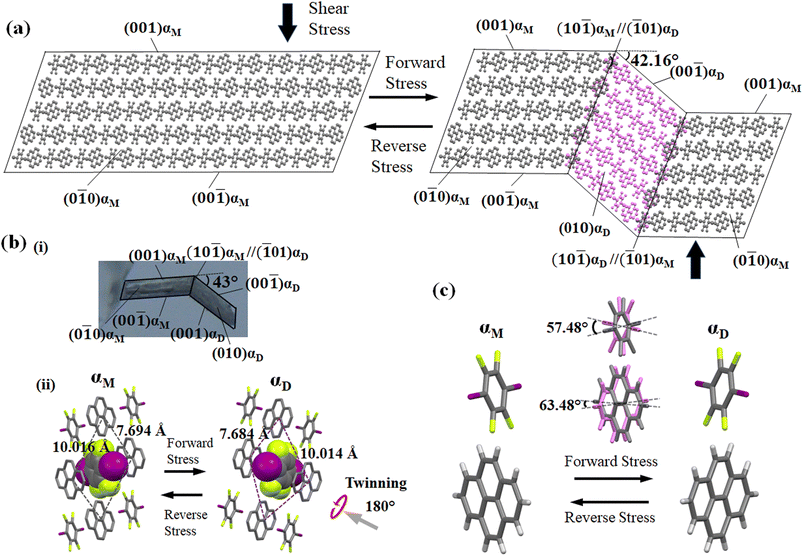
For studying the shear deformation behavior at a macroscopic level, mechanical shear stress on both the single crystals of 1 and 2 was applied independently at room temperature under a polarized microscope on the (01̄1) plane and (001) plane, respectively (Fig. 1(b)). An application of shear stress on the (01̄1) plane of single crystals of 1 caused a superelastic deformation (Fig. 2(a)). The superelastic deformation was initiated by the appearance of a stress-induced twinning domain (α_D) generated from the mother crystal (α_M) with a distinct boundary line at a bending angle of 11°. The deformed crystal was recovered to its original shape after the applied force was removed. On the other hand, single crystals of 2 showed a ferroelastic deformation on the application of shear stress on the (001) plane (Fig. 2(b)). A bending angle of 43° was demonstrated with the growth of daughter domains (α_D) from the mother domain (α_M) in the single crystal of 2, and a spontaneous strain was accumulated as residual strain until the removal of the force. Furthermore, on application of reverse force on the (001̄) plane, the daughter domain returned to its initial orientation, confirming the ferroelasticity.

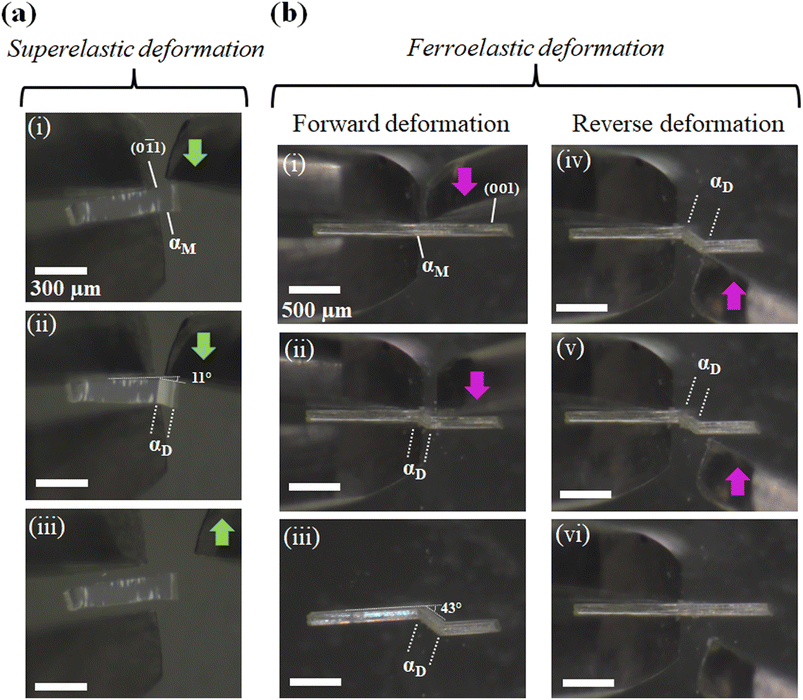Fig. 2 Microscope observation with tweezers at room temperature: (a) superelastic deformation of cocrystal 1 and (b) ferroelastic deformation of cocrystal 2.

Mechanical deformation analysis

The stress–strain relationship between cocrystals 1 and 2 was investigated by using a custom-designed setup: the shear force was applied with a jig to the specific crystal plane of the crystal fixed to a glass plate with epoxy glue. In a single crystal specimen of 1, the α_D domain started to grow from the α_M domain at an applied stress of 0.27 MPa on the (01̄1) plane. At a critical stress of 0.27 MPa, the stress-induced twinning phase transformation (α_D) propagated, and the stress–strain curves displayed a characteristic plateau resembling a superelastic deformation (Fig. 3(a)). The original shape was regained by decreasing the stress in depicting the typical superelastic stress–strain hysteresis loop, validating the superelastic deformation. On the other hand, with the gradual increase of stress on the (001) plane of the single crystal of 2, the α_D domain was generated at a coercive stress of 0.58 MPa, which was fairly steady. Furthermore, by applying a shear stress of 0.57 MPa force from the opposite direction, the α_D domain was reverted to the α_M domain with the corresponding release of the spontaneous strain. The hysteresis loop was established in the shear displacement graph, which is the confirmatory indicator of ferroelastic deformation (Fig. 3(b)). The observed stress strengths are similar to those of organosuperelastic/organoferroelastic crystals previously reported.^13–19

Fig. 3 Shear-strain test: (a) the superelastic hysteresis loop of the cocrystal of 1 (i) and snapshots during measurement (ii) and (b) the ferroelastic hysteresis loop of the cocrystal of 2 (i) and snapshots (ii).

Thermal diffusivity studies

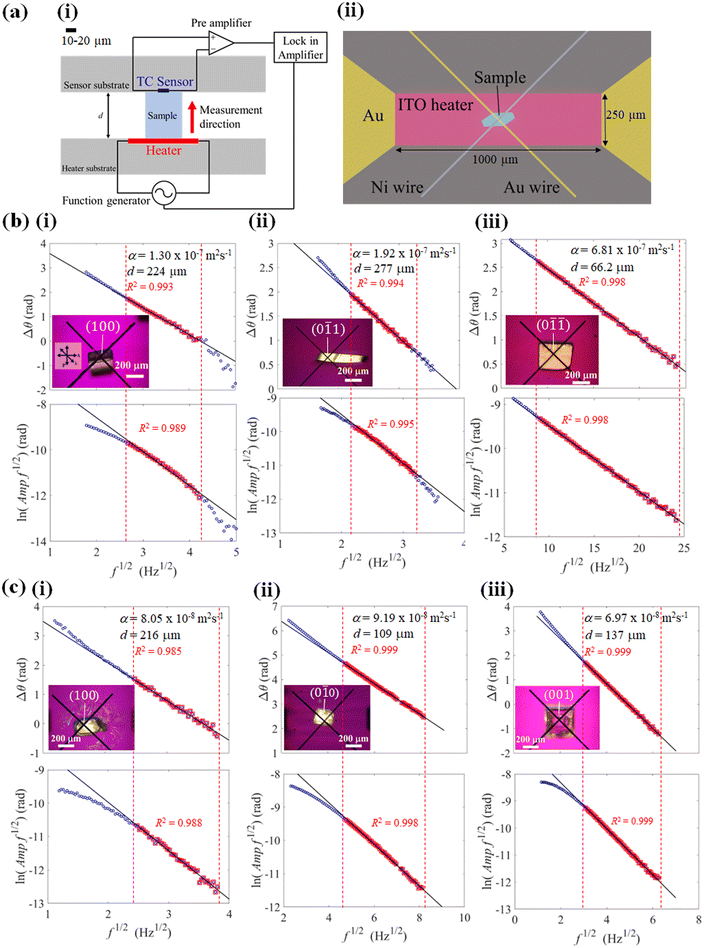
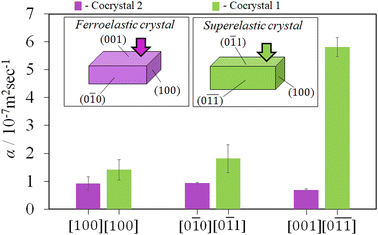
Thermal diffusivity is a specific property of materials related to the rate of thermal energy transfer through it. Determination of the thermal diffusivity value of the crystals would aid in understanding the heat transfer properties and their applicability in thermal management. In addition, it can also assist in understanding the changes in the thermal properties due to the structure, phase transitions, defects, etc. The anisotropic thermal diffusivity measurement of single crystals 1 and 2 were performed by μ-TWA measurements⁴⁰ along its longer, wider, and thinner axis. The frequency change in the phase delay of the temperature wave was obtained for the three crystallographic axes of the crystals (Fig. 4, S1, S2, and Tables S2, S3, ESI†).

Fig. 4 The frequency dependency of the phase delay measured for cocrystals 1 and 2 (a) schematic depiction of the experimental setup from the (i) cross-sectional view and (ii) top-view. The synchronized function generator and the lock-in amplifier determined the periodic heating and detection of the periodic temperature response from the sample as a phase delay. (b) (i), (ii), and (iii) cocrystals of 1 placed along its longer, wider and thinner axes corresponding to the [100], [01̄1] and [01̄1̄] directions, respectively, and (c) (i), (ii), and (iii) cocrystals of 2 placed along its longer, wider and thinner axes corresponding to the [100], [01̄0], and [001] directions, respectively. The inset shows the optical image of each sample under a crossed-Nicols with a sensitive plate (530 nm wave plate) taken by using a polarized microscope (top view).

From the measured data, the slope of the high-frequency region, which was decided according to the linearity of both phase and amplitude data, was used to determine the thermal diffusivity. In single crystals of 1, the measured thermal diffusivity was found to be the highest 6.30 × 10⁻⁷ m² s⁻¹ along the [01̄1̄] direction followed by, 2.04 × 10⁻⁷ m² s⁻¹ along the [01̄1] direction, and 1.12 × 10⁻⁷ m² s⁻¹ along the [100] direction (Fig. 5, S1, and Table S2, ESI†). In contrast, the thermal diffusivity of the ferroelastic crystal was similar along the [01̄0] direction and [100] directions (0.93 × 10⁻⁷ m² s⁻¹). However, a lower thermal diffusivity was observed along the [001] direction (0.69 × 10⁻⁷ m² s⁻¹) which is the shear stress deformation direction of cocrystal 2 (Fig. 5, S2, and Table S3, ESI†). The highest obtained thermal diffusivity along the [01̄0] direction in the ferroelastic crystal was almost 7-fold lower compared to that of superelastic crystal along the [01̄1̄] direction. In addition, the thermal diffusivity value of both the crystals was low in the direction of applied shear stress along [01̄1] of 1 and [001] of 2 compared to their orthogonal directions. Furthermore, the thermal diffusivity values in the daughter domains of cocrystals 1 and 2 were found to increase by 17% (7.38 × 10⁻⁷ m² s⁻¹) and 7% (0.99 × 10⁻⁷ m² s⁻¹) along the [01̄0] and [01̄1̄] directions of 1 and 2, respectively (Fig. S3, Table S4, ESI†). The switchable thermal diffusivity values of the mother and daughter domains indicate the potential for a thermal switch application of these crystals.

Fig. 5 The obtained thermal diffusivity values of cocrystals 1 (light green colored) and 2 (purple colored) with respect to the longer, wider, and thinner axes, respectively. Arrows indicate the direction of shear stress deformations.

Crystallographic studies

The underlying mechanism behind the different deformation behaviors of cocrystals 1 and 2 were investigated by single-crystal XRD analyses of the deformed crystals of 1 and 2. The cocrystal of 1 crystallizes in a triclinic crystal system with the space group P1̄. On the other hand, the cocrystal of 2 crystallizes in a monoclinic crystal system with space group P2₁/c. Both the crystal structures were similar to the previously reported one.^51,55 XRD investigations of 1 and 2 using face indexing revealed that the shear-induced twinning deformation initiated the development of the daughter crystal domain (α_D) from the mother crystal domain (α_M) upon application of shear stress on the (01̄1) and (001) planes, respectively (Fig. 6, 7, S4 and Table S1, ESI†). According to crystallographic investigations, the twinning interfaces of cocrystals 1 and 2 are located at (100)α_M/(100)α_D and (101̄)α_M/(1̄01)α_D, respectively, which are perpendicular to the stacked column. A 180° rotation about the rotation axis was associated with the mother domain and daughter domains. This relationship is attributed to the polar P1̄ and P2₁/c point group symmetry, which caused the molecules to tilt by 41.81° of the 1,4-diiodotetrafluorobenzene molecule and 7.81° of 1,2-bis(4-pyridyl)ethane molecule in the case of cocrystal 1, and 57.48° of the 1,4-diiodotetrafluorobenzene molecule and 63.48° of the pyrene molecule in the case of cocrystal 2, instead of the actual 180° rotation (Fig. S4, ESI†). 1,4-diiodotetrafluorobenzene interacted through C–I⋯N and C–H⋯F interactions with the nearby molecules in crystal structure 1, where it is surrounded by four 1,2-bis(4-pyridyl)ethane molecules in a rhomboid configuration with sides of 10.401 Å and 7.379 Å (Fig. 6(b)(ii)). 1,4-diiodotetrafluorobenzene was rotated by 41.81° in relation to its mother domain configuration due to the twinning orientational change. As a result, the crystal structure is balanced and has a configuration analogous to a rhomboid arrangement rotated by 90° in the daughter phase with sides of 7.384 Å and 10.403 Å. Similar observations were seen for cocrystal 2, which also resembled a tunable rhomboid structure with sides of 10.016 Å and 7.694 Å in the mother domain and 7.684 Å and 10.014 Å in the daughter domain (Fig. 7(b)(ii)).

Fig. 6 (a) Estimated connecting manners of the α_M domain and α_D domain based on the X-ray diffraction measurements of single crystal 1. (b) Face indexing of the superelastic bent crystal used for SCXRD (i) and estimated twinning manners of the α_D domain based on the α_M domain (ii). (c) Estimated molecular movements at the interface at (100)α_M//(100)α_D (light blue and light green colored molecules indicate the α_M and α_D domains, respectively).

Fig. 7 (a) Estimated connecting manners of the α_M domain and α_D domain based on the X-ray diffraction measurements of single crystal 2. (b) (i) Face indexing of the ferroelastic bent crystal used for SCXRD. (ii) Estimated twinning manners of the α_D domain based on the α_M domain. (c) Estimated molecular movements at the interface at (101̄) α_M/(1̄01)α_D. Light gray and light purple colored molecules indicate the α_M and α_D domains, respectively.

Although mechanical twinning manifested superelastic and ferroelastic deformations in both crystals, the deformation produced a different bending angle and dissipated energy (E_d). A bending angle of 10.53° between α_M and α_D can be anticipated based on crystallographic results in cocrystal 1, and this angle aligned well with the 11° bending angle that was measured by optical microscopy. However, the bending angle was higher by 32° in the case of cocrystal 2 compared to cocrystal 1, which was estimated to be 42.16° by crystallographic analysis and 43° by optical microscopy. Due to the molecular movement by such a large angle, significant coercive stress was observed during the daughter domain development in ferroelastic deformation. Furthermore, the lower tilt angle of molecules in the case of molecule 1 could be due to the presence of relatively strong and ordered C–I⋯N (4.898(4) Å, 175.6°) halogen interactions, and the stable twisted chair form of bipyridine moieties which would stabilize the crystal during the application of stress.

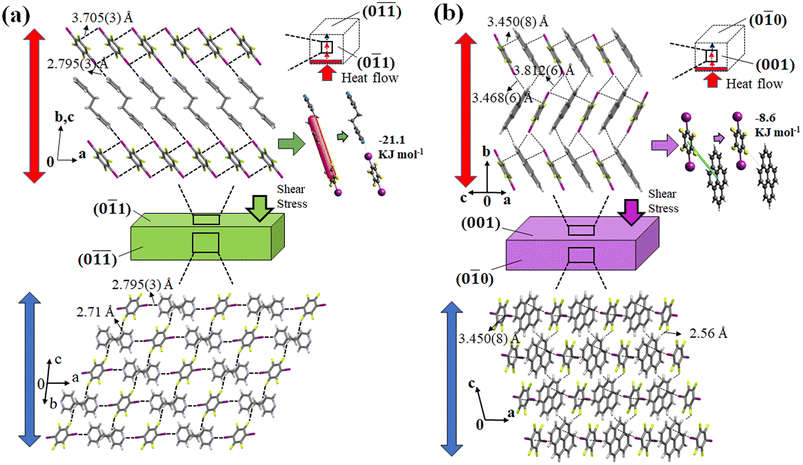
In cocrystal 1, the strong C–I⋯N halogen bond is clarified by the shorter I–N (2.795(3) Å) distance compared to other bipyridine-based halogen bonded complexes, relating to the two distantly placed twisted chair forms of the bipyridine rings in the structure. The strong C–I⋯N halogen-bonded interactions and weak C–H⋯F (3.528(3) Å, 141.98° (F1⋯H6a (2.71 Å))) hydrogen-bonded interactions in cocrystal 1 can make its crystal packing robust compared to cocrystal 2 (Fig. 8(a)).

Fig. 8 Crystal packing with the 3D topology of energy frameworks of cocrystal 1 (i) and 2 (ii). Red and blue colored bidirectional arrows indicate the highest and lowest thermal diffusivity direction of cocrystals 1 and 2, respectively. Red and green colored tubes indicate the electrostatic and dispersion energy, respectively.

In cocrystal 2, C–I/I–C (d(I–I) 3.812(6) Å) interactions hold the parallel-placed columns together. The connectivity between columns appears to be strengthened by C–I⋯π (3.468(6) Å) halogen bonding and C–H⋯F (3.367(5) Å, 145.05°) interactions d(F1⋯H19) = 2.56 Å to maintain the 3D crystal structure (Fig. 8(b)).

Correlation of anisotropic structural arrangement with mechanical behavior and thermal diffusivity

Since cocrystals 1 and 2 have a diversity of contacts, including halogen, π⋯π, and C–H⋯F interactions, it can be anticipated that the forces retaining them are diverse in strength. Hirshfeld surface analysis was utilized to evaluate the relative efficacy of the competing weak hydrogen bonding, π⋯π, and halogen-bonding interactions (Fig. S5, ESI†). Short interactions were discovered to be distinct in the mother phase of cocrystals 1 and 2. In cocrystal 1, the F⋯H (34.6%) interaction was found to be the highest interaction supporting the three-dimensional structure, followed by I⋯H (9.8%), C⋯I (9.1%), and I⋯N (4.7%) interactions. Nevertheless, the contributions of all interactions changed in cocrystal 2. However, F⋯H (23.4%) interaction was also seen to be the highest in cocrystal 2 followed by I⋯H (15.3%) and C⋯C (11.8%) interactions. It can be inferred that the halogen and weak hydrogen bond interactions play a significant role in determining the crystal structure of 1. On the other hand, weak hydrogen bonds and π⋯π interactions play a crucial role in maintaining the crystal structure of 2. Furthermore, energy framework analysis suggests that the C–I⋯N halogen interaction in cocrystal 1 is a strong, electrostatically dominant interaction with an energy of −21.1 kJ m⁻¹ that holds the structure together with weak C–H⋯F interactions (Fig. 8(a) and S6, ESI†). In contrast, weak electrostatic C–I/C–I interactions were found to be accompanied by the presence of the dispersion-dominated C–H⋯F and π⋯π interactions in cocrystal 2, which have a −8.6 kJ mol⁻¹ energy along the ac plane (Fig. 8 and S7, ESI†). The comparatively stronger interactions such as C–I⋯N, C–I, and C–H⋯F in cocrystal 1 could have promoted the superelastic deformation rather than ferroelastic deformation. Furthermore, the C–I⋯N halogen interaction tapes that make 2D sheets with the help of C–H⋯F interactions grow along the [01̄1̄] direction in a symmetrical stack in cocrystal 1. This could be the reason for the highest thermal diffusivity along the [01̄1̄] direction where the robust, strong, and electrostatically dominated C–I⋯N halogen bonds determine the thermal diffusivity value. In contrast, dispersion dominated C–I/C–I and π⋯π interactions contained in cocrystal 2 resulted in its lower thermal diffusivity than that of cocrystal 1.

Conclusions

In conclusion, we presented two cocrystals consisting of (1,2-bis(4-pyridyl)ethane and 1,4-diiodotetrafluorobenzene), and (pyrene and 1,4-diiodotetrafluorobenzene), which are denoted as 1 and 2, respectively. Cocrystals 1 and 2 demonstrated superelastic and ferroelastic deformations, respectively. From the crystal structure analysis, the underlying cause of the deformation was found to be mechanical twinning. The difference in the deformation behavior was discussed through the distinct combination of strong halogen bonds, such as C–I⋯N and C⋯I, and weak interactions, such as C–H⋯F and π⋯π interactions in the cocrystal structures. The thermal diffusivity measurements on the ferroelastic and superelastic crystals showed the axial-dependent anisotropic thermal diffusivity of the cocrystals. A 7-fold difference in thermal diffusivity was observed in superelastic crystal 1, the highest in the orthogonal plane to the shear-induced direction, whereas in crystal 2 the axial dependence was less pronounced. This study provides insights into the interplay with the variation of inter-molecular interactions in organosuperelastic and organoferroelastic behavior and the way for further design and regulation of functional organic solids with thermo-mechanical properties.

Data availability

All experimental, thermal diffusivity, and crystallographic data are available in the ESI.†

Author contributions

S. R. carried out the experiments, analyzed the results, and composed the manuscript. R. M., M. R., and J. M. conducted thermal diffusivity investigations. J. M. and S. T. organized the project and edited the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

Funding was provided by MEXT KAKENHI Grants, Numbers JP22K14200 for M. R., JP22H02137 for J. M., JP22K18333 and JP22H00318 for S. T. and J. M. M. R. acknowledge partial support of this work by JST CREST Grant Number JPMJCR19I3, Japan. S. R. thanks the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) for providing an MEXT fellowship.

References

1. L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Martensitic organic crystals as soft actuators, Chem. Sci., 2019, 10, 7327–7332.
2. M. Xie, K. Hisano, M. Zhu, T. Toyoshi, M. Pan, S. Okada, O. Tsutsumi, S. Kawamura and C. Bowen, Flexible multifunctional sensors for wearable and robotic applications, Adv. Mater. Technol., 2019, 4, 1800626.
3. B. Tang, X. Yu, K. Ye and H. Zhang, Manifold mechanical deformations of organic crystals with optical waveguiding and polarization rotation functions, Adv. Opt. Mater., 2022, 10, 2101335.
4. H. Koshima, T. Taniguchi and T. Asahi, Mechanically responsive crystals by light and heat, in Mechanically Responsive Materials for Soft Robotics, 2020, pp. 57–82.
5. S. Ghosh and C. M. Reddy, Elastic and bendable caffeine cocrystals: implications for the design of flexible organic materials, Angew. Chem., Int. Ed., 2012, 51, 10319–10323.
6. R. Samanta, S. Das, S. Mondal, T. Alkhidir, S. Mohamed, S. P. Senanayak and C. M. Reddy, Elastic organic semiconducting single crystals for durable all-flexible field-effect transistors: insights into the bending mechanism, Chem. Sci., 2023, 14, 1363–1371.
7. G. R. Krishna, R. Devarapalli, G. Lal and C. M. Reddy, Mechanically flexible organic crystals achieved by introducing weak interactions in structure: supramolecular shape synthons, J. Am. Chem. Soc., 2016, 138, 13561–13567.
8. R. O. Al-Kaysi and C. J. Bardeen, Reversible photoinduced shape changes of crystalline organic nanorods, Adv. Mater., 2007, 19, 1276–1280.
9. J. K. Sun, W. Li, C. Chen, C. X. Ren, D. M. Pan and J. Zhang, Photoinduced bending of a large single crystal of a 1,2-bis(4-pyridyl) ethylene-based pyridinium salt powered by a [2 + 2] cycloaddition, Angew. Chem., Int. Ed., 2013, 125, 6785–6789.
10. S. Takamizawa and Y. Miyamoto, Superelastic organic crystals, Angew. Chem., Int. Ed., 2014, 126, 7090–7093.
11. S. Takamizawa and Y. Takasaki, Superelastic Shape Recovery of Mechanically Twinned 3, 5-Difluorobenzoic Acid Crystals, Angew. Chem., Int. Ed., 2015, 127, 4897–4899.
12. H. Sun, S. K. Park, Y. Diao, E. P. Kvam and K. Zhao, Molecular mechanisms of superelasticity and ferroelasticity in organic semiconductor crystals, Chem. Mater., 2021, 33, 1883–1892.
13. S. H. Mir, Y. Takasaki, E. R. Engel and S. Takamizawa, Ferroelasticity in an organic crystal: a macroscopic and molecular level study, Angew. Chem., Int. Ed., 2017, 56, 15882–15885.
14. S. Ranjan and S. Takamizawa, Two-dimensional organoferroelasticity in a single crystal of 4-iodoaniline, Cryst. Growth Des., 2022, 22, 1831–1836.
15. S. Takamizawa, Y. Takasaki, T. Sasaki and N. Ozaki, Superplasticity in an organic crystal, Nat. Commun., 2018, 9, 3984.
16. S. Takamizawa and Y. Takasaki, Shape-memory effect in an organosuperelastic crystal, Chem. Sci., 2016, 7, 1527–1534.
17. S. Ranjan, H. Honda and S. Takamizawa, Thermo-mechanical reversibility in a shape memory organic salt, J. Mater. Chem. C, 2022, 10, 12765–12775.
18. E. R. Engel and S. Takamizawa, Versatile ferroelastic deformability in an organic single crystal by twinning about a molecular zone axis, Angew. Chem., Int. Ed., 2018, 57, 11888–11892.
19. T. Sasaki, S. Sakamoto, Y. Takasaki and S. Takamizawa, A Multidirectional Superelastic Organic Crystal by Versatile Ferroelastical Manipulation, Angew. Chem., Int. Ed., 2020, 132, 4370–4373.
20. S. K. Park, H. Sun, H. Chung, B. B. Patel, F. Zhang, D. W. Davies, T. J. Woods, K. Zhao and Y. Diao, Super-and ferroelastic organic semiconductors for ultraflexible single-crystal electronics, Angew. Chem., Int. Ed., 2020, 132, 13104–13112.
21. S. Ranjan and S. Takamizawa, Characterization of Organoferroelasticity in a TEMPO Crystal, Cryst. Growth Des., 2021, 22, 585–589.
22. T. Seki, C. Feng, K. Kashiyama, S. Sakamoto, Y. Takasaki, T. Sasaki, S. Takamizawa and H. Ito, Photoluminescent ferroelastic molecular crystals, Angew. Chem., Int. Ed., 2020, 59, 8839–8843.
23. M. D. Prasanna and T. N. Guru Row, C–halogen⋯π interactions and their influence on molecular conformation and crystal packing: A database study, Cryst. Eng., 2000, 3, 135–154.
24. M. D. Prasanna and T. N. Guru Row, Analysis of weak interactions involving fluorine: a comparative study of crystal packing of some benzodiazepinone drug intermediates and their non-fluorinated analogues, CrystEngComm, 2000, 2, 134–140.
25. D. Chopra and T. N. Guru Row, Evaluation of the interchangeability of C–H and C–F groups: insights from crystal packing in a series of isomeric fluorinated benzanilides, CrystEngComm, 2008, 10, 54–67.
26. V. R. Hathwar, D. Chopra, P. Panini and T. N. Guru Row, Revealing the polarizability of organic fluorine in the trifluoromethyl group: implications in supramolecular chemistry, Cryst. Growth Des., 2014, 14, 5366–5369.
27. A. Mukherjee, S. Tothadi and G. R. Desiraju, Halogen bonds in crystal engineering: like hydrogen bonds yet different, Acc. Chem. Res., 2014, 47, 2514–2524.
28. T. Caronna, R. Liantonio, T. A. Logothetis, P. Metrangolo, T. Pilati and G. Resnati, Halogen Bonding and π⋯π Stacking Control Reactivity in the Solid State, J. Am. Chem. Soc., 2004, 126, 4500–4501.
29. H. Adams, J. L. Jimenez Blanco, G. Chessari, C. A. Hunter, C. M. Low, J. M. Sanderson and J. G. Vinter, Quantitative determination of intermolecular interactions with fluorinated aromatic rings, Chem.–Eur. J., 2001, 7, 3494–3503.
30. H. Adams, S. L. Cockroft, C. Guardigli, C. A. Hunter, K. R. Lawson, J. Perkins, S. E. Spey, C. J. Urch and R. Ford, Experimental measurement of noncovalent interactions between halogens and aromatic rings, ChemBioChem, 2004, 5, 657–665.
31. S. E. Wheeler, Local nature of substituent effects in stacking interactions, J. Am. Chem. Soc., 2011, 133, 10262–10274.
32. Y. X. Li, Z. K. Liu, J. Cao, J. Tao and Z. S. Yao, Stress-Induced Inversion of Linear Dichroism by 4,4′-Bipyridine Rotation in a Superelastic Organic Single Crystal, Angew. Chem., Int. Ed., 2023, 62, e202217977.
33. T. Sasaki, S. Sakamoto, K. Nishizawa and S. Takamizawa, Ferroelasticity with a Biased Hysteresis Loop in a Cocrystal of Pimelic Acid and 1,2-Di(4-pyridyl) ethane, Cryst. Growth Des., 2020, 20, 3913–3917.
34. V. R. Thalladi, H.-C. Weiss, D. Bläser, R. Boese, A. Nangia and G. R. Desiraju, C−H⋯F Interactions in the crystal structures of some fluorobenzenes, J. Am. Chem. Soc., 1998, 120, 8702–8710.
35. H. Jain, D. Sutradhar, S. Roy and G. R. Desiraju, Synthetic Approaches to Halogen Bonded Ternary Cocrystals, Angew. Chem., Int. Ed., 2021, 133, 12951–12956.
36. A. Mukherjee and G. R. Desiraju, Halogen bonds in some dihalogenated phenols: applications to crystal engineering, IUCrJ, 2014, 1, 49–60.
37. S. Chakraborty and G. R. Desiraju, C–H⋯F hydrogen bonds in solid solutions of benzoic acid and 4-fluorobenzoic acid, Cryst. Growth Des., 2018, 18, 3607–3615.
38. S. Saha, M. K. Mishra, C. M. Reddy and G. R. Desiraju, From molecules to interactions to crystal engineering: mechanical properties of organic solids, Acc. Chem. Res., 2018, 51, 2957–2967.
39. S. Hasebe, Y. Hagiwara, J. Komiya, M. Ryu, H. Fujisawa, J. Morikawa, T. Katayama, D. Yamanaka, A. Furube and H. Sato, Photothermally driven high-speed crystal actuation and its simulation, J. Am. Chem. Soc., 2021, 143, 8866–8877.
40. M. Ryu, S. Takamizawa and J. Morikawa, Thermal diffusivity of organosuperelastic soft crystals during stress-induced phase transition, Appl. Phys. Lett., 2021, 119.
41. M. Ryu, Y. Cang, Z. Wang, G. Fytas and J. Morikawa, Temperature-dependent thermoelastic anisotropy of the phenyl pyrimidine liquid crystal, J. Phys. Chem. C, 2019, 123, 17148–17154.
42. Y. Cang, J. Liu, M. Ryu, B. Graczykowski, J. Morikawa, S. Yang and G. Fytas, On the origin of elasticity and heat conduction anisotropy of liquid crystal elastomers at gigahertz frequencies, Nat. Commun., 2022, 13, 5248.
43. R. G. Xiong, S. Q. Lu, Z. X. Zhang, H. Cheng, P. F. Li and W. Q. Liao, A chiral thermochromic ferroelastic with seven physical channel switches, Angew. Chem., Int. Ed., 2020, 59, 9574–9578.
44. Y. Wang and J. Ren, Strain-driven switchable thermal conductivity in ferroelastic PdSe₂, ACS Appl. Mater. Interfaces, 2021, 13, 34724–34731.
45. D. Zhang, Y. Mao, P. Bai, Q. Li, W. He, H. Cui, F. Ye, C. Li, R. Ma and Y. Chen, Multifunctional superelastic graphene-based thermoelectric sponges for wearable and thermal management devices, Nano Lett., 2022, 22, 3417–3424.
46. N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi and B. Li, Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond, Rev. Mod. Phys., 2012, 84, 1045.
47. Y. Li, W. Li, T. Han, X. Zheng, J. Li, B. Li, S. Fan and C.-W. Qiu, Transforming heat transfer with thermal metamaterials and devices, Nat. Rev. Mater., 2021, 6, 488–507.
48. S. Li, X. Ding, J. Ren, X. Moya, J. Li, J. Sun and E. K. Salje, Strain-controlled thermal conductivity in ferroic twinned films, Sci. Rep., 2014, 4, 6375.
49. X. Ding and E. Salje, Heat transport by phonons and the generation of heat by fast phonon processes in ferroelastic materials, AIP Adv., 2015, 5, 053604.
50. A. Sieradzki, A. Jeżowski and R. Poprawski, The influence of ferroelastic domain formation on thermal conductivity in Li₂TiGeO₅ ceramics, J. Therm. Anal. Calorim., 2014, 115, 467–470.
51. E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Halogen bonding versus hydrogen bonding in driving self-assembly processes, Angew. Chem., Int. Ed., 2000, 39, 1782–1786.
52. G. Kaur, P. Panini, D. Chopra and A. Roy Choudhury, Structural investigation of weak intermolecular interactions in fluorine substituted isomeric N-benzylideneanilines, Cryst. Growth Des., 2012, 12, 5096–5110.
53. P. Cardillo, E. Corradi, A. Lunghi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, The N⋯ I intermolecular interaction as a general protocol for the formation of perfluorocarbon–hydrocarbon supramolecular architectures, Tetrahedron, 2000, 56, 5535–5550.
54. J. Lombard, T. le Roex and D. A. Haynes, Competition between Hydrogen and Halogen Bonds: The Effect of Solvent Volume, Cryst. Growth Des., 2020, 20, 7384–7391.
55. Q. J. Shen, H. Q. Wei, W. S. Zou, H. L. Sun and W. J. Jin, Cocrystals assembled by pyrene and 1, 2-or 1,4-diiodotetrafluorobenzenes and their phosphorescent behaviors modulated by local molecular environment, CrystEngComm, 2012, 14, 1010–1015.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed information about the experimental section, and thermal and crystallographic studies (pdf). Movie S1: shear stress-induced mechanical deformation on the (01̄1) plane of cocrystal 1 by using a pair of tweezers. Movie S2: shear stress-induced mechanical deformation on the (001) plane of cocrystal 2 by using a pair of tweezers. CCDC 2256404–2256407. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03155a

---