Open Access Article
Open Access Article“Freedom of design” in chemical compound space: towards rational in silico design of molecules with targeted quantum-mechanical properties†
Leonardo
Medrano Sandonas
 *a,
Johannes
Hoja
*a,
Johannes
Hoja
 ab,
Brian G.
Ernst
ab,
Brian G.
Ernst
 c,
Álvaro
Vázquez-Mayagoitia
c,
Álvaro
Vázquez-Mayagoitia
 d,
Robert A.
DiStasio
Jr
d,
Robert A.
DiStasio
Jr
 *c and
Alexandre
Tkatchenko
*c and
Alexandre
Tkatchenko
 *a
*a
aDepartment of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg City, Luxembourg. E-mail: leonardo.medrano@uni.lu; alexandre.tkatchenko@uni.lu
bInstitute of Chemistry, University of Graz, 8010 Graz, Austria
cDepartment of Chemistry and Chemical Biology, Cornell University, Ithaca, NY 14853, USA. E-mail: distasio@cornell.edu
dComputational Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
First published on 18th August 2023
Abstract
The rational design of molecules with targeted quantum-mechanical (QM) properties requires an advanced understanding of the structure–property/property–property relationships (SPR/PPR) that exist across chemical compound space (CCS). In this work, we analyze these fundamental relationships in the sector of CCS spanned by small (primarily organic) molecules using the recently developed QM7-X dataset, a systematic, extensive, and tightly converged collection of 42 QM properties corresponding to ≈4.2M equilibrium and non-equilibrium molecular structures containing up to seven heavy/non-hydrogen atoms (including C, N, O, S, and Cl). By characterizing and enumerating progressively more complex manifolds of molecular property space—the corresponding high-dimensional space defined by the properties of each molecule in this sector of CCS—our analysis reveals that one has a substantial degree of flexibility or “freedom of design” when searching for a single molecule with a desired pair of properties or a set of distinct molecules sharing an array of properties. To explore how this intrinsic flexibility manifests in the molecular design process, we used multi-objective optimization to search for molecules with simultaneously large polarizabilities and HOMO–LUMO gaps; analysis of the resulting Pareto fronts identified non-trivial paths through CCS consisting of sequential structural and/or compositional changes that yield molecules with optimal combinations of these properties.
1 Introduction
In recent years, exploration of the remarkably vast chemical compound space (CCS) of molecules and materials with data-driven approaches has inspired countless academic and industrial initiatives to seek out the fundamental relationships that exist (among and) between the structural signatures of molecules (e.g., chemical composition, atom connectivity, molecular structure) and their physicochemical properties (e.g., energies, HOMO–LUMO gaps, polarizabilities).1–8 In doing so, the growing availability of accurate and reliable molecular property data, coupled with the use of machine learning (ML) algorithms to explore this data, have led to an increased qualitative and quantitative understanding of these structure–property/property–property relationships (SPR/PPR).9–14 Such advances have been particularly helpful in the design of novel drugs, antivirals, antibiotics, catalysts, battery materials, and molecules with desired properties15–21—scientific and technological endeavors that have traditionally been driven by chemical intuition and/or serendipitous discoveries. While there has been significant progress in this area, a comprehensive understanding of these complex SPR/PPR—even in the (relatively) more manageable sector of CCS spanned by small molecules—is still lacking despite the critical importance and high relevance of such molecules throughout the chemical sciences. Unravelling these complex relationships would not only provide us with the tools needed to explore and characterize molecular property space (i.e., the even higher dimensional space defined by the properties of each molecule in CCS), but would also greatly advance our ability to rationally design molecules with targeted arrays of physicochemical properties.To address this challenge, the GDB databases22–26 have enumerated the molecular graphs for a sizeable number of chemical compounds (≈166G)—an important first step towards the systematic exploration of swaths of CCS far too vast to be cataloged and studied experimentally. Since these graphs only contain chemical composition (i.e., molecular formula) and atom connectivity information, the three-dimensional (3D) molecular structure(s) consistent with each graph (as well as their corresponding physicochemical properties) still need to be determined before detailed SPR/PPR studies can be undertaken. Furthermore, while certain chemical rules/guidelines were used to generate graphs corresponding to stable (and potentially synthetically feasible) molecules, there will be graphs containing atom-connectivity motifs that are more prone to stability issues when translated into 3D molecular structures (e.g., small rings with high ring strain). To address these issues, several researchers have built upon these seminal databases by computing quantum-mechanical (QM) structure and property information for the subset of molecular graphs containing ≲10 heavy/non-hydrogen atoms, i.e., the graphs enumerating the sector of CCS spanned by small (primarily organic) molecules mentioned above.27–34 For instance, the QM7 dataset27,28 provides the equilibrium structures and 15 physicochemical properties for 7211 molecules corresponding to the molecular graphs from GDB-13 (ref. 24) that contain up to seven heavy/non-hydrogen atoms (including C, N, O, S, and Cl); such structural and property information was computed using a hierarchy of different QM methods (i.e., ZINDO, SCS, PBE0, GW), with more recent variants employing (LR-)CCSD for molecular property evaluation.32 The subsequent QM9 dataset29 generated the structures and 16 (geometric, energetic, electronic, and thermodynamic) properties for 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 molecules at the B3LYP/6-31G(2df,p) level, each of which corresponds to a molecular graph from GDB-17 (ref. 23) containing up to nine heavy atoms (including C, N, O, and F). Several years later, another extensive exploration of the small-molecule sector of CCS was accomplished by the ANI-1 dataset,30,31 which consists of more than 20M equilibrium and non-equilibrium molecular structures containing up to eight heavy atoms (albeit limited to C, N, and O only) based on molecular graphs from GDB-11.25,26 This was followed by the release of the ANI-1x and ANI-1ccx datasets,33 which contain 20 properties for ≈5M structures computed using the ωB97-X functional and energies of ≈5k structures computed at the CCSD(T)/CBS level, respectively.
885 molecules at the B3LYP/6-31G(2df,p) level, each of which corresponds to a molecular graph from GDB-17 (ref. 23) containing up to nine heavy atoms (including C, N, O, and F). Several years later, another extensive exploration of the small-molecule sector of CCS was accomplished by the ANI-1 dataset,30,31 which consists of more than 20M equilibrium and non-equilibrium molecular structures containing up to eight heavy atoms (albeit limited to C, N, and O only) based on molecular graphs from GDB-11.25,26 This was followed by the release of the ANI-1x and ANI-1ccx datasets,33 which contain 20 properties for ≈5M structures computed using the ωB97-X functional and energies of ≈5k structures computed at the CCSD(T)/CBS level, respectively.
Despite all of these foundational efforts to generate a fully QM description of the sector of CCS spanned by small molecules (and the corresponding sector of molecular property space), many challenges still exist when translating a series of molecular graphs (which only contain chemical composition and atom connectivity information) to a systematic sampling of such high-dimensional spaces that includes an accurate and reliable account of both structural information (i.e., equilibrium and non-equilibrium structures consistent with each molecular graph) and property information (i.e., an extensive and well-converged inventory of QM properties for each molecular structure). To address these challenges, the recently published QM7-X dataset34 provides a systematic, extensive, and tightly converged collection of 42 QM properties for ≈4.2M equilibrium and non-equilibrium structures corresponding to the ≈7k molecular graphs containing up to seven heavy atoms (C, N, O, S, Cl) in the GDB-13 database,24 providing what is arguably the most comprehensive QM description of the sectors of CCS and molecular property space spanned by small (primarily organic) molecules to date. Rather than just including a single molecular structure per graph, QM7-X contains an extensive sampling of ≈42k (meta-)stable equilibrium structures/isomers corresponding to this set of molecular graphs, as well as 100 additional non-equilibrium conformations per equilibrium structure. For each of the resulting ≈4.2M equilibrium and non-equilibrium molecular structures, QM7-X also includes an extensive number of physicochemical properties (i.e., 42 structural, global (molecular), local (atom-in-molecule), ground-state, and response properties) obtained using well-converged and highly accurate QM methodologies, thereby providing the prerequisite QM description of both structural and property information needed for impactful SPR/PPR research efforts.
In this work, we build upon this foundational effort by performing a detailed analysis of the molecular property space corresponding to small (primarily organic) molecules (i.e., as enumerated by the QM7-X dataset) in order to gain a deeper understanding of the SPR/PPR that exist throughout this sector of CCS. We start with a quantitative analysis of the pairwise correlations between select QM7-X properties, which revealed that most (>90%) properties exhibit little (to no) correlation, i.e., there are very few strict limitations preventing a single molecule from simultaneously exhibiting a desired pair of QM properties. By progressively investigating more complex manifolds of the QM7-X molecular property space and their underlying dependence on molecular structure and chemical composition (i.e., the tunable “knobs” in molecular design), we also found a remarkably large number of structurally and/or compositionally distinct molecules that share multiple QM properties. Taken together, these findings provide compelling evidence for “freedom of design” in CCS—an intrinsic degree of flexibility that enables the rational design of distinct molecules sharing an array of targeted physicochemical properties. To explore how this intrinsic flexibility manifests in the molecular design process, we used Pareto multi-property optimization to search for molecules in QM7-X with simultaneously large polarizabilities (α) and HOMO–LUMO gaps (Egap). Without any prior knowledge of the corresponding (α, Egap)-manifold of molecular property space, each Pareto front reflected the large degree of intrinsic flexibility within CCS by identifying a series of changes to the molecular structure and/or chemical composition that resulted in optimal combinations of these properties.
By demonstrating that “freedom of design” is a fundamental and emergent property of CCS, we hope this work will challenge the greater chemical sciences community to consider how such intrinsic flexibility can be used to expand the candidate pool of chemical compounds—beyond the paradigm of functional group modification based on a largely fixed molecular scaffold(s)—during the rational design of molecules with targeted physicochemical properties. We expect that the insight provided by this work will emphasize the critical importance of obtaining high-quality QM structural and property data when exploring the fundamental SPR/PPR existing throughout CCS and contribute to the development of advanced ML-based tools that will improve the in silico sampling, identification, and design of molecular systems for a number of applications, ranging from novel polymeric batteries and organic semiconductors to promising pharmaceuticals and small-molecule protein inhibitors.
2 Methods
2.1 Description of the QM7-X dataset
The QM7-X dataset34 was constructed via a systematic and extensive sampling of the (meta-)stable equilibrium structures (i.e., constitutional/structural isomers and stereoisomers, e.g., enantiomers and diastereomers (including cis-/trans- and conformational isomers)) corresponding to the ≈7k molecular graphs containing up to seven heavy/non-hydrogen atoms (including C, N, O, S, and Cl) in the GDB-13 database.24 As mentioned above, these molecular graphs only contain chemical composition and atom connectivity information, and therefore do not specify the 3D molecular structures (and their corresponding physicochemical properties) that are consistent with each graph. Furthermore, there will be graphs that contain certain moieties (e.g., small rings) that are more prone to stability issues (e.g., high ring strain) when translated into fully specified 3D molecular structures. To address these issues, we optimized each of the molecular structures in QM7-X using accurate and reliable QM methodologies, i.e., third-order self-consistent charge density-functional tight binding (DFTB3)35,36 that also accounts for many-body dispersion/van der Waals (vdW) interactions via the MBD approach,37,38 and performed subsequent harmonic frequency analyses on the resulting set of 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 optimized structures to confirm that each was a stationary point (i.e., a local minimum) on the corresponding molecular potential energy surface (PES). We also confirmed that each of these optimized molecular structures has a positive atomization energy (EAT > 0), and is therefore energetically downhill with respect to the infinite-separation limit of its constituent atoms (cf. Fig. 4(a) in ref. 34). While this protocol cannot guarantee that each molecular structure in QM7-X is stable with respect to the (Gibbs) free energy, this set of structures was taken to be a representative sample of the (meta-)stable equilibrium molecules in the sector of CCS spanned by small primarily organic molecules.
537 optimized structures to confirm that each was a stationary point (i.e., a local minimum) on the corresponding molecular potential energy surface (PES). We also confirmed that each of these optimized molecular structures has a positive atomization energy (EAT > 0), and is therefore energetically downhill with respect to the infinite-separation limit of its constituent atoms (cf. Fig. 4(a) in ref. 34). While this protocol cannot guarantee that each molecular structure in QM7-X is stable with respect to the (Gibbs) free energy, this set of structures was taken to be a representative sample of the (meta-)stable equilibrium molecules in the sector of CCS spanned by small primarily organic molecules.
To further sample each molecular PES, we also generated 100 non-equilibrium conformations for each of these ≈42k equilibrium structures (via the normal-mode displacements obtained during the harmonic frequency analysis, see schematic illustration in Fig. 1), yielding a total of ≈4.2M molecular structures. We note in passing that each of these non-equilibrium conformations also has a positive atomization energy (cf. Fig. 4(a) in ref. 34), despite the energetic destabilization resulting from the generative structural perturbations. For each of these ≈4.2M equilibrium and non-equilibrium structures, QM7-X also includes an extensive number of physicochemical properties (i.e., 42 structural, global (molecular), local (atom-in-molecule), ground-state, and response properties) obtained from QM calculations, most of which were performed with non-empirical hybrid density-functional theory (DFT) and a many-body treatment of vdW/dispersion interactions (i.e., PBE0+MBD)37,39–41 in conjunction with the tightly converged numeric atom-centered basis sets42 implemented in the FHI-aims code.43,44
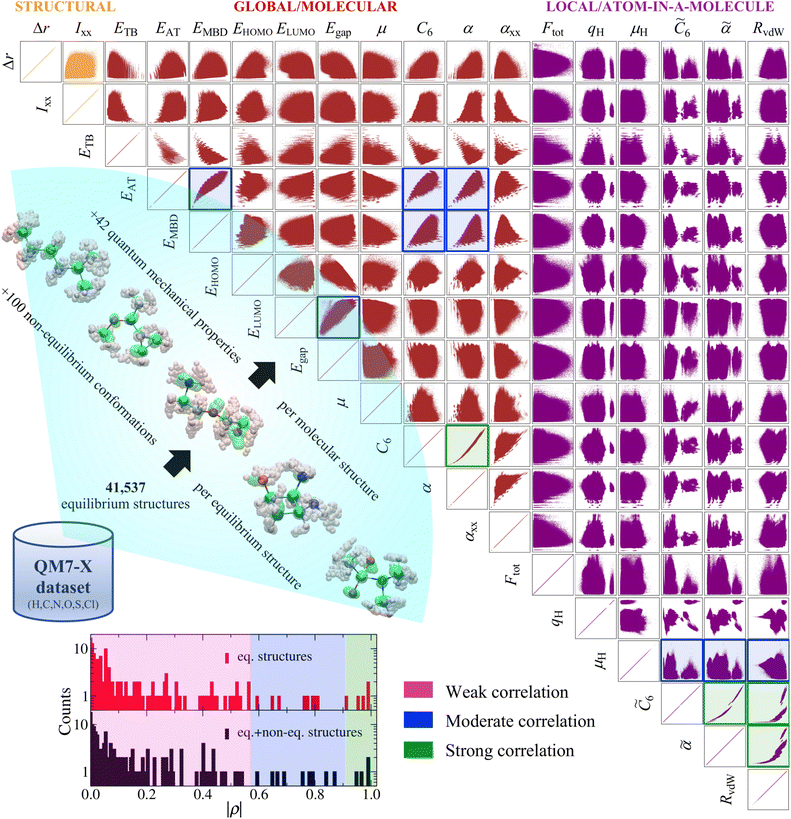 | ||
| Fig. 1 Pairwise property–property relationships (PPR) in molecular property space: 2D correlation plots. The recently developed QM7-X dataset34—a systematic, extensive, and tightly converged collection of 42 quantum mechanical (QM) properties corresponding to ≈4.2M equilibrium and non-equilibrium molecular structures containing up to seven heavy/non-hydrogen atoms (including C, N, O, S, and Cl)—is used in this work to study the PPR in the sector of chemical compound space (CCS) spanned by small (primarily organic) molecules. Select 2D projections of the 42D QM7-X molecular property space are depicted for a subset of 18 structural (orange), global/molecular (red), and local/atom-in-a-molecule (violet) properties (see Table 1 for a detailed description of each property) for the ≈4.2M structures in QM7-X. As depicted in the lower-left inset, measuring the degree of correlation between each pair of QM properties (via the Pearson correlation coefficient ρ in eqn (1)) results in three distinct clusters: weakly correlated (|ρ| ≤ 0.57), moderately correlated (0.57 < |ρ| ≤ 0.91, highlighted with blue frames), and strongly correlated (|ρ| > 0.91, highlighted with dark green frames). A vast majority (i.e., 140/153 or 91.5%) of these correlation plots resemble structureless “blobs” (i.e., weakly correlated PPR with |ρ| ≤ 0.57), indicating that small (primarily organic) molecules have the flexibility to exhibit nearly any pair of properties considered above. | ||
2.2 Analysis of the QM7-X molecular property space
Our detailed analysis of the QM7-X molecular property space includes the following four thrusts: (i) projecting the corresponding 42D molecular property space onto a series of 2D correlation plots for identifying pairwise PPR (Sec. 3.1); (ii) characterizing the structural and compositional dependence of select QM7-X properties (Sec. 3.2); (iii) quantifying the number of structurally and/or compositionally distinct molecules that share an array of QM7-X properties (Sec. 3.3); (iv) finding and analyzing Pareto fronts containing molecules in QM7-X with simultaneously large polarizabilities (α) and HOMO–LUMO gaps (Egap) (Sec. 3.4).For the analysis in Sec. 3.1, we considered the properties of all ≈4.2M (equilibrium and non-equilibrium) molecular structures in QM7-X. The degree of correlation between properties x and y was measured by the Pearson correlation coefficient,
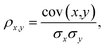 | (1) |
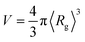 (in which 〈Rg〉 is the thermally-averaged radius of gyration at T = 300 K); and (ii) the total number of atoms Natoms in a given molecule. In Sec. 3.3, we used the following property-specific threshold values (each of which represents 0.5% of the total range observed for each thermally-averaged property at T = 300 K in the QM7-X dataset) when identifying a set of molecules sharing a given property value: δ〈EAT〉 = 0.42 eV for the thermally-averaged atomization energy 〈EAT〉, δ〈α〉 = 0.58 a03 for the thermally-averaged isotropic molecular polarizability 〈α〉, δ〈Egap〉 = 0.04 eV for the thermally-averaged HOMO–LUMO gap 〈Egap〉, and δ〈μ〉 = 0.008 e·Å for the thermally-averaged scalar molecular dipole moment 〈μ〉. For example, a three-molecule set that shares the same 〈EAT〉 value will be composed of molecules A, B, and C provided that the following three conditions are satisfied: |〈EAT〉A − 〈EAT〉B| < δ〈EAT〉, |〈EAT〉A − 〈EAT〉C| < δ〈EAT〉, and |〈EAT〉B − 〈EAT〉C| < δ〈EAT〉.
(in which 〈Rg〉 is the thermally-averaged radius of gyration at T = 300 K); and (ii) the total number of atoms Natoms in a given molecule. In Sec. 3.3, we used the following property-specific threshold values (each of which represents 0.5% of the total range observed for each thermally-averaged property at T = 300 K in the QM7-X dataset) when identifying a set of molecules sharing a given property value: δ〈EAT〉 = 0.42 eV for the thermally-averaged atomization energy 〈EAT〉, δ〈α〉 = 0.58 a03 for the thermally-averaged isotropic molecular polarizability 〈α〉, δ〈Egap〉 = 0.04 eV for the thermally-averaged HOMO–LUMO gap 〈Egap〉, and δ〈μ〉 = 0.008 e·Å for the thermally-averaged scalar molecular dipole moment 〈μ〉. For example, a three-molecule set that shares the same 〈EAT〉 value will be composed of molecules A, B, and C provided that the following three conditions are satisfied: |〈EAT〉A − 〈EAT〉B| < δ〈EAT〉, |〈EAT〉A − 〈EAT〉C| < δ〈EAT〉, and |〈EAT〉B − 〈EAT〉C| < δ〈EAT〉.
2.3 Multi-property optimization algorithm
Each Pareto front in Sec. 3.4 was found using a multi-objective evolutionary algorithm, i.e., the non-dominated sorting genetic algorithm II (NSGA-II),45,46 as implemented in the pymoo code.47 NSGA-II performs a fast sorting of non-dominant samples to define the Pareto fronts, while the diversity in each front is controlled by a crowding-distance calculation.48,49 In our search for molecules in QM7-X with simultaneously large 〈α〉 and 〈Egap〉 values, we employed the following two objective functions: f1(x) = x and f2(y) = y, in which x = 〈Egap〉 and y = 〈α〉.50,51 Here, we note in passing that these objective functions could also be tailored for other potential applications, i.e., f(x) = x2 could be employed for α when searching for molecules with large vdW/dispersion interactions, given the quadratic relationship between α and the isotropic molecular vdW/dispersion coefficient C6 (cf. C6 ∝ α2 in eqn (2)).3 Results & discussion
3.1 Pairwise correlations in molecular property space
As a first step towards gaining a deeper understanding of the structure–property/property–property relationships (SPR/PPR) in the sector of chemical compound space (CCS) spanned by small (primarily organic) molecules, we analyzed the pairwise correlations between select properties in the QM7-X dataset. To do so, we plotted an array of 2D projections of the 42D QM7-X molecular property space corresponding to 18 QM properties evaluated on the ≈4.2M (equilibrium and non-equilibrium) structures in Fig. 1. This set of QM7-X properties is quite diverse and includes both extensive and intensive properties, as well as representative examples of structural, global/molecular, local/atom-in-a-molecule, ground-state, and response properties (see Table 1). Even from a cursory glance at Fig. 1, one can see that nearly all of the 153 unique pair projections (i.e., 2D correlation plots) resemble structureless “blobs”, indicating that most of these QM properties are effectively uncorrelated. To quantify the degree of correlation in each plot, we computed the corresponding Pearson correlation coefficient in eqn (1), and found three distinct and fairly well-defined groups of ρ values (see Fig. 1 inset). For the purposes of this discussion, we will use these values to (roughly) classify a given PPR as strongly correlated (|ρ| > 0.91), moderately correlated (0.57 < |ρ| ≤ 0.91), or weakly correlated (|ρ| ≤ 0.57). Under this working classification system, a mere 4/153 (2.6%) projections displayed a strong degree of correlation with |ρ| > 0.91: (C6, α), (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6,
6, ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ), (
), (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6, RvdW), and (
6, RvdW), and (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) , RvdW); these correlation plots are highlighted with dark green frames in Fig. 1. In the same breath, only 9/153 (5.9%) projections were classified as moderately correlated, with intermediate |ρ| values and considerably more dispersion in their scatter plots: (EAT, EMBD), (EAT, C6), (EAT, α), (EMBD, C6), (EMBD, α), (ELUMO, Egap), (μH,
, RvdW); these correlation plots are highlighted with dark green frames in Fig. 1. In the same breath, only 9/153 (5.9%) projections were classified as moderately correlated, with intermediate |ρ| values and considerably more dispersion in their scatter plots: (EAT, EMBD), (EAT, C6), (EAT, α), (EMBD, C6), (EMBD, α), (ELUMO, Egap), (μH,![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6), (μH,
6), (μH,![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ), and (μH, RvdW); these plots are highlighted with blue frames in Fig. 1. Hence, the remaining 140/153 (91.5%)—the lion's share of the correlation plots in Fig. 1—correspond to weakly correlated PPR with |ρ| ≤ 0.57, which are particularly low values in the physical sciences. In other words, most of these properties are effectively uncorrelated, and there seem to be very few limitations preventing a single molecule from simultaneously exhibiting any pair of properties in Fig. 1. This finding is remarkable and implies that the sector of CCS spanned by small (primarily organic) molecules has a large degree of intrinsic flexibility—an important point that we return to throughout this manuscript.
), and (μH, RvdW); these plots are highlighted with blue frames in Fig. 1. Hence, the remaining 140/153 (91.5%)—the lion's share of the correlation plots in Fig. 1—correspond to weakly correlated PPR with |ρ| ≤ 0.57, which are particularly low values in the physical sciences. In other words, most of these properties are effectively uncorrelated, and there seem to be very few limitations preventing a single molecule from simultaneously exhibiting any pair of properties in Fig. 1. This finding is remarkable and implies that the sector of CCS spanned by small (primarily organic) molecules has a large degree of intrinsic flexibility—an important point that we return to throughout this manuscript.
| Symbol | Property description | Units | Dimension | Type | Class |
|---|---|---|---|---|---|
| Δr | RMSD with respect to equilibrium structure | Å | 1 | S,G | I |
| I xx | Moment of inertia tensor (xx component) | amu·Å2 | 1 | S,G | I |
| D max | Maximum distance between heavy/non-hydrogen atoms | Å | 1 | S,G | I |
| E TB | Total DFTB energy | eV | 1 | M,G | E |
| E AT | Atomization energy | eV | 1 | M,G | E |
| E MBD | MBD energy | eV | 1 | M,G | E |
| E HOMO | HOMO energy | eV | 1 | M,G | I |
| E LUMO | LUMO energy | eV | 1 | M,G | I |
| E gap | HOMO–LUMO gap | eV | 1 | M,G | I |
| μ | Scalar molecular dipole moment | e·Å | 1 | M,G | I |
| C 6 | Isotropic molecular vdW/dispersion coefficient | E h ·a60 | 1 | M,R | E |
| α | Isotropic molecular polarizability | a 30 | 1 | M,R | E |
| α xx | Molecular polarizability tensor (xx component) | a 30 | 1 | M,R | E |
| F tot | Norm of total atomic force vector | eV·Å−1 | 1 | A,G | I |
| q H | Hirshfeld atomic charges | e | N atoms | A,G | I |
| μ H | Scalar Hirshfeld atomic dipole moments | e·a0 | N atoms | A,G | I |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6
6
|
Isotropic atomic vdW/dispersion coefficients | E h ·a60 | N atoms | A,R | I |
![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif)
|
Isotropic atomic polarizabilities | a 30 | N atoms | A,R | I |
| R vdW | Isotropic atomic van der Waals (vdW) radii | a 0 | N atoms | A,R | I |
Among the 2D projections in Fig. 1 that do exhibit a strong (or moderate) degree of correlation, we observed several trends that can be explained using chemical/physical intuition. For instance, consider the strong degree of correlation (|ρ| = 0.99) between the isotropic molecular vdW/dispersion coefficient (C6) and isotropic molecular polarizability (α). In this case, the observed quadratic form can be rationalized by the Casimir–Polder formula52 for the C6 coefficient describing the vdW/dispersion interactions between molecules A and B:
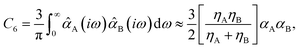 | (2) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) A(iω) is the frequency-dependent isotropic polarizability of A in the imaginary frequency domain. By substituting the leading-order Padé53,54 (or quantum harmonic oscillator)55,56 approximation for
A(iω) is the frequency-dependent isotropic polarizability of A in the imaginary frequency domain. By substituting the leading-order Padé53,54 (or quantum harmonic oscillator)55,56 approximation for ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) A(iω) into this expression (i.e.,
A(iω) into this expression (i.e., ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) A(iω) = αA/[1 − (ω/ηA)2], with ηA being the characteristic excitation frequency of A), one arrives at the well-known London formula on the right hand side of eqn (2) in which C6 ∝ α2.57 Since the leading-order term in the many-body expansion of the vdW/dispersion energy is given by C6/R6,57 it is also not surprising to observe a moderate degree of correlation (|ρ| = 0.65) between the many-body vdW/dispersion energy37,41,58,59 (EMBD) and C6, as well as a similar degree of correlation (|ρ| = 0.59) between EMBD and α (since C6 ∝ α2). Another related example is the moderate correlation observed between αxx (a single component of the molecular polarizability tensor) and C6 (|ρ| = 0.52); this is significantly less than the strong correlation (|ρ| = 0.99) between C6 and α (the isotropic average over the diagonal tensor components), and directly reflects the anisotropy in the shapes and spatial extents of the molecules in QM7-X. Here, we stress that such a reduced degree of correlation between fundamental QM properties is by no means uninteresting, and reflects a degree of flexibility that can be exploited when searching for molecules with specific properties, e.g., polarization directions/orientations that favor (or disfavor) the formation of specific molecular crystal polymorphs. If one considers the 2D projection between the atomization energy (EAT) and EMBD, one can (at least partially) rationalize the observed moderate degree of correlation (|ρ| = 0.87) by recognizing that EAT and EMBD both depend on molecular size; in this case, our physical intuition regarding extensive properties tells us that EAT will tend to increase with EMBD, and vice versa. In the same breath, the moderate degree of correlation (|ρ| = 0.67) between EAT and α can also be rationalized with the physical/chemical intuition that α is (in general) additive and tends to increase with molecular volume.60,61 As discussed below, one can normalize such extensive properties with respect to a number of different size-dependent quantities (e.g., molecular volume, total number of atoms, number of valence electrons); however, the resulting degree of correlation will depend on the normalization quantity and can therefore be quite variable and counterintuitive (see Sec. 3.2 and Fig. S4†).
A(iω) = αA/[1 − (ω/ηA)2], with ηA being the characteristic excitation frequency of A), one arrives at the well-known London formula on the right hand side of eqn (2) in which C6 ∝ α2.57 Since the leading-order term in the many-body expansion of the vdW/dispersion energy is given by C6/R6,57 it is also not surprising to observe a moderate degree of correlation (|ρ| = 0.65) between the many-body vdW/dispersion energy37,41,58,59 (EMBD) and C6, as well as a similar degree of correlation (|ρ| = 0.59) between EMBD and α (since C6 ∝ α2). Another related example is the moderate correlation observed between αxx (a single component of the molecular polarizability tensor) and C6 (|ρ| = 0.52); this is significantly less than the strong correlation (|ρ| = 0.99) between C6 and α (the isotropic average over the diagonal tensor components), and directly reflects the anisotropy in the shapes and spatial extents of the molecules in QM7-X. Here, we stress that such a reduced degree of correlation between fundamental QM properties is by no means uninteresting, and reflects a degree of flexibility that can be exploited when searching for molecules with specific properties, e.g., polarization directions/orientations that favor (or disfavor) the formation of specific molecular crystal polymorphs. If one considers the 2D projection between the atomization energy (EAT) and EMBD, one can (at least partially) rationalize the observed moderate degree of correlation (|ρ| = 0.87) by recognizing that EAT and EMBD both depend on molecular size; in this case, our physical intuition regarding extensive properties tells us that EAT will tend to increase with EMBD, and vice versa. In the same breath, the moderate degree of correlation (|ρ| = 0.67) between EAT and α can also be rationalized with the physical/chemical intuition that α is (in general) additive and tends to increase with molecular volume.60,61 As discussed below, one can normalize such extensive properties with respect to a number of different size-dependent quantities (e.g., molecular volume, total number of atoms, number of valence electrons); however, the resulting degree of correlation will depend on the normalization quantity and can therefore be quite variable and counterintuitive (see Sec. 3.2 and Fig. S4†).
Using the extensive structure–property data in QM7-X, Fig. 1 also provides new insight into the correlations (or lack thereof) that exist between fundamental QM properties. At the top of this list is the seemingly expected inverse proportionality between α and HOMO–LUMO gap (Egap),61–73 which has roots in the following sum-over-states expression for α from perturbation theory:74,75
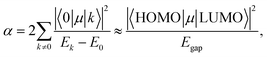 | (3) |
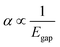 . Notably, this inverse proportionality also results from analytical evaluation of this sum-over-states expression for the quantum harmonic oscillator,65,66 which is effectively transformed into a two-state system by the selection rules. Furthermore, we note that this relationship has also become part of physical/chemical intuition, primarily through HSAB (hard–soft–acid–base) theory67,68 and the closely related concept of chemical hardness,61,69,72 both of which are often evoked to rationalize the stability/reactivity of chemical species; this relationship also appears via connections between α (and/or Egap) and a number of different theoretical quantities (e.g., ionization energy, electron affinity, electronegativity).61,70 While such an inverse proportionality has certainly been observed in homologous sets of molecules (e.g., polyenes71 and s-trans alkenes73 of increasing length), we find that this relationship does not hold for the diverse set of molecules in QM7-X. As depicted in Fig. 1, the correlation plot between α and Egap has only the faintest indication of an inverse proportionality and is more appropriately described as a structureless “blob”; with a correlation coefficient of |ρ| = 0.06 (which is abysmally low in the physical sciences), we would argue that these properties are effectively uncorrelated.
. Notably, this inverse proportionality also results from analytical evaluation of this sum-over-states expression for the quantum harmonic oscillator,65,66 which is effectively transformed into a two-state system by the selection rules. Furthermore, we note that this relationship has also become part of physical/chemical intuition, primarily through HSAB (hard–soft–acid–base) theory67,68 and the closely related concept of chemical hardness,61,69,72 both of which are often evoked to rationalize the stability/reactivity of chemical species; this relationship also appears via connections between α (and/or Egap) and a number of different theoretical quantities (e.g., ionization energy, electron affinity, electronegativity).61,70 While such an inverse proportionality has certainly been observed in homologous sets of molecules (e.g., polyenes71 and s-trans alkenes73 of increasing length), we find that this relationship does not hold for the diverse set of molecules in QM7-X. As depicted in Fig. 1, the correlation plot between α and Egap has only the faintest indication of an inverse proportionality and is more appropriately described as a structureless “blob”; with a correlation coefficient of |ρ| = 0.06 (which is abysmally low in the physical sciences), we would argue that these properties are effectively uncorrelated.
Unlike the majority of global/molecular properties (which have correlation plots resembling single connected “blobs”), the 2D projections involving local/atom-in-a-molecule properties, e.g., Hirshfeld atomic charges (qH), scalar Hirshfeld atomic dipole moments (μH), isotropic atomic vdW/dispersion coefficients (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6), and isotropic atomic polarizabilities (
6), and isotropic atomic polarizabilities (![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) ), often exhibit distinct clusters. As depicted in Fig. 1, such clusters are most visible when analyzing the correlation plots between two local properties, and are related to the different atomic environments present in the molecules in QM7-X. For example, the projections involving qH show the largest number of atomic environments, and represent the different local charge distributions that exist throughout this diverse dataset. Local response properties such as
), often exhibit distinct clusters. As depicted in Fig. 1, such clusters are most visible when analyzing the correlation plots between two local properties, and are related to the different atomic environments present in the molecules in QM7-X. For example, the projections involving qH show the largest number of atomic environments, and represent the different local charge distributions that exist throughout this diverse dataset. Local response properties such as ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6,
6, ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) , and RvdW (i.e., isotropic atomic vdW radii, see Table 1) also depend on the chemical environment surrounding each atom and tend to be strongly correlated. For instance, one can observe multiple quadratic-type functions in the (
, and RvdW (i.e., isotropic atomic vdW radii, see Table 1) also depend on the chemical environment surrounding each atom and tend to be strongly correlated. For instance, one can observe multiple quadratic-type functions in the (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 6,
6, ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) )-plot, which can be rationalized by applying the Casimir–Polder relationship in eqn (2) to each local chemical environment. In the same breath, we also find a strong degree of correlation between
)-plot, which can be rationalized by applying the Casimir–Polder relationship in eqn (2) to each local chemical environment. In the same breath, we also find a strong degree of correlation between ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) and RvdW (|ρ| = 0.97)—this is a fundamental relationship that continues to be a topic of discussion in the literature.76,77
and RvdW (|ρ| = 0.97)—this is a fundamental relationship that continues to be a topic of discussion in the literature.76,77
The distinct clustering of |ρ| values discussed above is quite robust and also holds when only considering the ≈41k equilibrium structures in QM7-X, i.e., the inclusion of the remaining ≈4.2M non-equilibrium conformations in QM7-X does not meaningfully alter the classification scheme used to discuss the PPR in this work (see the lower-left inset in Fig. 1 and S1† for representative examples). Statistically speaking, the mean absolute deviation (MAD) between |ρ| values in the two distributions depicted in the Fig. 1 inset is quite small (MAD = 0.04), and is primarily due to inconsequential changes among the weakly correlated PPR comprising the vast majority of cases. In the moderately and strongly correlated sectors, there are a handful of more substantive |ρ| changes worth mention, but none of which warrant changes to our working classification scheme. In most of these cases, we observed an increase in |ρ(x,y)| when this quantity was computed using the equilibrium structures only—this is an expected change as the omission of the non-equilibrium structures tends to increase cov(x,y) while simultaneously decreasing both σx and σy (cf.eqn (1)); see Fig. S1† and surrounding discussion for more details. Interestingly, the largest difference was observed for (ELUMO, Egap), for which |ρ| unexpectedly decreased from 0.84 to 0.67 when computed using the equilibrium structures only. This change in |ρ| highlights the non-trivial influence that non-equilibrium molecular structures can have on the observed pairwise correlations in molecular property space, and is (somewhat) easier to rationalize by considering it as an unexpected increase when the non-equilibrium structures were included in the evaluation of |ρ|. In this case, the non-equilibrium structures lead to a disproportionate increase in cov(ELUMO, Egap) (i.e., a measure of the diagonal spread) relative to the simultaneous increase in σELUMOσEgap (i.e., a measure of the axis-aligned spreads), which results in an overall increase in |ρ| but no change to the classification of this PPR (see Fig. S1†).
Although the inclusion of non-equilibrium molecular structures did not meaningfully alter the scheme used to classify the PPR in this work, it is important to recognize that their (partial or full) inclusion can lead to non-trivial effects on observed property values (and hence the rational design of molecules with targeted properties). To quantify this effect, we critically assessed the coefficient of variation (or relative standard deviation) cv ≡ σx/![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , i.e., the ratio of the standard deviation σx to the mean value
, i.e., the ratio of the standard deviation σx to the mean value ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) for a given property x, for several representative extensive (e.g., EAT, EMBD, α) and intensive (e.g., Egap, μ, EHOMO) properties (see Fig. S2†). In doing so, we found that the extensive properties have cv ≪ 0.1, and are therefore essentially unaffected by the structural diversity in the QM7-X non-equilibrium conformations, while the intensive properties are much more sensitive to such structural variations. Both of these findings are consistent with the fact that the non-equilibrium structural variations in QM7-X are largely perturbative (with respect to the corresponding equilibrium structures), and are characterized by changes to the molecular geometry that conserve atom connectivity and leave the molecule intact (i.e., non-equilibrium bond lengths, bond angles, and dihedrals). Hence, this analysis provides strong support for including such semi-local molecular PES information when characterizing and exploring the range/distribution of property values (particularly for intensive properties) that are accessible by a given molecule.
for a given property x, for several representative extensive (e.g., EAT, EMBD, α) and intensive (e.g., Egap, μ, EHOMO) properties (see Fig. S2†). In doing so, we found that the extensive properties have cv ≪ 0.1, and are therefore essentially unaffected by the structural diversity in the QM7-X non-equilibrium conformations, while the intensive properties are much more sensitive to such structural variations. Both of these findings are consistent with the fact that the non-equilibrium structural variations in QM7-X are largely perturbative (with respect to the corresponding equilibrium structures), and are characterized by changes to the molecular geometry that conserve atom connectivity and leave the molecule intact (i.e., non-equilibrium bond lengths, bond angles, and dihedrals). Hence, this analysis provides strong support for including such semi-local molecular PES information when characterizing and exploring the range/distribution of property values (particularly for intensive properties) that are accessible by a given molecule.
With only a handful of exceptions, the above analysis of the pairwise PPR in the sector of molecular property space spanned by the small (primarily organic) molecules in QM7-X demonstrates that most QM properties are effectively uncorrelated. While one might initially view this as a challenge for rational molecular design, we would argue that this finding highlights an intrinsic flexibility—or “freedom of design”—that exists in CCS, wherein there seems to be very few limitations preventing a molecule from simultaneously exhibiting any pair of properties considered in Fig. 1. Since this “freedom of design” conjecture has profound implications regarding the existence and uniqueness of molecules with a diverse array of targeted properties, it will be critically analyzed and assessed throughout the remainder of this work.
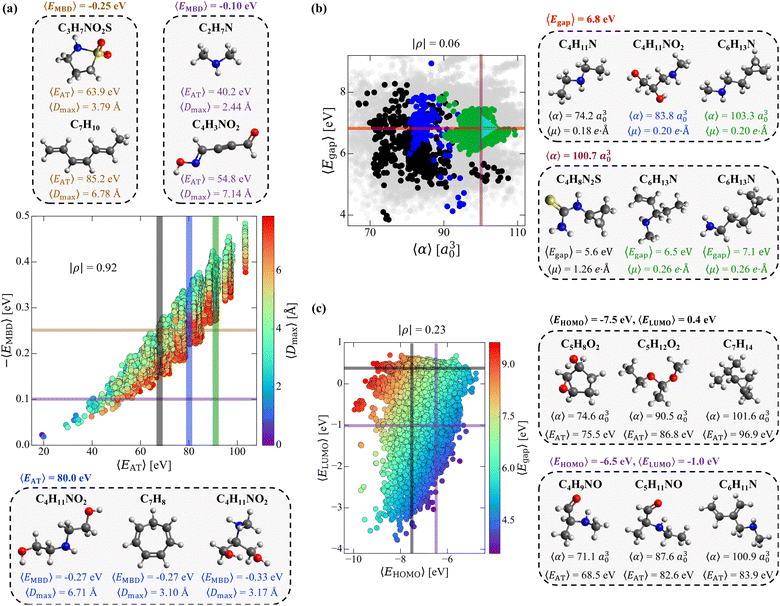
3.2 Structural and compositional dependence of molecular property space
While the complex set of pairwise PPR analyzed in Sec. 3.1 suggests that one has “freedom of design” when searching for small molecules with a targeted pair of properties, exactly how this intrinsic degree of flexibility is related to the molecular structure and chemical composition in this sector of CCS—the tunable knobs in the molecular design process—still requires further investigation. To do so, we start by considering a pair of properties that exhibited a moderate-to-strong degree of correlation in our previous analysis (i.e., (EMBD, EAT) with |ρ| = 0.87), as this relatively narrow sector of molecular property space is expected to have less intrinsic flexibility and will therefore serve as a more challenging test of our “freedom of design” conjecture. More specifically, we consider thermally-averaged versions of these quantities (i.e., (〈EMBD〉, 〈EAT〉) at T = 300 K) as thermally-averaged properties are commonly employed during molecular design procedures. In this case, thermal averaging increases |ρ| from 0.87 to 0.92, making these properties strongly correlated according to our classification system. Here, we note that the thermally-averaged |ρ| for these properties is effectively identical to that computed using the equilibrium structures only (see Fig. S1(d)†), which is not surprising as thermally-averaged property values (at T = 300 K) tend to be very similar to their corresponding equilibrium values for the majority of molecules and properties in QM7-X (see Fig. S2†).As depicted in Fig. 2(a), the range of |〈EMBD〉| and 〈EAT〉 values (0.02–0.48 eV and 19.3–103.3 eV, respectively) is quite large, indicating that the molecules in QM7-X are quite diverse and cover a sizeable sector of CCS. The molecules with the lowest |〈EMBD〉| and 〈EAT〉 values are small hydrocarbons such as CH4 (∼0.02 eV and ∼19.3 eV) and C2H2 (∼0.02 eV and ∼19.9 eV), while the largest values correspond to C7H16 isomers/conformers (∼0.48 eV and ∼103.3 eV); the molecules in QM7-X containing second-row elements (i.e., S and Cl) tend to have intermediate values for these quantities (see Fig. S3†). Despite the strong correlation between these extensive properties, there is still visible dispersion in Fig. 2(a), which indicates that diverse (〈EMBD〉, 〈EAT〉) combinations are possible, i.e., for a fixed value of one property, there is considerable flexibility in the value of the other. From this plot, one can also see that this dispersion is fairly well-correlated with 〈Dmax〉, a quantity that measures the spatial extent of each molecule via the thermally-averaged maximum pairwise distance between heavy/non-hydrogen atoms in a given molecular geometry (see Sec. 2). To explore these points further, we characterized the structure and composition of the molecules contained in two fixed 〈EMBD〉 windows, 〈EMBD〉 = −0.25 ± 0.01 eV and 〈EMBD〉 = −0.10 ± 0.01 eV, which represent the 50th and 20th percentiles of the observed vdW/dispersion energy spectrum. In doing so, we were able to easily find molecules with markedly distinct structures (i.e., compact vs. extended as quantified by 〈Dmax〉) and chemical compositions with the same 〈EMBD〉 but completely different 〈EAT〉. This is another manifestation of “freedom of design” in CCS, and is clearly illustrated by the C3H7NO2S and C7H10 isomers in the top inset of Fig. 2(a): while both are located in the 〈EMBD〉 = −0.25 ± 0.01 eV window (at opposite edges of the data dispersion), their 〈EAT〉 values differ by more than 20 eV. Since |〈EMBD〉| is an extensive property that tends to increase with the number of atoms in a molecule and decrease with molecular volume/spatial extent, C3H7NO2S (a compact molecule with less atoms, 〈Dmax〉 = 3.79 Å) and C7H10 (an extended molecule with more atoms, 〈Dmax〉 = 6.78 Å) represent a non-trivial compromise between these two effects that results in similar 〈EMBD〉. In the same breath, the sizeable difference in 〈EAT〉 between these molecules can be primarily attributed to the larger number of atoms in C7H10 as well as its conjugated/extended π-system, which further stabilizes this hydrocarbon and increases 〈EAT〉. When analyzing the less dense 〈EMBD〉 = −0.10 ± 0.01 eV window, one can just as easily find another distinct pair of molecules (again located at the edges of the data dispersion) that exhibit markedly different 〈EAT〉. Here, we observe an ≈15 eV 〈EAT〉 difference between C2H7N and C4H3NO2 (see Fig. 2(a), top inset), which can be rationalized by the larger number of heavy atoms and more complex bonding motifs (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C
O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) in C4H3NO2.
C) in C4H3NO2.
With such dispersion in the (〈EMBD〉, 〈EAT〉) correlation plot, a similar degree of flexibility also exists when holding 〈EAT〉 fixed. For instance, analyzing the molecules within the 〈EAT〉 = 80 ± 0.2 eV window (a region of high density in this correlation plot, see Fig. S3†) uncovered a group of molecules with different structures and/or chemical compositions and a range of 〈EMBD〉 (e.g., the C4H11NO2 and C7H8 isomers in the bottom inset of Fig. 2(a)). When comparing the extended (〈Dmax〉 = 6.71 Å) and compact (〈Dmax〉 = 3.17 Å) C4H11NO2 isomers, the latter exhibits a more negative 〈EMBD〉; this is consistent with the more sizeable vdW/dispersion energy contributions that arise from the relatively closer non-bonded atoms in compact molecular geometries. In contrast, the extended C4H11NO2 isomer has the same 〈EMBD〉 (and 〈EAT〉) as the more compact ring-like C7H8 hydrocarbon (〈Dmax〉 = 3.10 Å)—another illustrative example of the non-trivial compromises made between the number of atoms, chemical composition, and volume/spatial extent of a molecule in determining 〈EMBD〉. This example also illustrates another important aspect of “freedom of design” in CCS, i.e., that two distinct molecules can share multiple physicochemical properties (vide infra). Interestingly, despite having very similar 〈Dmax〉, the compact C4H11NO2 isomer has a more negative 〈EMBD〉 than the compact ring-like C7H8 isomer—a result of more nuanced topological effects (i.e., packed/globular vs. void space) on the vdW/dispersion interactions in molecules.78
By considering 〈Dmax〉 in this analysis, we have partially accounted for the fact that 〈EMBD〉 and 〈EAT〉 are extensive properties. However, one can perform the same analysis after explicitly normalizing these properties (i.e., 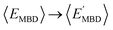 and
and 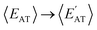 ) with respect to different size-dependent quantities (see Sec. 2). As depicted in Fig. S4†, the degree of correlation between
) with respect to different size-dependent quantities (see Sec. 2). As depicted in Fig. S4†, the degree of correlation between 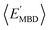 and
and 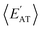 strongly depends on the chosen normalization quantity and can therefore be quite variable, ranging from a slight increase in |ρ| (i.e., |ρ| = 0.92 → 0.93, when normalized with respect to the thermally-averaged molecular volume 〈V〉) to a substantial decrease in |ρ| (i.e., |ρ| = 0.92 → 0.37, when normalized with respect to the total number of atoms Natoms). Despite such sizeable changes to the degree of correlation between these properties, we were still able to find example molecules located within fixed
strongly depends on the chosen normalization quantity and can therefore be quite variable, ranging from a slight increase in |ρ| (i.e., |ρ| = 0.92 → 0.93, when normalized with respect to the thermally-averaged molecular volume 〈V〉) to a substantial decrease in |ρ| (i.e., |ρ| = 0.92 → 0.37, when normalized with respect to the total number of atoms Natoms). Despite such sizeable changes to the degree of correlation between these properties, we were still able to find example molecules located within fixed 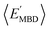 and
and 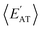 windows (for either normalization protocol) that were analogous to those obtained using the extensive variants (cf. the top and bottom insets in Fig. S4(a), (b)† and 2(a)). In other words, we were able to find structurally and/or compositionally distinct molecules with the same
windows (for either normalization protocol) that were analogous to those obtained using the extensive variants (cf. the top and bottom insets in Fig. S4(a), (b)† and 2(a)). In other words, we were able to find structurally and/or compositionally distinct molecules with the same 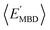 but different
but different 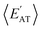 (and vice versa), as well as markedly distinct molecules sharing two (or more) normalized properties (see Fig. S4† and surrounding discussion). As such, these findings provide strong evidence that our “freedom of design” conjecture is quite robust and effectively independent of the use and choice of normalization protocol when dealing with extensive properties. For simplicity, we will therefore continue our analysis using non-normalized extensive properties for the remainder of this work.
(and vice versa), as well as markedly distinct molecules sharing two (or more) normalized properties (see Fig. S4† and surrounding discussion). As such, these findings provide strong evidence that our “freedom of design” conjecture is quite robust and effectively independent of the use and choice of normalization protocol when dealing with extensive properties. For simplicity, we will therefore continue our analysis using non-normalized extensive properties for the remainder of this work.
Having examined the intrinsic flexibility existing between two extensive properties, we now turn our attention to the 2D projection of molecular property space corresponding to 〈Egap〉 (an intensive property) and 〈α〉 (an extensive property). Fig. 2(b) depicts the corresponding (〈Egap〉, 〈α〉) correlation plot (with points colored according to the 〈EAT〉 windows in Fig. 2(a)); with a particularly low correlation coefficient of |ρ| = 0.06, these properties are effectively uncorrelated. Interestingly, we still find a large range of 〈Egap〉 and 〈α〉 (i.e., 3.8–8.4 eV and 68.0–110.0 a30), even though we are only considering the molecules contained in three narrow 〈EAT〉 windows. Similar to the (〈EMBD〉, 〈EAT〉) analysis performed above, we will fix one property and consider the flexibility in the other (and vice versa). Starting with the 〈Egap〉 = 6.8 ± 0.02 eV window (an intermediate HOMO–LUMO gap in this dataset), we again find molecules with distinct structures and compositions (see right inset in Fig. 2(b)) exhibiting a wide range of 〈α〉 (i.e., 74.2 a30 (C4H11N) to 103.3 a30 (C6H13N)) and 〈EAT〉 (i.e., 68.4 eV (C4H11N) to 90.0 eV (C6H13N)). Interestingly, the depicted C4H11NO2 and C6H13N isomers also share the same 〈μ〉 (in addition to 〈Egap〉), which is another example of the flexibility one has when searching for distinct molecules that share multiple physicochemical properties (see Sec. 3.3). Turning now to the fixed 〈α〉 = 100.7 ± 0.3 a30 window, we similarly found a set of distinct molecules (see right inset in Fig. 2(b)) that exhibit a wide range of 〈Egap〉 (i.e., 5.6 eV (C4H8N2S) to 7.1 eV (C6H13N)) and 〈EAT〉 (i.e., 68.3 eV (C4H8N2S) to 90.2 eV (C6H13N)). Within this group of molecules, we also found a two-molecule set (comprised of the two C6H13N isomers) that share four (extensive and intensive) properties: 〈EAT〉, 〈EMBD〉, 〈α〉, and 〈μ〉; in Sec. 3.3, we will show that this is not a rare occurrence or “cherry-picked example”, as there are thousands of three- and four-molecule sets (among the ≈41k equilibrium molecules in QM7-X) which share four properties. When considered together, the three C6H13N isomers depicted in the right insets of Fig. 2(b) also provide a simple but illustrative example of the inherent flexibility that exists throughout CCS. Through small and directed changes in the molecular structure—just one of the tunable knobs in the molecular design process—these constitutional isomers allow one to traverse a path through (〈Egap〉, 〈α〉)-space (i.e., the cyan triangle in Fig. 2(b)) in which an increase in 〈Egap〉 can be accompanied by an increase, a decrease, or no change in 〈α〉.
As a final case study, we now consider the flexibility one has in finding distinct molecules with the same EHOMO and ELUMO—two fundamentally important intensive properties that govern chemical reactivity and electron transfer in molecules. This choice of intensive properties poses an additional and more nuanced challenge to our “freedom of design” conjecture, since the number of structurally and/or compositionally distinct molecules sharing two properties (〈EHOMO〉 and 〈ELUMO〉) will be significantly less than those sharing the same 〈Egap〉 (vide supra). To proceed, we chose two distinct points in the (〈EHOMO〉, 〈ELUMO〉)-sector of molecular property space (see Fig. 2(c)). The first point corresponds to the window delineated by 〈EHOMO〉 = −7.5 ± 0.04 eV and 〈ELUMO〉 = 0.4 ± 0.04 eV, where we were able to find a set of structurally and compositionally distinct molecules, including (but not limited to): C5H8O2 (a cyclic molecule containing both epoxide and hydroxyl functional groups), C5H12O2 (an asymmetric ketal), and C7H14 (a cyclopropyl-containing alkane) that share these 〈EHOMO〉 and 〈ELUMO〉 values (see top right inset of Fig. 2(c)). With 〈EAT〉 and 〈α〉 ranging from 75.5–96.9 eV and 74.6–101.6 a30, this subset of molecules is rather diverse and indicative of considerable flexibility in this constrained sector of molecular property space. At the second of these points (〈EHOMO〉 = −6.5 ± 0.04 eV and 〈ELUMO〉 = −1.0 ± 0.04 eV), we were again able to find a diverse set of molecules with a similarly wide range of 〈EAT〉 (68.5–83.9 eV) and 〈α〉 (71.1–100.9 a30). In this case, some of the molecules that share these 〈EHOMO〉 and 〈ELUMO〉 values include: C4H9NO (an amine-containing aldehyde), C5H11NO (another amine-containing aldehyde), and C6H11N (an amine-containing conjugated alkene); see bottom right inset of Fig. 2(c). In many ways, this subset of molecules also illustrates how small and directed changes underlie rational molecular design. For one, the simple addition of a methyl group which converts C4H9NO to C5H11NO can be used to change the extensive properties (e.g., 〈α〉 and 〈EAT〉) without modifying the intensive properties (e.g., 〈EHOMO〉, 〈ELUMO〉, 〈Egap〉). In the same breath, more complex changes (i.e., functional group modifications, alchemical changes, increases in conjugation) can be used to induce selective and non-trivial modifications to some extensive properties (e.g., 〈α〉) while leaving others (e.g., 〈EAT〉) effectively unchanged.
In summary, these three complementary case studies show that the “freedom of design” conjecture proposed herein applies rather generally to both extensive and intensive properties, independent of whether these properties exhibit strong or weak mutual correlations. While also demonstrating that this conjecture is quite robust and effectively independent of the use and choice of normalization protocol when considering extensive properties, our analysis also indicates that the normalization protocol can potentially be used to enhance (or perhaps optimize) the flexibility in CCS when searching for distinct molecules with a targeted set of properties.
3.3 Multi-property analysis: exploring more complex manifolds of molecular property space
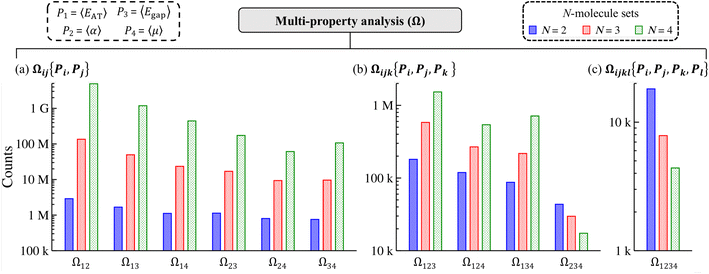
The fact that we were able to find numerous examples of distinct molecules that share two (or more) extensive and/or intensive properties in restricted sectors (i.e., selected windows) of QM7-X molecular property space in Sec. 3.2 provides strong support for an intrinsic flexibility in CCS that can be leveraged when searching for molecules with targeted QM properties. In this section, we demonstrate that these are not rare occurrences (or “cherry-picked examples”) by lifting such restrictions and exhaustively enumerating the number of N-molecule sets (i.e., sets containing N = 2, 3, 4 unique molecules) that share two, three, or four of the following thermally-averaged (T = 300 K) extensive (P1 = 〈EAT〉 and P2 = 〈α〉) and/or intensive (P3 = 〈Egap〉 and P4 = 〈μ〉) properties. This enumeration will be performed on the ≈41k equilibrium molecules in QM7-X and property-specific thresholds will be used to identify each N-molecule set (see Sec. 2 for more details).We start this analysis at the two-property tier, which consists of six different two-property combinations/levels (denoted by Ωij{Pi, Pj} throughout). Even from a quick glance at Fig. 3(a), one can see that the number of N-molecule sets that share any pair of these four properties is quite large, with total counts ranging from just under 1M to well over 4G. By far, the largest counts resulted from enumeration at the Ω12{〈EAT〉, 〈α〉} level, which yielded ≈2.9M unique 2-molecule sets, ≈134.5M unique 3-molecule sets, and ≈4.9G unique 4-molecule sets. In other words, there are nearly three million unique pairs of molecules (among the ≈863M possible unique molecular pairs) that have the same 〈EAT〉 and 〈α〉. In general, these counts tend to decrease as the extensive properties are replaced by the intensive properties, with the smallest counts resulting from enumeration at the Ω24{〈α〉, 〈μ〉} and Ω34{〈Egap〉, 〈μ〉} levels (although there are still millions of 2-, 3-, and 4-molecule sets in both cases). We also found that the number of N-molecule sets consistently increased with N across the entire two-property tier, such that the number of 4-molecule sets > the number of 3-molecule sets > the number of 2-molecule sets for all two-property combinations. Both of these trends illustrate the remarkable degree of flexibility that one has when searching for distinct molecules sharing any two of these properties, and will be discussed in more detail below.
While the number of N-molecule sets that share three properties are considerably less than those sharing two, the total counts at the three-property tier are still quite large and range from 10k to 1M (see Fig. 3(b)). The largest counts of 2-, 3-, and 4-molecule sets were found at the Ω123{〈EAT〉, 〈α〉, 〈Egap〉} level (which contains two extensive and one intensive properties), while the smallest counts were found at the Ω234{〈α〉, 〈Egap〉, 〈μ〉} level (which contains one extensive and two intensive properties). While we still observe a consistent rise in the total count of N-molecule sets from N = 2 to N = 4 at the Ω123{〈EAT〉, 〈α〉, 〈Egap〉}, Ω124{〈EAT〉, 〈α〉, 〈μ〉}, and Ω134{〈EAT〉, 〈Egap〉, 〈μ〉} levels, this trend is completely reversed at the Ω234{〈α〉, 〈Egap〉, 〈μ〉} level. This observation can be explained by considering the combinatorics that determine the number of N-molecule sets that share a given array of properties. Although our analysis here focuses on N-molecule sets with N = 2, 3, 4, enumeration of the ≈41k equilibrium molecules in QM7-X often finds significantly larger clusters (or parent sets) that contain M > N molecules sharing a given array of properties. Since the number of N-molecule sets that can be formed from one of these M-molecule clusters is given by 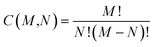 , each cluster with M ≥ 8 will generate more 4-molecule sets than 3-molecule sets and more 3-molecule sets than 2-molecule sets. Hence, the observed increase in the total count of N-molecule sets from N = 2 to N = 4 will start to break down when M < 8, which indicates that enumeration at the Ω234{〈α〉, 〈Egap〉, 〈μ〉} level tends to find M-molecule clusters containing fewer molecules than enumeration at the three other Ωijk{Pi, Pj, Pk} levels. The most likely explanation for these observed trends is twofold: (i) since the ≈41k equilibrium molecules in QM7-X correspond to ≈7k different molecular formulae, structural changes are sampled to a larger extent than compositional changes in the molecules enumerated in this analysis (see Sec. 2 and ref. 34); and (ii) intensive properties tend to be more sensitive to such structural changes than extensive properties.
, each cluster with M ≥ 8 will generate more 4-molecule sets than 3-molecule sets and more 3-molecule sets than 2-molecule sets. Hence, the observed increase in the total count of N-molecule sets from N = 2 to N = 4 will start to break down when M < 8, which indicates that enumeration at the Ω234{〈α〉, 〈Egap〉, 〈μ〉} level tends to find M-molecule clusters containing fewer molecules than enumeration at the three other Ωijk{Pi, Pj, Pk} levels. The most likely explanation for these observed trends is twofold: (i) since the ≈41k equilibrium molecules in QM7-X correspond to ≈7k different molecular formulae, structural changes are sampled to a larger extent than compositional changes in the molecules enumerated in this analysis (see Sec. 2 and ref. 34); and (ii) intensive properties tend to be more sensitive to such structural changes than extensive properties.
Quite interestingly, the number of N-molecule sets that share all four of these properties are also quite large. As depicted in Fig. 3(c), enumeration at the Ω1234{〈EAT〉, 〈α〉, 〈Egap〉, 〈μ〉} level—the most complex manifold of molecular property space considered in this work—found ≈20k 2-molecule sets, ≈8k 3-molecule sets, and ≈4k 4-molecule sets. Intrigued by these results, we also considered the same analysis with 〈EHOMO〉 and 〈ELUMO〉 (instead of 〈Egap〉 and 〈μ〉) as the intensive properties (see Fig. S5†). In doing so, we found that the number of N-molecule sets at the three- and four-property tiers in this more stringent case are actually larger than those shown in Fig. 3(b) and (c). For instance, there are nearly 2.5× more 4-molecule sets (i.e., ≈10k) at the Ω1234{〈EAT〉, 〈α〉, 〈EHOMO〉, 〈ELUMO〉} level than the Ω1234{〈EAT〉, 〈α〉, 〈Egap〉,〈μ〉} level.
In summary, this tiered multi-property analysis has demonstrated that it is quite feasible to find structurally and/or compositionally distinct molecules that share 2–4 extensive/intensive ground-state and response properties—yet another manifestation that “freedom of design” is a fundamental and emergent property of CCS. By considering the decay rate in the number of N-molecule sets, we also estimate that 7–10 properties are needed to uniquely identify each molecule in the sector of CCS spanned by QM7-X. This quantity corresponds to the effective dimensionality of a small (primarily organic) molecule in molecular property space and can potentially be used to guide the length of property-based molecular features (or fingerprints) for use in ML applications.
3.4 Multi-property optimization: finding optimal Pareto fronts in molecular property space
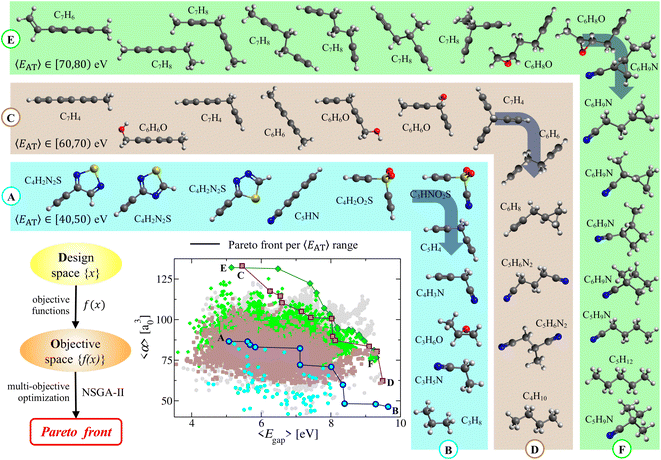
In the molecular design process, which often involves the simultaneous optimization of multiple (i.e., typically two or more) physicochemical properties, Pareto fronts (or frontiers) represent the so-called Pareto-optimal solutions for which no single property can be improved without degrading the other(s). Pareto fronts have therefore been used in a number of different fields (e.g., economics, medicine, materials science, chemical engineering)79–81 and have given rise to evolutionary multi-objective optimization.48,49 In this work, we use this approach in the complex manifold of molecular property space defined by 〈EAT〉, 〈α〉, and 〈Egap〉 to search for molecules in QM7-X with simultaneously large 〈α〉 and 〈Egap〉 values. Here, we note in passing that this approach is general and could be used to search for molecules with any number/combination of properties (e.g., promising small-molecule protein inhibitors with large 〈α〉 and reduced 〈μ〉).To begin, we partitioned the QM7-X molecules in the weakly correlated (〈α〉, 〈Egap〉)-space according to the following 〈EAT〉 windows: [40,50) eV, [60,70) eV, and [70,80) eV (see Fig. 4); these windows encompass the molecular diversity in QM7-X (see Fig. S3†), and contain molecules with distinct chemical compositions and a wide range of 〈α〉 and 〈Egap〉 values. The Pareto fronts resulting from independent multi-property optimizations carried out in each of these 〈EAT〉 windows are plotted in Fig. 4. Each of these fronts represents a unique and non-trivial path through CCS consisting of a sequence of molecules connected by structural and/or compositional changes that define the optimal balance between these properties. While consecutive molecules on a given front can often be rationalized a posteriori using chemical/physical intuition, several interesting and unexpected molecules appear in this analysis, reflecting the freedom one has when designing molecules with a targeted array of properties.
Consider the Ⓐ → Ⓑ front, which contains 11 diverse molecular structures with varied compositions and 〈EAT〉 ∈ [40,50) eV. This front starts with three constitutional isomers of C4H2N2S, each of which contains a terminal alkyne (ethynyl group) directly adjacent to an aromatic thiadiazole ring. Such conjugation facilitates charge delocalization and π-electron mobility across each molecule; as such, these isomers have large (but similar) 〈α〉 ≈ 86.0 a30 and (relatively) small 〈Egap〉. However, 〈Egap〉 is more sensitive to the structural differences connecting these isomers and can be tuned by ≈0.6 eV by changing the relative positions of the heteroatoms in the thiadiazole ring. Continuing along this front, a linear and highly conjugated molecule (penta-2,4-diynenitrile, C5HN) appears, with a structure and composition that is quite different from the C4H2N2S isomers. Despite such differences, this molecule has 〈α〉 and 〈Egap〉 values that are both very similar to its Pareto-adjacent C4H2N2S isomers, which again illustrates the flexibility provided by CCS when searching for distinct molecules sharing multiple properties. Ethynyl sulfone (C4H2O2S) is the next molecule on this front, and contains two terminal alkynes connected via a central sulfonyl (SO2) moiety in a kinked arrangement—another large change in both structure and composition when compared to C5HN. This non-linear molecular geometry reduces π-electron mobility and charge delocalization, resulting in a rather large change (i.e., >1 eV) in 〈Egap〉. In the same breath, this molecule shares a nearly identical 〈α〉 with C5HN—a simple and illustrative example of “freedom of design” provided by this non-trivial path through CCS. Also interesting is the natural emergence of the rational molecular design process when retrospectively analyzing a Pareto front. To see this, consider the sequence of small directed changes needed to arrive at the next three molecules on the Ⓐ → Ⓑ front. Since the polarizability of a N atom is smaller than that of C–H, replacing an ethynyl (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H) with a nitrile (C
C–H) with a nitrile (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) group (i.e., C4H2O2S → C3HNO2S) can be used to decrease 〈α〉 while leaving 〈Egap〉 effectively unchanged. Alternatively, one could instead replace SO2 with a more insulating methylene (CH2) group (i.e., C4H2O2S → C5H4) to decrease 〈α〉 while simultaneously increasing 〈Egap〉 by ≈1 eV. Finally, making both of these changes at the same time (i.e., C4H2O2S → C4H3N) leads to further changes in both 〈α〉 and 〈Egap〉. While the last segment on this front can be rationalized a posteriori as a series of structural/compositional changes resulting in more compact and less conjugated molecules that exhibit reduced 〈α〉 and increased 〈Egap〉 values, the a priori prediction of these molecules is far from trivial.
N) group (i.e., C4H2O2S → C3HNO2S) can be used to decrease 〈α〉 while leaving 〈Egap〉 effectively unchanged. Alternatively, one could instead replace SO2 with a more insulating methylene (CH2) group (i.e., C4H2O2S → C5H4) to decrease 〈α〉 while simultaneously increasing 〈Egap〉 by ≈1 eV. Finally, making both of these changes at the same time (i.e., C4H2O2S → C4H3N) leads to further changes in both 〈α〉 and 〈Egap〉. While the last segment on this front can be rationalized a posteriori as a series of structural/compositional changes resulting in more compact and less conjugated molecules that exhibit reduced 〈α〉 and increased 〈Egap〉 values, the a priori prediction of these molecules is far from trivial.
After performing a similar analysis on the QM7-X molecules with 〈EAT〉 ∈ [60,70) eV and 〈EAT〉 ∈ [70,80) eV, we again found numerous examples of how the intrinsic flexibility woven into CCS manifests during the molecular design process (see Fig. 4). In the 〈EAT〉 ∈ [60,70) eV sector, the Ⓒ → Ⓓ front forms an effectively straight line bisecting (〈α〉, 〈Egap〉)-space, indicating that most of its 12 constituent molecules correspond to Pareto-optimal solutions which simultaneously optimize both 〈α〉 and 〈Egap〉. Notable exceptions worth mention include the sixth, seventh, and eighth molecules on this front (i.e., C6H6O, C7H4, C6H6), wherein we first observe a sharp increase in 〈Egap〉 accompanied by almost no change in 〈α〉 as C6H6O (a kinked molecule with two alkynes connected by a central alcohol group) is transformed into C7H4 (a propeller-like molecule with three terminal alkynes connected by a central aliphatic (CH) group). As mentioned above, such changes can often be rationalized retrospectively, i.e., here we would argue that the broken conjugation (among the three triple bonds) in C7H4 will further localize the π-electrons, thereby increasing 〈Egap〉. In the same breath, it is perhaps less straightforward to rationalize why C6H6O and C7H4 have nearly identical 〈α〉 values, besides making the somewhat hand-waving argument that these molecules have similar molecular volumes. This was followed by a sharp decrease in 〈α〉 accompanied by almost no change in 〈Egap〉 as C7H4 is transformed into C6H6 (a staggered molecule with two terminal alkynes connected by a central ethylene (–CH2–CH2–) group). In this case, one could argue (with some conviction) that such a transition does not affect the overall mobility of the π-electrons (hence no appreciable change in 〈Egap〉); in the same breath, this transition clearly involves the loss of a C atom and the gain of two H atoms, which will tend to decrease 〈α〉 since ![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) C > 2
C > 2![[small alpha, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dc.gif) H. In the 〈EAT〉 ∈ [70,80) eV sector, the Ⓔ → Ⓕ front is more parabolic in shape and primarily consists of structural/constitutional isomers punctuated by simple functional group changes; for brevity, we leave a more detailed analysis of this front to the interested reader.
H. In the 〈EAT〉 ∈ [70,80) eV sector, the Ⓔ → Ⓕ front is more parabolic in shape and primarily consists of structural/constitutional isomers punctuated by simple functional group changes; for brevity, we leave a more detailed analysis of this front to the interested reader.
4 Summary and outlook
In this work, we used the recently developed QM7-X dataset—which includes 42 physicochemical properties obtained via high-level QM calculations for ≈4.2M (equilibrium and non-equilibrium) molecular structures containing up to seven heavy atoms—to study the structure–property/property–property relationships (SPR/PPR) that exist in the sector of chemical compound space (CCS) spanned by small (primarily organic) molecules. By quantitatively analyzing the pairwise correlations between a number of diverse physicochemical properties, we found that a vast majority (>90%) exhibited little (to no) correlation. While one might view this as a challenge for rational molecular design, we argued that this finding highlights an intrinsic flexibility—or “freedom of design”—that exists throughout CCS, as there are generally no hard-and-fast limitations preventing a molecule from exhibiting any pair of these properties.We then investigated how this intrinsic degree of flexibility depends on the structure and chemical composition (i.e., the tunable knobs underlying the molecular design process) of the molecules in this sector of CCS. Through a series of detailed case studies, we showcased numerous examples of structurally and/or compositionally distinct molecules that share multiple properties, demonstrating that the “freedom of design” conjecture proposed herein applies rather generally to both extensive and intensive properties, independent of whether such properties exhibit strong or weak mutual correlations. We also showed that these findings are quite robust and effectively independent of whether one works with normalized (or non-normalized) variants of the extensive properties. Quite interestingly, this analysis also indicated that the choice of normalization protocol might be another knob that can be used to selectively enhance/optimize the flexibility in CCS when searching for molecules with targeted properties.
Since molecular design often involves the simultaneous optimization of multiple properties, we also used the extensive QM7-X structure–property dataset to characterize and enumerate progressively more complex manifolds of molecular property space. By performing a tiered multi-property analysis involving exhaustive enumeration over the ≈41k equilibrium molecules in QM7-X, we found a remarkably large number of structurally and/or compositionally distinct molecules that share multiple properties—yet another manifestation of “freedom of design” in CCS. For instance, we were able to find ≈4k unique 4-molecule sets that share the same EAT, α, Egap, and μ values as well as ≈10k unique 4-molecule sets that share the same EAT, α, EHOMO, and ELUMO values. While a number of different extensive, intensive, ground-state, and response properties were included in our analysis, additional research will be needed to assess the full extent of “freedom of design” when considering more advanced (i.e., optical, excited-state) properties across larger swaths of CCS.
To explore how this intrinsic flexibility will manifest in the molecular design process, we then used Pareto multi-property optimization to search for molecules in QM7-X with simultaneously large α and Egap values. Analysis of the resulting Pareto fronts identified unique and non-trivial paths through CCS consisting of molecules connected by structural and/or compositional changes that yield simultaneously optimal values for these properties. While consecutive molecules on a given front can often be rationalized a posteriori using chemical/physical intuition, several interesting and unexpected molecules appeared in this analysis, reflecting the freedom one has in the rational design and discovery of molecules with targeted property values. A potentially interesting next step would use these Pareto-optimal structures in conjunction with current ML approaches (e.g., active learning) to build reliable multi-objective frameworks for identifying the molecules in CCS (beyond those in QM7-X) that are missing in each front.82,83
By demonstrating that “freedom of design” is a fundamental and emergent property of CCS, this work has a number of important implications in the field of rational molecular design. For one, we hope this work will challenge the greater chemical sciences community to consider how such intrinsic flexibility can be used to extend the dominant paradigm in the forward molecular design process (i.e., functional group modification based on a largely fixed molecular scaffold(s)). We also hope that this work will emphasize the critical importance of high-quality QM structure–property data in the training and development of next-generation ML approaches that will enable the exploration and characterization of more vast swaths of CCS. Additionally, this work estimated that 7–10 properties are needed to uniquely identify the small (primarily organic) molecules in QM7-X. This quantity is tantamount to the effective dimensionality associated with each molecule (in molecular property space) and is needed to define the inverse molecular design problem, in which one seeks to find a molecule (or set of molecules) corresponding to a targeted/pre-defined array of properties. At the current time, substantive progress towards solving this “holy grail” of molecular design seems possible with the use of invertible ML architectures (e.g., as accomplished by generative and diffusion models84–86) in conjunction with diverse molecular datasets (e.g., QM7-X and beyond).
Author contributions
The work was initially conceived by LMS and AT, and designed with contributions from JH, BGE, AVM, and RAD. AT and RAD supervised and revised all stages of the work. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
LMS, JH, and AT acknowledge financial support from the European Research Council (ERC-CoG grant BeStMo). This material is based upon work supported by the National Science Foundation under Grant No. CHE-1945676. RAD also gratefully acknowledges financial support from an Alfred P. Sloan Research Fellowship. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. This research also used computational resources provided by the University of Luxembourg and the Center for Information Services and High Performance Computing (ZIH) at TU Dresden.References
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed
.
- B. Huang and O. A. von Lilienfeld, Chem. Rev., 2021, 121, 10001–10036 CrossRef CAS PubMed
.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef
.
- A. Tkatchenko, Nat. Commun., 2020, 11, 4125 CrossRef CAS PubMed
.
- A. P. Bartók, S. De, C. Poelking, N. Bernstein, J. R. Kermode, G. Csányi and M. Ceriotti, Sci. Adv., 2017, 3, 1–8 Search PubMed
.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed
.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed
.
- M. Meuwly, Chem. Rev., 2021, 121, 10218–10239 CrossRef CAS PubMed
.
- E. N. Muratov, J. Bajorath, R. P. Sheridan, I. V. Tetko, D. Filimonov, V. Poroikov, T. I. Oprea, I. I. Baskin, A. Varnek, A. Roitberg, O. Isayev, S. Curtalolo, D. Fourches, Y. Cohen, A. Aspuru-Guzik, D. A. Winkler, D. Agrafiotis, A. Cherkasov and A. Tropsha, Chem. Soc. Rev., 2020, 49, 3525–3564 RSC
.
- A. Cherkasov, E. N. Muratov, D. Fourches, A. Varnek, I. I. Baskin, M. Cronin, J. Dearden, P. Gramatica, Y. C. Martin, R. Todeschini, V. Consonni, V. E. Kuz'min, R. Cramer, R. Benigni, C. Yang, J. Rathman, L. Terfloth, J. Gasteiger, A. Richard and A. Tropsha, J. Med. Chem., 2014, 57, 4977–5010 CrossRef CAS PubMed
.
- G. Lambrinidis and A. Tsantili-Kakoulidou, Expert Opin. Drug Discovery, 2018, 13, 851–859 CrossRef
.
-
R. D. Clark and P. R. Daga, in Building a Quantitative Structure-Property Relationship (QSPR) Model, ed. R. S. Larson and T. I. Oprea, Springer New York, New York, NY, 2019, pp. 139–159 Search PubMed
.
-
K. Roy, S. Kar and R. Das, A Primer on QSAR/QSPR Modeling: Fundamental Concepts, Springer International Publishing, 2015 Search PubMed
.
- T. Le, V. C. Epa, F. R. Burden and D. A. Winkler, Chem. Rev., 2012, 112, 2889–2919 CrossRef CAS PubMed
.
- J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Nat. Rev. Drug Discovery, 2019, 18, 463–477 CrossRef CAS
.
- V. O. Gawriljuk, D. H. Foil, A. C. Puhl, K. M. Zorn, T. R. Lane, O. Riabova, V. Makarov, A. S. Godoy, G. Oliva and S. Ekins, J. Chem. Inf. Model., 2021, 61, 3804–3813 CrossRef CAS
.
- J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz, N. M. Donghia, C. R. MacNair, S. French, L. A. Carfrae, Z. Bloom-Ackermann, V. M. Tran, A. Chiappino-Pepe, A. H. Badran, I. W. Andrews, E. J. Chory, G. M. Church, E. D. Brown, T. S. Jaakkola, R. Barzilay and J. J. Collins, Cell, 2020, 180, 688–702 CrossRef CAS
.
- T. Williams, K. McCullough and J. A. Lauterbach, Chem. Mater., 2020, 32, 157–165 CrossRef CAS
.
- D. Xue, P. V. Balachandran, J. Hogden, J. Theiler, D. Xue and T. Lookman, Nat. Commun., 2016, 7, 11241 CrossRef CAS PubMed
.
- H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, npj Comput. Mater., 2018, 4, 51 CrossRef
.
- L. Tallorin, J. Wang, W. E. Kim, S. Sahu, N. M. Kosa, P. Yang, M. Thompson, M. K. Gilson, P. I. Frazier, M. D. Burkart and N. C. Gianneschi, Nat. Commun., 2018, 9, 5253 CrossRef CAS
.
- J.-L. Reymond and M. Awale, ACS Chem. Neurosci., 2012, 3, 649–657 CrossRef CAS PubMed
.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS
.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed
.
- T. Fink, H. Bruggesser and J.-L. Reymond, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS PubMed
.
- T. Fink and J.-L. Reymond, J. Chem. Inf. Model., 2007, 47, 342–353 CrossRef CAS
.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, New J. Phys., 2013, 15, 095003 CrossRef CAS
.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef
.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed
.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 170193 CrossRef CAS PubMed
.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC
.
- Y. Yang, K. U. Lao, D. M. Wilkins, A. Grisafi, M. Ceriotti and R. A. DiStasio Jr, Sci. Data, 2019, 6, 152 CrossRef PubMed
.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 134 CrossRef CAS PubMed
.
- J. Hoja, L. Medrano Sandonas, B. G. Ernst, A. Vazquez-Mayagoitia, R. A. DiStasio Jr and A. Tkatchenko, Sci. Data, 2021, 8, 43 CrossRef CAS
.
- G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185–192 CrossRef CAS
.
- M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948 CrossRef CAS
.
- A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed
.
- M. Stöhr, G. S. Michelitsch, J. C. Tully, K. Reuter and R. J. Maurer, J. Chem. Phys., 2016, 144, 151101 CrossRef
.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio Jr and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed
.
- V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379 CrossRef CAS
.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS
.
- X. Ren, P. Rinke, V. Blum, J. Wieferink, A. Tkatchenko, A. Sanfilippo, K. Reuter and M. Scheffler, New J. Phys., 2012, 14, 053020 CrossRef
.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef
.
- V. Bhaskar, S. K. Gupta and A. K. Ray, Rev. Chem. Eng., 2000, 16, 1–54 CAS
.
- J. Blank and K. Deb, IEEE Access, 2020, 8, 89497–89509 Search PubMed
.
-
J. Mandal, S. Mukhopadhyay and P. Dutta, Multi-Objective Optimization: Evolutionary to Hybrid Framework, Springer Singapore, Singapore, 2018 Search PubMed
.
-
G. Rangaiah and A. Bonilla-Petriciolet, Multi-Objective Optimization in Chemical Engineering: Developments and Applications, John Wiley & Sons, Ltd, United Kingdom, 2013 Search PubMed
.
- M. D. Hager, B. Esser, X. Feng, W. Schuhmann, P. Theato and U. S. Schubert, Adv. Mater., 2020, 32, 2000587 CrossRef CAS
.
- J. Lopez, D. G. Mackanic, Y. Cui and Z. Bao, Nat. Rev. Mater., 2019, 4, 312–330 CrossRef CAS
.
- H. B. G. Casimir and D. Polder, Phys. Rev., 1948, 73, 360–372 CrossRef CAS
.
- K. T. Tang and M. Karplus, Phys. Rev., 1968, 171, 70–74 CrossRef CAS
.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed
.
- R. A. DiStasio Jr, V. V. Gobre and A. Tkatchenko, J. Phys.: Condens. Matter, 2014, 26, 213202 CrossRef PubMed
.
- A. Tkatchenko, A. Ambrosetti and R. A. DiStasio Jr, J. Chem. Phys., 2013, 138, 074106 CrossRef PubMed
.
-
A. Stone, The Theory of Intermolecular Forces, Clarendon Press, United Kingdom, 1996 Search PubMed
.
- R. A. DiStasio Jr, O. A. von Lilienfeld and A. Tkatchenko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14791–14795 CrossRef PubMed
.
- Y. S. Al-Hamdani and A. Tkatchenko, J. Chem. Phys., 2019, 150, 010901 CrossRef PubMed
.
- T. Brinck, J. S. Murray and P. Politzer, J. Chem. Phys., 1993, 98, 4305–4306 CrossRef CAS
.
- S. A. Blair and A. J. Thakkar, J. Chem. Phys., 2014, 141, 074306 CrossRef PubMed
.
- Y.-Q. Zhao, Y. Cheng, C.-E. Hu, B.-R. Yu and G.-F. Ji, Theor. Chem. Acc., 2021, 140, 51 Search PubMed
.
- X.-B. Li, H.-Y. Wang, R. Lv, W.-D. Wu, J.-S. Luo and Y.-J. Tang, J. Phys. Chem. A, 2009, 113, 10335–10342 CrossRef CAS PubMed
.
- I. Vasiliev, S. Öğüt and J. R. Chelikowsky, Phys. Rev. Lett., 1997, 78, 4805–4808 CrossRef CAS
.
- A. P. Jones, J. Crain, V. P. Sokhan, T. W. Whitfield and G. J. Martyna, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144103 CrossRef
.
- P. Szabó, S. Góger, J. Charry, M. R. Karimpour, D. V. Fedorov and A. Tkatchenko, Phys. Rev. Lett., 2022, 128, 070602 CrossRef PubMed
.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 581 CrossRef CAS
.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 643 CrossRef CAS
.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS
.
- P. Politzer, P. Jin and J. S. Murray, J. Chem. Phys., 2002, 117, 8197–8202 CrossRef CAS
.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS
.
- P. K. Chattaraj, P. Fuentealba, P. Jaque and A. Toro-Labbé, J. Phys. Chem. A, 1999, 103, 9307–9312 CrossRef CAS
.
- D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio Jr and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3401–3406 CrossRef CAS
.
- M. Brieger, A. Renn, A. Sodeik and A. Hese, Chem. Phys., 1983, 75, 1–9 CrossRef CAS
.
-
A. D. Buckingham, in Permanent and Induced Molecular Moments and Long-Range Intermolecular Forces, John Wiley & Sons, Ltd, United Kingdom, 1967, ch. 2, vol. 12, pp. 107–142 Search PubMed
.
- D. V. Fedorov, M. Sadhukhan, M. Stöhr and A. Tkatchenko, Phys. Rev. Lett., 2018, 121, 183401 CrossRef CAS PubMed
.
- K. U. Lao, Y. Yang and R. A. DiStasio Jr, Phys. Chem. Chem. Phys., 2021, 23, 5773–5779 RSC
.
- Y. Yang, K. U. Lao and R. A. DiStasio Jr, Phys. Rev. Lett., 2019, 122, 026001 CrossRef CAS
.
- A. H. Farmahini, S. Krishnamurthy, D. Friedrich, S. Brandani and L. Sarkisov, Chem. Rev., 2021, 121, 10666–10741 CrossRef CAS PubMed
.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Nat. Commun., 2021, 12, 2312 CrossRef CAS PubMed
.
- T. Erps, M. Foshey, M. K. Luković, W. Shou, H. H. Goetzke, H. Dietsch, K. Stoll, B. von Vacano and W. Matusik, Sci. Adv., 2021, 7, eabf7435 CrossRef CAS PubMed
.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed
.
- Z. del Rosario, M. Rupp, Y. Kim, E. Antono and J. Ling, J. Chem. Phys., 2020, 153, 024112 CrossRef
.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed
.
- E. Hoogeboom, V. G. Satorras, C. Vignac and M. Welling, Equivariant Diffusion for Molecule Generation in 3D, arXiv, 2022, preprint, arXiv:2203.17003, DOI:10.48550/arXiv.2203.17003.
- D. M. Anstine and O. Isayev, J. Am. Chem. Soc., 2023, 145, 8736–8750 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional analyses of the structure–property and property–property relationships in the sector of chemical compound space spanned by small (primarily organic) molecules. See DOI: https://doi.org/10.1039/d3sc03598k |
| This journal is © The Royal Society of Chemistry 2023 |