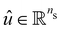Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Learning 3D shape proprioception for continuum soft robots with multiple magnetic sensors†
Thomas
Baaij‡
 a,
Marn Klein
Holkenborg‡
a,
Marn Klein
Holkenborg‡
 a,
Maximilian
Stölzle‡
a,
Maximilian
Stölzle‡
 *a,
Daan
van der Tuin‡
*a,
Daan
van der Tuin‡
 a,
Jonatan
Naaktgeboren
a,
Jonatan
Naaktgeboren
 a,
Robert
Babuška
a,
Robert
Babuška
 ab and
Cosimo
Della Santina
ab and
Cosimo
Della Santina
 ac
ac
aCognitive Robotics, Delft University of Technology, Mekelweg 2, 2628 CD Delft, The Netherlands. E-mail: T.A.Baaij@tudelft.nl; M.L.B.KleinHolkenborg@tudelft.nl; M.W.Stolzle@tudelft.nl; D.D.P.vanderTuin@tudelft.nl; J.Naaktgeboren-1@tudelft.nl; R.Babuska@tudelft.nl; C.DellaSantina@tudelft.nl
bCzech Institute of Informatics Robotics and Cybernetics, Czech Technical University in Prague, 160 00 Prague, Czech Republic
cInstitute of Robotics and Mechatronics, German Aerospace Center (DLR), 82234 Weßling, Germany
First published on 30th November 2022
Abstract
Sensing the shape of continuum soft robots without obstructing their movements and modifying their natural softness requires innovative solutions. This letter proposes to use magnetic sensors fully integrated into the robot to achieve proprioception. Magnetic sensors are compact, sensitive, and easy to integrate into a soft robot. We also propose a neural architecture to make sense of the highly nonlinear relationship between the perceived intensity of the magnetic field and the shape of the robot. By injecting a priori knowledge from the kinematic model, we obtain an effective yet data-efficient learning strategy. We first demonstrate in simulation the value of this kinematic prior by investigating the proprioception behavior when varying the sensor configuration, which does not require us to re-train the neural network. We validate our approach in experiments involving one soft segment containing a cylindrical magnet and three magnetoresistive sensors. During the experiments, we achieve mean relative errors of 4.5%.
1 Introduction
The past decade has seen an explosion of novel continuum soft robotic platforms.1–3 Inspired by invertebrate animals, these robots are almost entirely composed of soft deformable materials.4 This makes them robust and safe, but at the same time, it renders their modeling,5 control,6 and shape sensing7 substantially more complex than for their rigid counterparts. Shape sensing is especially intricate because it is both a technological and algorithmic challenge. Sensors must not obstruct the natural behavior or reduce the compliance of soft robots. At the same time, non-collocated and nonlinear sensors require algorithms for the measurements to be interpreted and connected to a description of the robot's shape.Several sensing modalities have been considered to implement shape sensing, such as resistive,8,9 capacitive,10,11 optical,12 and visual.13 Magnetic sensors14–18 are a promising solution as they are compact, highly sensitive, and can be easily integrated into existing soft robot designs. Thus, they can provide reliable and fully proprioceptive measurements at the cost of a minimal decrease in the robot's softness. Among the above-cited papers, the only work leveraging external magnetic fields is by Song et al.,14 where coils placed at a distance generate the magnetic field. Along this thought, an obvious choice would be to measure the earth's magnetic field for proprioception purposes. However, it would only allow estimating two rotational components, and any translational effects, such as an elongation of the continuum robot, could not be captured. Alternatively, some papers15–17 use co-axial pairs of magnets and sensors embedded in the robot to estimate planar deformations. Recently, Mitchell et al.18 have shown that a similar strategy can sense 3D deformations. Such simple arrangements greatly simplify the analysis, allowing for connecting sensor readings to the robot's shape through direct interpolation. Nevertheless, relying on isolated pairs of sensors and magnets also strongly limits the density and the amount of information gathered through this method.
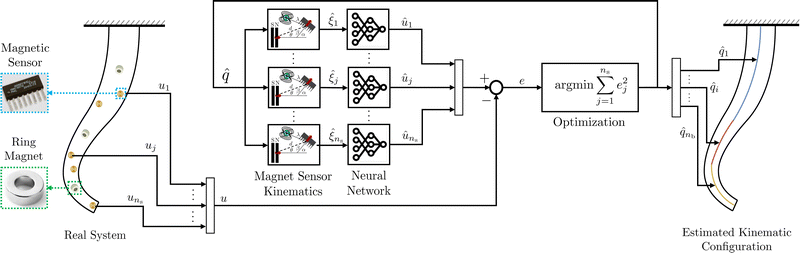
This paper proposes to use permanent ring magnets and multiple magnetic sensors for shape sensing of continuum soft robots. Importantly, we remove the requirement of magnets and sensors being placed in co-axial pairs. We have been inspired by recent work leveraging deep learning to interpret various types of non-magnetic sensor data for proprioception purposes.19–22 However, learning end-to-end mappings from sensors to configurations has three significant drawbacks: (i) it is data-intensive, (ii) it calls for recurrent architectures to encourage temporal consistency for the robot's configuration estimates, (iii) it requires re-training when changing the kinematic model of the robot. We propose a neural architecture that circumvents all three issues (see Fig. 1). First, we train shallow neural networks to predict the measurements of the magnetic sensors from a parameterization describing their relative pose with respect to the magnets. We then optimize the configuration estimate – and thus the sensor positions – to minimize the error between the predicted and actual sensor measurements. This way, we introduce a priori information on the modes of deformation of a continuum soft robot, effectively removing the kinematics from the black box. The presented strategy enables us to re-arrange and remove redundant sensors during inference without requiring us to re-train the neural network on the adjusted sensor configuration.
To summarize, this paper contributes to the state of the art in soft robot sensing with:
• A proprioceptive sensing modality relying on multiple magnetic sensors in conjunction with a neural network-based architecture that learns to estimate the full 3D shape of the robot from the sensor readings.
• Injection of kinematic priors through a description to spatially relate the poses of a sensor to the magnets. This proposed parametrization serves as an input to a neural network predicting the sensor measurements.
• Experimental verification of the approach for a one-segment robot with three integrated magnetoresistive sensors and proprioception of 3D curvature.
We open-source a Python / PyTorch implementation of the proposed algorithm and the corresponding datasets on GitHub.§
2 Proprioception with magnetic sensors
This section introduces a methodology to achieve proprioception for soft robots with magnetic sensors. We consider a continuum robot with the shape of its backbone described by the configuration variables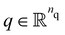 . In the commonly used piecewise constant curvature (PCC) kinematic state parametrization,23 the continuum robot is assumed to consist of nb segments with each segment exhibiting constant curvature and elongation along its length. Therefore, the configuration of the soft robot can be described with
. In the commonly used piecewise constant curvature (PCC) kinematic state parametrization,23 the continuum robot is assumed to consist of nb segments with each segment exhibiting constant curvature and elongation along its length. Therefore, the configuration of the soft robot can be described with 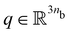 . Please refer to Appendix A.1 for more details. We indeed use PCC for most of our simulations and experiments. Note, however, that the proposed proprioception algorithm applies to any finite-dimensional kinematic description of a soft robot.5 In fact, we also specifically consider a robot with affine curvature24,25 with its shape described by the configuration
. Please refer to Appendix A.1 for more details. We indeed use PCC for most of our simulations and experiments. Note, however, that the proposed proprioception algorithm applies to any finite-dimensional kinematic description of a soft robot.5 In fact, we also specifically consider a robot with affine curvature24,25 with its shape described by the configuration 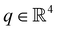 . We document this alternative kinematic model in Appendix A.2. The proprioception methodology described in the remaining section is agnostic to the chosen kinematic model.
. We document this alternative kinematic model in Appendix A.2. The proprioception methodology described in the remaining section is agnostic to the chosen kinematic model.
2.1 Proposed method at a glance
We integrate nm axially symmetric magnets and ns magnetic sensors into the robot. The magnets must be installed along the center line of the segment while the sensors can be arbitrarily placed. Fig. 1 concisely describes the proposed shape-sensing strategy with a pictorial example of a soft robot consisting of three segments and equipped with five magnetic sensors and three cylindrical magnets.The goal of the algorithmic part (center of the figure) is to regress the robot shape (left) by estimating the configuration ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) of all segments (right), starting from the measurements of the magnetic sensors u (e.g. usually the magnetic flux density). We achieve this by training a sensor measurement predictor and subsequently optimizing the configuration estimate
of all segments (right), starting from the measurements of the magnetic sensors u (e.g. usually the magnetic flux density). We achieve this by training a sensor measurement predictor and subsequently optimizing the configuration estimate ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) for the prediction û to match the actual sensor measurement u. Instead of predicting the sensor measurements end-to-end, we decouple the kinematics by explicitly describing the kinematic relationship
for the prediction û to match the actual sensor measurement u. Instead of predicting the sensor measurements end-to-end, we decouple the kinematics by explicitly describing the kinematic relationship ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) j = fξ,j(
j = fξ,j(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ) between sensor j and each magnet. Then, we train a neural network fπj to predict the measurement ûj based on the input
) between sensor j and each magnet. Then, we train a neural network fπj to predict the measurement ûj based on the input ![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) j. To achieve proprioception, we jointly optimize
j. To achieve proprioception, we jointly optimize ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) for all sensor measurement predictions.
for all sensor measurement predictions.
2.2 Magnet sensor kinematics
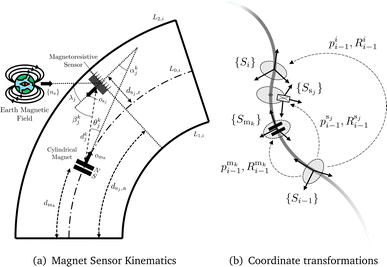
This subsection derives the kinematic relationship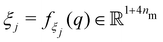 between the jth sensor and all nm magnets as we hypothesize that we can estimate the sensor measurement uj solely based on (a) the angle
between the jth sensor and all nm magnets as we hypothesize that we can estimate the sensor measurement uj solely based on (a) the angle 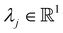 to the earth's magnetic field, (b) the distance dkj between the jth sensor and kth magnet, (c) the angle αkj between the sensor measurement direction and the cylindrical axis of the magnet, (d) the angle βkj between the sensor measurement direction and the vector from the magnet to the sensor, and (e) the angle θkj between the cylindrical axis of the magnet and the vector from the magnet to the sensor. Accordingly, ξj is defined as
to the earth's magnetic field, (b) the distance dkj between the jth sensor and kth magnet, (c) the angle αkj between the sensor measurement direction and the cylindrical axis of the magnet, (d) the angle βkj between the sensor measurement direction and the vector from the magnet to the sensor, and (e) the angle θkj between the cylindrical axis of the magnet and the vector from the magnet to the sensor. Accordingly, ξj is defined as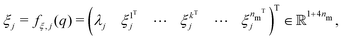 | (1) |
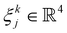 the kinematic relationship between the jth sensor and the kth magnet:
the kinematic relationship between the jth sensor and the kth magnet: 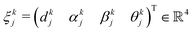 . We visualize the parameters incorporated in ξkj in Fig. 2(a).
. We visualize the parameters incorporated in ξkj in Fig. 2(a).
In the following, we present the derivation of all components of ξkj. Please note that all kinematic frames used in the following paragraphs are visualized in Fig. 2(b).
We define that the kth magnet is integrated into the ith segment. Now, we first derive a transformation matrix 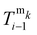 from the base frame {Si−1} to the magnet frame {Smk}. This can be achieved by evaluating the chosen kinematic model, two of which we report in the Appendix A, at the segment coordinate
from the base frame {Si−1} to the magnet frame {Smk}. This can be achieved by evaluating the chosen kinematic model, two of which we report in the Appendix A, at the segment coordinate 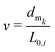 . This means that the cylindrical magnet is integrated at a distance, which is measured along the backbone, of dmk from the base of the segment.
. This means that the cylindrical magnet is integrated at a distance, which is measured along the backbone, of dmk from the base of the segment.
Subsequently, we describe the pose of the jth sensor with respect to the base of the ith segment. Denote with dsj,r the radial distance of the sensor from the center line, with φj the azimuth angle of the sensor in the cylindrical plane, and with dsj,a the axial distance along the center line from the base of the ith segment. We derive the transformation 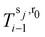 to the center of the cylindrical plane of the sensor analogously as for the magnets by evaluating the forward kinematics at
to the center of the cylindrical plane of the sensor analogously as for the magnets by evaluating the forward kinematics at 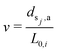 . This is followed by applying the radial offset dsj,r in the cylindrical plane of the sensor
. This is followed by applying the radial offset dsj,r in the cylindrical plane of the sensor
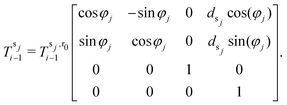 | (2) |
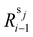 such that local z-axis osj corresponds to the sensor measurement direction.
such that local z-axis osj corresponds to the sensor measurement direction.
Knowing the transformation matrices from the base frame of the respective segment to the sensor and magnet frames, we express them in the inertial frame {S0} by multiplying with the kinematic chain 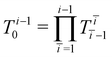 .
.
Next, we need to express the sensor measurement direction osj and the cylindrical axis of the magnet omk in the inertial frame
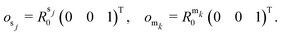 | (3) |
| cos(λj) = ne·osj, cos(αkj) = omkosj. | (4) |
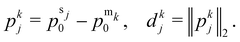 | (5) |
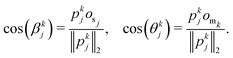 | (6) |
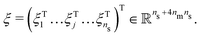 | (7) |
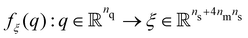 as the magnet sensor kinematics.
as the magnet sensor kinematics.
2.3 Data-driven sensor measurement model
We use a data-driven approach to learn the forward sensor model û = fπ(ξj) for each sensor using a neural network parameterized with π. We note that the same neural network weights can be shared for all sensors, but oftentimes performance can be improved by training a specialized model with weights πj for each sensor. During training on a dataset of length nt, we minimize the mean squared error (MSE) error between the predicted sensor measurement ûj and the actual sensor measurement uj: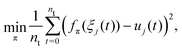 | (8) |
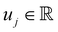 into an array
into an array 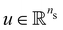 and stack the neural networks as fΠ(ξ):ξ → u. We discuss the choice of the specific network architecture later in Section 3.
and stack the neural networks as fΠ(ξ):ξ → u. We discuss the choice of the specific network architecture later in Section 3.
2.4 Proprioception by optimizing configuration estimate
Now, that we are able to predict the sensor measurement û using the composition of the kinematics fξ(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ) and the neural networks fΠ(
) and the neural networks fΠ(![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) ), we need to optimize the configuration estimate
), we need to optimize the configuration estimate ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) for the predictions û to match the actual sensor measurements u as closely as possible. We capture the error between the predicted sensor measurements û and the actual sensor measurements u by the MSE loss function we strive to minimize
for the predictions û to match the actual sensor measurements u as closely as possible. We capture the error between the predicted sensor measurements û and the actual sensor measurements u by the MSE loss function we strive to minimize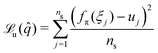 | (9) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) can be found with
can be found with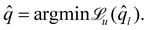 | (10) |
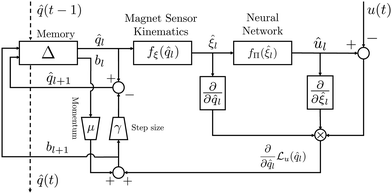
We optimize the cost function (9) through iterative gradient descent, as detailed in Fig. 3. The gradient descent is initialized with the best estimate of the previous time-step ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 0(t) =
0(t) = ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) (t − 1). As common in literature, we optimize the state belief
(t − 1). As common in literature, we optimize the state belief ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) l with a step size γ and the momentum μ using the Jacobian of the loss
l with a step size γ and the momentum μ using the Jacobian of the loss 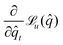
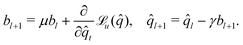 | (11) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) f
f![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) (
(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ) and the gradient of the neural network ∂
) and the gradient of the neural network ∂![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) fΠ(
fΠ(![[small xi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b9.gif) ):
):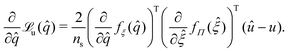 | (12) |
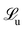 and accordingly select
and accordingly select 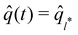 as the best configuration estimate of time-step t.
as the best configuration estimate of time-step t.
3 Piecewise constant curvature simulations
We evaluate the proposed methodology for estimating the PCC kinematic configuration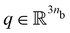 of soft continuum robots thoroughly in simulations. The PCC model allows for bending and elongation of each segment in 3D space. Please refer to Appendix A.1 for more details. We vary the number of robot segments nb, remove and add sensors (i.e. change ns), modify the arrangement of sensors, and the direction of the earth's magnetic field ne. To motivate some of the unique advantages of our method, we use the same learned neural network weights for all these trials.
of soft continuum robots thoroughly in simulations. The PCC model allows for bending and elongation of each segment in 3D space. Please refer to Appendix A.1 for more details. We vary the number of robot segments nb, remove and add sensors (i.e. change ns), modify the arrangement of sensors, and the direction of the earth's magnetic field ne. To motivate some of the unique advantages of our method, we use the same learned neural network weights for all these trials.
3.1 Simulation setup
In our simulations, we consider a robot consisting of one, two, or three segments. All cylindrical segments have an unextended length of L0,i = 110 mm and a radius of di = 22 mm. Each segment has a ring magnet of outer diameter 12 mm, inner diameter 6 mm and thickness 6 mm integrated along the backbone at a distance of dmk = 55 mm from the base of the segment. In the nominal case, three sensors are placed symmetrically in the tip plane of each segment at a radius of 13 mm from the center with the sensor measurement direction pointing along the local, negative z-axis of the tip plane {Si}. We also consider alternative placements of the sensors, which we further detail in Section 3.5.We build on Magpylib26 to simulate the magnetic field behavior. We model the magnets as cylindrical neodymium grade N50 rings with a magnetization of 1450 mT in the local z-direction. After simulating the magnetic field, we rotate the B-field into the local reference frame of each sensor and take the local z-component of the magnetic flux density as the sensor measurement.
3.2 Prediction network
The training set consists of 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random configurations sampled from uniform distribution
000 random configurations sampled from uniform distribution 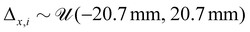 ,
, 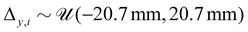 and
and 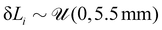 , where the upper bound represents a bending of the tip of 54° with respect to the base of a segment and an elongation of 5%. We also randomize the placement of the sensors in the training set. While in the nominal case, the first of the symmetrically placed sensors is placed on the local x-axis, we randomly sample an offset angle
, where the upper bound represents a bending of the tip of 54° with respect to the base of a segment and an elongation of 5%. We also randomize the placement of the sensors in the training set. While in the nominal case, the first of the symmetrically placed sensors is placed on the local x-axis, we randomly sample an offset angle 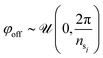 for each training sample, where nsi = 3 is the number of sensors per segment. Finally, we also randomly sample the radial displacement of the sensors from the center with
for each training sample, where nsi = 3 is the number of sensors per segment. Finally, we also randomly sample the radial displacement of the sensors from the center with 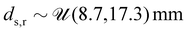 and consider a tilting of the sensors (i.e. a rotation around the tangential axis) with
and consider a tilting of the sensors (i.e. a rotation around the tangential axis) with 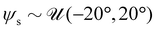 . Before training, we randomly split off 30% of the training set for validation purposes.
. Before training, we randomly split off 30% of the training set for validation purposes.
We conducted a selection study involving hyperparameters and feed-forward neural network architectures (number of layers, nodes, and nonlinear activation layer types) on the validation set. In particular, we aimed to generate a smooth loss landscape to improve the gradient descent convergence leading us to employ a stochastic gradient descent (SGD) optimizer in conjunction with the stochastic weight averaging (SWA)27 strategy. The neural network itself has 18 layers in total and contains, after an initial 1D batch norm layer, four blocks and is concluded with a fully-connected layer at the end. Each block consists of a dropout with a probability of 1%, a linear layer, a ReLU, and a 1D batch norm layer. The hidden state is first increased to 96 nodes, then to 256 nodes, and finally reduced again to 64 and 24 nodes. We minimize a mean squared error (MSE) loss of the neural network prediction ûj(t) for 250 epochs with batch size 650 while setting an initial learning rate of 0.18 for the cosine annealing learning rate scheduler.28 The SWA27 strategy is started after 125 epochs. We train the neural network such that all sensors in the ith segment share the same weights πi. When the training is finished, we select the model from the epoch with the lowest validation loss and save it for later testing.
3.3 Optimization
We optimize the configuration variables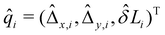 for each segment to minimize the sensor measurement prediction loss as defined in (9). The optimization strategy solely relies on gradient descent and uses the best solution from the last time step
for each segment to minimize the sensor measurement prediction loss as defined in (9). The optimization strategy solely relies on gradient descent and uses the best solution from the last time step ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) *(t − 1) as an initialization
*(t − 1) as an initialization ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) 0(t). For the first time step of the trajectory, we initialize with the ground truth. We use a step size γ = 3.5 × 10−4, 3 × 10−3, and 2 × 10−3 during gradient descent for a one-segment, two-segment and three-segment robot respectively. For all robots with more than one segment, the step size is reduced by a factor of ten when optimizing the elongation. The momentum μ is 0.3 for all trials and we perform 20 gradient descent iterations for each time step.
0(t). For the first time step of the trajectory, we initialize with the ground truth. We use a step size γ = 3.5 × 10−4, 3 × 10−3, and 2 × 10−3 during gradient descent for a one-segment, two-segment and three-segment robot respectively. For all robots with more than one segment, the step size is reduced by a factor of ten when optimizing the elongation. The momentum μ is 0.3 for all trials and we perform 20 gradient descent iterations for each time step.
3.4 Evaluation
We evaluate the performance of our method at estimating the configuration of the segment by computing a relative root mean-squared error (RMSE) metric with respect to the ground-truth configuration q(t) for each configuration variable separately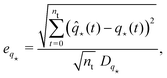 | (13) |
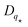 is the dynamic range of each configuration variable between the maximum and minimum value in the test set. All simulations are evaluated on a full lemniscate trajectory, which is very similar to what is plotted based on experimental data in Fig. 9(d). The maximum bending angle of this trajectory is 45 and the elongation of the segment follows a cosine wave with a minimum and maximum at 1.25% and 3.75% respectively.
is the dynamic range of each configuration variable between the maximum and minimum value in the test set. All simulations are evaluated on a full lemniscate trajectory, which is very similar to what is plotted based on experimental data in Fig. 9(d). The maximum bending angle of this trajectory is 45 and the elongation of the segment follows a cosine wave with a minimum and maximum at 1.25% and 3.75% respectively.
3.5 Results
We present all simulation results in Table 1. In the first section, robots with one to three segments, which all exhibit a nominal sensor placement, are considered separately. Neural networks are trained separately for each of these robots, as the input dimension needs to be adjusted to the number of magnets. The results show that the method works well for robots with 1–3 segments. It can be observed that the estimation error is usually lower for the distal segment(s).| Simulation | Specifications | e u [mT] | e Δ x,1 [%] | e Δ y,1 [%] | e δL1 [%] | e Δ x,2 [%] | e Δ y,2 [%] | e δL2 [%] | e Δ x,3 [%] | e Δ y,3 [%] | e δL3 [%] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Variation of # of segments | n b = 1, ns = 3 | 0.015 ± 0.002 | 1.7 ± 1.0 | 1.8 ± 1.1 | 2.8 ± 0.6 | — | — | — | — | — | — |
| n b = 2, ns = 6 | 0.015 ± 0.001 | 4.2 ± 1.3 | 3.9 ± 0.6 | 6.3 ± 1.3 | 2.3 ± 0.6 | 2.2 ± 0.3 | 4.1 ± 1.3 | — | — | — | |
| n b = 3, ns = 9 | 0.015 ± 0.002 | 3.7 ± 2.1 | 4.7 ± 1.6 | 6.0 ± 2.0 | 2.6 ± 1.6 | 2.5 ± 1.5 | 5.5 ± 1.6 | 1.6 ± 1.2 | 1.6 ± 1.1 | 2.7 ± 1.4 | |
| Variation of # of sensors | n b = 3, ns = 6 | 0.015 ± 0.002 | 3.9 ± 1.2 | 24.4 ± 2.7 | 8.4 ± 2.6 | 2.5 ± 1.3 | 53.2 ± 5.0 | 6.0 ± 1.7 | 1.5 ± 1.1 | 52.3 ± 7.3 | 3.1 ± 1.0 |
| n b = 3, ns = 9 | 0.015 ± 0.002 | 3.7 ± 2.1 | 4.7 ± 1.6 | 6.0 ± 2.0 | 2.6 ± 1.6 | 2.5 ± 1.5 | 5.5 ± 1.6 | 1.6 ± 1.2 | 1.6 ± 1.1 | 2.7 ± 1.4 | |
| n b = 3, ns = 12 | 0.015 ± 0.001 | 3.7 ± 1.6 | 3.9 ± 1.3 | 4.6 ± 2.4 | 2.6 ± 1.3 | 2.6 ± 1.2 | 4.4 ± 1.9 | 1.6 ± 1.2 | 1.5 ± 1.3 | 2.5 ± 1.6 | |
| n b = 3, ns = 18 | 0.016 ± 0.002 | 3.2 ± 1.5 | 3.5 ± 1.3 | 4.2 ± 1.8 | 2.4 ± 1.3 | 2.5 ± 1.2 | 4.4 ± 1.8 | 1.5 ± 1.3 | 1.3 ± 1.1 | 2.5 ± 1.5 | |
| Nominal | n b = 3, ns = 9 | 0.015 ± 0.002 | 3.7 ± 2.1 | 4.7 ± 1.6 | 6.0 ± 2.0 | 2.6 ± 1.6 | 2.5 ± 1.5 | 5.5 ± 1.6 | 1.6 ± 1.2 | 1.6 ± 1.1 | 2.7 ± 1.4 |
| Sensors tilted | ψ s = 10° | 0.015 ± 0.002 | 8.1 ± 4.0 | 6.4 ± 2.0 | 4.7 ± 0.7 | 5.1 ± 2.3 | 3.8 ± 0.8 | 5.6 ± 2.4 | 2.8 ± 1.2 | 1.9 ± 0.8 | 4.1 ± 0.6 |
| Sensors shifted | d s,r = 16 mm | 0.017 ± 0.003 | 3.4 ± 1.5 | 4.0 ± 1.3 | 6.2 ± 2.5 | 2.6 ± 1.0 | 2.8 ± 1.8 | 6.7 ± 0.9 | 1.6 ± 1.2 | 1.6 ± 1.0 | 4.0 ± 2.0 |
| Earth magnetic field | n e = (1,0,0) | 0.012 ± 0.002 | 2.0 ± 0.4 | 2.4 ± 1.1 | 4.3 ± 1.3 | 1.8 ± 0.7 | 1.9 ± 0.3 | 3.6 ± 2.0 | 1.5 ± 0.3 | 1.6 ± 0.4 | 3.2 ± 0.9 |
| n e = (0,1,0) | 0.012 ± 0.002 | 1.9 ± 0.5 | 2.5 ± 0.8 | 3.8 ± 1.1 | 1.9 ± 0.5 | 2.0 ± 0.2 | 3.4 ± 1.6 | 1.5 ± 0.3 | 1.6 ± 0.4 | 3.3 ± 0.8 | |
| n e = (0,0,1) | 0.012 ± 0.001 | 2.0 ± 0.7 | 2.6 ± 0.9 | 4.1 ± 0.9 | 1.6 ± 0.3 | 1.7 ± 0.3 | 4.9 ± 1.5 | 1.5 ± 0.5 | 1.4 ± 0.1 | 3.9 ± 0.3 | |
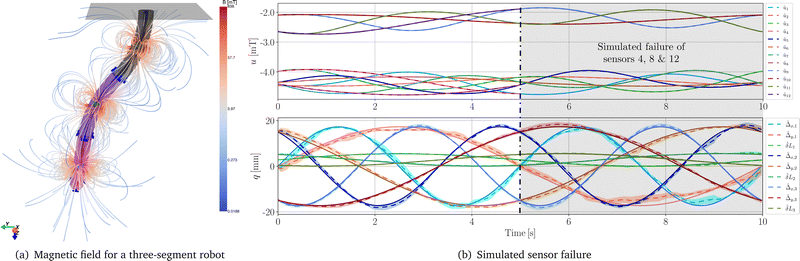
Next, the number of sensors ns is varied for a three-segment robot. We always apply a symmetrical placement of the sensors in the tip plane of each segment. In the first trial, two sensors are mounted in the tip plane of each segment opposite to each other (6 sensors in total). While the bending along Δx,i and the elongation of the segments δLi can still be estimated, the setup does not contain sufficient information to accurately determine the bending into Δy,i. While the nominal case of nine sensors in total already achieves relative RMSEs in the range of 1.6% to 6%, the proprioception performance can be slightly improved by adding more sensors. We emphasize that the neural networks are not retrained when adding or removing sensors. In Fig. 4(b) and 5, we plot the proprioceptive performance of a three-segment robot with four sensors per segment. Then, we simulated a failure of the 4th, 8th, and 12th sensor at 5s by removing these sensor measurements from (11) (i.e. the gradient descent). Our method is able to adapt without re-training and leverage the nominal redundancy of sensor measurements, as three sensors per segment are sufficient for shape estimation.
 | ||
| Fig. 5 Sequence of stills for simulated sensor failure as shown in Fig. 4(b): the number of sensors per segment, which are rendered in blue, is reduced from four to three at t = 5 s. We visualize the ground-truth shape of the soft robot with full opacity and the estimated configuration with slight transparency. The magnets are rendered in green and the three segments are visualized in a color sequence from black to violet. | ||
Then, two adjusted sensor placements are investigated, while keeping the neural network weights constant. First, the sensors are tilted from the nominal case of pointing along the local z-axis by ψs = 10° towards the inside. In a separate simulation, the sensors are moved radially from nominally 13 mm to 16 mm. As the results show, the configuration of all three segments can still be estimated accurately with a mean error of 3.3%.
Finally, an earth's magnetic field of magnitude 0.065 mT is added. A separate neural network is trained on a training set with randomly sampled magnetic field vector directions ne. As the last section of Table 1 demonstrates, the methodology is able to adapt to any earth's magnetic field direction by leveraging the λj input parameter.
4 Affine curvature simulations
To demonstrate the efficacy of the proposed method for higher-order kinematic models than PCC, we also conduct simulations of an affine curvature soft robot. The affine curvature kinematic parametrization24 has been shown capable of representing the shape of soft tentacles25,29 and provides a continuous function κ = κ0 + κ1v to describe the curvature of the soft robot, where κ0, κ1 are two configuration variables and v ∈ [0,1] is the backbone coordinate. We allow for movement in 3D space by also specifying an azimuth bending angle ϕ and the elongation δL. Please refer to Appendix A.2 for more implementation details about the affine curvature model.4.1 Simulation setup
We use the same simulation setup as described in Section 3.1. Therefore, we report in the following only the implemented modifications to simulate an affine curvature soft robot in Magpylib.26 Namely, we consider one affine curvature segment of length L0,i = 200 mm with in total ns = 9 magnetic sensors. The sensors are placed on three separate cylindrical planes at distances dsa of 0 mm, 100 mm, and 200 mm from the base of the robot. In each plane, the three sensors are spaced at an angle of 120° and at a radial distance dsr = 13 mm from the backbone, as it can be seen in Fig. 7. Two ring magnets are positioned at a distance of 50 mm and 150 mm from the robot's base respectively.4.2 Prediction network and optimization
We simulate 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random configurations of the affine curvature robot to generate the training set. For this purpose, we sample the configuration variables from uniform distributions: the affine curvature parameters
000 random configurations of the affine curvature robot to generate the training set. For this purpose, we sample the configuration variables from uniform distributions: the affine curvature parameters 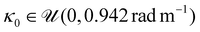 ,
, 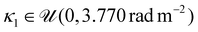 , the azimuth angle
, the azimuth angle 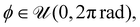 and the elongation
and the elongation 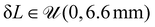 . Before training, we randomly split off 30% of the training set for validation purposes. We train a specialized neural network fπj(ξj) for each sensor and use the same neural network architecture as in Section 3.2 with the exception of the addition of a final layer y(x) = sign(x)e|x|. The training runs for in total 250 epochs and uses the SWA27 strategy with a learning rate of 0.01. All other training hyperparameters are the same as in Section 3.2.
. Before training, we randomly split off 30% of the training set for validation purposes. We train a specialized neural network fπj(ξj) for each sensor and use the same neural network architecture as in Section 3.2 with the exception of the addition of a final layer y(x) = sign(x)e|x|. The training runs for in total 250 epochs and uses the SWA27 strategy with a learning rate of 0.01. All other training hyperparameters are the same as in Section 3.2.
The four configuration variables are optimized to minimize the loss between the predictions and simulated measurements of the nine sensors as defined in eqn (9). For this optimization procedure, we employ gradient descent running at 40Hz with step sizes of γκ0 = 1, γκ1 = 5, γϕ = 1, and γδL = 2 × 10−4. The momentum is set to μ = 0.3 and 20 iterations are performed at each time step.
4.3 Evaluation
We evaluate the trained model on a flower trajectory of duration 10 s and sample rate 40 Hz. The evaluation trajectory has the following characteristics: κ0 is actuated by a sinusoidal wave of frequency 0.3Hz in the range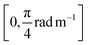 . Similarly, κ1 is also varied through a sinusoidal function of the same frequency and has a dynamic range of [0.1π,π] rad m−2. The azimuth angle ϕ is linearly scaled from 0 rad to 2π rad over the duration of the trajectory. Finally, δL follows a sinusoidal sequence of frequency 0.1 Hz in the range of [0,5.5] mm. We use the same evaluation metrics as first introduced in Section 3.4. We report the error as mean ± stdev and compute the statistics over three different random seeds. The random seed determines at the start of the training the initialization of the neural network weights.
. Similarly, κ1 is also varied through a sinusoidal function of the same frequency and has a dynamic range of [0.1π,π] rad m−2. The azimuth angle ϕ is linearly scaled from 0 rad to 2π rad over the duration of the trajectory. Finally, δL follows a sinusoidal sequence of frequency 0.1 Hz in the range of [0,5.5] mm. We use the same evaluation metrics as first introduced in Section 3.4. We report the error as mean ± stdev and compute the statistics over three different random seeds. The random seed determines at the start of the training the initialization of the neural network weights.
4.4 Results
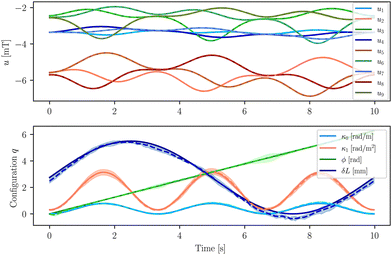
The trained neural networks achieve an RMSE error for predicting the magnetic sensor measurements of 0.025 ± 0.002 mT on the test set. When we run inference (see Fig. 6) on the flower trajectory, the configuration variables can be estimated with an absolute RMSE of eκ0 = 0.042 ± 0.005 rad m−1, eκ1 = 0.11 ± 0.04 rad m−2, eϕ = 0.08 ± 0.02 rad, and eδL = 0.001 ± 0.001 mm. We state the relative RMSE errors for the configuration estimates as eκ0 = 5.4 ± 0.7%, eκ1 = 4.0 ± 1.4%, eϕ = 1.3 ± 0.4%, and eδL = 3.8 ± 1.6%. In Fig. 7, we render at six different points along the trajectory the robot's shape according to the ground truth and estimated configurations respectively. The sequence qualitatively shows that our proposed method is able to estimate the affine curvature robot's shape very accurately.5 Experiments
We verify the performance of our proposed proprioception method in experiments involving one soft robot segment with three magnetoresistive sensors attached to the tip. We aim to estimate the CC configuration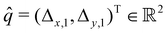 from the measured sensor values
from the measured sensor values 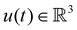 . We let the robot follow a diverse set of trajectories and evaluate the proprioception performance. After measuring the ground-truth pose of the tip of the segment with a motion capture system, we perform inverse kinematics with the closed-form solution reported by Della Santina et al.30 and quantitatively compare the proprioceptive configuration estimate of the segment with the ground-truth configuration.
. We let the robot follow a diverse set of trajectories and evaluate the proprioception performance. After measuring the ground-truth pose of the tip of the segment with a motion capture system, we perform inverse kinematics with the closed-form solution reported by Della Santina et al.30 and quantitatively compare the proprioceptive configuration estimate of the segment with the ground-truth configuration.
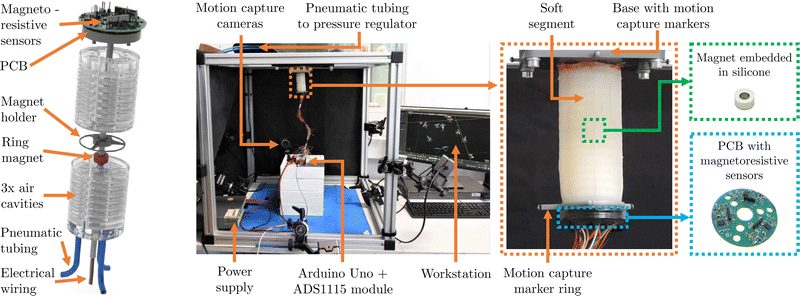
5.1 Robot design
We use a cylindrical, pneumatically-actuated soft robotic silicon segment of length L0 = 110 mm and radius d1 = 22 mm consisting of three independently inflatable cavities evenly spaced in the radial direction from the center line.31 The proprioceptive sensing system is achieved by embedding one ring magnet in the backbone at a distance dm0 = 55 mm from the base of the segment and three symmetrically-placed Magnetoresistive Sensors (MRSs) at the tip of the segment as visualized in Fig. 8. Although we use MRSs in our experimental setup for their high sensitivity,32 this is not a strict condition and other sensor types measuring the magnetic field such as Hall-effect sensors can be combined with the methodology proposed in this paper too. For casting the silicone segment, we use a 3D-printed mold with a holder for the magnet which keeps it in place inside the segment. The magnet used is a neodymium ring of grade N50 with a thickness and inner diameter of 6 mm each, and an outer diameter of 12 mm. The MRSs of type Honeywell HMC1021Z are integrated into a printed circuit board (PCB) and output a voltage difference of 50 mV mT−1. The three sensors are equally spaced at 120° from each other and are placed at a radial distance of ds,r = 13 mm, and at a longitudinal distance of ds,a = 116 mm from the base in a straight configuration. For each sensor, we implemented a Set/Reset and an amplification circuit on the PCB. The Set/Reset circuit is used for calibration of the sensor by re-aligning the magnetic domains. After amplification of the sensor output by a factor of 100, the output of the sensors is processed with a Texas Instruments ADS1115 module resulting in a digital signal of 16bit resolution. All sensor measurements u are in the range [0 mV,2048 mV], which corresponds to magnetic flux densities of [0 mT,41 mT].5.2 Experimental setup
We conducted our experiments in a lab environment with the base of the soft robot segment mounted in a tip-down configuration to a cubical cage as shown in Fig. 8. A 3D-printed ring with four reflective markers is mounted on the tip of the segment. Eight motion capture cameras are attached to the cage tracking at 40 Hz the 3D pose of the ring. We transform the pose measurements of the tip to the base frame of the robot and compute the closed-form inverse kinematics30 to receive a ground-truth configuration estimate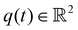 . Each of the three pneumatic chambers of the segment is connected via tubing to a separate valve of a proportional pressure regulator operated at 100 Hz. We read out the analog signals of the magnetoresistive sensors with an Arduino Uno at 40 Hz and save them for later offline processing. We temporally align the motion capture and the magnetic sensor data by detecting the initial extension of the robot with a suitable threshold. The sensor noise is determined for both an unelongated straight configuration, and during fully inflated bending. Here the standard deviations of the white noise are 0.24 mV and 3.55 mV, which normalizes to 0.03% and 2% of the dynamic range respectively. Furthermore, we identify the earth's magnetic field direction in the base from as
. Each of the three pneumatic chambers of the segment is connected via tubing to a separate valve of a proportional pressure regulator operated at 100 Hz. We read out the analog signals of the magnetoresistive sensors with an Arduino Uno at 40 Hz and save them for later offline processing. We temporally align the motion capture and the magnetic sensor data by detecting the initial extension of the robot with a suitable threshold. The sensor noise is determined for both an unelongated straight configuration, and during fully inflated bending. Here the standard deviations of the white noise are 0.24 mV and 3.55 mV, which normalizes to 0.03% and 2% of the dynamic range respectively. Furthermore, we identify the earth's magnetic field direction in the base from as ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) e = (−0.311,−0.234,0.921)T using a compass and the world magnetic model (WMM).33
e = (−0.311,−0.234,0.921)T using a compass and the world magnetic model (WMM).33
5.3 Pneumatic actuation and trajectories
We consider, as visualized in Fig. 9, six continuous actuation sequences in this paper: random configuration way-points which are connected through linear interpolation (T0), planar side bending (T1), the tip following a half lemniscate (T2) and full lemniscate (T3), a spiral with constant linear velocity34 (T4) and finally a flower-shape (T5). We define our trajectories as wrenches τxyz = [τxτy]T on the tip of the segment in Cartesian space, where τx and τy cause bending around the local x- and y-axis of the tip respectively. The pressures we command from the pressure regulator are given by inversely evaluating the force produced at the center of pressure at the tip of the segment for each chamber for a given chamber pressure.35 All actuation sequences are preceded by first applying an offset pressure of 225 mBar in all chambers, which causes a near-constant elongation of the segment. The peak pressure, which causes maximum bending, is set for all trajectories to 450 mBar.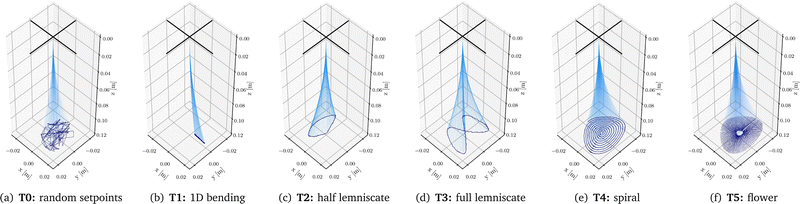 | ||
| Fig. 9 Trajectories used during the experiments. We plot the shape of the segment under PCC approximation in light blue and the position of the tip of the segment in dark blue. | ||
The 1D bending (T1), half lemniscate (T2) and full lemniscate (T3) are all executed periodically with a period of 5 s, 10 s, and 10 s respectively. Trajectories T0 and T4 are characterized by a constant velocity in torque-space of 0.025 N m s−1 and 0.0125 kN m s−1 respectively. The flower trajectory T5 can be described as periodic 1D bending with a linearly changing azimuth angle. It exhibits an angular velocity of 0.0126 rad s−1 and a period of 10 s for the bending, which results in 50 bending cycles per circumnavigation. While the random configuration set points of T0 are recorded for 200 s, T1, T2 and T3 have total a duration of 90s each, and the spiral T4 and flower T5 last for 120 s and 1500 s respectively. We split off the final 20% of all datasets as a test set.
5.4 Prediction network and optimization
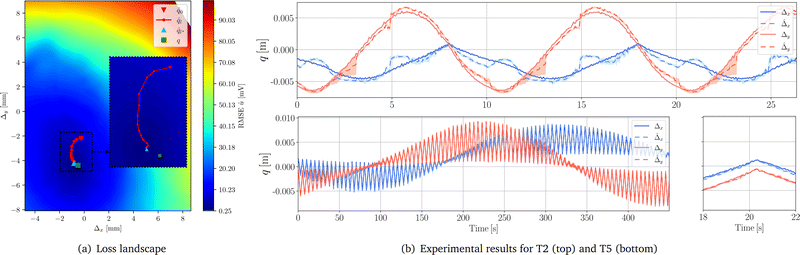
We use the same neural network architecture and training procedure as in Section 3.2, but with an adjusted initial learning rate of 5 × 10−5 and train the model separately for each sensor on the 1200 s long T5/flower trajectory, which results in 48000 training samples for each neural network.We optimize the configuration variables Δx and Δy for the one segment to minimize the sensor measurement prediction loss as defined in (9). The optimization strategy solely relies on gradient descent running at 40 Hz with a step size γ = 1.5 × 10−8 and momentum μ = 0.2. We visualize a sample loss landscape in Fig. 10(a).
5.5 Results
First, we quantify the performance of the neural network predicting the sensor measurements û(t) for a known, ground-truth configuration q(t), which we report in Table 2. We observe, that the relative RMSE lies between 0.6% and 4.6% of the range of the respective datasets with a mean of 3.1%. As expected, the predictions are generally the most accurate when evaluated on a trajectory of the same type as the neural network was trained on (T5). Next, we analyze the proprioception performance on the same trajectories. We report relative RMSEs between 1.9% and 13.6% for estimating the bending of the robot. Additionally, we visualize the configuration estimates for two trajectories: in the top-right of Fig. 10(b), we run inference for our trained model on T2. While the proprioception estimate tracks the general shape of the trajectory well, the optimization, particularly for Δy, gets trapped in local minima sometimes leading to periods of higher error. Next, we consider a model trained and evaluated on separated sets of the T5 trajectory. The configuration estimate tracks the ground truth very well as can be seen in the bottom right. Finally, we present a sequence of stills based on camera views and renderings of the soft segment for inference on T3 in Fig. 11.| Trajectory | e u [mV] | e u [%] | e Δ x [mm] | e Δ x [%] | e Δ y [mm] | e Δ y [%] |
|---|---|---|---|---|---|---|
| T5.train → T0.test | 9.90 ± 0.90 | 3.90 ± 0.40 | 0.37 ± 0.06 | 3.70 ± 0.60 | 0.44 ± 0.01 | 3.50 ± 0.10 |
| T5.train → T1.test | 8.80 ± 0.30 | 4.40 ± 0.10 | 0.36 ± 0.08 | 6.50 ± 1.50 | 0.43 ± 0.05 | — |
| T5.train → T2.test | 11.10 ± 0.30 | 4.30 ± 0.10 | 0.78 ± 0.03 | 13.60 ± 0.60 | 0.74 ± 0.23 | 5.90 ± 1.80 |
| T5.train → T3.test | 12.30 ± 0.30 | 4.60 ± 0.10 | 0.52 ± 0.06 | 4.50 ± 0.50 | 0.47 ± 0.03 | 3.10 ± 0.20 |
| T5.train → T4 | 3.01 ± 0.05 | 1.08 ± 0.02 | 0.33 ± 0.02 | 2.40 ± 0.10 | 0.52 ± 0.06 | 3.10 ± 0.40 |
| T5.train → T5.test | 1.60 ± 0.10 | 0.58 ± 0.05 | 0.24 ± 0.05 | 1.90 ± 0.30 | 0.24 ± 0.01 | 1.40 ± 0.05 |
6 Conclusion
This work proposed a sensing strategy for soft-bodied robots that relies on multiple magnetic sensors embedded directly in the robot. Thanks to a novel kinematics-aware neural architecture, we can simultaneously use information coming from all the sensors to reliably reconstruct the full robot shape. The decoupling of the kinematics from the learned sensor measurement predictor allows modifications to the placement of the sensors without requiring a re-training of the neural network. The proposed method is agnostic to the used kinematic state parametrization, which we verified in simulations using either PCC or affine curvature models. Extensive experiments with a soft segment showed that a model can be trained on one trajectory type and then be used for inference on a variety of other trajectories in the same workspace. In future work, we will validate the proposed proprioception methodology to execute closed-loop control. We also invite future research studying the optimal placement of sensors in continuum soft robots, where the optimization procedure might take advantage of the gradients provided by our algorithm.Author contributions
T. B., M. K. H, M. S., and D. V. D. T contributed equally to this work. C. D. S., and R. B. conceived and led the project. M. S. invented the proprioception algorithm and implemented all simulations. T. B., M. K. H, J. N., and D. V. D. T designed the strategy to integrate sensors and magnets into the robot. T. B., M. K. H, J. N., and D. V. D. T. developed the PCB and sensing electronics. T. B., M. K. H, and D. V. D. T. fabricated the soft robot. T. B., M. K. H, J. N., and D. V. D. T. implemented the experimental data processing pipeline. T. B., M. K. H., M. S., and D. V. D. T. conducted experiments. T. B., M. K. H., M. S., and D. V. D. T. tuned the learning strategy and developed suitable trajectories. T. B., M. K. H., M. S., and D. V. D. T. wrote the manuscript. C. D. S., and R. B. revised the manuscript.Conflicts of interest
There are no conflicts to declare.Appendices
A Kinematics
A kinematic description provides us with the forward kinematic transformation Tsi−1(qi,s) from base frame {Si−1} at the proximal end of the ith segment to the local frame {Sv} at a coordinate v ∈ [0,1] for a given configuration qi. Furthermore, the tip frame of the ith segment located at the coordinate v = 1 is denoted as {Si}, as shown in Fig. 2(b).A.1 Δ-Parametrization of the piecewise constant curvature kinematics
Under the PCC hypothesis, the shape of each segment i of length Li and radius di can be fully parameterized through three variables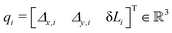 | (14) |
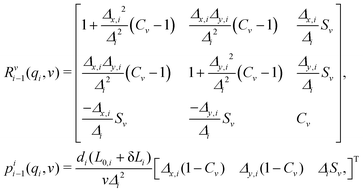 | (15) |
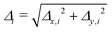 ,
, 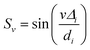 , and
, and 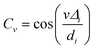 for conciseness.
for conciseness.
A.2 Affine curvature kinematics
The affine curvature hypothesis24,25 models the bending of the soft segment to be conforming to the affine function κ(t,v) = κ0(t) + κ1(t)v, where κ describes the local curvature of the backbone at the coordinate v ∈ [0,1] along the segment and κ0(t), κ1(t) are the zero-order and first-order term of the curvature polynomial respectively.36 Specifically, we implement the recently proposed extension to 3D environments,25 which specifies an azimuth angle of the bending direction ϕ(t) and additionally allows for an elongation δL(t) of the segment. Accordingly, the configuration of the ith segment is described at any point in time by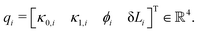 | (16) |
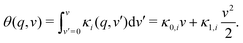 | (17) |
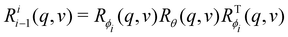 . After substituting S· = sin(·), C· = cos(·) for conciseness, we state the homogeneous transformation as
. After substituting S· = sin(·), C· = cos(·) for conciseness, we state the homogeneous transformation as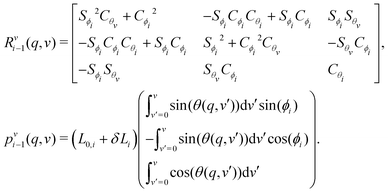 | (18) |
Acknowledgements
This work has received funding under the European Union's Horizon Europe Programme from Project EMERGE – Grant Agreement No. 101070918. We would like to thank Ehsan Heseini, Jasper Insinger and Tom Salden from Delft University of Technology, NL for their guidance in designing the PCB.References
- J. Luong, P. Glick, A. Ong, M. S. DeVries, S. Sandin, E. W. Hawkes and M. T. Tolley, 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), 2019, pp. 801–807.
- D. S. Shah, J. P. Powers, L. G. Tilton, S. Kriegman, J. Bongard and R. Kramer-Bottiglio, Nat. Machine Intell., 2021, 3, 51–59 CrossRef.
- J. Hughes, C. Della Santina and D. Rus, 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), 2020, pp. 733–739.
- C. Della Santina, M. G. Catalano and A. Bicchi, Encyclopedia Robot., 2021, 489 DOI:10.1007/978-3-642-41610-1_146-2.
- C. Armanini, C. Messer, A. T. Mathew, F. Boyer, C. Duriez and F. Renda, arXiv, 2021, preprint, arXiv:2112.03645, DOI:10.48550/arXiv:2112.03645.
- C. Della Santina, C. Duriez and D. Rus, arXiv, 2021, preprint, arXiv:2110.01358 DOI:10.48550/arXiv:2110.01358.
- H. Wang, M. Totaro and L. Beccai, Adv. Sci., 2018, 5, 1800541 CrossRef.
- B. Shih, C. Christianson, K. Gillespie, S. Lee, J. Mayeda, Z. Huo and M. T. Tolley, Front. Robot. AI, 2019, 6, 30 CrossRef.
- R. K. Kramer, C. Majidi, R. Sahai and R. J. Wood, 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011, pp. 1919-1926.
- L. Scimeca, J. Hughes, P. Maiolino and F. Iida, IEEE Robot. Autom. Lett., 2019, 4, 2479–2484 Search PubMed.
- J. Shintake, Y. Piskarev, S. H. Jeong and D. Floreano, Adv. Mater. Technol., 2018, 3, 1700284 CrossRef CAS.
- S. Li, S. A. Awale, K. E. Bacher, T. J. Buchner, C. Della Santina, R. J. Wood and D. Rus, Soft Robot., 2021, 9(2), 324–336 CrossRef PubMed.
- E. R. Rosi, M. Stölzle, F. Solari and C. Della Santina, 2022 IEEE 5th International Conference on Soft Robotics (RoboSoft), 2022, pp. 795-801.
- S. Song, Z. Li, H. Yu and H. Ren, IEEE Sens. J., 2015, 15, 4565–4575 Search PubMed.
- S. Ozel, N. A. Keskin, D. Khea and C. D. Onal, Sens. Actuators, A, 2015, 236, 349–356 CrossRef CAS.
- M. Luo, E. H. Skorina, W. Tao, F. Chen, S. Ozel, Y. Sun and C. D. Onal, Soft Robot., 2017, 4, 117–125 CrossRef.
- H. Guo, F. Ju, Y. Cao, F. Qi, D. Bai, Y. Wang and B. Chen, Sens. Actuators, A, 2019, 285, 519–530 CrossRef CAS.
- M. D. Mitchell, F. E. Hurley and C. D. Onal, 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), 2021, pp. 215–220.
- R. L. Truby, C. Della Santina and D. Rus, IEEE Robot. Autom. Lett., 2020, 5, 3299–3306 Search PubMed.
- Z. Y. Ding, J. Y. Loo, V. M. Baskaran, S. G. Nurzaman and C. P. Tan, IEEE Robot. Autom. Lett., 2021, 6, 951–957 Search PubMed.
- G. Soter, A. Conn, H. Hauser and J. Rossiter, 2018 IEEE international conference on robotics and automation (ICRA), 2018, pp. 2448–2453.
- T. G. Thuruthel, B. Shih, C. Laschi and M. T. Tolley, Sci. Rob., 2019, 4, eaav1488 CrossRef.
- R. J. Webster III and B. A. Jones, Int. J. Robot. Res., 2010, 29, 1661–1683 CrossRef.
- C. Della Santina, 2020 59th IEEE Conference on Decision and Control (CDC), 2020, pp. 4135–4142.
- F. Stella, Q. Guan, J. Leng, C. Della Santina and J. Hughes, Piecewise Affine Curvature model: a reduced-order model for soft robot-environment interaction beyond PCC, 2022, https://arxiv.org/abs/2211.10188.
- M. Ortner and L. G. Coliado Bandeira, SoftwareX, 2020, 11, 100466, DOI:10.1016/j.softx.2020.100466.
- P. Izmailov, D. Podoprikhin, T. Garipov, D. Vetrov and A. G. Wilson, arXiv, 2018, preprint, arXiv:1803.05407, DOI:10.48550/arXiv:1803.05407.
- I. Loshchilov and F. Hutter, arXiv, 2016, preprint, arXiv:1608.03983 DOI:10.48550/arXiv:1608.0398.
- F. Stella, N. Obayashi, C. Della Santina and J. Hughes, IEEE Robot. Autom. Lett., 2022, 7, 11410–11417 Search PubMed.
- C. Della Santina, A. Bicchi and D. Rus, IEEE Robot. Autom. Lett., 2020, 5, 1001–1008 Search PubMed.
- A. D. Marchese, R. K. Katzschmann and D. Rus, Soft Robot., 2015, 2, 7–25 CrossRef PubMed.
- R. Popovic, P. Drljaca and C. Schott, 2002 23rd International Conference on Microelectronics, 2002, pp. 55–58.
- A. Chulliat, W. Brown, P. Alken, C. Beggan, M. Nair, G. Cox, A. Woods, S. Macmillan, B. Meyer and M. Paniccia, The US/UK world magnetic model for 2020–2025, British Geological Survey, 2020 Search PubMed.
- O. M. Carrasco-Zevallos, C. Viehland, B. Keller, R. P. McNabb, A. N. Kuo and J. A. Izatt, Biomed. Opt. Express, 2018, 9, 5052–5070 CrossRef.
- C. Della Santina, A. Bicchi and D. Rus, 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019, pp. 6622–6629.
- C. Della Santina and D. Rus, IEEE Robot. Autom. Lett., 2019, 5, 290–298 Search PubMed.
- P. Gómez, H. H. Toftevaag and G. Meoni, J. Open Source Software, 2021, 6, 3439 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00914e |
| ‡ These authors contributed equally to this work and are co-first authors. |
| § https://www.github.com/tud-cor-sr/promasens. |
| This journal is © The Royal Society of Chemistry 2023 |