Crossover behavior in stress relaxations of poroelastic and viscoelastic dominant hydrogels
Hangyu
Li
ab,
Xinyi
Lian
ab and
Dongshi
Guan
 *ab
*ab
aState Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
bSchool of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China. E-mail: dsguan@imech.ac.cn
First published on 19th June 2023
Abstract
The mechanical response and relaxation behavior of hydrogels are crucial to their diverse functions and applications. However, understanding how stress relaxation depends on the material properties of hydrogels and accurately modeling relaxation behavior at multiple time scales remains a challenge for soft matter mechanics and soft material design. While a crossover phenomenon in stress relaxation has been observed in hydrogels, living cells, and tissues, little is known about how the crossover behavior and characteristic crossover time depend on material properties. In this study, we conducted systematic atomic-force-microscopy (AFM) measurements of stress relaxation in agarose hydrogels with varying types, indentation depths, and concentrations. Our findings show that the stress relaxation of these hydrogels features a crossover from short-time poroelastic relaxation to long-time power-law viscoelastic relaxation at the micron scale. The crossover time for a poroelastic-dominant hydrogel is determined by the length scale of the contact and diffusion coefficient of the solvent inside the gel network. In contrast, for a viscoelastic-dominant hydrogel, the crossover time is closely related to the shortest relaxation time of the disordered network. We also compared the stress relaxation and crossover behavior of hydrogels with those of living cells and tissues. Our experimental results provide insights into the dependence of crossover time on poroelastic and viscoelastic properties and demonstrate that hydrogels can serve as model systems for studying a wide range of mechanical behaviors and emergent properties in biomaterials, living cells, and tissues.
1 Introduction
The mechanical properties of hydrogels have gained increasing attention due to their significant role in various applications, including drug delivery carriers,1,2 microfluidic devices and sensors,3–5 and biofunctional materials and cell culture scaffolds.6–9 Understanding how hydrogels respond to mechanical stresses and deformations is essential for optimizing these applications. Hydrogels are cross-linked polymeric networks that swell in water and are generally soft, with Young's modulus E ranging from tens of Pa to several MPa.10 In addition to their elastic properties, the hierarchical porous structures within hydrogels allow water transport and reorganization of the polymeric network, resulting in viscous behavior and stress relaxation under deformation. Additionally, their structural similarities to cells and tissues make hydrogels a particularly interesting soft material to investigate.Various experimental techniques have been employed to measure the mechanical response and stress relaxation of hydrogels. These techniques include the use of an indenter,11,12 parallel plates,13 atomic force microscopy (AFM),14–16 and interferometric imaging.17 AFM, in particular, has proven to be an effective and versatile platform for studying a range of mechanical properties and behaviors of hydrogels. This is accomplished by pressing an indenter into the hydrogel, causing a deformation at the nano to micron scale. Two types of mechanical characterizations can be performed using AFM. The first is force indentation measurement, in which the response force F(δ) is measured as a function of the indentation δ as the AFM probe approaches and retracts from the sample surface. This simple and efficient method is widely used to characterize the elastic properties of hydrogels, such as the modulus E. The second method is force or stress relaxation measurement. In this technique, a constant indentation δ is applied to the hydrogel, and AFM records the force variation F(t) as a function of time t. Compared to force indentation, relaxation measurements can measure mechanical response over a longer time span and characterize the time-dependent relaxation behaviors of hydrogels.
Various theoretical models have been developed to understand the underlying physics of stress relaxation behaviors observed in hydrogels. Typically, two mechanisms contribute to stress relaxation: poroelasticity, which arises from solvent movement and redistribution through the gel network, and viscoelasticity, which involves energy dissipation by rearrangement of polymer chains and reformation of crosslinks. Based on the concept of poroelasticity, Suo and collaborators developed an approximate solution for measuring the diffusion coefficient of solvent inside soft gels from force relaxation curves for indenters with different geometries.11 On the other hand, the Maxwell model, which consists of a series of elastic spring and viscous damper, characterizes exponential relaxation of stress with an elastic modulus and a relaxation time. A soft glassy rheology model has been developed to explain the power-law behavior in viscoelastic stress relaxation of soft materials such as foams, emulsions, pastes, slurries, and microgels. This behavior arises as a natural consequence of structural disorder and metastability.18
Previous research has primarily focused on one relaxation mechanism, neglecting the other. However, recent studies have shown that both viscoelasticity and poroelasticity contribute to hydrogel relaxation over a wide range of time and length scales. Strange et al.12 and Wang et al.13 have proposed methods to separate the two mechanisms by exploiting the fact that poroelasticity is scale-dependent, whereas viscoelasticity is not. Xu et al.17 have directly observed the crossover from viscoelastic to poroelastic relaxation in a soft surface using fast interferometric imaging techniques. While considerable efforts have been made to describe the relaxation behavior with a combination of poroelasticity and viscoelasticity,10 there is currently no clear framework for determining which mechanism dominates in a given situation, and little is known about how the crossover behavior and characteristic crossover time depend on the material properties of hydrogels.
Living matters, such as cells and tissues, share many similarities with hydrogels in terms of their complex network structures and high water content, and also exhibit relaxation behaviors in their mechanical response.19–25 Understanding the mechanical properties of living matter is important as they play crucial roles in various cellular functions, including cell contraction, spreading, invasion, division, and wound healing.26–30 However, compared with hydrogels, living matters are filled with irregular macromolecular substances, organelles and active motors, so that revealing their emergent mechanical properties is challenging. Hydrogels, on the other hand, are relatively simple polymeric systems and can serve as a model to investigate the relaxation and crossover behavior of living matter.
In this paper, we report a systematic study of stress relaxation and crossover behavior of hydrogels by using AFM-based force apparatus. It is found that the relaxation curves of hydrogels at the micron scale feature a crossover from a short-time poroelastic relaxation to a long-time power-law viscoelastic relaxation. By tuning the material properties of hydrogels with different molecules and concentrations, we are able to reveal the underlying physics behind the crossover behavior and characteristic crossover time. For a poroelastic dominant hydrogel, the crossover time is determined by the length scale of the contact and diffusion coefficient of solvent inside the gel network. On the other hand, for a viscoelastic dominant hydrogel, the crossover time is closely related to the shortest relaxation time of the disordered network. On this basis, we further compare the hydrogels with living matters and find they share several similarities in terms of stress relaxation and crossover behavior. Our quantitative description on stress relaxation of hydrogels provides new insights into the origin of the multiscale mechanics of living cells and tissues.
2 Materials and methods
2.1 Hydrogel preparation
Two types of agarose were used in the experiment: regular agarose (Sigma, V900510) and low gelling temperature (LGT) agarose (Sigma, A9414). The regular agarose has a congealing temperature of 34.5–37.5 °C, while LGT agarose has a congealing temperature of 26–30 °C, because the molecular structure of LGT agarose has been modified. A portion of the hydrogen atoms on agarose chains are replaced by the hydroxyethyl group,31 so LGT agarose is also known as 2-hydroxyethyl agarose.Agarose hydrogels are prepared by adding agarose powder into deionized water (Milli-Q™). The mixed solution is heated in a boiling water bath for 10 min and is continuously stirred using a glass rod until the agarose powder is completely dissolved. After heating, sufficient hot deionized water is added to supplement the water lost during heating. Next, the mixed solution is cooled to 50–55 °C and then is poured into a preheated container. The container is assembled from a glass substrate and a PDMS plate with a circular hole of 1 cm in diameter and 3 mm in height. The circular boundary can prevent the soft hydrogel sample from sliding during the measurement, meanwhile it is large enough compared with a typical impact region of the compression so that the effect of confinement can be ignored. The mixed solution poured into the container is naturally cooled to room temperature and forms into a gel state. Then, the hydrogel is fully immersed in deionized water and placed in a 4 °C refrigerator for 24 hours to achieve swelling equilibrium. Prior to each experiment, the hydrogel is kept at room temperature for about 2 hours and is placed in a closed fluid chamber to minimize evaporation during AFM measurement.
2.2 AFM setup and operation
Force relaxation and indentation measurements for hydrogels are performed by using an AFM (MFP-3D, Asylum Research) with a colloidal probe, as sketched in Fig. 1a. The AFM is set up on an inverted microscope (IX71, Olympus) equipped with an EMCCD camera (Ixon3, Andor). The colloidal probe consists of a glass sphere of radius R (≃25 μm), which is glued on the front end of a rectangular cantilever beam (NSC35/Pt, MikroMasch) featuring a spring constant of 10 N m−1. The glass sphere is used to ease alignment between surfaces in a micron scale system. Compared with other shapes of AFM tips, such as a cone and cylinder, the force field of the spherical probe is more uniform and will not cause stress concentration at the edge of the probe. The freshly assembled colloidal probe32 is plasma cleaned using a low-vacuum plasma cleaner (Harrick Plasma, PDC-32G) at the power of 40 W for 15 min. The vacuum level of the cleaner is kept at about 600 milli-torr during the plasma cleaning. The colloidal probe is then coated with a thin layer of poly(L-lysine)-graft-poly(ethylene glycol) (PLL-g-PEG), which effectively reduces the adhesion of the hydrogel surface to the probe.23 Therefore, the effect of time-dependent adhesion is not considered in the current study, compared with a more obvious poroelastic and viscoelastic mechanical response. The PLL-g-PEG coated glass surface is hydrophilic with a contact angle of 50° for the water–air interface, thus we do not expect an obvious slip effect for this hydrophilic surface.33 The PLL-g-PEG monolayer is so soft and thin (∼nm) that it does not affect the value of the mechanical force.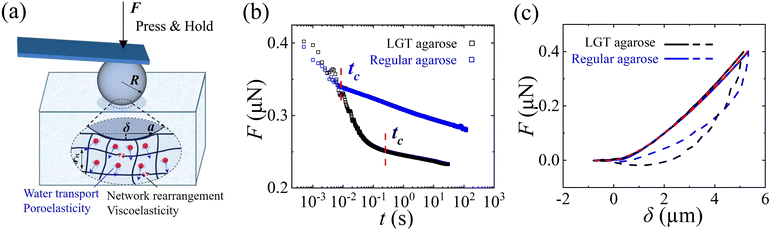 | ||
Fig. 1 Hydrogel stress relaxation reveals a crossover from a short-time poroelastic decay to a long-time power-law viscoelastic decay. (a) Sketch of force relaxation measurement by AFM with a colloidal probe on a hydrogel. When a colloidal probe of radius R presses on a hydrogel with a typical mesh size ξ and generates a downward indentation δ, the characteristic length scale of the indentation is the contact radius 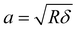 . Two different mechanisms contribute to the stress relaxation of a hydrogel: poroelasticity due to water transport and viscoelasticity due to network rearrangement; (b) linear-log plots of the force relaxation curves for LGT agarose (blue squares) and regular agarose (black squares), respectively, and tc is the crossover time from an initial fast decay to a slow power-law decay; (c) the force indentation curves measured during approaches to (solid lines) and retracts away from (dashed lines) the hydrogel surfaces. By fitting the indentation curves with the Hertz model38 (red dashed lines), the elastic modulus of both samples is obtained as E ≃ 4 kPa. . Two different mechanisms contribute to the stress relaxation of a hydrogel: poroelasticity due to water transport and viscoelasticity due to network rearrangement; (b) linear-log plots of the force relaxation curves for LGT agarose (blue squares) and regular agarose (black squares), respectively, and tc is the crossover time from an initial fast decay to a slow power-law decay; (c) the force indentation curves measured during approaches to (solid lines) and retracts away from (dashed lines) the hydrogel surfaces. By fitting the indentation curves with the Hertz model38 (red dashed lines), the elastic modulus of both samples is obtained as E ≃ 4 kPa. | ||
Prior to each force measurement, the actual spring constant of the colloidal probe is calibrated in situ using the thermal power spectral density method. The contact point (δ = 0) is determined by the Hertzian contact point. In each relaxation measurement, the force vs. distance curve before the relaxation process is fitted with a Hertz model, from which the contact point is determined. It is found that the measured force deviated from the theoretical Hertz model a bit near the contact point, due to the hydrodynamic effect that an extra force is needed to drain out the water in the gap, or an apparent slip layer on the surface of the hydrogel whose mechanical properties deviate from the bulk of the hydrogel. The uncertainty of the indentation depth is within ±0.2 μm, while the typical indentation δ on the hydrogel is within the range of 1 μm to 10 μm. Therefore, the uncertainty is acceptable and does not play a big role in the normalization of the relaxation curves in our data analysis. Each force relaxation and indentation measurement was performed at least three times to ensure the reproducibility and accuracy of the experiment results. All experiments were carried out at room temperature (∼25 °C).
2.3 Poroelastic and viscoelastic modeling
Considering a hydrogel is suddenly deformed by a spherical indentor with a radius R, the response force F(t) is time-dependent and relaxes as a function of time. Based on the theory of poroelasticity, Suo and collaborators11 obtained an approximate solution of F(t) by using the finite element method, which is given by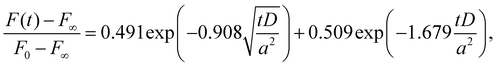 | (1) |
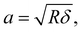 and D is the poroelastic diffusion coefficient of the solvent through the network. The characteristic poroelastic relaxation time is given by τp = Rδ/D, which is related to the characteristic length scale of indentation. This formula has been successfully used to characterize the poroelastic relaxation process and obtain the diffusion coefficient D of various soft materials, including hydrogels, cells and biological tissues.14,22,34,35
and D is the poroelastic diffusion coefficient of the solvent through the network. The characteristic poroelastic relaxation time is given by τp = Rδ/D, which is related to the characteristic length scale of indentation. This formula has been successfully used to characterize the poroelastic relaxation process and obtain the diffusion coefficient D of various soft materials, including hydrogels, cells and biological tissues.14,22,34,35
Meanwhile, hydrogels can also dissipate energy and produce force or stress relaxation by viscoelasticity. Power-law relaxation with an exponent α (0 ≤ α ≤ 1) is used to characterize the slow reorganization of soft materials18 and force F(t) is given by:
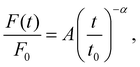 | (2) |
3 Results
3.1 Crossover behavior in the stress-relaxation experiment for hydrogels
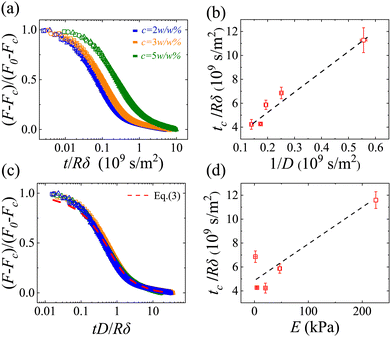
In the experiment, force relaxation measurements were conducted on LGT agarose and regular agarose using an AFM-based force apparatus, as depicted in Fig. 1a. The hydrogels were subjected to a constant indentation δ applied at a loading speed of v = 100 μm s−1. The goal was to quickly apply the indentation to reduce the influence of water redistribution in the hydrogel during indentation while avoiding unwanted hydrodynamic effects on the probe.23 Once the elastic restoring force of the hydrogel reached a preset maximal value F0, the AFM recorded the force relaxation F(t) while keeping the indentation δ constant. The typical δ used was a few microns, which bridges nanometer-sized molecular structures with macroscopic material. F(t) was measured over a five-decade time span ranging from 0.1 ms to tens of seconds until the variations of F(t) reached the noise level of the system. It can be seen from the Fig. 1b that the normalized force F(t)/F0 decays quickly in a short time and then slows down for both types of agarose hydrogels. This bimodal relaxation behavior cannot be explained by a single mechanism. Interestingly, the crossover time tc between the fast and slow decay varied significantly for the two hydrogels, with LGT agarose having a tc one order of magnitude larger than that of regular agarose, even though both hydrogels were almost the same in terms of the materials used and their elastic modulus E(≃4 kPa) measured by the force-indentation measurements, as shown in Fig. 1c. To investigate the underlying physics of the crossover behavior and variations in tc during force relaxation, we conducted a series of experiments on the two types of agarose hydrogels with different indentation depths and concentrations.3.2 Crossover in poroelastic dominant force relaxation
Fig. 2a shows the force relaxation curves of LGT agarose under five different indentation forces F0 (or different indentation δ). It is found that the crossover times tc are sensitive to the magnitude of δ and the corresponding F0 in the measurement, indicating that the force relaxation depends on the length scales of the probed area. The relevant characteristic length scale during the contact between AFM probe and hydrogel is given by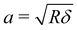 . Indeed, the relaxation curves collapse into a single master curve when normalizing the force [F(t) − F∞] by (F0 − F∞) and the time t by Rδ, as shown in Fig. 2b. This attained collapse of all the normalized force relaxation curves is a signature of the poroelastic response of the hydrogel.14,15 To further quantify the poroelastic diffusion coefficient D of the gel, eqn (1) is utilized to fit the relaxation curves. It is found that eqn (1) fits the data well in a short time while it deviates after the apparent crossover time tc, as shown in Fig. 2c. This behavior further confirms that there is a transition during the force relaxation and the short time relaxation is governed by the poroelastic response of the hydrogel.
. Indeed, the relaxation curves collapse into a single master curve when normalizing the force [F(t) − F∞] by (F0 − F∞) and the time t by Rδ, as shown in Fig. 2b. This attained collapse of all the normalized force relaxation curves is a signature of the poroelastic response of the hydrogel.14,15 To further quantify the poroelastic diffusion coefficient D of the gel, eqn (1) is utilized to fit the relaxation curves. It is found that eqn (1) fits the data well in a short time while it deviates after the apparent crossover time tc, as shown in Fig. 2c. This behavior further confirms that there is a transition during the force relaxation and the short time relaxation is governed by the poroelastic response of the hydrogel.
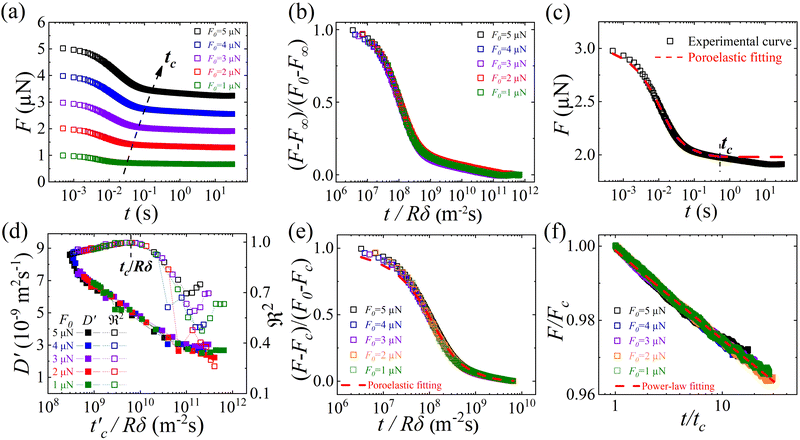 | ||
Fig. 2 Crossover in poroelastic dominant force relaxation. (a) Force relaxation curves of LGT agarose under five different indentation forces F0. The black dashed line indicates the apparent crossover time tc, and tc increases with F0 (or corresponding δ); (b) normalized plot of [F(t) − F∞]/(F0 − F∞) as a function of t/R using the force relaxation curves in (a), and the normalized curves collapse into a single master curve; (c) the poroelastic model [eqn (1), red dashed line] fits the experimental data well in a short time while it deviates after an apparent crossover time tc; (d) the fitted diffusion coefficient D′ (solid symbols) and coefficient of determination 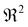 (open symbols) as a function of the attempt normalized crossover time (open symbols) as a function of the attempt normalized crossover time 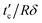 . The dashed line indicates the choice of real crossover time tc at which . The dashed line indicates the choice of real crossover time tc at which 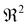 reaches the highest value reaches the highest value 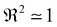 ; (e) normalized plots of [F(t) − Fc]/(F0 − Fc) as a function of t/R using the short-time relaxation curves (t < tc) in (a). The red dashed line indicates the fit of eqn (3) to the data points with a signal fitting parameter D = (5.08 ± 0.36) × 10−9 m2 s−1; (f) normalized plots of F/Fc as a function of t/tc using the long-time relaxation curves (t > tc) in (a). The red dashed line indicates the fit of eqn (4) to the data points with a signal fitting parameter α ≃ 0.0128. ; (e) normalized plots of [F(t) − Fc]/(F0 − Fc) as a function of t/R using the short-time relaxation curves (t < tc) in (a). The red dashed line indicates the fit of eqn (3) to the data points with a signal fitting parameter D = (5.08 ± 0.36) × 10−9 m2 s−1; (f) normalized plots of F/Fc as a function of t/tc using the long-time relaxation curves (t > tc) in (a). The red dashed line indicates the fit of eqn (4) to the data points with a signal fitting parameter α ≃ 0.0128. | ||
To precisely determine the crossover time tc of stress relaxation for this type of hydrogel, we modify eqn (1) by taking the force at the crossover time Fc to replace F∞ and force F(t) is given by:
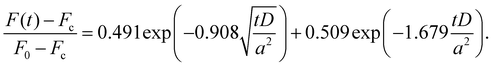 | (3) |
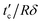 . From the fitting, the
. From the fitting, the 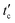 -dependent diffusion coefficient
-dependent diffusion coefficient 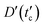 is obtained with a corresponding coefficient of determination
is obtained with a corresponding coefficient of determination 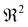 , which quantifies the accuracy of fitting. It is found that with an increase of
, which quantifies the accuracy of fitting. It is found that with an increase of 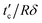 , the coefficient of determination
, the coefficient of determination 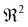 first increases to the highest value
first increases to the highest value 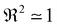 at
at 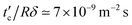 and then decreases, while the diffusion coefficient D′(t) decreases gradually, as shown in Fig. 2d. We define the time of reaching the highest value of
and then decreases, while the diffusion coefficient D′(t) decreases gradually, as shown in Fig. 2d. We define the time of reaching the highest value of 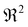 as the crossover time tc, and obtain the poroelastic diffusion coefficient of the gel D = D′(t = tc). It is found that D = (5.08 ± 0.36) × 10−9 m2 s−1, which agrees with the previous studies.10 Furthermore, Fig. 2d shows that the relaxation curves with different indentation forces F0 or depth δ share the same normalized crossover time tc/Rδ, indicating the tc is linear with the indentation δ for this poroelastic dominant relaxation process.
as the crossover time tc, and obtain the poroelastic diffusion coefficient of the gel D = D′(t = tc). It is found that D = (5.08 ± 0.36) × 10−9 m2 s−1, which agrees with the previous studies.10 Furthermore, Fig. 2d shows that the relaxation curves with different indentation forces F0 or depth δ share the same normalized crossover time tc/Rδ, indicating the tc is linear with the indentation δ for this poroelastic dominant relaxation process.
With the precisely determined tc, the whole relaxation curves could be chopped into two regions as shown in Fig. 2e and f. As mentioned above, the relaxation curves in the short-time region are well described by the poroelastic model of eqn (3). For the relaxation curves in the long-time region, they overlap after normalizing the force by Fc and the time by tc. The normalized curves are well described by a power-law form,
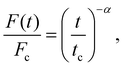 | (4) |
The above results show that the crossover behavior of LGT agarose is mainly affected by the poroelastic process. To investigate how the poroelastic properties of the hydrogel network impact the crossover time tc, we varied the concentration c of the agarose (ranging from 1–5 w/w%) during sample preparation, systematically modifying the hydrogel's poroelastic properties such as the diffusion coefficient D and elastic modulus E. Fig. 3a shows the normalized short-time relaxation curves of LGT agarose hydrogels with different concentrations c. While the normalized curves maintain a similar functional form, the relaxation slows down for higher concentration hydrogels, resulting in a larger tc/Rδ at the end. After fitting the curves with the poroelastic model of eqn (3), we obtained the values of diffusion coefficient D. Interestingly, we found an almost linear relationship between the normalized crossover time tc/Rδ and 1/D, as shown in Fig. 3b. Since the drag coefficient of fluid is proportional to 1/D, our result suggests that an increase in the drag force for higher concentration poroelastic networks slows down the crossover. From the slope of the dashed line, we further find that tcD/Rδ = tc/τp ≃ 25 ± 5 for the LGT agarose hydrogels with different concentrations c, where τp = Rδ/D is the characteristic poroelastic relaxation time. Since tc is much larger than τp, the poroelastic relaxation almost vanishes and transforms into a power-law relaxation at tc. Fig. 3c further shows the normalized plot of [F(t) − Fc]/(F0 − Fc) as a function of tD/R using the relaxation curves in Fig. 3a. The normalized curves collapse into a single master curve, and the red dashed line is a plot of eqn (3) without any fitting parameter. Therefore, D can be treated as another tuning parameter besides the length scales of contact, R and δ, to control the crossover behavior during poroelastic dominant relaxation.
 | ||
| Fig. 3 Relaxations of poroelastic dominant hydrogels with different concentrations. (a) Normalized plots of [F(t) − Fc]/(F0 − Fc) as a function of t/R for LGT agarose with different concentrations c. Data points in different symbols indicate the measurements with different initial indentation forces F0 = 1 μN (triangles), 2 μN (circles), and 3 μN (squares); (b) Normalized crossover time tc/Rδ as a function of 1/D. The black dashed line is a guide to the eye, showing a linear relationship between tc/Rδ and 1/D; (c) Normalized plot of [F(t) − Fc]/(F0 − Fc) as a function of tD/R using the relaxation curves in (a), and the normalized curves collapse into a single master curve. The red dashed line is a plot of eqn (3) without any fitting parameter. (d) Normalized crossover time tc/Rδ as a function of E. The black dashed line is a guide to the eye. | ||
We also investigate the effect of the elastic modulus E on the crossover behavior of LGT agarose. To do so, we calculate the elastic modulus E from the indentation data of LGT agarose with different concentrations and plot the normalized crossover time tc/Rδ as a function of E, as shown in Fig. 3d. It is observed that tc/Rδ increases with E, showing a similar trend as the tc/Rδ vs. 1/D curve, as shown in Fig. 3b. When the concentration of the hydrogel sample increases, the mesh size ξ decreases,40,41 leading to an increase in the elastic modulus E of the network and a decrease in the diffusion coefficient D.35 The similar dependence of the normalized crossover time tc/Rδ on E and 1/D further demonstrates that the crossover behavior is predominantly affected by the poroelastic relaxation of the LGT agarose.
3.3 Crossover in viscoelastic dominant force relaxation
Fig. 4a shows the force relaxation curves of regular agarose under four different indentation forces F0. The apparent crossover times tc for this agarose do not vary significantly with the magnitude of F0 (or indentation δ), unlike LGT agarose shown in Fig. 2a. Meanwhile, the crossover time for regular agarose is around 10 ms, and the long power-law relaxation after tc presumably dominates the force relaxation process. Fig. 4b shows the normalized plots of F/Fc as a function of t/tc using the long-time relaxation curves when t > tc. The four curves for different F0 collapse onto a single master curve over a three-decade time span, which is well described by eqn (4) with α ≃ 0.022. Power-law rheology (with 0 ≤ α ≤ 1) is a feature of viscoelastic relaxation.17,18 The characteristic time tc represents the time at which the power-law rheology dominates the relaxation process. Physically, the smallest scale of the hydrogel network, which is the mesh size ξ, determines the fastest viscoelastic relaxation and hence tc. We propose that tc ∼ ξ2/Dag, where Dag is the local mobility of the agarose chains, which is much lower than the water diffusivity D inside the network, in the order of ∼1 × 10−11 m2 s−1.42–44 Using different techniques, the typical mesh size ξ of agarose gel is measured to be around 300 nm.40,41 Therefore, we estimate tc ∼ 10 ms, which is of the same order of magnitude as the crossover time measured in our force relaxation experiment. Since both ξ and Dag are intrinsic material properties of the agarose hydrogel and do not depend on the length scales of the contact measurement, tc does not depend on the indentation depth δ or forces F0, as shown in Fig. 4a.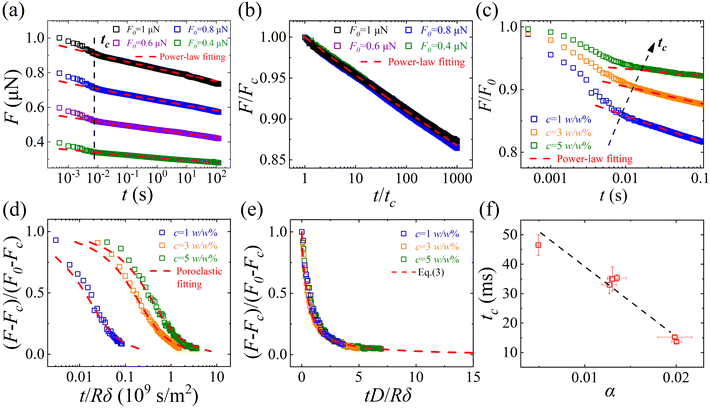 | ||
| Fig. 4 Crossover in viscoelastic dominant force relaxation. (a) Force relaxation curves of regular agarose under four different indentation forces F0. The black dashed line indicates the apparent crossover time tc, and tc is not sensitive to F0 (or the corresponding δ). The red dashed lines indicate the power-law fitting to the data points; (b) Normalized plots of F/Fc as a function of t/tc using the long-time relaxation curves (t > tc) in (a). The red dashed line indicates the fit of eqn (4) to the data points with a signal fitting parameter α ≃ 0.022; (c) force relaxation curves of regular agarose with different concentrations c. The black dashed line indicates the apparent crossover time tc, and tc increases with c. The red dashed lines indicate the fits of eqn (4) to the data points, and the obtained α decreases with c; (d) normalized plots of [F(t) − Fc]/(F0 − Fc) as a function of t/R using the short-time relaxation curves (t < tc) in (c); (e) normalized plot of [F(t) − Fc]/(F0 − Fc) as a function of tD/R, and the red dashed line is a plot of eqn (3) without any fitting parameter. (f) Crossover time tc as a function of power-law exponent α. The black dashed line is a guide to the eye. | ||
Furthermore, we investigated whether the short-time relaxation (t < tc) is still due to the poroelasticity of the hydrogel, even though the long-time viscoelastic relaxation dominates. To do this, we conducted relaxation measurements on hydrogels with different agarose concentrations c, as shown in Fig. 4c. We found that tc increases with c, and the overall relaxation slows down. Using the data analysis from above, we divided the relaxation curves into two regions and plotted the normalized relaxation curves in the short-time region in Fig. 4d. It was found that the short-time curves are still well described by the poroelastic model of eqn (3). However, at the crossover time tc (end of the short-time relaxation), the poroelastic relaxation is not completely over with a small residual force (<10%) left. We further plotted the normalized plot of [F(t) − Fc]/(F0 − Fc) as a function of tD/R in Fig. 4e. As expected, the normalized curves collapsed into a single master curve, similarly to Fig. 3c, while the curves terminated around tD/Rδ = t/τp ≃ 5 ± 2.5, indicating that the poroelastic relaxation is not completely over while the viscoelastic relaxation starts to play a dominant role. Therefore, even in cases of viscoelastic dominant force relaxation, the short-time behavior is still governed by the poroelasticity of the hydrogel, but the crossover time tc is mainly determined by the viscoelastic properties. For example, we also plotted the crossover time tc as a function of the viscoelastic power-law exponent α in Fig. 4f, and found a negative correlation between them for different samples. For hydrogels with higher concentrations, the mesh size ξ decreases, and the gel becomes more solid-like with a decrease in α. Meanwhile, the network becomes more crowded with a decrease in the local mobility of polymer chains Dag. The increase in tc(∼ξ2/Dag) with a decrease in α (or an increase in c) indicates that compared with ξ2, the mobility Dag is more sensitive to the hydrogel concentration.
4 Discussions and biological implications
The experimental results demonstrate that the agarose hydrogels with similar elastic modulus exhibit different stress relaxation patterns. The relaxation behavior can be understood by analyzing the normalized relaxation curves, which can be separated into two distinct regions. The short-time relaxation (t < tc) is mainly due to the poroelasticity of the hydrogel, while the long-time relaxation (t > tc) is dominated by viscoelasticity. Significant differences in crossover behaviors between the two agarose hydrogels are obtained. The crossover time tc of LGT agarose is dominated by short-time poroelastic decay, while that of regular agarose is dominated by long-time viscoelastic power-law decay. The poroelasticity is generated by the solvent (water) movement and redistribution through the hydrogel mesh, whose relaxation time is set by the characteristic length of the indentation, such as the probe radius R and indentation depth δ. By contrast, the viscoelasticity is produced by the reformation of crosslinks and rearrangement of the polymer chains, which is determined by intrinsic material properties. The competition between poroelasticity and viscoelasticity is crucial for understanding the mechanical properties of hydrogels.The two mechanisms can be well separated at different time scales by setting the lengths of indentation measurement to be much larger or smaller than the material lengths of the hydrogels.14,15 However, for a micron-scale mechanical characterizations on hydrogels, tissues and living cells, the two relaxation mechanisms may not be easily distinguished.17,22,23 In our experiment, we hope to clarify the competition between poroelasticity and viscoelasticity and the crossover behavior in stress relaxation. To achieve this, we chose a specific radius for the AFM colloidal probe, which is approximately 25 μm. This choice is made for several reasons. Firstly, the radius is much larger than the mesh size of the hydrogel (ξ ∼ 300 nm40,41), meaning that the probe senses the mechanical responses of the composite material, i.e. the hydrogel network together with the solvent in the pores. If the radius of the AFM tip were smaller or equal to the pore size of the hydrogel, the obtained mechanical properties would originate from the single molecular chain or hollow of the hydrogel,45 which would deviate from the main results reported here. Secondly, the poroelastic relaxation time depends on the length scale of indentation, and the time required for full relaxation exceeds tens of hours for macroscale experiments.14 In contrast, our micron-scale experiments only require a few seconds for full relaxation. Thirdly, the contact radius  between the colloidal probe and hydrogel surface is similar in size to that of a living cell, which is used to mimic the cells seeding on the hydrogel during indentation measurements. Furthermore, the relatively large probe and indentation depth (approximately 1 to 10 μm) average out the local anisotropy and inhomogeneity of the hydrogel surface, so that mechanical property gradients, which can develop close to the surface of gel systems during their synthesis,46,47 are not considered in the current study. These features of the micron-scale indentation are particularly useful for the study attempted here.
between the colloidal probe and hydrogel surface is similar in size to that of a living cell, which is used to mimic the cells seeding on the hydrogel during indentation measurements. Furthermore, the relatively large probe and indentation depth (approximately 1 to 10 μm) average out the local anisotropy and inhomogeneity of the hydrogel surface, so that mechanical property gradients, which can develop close to the surface of gel systems during their synthesis,46,47 are not considered in the current study. These features of the micron-scale indentation are particularly useful for the study attempted here.
Fig. 5a shows the proportions of relaxed force due to poroelasticity and viscoelasticity for the two types of hydrogels, respectively. The results show that poroelasticity dominates the stress relaxation for LGT agarose, whereas for regular agarose, viscoelastic relaxation slightly exceeds poroelastic relaxation. The difference in relaxation behavior arises from their differences in micro structures. The agarose hydrogels are formed by weak hydrogen bonds,10 which are prone to rearrange under deformation and exhibit a viscoelastic behavior. In the case of LGT agarose, some of the hydrogen atoms are replaced by hydroxyethyl groups,31 leading to a more porous network and more pronounced water movement due to a reduction of hydrogen bonds. Moreover, LGT agarose has a relatively uniform pore size, while regular agarose has a more disordered structure with a larger variation in pore size,40,41 which facilitates power-law stress relaxation.
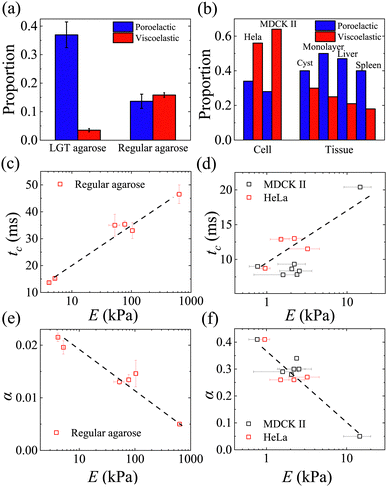 | ||
| Fig. 5 Comparison between hydrogels and living matter in terms of stress relaxation. (a) The proportion of relaxed force due to poroelasticity and viscoelasticity for LGT agarose and regular agarose; (b) the proportion of relaxed force due to poroelasticity and viscoelasticity for cells and tissues. The data is obtained by further analyzing the experimental results in previous works;22–25 (c and d) crossover time tc as a function of modulus E for regular agarose and cells; (e and f) power-law exponent α as a function of modulus E for regular agarose and cells. | ||
It is of great interest to compare the mechanical properties of living matter with conventional hydrogels. The mechanical structures of living matter, such as cells and tissues, are similar to hydrogels. For example, cells have a cytoskeletal network made of cross-linked protein filaments, such as actin filaments (F-actin), microtubules, and intermediate filaments. The cytoskeletal network is filled with cytosol, and transportation through the soft porous structures is essential for cell locomotion, division, and deformation.35 Previous studies have shown that living cells and tissues exhibit stress relaxation with a crossover behavior similar to that of hydrogels in response to deformation.22–25,35 However, little is known about the characteristic crossover time and how it relates to the structures of living matter.
Fig. 5b shows the proportions of relaxed force for single cells and tissues. The data were obtained by further analyzing experimental results from previous studies.22–25 These stress relaxation measurements were conducted following a relatively fast deformation (compression or sketching) so that the influence of water redistribution in the soft materials during deformation can be ignored. Interestingly, it was found that viscoelasticity plays a leading role in stress relaxation for HeLa and MDCK II cells,23 similar to regular agarose, indicating that the slow reorganization of the cytoskeletal network dominates the mechanical response at the single-cell level. Furthermore, we plotted the characteristic parameters for describing viscoelastic dominant relaxation, tc and α, as a function of material property, modulus E, for both hydrogels and living cells, as shown in Fig. 5c–f. Hydrogels with different E were obtained by changing the concentration of regular agarose, and cells with different E were obtained by using different drug treatments on the actin network. The hydrogels and living cells exhibit similar behaviors. For example, the crossover time tc of MDCK II cells and HeLa cells increases with modulus E, similar to agarose hydrogels. Moreover, the values of tc for both cells and regular agarose are on the order of tens of milliseconds.23 The power-law exponent α of both cells and agarose decreases with modulus E, and the values of α for cells, which are in the range of 0.1–0.4 as reported in the literature,37,48 are much larger than those of agarose hydrogels, indicating that living cells are more fluid-like.
In Fig. 5b, the proportions of relaxed force for tissues are shown in comparison to those of single cells. Examples of two types of engineered artificial tissues, epithelial cyst22 and monolayer24 formed by MDCK II cells, and two types of tissues from organs, liver and spleen,25 are given. It is found that poroelasticity plays an important role in stress relaxation after a fast deformation for these tissues regardless of their geometry. In addition to the aquaporin channels located on the cell membranes, the tissues have gap junctions between neighboring cells, which facilitates the exchange of fluid.22 Therefore, poroelastic relaxation becomes pronounced for the tissues. Similar to poroelastic dominant LGT agarose, the crossover time tc for the tissues is in the order of 100 ms to a few seconds, which is much larger than that of single cells and regular agarose.
Both the proportions of relaxed force and tc suggested that the relaxation behavior of viscoelastic dominate hydrogel (regular agarose) is very similar to that of a single cell, while the poroelastic dominate hydrogel (LGT agarose) shares more similarities with tissue. However, living matter has active stress produced by molecular motors, such as myosins, which can actively contract and generate forces, leading to complex mechanical responses that cannot be easily captured by passive hydrogels. It is of interest to investigate the unique active mechanical properties of living materials compared with conventional hydrogels.
5 Conclusion
We have carried out systematic AFM measurements of stress relaxation on agarose hydrogels. Two different types of agarose hydrogels with different concentrations are used. The stress relaxation features a short-time poroelastic relaxation followed by a viscoelastic power-law relaxation, and each type of hydrogel shows its own characteristic crossover behavior. An important result shown in Fig. 2–4 is that the crossover time tc is uniquely connected to the predominant mechanism of stress relaxation. For poroelastic dominate hydrogels (LGT agarose), tc is proportional to characteristic lengths of the contact measurement, such as indentation depth δ, and inversely proportional to the diffusion coefficient of water inside porous networks D. In contrast, for viscoelastic dominate hydrogels (regular agarose), tc is not sensitive to δ but increases as the power-law exponent α decreases. Based on these findings, we further discuss the stress relaxation and crossover behavior of living cells and tissues. We found that although living materials have more complex compositions, their mechanical responses share several similarities with hydrogels. Single cells behave like viscoelastic dominant hydrogels, while tissues behave like poroelastic dominant hydrogels. Through careful design of hydrogels, one would utilize the hydrogel as a model system to study a range of interesting mechanical problems related to biomaterials, living cells and tissues, such as the nonlinear mechanical response, diffusio-rheological coupling, abnormal diffusion of nanoparticles in cytoplasm and transportation of drugs in tissue.Author contributions
H. L. and D. G. conceived the research idea. H. L. performed the experiment. H. L., X. L. and D. G. carried out data analysis and discussed the results. H. L. and D. G. wrote the manuscript with further revisions from X. L. and D. G. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank P. Tong, M. Doi, X. Zheng, and Q. Fan for the illuminating discussions and Q. Fan and X. Wang for providing the LGT agarose. This work was supported in part by the National Key R&D Program of China No. 2021YFA0719302 and NSFC under Grant No. 11972351.Notes and references
- B. Jeong, H. B. You, D. S. Lee and S. W. Kim, Nature, 1997, 388, 860–862 CrossRef CAS PubMed
.
- R. W. Langer, Nature, 1998, 392, 5–10 CAS
.
- D. J. Beebe, J. S. Moore, J. M. Bauer, Q. Yu, R. H. Liu, C. Devadoss and B. H. Jo, Nature, 2000, 404, 588–590 CrossRef CAS PubMed
.
- G. Gerlach, M. Guenther, J. Sorber, G. Suchaneck, K. F. Arndt and A. Richter, Sens. Actuators, B, 2005, 111, 555–561 CrossRef
.
- R. Andreas, P. Georgi, K. Stephan, L. Jens and H. J. P. Adler, Sensors, 2008, 8, 561–581 CrossRef PubMed
.
- A. P. Nowak, V. Breedveld, L. Pakstis, B. Ozbas, D. J. Pine, D. Pochan and T. J. Deming, Nature, 2002, 417, 424–428 CrossRef CAS PubMed
.
- Y. Luo and M. S. Shoichet, Nat. Mater., 2004, 3, 249–253 CrossRef CAS PubMed
.
- O. Chaudhuri, J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Nature, 2020, 584, 535–546 CrossRef CAS PubMed
.
- T. Nonoyama and J. P. Gong, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 393–410 CrossRef CAS PubMed
.
- D. Caccavo, S. Cascone, G. Lamberti and A. A. Barba, Chem. Soc. Rev., 2018, 47, 2357–2373 RSC
.
- Y. Hu, X. Zhao, J. J. Vlassak and Z. Suo, Appl. Phys. Lett., 2010, 96, 37 Search PubMed
.
- D. G. Strange, T. L. Fletcher, K. Tonsomboon, H. Brawn, X. Zhao and M. L. Oyen, Appl. Phys. Lett., 2013, 102, 031913 CrossRef
.
- Q.-M. Wang, A. C. Mohan, M. L. Oyen and X.-H. Zhao, Acta Mech. Sin., 2014, 30, 20–27 CrossRef CAS
.
- Z. I. Kalcioglu, R. Mahmoodian, Y. Hu, Z. Suo and K. J. Van Vliet, Soft Matter, 2012, 8, 3393–3398 RSC
.
- J. D. Berry, M. Biviano and R. R. Dagastine, Soft Matter, 2020, 16, 5314–5324 RSC
.
- M. H. Esteki, A. A. Alemrajabi, C. M. Hall, G. K. Sheridan, M. Azadi and E. Moeendarbary, Acta Biomater., 2020, 102, 138–148 CrossRef CAS PubMed
.
- Q. Xu, L. A. Wilen, K. E. Jensen, R. W. Style and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 238002 CrossRef CAS PubMed
.
- P. Sollich, F. Lequeux, P. Hébraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020–2023 CrossRef CAS
.
- J. De Sousa, R. Freire, F. Sousa, M. Radmacher, A. Silva, M. Ramos, A. Monteiro-Moreira, F. Mesquita, M. Moraes and R. Montenegro,
et al.
, Sci. Rep., 2020, 10, 1–10 CrossRef PubMed
.
- M. R. Islam, J. Virag and M. L. Oyen, J. Biomech., 2020, 113, 110090 CrossRef PubMed
.
- Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81 RSC
.
- Y. Shen, D. Guan, D. Serien, S. Takeuchi, P. Tong, L. Yobas and P. Huang, Biophys. J., 2017, 112, 398 CrossRef CAS PubMed
.
- D. Guan, Y. Shen, R. Zhang, P. Huang, P. Lai and P. Tong, Phys. Rev. Res., 2021, 3, 043166 CrossRef CAS
.
- A. R. Harris, L. Peter, J. Bellis, B. Baum, A. J. Kabla and G. T. Charras, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16449–16454 CrossRef CAS PubMed
.
- Y.-C. Lu and C. D. Untaroiu, Proc. Inst. Mech. Eng., Part H, 2013, 227, 293–301 CrossRef PubMed
.
- V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265–275 CrossRef CAS PubMed
.
- K. E. Kasza, A. C. Rowat, J. Liu, T. E. Angelini, C. P. Brangwynne, G. H. Koenderink and D. A. Weitz, Curr. Opin. Cell Biol., 2007, 19, 101–107 CrossRef CAS PubMed
.
- E. Moeendarbary and A. R. Harris, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2014, 6, 371–388 Search PubMed
.
- Y. Shu, H. N. Chan, D. Guan, H. Wu and M. Lan, Sci. Bull., 2017, 62, 222–228 CrossRef CAS PubMed
.
- J. Cao, H. Li, H. Tang, X. Gu, Y. Wang, D. Guan, J. Du and Y. Fan, Bioengineering, 2023, 10, 384 CrossRef CAS PubMed
.
- Y. Gu, K.-L. Cheong and H. Du, Chem. Cent. J., 2017, 11, 1–10 CrossRef PubMed
.
- D. Guan, Z. H. Hang, Z. Marcet, H. Liu, I. I. Kravchenko, C. T. Chan, H. B. Chan and P. Tong, Sci. Rep., 2015, 5, 1–12 Search PubMed
.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC
.
- M. L. Oyen, Curr. Opin. Solid State Mater. Sci., 2015, 19, 317–323 CrossRef
.
- E. Moeendarbary, L. Valon, M. Fritzsche, A. R. Harris, D. A. Moulding, A. J. Thrasher, E. Stride, L. Mahadevan and G. T. Charras, Nat. Mater., 2013, 12, 253–261 CrossRef CAS PubMed
.
- F. Amblard, A. C. Maggs, B. Yurke, A. N. Pargellis and S. Leibler, Phys. Rev. Lett., 1996, 77, 4470–4473 CrossRef CAS PubMed
.
- J.-T. Hang, Y. Kang, G.-K. Xu and H. Gao, Nat. Commun., 2021, 12, 6067 CrossRef CAS PubMed
.
- H. Hertz, Z. Reine Angew. Mathematik, 1881, 92, 156–171 Search PubMed
.
- F. de Sousa, P. Babu, M. Radmacher, C. Oliveira and J. de Sousa, J. Phys. D: Appl. Phys., 2021, 54, 335401 CrossRef CAS
.
- M. M. Chui, R. J. Phillips and M. J. Mccarthy, J. Colloid Interface Sci., 1995, 174, 336–344 CrossRef CAS
.
- N. Pernodet, M. Maaloum and B. Tinland, Electrophoresis, 1997, 18, 55–58 CrossRef CAS PubMed
.
- B. Dai and S. Matsukawa, Carbohydr. Res., 2013, 365, 38–45 CrossRef CAS PubMed
.
- F. B. A. Descallar and S. Matsukawa, Carbohydr. Polym., 2020, 245, 116497 CrossRef CAS PubMed
.
- F. B. A. Descallar, A. Wang and S. Matsukawa, Food Hydrocolloids, 2022, 123, 106930 CrossRef CAS
.
- K. Wang, X. Pang, Y. Ge, F. Ma, X. Shen, X. Xia, B. Tang, K. Wang, X. Pang, Y. Ge, F. Ma, X. Shen, X. Xia and B. Tang, J. Biomater. Tissue Eng., 2018, 8, 1617–1621 CrossRef
.
- J. P. Gong, Soft Matter, 2006, 2, 544–552 RSC
.
- Y. Gombert, R. Simi, F. Roncoroni, M. Dübner, T. Geue and N. D. Spencer, Adv. Mater. Interfaces, 2019, 6, 22 Search PubMed
.
- P. Kollmannsberger and B. Fabry,
et al.
, Annu. Rev. Mater. Res., 2011, 41, 75–97 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2023 |
