Open Access Article
Open Access ArticleEnhanced inverted singlet–triplet gaps in azaphenalenes and non-alternant hydrocarbons†
Marc H.
Garner‡§
 *,
J. Terence
Blaskovits‡¶
*,
J. Terence
Blaskovits‡¶
 and
Clémence
Corminboeuf
and
Clémence
Corminboeuf
 *
*
Laboratory for Computational Molecular Design, Institute of Chemical Sciences and Engineering, École Polytechnique Fedéralé de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: marc.garner@epfl.ch; clemence.corminboeuf@epfl.ch
First published on 15th January 2024
Abstract
Inverted singlet–triplet gaps may lead to novel molecular emitters if a rational design approach can be achieved. We uncover a substituent strategy that enables tuning of the gap and succeed in inducing inversion in near-gapless molecules. Based on known inverted-gap emitters, we design substituted analogs with even more negative singlet–triplet gaps than in the parent systems. The inversion is lost if the reverse substituent-strategy is used. We thus demonstrate a definite set of conceptual design rules for inverted gap molecules.
A range of molecules where the first excited singlet (S1) and triplet (T1) states violate Hund's rule have recently been discovered.1–5 Such compounds hold great promise as molecular emitters because the potentially emissive singlet state is thermodynamically favored over the non-emissive triplet, as illustrated in Fig. 1.1,6–9 Inverted singlet–triplet gaps had been overlooked in azaphenalenes,10,11 and were recently reexamined as emitters using coupled-cluster (CC)-based methods that can correctly predict Hund's rule violations.12–14 The inversion can occur in species where the overlap between the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO) is minimal, which is the case in azaphenalenes.2 Finally, Aizawa et al. confirmed the potential of the inverted gap mechanism in an OLED device.1 It is now imperative to establish a rational design paradigm for promoting the inverted gap mechanism in molecules.
We recently uncovered several non-alternant polycyclic hydrocarbons,3,4 which constitute a class of inverted singlet–triplet gap molecules (Fig. 1).15–17 These molecules have symmetric pentalenic or heptalenic cores that are stabilized by aromatic ring patterns or by substituent-induced double-bond delocalization. Heilbronner described how this double-bond delocalization is promoted by using donors at positions with pronounced LUMO coefficients or acceptors at HOMO positions,18,19 which alleviate the antiaromaticity of the parent molecules.4 In this way, we designed several double-bond delocalized pentalenes and s-indacenes that exhibit inverted gaps.4 However, there are many other non-alternant hydrocarbons that are highly symmetric but nonetheless exhibit small positive singlet–triplet gaps, despite having minimal HOMO–LUMO overlap.
Here, we uncover the full potential of Heilbronner's substituent strategy. We demonstrate that the substituent effect not only leads to inversion through the induction of structural changes in low-symmetry cores, but can directly influence the singlet–triplet gap of high-symmetry structures via electronic tuning. The Hund's rule violation can thus be induced in compounds that would otherwise respect Hund's rule, and the magnitude of the violation can be increased in compounds that already exhibit negative singlet–triplet gaps.
To model the singlet–triplet gaps, we compute the vertical excitation energies at the equations of motion coupled cluster with singles and doubles (EOM-CCSD) level with the cc-pVDZ basis set as implemented in Q-Chem 5.1.20,21 The computational resources required for EOM-CCSD restrict the size and number of molecules we can assess; we therefore sample select molecular cores and small substituents. This limits the scope to proof-of-concept of the design strategy. EOM-CCSD provides a conservative assessment of singlet–triplet gaps in conjugated molecules.4,22 The singlet–triplet gap (E(S1–T1)) of azulene was determined experimentally in the gas-phase to be 49 meV;23 while this value is specific to the experimental setup, it is 6 meV below the vertical gap obtained with EOM-CCSD/cc-pVDZ, 55 meV. All structures are optimized without symmetry constraints at the ωB97X-D/def2-TZVP level using Gaussian16 and are identified as energy minima with no imaginary frequencies.24 The basis set dependence of E(S1–T1) is small in planar conjugated molecules, which we test both at the EOM-CCSD and CC2 level in Fig. S1 and Table S1 (ESI†).
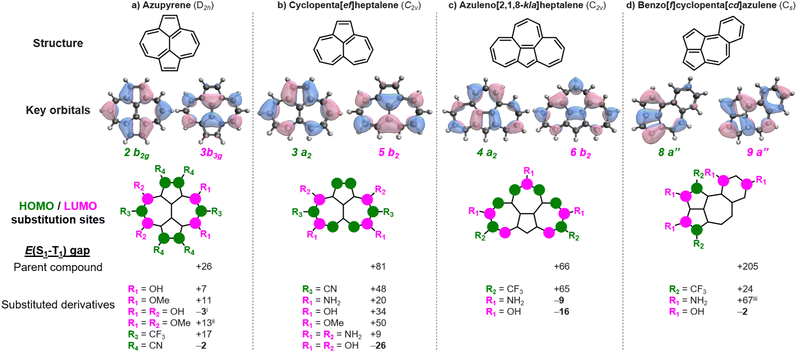
Azupyrene has previously been suggested as an inverted gap molecule.17 And yet, despite having a double-bond delocalized structure and negligible HOMO–LUMO overlap, it has a positive gap of +26 meV at the EOM-CCSD/cc-pVDZ level.4,25 In accordance with the Heilbronner strategy,18,19 we substitute azupyrene with archetypical donor substituents (–OH, –OMe, –NH2, –NMe2) at positions with significant LUMO coefficients, and with acceptors (–CN, –CF3) at positions with large HOMO coefficients, as shown in Fig. 2a. In this way, we find several new substituted azupyrenes with lower singlet–triplet gaps than the parent compound. Most notably, we find that azupyrene-3,5,8,10-tetraol and azupyrene-1,2,6,7-tetracarbonitrile have inverted gaps.
There are several substituted azupyrenes where the gap between S1 and the triplet of the same configuration is negative – thus constituting a Hund's rule violation – but where another triplet state is lower in energy (Table S1, ESI†). This includes the abovementioned azupyrene-3,5,8,10-tetraol, which has an inverted gap of −3 meV, but Hund's rule violation exists between S1 and T2 and is at E(S1–T2) = −120 meV; similar values are obtained for the analogous amine- and methoxy-substituted molecules. The tetrakis(trifluoromethyl)-azupyrene has a more negative gap than azupyrene-1,2,6,7-tetracarbonitrile at the CC2/cc-pVDZ level, but we were unable to obtain a result with EOM-CCSD. There is a huge chemical space to explore with larger substituents that may enable inverted singlet–triplet gaps in azupyrenes.
There are many polycyclic hydrocarbons that have a double-bond delocalized structure and small positive singlet–triplet gap.4,26,27 Again, we substitute with donors at LUMO positions, and with acceptors at HOMO positions. Cyclopenta[ef]heptalene has a small positive singlet–triplet gap, E(S1–T1) = +81 meV. We show several cases where the gap is lowered (Fig. 2b), and a cyclopenta[ef]heptalene-3,5,8,10-tetraol with a negative singlet–triplet gap of E(S1–T1) = −26 meV. Similarly, bare azuleno[2,1,8-kla]heptalene has a positive gap of E(S1–T1) = +66 meV, while the 2,8,11-triol and 2,8,11-triamine derivatives achieve negative gaps of E(S1–T1) = −9 meV and −16 meV, respectively (Fig. 2c). Benzo[f]cyclopenta[cd]azulene has a significant gap of E(S1–T1) = +205 meV. Still, we find an inverted gap in the 2,3,8,10-tetraol derivative with E(S1–T1) = −2 meV. These examples underline the range of molecules to which the Heilbronner strategy can be applied to fine-tune the singlet–triplet gaps towards the desirable inverted gap regime.
We also apply this strategy to derivatives of azulene. Although we find Hund's rule violations with the S1 state, the MO order changes and a lower-lying triplet state means that E(S1–T1) remains positive (Fig. S2, ESI†). However, it is clear that the Heilbronner strategy can be applied to tune its excited states, which may be relevant to controlling its anti-Kasha emission.28–31
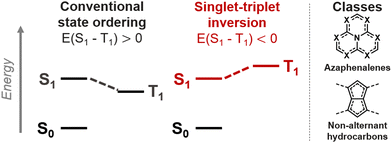
Next, we test the strategy on molecules that already possess negative singlet–triplet gaps. Isopyrene has a negative singlet–triplet gap of −21 meV (Fig. 3a).3 Although the gap is already inverted in the parent system, we find several derivatives with enhanced negative gaps when substituted with acceptors at HOMO positions, or with donors at LUMO positions. Most notably, the 5,10-bis(trifluoromethyl) and 5,10-dicarbonitrile derivatives achieve E(S1–T1) as low as −51 meV and −63 meV, respectively. As in azupyrene, there are several cases where another triplet state becomes T1. These Hund's rule violations are listed in Table S1 (ESI†).
Interestingly, we also find that the reverse strategy can suppress the singlet–triplet gap inversion. This is done by applying donors at HOMO coefficient positions and acceptors at LUMO positions. The 5,10-diol and 5,10-diamine substituted isopyrenes thereby attain positive singlet triplet-gaps of E(S1–T1) = +189 meV and E(S1–T1) = +149 meV, respectively. Although these derivatives have double-bond delocalized structures like the parent isopyrene, the substituents remove the Hund's rule violation. This testifies to the effectiveness of the Heilbronner strategy in manipulating singlet–triplet gaps, and underlines that it constitutes a rational design strategy.
We further test these findings on a few well-studied azaphenalenes, namely heptazine, cyclazine and pentaazaphenalene (Fig. 3b–d).1,8,12,22,32,33 While the number of available substituent positions is more limited in these molecules, particularly in heptazine, the derivatives reveal a gap enhancement of almost 100 meV compared to the parent compounds. We thus show a range of molecules with very negative gaps. Heptazine-2,5,8-triamine (melem) is the most negative singlet–triplet gap we have on record at the EOM-CCSD level with E(S1–T1) = −265 meV. Melem has been studied in OLEDs and has achieved very high photoluminescence quantum yields, which have yet to be rationalized.34–37 If the inverted gap of melem is retained in devices, it may contribute to this result. However, we note that there is no oscillator strength from S1 in melem due to its high symmetry (Table S2, ESI†).
The reverse strategy also applies to azaphenalenes, and causes the singlet–triplet gaps to become less negative. We find several substituted cyclazines (Fig. 2c) and pentaazaphenalenes (Fig. 2d and Table S1, ESI†) where the gap becomes positive when we substitute with donors (acceptors) at HOMO (LUMO) positions. Again, it is essential to consider where to substitute, as the inversion is highly sensitive to this choice. It is likely that many previously studied substituted azaphenalene-based emitters may not possess inverted gaps.38,39 However, with the possibility of tuning the gap to be more negative than the parent compound, our result guides the way to molecules with inverted gaps robust enough to persist in a device environment.
The Heilbronner strategy in its current form does not consider oscillator strength (fosc). Like most other inverted gap molecules, the compounds discussed here have almost exclusively dark S1 states due to the lack of overlap between the HOMO and LUMO (Table S2, ESI†), with the exception of a few promising candidates (Fig. S3, ESI†). These include triamine (trimethylamine)-substituted pentaazaphenalene (Fig. 3d), which retains a negative gap of −8 (−57) meV, while exhibiting an fosc for S1 of 0.043 (0.027). Nevertheless, we expect that the increased negative gaps presented here will provide more space to maneuver within the trade-off that exists between negative gap and fosc.1 In this way, sufficient orbital overlap to promote fosc may be achieved, while a reduced negative gap can be retained. This will likely require the exploration of larger substituents than those considered in this work and the identification of suitable combinations of donor- and acceptor-type substituents.
While the Heilbronner strategy seems generally applicable across different classes of compounds, it does not always lead to the expected result; these are indicated in Table S1 (ESI†). In some cases, ostensibly favorable substitutions result in more positive singlet–triplet gaps than the unsubstituted parent compound. For example, while azupyrene-3,5-diol and -3,5-dimethoxyl have less positive gaps than azupyrene (Fig. 2a), that of azupyrene-3,5-diamine is more positive at +53 meV (Table S1, ESI†). Some exceptions can be attributed to the substituents breaking the symmetry of the molecular cores (Fig. S4 and S5, ESI†), as also explored by Ricci et al.32 Substituted heptazines are an example of this: trisubstituted heptazines retain the local symmetry of bare heptazine (Fig. 3b), while mono- and disubstituted derivatives induce deformations in the core (Fig. S4, ESI†). This reduces the magnitude of the negative gap relative to bare heptazine, and in some cases induces a positive gap.
Deviations in substituent effects should not be surprising considering that excited state energies are being fine-tuned in a very small range. A structural distortion, however small, may have a detrimental effect on the singlet–triplet gap, which outweighs the electronic effect brought about by the substitution. The set of molecules examined here is focused on identifying new molecules with inversions using high-level methods, and we thus cannot make a quantitative evaluation of the interplay between these effects.
In summary, we have described a rational substituent strategy that induces and enhances inverted singlet–triplet gaps in a range of non-alternant polycyclic hydrocarbons and azaphenalenes. This is achieved by functionalizing with electron donors in positions with large LUMO coefficients, or with electron acceptors in positions with large HOMO coefficients. Using this strategy, we identified several molecular cores which achieve an inverted singlet–triplet gap only when appropriately substituted. We furthermore demonstrate that the reverse strategy can remove the singlet–triplet inversion.
This result underlines the importance of rational design rules, as substituents can enhance or suppress singlet–triplet inversions. We project that this knowledge of substituent effects will enable efficient screening in the hunt for novel inverted gap systems. We have provided an approach for the a priori elimination of undesired core-substituent combinations from the search pool, thus reducing computational cost and reserving highly accurate methods for the most promising candidates. This strategy will facilitate the optimization of other properties, such as oscillator strength, while retaining singlet–triplet gap inversions.
We are grateful to the EPFL for financial support and the allocation of computational resources. M. H. G. acknowledges the Carlsberg Foundation for funding (CF21-0202).
Conflicts of interest
There are no conflicts to declare.Notes and references
- N. Aizawa,
et al.
, Nature, 2022, 609, 502–506 CrossRef CAS PubMed
.
- T. Won,
et al.
, Chem. Phys. Rev., 2023, 4, 021310 CrossRef CAS
.
- J. T. Blaskovits,
et al.
, Angew. Chem., Int. Ed., 2023, 62, e202218156 CrossRef PubMed
.
- M. H. Garner,
et al.
, Chem. Sci., 2023, 14, 10458–10466 RSC
.
- A. Actis,
et al.
, Angew. Chem., Int. Ed., 2023, 62, e202313540 CrossRef CAS PubMed
.
- J.-C. Sancho-García, Nature, 2022, 609, 473–475 CrossRef PubMed
.
- J. Eng and T. J. Penfold, Commun. Chem., 2021, 4, 91 CrossRef PubMed
.
- R. Pollice,
et al.
, Matter, 2021, 4, 1654–1682 CrossRef CAS
.
- X. Chen,
et al.
, Adv. Opt. Mater., 2023, 2301784 CrossRef
.
- W. Leupin and J. Wirz, J. Am. Chem. Soc., 1980, 102, 6068–6075 CrossRef CAS
.
- W. Leupin,
et al.
, J. Am. Chem. Soc., 1986, 108, 17–22 CrossRef CAS
.
- J. Ehrmaier,
et al.
, J. Phys. Chem. A, 2019, 123, 8099–8108 CrossRef CAS PubMed
.
- P. de Silva, J. Phys. Chem. Lett., 2019, 10, 5674–5679 CrossRef CAS PubMed
.
- G. Ricci,
et al.
, ChemPhysChem, 2021, 22, 553–560 CrossRef CAS PubMed
.
- S. Koseki,
et al.
, Can. J. Chem., 1985, 63, 1572–1579 CrossRef CAS
.
- A. Toyota and T. Nakajima, J. Chem. Soc., Perkin Trans. 2, 1986, 1731–1734 RSC
.
- A. Toyota, Theor. Chim. Acta, 1988, 74, 209–217 CrossRef CAS
.
- E. Heilbronner and Z.-Z. Yang, Angew. Chem., Int. Ed. Engl., 1987, 26, 360–362 CrossRef
.
- E. Heilbronner, J. Chem. Educ., 1989, 66, 471 CrossRef CAS
.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS
.
- E. Epifanovsky,
et al.
, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed
.
- P.-F. Loos,
et al.
, J. Phys. Chem. Lett., 2023, 14, 11069–11075 CrossRef CAS PubMed
.
- S. Vosskötter,
et al.
, Phys. Chem. Chem. Phys., 2015, 17, 23573–23581 RSC
.
-
M. J. Frisch, et al., Gaussian 16, Revision A.03, 2016, Gaussian Inc., Wallingford, CT Search PubMed
.
- M. E. Sandoval-Salinas,
et al.
, Phys. Chem. Chem. Phys., 2023, 25, 26417–26428 RSC
.
- H. Omar,
et al.
, J. Am. Chem. Soc., 2023, 145, 19790–19799 CrossRef PubMed
.
- A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2023, 25, 21875–21882 RSC
.
- M. Beer and H. C. Longuet-Higgins, J. Chem. Phys., 1955, 23, 1390–1391 CrossRef CAS
.
- T. Itoh, Chem. Rev., 2012, 112, 4541–4568 CrossRef CAS PubMed
.
- T. Tsuchiya,
et al.
, Chem. Commun., 2023, 59, 10604–10607 RSC
.
- D. Dunlop,
et al.
, J. Am. Chem. Soc., 2023, 145, 21569–21575 CrossRef CAS PubMed
.
- G. Ricci,
et al.
, J. Mater. Chem. C, 2022, 10, 12680–12698 RSC
.
- D. Blasco,
et al.
, Chem. Sci., 2023, 14, 3873–3880 RSC
.
- H. B. Zheng,
et al.
, J. Mater. Chem. C, 2017, 5, 10746–10753 RSC
.
- J. Wen,
et al.
, Chem. – Asian J., 2018, 13, 1060–1066 CrossRef CAS PubMed
.
- H. Kiuchi,
et al.
, Phys. Chem. Chem. Phys., 2022, 24, 23602–23611 RSC
.
- H. Kiuchi,
et al.
, Org. Electron., 2023, 122, 106901 CrossRef CAS
.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. Lett., 2021, 12, 6852–6860 CrossRef CAS PubMed
.
- A. Dreuw and M. Hoffmann, Front. Chem., 2023, 11, 1239604 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cc05747j |
| ‡ These authors contributed equally to this work. |
| § Present address: Department of Energy Conversion and Storage, Technical University of Denmark, 2800 Kongens Lyngby, Denmark. |
| ¶ Present address: Max-Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S1 has the same electron configuration as T2, but is lower in energy than T1. ii
S1 has the same electron configuration as T2, but is lower in energy than T1. ii