Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of the mechanically induced ibuprofen–nicotinamide co-crystal formation by in situ X-ray diffraction†
Lucia
Casali
a,
Maria
Carta
bc,
Adam A. L.
Michalchuk
 ad,
Francesco
Delogu
ad,
Francesco
Delogu
 *bc and
Franziska
Emmerling
*bc and
Franziska
Emmerling
 *ae
*ae
aFederal Institute for Materials Research and Testing, Richard-Willstätter-Straße 11, 12489 Berlin, Germany. E-mail: franziska.emmerling@bam.de
bDepartment of Mechanical, Chemical and Materials Engineering, University of Cagliari, via Marengo 2, 09123 Cagliari, Italy. E-mail: francesco.delogu@unica.it
cCenter for Colloid and Surface Science (CSGI), Cagliari Research unit, Department of Chemistry, University of Florence, via della Lastruccia 3, 50019 – Sesto Fiorentino, FI, Italy
dSchool of Chemistry, University of Birmingham, B15 2TT Edgbaston, Birmingham, UK
eDepartment of Chemistry, Humboldt-Universität zu Berlin, 12489 Berlin, Germany
First published on 26th July 2024
Abstract
Mechanochemistry is drawing attention from the pharmaceutical industry given its potential for sustainable material synthesis and manufacture. Scaling mechanochemical processes to industrial level remains a challenge due to an incomplete understanding of their underlying mechanisms. We here show how time-resolved in situ powder X-ray diffraction data, coupled with analytical kinetic modelling, provides a powerful approach to gain mechanistic insight into mechanochemical reactions. By using the ibuprofen–nicotinamide co-crystal mechanosynthesis as a benchmark system, we investigate the behaviour of the solids involved and identify the factors that promote the reaction. As mechanochemical mechanisms become increasingly clear, it promises to become a breakthrough in the industrial preparation of advanced pharmaceuticals.
Introduction
Co-crystals (i.e. crystals comprising multiple different molecules) are of significant interest to the pharmaceutical industry as a platform to supply active pharmaceutical ingredients (APIs). By combining an API in the solid state with other chemically distinct entities, their physico-chemical properties can be enhanced, including their thermal stability, water solubility, dissolution rate, bioavailability and processability.1Among the APIs in the WHO (World Health Organisation) model list of essential medicines, R/S ibuprofen (hereafter, ibuprofen) is an excellent example of how co-crystallization can markedly improve API physico-chemical properties. Ibuprofen (Fig. 1a) is an analgesic drug with a market size estimated at around 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MT (December 2023), growing at an annual rate of 2%.2 The poor aqueous solubility, bioavailability and thermal stability adversely affect the therapeutic efficacy of ibuprofen. Correspondingly, several strategies have been developed over the decades to overcome these issues,3–5 with co-crystallisation emerging as one of the most effective approaches.6
000 MT (December 2023), growing at an annual rate of 2%.2 The poor aqueous solubility, bioavailability and thermal stability adversely affect the therapeutic efficacy of ibuprofen. Correspondingly, several strategies have been developed over the decades to overcome these issues,3–5 with co-crystallisation emerging as one of the most effective approaches.6
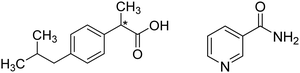 | ||
| Fig. 1 Schematic representation of ibuprofen (left) and nicotinamide (right). The star indicates a chiral carbon centre. | ||
The cocrystal of ibuprofen with nicotinamide (Fig. 1b) is particularly promising since it presents a 7.5-fold increase in water solubility as compared with pure ibuprofen, along with increased thermal stability.7,8 Given the advantages of the ibuprofen–nicotinamide cocrystal,9 strategies to reliably prepare this compound have been extensively investigated.10 To date, the ibuprofen–nicotinamide cocrystal has been successfully made by solution11,12 and vapor crystallization methods,13 from melts7 and even by mechanochemical methods i.e. extrusion14–16 and ball milling.17,18
Co-crystal syntheses based on mechanochemistry are of particular interest for future industrial applications. The drastically reduced use of solvents and energy, along with reactions that often result in 100% yields of single products, make mechanochemistry a sustainable and eco-friendly method.19 In fact, a recent study demonstrated how the ibuprofen–nicotinamide co-crystal can be prepared mechanochemically without waste,20 and with improved green metrics and reduced environmental impact in comparison with large-scale processes in solution (in batch) or solvent-free in continuous by HME (hot melt extrusion).21
Though mechanochemical methods are very promising, their translation to industry remains hindered by a lack in mechanistic understanding and selectivity. This is exacerbated by the fact that the kinetic and thermodynamic rules of analogous solution-based syntheses tend not to apply to mechanochemical routes. To tackle this challenge, methods for time-resolved in situ (TRIS) monitoring of mechanochemical reactions have been developed,22 paving the way to obtaining otherwise inaccessible information on intermediates or new products, as well as on reaction rates.
TRIS methods for monitoring ball milling reactions via X-ray diffraction (XRD) are particularly powerful to follow mechanochemical co-crystallization,22 and are excellent tools to probe and optimize mechanochemical reactions.23,24 Moreover, the collection of TRIS-XRD data provides access to kinetic profiles, which, when modelled analytically, offer exciting insight into the fundamental behaviors of solids under mechanochemical conditions.25,26 To date, such analyses have shown that mechanochemical kinetics derive from the complex interplay of physical parameters, including changes of the internal and surface energy, the reduction of the crystallite sizes, as well the reduction in the coherence energy of the solids.27–29
Using the synergies of TRIS-XRD and analytical kinetic modelling, we here investigate the mechanochemical synthesis of the ibuprofen–nicotinamide cocrystal and demonstrate that the transformation likely occurs via the mechanically induced melting of ibuprofen.
Materials and methods
Reagents
R/S ibuprofen (4-isobutyl-alpha-methylphenyl acetic acid 99%) and nicotinamide 99% were purchased from Alfa Aesar (Thermo Fisher Scientific). The experimental powder diffractograms were compared with simulated patterns to verify the purity of the samples (see Fig. SI1a, ESI†): we had pure polymorph I for R/S ibuprofen (IBPRAC06)30 and the α polymorph for nicotinamide (NICOAM02).31 The compounds were used without further purification.Mechanochemical reaction
The stoichiometric mechanochemical reactions between R/S ibuprofen (75.38 mg) and nicotinamide (44.62 mg) were performed in a vibrational ball mill (Pulverisette 23, Fritsch, Germany) with a custom-made PMMA jar with hemispherical steel ends (12 mm diameter)32 in neat grinding conditions with the frequencies and steel ball sizes reported in the Results and discussion section. The experiments were performed using a single milling ball (details in the main text).Ex situ powder X-ray diffraction (PXRD) measurements
PXRD data were collected on a laboratory diffractometer (D8 Discover, Bruker AXS) in transmission geometry equipped with a Cu Kα1,2 source (λ1 = 1.54056 Å, λ2 = 1.54443 Å) and a Lynxeye XET detector. The sample powder was loaded into capillaries of 0.5 mm diameter, and data were measured in a 2θ range 2–60°, 6000 steps, 4 s per step.Time resolved in situ (TRIS) PXRD measurements
TRIS-PXRD measurements were performed at the μ-Spot beamline (BESSY II, Helmholtz Centre Berlin for Materials and Energy).33 The reactions were carried out in a vibrational ball mill (Pulverisette 23, Fritsch, Germany) using a custom-made PMMA jar with hemispherical steel ends (12 mm diameter). Data were measured using an incident wavelength of λ = 0.7314 Å, obtained with a double crystal monochromator (Si 111). Each data frame was obtained by accumulating scattering for 30 s. The resulting scattering images were integrated using the Dpdak-software,34 and background corrected with a custom-built python script using the ARPLS and ALS algorithms.35Kinetic study
For single peak analysis, data points collected one minute apart were selected from the in situ data set. For each data point, the area under the Bragg peak of the co-crystal at scattering vector q = 2–2.40 nm−1 was calculated using OriginPro 2020. For multivariate analysis, we used the software The UnscrumblerX to perform MCR-ALS (multivariate curve resolution – alternating least squares) on the background corrected data set. We note that the experimental set-up used for TRIS-PXRD caused distortion of the PXRD profiles that made reliable quantitative analysis by Rietveld methods unreliable.Differential scanning calorimetry (DSC)
The DSC profiles for 5 mg of the physical mixture of R/S ibuprofen and nicotinamide were recorded at a speed of 10 K min−1 and 1 K min−1 in the Mettler Toledo TGA/DSC 3+ thermal analysis system. The DSC profiles of the reagents ibuprofen and nicotinamide, and of the pure product ibuprofen–nicotinamide, were collected at a rate of 10 K min−1. All the samples were placed in a 100 μL Al pan, and analysed under an N2 atmosphere at a rate of 80 μL min−1.High-speed camera measurements
Frames of the mechanochemical reactions were recorded with a Basler acA2040-180kmNIR with an acquisition speed of 602 or 1782 frames per second depending on the chosen set-up.Piezoelectric sensor measurements
The milling jar containing one 10 mm ball was equipped with piezoelectric transducers attached to one of the hemispherical caps. The sensors were connected to a computer and the signals generated by contacts between the jar and ball were recorded and subsequently analysed using in house software.Kinetic modelling
Analysis of the experimental kinetic data was performed using a phenomenological analytical model based on the statistical character of the mechanical processing by ball milling. Kinetic equations were written to describe the specific case study and fit to the experimental kinetic curves. The final objective was to provide a quantitative rationalization of the observed physical behaviour.Simulation of milling dynamics
The trajectories of the single milling ball (steel, 10 mm in diameter, 4 g) inside the jar were reconstructed through the numerical solution of the equations of motion of the ball and jar. To this aim, an in-house code was written to simulate the motion of the jar in the inertial Cartesian reference frame of the laboratory and the motion of the ball in the non-inertial Cartesian reference frame that moves with the jar. Impacts were described as instantaneous events with a degree of elasticity measured by a coefficient of restitution (see more details in the ESI†).Results and discussion
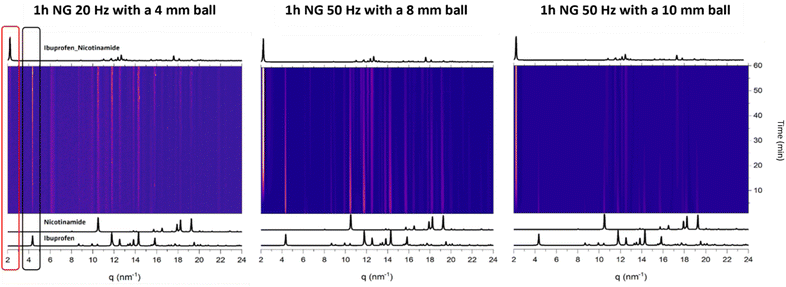
It is widely known that the choice of milling conditions can influence the progress of a mechanochemical reaction, in terms of both kinetics and the appearance of intermediate phases.36–38 To determine the sensitivity of ibuprofen + nicotinamide co-crystallisation to mechanochemical conditions, we followed the reaction using time-resolved in situ (TRIS) powder X-ray diffraction (PXRD), Fig. 2. All of our reactions were performed under neat grinding conditions for 1 hour, and we varied the milling frequency and the ball size (Fig. 2).The first reaction that we investigated by TRIS-PXRD was the mechanochemical co-crystallisation of ibuprofen + nicotinamide performed at 20 Hz with a 4 mm stainless steel ball (Fig. 2, left). From literature,39 we did not expect these mild conditions to yield a complete reaction within 1 h, and indeed under these mild conditions, the first hour of milling was dominated by scattering from the reagents alone. Only early signs of co-crystal formation were seen to appear after 40 min milling.
Aiming to drive the reaction further, we increased the milling frequency to 50 Hz, and doubled the diameter of the milling ball (to 8 mm), Fig. 2, middle. Under these harsher conditions, the co-crystal appeared within the first few minutes of milling, indicating a significant speed-up of the reaction. However, these conditions still did not yield a complete reaction within 1 h; scattering from the reagents remained until the end.
Finally, we increased the ball size to 10 mm, keeping the frequency at 50 Hz, Fig. 2, right. Under these conditions the reaction reached completion within 1 h, providing us a complete dataset on which to perform analytical kinetic analysis (for details see Fig. SI1b, ESI†). To apply our analytical kinetic model to the experimental data, we had to extract quantitative phase information from the TRIS PXRD data.
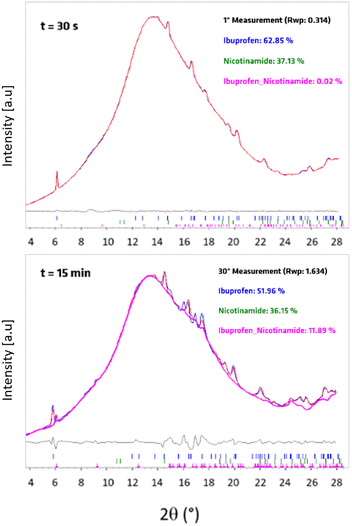
The most robust approach to extract quantitative phase data for crystalline materials from PXRD data is via Rietveld methods. However, owing to the distortions to Bragg scattering data that are common for TRIS-PXRD datasets,32,40 along with the poor crystallinity of the product, our attempts at performing quantitative Rietveld refinements of our TRIS data were unreliable. As shown in Fig. 3, quantitative phase analysis (QPA) by Rietveld methods on profiles containing reagents was effective, with a good quality of the fitting, and reliable weight percentages of the components. In contrast, with the appearance of products, the Rietveld refinement was no longer suitable.
We subsequently performed QPA via Rietveld methods on ex situ data sets, but in doing so we encountered an unexpected behaviour. Namly, the reaction continued spontaneously once the powder was mechanically activated, even after the mill was stopped. For example, we observed that after ball milling for five minutes, the ex situ PXRD profile measured immediately after milling differed from that measured on the same sample aged for 48 h (see Fig. SI2a, ESI†). This behaviour unfortunately limited the reliability of ex situ data to track the progress of the mechanochemical reaction and required us to identify an alternative strategy for robust QPA of our TRIS-PXRD datasets.
To this end, we applied two alternative approaches to extract phase composition from our TRIS data: (1) we evaluated the variation of the area under a single, isolated Bragg peak of the product phase,41 and (2) we applied the multivariate method MCS-ALS.42 Although these methods are not as robust as QPA via Rietveld methods, reliable kinetic modelling has been performed using them,43–45 especially when non-crystalline or unknown crystalline materials are involved in the mechanochemical reactions. In a recent work, it was shown that MCS-ALS can be used to derive kinetic insights with comparable validity as from Rietveld refinements.42
As shown in Fig. 4, the two analytical methods provide consistent trends in the reaction kinetics, lending significant degree of confidence to the observed trend and the methods themselves (for details see Fig. SI2b, ESI†). In both cases, the relative total amount of reactants is plotted in a semi-logarithmic plot to emphasize the dependence of the fraction of reactants on time. When plotted in this way, the data are approximately linear, revealing exponential kinetics. We note that particle size can influence reaction kinetics in mechanochemical processes, affecting parameters such as rate constants without fundamentally altering the underlying reaction mechanism or compromising the extraction of mechanistic insights from kinetic data.46
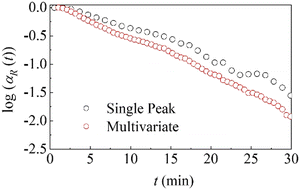 | ||
| Fig. 4 Comparison between single peak (black dots) and MCS-ALS (red dots) analyses in a semi-logarithmic plot for the data collected the first 30 minutes of the reaction. | ||
To interpret the kinetic trends and gain deeper insight into the observed transformation, we used a kinetic model as follows. We assumed that the mechanical loading exceeds a certain threshold in a set of small volumes v* that are located at the points of contact between powder particles, or inside them. Once the volumes v* experience such critical loading conditions (CLCs), the reactants undergo effective mixing. The total volume of powder affected by CLCs, v, during an individual impact is simply the sum of the volumes v*. Under the assumption that the powder is effectively stirred and that the involvement of volumes v* in any given impact is stochastic, the statistics of v* affected by CLCs can be described analytically. If we denote with κ the ratio between v and the total volume of powder, V, inside the jar, the volume fraction of powder, χi(m), that has undergone CLCs i times after m impacts can be expressed, to a first approximation, as
| χi(m) = [(κm)i/i!]exp(−κm). | (1) |
Although eqn (1) describes how volumes v* undergo CLCs, it does not consider the possible changes induced by CLCs in volumes v*. In this regard, it is reasonable to expect that specific values αi of the degree of chemical conversion in volumes v* after i CLCs can be associated to volume fractions χi(m).
Accordingly, the total degree of chemical conversion, α(m), can be expressed as
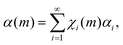 | (2) |
Eqn (2) allows us to relate the volume v effectively involved in CLCs to the degree of chemical conversion. Since the total number of impacts, m, undergone by powders can be calculated as the product Nt between the impact frequency, N, and time, t, the fraction of final co-crystal can be expressed as
| α(t) = 1 − exp(−κNt) = 1 − exp(−kt) | (3) |
| ln[1 − α(t)] = −κNt = −kt, | (4) |
Thus, the slope of the linear plots shown in Fig. 4 is equal to k. Since k represents a measure of the effective amount of powder affected by CLCs per unit time, and then transformed, it can be regarded as the rate constant of the co-crystal formation.
The best-fitted k values are equal to about 0.056 min−1 and 0.059 min−1 for the data obtained from single-peak and multivariate analyses, respectively. The two values are close enough to suggest that we can consider a single average value equal to about 0.057 min−1. By considering that the total mass of reactants in the jar was 120 mg, the mass of powder affected by CLCs per unit time is approximately equal to 6.8 mg min−1.
Since the impact frequency, N, is determined by the details of the jar movement, which are characteristic of each ball mill, and the specific processing conditions, it is more appropriate to refer the kinetics to individual impacts.25 This can be done by estimating N and subsequently extracting κ from k. In this way, we can in principle use the quantity κ, which corresponds to the effective amount of powder affected by CLCs per single impact, to compare the kinetics of co-crystal formation obtained using different ball mills and under different processing conditions.
To this aim, we combined experimental and numerical methods to study the dynamics of the single milling ball inside the moving jar under the selected working conditions.
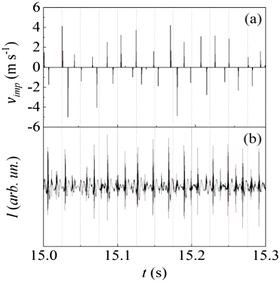
The ball can be expected to behave like a forced-damped oscillator that undergoes, to a first approximation, harmonic motion along the main jar axis. The amount of powder inside the jar affects the impact elasticity and, in turn, the overall ball dynamics. On a phenomenological basis, the effects of damping can be described by a coefficient of restitution that measures the average degree of elasticity for the impacts between ball and jar, and thus the amount of mechanical energy transferred from the ball to the powder. While details can be found in the ESI,† the most relevant results of numerical simulations performed with a coefficient of restitution of 0.4 are shown in Fig. 5. The sequence of vertical segments has been constructed by plotting the modulus of the velocity vector, vimp, of any detected impact as a function of the time, t, at which the impact was detected. Positive and negative vimp values correspond to impacts on the top and bottom hemispherical caps of the cylindrical jar, respectively. Approximately half of the detected impacts take place at a velocity vimp between ca. 2.0 m s−1 and 5.0 m s−1. Less severe impacts can be considered in the same way as rebounds, probably having minor effects on the compressed powder.
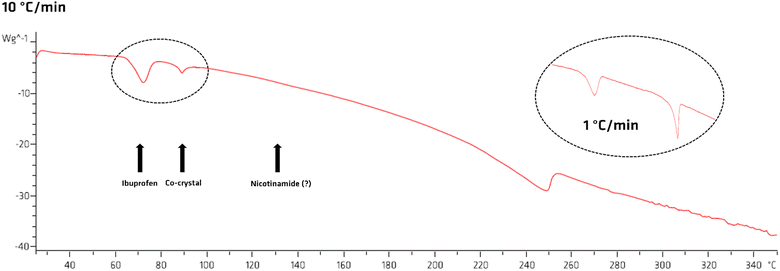
We then performed a DSC analysis on a physical mixture of ibuprofen and nicotinamide (Fig. 6). Along with the information on the thermal behaviour of the compounds, the thermal analysis was instrumental to estimate the effective thermal properties of ibuprofen and nicotinamide. After melting of ibuprofen (78 °C) we observe the melting of the co-crystal at around 90 °C. However, we do not observe melting of nicotinamide (ca. 130 °C). This strongly suggests that nicotinamide reacts entirely with the ibuprofen melt (see Fig. SI4 for more details, ESI†). To better understand the thermal events, we lowered the heating speed from 10 K min−1 to 1 K min−1, and we observed an increase in the co-crystal melting contribution (black circle in Fig. 6), which agrees with our hypothesis.
DSC analysis show a melting enthalpy of ca. 22.3 kJ mol−1 for ibuprofen, in good agreement literature values (25.0 kJ mol−1 to 39.5 kJ mol−1),47,48 and a heat capacity in the range of 200 J K−1 mol−1 to 300 J K−1 mol−1.47 Accordingly, melting 1 mol of ibuprofen (∼206.3 g), requires between 35.6 kJ to 55.4 kJ.47
Our above analysis shows that, per unit time, the volume of powder affected by CLCs is 6.8 mg min−1, and that the effective amount of powder affected by CLCs per single impact, κ, is ∼1.2 μg. The mass of ibuprofen affected by CLCs, and eventually involved in the formation of the co-crystal, is equal to about 0.7 μg min−1. It follows that the amount of energy needed to melt this much ibuprofen is between 0.12 mJ and 0.19 mJ. Notably, these values are well below the amount of energy transferred to powders during a single impact, (ca. 3.0 mJ to 20.0 mJ, see ESI†). The hypothesis of powder melting at impact is supported by high-speed video monitoring, which shows that powder sticks to the jar walls within the first minute of the reaction (Fig. SI5, ESI†).
Mechanical stimulation can induce both bulk amorphization through defect accumulation and surface melting at particle–particle interfaces during milling processes. While bulk amorphization has been the focus of attention in multicomponent reactions, the importance of surface melting, first observed by Bowden in the 1940s,49,50 has been largely overlooked. In this respect, our findings are particularly notable in the field of mechanochemistry. We also note that our experimental results do not indicate formation of amorphous phases (i.e. there is no notable no peak broadening or visible increase in background scattering contributions of the PXRD data). Moreover, our thermal analyses show no indication of glass transitions or recrystallisations of amorphous compositions. Thus, all our experimental data support that the only ‘fluid’ phase being generated in this system is a molten state.
Ultimately, we conclude that processing conditions are compatible with the melting of ibuprofen, which provides a mechanism for co-crystal formation through the dissolution of nicotinamide in molten ibuprofen and the subsequent nucleation of the co-crystal. Though this aspect will be subject to further study, when combined with other observations we hypothesise that ball milling is just a way of promoting a melt-mediated reaction of ibuprofen, consistent with literature data.48
Conclusions
In this work we demonstrate the feasibility of using kinetic modelling on in situ PXRD data to gain insight into the microscopic features of mechanical activation. The behaviour of the solids involved in the mechanochemical preparation of the co-crystal ibuprofen–nicotinamide was investigated as a benchmark system, and the factors that promote solid-state transformations were understood.Firstly, we monitored the mechanochemical reactions between ibuprofen and nicotinamide carried out at different grinding conditions to assess the optimal grinding conditions and eventually to detect the formation of transient phases or intermediates. We observed that the use of different milling frequencies and ball sizes only affected the reaction kinetics, so we selected the data set of the most optimised reaction (10 mm steel ball at 50 Hz) for kinetic modelling.
The kinetic analysis on PXRD data, along with a detailed characterization of the ball motion inside the jar, revealed that the formation of the final co-crystal was reasonably facilitated by the presence of a molten phase capable of enhancing the mixing. Further experiments, i.e. thermal analysis (DSC) and monitoring of the mechanochemical reaction with a high-speed camera, supported this suggestion. Therefore, we assumed that ball milling was an effective method for the preparation of the co-crystal as it locally promoted the melting of ibuprofen.
In conclusion, the combination of TRIS-PXRD measurements with kinetic modelling proved to be a powerful tool for the mechanistic understanding of mechanochemical reactions, as well as for their optimisation. We demonstrated that the ibuprofen–nicotinamide system was reasonably formed via the mechanically induced melting of ibuprofen. Although further investigation is required, this study on the benchmark system ibuprofen–nicotinamide can be considered a valuable protocol for understanding and subsequently scaling up mechanochemical reactions. As mechanochemistry becomes clearer, it is believed to represent a breakthrough in the industrial preparation of pharmaceuticals.
Author contributions
LC, FD, and FE conceived the project; LC and MC planned the experiments and analysed data. LC, MC, AM, FD, and FE prepared the manuscript and discussed the results. FE and FD supervised the project. All authors have given approval to the final version of the manuscript.Data availability
All data will be made available by the authors upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Simon Oster and Dr Simon Altenburg for their help in collecting frames of the mechanochemical reactions with the high-speed camera. This project has received funding from the European Union's Horizon 2021–2027 research and innovation program under grant agreement No 101057286 (IMPACTIVE).References
- D. Braga, L. Casali and F. Grepioni, Int. J. Mol. Sci., 2022, 23, 9013 CrossRef CAS PubMed
.
- Ibuprofen Market Size | API Market | Demand, Price Chart, https://www.beroeinc.com/category-intelligence/ibuprofen-market/, (accessed 10 November 2023).
- I. Theochari, E. Mitsou, I. Nikolic, T. Ilic, V. Dobricic, V. Pletsa, S. Savic, A. Xenakis and V. Papadimitriou, J. Mol. Liq., 2021, 334, 116021 CrossRef CAS
.
- A. Ouranidis, N. Gkampelis, E. Vardaka, A. Karagianni, D. Tsiptsios, I. Nikolakakis and K. Kachrimanis, Pharmaceutics, 2020, 12, 969 CrossRef CAS PubMed
.
- Ionic Liquids and Salts from Ibuprofen as Promising Innovative Formulations of an Old Drug – Santos – 2019 – ChemMedChem – Wiley Online Library, https://chemistry-europe.onlinelibrary.wiley.com/doi/full/10.1002/cmdc.201900040, (accessed 10 November 2023).
- G. Bolla, B. Sarma and A. K. Nangia, Chem. Rev., 2022, 122, 11514–11603 CrossRef CAS PubMed
.
- D. J. Berry, C. C. Seaton, W. Clegg, R. W. Harrington, S. J. Coles, P. N. Horton, M. B. Hursthouse, R. Storey, W. Jones, T. Friščić and N. Blagden, Cryst. Growth Des., 2008, 8, 1697–1712 CrossRef CAS
.
- S. F. Alshahateet, Mol. Cryst. Liq. Cryst., 2010, 533, 152–161 CrossRef CAS
.
- S. F. Chow, M. Chen, L. Shi, A. H. L. Chow and C. C. Sun, Pharm. Res., 2012, 29, 1854–1865 CrossRef CAS PubMed
.
- M. Guerain, Y. Guinet, N. T. Correia, L. Paccou, F. Danède and A. Hédoux, Int. J. Pharm., 2020, 584, 119454 CrossRef CAS PubMed
.
- F. L. F. Soares and R. L. Carneiro, Cryst. Growth Des., 2013, 13, 1510–1517 CrossRef CAS
.
- Y. Wei, L. Zhang, N. Wang, P. Shen, H. Dou, K. Ma, Y. Gao, J. Zhang and S. Qian, Cryst. Growth Des., 2018, 18, 7343–7355 CrossRef CAS
.
- K. Lin, Y. Wang and Q. Yu, J. Cryst. Growth, 2021, 570, 126229 CrossRef CAS
.
- S. Ishihara, Y. Hattori and M. Otsuka, Spectrochim. Acta, Part A, 2019, 221, 117142 CrossRef CAS PubMed
.
- M. Asgarpour Khansary, G. Walker and S. Shirazian, Int. J. Pharm., 2020, 591, 119992 CrossRef CAS PubMed
.
- A. L. Kelly, T. Gough, R. S. Dhumal, S. A. Halsey and A. Paradkar, Int. J. Pharm., 2012, 426, 15–20 CrossRef CAS PubMed
.
- Y. Xiao, C. Wu, X. Hu, K. Chen, L. Qi, P. Cui, L. Zhou and Q. Yin, Cryst. Growth Des., 2023, 23, 4680–4700 CrossRef CAS
.
- D. Braga, L. Maini and F. Grepioni, Chem. Soc. Rev., 2013, 42, 7638–7648 RSC
.
- O. Galant, G. Cerfeda, A. S. McCalmont, S. L. James, A. Porcheddu, F. Delogu, D. E. Crawford, E. Colacino and S. Spatari, ACS Sustainable Chem. Eng., 2022, 10, 1430–1439 CrossRef CAS
.
- Scalability of Pharmaceutical Co-Crystal Formation by Mechanochemistry in batch. – Bodach – ChemSusChem – Wiley Online Library, https://chemistry-europe.onlinelibrary.wiley.com/doi/abs/10.1002/cssc.202301220, (accessed 27 November 2023).
- O. Galant, G. Cerfeda, A. S. McCalmont, S. L. James, A. Porcheddu, F. Delogu, D. E. Crawford, E. Colacino and S. Spatari, ACS Sustainable Chem. Eng., 2022, 10, 1430–1439 CrossRef CAS
.
- A. A. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61, e202117270 CrossRef CAS PubMed
.
- M. Rautenberg, B. Bhattacharya, J. Witt, M. Jain and F. Emmerling, CrystEngComm, 2022, 24, 6747–6750 RSC
.
- A. M. Belenguer, G. I. Lampronti, A. A. Michalchuk, F. Emmerling and J. K. Sanders, CrystEngComm, 2022, 24, 4256–4261 RSC
.
- M. Carta, L. Vugrin, G. Miletić, M. J. Kulcsár, P. C. Ricci, I. Halasz and F. Delogu, Angew. Chem., Int. Ed., 2023, 62, e202308046 CrossRef CAS PubMed
.
- M. Carta, E. Colacino, F. Delogu and A. Porcheddu, Phys. Chem. Chem. Phys., 2020, 22, 14489–14502 RSC
.
- X. Liu, Y. Li, L. Zeng, X. Li, N. Chen, S. Bai, H. He, Q. Wang and C. Zhang, Adv. Mater., 2022, 34, 2108327 CrossRef CAS PubMed
.
- L. M. Martínez, J. Cruz-Angeles, M. Vázquez-Dávila, E. Martínez, P. Cabada, C. Navarrete-Bernal and F. Cortez, Pharmaceutics, 2022, 14, 2003 CrossRef PubMed
.
- A. L. Sanna, M. Carta, G. Pia, S. Garroni, A. Porcheddu and F. Delogu, Sci. Rep., 2022, 12, 9445 CrossRef CAS PubMed
.
- K. Ostrowska, M. Kropidłowska and A. Katrusiak, Cryst. Growth Des., 2015, 15, 1512–1517 CrossRef CAS
.
- N. Tumanova, N. Tumanov, F. Fischer, F. Morelle, V. Ban, K. Robeyns, Y. Filinchuk, J. Wouters, F. Emmerling and T. Leyssens, CrystEngComm, 2018, 20, 7308–7321 RSC
.
- G. I. Lampronti, A. A. Michalchuk, P. P. Mazzeo, A. M. Belenguer, J. K. Sanders, A. Bacchi and F. Emmerling, Nat. Commun., 2021, 12, 6134 CrossRef CAS PubMed
.
- I. Zizak, J. Large-Scale Res. Facil., 2016, 2, A102 CrossRef
.
- G. Benecke, W. Wagermaier, C. Li, M. Schwartzkopf, G. Flucke, R. Hoerth, I. Zizak, M. Burghammer, E. Metwalli and P. Müller-Buschbaum, J. Appl. Crystallogr., 2014, 47, 1797–1803 CrossRef CAS PubMed
.
- S.-J. Baek, A. Park, Y.-J. Ahn and J. Choo, Analyst, 2014, 140, 250–257 RSC
.
- L. Casali, T. Feiler, M. Heilmann, D. Braga, F. Emmerling and F. Grepioni, CrystEngComm, 2022, 24, 1292–1298 RSC
.
- K. Linberg, B. Röder, D. Al-Sabbagh, F. Emmerling and A. Michalchuk, Faraday Discuss., 2022, 1–16 Search PubMed
.
- H. Kulla, A. A. Michalchuk and F. Emmerling, Chem. Commun., 2019, 55, 9793–9796 RSC
.
- F. Fischer, K.-J. Wenzel, K. Rademann and F. Emmerling, Phys. Chem. Chem. Phys., 2016, 18, 23320–23325 RSC
.
- I. Halasz, T. Friščić, S. A. J. Kimber, K. Užarević, A. Puškarić, C. Mottillo, P. Julien, V. Štrukil, V. Honkimäki and R. E. Dinnebier, Faraday Discuss., 2014, 170, 203–221 RSC
.
- A. A. L. Michalchuk, I. A. Tumanov, S. Konar, S. A. J. Kimber, C. R. Pulham and E. V. Boldyreva, Adv. Sci., 2017, 4, 1700132 CrossRef PubMed
.
- L. Macchietti, L. Casali, F. Emmerling, D. Braga and F. Grepioni, RSC Mechanochem., 2024, 1, 106–115 RSC
.
- I. C. B. Martins, M. Carta, S. Haferkamp, T. Feiler, F. Delogu, E. Colacino and F. Emmerling, ACS Sustainable Chem. Eng., 2021, 9, 12591–12601 CrossRef CAS
.
- P. Guccione, M. Lopresti, M. Milanesio and R. Caliandro, Crystals, 2020, 11, 12 CrossRef
.
- S. J. Mazivila, R. A. E. Castro, J. M. M. Leitão and J. C. G. Esteves Da Silva, Vib. Spectrosc., 2020, 106, 102992 CrossRef CAS
.
- M. Alrbaihat, F. Khalil Al-Zeidaneen and Q. Abu-Afifeh, Mater. Today: Proc., 2022, 65, 3651–3656 CAS
.
- V. Štejfa, V. Pokorný, A. Mathers, K. Růžička and M. Fulem, J. Chem. Thermodyn., 2021, 163, 106585 CrossRef
.
- F. Cilurzo, E. Alberti, P. Minghetti, C. G. M. Gennari, A. Casiraghi and L. Montanari, Int. J. Pharm., 2010, 386, 71–76 CrossRef CAS PubMed
.
- F. P. Bowden and O. Gurton, Proc. R. Soc. London, Ser. A, 1949, 198, 337–349 CAS
.
- F. P. Bowden, M. Stone and G. Tudor, Proc. R. Soc. London, Ser. A, 1947, 188, 329–349 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01457j |
| This journal is © the Owner Societies 2024 |