Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards efficient quantum computing for quantum chemistry: reducing circuit complexity with transcorrelated and adaptive ansatz techniques†
Erika
Magnusson
 a,
Aaron
Fitzpatrick
b,
Stefan
Knecht
a,
Aaron
Fitzpatrick
b,
Stefan
Knecht
 b,
Martin
Rahm
b,
Martin
Rahm
 *a and
Werner
Dobrautz
*a and
Werner
Dobrautz
 *a
*a
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 41296 Gothenburg, Sweden. E-mail: martin.rahm@chalmers.se; werner.dobrautz@gmail.com
bAlgorithmiq Ltd, Kanavakatu 3C, FI-00160 Helsinki, Finland
First published on 16th April 2024
Abstract
The near-term utility of quantum computers is hindered by hardware constraints in the form of noise. One path to achieving noise resilience in hybrid quantum algorithms is to decrease the required circuit depth – the number of applied gates – to solve a given problem. This work demonstrates how to reduce circuit depth by combining the transcorrelated (TC) approach with adaptive quantum ansätze and their implementations in the context of variational quantum imaginary time evolution (AVQITE). The combined TC-AVQITE method is used to calculate ground state energies across the potential energy surfaces of H4, LiH, and H2O. In particular, H4 is a notoriously difficult case where unitary coupled cluster theory, including singles and doubles excitations, fails to provide accurate results. Adding TC yields energies close to the complete basis set (CBS) limit while reducing the number of necessary operators – and thus circuit depth – in the adaptive ansätze. The reduced circuit depth furthermore makes our algorithm more noise-resilient and accelerates convergence. Our study demonstrates that combining the TC method with adaptive ansätze yields compact, noise-resilient, and easy-to-optimize quantum circuits that yield accurate quantum chemistry results close to the CBS limit.
I. Introduction
The challenge at the heart of quantum chemistry is the electronic structure problem. This problem, encapsulated in the Schrödinger equation, scales exponentially with system size. Numerous computational approaches exist for tackling this challenge, ranging from approximate mean-field theories like Hartree–Fock (HF),1 more accurate but costly methods like coupled cluster (CC),2,3 density matrix renormalization group (DMRG)4–6 and quantum Monte Carlo (QMC) methods,7–9 to exact, but exponentially-scaling, full configuration interaction (FCI)/exact diagonalization (ED). In recent years, attempts have been made to circumvent the unfavourable scaling of highly accurate quantum chemistry using quantum computers. Quantum hardware is believed to be particularly well suited for simulating quantum systems like molecules and may enable a significant computational speedup.10,11 However, given the existence of conventional numerical methods that have been refined over decades, it is still uncertain if quantum algorithms can provide a genuine quantum advantage over established techniques.12–15Unfortunately, noise severely limits practicable circuit depths on current and near-term quantum processors. Furthermore, the number of qubits needed to encode quantum chemistry on quantum hardware is proportional to the basis set size or the number of orbitals in the case of an active space approach. Thus, the achievable accuracy on quantum hardware is severely limited as either small, often minimal, basis sets have to be used or calculations must be done with very small active spaces to fit the problem on current quantum hardware. Despite these constraints, quantum hardware may, in the future, outperform conventional computation in specialized instances, such as modelling highly correlated systems.16
Various algorithms have been devised to advance toward practical quantum advantage in the current noisy intermediate-scale quantum (NISQ) regime. Most of these NISQ algorithms are variational, i.e., based on the variational theorem. Variational quantum algorithms (VQAs)17,18 can significantly reduce quantum circuit depth by offloading calculations that do not strictly need quantum properties to a conventional computer. This idea follows naturally from trying to use the quantum computer as little as possible. VQAs are heuristic and rely on an ansatz circuit, which is optimized following some scheme. A considerable drawback of VQAs is that many measurements are needed for this optimization procedure, a factor that may limit or remove the chances for practical quantum advantage.14 Despite this drawback, for reasons related to the limitations of current hardware, VQAs are by far the most investigated type of quantum algorithm to date. The variational quantum eigensolver (VQE)19,20 is the most well-known VQA. However, other methods, such as variational quantum imaginary time evolution (VarQITE), are competitive alternatives.21
A myriad variations of and additions to these VQAs have been made to improve them in search of practical quantum advantage. A non-exhaustive list of such approaches includes reducing circuit depth by gradually building the ansatz circuit to be only as deep as needed,22–27 reducing qubit requirements by similarity transforms,28–37 or post-processing.38,39 Among these additions, explicitly correlated methods40–48 like the transcorrelated (TC) method49–61 make it possible to obtain more accurate results with smaller basis sets by incorporating the problematic electronic cusp condition62 into the Hamiltonian. The TC approach also has the added benefit of providing more compact ground state wavefunctions.52 A consequence of this compactness is that the ground state of the TC Hamiltonian is easier to prepare with shallower quantum circuits.31,32,63
Explicitly correlated and TC-based approaches have also recently been applied to increase the accuracy while lowering the resource requirements of quantum chemistry calculations on quantum hardware.28–32,63,64 Motta et al. employed canonical transcorrelated F12 (CT-F12) theory28 to accurately calculate the ground state energy of various small molecular systems with fewer required qubits. Kumar et al. extended CT-F12 theory on quantum hardware to excited state energies,30 and Schleich and coworkers used an explicitly correlated a posteriori correction29 to improve ground state energy estimates from VQE calculations. McArdle and Tew63 have merged the TC and VarQITE methods to study small Hubbard lattices, utilizing the improved compactness of the ground state solution due to the TC approach.52 Some of the present authors have developed an optimized TC-VarQITE approach31 for ab initio problems that drastically reduces the necessary qubit number to obtain accurate spectroscopic data of small molecular systems on quantum hardware.32 Our previous work relied on pre-determined and fixed quantum circuit ansätze like the unitary coupled cluster (UCC)65,66 or hardware efficient ansätze.67 However, full UCC ansätze are not a viable option for current noisy quantum hardware due to their required long circuit depths. On the other hand, hardware efficient ansätze can have convergence problems due to their heuristic nature and lack of chemical/physical motivation.
In this work, we present an extension of the TC-VarQITE approach by combining Gomes et al.’s adaptive variational quantum imaginary time evolution algorithm (AVQITE)24 with the TC method. The rationale for this approach is that the increased compactness of the ground state wavefunction due to the TC method31,52 should lead to shallower adaptive quantum circuits. The capability and strength of the resulting algorithm, transcorrelated adaptive variational quantum imaginary time evolution (TC-AVQITE), is then evaluated through simulations of near-term quantum devices.
This paper is structured as follows. First, we discuss in Section II the constituent parts of the TC-AVQITE algorithm and introduce relevant terminology. Next, we detail the implementation of TC-AVQITE in Section III, and provide computational details for the numerical studies. After discussing the numerical data in Section IV, we conclude, address possible improvements, and outline future work.
II. Theory
TC-AVQITE is built upon multiple methods and algorithms. To begin with, AVQITE is a combination of adaptive ansätze22,23 and VarQITE.18,21 VarQITE is, in turn, a variational rephrasing of quantum imaginary time evolution (QITE).68–72 In what follows, we briefly introduce the electronic structure problem, followed by QITE, VarQITE, adaptive ansätze, and AVQITE. To conclude, we describe the TC method.A. The electronic structure problem
The electronic structure problem can often be reduced to solving the non-relativistic Schrödinger equation, either in stationary form,| Ĥ|ψ〉 = E|ψ〉, | (1) |
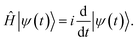 | (2) |
Decoupling electronic and nuclear degrees of freedom is often justified by invoking the Born–Oppenheimer approximation. When expressed within second quantization, the electronic Hamiltonian then reads as
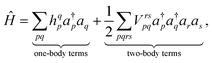 | (3) |
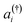 is the annihilation (creation) operator of an electron in spin-orbital i, with the integrals
is the annihilation (creation) operator of an electron in spin-orbital i, with the integrals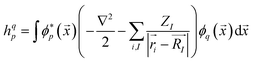 | (4) |
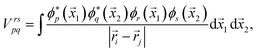 | (5) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) are the basis functions, ZI the charge number,
) are the basis functions, ZI the charge number, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i the electron positions,
i the electron positions, ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) I the nucleon positions. From the shape of these integrals, we can note that the “one-body terms” include the kinetic energy and nuclear repulsion, while the “two-body terms” describe the electron–electron interaction.
I the nucleon positions. From the shape of these integrals, we can note that the “one-body terms” include the kinetic energy and nuclear repulsion, while the “two-body terms” describe the electron–electron interaction.
B. Imaginary time evolution, QITE and VarQITE
QITE68–72 is a quantum computer implementation of imaginary time evolution (ITE),9,73–75 a method used in various fields of science, such as statistical mechanics, cosmology, and quantum mechanics.21 In the context of electronic structure theory, ITE works by expressing the time-dependent Schrödinger equation, eqn (2), as dependent on imaginary time instead of time, t → iτ, in the so-called Wick-rotated form76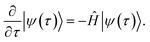 | (6) |
By integrating eqn (6) and given an initial state, |ψ(0)〉, one can obtain the state |ψ(τ)〉 for any imaginary time τ as
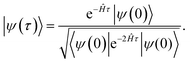 | (7) |
As τ → ∞, the state |ψ(τ)〉 converges to the ground state of the Hamiltonian Ĥ, given that the initial state, |ψ(0)〉, overlaps with the ground state.21 Fortunately, for quantum chemistry problems, this requirement is usually not particularly restrictive as easily preparable states with (in most cases) non-vanishing overlap to the ground state exist. One example is the wave function obtained by solving the Hartree–Fock equations. However, counterexamples to this assumption of easily preparable states with non-vanishing overlap exist.13
ITE is a so-called projector method related to the power,77 Lanczos78 and Davidson method,79 which yields the ground state of a system by repeated application of the operator e−Ĥτ on the initial state |ψ(0)〉. Consequently, ITE does not rely on the variational principle and thus can be used to obtain ground states of non-Hermitian Hamiltonians, as present in open quantum systems,27,80,81 transport problems,82,83 and the transcorrelated method.31,63
To perform ITE on a quantum computer (i.e., QITE), the exponential e−Ĥτ is approximated by its Taylor series for a small imaginary time step Δτ.68 Implementing QITE on quantum hardware is not straightforward because the operator e−Ĥτ is non-unitary. Consequently, e−Ĥτ must be approximated by unitary operations, which can require deep quantum circuits.68
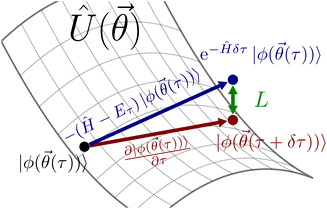
An alternative to unitary approximation is to express QITE in variational form – VarQITE.21 In VarQITE, one approximates the targeted state |ψ〉 with a quantum circuit ansatz, Û(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) ), that depends on a set of parameters
), that depends on a set of parameters ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) with elements θi, i.e. representing the angles of single qubit rotational gates (Fig. 1),
with elements θi, i.e. representing the angles of single qubit rotational gates (Fig. 1),
|ψ(τ)〉 ≈ Û(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) (τ))|0〉 = |ϕ( (τ))|0〉 = |ϕ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) (τ))〉 = |ϕ(τ)〉. (τ))〉 = |ϕ(τ)〉. | (8) |
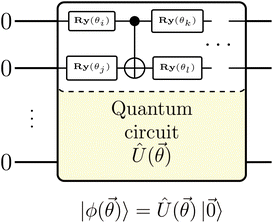 | ||
Fig. 1 Sketch of the quantum circuit ansatz |ϕ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )〉 = Û( )〉 = Û(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )| )|![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) 〉 depending on a set of parameters, 〉 depending on a set of parameters, ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) , in form of single qubit rotations around the y-axis, Ry(θi). , in form of single qubit rotations around the y-axis, Ry(θi). | ||
The ITE can then be approximated using McLachlan’s variational principle.18,84 This approach minimizes the distance between the QITE evolution and the approximated path in parameter space Û(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) ),
),
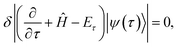 | (9) |
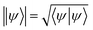 . Eqn (9) minimizes the distance between the left-hand- and right-hand-side of the Wick-rotated Schrödinger equation, eqn (6), and the energy expectation value at imaginary time τ. Eτ = 〈ψ(τ)|Ĥ|ψ(τ)〉 ensures normalization.11 VarQITE iteratively steps through imaginary time, approximating the ideal path of QITE. The update rule for each iteration can be obtained from first expanding eqn (9) in the parameter space by inserting eqn (8), which simplifies to 18,21
. Eqn (9) minimizes the distance between the left-hand- and right-hand-side of the Wick-rotated Schrödinger equation, eqn (6), and the energy expectation value at imaginary time τ. Eτ = 〈ψ(τ)|Ĥ|ψ(τ)〉 ensures normalization.11 VarQITE iteratively steps through imaginary time, approximating the ideal path of QITE. The update rule for each iteration can be obtained from first expanding eqn (9) in the parameter space by inserting eqn (8), which simplifies to 18,21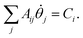 | (10) |
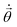 with elements
with elements ![[small theta, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a7.gif) j represents the imaginary time derivative of the quantum circuit parameters
j represents the imaginary time derivative of the quantum circuit parameters ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) (Fig. 1), and
(Fig. 1), and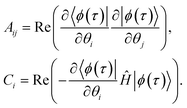 | (11) |
The matrix with elements Aij and vector with elements Ci, which both depend on the imaginary time τ, are the metric tensor in parameter space A(τ)85,86 related to the quantum Fisher information matrix87–95 and the gradient ![[C with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0043_20d1.gif) (τ), respectively. From eqn (10), one can solve for
(τ), respectively. From eqn (10), one can solve for 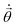 by inverting A, and then update
by inverting A, and then update ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) by i.e. the Euler or Runge–Kutta methods.96
by i.e. the Euler or Runge–Kutta methods.96
The drawback of the VarQITE approximation compared to QITE is that the strict convergence guarantee to the ground state is lost, as one is limited by how expressive the employed ansatz Û(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) ) is. When quantifying how close the iterative VarQITE is to the QITE path, it is helpful to consider the McLachlan distance L,18
) is. When quantifying how close the iterative VarQITE is to the QITE path, it is helpful to consider the McLachlan distance L,18
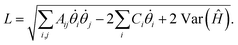 | (12) |
Fig. 2 illustrates how the quantity L can be interpreted as the distance between the optimal path of QITE and the approximate path of VarQITE.18 We will return to describe why L is particularly important for TC-AVQITE when introducing our method of choice for adaptive ansatz construction.
The cost in terms of circuit evaluations for measuring A on quantum hardware scales as 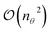 , where nθ is the number of ansatz parameters. Fortunately, various approximations are available that reduce this scaling to linear,87,97–99 or even a constant cost.88 However, it was recently shown by van Straaten and Koczor100 that the measurement cost of the gradient will dominate for large-scale quantum chemistry applications.
, where nθ is the number of ansatz parameters. Fortunately, various approximations are available that reduce this scaling to linear,87,97–99 or even a constant cost.88 However, it was recently shown by van Straaten and Koczor100 that the measurement cost of the gradient will dominate for large-scale quantum chemistry applications.
C. Adding adaptive ansätze
Adaptive ansätze are iteratively built to identify a circuit that is as shallow as possible yet sufficiently deep to describe a given problem. Adaptive quantum algorithms gradually add operators from a pre-defined operator pool to an initial, easy-to-prepare ansatz circuit. Operator pools can be constructed in various ways.101,102 For example, they might include fermionic excitation operators22 or operators constructed from Pauli strings.23 Which operator(s) to append and when to do so is decided iteratively based on some selection and expansion criteria. Using an adaptive approach naturally decreases circuit depth compared to a case in which all operators in the pool are used.The first adaptive ansatz implementation was Adaptive Derivative-Assembled Problem-Tailored ansatz (ADAPT)-VQE by Grimsley et al.,22 which has been followed by several variants.23–26,103 Herein, we rely on the adaptive algorithm AVQITE by Gomes et al.,24 which implements adaptive algorithms in the context of VarQITE.
In AVQITE as implemented in ref. 24 and in our work, the operator pool consists of all Pauli strings of a unitary coupled cluster singles doubles (UCCSD) ansatz66 constructed for the problem. The AVQITE ansatz circuit is expanded by selecting those operators that keep the VarQITE evolution as close to QITE as possible. Operators are added when the McLachlan distance L, eqn (12), becomes too large compared to some defined cutoff value Lcut.
Adaptive ansätze have been shown to successfully decrease the circuit depth compared to including the entire operator pool at the cost of more measurements. The reason for these extra measurements is that the adaptive algorithm needs to evaluate the expansion and selection criteria to keep track of when to modify the ansatz circuit. However, as circuit depth is currently one of the most limiting factors for NISQ hardware, there is much to be gained from the approach despite the increased measurement cost. Additionally, work has been done to reduce measurement costs,102,104,105 for example, through classical shadows,106 Pauli grouping,107–110 and informationally complete positive operator valued measures.111–115
D. The transcorrelated method
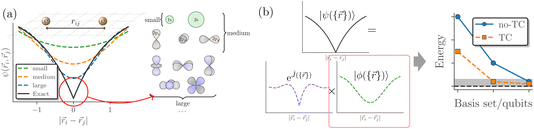
The TC method introduced by Hirschelder,116 Boys and Handy,49–51,117 is an explicitly correlated method40–48 based on factorizing the electronic wave function in Jastrow form,118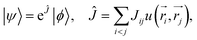 | (13) |
Ĥ|ψ〉 = E|ψ〉 ⇒ Ĥ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eĴ|ϕ〉 = E eĴ|ϕ〉 = E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eĴ|ϕ〉 eĴ|ϕ〉 | (14) |
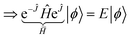 | (15) |
Note that eqn (15) is not an approximation but an exact similarity transformation of the electronic Hamiltonian, eqn (3).52 However, and importantly, this recasting is not a unitary transformation, so Hermiticity is lost.53 The “normal” Rayleigh–Ritz variational principle requires Hermiticity, which means many variational methods, such as the VQE, do not apply to (non-truncated) transcorrelated Hamiltonians. There are ways to perform an approximate Hermitian truncation of a transcorrelated similarity transform if Hermiticity is deemed essential, i.e. via CT-F12 theory119,120 as used by Motta et al.28 and Kumar et al.30 However, as a projective method, VarQITE can be used with both non-Hermitian as well as Hermitian Hamiltonians.31,63
In quantum chemistry, explicitly correlated methods are essential for correctly dealing with Kato’s cusp condition:62,121 that when two electrons approach each other, they (should) give rise to a sharp, non-differentiable dip (cusp) in the wave function (Fig. 3a). This sharp feature is one of the reasons why large basis sets are needed in conventional quantum chemistry calculations. As basis sets are generally composed of smooth functions, such as Gaussians, many basis functions are needed to capture this cusp (Fig. 3a). However, through the TC method, the cusp condition can be directly treated by choosing an appropriate Jastrow factor Ĵ (see eqn (13) and Fig. 3b), so that the non-differentiable behaviour of |ψ〉 can be incorporated in the Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) . The cusp condition description has then moved from the wave function into the Hamiltonian via the similarity transformation, as seen in eqn (15).
. The cusp condition description has then moved from the wave function into the Hamiltonian via the similarity transformation, as seen in eqn (15).
Dealing with the cusp condition in the Hamiltonian instead of the wavefunction is why the TC method can provide results much closer to the complete basis set (CBS) limit with smaller basis sets (Fig. 3b). This potential for lowering computational resources is one reason behind the TC methods’ recent revival in electronic structure theory.52–61,122–130 Additionally, a smaller basis set means that one needs significantly fewer qubits to obtain reliable and accurate quantum chemistry results, as the number of qubits scales with active space size.28–32,63 This resource reduction has recently been demonstrated by Motta et al.28 and Kumar and coworkers30 using CT-F12 theory, Schleich et al. using the [2]R12 correction and by some of the present authors with an un-approximated TC-VarQITE combination.31,32
Moving the description of the cusp from the wave function to the Hamiltonian does not come for free. The price we pay is that the Hamiltonian becomes more complex, both in terms of the aforementioned non-Hermiticity (in the form of modified two-body terms) as well as the appearance of three-body terms, see ref. 53 for details.
The additional three-body terms of the TC method raise the justified question of whether applying the method will be beneficial at all – does the incurred cost outweigh the benefits? Recent work122,125,131 has shown that the TC Hamiltonian can be reduced to an 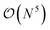 or even
or even 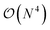 scaling (with N being the number of orbitals) by either neglecting three-body excitations with six unique indices122 altogether or by neglecting the pure normal ordered132 three-body operators and incorporating the remaining three-body contributions in the two-, one-, and zero-body integrals.131 Additionally, in ref. 32, some of the present authors have demonstrated that the resource reduction of the TC method (without approximations) outweighs the cost of additional measurements until (roughly) the 1000 qubit mark.
scaling (with N being the number of orbitals) by either neglecting three-body excitations with six unique indices122 altogether or by neglecting the pure normal ordered132 three-body operators and incorporating the remaining three-body contributions in the two-, one-, and zero-body integrals.131 Additionally, in ref. 32, some of the present authors have demonstrated that the resource reduction of the TC method (without approximations) outweighs the cost of additional measurements until (roughly) the 1000 qubit mark.
E. Conserved quantum numbers
The Jastrow factor eĴ, eqn (13), used in the TC approach is optimized for a state with a specific chosen number of electrons, nmol,125 usually corresponding to the molecular ground state. Under certain extremal conditions, e.g., in the broken bond regime, the TC similarity transformation, eqn (15), can cause sectors of the Hamiltonian describing different electron numbers, which should have higher energy, to be below the original ground state sector with nmol electrons. Thus, unless measures are taken to conserve the correct number of electrons, TC calculations may converge to false ground states.These Hamiltonian symmetry sector issues can be avoided by modifying the energy calculation to include a penalty term, E′ = E + Epenalty. The energy penalty is in this work given by
Epenalty = α〈ϕ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )|( )|(![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) − nmol)2|ϕ( − nmol)2|ϕ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )〉, )〉, | (16) |
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) is the electron number operator, nmol is the chosen number of electrons, and α is a constant we have set to 1. Eqn (16) penalizes solutions with an electron number different than the chosen, n ≠ nmol, by increasing their respective energy expectation value E′. This penalty term ensures that TC-AVQITE converges to physically/chemically sound solutions with the correct number of electrons, nmol, but does not affect the described physics or chemistry of the studied systems.
is the electron number operator, nmol is the chosen number of electrons, and α is a constant we have set to 1. Eqn (16) penalizes solutions with an electron number different than the chosen, n ≠ nmol, by increasing their respective energy expectation value E′. This penalty term ensures that TC-AVQITE converges to physically/chemically sound solutions with the correct number of electrons, nmol, but does not affect the described physics or chemistry of the studied systems.
III. Computational details
The combination of the TC method with AVQITE follows naturally by applying each method sequentially: the TC method first produces a Hamiltonian![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) , which can then be used in a modified AVQITE implementation. Our program for performing TC-AVQITE is based on the code by Gomes et al., as implemented in ref. 24 and 133. Our development, available as a Python code,134 includes additions to handle non-Hermiticity, generation of Hamiltonians and appropriate operator pools and restartable calculations. Our implementation of TC-AVQITE relies on Qiskit v.0.42.0, Qiskit Nature v.0.5.2,135,136 and Qutip v.4.7.1 (ref. 137) to produce operator pools and obtain exact reference energies. TC Hamiltonians were generated following the workflow outlined in ref. 32 and 125. PySCF v.2.4.0 (ref. 138–140) was used for the initial Hartree–Fock calculations to construct the molecular orbital basis for generating the Hamiltonians and operator pools, as well as the FCI/cc-p(C)VTZ and FCI/CBS estimate calculations.
, which can then be used in a modified AVQITE implementation. Our program for performing TC-AVQITE is based on the code by Gomes et al., as implemented in ref. 24 and 133. Our development, available as a Python code,134 includes additions to handle non-Hermiticity, generation of Hamiltonians and appropriate operator pools and restartable calculations. Our implementation of TC-AVQITE relies on Qiskit v.0.42.0, Qiskit Nature v.0.5.2,135,136 and Qutip v.4.7.1 (ref. 137) to produce operator pools and obtain exact reference energies. TC Hamiltonians were generated following the workflow outlined in ref. 32 and 125. PySCF v.2.4.0 (ref. 138–140) was used for the initial Hartree–Fock calculations to construct the molecular orbital basis for generating the Hamiltonians and operator pools, as well as the FCI/cc-p(C)VTZ and FCI/CBS estimate calculations.
We have performed noiseless, state-vector AVQITE and TC-AVQITE simulations to compute the ground state energy of the three molecular test cases. To limit costs associated with computing the six-body integrals in the TC approach and the state-vector simulations, we have used a minimal STO-6G basis set in all simulated systems. We note that more elaborate basis sets are required to approach the CBS, even in TC-based approaches. As such, a cost-effective alternative would be using an active space approach combined with a larger basis set. The use of minimal basis sets suffices for our goals here: to demonstrate the circuit width and depth reduction made possible with TC-AVQITE.
In our calculations of the water molecule, the oxygen 1s orbital was frozen, i.e., omitted from the correlated description, which resulted in a reduction of two qubits. To decrease calculation costs further, parity encoding141 was used for all systems to decrease the number of simulated qubits by two.
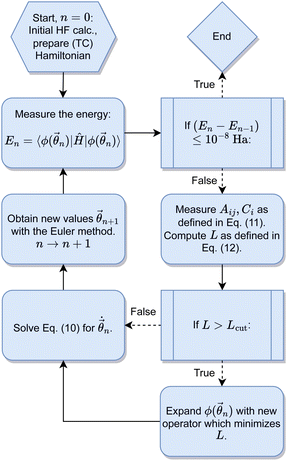
The TC-AVQITE iteration procedure is visualized in Fig. 4: first, we perform a conventional HF calculation, and in the case of TC-AVQITE, we use the workflow of ref. 125 to construct the TC Hamiltonian. In all cases except for broken-bond H2O, we use the single determinant HF state as the initial state, |ϕ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) 0)〉. Since the HF solution is not a good approximation to the true ground state for H2O at 2.5 Å, we use a single determinant open-shell initial state in this case. Then, we enter the TC-AVQITE self-consistent loop by measuring the energy expectation value of the current ansatz circuit. If this expectation value does not change by more than 1 × 10−8 Ha during the iteration procedure, we consider the calculation converged and exit the loop. If not, we measure the metric tensor with elements Aij and the gradient with elements Ci, and from these, compute the McLachlan distance L. If the McLachlan distance is larger than the defined cutoff value, L > Lcut, we expand the ansatz circuit with a new operator. We use the operator with the largest decrease to L when added. This step is skipped if L ≤ Lcut. Next, we solve eqn (10) to obtain
0)〉. Since the HF solution is not a good approximation to the true ground state for H2O at 2.5 Å, we use a single determinant open-shell initial state in this case. Then, we enter the TC-AVQITE self-consistent loop by measuring the energy expectation value of the current ansatz circuit. If this expectation value does not change by more than 1 × 10−8 Ha during the iteration procedure, we consider the calculation converged and exit the loop. If not, we measure the metric tensor with elements Aij and the gradient with elements Ci, and from these, compute the McLachlan distance L. If the McLachlan distance is larger than the defined cutoff value, L > Lcut, we expand the ansatz circuit with a new operator. We use the operator with the largest decrease to L when added. This step is skipped if L ≤ Lcut. Next, we solve eqn (10) to obtain 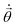 , and obtain new parameter values
, and obtain new parameter values ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) by the Euler method. The loop is repeated until the energy convergence criterion is met.
by the Euler method. The loop is repeated until the energy convergence criterion is met.
We used Δτ = 0.05 as the imaginary time step and Lcut = 1 × 10−5 for the McLachlan distance cutoff in all AVQITE and TC-AVQITE calculations. Both TC-AVQITE and the original AVQITE algorithm by Gomes et al.24 were tested and found to be robust with respect to different parameter settings, details of which can be found in the ESI.† TC-VarQITE calculations were performed as outlined in ref. 32 using the same imaginary time step of Δτ = 0.05.
Notes on convention: We follow the convention of ref. 142 and use the term “computational accuracy” in this work when the difference of a quantum calculation and the exact solution in a given (finite) basis set do not exceed 10−3 Ha. We highlight this nomenclature because a different term, chemical accuracy, is often used in quantum chemistry to measure calculation quality. Chemical accuracy is commonly defined as an error of 1 kcal mol−1 (approximately 10−3 Ha) with respect to the exact (e.g., FCI/CBS) solution or experiment.142 In quantum computing literature, this term is sometimes used instead of what we prefer to call computational accuracy. Such a mix-up can be misleading – especially as these energies usually differ significantly.143
Furthermore, to avoid confusion, we want to make clear how we use the terms FCI and ED in the remainder of the text: Both terms, FCI and ED, are somewhat interchangeably used in computational chemistry and physics. They refer to a given Hamiltonian’s exact ground state (energy) solution expressed in a specific basis set. However, as stated above, the main benefit of explicitly correlated/TC approaches is that they usually yield lower energies in a given basis set. To avoid confusion, we refer to the energy obtained by exactly diagonalizing the TC Hamiltonian (eqn (15)) as the ED – TC result (here only performed in the STO-6G basis). Meanwhile, we resort to the “usual” convention FCI/basis when referring to the exact solution of the original Hamiltonian (eqn (3)) in a specific basis set. We want to note that these two energies agree in the CBS limit.
IV. Results and discussion
One assumption motivating our development of TC-AVQITE is that by explicitly dealing with Kato’s cusp condition with a TC transformation,32,52 total energies should reach closer to the CBS limit compared to AVQITE. Furthermore, we expect that transferring complexity from the wavefunction to the Hamiltonian in the TC method (eqn (15)), should translate to shallower quantum circuits.31 In other words, the two metrics relevant for comparing TC-AVQITE and AVQITE are the computed energies and the number of operators adaptively appended to the ansatz circuits.To compare TC-AVQITE with AVQITE, we study bond dissociation in three test cases: quadratic H4, LiH and H2O. In the latter case, the bond dissociation is defined with respect to symmetric stretching of the rOH distances at a fixed angle of ∠(HOH) = 104.4°. This test set was chosen so to include different kinds of chemical bonds, including ionic (LiH) and polar covalent (H2O), as well as to stress-test the methodology in strongly correlated systems (H4). In what follows, we study different points along these systems’ potential energy surfaces to capture behaviours of bonded, broken bond, and half-broken bond regimes. For benchmarking purposes, all TC-AVQITE calculations are additionally compared to FCI computations performed with different basis sets (STO-6G, cc-p(C)VTZ or CBS-limit extrapolation) and our original TC-VarQITE implementation31,32 using a full UCCSD ansatz.
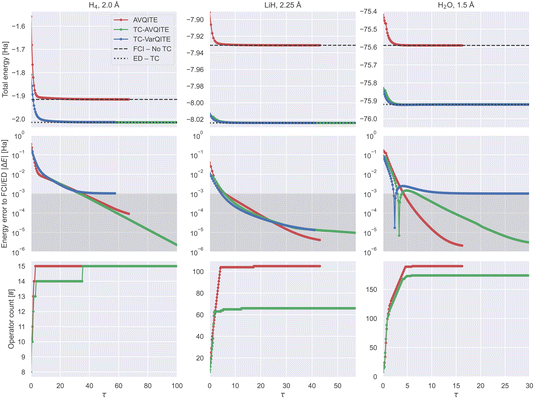
A. Convergence in imaginary time
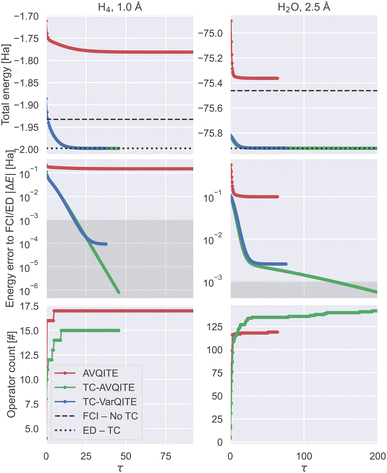
Fig. 5 compares the imaginary time evolution of each tested molecule in the half-broken bond regime.The main strength of TC-AVQITE and TC-VarQITE is apparent from the first row of Fig. 5: There is a substantial difference between the conventional FCI result (FCI – No-TC) and the energy obtained by exactly diagonalizing the TC Hamiltonian (ED – TC), despite both using the same basis set. These improved energies due to the TC approach are the primary cause of the difference between TC-AVQITE/STO-6G and AVQITE/STO-6G when compared to FCI/CBS in Fig. 6, which we will discuss below.
The second and third rows of Fig. 5 clearly illustrate how an initial rapid ramp-up of appended operators corresponds to a sharp decline in error. After this initial phase, the number of operators in the ansatz plateaus while the energy continues to converge steadily. One anomaly is apparent in the energy error for the calculation of H2O. This sharp discontinuity arises because the energies of both TC-VarQITE and TC-AVQITE cross the reference energy obtained by exactly diagonalizing the TC Hamiltonian, expressed in the STO-6G basis set (ED – TC). Such crossings can occur because the non-Hermiticity of the TC Hamiltonian ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) invalidates the Rayleigh–Ritz variational theorem. In such situations, the TC-AVQITE and TC-VarQITE energy approaches the final ED – TC value from below after the discontinuity. The final error of both adaptive methods (AVQITE and TC-AVQITE) is well below computational accuracy concerning the corresponding reference values (FCI – no-TC/ED – TC).
invalidates the Rayleigh–Ritz variational theorem. In such situations, the TC-AVQITE and TC-VarQITE energy approaches the final ED – TC value from below after the discontinuity. The final error of both adaptive methods (AVQITE and TC-AVQITE) is well below computational accuracy concerning the corresponding reference values (FCI – no-TC/ED – TC).
Opposed to TC-AVQITE, TC-VarQITE (using the entire operator pool) struggles to converge for H4 at 2.0 Å and H2O at 1.5 Å, where it retains an energy error to the ED – TC result of around 1 mH. This behaviour is consistent with previous findings for ADAPT-VQE,22 suggesting that adaptive ansätze can improve convergence. In addition to the results shown here, we compare TC-VarQITE with TC-AVQITE for all H4 bond lengths, see the ESI for details.† In general, our results indicate that TC-AVQITE is more accurate with respect to the ED – TC energy than the TC-VarQITE calculation. The exception to this case is the broken-bond regime, where both perform roughly equivalently.
The third row of Fig. 5 shows the lower operator count made possible with TC-AVQITE. For perspective and to appreciate the power of adaptive methods for reducing circuit depth without losing (and potentially even improving) accuracy, we note that the number of available operators (the full pool) that TC-VarQITE uses is 152 for H4 and 640 for LiH and H2O.
Table 1 shows the final errors for FCI – No-TC/ED – TC results both to the STO-6G basis and to FCI/CBS results, as well as corresponding estimates of required quantum resources. The listed resource estimates assume full circuit connectivity and are given as the total number of 1- and 2-qubit gates, the number of CNOTs, and the circuit depth (the number of gates that cannot be performed in parallel). Even for tiny target energy errors, |ΔE| < 10−6, the required CNOT count for TC-AVQITE calculations is within reasonable limits of near-term quantum devices. Due to the adaptive nature of TC-AVQITE, even lower CNOT counts are possible for less tight target |ΔE|. In addition, specialised quantum circuited compilation/transpilation methods144–146 could significantly reduce the required gate counts further.
| System | #Qubits | Method | #Operators | #Gates | #CNOTs | Circuit depth | |ΔE| to STO-6G/FCI or ED | |ΔE| to CBS/FCI |
|---|---|---|---|---|---|---|---|---|
| H4, 2.0 Å | 6 | AVQITE | 15 | 271 | 118 | 161 | 9.078 × 10−5 | 1.324 × 10−1 |
| TC-AVQITE | 15 | 269 | 116 | 151 | 2.167 × 10−6 | 3.349 × 10−2 | ||
| TC-VarQITE | 152 | 2797 | 1250 | 1643 | 1.026 × 10−3 | 3.452 × 10−2 | ||
| LiH, 2.25 Å | 10 | AVQITE | 105 | 2993 | 1246 | 1476 | 4.056 × 10−6 | 1.141 × 10−1 |
| TC-AVQITE | 66 | 1752 | 704 | 842 | 9.487 × 10−6 | 2.077 × 10−2 | ||
| TC-VarQITE | 640 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
7080 | 8468 | 1.308 × 10−5 | 2.077 × 10−2 | ||
| H2O, 1.5 Å | 10 | AVQITE | 190 | 5724 | 2450 | 3069 | 2.082 × 10−6 | 5.898 × 10−1 |
| TC-AVQITE | 174 | 4792 | 2054 | 2537 | 3.041 × 10−6 | 2.603 × 10−1 | ||
| TC-VarQITE | 640 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 572 572 |
7080 | 8460 | 1.002 × 10−3 | 2.593 × 10−1 |
These results demonstrate that using adaptive quantum ansätze in TC-AVQITE improves convergence and drastically reduces the number of CNOTs and circuit depth. The circuit depth using TC-AVQITE is reduced by an order of magnitude for LiH and H4 and a factor of 5 for H2O compared to TC-VarQITE.
B. Bond dissociation
Next, we compare TC-AVQITE with AVQITE along our test set’s entire bond dissociation curves. We omit direct comparison with TC-VarQITE here, as both TC-AVQITE and TC-VarQITE target the same ED – TC energies. Fig. 6 demonstrates a substantial advantage of TC-AVQITE, both in terms of lower total energies and fewer adaptively added operators. The error with respect to FCI/CBS results is up to an order of magnitude smaller using TC-AVQITE when applied to LiH across the entire binding curve, as well as in the stretched and broken-bond regimes of H4 and H2O. These drastically improved total energies are remarkable considering that only a minimal basis set is used, and clearly demonstrate the benefit of the TC method in reducing quantum circuit width (i.e., the number of necessary qubits).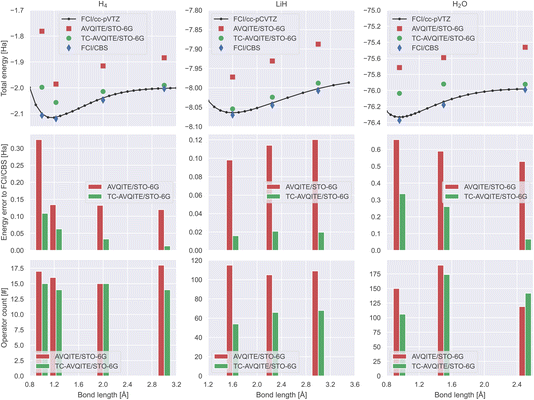 | ||
| Fig. 6 Comparison of results from TC-AVQITE/STO-6G (green), AVQITE/STO-6G (red), FCI/cc-p(C)VTZ (black) and FCI/CBS results (blue) for H4 (left column), LiH (middle column) and H2O (right column). (Top row) Total energy as a function of bond distance. (Middle row) Energy error with respect to FCI/CBS estimates as a function of bond distance. (Bottom row) The final number of adaptively added operators in AVQITE and TC-AVQITE calculations as a function of bond distance. Note: For visualization purposes, the bar plots in the middle and bottom rows are plotted as a function of bond distance. Adjacent pairs of red (AVQITE) and green (TC-AVQITE) bars correspond to the distances of the corresponding markers in the top row. Corresponding imaginary time trajectories are provided in ESI.† | ||
As shown in the bottom row of Fig. 6, this reduction in circuit width is accompanied by a simultaneous contraction of the required circuit depth. The benefit is modest for H4 and H2O, where the number of final operators is reduced by 8% to 26% on average, respectively. In the case of LiH, TC-AVQITE reduces the needed circuit depth by half compared to AVQITE while yielding results considerably closer to the CBS limit. However, there are exceptions. For example, for our calculation of quadratic H4 with a side length of 2.0 Å, both TC-AVQITE and AVQITE require 15 operators to reach convergence. We argue that the lack of improvement in situations such as these is due to a combination of (a) the minimal basis set size (only one spatial orbital per H atom); and (b) H4 being a notoriously difficult system for unitary coupled cluster theory limited to single and double (UCCSD) excitations,65 which our operator pool is based upon.
In the molecular disassociation limit of H4 and H2O, a curious behaviour can be observed: the TC-AVQITE energy errors to FCI/CBS are generally lower for larger bond lengths. This behaviour is most likely a basis set effect as the utilized minimal basis can better describe disassociated atoms than molecules. The presence of basis set effects motivates using larger basis sets, even with the TC method.
In Fig. 7, we look more closely at two challenging examples where the operator count produced by TC-AVQITE might not look advantageous compared to AVQITE at first glance.
First, in the case of the modest circuit depth reduction for quadratic H4 at 1.0 Å, TC-AVQITE adds something essential: in contrast to AVQITE, TC-AVQITE actually converges to the ground state solution! In contrast, AVQITE struggles to converge and retains a sizeable energy error exceeding 0.1 Ha at convergence. The same convergence issue also occurs for AVQITE (though far less noticeably) when applied to H4 at a bond length of 3.0 Å, where computational accuracy cannot be reached; see the ESI for details.† By moving complexity from the wavefunction to the Hamiltonian, TC-AVQITE converges well below computational accuracy while, at the same time, requiring two operators less to do so.
The second exception to circuit depth reduction seen in Fig. 6 is H2O at bond length 2.5 Å. In this case, the final operator count of TC-AVQITE is higher than the count for AVQITE, seemingly contradicting our assumption that TC approaches reduce circuit depth. However, a closer look at the imaginary time evolutions (Fig. 7 left column) reveals that similar to H4 at 1.0 Å, AVQITE here fails to converge to the FCI/STO-6G ground state. In other words, the high operator count for TC-AVQITE in these examples is caused by the algorithm successfully identifying suitable operators to append. If AVQITE were to converge in this example (for H2O at 2.5 Å), we expect its final operator count to be substantially larger.
Similar as in the case for H4 at 2.0 Å and H2O at 1.5 Å (Fig. 5), TC-VarQITE also fails to converge for H2O at 2.5 Å. This case demonstrates that using adaptive ansätze in TC-AVQITE reduces circuit depth and improves convergence for strongly correlated systems like stretched H2O.
The examples we have discussed highlight the strengths of the TC method – how a similarity transformation can simplify the solution by transferring complexity from the wavefunction to the Hamiltonian. In other words, results from our test set of calculations support our premise that TC-AVQITE reduces both circuit width and depth, by yielding better results with smaller basis sets and shallower quantum circuits. At the same time, TC-AVQITE can improve convergence behaviour compared to TC-VarQITE, which uses a full and pre-defined UCCSD operator pool.
V. Conclusion
The most significant barrier to the practical quantum computation of chemistry is the performance of current hardware, which imparts particularly harsh restrictions on the quantum circuit width (number of qubits) and depth. This work demonstrates that combining an explicitly correlated approach, the transcorrelated (TC) method, with adaptive quantum ansätze in the context of variational quantum imaginary time evolution (AVQITE) significantly reduces the necessary circuit depth and width.The TC method transfers complexity away from the wave function by incorporating Kato’s cusp condition into the Hamiltonian description of a system. Consequently, the transformed TC Hamiltonian’s eigenfunctions are easier to represent with smaller basis sets and require shallower adaptive quantum circuit ansätze. This quantum resource reduction enhances noise resilience and enables higher accuracy in calculating ground state energies for small molecular systems.
By applying TC-AVQITE to the electronic structure problems of H4, LiH, and H2O, we demonstrate a close agreement with complete basis set limit results despite using a minimal basis set; in stark contrast to traditional (non-transcorrelated) methods. Additionally, we show that, by transferring complexity from the wavefunction into the Hamiltonian, TC-AVQITE is able to converge when applied to strongly correlated systems (H4, stretched H2O), where “conventional” AVQITE or non-adaptive approaches (TC-VarQITE) fail. Additionally, for the systems studied in this work, TC with adaptive quantum ansätze reduces the required quantum resources by a factor of 5 to 10 compared to a fixed quantum ansatz strategy employed in TC-VarQITE.
While the current study focuses on small molecular systems, we emphasise that TC-AVQITE holds promise for addressing larger, more complex quantum chemistry problems in the future. To achieve such up-scaling, we intend to combine the TC approach with more elaborate basis sets, active space approaches and self-consistent orbital optimization,147–151 embedding methods,152–155 as well as spin-conserving schemes.103,156–160 Because the TC method coupled with adaptive ansätze leads to more compact quantum circuits, the method should be inherently less susceptible to noise. Therefore, another future research direction will be to study the effect of hardware noise on the method’s performance, moving closer to practical quantum chemistry applications.
Data availability
Data and software to reproduce this work are available in the accompanying public Git repository.134Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Yongxin Yao for sharing their AVQITE implementation, as well as providing helpful feedback. Funded by the European Union. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or European Research Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. This work was funded by the EU Flagship on Quantum Technology HORIZON-CL4-2022-QUANTUM-01-SGA project 101113946 OpenSuperQPlus100 and the Wallenberg Center for Quantum Technology (WACQT). WD acknowledges funding from the European Union’s Horizon Europe research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101062864. This research relied on computational resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at C3SE and NSC, partially funded by the Swedish Research Council through grant agreement no. 2022-06725. We thank Mårten Skogh for valuable discussions and feedback.References
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, 2000 Search PubMed.
- J. Čížek, On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods, J. Chem. Phys., 1966, 45, 4256 CrossRef.
- R. J. Bartlett and M. Musiał, Coupled-cluster theory in quantum chemistry, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- S. R. White, Density matrix formulation for quantum renormalization groups, Phys. Rev. Lett., 1992, 69, 2863 CrossRef PubMed.
- G. K.-L. Chan and S. Sharma, The density matrix renormalization group in quantum chemistry, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed.
- A. Baiardi and M. Reiher, The density matrix renormalization group in chemistry and molecular physics: Recent developments and new challenges, J. Chem. Phys., 2020, 152, 040903 CrossRef CAS PubMed.
- M. Nightingale and C. J. Umrigar, Quantum Monte Carlo Methods in Physics and Chemistry, Springer, Dordrecht, 1998 Search PubMed.
- F. Becca and S. Sorella, Quantum Monte Carlo Approaches for Correlated Systems, Cambridge University Press, 2017 Search PubMed.
- K. Guther, R. J. Anderson, N. S. Blunt, N. A. Bogdanov, D. Cleland, N. Dattani, W. Dobrautz, K. Ghanem, P. Jeszenszki, N. Liebermann, G. L. Manni, A. Y. Lozovoi, H. Luo, D. Ma, F. Merz, C. Overy, M. Rampp, P. K. Samanta, L. R. Schwarz, J. J. Shepherd, S. D. Smart, E. Vitale, O. Weser, G. H. Booth and A. Alavi, NECI: N-electron configuration interaction with an emphasis on state-of-the-art stochastic methods, J. Chem. Phys., 2020, 153, 034107 CrossRef CAS PubMed.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Quantum Algorithms for Quantum Chemistry and Quantum Materials Science, Chem. Rev., 2020, 120, 12685 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- H. Liu, G. H. Low, D. S. Steiger, T. Häner, M. Reiher and M. Troyer, Prospects of quantum computing for molecular sciences, Mater. Theory, 2022, 6, 11 CrossRef.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry, Nat. Commun., 2023, 14, 1952 CrossRef CAS PubMed.
- J. F. Gonthier, M. D. Radin, C. Buda, E. J. Doskocil, C. M. Abuan and J. Romero, Measurements as a roadblock to near-term practical quantum advantage in chemistry: Resource analysis, Phys. Rev. Res., 2022, 4, 033154 CrossRef CAS.
- L. Bittel and M. Kliesch, Training variational quantum algorithms is np-hard, Phys. Rev. Lett., 2021, 127, 120502 CrossRef CAS PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Quantum Chemistry in the Age of Quantum Computing, Chem. Rev., 2019, 119, 10856 CrossRef CAS PubMed.
- M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan, L. Cincio and P. J. Coles, Variational quantum algorithms, Nat. Rev. Phys., 2021, 3, 625–644 CrossRef.
- X. Yuan, S. Endo, Q. Zhao, Y. Li and S. C. Benjamin, Theory of variational quantum simulation, Quantum, 2019, 3, 191 CrossRef.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth and J. Tennyson, The variational quantum eigensolver: A review of methods and best practices, Phys. Rep., 2022, 986, 1–128 CrossRef.
- S. McArdle, T. Jones, S. Endo, Y. Li, S. C. Benjamin and X. Yuan, Variational ansatz-based quantum simulation of imaginary time evolution, npj Quantum Inf., 2019, 5, 75 CrossRef.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, An adaptive variational algorithm for exact molecular simulations on a quantum computer, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- H. L. Tang, V. Shkolnikov, G. S. Barron, H. R. Grimsley, N. J. Mayhall, E. Barnes and S. E. Economou, Qubit-ADAPT-VQE: An Adaptive Algorithm for Constructing Hardware-Efficient Ansätze on a Quantum Processor, PRX Quantum, 2021, 2, 020310 CrossRef.
- N. Gomes, A. Mukherjee, F. Zhang, T. Iadecola, C.-Z. Wang, K.-M. Ho, P. P. Orth and Y.-X. Yao, Adaptive Variational Quantum Imaginary Time Evolution Approach for Ground State Preparation, Adv. Quantum Technol., 2021, 4, 2100114 CrossRef.
- H. R. Grimsley, G. S. Barron, E. Barnes, S. E. Economou and N. J. Mayhall, Adaptive, problem-tailored variational quantum eigensolver mitigates rough parameter landscapes and barren plateaus, npj Quantum Inf., 2023, 9, 19 CrossRef.
- C. Feniou, M. Hassan, D. Traoré, E. Giner, Y. Maday and J.-P. Piquemal, Overlap-ADAPT-VQE: practical quantum chemistry on quantum computers via overlap-guided compact Ansätze, Commun. Phys., 2023, 6, 192 CrossRef CAS.
- H. Chen, N. Gomes, S. Niu and W. A. de Jong, Adaptive variational simulation for open quantum systems, arXiv, 2024, preprint, arXiv:2305.06915 [quant-ph] DOI:10.48550/arXiv.2305.06915.
- M. Motta, T. P. Gujarati, J. E. Rice, A. Kumar, C. Masteran, J. A. Latone, E. Lee, E. F. Valeev and T. Y. Takeshita, Quantum simulation of electronic structure with a transcorrelated Hamiltonian: improved accuracy with a smaller footprint on the quantum computer, Phys. Chem. Chem. Phys., 2020, 22, 24270 RSC.
- P. Schleich, J. S. Kottmann and A. Aspuru-Guzik, Improving the accuracy of the variational quantum eigensolver for molecular systems by the explicitly-correlated perturbative [2]R12 correction, Phys. Chem. Chem. Phys., 2022, 24, 13550 RSC.
- A. Kumar, A. Asthana, C. Masteran, E. F. Valeev, Y. Zhang, L. Cincio, S. Tretiak and P. A. Dub, Quantum simulation of molecular electronic states with a transcorrelated Hamiltonian: higher accuracy with fewer qubits, J. Chem. Theory Comput., 2022, 18, 5312 CrossRef CAS PubMed.
- I. O. Sokolov, W. Dobrautz, H. Luo, A. Alavi and I. Tavernelli, Orders of magnitude increased accuracy for quantum many-body problems on quantum computers via an exact transcorrelated method, Phys. Rev. Res., 2023, 5, 023174 CrossRef CAS.
- W. Dobrautz, I. O. Sokolov, K. Liao, P. L. Ríos, M. Rahm, A. Alavi and I. Tavernelli, Ab Initio Transcorrelated Method enabling accurate Quantum Chemistry on near-term Quantum Hardware, arXiv, 2023, preprint, arXiv:2303.02007 DOI:10.48550/arXiv.2303.02007.
- R. Huang, C. Li and F. A. Evangelista, Leveraging small-scale quantum computers with unitarily downfolded hamiltonians, PRX Quantum, 2023, 4, 020313 CrossRef.
- N. P. Bauman, E. J. Bylaska, S. Krishnamoorthy, G. H. Low, N. Wiebe, C. E. Granade, M. Roetteler, M. Troyer and K. Kowalski, Downfolding of many-body Hamiltonians using active-space models: Extension of the sub-system embedding sub-algebras approach to unitary coupled cluster formalisms, J. Chem. Phys., 2019, 151, 014107 CrossRef PubMed.
- N. P. Bauman, G. H. Low and K. Kowalski, Quantum simulations of excited states with active-space downfolded Hamiltonians, J. Chem. Phys., 2019, 151, 234114 CrossRef PubMed.
- N. P. Bauman, C. Jaroslav, V. Libor, P. Jiří and K. Kowalski, Variational quantum eigensolver for approximate diagonalization of downfolded Hamiltonians using generalized unitary coupled cluster ansatz, Quantum Sci. Technol., 2021, 6, 034008 CrossRef.
- N. P. Bauman and K. Kowalski, Coupled cluster downfolding theory: towards universal many-body algorithms for dimensionality reduction of composite quantum systems in chemistry and materials science, Mater. Theory, 2022, 6, 17 CrossRef.
- J. Bierman, Y. Li and J. Lu, Improving the Accuracy of Variational Quantum Eigensolvers With Fewer Qubits Using Orbital Optimization, arXiv, 2023, preprint, arXiv:2208.14431 [physics, physics:quant-ph] version: 2 DOI:10.48550/arXiv:2208.14431.
- C. Mejuto-Zaera and A. F. Kemper, Quantum Eigenvector Continuation for Chemistry Applications, arXiv, 2023, preprint, arXiv:2305.00060 [physics, physics:quant-ph] DOI:10.48550/arXiv:2305.00060.
- E. A. Hylleraas, Neue Berechnung der Energie des Heliums im Grundzustande, sowie des tiefsten Terms von Ortho-Helium, Z. Phys., 1929, 54, 347 CrossRef CAS.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Explicitly correlated electrons in molecules, Chem. Rev., 2011, 112, 4 CrossRef PubMed.
- L. Kong, F. A. Bischoff and E. F. Valeev, Explicitly correlated R12/F12 methods for electronic structure, Chem. Rev., 2011, 112, 75 CrossRef PubMed.
- S. Ten-no and J. Noga, Explicitly correlated electronic structure theory from R12/F12 ansätze, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 114 Search PubMed.
- S. Ten-no, Explicitly correlated wave functions: summary and perspective, Theor. Chem. Acc., 2012, 131, 1070 Search PubMed.
- A. Grüneis, S. Hirata, Y. ya Ohnishi and S. Ten-no, Perspective: explicitly correlated electronic structure theory for complex systems, J. Chem. Phys., 2017, 146, 080901 CrossRef PubMed.
- W. Kutzelnigg, r 12-dependent terms in the wave function as closed sums of partial wave amplitudes for large l, Theor. Chim. Acta, 1985, 68, 445 CrossRef CAS.
- S. Ten-no, Initiation of explicitly correlated Slater-type geminal theory, Chem. Phys. Lett., 2004, 398, 56 CrossRef CAS.
- S. Ten-no, Explicitly correlated second order perturbation theory: introduction of a rational generator and numerical quadratures, J. Chem. Phys., 2004, 121, 117 CrossRef CAS PubMed.
- S. Boys and N. Handy, A condition to remove the indeterminacy in interelectronic correlation functions, Proc. R. Soc. London, Ser. A, 1969, 309, 209 Search PubMed.
- S. Boys and N. Handy, The determination of energies and wavefunctions with full electronic correlation, Proc. R. Soc. London, Ser. A, 1969, 310, 43 CAS.
- N. C. Handy, Energies and expectation values for Be by the transcorrelated method, J. Chem. Phys., 1969, 51, 3205 CrossRef CAS.
- W. Dobrautz, H. Luo and A. Alavi, Compact numerical solutions to the two-dimensional repulsive Hubbard model obtained via nonunitary similarity transformations, Phys. Rev. B, 2019, 99, 075119 CrossRef CAS.
- A. J. Cohen, H. Luo, K. Guther, W. Dobrautz, D. P. Tew and A. Alavi, Similarity transformation of the electronic Schrödinger equation via Jastrow factorization, J. Chem. Phys., 2019, 151, 061101 CrossRef.
- K. Guther, A. J. Cohen, H. Luo and A. Alavi, Binding curve of the beryllium dimer using similarity-transformed FCIQMC: spectroscopic accuracy with triple-zeta basis sets, J. Chem. Phys., 2021, 155, 011102 CrossRef CAS PubMed.
- A. Baiardi and M. Reiher, Transcorrelated density matrix renormalization group, J. Chem. Phys., 2020, 153, 164115 CrossRef CAS PubMed.
- A. Baiardi, M. Lesiuk and M. Reiher, Explicitly correlated electronic structure calculations with transcorrelated matrix product operators, J. Chem. Theory Comput., 2022, 18, 4203 CrossRef CAS PubMed.
- K. Liao, H. Zhai, E. M. Christlmaier, T. Schraivogel, P. L. Ríos, D. Kats and A. Alavi, Density matrix renormalization group for transcorrelated hamiltonians: Ground and excited states in molecules, J. Chem. Theory Comput., 2023, 19, 1734 CrossRef CAS PubMed.
- K. Liao, T. Schraivogel, H. Luo, D. Kats and A. Alavi, Towards efficient and accurate ab initio solutions to periodic systems via transcorrelation and coupled cluster theory, Phys. Rev. Res., 2021, 3, 033072 CrossRef CAS.
- T. Schraivogel, E. M. Christlmaier, P. L. Ríos, A. Alavi and D. Kats, Transcorrelated coupled cluster methods. II. molecular systems, J. Chem. Phys., 2023, 158, 214106 CrossRef CAS PubMed.
- T. Schraivogel, A. J. Cohen, A. Alavi and D. Kats, Transcorrelated coupled cluster methods, J. Chem. Phys., 2021, 155, 191101 CrossRef CAS PubMed.
- A. Ammar, A. Scemama and E. Giner, Extension of selected configuration interaction for transcorrelated methods, J. Chem. Phys., 2022, 157, 134107 CrossRef CAS PubMed.
- T. Kato, On the eigenfunctions of many-particle systems in quantum mechanics, Commun. Pure Appl. Math., 1957, 10, 151 CrossRef.
- S. McArdle and D. P. Tew, Improving the accuracy of quantum computational chemistry using the transcorrelated method, arXiv, 2020, preprint, arXiv:2006.11181 [quant-ph] DOI:10.48550/arXiv:2006.11181.
- H. Volkmann, R. Sathyanarayanan, A. Saenz, K. Jansen and S. Kühn, Chemically accurate potential curves for h2 molecules using explicitly correlated qubit-adapt, J. Chem. Theory Comput., 2024, 20, 1244–1251 CrossRef CAS PubMed.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, Quantum orbital-optimized unitary coupled cluster methods in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents?, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, A quantum computing view on unitary coupled cluster theory, Chem. Soc. Rev., 2022, 51, 1659–1684 RSC.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549, 242 CrossRef CAS PubMed.
- M. Motta, C. Sun, A. T. K. Tan, M. J. O’Rourke, E. Ye, A. J. Minnich, F. G. S. L. Brandão and G. K.-L. Chan, Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution, Nat. Phys., 2019, 16, 205 Search PubMed.
- Y. Huang, Y. Shao, W. Ren, J. Sun and D. Lv, Efficient quantum imaginary time evolution by drifting real-time evolution: An approach with low gate and measurement complexity, J. Chem. Theory Comput., 2023, 19, 3868–3876 CrossRef CAS PubMed.
- H. Nishi, T. Kosugi and Y.-i. Matsushita, Implementation of quantum imaginary-time evolution method on NISQ devices by introducing nonlocal approximation, npj Quantum Inf., 2021, 7, 85 CrossRef.
- T. Tsuchimochi, Y. Ryo, S. L. Ten-no and K. Sasasako, Improved algorithms of quantum imaginary time evolution for ground and excited states of molecular systems, J. Chem. Theory Comput., 2023, 19, 503–513 CrossRef CAS PubMed.
- C. Cao, Z. An, S.-Y. Hou, D. L. Zhou and B. Zeng, Quantum imaginary time evolution steered by reinforcement learning, Commun. Phys., 2022, 5, 57 CrossRef.
- W. von der Linden, A quantum Monte Carlo approach to many-body physics, Phys. Rep., 1992, 220, 53 CrossRef.
- D. M. Ceperley, Path integrals in the theory of condensed helium, Rev. Mod. Phys., 1995, 67, 279 CrossRef CAS.
- N. Trivedi and D. M. Ceperley, Ground-state correlations of quantum antiferromagnets: A Green-function Monte Carlo study, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 4552 CrossRef PubMed.
- G. C. Wick, Properties of Bethe-Salpeter Wave Functions, Phys. Rev., 1954, 96, 1124 CrossRef CAS.
- R. V. Mises and H. Pollaczek-Geiringer, Praktische verfahren der gleichungsauflösung, J. Appl. Math. Mech., 1929, 9, 152–164 Search PubMed.
- C. Lanczos, An iteration method for the solution of the eigenvalue problem of linear differential and integral operators, J. Res. Natl. Bur. Stand., 1950, 45, 255 CrossRef.
- E. R. Davidson, The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- H. Feshbach, Unified theory of nuclear reactions, Ann. Phys., 1958, 5, 357–390 CAS.
- H. Kamakari, S.-N. Sun, M. Motta and A. J. Minnich, Digital quantum simulation of open quantum systems using quantum imaginary–time evolution, PRX Quantum, 2022, 3, 010320 CrossRef.
- C. W. J. Beenakker, Random-matrix theory of quantum transport, Rev. Mod. Phys., 1997, 69, 731 CrossRef CAS.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley, 2011 Search PubMed.
- A. D. McLachlan, A variational solution of the time-dependent Schrodinger equation, Mol. Phys., 1964, 8(1), 39–44 CrossRef.
- G. Fubini, Sulla teoria delle funzioni automorfe e delle loro trasformazioni, Ann. Mat. Pura Appl., 1908, 14, 33 CrossRef.
- E. Study, Kürzeste wege im komplexen gebiet, Math. Ann., 1905, 60, 321 CrossRef.
- J. Stokes, J. Izaac, N. Killoran and G. Carleo, Quantum Natural Gradient, Quantum, 2020, 4, 269 CrossRef.
- J. Gacon, C. Zoufal, G. Carleo and S. Woerner, Simultaneous perturbation stochastic approximation of the quantum Fisher information, Quantum, 2021, 5, 567 CrossRef.
- Y. Yao, P. Cussenot, R. A. Wolf and F. Miatto, Complex natural gradient optimization for optical quantum circuit design, Phys. Rev. A, 2022, 105, 052402 CrossRef CAS.
- F. Wilczek and A. Shapere, Geometric Phases in Physics, World Scientific Publishing, 1989 Search PubMed.
- L. Hackl, T. Guaita, T. Shi, J. Haegeman, E. Demler and J. I. Cirac, Geometry of variational methods: dynamics of closed quantum systems, SciPost Phys., 2020, 9, 048 CrossRef.
- S. Zhou and L. Jiang, An exact correspondence between the quantum Fisher information and the Bures metric, arXiv, 2019, preprint, arXiv:1910.08473 [quant-ph] DOI:10.48550/arXiv:1910.08473.
- J. Liu, H. Yuan, X.-M. Lu and X. Wang, Quantum Fisher information matrix and multiparater estimation, J. Phys. A: Math. Theor., 2020, 53, 023001 CrossRef.
- V. Giovannetti, S. Lloyd and L. Maccone, Advances in quantum metrology, Nat. Photonics, 2011, 5, 222 CrossRef CAS.
- D. Petz and C. Sudár, Geometries of quantum states, J. Math. Phys., 1996, 37, 2662 CrossRef.
- C. Zoufal, D. Sutter and S. Woerner, Error bounds for variational quantum time evolution, Phys. Rev. Appl., 2023, 20, 044059 CrossRef CAS.
- D. Fitzek, R. S. Jonsson, W. Dobrautz and C. Schäfer, Quantum, 2024, 8, 1313 CrossRef.
- J. Gacon, J. Nys, R. Rossi, S. Woerner and G. Carleo, Variational quantum time evolution without the quantum geometric tensor, arXiv, 2023, preprint, arXiv:2303.12839 [quant-ph] DOI:10.48550/arXiv:2303.12839.
- J. Gacon, C. Zoufal, G. Carleo, and S. Woerner, Stochastic approximation of variational quantum imaginary time evolution, arXiv, 2023, preprint, arXiv:2305.07059 [quant-ph] DOI:10.48550/arXiv:2305.07059.
- B. van Straaten and B. Koczor, Measurement cost of metric-aware variational quantum algorithms, PRX Quantum, 2021, 2, 030324 CrossRef.
- J. S. Van Dyke, K. Shirali, G. S. Barron, N. J. Mayhall, E. Barnes and S. E. Economou, Scaling adaptive quantum simulation algorithms via operator pool tiling, Phys. Rev. Res., 2024, 6, L012030 CrossRef CAS.
- V. O. Shkolnikov, N. J. Mayhall, S. E. Economou and E. Barnes, Avoiding symmetry roadblocks and minimizing the measurement overhead of adaptive variational quantum eigensolvers, Quantum, 2023, 7, 1040 CrossRef.
- H. G. A. Burton, D. Marti-Dafcik, D. P. Tew and D. J. Wales, Exact electronic states with shallow quantum circuits from global optimisation, npj Quantum Inf., 2023, 9, 75 CrossRef.
- P. G. Anastasiou, N. J. Mayhall, E. Barnes and S. E. Economou, How to really measure operator gradients in ADAPT-VQE, arXiv, 2023, preprint, arXiv:2306.03227 [quant-ph] DOI:10.48550/arXiv:2306.03227.
- M. Ramôa, L. P. Santos, N. J. Mayhall, E. Barnes and S. E. Economou, Reducing measurement costs by recycling the hessian in adaptive variational quantum algorithms, arXiv, 2024, preprint, arXiv:2401.05172 [quant-ph] DOI:10.48550/arXiv:2401.05172.
- H.-Y. Huang, R. Kueng and J. Preskill, Predicting many properties of a quantum system from very few measurements, Nat. Phys., 2020, 16, 1050–1057 Search PubMed.
- T.-C. Yen, A. Ganeshram and A. F. Izmaylov, Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates, npj Quantum Inf., 2023, 9, 1–7 Search PubMed.
- T.-C. Yen, V. Verteletskyi and A. F. Izmaylov, Measuring all compatible operators in one series of single-qubit measurements using unitary transformations, J. Chem. Theory Comput., 2020, 16, 2400 CrossRef CAS PubMed.
- T.-C. Yen and A. F. Izmaylov, Cartan subalgebra approach to efficient measurements of quantum observables, PRX Quantum, 2021, 2, 040320 CrossRef.
- A. F. Izmaylov, T.-C. Yen and I. G. Ryabinkin, Revising the measurement process in the variational quantum eigensolver: is it possible to reduce the number of separately measured operators?, Chem. Sci., 2019, 10, 3746 RSC.
- Z. Lan and W. Liang, Amplitude reordering accelerates the adaptive variational quantum eigensolver algorithms, J. Chem. Theory Comput., 2022, 18, 5267 CrossRef CAS PubMed.
- M. D. Sapova and A. K. Fedorov, Variational quantum eigensolver techniques for simulating carbon monoxide oxidation, Commun. Phys., 2022, 5, 199 CrossRef.
- J. Liu, Z. Li and J. Yang, An efficient adaptive variational quantum solver of the Schrödinger equation based on reduced density matrices, J. Chem. Phys., 2021, 154, 244112 CrossRef CAS PubMed , https://pubs.aip.org/aip/jcp/article-pdf/doi/10.1063/5.0054822/15965352/244112_1_online.pdf.
- A. Nykänen, M. A. C. Rossi, E.-M. Borrelli, S. Maniscalco and G. García-Pérez, Mitigating the measurement overhead of adapt-vqe with optimised informationally complete generalised measurements, arXiv, 2023, preprint, arXiv:2212.09719 [quant-ph] DOI:10.48550/arXiv:2212.09719.
- L. E. Fischer, T. Dao, I. Tavernelli and F. Tacchino, Dual frame optimization for informationally complete quantum measurements, arXiv, 2024, preprint, arXiv:2401.18071 [quant-ph] DOI:10.48550/arXiv:2401.18071.
- J. O. Hirschfelder, Removal of electron-electron poles from many-electron Hamiltonians, J. Chem. Phys., 1963, 39, 3145 CrossRef CAS.
- S. Boys and N. Handy, A calculation for the energies and wavefunctions for states of neon with full electronic correlation accuracy, Proc. R. Soc. London, Ser. A, 1969, 310, 63 CAS.
- R. Jastrow, Many-Body Problem with Strong Forces, Phys. Rev., 1955, 98, 1479 CrossRef.
- E. Neuscamman, T. Yanai and G. K.-L. Chan, A review of canonical transformation theory, Int. Rev. Phys. Chem., 2010, 29, 231–271 Search PubMed.
- T. Yanai and T. Shiozaki, Canonical transcorrelated theory with projected Slater-type geminals, J. Chem. Phys., 2012, 136, 084107 CrossRef PubMed.
- R. T. Pack and W. B. Brown, Cusp Conditions for Molecular Wavefunctions, J. Chem. Phys., 1966, 45, 556 CrossRef CAS.
- W. Dobrautz, A. J. Cohen, A. Alavi and E. Giner, Performance of a one-parameter correlation factor for transcorrelation: study on a series of second row atomic and molecular systems, J. Chem. Phys., 2022, 156, 234108 CrossRef CAS PubMed.
- P. Jeszenszki, U. Ebling, H. Luo, A. Alavi and J. Brand, Eliminating the wave-function singularity for ultracold atoms by a similarity transformation, Phys. Rev. Res., 2020, 2, 043270 CrossRef CAS.
- E. Giner, A new form of transcorrelated Hamiltonian inspired by range-separated DFT, J. Chem. Phys., 2021, 154, 084119 CrossRef CAS PubMed.
- J. P. Haupt, S. M. Hosseini, P. L. Ríos, W. Dobrautz, A. Cohen and A. Alavi, Optimizing Jastrow factors for the transcorrelated method, J. Chem. Phys., 2023, 158, 224105 CrossRef CAS PubMed.
- S. L. Ten-no, Nonunitary projective transcorrelation theory inspired by the F12 ansatz, J. Chem. Phys., 2023, 159, 171103 CrossRef CAS PubMed.
- M. Ochi, Fully self-consistent optimization of the jastrow-slater-type wave function using a similarity-transformed hamiltonian, Phys. Rev. A, 2023, 108, 032806 CrossRef CAS.
- M. Ochi, Tc++: First-principles calculation code for solids usingthe transcorrelated method, Comput. Phys. Commun., 2023, 287, 108687 CrossRef CAS.
- A. Ammar, A. Scemama and E. Giner, Transcorrelated selected configuration interaction in a bi-orthonormal basis and a cheap three-body correlation factor, arXiv, 2023, preprint, arXiv:2306.10888 [physics.chem-ph] DOI:10.48550/arXiv:2306.10888.
- N. Lee and A. J. W. Thom, Studies on the transcorrelated method, arXiv, 2023, preprint, arXiv:2301.02590 [physics.chem-ph] DOI:10.48550/arXiv:2301.02590.
- E. M. Christlmaier, T. Schraivogel, P. López Ríos, A. Alavi and D. Kats, xtc: An efficient treatment of three-body interactions in transcorrelated methods, J. Chem. Phys., 2023, 159, 014113 CrossRef CAS PubMed.
- W. Kutzelnigg and D. Mukherjee, Normal order and extended wick theorem for a multiconfiguration reference wave function, J. Chem. Phys., 1997, 107, 432 CrossRef CAS.
- Y. Yao, Avqite, 2022, git repository, https://gitlab.com/gqce/avqite Search PubMed.
- W. Dobrautz, Avqite (Fork), 2023, git repository, https://gitlab.com/werner.dobrautz/avqite Search PubMed.
- Qiskit contributors, Qiskit: an Open-Source Framework for Quantum Computing, 2023 Search PubMed.
- T. Q. N. developers and contributors, Qiskit Nature 0.6.0, 2023 Search PubMed.
- F. N. J. R. Johansson and P. D. Nation, QuTiP 2: A Python Framework for the Dynamics of Open Quantum Systems, 2013, vol. 184, issue 1234 Search PubMed.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, Pyscf: the python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- Q. Sun, Libcint: An efficient general integral library for gaussian basis functions, J. Comput. Chem., 2015, 36, 1664–1671 CrossRef CAS PubMed.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi-Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
- P. Lolur, M. Skogh, W. Dobrautz, C. Warren, J. Biznárová, A. Osman, G. Tancredi, G. Wendin, J. Bylander and M. Rahm, Reference-State Error Mitigation: A Strategy for High Accuracy Quantum Computation of Chemistry, J. Chem. Theory Comput., 2023, 19, 783 CrossRef CAS PubMed.
- N. C. C. Comparison and B. Database, NIST Standard Reference Database Number 101, 2022, issue 22 Search PubMed.
- T. Häner, D. S. Steiger, K. Svore and M. Troyer, A software methodology for compiling quantum programs, Quantum Sci. Technol., 2018, 3, 020501 CrossRef.
- N. Earnest, C. Tornow and D. J. Egger, Pulse-efficient circuit transpilation for quantum applications on cross-resonance-based hardware, Phys. Rev. Res., 2021, 3, 043088 CrossRef CAS.
- A. Miller, A. Glos and Z. Zimborás, Treespilation: Architecture- and state-optimised fermion-to-qubit mappings, arXiv, 2024, preprint, arXiv:2403.03992 [quant-ph] DOI:10.48550/arXiv:2403.03992.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157 CrossRef CAS.
- J. Olsen, The CASSCF method: A perspective and commentary, Int. J. Quantum Chem., 2011, 111, 3267 CrossRef CAS.
- W. Dobrautz, O. Weser, N. A. Bogdanov, A. Alavi and G. L. Manni, Spin-pure stochastic-CASSCF via GUGA-FCIQMC applied to iron–sulfur clusters, J. Chem. Theory Comput., 2021, 17, 5684 CrossRef CAS PubMed.
- A. Fitzpatrick, A. Nykänen, N. W. Talarico, A. Lunghi, S. Maniscalco, G. García-Pérez and S. Knecht, A self-consistent field approach for the variational quantum eigensolver: orbital optimization goes adaptive, arXiv, 2022, preprint, arXiv:2212.11405 [quant-ph] DOI:10.48550/arXiv:2212.11405.
- J. A. de Gracia Triviño, M. G. Delcey and G. Wendin, Complete active space methods for NISQ devices: The importance of canonical orbital optimization for accuracy and noise resilience, J. Chem. Theory Comput., 2023, 19, 2863 CrossRef PubMed.
- B. Bauer, D. Wecker, A. J. Millis, M. B. Hastings and M. Troyer, Hybrid quantum-classical approach to correlated materials, Phys. Rev. X, 2016, 6, 031045 Search PubMed.
- J. Tilly, P. V. Sriluckshmy, A. Patel, E. Fontana, I. Rungger, E. Grant, R. Anderson, J. Tennyson and G. H. Booth, Reduced density matrix sampling: Self-consistent embedding and multiscale electronic structure on current generation quantum computers, Phys. Rev. Res., 2021, 3, 033230 CrossRef CAS.
- M. Rossmannek, F. Pavošević, A. Rubio and I. Tavernelli, Quantum embedding method for the simulation of strongly correlated systems on quantum computers, J. Phys. Chem. Lett., 2023, 14, 3491 CrossRef CAS PubMed.
- M. Rossmannek, P. K. Barkoutsos, P. J. Ollitrault and I. Tavernelli, Quantum HF/DFT-embedding algorithms for electronic structure calculations: Scaling up to complex molecular systems, J. Chem. Phys., 2021, 154, 114105 CrossRef CAS PubMed.
- W. Dobrautz, S. D. Smart and A. Alavi, Efficient formulation of full configuration interaction quantum Monte Carlo in a spin eigenbasis via the graphical unitary group approach, J. Chem. Phys., 2019, 151, 094104 CrossRef PubMed.
- W. Dobrautz, V. M. Katukuri, N. A. Bogdanov, D. Kats, G. Li Manni and A. Alavi, Combined unitary and symmetric group approach applied to low-dimensional Heisenberg spin systems, Phys. Rev. B, 2022, 105, 195123 CrossRef CAS.
- G. L. Manni, W. Dobrautz, N. A. Bogdanov, K. Guther and A. Alavi, Resolution of low-energy states in spin-exchange transition-metal clusters: Case study of singlet states in [Fe(III)4S4] cubanes, J. Phys. Chem. A, 2021, 125, 4727 CrossRef PubMed.
- G. L. Manni, W. Dobrautz and A. Alavi, Compression of spin-adapted multiconfigurational wave functions in exchange-coupled polynuclear spin systems, J. Chem. Theory Comput., 2020, 16, 2202 CrossRef PubMed.
- G.-L. R. Anselmetti, D. Wierichs, C. Gogolin and R. M. Parrish, Local, expressive, quantum-number-preserving vqe ansätze for fermionic systems, New J. Phys., 2021, 23, 113010 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00039k |
| This journal is © The Royal Society of Chemistry 2024 |