DOI:
10.1039/D4FD00044G
(Paper)
Faraday Discuss., 2024,
254, 170-190
Multi-reference coupled cluster theory using the normal ordered exponential ansatz
Received
1st March 2024
, Accepted 28th May 2024
First published on 1st October 2024
Abstract
Properly spin-adapted coupled-cluster theory for general open-shell configurations remains an active area of research in electronic structure theory. In this contribution we examine Lindgren's normal-ordered exponential ansatz to correlate specific spin states using spin-free excitation operators, with the aid of automatic equation generation software. We present an intermediately normalised and size-extensive reformulation of the unlinked working equations, and analyse the performance of the method with single and double excitations for simple molecular systems in terms of accuracy and size-consistency.
1 Introduction
Coupled cluster (CC) theory based on a single Slater-determinant reference wavefunction is firmly established and is widely used in high-accuracy electronic structure calculations.1 Many chemical systems, including diradicals, transition metals, and molecules at non-equilibrium geometries, display open-shell configurations for which multi-determinant reference states are required. The analogous multi-reference coupled-cluster (MRCC) theory for correlating open-shell systems remains an area of active research due to challenges arising from the complexity of defining wave operators and working equations for multi-determinant reference spaces.2–4 Our work concerns the generalisation of closed-shell coupled-cluster theory to arbitrary open-shell states while retaining full spin-adaption, through a state-specific formulation. State-specific MRCC ansätze can be broadly classified into two categories: those that define a different wave operator for each reference configuration are known as Jeziorski–Monkhorst (JM) ansätze;5 the other type, in which a single wave operator is applied to a linear combination of the reference functions, are known as internally contracted ansätze.6–8 These methods are multi-reference because they include linear or non-linear parameters that are optimised separately for each contributing reference determinant.
Owing to the limitations of the single Slater determinant picture, open-shell systems are often misidentified as multi-reference. Multi-reference treatments are necessary when competing configurations are involved in bonding or when targeting excited state spectra, but are not necessary9 for states that are correctly represented by a single open-shell configuration state function (CSF), which are eigenfunctions of the spin operators. Many open-shell systems, such as organic radicals and transition metal spin states may be treated using single-reference open-shell coupled-cluster theory. In these cases, it is not necessary to perform a full CAS calculation, whose cost formally scales exponentially with the number of open-shell electrons. In this work, we explore fully spin-adapted coupled-cluster theory for correlating single open-shell CSF reference states. Our ansatz takes the form of the internally contracted theories, but where the coefficients of the multi-determinant reference state are pre-determined by spin and spatial symmetry constraints. Full spin-adaptation is achieved through the use of spin-free excitation operators in our cluster operator, in a manner similar to unitary group approaches.10–14
Since excitations involving singly-occupied orbitals do not commute, we adopt Lindgren's normal-ordered exponential (NOE) form of the coupled-cluster wave operator.15 This choice ensures that there are no contractions among cluster operators and thus the working equations terminate at finite order in the cluster amplitudes. Single CSF references are invariant with respect to rotations among the doubly-occupied orbitals, but not in general among the open-shell (active) orbitals. We include purely active-to-active excitations in our cluster operator, since these are required to fully allow for correlation-induced orbital relaxation of the CSF reference. The normal-ordered ansatz allows the inclusion of these otherwise problematic excitations. It is our opinion that this ansatz, with its origins in the factorisation theorem, best aligns with the physical motivation for coupled cluster as modelling independent excitation events.
The NOE ansatz has previously been considered in the context of Fock-Space MRCC16–21 and the Similarity Transformed Equation-of-Motion Coupled Cluster22–27 (ST-EOM-CC) approaches. In these two methods, normal-ordering of the exponential allows for a partial decoupling of the different valence sectors, simplifying the working equations. Mukherjee and co-workers have explored the NOE ansatz with unitary group adapted cluster operators for state-universal and state-specific MRCC theories, using a JM ansatz in an effective Hamiltonian formulation.28–33 Very recently, they succeeded in replacing the sufficiency conditions used in their earlier work with a rigorous effective Hamiltonian formulation.34–36 The single-reference limit of Mukherjee's approach34 reduces to the same NOE ansatz as used in this work.
In this contribution we present an alternative and much simpler formulation of the working equations for NOECC theory that permits systematic approximation. We generate our working equations via an intermediately normalised unlinked CC formalism in such a way as to preserve size extensivity. We demonstrate through analysis and numerical testing that our methods are rigorously spin-adapted, and that the errors in size-extensivity and size-consistency for homolytic bond fission introduced by truncation of our theory may be systematically removed at a finite order in the cluster operator. Our approach also differs from previous work in that we formally allow purely active-to-active excitations in order to treat active orbital relaxation, and that we do not insist on spin-completeness of the excited state projection manifold. Due to the complexity of obtaining spin-free working equations with the NOE ansatz, we have implemented our own domain-specific Wick contraction engine and automated equation generator, using similar ideas to those of Hermann and Hanrath.37–39
2 Theory
2.1 Preliminaries
We employ the following convention for orbital labelling: i, j, k, … for core (doubly-occupied) orbitals, a, b, c, … for virtual (unoccupied) orbitals, t, u, v, … for active orbitals, and p, q, r, … for general orbitals. The core, active, and virtual spaces will be denoted 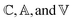 respectively. We express creation and annihilation operators using the tensor notation âpσ = â†pσ and âpσ = âpσ, and define spin-free unitary group generators
respectively. We express creation and annihilation operators using the tensor notation âpσ = â†pσ and âpσ = âpσ, and define spin-free unitary group generators| | 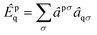 | (1) |
| | 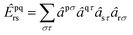 | (2) |
and so on for higher-body operators. Our cluster operator is a sum of n-body spin-free excitation operators ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) n that each commute with the total spin squared operator Ŝ2.
n that each commute with the total spin squared operator Ŝ2.| | 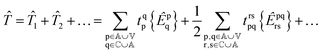 | (3) |
where the braces {} denote normal ordering with respect to the closed shell vacuum corresponding to doubly occupying the core orbitals and leaving the active and virtual orbitals vacant.
We consider the spin-free molecular electronic Hamiltonian Ĥ in normal order40 with respect to the same vacuum:
| | 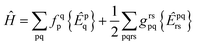 | (4) |
with
hqp = 〈p|
ĥ|q〉 and
grspq = 〈pq|
r−112|rs〉 = (pr|
r−112|qs), and the core Fock matrix is defined by
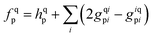
.
The open-shell part of the reference is a CSF of N electrons in N orbitals with total spin S and projected spin M, expressed through a linear combination of creation operator strings acting upon a closed shell vacuum, |Φ0〉 = |N,S,M;t〉 = ÔS,MN(t)|0〉.41 The genealogical coupling vector t specifies a particular Gel'fand–Tsetlin state in cases of spin degeneracy when there are more than two open-shell electrons. The creation operator ÔS,MN(t) is built up by recursively applying the definition
| | 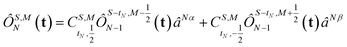 | (5) |
This recursive construction is known as a genealogical coupling scheme as it depends on the history, specified by
t, of the configurations as the angular momentum of each electron is added in turn. Each component
tN denotes whether each electron increases the total spin
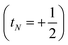
or decreases it
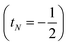
when added (
âNα/β) in the
N-th orbital to the previous (
N − 1)-electron CSF. The Clebsch–Gordan coefficients
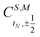
for addition of a single electron simplify to
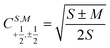
and
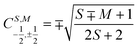
. For example, an open-shell singlet in orbitals p and q is formed from the closed shell vacuum |0〉 by the operator
| | 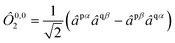 | (6) |
and the
M = 0 component of a triplet by
| | 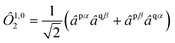 | (7) |
2.2 Normal ordered exponential coupled cluster
The traditional coupled cluster wavefunction for a cluster operator containing terms that mutually commute is written as an exponential wave operator applied to the reference determinant| | |Ψ〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (8) |
Projecting the Schrödinger equation for this ansatz onto a manifold of excited states |ΦI〉 yields the coupled cluster equations in their energy-dependent, “unlinked” formulation| | E = 〈Φ0|Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (9) |
| | 0 = RI = 〈ΦI|(Ĥ − E)e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (10) |
It is common to use the alternative “linked” formalism, which pre-multiplies the Schrödinger equation by the inverse wave operator e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) to give an effective Hamiltonian
to give an effective Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe
Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) = (Ĥe
= (Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )C that contains only linked diagrams, with the CC equations
)C that contains only linked diagrams, with the CC equations| | E = 〈Φ0|![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) |Φ0〉 |Φ0〉 | (11) |
| | 0 = RI = 〈ΦI|![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) |Φ0〉 |Φ0〉 | (12) |
retaining size-extensivity for each term in the cluster operator, and terminating at fourth order in the amplitudes, as shown by the Baker–Campbell–Hausdorff (BCH) expansion for ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) in nested commutators. The single-reference closed-shell and spin-unrestricted open-shell CC theories use cluster operators that mutually commute, and so are almost always implemented in the linked formalism. The appropriate generalisation for an open-shell CSF reference state |Φ0〉 is Lindgren's normal-ordered exponential coupled-cluster (NOECC) wave operator
in nested commutators. The single-reference closed-shell and spin-unrestricted open-shell CC theories use cluster operators that mutually commute, and so are almost always implemented in the linked formalism. The appropriate generalisation for an open-shell CSF reference state |Φ0〉 is Lindgren's normal-ordered exponential coupled-cluster (NOECC) wave operator| | |Ψ〉 = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (13) |
where braces indicate normal-ordering with respect to the closed-shell vacuum. The normal-ordered exponential form excludes contractions between cluster operators and properly parametrises independent correlation processes according to the factorisation theorem.15 Without normal-ordering, contractions among active-to-active excitations in the cluster operator, such as ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ut and
ut and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) uytx, would give rise to non-terminating working equations. Normal-ordering ensures that the energy and amplitude equations terminate at finite order in the cluster operators. The order at which the equations terminate is 4 + min(n,2Nr), where n is the number of active orbitals and Nr is the maximum rank of the excitation operators. When applied to a closed-shell reference, {e
uytx, would give rise to non-terminating working equations. Normal-ordering ensures that the energy and amplitude equations terminate at finite order in the cluster operators. The order at which the equations terminate is 4 + min(n,2Nr), where n is the number of active orbitals and Nr is the maximum rank of the excitation operators. When applied to a closed-shell reference, {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = e
} = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and NOECC is equivalent to the standard coupled-cluster ansatz. Internally contracted MRCC can be formulated with linked equations because active-to-active excitations are excluded. Using a linked formalism for NOECC theory in an analogous way to the standard theory would require knowledge of the inverse wave operator {e
and NOECC is equivalent to the standard coupled-cluster ansatz. Internally contracted MRCC can be formulated with linked equations because active-to-active excitations are excluded. Using a linked formalism for NOECC theory in an analogous way to the standard theory would require knowledge of the inverse wave operator {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }−1, which is non-trivial.23 Several attempts have been made to construct linked equations equivalent to a similarity transformed Hamiltonian by other means. The work by Mukherjee et al. uses the Bloch formalism
}−1, which is non-trivial.23 Several attempts have been made to construct linked equations equivalent to a similarity transformed Hamiltonian by other means. The work by Mukherjee et al. uses the Bloch formalism| | Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 = {e }|Φ0〉 = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }Ĥeff|Φ0〉 }Ĥeff|Φ0〉 | (14) |
where Ĥeff is an effective Hamiltonian in the reference space |Φ0〉 with the same eigenenergy as the target space {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉. By applying Wick's theorem to factor out {e
}|Φ0〉. By applying Wick's theorem to factor out {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } they obtain a rigorous expression for the effective Hamiltonian as an infinite series, along with a hierarchy of finite order approximations of increasing accuracy.34,35 Intermediate normalisation
} they obtain a rigorous expression for the effective Hamiltonian as an infinite series, along with a hierarchy of finite order approximations of increasing accuracy.34,35 Intermediate normalisation ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) {e
{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) =
= ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) is not imposed since it is in general incompatible with size-extensivity, which requires (1 −
is not imposed since it is in general incompatible with size-extensivity, which requires (1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )Ĥeff
)Ĥeff![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) = 0, where
= 0, where ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) projects onto the reference space.42,43 Our approach is much simpler. Recognising that for the single-reference case intermediate normalisation can be imposed, we use the unlinked form.
projects onto the reference space.42,43 Our approach is much simpler. Recognising that for the single-reference case intermediate normalisation can be imposed, we use the unlinked form.
The unlinked energy and amplitude equations are given by
| | E = 〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (15) |
| | RI = 〈ΦI|(Ĥ − E){e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (16) |
where the first-order interacting space is 〈Φ
I| = 〈Φ
0|
ʆI, with
I standing for one of the cluster excitations. The unlinked residual equations can be rewritten as
| | RI = 〈ΦI|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e }|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉E }|Φ0〉E | (17) |
| | = 〈ΦI|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e }|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e }|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (18) |
A proof that
eqn (18) is equivalent to a connected form of the residual equations and that the formulation is therefore size extensive is provided in Appendix A. The equations terminate, but at a high order in
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
of 4 + min(
n,2
Nr). In this contribution, we study truncated equations. Naively truncating the exponential in the unlinked formalism to obtain a lower-cost approximation would result in non-size extensive equations. However, the size-extensivity error can be kept small by retaining all terms in
eqn (18) up to a given power in the amplitudes (see Appendix A).
Specifically, the linearised equations (l-NOECC) are:
| | E = 〈Φ0|Ĥ{1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (19) |
| | RI = 〈ΦI|Ĥ{1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{ }|Φ0〉 − 〈ΦI|{![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ|Φ0〉 }|Φ0〉〈Φ0|Ĥ|Φ0〉 | (20) |
and the quadratic equations (q-NOECC) are:
| | 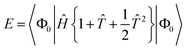 | (21) |
| | 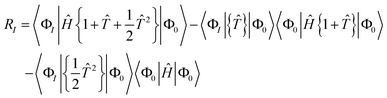 | (22) |
Since standard CCD only includes terms up to quadratic in the amplitudes, our truncated q-NOECCD method exactly replicates closed-shell CCD, and q-NOECCSD differs from CCSD only by neglecting third- and fourth-order terms involving singles amplitudes and the failure to cancel the disconnected 〈Φ
I|{
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
}|Φ
K〉〈Φ
K|
Ĥ{
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
}|Φ
0〉 term in the residual equation, where |Φ
K〉 is a singly excited state and |Φ
I〉 is doubly excited.
Our unlinked formulation explicitly imposes intermediate normalisation. It therefore allows for the possibility to include purely active-to-active excitations in the cluster operator that would formally break intermediate normalisation, since the amplitudes that would violate intermediate normalisation are necessarily zero at convergence.
2.3 The cluster operator
We choose the cluster operator so that it generates the entire first-order interacting space out of the reference state. For excitations from core orbitals to virtual, this leads to the usual inclusion of singles and doubles as in standard CCSD approaches. We also include core-to-active, active-to-virtual, and active-to-active excitations in both the singles and doubles. The active-to-active excitations are important to allow the possibility of correlation-induced orbital relaxation of the reference state. The Goldstone diagrams for the general excitation operators for NOECCSD are depicted in Fig. 1. For reference states with only one active orbital, we exclude purely active-to-active excitations in the singles and doubles.
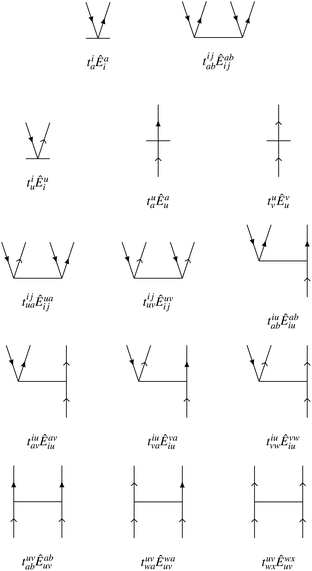 |
| | Fig. 1 Goldstone diagrams for the singles and doubles amplitudes used in our NOECCSD. Core and virtual electrons are represented by solid arrows; active electrons are represented by skeleton arrows. | |
The active-to-active amplitudes introduce spectator excitations, where a double excitation involves an electron being annihilated and created in the same active orbital and acts as a single excitation when applied to the reference. The same residual equation is therefore obtained by projection with either the single excitation Êqp or the double excitation with a spectator Êqupu, and there are an insufficient number of equations to uniquely determine the amplitudes.5,16,43–45 In the linearised approximation l-NOECCSD, the redundant excitations are interchangeable and the infinite set of amplitudes that solve the residual equations all result in exactly the same energy. We have also observed that different amplitude solutions also yield exactly the same energies for the q-NOECCSD method, although we do not expect this to be true in general. Despite the fact that in the current formulation the equations contain redundant excitations and are under-determined, we find that is always possible to converge the residual equations. Typically, convergence requires use of an appropriate level shift and the Direct Inversion in the Iterative Subspace (DIIS) technique.46 It should be noted that, while spectator excitations are present, we choose to include these only at the ranks denoted by the ansatz, i.e. the NOECCSD cluster operator only includes one- and two-body operators, even though there may be higher rank operators that produce the same configuration from the reference.
We make no attempt at spin completeness of the excitation manifold. For single-reference cases the dominant spin-coupling is present in the CSF and the remaining dynamic correlation processes are contained within the first-order interacting space. The higher-rank excitations necessary for spin completeness lead to computationally expensive terms in the NOECC equations and are not necessary to guarantee spin adaptation. We expect that higher-order excitations will be of much less significance that the ones generating the first-order interacting space. Hermann and Hanrath found that although excluding spectators in spin-adapted CC treatments gave a significant spin-incompleteness error in the energy, including them only up to the tensor rank was sufficient to remove it almost entirely, despite the excitation manifold not being fully spin-complete.38
3 Method
3.1 Automated equation generator
The large numbers of terms appearing in the spin-free open-shell coupled cluster equations make it necessary to automate the generation of working equations. We therefore constructed an object-oriented Python code that implements a second-quantised operator algebra along with a tensor algebra to represent the associated coefficients. In this framework, a particular coupled-cluster ansatz may be represented as a sum of tensor products, with associated second-quantised operator products. The open-shell reference is included through the application of second-quantised operators with specific orbital indices that create the appropriate configuration state function out of the closed shell Fermi vacuum. Rigorous spin adaptation of the theory is performed at the level of the coupled-cluster ansatz by including all terms in the spin summation. This brute force approach leads to very many terms in the equations, but produces a fully spin-adapted coupled cluster theory. The equations are projected onto the excited state manifold generated by the cluster operators and Wick's theorem is applied to obtain the terms that contribute to the energy and amplitude equations.
As an example, consider a doublet with one open-shell electron, with spin α, in an orbital labelled t. Each contribution rI to a residual RI is found by evaluating its contribution to the expectation value when projected onto the excitation manifold,
For example, the linear contribution
riuab of amplitude
tiuab with
gbjia to the residual
Riuab is found from
| | | 〈atα|ϕabiu{Êiuba}gdkjc{Êjckd}tlvef{Êefvl}|atα〉 | (24) |
One of the spin cases is
| | | 〈atα|ϕabiu{aiαauαabαaaα}gdkjc{ajαacαakαadα}tlvef{aeαafαavαalα}|atα〉 | (25) |
where possible full contraction is
| | | ϕabiuriuab = ϕabiugdkjctlvefδutδikδfbδcaδjlδedδtv | (26) |
for a residual contribution of
| | | riuab = gdkjctlvefδutδikδfbδcaδjlδedδtv | (27) |
The automated procedure to generate this expression is equivalent to the Goldstone diagram construction in
Fig. 2.
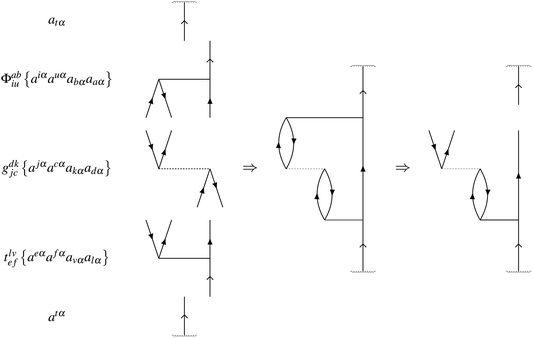 |
| | Fig. 2 Goldstone diagram construction representing the automated generation of the residual term riuab = gdkjctlvefδutδikδfbδcaδjlδedδtv. | |
This and other possible spin components are accounted for automatically, together with the factor of 4 associated with this diagram. In our pilot implementation, we do not identify equivalent terms in the equations by the topologies of their diagrammatic construction. Furthermore, the equations are not factorized in this naive implementation, giving a suboptimal scaling of computational cost that remains to be addressed in future versions of the code. It is expected that the efficiency will be improved by a substantial factor when these steps are introduced through future code developments.
3.2 Solution of CC equations
The solution scheme used for these NOECC equations is based on the iterative quasi-Newton method commonly employed in coupled cluster methods. With no true spin-free Fock matrix available, the preconditioner was the generalized Fock matrix, given by| | 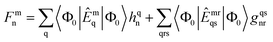 | (28) |
Iterative solution of the generated equations is aided by use of a level shift, chosen to be larger than the difference between the Fock matrix eigenvalues corresponding to the highest core orbital and lowest virtual orbital. Direct Inversion in the Iterative Subspace (DIIS) was used to accelerate convergence.46,47
4 Results
4.1 Doublets
We start with doublet electronic states because the single determinant ROHF reference can be correlated using standard unrestricted and spin-restricted spin–orbital coupled cluster implementations, which enables us to compare directly to our spin-free approach. In Table 1 we present results for unrestricted CCSD (uCCSD), Szalay and Gauss's spin-restricted CCSD (rCCSD)48 and our normal-ordered exponential NOECCSD, truncated to linear and quadratic order. Szalay and Gauss's spin-restricted approach constrains the cluster amplitudes by imposing the exact S2 expectation value, rather than fully spin-adapting the amplitudes. We also present results for the quadratic spin-free CCSD without normal-ordering. The geometries were obtained from Szalay and Gauss48 and we use the same cc-pVTZ basis as that work. In all cases, the ROHF state is used as the reference determinant. Energies were converged to 10−10 EH.
Table 1 l-NOECCSD and q-NOECCSD correlation energies in mEH for ROHF doublets states in a cc-pVTZ basis compared to unrestricted spin–orbital based CCSD (uCCSD), Szalay and Gauss's restricted CCSD (rCCSD) and spin-free quadratic CCSD (q-CCSD)
| Molecule |
uCCSD |
rCCSD |
l-NOECCSD |
q-NOECCSD |
q-CCSD |
|
2CH |
−141.105 |
−140.973 |
−137.013 |
−140.851 |
−141.049 |
|
2OH |
−230.302 |
−230.156 |
−223.133 |
−230.306 |
−230.331 |
|
2CN |
−354.724 |
−353.995 |
−325.369 |
−353.749 |
−354.454 |
|
2NO |
−433.834 |
−433.354 |
−402.668 |
−433.327 |
−434.265 |
|
2CH3 |
−199.002 |
−198.832 |
−191.233 |
−198.833 |
−198.974 |
|
2NH2 |
−220.008 |
−219.831 |
−211.911 |
−219.806 |
−219.991 |
The rCCSD correlation energies are smaller than uCCSD due to the spin-restriction imposed on the amplitudes. The spin-free NOECCSD energies are in close agreement with rCCSD, differing by only 0.3 mEH. Exact agreement between spin-restricted and spin-adapted theories is not expected, even if we had not truncated the NOECCSD equations to quadratic order. The difference between the two approaches is small in comparison to the expected magnitude of the contribution from the three-body excitations that are absent in both methods. The non normal-ordered spin-free CCSD correlation energies are universally lower than for NOECCSD, in some cases by as much as 0.8 mEH. This is because, without normal-ordering, quadratic terms involving active orbitals result in spurious additional energy contributions. For example tuatiuEauEui gives rise to an additional core to virtual excitation tuatiuEai that lowers the energy. Normal-ordering has no impact on the linear terms, but linearised NOECCSD only recovers 90% of the correlation energy.
4.2 Open shell singlets and triplets
4.2.1 Beryllium atom.
Having demonstrated our spin-free NOECC framework for one-electron doublets, we now turn to the two-electron cases: the triplet and the open-shell singlet. The 3P and 1P 2s2p excited states of the beryllium atom exemplify these electronic configurations, in a system simple enough to allow comparison of the singlet–triplet splitting with full configuration interaction (FCI).
Table 2 lists energies computed for the CSF references, and all-electron FCI and NOECCSD energies of the singlet 1P and triplet 3P states. uCCSD energies are also included for the triplet state, which has a single reference determinant. We use the cc-pCVTZ basis and the orbitals for both CSF references were generated from an ROHF calculation for the M = 1 triplet state. The CSF for the open-shell singlet is that generated by eqn (6). Energies are converged to 10−10 EH.
Table 2 l-NOECCSD and q-NOECCSD 2s2p excited state energies and singlet–triplet gap Δ of the beryllium atom in EH in a cc-pCVTZ basis, compared to the energies of the CSF references, the full CI energies, and the unrestricted CCSD energy for the triplet state
| 2S + 1 |
CSF |
uCCSD |
l-NOECCSD |
q-NOECCSD |
FCI |
| 3 |
−14.513129 |
−14.561352 |
−14.561504 |
−14.561358 |
−14.561412 |
| 1 |
−14.356425 |
— |
−14.473941 |
−14.462727 |
−14.463057 |
|
|
|
Δ
|
0.156703 |
— |
0.087563 |
0.098630 |
0.098355 |
The uCCSD, q-NOECCSD and FCI energies for the single-reference triplet state are all in excellent agreement, within 60 μEH. The agreement between CCSD and FCI is a consequence of the higher-order excitations all involving core–valence correlation, which is small for Be. We can also conclude that spin-contamination in the uCCSD wavefunction for this state is very small, and that the neglected cubic and higher NOECCSD contributions must also either be small in magnitude, or cancel.
The singlet CSF reference is almost 0.1 EH above FCI, whereas the triplet reference was 0.05 EH above the corresponding FCI energy. This is in part a consequence of using the ROHF orbitals optimised for the triplet, but also because the correlation among singlet spin-coupled electrons is larger than triplet spin-coupled due to the Fermi heap in their joint probability distribution.49 The effect of both orbital relaxation and correlation are well captured in the spin-free NOECCSD approach. At linear order, l-NOECCSD is within 10 mEH of FCI, which reduces to 0.3 mEH for q-NOECCSD. The singlet–triplet gap is also accurate to 0.3 mEH compared to FCI.
A fully spin-adapted theory should recover the same energy for each of the (2S + 1) spin-projections of a state with total spin S. Our approach enables us to correlate arbitrary CSFs, and as a test of our method, we computed all-electron l-NOECCD energies of the M = 1 and M = 0 components of the triplet state. The M = 1 CSF is a single ROHF determinant, whereas the M = 0 CSF is a linear combination of two determinants (eqn (7)). The two calculations converged with energies that were identical at every iteration, confirming that our method is fully spin-adapted.
4.2.2 Oxygen molecule.
Another archetypical singlet–triplet system is provided by the oxygen molecule. The lowest energy singlet state 1Δg lies 0.0359 EH above the triplet 3Σg− ground state. Both states correspond to the open-shell configuration π1g,xπ1g,y. The O1,12 reference CSF for the 3Σg− is a single ROHF determinant, whereas the O0,02 reference CSF for the 1Δg state is a linear combination of two determinants. Table 3 reports all-electron NOECCSD energies for the singlet and triplet states of O2 at a bond length of 1.2075 Å using a cc-pCVTZ basis. For both CSFs, the orbitals were obtained from a ROHF calculation on the triplet state. We also report energies for the 3Σg− ground state computed by ROHF-uCCSD for comparison. All energies are converged to 10−10 EH.
Table 3 l-NOECCSD and q-NOECCSD energies in EH of the triplet ground state and lowest-lying open and closed shell singlet excited states of O2 in a cc-pCVTZ basis set, compared to the CSF reference energies and the unrestricted CCSD energy of the triplet state
|
2S+1Λ |
Reference energy |
uCCSD |
l-NOECCSD |
q-NOECCSD |
|
3Σg− |
−149.653208 |
−150.223429 |
−150.238029 |
−150.222443 |
|
1Δg |
−149.605647 |
— |
−150.204043 |
−150.183136 |
|
1Σg+ |
−149.558086 |
— |
−150.187127 |
−150.156285 |
|
|
|
1Δg − 3Σg− |
0.047561 |
— |
0.033986 |
0.039307 |
|
1Σg+ − 3Σg− |
0.095122 |
— |
0.050903 |
0.066158 |
As before, the q-NOECCSD energy is within 1 mEH of the uCCSD energy, where they can be compared. The computed singlet–triplet gap of 0.0393 EH is in good agreement with the experimental value of 0.0359 EH, considering that the experimental value is the adiabatic 0–0 energy, whereas we have computed the vertical electronic energy, and that triple excitations are not fully accounted for in our method. The 1Σg+ state, which lies 0.0598 EH above the triplet ground state, is a π2g,x + π2g,y configuration that is a symmetry-adapted linear combination of two closed-shell CSFs. Our single-reference open-shell formalism extends straightforwardly to this multi-determinant state and we obtain a singlet–triplet gap with q-NOECCSD of 0.0662 EH.
5 Discussion
We discuss the characteristics of the NOECC method using criteria set out by Köhn2 and coworkers for MRCC theory: size extensivity; size consistency; orbital invariance; compatibility with SRCC; satisfying the proper residual condition.
5.1 Size extensivity
As shown in Appendix A, solving for the amplitude equations is equivalent to solving for a corresponding set of equations comprising only connected terms. Since the energy of the CSF reference is also size extensive, our NOECC method is fully size extensive when all terms are included up to the finite order at which the equations terminate. Truncating our equations at a lower order introduces a size-extensivity error.
5.2 Size consistency
Size consistency requires that the energy of a molecule composed of two infinitely separated spin-coupled fragments is equal to the sum of the energies of the isolated fragments. For size consistency to be satisfied, the reference CSF must dissociate into the corresponding CSFs for the constituent fragments, and non-vanishing higher-order excitations present in the NOECC wave operator for the molecule must be representable through products of lower-order excitations of the fragments.
The appropriate CSF for spin-coupled, but non-interacting fragments is the one constructed from Clebsch–Gordan coupling of the spins of the fragments. For example, a two-electron open-shell triplet and singlet are formed by high-spin or low-spin coupling two one-electron doublet states, respectively. To assess the size consistency of the NOECC ansatz, we examine the energies for the homolytic bond fission of Li2 as the simplest non-trivial test case.
At dissociation, the 1Σg+ and 3Σu+ states of a lithium dimer should have the same energy, and this should be equal to twice that of an isolated lithium atom in the 2S state. The results of all-electron spin-free NOECCD and NOECCSD calculations assessing the extent to which this is true are presented in Tables 4 and 5, respectively. The orbitals of the 3Σu+ state of Li2 and the 2S state of the Li atom were obtained from ROHF calculations. The 1Σg+ state was constructed using the localised 1s and 2s orbitals of the 3Σu+ state, ensuring that the energy expectation value of the open-shell singlet CSF exactly matches the ROHF energy of the triplet, and that both are exactly twice that of the doublet. The cc-pCVTZ basis was used and an interatomic distance of 109 Å was chosen to represent the system of the two dissociated, but still spin-coupled, lithium atoms. All energies are converged to 10−10 EH. uCCD and uCCSD energies are also provided for comparison.
Table 4 l-NOECCD and q-NOECCD correlation energies in mEH for Li and Li2 at a separation of 109 Å in cc-pCVTZ basis, compared to unrestricted CCD
|
|
uCCD |
l-NOECCD |
q-NOECCD |
| Li(2S) |
−41.505947 |
−41.680942 |
−41.532939 |
| Li2(3Σg−), r = 109 Å |
−83.011893 |
−83.389282 |
−83.091473 |
| Li2(1Σg+), r = 109 Å |
— |
−83.389289 |
−83.091788 |
|
|
| 2E(2S) − E(3Σg−) |
0.000000 |
0.027398 |
0.025595 |
| 2E(2S) − E(1Σg+) |
— |
0.027404 |
0.025910 |
Table 5 l-NOECCSD and q-NOECCSD correlation energies in mEH for Li and Li2 at a separation of 109 Å in cc-pCVTZ basis, compared to unrestricted CCSD
|
|
uCCSD |
l-NOECCSD |
q-NOECCSD |
| Li(2S) |
−41.546366 |
−41.694641 |
−41.545784 |
| Li2(3Σg−), r = 109 Å |
−83.092731 |
−83.389282 |
−83.091498 |
| Li2(1Σg+), r = 109 Å |
— |
−83.389289 |
−83.091947 |
|
|
| 2E(2S) − E(3Σg−) |
0.000000 |
0.000001 |
−0.000070 |
| 2E(2S) − E(1Σg+) |
— |
0.000007 |
0.000379 |
Both l-NOECCD and q-NOECCD show significant size-inconsistency errors of 0.03 mEH. Size consistency is violated because the cluster operator includes terms that excite fragment A with spectator orbitals on fragment B, and vice versa
| |  | (29) |
The terms
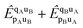
are non-vanishing in the molecule, but are absent in the cluster operators of fragments and the cluster operator is therefore not additively separable in the dissociative limit, which for CCD would require
| | 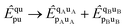 | (30) |
The doubles spectator excitations correspond to single excitations when acting on the reference. Since the l-NOECCSD and q-NOECCSD methods explicitly include the single excitations
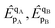
that were absent in NOECCD, size consistency can be restored numerically through the combined action of the singles and doubles. The size-inconsistency errors are reduced to 7 nE
H for l-NOECCSD and 4 μE
H for q-NOECCSD. While the NOECCSD method is not rigorously size consistent, it is numerically very close to being size consistent in practice. Similar observations have been made by Hanauer and Köhn
8 for the ic-MRCC method, where they found that the magnitude of size-inconsistency errors depended critically on the way they removed the redundancies from their working equations. These small size-inconsistency errors may be due in part to the size-extensivity errors introduced by truncating our theory. The fact that q-NOECCSD has a larger error than l-NOECCSD would align with the presence of disconnected terms in the q-NOECCSD equations that do not appear in l-NOECCSD. This suggests that taking the full NOECCSD equations (5-NOECCSD for the Li atom and 6-NOECCSD for the dimer) could remove the errors, although this would be prohibitively expensive in our current version of the code.
5.3 Orbital invariance
The NOECC method proposed is invariant to core–core and virtual–virtual rotations in the same way as standard coupled-cluster theory. The reference CSF is not in general invariant to active–active rotations. This is in contrast to a CASSCF reference function, used in ic-MRCC methods, which is invariant to active–active rotations.50 For any given excitation order, the NOE cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) consists of all possible excitations from the set of core and active orbitals to the set of active and virtual orbitals. The NOE wave operator {e
consists of all possible excitations from the set of core and active orbitals to the set of active and virtual orbitals. The NOE wave operator {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } is therefore invariant to orbital rotations within each of these sets. If a certain subset of these excitations were excluded, the wave operator ceases to be orbital invariant. Our proposed NOECC method includes all excitations of a given type and therefore retains all orbital invariance properties of the reference CSF.
} is therefore invariant to orbital rotations within each of these sets. If a certain subset of these excitations were excluded, the wave operator ceases to be orbital invariant. Our proposed NOECC method includes all excitations of a given type and therefore retains all orbital invariance properties of the reference CSF.
5.4 Compatibility with SRCC
The state-specific NOECC method we have proposed is a single-reference method in the sense that we correlate a single reference CSF representative of the electronic eigenstate under consideration. In general, the CSF is a specific linear combination of many determinants. In the case that the CSF is a single closed-shell determinant, NOECC reduces identically to conventional spin-free coupled-cluster theory, making it seamlessly compatible with SRCC methods. Many of the problems associated with combining results from MRCC methods with SRCC methods stem from the use of a CASSCF reference, where it is often challenging to keep the reference space consistent across different regions of the potential energy surface. In the context of state-specific NOECC, this problem becomes one of choosing an appropriate CSF reference. Some regions of the potential energy surface will not be well represented by a single CSF9 and there the state-specific approach is expected to be less accurate.
5.5 Projected Schrödinger equation
A proper residual equation2,3,51 is defined as one that is equivalent to solving a projected Schrödinger equation. In general, the amplitude equations for methods using the JM ansätze, where each reference determinant has its own wave operator, do not correspond to a projected Schrödinger equation (a notable exception being Hanrath's MRexpT52,53 method). The NOECC approach uses an internally-contracted ansatz with a complete first-order interacting space and therefore does satisfy the condition of having a proper residual equation.
6 Conclusion
We have developed a novel formulation of the single-reference normal-ordered exponential coupled-cluster method to correlate multi-determinant states, NOECC. The ansatz is rigorously spin-adapted and recovers the dynamic correlation and orbital relaxation of an arbitrary configuration state function, without spin contamination. Both high- and low-spin states of an atom or molecule can be correlated. Our working equations are derived from a reformulation of the unlinked coupled-cluster equations, which we prove are equivalent to solving fully connected equations. The method formally terminates at 4 + min(n,2Nr) in the cluster amplitudes, where n is the number of open-shell orbitals and Nr is the maximum excitation rank of the cluster operator, at which order the theory is fully size extensive. In this way, we circumvent the requirement for the inverse of the normal ordered exponential, for which the closed form is not known. We have developed code to automatically generate spin-adapted equations in a truncated form, while keeping the size extensivity errors as small as possible. The NOECCSD method truncated at second-order has been examined numerically using a set of small atoms and molecules, with encouraging results. Our energies for doublet systems are comparable to those found by Szalay and Gauss using a spin-restricted formalism and the singlet–triplet energy splittings are shown to be in excellent agreement with FCI for the 1s2s configuration of beryllium and within 10 kJ mol−1 of experiment for the oxygen molecule. Numerical tests of size consistency reveal that, while the method is not rigorously size consistent, size-inconsistency errors are on the order of μEH for the cases tested. In common with many MRCC methods, the NOECC wavefunction contains spectator excitations that lead to a set of redundant amplitudes in the residual equations. Although this leads to an infinite family of solutions, we find that different amplitude solutions yield exactly the same energies. NOECC is a single-reference method in the sense that coefficients of the multi-determinant reference state are not relaxed. Since our formulation does not rely on the absence of active-to-active excitations in the cluster operator, it can in principle therefore be used to correlate single CSFs, or CASSCF, RASSCF54 or GASSCF55 references to recover the dynamic correlation of highly multi-reference states, without spin contamination. While for cases such as bond dissociation, or near degeneracies, a fully multi-reference approach is more appropriate, NOECC is highly suited for correlating specific spin states, such as those in organic radicals and high- or low-spin transition metal spin states.
Conflicts of interest
There are no conflicts of interest to declare.
Appendix A Connectedness of the residual equation
We demonstrate here that our working equations (eqn (18)) are equivalent to a connected form of the residual equations. We also show that truncating our equations does introduce disconnected terms, but that size extensivity can be restored if the equations are taken to the full (finite) order at which they terminate. The proof uses a derivation found in Lindgren's paper15 that extracts the connected terms from the product of the Hamiltonian and the normal ordered exponential form of the wave operator:| | 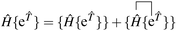 | (31) |
The contracted terms can be separated into products of the connected parts and the remaining cluster operators:| | 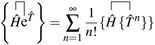 | (32) |
| | 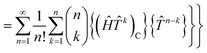 | (33) |
| | 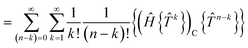 | (34) |
| | 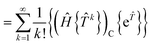 | (35) |
The first term of eqn (31) corresponds to extending the sum to k = 0, leading to the classic result that15,44| | 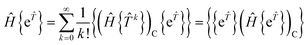 | (36) |
where the subscript C denotes connected terms. We have also used the fact that, within a normal ordered product, operators consisting of even numbers of creation and annihilation operators commute.
A.1 Size extensivity in the closed shell case
Our residual equation is| | RI = 〈ΦI|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e }|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e }|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (37) |
| | = 〈ΦI|{{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }(Ĥ{e }(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C}|Φ0〉 − 〈ΦI|{e })C}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e }|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (38) |
| | 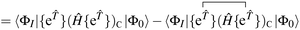 | (39) |
| | −〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e }|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (40) |
In the closed shell case, amplitudes cannot be contracted with from the right so the middle term is zero. The disconnected terms in 〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 will also vanish. We then have
}|Φ0〉 will also vanish. We then have| | RI = 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }(Ĥ{e }(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 − 〈ΦI|{e })C|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|(Ĥ{e }|Φ0〉〈Φ0|(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 })C|Φ0〉 | (41) |
| | 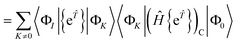 | (42) |
| | 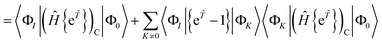 | (43) |
If |ΦI〉 is to be reached from |ΦK〉 using only excitations and |ΦK〉 ≠ |Φ0〉, then |ΦK〉 must be in the manifold spanned by the states |ΦI〉. If |ΦK〉 is an excited state that can only be reached from |Φ0〉, then 〈ΦK|(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 = RK. The disconnected terms vanish at convergence because they are comprised of smaller connected terms that are already solved in our equations. Solving our (not fully connected) equation is equivalent to solving the connected equation
})C|Φ0〉 = RK. The disconnected terms vanish at convergence because they are comprised of smaller connected terms that are already solved in our equations. Solving our (not fully connected) equation is equivalent to solving the connected equation| | 0 = RI = 〈ΦI|(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 })C|Φ0〉 | (44) |
A.2 The general case
We first use the fact that the product of Hamiltonian and normal ordered wave operator Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } can be expressed as the product of {e
} can be expressed as the product of {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } with a fully connected operator:where
} with a fully connected operator:where ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) is a sum of fully connected terms. This result was first published by Mukherjee,34,35 and we will reproduce the proof here. It is convenient to define the fully connected term
is a sum of fully connected terms. This result was first published by Mukherjee,34,35 and we will reproduce the proof here. It is convenient to define the fully connected term ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = (Ĥ{e
0 = (Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C and the modified exponential {ẽ
})C and the modified exponential {ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = {e
} = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − 1}.
− 1}.
Repeatedly applying Wick's theorem to eqn (36) yields the relation obtained by Chakravarti, Sen, and Mukherjee,34,35 that
where
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif)
is the sum of connected terms defined by
| | ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) = { = {![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0} − {({ẽ 0} − {({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } }![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C}+{({ẽ 0)C}+{({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ }({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } }![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C)C} 0)C)C} | (57) |
| | −{({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ }({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ }({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } }![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C)C)C} + … 0)C)C)C} + … | (58) |
Using this result, the residual equation can be written
| | RI = 〈ΦI|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e }|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e }|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 }|Φ0〉 | (59) |
| | = 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } }![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 − 〈ΦI|{e |Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|{e }|Φ0〉〈Φ0|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } }![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 |Φ0〉 | (60) |
| | 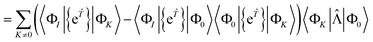 | (61) |
| | = 〈ΦI|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 |Φ0〉 | (62) |
| | 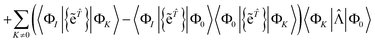 | (63) |
where the
K = 0 terms cancel due to the intermediate normalisation condition 〈Φ
0|{e
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
}|Φ
0〉 = 1.
Assuming intermediate normalisation also gives that 〈Φ0|{ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|ΦK〉 = 0, so we can write
}|ΦK〉 = 0, so we can write
| | 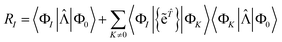 | (64) |
As for the closed shell case, if |Φ
K〉 cannot be reached from another excited state, then we have 〈Φ
K|
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif)
|Φ
0〉 =
RK, which vanishes at convergence.
Solving the residual eqn (18) is therefore equivalent to solving the fully connected equation
| | 0 = RI = 〈ΦI|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 |Φ0〉 | (65) |
The contribution of order ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) n to the residual is
n to the residual is
| | 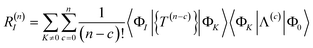 | (66) |
where Λ
(c) is the sum of (connected) terms in Λ of order
c with respect to
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
.
The residual truncated at order N is then
| | 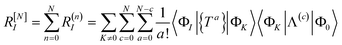 | (67) |
where the relabelling
a = (
n −
c) has been made inside the sum. Equivalently,
| | 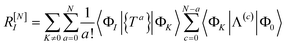 | (68) |
| | 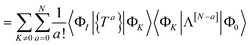 | (69) |
where Λ
[N−a] indicates the sum of terms in Λ up to order
N −
a in
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
. Since we have not solved the connected equations 〈Φ
K|Λ
[N−a]|Φ
0〉 = 0 truncated to lower order, the truncation of our equations has once again introduced a size-extensivity error.
Acknowledgements
The authors would like to acknowledge Professor Andreas Köhn and Professor Debashis Mukherjee for providing insightful comments on this manuscript. This work was supported by the EPSRC Centre for Doctoral Training in Theory and Modelling in the Chemical Sciences [grant number EP/L015722/1].
Notes and references
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- A. Köhn, M. Hanauer, L. A. Mück, T.-C. Jagau and J. Gauss, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2013, 3, 176–197 CrossRef.
- D. I. Lyakh, M. Musial, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS.
- F. A. Evangelista, J. Chem. Phys., 2018, 149, 030901 CrossRef PubMed.
- B. Jeziorski and H. J. Monkhorst, Phys. Rev. A, 1981, 24, 1668 CrossRef CAS.
- A. Banerjee and J. Simons, Int. J. Quantum Chem., 1981, 19, 207–216 CrossRef CAS.
- F. A. Evangelista, M. Hanauer, A. Köhn and J. Gauss, J. Chem. Phys., 2012, 136, 204108 CrossRef PubMed.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed.
-
D. Marti-Dafcik, N. Lee, H. G. A. Burton and D. P. Tew, Spin-coupled Molecular Orbitals: Chemical Intuition Meets Quantum Chemistry, arXiv, 2024, preprint, arXiv:2402.08858, DOI:10.48550/arXiv.2402.08858.
- X. Li and J. Paldus, Int. J. Mol. Sci., 1993, 48, 269–285 Search PubMed.
- X. Li and J. Paldus, J. Chem. Phys., 1994, 101, 8812–8826 CrossRef CAS.
-
X. Li and J. Paldus, Recent Advances in Coupled-Cluster Methods, World Scientific, 1997, vol. 3, pp. 183–219 Search PubMed.
- X. Li and J. Paldus, Mol. Phys., 1998, 94, 41–54 CrossRef CAS.
- X. Li and J. Paldus, Int. J. Quantum Chem., 1998, 70, 65–75 CrossRef CAS.
- I. Lindgren, Int. J. Quantum Chem., 1978, 14, 33–58 CrossRef.
- M. A. Haque and D. Mukherjee, J. Chem. Phys., 1984, 80, 5058–5069 CrossRef CAS.
- L. Z. Stolarczyk and H. J. Monkhorst, Phys. Rev. A, 1985, 32, 725 CrossRef.
- L. Z. Stolarczyk and H. J. Monkhorst, Phys. Rev. A, 1985, 32, 743 CrossRef.
- L. Z. Stolarczyk and H. J. Monkhorst, Phys. Rev. A, 1988, 37, 1908 CrossRef.
- L. Z. Stolarczyk and H. J. Monkhorst, Phys. Rev. A, 1988, 37, 1926 CrossRef.
- U. Kaldor, Theor. Chim. Acta, 1991, 80, 427–439 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1996, 104, 2652–2688 CrossRef CAS.
- M. Nooijen, J. Chem. Phys., 1996, 104, 2638–2651 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 106, 6441–6448 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 106, 6449–6455 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- M. Nooijen, D. Ondrej, D. Datta, L. Kong, K. R. Shamasundar, V. F. Lotrich, L. M. Huntington and F. Neese, J. Chem. Phys., 2014, 140, 081102 CrossRef PubMed.
- D. Jana, U. S. Mahapatra and D. Mukherjee, Chem. Phys. Lett., 2002, 353, 100–110 CrossRef CAS.
- D. Datta and D. Mukherjee, Int. J. Quantum Chem., 2008, 108, 2211–2222 CrossRef CAS.
- D. Datta and D. Mukherjee, J. Chem. Phys., 2009, 131, 044124 CrossRef PubMed.
- R. Maitra, D. Sinha and D. Mukherjee, J. Chem. Phys., 2012, 137, 024105 CrossRef PubMed.
- D. Sinha, R. Maitra and D. Mukherjee, J. Chem. Phys., 2012, 137, 094104 CrossRef PubMed.
- S. Sen, A. Shee and D. Mukherjee, J. Chem. Phys., 2012, 137, 074104 CrossRef.
- S. Sen, A. Shee and D. Mukherjee, J. Chem. Phys., 2018, 148, 054107 CrossRef PubMed.
- D. Chakravarti, S. Sen and D. Mukherjee, Mol. Phys., 2021, 119, e1979676 CrossRef.
- D. Chakravarti, S. Sen and D. Mukherjee, J. Chem. Phys., 2023, 159, 134102 CrossRef CAS.
- N. Hermann and M. Hanrath, J. Chem. Phys., 2020, 153, 164114 CrossRef PubMed.
- N. Hermann and M. Hanrath, Mol. Phys., 2022, 120, e2005836 CrossRef.
- N. Hermann and M. Hanrath, J. Chem. Phys., 2022, 156, 054111 CrossRef PubMed.
- W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1997, 107, 432–449 CrossRef CAS.
-
T. Helgaker, J. Olsen and P. Jorgensen, Modern Electronic Structure Theory, Wiley-Blackwell, 2013 Search PubMed.
- I. Lindgren, Phys. Scr., 1985, 32, 291–302 CrossRef.
- I. Lindgren and D. Mukherjee, Phys. Rep., 1987, 151, 93–127 CrossRef CAS.
- D. Mukherjee, R. K. Moitra and A. Mukhopadhyay, Mol. Phys., 1975, 30, 1861–1888 CrossRef CAS.
- S. Pal, M. D. Prasad and D. Mukherjee, Theor. Chim. Acta, 1984, 66, 311–332 CrossRef CAS.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 CrossRef CAS.
- G. E. Scuseria, T. J. Lee and H. F. Schaefer III, Chem. Phys. Lett., 1986, 130, 236–239 CrossRef CAS.
- P. G. Szalay and J. Gauss, J. Chem. Phys., 1997, 107, 9028–9038 CrossRef CAS.
- D. P. Tew, W. Klopper and T. Helgaker, J. Comput. Chem., 2007, 28, 1307–1320 CrossRef CAS PubMed.
- L. Kong, Int. J. Quantum Chem., 2010, 110, 2603–2613 CrossRef CAS.
- L. Kong, Int. J. Quantum Chem., 2008, 109, 441–447 CrossRef.
- M. Hanrath, J. Chem. Phys., 2005, 123, 084102 CrossRef PubMed.
- M. Hanrath, Chem. Phys. Lett., 2006, 420, 426–431 CrossRef CAS.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- D. Ma, G. Li Manni and L. Gagliardi, J. Chem. Phys., 2011, 135, 044128 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
 respectively. We express creation and annihilation operators using the tensor notation âpσ = â†pσ and âpσ = âpσ, and define spin-free unitary group generators
respectively. We express creation and annihilation operators using the tensor notation âpσ = â†pσ and âpσ = âpσ, and define spin-free unitary group generators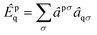
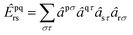
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) n that each commute with the total spin squared operator Ŝ2.
n that each commute with the total spin squared operator Ŝ2.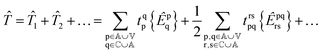
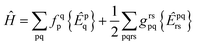
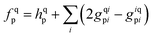 .
.
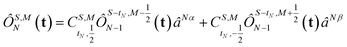
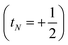 or decreases it
or decreases it 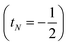 when added (âNα/β) in the N-th orbital to the previous (N − 1)-electron CSF. The Clebsch–Gordan coefficients
when added (âNα/β) in the N-th orbital to the previous (N − 1)-electron CSF. The Clebsch–Gordan coefficients 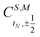 for addition of a single electron simplify to
for addition of a single electron simplify to 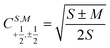 and
and 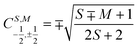 . For example, an open-shell singlet in orbitals p and q is formed from the closed shell vacuum |0〉 by the operator
. For example, an open-shell singlet in orbitals p and q is formed from the closed shell vacuum |0〉 by the operator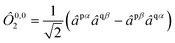
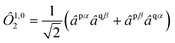
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) to give an effective Hamiltonian
to give an effective Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe
Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) = (Ĥe
= (Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )C that contains only linked diagrams, with the CC equations
)C that contains only linked diagrams, with the CC equations![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) |Φ0〉
|Φ0〉![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) |Φ0〉
|Φ0〉![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) in nested commutators. The single-reference closed-shell and spin-unrestricted open-shell CC theories use cluster operators that mutually commute, and so are almost always implemented in the linked formalism. The appropriate generalisation for an open-shell CSF reference state |Φ0〉 is Lindgren's normal-ordered exponential coupled-cluster (NOECC) wave operator
in nested commutators. The single-reference closed-shell and spin-unrestricted open-shell CC theories use cluster operators that mutually commute, and so are almost always implemented in the linked formalism. The appropriate generalisation for an open-shell CSF reference state |Φ0〉 is Lindgren's normal-ordered exponential coupled-cluster (NOECC) wave operator![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ut and
ut and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) uytx, would give rise to non-terminating working equations. Normal-ordering ensures that the energy and amplitude equations terminate at finite order in the cluster operators. The order at which the equations terminate is 4 + min(n,2Nr), where n is the number of active orbitals and Nr is the maximum rank of the excitation operators. When applied to a closed-shell reference, {e
uytx, would give rise to non-terminating working equations. Normal-ordering ensures that the energy and amplitude equations terminate at finite order in the cluster operators. The order at which the equations terminate is 4 + min(n,2Nr), where n is the number of active orbitals and Nr is the maximum rank of the excitation operators. When applied to a closed-shell reference, {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = e
} = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and NOECC is equivalent to the standard coupled-cluster ansatz. Internally contracted MRCC can be formulated with linked equations because active-to-active excitations are excluded. Using a linked formalism for NOECC theory in an analogous way to the standard theory would require knowledge of the inverse wave operator {e
and NOECC is equivalent to the standard coupled-cluster ansatz. Internally contracted MRCC can be formulated with linked equations because active-to-active excitations are excluded. Using a linked formalism for NOECC theory in an analogous way to the standard theory would require knowledge of the inverse wave operator {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }−1, which is non-trivial.23 Several attempts have been made to construct linked equations equivalent to a similarity transformed Hamiltonian by other means. The work by Mukherjee et al. uses the Bloch formalism
}−1, which is non-trivial.23 Several attempts have been made to construct linked equations equivalent to a similarity transformed Hamiltonian by other means. The work by Mukherjee et al. uses the Bloch formalism![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 = {e
}|Φ0〉 = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }Ĥeff|Φ0〉
}Ĥeff|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉. By applying Wick's theorem to factor out {e
}|Φ0〉. By applying Wick's theorem to factor out {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } they obtain a rigorous expression for the effective Hamiltonian as an infinite series, along with a hierarchy of finite order approximations of increasing accuracy.34,35 Intermediate normalisation
} they obtain a rigorous expression for the effective Hamiltonian as an infinite series, along with a hierarchy of finite order approximations of increasing accuracy.34,35 Intermediate normalisation ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) {e
{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) =
= ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) is not imposed since it is in general incompatible with size-extensivity, which requires (1 −
is not imposed since it is in general incompatible with size-extensivity, which requires (1 − ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) )Ĥeff
)Ĥeff![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) = 0, where
= 0, where ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) projects onto the reference space.42,43 Our approach is much simpler. Recognising that for the single-reference case intermediate normalisation can be imposed, we use the unlinked form.
projects onto the reference space.42,43 Our approach is much simpler. Recognising that for the single-reference case intermediate normalisation can be imposed, we use the unlinked form.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e
}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉E
}|Φ0〉E![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e
}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e
}|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) of 4 + min(n,2Nr). In this contribution, we study truncated equations. Naively truncating the exponential in the unlinked formalism to obtain a lower-cost approximation would result in non-size extensive equations. However, the size-extensivity error can be kept small by retaining all terms in eqn (18) up to a given power in the amplitudes (see Appendix A).
of 4 + min(n,2Nr). In this contribution, we study truncated equations. Naively truncating the exponential in the unlinked formalism to obtain a lower-cost approximation would result in non-size extensive equations. However, the size-extensivity error can be kept small by retaining all terms in eqn (18) up to a given power in the amplitudes (see Appendix A).
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{
}|Φ0〉 − 〈ΦI|{![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ|Φ0〉
}|Φ0〉〈Φ0|Ĥ|Φ0〉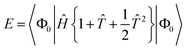
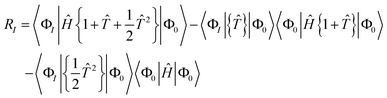
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|ΦK〉〈ΦK|Ĥ{
}|ΦK〉〈ΦK|Ĥ{![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 term in the residual equation, where |ΦK〉 is a singly excited state and |ΦI〉 is doubly excited.
}|Φ0〉 term in the residual equation, where |ΦK〉 is a singly excited state and |ΦI〉 is doubly excited.


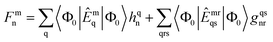
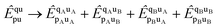
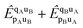 are non-vanishing in the molecule, but are absent in the cluster operators of fragments and the cluster operator is therefore not additively separable in the dissociative limit, which for CCD would require
are non-vanishing in the molecule, but are absent in the cluster operators of fragments and the cluster operator is therefore not additively separable in the dissociative limit, which for CCD would require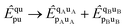
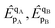 that were absent in NOECCD, size consistency can be restored numerically through the combined action of the singles and doubles. The size-inconsistency errors are reduced to 7 nEH for l-NOECCSD and 4 μEH for q-NOECCSD. While the NOECCSD method is not rigorously size consistent, it is numerically very close to being size consistent in practice. Similar observations have been made by Hanauer and Köhn8 for the ic-MRCC method, where they found that the magnitude of size-inconsistency errors depended critically on the way they removed the redundancies from their working equations. These small size-inconsistency errors may be due in part to the size-extensivity errors introduced by truncating our theory. The fact that q-NOECCSD has a larger error than l-NOECCSD would align with the presence of disconnected terms in the q-NOECCSD equations that do not appear in l-NOECCSD. This suggests that taking the full NOECCSD equations (5-NOECCSD for the Li atom and 6-NOECCSD for the dimer) could remove the errors, although this would be prohibitively expensive in our current version of the code.
that were absent in NOECCD, size consistency can be restored numerically through the combined action of the singles and doubles. The size-inconsistency errors are reduced to 7 nEH for l-NOECCSD and 4 μEH for q-NOECCSD. While the NOECCSD method is not rigorously size consistent, it is numerically very close to being size consistent in practice. Similar observations have been made by Hanauer and Köhn8 for the ic-MRCC method, where they found that the magnitude of size-inconsistency errors depended critically on the way they removed the redundancies from their working equations. These small size-inconsistency errors may be due in part to the size-extensivity errors introduced by truncating our theory. The fact that q-NOECCSD has a larger error than l-NOECCSD would align with the presence of disconnected terms in the q-NOECCSD equations that do not appear in l-NOECCSD. This suggests that taking the full NOECCSD equations (5-NOECCSD for the Li atom and 6-NOECCSD for the dimer) could remove the errors, although this would be prohibitively expensive in our current version of the code.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) consists of all possible excitations from the set of core and active orbitals to the set of active and virtual orbitals. The NOE wave operator {e
consists of all possible excitations from the set of core and active orbitals to the set of active and virtual orbitals. The NOE wave operator {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } is therefore invariant to orbital rotations within each of these sets. If a certain subset of these excitations were excluded, the wave operator ceases to be orbital invariant. Our proposed NOECC method includes all excitations of a given type and therefore retains all orbital invariance properties of the reference CSF.
} is therefore invariant to orbital rotations within each of these sets. If a certain subset of these excitations were excluded, the wave operator ceases to be orbital invariant. Our proposed NOECC method includes all excitations of a given type and therefore retains all orbital invariance properties of the reference CSF.
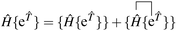
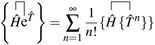
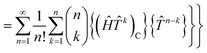
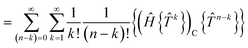
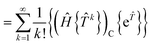
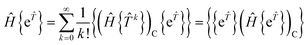
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e
}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e
}|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }(Ĥ{e
}(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C}|Φ0〉 − 〈ΦI|{e
})C}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e
}|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉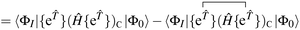
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e
}|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 will also vanish. We then have
}|Φ0〉 will also vanish. We then have![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }(Ĥ{e
}(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 − 〈ΦI|{e
})C|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|(Ĥ{e
}|Φ0〉〈Φ0|(Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉
})C|Φ0〉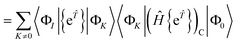
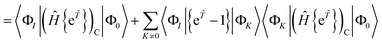
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉 = RK. The disconnected terms vanish at convergence because they are comprised of smaller connected terms that are already solved in our equations. Solving our (not fully connected) equation is equivalent to solving the connected equation
})C|Φ0〉 = RK. The disconnected terms vanish at convergence because they are comprised of smaller connected terms that are already solved in our equations. Solving our (not fully connected) equation is equivalent to solving the connected equation![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C|Φ0〉
})C|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) :
: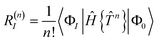
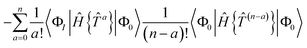
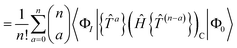
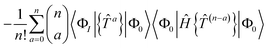
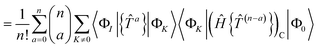
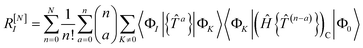
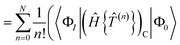
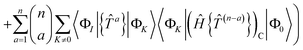
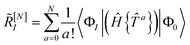
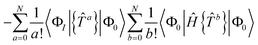
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) a}, R[N]K only has terms up to order N − a, so R[N]K = R[N−a]K and our equation is equivalent to the connected form.
a}, R[N]K only has terms up to order N − a, so R[N]K = R[N−a]K and our equation is equivalent to the connected form.![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } can be expressed as the product of {e
} can be expressed as the product of {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } with a fully connected operator:
} with a fully connected operator:![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = {e
} = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif)
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) is a sum of fully connected terms. This result was first published by Mukherjee,34,35 and we will reproduce the proof here. It is convenient to define the fully connected term
is a sum of fully connected terms. This result was first published by Mukherjee,34,35 and we will reproduce the proof here. It is convenient to define the fully connected term ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = (Ĥ{e
0 = (Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) })C and the modified exponential {ẽ
})C and the modified exponential {ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = {e
} = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − 1}.
− 1}.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) } = {{e
} = {{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0} = {e
0} = {e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif)
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) is the sum of connected terms defined by
is the sum of connected terms defined by![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) = {
= {![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0} − {({ẽ
0} − {({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C}+{({ẽ
0)C}+{({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ
}({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C)C}
0)C)C}![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ
}({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }({ẽ
}({ẽ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0)C)C)C} + …
0)C)C)C} + …![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 − 〈ΦI|{e
}|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|Ĥ{e
}|Φ0〉〈Φ0|Ĥ{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉
}|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 − 〈ΦI|{e
|Φ0〉 − 〈ΦI|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉〈Φ0|{e
}|Φ0〉〈Φ0|{e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }
}![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉
|Φ0〉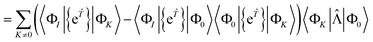
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉
|Φ0〉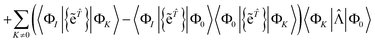
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|Φ0〉 = 1.
}|Φ0〉 = 1.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) }|ΦK〉 = 0, so we can write
}|ΦK〉 = 0, so we can write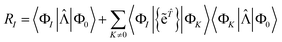
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉 = RK, which vanishes at convergence.
|Φ0〉 = RK, which vanishes at convergence.
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) n to the residual is
n to the residual is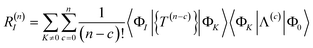
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) .
.
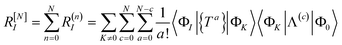
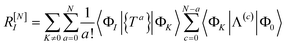
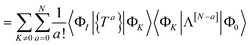
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . Since we have not solved the connected equations 〈ΦK|Λ[N−a]|Φ0〉 = 0 truncated to lower order, the truncation of our equations has once again introduced a size-extensivity error.
. Since we have not solved the connected equations 〈ΦK|Λ[N−a]|Φ0〉 = 0 truncated to lower order, the truncation of our equations has once again introduced a size-extensivity error.
