Imaging of voltage-controlled switching of magnetization in highly magnetostrictive epitaxial Fe–Ga microstructures

Abstract

The magnetoelectric behavior of epitaxial Fe–Ga microstructures on top of a (001)-oriented PMN–PT piezoelectric substrate is imaged with magnetic X-ray microscopy. Additionally, the micron-scale strain distribution in PMN–PT is characterized by X-ray microdiffraction and examined with respect to the results of the Fe–Ga magnetoelectric switching. The magnetic reorientation of Fe–Ga is found to be strongly correlated with size, shape, and crystallographic orientation of the microstructures. In the case of square-shaped structures, size dictates the influence of the strain distribution on both the initialization of the ground state and on the magnetic reorientation during application of voltage. On the other hand, elliptical microstructures demonstrate completely different magnetic responses depending on the relative orientation of their long axis with respect to the crystallographic directions of the PMN–PT. This study demonstrates that engineering the behavior of highly magnetostrictive epitaxial microdevices is possible. It further elucidates that voltage-induced actuation can be largely tuned to achieve the desired type of magnetic switching ranging from vortex circulation reversal, domain wall motion, to a large rotation of magnetization. Because of the outstanding properties of the investigated material system, the reported findings are expected to be of great interest for the realization of next-generation energy-efficient magnetic memory and logic devices.

---

Introduction

The creation of energy-efficient memory and logic devices requires new alternatives to conventional current-based magnetization reversal approaches that suffer from significant energy loss from heating.^1,2 Magnetoelectric multiferroic systems, which allow for the control of magnetization through voltage rather than large currents, have emerged as a promising candidate to lead this transition.^3,4 Specifically, composite multiferroic materials constitute a potential niche for developing the next-generation spintronic devices, in contrast to their single-phase counterparts which are rare under ambient conditions.^5–8 As a result, various multiferroic heterostructures have been proposed in the literature, exhibiting magnetic reorientation driven solely by voltage.^9,10

In composite multiferroic heterostructures, a ferroelectric substrate with a large piezoelectric coefficient is mechanically coupled to a magnetostrictive ferromagnetic layer such that voltage-induced strains in the former are transferred to the latter, modulating its magnetocrystalline anisotropy. Consequently, the larger the magnetostrictive and the piezoelectric coefficients of the constituent elements, the stronger the magnetoelectric effect can be, which is a key feature for device applications. Among transition metals and alloys, materials in the Fe–Ga system (galfenol) have the highest magnetostriction coefficients, with typical values of λ₁₀₀ ≈ 200 × 10⁻⁶ in Fe–Ga.¹¹ These values are rivalled only by rare-earth compounds such as Terfenol-D which is significantly more difficult to fabricate.¹² However, the magnetostrictive coefficient can be limited by the interface quality between the piezoelectric substrate and the ferromagnetic layer, which determines the strain transfer efficiency. Epitaxial growth of the magnetic thin film can potentially optimize the ferromagnetic–piezoelectric interface, enabling a full transfer of the strain generated in the piezoelectric substrate. Several works have reported on multiferroic heterostructures based on epitaxially grown Fe–Ga films, demonstrating impressive electrically driven magnetic reorientation capabilities.^13–16 Nonetheless, they consist of either a continuous thin film or large structures of Fe–Ga, with sizes of tens of micrometers, far from the small features required for the development of memory and logic devices. At smaller scales, down to a few micrometers and below, only polycrystalline Fe–Ga has been reported thus far.^17–20

Here, we study the electrical switching of highly magnetostrictive epitaxial Fe–Ga microstructures, with sizes down to 1 µm, coupled to a piezoelectric substrate, by imaging the magnetic reorientation under magnetic X-ray microscopy. Despite the great potential of such materials for next generation spintronic devices, their magnetoelectric performance at small scales has not been investigated prior to the present study.

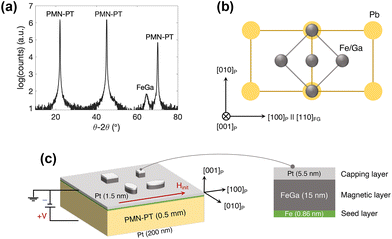
The single crystal epitaxial Fe–Ga film (15 nm thick) with a Ga composition of 24% is grown on single crystal (001)-oriented [Pb(Mg_1/3Nb_2/3)O₃]_0.7–[PbTiO₃]_0.3 (PMN–PT) substrate (TRS ceramics) by molecular beam epitaxy (MBE). A sub-nanometer thick Fe seed layer is used to achieve better crystalline perfection, and a 4 nm Pt capping layer is deposited on top to prevent surface oxidation. The crystallographic structure of the PMN–PT/Fe–Ga heterostructure is characterized by ex situ X-ray diffraction (XRD) θ–2θ scan, and the magnetic properties of the film are measured by vibrating sample magnetometry (VSM) and magnetic spectroscopy (beamline 6.3.1 at the Advanced Light Source) (ESI, Section 1†). Next, the epitaxial thin film is patterned into microstructures of sizes ranging from 6 µm down to 1 µm through electron-beam lithography (EBL) and Ar ion milling. The magnetic switching in the resulting device is imaged under an X-ray magnetic circular dichroism photoemission electron microscopy (XMCD-PEEM) (beamline 11.0.1 at the Advanced Light Source) with an in operando applied voltage. Furthermore, X-ray microdiffraction techniques (beamline 12.3.2 at the Advanced Light Source) are used in order to measure voltage-induced micron-scale strain in the PMN–PT substrate, and to correlate them with the observed magnetic switching in the microstructures. Finally, micromagnetic simulations are performed to qualitatively compare to the experimental results (ESI, Section 4†).

Results and discussion

Crystallographic and magnetic properties of the Fe–Ga thin film

Ex situ X-ray diffraction θ–2θ data in Fig. 1a show a 002 peak near 65° which corresponds to chemically disordered body centered cubic (BCC) structure, i.e. A2 structure, with a lattice parameter of a_Fe–Ga = 2.90 Å.²¹ On the other hand, PMN–PT has a pseudo-cubic lattice structure with a lattice parameter of a_PMN–PT = 4.022 Å.²² In order to minimize the lattice mismatch, Fe–Ga grows with a 45° in-plane rotation with respect to PMN–PT resulting in a lattice mismatch of 1.7% (Fig. S1, ESI†).^15,23 This relationship is shown schematically in Fig. 1b, where the magnetic easy axis along the [110] direction corresponds to the [100] direction of the PMN–PT (crystallographic axes hereafter denoted as [ijk]_FG and [ijk]_P for Fe–Ga and PMN–PT respectively). The magnetic easy axis of the Fe–Ga film determined by VSM (Fig. S2, ESI†) gives a saturation magnetization of 1100 kA m⁻¹.

Fig. 1 (a) Ex situ XRD θ–2θ scan of the multiferroic heterostructure composed of epitaxial (001) Fe–Ga and (001)-oriented PMN–PT. (b) Top-view schematic of the crystallographic orientation of the Fe–Ga cell (grey) with respect to the PMN–PT cell (yellow) (O, Mn, Nb and Ti atoms have been omitted for simplicity). The easy axis of Fe–Ga [110]_FG is aligned with the [100]_P direction of PMN–PT and the Fe–Ga [001]_FG axis is oriented out of plane. (c) Schematic description of the investigated multiferroic system. The PMN–PT has the [001]_P direction parallel to the surface normal, along which voltage is applied. After patterning, the magnetic microstructures are initialized by an external magnetic field, μ₀H_init ≈ 250 mT, applied in the direction as indicated by the red arrow. The multi-layered stack of the microstructures is zoomed in on the right.

Voltage-controlled switching of magnetization

Following the initial characterization of the Fe–Ga thin film, the magnetoelectric behavior of the system is investigated through voltage-controlled magnetization reorientation experiments in patterned microstructures. The Fe–Ga thin film is patterned into squares (lateral size of 1 µm and 2 µm) and ellipses (6 × 3 µm²) with the long axis along [100]_P and [010]_P using standard e-beam photolithography and etching processes. The PMN–PT substrate has the bottom and top surfaces covered with a 200 nm and 1.5 nm layer of Pt respectively, which were sputter-deposited after the initial microstructure patterning. This leaves 1.5 nm of Pt on the majority of the substrate surface, and the microstructures have a total capping layer thickness of 5.5 nm because of the initial 4 nm Pt grown by MBE. These Pt layers serve as the electrodes for voltage application as shown schematically in Fig. 1c. The PMN–PT substrate has the [001]_P crystallographic direction pointing out of the surface plane, along which the voltage is applied experimentally.

The magnetic state of the microstructures is imaged by XMCD-PEEM, probing at the Fe L₃-edge. The results are displayed in Fig. 2. After magnetically initializing the samples by applying an external magnetic field (ramped up to µ₀H_init ≈ 250 mT and down to 0 mT) as indicated in Fig. 2g, the majority of the structures relax into a magnetic flux closure arrangement (Fig. 2a–c). This is clear in the case of 1 µm squares where a magnetic vortex state is nucleated (Fig. 2a). A vortex state was also expected in 2 µm squares. However, 2 µm squares display a bidomain-like configuration with a domain wall (DW) along the diagonal, as shown in Fig. 2b. This can result from residual strains from fabrication processes that could induce a net uniaxial anisotropy along this direction. It has been shown that the configuration of domains in lithographically patterned structures is determined not only by the balance of the magnetocrystalline, magnetoelastic and shape anisotropies, but also by the strain-induced anisotropy term from the fabrication process.²⁴ In fact, the addition of a uniaxial anisotropy term along the diagonal is required in the micromagnetic model to initialize the 2 µm Fe–Ga square in a stable bidomain configuration (ESI, Section 4†). In the case of the ellipses aligned parallel to [100]_P (horizontally oriented in Fig. 2c), they seem to be in a nearly single-domain state with the magnetization along the long axis. This state is favored by shape and magnetocrystalline anisotropy and disrupted only by small light-colored domains (see Fig. 2h for a visual relationship between contrast and magnetic orientation with respect to the incident X-rays in XMCD-PEEM). The formation of these small domains might be due to DW pinning effects at structural imperfections and also due to inhomogeneous strains at the submicron scale, which have been previously measured in PMN–PT.²⁵ On the other hand, the magnetic configuration of the ellipses aligned with the [010]_P direction (vertically oriented in Fig. 2c) exhibits a flux-closure pattern with a characteristic rectangular domain in the center (white colored domain), indicated with more detail in marked PEEM images and in the simulated microstructures (Fig. S5b and S6a of ESI†).

Fig. 2 XMCD-PEEM images at Fe L₃-edge showing the magnetic configuration in epitaxial Fe–Ga microstructures before and after applying voltage: 1 µm squares (a and d), 2 µm squares (b and e), 6 × 3 µm² ellipses aligned along [100]_P (c-3 and f-3) and 3 × 6 µm² ellipses aligned along [010]_P (c-4 and f-4). (g) Sample orientation during XMCD-PEEM experiment: the crystallographic axes correspond to those of PMN–PT, the red arrow indicates the initializing magnetic field (250 mT) applied before the PEEM experiment, and the blue arrow indicates the direction of incident X-rays. (h) Gray scale bar describing the contrast levels of magnetic orientation with respect to the direction of the incident X-rays in the XMCD-PEEM images.

To study the voltage-driven magnetic reorientation in the initialized microstructures, we exploit the piezoelectric properties of the (001)-oriented PMN–PT substrate which, besides enabling epitaxial growth of Fe–Ga, can reach high levels of strain.²⁶ As explained previously, in a multiferroic composite, upon application of voltage the generated strains are transferred to the magnetic layer deposited on top and reorient the direction of the magnetization via the inverse magnetostrictive effect.²⁷ In our system, since Fe–Ga has a positive magnetostriction coefficient,¹¹ the magnetization will tend to align with the tensile strain. Nonetheless, the resulting magnetic anisotropy will not only be governed by voltage-induced magnetoelastic anisotropy, but also by shape and magnetocrystalline anisotropy and other material- and fabrication-related effects (e.g., strain homogeneity, pinning sites, residual strains from fabrication, etc.).

The final magnetic configurations of the Fe–Ga microstructures obtained upon application of voltage along [001]_P are shown in Fig. 2d–f. It should be noted that the voltage values required to trigger the reorientation of magnetization in all the structures range from 0.36 MV m⁻¹ to 0.52 MV m⁻¹, except for the 1 µm squares. Nevertheless, Fig. 2d–f display the images corresponding to the largest applied voltage of 0.76 MV m⁻¹ for it is this voltage that drives a magnetic reorientation in 1 µm squares as well (the whole set of images is available in ESI, Fig. S4†). Compared to the 2 µm squares and the 3 × 6 µm² ellipses, the larger reorientation field observed for the 1 µm squares is consistent with the higher demagnetization energy density associated to the vortex configuration, making them energetically more stable. In fact, not all the 1 µm squares undergo a magnetic reorientation even at 0.76 MV m⁻¹. Fig. 2d is a representative picture of different events observed during the experiment, where some squares remain in the initial vortex state (e.g. square number 1) while others reverse chirality (e.g. square number 2). This switching is particularly interesting due to its potential in data writing and storage applications.²⁸ A similar strain-mediated switching of vortex circulation has been previously observed in 1 µm Co disks on PMN–PT.²⁹ The authors propose that stepwise application of voltage across the sample could lead to a similar effect caused by the application of a time-varying strain, which has been proven to induce vortex circulation reversal in the specific case of epitaxial Fe–Ga microsquares in a theoretical study.³⁰ As for the heterogeneous behavior of the 1 µm squares, we anticipate that the inhomogeneous strain distribution at the submicron scale in the PMN–PT substrate is playing a major role.

In the case of 2 µm squares, application of voltage is observed to curve and shift the DW away from the diagonal as shown in Fig. 2e. A very similar DW motion and curving has been observed in Ni squares of the same size on (011)-cut PMN–PT which is attributed to spatial differences in strain inside the square.²⁵ This is explored in more detail in the following section.

Voltage-driven reorientation of magnetization in the ellipses parallel to [100]_P is observed as a switching from a predominantly dark- (Fig. 2c-3) to a predominantly light-colored domain (Fig. 2f-3) which would imply a 180° rotation of the magnetization (from 180° to 0° in relation with the incident X-rays). However, quantification of the magnetization angle based on XMCD-PEEM images reveals that neither the initial nor the final magnetization directions are completely aligned with the long axis of the ellipse. Fig. 3 serves as a visual example of the magnetic reorientation that takes place in the ellipses parallel to [100]_P. According to the calculations, the initial dark-colored domain (Fig. 3a) and the final light-colored domain (Fig. 3b) form an angle of 146 ± 13° and 59 ± 6° with respect to the incident X-rays direction (these are average values of several ellipses, see ESI, Section 3,† for more details). That is, the reorientation of the magnetization is in reality closer to 90° (Fig. 3c), which is still an outstanding magnetoelectric effect. The calculations of the magnetic angle also show that the ellipses form a more sophisticated multidomain configuration (Fig. S5a†) rather than a single-domain state, which is consistent with the size of the structures. Interestingly, the net magnetization direction of the small light-colored domains that are observed in the initial state, form an angle of about 60° with respect to the X-rays, suggesting they might be the nucleation sites of the magnetic reorientation upon application of voltage.

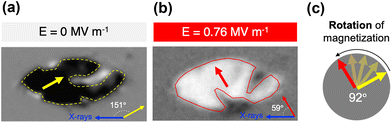Fig. 3 Quantification of the magnetic reorientation in an ellipse oriented along the [100]_P direction (ellipse at the top of Fig. 2c-3 and f-3). (a) Before application of voltage, the magnetization of the major magnetic domain (yellow arrow) forms an angle of 151 ± 14° with respect to the incident X-rays direction (blue arrow). (b) After application of voltage, the magnetization direction (red arrow) and the X-rays form an angle of 59 ± 5°. (c) Schematic representation of the magnetic rotation of 92 ± 15° in the major magnetic domain of the ellipse.

Lastly, in the case of the ellipses with the long axis parallel to [010]_P, application of voltage rearranges the DWs of the initial magnetic flux closure pattern to align along [100]_P which creates a stripe-like domain configuration shown in Fig. 2f-4. This suggests that voltage induces a net tensile strain along [100]_P. Although DWs align with [100]_P, the net direction of magnetization of the domains seem to reorient towards the long vertical axis of the ellipse, that is [010]_P. For instance, the angle of the rectangular light-colored magnetic domain reorients from 31 ± 11° to 64 ± 6° (ESI, Section 3†). The two contrasting effects may be a result of the balance between voltage-induced magnetoelastic anisotropy and shape anisotropy.

Voltage-induced strains in PMN–PT

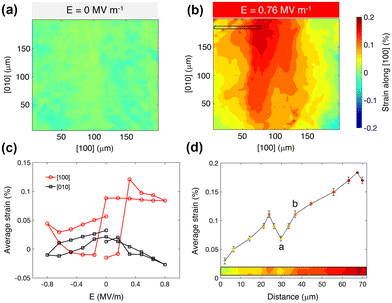
In order to gain a deeper insight into the magnetic reorientation in the microstructures, we perform X-ray microdiffraction of the sample to measure strains with micrometer resolution under an applied voltage.

When voltage is applied along the [001]_P crystallographic direction of the (001)-oriented PMN–PT crystal, the ferroelectric polarization can rotate either by 71°/180° or by 109°. The 71°/180° rotation of the polarization induces a biaxial in-plane compressive strain, whereas the 109° rotation of polarization leads to a uniaxial in-plane tensile strain. Both rotations may take place in different ferroelectric domains in a PMN–PT single crystal.^31,32 The 71°/180° rotation is characterized by a symmetric butterfly-like S–E (strain–voltage) loop, whereas the S–E curve associated to the 109° rotation is an asymmetric butterfly-like loop. The asymmetric butterfly-like loop is, at the same time, composed of a symmetric butterfly-like and a loop-like curve, the latter being related to the net 109° switching.³¹ One advantage of the asymmetric behavior is its non-volatile nature, i.e., it has a remanent strain upon removal of voltage which is highly desired for data storage. So far, the most common reported behavior of (001)-oriented PMN–PT in multiferroic heterostructures is the symmetric one.^33–37 However, works reporting on (001)-oriented PMN–PT with asymmetric behavior are arising in the literature.^32,38,39

The results of (001)-oriented PMN–PT characterization by X-ray microdiffraction are presented in Fig. 4. Fig. 4a and b show the strain maps corresponding to the lattice distortion along [100]_P at 0 MV m⁻¹ and 0.76 MV m⁻¹ respectively. The strain is scanned in a 200 × 200 µm² area underneath the Fe–Ga microstructures. Fig. 4c shows the average strain values along [100]_P and [010]_P as a function of the applied voltage. On the one hand, a tensile strain with an average value of 0.085% is induced along [100]_P. In contrast, the strain profile along [010]_P remains almost unchanged. On the other hand, the S–E curve along [100]_P exhibits an asymmetric butterfly-like loop with a strong loop-like component, further confirming the occurrence of a net 109° polarization switching which would be the origin of the measured tensile strain. Additionally, although the switching field varies from structure to structure (ESI, Fig. S4†), it is always above the coercive field of (001)-oriented PMN–PT of around 0.1–0.2 MV m⁻¹,^31–33,39i.e., the voltage region where 109° rotation of polarization takes place. Therefore, the net tensile strain generated along [100]_P is considered as the main driving force of the observed magnetic switching events in the positive magnetostrictive Fe–Ga. The micromagnetic simulations further confirm this observation by reproducing the qualitative transformation of all the different microstructures by using the measured strains (ESI, Section 4†). Lastly, the non-volatility of the asymmetric behavior, evidenced by the remanent strain along [100]_P in Fig. 4c, is consistent with the non-volatile actuation of the Fe–Ga microstructures, which stay in the electrically activated magnetic configuration after voltage is removed (Fig. S4, ESI†).

Fig. 4 Strain maps corresponding to lattice distortion along [100]_P (a) at 0 MV m⁻¹ and (b) 0.76 MV m⁻¹. (c) S–E curves along the in-plane [100]_P and [010]_P directions. (d) Variation of the strain magnitude at 0.76 MV m⁻¹ along a 70 µm long line, extracted from the strain map in (b).

Another relevant result from the X-ray microdiffraction experiment is that the distribution of the strains is non-uniform, as observed in Fig. 4b and highlighted in Fig. 4d. The absolute difference in strain can be as large as 0.04% between two points that are less than 6 µm apart. For example, the strain value increases by almost 60% from point a to point b indicated in Fig. 4d. Considering that the length of the ellipses is of 6 µm and that the lateral distance between the microstructures is also around 6 µm, this effect can have significant implications on the magnetic reorientation events imaged by XMCD-PEEM. For instance, it could be the main cause of the DW motion and curving in the 2 µm squares. Indeed, as mentioned previously, a similar phenomenon was reported by Lo Conte and co-authors in a multiferroic system composed of Ni squares and (011)-cut PMN–PT.²⁵ They observed that the spatial differences in strain increase with voltage and induce a DW motion, from strain regions with larger anisotropy to regions with smaller anisotropy, which is accompanied by a shortening of the DW, and, thus, by a minimization of its energy. We suspect that a similar mechanism is behind the DW motion in the 2 µm Fe–Ga squares. Furthermore, the non-uniform strain distribution could also explain the heterogeneous magnetoelectric behavior of the 1 µm squares that are 6 µm apart, hence possibly subjected to significantly different magnitudes of strain. A square sitting on a region with larger local strain could experience sufficient stimulus to reverse its vortex circulation, in contrast to another square localized on a region with a lower strain that remains in the same initial state.

The non-uniform strain distribution, attributed to the presence of ferroelectric domains and domain walls that vary spatially and whose influence has been observed in different multiferroic systems,^{25,29,32,40,41} can be considered a limitation as well as an opportunity. For instance, the DW motion observed in the 2 µm squares could be useful for applications since the control of DW propagation in confined structures is recognized for the realization of magnetic logic⁴² and memory schemes.⁴³ This could be potentially feasible, provided certain degree of control over the distribution of the micron-scale strain is achieved, by engineering and pre-characterizing the ferroelectric domains. On the other side, efforts are being made to achieve a more uniform response in multiferroic schemes, for example by reducing interface defects introduced by PMN–PT surface through depositing a thin film polymer between the PMN–PT and the Pt layers.⁴⁴

In contrast to square-shaped microstructures, the voltage-induced magnetic reorientation of the elliptical microstructures does not seem to be strongly affected by strain inhomogeneity. Instead, shape anisotropy and crystallographic orientation of the long axis with respect to PMN–PT axes appear to dominate. The ellipses parallel to [100]_P show the most striking switching event of all, with a experimentally quantified rotation of magnetization close to 90° in the major area of the structure (Fig. 3 and ESI, Section 3†). This is in line with the largest degrees of magnetic reorientation reported in the literature in multiferroic composites based on (001)-oriented PMN–PT.^15,16,37,39 When the applied voltage reaches a value in between 0.36 MV m⁻¹ and 0.52 MV m⁻¹, generating a net tensile strain parallel to the long axis of the ellipse, the net magnetization direction of the largest area rotates by 90°. As mentioned previously, the light-colored domains that are found in the initial state seem to be the nucleation sites of this switching, whose expansion is favored by the voltage-induced strains. On the other hand, if the long axis of the ellipse is perpendicular to [100]_P, the magnetic reorientation is completely different. In this case, when voltage reaches a value in between 0.36 MV m⁻¹ and 0.52 MV m⁻¹, the DWs that are forming the initial flux-closure pattern rearrange to align with the newly induced magnetoelastic anisotropy axis along [100]_P. Meanwhile, voltage-induced strains may be enhancing shape anisotropy which is observed as a reorientation of the net magnetization directions in different domains towards the long axis of the ellipse (quantified in Section 3 of ESI†). The different magnetic reorientations observed in the two types of ellipses not only reveal the importance of shape and orientation of the microstructures in the optimization of the magnetoelectric performance, but also the capability of tuning the magnetoelectric response.

Conclusions

In summary, voltage-driven magnetization switching in single crystal epitaxial Fe–Ga microstructures on top of a (001)-oriented PMN–PT piezoelectric substrate is investigated. The structures are square- or ellipse-shaped, with different crystallographic orientations, and with sizes varying from 6 µm to 1 µm. This setup makes them the smallest epitaxial Fe–Ga structures studied in the context of a multiferroic composite. Accordingly, different magnetoelectric responses are observed depending on the shape and size of the microstructure, from vortex circulation reversal, DW motion or re-alignment, to 90° rotation of magnetization. The magnetic response is primarily governed by voltage-induced strains, influenced by the shape and magnetocrystalline anisotropies, and by a non-uniform strain distribution in the PMN–PT substrate. We show that the balance of those terms can be largely tuned by shape, size and orientation of the Fe–Ga structures. Furthermore the observed non-volatile magnetoelectric actuation, the huge magnetostriction of Fe–Ga and the strong magnetoelastic coupling due to the epitaxial multiferroic interface, makes the investigated heterostructure an almost ideal material system for the realization of energy-efficient electronic devices. One particularly promising application could be data storage. Indeed, 1 μm squares and [100]_P-oriented ellipses can be regarded as individual data storage bits; the out-of-plane component of the magnetic vortex core of the squares (up or down) and the net in-plane magnetization of the ellipses (with a 90° rotation capability) would represent the 0 or 1 of a bit element. On the other hand, the DW propagation observed in the 2 μm squares could be harnessed in a racetrack-like memory scheme, where data bits (DWs) move back and forth intersecting with reading and writing elements.⁴³ Hence, our envisioned multiferroic device would consist of arrays of single crystal Fe–Ga bit elements (either 1 μm squares or [100]_P ellipses) or racetrack-inspired 2D structures on (001)-oriented PMN–PT substrate, where localized strain control could be improved by surface electrodes.⁴⁵ Finally, with the goal of reducing the lateral dimensions of the epitaxial Fe–Ga structures to the nanoscale, P. B. Meisenheimer et al. propose an idealized magnetic bit of 45 × 45 nm², which would be the smallest magnetic size to preserve thermal stability.¹⁵

This work is expected to motivate more experimental studies focused on optimizing and nano-scaling of epitaxial Fe–Ga-based multiferroic composites. Specifically, optimization should prioritize improving the degree of control over the micron-scale strain distribution in the piezoelectric substrate (potentially with the integration of surface electrodes), as well as investigating the reversibility of the magnetoelectric response of the Fe–Ga microstructures.

Experimental section

Deposition of the Fe–Ga thin film

A TRS technologies X2B (001)-oriented [Pb(Mg_1/3Nb_2/3)O₃]_0.7–[PbTiO₃]_0.3 single crystal was polished and used as a substrate onto which an iron seed layer, the Fe–Ga, and the platinum cap was deposited using a Veeco GEN10 MBE system. The PMN–PT was heated to 300 °C inside the chamber before the deposition to prepare the surface, and then it was cooled down to the growth temperature of nominally 50 °C. The iron and gallium were heated in effusion cells and calibrated to the desired fluxes of around 1.8 × 10¹³ atoms per cm² per s for iron and 0.37 × 10¹³ atoms per cm² per s for gallium using a quartz crystal microbalance. A thin iron seed layer was deposited, followed by co-deposition of iron and gallium for the Fe–Ga film. The sample was then left in a vacuum to cool before platinum was deposited without heating at a flux of around 10¹³ atoms per cm² per s using a Telemark electron-beam evaporator located below the MBE main chamber.

Patterning of the Fe–Ga microstructures

To pattern the Fe–Ga microstructures with lateral dimensions ranging from 1 μm to 6 μm, e-beam lithography was used. To prepare the sample for e-beam lithography, MMA/MAA copolymer and PMMA950 were spin coated on to the sample surface. After the e-beam exposure, the sample was developed in MIBK/IPA 1 : 3 and poled through the thickness. Then the sample was etched by argon gas via the ion milling process in an advanced oxide etcher (STS-AOE) to expose the Fe–Ga microstructures and surrounding iron seed layer. The etched sample was then chemically cleaned with acetone, methanol, and isopropanol. Since PEEM requires a reasonable conductive sample surface and the need to prevent the exposed iron seed layer from oxidizing, an additional ∼2 nm thick platinum was deposited by electron beam evaporation right after the etching step on the entire sample surface. The Pt capping layer was then mostly removed via argon ion sputter cleaning in the high vacuum ion milling chamber prior to being transferred into the PEEM3 chamber (beamline 11.0.1.1 of the Advanced Light Source) in order to maximize signal from the Fe–Ga structures under the thinned capping layer.

Author contributions

M. G., Z. X. and R. S. contributed equally to this work. R. S. deposited the Fe–Ga thin film and performed its crystallographic and magnetic characterization. Z. X. carried out XMCD measurements of the Fe–Ga thin film under the supervision of A. T. N., and patterned the Fe–Ga microstructures. M. G. and Z. X. performed the XMCD-PEEM and X-ray microdiffraction measurements, under the supervision of R. V. C. and N. T., respectively. M. G. analysed the XMCD-PEEM and X-ray microdiffraction data with the help of R. V. C. and N. T., respectively. V. E. carried out the micromagnetic simulations. M. G. wrote the original draft of the manuscript; R. S. and Z. X. contributed with the critical review; V. E. helped with editing. R. N. C., D. G. S., A. S. and J. B. coordinated the project and provided financial support.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the support from the NSF Nanosystems Engineering Research Center for Translational Applications of Nanoscale Systems (TANMS) under the Cooperative Agreement Award No. EEC-1160504. The work at the Advanced Light Source at Lawrence Berkeley National Laboratory (XMCD-PEEM at beamline 11.0.1, X-ray microdiffraction at beamline 12.3.2 and X-ray magnetic spectroscopy at beamlines 4.0.2 and 6.3.1) is supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy, under contract number DE-AC02-05CH11231. Z. X. acknowledges the support of the ALS Doctoral Fellowship in Residence for part of the work carried out at the ALS. M. G. acknowledges the support from the Ministry of Science and Innovation of the Spanish Government (grant PID2020-115704RB-C32). We also acknowledge the use of the fabrication facility at the Integrated Systems Nanofabrication Cleanroom of the California NanoSystems Institute.

References

1. A. Brataas, A. D. Kent and H. Ohno, Nat. Mater., 2012, 11, 372.
2. M. Baumgartner, K. Garello, J. Mendil, C. O. Avci, E. Grimaldi, C. Murer, J. Feng, M. Gabureac, C. Stamm, Y. Acremann, S. Finizio, S. Wintz, J. Raabe and P. Gambardella, Nat. Nanotechnol., 2017, 12, 980.
3. M. Bibes and A. Barthélémy, Nat. Mater., 2008, 7, 425.
4. S. Manipatruni, D. E. Nikonov, C.-C. Lin, T. A. Gosavi, H. Liu, B. Prasad, Y.-L. Huang, E. Bonturim, R. Rames and I. A. Young, Nature, 2019, 565, 35.
5. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694.
6. W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759.
7. N. Spaldin and M. Fiebig, Science, 2005, 309, 391.
8. R. Ramesh, Nature, 2009, 461, 1218.
9. P. B. Meisenheimer, S. Novakov, N. M. Vu and J. T. Heron, J. Appl. Phys., 2018, 123, 240901.
10. J.-M. Hu, L.-Q. Chen and C. W. Nan, Adv. Mater., 2016, 26, 15.
11. A. E. Clark, K. B. Hathaway, M. Wun-Fogle, J. B. Restorff, T. A. Lograsso, V. M. Keppens, G. Petculescu and R. A. Taylor, J. Appl. Phys., 2003, 93, 8621.
12. C. W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103, 031101.
13. D. E. Parkes, S. A. Cavill, A. T. Hindmarch, P. Wadley, F. McGee, C. R. Staddon, K. W. Edmonds, R. P. Campion, B. L. Gallagher and A. W. Rushforth, Appl. Phys. Lett., 2012, 101, 072402.
14. S. A. Cavill, D. E. Parkes, J. Miguel, S. S. Dhesi, K. W. Edmonds, R. P. Campion and A. W. Rushforth, Appl. Phys. Lett., 2013, 102, 032405.
15. P. B. Meisenheimer, R. A. Steinhard, S. H. Sung, L. D. Williams, S. Zhuang, M. E. Nowakowski, S. Novakov, M. M. Torunbalci, B. Prasad, C. J. Zollner, Z. Wang, N. M. Dawley, J. Schubert, A. H. Hunter, S. Manipatruni, D. E. Nikonov, I. A. Young, L. Q. Chen, J. Bokor, S. A. Bhave, R. Ramesh, J.-M. Hu, E. Kioupakis, R. Hovden, D. G. Schlom and J. T. Heron, Nat. Commun., 2021, 12, 2757.
16. A. Begué and M. Ciria, ACS Appl. Mater. Interfaces, 2021, 13, 6778.
17. H. Ahmad, J. Atulasimha and S. Bandyopadhyay, Nanotechnology, 2015, 26, 401001.
18. H. Ahmad, J. Atulasimha and S. Bandyopadhyay, Sci. Rep., 2016, 5, 18264.
19. Z. Xiao, R. Khojah, M. Chooljian, R. Lo Conte, J. D. Schneider, K. Fitzell, R. V. Chopdekar, Y. Wang, A. Scholl, J. Chang, G. P. Carman, J. Bokor, D. Di Carlo and R. N. Candler, Multifunct. Mater., 2018, 1, 014004.
20. M. Guevara De Jesus, Z. Xiao, M. Goiriena-Goikoetxea, R. V. Chopdekar, M. K. Panduranga, P. Shirazi, A. Acosta, J. P. Chang, J. Bokor and G. P. Carman, Smart Mater. Struct., 2022, 31, 035005.
21. M. Ciria, M. G. Proietti, E. C. Corredor, D. Coffey, A. Begué, C. de la Fuente, J. I. Arnaudas and A. Ibarra, J. Alloys Compd., 2018, 767, 905.
22. A. A. Levin, D. C. Meyer, C. Thiele and P. Paufler, Appl. Phys. A, 2006, 84, 37.
23. D. Seguin, M. Sunder, L. Krishna, A. Tatarenko and P. D. Moran, J. Cryst. Growth, 2009, 311, 3235.
24. R. P. Beardsley, D. E. Parkes, J. Zemen, S. Bowe, K. W. Edmonds, C. Reardon, F. Maccherozzi, I. Isakov, P. A. Warburton, R. P. Campion, B. L. Gallagher, S. A. Cavill and A. W. Rushforth, Sci. Rep., 2017, 7, 42107.
25. R. Lo Conte, Z. Xiao, C. Chen, C. V. Stan, J. Gorchon, A. El-Ghazaly, M. E. Nowakowski, H. Sohn, A. Pattabi, A. Scholl, N. Tamura, A. Sepulveda, G. P. Carman, R. N. Candler and J. Bokor, Nano Lett., 2018, 18, 1952.
26. S.-E. Park and T. R. Shrout, J. Appl. Phys., 1997, 82, 1804.
27. E. W. Lee, Rep. Prog. Phys., 1955, 18, 184.
28. B. Van Waeyenberge, A. Puzic, H. Stoll, K. W. Chou, T. Tyliszczak, R. Hertel, M. Fähnle, H. Brückl, K. Rott, G. Reiss, I. Neudecker, D. Weiss, C. H. Back and G. Schütz, Nature, 2006, 444, 461.
29. Q. Li, A. Tan, A. Scholl, A. T. Young, M. Yang, C. Hwang, A. T. N'Diaye, E. Arenholz, J. Li and Z. Q. Qiu, Appl. Phys. Lett., 2017, 110, 262405.
30. T. A. Ostler, R. Cuadrado, R. W. Chantrell, A. W. Rushforth and S. A. Cavill, Phys. Rev. Lett., 2015, 115, 067202.
31. L. Yang, Y. Zhao, S. Zhang, P. Li, Y. Gao, Y. Yang, H. Huang, P. Miao, Y. Liu, A. Chen, C. W. Nan and C. Gao, Sci. Rep., 2015, 4, 4591.
32. Y. Ba, Y. Liu, P. Li, L. Wu, J. Unguris, D. T. Pierce, D. Yang, C. Feng, Y. Zhang, H. Wu, D. Li, Y. Chang, J. Zhang, X. Han, J. Cai, C.-W. Nan and Y. Zhao, Adv. Funct. Mater., 2018, 28, 1706448.
33. C. Thiele, K. Dörr, O. Bilani, J. Rödel and L. Schultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054408.
34. O. Bilani-Zeneli, A. D. Rata, A. Herklotz, O. Mieth, L. M. Eng, L. Schultz, M. D. Biegalski, H. M. Christen and K. Dörr, J. Appl. Phys., 2008, 104, 054108.
35. J.-H. Kim, K.-S. Ryu, J.-W. Jeong and S.-C. Shin, Appl. Phys. Lett., 2010, 97, 252508.
36. W.-C. Tsai, S.-C. Liao, K.-F. Huang, D.-S. Wang and C.-H. Lai, Appl. Phys. Lett., 2013, 103, 252405.
37. Z. Zhao, M. Jamali, N. D'Souza, D. Zhang, S. Bandyopadhyay, J. Atulasimha and J.-P. Wang, Appl. Phys. Lett., 2016, 109, 092403.
38. S. Zhang, Y. G. Zhao, P. S. Li, J. J. Yang, S. Rizwan, J. X. Zhang, J. Seidel, T. L. Qu, Y. J. Yang, Z. L. Luo, Q. He, T. Zou, Q. P. Chen, J. W. Wang, L. F. Yang, Y. Sun, Y. Z. Wu, X. Xiao, X. F. Jin, J. Huang, C. Gao, X. F. Han and R. Ramesh, Phys. Rev. Lett., 2012, 108, 137203.
39. X. Guo, Y. Zuo, D. Li, B. Cui, K. Wu, J. Yun, T. Wang and L. Xi, Appl. Phys. Rev., 2016, 108, 042403.
40. H. Sohn, M. E. Nowakowski, C.-Y. Liang, J. L. Hockel, K. Wetzlar, S. Keller, B. M. McLellan, M. A. Marcus, A. Doran, A. Young, M. Klaüi, G. P. Carman, J. Bokor and R. N. Candler, ACS Nano, 2015, 9, 4814.
41. M. Buzzi, R. V. Chopdekar, J. L. Hockel, A. Bur, T. Wu, N. Pilet, P. Warnicke, G. P. Carman, L. J. Heyderman and F. Nolting, Phys. Rev. Lett., 2013, 111, 027204.
42. D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit and R. P. Cowburn, Science, 2005, 309, 1688.
43. S. S. P. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190.
44. Z. Xiao, K. P. Mohanchandra, R. Lo Conte, C. Ty Karaba, J. D. Schneider, A. Chavez, S. Tiwari, H. Sohn, M. E. Nowakowski, A. Scholl, S. H. Tolbert, J. Bokor, G. P. Carman and R. N. Candler, AIP Adv., 2018, 8, 055907.
45. Z. Xiao, C. Lai, R. Zheng, M. Goiriena-Goikoetxea, N. Tamura, C. Torres Juarez, C. Perry, H. Singh, J. Bokor, G. P. Carman and R. N. Candler, Appl. Phys. Lett., 2021, 118, 182901.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic and magnetic characterization of the Fe–Ga thin film (ESI1), stepwise voltage-induced reorientation of magnetization (ESI2), quantitative analysis of the magnetic moment reorientation angle based on XMCD-PEEM images (ESI3), micromagnetic simulations of the magnetoelectric behaviour (ESI4). See DOI: https://doi.org/10.1039/d4nr00739e

---