Open Access Article
Open Access ArticleExploring the effect of the covalent functionalization in graphene-antimonene heterostructures†
M. Fickert‡
a,
R. Martinez-Haya‡ b,
A. M. Ruiz
b,
A. M. Ruiz b,
J. J. Baldoví
b,
J. J. Baldoví b and
G. Abellán
b and
G. Abellán *b
*b
aDepartment of Chemistry and Pharmacy, Joint Institute of Advanced Materials and Processes (ZMP), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Fürth 90762, Germany
bInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, Valencia 46980, Spain. E-mail: gonzalo.abellan@uv.es
First published on 26th April 2024
Abstract
The growing field of two-dimensional (2D) materials has recently witnessed the emergence of heterostructures, however those combining monoelemental layered materials remain relatively unexplored. In this study, we present the chemical fabrication and characterization of a heterostructure formed by graphene and hexagonal antimonene. The interaction between these 2D materials is thoroughly examined through Raman spectroscopy and first-principles calculations, revealing that this can be considered as a van der Waals heterostructure. Furthermore, we have explored the influence of the antimonene 2D material on the reactivity of graphene by studying the laser-induced covalent functionalization of the graphene surface. Our findings indicate distinct degrees of functionalization based on the underlying material, SiO2 being more reactive than antimonene, opening the door for the development of controlled patterning in devices based on these heterostructures. This covalent functionalization implies a high control over the chemical information that can be stored but also removed on graphene surfaces, and its use as a patterned heterostructure based on antimonene and graphene. This research provides valuable insights into the antimonene–graphene interactions and their impact on the chemical reactivity during graphene covalent functionalization.
1. Introduction
The interest in two-dimensional (2D) materials has risen exponentially in the last years and, what is more, this trend is expected to continue growing.1,2 Beyond that, the combination of different 2D materials is even more revolutionary, since the resulting heterostructures could meet the properties of each component or even exhibit new ones derived from their interaction.3,4 In this context, a crucial aspect involves comprehending the interactions between 2D materials to envision their potential applications.5Exciting examples of heterostructures have recently been reported by using various multielemental 2D materials, including hexagonal boron nitride (hBN), transition metal dichalcogenides (TMD), and MXenes, as building blocks. Indeed, combinations like hBN/TMD,6 TMD/TMD,7–9 Ti2C/Ta2C,10 or a blend of a multielemental 2D material with a monoelemental one, such as hBN/graphene,11,12 TMD/graphene,13–20 or TMD/phosphorene21 have showcased the potential of these artificial hybrids, pushing the limits of new materials. However, the experimental studies involving heterostructures formed by two monoelemental 2D materials are scarcer,22–27 computational ones being the most abundant. In this regard, graphene is probably the most studied 2D building block and its reactivity is well stablished in the literature. Specifically, works on graphene/silicene,28,29 graphene/phosphorene,30–34 graphene/antimonene35–40 or antimonene/germanene41 have been reported. Within the realm of the 2D-pnictogens, the heavy ones (Sb42,43 and Bi44) are particularly interesting because of their pronounced interlayer interactions, inasmuch their atomic orbitals between individual layers contribute to a strong covalent character, surpassing the typical van der Waals (vdW) interaction. In this context, antimonene emerges as an ideal candidate for the preparation of this sort of heterostructure because it can be produced either by top-down (micromechanical exfoliation or liquid phase exfoliation, among others), or bottom-up (epitaxial growth and solution-phase synthesis) approaches.43 Among these, the colloidal synthesis yields high-quality, ultrathin antimonene hexagons, making it particularly appealing for constructing 2D heterostructures. Moreover, the impact of combining graphene with a quasi-van der Waals 2D material such as antimonene on the chemical reactivity of the former remains unexplored. Besides, within this strategy, we can take advantage of the well-stablished reactivity of graphene to address a proper description of the antimonene reactivity.
In this contribution, we fabricated a graphene-antimonene heterostructure combining CVD graphene with antimonene hexagons. Following structural and spectroscopic characterization, a covalent reaction scheme was explored, revealing that the reactivity of graphene towards benzyl radical molecules—derived from dibenzoyl peroxide (DBPO)—is lower in the case of the graphene-antimonene heterostructure compared to pristine graphene supported on Si/SiO2 substrates. Moreover, by means of DFT calculations we rationalized the nature of the interactions between the 2D materials, highlighting their predominant vdW character. This work provides valuable insights into the interactions between antimonene and graphene, as well as their impact on the chemical reactivity during graphene covalent functionalization. Last but not least, towards this precise covalent 2D patterning of graphene, a controlled double chemical laser writing can be achieved: the benzyl—graphene functionalization and its subsequent antaratopic bonding between graphene and antimonene. Moreover, this covalent functionalization is entirely reversible, which implies the write/read/erase control over the chemical information provided by the covalent functionalization on the graphene surface.
2. Experimental
2.1. Chemicals and materials
SbCl3,1-octadecene (ODE), 1-dodecanethiol (DDT), oleylamine (OA), dibenzoyl peroxide (DBPO), acetone, dichloromethane (DCM) and chloroform (CHCl3) were purchased from Sigma–Aldrich. Graphene monolayers (Trivial Transfer® Graphene) were purchased by ACSMaterial. Si/SiO2 substrates with an oxide layer thickness of 300 nm was bought and cut into 10 × 10 mm wafer by the “Fraunhofer-Institut für Integrierte Schaltungen IIS” in Erlangen. Additionally, the substrates were bath sonicated in acetone for 5 min and in isopropanol for 5 min. Subsequently, the Si/SiO2 wafer were dried using an argon flow.2.2. Instrumentation
An MB-Labmaster Pro DP glovebox (MBraun) was used to achieve an argon atmosphere with less than 0.1 ppm of water and less than 0.1 ppm of oxygen. The glovebox is equipped with a gas purification system to remove gasses like O2 and H2O as well as solvent vapor. Additionally, the system has an oxygen sensor and a water sensor to determine the respective content. Atomic force microscopy was carried out using a Bruker Dimension Icon microscope in scan-assist-mode. A Bruker ScanAsyst-Air silicon tip with a diameter of around 10 nm was used to obtain images with a resolution of 512 × 512 or 1024 × 1024 pixels. The Gwydion software was used for post-processing like flattening, image correction and extraction of the corresponding thicknesses and lengths. Raman spectroscopic characterization was carried out with a Horiba LabRAM Aramis confocal Raman microscope. The system was equipped with laser of the wavelength λ = 532 nm. The laser spot size was ca. 1 μm (objective: Olympus LMPlanFI 100×, NA 0.80) and the grating was 1800 or 600. The system has a filter wheel that can reduce the laser energy from 100% to 50%, 25%, 10%, 5%, 3.2%, 1%, 0.1% or 0.01%. Temperature-dependent Raman measurements were performed using a Linkam stage THMS 600, equipped with a liquid nitrogen pump TMS94 for temperature stabilization. A constant flow of nitrogen was applied to remove the oxygen in the chamber and to maintain an inert atmosphere. The samples were measured using a grating of 1800, a heating rate of 10 °C min−1 and an objective with a magnification of 50×. After each heating step, a waiting period of 5 minutes ensured the temperature stabilization of the sample. Furthermore, the laser energy was kept as low as possible to avoid damaging the flake. For the functionalization and the following characterization of the Sb hexagonal NS and graphene hybrid, a WITec alpha300R confocal microscope equipped with an XYZ table was used. The laser wavelength was 532 nm. For the functionalization a 5 × 5 μm map with 20 × 20 points, an acquisition time of 1 s and a laser power of 1 mW were used. For the following temperature dependent Raman measurements, a 5 × 5 μm map with 20 × 20 points, an acquisition time of 1 s and a laser power of 1.5 mW was used. For this experiment a higher laser power was used, since the laser had to go through the extra window of the Linkam stage, which reduces the energy that reaches the sample. Computational details: we carried out spin polarized density-functional theory (DFT) calculations within the generalized gradient approximation on single-layer Sb and graphene using the Quantum ESPRESSO package.45 The atomic coordinates and lattice parameters were fully optimized using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the forces on each atom were smaller than 1 × 10−3 Ry au−1 and the energy difference between two consecutive relaxation steps was less than 1 × 10−4 Ry. The electronic wave functions were expanded with well-converged kinetic energy cut-offs for the wave functions (charge density) of 40 (350) Ry. A vacuum spacing of 22 Å was set along c direction to avoid unphysical interlayer interactions. The Brillouin zone was sampled by a fine Γ-centered 8 × 8 × 1 k-point Monkhorst–Pack.46 We employed fully relativistic ultrasoft pseudopotentials to account for spin–orbit coupling effects. For the heterostructure Sb/graphene, we constructed supercells of dimensions 1 × 1 and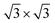 for Sb and graphene, respectively. The dimensions of the supercell were necessary to ensure a minimum mismatch between both lattices (∼3%). Grimme-D2 dispersion corrections were added in order to account for van der Waals interactions between the different systems in the heterostructures.47 We considered the chemical functionalization of Sb with an hexanethiol chain (thus forming a Sb–S covalent bond), the latter formed by one atom of S, 6C and 13H.
for Sb and graphene, respectively. The dimensions of the supercell were necessary to ensure a minimum mismatch between both lattices (∼3%). Grimme-D2 dispersion corrections were added in order to account for van der Waals interactions between the different systems in the heterostructures.47 We considered the chemical functionalization of Sb with an hexanethiol chain (thus forming a Sb–S covalent bond), the latter formed by one atom of S, 6C and 13H.
2.3. Synthesis of Sb hexagonal nanosheets
The Sb hexagonal nanosheets were prepared according to a two-step procedure reported in literature.48,49 Briefly: the first step consists of the preparation of the Sb-DDT precursor. For this, vacuum was applied to a 50 mL nitrogen round flask with a stopcock. Afterwards, the flask was heated with a heat gun, after which the flask was filled with argon. These steps (evacuating/heating/refilling with argon) were repeated three times to remove all residues of water and oxygen in the flask. After cooling down to room temperature SbCl3 (0.91 g, 4 mmol), ODE (6 mL) and DDT (4 mL) were added. The flask was sealed with a septum and heated to 110 °C while stirring continuously. Then vacuum was applied for two hours to degas the chemicals. Afterwards, argon was introduced in the flask and the temperature was increased to 150 °C to let all DDT react with SbCl3. At this point, the precursor solution has a yellow color. After cooling down to room temperature, the precursor precipitates out of the solution as a white solid. Therefore, the mixture must be heated to minimum 60 °C until all of the Sb-DDT precursor is dissolved again before it can be used for further reactions. The second step consists of the synthesis of hexagonal antimonene nanosheets. Herein, OA (0.5 mL) and ODE (4.0 mL) were added in a 3-neck flask equipped with a septum, a condenser and a nitrogen adapter. Similar to the Sb-DDT precursor the OA and ODE mixture was degassed at 110 °C for 30 minutes. Afterwards, the apparatus was flushed with argon and a bubbler was put on the condenser, so that pressure equalization can take place. Thereafter, the reaction mixture was heated to 300 °C, whereupon Sb-DDT (1 mL) was injected. After 10 s at 300 °C the flask was cooled down rapidly using a water-ice bath. To obtain clean and well-defined hexagons, a solvent exchange was performed to remove all residues of unreacted chemicals. The sample was centrifuged (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 5 min) and the solvent mixture was exchanged with CHCl3. This was repeated two additional times to obtain the Sb hexagonal NSs in CHCl3.
000 rpm for 5 min) and the solvent mixture was exchanged with CHCl3. This was repeated two additional times to obtain the Sb hexagonal NSs in CHCl3.
2.4. Preparation of the Sb NS/graphene hybrid
A dispersion of Sb hexagonal NSs in CHCl3 was drop casted onto Si/SiO2 wafer. In the next step, graphene was transferred with a wet chemical transfer method. Thereby, the graphene monolayer was made to float on bi-distilled water, whereupon the prepared Si/SiO2 wafer with Sb NS was used to fish the graphene layer. Bi-distilled water was used to avoid any contaminations. After the transfer on the Si/SiO2 wafer the graphene was backed in a vacuum drying oven to remove the residues of water. The temperature of the oven was increased slowly over 30 min from 30 °C to 80 °C to avoid damaging the graphene layer. Thereon, the baking process continued for 16 h at 80 °C. In the end, the PMMA protective layer of the commercial graphene monolayer was removed with acetone vapor (90 min) and the wafer was dried with airflow.2.5. Functionalization of graphene on top of Sb hexagonal NS
For the functionalization of graphene on top of the hexagonal NS an easy method using DBPO and a laser with a wavelength of 532 nm was used. For this functionalization, a WITec Raman setup was used. A solution of DBPO (0.242 mg) in DCM (10 mL) with a concentration of 0.0001 mol L−1 was prepared. Next, the solution was drop casted on previously prepared Si/SiO2 wafer with Sb hexagonal NSs and graphene on the surface, resulting in a coverage of the whole wafer. Then, the material was irradiated with the laser beam (λ = 532 nm) at 1 mW with 1 second pulses, at room temperature and under atmospheric conditions. After the solvent evaporated, the wafer shows a homogeneous coating of DBPO on the surface. After functionalization the DBPO was removed by putting the wafer in a flask with DCM and sonicating it for 10 s in a bath using the lowest power possible. In the following, the surface was cleaned with ten additional drops of DCM and the surface was dried using an airflow.3. Results and discussion
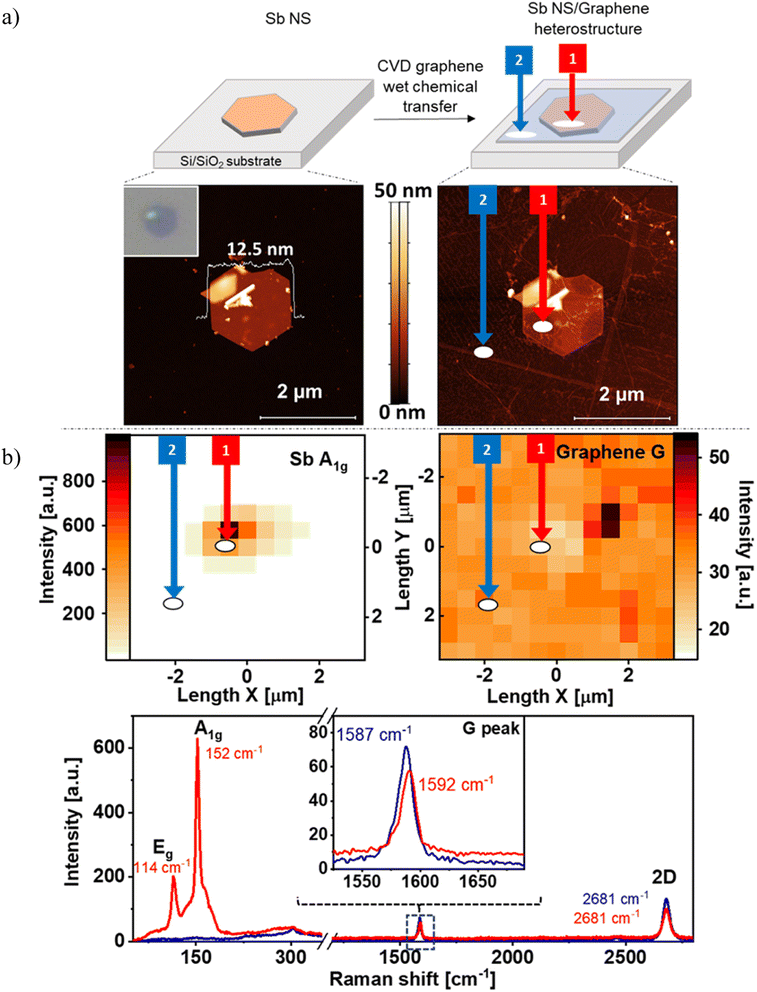
3.1. Sb NSs and graphene hybrids production
Our research starts with the production of the antimonene hexagonal nanosheets (Sb NS), following the colloidal synthesis procedure, and its ulterior combination with monolayer CVD graphene to finally form the desired heterostructures. Specifically, the novel Sb/graphene heterostructure was prepared in three steps. First, we synthetized the Sb hexagons using our optimized protocol.42 Secondly, we drop-casted the colloidal dispersion onto a Si/SiO2 substrate (Fig. 1a top) and the optical observation, as depicted in the inset of Fig. 1a bottom left, revealed the thin height of this hexagon, indicated by its deep purple color. The bright yellow area in the top left part of the nanosheet corresponds to an overlapped section of another Sb nanosheet. Indeed, AFM measurements of the same image exhibit a thickness of only 12.5 nm together with the fragment of the overlapped NS and some bulk material in the middle of the flake, see Fig. 1a bottom left. This hexagonal Sb NS served as the bottom layer of the hybrid structure. Finally, CVD graphene was transferred on top of the Sb NS using a wet chemical transfer method. As a result, not only the whole Sb flake was covered with a thin graphene layer, but also the SiO2/Si substrate, as can be seen in Fig. 1a top. The AFM of the hybrid reveals that some parts of graphene at the right and the left side of the Sb NS overlaps better with the Sb NS than in the center of it, which seems to include a hollow space, see Fig. 1a bottom left. This is related to some solvent impurities on the top side of the Sb flake, hindering the uniform distribution of graphene across the entire sample.Subsequently, Raman measurements were conducted to examine the interactions resulting from the overlap of the two elemental layers. The Raman maps of the hybrid can be seen in Fig. 1b top showing the intensity of the A1g-peak of Sb and the G-peak of graphene. The Sb NS can be observed in the middle of the map with a good intensity. On the other hand, the Raman signal of the G-peak of graphene is present everywhere as expected, nevertheless, the intensity of this signal exhibits a slight decrease at the position of the Sb nanosheet. Those statements are even clearer when comparing the mean Raman spectra at the area of the prepared Sb NS/graphene hybrid (circled area labeled as 1) with the area located at the bottom of the waffle (circled area labeled as 2), where there is not Sb NS but a thin layer of the transferred graphene. Fig. 1b bottom left shows the region where typical bulk Sb signals can be found at 110 cm−1 (Eg peak) and 150 cm−1 (A1g peak, red trace, area 1). Furthermore, a broad shoulder at higher wavenumbers and a signal between the main Sb signals is present at ca. 130 cm−1. Actually, a monolayer of antimonene shows an average heigh of ca. 0.9 nm (ref. 50 and 51) and few-layer antimonene displays a blueshift in Raman bands43 in agreement with AFM. Next, the mean Raman spectra in the region between 1200–2800 cm−1 reveals the G and the 2D peaks, see Fig. 1b bottom right. In both recorded areas (1, Sb NS/graphene hybrid vs. 2, pristine graphene) the intensities of both peaks are higher for pristine graphene (blue trace) than those of the Sb NS/graphene hybrid (red trace). Indeed, the graphene signals at the Sb NS/graphene hybrid reach only 80% of the intensity of pristine graphene. This attenuation of the Raman signal is attributed to an interaction between the two distinct 2D materials. This interaction suggests a non-covalent interaction inasmuch there is no appreciable sp2 defects, since no D-peak is observed and no covalent addends are present.52 Moreover, a slight shift in the G peak is observed when comparing both signals (see inset of Fig. 1b bottom) that may involve a charge transfer interaction.53–55
In order to clarify if the weak shift observed at the G peak in the Raman spectrum involves a real electron transfer interaction between both materials, first-principles calculations were performed. Firstly, we studied the structural and electronic properties of single layers Sb and graphene. Our DFT calculations predicted lattice parameters values of a = b = 4.12 Å for monolayer Sb and a = b = 2.47 Å in case of graphene, which agree well with previous reports.56,57 Then, we calculated the electronic band structure of Sb (graphene) along the high symmetry points K–Γ–M–K (Γ–K–M–Γ) for the hexagonal unit cell. From the band structures we can conclude that single layer Sb presents a semiconductor behaviour, with an indirect semiconducting band gap of around 0.9 eV. On the other hand, graphene shows a semimetallic character where a massless Dirac cone can be observed at K (see Fig. S1†). Note that, for simplicity, in our heterostructure we computed a single layer of Sb instead of nanosheets of Sb (as experimentally observed), which represents an efficient model to analyse the interactions between Sb and graphene.
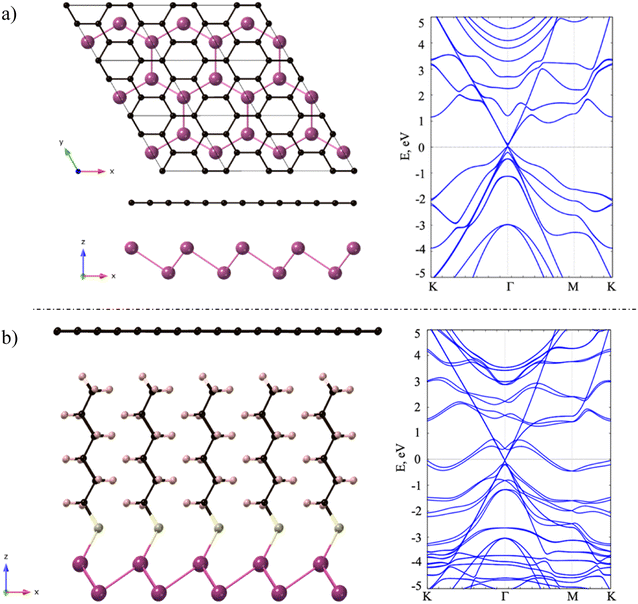
Next, we investigated the deposition of graphene above a single layer of Sb forming a heterostructure. For such purpose, we aimed to generate the most compact supercell configurations for each system that accurately represent their lattice structures and capture important attributes of their stress-free structures. Thus, we constructed a supercell of dimensions of 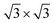 of graphene, meanwhile a 1 × 1 unit cell of Sb was enough to create such heterostructures. As we are mainly interested in the properties of Sb, the lattice parameters of our heterostructure are a = b = 4.12 Å. In the case of stress-free graphene, the values of a = b = 4.28 Å (for a
of graphene, meanwhile a 1 × 1 unit cell of Sb was enough to create such heterostructures. As we are mainly interested in the properties of Sb, the lattice parameters of our heterostructure are a = b = 4.12 Å. In the case of stress-free graphene, the values of a = b = 4.28 Å (for a 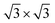 supercell), and the graphene is compressed to have values of a = b = 4.12 Å (thus resulting in a 3.9% of reduction) to match the lattice of Sb. We studied two possible stacking configurations of graphene over Sb. For the first case of study, we considered that one Sb atom is below one atom of C (site A), see Fig. S2,† meanwhile in the second case we considered that one Sb atom is placed below the centre of the hexagon of graphene (site B), see Fig. 2a left. We optimized the atomic coordinates for the two proposed configurations and obtained the most stable one by means of total energy difference. Our calculations predict that site B is the most stable structure with a difference of energy of ΔE = 2.46 meV per atom with respect to site A. The distance between Sb and graphene was found to be 3.49 Å and 3.40 Å for site A and B, respectively. Furthermore, for the most stable heterostructure (site B), we calculated its electronic band structure along the high symmetry path K–Γ–M–K (Fig. 2a right). Note that due to the new dimensions of the cell of graphene (
supercell), and the graphene is compressed to have values of a = b = 4.12 Å (thus resulting in a 3.9% of reduction) to match the lattice of Sb. We studied two possible stacking configurations of graphene over Sb. For the first case of study, we considered that one Sb atom is below one atom of C (site A), see Fig. S2,† meanwhile in the second case we considered that one Sb atom is placed below the centre of the hexagon of graphene (site B), see Fig. 2a left. We optimized the atomic coordinates for the two proposed configurations and obtained the most stable one by means of total energy difference. Our calculations predict that site B is the most stable structure with a difference of energy of ΔE = 2.46 meV per atom with respect to site A. The distance between Sb and graphene was found to be 3.49 Å and 3.40 Å for site A and B, respectively. Furthermore, for the most stable heterostructure (site B), we calculated its electronic band structure along the high symmetry path K–Γ–M–K (Fig. 2a right). Note that due to the new dimensions of the cell of graphene (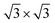 ), the Dirac cone is translated from K to Γ. From the result of the band structure, we can conclude that there is no charge transfer between both components of the heterostructure, as the Dirac cone of graphene remains localized at the Fermi level.
), the Dirac cone is translated from K to Γ. From the result of the band structure, we can conclude that there is no charge transfer between both components of the heterostructure, as the Dirac cone of graphene remains localized at the Fermi level.
To confirm the absence of charge transfer in the heterostructure we computed a Bader charge transfer analysis for the most stable configuration (site B). This allows to quantify the electron density flow along the heterostructure. We observe that there is only a negligible number of electrons gained by graphene (0.0185 e− per cell) and depleted from Sb (−0.0185 e− per cell), see Table S1 of the ESI.† The analysis reveals that the overall transferred electrons is zero, as expected in a neutral system. Furthermore, it also reveals that the charge flows from Sb to C, as would be expected from the higher electron affinity of the latter.
Once demonstrated that there is no charge transfer between Sb and graphene in the described heterostructure, we analysed the properties of a Sb/graphene heterostructure where the former is functionalized with an hexanethiol chain using the same stacking that in the pristine Sb/graphene heterostructure (Fig. 2b left).42,44 Note that after performing the relaxation of the heterostructure the bond length Sb–S is 2.55 Å, resulting in a covalent attachment of the sulfur to the terminated Sb. On the other hand, the spacing between the terminal H atom of the hexanethiol chain and the graphene is 2.62 Å. In this case the interfacial interactions are mainly governed by van der Waals (vdW) forces.
We calculated the electronic band structure of the hybrid system along high symmetry path K–Γ–M–K (Fig. 2b right). We can observe that with respect the pristine heterostructure, there are two new bands at the Fermi level which are coming from Sb atoms and there is a splitting of the bands of Sb due to SOC. Furthermore, we observe that there is no charge transfer from the hybrid antimonene to graphene or vice versa, as the Dirac cone of graphene keeps localized at Γ point and at the Fermi level.
We computed a Bader charge transfer analysis in the hybrid heterostructure to quantify the electron density flow along the system, see Table S2 of the ESI.† We show Bader charges for pristine hybrid antimonene and hybrid antimonene/graphene heterostructure. Focusing on the former, the analysis reveals that the overall transferred electrons is zero, as expected in a neutral system. It also reveals that Sb loses 0.970e−, which are gained by S (thus forming the covalent Sb–S bond we described above). Furthermore, in the hexanethiol chain the charge flows from H to C. Finally, in the hybrid antimonene/graphene heterostructure the distribution of the charge remains almost constant compared with the hybrid antimonene. This indicates that the graphene is not interacting strongly with the substrate and that there is not a flow of electrons between graphene and the substrate.
3.2. Covalent functionalization of Sb NS/graphene hybrid
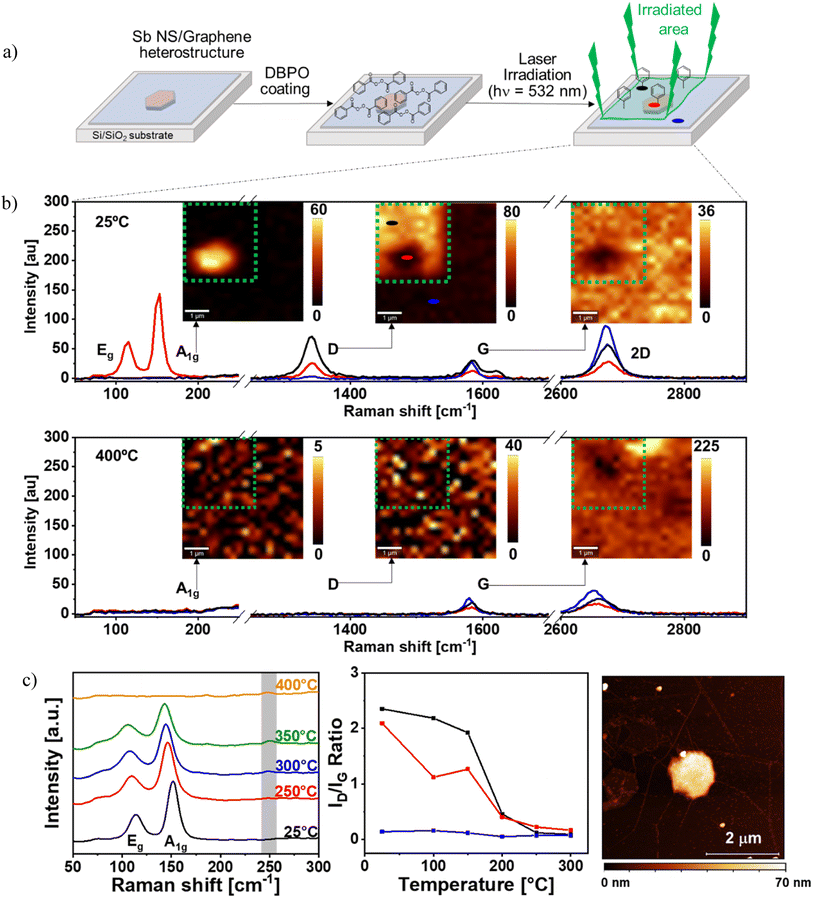
Once identified the nature of the interactions between the monoelemental 2D materials, we are in the perfect scenario to analyze the chemical reactivity of the heterostructure. Actually, the covalent bond formation in graphene mediated by radicals has been widely reported in the literature.58–61 For this, we applied a recent laser-induced functionalization protocol developed by Hirsch and co-workers62–69 using dibenzoyl peroxide (DBPO) to graft phenyl groups on the surface of graphene according to Fig. 3a. Briefly, first the Sb NS/graphene hybrid was prepared on a Si/SiO2 substrate as previously described and then a DBPO solution was used to coat the sample. After that, the hybrid and the pristine graphene around it were irradiated (green area in Fig. 3a), photo-inducing the homolytic decomposition of DBPO and generating the two benzoyloxyl radicals whose subsequent decarboxylation leads to the formation of two phenyl radicals70,71 that easily functionalize graphene through covalent bonding.62 Attending to this, three areas with different covalent reaction schemes were obtained (Fig. 3a top right): (i) the functionalized Sb NS/graphene hybrid (exemplified with a red circle), (ii) the functionalized pristine CVD graphene (black circle); and (iii) the unfunctionalized CVD graphene (blue circle).To follow the functionalization of graphene we took advantage of scanning Raman microscopy (using a WITec alpha300R confocal microscope) monitoring with mappings the A1g, G and D signals of the sample and extracting the mean Raman spectra from the three mentioned areas (see Fig. 3b top).52,72,73 More specifically, since the intensity of the D-signal measures the introduced defects in the sp2 graphene surface, this signal is usually weak in pristine graphene, but as long as the covalent bonds are formed, an increase in the D-signal intensity is observed. Besides, comparing the intensity of the D-band to the G-band (ID/IG ratio) the density of defects can be detected.52,72,73 In this regard, within the functionalization using benzyl radical, the increase of the D band and the appearance of the D′ band in Raman spectroscopy using light at 532 nm has been demonstrated to be an undirect probe of the functionalization process.74,75
To study our system, we firstly attend to the A1g-peak map that clearly shows the presence of Sb NS located in the middle-left part of the map and this signal is only noticeable at the mean Raman spectrum of the Sb NS/graphene hybrid (red trace). Focusing now on the G-peak intensity map, we observe that graphene is homogeneously distributed in the whole sample but over the hexagonal Sb NS the intensity of the signal decreases. This is attributed to interaction between the Sb NS and graphene, as previously demonstrated. This can be confirmed with the mean Raman spectra exhibiting a clear decrease in the intensity of the G band (blue and black trace vs. red trace) with the presence of the characteristic D′ at 1610 cm−1, showing a good functionalization. Finally, the D-peak map shows a rather intense signal in the graphene functionalized area except over the Sb NS, where it is reduced. On the contrary, it is almost negligible in the non-functionalized area. Actually, the ID/IG ratio (Fig. S3a†) is close to zero in the non-functionalized area, while it reaches a ratio higher than two in the free-Sb NS functionalized one, revealing a high density of defects on graphene and optimal functionalization. In the case of the functionalized graphene over the Sb NS, the ID/IG ratio decrease indicates a lower degree of functionalization over the Sb NS. This is corroborated through the intensities of the D-peak at the mean Raman spectra for these three zones, where there is no signal in the non-functionalized zone (blue trace), and in the functionalized areas, the intensity in the presence of Sb NS (red trace) is lower than in its absence (black trace).
To understand this effect, two subsequent phenomena should be analyzed. The first is the lattice electron distortion on graphene caused by functionalization with the radical, and second is the ability of the material below graphene to trap an electron through a covalent bond and recover stability. The monotopic functionalization of graphene with the radical would generate strain energy over carbon lattice.62,76 In our structure, the material below graphene can stabilize the adduct, embedding those dangling bonds antaratopic to the functionalization, this effect is also known as substrate back-bonding62,74–78 and ends in the covalent bonding of graphene with the material below it. Actually, the antaratopic reaction has been extensively studied in the literature for graphene monolayers over Si/SiO2 and Ni substrates,74 fluorine derivatives75 and even freestanding graphene monolayers in which the back bonding takes place abstracting hydrogen atoms from the polycyclic aromatic hydrocarbon contamination.79 However, to the best of our knowledge, this effect has not been exploited to functionalize 2D-pnictogen/graphene heterostructures.
Herein, the chemical nature of the back side material of graphene plays a key role in the functionalization degree.80 In this sense, both the Si/SiO2 substrate and the Sb NS allow the antaratopic back-bonding, since functionalization takes place in both areas. Nevertheless, the Si/SiO2 substrate may promote a higher strain relieve than the Sb NS, minimizing the lattice distortion caused by the functionalization.62,74 This is due to the presence of SiOH groups and residual water in the Si/SiO2 substrate that easily form the back-bond.81 However, the situation is different when the Sb NS is below graphene due to the absence of these functional groups in the Sb NS surface, yielding a lower functionalization. Another drawback for the functionalization over the Sb NS comes from the physical distance between a C atom of graphene and an Sb atom of the Sb NS. According to our computational studies, the distance between the superficial Sb of the NS to the terminal H atom of the hexanethiol is 5.17 Å, therefore, this distance will be even higher for the experimental used thiol (1-dodecanethiol), while the typical values for a C–Sb bond are 2.20 Å.82 This distance may prevent the C–Sb antaratopic backbonding.
The reversibility of the functionalization process was also studied through temperature-dependent Raman measurements recording the same Raman maps and mean spectra at 400 °C, see Fig. 3b bottom. The Raman map and the spectra of the D-peak shows that no signal is observed after the temperature treatment regardless the former functionalization, revealing the removal of sp2 defects and thus the phenyl functionalizing groups. On the contrary, the signal of the G-peak, is still present on each area, confirming the integrity of the graphene layer as a sp2 lattice. Regarding the Sb signal, the A1g peak is not noticeable. The disappearance of this signal is attributed to the oxidation and decomposition of Sb below 400 °C.83
These statements can be confirmed attending to the mean Raman spectra of the three studied zones before and after heating the samples, see Fig. 3b. Looking at the spectra of the non-functionalized graphene (blue traces), both the G and the 2D peaks are detected in both spectra, revealing the stability of graphene during the heating experiment. The D signal is not present due to the absence of functionalization. Focusing now on the graphene functionalized area (black trace), one can observe an intense D peak before heating, indicating proper functionalization. This peak disappears after heating, revealing a reversible functionalization process. Finally, the analysis of the functionalized Sb/graphene hybrid area (red trace) exhibits the presence of Sb before heating and the disappearance of this signal after heating, since it decomposes and oxidizes below 400 °C. Actually, weak signals can be seen at 190 and 255 cm−1 in the spectrum after heating, which are attributed to Sb2O3.25,84
For a better understanding of the degree of functionalization, the ID/IG ratio of three studied zones over the course of the T-dependent Raman measurement were plotted in Fig. 3c middle. The non-functionalized graphene (blue trace) ID/IG ratio is almost negligible at 25 °C, ca. 0.2 and as the temperature increases, the ratio slightly decreases at 200 °C and remains constant until 300 °C. This is attributed to the presence of possible defects present on the graphene surface, which can be minimized due to the heating procedure. The functionalized graphene (black trace) exhibits a high ID/IG ratio at 25 °C of ca. 2.3 which slightly decreases to 2.0 at 150 °C. As the temperature increases, the ratio decreases sharply up to ca. 0.4 at 200 °C, whilst from 200 to 300 °C it decreases slowly to reach ca. 0.1. Finally, the functionalized hybrid area shows an ID/IG ratio of ca. 2.1 at 25 °C. However, in this case, the ratio decreases much faster than in the other functionalized area leading to an ID/IG value of ca. 1.3 at 150 °C. At this point, the ratio decreases to 0.4 at 200 °C to finally reach 0.2 at 300 °C. Comparison of the decrease of the ID/IG ratio of the functionalized graphene with the functionalized hybrid reveals that the ratio of the hybrid falls faster. Nevertheless, both ratios show hardly noticeable differences above 200 °C and at even higher temperatures, the difference is negligible. This proves a complete retro-functionalization process for both areas that takes place at the same temperature, which matches well with other published results for the defunctionalisation of DBPO.62
The temperature dependent mean Raman spectra of the functionalized Sb NS/graphene hybrid area were studied in detail at the region of 50–300 cm−1 in order to evaluate the behaviour of the Sb A1g and Eg signals due to the heating process, see Fig. 3c left. The analysis shows a slight redshift of the signals and their complete disappearance at 400 °C. By heating the sample, the material expands and thus reduces the frequency of the phonons interacting with the incident photons, which results in the observed redshift. This effect has also been reported for other 2D materials like graphene, BP and MoS2.85–87 As anticipated, a small oxide signal arises at 300 °C and 350 °C at 250 cm−1. Sb NS usually decomposes at 350 °C, but in this hybrid, a portion of the laser energy is absorbed by the graphene layer covering the Sb NS, decreasing the decomposition temperature.
To gather additional evidence of the final state of the Sb NS after heating, an AFM image of the sample was recorded, see Fig. 3c right. Surprisingly, the Sb NS can still be observed, even though it typically decomposes at around 350 °C. However, its well-defined hexagonal structure and flat surface have changed, now remaining as an amorphous flake. This transformation is attributed to the graphene layer covering the Sb NS, which prevents Sb evaporation, forming an amorphous Sb flake below graphene and preventing its total decomposition.
4. Conclusions
In this study, we investigated a heterostructure comprising Sb NS and graphene, analyzing their interactions through Raman spectroscopy and DFT calculations, revealing a predominant van der Waals interaction between the two 2D materials. Subsequently, we achieved the functionalization of the graphene surface by covalently bonding phenyl radicals, triggered by light. Raman experiments on the functionalized hybrid provided insights into the nature of the interaction between graphene and the Sb NS, indicating a reduced, but still present, degree of functionalization with phenyl radicals compared to the Si/SiO2 substrate. We attribute this behavior to the antaratopic back bonding effect required for graphene functionalization. Specifically, there are fewer functional groups on the Sb NS surface compared to the Si/SiO2 substrate, hindering the formation of antaratopic back bonding due to the longer distance between graphene-Sb NS compared to graphene–Si/SiO2. Our findings suggest that through the well-stablished covalent functionalization of graphene with the benzyl radical using laser irradiation, the covalent bonding between graphene and the antimonene hexagon interface could also be promoted through the antaratopic backbonding. Besides, this covalent bonding can be spatially controlled since it will only take place where the laser beam has been applied. On the top of that, since the functionalization with the benzyl radical is reversible, the covalent bonding is also reversible through a temperature treatment. This opens avenues for producing graphene-based heterostructures with varying degrees of functionalization or patterns based on the combined materials. Additionally, we demonstrated the reversibility of the covalently linked phenyl groups through temperature dependent Raman spectroscopy.Author contributions
G. A. conceived the presented idea and supervised the project. M. F. performed the experimental part supervised by G. A. A. M. performed the computational part according to R. M.-H. suggestions and J. J. B. supervision. R. M.-H. and M. F. analyzed the data R. M.-H. wrote the manuscript supervised by G. A. R. M.-H. and M. F. contribute equally as co-first authors. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the European Research Council (ERC Starting Grant No. 2D-PnictoChem 804110, ERC Proof of Concept Grant 2D4H2 No. 101101079 and ERC Starting Grant No. 2D-SMARTiES 101042680), and the Generalitat Valenciana (CIDEGENT/2018/001 and CDEIGENT/2019/022). Grants PID2022-143297NB-I00, MRR/PDC2022-133997I00, TED2021-131347B-I00 and Unit of Excellence “Maria de Maeztu” CEX2019-000919-M funded by MICIU/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”, and the “European Union NextGenerationEU/PRTR”. G. A. acknowledges the Deutsche Forschungsgemeinschaft DFG (FLAG-ERA AB694/2-1). R. M.-H. acknowledges the grant FJC2021-047262-I funded by MCIN/AEI/10.13039/501100011033 and by “European Union NextGenerationEU/PRTR”. A. M. R. thanks the Spanish MIU (FPU21/04195).References
- D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11, 218–230 CrossRef CAS PubMed
.
- N. Briggs, S. Subramanian, Z. Lin, X. Li, X. Zhang, K. Zhang, K. Xiao, D. Geohegan, R. Wallace, L.-Q. Chen, M. Terrones, A. Ebrahimi, S. Das, J. Redwing, C. Hinkle, K. Momeni, A. Van Duin, V. Crespi, S. Kar and J. A. Robinson, 2D Mater., 2019, 6, 022001 CrossRef CAS
.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed
.
- X. Zhou and G. Yu, ACS Nano, 2021, 15, 11040–11065 CrossRef CAS PubMed
.
- G. P. Neupane, K. Zhou, S. Chen, T. Yildirim, P. Zhang and Y. Lu, Small, 2019, 15, 1804733 CrossRef PubMed
.
- Z. Huang, C. He, X. Qi, H. Yang, W. Liu, X. Wei, X. Peng and J. Zhong, J. Phys. D: Appl. Phys., 2014, 47, 075301 CrossRef CAS
.
- N. Lu, H. Guo, L. Li, J. Dai, L. Wang, W.-N. Mei, X. Wu and X. C. Zeng, Nanoscale, 2014, 6, 2879–2886 RSC
.
- C. T. Le, J. Kim, F. Ullah, A. D. Nguyen, T. N. Nguyen Tran, T.-E. Le, K.-H. Chung, H. Cheong, J. I. Jang and Y. S. Kim, ACS Nano, 2020, 14, 4366–4373 CrossRef CAS PubMed
.
- W. Choi, I. Akhtar, D. Kang, Y. Lee, J. Jung, Y. H. Kim, C.-H. Lee, D. J. Hwang and Y. Seo, Nano Lett., 2020, 20, 1934–1943 CrossRef CAS PubMed
.
- S. Özcan and B. Biel, RSC Adv., 2023, 13, 17222–17229 RSC
.
- S. Park, C. Park and G. Kim, J. Chem. Phys., 2014, 140, 134706 CrossRef PubMed
.
- N. Shen, ACS Appl. Electron. Mater., 2023, 5, 2648–2655 CrossRef CAS
.
- Y. Shi, W. Zhou, A.-Y. Lu, W. Fang, Y.-H. Lee, A. L. Hsu, S. M. Kim, K. K. Kim, H. Y. Yang, L.-J. Li, J.-C. Idrobo and J. Kong, Nano Lett., 2012, 12, 2784–2791 CrossRef CAS PubMed
.
- W. J. Yu, Y. Liu, H. Zhou, A. Yin, Z. Li, Y. Huang and X. Duan, Nat. Nanotechnol., 2013, 8, 952–958 CrossRef CAS PubMed
.
- S. Bertolazzi, D. Krasnozhon and A. Kis, ACS Nano, 2013, 7, 3246–3252 CrossRef CAS PubMed
.
- L. Yu, Y.-H. Lee, X. Ling, E. J. G. Santos, Y. C. Shin, Y. Lin, M. Dubey, E. Kaxiras, J. Kong, H. Wang and T. Palacios, Nano Lett., 2014, 14, 3055–3063 CrossRef CAS PubMed
.
- Z. Wang, Q. Chen and J. Wang, J. Phys. Chem. C, 2015, 119, 4752–4758 CrossRef CAS
.
- S. Ulstrup, A. G. Čabo, J. A. Miwa, J. M. Riley, S. S. Grønborg, J. C. Johannsen, C. Cacho, O. Alexander, R. T. Chapman, E. Springate, M. Bianchi, M. Dendzik, J. V. Lauritsen, P. D. C. King and P. Hofmann, ACS Nano, 2016, 10, 6315–6322 CrossRef CAS PubMed
.
- C. Li, Q. Cao, F. Wang, Y. Xiao, Y. Li, J.-J. Delaunay and H. Zhu, Chem. Soc. Rev., 2018, 47, 4981–5037 RSC
.
- E. Lorchat, L. E. P. López, C. Robert, D. Lagarde, G. Froehlicher, T. Taniguchi, K. Watanabe, X. Marie and S. Berciaud, Nat. Nanotechnol., 2020, 15, 283–288 CrossRef CAS PubMed
.
- Y. C. Huang, X. Chen, C. Wang, L. Peng, Q. Qian and S. F. Wang, Nanoscale, 2017, 9, 8616–8622 RSC
.
- Y. Liu, B. N. Shivananju, Y. Wang, Y. Zhang, W. Yu, S. Xiao, T. Sun, W. Ma, H. Mu, S. Lin, H. Zhang, Y. Lu, C.-W. Qiu, S. Li and Q. Bao, ACS Appl. Mater. Interfaces, 2017, 9, 36137–36145 CrossRef CAS PubMed
.
- K. Ge, Y. Zhang, D. Wang, Z. Li, J. He, C. Fu, Y. Yang, M. Pan and L. Zhu, ACS Appl. Mater. Interfaces, 2020, 12, 20035–20043 CrossRef CAS PubMed
.
- H. Qiao, H. Liu, Z. Huang, R. Hu, Q. Ma, J. Zhong and X. Qi, Energy Environ. Mater., 2021, 4, 522–543 CrossRef CAS
.
- T. Gupta, K. Elibol, S. Hummel, M. Stöger-Pollach, C. Mangler, G. Habler, J. C. Meyer, D. Eder and B. C. Bayer, npj 2D Mater. Appl., 2021, 5, 53 CrossRef CAS
.
- Y. Yu, Q. Meng and T. Liu, J. Mater. Res. Technol., 2022, 17, 2466–2479 CrossRef CAS
.
- S. Akhavan, A. Ruocco, G. Soavi, A. Taheri Najafabadi, S. Mignuzzi, S. Doukas, A. R. Cadore, Y. A. K. Samad, L. Lombardi, K. Dimos, I. Paradisanos, J. E. Muench, H. F. Y. Watson, S. Hodge, L. G. Occhipinti, E. Lidorikis, I. Goykhman and A. C. Ferrari, 2D Mater., 2023, 10, 035015 CrossRef
.
- W. Hu, Z. Li and J. Yang, J. Chem. Phys., 2013, 139, 154704 CrossRef PubMed
.
- G. R. Berdiyorov, M. Neek-Amal, F. M. Peeters and A. C. T. Van Duin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 024107 CrossRef
.
- Y. Cai, G. Zhang and Y.-W. Zhang, J. Phys. Chem. C, 2015, 119, 13929–13936 CrossRef CAS
.
- B. Van Troeye, A. Lherbier, J.-C. Charlier and X. Gonze, Phys. Rev. Mater., 2018, 2, 074001 CrossRef CAS
.
- L. Cui and M. Sun, J. Phys. Chem. C, 2021, 125, 22370–22378 CrossRef CAS
.
- A. Muroni, S. Brozzesi, F. Bechstedt, P. Gori and O. Pulci, Nanomaterials, 2023, 13, 2358 CrossRef CAS PubMed
.
- H. Lu and W. Guo, Nano Res., 2023, 16, 12587–12593 CrossRef CAS
.
- F. Zhang, W. Li and X. Dai, Superlattices Microstruct., 2016, 100, 826–832 CrossRef CAS
.
- W. Li, X. Wang and X. Dai, Solid State Commun., 2017, 254, 37–41 CrossRef CAS
.
- P. Wu, P. Li and M. Huang, Nanomaterials, 2019, 9, 1430 CrossRef CAS PubMed
.
- J. Su, W. Li, T. Duan, B. Xiao, X. Wang, Y. Pei and X. C. Zeng, Carbon, 2019, 153, 767–775 CrossRef CAS
.
- S. Hashemi, R. Faez and G. Darvish, J. Comput. Electron., 2023, 22, 80–87 CAS
.
- Y.-B. Liang, K. Liu, Z. Liu, J. Wang, C.-S. Liu and Y. Liu, Appl. Surf. Sci., 2022, 577, 151880 CrossRef CAS
.
- J. Yan, D. Cao, X. Yang, J. Wang, Z. Jiang, Z. Jiao and H. Shu, Appl. Phys. A, 2022, 128, 958 CrossRef CAS
.
- I. Torres, M. Alcaraz, R. Sanchis-Gual, J. A. Carrasco, M. Fickert, M. Assebban, C. Gibaja, C. Dolle, D. A. Aldave, C. Gómez-Navarro, E. Salagre, E. García Michel, M. Varela, J. Gómez-Herrero, G. Abellán and F. Zamora, Adv. Funct. Mater., 2021, 31, 2101616 CrossRef CAS
.
- J. A. Carrasco, P. Congost-Escoin, M. Assebban and G. Abellán, Chem. Soc. Rev., 2023, 52, 1288–1330 RSC
.
- C. Dolle, V. Oestreicher, A. M. Ruiz, M. Kohring, F. Garnes-Portolés, M. Wu, G. Sánchez-Santolino, A. Seijas-Da Silva, M. Alcaraz, Y. M. Eggeler, E. Spiecker, J. Canet-Ferrer, A. Leyva-Pérez, H. B. Weber, M. Varela, J. J. Baldoví and G. Abellán, J. Am. Chem. Soc., 2023, 145, 12487–12498 CrossRef CAS PubMed
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, m. Cococcioni, I. Dabo, A. D. Corso, S. Fabris, G. Fratesi, S. de Gironcoli, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter., 2009, 21, 395502 CrossRef PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- L. Peng, S. Ye, J. Song and J. Qu, Angew. Chem., Int. Ed., 2019, 58, 9891–9896 CrossRef CAS PubMed
.
- I. Torres, M. Alcaraz, R. Sanchis-Gual, J. A. Carrasco, M. Fickert, M. Assebban, C. Gibaja, C. Dolle, D. A. Aldave, C. Gómez-Navarro, E. Salagre, E. García Michel, M. Varela, J. Gómez-Herrero, G. Abellán and F. Zamora, Adv. Funct. Mater., 2021, 31, 2101616 CrossRef CAS
.
- P. Ares, F. Aguilar-Galindo, D. Rodríguez-San-Miguel, D. A. Aldave, S. Díaz-Tendero, M. Alcamí, F. Martín, J. Gómez-Herrero and F. Zamora, Adv. Mater., 2016, 28, 6332–6336 CrossRef CAS PubMed
.
- C. Gibaja, D. Rodriguez-San-Miguel, P. Ares, J. Gómez-Herrero, M. Varela, R. Gillen, J. Maultzsch, F. Hauke, A. Hirsch, G. Abellán and F. Zamora, Angew. Chem., Int. Ed., 2016, 55, 14345–14349 CrossRef CAS PubMed
.
- A. C. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef CAS
.
- R. Voggu, B. Das, C. S. Rout and C. N. R. Rao, J. Phys.: Condens. Matter, 2008, 20, 472204 CrossRef
.
- H. Liu, Y. Liu and D. Zhu, J. Mater. Chem., 2011, 21, 3335–3345 RSC
.
- E. Nuin, V. Lloret, K. Amsharov, F. Hauke, G. Abellán and A. Hirsch, Chem.–Eur. J., 2018, 24, 4671–4679 CrossRef CAS PubMed
.
- R. M. Ribeiro, V. M. Pereira, N. M. R. Peres, P. R. Briddon and A. H. Castro Neto, New J. Phys., 2009, 11, 115002 CrossRef
.
- T. Niu, W. Zhou, D. Zhou, X. Hu, S. Zhang, K. Zhang, M. Zhou, H. Fuchs and H. Zeng, Adv. Mater., 2019, 31, 1902606 CrossRef PubMed
.
- J. Park and M. Yan, Acc. Chem. Res., 2013, 46, 181–189 CrossRef CAS PubMed
.
- C. K. Chan, T. E. Beechem, T. Ohta, M. T. Brumbach, D. R. Wheeler and K. J. Stevenson, J. Phys. Chem. C, 2013, 117, 12038–12044 CrossRef CAS
.
- F. Hof, R. A. Schäfer, C. Weiss, F. Hauke and A. Hirsch, Chem.–Eur. J., 2014, 20, 16644–16651 CrossRef CAS PubMed
.
- S. Al-Fogra, S. Rohde, M. Speck, F. Hauke, A. Hirsch and T. Wei, Chem. Commun., 2024, 60, 734–737 RSC
.
- K. F. Edelthalhammer, D. Dasler, L. Jurkiewicz, T. Nagel, S. Al-Fogra, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2020, 59, 23329–23334 CrossRef CAS PubMed
.
- T. Wei, S. Al-Fogra, F. Hauke and A. Hirsch, J. Am. Chem. Soc., 2020, 142, 21926–21931 CrossRef CAS PubMed
.
- T. Wei, X. Liu, S. Al-Fogra, J. Bachmann, F. Hauke and A. Hirsch, Chem. Commun., 2021, 57, 4654–4657 RSC
.
- L. Bao, B. Zhao, M. Assebban, M. Halik, F. Hauke and A. Hirsch, Chem.–Eur. J., 2021, 27, 8709–8713 CrossRef CAS PubMed
.
- L. Bao, B. Zhao, B. Yang, M. Halik, F. Hauke and A. Hirsch, Adv. Mater., 2021, 33, 2101653 CrossRef CAS PubMed
.
- T. Dierke, D. Dasler, T. Nagel, F. Hauke, A. Hirsch and J. Maultzsch, ACS Appl. Nano Mater., 2022, 5, 4966–4971 CrossRef CAS
.
- T. Wei, X. Liu, M. Kohring, S. Al-Fogra, M. Moritz, D. Hemmeter, U. Paap, C. Papp, H. Steinrück, J. Bachmann, H. B. Weber, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2022, 61, e202201169 CrossRef CAS PubMed
.
- S. Al-Fogra, B. Yang, L. Jurkiewicz, F. Hauke, A. Hirsch and T. Wei, J. Am. Chem. Soc., 2022, 144, 19825–19831 CrossRef CAS PubMed
.
- J. A. Den Hollander and J. P. M. Van Der Ploeg, Tetrahedron, 1976, 32, 2433–2436 CrossRef CAS
.
- A. Kitamura, H. Sakuragi, M. Yoshida and K. Tokumaru, Bull. Chem. Soc. Jpn., 1980, 53, 1393–1398 CrossRef CAS
.
- M. A. Pimenta, G. Dresselhaus, M. S. Dresselhaus, L. G. Cançado, A. Jorio and R. Saito, Phys. Chem. Chem. Phys., 2007, 9, 1276–1290 RSC
.
- M. M. Lucchese, F. Stavale, E. H. M. Ferreira, C. Vilani, M. V. O. Moutinho, R. B. Capaz, C. A. Achete and A. Jorio, Carbon, 2010, 48, 1592–1597 CrossRef CAS
.
- R. A. Schäfer, K. Weber, M. Koleśnik-Gray, F. Hauke, V. Krstić, B. Meyer and A. Hirsch, Angew. Chem., Int. Ed., 2016, 55, 14858–14862 CrossRef PubMed
.
- L. Bao, B. Zhao, V. Lloret, M. Halik, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2020, 59, 6700–6705 CrossRef CAS PubMed
.
- K. Amsharov, D. I. Sharapa, O. A. Vasilyev, M. Oliver, F. Hauke, A. Goerling, H. Soni and A. Hirsch, Carbon, 2020, 158, 435–448 CrossRef CAS
.
- G. Gao, D. Liu, S. Tang, C. Huang, M. He, Y. Guo, X. Sun and B. Gao, Sci. Rep., 2016, 6, 20034 CrossRef CAS PubMed
.
- K. C. Knirsch, R. A. Schäfer, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2016, 55, 5861–5864 CrossRef CAS PubMed
.
- C. Dolle, P. Schweizer, D. Dasler, S. Gsänger, R. Maidl, G. Abellán, F. Hauke, B. Meyer, A. Hirsch and E. Spiecker, npj 2D Mater. Appl., 2022, 6, 29 CrossRef CAS
.
- Q. H. Wang, Z. Jin, K. K. Kim, A. J. Hilmer, G. L. C. Paulus, C.-J. Shih, M.-H. Ham, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, J. Kong, P. Jarillo-Herrero and M. S. Strano, Nat. Chem., 2012, 4, 724–732 CrossRef CAS PubMed
.
- M. Yamamoto, T. L. Einstein, M. S. Fuhrer and W. G. Cullen, ACS Nano, 2012, 6, 8335–8341 CrossRef CAS PubMed
.
- S. Furan, E. Hupf, J. Boidol, J. Brünig, E. Lork, S. Mebs and J. Beckmann, Dalton Trans., 2019, 48, 4504–4513 RSC
.
- M. Fickert, M. Assebban, J. Canet-Ferrer and G. Abellán, 2D Mater., 2021, 8, 015018 CrossRef CAS
.
- M. Assebban, C. Gibaja, M. Fickert, I. Torres, E. Weinreich, S. Wolff, R. Gillen, J. Maultzsch, M. Varela, S. Tan Jun Rong, K. P. Loh, E. G. Michel, F. Zamora and G. Abellán, 2D Mater., 2020, 7, 025039 CrossRef CAS
.
- S. Sahoo, A. P. S. Gaur, M. Ahmadi, M. J.-F. Guinel and R. S. Katiyar, J. Phys. Chem. C, 2013, 117, 9042–9047 CrossRef CAS
.
- D. J. Late, ACS Appl. Mater. Interfaces, 2015, 7, 5857–5862 CrossRef CAS PubMed
.
- S. Tian, Y. Yang, Z. Liu, C. Wang, R. Pan, C. Gu and J. Li, Carbon, 2016, 104, 27–32 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra01029a |
| ‡ R. M.-H. and M. F. contribute equally as co-first authors. |
| This journal is © The Royal Society of Chemistry 2024 |