Open Access Article
Open Access ArticleThe thermodynamics and kinetics of depolymerization: what makes vinyl monomer regeneration feasible?
Victoria
Lohmann
 a,
Glen R.
Jones
a,
Glen R.
Jones
 a,
Nghia P.
Truong
a,
Nghia P.
Truong
 ab and
Athina
Anastasaki
ab and
Athina
Anastasaki
 *a
*a
aLaboratory of Polymeric Materials, Department of Materials, ETH Zürich, Vladimir-Prelog-Weg 5, 8093 Zürich, Switzerland. E-mail: athina.anastasaki@mat.ethz.ch
bMonash Institute of Pharmaceutical Sciences, Monash University, 399 Royal Parade, Parkville, VIC 3152, Australia
First published on 5th December 2023
Abstract
Depolymerization is potentially a highly advantageous method of recycling plastic waste which could move the world closer towards a truly circular polymer economy. However, depolymerization remains challenging for many polymers with all-carbon backbones. Fundamental understanding and consideration of both the kinetics and thermodynamics are essential in order to develop effective new depolymerization systems that could overcome this problem, as the feasibility of monomer generation can be drastically altered by tuning the reaction conditions. This perspective explores the underlying thermodynamics and kinetics governing radical depolymerization of addition polymers by revisiting pioneering work started in the mid-20th century and demonstrates its connection to exciting recent advances which report depolymerization reaching near-quantitative monomer regeneration at much lower temperatures than seen previously. Recent catalytic approaches to monomer regeneration are also explored, highlighting that this nascent chemistry could potentially revolutionize depolymerization-based polymer recycling in the future.
Introduction
The first century of polymer science has changed the world, with polymers now being integral to numerous aspects of modern life, from packaging materials and medical devices to electronics and construction materials. However, polymers are often incredibly resilient to degradation by design, and consequently their widespread use has come at a cost to the environment. The ecological repercussions of non-biodegradable and single-use polymeric materials are increasingly evident, with plastic pollution contaminating our oceans and land, and harming wildlife on both a macroscopic and microscopic level.1 It is therefore crucial that polymer scientists innovate and seek alternatives to the currently unsustainable lifecycle of polymers. One approach to this is the development of plastic materials which can exhibit similar properties to commercial plastics, but are inherently designed to be efficiently recycled or biodegraded to give innocuous products.2–8 While this could reduce plastic waste in the future, it doesn't solve the end-of-life problem of plastic materials that have already been produced. The majority of plastic waste cannot currently be effectively recycled in a cost-effective manner, and as a result of this waste in landfills and the general environment is estimated to rise to 12 Gt by 2050.9 Better methods of processing and utilizing plastic waste streams are of paramount importance for solving the global problem of our unsustainable polymer economy.One strategy that is currently attracting attention is depolymerization, also referred to as chemical recycling to monomer (CRM). Depolymerization can be defined as the reverse of polymerization, whereby polymers are converted back into their constituent monomers.10 This is in contrast to polymer degradation strategies where lower molecular weight polymeric species and small molecule side products are formed.11–17 Conventional mechanical recycling of polymers is another possibility which often results in deterioration of mechanical properties, as polymer chains are sheared and reduced in molecular weight.18 CRM circumvents this problem entirely as regenerated monomers can be re-polymerized to give pristine polymeric materials. It could be envisioned that widespread adoption of CRM would not only greatly reduce plastics entering landfill sites but would also potentially offset the polymer industry's reliance on fossil fuels as plastic waste would become a valuable resource to produce new materials.
Although the depolymerization of polymers with heteroatom backbones (such as polyesters)19–23 has been successfully demonstrated on an industrial scale, polymers with C–C backbones (e.g., vinyl polymers) are much more challenging. This perspective will primarily focus on discussing the thermodynamics and kinetics of depolymerization of vinyl type polymers. The reader is referred to other recent reviews for other polymer classes and further challenges of the recycling process.24–27 While chemical recycling via pyrolysis, where the polymer is exposed to high temperatures (typically T > 300 °C) under the exclusion of oxygen to produce monomer and other small molecules, has been described and reviewed for a vast range of addition polymers,28–33 reports of depolymerization at lower temperatures and with monomer as the product are much more recent. Recent exciting work has sought to overcome this challenge by utilizing addition polymers predominantly made by reversible-deactivation radical polymerization (RDRP) methods. RDRP is a form of radical polymerization where critical characteristics of the polymer such as molecular weight, dispersity, and nature of the end-group can be controlled by reversibly deactivating propagating chains. The most common methods to achieve such reversible deactivation are atom transfer radical polymerization (ATRP), reversible addition–fragmentation chain-transfer (RAFT) polymerization, and nitroxide-mediated polymerization (NMP). The functional end-group present on the polymer in the deactivated state remains on the chain even after polymerization and suitable purification.34–40 The existence of reactive end-groups in these polymers has been demonstrated to provide a handle to initiate depolymerization at lower temperatures than was previously achieved.10,41–44 As further advancements are made in CRM, researchers new to this field will naturally ask what makes monomer regeneration feasible, and what are the possible limits of depolymerization?
The practical feasibility of depolymerization is governed by thermodynamic and kinetic principles which were first formulated in the mid-20th century. These principles, derived from careful kinetic analysis of polymerizations, dictate the energy requirements, reaction rates, and equilibrium considerations associated with breaking down long polymer chains into monomeric units. This pioneering work lays the essential foundations for what is possible in depolymerization. The purpose of this perspective is to revisit this foundational literature and summarize the thermodynamic and kinetic considerations of depolymerization in a way that is accessible to both experts and non-experts interested in this area and put this work in the context of more modern studies. Ultimately, envisioning that many of the conclusions reached 50 years ago, in combination with modern chemistry, can be utilized to further improve CRM today. First, the concepts of thermodynamics of depolymerization are introduced in a broadly didactic format, with an emphasis on the concept of ceiling temperature as a measure of depolymerizability (Section 2). Then, the perspective expands upon this theory to discuss the kinetic considerations of depolymerization (Section 3). In Section 4, current literature reporting lower temperature depolymerizations and how this fits with existing theory is explored. Finally, in Section 5, future opportunities in depolymerization through catalysis via non-radical pathways are discussed.
Thermodynamics of depolymerization
Monomer formation from vinyl polymers was postulated as early as 1914, when Stobbe detected the formation of small molecular vinyl species and a change in refractive index in a solution of polystyrene (PS) after it was placed under sunlight irradiation in a sealed vial for extended periods of time.45 He investigated the reversibility of addition polymerization since he and his colleagues had never been able to fully consume the monomer when making PS and thought that might have been due to a competing reverse reaction. Strikingly, interest in the reversibility of the polymerization reaction is therefore older than the concept of covalently bound macromolecules initially proposed by Staudinger in 1920 and used by all of us today.46 However, by todays analytical standards, Stobbe45 and others never conclusively proved the formation of monomer. It took until the 1940s for monomer formation to be proven, when polymer theory was firmly established, and depolymerization studies on PS solutions were conducted at high temperatures with the first mechanistic models being proposed.47,48 Since the activation energy should not be more than the sum of the activation energy and the enthalpy of the forward reaction (approximately 25 kcal mol−1), the authors postulated that the probability of a depropagation was predicted to be significant enough even at polymerization temperatures below 100 °C and the depropagation must be considered: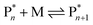 | (1) |
As the propagation reaction is reversible, the activated polymer and the monomer are in chemical equilibrium with each other, quantified by an equilibrium constant (Kpoly). Formulating the law of mass action for this equilibrium in terms of species concentration, an expression for the equilibrium constant is found:
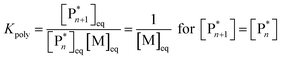 | (2) |
For sufficiently large n, the propagating species can be considered the same before and after addition of a repeat unit due to the long chain assumption (i.e., small changes in DP have a negligible effect on the reactivity),49 and it can be seen that the equilibrium position is solely defined by the monomer concentration at equilibrium. Such a description of the polymerization equilibrium was found to be valid for different polymerization mechanisms.50–54
Now, Stobbe's investigation into reversibility as an explanation for the conversion limits observed in polymerization can be fully appreciated.45 If both propagation and depropagation take place simultaneously, the reaction proceeds until the monomer concentration is reached at which the equilibrium is established. For any closed system, no more overall macroscopic change in the composition takes place, which appears as though the reaction stops at a finite monomer concentration. As per definition, the Gibb's free energy change reaches zero at the equilibrium:
| ΔG = 0 = ΔH − TΔS | (3) |
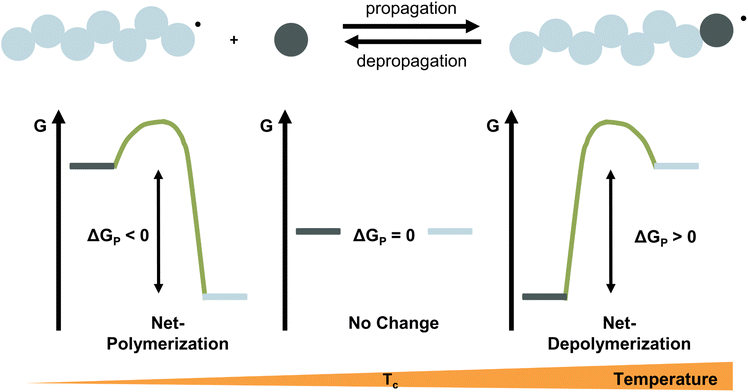
For any reaction to occur spontaneously, the Gibb's free energy change must be negative. For polymerization reactions specifically, this means that the free energy of the monomeric state has to be higher than that of the polymeric state for propagation and vice versa for depropagation (Fig. 1).55 For addition polymerization reactions of vinyl monomers, the enthalpy change (ΔH) is always negative as the formation of a σ-bond by addition to a π-bond releases energy. Generally speaking, the change in entropy (ΔS) is also negative for most vinyl monomers as the system's degrees of freedom decrease when a propagating species and a monomer molecule are combined into a single species. As long as the absolute value of the enthalpy change is larger than the absolute value of the change in entropy times the temperature, the overall change in free energy is negative. Therefore, the lower the temperature, the smaller the value of TΔS, the more negative the free energy change, the more favoured the polymerization reaction. Since the equilibrium responds to shifts in the reaction conditions according to Le Chatelier's principle, more polymerization is achieved by increasing the monomer concentration, and more depolymerization by removing monomer from the system.
Ceiling temperature and monomer equilibrium concentration
Thus far, the equilibrium constant has only been presented as a quantitative description of the equilibrium state. However, the constant changes with temperature, and concluding whether a system polymerizes or depolymerizes is difficult to determine from this value alone. In addition, comparing polymers to each other also becomes more difficult. Dainton and Ivin developed the concept of ceiling temperature as an alternative, quantitative description.56 As the ceiling temperature is such an important concept for depolymerization, a short historical account of its development is given below.In the 1930s, copolymerization of sulfur dioxide with olefins was attempted by many researchers.57–60 Snow and Frey in particular, observed that such reactions were only feasible at low temperatures and ceased abruptly once a certain temperature was reached. They termed this temperature barrier the ceiling temperature and attributed it to inhibitor formation.61 In Dainton's obituary, Ivin, who was a PhD student of Dainton in Cambridge at the time, describes how the ceiling temperature was formalized as a concept:62 Dainton's research group was well aware of the temperature barrier in polymerization and had already conducted experiments during which they found such a ceiling temperature independent of the initiation method but dependent on monomer concentration. However, they were struggling to explain why. One day during a group meeting, Dainton proposed the consideration of reversibility and wrote down the resulting rate equation for monomer consumption in such a system:
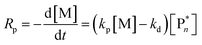 | (4) |
It immediately became obvious to Ivin and Dainton that the rate would fall to zero if the depropagation constant (kd) became equal to the propagation constant times the monomer concentration (kp[M]), independent of the active species concentration for reversible propagation. The ceiling temperature must therefore be the temperature at which this condition is reached since a propagation rate of zero results in no polymerization. As an equal rate of the forward and backward reactions means that the equilibrium is established, they then reformulated eqn (3) to give an expression for this temperature.56
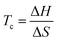 | (5) |
The entropy change can be expressed in terms of the standard entropy at unit concentration (ΔS°) and a concentration-dependent term:
ΔS = ΔS° + R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[M] ln[M] | (6) |
By substituting the entropy in eqn (5) with eqn (6), the most commonly used expression for the ceiling temperature is found. Because the ceiling temperature is a characteristic of the equilibrium, the monomer concentration becomes the monomer concentration at equilibrium ([M]eq):
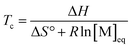 | (7) |
Typically, this is referred to as the monomer equilibrium concentration (MEC). Eqn (7) makes one thing very clear, which is that ceiling temperature and MEC are a pair. As the ceiling temperature changes, the MEC changes. Hence, instead of being a clear barrier of depolymerization as often stated in literature, the ceiling temperature is merely a quantitative description of the equilibrium position. Meaning that if an active species was put into solution at a given temperature, depolymerization would proceed until the MEC is reached for this temperature. The addition of monomer to a solution of propagating species at a given temperature, would result in overall polymerization until enough monomer is consumed to reach the MEC for this temperature. Therefore, the ceiling temperature is a characteristic of monomer at a specific concentration.63 IUPAC defines it as the ‘temperature above which, in a given chain polymerization, polymer of high molar mass is not formed’.64 Oftentimes in literature, authors refer to a bulk ceiling temperature even if reactions are carried out under different conditions.65
As already mentioned, the ceiling temperature is independent of the initiation mechanism (Fig. 2) because it is a characteristic of the propagation reaction, which only considers the already activated species. Furthermore, it is even independent of the propagation mechanism since substrate and product are the same regardless of whether propagation takes place via a radical or an ion.66,67
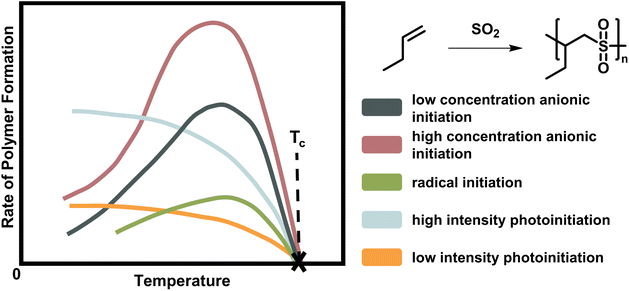 | ||
| Fig. 2 Scheme of the rate of polymer formation with temperature for the copolymerisation of butene polysulfone. As the depropagation becomes more significant at higher temperature, the polymer formation rate falls to zero. The ceiling temperature is independent of the initiation mechanism and active species for a chain polymerization conducted at the same initial monomer concentration with low (dark blue) and high (rose) anionic initiator concentration, radical initiator (green), and light of low (orange) and high intensity (light blue). Adapted from ref. 66 with permission from the Royal Society of Chemistry, copyright 1953. | ||
Disregarding the initiation and termination of active species and describing the thermodynamics of a polymerization or depolymerization reaction purely in terms of the propagation–depropagation equilibrium as the ceiling temperature does, is a valid treatment for long polymer chains. However, for short chain lengths and especially oligomer formation, initiation and termination reactions have significant contributions to the total reaction entropy and enthalpy.68 Generally, the effect is considered negligible for chain lengths with a DP larger than or equal to 3.49,53,69,70
The approximations made for the thermodynamic treatment of polymerization and by extension depolymerization reactions already expose a significant limitation of the ceiling temperature concept with respect to being able to predict the feasibility of monomer generation. As the concept only considers already activated species, no information is given on what is required to generate these species or what termination reactions might limit the amount of monomer generated.
Influences on the ceiling temperature
The ceiling temperature is represented by the enthalpy and entropy change of the reaction. Many factors can influence this such as solubility,71 changes in aggregation states during polymerization (i.e., from liquid monomer to solid polymer),55 and pressure.72 The main considerations on the ceiling temperature were well summarized by Ivin: ‘one should never speak of the Tc of a polymer: this has no thermodynamic meaning; and when speaking of the Tc of a monomer one must always quote the precise conditions of monomer concentration, solvent medium, and pressure if this is to have real thermodynamic meaning’.63 This section aims to give a comprehensive overview of the ways ceiling temperatures have been tuned in the past, while delving deeper into theory where appropriate.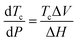 | (8) |
As double bonds have a larger volume than single bonds, more vinyl species can be obtained in addition depolymerization by reducing the reaction pressure, as exemplified for the thermal degradation of polyethylene,73 and polymerization is favoured for higher pressure. Hence, higher pressure is one factor that enables the increase of reaction temperature for the polymerization of α-methyl styrene (AMS) (Fig. 3).74
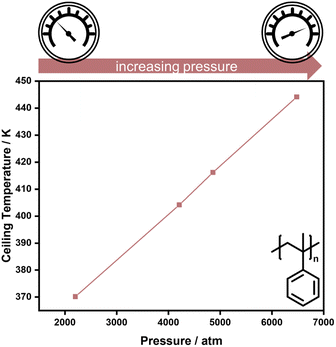 | ||
| Fig. 3 High pressure increases the ceiling temperature in the polymerization of α-methyl styrene. Adapted from ref. 74 with permission from the Royal Society of Chemistry, copyright 1960. | ||
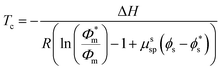 | (9) |
In this work, only entropic contributions are considered. The choice of solvent affects the volume fraction (ϕ), volume fraction at standard conditions (1 M, ϕ*), and the interaction between polymer and solvent, as well as the polymer concentration accounted for by a correction term (μssp). The correction term is a weakness of this treatment as it combines all effects of the polymer in one value, which again becomes difficult to estimate. However, it has been established that the choice of solvent also has an effect on the reaction enthalpy, where a better solvent results in less chain coiling and therefore, longer backbone bonds, which in turn resulted in lower enthalpy and therefore lower ceiling temperature.77
A more comprehensive treatment is perhaps given by a relation of all interaction parameters (χ), and fractional volumes to each other, also considering the volumes (V) and molar volumes (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) of each component:78
) of each component:78
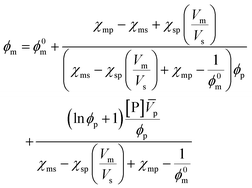 | (10) |
The index 0 thereby denotes the theoretical molar fraction for all polymer being converted to monomer, also a temperature dependent characteristic.79 So, what information does this relation reveal about the equilibrium position? Since is the volume fraction of the monomer at the equilibrium, the MEC is nothing other than this fraction divided by the molar volume of the monomer. Eqn (10) therefore establishes a direct relation between the equilibrium position of the monomer–polymer solution, expressed through the ceiling temperature, and the interaction parameters between all components as established by Flory–Huggins theory.80 The complexity is also the greatest barrier to the practicality of this treatment as interaction parameters are not readily available from literature, and hence either have to determined experimentally or modelled under assumptions. It follows that the weaker the interaction between monomer and solvent, the more exothermic and exoentropic the reaction, which favours polymerization and increases the ceiling temperature.81
Experimentally, the solvent effect has recently been leveraged for the reduction of ceiling temperature by Odelius and co-workers. Even though the conducted depolymerization of poly lactic acid was not that of an all-carbon backbone polymer, the work was the first demonstration of deliberate application of the solvent effect for ceiling temperature tuning. By using solubility parameters, which are much more accessible and related to the interaction parameters, the effect on the ceiling temperature could be accurately modelled, and essentially the ceiling temperature could be lowered over a 200 °C temperature range by selection of suitable solvents (Fig. 4).71,82 Such a large temperature range might be attributable to the large solubility difference between this specific monomer and polymer.
 | ||
| Fig. 4 The effect of phenyl methacrylate's substituents on the ceiling temperature, the larger the substituent the lower the ceiling temperature of the polymerization. Graph reprinted from ref. 90Eur. Polym. J., 25, 2, B. Yamada, T. Tanaka, T. Otsu, Correlations of ceiling temperature and reactivity with bulkiness of ortho-substituent in radical polymerization of phenyl methacrylate, 117–120, Copyright 1989, with permission from Elsevier. | ||
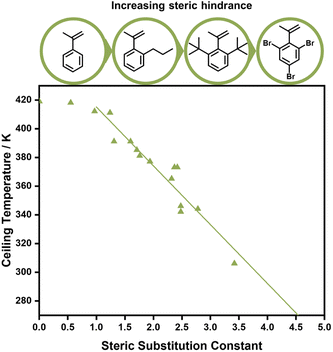
Aside from electronic effects, side chain substituents can have a structural influence on the ceiling temperature. These are attributed to steric effects, which can cause increased depropagation to reduce steric hindrance, and the reduction of rotational freedoms of the polymer chain for bulky side chains. The closer such substituents to the double bond, the larger the effect.88–90 While a decrease of the ceiling temperature for linear side chains could only be observed for lengths between one and four carbons,91 much more pronounced effects were discovered for branched side chains. When different ortho substituents on phenyl methacrylate were investigated, the ceiling temperature decreased linearly with the size of the substituent, which was concluded to be a purely steric effect (Fig. 5).92 In fact, Kunisada and co-workers realized that such an effect was further exaggerated for conformational constraints. Where substituents prevented the free rotation of the side chain, ceiling temperatures were even lower than for unconstrained chains.93–96 Steric factors aside, functional groups on the side chain can also be exploited for tuning the equilibrium position. If the presence of functional groups results in strong non-covalent bonding between individual side chains, the polymerization state will be favoured since more energy is required to break the backbone bonds, and the ceiling temperature will be increased.97
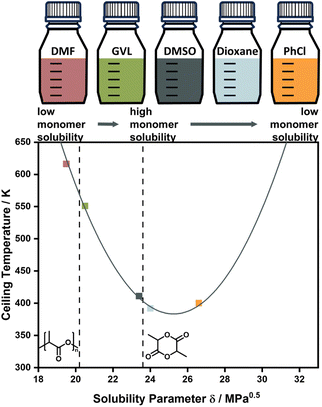 | ||
| Fig. 5 Changing the ceiling temperature through choice of solvent. The smaller the solubility difference between monomer and solvent, the lower the ceiling temperature. Adapted from ref. 71 “Like recycles like”: selective ring-closing depolymerization of poly(L-lactic acid) to L-lactide, L. Cederholm, J. Wohlert, P. Olsén, M. Hakkarainen, K. Odelius, Angew. Chem. Int. Ed., 61, 33. Copyright© 2022 the authors. | ||
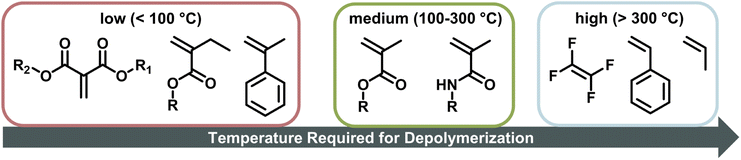
When the α-position has a second substituent, as is the case for AMS or methacrylates, lower ceiling temperatures have generally been observed due to weaker C–C bonds arising from the more strained backbones. For itaconates, a monomer class derived from itaconic acid, depropagation already has a strong effect on polymer formation well below 100 °C due to their large α-substituents.98 How much the ceiling temperature is lowered can also depend on the electronic properties of the second substituent. When the substituent was an ether, the resulting ceiling temperature was higher than in the case of an alkyl.99 Generally, monomers become hard to polymerize for any substituent larger than methyl.100 α-Ethacrylates already have ceiling temperatures that are around 150 °C lower than their methacrylate counterparts.101 As for the primary substituents this effect is exaggerated for branched substituents.102 The exception is substitution on the double bond in a ring opening polymerization, where the effect is reversed since substituents reduce the steric hindrance in the transition state.103 In summary, the less substituted a monomer, the higher the electronic stabilization by the side chain, and the less bulky a vinyl monomer, the higher the required temperature to achieve effective depolymerization (Fig. 6). For this reason, the depolymerization of polypropylene and polyethylene, which are the most widely used consumer plastics, is very challenging since high temperatures are required for depropagation, and such a high temperature environment gives rise to many side reactions, and low monomer recovery.104
Determining ceiling temperature
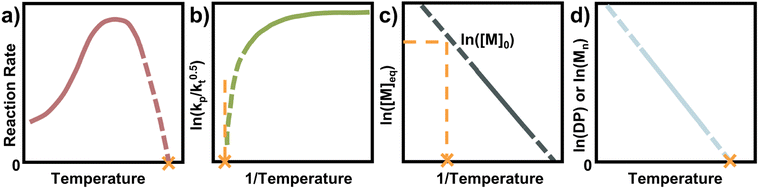
Seeing how small changes in the reaction conditions can have significant influences on the equilibrium position, it is important to determine ceiling temperatures and thermodynamic parameters for effective depolymerization systems. A multitude of methodologies are available to determine ceiling temperatures, and some of the most straightforward and commonly used are discussed in this section.Before choosing a method, it must be clear whether free radical polymerization (FRP) or a living/controlled polymerization is used. In a controlled polymerization, the assumption is that irreversible termination is minimized, and the MEC can be directly determined from the final conversion. In FRP this cannot necessarily be done, and it has been shown that the final conversion can lie rather far away from the MEC since termination and loss of propagating species play an important role.81 Especially at high temperatures, the half-life of the radical initiator approaches the lifetime of the propagating radical which results in a limited conversion, away from the equilibrium.87
Therefore, for FRP another parameter must be used to determine the ceiling temperature. One option is to measure the polymerization rate for different temperatures, in the same way Dainton demonstrated for his initial experimental determinations.66 This is much easier today as modern analysis methods such as NMR make kinetic studies fast, accurate, and accessible. The rate first increases as the temperature increases until a rate maximum is reached, from thereon depropagation becomes significant and the rate decreases until the ceiling temperature is reached. It is not necessary to perform experiments up to the ceiling temperature as the curve can be extrapolated to zero (Fig. 7a).
Another way to conduct ceiling temperature measurements from FRP was pioneered by Yamada and co-workers.89,105 Here, the varying initiation rate at different temperatures is accounted for.100,106 From the apparent rate constant of the polymerization, knowledge of initial initiator concentration ([I]0), decomposition rate (ki), and initiator efficiency (f), as well as the reaction time (t), initial monomer concentration ([M]0), and final monomer conversion ([M]), the value (kp/kt0.5) can be determined from the following equation:
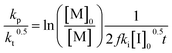 | (11) |
By determining kp/kt0.5 at different reaction temperatures, its natural logarithm can be plotted against 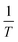 resulting in a graph like that shown in Fig. 7b. The ceiling temperature is then the temperature for which the slope of this graph becomes infinite.
resulting in a graph like that shown in Fig. 7b. The ceiling temperature is then the temperature for which the slope of this graph becomes infinite.
For a controlled polymerization where termination is negligible, a simpler treatment is possible. Here, the polymerization is conducted at different temperatures for the same initial concentration and the final conversion is measured. The remaining monomer concentration is then equivalent to the MEC at this temperature. To determine the ceiling temperature for a MEC equivalent to the initial concentration, the concentration is plotted logarithmically in an Arrhenius plot and fitted using the van’t Hoff expression derived from eqn (2) and (3):71,107–109
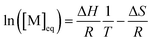 | (12) |
The temperature value for which this expression is then equal to the logarithm of the initial concentration, is the ceiling temperature for this MEC (Fig. 7c). A big advantage of this method is the simultaneous determination of the polymerization entropy and enthalpy, giving an even more accurate picture of the reaction's thermodynamic characteristics.
For a rapid but rough determination of ceiling temperature for specific reaction conditions, an even simpler method can be utilized. When molecular weight and/or degree of polymerization can be accurately determined, the logarithm of either can be plotted against the temperature.72,87 A linear relation should be observable and extrapolation to zero gives the ceiling temperature (Fig. 7d). The reasoning behind this being that at the ceiling temperature, no formation of high molecular weight polymer should take place. However, the molecular weight is not solely dependent on the equilibrium position but also on termination and transfer reactions.110 Since these reactions can exhibit a temperature dependence too, it is not always clear whether the molecular weight change with temperature can be fully attributed to reaching the equilibrium position of the polymerization. Equilibrium positions generated from this method should therefore be viewed more as an approximation than precise determination.
Ceiling temperature as a measure of depolymerizability
The position of the equilibrium, given by the ceiling temperature and MEC, is an important characteristic of any depolymerization reaction, as it gives information on whether monomer can be regenerated under certain reaction conditions. Additionally, a solid understanding of the parameters involved in tuning the equilibrium position is paramount for the development of depolymerization systems with effective monomer regeneration. However, the ceiling temperature can only be a good quantitative measure if the limitations are well understood. The ceiling temperature is a characteristic of the propagation–depropagation equilibrium, completely disregarding any initiation or termination reactions. Therefore, the MEC is not a theoretical monomer yield of a depolymerization under the given conditions, but more akin to a theoretical depolymerization limit. It is the maximum amount of monomer which can be obtained. Only looking at thermodynamic parameters can therefore make monomer generation appear much more feasible than it actually is under the experimental conditions. Hence, a kinetic analysis and mechanistic understanding of any depolymerization reaction is essential to complete the picture since it takes initiation and termination into account.Mechanism and kinetics of depolymerization
Keeping the thermodynamic principles discussed in the previous section in mind, why does poly(methyl methacrylate) (PMMA) depolymerize readily in solution at moderate temperatures when it has been prepared by RDRP but does not depolymerize to high conversion under the same conditions when it has been prepared by FRP?41 Both polymers exhibit identical equilibrium positions because the ceiling temperature is independent of the synthesis method, therefore, both should show equal affinity for monomer regeneration. So why do they not exhibit the same depolymerizability? The answer lies in the kinetics of the reactions, which are different for the polymers prepared by FRP and RDRP respectively. Therefore, this clearly illustrates that a thermodynamic treatment alone does not provide sufficient evidence for or against the feasibility of monomer generation and needs to be complimented by kinetic considerations.Generally, the kinetic characteristics connect to the thermodynamic ones. Only looking at the propagation–depropagation equilibrium, the forward and the backward reactions proceed with individual rate constants (Scheme 1). The rate of the propagation reaction can therefore be expressed as follows:
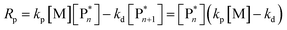 | (13) |
 | ||
| Scheme 1 Propagation–depropagation equilibrium for the addition of monomer to an active species with the reaction constants for the propagation reaction (kp) and the depropagation reaction (kd). | ||
The equation can be simplified since for the long chain assumption the propagating species is considered the same before and after the addition of one monomer unit. At the chemical equilibrium, the reaction rate falls to zero since no more macroscopic change is observed. The equilibrium constant is then expressed as the ratio between the propagation and depropagation constant.
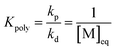 | (14) |
The reaction constants are temperature dependent characteristics, and their magnitude depends on the activation energy of the reaction (Ea,p/d) as well as a pre-exponential factor (A), and the Boltzmann constant (kb).
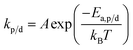 | (15) |
Eqn (14) and (15) together also explain why the equilibrium position is temperature dependent as the rate of propagation and depropagation both vary with temperature but kd increases much faster with temperature than kp.56
However, the kinetic description of the propagation and depropagation reaction still does not explain the difference observed during depolymerization of PMMA made by RDRP and FRP. This is because the depropagation reaction has been the only consideration and any other contributions have been neglected.
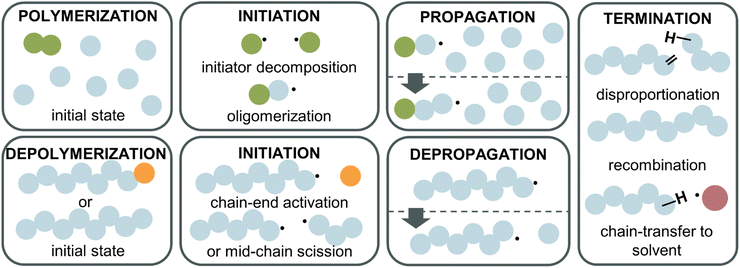
Depolymerization mechanism
To fully understand why the difference between RDRP-synthesized and FRP-synthesized PMMA exists, a closer examination of the reactions involved in the depolymerization mechanism is necessary. In the following, radical depolymerization is exclusively covered since it is the most common. Each depolymerization reaction consists of three main steps, similar to FRP: initiation, depropagation, and termination (Fig. 8). The possible termination pathways are even identical in polymerization and depolymerization.Starting with initiation, two pathways exist. First, if a polymer chain has a functional end-group, which could be a terminal vinyl group, a halogen, a CTA etc., i.e., any group with a lower bond dissociation energy than the backbone bonds, the initiation will take place at the chain-end generating a terminal propagating species. Second, if no functional group is present on the chain-end, the polymer will undergo mid-chain initiation by scission at higher temperatures. Two scenarios are possible for mid-chain initiation. If weak links are present scission will first occur here since the bond energy is lower than for the rest of the backbone. A weak link in a polymer backbone is usually the result of a head-to-head reaction such as termination by recombination during the polymerization. Since such a scission produces two considerably stable radicals, and as the bonds are normally more sterically hindered, less energy is required to cleave a weak link. In the absence of weak links or after these sites have all been initiated, scission occurs statistically along the backbone to initiate radicals (random scission). The different initiation pathways also explain why FRP-made PMMA does not depolymerize under the same conditions as RDRP-made PMMA. Most of the chains do not have a functional end-group, therefore, higher energy is required to initiate radicals than for the functional chain-ends of RDRP-made PMMA. Once radicals are generated, the depropagation is then equal, which is why no difference in ceiling temperature is expected. When the depolymerization is modelled,111 chain-end initiation is independent of the molecular weight and degree of polymerization, as a chain has the same probability of being initiated whether it has 100 or 500 repeat units. For mid-chain initiation, the opposite is true. Every repeat unit is a potential initiation site therefore, the higher the polymer concentration, and/or the higher the DP, the higher the initiation rate (eqn (20)), as the repeat unit concentration (RUC) is higher. As an example, 0.1 M of a 100k PMMA and 1 M of a 10k PMMA exhibit the same mid-chain scission initiation rate. Furthermore, the dispersity (Mw/Mn) of the polymer determines the reaction order in this case. A narrow molar mass distribution means all chains have the same initiation probability while for broader distributions, the probability of each chain varies as the chain length varies.112,113
For the termination of radicals, disproportionation and recombination take place, which can create polymeric residue during the reaction. In addition, chain transfer must be considered. Like polymerization, the radical can be transferred to the solvent, terminating the polymer chain. Further, a propagating chain can transfer the radical to any position on another polymer chain or engage in backbiting, an intramolecular chain transfer.114,115
Depending on the exact initiation and termination pathway or combination thereof, the rate equations look different. Unfortunately, the consequence is that intricate knowledge of the reaction pathway is necessary (e.g., order of reaction, radical concentration, side reactions etc.) to analytically describe or model kinetics. For simplified cases, derivations have been conducted by various authors and were summarized by Friedman.116 However, oftentimes details such as the reaction order remain elusive especially for more complicated systems. To counter this problem, Criado and co-workers117 have developed a universal, numerical modelling methodology for initiation via random scission by utilizing conversion functions for the different reaction pathways. To apply it, only the degradation activation energy must be determined experimentally. This methodology is complimented by a numerically verified analytical model for chain-end initiation.118
Monomer is produced during the depropagation step. For depropagation happening sequentially in a rapid chain of reactions and thereby, generating monomer, this process is called unzipping. The average number of eliminated monomer units taking place between an initiation and termination event is called the zip length. Conceptually, the zip length is the depropagation equivalent of the kinetic chain length in the propagation reaction. Therefore, it is also sometimes referred to as the kinetic chain length of depropagation in literature. As a quantification of the average number of repeat units lost, it depends on the ratio of initiation and termination to propagation rate constants. The ratio can be expressed as the probability of a depropagation event taking place over a termination event after initiation:114,115,119
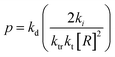 | (16) |
The zip length (1/ε) can then be expressed in terms of this probability:
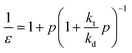 | (17) |
For depolymerization reactions where the zip length is larger than the degree of polymerization, it is likely that an initiated polymer chain depolymerizes fully without leaving a shorter polymeric species behind. In this case, the zip length is the same whether the propagating species is generated via chain-end initiation or mid-chain scission.116 In addition, longer zip length than the degree of polymerization combined with chain-end initiation results in an unchanged molar mass distribution during the depolymerization. Any chain that is initiated fully depolymerizes leaving no residue that can contribute to the molar mass distribution.120 If a chain does not fully depolymerize, it appears as low molecular weight tailing indicating dominant termination reactions. Theoretically, the zip length is a good indication of how well a polymer depolymerizes fully to monomer. However, zip lengths are strongly dependent on reaction conditions since they are given by the ratio of termination to initiation and propagation. Considering the difference in the extent of chain transfer in benzene and toluene, for the same polymer shorter zip lengths would be expected in toluene as the radical transfers more readily. In literature, zip lengths have been reported that differ by up to two orders of magnitude for the same polymer. For that reason, no values are provided here, but it should be pointed out that a systematic investigation of zip lengths and influencing effects would be vastly beneficial for the kinetic understanding of the depolymerization process and could reveal strong influencing factors that have not been previously considered. For enhanced understanding, a few general consequences of different zip lengths are still discussed here. If the zip length is small, termination reactions are dominant, and a large fraction of side products will be formed such as in the depolymerization of PS.121,122 Even though reported values vastly differ for the same polymer, reported zip lengths for PMMA are generally much larger than those for PS since the backbone in PS is less substituted, the number of hydrogen atoms in the backbone is larger. The less substituted the backbone, the more prone it is to backbiting and chain transfer from another propagating species. Polytetrafluoroethylene for example exclusively depolymerizes to monomer as chain transfer to the polymer is not possible due to a fully substituted backbone.28 Combining a sparsely substituted polymer backbone with a low stability radical such as in the case of acrylates then makes depolymerization via a depropagation mechanism unfeasible, which is possibly why it has not been reported for many monosubstituted monomers.
Experimental studies of depolymerization mechanisms and kinetics
In literature, depolymerization and degradation studies have mostly been reported for PMMA, PS, and PAMS. PAMS has only been considered for depolymerization studies however, there is little practical interest in PAMS materials. The mechanism of FRP-made PMMA depolymerization in bulk strongly depends on the reaction temperature and roughly follows three regimes. At low temperature (around 170 °C), head-to-head linkages are broken to initiate chains. As these are a result of recombination reactions in radical polymerization, such degradation is not observed in polymers prepared by anionic polymerization.123 However, the importance of such weak-link scission is small compared to the contribution of chain-end and random initiation.124 At higher temperature (around 260 °C), vinyl-terminated chains are mainly initiated at the chain-end by radical transfer reactions, with no change in the molar mass distribution observable over the course of the reaction.125 While non vinyl-terminated chains are only initiated at even higher temperatures (above 300 °C) through random scission during which a side chain bond is cleaved that places a radical on the chain.126 In addition to detailed investigations in bulk, Grant and Bywater investigated the thermal depolymerization of free-radical PMMA in solution and while the mechanism was similar, they found two main differences.127 In solution, the depropagation rate was dependant on the initial polymer concentration. It was hypothesized that this was due to the difference in the reaction medium when different amounts of polymer were present, which affects the equilibrium position, as discussed in the thermodynamics section, although the effect was not quantified.128,129 Secondly, chain termination by radical transfer to solvent during the depolymerization had to be considered. They derived a rate expression for the depolymerization via chain-end initiation and subsequent unzipping: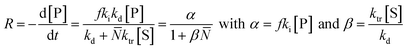 | (18) |
![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) is the number average chain length of the disproportionated chains, ki is the initiation constant, and kd is the depropagation constant. The conversion limit follows from the exclusive activation of vinyl terminated chain-ends under the reaction conditions in solution depolymerization of PMMA:127
is the number average chain length of the disproportionated chains, ki is the initiation constant, and kd is the depropagation constant. The conversion limit follows from the exclusive activation of vinyl terminated chain-ends under the reaction conditions in solution depolymerization of PMMA:127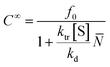 | (19) |
It follows that the depolymerization rate and final conversion are larger for solvents with lower chain transfer constants.130
For depolymerization initiated by random mid-chain scission, a modified rate equation of initiation was obtained:
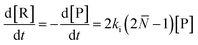 | (20) |
For PS, the depolymerization behaviour looks different. In bulk, temperatures between 250 °C and 300 °C are required to achieve significant monomer generation. A large initial drop in molecular weight is observed, which was attributed to random scission followed by disproportionation of the two chain-fragment radicals.122 Since random scission is chain length dependent, the rate of the initial degradation is dependent on the molecular weight though the scission does not produce a significant amount of monomer.132 After the initial drop in molecular weight (Fig. 9) the reaction rate depends on the chain-end concentration indicating a chain-end initiation and the molecular weight remains fairly constant pointing towards complete unzipping from the end with a large zip length, monomer was only regenerated in this reaction step.86 While there is some debate over the zip length of PS,133–135 these findings were supported by the observation that the molecular weight decrease levelled off at approximately 5000. Therefore, smaller chains must fully depropagate, making a zip length of around 50 necessary.136 For PS, the activation energy for the chain-end initiation was lower than for random scission on the backbone.137
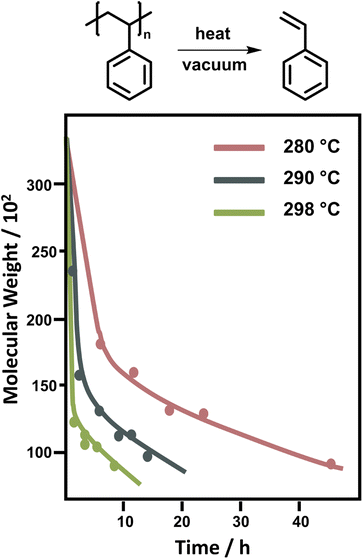 | ||
| Fig. 9 Change of molecular weight of PS during the depolymerization at different temperatures. Adapted from ref. 86 with permission from the Royal Society of Chemistry, copyright 1957. | ||
Depolymerization of PS in solution was limited to a few solvents as high reaction temperatures were still required. Similar molecular weight change profiles as in Fig. 9 were obtained. When the reaction was conducted in naphthalene and tetralin, the same initial drop in molecular weight occurred as in bulk. However, in the solvents the subsequent depolymerization process was strongly inhibited, as both solvents can act as chain transfer agents, and greater mobility of radical chain-ends in solution facilitated more termination.138 To conclude, mid-chain scission in PS did not produce monomer but resulted in rapid reduction of molecular weight at the start of the reaction. Generally, the depolymerization of PS requires higher temperatures both in bulk and solution than PMMA. Lastly, reported kinetic factors vary greatly between publications and more systematic kinetic investigations using modern analysis methods could potentially further support and clarify our current mechanistic understanding.
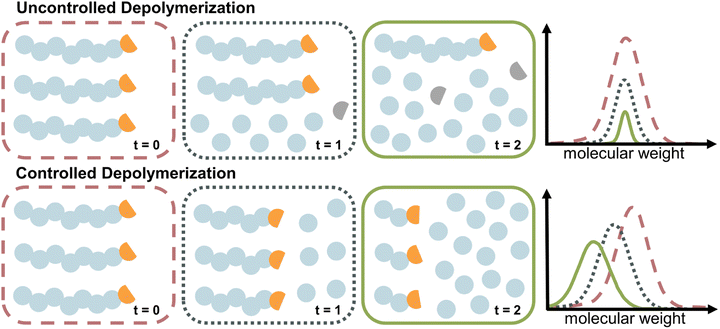
The case of controlled depolymerization
The depolymerization studies discussed so far are mechanistically a reversal of FRP, which is characterized by a lack of control over the chain growth. Once a chain is initiated, it grows until it is terminated. The same is true for uncontrolled depolymerization where a chain rapidly depolymerizes without control (i.e., deactivation) over the depropagation step. Controlled depolymerization on the other hand would be equivalent to controlled polymerizations such as RDRP. In RDRP, chains grow in a controlled manner, as the propagation centre can be temporarily deactivated and then re-activated. Such deactivation dominates over propagation, which enables precise control over the molecular weight of the polymer, which progresses linearly with conversion. Conceptually, controlled depolymerization would work in a similar way where the depropagation could be metered by repeated, reversible deactivation and therefore, chains would shift to lower molecular weight linearly with conversion instead of rapid unzipping until chain loss while the polymer concentration remains constant throughout (Fig. 10). Thereby, the zip length is reduced to very low values. In such a system, mirroring the behaviour in RDRP, the reversible deactivation of the depropagating chains must dominate over the depropagation. Such a system is highly desirable since it enables control over the zip length, and thereby over the monomer release, molecular weight during depolymerization, a potential reduction in the frequency of side reactions due to sufficient deactivation, and a retention of chain-end functionality. Such a case of controlled depolymerization was recently reported, where the molecular weight could be controlled during depolymerization, which was applied to analyze the sequence and monomer distribution in copolymers.139Thermodynamic approaches to solution depolymerization
Since polymers with a functional end-group can be used for chain-end initiation at lower temperatures, it is not surprising that the current literature for depolymerization of addition polymers is mainly focussed on polymers made by RDRP. Depolymerization has been reported for polymers made by ATRP, and by RAFT polymerization. Before delving deeper into this research, some crucial terminology must be pointed out. Reaction systems are almost exclusively described in terms of the RUC. The RUC refers to a theoretical concentration of monomer if all polymer was depolymerized. Such notation is used rather than the polymer concentration since it can be directly compared to the MEC at the reaction temperature while the polymer concentration itself does not necessarily provide this information. Final monomer concentrations can then be easily inferred from final polymer conversions or monomer yields and resultingly the thermodynamic feasibility of a reaction can be assessed.The functional end-groups of RDRP-made polymers can be selectively cleaved to generate propagating chain-end radicals at much lower temperatures than the all-carbon bonds of the backbone. Therefore, they can be depolymerized fairly easily by leveraging the reaction conditions, such as reaction temperature, in situ monomer removal, and dilution to tune the propagation–depropagation equilibrium. It is important to note however that depolymerization has only been reported for polymethacrylates and not for any other polymer class. Subsequently, the scope of such approaches is presently somewhat limited.
For RDRP methods based on chain transfer, depolymerization has been reported for RAFT polymerization and for iodine transfer polymerization (ITP). In fact, the depolymerization of a RAFT-synthesized polymer was the first report of CRM for RDRP-made polymers. Gramlich and coworkers first came across the propensity of methacrylate-terminated oligo-dimethylsiloxane to depolymerize under polymerization relevant temperatures (70 °C) at a RUC of 100 mM.140 However, only 27% of monomer was regenerated. These results tie in neatly with the thermodynamic theory discussed above. Depropagation can be favoured at any temperature given that the monomer concentration is below the corresponding MEC, and propagating species can be generated. The authors showed that the obtained monomer concentration was the MEC at this temperature, and the presence of the RAFT agent on the chain-end made initiation feasible even below 100 °C, and the bulky side chain drove the depolymerization. Such substantial monomer regeneration would not be possible for this polymer made by FRP, since the chain-end is stable at the utilized reaction temperature.
After this first report, it took almost four years until near-quantitative depolymerization conversion was reported for RAFT-made polymethacrylates. Strikingly, this report included poly(methacrylates) with much smaller side chains than the polysiloxane-based macromonomer investigated in the first report, making depolymerization much less thermodynamically favored. By increasing the temperature to 120 °C, it was possible to depolymerize poly(methyl methacrylate) at a RUC of 5 mM to almost full conversion and monomer generation was even feasible for heat-sensitive monomers that could never previously be depolymerized (Fig. 11).41 In follow-up work, depolymerization was proven to be feasible for a range of methacrylate side-chains, solvents, and RAFT-agents. However, it was also shown that the chosen reaction conditions strongly influenced the final monomer yield due to varying degrees of end-group degradation141 and initiation by solvent-derived radicals.142 Corresponding to the end-group degradation, larger DPs at the same RUC led to lower monomer yields as the end-group concentration was lower and the degradation effect was exacerbated. Here, effects on the equilibrium position were not under investigation. To achieve these high depolymerization conversions, the temperature had to be raised significantly (70 °C vs. 120 °C) compared to the work by Gramlich, yet it remains at significantly lower values than what is required for FRP-made polymers (300 °C).127 Monomer generation is feasible at even lower depolymerization temperatures, when light is used to increase the chain activation either in combination with a photocatalyst,143 or without.43 The increased activation led to much faster depolymerization rates, showing that the initiation reaction can be considered the rate limiting step, as the depropagation is swift even if the temperature is lowered. This process is well known for RAFT polymerizations under irradiation.144–147 Even though the polymers were made by a RDRP method, which meant that the molar mass distribution could be precisely controlled, all presented depolymerizations did not proceed in a controlled manner. Hence, the RAFT agents supplied by the chain activation did not appear to be capable of sufficiently deactivating the propagating chains to exert control over the molecular weight. Why control over the depolymerization could not be achieved in these systems is not known at this point.
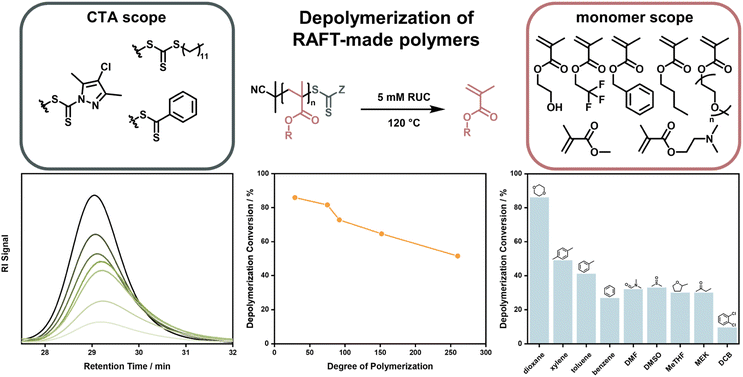 | ||
| Fig. 11 Depolymerization of polymethacrylates made by RAFT polymerization with different monomers, and CTA end-groups. The polymer signal reduces over the course of the reaction (bottom left), the final depolymerization conversion decreases for increasing DPs (bottom middle), and the final depolymerization conversion changes depending on the used solvent (bottom right). Adapted with permission from ref. 41 Reversing RAFT polymerization: near-quantitative monomer generation via a catalyst-free depolymerization approach, H. S, Wang, N. P. Truong, Z. Pei, M. L. Coote, A. Anastasaki, J. Am. Chem. Soc., 144, 10, copyright 2022 the authors and ref. 141 Investigating the effect of end-group, molecular weight, and solvents on the catalyst-free depolymerization of RAFT polymers: possibility to reverse the polymerization of heat-sensitive polymers, H. S, Wang, N. P. Truong, G. R. Jones, A. Anastasaki, ACS Macro Lett., 11, 10, copyright 2022 the authors. | ||
In contrast to the RAFT-made polymers, a significant molecular weight shift was observed for the depolymerization of PMMA made via ITP.44 The molecular weight shift amounted to around 40% weight loss, however depolymerization conversion was not reported so conclusions cannot be made as to whether the depolymerization proceeded with control. Strikingly, this depolymerization was achieved with a much higher RUC concentration (200 mM) than reported for the RAFT polymers. Since PMMA was depolymerized at 120 °C in both cases, the limited conversion at higher RUC for RAFT polymers cannot be a thermodynamic effect – remembering that the ceiling temperature is independent of the method which creates the active centre – but must be a limitation specific to the RAFT end-group (e.g., a side reaction). Additionally, such a depolymerization was only successful for a highly active ITP catalyst developed specifically for this work, and failed when more conventional catalysts were applied. Depolymerization of ITP-made polymers is therefore a promising topic for future research.
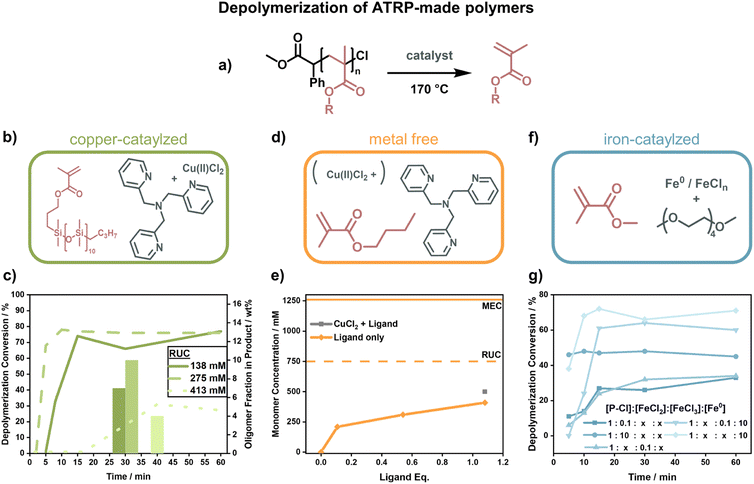
The first depolymerization of PMMA synthesized by ATRP was reported by Ouchi and his team. In 2019, they reported the regeneration of monomer from chlorine-terminated polymer using a ruthenium catalyst at 120 °C and a RUC of 500 mM, albeit with a low conversion of 25% in 24 h and substantial side-reactions. As opposed to the RAFT depolymerization, the molecular weight also shifted linearly with conversion and end-group functionality was retained evident by stopping and restarting the reaction multiple times.148 While the authors determined the low conversion to be due to reaching the MEC, comparing this with results obtained from the RAFT-made polymers, this seems to be an underestimation as higher final concentrations were reached. Since the activation of end-groups was very effective in this system, they followed-up this work by incorporating a few percent of methyl chloroacrylate in the FRP of PMMA. With these units, radicals were then selectively generated by group 8 metal catalysts on the backbone and the polymer degraded effectively at 100 °C.149 The use of ‘degraded’ instead of ‘depolymerized’ is intentional here because the authors did not show any monomer regeneration.
When Matyjaszewski and co-workers replaced the ruthenium catalyst with different catalysts and raised the temperature to 170 °C (Fig. 12a), they were able to recover high yields of monomer.42 Such a system was first developed for the macromonomer poly(dimethylsilane) methacrylate (PDMSMA, Fig. 12b) since the ceiling temperature is lower due to the much bulkier side chain compared to MMA (Section 2.2). When the depolymerization was conducted with a Cu(II)–ATRP complex, the depolymerization proceeded swiftly to high conversion (∼80% in 15 minutes under optimized condition).42 The depolymerization was conducted at a much higher RUC (275 mM) than for the RAFT systems, potentially because the presence of catalyst allowed for an immediate and selective activation of chain-ends compared to the thermal activation. Besides proving that ATRP-synthesized polymers can be effectively depolymerized as well, the authors conducted a more systematic investigation into the role of the individual reaction components. The ligand plays an important role in the system in generating the activating species via electron transfer, and an excess was required for the depolymerization to selectively proceed to high monomer conversion. Higher RUC drastically reduced the conversion (only 21% at 413 mM), and lower conversions with less selectivity for the monomer were also observed when the catalyst loading was reduced. It was also discovered that the decrease in depolymerization rate resulted in reduced oligomeric side-product formation (Fig. 12c).42
Initial depolymerization reports were soon followed up with the depolymerization of the poly(n-butyl methacrylate). Impressively, moving to the shorter n-butyl side-chain, and using TPMA as a ligand (Fig. 12d), they were able to almost triple the RUC (750 mM).150 Besides achieving conversions of nearly 70%, the system could even operate in the absence of metal catalyst where ligand alone was enough to activate the propagating radical (Fig. 12e). In this case, the chain-end functionality was unfortunately also lost more rapidly, so the more limited conversion compared to the previous system was also a result of non-functionalized chain-ends. The strong dependence of the depolymerization rate on the chain-end activation also points towards initiation being the rate determining step in the depolymerization of methacrylate-based polymers. Such dependence on the initiation step was further observed when copper was replaced by iron as a catalyst (Fig. 12f).151 Interestingly, instead of iron salts, zero-valent iron metal yielded higher depolymerization yields, faster reaction rates, and shorter inhibition periods (Fig. 12g). When light was used for activation in addition to an iron catalyst in a photothermal system, the temperature could be lowered to 100 °C, and almost perfect temporal control was achieved with low catalyst loadings at 120 °C.152 Once again, the results for the polymers produced by ATRP show that the depolymerization temperature can be lowered significantly compared to conditions used for FRP (∼300 °C (ref. 127) vs. 100 °C for polymethacrylates) as the activation energy of the initiation step is decreased by the functional end-groups. The studies have proven that limited monomer regeneration is less an issue of impractical equilibrium positions but more of inhibition of the propagating radical generation.
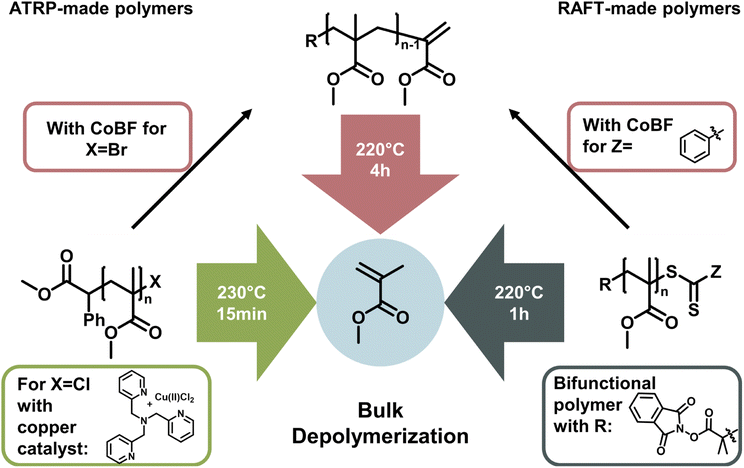
The latest development in depolymerization of RDRP-made polymers is conducting the reaction in bulk. While this seems counterintuitive since the absence of solvent means that the monomer concentration is immediately high, the reaction can be driven by evaporation of monomer at the reaction temperature and therefore instantaneous removal from the monomer equilibrium. Pioneering work in bulk depolymerization (Fig. 13) was recently conducted in parallel by the groups of Anastasaki,153 Matyjaszewski,154 and Sumerlin.155 For polymers synthesized by RAFT and ATRP, the functional groups can be transformed to a vinyl end-group, which can be activated at temperatures around 200 °C and subsequently depolymerized.153 The main advantage here is the lack of solvent, making it much more environmentally friendly, and even though the required energy is higher, a purification step to obtain the monomer is unnecessary. Thermodynamically, the reaction is driven by evaporation of the generated monomer.
Therefore, bulk depolymerization is a highly attractive method. For a faster depolymerization of ATRP-made polymers in bulk, copper can be directly added to the mixture to generate chain-end radicals instead of transforming the end-group to a vinyl group.154 When a bifunctional RAFT agent was used in the polymerization of poly(methyl methacrylate), radicals could be formed on both ends of the polymer chain, maximizing the initiation efficiency and therefore reaching high conversions in shorter periods of time. It is also particularly advantageous for the depolymerization of higher molecular weight polymers.155
In all the cases discussed above, the depolymerization is arguably achieved by simply putting the long developed and sophisticated polymerization systems of RDRPs at reaction conditions that shift the propagation–depropagation equilibrium to favour depropagation. Reaction systems are not necessarily enhanced by developing new catalysts or reaction procedures, but rather by choosing the reaction conditions in a way which influences the enthalpy and entropy to reach the favoured depropagation. Therefore, these approaches are ultimately governed by ceiling temperature and MEC, even if new kinetic effects are discovered and overcome in the process. To summarize, the field of depolymerization of RDRP polymers is still in its infancy. Progress is rapid and oftentimes raises more questions than it answers. While all the presented solution methods have drawbacks such as reaction temperatures over 100 °C, the lack of control over the reaction, the requirement for high dilution, or monomer removal during the reaction, many of these issues are expected to be addressed in the future.
Low-energy depolymerization through catalysis
Depolymerization via a radical pathway of vinyl polymers made by addition polymerization has only been effectively demonstrated for polymethacrylates. Whether this is because the ceiling temperature of other polymers can be very high and therefore the solution depolymerization is not feasible at moderate temperatures or that a ceiling temperature has not even been reported or lies far beyond the degradation temperature, does not mean that monomer generation is impossible for these polymers. In the following section, the discussion is guided towards reports of depolymerization of addition polymers, which from a radical depropagation standpoint seem thermodynamically and/or kinetically impossible. Generally, depolymerizations are conducted which do not proceed via radical pathways, polymers are modified before depolymerization to increase the selectivity of breaking backbone bonds, or strategies are employed that only indirectly produce monomer from the polymer.To illustrate what is meant by depolymerizations that could appear to be thermodynamically impossible the depolymerization of PS in ball-mills is considered as an example. A ball mill is essentially a container which is charged with the substrate and milling material such as metal beads and then shaken at a high frequency. By ball-milling commercial PS under ambient atmosphere and room temperature for 12 h, 7% of styrene monomer was regenerated.156 While this might not seem like an impressive yield, considering the thermodynamics of the propagation–depropagation equilibrium and assuming ideal generation of radicals, the equivalent of producing this much monomer at ambient temperature via a radical mechanism would require the dissolution of the reported 3 g of PS in 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 L of solvent, which corresponds to a RUC of 2.9 μM.† As opposed to the bulk depolymerization of PMMA at high temperatures, the monomer is also not removed from the reaction mixture in this case, so the removal cannot drive the equilibrium to monomer generation. So why is it possible to generate monomer? The authors proposed a catalytic cycle in which trace metal from the milling beads and oxygen from the ambient atmosphere result in metal-capped chain-ends, which subsequently eliminated monomer, foregoing the thermodynamics of the depropagation reaction.
793 L of solvent, which corresponds to a RUC of 2.9 μM.† As opposed to the bulk depolymerization of PMMA at high temperatures, the monomer is also not removed from the reaction mixture in this case, so the removal cannot drive the equilibrium to monomer generation. So why is it possible to generate monomer? The authors proposed a catalytic cycle in which trace metal from the milling beads and oxygen from the ambient atmosphere result in metal-capped chain-ends, which subsequently eliminated monomer, foregoing the thermodynamics of the depropagation reaction.
These results were supported by Choi and co-workers, who conducted a mechanochemical study on depolymerization of mainly poly α-methylstyrene.157 They also obtained a significant monomer yield below the bulk ceiling temperature (55%, Tc = 66 °C) and a comparable yield of styrene from PS. If metal catalysis is able to effectively generate monomer from PS at low temperature, it might also explain why the addition of table salt or copper salts to PS gave higher styrene yields under pyrolysis conditions (420 °C).158 However, it is important to note that the mechanism of these depolymerizations are unknown, and further studies are required.
A metal-catalyzed monomer regeneration via a non-radical mechanism also ties in with depolymerization reports for polyacrylates and polyacrylamides. Zhu and co-workers serendipitously discovered that polyacrylamides could be depolymerized when a radical trap such as TEMPO was added to aqueous Cu(0) polymerizations. They also hypothesized that trapping of the radical resulted in copper-capped chains followed by β-alkyl elimination of monomer, facilitating substantial monomer yields at 0 °C (Fig. 14).159 Another similar report saw the regeneration of monomer when acrylates and acrylamides where polymerized by Cu(0)-mediated polymers in carbonated water at 0 °C and the reaction was left at reaction conditions after the polymer was obtained.160 While the mechanism was not fully specified, it seems reasonable that the depolymerization proceeded in a similar fashion. Two obvious similarities between the aforementioned methods are the use of Cu(0) as the catalyst and the requirement of sub-room temperature conditions. Excitingly, these results together with the ball-milling results suggest that there are pathways other than radical depropagation which might enable monomer generation from vinyl polymers at low temperatures, and that this could operate via hitherto unknown transition metal mediated catalytic pathways governed by different thermodynamics and kinetics.
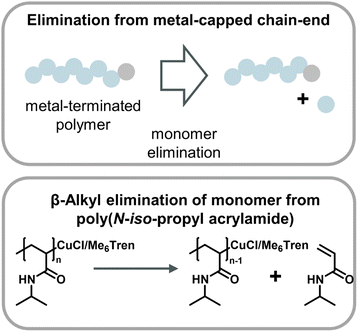 | ||
| Fig. 14 Scheme of monomer generation from metal-capped polymer chains (top) with the example of poly(N-iso-propyl acrylamide) depolymerization in an aqueous Cu-ATRP system through β-alkyl elimination from copper-terminated chain-ends as described in ref. 159. | ||
Catalytic pathways to monomer regeneration that do not require metal-capping of the chain-end have also been developed. However, catalytic depolymerization is challenging because the C–C backbone of vinyl polymers, such as polyethylene (PE) or polypropylene, does not present selective sites for the catalyst to attack. As a result, the catalyst can also degrade the side chains, which makes monomer recovery unfeasible. Recently, this problem was overcome in the generation of propylene monomer from PE (Fig. 15). By functionalizing the backbone prior to depolymerization via dehydrogenation, the catalyst was then able to selectively break the formed vinyl backbone bonds.161,162 In both publications, the authors managed to streamline this process in which functionalization and monomer generation took place simultaneously. Remarkably, high monomer yields could not only be generated from pre-synthesized PE, but when the method was applied to post-consumer plastic waste, more than 50% was converted to monomer at 130 °C,162 which is a few hundred degrees lower than reported bulk ceiling temperature for PE (∼300 °C).163 Again here, the reaction did not proceed via the propagation–depropagation equilibrium and was therefore not subject to the same thermodynamic limitations. PE and polypropylene are the most widely used consumer polymers and make up the vast majority of plastic waste worldwide.9 Developing effective and efficient depolymerization strategies for these materials, while challenging, are most impactful for a circular polymer economy. Another example of backbone functionalization to introduce selective sites for catalytic depolymerization is the incorporation of hydroxy groups in the polymer backbone.164 A photocatalyst then cleaved the hydroxylated sites and hydroxy-containing monomer was obtained at 40 °C.
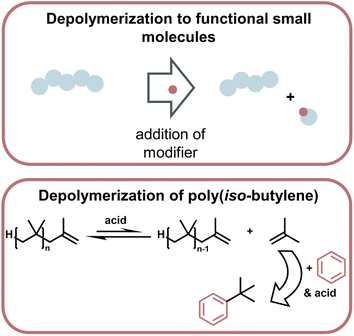 | ||
| Fig. 15 Schematic overview of depolymerization driven by modification of monomer to make functional small molecules, which then thermodynamically drives the depolymerization (top). Such a system was applied to the depolymerization of poly(iso-butylene) which was driven by the highly enthalpically favoured Friedel–Craft type reaction of the monomer with benzene in the presence of strong acid (bottom) as described in ref. 169. | ||
Lastly, a multitude of reports exist where different methods are used to generate small molecules with synthetic value from vinyl polymer waste.165–168 As a specific example (Fig. 16), polyisobutylene was degraded at 0 °C with a strong acid by modifying monomeric products to form more stable bonds than in the polymer so the small molecule formation becomes exothermic, and monomer is removed from the equilibrium.169
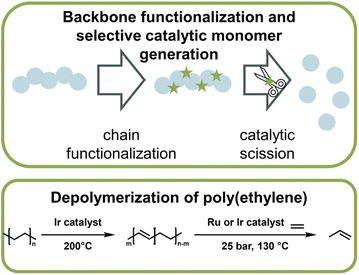 | ||
| Fig. 16 Schematic overview of catalytic monomer regeneration from previously functionalized polymer backbones with selective catalytic sites (top). Example of depolymerization of dehydrogenated polyethylene with ruthenium and iridium catalysts (bottom) as described in ref. 162. | ||
Conclusions
Going back to the initial question, what makes monomer regeneration feasible for a depolymerization reaction? The position of the chemical equilibrium determines whether and to what extent monomer generation is thermodynamically feasible at given reaction conditions. By changing reaction parameters which influence the entropy or enthalpy of the propagation reaction, the equilibrium position can be tuned. However, thermodynamic feasibility alone does not mean that monomer can be generated, as the assessment neglects every other reaction of the depolymerization such as initiation or termination. Therefore, favourable reaction kinetics are also essential for monomer regeneration. The propagation can only take place once active centres have been initiated. Numerous studies have been conducted on both the thermodynamics and kinetics of depolymerization reactions in the last century. While modern depolymerization benefits from easy chain activation by applying principles from RDRP, the fundamental conclusions of the older studies still hold and explain many of the observed phenomena today. Finding the ideal initiation mechanism, exerting control over the depolymerization reactions, expanding the methodology to different materials, and tuning reaction parameters for maximized monomer yield are all exciting prospects for future research in this field. Unfortunately, some polymer classes such as polyacrylates are highly unlikely to ever become depolymerizable by radical depropagation due to unfavourable thermodynamic characteristics and limiting kinetics. However, there are some reports of approaches which generate monomer from these materials, which are mechanistically proposed to eliminate monomer from the polymer via non-radical mechanisms, foregoing some of the thermodynamic and kinetic limitations. However, much more research is needed on this topic to elucidate the processes behind these reactions and as a result making them adaptable, and widely applicable. All in all, exciting times are surely ahead for depolymerization, and a fundamental grasp of the thermodynamic and kinetic concepts so carefully elucidated by pioneers of the field is undoubtedly guiding future research.Author contributions
VL: conceptualization, writing – original draft, writing – review & editing, and visualization. GRJ: conceptualization, writing – original draft, writing – review & editing. NPT: conceptualization, writing – review & editing. AA: conceptualization, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. A. gratefully acknowledges ETH Zurich for financial support. N. P. T. acknowledges the award of a DECRA Fellowship and DP from the ARC (DE180100076 and DP200100231). This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Program (DEPO: grant agreement no. 949219).Notes and references
- M. MacLeod, H. P. H. Arp, M. B. Tekman and A. Jahnke, Science, 2021, 373, 61–65 CrossRef CAS PubMed.
- X.-L. Li, R. W. Clarke, H.-Y. An, R. R. Gowda, J.-Y. Jiang, T.-Q. Xu and E. Y. X. Chen, Angew. Chem., Int. Ed., 2023, 62, e202303791 CrossRef CAS PubMed.
- X. Tang and E. Y. X. Chen, Chem, 2019, 5, 284–312 CAS.
- B. A. Abel, R. L. Snyder and G. W. Coates, Science, 2021, 373, 783–789 CrossRef CAS PubMed.
- W. Xiong, W. Chang, D. Shi, L. Yang, Z. Tian, H. Wang, Z. Zhang, X. Zhou, E.-Q. Chen and H. Lu, Chem, 2020, 6, 1831–1843 CAS.
- J. Yuan, W. Xiong, X. Zhou, Y. Zhang, D. Shi, Z. Li and H. Lu, J. Am. Chem. Soc., 2019, 141, 4928–4935 CrossRef CAS PubMed.
- T. Yan, A. H. Balzer, K. M. Herbert, T. H. Epps and L. T. J. Korley, Chem. Sci., 2023, 14, 5243–5265 RSC.
- C. Jehanno, J. W. Alty, M. Roosen, S. De Meester, A. P. Dove, E. Y. X. Chen, F. A. Leibfarth and H. Sardon, Nature, 2022, 603, 803–814 CrossRef CAS.
- R. Geyer, J. R. Jambeck and K. L. Law, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed.
- G. R. Jones, H. S. Wang, K. Parkatzidis, R. Whitfield, N. P. Truong and A. Anastasaki, J. Am. Chem. Soc., 2023, 145, 9898–9915 CrossRef CAS PubMed.
- A. B. Korpusik, A. Adili, K. Bhatt, J. E. Anatot, D. Seidel and B. S. Sumerlin, J. Am. Chem. Soc., 2023, 145, 10480–10485 CrossRef CAS PubMed.
- A. Adili, A. B. Korpusik, D. Seidel and B. S. Sumerlin, Angew. Chem., Int. Ed., 2022, 61, e202209085 CrossRef CAS PubMed.
- B. Fan, J. F. Trant, R. E. Yardley, A. J. Pickering, F. Lagugné-Labarthet and E. R. Gillies, Macromolecules, 2016, 49, 7196–7203 CrossRef CAS.
- V. Delplace and J. Nicolas, Nat. Chem., 2015, 7, 771–784 CrossRef CAS PubMed.
- J. Zhou, T.-G. Hsu and J. Wang, Angew. Chem., Int. Ed., 2023, 62, e202300768 CrossRef CAS.
- S. Kobben, A. Ethirajan and T. Junkers, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 1633–1641 CrossRef CAS.
- A. M. Schenzel, C. Klein, K. Rist, N. Moszner and C. Barner-Kowollik, Advanced Science, 2016, 3, 1500361 CrossRef PubMed.
- Z. O. G. Schyns and M. P. Shaver, Macromol. Rapid Commun., 2021, 42, 2000415 CrossRef CAS.
- M. Kirstein, C. Lucking, L. Biermann, E. Brepohl, V. Salikov, C. Eichert, M. Paschetag and S. Scholl, Chem. Ing. Tech., 2023, 95, 1290–1296 CrossRef CAS.
- C. DelRe, Y. Jiang, P. Kang, J. Kwon, A. Hall, I. Jayapurna, Z. Ruan, L. Ma, K. Zolkin, T. Li, C. D. Scown, R. O. Ritchie, T. P. Russell and T. Xu, Nature, 2021, 592, 558–563 CrossRef CAS PubMed.
- Y. Yang, Y. Lu, H. Xiang, Y. Xu and Y. Li, Polym. Degrad. Stab., 2002, 75, 185–191 CrossRef CAS.
- M. N. Siddiqui, D. S. Achilias, H. H. Redhwi, D. N. Bikiaris, K. A. G. Katsogiannis and G. P. Karayannidis, Macromol. Mater. Eng., 2010, 295, 575–584 CrossRef CAS.
- F. Cao, L. Wang, R. Zheng, L. Guo, Y. Chen and X. Qian, RSC Adv., 2022, 12, 31564–31576 RSC.
- G. W. Coates and Y. D. Y. L. Getzler, Nat. Rev. Mater., 2020, 5, 501–516 CrossRef CAS.
- A. C. Fernandes, Green Chem., 2021, 23, 7330–7360 RSC.
- B. D. Vogt, K. K. Stokes and S. K. Kumar, ACS Appl. Polym. Mater., 2021, 3, 4325–4346 CrossRef CAS.
- Z. Deng and E. R. Gillies, JACS Au, 2023, 3, 2436–2450 CrossRef CAS.
- C. M. Simon and W. Kaminsky, Polym. Degrad. Stab., 1998, 62, 1–7 CrossRef CAS.
- N. Kiran, E. Ekinci and C. E. Snape, Resour., Conserv. Recycl., 2000, 29, 273–283 CrossRef.
- D. S. Achilias, I. Kanellopoulou, P. Megalokonomos, E. Antonakou and A. A. Lappas, Macromol. Mater. Eng., 2007, 292, 923–934 CrossRef CAS.
- W. Kaminsky and J. Franck, J. Anal. Appl. Pyrolysis, 1991, 19, 311–318 CrossRef CAS.
- A. Bhargava, P. van Hees and B. Andersson, Polym. Degrad. Stab., 2016, 129, 199–211 CrossRef CAS.
- O. Dogu, M. Pelucchi, R. Van de Vijver, P. H. M. Van Steenberge, D. R. D'Hooge, A. Cuoci, M. Mehl, A. Frassoldati, T. Faravelli and K. M. Van Geem, Prog. Energy Combust. Sci., 2021, 84, 100901 CrossRef.
- W. A. Braunecker and K. Matyjaszewski, Prog. Polym. Sci., 2007, 32, 93–146 CrossRef CAS.
- K. Parkatzidis, H. S. Wang, N. P. Truong and A. Anastasaki, Chem, 2020, 6, 1575–1588 CAS.
- K. Matyjaszewski, Macromolecules, 2012, 45, 4015–4039 CrossRef CAS.
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef CAS.
- G. Moad and E. Rizzardo, Polym. Int., 2020, 69, 658–661 CrossRef CAS.
- J. Nicolas, Y. Guillaneuf, C. Lefay, D. Bertin, D. Gigmes and B. Charleux, Prog. Polym. Sci., 2013, 38, 63–235 CrossRef CAS.
- N. Corrigan, K. Jung, G. Moad, C. J. Hawker, K. Matyjaszewski and C. Boyer, Prog. Polym. Sci., 2020, 111, 101311 CrossRef CAS.
- H. S. Wang, N. P. Truong, Z. Pei, M. L. Coote and A. Anastasaki, J. Am. Chem. Soc., 2022, 144, 4678–4684 CrossRef CAS.
- M. R. Martinez, S. Dadashi-Silab, F. Lorandi, Y. Zhao and K. Matyjaszewski, Macromolecules, 2021, 54, 5526–5538 CrossRef CAS.
- J. B. Young, J. I. Bowman, C. B. Eades, A. J. Wong and B. S. Sumerlin, ACS Macro Lett., 2022, 11, 1390–1395 CrossRef CAS.
- S. Huang, X. Su, Y. Wu, X.-G. Xiong and Y. Liu, Chem. Sci., 2022, 13, 11352–11359 RSC.
- H. Stobbe, Chem. Ber., 1914, 47, 2701–2703 CrossRef CAS.
- H. Staudinger, Chem. Ber., 1920, 53, 1073–1085 CrossRef.
- H. S. Taylor and A. V. Tobolsky, J. Am. Chem. Soc., 1945, 67, 2063–2067 CrossRef CAS.
- R. Mesrobian and A. Tobolsky, J. Am. Chem. Soc., 1945, 67, 785–787 CrossRef CAS.
- S. Beuermann and M. Buback, Prog. Polym. Sci., 2002, 27, 191–254 CrossRef CAS.
- A. V. Tobolsky, J. Polym. Sci., 1957, 25, 220–221 CrossRef CAS.
- A. V. Tobolsky, J. Polym. Sci., 1958, 31, 126 CrossRef.
- A. V. Tobolsky and A. Eisenberg, J. Am. Chem. Soc., 1959, 81, 780–782 CrossRef CAS.
- A. V. Tobolsky and A. Eisenberg, J. Am. Chem. Soc., 1960, 82, 289–293 CrossRef.
- A. V. Tobolsky and A. Eisenberg, J. Am. Chem. Soc., 1959, 81, 2302–2305 CrossRef CAS.
- D. Heikens and H. Geelen, Polymer, 1962, 3, 591–594 CrossRef CAS.
- F. S. Dainton and K. J. Ivin, Nature, 1948, 162, 705–707 CrossRef CAS.
- D. Frederick, H. Cogan and C. Marvel, J. Am. Chem. Soc., 1934, 56, 1815–1819 CrossRef CAS.
- M. Hunt and C. Marvel, J. Am. Chem. Soc., 1935, 57, 1691–1696 CrossRef CAS.
- L. Ryden and C. Marvel, J. Am. Chem. Soc., 1935, 57, 2311–2314 CrossRef CAS.
- R. D. Snow and F. E. Frey, Ind. Eng. Chem., 1938, 30, 176–182 CrossRef CAS.
- R. Snow and F. Frey, J. Am. Chem. Soc., 1943, 65, 2417–2418 CrossRef CAS.
- P. Gray and K. J. Ivin, Biogr. Mem. Fellows R. Soc., 2000, 46, 85–124 CrossRef.
- K. J. Ivin, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 2137–2146 CrossRef CAS.
- S. Penczek and G. Moad, Pure Appl. Chem., 2008, 80, 2163–2193 CrossRef CAS.
- G. Odian, in Principles of Polymerization, 2004, p. 281 Search PubMed.
- F. Dainton and K. Ivin, Discuss. Faraday Soc., 1953, 14, 199–207 RSC.
- F. S. Dainton and K. J. Ivin, Chem. Soc. Rev., 1958, 12, 61–92 RSC.
- F. S. Dainton and K. J. Ivin, Trans. Faraday Soc., 1950, 46, 331–348 RSC.
- M. Szwarc, Proc. R. Soc. London, Ser. A, 1997, 279, 260–290 Search PubMed.
- E. I. Izgorodina and M. L. Coote, Macromol. Theory Simul., 2006, 15, 394–403 CrossRef CAS.
- L. Cederholm, J. Wohlert, P. Olsén, M. Hakkarainen and K. Odelius, Angew. Chem., Int. Ed., 2022, 61, e202204531 CrossRef CAS PubMed.
- M. Rahman and K. E. Weale, Polymer, 1970, 11, 122–124 CrossRef CAS.
- K. Murata, K. Sato and Y. Sakata, J. Anal. Appl. Pyrolysis, 2004, 71, 569–589 CrossRef CAS.
- J. Kilroe and K. Weale, J. Chem. Soc., 1960, 3849–3854 RSC.
- K. J. Ivin, Macromol. Symp., 1991, 42–43, 1–14 Search PubMed.
- S. Bywater and D. J. Worsfold, J. Polym. Sci., 1962, 58, 571–579 CrossRef CAS.
- M. R. Martinez, P. Krys, S. S. Sheiko and K. Matyjaszewski, ACS Macro Lett., 2020, 9, 674–679 CrossRef CAS PubMed.
- K. J. Ivin and J. Léonard, Eur. Polym. J., 1970, 6, 331–341 CrossRef CAS.
- J. Leonard, Macromolecules, 1969, 2, 661–666 CrossRef CAS.
- P. J. Flory, Chem. Phys., 2004, 10, 51–61 Search PubMed.
- M. R. Martinez, Y. Cong, S. S. Sheiko and K. Matyjaszewski, ACS Macro Lett., 2020, 9, 1303–1309 CrossRef CAS.
- L. Cederholm, P. Olsén, M. Hakkarainen and K. Odelius, Polym. Chem., 2023, 14, 3270–3276 RSC.
- C. Rüchardt and H.-D. Beckhaus, Angew. Chem., Int. Ed., 1980, 19, 429–440 CrossRef.
- C. Rüchardt and H.-D. Beckhaus, in Synthetic Organic Chemistry, Topics in Current Chemistry, Springer, Berlin, Heidelberg, 1986, vol. 130, pp. 1–22 Search PubMed.
- A. Rudin and S. S. M. Chiang, J. Polym. Sci., Part A: Polym. Chem., 1974, 12, 2235–2254 CAS.
- N. Grassie and W. W. Kerr, Trans. Faraday Soc., 1957, 53, 234–239 RSC.
- A. Gallardo and J. San Roman, Macromolecules, 1992, 25, 5836–5840 CrossRef CAS.
- T. Otsu, B. Yamada, S. Sugiyama and S. Mori, J. Polym. Sci., Part A: Polym. Chem., 1980, 18, 2197–2207 CAS.
- B. Yamada, S. Sugiyama, S. Mori and T. Otsu, J. Macromol. Sci., Part A: Pure Appl. Chem., 1981, 15, 339–345 CrossRef.
- T. Otsu, B. Yamada, T. Mori and M. Inoue, J. Polym. Sci., Polym. Lett. Ed., 1976, 14, 283–285 CrossRef CAS.
- R. E. Cook, F. S. Dainton and K. J. Ivin, J. Polym. Sci., 1957, 26, 351–364 CrossRef CAS.
- B. Yamada, T. Tanaka and T. Otsu, Eur. Polym. J., 1989, 25, 117–120 CrossRef CAS.
- H. Kunisada, Y. Yuki, S. Kondo, K. Adachi and N. Takahashi, Polymer, 1992, 33, 3512–3519 CrossRef CAS.
- Y. Yuki, H. Kunisada and T. Furihata, Polym. J., 1992, 24, 791–799 CrossRef CAS.
- H. Kunisada, Y. Yuki, S. Kondo and K.-i. Goto, Makromol. Chem., 1992, 193, 2621–2630 CrossRef CAS.
- H. Kunisada, Y. Yuki, S. Kondo, K.-i. Goto and S. Oda, Polym. J., 1992, 24, 239–246 CrossRef CAS.
- X. Luo, Z. Wei, B. Seo, Q. Hu, X. Wang, J. A. Romo, M. Jain, M. Cakmak, B. W. Boudouris, K. Zhao, J. Mei, B. M. Savoie and L. Dou, J. Am. Chem. Soc., 2022, 144, 16588–16597 CrossRef CAS.
- Z. Szablan, M. Huaming, M. Adler, M. H. Stenzel, T. P. Davis and C. Barner-Kowollik, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 1931–1943 CrossRef CAS.
- R. D. Thompson, T. B. Barclay, K. R. Basu and L. J. Mathias, Polym. J., 1995, 27, 325–338 CrossRef CAS.
- B. Yamada, M. Satake and T. Otsu, Polym. J., 1992, 24, 563–571 CrossRef CAS.
- J. Penelle, J. Collot and G. Rufflard, J. Polym. Sci., Part A: Polym. Chem., 1993, 31, 2407–2412 CrossRef CAS.
- J.-S. Cheng, B. Yamada and T. Otsu, J. Polym. Sci., Part A: Polym. Chem., 1991, 29, 1837–1843 CrossRef CAS.
- H. Ito and M. Ueda, Macromol. Symp., 1992, 54–55, 551–560 CrossRef.
- L. S. Diaz-Silvarrey, K. Zhang and A. N. Phan, Green Chem., 2018, 20, 1813–1823 RSC.
- B. Yamada, A. Matsumoto and T. Otsu, Makromol. Chem., 1991, 192, 1921–1929 CrossRef CAS.
- T. Otsu, B. Yamada, T. Mori and M. Inoue, J. Polym. Sci., Part C: Polym. Lett., 1976, 14, 283–285 CAS.
- H. W. McCormick, J. Polym. Sci., 1957, 25, 488–490 CrossRef CAS.
- R. E. Cunningham and H. A. Colvin, Polymer, 1992, 33, 5073–5075 CrossRef.
- J. M. Schwartz, A. Engler, O. Phillips, J. Lee and P. A. Kohl, J. Polym. Sci., Part A: Polym. Chem., 2018, 56, 221–228 CrossRef CAS.
- P. A. Clay and R. G. Gilbert, Macromolecules, 1995, 28, 552–569 CrossRef CAS.
- M. Gordon, Trans. Faraday Soc., 1957, 53, 1662–1675 RSC.
- J. R. MacCallum, Eur. Polym. J., 1966, 2, 413–422 CrossRef CAS.
- R. H. Boyd and T. P. Lin, Chem. Phys., 1966, 45, 778–781 CAS.
- R. Simha, Trans. N.Y. Acad. Sci., 1952, 14, 151–157 CrossRef CAS.
- R. H. Boyd, Chem. Phys., 1959, 31, 321–328 CAS.
- H. L. Friedman, J. Polym. Sci., 1960, 45, 119–125 CrossRef CAS.
- P. E. Sánchez-Jiménez, L. A. Pérez-Maqueda, A. Perejón and J. M. Criado, J. Phys. Chem. A, 2010, 114, 7868–7876 CrossRef.
- J. Wang, T.-T. Wang, Z.-H. Luo and Y.-N. Zhou, AIChE J., 2023, 69, e17854 CrossRef CAS.
- L. A. Wall, S. Straus, J. H. Flynn, D. McIntyre and R. Simha, J. Phys. Chem., 1966, 70, 53–62 CrossRef CAS.
- M. Gordon and L. R. Shenton, J. Polym. Sci., 1959, 38, 157–178 CrossRef CAS.
- T. Faravelli, M. Pinciroli, F. Pisano, G. Bozzano, M. Dente and E. Ranzi, J. Anal. Appl. Pyrolysis, 2001, 60, 103–121 CrossRef CAS.
- I. C. McNeill, M. Zulfiqar and T. Kousar, Polym. Degrad. Stab., 1990, 28, 131–151 CrossRef CAS.
- T. Kashiwagi, A. Inaba, J. E. Brown, K. Hatada, T. Kitayama and E. Masuda, Macromolecules, 1986, 19, 2160–2168 CrossRef CAS.
- L. E. Manring, D. Y. Sogah and G. M. Cohen, Macromolecules, 1989, 22, 4652–4654 CrossRef CAS.
- L. E. Manring, Macromolecules, 1989, 22, 2673–2677 CrossRef CAS.
- L. E. Manring, Macromolecules, 1988, 21, 528–530 CrossRef CAS.
- D. Grant and S. Bywater, Trans. Faraday Soc., 1963, 59, 2105–2112 RSC.
- F. S. Dainton, G. A. Harpell and K. J. Ivin, Eur. Polym. J., 1969, 5, 395–403 CrossRef CAS.
- A. Vrancken, J. Smid and M. Szwarc, Trans. Faraday Soc., 1962, 58, 2036–2048 RSC.
- S. Bywater and P. Black, J. Phys. Chem., 1965, 69, 2967–2970 CrossRef CAS.
- J. M. G. Cowie and S. Bywater, J. Polym. Sci., 1961, 54, 221–227 CrossRef CAS.
- G. Madras, G. Y. Chung, J. M. Smith and B. J. McCoy, Ind. Eng. Chem. Res., 1997, 36, 2019–2024 CrossRef CAS.
- G. Audisio and F. Bertini, J. Anal. Appl. Pyrolysis, 1992, 24, 61–74 CrossRef CAS.
- D. H. Richards and D. A. Salter, Polymer, 1967, 8, 153–159 CrossRef CAS.
- R. Simha and L. Wall, J. Phys. Chem., 1952, 56, 707–715 CrossRef CAS.
- S. Ide, T. Ogawa, T. Kuroki and T. Ikemura, J. Appl. Polym. Sci., 1984, 29, 2561–2571 CrossRef CAS.
- G. Madras, J. M. Smith and B. J. McCoy, Polym. Degrad. Stab., 1997, 58, 131–138 CrossRef CAS.
- G. G. Cameron and N. Grassie, Polymer, 1961, 2, 367–373 CrossRef.
- H. S. Wang, K. Parkatzidis, T. Junkers, N. P. Truong and A. Anastasaki, Chem, 2023 DOI:10.1016/j.chempr.2023.09.027.
- M. J. Flanders and W. M. Gramlich, Polym. Chem., 2018, 9, 2328–2335 RSC.
- H. S. Wang, N. P. Truong, G. R. Jones and A. Anastasaki, ACS Macro Lett., 2022, 11, 1212–1216 CrossRef CAS PubMed.
- F. Häfliger, N. P. Truong, H. S. Wang and A. Anastasaki, ACS Macro Lett., 2023, 12, 1207–1212 CrossRef.
- V. Bellotti, K. Parkatzidis, H. S. Wang, N. De Alwis Watuthanthrige, M. Orfano, A. Monguzzi, N. P. Truong, R. Simonutti and A. Anastasaki, Polym. Chem., 2023, 14, 253–258 RSC.
- M. L. Allegrezza and D. Konkolewicz, ACS Macro Lett., 2021, 10, 433–446 CrossRef CAS.
- M. Hartlieb, Macromol. Rapid Commun., 2022, 43, 2100514 CrossRef CAS.
- J. Xu, K. Jung, A. Atme, S. Shanmugam and C. Boyer, J. Am. Chem. Soc., 2014, 136, 5508–5519 CrossRef CAS.
- N. Corrigan, J. Yeow, P. Judzewitsch, J. Xu and C. Boyer, Angew. Chem., Int. Ed., 2019, 58, 5170–5189 CrossRef CAS.
- Y. Sano, T. Konishi, M. Sawamoto and M. Ouchi, Eur. Polym. J., 2019, 120, 109181 CrossRef CAS.
- T. Kimura, K. Kuroda, H. Kubota and M. Ouchi, ACS Macro Lett., 2021, 10, 1535–1539 CrossRef CAS.
- M. R. Martinez, F. De Luca Bossa, M. Olszewski and K. Matyjaszewski, Macromolecules, 2022, 55, 78–87 CrossRef CAS.
- M. R. Martinez, D. Schild, F. De Luca Bossa and K. Matyjaszewski, Macromolecules, 2022, 55, 10590–10599 CrossRef CAS.
- K. Parkatzidis, N. P. Truong, K. Matyjaszewski and A. Anastasaki, J. Am. Chem. Soc., 2023, 145, 21146–21151 CrossRef CAS.
- R. Whitfield, G. R. Jones, N. P. Truong, L. E. Manring and A. Anastasaki, Angew. Chem., Int. Ed., 2023, e202309116 CAS.
- F. De Luca Bossa, G. Yilmaz and K. Matyjaszewski, ACS Macro Lett., 2023, 1173–1178 CrossRef CAS PubMed.
- J. B. Young, R. W. Hughes, A. M. Tamura, L. S. Bailey, K. A. Stewart and B. S. Sumerlin, Chem, 2023, 9, 2669–2682 CAS.
- V. P. Balema, I. Z. Hlova, S. L. Carnahan, M. Seyedi, O. Dolotko, A. J. Rossini and I. Luzinov, New J. Chem., 2021, 45, 2935–2938 RSC.
- E. Jung, D. Yim, H. Kim, G. I. Peterson and T.-L. Choi, J. Polym. Sci., 2023, 61, 553–560 CrossRef CAS.
- V. Kumar, A. Khan and M. Rabnawaz, ACS Sustainable Chem. Eng., 2022, 10, 6493–6502 CrossRef CAS.
- L. Li, X. Shu and J. Zhu, Polymer, 2012, 53, 5010–5015 CrossRef CAS.
- D. J. Lloyd, V. Nikolaou, J. Collins, C. Waldron, A. Anastasaki, S. P. Bassett, S. M. Howdle, A. Blanazs, P. Wilson, K. Kempe and D. M. Haddleton, Chem. Commun., 2016, 52, 6533–6536 RSC.
- N. M. Wang, G. Strong, V. DaSilva, L. Gao, R. Huacuja, I. A. Konstantinov, M. S. Rosen, A. J. Nett, S. Ewart, R. Geyer, S. L. Scott and D. Guironnet, J. Am. Chem. Soc., 2022, 144, 18526–18531 CrossRef CAS.
- R. J. Conk, S. Hanna, J. X. Shi, J. Yang, N. R. Ciccia, L. Qi, B. J. Bloomer, S. Heuvel, T. Wills, J. Su, A. T. Bell and J. F. Hartwig, Science, 2022, 377, 1561–1566 CrossRef CAS.
- C. W. S. Yeung, J. Y. Q. Teo, X. J. Loh and J. Y. C. Lim, ACS Mater. Lett., 2021, 3, 1660–1676 CrossRef CAS.
- S. T. Nguyen, E. A. McLoughlin, J. H. Cox, B. P. Fors and R. R. Knowles, J. Am. Chem. Soc., 2021, 143, 12268–12277 CrossRef CAS.
- S. Oh and E. E. Stache, J. Am. Chem. Soc., 2022, 144, 5745–5749 CrossRef CAS PubMed.
- L. H. Kugelmass, C. Tagnon and E. E. Stache, J. Am. Chem. Soc., 2023, 145, 16090–16097 CrossRef CAS PubMed.
- K. W. J. Ng, J. S. K. Lim, N. Gupta, B. X. Dong, C.-P. Hu, J. Hu and X. M. Hu, Commun. Chem., 2023, 6, 158 CrossRef CAS.
- M.-Q. Zhang, M. Wang, B. Sun, C. Hu, D. Xiao and D. Ma, Chem, 2022, 8, 2912–2923 CAS.
- C. B. Watson, D. Tan and D. E. Bergbreiter, Macromolecules, 2019, 52, 3042–3048 CrossRef CAS.
- K. J. Ivin, in Polymer Handbook, ed. J. Bandrup and E. H. Immergut, John Wiley & Sons, New York, 2nd edn, 1975, ch. 2, pp. 421–450 Search PubMed.
Footnote |
† Calculated from the MEC for a ceiling temperature of 25 °C, which was determined from eqn (12) with tabulated values for the enthalpy (ΔHlc = −70 kJ mol−1) and entropy (ΔSlc = −104 J mol−1 K−1).170 This gave a MEC at 25 °C of 0.145 μM. Considering the reported monomer yield of 7%, this corresponds to 2 mmol of monomer generated. Assuming the reaction stops at the MEC, generating this much monomer would then require 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 793 L of solvent as: V = nSTY/c where c is the MEC. Since the authors originally started from 3 g of polystyrene, the RUC is calculated as follows: 793 L of solvent as: V = nSTY/c where c is the MEC. Since the authors originally started from 3 g of polystyrene, the RUC is calculated as follows: 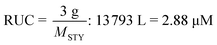 . . |
| This journal is © The Royal Society of Chemistry 2024 |