Open Access Article
Open Access ArticleEffects of current density on Zn reversibility
Licheng
Miao
 ,
Wenqi
Jia
,
Wenqi
Jia
 and
Lifang
Jiao
and
Lifang
Jiao
 *
*
Key Laboratory of Advanced Energy Materials Chemistry (Ministry of Education), Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), College of Chemistry, Nankai University, Tianjin 300071, China. E-mail: jiaolf@nankai.edu.cn
First published on 21st October 2024
Abstract
Aqueous zinc (Zn) batteries (AZBs) exhibit potential as viable candidates for stationary energy storage. Improvements in the plating/stripping efficiency and lifespan of Zn anodes at high applied current density (j) render AZBs attractive for rapid charge and discharge scenarios. However, the existing literature presents inconsistent experimental results and interpretations regarding the impact of j on Zn reversibility. While some studies indicate that increasing j reduces Zn reversibility, others argue the opposite. In this perspective, we delve into this conflicting phenomenon with a specific focus on the fundamentals of Zn electrodeposition, nucleation-growth models and theories related to j, and future development. Our stance supports the notion that an increase in j leads to a volcano-shaped pattern in the reversibility of Zn plating and stripping, and such a relationship lies in the dual and contradictory roles that high j plays in thermodynamics and interfacial kinetics. Our in-depth discussion provides valuable insights for accurate data interpretation and holds significant promise for advancing high-power AZBs.
1 Introduction
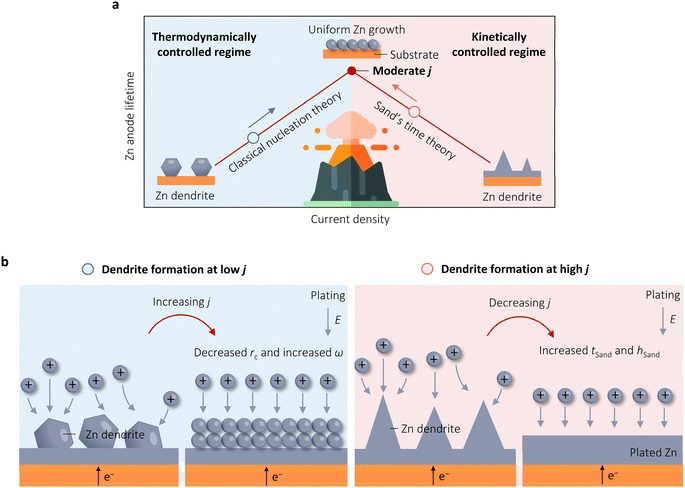
Aqueous zinc (Zn) batteries (AZBs) have emerged as a promising battery system for large-scale energy storage owing to their safety, ease of assembly, cost-effectiveness, non-toxicity, and the intrinsic advantages of the Zn metal anode with a high theoretical capacity (820 mA h g−1 and 5854 mA h cm−3) and high natural abundance.1–5 However, current AZBs face challenges in practical application due to the severe reversibility issues of Zn anodes in aqueous electrolytes, such as random dendrite growth and dead Zn, resulting in low coulombic efficiency (CE). The sharp dendrites with high Young's modulus can potentially penetrate the separator, causing a short-circuit.6–11 These obstacles significantly reduce the efficiency of Zn plating/stripping, hindering the progress of AZBs.Various successful approaches, such as optimizing Zn electrode materials, electrolytes, and separator designs, have been proposed to improve the stability of Zn anodes.12–15 These intricate strategies aim to control the morphology of Zn deposition and inhibit side reactions, ultimately enhancing Zn reversibility to some degree. Alternatively, a simple adjustment of operation conditions through changing the applied or polarization current density (j) has shown considerable improvements in Zn reversibility.16–26 Nevertheless, the question of how Zn reversibility depends on j has no exact answer. Three viewpoints have arisen regarding the correlation between j and Zn reversibility in AZBs. Historically, it was widely accepted that high j causes a rapid depletion of the Zn2+ ion concentration at the electrode–electrolyte interface, leading to diffusion-controlled (mass-transport-limited) deposition of Zn on the electrode. This process can trigger the formation of morphologically unstable branching or dendrites, ultimately resulting in a shorter lifetime of Zn anodes.16,17,22 Paradoxically, recent observations have shown that high j can facilitate the nucleation process, resulting in smaller nuclei size, a higher nuclei density, and consequently, more uniform and smaller Zn deposition flakes.18–21,25 Notably, Chen et al. has demonstrated that Zn anodes could cycle steadily even under an unprecedented high j of 1 A cm−2.26 More recently, however, Zhang and Sun's groups successively introduced an alternative perspective, suggesting that the relationship between j and the cycling life of Zn anodes follows an analogous volcano-shaped pattern.23,24 They argue that this phenomenon is due to the dual and contradictory roles that high j plays in crystallographic thermodynamics and interfacial kinetics. These viewpoints indicate the relationship between j and the stability of Zn anodes is not straightforward. However, a systematic investigation into the underlying mechanism is still lacking, rendering it elusive.
This perspective aims to enhance the understanding of the rate-dependent stability of Zn anodes by collating and contrasting several prospective nucleation-growth theories and models relevant to j. It provides a brief introduction to the Zn electrodeposition process in alkaline and acidic electrolytes (Section 2), followed by a comprehensive analysis of models and theories regarding Zn nucleation and growth influenced by j, along with recent advancements in Zn anodes (Section 3). Finally, it discusses the remaining challenges and opportunities for the practical implementation of high-power AZBs and offers future perspectives for the advancement of this burgeoning field (Section 4).
2 Fundamentals of Zn electrodeposition
Zn metal has been extensively utilized as an anode material in AZBs. The deposition of Zn plays a crucial role in the energy and storage and release processes of AZBs. Achieving a compact and uniform Zn deposition is crucial for maximizing CE and prolonging the lifespan of AZBs. Section 2 provides a succinct introduction to the fundamental background of Zn electrodeposition, covering the mechanistic reactions that occur in acidic and alkaline electrolytes, as well as the crucial Zn nucleation-growth process and its associated influencing factors.2.1 Reaction mechanisms
The Zn anode undergoes different reaction mechanisms in alkaline and acidic electrolytes.27–31 In an alkaline environment, zinc oxide (ZnO) initially combines with two hydroxyl ions (OH−) and one water molecule (H2O) to form a zincate ion (Zn(OH)42−). Zn(OH)42− is subsequently reduced to metallic Zn by gaining electrons on the Zn surface during the charging process as follows:| Zn(OH)42− + 2e− → Zn(s) + 4OH−, E0 = −1.20 V vs. SHE | (2.1) |
The electrochemical deposition of Zn in alkaline electrolyte undergoes four sequential stages. Firstly, mass transfer occurs, where Zn(OH)42− migrates from the bulk solution to the anode surface via electromigration, diffusion, and convection. Secondly, in the pre-transformation stage, Zn(OH)2 with a lower coordination number is the ion directly involved in the reduction process, rather than Zn(OH)42− with a higher coordination number. This preference is due to Zn(OH)2, which dissociates two OH−, being more likely to gain electrons on the electrode surface. The third stage involves charge transfer, where the converted Zn(OH)2 species exchange electrons at the anode interface to form Zn atoms. Finally, in the electrocrystallization stage, the new Zn atoms diffuse to the appropriate positions along the electrode surface, integrating into the metal lattice to either grow individually or aggregate with other atoms to form nuclei, eventually developing into crystals (Fig. 1a). The Zn electrodeposition in acidic media is initiated by applying a negative (reduction) current to the Zn anode, following the half-reaction equation:
| Zn2+ + 2e− → Zn(s), E0 = −0.76 V vs. SHE | (2.2) |
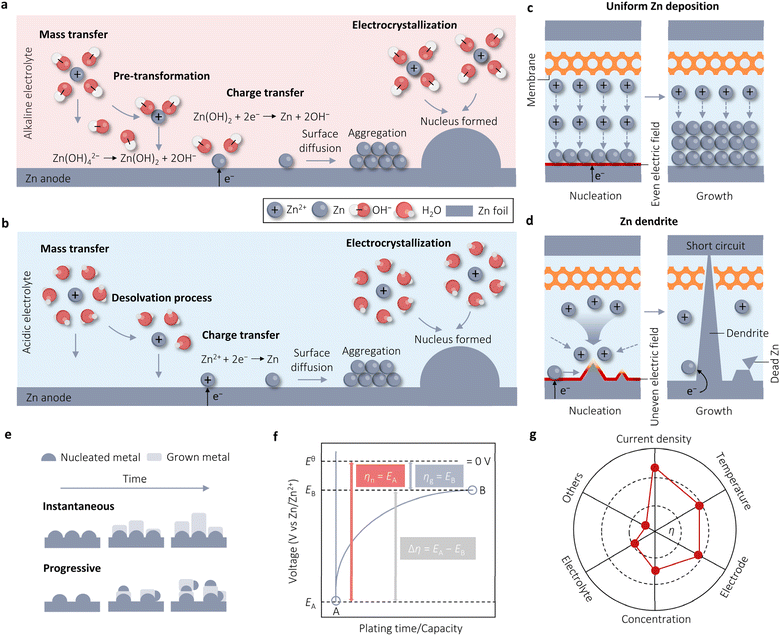 | ||
| Fig. 1 Concepts associated with Zn electrodeposition. Four steps of Zn electrodeposition in alkaline (a) and acidic (b) solutions. Schematics for uniform Zn electrodeposition (c) and Zn dendrite formation (d). (e) Instantaneous and progressive nucleation processes. Adapted from ref. 32 with permission from Wiley-VCH, Copyright 2023. (f) Schematic time–voltage curve during Zn electrodeposition. Adapted from ref. 33 with permission from Elsevier, Copyright 2023. (g) The influence factors on overpotential (η). Adapted from ref. 33 with permission from Elsevier, Copyright 2023. | ||
As shown in Fig. 1b, this reaction also comprises four successive procedures: Zn2+ ion diffusion (mass transfer), Zn2+ ion desolvation, Zn2+ ion reduction (charge transfer), and Zn nucleation and crystal growth (electrocrystallization). In contrast to alkaline electrolytes, only Zn plating occurs in acidic systems without the formation of insoluble products, such as Zn(OH)2, during this process. It is evident that Zn electrodes in alkaline and acidic electrolytes have different reaction mechanisms, which leads to different reaction potentials.31 In alkaline electrolytes, the standard reduction potential of Zn/Zn(OH)42− is −1.20 V vs. the standard hydrogen electrode (SHE). In contrast, the standard reduction potential of Zn/Zn2+ is −0.76 V vs. SHE in acidic electrolytes, which is less negative than that of the Zn electrode in alkaline electrolytes. This disparity suggests that alkaline AZBs are more likely to deliver a higher output voltage.
2.2 Zn nucleation and growth process
The electrocrystallization process of Zn, which involves nucleation and growth, is crucial for the stability of Zn deposition. Nucleation significantly influences the subsequent growth of Zn.32 A flat surface, as shown in Fig. 1c, exhibits a uniform electric field that promotes even Zn deposition during charging. Conversely, an uneven initial surface results in the formation of non-uniform Zn seeds during charging owing to the uneven distribution of the electric field. The growth priority of Zn is contingent upon the intensity of the electric field and ion concentration in electrolytes. This leads to the accumulation of electrons and ions at the tips of Zn seeds, resulting in the formation of tiny protrusions known as initial dendrites. The j surrounding these protrusions is significantly larger than in other areas. This large local j induces a low Zn2+ ion concentration and the localization of j, intensifying the “accumulation effect” and consequently promoting dendrite growth. The formation of “dead” Zn is facilitated by the shedding of Zn dendrites from the electrode into the electrolyte, causing a rapid decline in the CE and reversible capacity of batteries. Moreover, continuous dendrite growth can pierce the separator, leading to direct contact between the anode and cathode, resulting in a short-circuit and eventual battery failure (Fig. 1d). Therefore, a flat surface with a uniform electric field and ion distribution can mitigate the uneven nucleation and growth of Zn, thereby enhancing the stability of Zn deposition. The formation and growth of Zn dendrites are more severe in alkaline electrolytes compared to acidic electrolytes, primarily due to the high electrochemical activity of Zn in alkaline environments, by the way.In metal electrodeposition, there are two primary nucleation modes: instantaneous and progressive (Fig. 1e).33,34 Progressive nucleation, as the name suggests, involves the gradual development of nuclei over time, with additional nuclei forming on the substrate or on top of previously deposited material, competing with the growth of existing nuclei. In contrast, instantaneous nucleation occurs all at once in the beginning before growth takes place at these nucleation sites. This process demands a high force to initiate nucleation; subsequently, adding Zn adatom to existing nuclei becomes favorable, leading to a significantly more negative overpotential (η) for nucleation than for growth. Fig. 1f illustrates the general characteristic voltage profiles for Zn deposition, showing that the polarization in the growth step of nuclei (ηg) is much lower than in the nucleation process (ηn); indicating that new nucleation sites at this growth step are very few and negligible and Zn electrodeposition follows the instantaneous nucleation process.33 Furthermore, utilizing the Scharifker and Hills (SH) model to distinguish nucleation modes, Zhang et al. found that the experimental Zn nucleation process closely aligns with the theoretical response for three-dimensional (3D) instantaneous nucleation across all measured η, consistent with the ηn results.24 Theoretically, the instantaneous nucleation process results in the formation of highly crystalline deposits. However, if specific growth areas are prioritized over others, the deposited surface may become rough. In fact, the electrodeposited Zn exhibits indeed high crystallinity but rough surfaces, as evidenced by both the literature and our experimental data.
In Fig. 1f, the η of Zn‖Zn cells plays a crucial role in evaluating the cycle performance of Zn anodes. However, the relationship between η and cycle performance is currently a topic of debate. Some argue that higher η results in rapid Zn deposition, leading to more serious concentration polarization and uneven distribution of deposited Zn.29 Conversely, others support the classical nucleation theory, suggesting that an increase in η causes Zn nuclei to become smaller and denser, potentially enhancing electrochemical performance by yielding a smoother surface.16η serves as the driving force for the four steps involved in Zn electrodeposition, whether in alkaline or acidic media.35 It represents the difference between the actual electrode potential (E) and the equilibrium electrode potential (E0, 0 V vs. Zn/Zn2+). As the voltage is applied, E rapidly shifts, initiating the formation of crystal nuclei on the Zn metal surface (initial substrate) once E reaches its peak value at point A (EA), corresponding to the nucleation process (instantaneous nucleation), where EA is denoted as ηn. η Decreases since crystal growth necessitates less driving force compared to crystal nuclei formation. Upon reaching a plateau at point B (EB), this plateau is identified as ηg. The transition from point A to point B is influenced by both nucleation and growth processes, with the driving force required during this process expressed as Δη. In the absence of mass transfer effects, the Butler–Volmer equation (BVE) can be reformulated as follows:
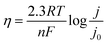 | (2.3) |
3 Models and theories regarding Zn nucleation and growth influenced by j
Three perspectives have arisen concerning the relationship between j and Zn reversibility in AZBs. The main cause of this debate stems from a lack of comprehensive understanding of the intricacies of Zn nucleation and growth in AZBs. This section provides an in-depth discussion of Zn nucleation and growth theories and models that are pertinent to j. By revisiting previous controversies, thermodynamic properties of Zn nucleation and kinetic concepts of Zn growth are distinguished and substantiated with relevant examples.3.1 Thermodynamic theories and models of Zn nucleation
In the process of Zn electrodeposition, Zn2+ ions in the electrolyte are reduced to Zn atoms, which aggregate into Zn nuclei on the nanoscale, undergoes continuous growth, and ultimately crystallizes into Zn metals on the microscale with a hexagonal shape (Fig. 2a).35 Classical nucleation theory (CNT) provides an explanation of Zn nucleation by considering the net change in Gibbs free energy. Most models that describe the nucleation and growth process of metal electrodeposition are constructed using the conventional 3D sphere or hemisphere models of CNT. However, the nucleation process of different metals is influenced by crystal faces with different orientations, favoring the crystal face with the lowest surface energy for nucleus formation. For instance, in the nucleation of Zn, the nucleation rate (ω, number of nuclei per unit volume per unit time) differs among different crystal faces. The (002) crystal face, which has the lowest surface energy, is preferentially exposed, resulting in the formation of hexagonal Zn flakes. Unlike the body-centered cubic (BCC) crystal structure of Li metal, Zn metal adopts a hexagonal close-packed (HCP) structure, showing distinct configurations of the crystal nucleus at the nanoscale and the metal crystal at the macroscale (Fig. 2a).36 Therefore, 3D models of CNT do not match well with Zn metal, while a two-dimensional (2D) hexagonal nucleation model is more appropriate for Zn metal. Zn plating consistently shows well-defined anisotropic hexagonal flakes in line with the 2D hexagonal nucleation model. Therefore, it is imperative to standardize the structural and crystal model of Zn as the HCP structure before progressing any relevant experimental modes and theoretical simulations. As shown in Fig. 2b, there exists an energy barrier (ΔGn) that needs to be surpassed for the successful nucleation of Zn.32 In the case of the 2D hexagonal nucleation model, the calculation of ΔGn is as follows: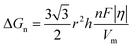 | (3.1) |
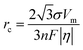 | (3.2) |
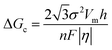 | (3.3) |
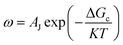 | (3.4) |
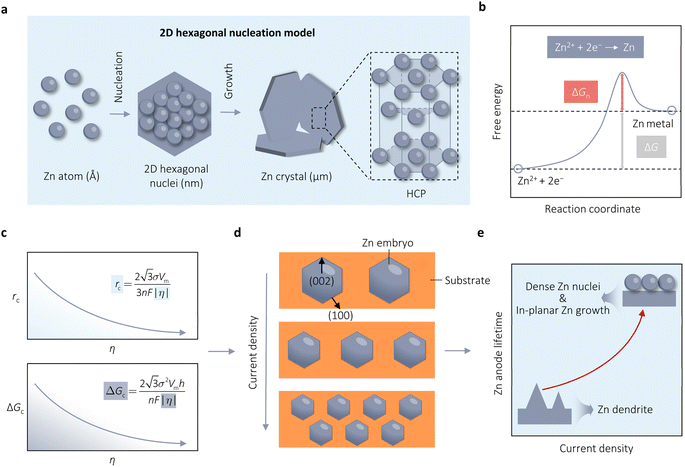 | ||
| Fig. 2 Thermodynamic theories and models concerning Zn nucleation. (a) Schematic illustrating the Zn nucleation and growth process based on the 2D hexagonal nucleation model. Adapted from ref. 35 with permission from Elsevier, Copyright 2023. (b) The energy barrier in the process of Zn nucleation. Adapted from ref. 32 with permission from Wiley-VCH, Copyright 2020. (c) Curves and formulas representing the relationship between η with either rc, or ΔGc. (d) Schematic illustrating the dependence of Zn nucleation and growth on j. Adapted from ref. 25 with permission from Wiley-VCH, Copyright 2023. (e) Experimental results of nucleation theories advocating for a high density of Zn nuclei at high j, leading to in-planar Zn growth with an extended lifespan of Zn anodes. | ||
Apart from CNT, two other mechanisms explain the beneficial effect of j on the stability of Zn. Huang et al. found that Zn electrodeposits exhibited plate-hexagonal units of Zn crystal at all values of j, but the consistency of crystal plane inclination increased as j intensified.18 At a high j of 16 mA cm−2, the Zn‖Cu cell delivered a cycle life of up to 1000 cycles and an average CE of 99.8%. They engage in a discussion about the reorganization of a condensed region with tight-absorbed Zn2+ ions from the viewpoint of the electrical double layer (EDL). Molecular dynamics (MD) simulations reveal that at high j, the EDL undergoes reconstruction, resulting in a decrease in thickness. This compressed EDL effectively shortens the diffusion distance of Zn2+ ions through the EDL, thereby enhancing the reaction kinetics for Zn deposition and facilitating the dense and compact Zn electrodeposition. Kundu et al. also found that a high j significantly prolongs the cycling lifetime of Zn.21 They successfully achieved Zn reversibility over 8000 cycles at a high j of 20 mA cm−2 for 1 mA h cm−2. By investigating the evolution of Zn morphology, they attributed the enhanced Zn reversibility to a smoother, step-like surface without sharp features. They propose that this outcome is due to the short duration of Zn deposition at 20 mA cm−2 for 1 mA h cm−2 (3 min), which might not be enough to initiate the diffusion-controlled deposition regime.
In short, researchers have observed that Zn anodes can endure thousands of rechargeable cycles at high j, yet exhibit poor rechargeability at low j (Fig. 2e). This behavior is attributed to the orderly coherent Zn electrodeposits formed under high j. The thermodynamic theories, spearheaded by CNT, underscore the necessity of uniform and compact Zn nucleation for achieving high Zn reversibility. Nevertheless, the examples provided also show that Zn reversibility is only maintained within a critical range of j. There is a maximum threshold to the positive impact of j on Zn stability. Simply encouraging dense Zn nucleation is inadequate for ensuring Zn stability. In addition, while j does influence the growth orientation of Zn crystals, a definitive correlation between the two is currently lacking. External factors such as substrates often alter the crystallography of Zn nucleation and growth, thereby affecting the assessment of j's impact on the texture of Zn electrodeposition. The relationship between them requires further investigation in future studies.
3.2 Kinetic theories and models of Zn growth
Despite the well-established knowledge of dendrite-free morphology and high reversibility of Zn at high j, previous research has shown that low j can actually promote a more controlled in-plane morphology and increased Zn reversibility (Fig. 3a). The researchers are confident that the deposition of dendritic Zn from acidic or alkaline electrolytes can be attributed to a diffusion-controlled process.16,17 Sand's time (tSand) theory, proposed in 1901, is well-known for describing the evolution of Zn growth in diffusion-limited systems.42 When j is applied to the Zn anode, it induces a concentration gradient in the electrolytic salt near the Zn surface, following a diffusion equation. If the applied j is sufficiently large, the salt concentration at the Zn electrode surface can be reduced to zero, hindering uniform Zn deposition. The moment at which the surface concentration reaches zero is termed as tSand. After this time, Zn deposition will preferentially occur on surface protrusions that reach into regions of higher salt concentration, consequently leading to dendritic growth (Fig. 3b). In a binary electrolyte, tSand is inversely proportional to the square value of j (j2), as demonstrated in the formula: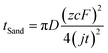 | (3.5) |
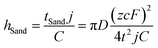 | (3.6) |
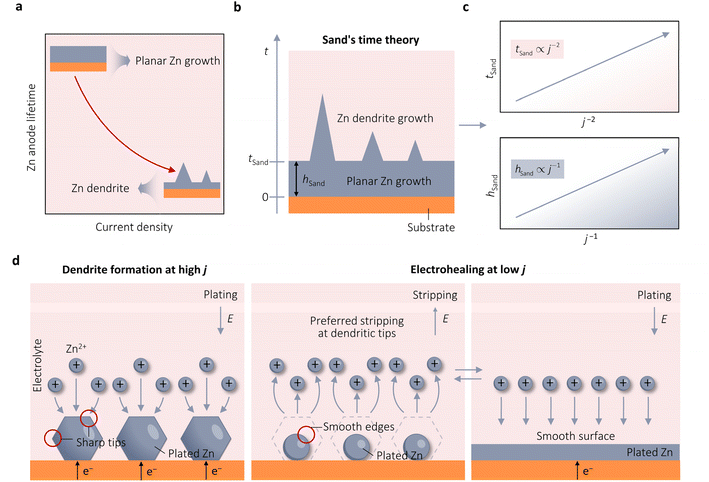 | ||
| Fig. 3 Kinetic theories and models pertaining to the growth of Zn. (a) Observed results of growth theories indicating the adverse impact of j on the longevity of Zn anodes. (b) Diagram of the electrodeposition process of Zn on substrates like Cu. Adapted from ref. 26 with permission from Wiley-VCH, Copyright 2023. (c) Plots of the correlation between j with either tSand or hSand. (d) Schematic representation of the electrohealing process, in which the sharp tips of dendrites are passivated to form smooth edges, resulting in a smooth anode surface. Adapted from ref. 22 with permission from Wiley-VCH, Copyright 2019. | ||
Brandon et al. conducted an in situ study of Zn dendrite growth, dissolution, and regrowth on Zn anodes using synchrotron X-ray computed tomography (SXCT), further supporting the perspective proposed by tSand theory.30 They observed that Zn dendrites first became visible in radiography after 180 s and 71 s at a j of 15 mA cm−2 and 80 mA cm−2, respectively, indicating a longer initiation time at low j compared to higher ones. Furthermore, their results showed that under constant j, larger dendrites exhibit a higher growth rate than smaller dendrites, indicating that a large portion of j flows through larger dendrites, enabling them to grow and form more branches at the expense of the growth of smaller dendrites. This behavior poses a significant challenge for battery charging at high j, as a single dendrite under high localized j can quickly reach the counter electrode and cause a permanent short circuit within minutes of operation. Shearing et al. utilized operando optical microscopy (OM) and in situ lab-based X-ray computed tomography (X-ray CT) to investigate and quantify the morphologies of Zn electrodeposition/dissolution in symmetric Zn‖Zn cells under various j.17 Their study revealed that higher j leads to a shorter initiation time and the formation of larger Zn dendrites. Increased j promotes the development of sharp dendrites with a larger mean curvature at their tips, leading to dendritic tip splitting and a hyper-branching morphology. Consequently, the Zn‖Zn cell exhibited stable cycling for 480 h at a low j of 2 mA cm−2. However, when subjected to a high j of 20 mA cm−2, the cell experienced short-circuiting after 25 h. This outcome is similar to Qie et al., who observed that the Zn‖Zn cell could cycle for 300 at a j of 0.885 cm−2 and only 25 h at 20 mA cm−2.43
Zhi et al. also highlighted the instability of Zn at high j.22 They observed that the Zn‖Zn cells showed a stable Zn plating/stripping process with a lifespan lasting 120 h at 1 mA cm−2. However, the lifespan decreased to 2.1 and 1.2 h at higher j of 7.5 and 10 mA cm−2, respectively. The η also increased significantly by 284% (from 134 mV at 1 mA cm−2 to 380 mV at 10 mA cm−2). This rise in η was due to the slower diffusion kinetics of Zn2+ from the bulk electrolyte to the Helmholtz layer and the solid–liquid interface, compared to electron transfer in the Zn anode. Increasing j led to a higher local j, intensifying η and causing uneven Zn plating. They subsequently proposed an electrohealing protocol to remove already formed dendrites by applying a low j. By subjecting a short-circuited Zn‖Zn cell at 10 mA cm−2 to dendritic electrohealing at 1 mA cm−2, they successfully eliminated dendrites. Further cycling at a high j of 10 mA cm−2 resulted in stable electrochemical performance for an additional 6.2 h before an internal short circuit. Through scanning electron microscopy (SEM) analysis of the evolution of Zn morphology, they concluded that low j favored Zn stripping at the sharp tips of Zn dendrites, producing smooth edges that hindered tip-growth behavior. Repeated Zn plating/stripping procedures at low j resulted in a smooth, large-area electrode surface that could reduce localized j (Fig. 3d). After this, Yang et al. used SEM to study the evolution morphology of Zn electrodeposition across a range of j from 0.025 to 10 mA cm−2.16 At lower j of 0.025–0.1 mA cm−2, large hexagonal Zn nuclei were observed on the Zn matrix. With an increase in j to 0.3 mA cm−2, the size of the nuclei decreased significantly. Subsequently, as j further rose from 0.3 to 2 mA cm−2, there was a gradual reduction in the nuclei size, with hexagonal-shaped Zn nuclei irregularly dispersed on the Zn matrix surface. However, at higher j of 5 and 7 mA cm−2, smaller Zn nuclei began to aggregate, forming tiny protrusions. This trend persisted at 10 mA cm−2, where the Zn nuclei displayed tiny protrusions that were not yet fully developed, resulting from the accumulation of ultra-thin Zn nuclei. The authors suggested the uneven distribution of Zn nuclei on the Zn substrate at different j. Higher j results in smaller nucleus sizes, and these small Zn nuclei easily accumulate to form tiny protrusions.
To sum up, tSand theory provides a mechanism to explain the negative effect of j on the stability of Zn from the perspective of Zn deposition diffusion kinetics and quantifies the critical j required for Zn dendrite formation. On the other hand, Zhi and Yang et al. appeared to use thermodynamic-based CNT and BVE to rationalize the proliferation of Zn dendrites under high j, a viewpoint that seems contradictory to the discussion in Section 3.1.16,22 This discrepancy may arise from an incomplete understanding of the nuances of nucleation and growth in Zn. It is recommended that researchers first establish tSand values at different j and calculate η when tSand is reached using BVE, akin to the approach employed by Chen et al.,26 before making conclusions. This approach will definitively determine whether the diffusion-controlled process has commenced, enabling a clear differentiation between the specific impact of j on Zn nucleation and growth during Zn electrodeposition, ultimately leading to the identification of the mechanism by which j affects Zn stability.
3.3 Combining thermodynamics and kinetics
The preceding observations suggest that the effect of j on the stability of Zn anodes is not straightforward, with conflicting results and interpretations. In response to this, Zhang et al. conducted a thorough investigation into the influence of j on Zn cyclic stability in 2021.24 Their study revealed that neither low j (as low as 0.04 mA cm−2) nor high j (up to 30 mA cm−2) improved the cycle life of Zn anodes. Instead, a moderate j of 5 mA cm−2 yielded the optimal Zn cyclic stability of 1600 h. The authors suggested that j has dual effects on Zn stability. On one hand, high j can lead to Zn instability by reducing tSand due to the adverse kinetic impact of j. Conversely, increasing j can enhance η and boost nucleation densities from a thermodynamic standpoint, contributing to the improved stability. An initial high j discharge strategy, which is similar to the work by Liu et al.,19 was thus developed to produce abundant nuclei for uniform metal growth at standard j in the subsequent process. This protocol increases the Zn deposition/stripping lifetime from 303 to 2500 h under a cycling capacity of 1 mA h cm−2 without resorting to electrode/electrolyte modification. In 2022, Sun et al. investigated the process of Zn electrodeposition using in situ OM to analyze its behavior under varying j.23 Their results were consistent with those of Zhang et al.,24 demonstrating that at a low j of 1 mA cm−2, aggregation favored hexagonal plates with a dominant <0001> facet, leading to randomly stacked nanosheets. Conversely, at a higher j of 10 mA cm−2, the Zn electrodeposition behavior was governed by high index facets, resulting in a uniform and closely packed morphology. Subsequently, increasing j to 100 mA cm−2 resulted in the expansion of the ion-depleted zone, inducing concentration polarization and initiating a diffusion-controlled regime.In brief, the two examples above emphasize the beneficial thermodynamic and adverse kinetic characteristics of j on Zn stability, with the highest stability observed at a moderate j (Fig. 4a). From the literature, it can be deduced that an increase in j leads to a volcano-shaped pattern in the reversibility of Zn plating and stripping. It is insufficient to analyze the stability of Zn deposition/stripping at high j solely from the perspectives of thermodynamics or kinetics. This volcano relationship arises from the conflicting roles that high j plays in thermodynamics and interfacial kinetics. Building upon these findings and existing literature protocols, we propose a more comprehensive strategy of regulating j to prolong the lifespan of Zn anodes. As shown in Fig. 4b, during Zn stripping, if dendrite formation occurs at a low j, increasing j will activate the beneficial thermodynamic nucleation characteristics, leading to a decrease in rc and an increase in ω to produce a smooth Zn surface. Conversely, if dendrites form at high j, reducing j will inhibit the adverse effect of Zn growth kinetics, raise tSand, and increase hSand, thereby impeding the diffusion-controlled process and promoting the uniform growth of Zn.
4 Conclusions and outlook
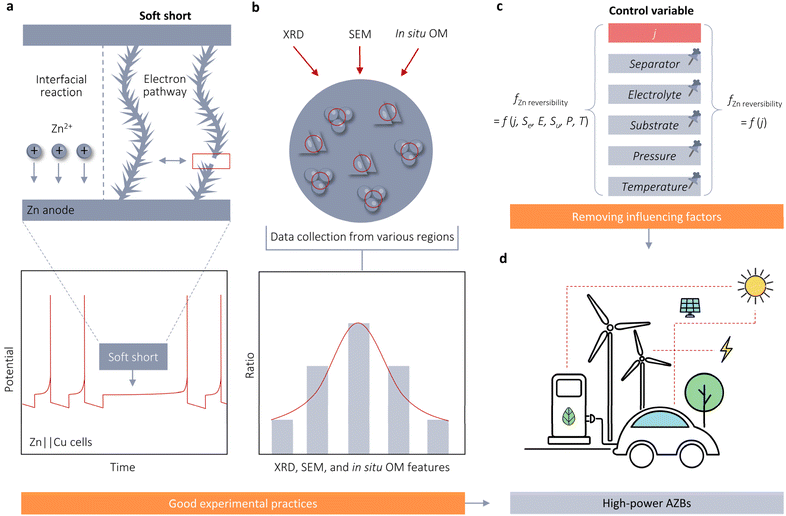
The improvement both in Zn reversibility and stability at high j is crucial for rapid charge and discharge applications of AZBs. However, there is an ongoing debate regarding the dependency of Zn reversibility on j. This perspective provides a comprehensive examination of the rate-dependent stability of Zn anodes by comparing and contrasting various nucleation-growth theories and models relevant to j. Our standpoint supports the notion that an increase in j results in a volcano-shaped pattern in the reversibility of Zn plating and stripping. However, given the conflicting conclusions from previous studies, it is essential to discuss certain experimental practices and influencing factors that may disturb the accurate assessment of the association between Zn reversibility and j in the following aspects (Fig. 5).4.1 Hidden “soft shorts” (SS) in AZBs and the necessity of reversibility assessment for Zn stability using asymmetric cells
The current performance gap—approximately 20-fold—between Zn‖Zn symmetric cells and Zn‖Cu asymmetric cells.44 State-of-the-art symmetric cells have been reported to stably operate at 80 mA cm−2, whereas asymmetric cells typically operate within the range of 1–5 mA cm−2 or even less. This substantial difference in performance raises concerns regarding the reliability of the exceptionally long lifespans claimed for symmetric cells. One likely factor contributing to this disparity is the phenomenon known as soft shorts (SS), which refers to a small localized electrical connection between two electrodes that enables direct electron transfer and interfacial reactions (Fig. 5a). SS commonly occurs in AZBs, particularly under aggressive performance conditions such as high j. However, detecting SS is challenging using Zn‖Zn symmetric cell tests, which could create an illusion of exceptional stability for Zn anodes. For instance, Zhi et al. conducted tests on Zn‖Zn cells at 50 mA cm−2 and observed a voltage profile with no abrupt drop and a quasi-rectangular shape with minimal fluctuations per cycle.44 According to commonly accepted evaluation criteria, this symmetric cell would be considered highly stable with exceptional Zn stripping/plating reversibility. However, these conclusions become problematic upon examining the electrochemical impedance spectrum (EIS). The Nyquist plot of the initial cell displayed a large semicircle with a diameter of approximately 240 Ω, indicative of the charge transfer resistance (Rct). This Rct then significantly decreased to 0 Ω after 50 cycles, demonstrating a typical signature of SS behavior. Due to the questionable high Zn reversibility after SS, they proposed that the symmetric cell in fact only exhibits a cycling life of less than 18 h at 50 mA cm−2, rather than the anticipated 100 h.In contrast to the symmetric cell controlled by time or plating/stripping capacities, the asymmetric cell is regulated by cutoff voltages. The SS behavior of the asymmetric cell is easily identifiable through galvanostatic charge and discharge (GCD) testing. A notable characteristic of SS in asymmetric cells is their inability to charge the cells to the upper cutoff voltage (Fig. 5a).45 Therefore, the protocols of asymmetric cells offer more accurate and timely insights into determining the actual lifespan of Zn anodes. When investigating the impact of j on the timescale and likelihood of dendrite formation or failure, the use of asymmetric cells becomes essential.
4.2 Randomness in XRD, SEM, and in situ OM results on accurate assessment of Zn stability and the importance of using in situ technologies
SEM and XRD are widely used techniques for evaluating cycle performance and visualizing Zn deposition morphology. However, these methods are constrained by significant spatial variability due to the enlargement factor and X-ray spot size. For example, Sun et al. observed diverse deposition morphologies on the same Zn surface using SEM, including both dense, uniform deposits and large dendrites. A similar issue is observed with XRD, where the intensities of Zn(002) and Zn(101) peaks, as well as their ratios, differ markedly across different regions of the Zn surface.35 These inconsistencies complicate the accurate assessment of Zn deposition morphologies. The spatial heterogeneity introduces substantial subjectivity and can lead to unreliable characterization results.In situ OM is another prevalent technique for microscale characterization of the plating/stripping behavior of Zn2+, enabling the visualization of dendrites. However, similar to SEM and XRD, in situ OM results demonstrate inherent variability, lack of reproducibility, and are constrained by the viewing angle. These factors can compromise the credibility, dependability, and impartiality of research outcomes. Therefore, we advocate for the collection of extensive data from multiple regions of the plated Zn metal surface, as illustrated in Fig. 5b, to address the constraints associated with characterization results.
Apart from in situ OM, we advocate for the utilization of a range of in situ characterization techniques such as in situ Fourier transform infrared spectroscopy (FTIR), Raman spectroscopy, and XRD. It is essential to establish a set of in situ characterization technology paradigms to monitor the dynamic variations at the Zn anode surface. This approach will enhance our comprehension of the fundamental mechanisms involved in the electrodeposition of Zn2+, thereby offering more valuable insights to facilitate rapid charge and discharge applications of AZBs.
4.3 The influence of battery configuration and environmental factors on evaluating the effect of j on Zn reversibility
In addition to the misleading impressions created by the aforementioned experimental practices, battery configuration can also impact the evaluation of the correlation between j and the reversibility of Zn. For instance, Zhou et al. attributed the paradox of smooth Zn deposition coupled with a short lifespan at high j to the separator permeation effect.46 They posited that the multiplied local j resulting from the narrow separator channels would inevitably initiate the diffusion-controlled region, causing the deposits to accumulate along the separator channels, ultimately resulting in a short circuit in the cell. To mitigate this issue, they proposed using a micro-pore sponge foam (150 μm) as the separator for high-j Zn anodes. This separator successfully enabled Zn‖Zn symmetrical cells to achieve a long lifetime of 238 h under 40 mA cm−2.Apart from the separator effect, the stability of Zn is significantly influenced by both the initially selected substrate and the orientation of the Zn. For instance, Robertson et al. demonstrated that utilizing only an appropriate metallic anode—without additional architecture, electrolyte, or interface modifications—can effectively address the dendrite issue and achieve exceptional cell performance in AZBs.47 When employing a metallic single-Zn anode, it becomes possible to achieve excellent planar deposition of dendrite-free Zn at an unprecedented j of 200 mA cm−2. Furthermore, this dendrite-free epitaxial surface is well preserved even after extended cycling of over 1200 cycles at 50 mA cm−2. Electrolytes also impact the stability of Zn. The tSand, as described by eqn (3.5), can be enhanced by employing a higher concentration electrolyte. Chen et al. demonstrated that planar, dendrite-free Zn can be rapidly achieved in a 10 m ZnCl2 electrolyte at an exceptionally high j of 1 A cm−2.26 In summary, Zn stability in AZBs is profoundly impacted by the battery configuration, including the substrate, electrolyte, and separator. Apart from battery configuration, external factors such as pressure and temperature can significantly impact Zn growth and nucleation, complicating the assessment of how j influences Zn electrode stability. Robertson et al. demonstrated that altering pressure can modify ηg, reducing the energy required for Zn growth and promoting a more uniform morphology on Zn surfaces.48 Wei et al. observed a temperature-dependent nucleation process and electrochemical performance in Zn metal anodes.49 Higher temperatures decrease η, leading to larger nuclei size and reduced nucleation density. Conversely, lower temperatures promote smaller and denser nucleation, facilitating the formation of fine-grained Zn deposits. Building on these insights, they proposed an in situ dendrite self-healing technique based on cooling treatment to eliminate dendrites formed during cycling at elevated temperatures. These factors account for discrepancies in cycling life and j tolerance reported in the literature for half-cells, and also elucidate why the upper limit of j for maintaining dendrite-free Zn anodes is continually updated in the literature, despite assumptions of a fixed limit for stable Zn electrodeposition. To accurately assess the impact of j on the stability and reversibility of Zn anodes, it is essential to employ the control variable method. This approach will enhance the reliability of experimental results by isolating the effects of j from other influencing factors (Fig. 5c) and thus facilitate a comprehensive understanding of the mechanisms underlying the influence of j on Zn reversibility, ultimately advancing the development of AZBs for rapid charge and discharge applications (Fig. 5d).
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this perspective.Author contributions
All authors participated in this perspective work. L. M. and W. J. performed the literature search. L. M. analyzed the published results and wrote the manuscript. L. J. reviewed and refined the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (52025013, 52071184, 52171228), and the Fundamental Research Funds for the Central Universities.Notes and references
- J. Shin, J. Lee, Y. Park and J. W. Choi, Chem. Sci., 2020, 11, 2028–2044 RSC.
- J. Zheng, Q. Zhao, T. Tang, J. Yin, C. D. Quilty, G. D. Renderos, X. Liu, Y. Deng, L. Wang, D. C. Bock, C. Jaye, D. Zhang, E. S. Takeuchi, K. J. Takeuchi, A. C. Marschilok and L. A. Archer, Science, 2019, 366, 645–648 Search PubMed.
- Y. Zhu, G. Liang, X. Cui, X. Liu, H. Zhong, C. Zhi and Y. Yang, Energy Environ. Sci., 2024, 17, 369–385 RSC.
- Z. Cai, J. Wang and Y. Sun, eScience, 2023, 3, 100093 CrossRef.
- S. Wu, Z. Hu, P. He, L. Ren, J. Huang and J. Luo, eScience, 2023, 3, 100120 CrossRef.
- Y. Dai, J. Li, L. Chen, K. Le, Z. Cai, Q. An, L. Zhang and L. Mai, ACS Energy Lett., 2021, 6, 684–686 CrossRef.
- L. Miao, Z. Guo and L. Jiao, Energy Mater., 2023, 3, 300014 Search PubMed.
- Q. Zhang, Y. Ma, Y. Lu, L. Li, F. Wan, K. Zhang and J. Chen, Nat. Commun., 2020, 11, 4463 CrossRef CAS.
- Y. Li, P. Wu, W. Zhong, C. Xie, Y. Xie, Q. Zhang, D. Sun, Y. Tang and H. Wang, Energy Environ. Sci., 2021, 14, 5563–5571 RSC.
- M. Wang, Y. Meng, K. Li, T. Ahmad, N. Chen, Y. Xu, J. Sun, M. Chuai, X. Zheng, Y. Yuan, C. Shen, Z. Zhang and W. Chen, eScience, 2022, 2, 509–517 CrossRef.
- L. Miao, R. Wang, S. Di, Z. Qian, L. Zhang, W. Xin, M. Liu, Z. Zhu, S. C. Y. Du and N. Zhang, ACS Nano, 2022, 16, 9667–9678 CrossRef PubMed.
- Z. Xiang, Y. Qiu, X. Guo, K. Qi, Z.-L. Xu and B. Y. Xia, Energy Environ. Sci., 2024, 17, 3409–3418 RSC.
- J. Wu, C. Yuan, T. Li, Z. Yuan, H. Zhang and X. Li, J. Am. Chem. Soc., 2021, 143, 13135–13144 Search PubMed.
- L. Miao, Z. Xiao, D. Shi, M. Wu, D. Liu, Y. Li, X. Liu, Y. Sun, S. Zhong, Z. Qian and R. Wang, Adv. Funct. Mater., 2023, 33, 2306952 CrossRef.
- Y. Liang, M. Qiu, P. Sun and W. Mai, Chem. Sci., 2024, 15, 1488–1497 RSC.
- P. Cao, J. Tang, A. Wei, Q. Bai, Q. Meng, S. Fan, H. Ye, Y. Zhou, X. Zhou and J. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 48855–48864 CrossRef PubMed.
- W. Du, Z. Zhang, F. Iacoviello, S. Zhou, R. E. Owen, R. Jervis, D. J. L. Brett and P. R. Shearing, ACS Appl. Mater. Interfaces, 2023, 15, 14196–14205 Search PubMed.
- Y. F. Cui, R. F. Cao, J. Y. Du, Z. B. Zhuang, Z. L. Xie, Q. S. Wang, D. Bao, W. Q. Liu, Y. H. Zhu and G. Huang, Chem. Commun., 2023, 59, 2437–2440 RSC.
- H. Liu, Y. Zhang, C. Wang, J. N. Glazer, Z. Shan and N. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 32930–32936 CrossRef PubMed.
- Y. Yang, H. Yang, R. Zhu and H. Zhou, Energy Environ. Sci., 2023, 16, 2723–2731 RSC.
- H. Glatz, E. Tervoort and D. Kundu, ACS Appl. Mater. Interfaces, 2020, 12, 3522–3530 CrossRef.
- Q. Yang, G. Liang, Y. Guo, Z. Liu, B. Yan, D. Wang, Z. Huang, X. Li, J. Fan and C. Zhi, Adv. Mater., 2019, 31, e1903778 CrossRef PubMed.
- Z. Cai, J. Wang, Z. Lu, R. Zhan, Y. Ou, L. Wang, M. Dahbi, J. Alami, J. Lu, K. Amine and Y. Sun, Angew. Chem., Int. Ed., 2022, 61, e202116560 CrossRef CAS PubMed.
- Z. Hou, Y. Gao, R. Zhou and B. Zhang, Adv. Funct. Mater., 2022, 32, 2107584 CrossRef.
- W. Yuan, X. Nie, G. Ma, M. Liu, Y. Wang, S. Shen and N. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202218386 CrossRef.
- Z. Hao, Y. Zhang, Z. Hao, G. Li, Y. Lu, S. Jin, G. Yang, S. Zhang, Z. Yan, Q. Zhao and J. Chen, Adv. Mater., 2023, 35, e2209985 CrossRef.
- C. Han, W. Li, H. K. Liu, S. Dou and J. Wang, Nano Energy, 2020, 74, 104880 CrossRef.
- Y. Zuo, K. Wang, P. Pei, M. Wei, X. Liu, Y. Xiao and P. Zhang, Mater. Today Energy, 2021, 20, 100692 CrossRef.
- W. Lu, C. Xie, H. Zhang and X. Li, ChemSusChem, 2018, 11, 3996–4006 CrossRef.
- V. Yufit, F. Tariq, D. S. Eastwood, M. Biton, B. Wu, P. D. Lee and N. P. Brandon, Joule, 2019, 3, 485–502 CrossRef.
- J. Hao, X. Li, X. Zeng, D. Li, J. Mao and Z. Guo, Energy Environ. Sci., 2020, 13, 3917–3949 Search PubMed.
- E. R. Cooper, M. Li, I. Gentle, Q. Xia and R. Knibbe, Angew. Chem., Int. Ed., 2023, 62, e202309247 Search PubMed.
- X. Yu, Z. Li, X. Wu, H. Zhang, Q. Zhao, H. Liang, H. Wang, D. Chao, F. Wang, Y. Qiao, H. Zhou and S.-G. Sun, Joule, 2023, 7, 1145–1175 Search PubMed.
- Q. Zhang, J. Luan, Y. Tang, X. Ji and H. Wang, Angew. Chem., Int. Ed., 2020, 59, 13180–13191 CrossRef PubMed.
- X. B. Cheng, R. Zhang, C. Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef PubMed.
- Y. Onabuta, M. Kunimoto, S. Wang, Y. Fukunaka, H. Nakai and T. Homma, J. Phys. Chem. C, 2022, 126, 5224–5232 CrossRef.
- S. Amini and R. Abbaschian, Carbon, 2013, 51, 110–123 Search PubMed.
- E. Budevski, G. Staikov and W. J. Lorenz, Electrochim. Acta, 2000, 45, 2559–2574 CrossRef.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef.
- K. Raeissi, A. Saatchi, M. A. Golozar and J. A. Szpunar, J. Appl. Electrochem., 2004, 34, 1249–1258 CrossRef.
- Q. Li, A. Chen, D. Wang, Y. Zhao, X. Wang, X. Jin, B. Xiong and C. Zhi, Nat. Commun., 2022, 13, 3699 CrossRef PubMed.
- H. J. S. Sand, London, Edinburgh Dublin Philos. Mag. J. Sci., 1901, 1, 45–79 CrossRef.
- R. Zhao, Y. Yang, G. Liu, R. Zhu, J. Huang, Z. Chen, Z. Gao, X. Chen and L. Qie, Adv. Funct. Mater., 2021, 31, 2001867 Search PubMed.
- Q. Li, A. Chen, D. Wang, Z. Pei and C. Zhi, Joule, 2022, 6, 273–279 CrossRef.
- L. Ma, M. A. Schroeder, O. Borodin, T. P. Pollard, M. S. Ding, C. Wang and K. Xu, Nat. Energy, 2020, 5, 743–749 Search PubMed.
- Z. Liu, J. Liu, X. Xiao, Z. Zheng, X. Zhong, Q. Fu, S. Wang and G. Zhou, Adv. Mater., 2024, 36, e2404140 Search PubMed.
- S. D. Pu, C. Gong, Y. T. Tang, Z. Ning, J. Liu, S. Zhang, Y. Yuan, D. Melvin, S. Yang, L. Pi, J. J. Marie, B. Hu, M. Jenkins, Z. Li, B. Liu, S. C. E. Tsang, T. J. Marrow, R. C. Reed, X. Gao, P. G. Bruce and A. W. Robertson, Adv. Mater., 2022, 34, e2202552 Search PubMed.
- Z. Li, Y. Yuan, S. D. Pu, R. Qi, S. Ding, R. Qin, A. Kareer, P. G. Bruce and A. W. Robertson, Adv. Mater., 2024, 36, 2401576 Search PubMed.
- J. Su, X. Yin, H. Zhao, H. Yang, D. Yang, L. He, M. Wang, S. Jin, K. Zhao, Y. Wang and Y. Wei, Nano Lett., 2022, 22, 1549–1556 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2024 |