Enhancing precision in PANI/Gr nanocomposite design: robust machine learning models, outlier resilience, and molecular input insights for superior electrical conductivity and gas sensing performance†
Abir
Boublia‡
a,
Zahir
Guezzout
b,
Nacerddine
Haddaoui
a,
Michael
Badawi
 c,
Ahmad S.
Darwish
de,
Tarek
Lemaoui
c,
Ahmad S.
Darwish
de,
Tarek
Lemaoui
 de,
Fawzi
Banat
df,
Krishna Kumar
Yadav
de,
Fawzi
Banat
df,
Krishna Kumar
Yadav
 gh,
Byong-Hun
Jeon
gh,
Byong-Hun
Jeon
 i,
Noureddine
Elboughdiri
i,
Noureddine
Elboughdiri
 jk,
Yacine
Benguerba
jk,
Yacine
Benguerba
 *lj and
Inas M.
AlNashef
*lj and
Inas M.
AlNashef
 def
def
aLaboratoire de Physico-Chimie des Hauts Polymères (LPCHP), Département de Génie des Procédés, Faculté de Technologie, Université Ferhat ABBAS Sétif-1, Sétif, 19000, Algeria
bUnité de Recherche sur les Matériaux Emergents –Sétif-; URMES, Equipe de Valorisation Des Polymères, Université Ferhat ABBAS Sétif-1, Sétif, 19000, Algeria
cUniversité de Lorraine, CNRS, L2CM, F-57000 Metz, France
dDepartment of Chemical Engineering, Khalifa University of Science and Technology, Al Saada St., Abu Dhabi, 127788, United Arab Emirates
eResearch & Innovation Center for Graphene and 2D Materials (RIC-2D), Khalifa University, P.O. Box 127788, Abu Dhabi, United Arab Emirates
fCenter for Membrane and Advanced Water Technology (CMAT), Khalifa University, Al Saada St., Abu Dhabi, 127788, United Arab Emirates
gFaculty of Science and Technology, Madhyanchal Professional University, Ratibad, Bhopal, 462044, India
hEnvironmental and Atmospheric Sciences Research Group, Scientific Research Center, Al-Ayen University, Thi-Qar, Nasiriyah, 64001, Iraq
iDepartment of Earth Resources & Environmental Engineering, Hanyang University, 222-Wangsimni-ro, Seongdong-gu, Seoul 04763, Republic of Korea
jChemical Engineering Department, College of Engineering, University of Ha'il, P.O. Box 2440, Ha'il 81441, Saudi Arabia
kChemical Engineering Process Department, National School of Engineers Gabes, University of Gabes, Gabes 6029, Tunisia
lLaboratoire de Biopharmacie Et Pharmacotechnie (LBPT), Université Ferhat ABBAS Sétif-1, Sétif, Algeria. E-mail: yacinebenguerba@univ-setif.dz
First published on 11th December 2023
Abstract
This study employs various machine learning algorithms to model the electrical conductivity and gas sensing responses of polyaniline/graphene (PANI/Gr) nanocomposites based on a comprehensive dataset gathered from over 100 references. Artificial neural networks (ANNs) demonstrated superior predictive accuracy among the models. The investigation delves into identifying and mitigating outliers, both structural and response-related, showcasing the robustness of the proposed ANN models. The study emphasizes the critical role of applicability domain (AD) analysis in evaluating model reliability. Results indicate high accuracy for electrical conductivity (RMSE: 0.408, R2: 0.984) and gas sensing responses for ammonia, toluene, and benzene gases (RMSE: 0.350, 0.232, and 0.081, R2: 0.967, 0.983, and 0.976, respectively). Input contribution analysis highlights key parameters influencing performance. The σ-profiles of additives emerge as significant contributors, emphasizing the importance of molecular-input understanding in machine learning models. These findings contribute to developing high-performance PANI/Gr nanocomposites with implications for diverse applications like supercapacitors, gas sensors, and energy storage devices. The study underscores the need for further research to deepen the understanding of molecular inputs' impact on PANI/Gr system performance, enabling more precise material design.
1. Introduction
Designing high-performance conducting and multifunctional nanocomposites is an exciting area of research that has garnered significant attention in recent years.1 Advanced materials encompass a diverse array of nanostructured materials, spanning one-dimensional, two-dimensional, and three-dimensional nanosized configurations, each customizable to showcase distinct and coveted attributes, including electrical conductivity, mechanical robustness, and sensing prowess. The resultant nanocomposites emerge as versatile candidates with widespread applications across various industries, such as automotive, integrated circuits, sensors, medical devices, and biomedical. These materials' tunable properties and multifaceted applications underscore their significance and potential contributions to advancements in diverse technological domains.2,3 The ability to create materials with customized properties is of great interest to researchers and industry alike, as it enables the production of high-performance materials that can meet specific requirements for a given application.4–6One of the most promising combinations among nanocomposites is the incorporation of conducting polymers and carbon-based materials, which has garnered significant attention due to their unique combination of properties.7–9 The ease of processing, ductility, and electrical conductivity of conducting polymers and the mechanical strength, optical properties, and sensing capabilities of carbon materials make this combination highly desirable. Pioneering the domain of conducting polymers, polyaniline (PANI) stands as a focal point of extensive investigation due to its remarkable properties. This versatile polymer has garnered significant attention for its potential applications in diverse electronic devices, including batteries, supercapacitors, and sensors. Its exceptional conductivity and tunable characteristics make it an attractive candidate for pushing the boundaries of modern electronic technologies.10–12 In particular, combining PANI with carbonaceous components within nanocomposites has emerged as an attractive approach for developing advanced materials due to the unique combination of their complementary properties. PANI is known for its exceptional electrical conductivity, high pseudocapacitance, and impressive resistance to environmental degradation,8,13 while carbonaceous materials, encompassing graphene, carbon nanotubes, and carbon black, stand out for their remarkable mechanical strength, expansive surface area, and superior electrical conductivity. Researchers have significantly improved electrochemical performance by combining these materials, making them ideal candidates for various applications.14,15 Graphene has emerged as a particularly exceptional material among the varied carbon-based materials due to its excellent electrical, thermal, and mechanical properties.16,17 Graphene's low density,18 remarkable specific surface area,19 and strong electron mobility20 make it an excellent substrate for housing the active polymer in nanocomposites.21 Since its discovery in 2004 by Geim and Novoselov,22 numerous studies have attempted to incorporate graphene as a nanofiller into PANI to develop multifunctional-based nanocomposites.
Furthermore, owing to the synergistic interaction of the two components, dramatic improvements in their properties and performance may be recognized. Compared to pristine PANI or graphene alone, these nanocomposites showcase enhanced thermal, electrical, mechanical, optical, and electrochemical properties.21,23 However, graphene's potential has been somewhat hindered by its insolubility in aqueous environments and its propensity to agglomerate, attributed to van der Waals (VDW) interactions between its sheets. To surmount these limitations, a series of graphene derivatives, including functionalized graphene, graphene oxide (GO), and reduced graphene oxide (rGO), have emerged as promising nanofillers for polymer nanocomposites.24,25 Numerous investigations have been carried out to augment the electrical characteristics of diverse nanocomposites based on PANI/graphene and its derivatives at ambient conditions, where many parameters would certainly influence these properties' performances such as the synthesis methods, morphologies, component ratios, doping type, protonation degree, redox state, and temperature, etc.26 For instance, doped PANI/GO revealed an electrical conductivity (k) of 10 S cm−1 and a specific capacitance of 531 F g−1 while for pristine PANI exhibited comparatively lower values of 2 S cm−1 and 216 F g−1.27 As a result, the improved conductivity and capacitance of PANI/graphene-based nanocomposites have paved the path for their wide-ranging applications in electronic devices, supercapacitors, sensing systems, detectors, fuel cells, and various other domains.28
Researchers must meticulously control the synthesis and processing conditions to design high-performance nanocomposites to achieve the desired properties. This involves optimizing the nanocomposite materials' composition, morphology, and structure while developing novel techniques for characterizing their properties at the nanoscale. Predicting the properties of these materials is crucial, especially given the almost limitless number of material structures that could exist. Traditional experimental trial-and-error approaches can be extremely time-consuming and laborious, requiring the synthesis and characterization of many samples.29,30 However, leveraging recent advancements in machine learning (ML) techniques, structure–property relationships in nanoscale materials can be discovered more efficiently. It is possible to train ML models on large datasets of experimental or simulated materials to estimate the properties of novel materials by analyzing their structural attributes.
Moreover, interpretable models can help identify the underlying structural reasons for specific properties, thus providing researchers with a better understanding of the materials they are working with.31–33 By integrating ML with experimental and theoretical approaches, researchers can accelerate the discovery of new high-performance nanocomposites with tailored properties for specific applications.34 While polymer materials' properties are closely related to the multiple parameters required for synthesizing and processing polymers, ML might be very advantageous to polymer research. Therefore, the capacity to forecast polymer characteristics before their synthesis will save energy and money in industrial development, expediting the investigation of structure–property connections among diverse polymers. This has resulted in the extensive application of polymers in electrical engineering, medical technology, and other manufacturing engineering fields.35,36 Numerous successful endeavors have been undertaken by scientists to employ machine learning for investigating polymer synthesis and properties.37 The application of ML in conjunction with mechanical properties of polymer composites,38,39 liquid crystal behavior of copolyether,40 thermal conductivity and dielectric properties,41–44 glass transition,45–47 melting and degradation temperature, as well as quantum physical and chemical properties,48–51 has led to significant achievement in prediction accuracy.
PANI/graphene-based nanocomposites have risen as up-and-coming materials due to their distinctive electrical and gas-sensing properties, rendering them well-suited for diverse industrial applications. However, developing PANI/graphene-based nanocomposites with enhanced properties and attaining a comprehensive comprehension of the interconnections between their properties and constituents necessitates in-depth analysis. Experimentally investigating every possible combination of PANI/graphene mixtures is challenging, time-consuming, and expensive. Hence, establishing prediction models for PANI/graphene-based nanocomposites' physicochemical features is critical. In this context, adopting ML techniques, particularly Artificial Neural Networks (ANNs), is an efficient and cost-effective alternative. ANNs, with their capacity to mimic the structure and function of the human brain, have garnered significant attention in this domain. ANNs are a type of ML algorithm capable of identifying patterns in datasets and making accurate predictions for new data based on these patterns.
ANNs have demonstrated remarkable success across diverse fields, effectively addressing material design, optimization, and process control challenges. By using ANNs, researchers can build accurate predictive models that can simulate the behavior of complex systems, such as PANI/graphene-based nanocomposites, with remarkable accuracy and efficiency. This research aims to thoroughly comprehend the performance prediction of PANI/graphene-based nanocomposites using ANNs and demonstrate the potential of this approach for designing and developing new high-performance nanocomposites. Twelve years of published data on PANI/graphene nanocomposites were utilized to build databases and create a data-driven platform to predict the electrical conductivity and gas sensing response performances of any new PANI/graphene-based nanocomposite. A comprehensive methodology is employed utilizing the COSMO-RS-derived σ-profiles of additives in the systems as inputs into eight different ML algorithms, including simple linear models such as Multi Linear regression (MLR), Multiple Non-Linear Regression (MLNR), Decision Tree (DT), Random Forest (RF), Gradient Boosting Machine (GBM), k-Nearest Neighbors (k-NN), Support Vector Regression (SVR), and ANNs. A thorough statistical evaluation and examination of the molecular space of applicability were performed to validate the predictive accuracy and robustness of the developed models.
Furthermore, a bootstrap forest was employed to categorize PANI/graphene systems based on their inputs, unveiling insights into the influences of individual inputs on the enhancement or reduction of electrical conductivity and gas sensing response in the nanocomposite systems. This groundbreaking study introduces pioneering holistic models, showcasing their proof-of-concept potential that effectively map the properties of graphene-based nanocomposites. It is also the first reported model to predict the electrical conductivity and gas-sensing response of polyaniline/graphene-based nanocomposites. The model's outstanding performance underscores the prospect of this methodological approach in guiding the design of novel PANI/graphene systems, reduces the necessity for extensive experimental measurements, leading to a substantial reduction in the nanocomposite manufacturing cycle, thereby facilitating the design of tailor-made conducting nanocomposites for specific applications.
2. Methodologies
This research aims to build a machine-learning technique for estimating the performance of polyaniline and graphene nanocomposite systems in high-end applications based on their electrical and gas sensing properties. The accurate prediction of the performance of such systems is a significant and currently unresolved challenge that involves modeling various processes occurring at distinct time and length scales. Instead of pursuing a multi-scale approach, a different strategy focuses on the conditions that can be imposed on the polyaniline/graphene systems and accurately predicted. Fig. 1 represents the overall procedure used for the development of the models. The first and foremost step of the methodology involves generating a comprehensive dataset from published literature sources and organizing it in a readable format. Subsequently, machine learning algorithms were evaluated and validated utilizing K-fold cross-validation. The best model was selected based on its performance and then further hyper-tuned to improve accuracy. The final models were employed to predict the systems' conductivity, gas-sensing effectiveness, and responsiveness to various parameters. The methodology will be thoroughly discussed in the subsequent sections of the manuscript.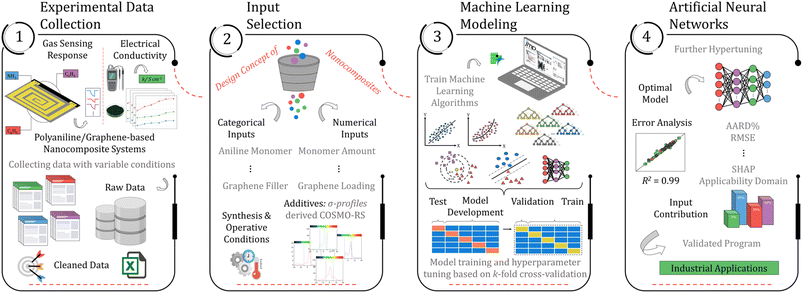 | ||
| Fig. 1 A comprehensive summary of the ML-assisted workflow for developing robust models capable of predicting electrical conductivity and gas sensing response. | ||
2.1. Datasets processing and treatment
One of the key steps in building a machine learning model is obtaining relevant datasets. To construct the datasets for this study, a comprehensive search was conducted to gather information on synthesis conditions that could affect the effectiveness of PANI and graphene nanocomposites. This was achieved by mining all available data published between 2010 and 2023 from credible sources such as Scopus, Google Scholar, and Web of Science using relevant keywords such as “polyaniline, PANI, graphene, nanocomposite, and PANI/graphene.” This study's performance evaluation of novel polyaniline/graphene nanocomposites was based on the collected experimental data. Data were sourced from tables and figures, while for specific figures where direct data retrieval proved challenging, a digitized image tool, in conjunction with the professional software Origin Lab® 2022b, was employed effectively to ascertain their values.Furthermore, the resulting experimental data was systematically organized into two primary datasets: electrical conductivity and gas sensing response. The raw data points in each dataset varied due to the availability of information reported in the literature, including a sum of 989 data points for electrical conductivity and 931 data points for gas sensing. Within the extensive gas sensing dataset, 26 different gases were identified in the literature, encompassing a range of substances such as hydrogen, ammonia, methane, nitrogen dioxide, sulfur dioxide, hydrogen sulfide, carbon dioxide, carbon monoxide, benzene, toluene, among others. Upon a comprehensive examination of the gas-specific datapoints, it became evident that ammonia, benzene, and toluene gases have received considerable attention in the literature. This is reflected in the substantial number of datapoints associated with these gases, establishing a robust foundation for comparative analysis with existing research. Furthermore, the prominence of these gases in real-world applications underscores their relevance and renders them meaningful choices for in-depth investigation within the scope of our study. Furthermore, various parameters, such as the concentrations of the monomer, oxidant, and doping agents, the graphene filler's type and loading, the synthesis conditions (temperature and time), and the operative temperature, were extracted from each report. The gas sensors' response also considered the tested gas's type and concentration. The experimental data that met the criteria for analysis was then organized in Excel, and a percentage distribution was generated to aid in the examination. The next step in the process was data cleaning and pretreatment since most unprocessed data sets contain duplicate or even inaccurate information that can negatively impact the machine learning model's performance. All the data points collected for this study were obtained from in situ polymerization, which involves synthesizing the PANI/Gr nanocomposites directly on the graphene surface. This approach simplifies the systems and eliminates potential contamination from external sources, resulting in more reliable and accurate experimental data. Additionally, this methodology ensures a higher degree of homogeneity in the resulting nanocomposites. It reduces the variability in the measured properties, which is crucial for developing robust ML models for predicting the electrical conductivity and gas sensing response values. The final data utilized in this study consisted of 616 data points of various systems and synthesis conditions for electrical conductivity and 668 datapoints for gas sensing, with the gas sensing data further subdivided and analyzed for the presence of ammonia, benzene, and toluene gases (338, 146, and 122 datapoints, respectively).
The entire dataset is provided in Tables S1 and S2 of the ESI.† Further, the datasets were converted and used on the logarithmic scale during training for all property sets used in the models to aid machine learning. Fig. 2 presents a comprehensive summary of the histogram distribution for the employed datasets, showcasing their frequency counts, averages, and one-sigma standard deviations. Utilizing a logarithmic scale during model training leads to a more uniform distribution, effectively mitigating any unbalanced skewness in the models.
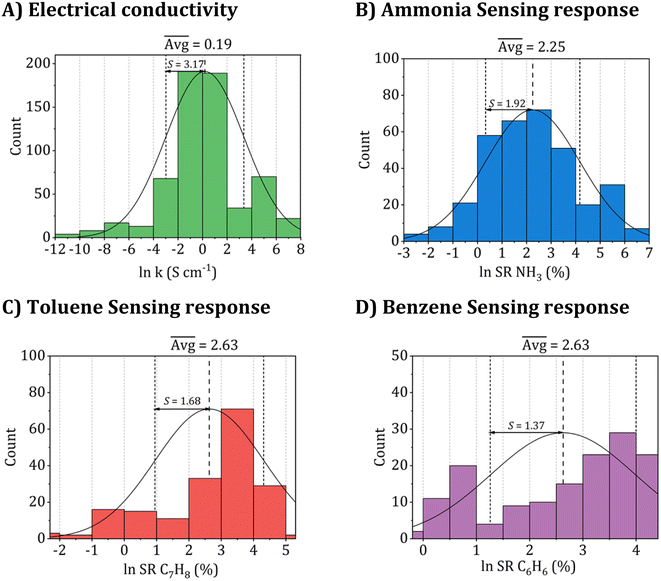 | ||
| Fig. 2 Histogram distribution of the collected datasets utilized for (A) electrical conductivity, (B) ammonia (NH3), (C) toluene (C7H8), and (D) benzene (C6H6) sensing responses. | ||
2.2. Input selection
When building an ML model, identifying relevant inputs is vital in ensuring the model's accuracy and effectiveness. To determine the relevant factors that affect the performance of polyaniline/graphene systems, a comprehensive literature review was conducted to identify commonly reported input parameters. These inputs were then incorporated into the ML models, considering the design concept of nanocomposites and experimental operation. As shown in Fig. 3, four sections were chosen as input descriptors. They are as follows: (1) matrix: aniline amount, type, and amount of oxidant, volume, and concentration of the doping agent, and additives, (2) filler: graphene filler type and loading, (3) synthesis conditions: temperature and time, and (4) operating conditions: temperature and gas concentration for the gas sensing response properties. It is worth noting that some inputs that may affect the electrical conductivity or gas response were not included in the datasets as they were either not widely reported in the literature or not uniformly documented. However, many of the inputs used in these datasets were categorical, and a short abbreviation was utilized to incorporate categorical data in the ML algorithms effectively. This involved assigning numerical values to the categorical inputs, such as the type of graphene nanofiller and doping agents. The numerical inputs, such as temperature and time, were entered as reported in the literature. A comprehensive list of numerical and categorical inputs is shown in Table S3 in the ESI.†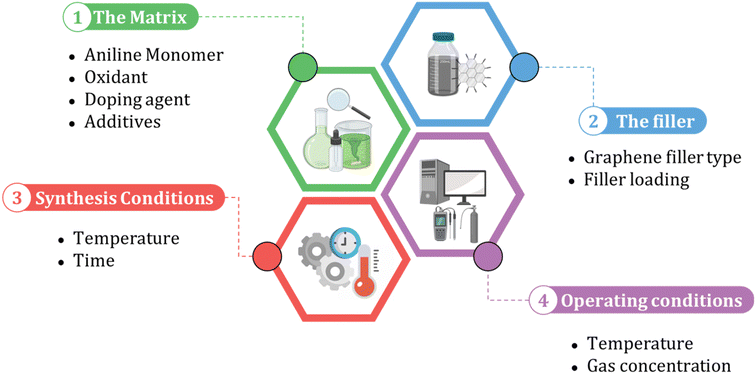 | ||
| Fig. 3 The input selection process for machine learning models of polyaniline/graphene nanocomposites. | ||
Given the limited number of variations for inputs, including monomers, oxidants, and graphene fillers, incorporating them as molecular inputs into the model would not significantly increase its complexity and result in overfitting. However, the wide range of various additives used in the systems can dramatically impact the material properties. To properly account for these impacts, it was crucial to include the additives as molecular inputs in the model. Utilizing sigma profiles derived from the COSMO-RS offered a powerful method for characterizing the complex mixture of additives in the system. This approach accurately describes the mixture and provides valuable insights into the behavior and properties of the material under study. This molecular method allows for a complete examination of the effects of additives on polyaniline/graphene systems, yielding a clearer understanding of their influence on material characteristics and behavior. The methodology behind the molecular inputs is thoroughly described in a subsequent section.
In this study, the density functional theory (DFT) computations were conducted using the DMol3 code, part of the Material Studio® 2020 software developed by BIOVIA Corporation. This code employs localized numerical orbitals as basis functions and can predict the energy and structure of atoms without any experimental data inputs.52–55 To improve upon the limitations of the LDA in accurately predicting bond energies and equilibrium distances, the GGA with the PBE method was used to treat the correlation.56,57 The GGA functional is known for its reliable numerical behavior and is commonly employed in DFT methodology. The computations were performed using the high-quality DNP basis set, including hexadecapole for multipolar expansion. Using a numerical basis set and precise DFT spherical atomic orbitals to mitigate any potential basis set superposition effects and enhance the accuracy of the system description, even for weak bonds. To optimize computational performance and achieve convergence efficiently, a thermal smearing of 5 × 10−3 Ha was utilized. Additionally, we set the density at 0.2 charges and 0.5 spins, respectively, to improve the overall computational efficiency. These computational approaches contributed to a more reliable and accurate analysis of the system under investigation. In addition, for the graphene-based compounds, we employed specific models to simulate their structures. The graphene (Gr) model contained 92 atoms and was adopted from previous studies.58 The model of graphene oxide (GO) consisted of 114 atoms, which include two epoxy groups (C–O–C), two hydroxyl groups (–OH), and four carboxyl groups (–COOH).59 For reduced graphene oxide (rGO), a model of 93 atoms with the charge set at −2, where oxygen atoms bonded to 2 carbon atoms to represent the C–O–C group.60 After geometry optimization, energy computations were performed utilizing a conductor-like screening model for real solvents (COSMO-RS) solvation with a dielectric constant of 78.54, representative of water,61 to generate COSMO files. These files were subsequently leveraged to calculate sigma profiles (σ-profiles).
2.3. Machine learning models
This study aimed to identify polyaniline/graphene-based nanocomposites with high electrical conductivity and gas-sensing solid capabilities for ammonia, toluene, and benzene. To achieve this, we evaluated eight different ML algorithms concurrently (Fig. 4), including simple linear models such as MLR, MLNR, DT, RF, GBM, k-NN, SVR, and ANN. The details of these ML algorithms are introduced in more facts in Table 1.| Machine learning algorithm | Method description | Sources |
|---|---|---|
| Multi linear regression | A widely used technique for predicting an outcome based on one or more input variables. It assumes a linear interaction between the inputs (X) and the output variable (Y) | 63 and 64 |
| Multiple non-linear regression | A ML technique that accurately models complex relationships between multiple inputs and an output variable, allowing for non-linear behaviors. Through iterative optimization algorithms, MNLR estimates the model coefficients, providing a robust tool for process optimization and control. Compared to MLR, MNLR can provide more accurate models for processes with nonlinear behavior | 65 |
| Decision tree | A straightforward ML method involves gathering and organizing data into a tree-like structure. The data is arranged into roots and nodes, and the technique follows the path of the nodes that meet specific conditions until the outcome (represented by a leaf node) is reached | 66 |
| Random forest | A powerful ML approach that uses multiple decision trees to make predictions. It uses bootstrapped samples and random feature selection to reduce overfitting and improve accuracy. By combining the predictions of multiple DTs, RF creates a more robust and accurate model compared to a single DT | 64 and 67 |
| Gradient boosting machine | A ML algorithm employs a sequence of decision trees, similar to RF. However, in GBM, each subsequent tree aims to reduce the residual errors of the preceding tree | 68 |
| k-Nearest neighbors | A memory-based method is used for classification and regression. It is based on the idea that similar instances tend to have similar outputs. The k-NN algorithm assigns the class/value of an observation based on the majority class/value of its k nearest neighbors. The number of nearest neighbors (k) is a user-specified parameter, and a common choice is k = 5 or k = 10 | 69 and 70 |
| Support vector regression | A ML algorithm creates a boundary that separates different classes by maximizing the margin between them. Using the kernel trick, it can handle non-linear decision boundaries, making it robust to overfitting and valuable. It efficiently runs high-dimensional data but requires more computational resources than other methods like k-NN | 68 and 69 |
| Artificial neural networks | A powerful ML technique inspired by the structure and function of the human brain, it consists of layers of interconnected neurons that process input and make predictions. It is divided into input, hidden, and output neuron layers | 71–73 |
These ML algorithms, including MLR, MLNR, DT, RF, GBM, K-NN, SVR, and ANN models, were all implanted and directly programmed using the JMP® statistical software (version 16). To optimize the model hyperparameters, we employed several techniques, including stepwise parameter variation for MLR to achieve the smallest value of root mean squared error (RMSE), varying the number of splits between 1 and 100 for DT, using default settings with 100 trees for RF and GBM; performing k-NN regression for all k-values of 10; and adjusting the neuron's number in the first hidden layer of ANNs between 5 and 25. Additionally, to further optimize the performance of the ANNs, we performed further adjustments by varying the configuration of neurons in the second hidden layer, along with their activation functions. These refinements were accomplished through a conventional iterative approach, systematically seeking the most effective settings62 through a seven-level factorial design, which evaluated 25 two-hidden layer configurations. All other software options in JMP® 16 were kept as default.
2.4. Criteria for model evaluation
To analyze the reliability and applicability of the developed ML models, a k-fold cross-validation technique was employed.74 In this strategy, the dataset is divided into k = 5 subsets of equal size, one of which serves as the test set, while the remaining k-1 subsets form the training set, which also includes the validation set. The primary objective of this technique is to train the model using different subsets of the data and evaluate its performance using the held-out test set. By repeating this process k times, we can estimate the model's performance using data not included in the specific fold. The final model is then selected based on the parameter set that provides the lowest average error across all k iterations (Fig. 4H). This method effectively prevents overfitting and gives a more thorough assessment of the models' capacity to adapt to new data.Moreover, various metrics were employed to assess the models' reliability. These metrics encompass root mean square error (RMSE), coefficient of determination (R2), the standard deviation (ASD), average absolute relative deviation (AARD), and Mean Absolute Error (MAE), which are determined through eqn (1)–(5). In these equations, Yexp, Ypred, and Ȳ are utilized to denote the target properties' experimental, predicted, and average values, respectively. The symbol N represents the total number of data points in the datasets.
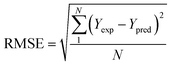 | (1) |
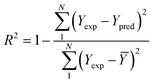 | (2) |
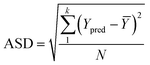 | (3) |
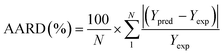 | (4) |
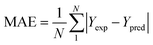 | (5) |
Although all of these metrics are generally useful for evaluating model accuracy, it was found that the RMSE is mainly affected by a small number of highly inaccurate predictions. In practical applications, such predictions can have significant consequences. Therefore, RMSE has been adopted as the primary metric for quantifying accuracy in this study, in which the analysis of the current data sets indicates that the RMSE provides a conservative estimate of the model's performance, making it a suitable choice for evaluating the accuracy of the developed models.
2.5. Artificial neural network
Upon evaluating the constructed models, the most effective model, ANN, was chosen for interpretation. The hidden neurons within layers 1 and 2, denoted as Hn,l and HHn,l respectively, are mathematically represented by eqn (6) and (7). The weights between neurons m and n, denoted as Wm,n,l, along with the biases of neurons (b), are specified in the equations. The hyperbolic tangent function (tanh) utilized in eqn (6) and (7) confines the neuron's activation or deactivation values within the range of [−1, 1]. Ultimately, the ANN model's output response (ypred) is determined through eqn (8), derived from eqn (6) and (7).33,75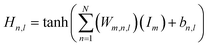 | (6) |
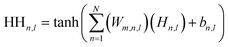 | (7) |
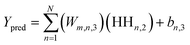 | (8) |
The optimization process during ANN training involved the implementation of the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm, well-regarded for its efficacy in handling datasets. To ascertain the suitability of the dataset for training ANNs, a meticulous evaluation was conducted, considering factors such as the model's complexity, dimensionality of the input space, and intrinsic relationships within the data. Despite the considerable number of data points, we underscored the significance of scrutinizing the distribution across training, validation, and testing sets. To gauge the model's generalization performance, we employed appropriate cross-validation techniques, ensuring a robust assessment of the ANN training efficiency. The effectiveness of training ANNs with a specific number of hidden neurons underwent comprehensive testing and cross-validation procedures. This rigorous validation process guarantees the models' robustness and their ability to generalize effectively to new, unseen data. For internal validation, a k-fold of 5 was adopted, and an ANN network learning rate of 0.10 was set, employing squared penalty optimization [∑(Yexp − Ypred)2] to enhance learning stability. The model weights were initialized randomly to ensure diversification in the preliminary state and prevent convergence to local minima. A maximum of 1000 epochs were carried out throughout the training process, and early stopping was incorporated to avoid overfitting. The training was stopped if the validation loss did not improve in consecutive epochs. The model with the lowest achieved Mean Squared Error (MSE) value was chosen as the best, while all other settings in JMP 16 Pro® remained at their default values.
2.6. Applicability domain analysis
To determine the outliers in the datasets and establish the range of molecules/systems for accurate predictions, an applicability domain (AD) evaluation was conducted. The AD approach relies on two key specifications, namely, the leverage values hi, and the SDR. The AD range is defined as 0 < hi < h*, and −3 < SDR < +3. The critical leverage value h* and the leverage value hi are determined using eqn (9)–(11), respectively. A matrix represents the input parameters considered for this study xi of dimensions 1 × D while D is the number of input parameters. The training data points are represented by a matrix V of dimensions N × D, where N is the total number of data points in the datasets, moreover, the superscript “T” signifies the transpose of matrices.76,77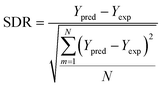 | (9) |
| hi = xi(XTX)−1 × xiT | (10) |
| h* = 3(D + 1)/N | (11) |
The William plot is widely used to represent the applicability domain (AD) visually due to its simplicity.76,78 It involves plotting the SDR versus hi values to determine the AD coverage. The AD coverage is calculated using the following equation eqn (12), where Ninside refers the count of data points that lie within the specified boundaries, while Ntotal represents the total number of data points considered for analysis.
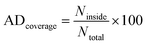 | (12) |
3. Results and discussion
3.1. Database treatment and visualization
To develop accurate ML-based prediction models, it is necessary to visualize and analyze the constructed datasets to investigate the correlations and structures of each input. The collected datasets for both electrical conductivity and gas sensing capabilities of PANI/graphene nanocomposites involve several forms of nanocomposites based on various parameters such as aniline concentrations, oxidant types and concentrations, graphene types, and loading, dopant types and concentrations, and additive types. Including such comprehensive and diverse data is essential for developing reliable prediction models. The datasets consist of graphene-based nanofillers, including Gr, GO, and rGO. The commonly used oxidants and dopants for PANI/graphene nanocomposite fabrication are ammonium persulphate and hydrochloric acid, respectively. The loading of graphene varies from 0 to 50 wt%, with most loadings being between 0.1 and 3 wt%, although exceptional cases of high loading rates were noticed for GO fillers. Moreover, more information has been gathered about the concentrations of aniline monomers/oxidants, such as APS or potassium persulphate (KPS), which range from 10−3 to 2 M, with the majority of the concentrations ranging between 0.5 and 1 M. The aniline monomers/dopants include 9 different doping agents with concentrations ranging from 0.1 to 10 M, with most concentrations of 1 M. We also observed high concentrations of formic acid as a dopant (10 M), which is not typically applied in experiments. The additives vary from organic solvents surfactants to nanoparticles, with different concentrations. The datasets underwent essential preprocessing steps to enhance the accuracy and reliability of ML models for predicting the performance of PANI/graphene nanocomposites. These steps encompassed handling missing data, detecting and removing outliers, and normalizing data to ensure equitable consideration of each input variable in the analysis. For instance, the deliberate selection of ammonia, benzene, and toluene as selected gases in this study was grounded in their prevalence in industrial and environmental contexts, aligning them closely with gas-sensing applications. Their distinct chemical properties permit an exploration of the versatility of polyaniline/graphene-based nanocomposites across diverse chemical environments.79,80 Moreover, the extensive literature on these gases serves as a robust foundation for comparative analysis, contributing meaningfully to existing research and advancing the understanding of gas-sensing materials. The practical significance of ammonia, benzene, and toluene in real-world applications, including environmental monitoring and industrial processes, further justifies their selection for in-depth investigation. While recognizing the importance of other gases, our focused exploration of ammonia, benzene, and toluene enables valuable insights into the materials' performance within the defined scope and objectives of this study.Consequently, the application of such preprocessing steps is crucial for developing accurate prediction models by reducing noise and improving the reliability of results. The comprehensive information gathered about the inputs forms the basis for building highly accurate and reliable ML models. Such models aid in the design and optimization of new and innovative materials. Thus, the use of advanced visualization and data preprocessing techniques along with comprehensive datasets is essential for developing accurate prediction models.
3.2. Input selection
Input selection is a critical process that selects the key features that contribute most to the PANI/graphene systems. As mentioned earlier, the input variables were chosen based on the design principles of nanocomposites and the requirements of experimental operations. Although the number of variations for inputs, such as monomers, oxidants, and graphene fillers, is limited, incorporating them as molecular inputs into the model is still essential. This approach ensures that the model's complexity does not significantly increase and results in overfitting. However, using various additives in the systems can dramatically impact their material properties. Therefore, it is crucial to include the additives as molecular inputs in the model to account for these impacts properly. The following section will analyze the σ-profiles of some selected additives and other features. This analysis will better understand the proportion of each input variable to the PANI/graphene systems' performance and behavior.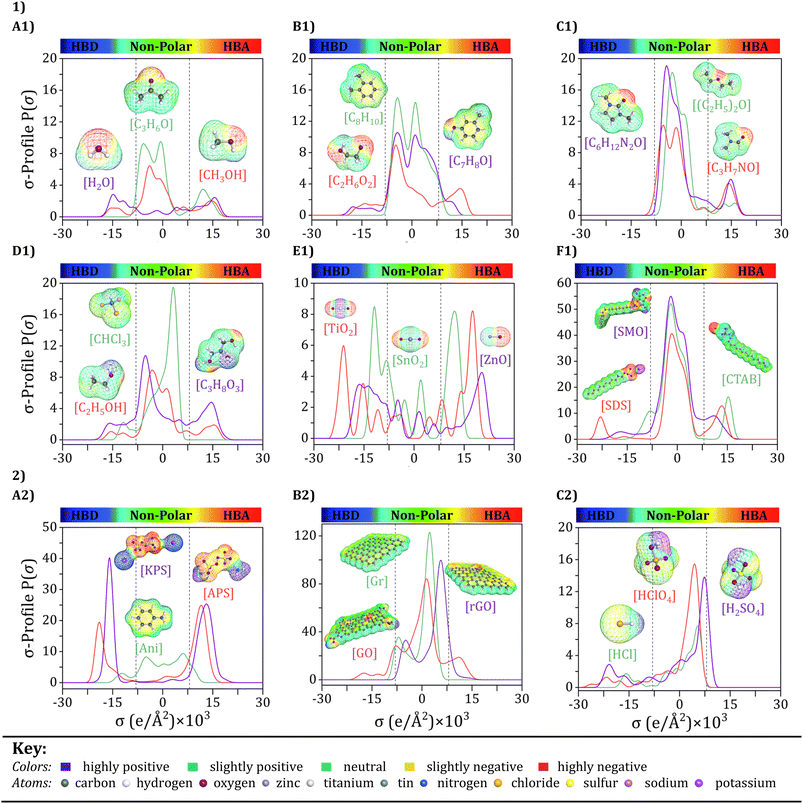 | ||
| Fig. 5 COSMO-RS molecular structures and σ-profiles of selected components: (1) various additives (A1–F1), and (2) aniline monomer, two oxidants, graphene fillers, and three dopants (A2–C2). | ||
Upon observing Fig. 5, it becomes evident that the σ-profiles can be classified into three distinct regions, each delineated by the electrostatic properties of the molecular surface. These regions are identified as the hydrogen bond donor (HBD) region (−0.030 < σ < −0.008 e Å−2), the non-polar region −0.0075 < σ < +0.008 eÅ−2), and the hydrogen bond acceptor (HBA) region (+0.008 < σ < +0.030 e Å−2).88–90 As depicted in Fig. 5, the HBD, non-polar, and HBA regions are clearly distinguished using vertical dashed lines. As described earlier, the peaks in the σ-Profile include more of a measure of the relative concentration of different atom types within the molecular system, therefore revealing underlying molecular insights into the behavior of compounds. The additives used in these systems can vary greatly, including solvents, inorganic nanoparticles, and surfactants. Solvents play a key aspect in the preparation and effectiveness of polyaniline/graphene systems. They serve a dual purpose as they are employed both for dissolving the polyaniline and graphene and for doping/dedoping the system, thereby affecting its conductivity. Additionally, solvents can also serve as washing agents. The choice of solvent has a major impact on the properties of the system, including its stability, dispersion, and conductivity.91 Each of these solvents has unique properties and characteristics, such as boiling point, solubility, and polarity, which can affect the properties of the polyaniline/graphene system. In the case of water (H2O), acetone (C3H6O), and methanol (CH3OH), as shown in Fig. 5A1, The σ-Profile graphs exhibit wide peaks that span across both the HBA and HBD areas, showing the potential of these solvents to act as both HBAs and HBDs, this phenomenon is primarily governed by the concentration and polarization of the partially positive hydrogen (Hδ+) and partially negative oxygen (Oδ−) atoms in the molecule, respectively. The sigma profile graphs for xylene (C8H10), ethylene glycol (C2H6O2), and m-cresol (C7H8O) show that these solvents also have the potential to act as both HBAs and HBDs, with distinct peaks and regions in their profiles (Fig. 5B1). The exact nature of these peaks and regions depends on the specific functional groups in the molecule, includs the –OH group in ethylene glycol and the phenol group in m-cresol. Furthermore, dimethyl propylene urea (C6H12N2O), ethyl ether ((C2H5)2O), and dimethylformamide (C3H7NO) reveals small peaks in the HBA region and minimal or no presence in the HBD region (Fig. 5C1). The presence of functional groups, such as amines and ethers, accounts for this observation, for instance, in the case of C3H7NO, it can be attributed to the nitrogen (N) atom, which has a relatively high electronegativity, allowing it to attract electrons and partially negative charges. However, these solvents have a weak HBA ability, suggesting that they can be classified as intermediate polar with different solubility properties.
Further, the σ-Profile of ethanol (C2H5OH) and glycerol (C3H8O3) suggest that they can act as both HBAs and HBDs, with distinctive peaks and regions in their profiles determined by the functional groups in the molecule. On the other hand, chloroform (CHCl3) is dominated by a peak close to the HBA region, which is primarily attributed to the presence of a highly polarizable chloroform molecule due to the fact of a highly electronegative chlorine (Cl) atom in the molecule Fig. 5D1. This polarizability enables chloroform to act as an effective HBA, leading to the observed peak close to the HBA region. Inorganic nanoparticles are essential in controlling the properties and behavior of polyaniline/graphene systems, promoting oxidation and improving the material's conductivity for practical functionality. In terms of their σ-profiles, as shown in Fig. 5E1, tin oxide (SnO2), zinc oxide (ZnO), and titanium oxide (TiO2) show unique peaks and regions in both HBD or HBA regions, which can influence the interactions between the polyaniline and graphene components. For example, due to its excellent conductivity-promoting properties, SnO2 is a widely used oxidant in polyaniline/graphene systems. It is a wide bandgap semiconductor made up of tin and oxygen atoms and is commonly used in various fields, including catalysis, gas sensing, and environmental remediation.92 The σ-Profile of SnO2 shows broad peaks in both the HBD and HBA areas, indicating that it can act as both an HBD and HBA. These peaks are primarily attributed to hydroxyl groups and oxygen atoms appearing on the SnO2 surface. The –OH groups can act as HBDs by donating a hydrogen atom, while the oxygen atoms can act as HBAs by accepting a hydrogen atom. However, it is essential to note that these specific characteristics can vary depending on various factors, such as the nanoparticle synthesis process, particle size, and crystal structure.93
Moreover, considering surfactant substances as additives in these systems, it is essential to note that their σ-Profile, as represented by sodium dodecyl sulfate (SDS), sodium cetyltrimethylammonium bromide (CTAB), and sorbitan monooleate (SMO), will typically have a larger neutral region, indicating that they are not likely to participate in hydrogen bonding interactions with other substances (Fig. 5F1). However, some HBD or HBA regions may be present, suggesting that these substances can form weak hydrogen bonds with other molecules due to their unique molecular structure. However, they are not typically considered strong HBDs or HBAs. Surfactant molecules tend to interact more strongly with each other through hydrophobic and VDW interactions rather than with H bonding with other molecules, owing to the polar head groups and nonpolar tails in their molecular structure. Despite not directly participating in hydrogen bonding interactions, surfactants are pivotal in improving the dispersion, stability, and characteristics of polyaniline/graphene nanocomposites, making them an essential component of these materials.
In the context of the statement provided, the σ-profiles also yield significant insights into these components' molecular interactions and behavior, which are invaluable contributions to advancing the field. The key components analyzed in this study include an aniline monomer, two oxidants, three representative graphene fillers, and three dopants (Fig. 5(2)). Even though these components may not be directly included as molecular inputs, their σ-profiles offer a deeper understanding of their electronic structure and interactions with the surrounding environment. By analyzing Fig. 5A2, aniline, for example, can act as an HBD and an HBA. The HBD and HBA properties of aniline are essential in the polymerization process, as they allow for hydrogen bond creation between aniline monomers, which can facilitate the polymerization reaction. Specifically, the density of electrons on the nitrogen atom and the benzenoid and quinoid unit of aniline can contribute to its ability to undergo oxidative polymerization with oxidants, including ammonium persulfate (APS) or potassium persulfate (KPS). Alternatively, the σ-profiles of APS and KPS can offer valuable information on their reactivity and capability to oxidize aniline monomers.
The electron density on the sulfate groups of these oxidants, as revealed by their σ-profiles, can facilitate the H bond creation with the electron's lone pairs on the aniline nitrogen atom. Furthermore, the σ-profiles can indicate the ability of these oxidants to accept electrons during the oxidation process. In the case of graphene and its derivatives (Fig. 5B2), σ-Profile can give insight into the interactions between the graphene sheets and the surrounding solvent or other molecules. For Gr, σ-Profile shows a uniform electron density distribution around the sheet, with a slight electron density depletion at the edges. This is because the carbon–carbon bonds in Gr are powerful, and the electron density is uniformly dispersed over the sheet.
In contrast, GO shows a more significant variation in electron density, as the O-containing functional groups on the sheet surface can create regions of higher or lower electron density. These functional groups can interact with solvent molecules or other molecules in solution through hydrogen bonding or other interactions, which can affect the stability and reactivity of the GO.94 For rGO shows a decrease in electron density compared to GO, as the reduction process removes some of the oxygen-containing functional groups from the sheet surface. This can lead to a uniform electron density around the sheet, similar to Gr.95 Doping is a process in which impurities, or dopants, are intentionally introduced into a material to modify its properties. Hydrochloric acid (HCl), sulfuric acid (H2SO4), and perchloric acid (HClO4) are widely recognized and used as dopants to modify the electronic and structural properties in the case of the polyaniline/graphene nanocomposite systems. When examining the σ-Profile (Fig. 5C2) of HCl, H2SO4, and HClO4, it can be observed that there are regions of high electron density around the sulfur, chlorine, and oxygen atoms. These regions of high electron density indicate that these atoms have a partial negative charge and are, therefore, capable of acting as HBAs. Therefore, these molecules can participate in H-bonding interactions with suitable donor molecules, which can play a key function in chemical reactions and the behavior of these compounds in various applications. Overall, σ-profiles reveal important information about the electronic structure and interactions of key components in conducting polymer composites like polyaniline/graphene. This analysis can assist in designing and enhancing the material properties in wide variety of applications, including electronics and energy storage materials. Additionally, accurately predicting the hydrogen bonding ability of these molecules based on its σ-Profile can also be beneficial for gas sensing applications. This can aid in the discovery and development of gas sensors with improved sensitivity and selectivity, leading to better detection and identification of various gases in industrial and environmental settings.
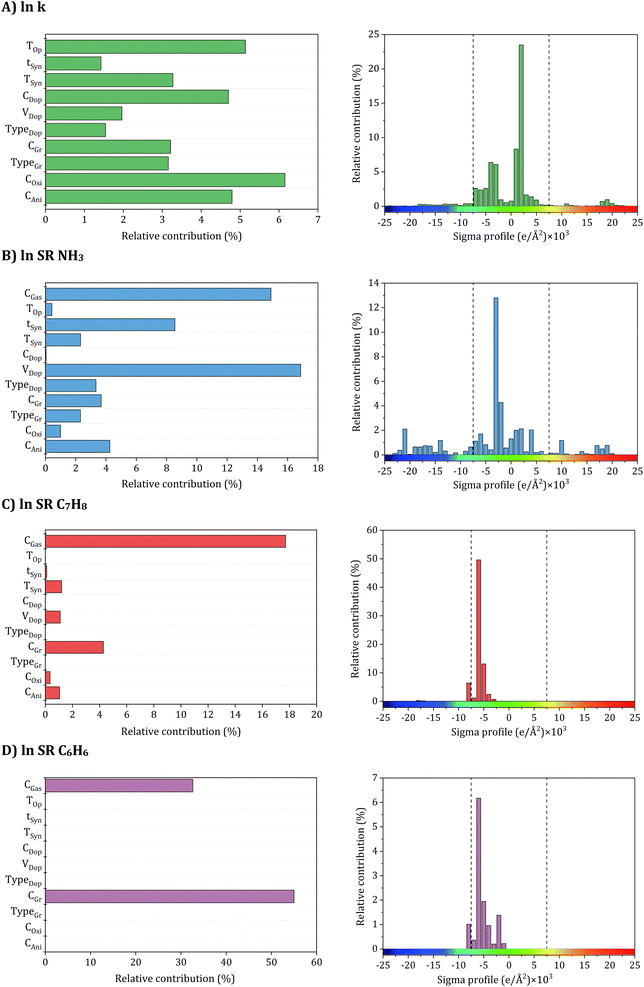 | ||
| Fig. 6 Relative contribution of input parameters to accuracy (A) electrical conductivity, (B) NH3, (C) C7H8, and (D) C6H6 sensing response models. | ||
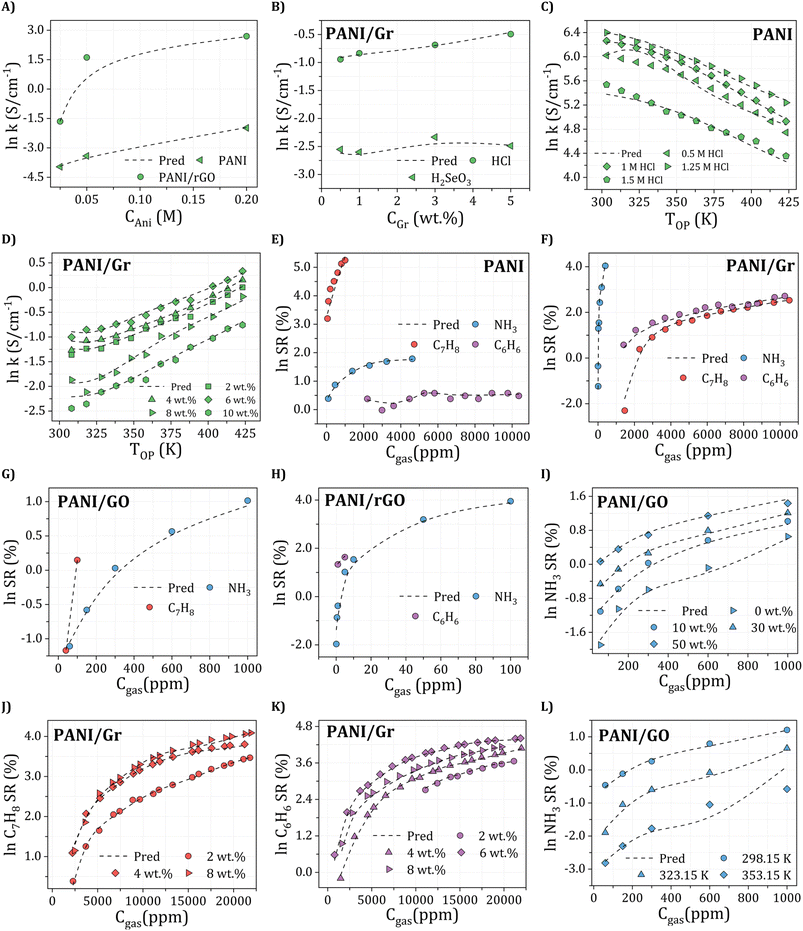
To achieve high electrical conductivity and gas sensing response values, It is essential to understand the influences of synthesis and operational conditions and use them to reduce the generation of undesired properties. For electrical conductivity (Fig. 6A), the oxidant amount, aniline amount, doping agent concentration, and operating temperature were the most critical features, followed by graphene filler type with corresponding loading and synthesis conditions, including temperature and time. This indicates that synthesis and operating conditions play important roles in the electrical conductivity property. For instance, According to Zheng et al.,97 PANI's electrical conductivity increases with the rise in the oxidant (APS) molar ratio, attributed to higher concentrations of cation radicals and increased PANI chain length. These factors contribute to the enhancement of interchain transfer in electrical conductivity. However, an increase in APS concentration above 0.5 M leads to the production of phenazine, which reduces the electrical conductivity.98,99 Additionally, Nazari et al.100 demonstrated that the conductivity of PANI shows an initial increase with an aniline amount of up to 0.15 M, but it decreases with further additions of aniline. Moreover, the rise in PANI particle conductivity with Oxi/Ani ratio can be attributed to an augmentation in both the crystalline regions and the doping level of microstructures. Extensive investigations into the impact of diverse dopants on electrical conductivities have been conducted, revealing a positive correlation between each dopant's concentration and PANI's electrical conductivity.101 Significantly, the electrical conductivity of PANI experiences a notable decline with increasing the DBSA/Ani ratio, indicating that the intramolecular mobility of charged species along the chain exerts a more substantial impact on electrical conductivity than the intermolecular hopping of charge carriers within crystalline regions. However, at very high DBSA concentrations (DBSA/Ani = 3), a more pronounced reduction in conductivity can be achieved by simultaneously reducing both the doping level and crystallinity.102 Additionally, the electrical conductivity of PANI/Gr nanocomposites was evaluated across different operating temperatures and varying loadings of graphene. The observed enhancement in conductivity with increasing temperature can be attributed to thermally-assisted charge carrier hopping, a characteristic commonly found in disordered materials. Al-Hartomy et al.103 assessed the electrical conductivity of PANI–Gr systems at various temperatures and diverse Gr loadings. Incorporating Gr into the PANI matrix remarkably enhances the composite's conductivity, attributed to the synergetic interactions between PANI and Gr phases involving charge transfer between delocalized P-orbitals. The system's conductivity demonstrates an increasing trend up to a 6 wt% content of Gr in PANI, after which it exhibits a subsequent decrease.103,104 Moreover, the synthesis time and temperature can also impact the size and structure of the PANI/Gr nanocomposites, which in turn affect the electrical conductivity. Longer synthesis times and lower temperatures can lead to larger and more well-defined PANI/Gr systems, typically exhibiting higher electrical conductivity. The gas concentration is the most significant input affecting all gas sensing properties, including NH3, C7H8, and C6H6. As gas concentration decreases, a stepwise reduction trend is observed in the actual sensor resistance values. Additionally, the sensor's resistance decreases with rising temperature. Higher gas concentrations result in gas molecules covering the largest surface area of the sensor, promoting an increased surface reaction. This, in turn, leads to higher resistance and a more pronounced response from the sensor. Conversely, lower gas concentrations result in fewer gas molecules adsorbing on the sensor's surface, diminishing surface reactions and reducing the sensor's resistance.105 Additionally, for NH3 gas sensing response (Fig. 6B), the most critical features contributing to high sensitivity are the dopant amount and synthesis time. These input variables are followed by aniline amount, graphene filler type with its corresponding loading, dopant type, and synthesis temperature. Doping PANI changes it from an insulator to a conductor, increasing its sensitivity to gases. This phenomenon arises from the protonation/deprotonation process of PANI, wherein the introduction of a proton acid stabilizes the regular and output resistance response curve. Consequently, the system's conductivity and NH3 adsorption capacity exhibit an increase.106,107 For instance, during the in situ polymerization of PANI with the addition of HCl as a dopant, a doping reaction (protonation) takes place, leading to neutral PANI molecules gaining protons and forming N+–H bonds. Subsequently, as NH3 molecules adsorb on the PANI surface and interact with one another, PANI loses protons and converts into an emeraldine base, resulting in a sharp increase in resistance (deprotonation) and NH3 transforming into ion (NH4+).108 According to a previous study, the response values of five different samples of 1 wt% PANI/rGO produced from varying HCl molarities (0.1, 0.5, 1, 1.5, and 2 M) exhibit varying trends, with response values changing with HCl concentration, particularly at the lowest and highest NH3 concentrations. Response values are observed to decrease on either side of this optimal concentration, which has been found that 1 wt% PANI/rGO sensors prepared using a 1 M HCl concentration demonstrate good NH3 response capabilities, with different sensing response values increasing with increasing NH3 concentration.109 The introduction of GO in the PANI/GO system was observed to improve its response values, similar to the enhancement observed in electrical conductivity. The optimal loading of 1 wt% GO resulted in the strongest response value, reaching 31.2 ± 1.8%.46 Notably, Gr has shown to play a beneficial role in C7H8 and C6H6 gases typically similar to NH3 sensing measurements which achieved a significantly higher maximum response compared to other nanocomposite samples.110 Several experimental studies have demonstrated that PANI/Gr-based gas sensors are more suitable for measuring room temperature gases, as they are less affected by operating temperatures and maintain reliable gas response sensing properties.111 Additionally, it should be noted that there is a lack of experimental data in relation to the influence of other input variables on the sensing properties of C7H8 and C6H6 gases (Fig. 6C and D). Hence, further research is required to comprehensively understand the behavior of PANI/Gr nanocomposites towards these gases and to identify the crucial input variables that can be optimized to improve gas sensing properties. Such studies could facilitate The advancement of more effective and reliable gas sensors for detecting C7H8 and C6H6, which are important industrial pollutants. Therefore, in addition to synthesis and operational conditions, the σ-profiles of additives play a pivotal role in predicting the electrical conductivity and gas sensing responses of PANI/Gr systems. These additives exert a substantial influence on both the preparation and performance of nanocomposites. The types of additives used in PANI/Gr systems can vary greatly, including solvents, inorganic nanoparticles, or surfactants. Interestingly, for both electrical conductivity and gas sensing response values, the nonpolar regions of the additive molecules were observed as the most significant inputs. This can be attributed to the fact that most additives act as solvents (e.g., H2O, C3H6O or CH3OH) as washing agents to remove any unreacted aniline or other compounds from the system. This study imparts invaluable insights into the structural features of PANI/Gr nanocomposites, enabling the optimization of both electrical conductivity and gas sensing response values. By prioritizing the significance of synthesis and operational conditions, along with additives possessing specific σ-Profile features, the design of new PANI/Gr nanocomposites with exceptional electrical conductivities and NH3, C7H8, and C6H6 sensing responses becomes feasible. This approach facilitates the selection of more focused and efficient PANI/Gr prospects, presenting the opportunity for the advancement of highly effective gas sensor technologies.
3.3. ML algorithms analysis
After analyzing the input parameters, eight different ML algorithms were utilized to predict the electrical conductivity and gas sensing responses (NH3, C7H8, and C6H6) of PANI/Gr nanocomposite systems. These algorithms include MLR, MLNR, DT, RF, GBM, k-NN, SVR, and ANN, each of which requires the selection of hyperparameters to ensure optimal performance.112 These algorithms include MLR, MLNR, DT, RF, GBM, k-NN, SVR, and ANN, each of which requires the selection of hyperparameters to ensure optimal performance. These hyperparameters were determined through train and test sets. The R2, ASD, and residual error used for evaluation of the robustness and cognitive ability of each developed ML model. Table 2 shows the predictive performance of the electrical conductivity and gas sensing response models trained by the different ML algorithms. The average R2 from the various models ranged from 0.616 to 0.998. As shown in Table 2, some of the developed ML models demonstrated good training performance for predicting the different properties, while others did not achieve high accuracy.| Electrical conductivity | Ammonia sensing response | Toluene sensing response | Benzene sensing response | |||||
|---|---|---|---|---|---|---|---|---|
| R 2 | ASD (±) | R 2 | ASD (±) | R 2 | ASD (±) | R 2 | ASD (±) | |
| MLR | ||||||||
| 45 Parameters | 37 Parameters | 26 Parameters | 25 Parameters | |||||
| Train | 0.9166 | 0.4320 | 0.7827 | 0.4692 | 0.9276 | 0.2543 | 0.8872 | 0.2161 |
| Test | 0.8811 | 0.5069 | 0.6160 | 0.5779 | 0.7872 | 0.3303 | 0.8744 | 0.2693 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| MNLR | ||||||||
| 73 Parameters | 54 Parameters | 37 Parameters | 34 Parameters | |||||
| Train | 0.9667 | 0.2642 | 0.9231 | 0.2738 | 0.9356 | 0.2361 | 0.9192 | 0.1760 |
| Test | 0.9538 | 0.2947 | 0.8667 | 0.3387 | 0.8082 | 0.3039 | 0.9102 | 0.2224 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| DT | ||||||||
| 42 Splits | 31 Splits | 12 Splits | 16 Splits | |||||
| Train | 0.9040 | 0.3781 | 0.8723 | 0.3490 | 0.8085 | 0.2617 | 0.9346 | 0.1682 |
| Test | 0.8900 | 0.3835 | 0.8107 | 0.4426 | 0.6309 | 0.3013 | 0.9254 | 0.1817 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| RF | ||||||||
| 94 Trees | 81 Trees | 70 Trees | 73 Trees | |||||
| Train | 0.9528 | 0.2548 | 0.9290 | 0.2476 | 0.9543 | 0.1630 | 0.9511 | ±0.1679 |
| Test | 0.9448 | 0.2716 | 0.8908 | 0.3210 | 0.8153 | 0.2403 | 0.9314 | ±0.1907 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| GBM | ||||||||
| 122 Trees | 113 Trees | 104 Trees | 98 Trees | |||||
| Train | 0.9562 | 0.2119 | 0.9061 | 0.3038 | 0.9137 | 0.2529 | 0.9205 | 0.1784 |
| Test | 0.9477 | 0.2315 | 0.8610 | 0.3736 | 0.7663 | 0.3205 | 0.8899 | 0.2221 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| k-NN | ||||||||
| 3 Neighbors | 3 Neighbors | 2 Neighbors | 2 Neighbors | |||||
| Train | 0.9611 | 0.2054 | 0.9693 | 0.1257 | 0.9750 | 0.1275 | 0.9550 | 0.1632 |
| Test | 0.9525 | 0.2364 | 0.9203 | 0.1731 | 0.9560 | 0.1784 | 0.9245 | 0.1878 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| SVR | ||||||||
| C = 4.84, γ = 0.434 | C = 4.40, γ = 0.495 | C = 4.36, γ = 0.423 | C = 4.41, γ = 0.495 | |||||
| Train | 0.9642 | 0.2282 | 0.9574 | 0.1862 | 0.9685 | 0.1369 | 0.9583 | 0.1156 |
| Test | 0.9601 | 0.2313 | 0.9275 | 0.2138 | 0.9556 | 0.1451 | 0.9377 | 0.1788 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| ANN | ||||||||
| 20–20 Neurons | 20–10 Neurons | 10–10 Neurons | 15–5 Neurons | |||||
| Train | 0.9850 | 0.1064 | 0.9725 | 0.1339 | 0.9877 | 0.0721 | 0.9977 | 0.0346 |
| Test | 0.9776 | 0.1307 | 0.9444 | 0.1799 | 0.9692 | 0.1166 | 0.9919 | 0.0631 |
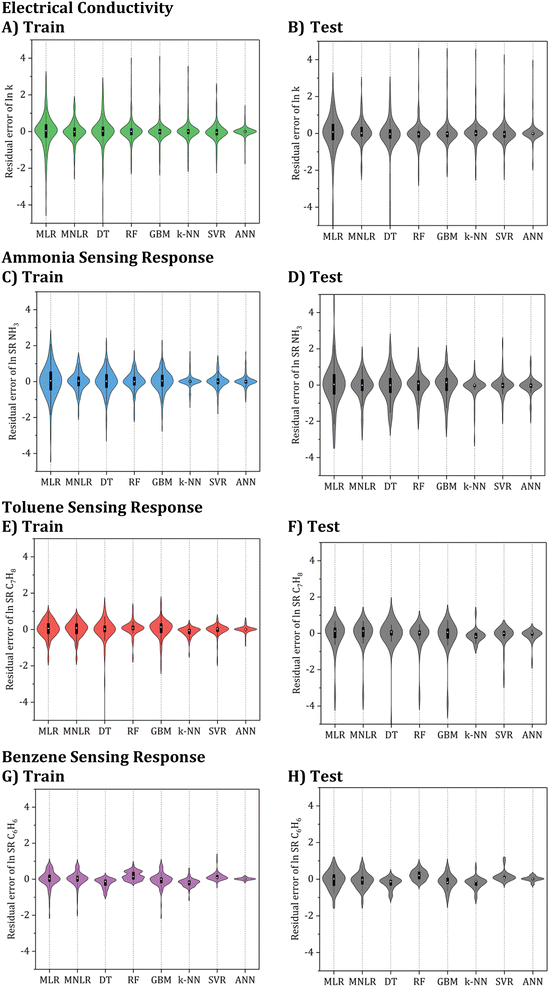
To select the best model among the developed ML algorithms, a visualization of their prediction residual errors (RSE) can be displayed using a violin plot, as shown in Fig. 7. A fatter plot in the violin plot indicates that the distribution of the prediction residual errors is more spread out, which suggests higher variability and potentially larger errors in the model predictions. Conversely, a thinner plot indicates a more centralized distribution, which suggests lower variability and potentially more accurate predictions.
By analyzing Table 2 and Fig. 7, it can be observed that while MLR is one of the algorithms that were tested, its R2 values for the test set analysis of electrical conductivity, NH3, C7H8, and C6H6 models are only 0.881, 0.616, 0.787, and 0.874, respectively. Furthermore, the corresponding ASD of the testing sets is between 0.2 and 0.5. Based on these results, it can be confirmed that linear models are unsuitable for accurate electrical conductivity and gas sensing response prediction, except for very narrow ranges of conditions where the problem might be nearly linear.
Furthermore, the nonlinear ML models examined demonstrated significantly superior effectiveness to the linear ones. Based on the evaluation of the different nonlinear models, it was found that the k-NN, SVR, and ANN models provided lower ASD values compared to the tree-based and other models. However, when considering the testing set standard deviations, the ANN model outperformed the k-NN or SVR models. This, along with the high R2 value of over 0.98, and the excellent fit demonstrated by the ANN model makes it the best candidate for further hypertuning. Hence, the ANN algorithm was selected for further optimization.
3.4. ANN hypertuning
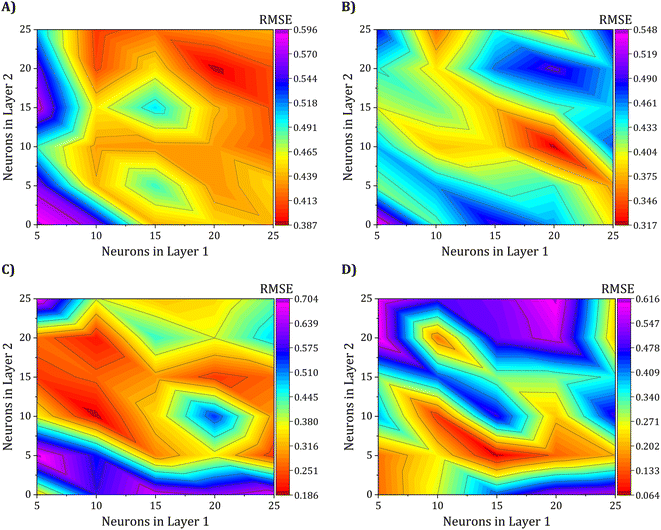
Achieving the optimal network architecture requires meticulous tuning of the number of hidden layers and neurons in each layer to suit the specific problem under investigation precisely. To investigate the influence of the second hidden layer's neuron count on network performance, we conducted a seven-level factorial design for both the first and second layers, with the number of neurons varying from 5 to 25. This resulted in 25 different network configurations, with the 5–5 architecture being the simplest and the 25–25 architecture being the most intricate. Consequently, the results of this study have been meticulously showcased through the use of contour maps in Fig. 8, providing a comprehensive and intuitive representation of the findings. These maps illustrate the RMSE of the 25 ANN configurations, based on the training set, for predicting electrical conductivity and the three gas sensing response properties.
Fig. 8A shows that the two-layer ANN configuration with 20–20 neurons best predicted electrical conductivity, with a lower RMSE in the test set, exhibiting a value of 0.3876 S cm−1. Regarding the gas sensing response properties, Fig. 8B–D show that the ANN models with 20–10, 10–10, and 15–5 neurons, respectively, outperformed other models and had the lowest RMSE values of 0.3170, 0.1862, and 0.0642% for ammonia, toluene, and benzene gases, respectively. The presented findings underscore the promising potential of ANNs in effectively predicting the electrical conductivity and gas-sensing response properties of polyaniline-graphene nanocomposites with high accuracy.
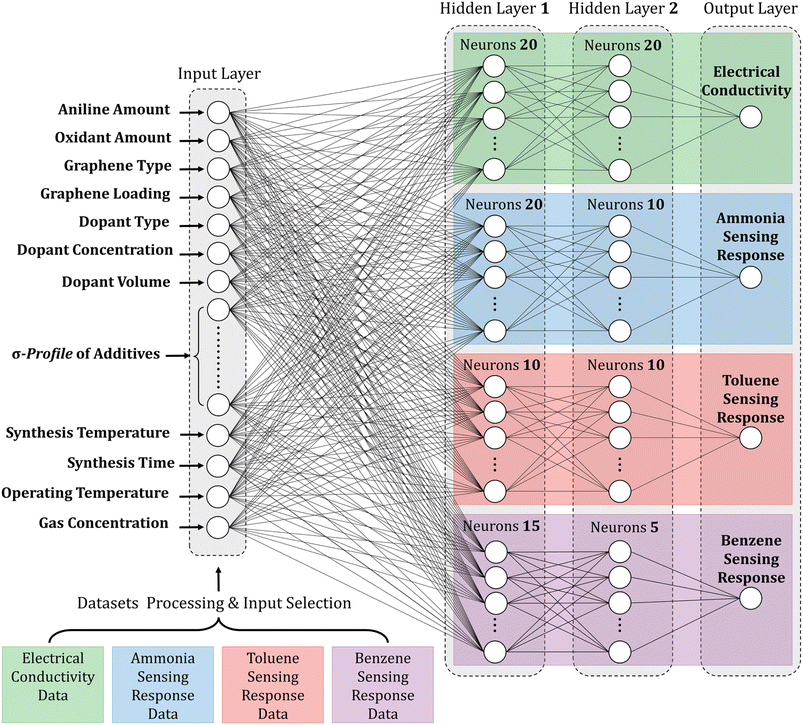
The findings emphasize the importance of meticulous optimization of neuron count per layer and thoughtful selection of suitable activation functions when employing ANNs for predictive modeling. The configurations that demonstrated the highest accuracy and reliability were the 62–20–20–1, 63–20–10–1, 63–10–10–1, and 63–15–5–1 ANN configurations, which are illustrated clearly and concisely in Fig. 9. Table S4† provides a comprehensive compilation of equations detailing the weights and biases of individual neurons. Hence, this methodology can significantly facilitate the rational design and exploration of innovative multifunctional nanocomposite systems. These systems can be precisely customized to fulfill specific requirements in diverse applications, including electronics, sensors, and energy storage.
3.5. Model analysis
| Parameter | Electrical conductivity | Ammonia sensing response | Toluene sensing response | Benzene sensing response |
|---|---|---|---|---|
| Training | ||||
| R 2 train | 0.985 | 0.973 | 0.988 | 0.998 |
| RMSE | 0.388 | 0.317 | 0.186 | 0.064 |
| ASD | ±0.1064 | ±0.1339 | ±0.0721 | ±0.035 |
| MAE | 0.1505 | 0.1893 | 0.1019 | 0.0489 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Testing | ||||
| R 2 test | 0.978 | 0.944 | 0.969 | 0.992 |
| RMSE | 0.479 | 0.459 | 0.358 | 0.127 |
| ASD | ±0.1307 | ±0.1799 | ±0.1166 | ±0.0631 |
| MAE | 0.1848 | 0.2544 | 0.1649 | 0.0892 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Total | ||||
| R 2 | 0.984 | 0.967 | 0.983 | 0.996 |
| RMSE | 0.408 | 0.350 | 0.232 | 0.081 |
| ASD | ±0.1113 | ±0.1431 | ±0.0812 | ±0.0404 |
| MAE | 0.1574 | 0.2024 | 0.1148 | 0.0572 |
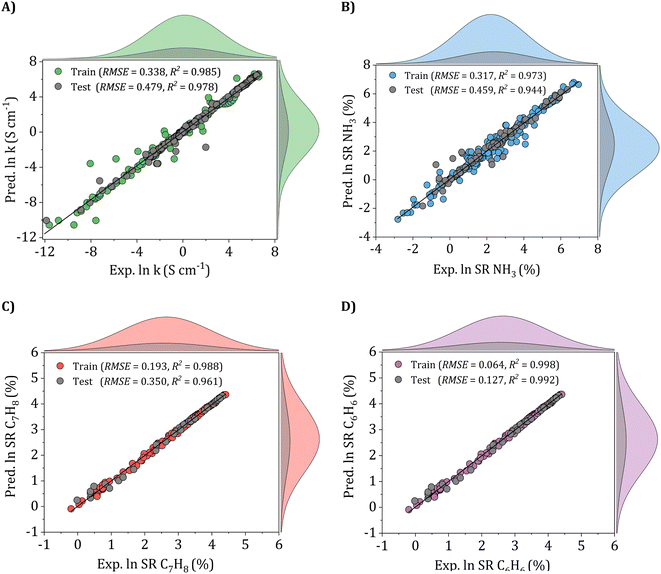
To validate the performance of the ANN models, scatter plots of the training and testing sets were meticulously examined, as depicted in Fig. 10. Each joint scheme consists of 5 plots, including a scatter plot and four marginal distribution plots. For instance, in Fig. 10A, the gray and green-colored scatter plots demonstrate the correlation between experimental and predicted electrical conductivity values in both the training and testing sets. Additionally, the four marginal distribution plots on the top and right-hand side offer a comprehensive insight into the distribution of experimental and predicted values in their respective sets. The findings reveal excellent agreement of the ANN models, with data points mostly aligning along the y = x diagonal, exhibiting minimal dispersion and scattering. For the electrical conductivity model, as shown in Fig. 10A, the ANN model achieved an RMSE of 0.338 and R2 of 0.985 for the train set and 0.479 and 0.978 for the testing set, respectively.
Similarly, in the case of the ammonia gas model (Fig. 10B), the ANN model achieved RMSE and R2 values of 0.317 and 0.973 for the train set and 0.459 and 0.944 for the testing set, respectively. For the gas sensing response of toluene and benzene gases, as presented in Fig. 10C and D, the ANN models achieved higher accuracy, with all data points closely centered around the perfect fitting line and lower RMSE values of 0.193 and 0.064 and higher R2 values, reaching 0.988 and 0.998 for the train sets and 0.350 and 0.127 and 0.961 and 0.992 for the testing sets, respectively. These findings demonstrate the ANN models' exceptional performance, which suggests the models' substantial accuracy and reliability in predicting the conductivity and gas sensing performances of all three gases, including ammonia, toluene, and benzene.
To achieve this, we employed the ‘Kernel Explainer’ method from the SHAP toolkit in Python, designed to handle intricate and computationally intensive models like ANNs. This method utilizes a unique kernel function to compute SHAP values, allowing an in-depth analysis of the model by approximating the contribution of each input to the final prediction. The primary objective of integrating SHAP was to enhance the interpretability of the ANN, making its decision-making process more transparent and understandable.
One significant advantage of SHAP is its ability to reflect the impact of each input in each sample, showcasing both positive and negative impacts. The SHAP values for each input were then summarized and ranked based on their mean values, as depicted in Fig. 11.
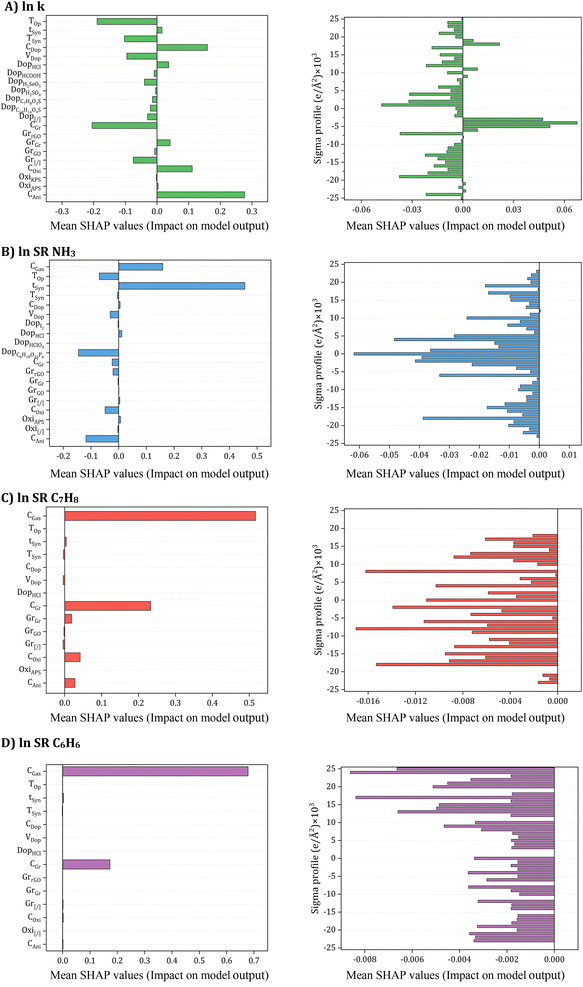 | ||
| Fig. 11 SHAP input importance to accuracy (A) electrical conductivity, (B) NH3, (C) C7H8, and (D) C6H6 Sensing response models. | ||
The SHAP values for each input are summarized with a bar char are ranked according to the mean value of SHAP as shown in Fig. 11. Specifically, concerning electrical conductivity (Fig. 11A), crucial inputs such as oxidant amount, aniline amount, doping agent concentration, and operating temperature emerged as the most critical contributors. Synthesis and operating conditions played pivotal roles in influencing electrical conductivity, with varying effects observed for different input parameters. For instance, aniline amount, oxidant amount, Gr filler, HCl doping agent, doping agent concentration, and synthesis time exhibited a positive impact on electrical conductivity, whereas systems without Gr filler (Gr[/]) and doping agent, GO filler, dopant volume, and other doping agents had a negative effect. The influence of temperature was also explored, revealing that an increase in synthesis and operating temperature tended to decrease electrical conductivity, aligning with both input contribution analysis and existing literature reports.97–103 Turning to NH3 gas sensing response ((Fig. 11C), synthesis time and gas concentration emerged as pivotal inputs positively affecting the sensing response. Conversely, aniline and oxidant amount, camphorsulfonic acid (C10H16O4S) doping agent, dopant volume, and operating temperature were identified as inputs exerting a negative impact on the sensing response. The role of doping agents in transforming PANI from an insulator to a conductor, particularly through the protonation/deprotonation process, was discussed, with the impact on NH3 adsorption capacity well-established in the literature.106–108 For the prediction of C7H8 and C6H6 sensing response (Fig. 11C and D), it was highlighted that a lack of experimental data regarding the influence of other input features necessitates further research. Comprehensive studies are required to unravel the behavior of PANI/Gr nanocomposites towards these gases and identify crucial input variables for optimization. Such endeavors hold the promise of advancing more effective and reliable gas sensors for detecting C7H8 and C6H6, crucial industrial pollutants.
Conclusively, as elucidated in earlier sections, the σ-profiles of additives play a pivotal role alongside synthesis and operational conditions in predicting the electrical conductivity and gas sensing responses of PANI/Gr systems. These additives, including solvents, inorganic nanoparticles, or surfactants, exert a substantial influence on both the synthesis and performance of nanocomposites. Intriguingly, for electrical conductivity, nonpolar regions of additive molecules emerged as the most significant inputs, predominantly influencing conductivity positively. Conversely, HBA and HBD regions were identified as exerting a negative impact on conductivity. This observed phenomenon can be attributed to the solvent-like role of most additives, acting as washing agents to eliminate any unreacted aniline or other compounds from the system. In terms of gas sensing responses, all regions of additive molecules were noted to negatively affect the gas sensing response. In addition, the SHAP analysis also revealed that, even with 61 dimensions of σ-profiles, other inputs played more crucial roles in the ANN predictions. This underscores the complexity of our system and emphasizes the need for a multifaceted approach. Consequently, the extensive SHAP analysis aligns with the input contribution analysis, shedding light not only on the intricate relationships between input variables and model predictions but also providing actionable insights for the future optimization of gas sensors. This contribution adds to the ongoing discourse, advancing our understanding and strategies for enhancing the performance of PANI/Gr nanocomposite systems.
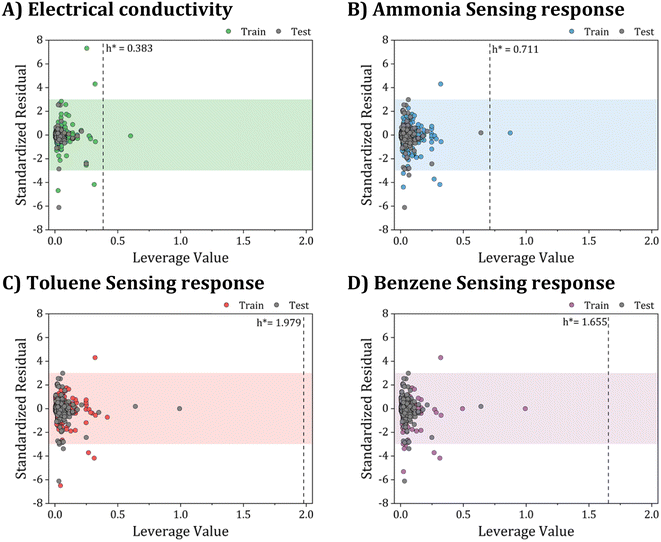 | ||
| Fig. 12 Applicability domain assessment using William plots: (A) electrical conductivity, (B) ammonia sensing response, (C) toluene sensing response, and (D) benzene sensing response models. | ||
Fig. 12A–D provide a helpful comparison of the applicability domains of various models, including the electrical conductivity model and models for sensing response to ammonia, toluene, and benzene. Upon examining these models, it becomes evident that the critical leverage of the toluene sensing model exceeds that of the other models, with the benzene sensing model showing the second-highest critical leverage value 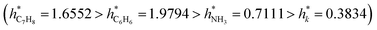 . However, despite the differences in critical leverage among the models, the analysis reveals that the majority of data points (over 97%) conform within the AD boundaries, signifying the dataset's limited inclusion of outliers based on the leverage method (i.e., hi > h*), this metric holds significant importance in evaluating the data quality employed to train ML models. As presented in Table 4, the electrical conductivity model has a lower percentage of structural outliers (0.16%) compared to the ammonia sensing model (0.30%). These findings suggest that the electrical conductivity model may be more reliable in its predictions than the ammonia sensing model. Furthermore, it is essential to highlight that both the toluene and benzene sensing models exhibited no structural outliers, as their leverages consistently remained below the critical boundary of hi < h*. This observation is consistent with the expected behavior of well-trained ANN models. It supports their reliability for predicting the toluene and benzene sensing properties of polyaniline/graphene systems within their AD.
. However, despite the differences in critical leverage among the models, the analysis reveals that the majority of data points (over 97%) conform within the AD boundaries, signifying the dataset's limited inclusion of outliers based on the leverage method (i.e., hi > h*), this metric holds significant importance in evaluating the data quality employed to train ML models. As presented in Table 4, the electrical conductivity model has a lower percentage of structural outliers (0.16%) compared to the ammonia sensing model (0.30%). These findings suggest that the electrical conductivity model may be more reliable in its predictions than the ammonia sensing model. Furthermore, it is essential to highlight that both the toluene and benzene sensing models exhibited no structural outliers, as their leverages consistently remained below the critical boundary of hi < h*. This observation is consistent with the expected behavior of well-trained ANN models. It supports their reliability for predicting the toluene and benzene sensing properties of polyaniline/graphene systems within their AD.
| Parameter | Electrical conductivity | Ammonia sensing response | Toluene sensing response | Benzene sensing response |
|---|---|---|---|---|
| h* | 0.3834 | 0.7111 | 1.9794 | 1.6552 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Training | ||||
| Structural outliers | 0.16% | 0.30% | 0.0% | 0.0% |
| Response outliers | 0.65% | 0.89% | 0.82% | 2.05% |
| ADcoverage | 99.19% | 98.82% | 99.18% | 97.95% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Testing | ||||
| Structural outliers | 0.81% | 0.30% | 0.0% | 0.0% |
| Response outliers | 0.81% | 1.47% | 4.0% | 0.0% |
| ADcoverage | 99.19% | 97.06% | 96% | 100% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Total | ||||
| Structural outliers | 0.16% | 0.30% | 0.0% | 0.0% |
| Response outliers | 0.81% | 1.18% | 1.64% | 2.05% |
| ADcoverage | 99.03% | 98.52% | 98.36% | 97.95% |
In addition to the structural outliers discussed earlier, response outliers were also identified in the models. Specifically, specific data points at exception compositions and conditions were identified as outliers based on their SDR values exceeding the acceptable ±3 SDR boundary. As a result, the coverage of the models within their AD was reduced to 99.03%, 98.52%, 98.36%, and 97.95% for the electrical conductivity, ammonia, toluene, and benzene sensing response models, respectively. Outliers can substantially influence the accuracy of model predictions, emphasizing the criticality of meticulous identification and evaluation of the AD of models to ensure dependable and precise predictions. It is worth emphasizing that the absence of data points in the double outlier region (i.e., hi > h* and SDRi > ±3) as illustrated in Fig. 12. This observation underscores the robustness of the proposed ANN models, indicating minimal impact from outliers on their performance.
In summary, accounting and identifying structural and response outliers are crucial for improving the reliability and accuracy of ANN models in chemical engineering applications. This study underscores the significance of the AD method as an invaluable instrument for assessing data quality during model training, enabling the identification and evaluation of outliers that could potentially impact model predictions. The concurrent use of k-fold validation and AD analysis provides a robust framework for the holistic evaluation of our models. It is important to note that the AD analysis, in particular, considers the distribution of training data and helps identify how different a data point is from the majority of the points. This method has been chosen deliberately to enhance the understanding of model performance within specific boundaries. Consequently, the findings from this study indicate that the predictions of new polyaniline/graphene systems, falling within the same domain of applicability, can be deemed reliable for preliminary polymer nanocomposite investigations, even without experimental data. This highlights the significance of dependable and precise predictions for advancing new nanocomposites, mainly when the properties of the materials are challenging to measure experimentally.
The results showcase the multifaceted behavior of PANI/Gr in varying experimental conditions, providing insights into the potential applications of these composites in sensor technology. The conductivity exhibits a non-linear response to the concentration of aniline, which suggests a threshold behavior where the conductivity stabilizes beyond a certain concentration.118 While the ANN models capture this phenomenon to some extent, there is a noticeable divergence from experimental data. This discrepancy suggests the intricate nature of molecular-level interactions that might not be entirely accounted for by the ANN. Molecularly, this can be associated with increased π–π stacking between the aniline-derived PANI chains and the graphene sheets, leading to improved charge transport pathways.119 When considering dopant effects, the nature of the dopant and its concentration have pronounced effects on the conductivity of PANI.120 The protonation of the nitrogen atoms in the PANI backbone by acid dopants like HCl and H2SeO3 enhances the delocalization of electrons, which is crucial for conductivity.121 The temperature dependence of conductivity is consistent with a semiconducting behavior where thermal energy aids in the hopping of charge carriers, enhancing conductivity.104,122,123 The ANN predictions closely follow the experimental data, suggesting that the temperature effect is well-characterized by the network parameters, capturing the thermally activated processes within the material.
In terms of gas sensing, the nanocomposites exhibit distinct responses to NH3, C7H8 and C6H6. The molecular interactions between these gases and the PANI/Gr nanocomposite are crucial for the sensing mechanism.111 NH3, being a polar molecule with a lone pair of electrons, can interact with the π-electron rich regions of the composites, likely forming charge transfer complexes. This interaction alters the distribution of charge carriers in the PANI chains, leading to a measurable change in conductivity which is utilized for sensing.124,125 C7H8 and C6H6, being aromatic compounds, may also interact with the nanocomposite through π–π stacking interactions. The presence of the methyl group in toluene introduces steric hindrance and a slight electron-donating effect, potentially altering its interaction with the nanocomposite compared to C6H6. The differential sensing response between C6H6 or C7H8 can be attributed to the size and electron density of these molecules, which influences their adsorption onto the system surface and subsequent interaction with the conductive network.126–128 The enhancement in gas response with increasing graphene content can be rationalized by the expanded surface area provided by graphene, which facilitates greater adsorption of gas molecules.122 Additionally, graphene's high electron mobility may contribute to more efficient charge transfer upon interaction with gas molecules, leading to a stronger sensing response. Meanwhile, the response to gases such as NH3, C7H8, and C6H6 indicates that the nanocomposites are sensitive to changes in gas concentration, with the response magnitude varying according to the type of gas.105 The response to NH3 is especially significant, which is a desirable trait for sensors targeting this gas. However, the ANN predictions are less accurate at higher concentrations, potentially due to saturation effects that are not fully represented in the mode.
Consequently, the experimental findings enriched by molecular insights into the nanocomposite's interaction with aniline, dopants, temperature, and gases, demonstrate the complexity and potential of PANI/Gr as a material for gas sensors. Although ANNs prove valuable in predicting overarching trends and behaviors, the existing disparities between experimental and predicted data emphasize the imperative for further model refinement. Supplementary approaches such as molecular dynamics simulations or quantum mechanical modeling could complement ANN predictions, offering a more thorough understanding of the intricate interactions involved. The imperative for further refinement is driven by the complex and dynamic nature of nanocomposites' responses, necessitating a nuanced comprehension. These findings not only yield insights into the intricate behavior of PANI/Gr nanocomposites but also lay the foundation for optimizing these materials for specific applications, particularly in the domain of sensitive and selective gas detection.
4. Conclusions
In conclusion, this study comprehensively explores machine learning models for predicting the properties of polyaniline/graphene (PANI/Gr) nanocomposites, leveraging a rich dataset from numerous sources. The artificial neural network (ANN) models emerge as highly accurate tools for forecasting electrical conductivity and gas sensing responses, with meticulous attention given to identifying and handling outliers. The robustness of these models, particularly in the face of structural and response outliers, underscores their reliability.The input contribution analysis provides crucial insights into the key parameters shaping the performance of PANI/Gr nanocomposites, highlighting the significance of oxidant, aniline, doping agent concentration, and operating temperature. Complementing this, the SHAP analysis reveals intricate relationships among input variables and model predictions, offering valuable insights for gas sensor optimization and contributing to the ongoing discourse on enhancing PANI/Gr nanocomposite systems' performance. Furthermore, the study underscores the influential role of molecular inputs, particularly the σ-profiles of additives, in predicting material properties.
Applicability domain (AD) analysis is a critical facet of model evaluation, revealing high coverage percentages and emphasizing the models' dependability within specific parameter ranges. The significance of understanding and managing outliers is highlighted, as they can significantly impact model predictions. Notably, the absence of data points in the double outlier region underscores the resilience of the proposed ANN models.
The implications of this research extend to the practical development of high-performance PANI/Gr nanocomposites, offering valuable contributions to fields such as supercapacitors, gas sensors, and energy storage devices. The call for further investigations into the nuanced impacts of molecular inputs on material performance reflects the ongoing pursuit of precision in nanocomposite design. Overall, this study significantly advances our understanding of machine learning applications in chemical engineering, providing a foundation for informed decision-making and reliable predictions in developing novel materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the invaluable support from the Ministry of Higher Education and Scientific Research, Ferhat ABBAS Setif 1 University, and the Directorate General for Scientific Research and Technological Development (DGRSDT), Algeria. The authors gratefully acknowledge the support from the Center for Membranes and Advanced Water Technology (CMAT) at Khalifa University of Science and Technology in Abu Dhabi (UAE).References
- S. Raza, X. Li, F. Soyekwo, D. Liao, Y. Xiang and C. Liu, Eur. Polym. J., 2021, 160, 110773 CrossRef CAS.
- D. R. Paul and L. M. Robeson, Polymer, 2008, 49, 3187–3204 CrossRef CAS.
- T. Ahuja and D. Kumar, Sens. Actuators, B, 2009, 136, 275–286 CrossRef.
- W. K. Chee, H. N. Lim, N. M. Huang and I. Harrison, RSC Adv., 2015, 5, 68014–68051 RSC.
- S. Fu, Z. Sun, P. Huang, Y. Li and N. Hu, Nano Mater. Sci., 2019, 1, 2–30 CrossRef.
- Z. Guezzout, A. Boublia and N. Haddaoui, J. Polym. Res., 2023, 1–16 Search PubMed.
- S. Meer, A. Kausar and T. Iqbal, Polym.-Plast. Technol. Eng., 2016, 55, 1416–1440 CrossRef CAS.
- X. Hong, J. Fu, Y. Liu, S. Li, X. Wang, W. Dong and S. Yang, Materials, 2019, 12, 1451 CrossRef CAS PubMed.
- H.-Y. Zhao, M.-Y. Yu, J. Liu, X. Li, P. Min and Z.-Z. Yu, Nano-Micro Lett., 2022, 14, 129 CrossRef CAS PubMed.
- A. Boublia, Z. Guezzout, N. Haddaoui, M. Badawi, A. S. Darwish, T. Lemaoui, S. El, I. Lebouachera, K. Kumar, M. A. Alreshidi, J. S. Algethami, M. Abbas, I. M. Alnashef, B. Jeon, Y. Benguerba, M. A. Alreshidi, J. S. Algethami, M. Abbas, F. Banat and I. M. Alnashef, Crit. Rev. Solid State Mater. Sci., 2023, 0, 1–25 Search PubMed.
- H. D. Kyomuhimbo and U. Feleni, Electroanalysis, 2023, 35, e202100636 CrossRef CAS.
- T. Sen, S. Mishra and N. G. Shimpi, RSC Adv., 2016, 6, 42196–42222 RSC.
- H. N. Heme, M. S. N. Alif, S. M. S. M. Rahat and S. B. Shuchi, J. Energy Storage, 2021, 42, 103018 CrossRef.
- H. Chen, F. Zhuo, J. Zhou, Y. Liu, J. Zhang, S. Dong, X. Liu, A. Elmarakbi, H. Duan and Y. Fu, Chem. Eng. J., 2023, 142576 CrossRef CAS.
- Y. Zhang, X. Chen, H. Chen, M. Jia, H. Cai, Z. Mao and Y. Bai, Chem. Eng. J., 2023, 470, 143912 CrossRef CAS.
- K. S. Novoselov and A. K. Geim, Nat. Mater., 2007, 6, 183–191 CrossRef PubMed.
- Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924 CrossRef CAS PubMed.
- M. Sabet, H. Soleimani and S. Hosseini, J. Vinyl Addit. Technol., 2018, 24, E177–E185 CAS.
- M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498–3502 CrossRef CAS PubMed.
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261–482 CrossRef CAS.
- N. A. Kumar and J. B. Baek, Chem. Commun., 2014, 50, 6298–6308 RSC.
- K. S. Novoselov, A. K. Geim, S. V Morozov, D. Jiang, Y. Zhang, S. V Dubonos, I. V Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- L. Wang, X. Lu, S. Lei and Y. Song, J. Mater. Chem. A, 2014, 2, 4491–4509 RSC.
- A. M. Díez-Pascual and J. A. Luceño-Sánchez, Polymers, 2021, 13, 2105 CrossRef PubMed.
- L. Chen, N. Li, X. Yu, S. Zhang, C. Liu, Y. Song, Z. Li, S. Han, W. Wang and P. Yang, Chem. Eng. J., 2023, 462, 142139 CrossRef CAS.
- Z. Tian, H. Yu, L. Wang, M. Saleem, F. Ren, P. Ren, Y. Chen, R. Sun, Y. Sun and L. Huang, RSC Adv., 2014, 4, 28195–28208 RSC.
- H. Wang, Q. Hao, X. Yang, L. Lu and X. Wang, Electrochem. Commun., 2009, 11, 1158–1161 CrossRef CAS.
- F. Kazemi, S. M. Naghib, Y. Zare and K. Y. Rhee, Polym. Rev., 2021, 61, 553–597 CrossRef CAS.
- A. Boublia, S. E. I. Lebouachera, N. Haddaoui, Z. Guezzout, M. A. Ghriga, M. Hasanzadeh, Y. Benguerba and N. Drouiche, Polym. Bull., 2022, 1–33 Search PubMed.
- A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 53208 CrossRef.
- T. Lemaoui, A. S. Darwish, A. Attoui, F. Abu Hatab, N. E. H. Hammoudi, Y. Benguerba, L. F. Vega and I. M. Alnashef, Green Chem., 2020, 22, 8511–8530 RSC.
- Y. Benguerba, I. M. Alnashef, A. Erto, M. Balsamo and B. Ernst, J. Mol. Struct., 2019, 1184, 357–363 CrossRef CAS.
- T. Lemaoui, F. Abu Hatab, A. S. Darwish, A. Attoui, N. E. H. Hammoudi, G. Almustafa, M. Benaicha, Y. Benguerba and I. M. Alnashef, ACS Sustain. Chem. Eng., 2021, 9, 5783–5808 CrossRef CAS.
- B. Motevalli, B. Sun and A. S. Barnard, J. Phys. Chem. C, 2020, 124, 7404–7413 CrossRef CAS.
- T. Zhou, Z. Song and K. Sundmacher, Engineering, 2019, 5, 1017–1026 CrossRef CAS.
- D. J. Audus and J. J. de Pablo, ACS Macro Lett., 2017, 6, 1078–1082 CrossRef CAS.
- M. M. Cencer, J. S. Moore and R. S. Assary, Polym. Int., 2022, 71, 537–542 CrossRef CAS.
- K. Hiraide, K. Hirayama, K. Endo and M. Muramatsu, Comput. Mater. Sci., 2021, 190, 110278 CrossRef CAS.
- S. Altarazi, M. Ammouri and A. Hijazi, Comput. Mater. Sci., 2018, 153, 1–9 CrossRef CAS.
- F. Leon, S. Curteanu, C. Lisa and N. Hurduc, Mol. Cryst. Liq. Cryst., 2007, 469, 1–22 CrossRef CAS.
- S. Wu, Y. Kondo, M. aki Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 66 CrossRef.
- J. Liang, S. Xu, L. Hu, Y. Zhao and X. Zhu, Mater. Chem. Front., 2021, 5, 3823–3829 RSC.
- L. Chen, C. Kim, R. Batra, J. P. Lightstone, C. Wu, Z. Li, A. A. Deshmukh, Y. Wang, H. D. Tran, P. Vashishta, G. A. Sotzing, Y. Cao and R. Ramprasad, npj Comput. Mater., 2020, 6, 30–32 CrossRef.
- S. A. Armida, D. Ebrahimibagha, M. Ray and S. Datta, Adv. Compos. Mater., 2023, 1–23 CrossRef.
- G. Chen, L. Tao and Y. Li, Polymers, 2021, 13, 1–14 Search PubMed.
- X. Xing, L. Du, D. Feng, C. Wang, Y. Tian, Z. Li, H. Liu and D. Yang, Sens. Actuators, B, 2022, 351, 130944 CrossRef CAS.
- A. Boublia, T. Lemaoui, J. AlYammahi, A. S. Darwish, A. Ahmad, M. Alam, F. Banat, Y. Benguerba and I. M. AlNashef, ACS Sustain. Chem. Eng., 2022, 11(1), 208–227 CrossRef.
- R. Ma, Z. Liu, Q. Zhang, Z. Liu and T. Luo, J. Chem. Inf. Model., 2019, 59, 3110–3119 CrossRef CAS PubMed.
- K. K. Bejagam, J. Lalonde, C. N. Iverson, B. L. Marrone and G. Pilania, J. Phys. Chem. B, 2022, 126, 934–945 CrossRef CAS PubMed.
- C. Kuenneth, W. Schertzer and R. Ramprasad, Macromolecules, 2021, 54, 5957–5961 CrossRef CAS.
- R. Ma and T. Luo, J. Chem. Inf. Model., 2020, 60, 4684–4690 CrossRef CAS PubMed.
- B. Delley, Theor. Comput. Chem., 1995, 2, 221–254 CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- O. Moumeni, M. Mehri, R. Kerkour, A. Boublia, F. Mihoub, K. Rebai, A. A. Khan, A. Erto, A. S. Darwish and T. Lemaoui, J. Taiwan Inst. Chem. Eng., 2023, 147, 104918 CrossRef CAS.
- T. Yasmin, A. Mahmood, M. Farooq, U. Rehman, R. M. Sarfraz, H. Ijaz, M. R. Akram, A. Boublia, M. M. S. Bekhit and B. Ernst, Int. J. Biol. Macromol., 2023, 127032 CrossRef CAS PubMed.
- A. Dal Corso, A. Pasquarello, A. Baldereschi and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1180 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. Legarreta-Mendoza, N. Flores-Holguín and D. Lardizabal-Gutiérrez, Int. J. Hydrogen Energy, 2019, 44, 12374–12380 CrossRef CAS.
- L. Tabari and D. Farmanzadeh, Appl. Surf. Sci., 2020, 500, 144029 CrossRef CAS.
- Q. Shi, L. Yan and C. Jing, Adv. Sci., 2020, 7, 1–8 Search PubMed.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- H. Matsukawa, M. Kitahara and K. Otake, Fluid Phase Equilib., 2021, 548, 113179 CrossRef CAS.
- D. Maulud and A. M. Abdulazeez, J. Appl. Sci. Technol. Trends, 2020, 1, 140–147 CrossRef.
- M. Li, L. Dai and Y. Hu, ACS Energy Lett., 2022, 7, 3204–3226 CrossRef CAS PubMed.
- P. K. Pandey, T. Nyori and V. Pandey, Model. Earth Syst. Environ., 2017, 3, 1449–1461 CrossRef.
- I. D. Mienye, Y. Sun and Z. Wang, Procedia Manuf., 2019, 35, 698–703 CrossRef.
- M. Belgiu and L. Drăguţ, ISPRS J. Photogramm. Remote Sens., 2016, 114, 24–31 CrossRef.
- A. Manoharan, K. M. Begam, V. R. Aparow and D. Sooriamoorthy, J. Energy Storage, 2022, 55, 105384 CrossRef.
- M. Bansal, A. Goyal and A. Choudhary, Decis. Anal., 2022, 3, 100071 Search PubMed.
- Y. Song, J. Liang, J. Lu and X. Zhao, Neurocomputing, 2017, 251, 26–34 CrossRef.
- N. M. Quang, T. X. Mau, N. T. Ai Nhung, T. N. Minh An and P. Van Tat, J. Mol. Struct., 2019, 1195, 95–109 CrossRef.
- M. R. Fissa, Y. Lahiouel, L. Khaouane and S. Hanini, J. Mol. Graphics Modell., 2019, 87, 109–120 CrossRef PubMed.
- V. Rashidian and M. Hassanlourad, Int. J. Geomech., 2014, 14, 142–150 CrossRef.
- M. Stone, J. R. Stat. Soc., B, 1976, 38, 102 Search PubMed.
- S. Haykin, Neural Networks and Learning Machines, 3/E, Pearson Education India, 2009 Search PubMed.
- A. Tropsha, P. Gramatica and V. K. Gombar, QSAR Comb. Sci., 2003, 22, 69–77 CrossRef CAS.
- I. Almi, S. Belaidi, E. Zerroug, M. Alloui, R. Ben Said, R. Linguerri and M. Hochlaf, J. Mol. Struct., 2020, 1211, 128015 CrossRef CAS.
- I. Mitra, A. Saha and K. Roy, Mol. Simul., 2010, 36, 1067–1079 CrossRef CAS.
- N. R. Tanguy, M. Thompson and N. Yan, Sens. Actuators, B, 2018, 257, 1044–1064 CrossRef CAS.
- T. Wang, D. Huang, Z. Yang, S. Xu, G. He, X. Li, N. Hu, G. Yin, D. He and L. Zhang, Nano-Micro Lett., 2016, 8, 95–119 CrossRef PubMed.
- J. S. Torrecilla, J. Palomar, J. Lemus and F. Rodríguez, Green Chem., 2010, 12, 123–134 RSC.
- I. Adeyemi, R. Sulaiman, M. Almazroui, A. Al-Hammadi and I. M. AlNashef, J. Mol. Liq., 2020, 311, 113180 CrossRef CAS.
- D. O. Abranches, Y. Zhang, E. J. Maginn and Y. J. Colón, Chem. Commun., 2022, 5630–5633 RSC.
- T. Lemaoui, A. S. Darwish, G. Almustafa, A. Boublia, P. R. Sarika, N. A. Jabbar, T. Ibrahim, P. Nancarrow, K. K. Yadav, A. M. Fallatah, M. Abbas, J. S. Algethami, Y. Benguerba, B. H. Jeon, F. Banat and I. M. AlNashef, Energy Storage Mater., 2023, 59, 102795 CrossRef.
- T. Lemaoui, A. Boublia, S. Lemaoui, A. S. Darwish, B. Ernst, M. Alam, Y. Benguerba, F. Banat and I. M. AlNashef, ACS Sustain. Chem. Eng., 2021, 9(17), 5783–5808 CrossRef CAS.
- N. E. Awaja, G. Almustafa, A. S. Darwish, T. Lemaoui, Y. Benguerba, F. Banat, H. A. Arafat and I. AlNashef, Chem. Eng. J., 2023, 146429 CrossRef CAS.
- A. Boublia, T. Lemaoui, F. Abu Hatab, A. S. Darwish, F. Banat, Y. Benguerba and I. M. AlNashef, J. Mol. Liq., 2022, 366, 120225 CrossRef CAS.
- T. Lemaoui, A. S. Darwish, N. E. H. Hammoudi, F. Abu Hatab, A. Attoui, I. M. Alnashef and Y. Benguerba, Ind. Eng. Chem. Res., 2020, 59, 13343–13354 CrossRef CAS.
- T. Lemaoui, A. Boublia, A. S. Darwish, M. Alam, S. Park, B.-H. Jeon, F. Banat, Y. Benguerba and I. M. AlNashef, ACS Omega, 2022, 7, 32194–32207 CrossRef CAS PubMed.
- D. Uka, B. Blagojević, O. Alioui, A. Boublia, N. Elboughdiri, Y. Benguerba, T. Jurić and B. M. Popović, J. Mol. Liq., 2023, 123411 CrossRef CAS.
- S. Goswami, S. Nandy, E. Fortunato and R. Martins, J. Solid State Chem., 2023, 317, 123679 CrossRef CAS.
- R. Arora, A. Srivastav and U. K. Mandal, Int. J. Eng. Res., 2012, 2, 2384–2395 Search PubMed.
- S. Krithika and J. Balavijayalakshmi, Inorg. Chem. Commun., 2022, 110324 Search PubMed.
- J. J. Prías Barragán, K. Gross, J. Darío Perea, N. Killilea, W. Heiss, C. J. Brabec, H. A. Calderón and P. Prieto, ChemistrySelect, 2020, 5, 11737–11744 CrossRef.
- S. Masson, C. Vaulot, L. Reinert, S. Guittonneau, R. Gadiou and L. Duclaux, Environ. Sci. Pollut. Res., 2017, 24, 10005–10017 CrossRef CAS PubMed.
- 2022, https://www.jmp.com/support/help/en/16.2/.
- X. Zheng, M. E. Ali Mohsin, A. Arsad and A. Hassan, J. Appl. Polym. Sci., 2021, 138, 50637 CrossRef CAS.
- E. J. Jelmy, S. Ramakrishnan, S. Devanathan, M. Rangarajan and N. K. Kothurkar, J. Appl. Polym. Sci., 2013, 130, 1047–1057 CrossRef CAS.
- M. Reza, N. Srikandi, A. N. Amalina, D. P. Benu, F. V. Steky, A. Rochliadi and V. Suendo, in IOP Conference Series: Materials Science and Engineering, IOP Publishing, 2019, Vol. 599, p. 12002 Search PubMed.
- H. Nazari and R. Arefinia, Int. J. Polym. Anal. Charact., 2019, 24, 178–190 CrossRef CAS.
- M. M. Rahman, T. Mahtab, M. Z. Bin Mukhlish, M. O. Faruk and M. M. Rahman, Polym. Bull., 2021, 78, 5379–5397 CrossRef CAS.
- G. M. Neelgund and A. Oki, Polym. Int., 2011, 60, 1291–1295 CrossRef CAS PubMed.
- O. A. Al-Hartomy, S. Khasim, A. Roy and A. Pasha, Appl. Phys. A, 2019, 125, 1–9 CrossRef CAS.
- N. Badi, S. Khasim and A. S. Roy, J. Mater. Sci.: Mater. Electron., 2016, 27, 6249–6257 CrossRef CAS.
- N. R. Tanguy, M. Thompson and N. Yan, Sens. Actuators, B, 2018, 257, 1044–1064 CrossRef CAS.
- B. Li, Y. Li and P. Ma, J. Mater. Sci.: Mater. Electron., 2022, 33, 18673–18685 CrossRef CAS.
- B. Li, Y. Li and P. Ma, Org. Electron., 2023, 114, 106749 CrossRef CAS.
- I. Fratoddi, I. Venditti, C. Cametti and M. V. Russo, Sens. Actuators, B, 2015, 220, 534–548 CrossRef CAS.
- S. Kundu, R. Majumder, B. R. Bhagat, S. Roy, R. Gayen, A. Dashora and M. Pal Chowdhury, J. Mater. Sci., 2023, 1–24 Search PubMed.
- L.-H. Xu and T.-M. Wu, J. Mater. Sci.: Mater. Electron., 2020, 31, 7276–7283 CrossRef CAS.
- X. Liu, W. Zheng, R. Kumar, M. Kumar and J. Zhang, Coord. Chem. Rev., 2022, 462, 214517 CrossRef CAS.
- D. J. C. MacKay, Maximum Entropy Bayesian Methods, St. Barbar. California, USA, 1993, 1996, pp. 43–59 Search PubMed.
- S. Kakkar, W. Kwapinski, C. A. Howard and K. V. Kumar, Educ. Chem. Eng., 2021, 36, 115–127 CrossRef.
- E. Mosca, F. Szigeti, S. Tragianni, D. Gallagher and G. Groh, in Proceedings of the 29th International Conference on Computational Linguistics, 2022, pp. 4593–4603 Search PubMed.
- T. A. Meyer, C. Ramirez, M. J. Tamasi and A. J. Gormley, ACS Polym. Au, 2022, 3, 141–157 CrossRef PubMed.
- T. B. Martin and D. J. Audus, ACS Polym. Au., 2023, 3(3), 239–258 CrossRef CAS PubMed.
- A. Oluwaseye, A. Uzairu, G. A. Shallangwa and S. E. Abechi, J. King Saud Univ., Sci., 2020, 32, 75–83 CrossRef.
- J. Cao and C. Wang, Org. Electron., 2018, 55, 26–34 CrossRef CAS.
- S. M. Imran, Y. Kim, G. N. Shao, M. Hussain, Y. Choa and H. T. Kim, J. Mater. Sci., 2014, 49, 1328–1335 CrossRef CAS.
- H. F. Alesary, H. K. Ismail, A. F. Khudhair and M. Q. Mohammed, Orient. J. Chem., 2018, 34, 2525 CAS.
- N. T. Tung, T. Van Khai, H. Lee and D. Sohn, Synth. Met., 2011, 161, 177–182 CrossRef CAS.
- O. A. Al-Hartomy, S. Khasim, A. Roy and A. Pasha, Appl. Phys. A: Mater. Sci. Process., 2019, 125, 1–9 CrossRef CAS.
- G. Gaikwad, P. Patil, D. Patil and J. Naik, Mater. Sci. Eng., B, 2017, 218, 14–22 CrossRef CAS.
- X. Huang, N. Hu, L. Zhang, L. Wei, H. Wei and Y. Zhang, Synth. Met., 2013, 185–186, 25–30 CrossRef CAS.
- M. O. Ansari, M. M. Khan, S. A. Ansari, I. Amal, J. Lee and M. H. Cho, Mater. Lett., 2014, 114, 159–162 CrossRef CAS.
- C. Murugan, E. Subramanian and D. P. Padiyan, Sens. Actuators, B, 2014, 205, 74–81 CrossRef CAS.
- E. Subramanian, P. Santhanamari and C. Murugan, J. Electron. Mater., 2018, 47, 4764–4771 CrossRef CAS.
- F. Xu, S. Guo and Y.-L. Luo, Mater. Chem. Phys., 2014, 145, 222–231 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Table S1: experimental dataset and literature citations for published electrical conductivity values, Table S2: experimental dataset and literature citations for published gas sensing response values, Table S3: types of input variables used in data mining for machine learning modeling of polyaniline/graphene nanocomposites, Table S4: numerical values of σ Profile for additives, and Table S5: ANN equations. See DOI: https://doi.org/10.1039/d3ta06385b |
| ‡ First authorship. |
| This journal is © The Royal Society of Chemistry 2024 |