Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heteroepitaxial tuning of resonant forbidden reflections in a spinel†
Ryosuke
Oka
ab,
Minu
Kim‡
 a,
Peter
Wochner
a,
Sonia
Francoual
a,
Peter
Wochner
a,
Sonia
Francoual
 c,
Thomas T. M.
Palstra
ad,
Hidenori
Takagi
abe and
Dennis
Huang
c,
Thomas T. M.
Palstra
ad,
Hidenori
Takagi
abe and
Dennis
Huang
 *a
*a
aMax Planck Institute for Solid State Research, 70569 Stuttgart, Germany. E-mail: D.Huang@fkf.mpg.de
bDepartment of Physics, The University of Tokyo, 113-0033 Tokyo, Japan
cDeutsches Elektronen-Synchrotron DESY, 22607 Hamburg, Germany
dNano Electronic Materials, University of Twente, 7522 NB Enschede, The Netherlands
eInstitute for Functional Matter and Quantum Technologies, University of Stuttgart, 70569 Stuttgart, Germany
First published on 4th September 2024
Abstract
In resonant elastic X-ray scattering (REXS), low site symmetries in a crystal may be revealed through resonant Bragg reflections that are normally forbidden in conventional X-ray diffraction due to screw axes and/or glide planes. These resonant forbidden reflections have been observed in spinel compounds, but to better understand and utilize their connection to microscopic material parameters and possible charge and/or orbital ordering, a systematic study of their dependence on growth conditions and applied strain is desired. We performed REXS at the V K edge and examined the resonant forbidden (002) reflection in thin films of the spinel LiV2O4 grown on three substrates: MgAl2O4, SrTiO3, and MgO. The energy dependence of the (002) reflection shows a systematic evolution as epitaxial strain modifies the local anisotropy of the V site. More strikingly, the integrated intensity of the (002) reflection varies by more than an order of magnitude in films on different substrates. We speculate that the large variation in integrated intensity reflects the varying degree of antiphase domains that arise during the epitaxy.
1 Introduction
Resonant elastic X-ray scattering (REXS) has been rapidly developed over the recent decades to become a powerful probe of electronic and magnetic ordering and associated small symmetry reduction in correlated electron materials.1–3 REXS combines (1) the sensitivity of X-ray absorption spectroscopy to specific elements and their valence configurations with (2) the ability of scattering techniques to probe momentum space with high resolution.The spinel group AB2X4 has been the subject of several REXS investigations.4–11 It holds both fundamental significance as a platform for realizing frustrated charge/spin/orbital phases,12 as well as technological applications in multiferroics,13 spin-polarized transport,14,15 battery cathodes,16 and chemical sensors.17,18 The A ions are tetrahedrally coordinated to X ligands and form a diamond sublattice. The B ions have a slightly distorted octahedral coordination to X ligands and form a pyrochlore sublattice of corner-sharing B4 tetrahedra [Fig. 1(a)]. The pyrochlore sublattice can also be visualized as layers of B-ion chains stacked along [001]; from layer to layer, the chains alternate between running along the [110] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] directions [Fig. 1(b)]. Neighboring layers of B-ion chains are related to each other by a diamond glide reflection (or 41 screw rotation), which causes the (004l+2) Bragg reflections to be extinct in conventional X-ray diffraction (XRD).
10] directions [Fig. 1(b)]. Neighboring layers of B-ion chains are related to each other by a diamond glide reflection (or 41 screw rotation), which causes the (004l+2) Bragg reflections to be extinct in conventional X-ray diffraction (XRD).
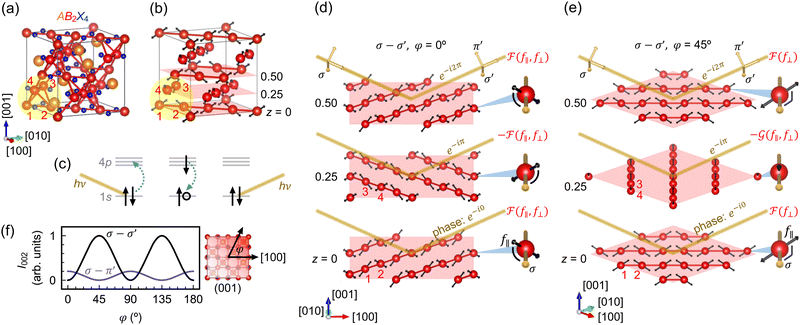 | ||
Fig. 1 (a) Crystal structure of cubic spinel AB2X4. The numbers 1–4 label the four B ions in a primitive unit cell of the pyrochlore sublattice. (b) Crystal structure with only the B sublattice shown, highlighting the B-ion chains, which run along [110] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10]. The double-headed arrows represent the local threefold rotation axes. (c) Schematic illustration of REXS at the B K edge. The photon energy hν is tuned to the energy difference between the 1s and 4p levels. (d) and (e) Schematic depiction of resonant scattering at the (002) Bragg condition with σ-polarized photons. The z = 0, 0.25, and 0.50 planes are artificially expanded for clarity. The scattered photons from the z = 0 and 0.50 planes are in phase (e−i0 and e−i2π), whereas those from the z = 0.25 plane are out of phase (e−iπ). (d) When the azimuthal angle φ = 0°, the scattering amplitudes from the z = 0 and 0.25 planes are equal in magnitude, 10]. The double-headed arrows represent the local threefold rotation axes. (c) Schematic illustration of REXS at the B K edge. The photon energy hν is tuned to the energy difference between the 1s and 4p levels. (d) and (e) Schematic depiction of resonant scattering at the (002) Bragg condition with σ-polarized photons. The z = 0, 0.25, and 0.50 planes are artificially expanded for clarity. The scattered photons from the z = 0 and 0.50 planes are in phase (e−i0 and e−i2π), whereas those from the z = 0.25 plane are out of phase (e−iπ). (d) When the azimuthal angle φ = 0°, the scattering amplitudes from the z = 0 and 0.25 planes are equal in magnitude, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (f‖,f⊥), but carry opposite phase prefactors, leading to complete destructive interference. Magnified insets: The angles subtended by the polarization vector and threefold rotation axes are identical. (e) When φ = 45°, the scattering amplitude (f‖,f⊥), but carry opposite phase prefactors, leading to complete destructive interference. Magnified insets: The angles subtended by the polarization vector and threefold rotation axes are identical. (e) When φ = 45°, the scattering amplitude ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (f⊥) from the z = 0 plane is distinct from the scattering amplitude (f⊥) from the z = 0 plane is distinct from the scattering amplitude ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (f‖,f⊥) from the z = 0.25 plane, so the intensity of the (002) reflection can still be nonzero when the two are summed with opposite phases. Magnified insets: The scattering amplitude from the z = 0 plane has no contribution from f‖, because the polarization vector is fully perpendicular to the threefold rotation axes. (f) Azimuthal dependence of the intensity (I) of the resonant forbidden (002) reflection in the σ–σ′ and σ–π′ polarization channels, as described by eqn (4) and (5). (f‖,f⊥) from the z = 0.25 plane, so the intensity of the (002) reflection can still be nonzero when the two are summed with opposite phases. Magnified insets: The scattering amplitude from the z = 0 plane has no contribution from f‖, because the polarization vector is fully perpendicular to the threefold rotation axes. (f) Azimuthal dependence of the intensity (I) of the resonant forbidden (002) reflection in the σ–σ′ and σ–π′ polarization channels, as described by eqn (4) and (5). | ||
Early REXS studies of magnetite Fe3O4 (A = B = Fe) at the Fe K edge reported resonant forbidden reflections at (002) and (006).4–7 Although studies of magnetite typically aim to probe charge and/or orbital order below the Verwey transition around 120 K, these specific reflections at (002) and (006) appear even above the transition temperature and have a structural origin in a phenomenon known as anisotropic tensor of susceptibility (ATS) scattering:19,20 at photon energies far away from any elemental absorption edge, the atomic form factor as described by classical Thomson scattering is energy independent and can be treated as a scalar. At energies near the K edge of a specific element, however, the scattering of photons involves a virtual transition between the 1s and 4p levels [Fig. 1(c)], resulting in an anomalous energy dependence of the atomic form factor. Since the p orbitals have an anisotropic spatial distribution, the atomic form factor near the K edge further acquires the possibility of being sensitive to the polarizations of the incident and scattered photons, depending on the site symmetry. In the case of octahedral site symmetry, the atomic form factor remains isotropic. In the case of trigonal site symmetry, the atomic form factor can be anisotropic, i.e., with different matrix elements f‖ ≠ f⊥, where (‖) or (⊥) represent the cases where the polarizations of the incident and scattered photons are parallel or perpendicular to the local threefold rotation axis. In cubic spinels AB2X4 with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, the B sites have
m, the B sites have ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, with the threefold rotation axes locally directed towards the center of the B4 tetrahedra [double-headed arrows in Fig. 1(b)]. Depending on the relative orientation of the photon polarization to these threefold rotation axes, the (002) and (006) reflections may no longer be extinct, which is the essence of ATS scattering.
m symmetry, with the threefold rotation axes locally directed towards the center of the B4 tetrahedra [double-headed arrows in Fig. 1(b)]. Depending on the relative orientation of the photon polarization to these threefold rotation axes, the (002) and (006) reflections may no longer be extinct, which is the essence of ATS scattering.
Fig. 1(d) and (e) provide a schematic illustration of ATS scattering of spinels. We consider the case where the incident and scattered photons both have σ polarization pointing perpendicular to the scattering plane. At the (002) Bragg condition, scattered photons from the z = 0.5 plane are in phase with those from the z = 0 plane and sum constructively, while scattered photons from the z = 0.25 plane are out of phase with those from the z = 0 plane and sum destructively. The scattering amplitudes from the z = 0 and 0.5 planes are always identical by symmetry, whereas the scattering amplitude from the z = 0.25 plane may differ from that of the z = 0 plane, depending on the azimuthal angle φ of the momentum transfer. When φ = 0° (‖ [100]), the angles subtended by the polarization vector and the local threefold rotation axes are identical for B ions in the z = 0 and 0.25 planes. The scattering amplitudes from the z = 0 and 0.25 planes are thus equal in magnitude. We denote them as ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (f‖,f⊥), where the dependence on both f‖ and f⊥ comes from the fact that the polarization vector has components both parallel and perpendicular to the threefold rotation axes. Given the opposite phases at z = 0 and 0.25, complete destructive interference ensues and the (002) reflection is extinct at φ = 0°. When φ = 45° (‖ [110]), the polarization vector always points perpendicular to the threefold rotation axes of the B ions in the z = 0 plane. The scattering amplitude from the z = 0 plane is thus given by
(f‖,f⊥), where the dependence on both f‖ and f⊥ comes from the fact that the polarization vector has components both parallel and perpendicular to the threefold rotation axes. Given the opposite phases at z = 0 and 0.25, complete destructive interference ensues and the (002) reflection is extinct at φ = 0°. When φ = 45° (‖ [110]), the polarization vector always points perpendicular to the threefold rotation axes of the B ions in the z = 0 plane. The scattering amplitude from the z = 0 plane is thus given by ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (f⊥). For the B ions in the z = 0.25 plane, the polarization vector again has components both parallel and perpendicular to the threefold rotation axes, and the scattering amplitude from the z = 0.25 plane is given by
(f⊥). For the B ions in the z = 0.25 plane, the polarization vector again has components both parallel and perpendicular to the threefold rotation axes, and the scattering amplitude from the z = 0.25 plane is given by ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (f‖,f⊥). Since
(f‖,f⊥). Since ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (f⊥) ≠
(f⊥) ≠ ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (f‖,f⊥), the scattering amplitudes from the z = 0 and 0.25 planes no longer cancel out when summed with opposite phases, leading to a finite intensity of the (002) reflection at φ = 45°. ATS scattering of spinels predicts a resonant forbidden (002) reflection in the σ–σ′ channel that is maximal at φ = 45° and zero at φ = 0°.
(f‖,f⊥), the scattering amplitudes from the z = 0 and 0.25 planes no longer cancel out when summed with opposite phases, leading to a finite intensity of the (002) reflection at φ = 45°. ATS scattering of spinels predicts a resonant forbidden (002) reflection in the σ–σ′ channel that is maximal at φ = 45° and zero at φ = 0°.
The precise azimuthal angular and polarization dependence of the resonant forbidden (002) reflection due to ATS scattering can be modeled as follows.6 In the dipole–dipole approximation, we represent the atomic form factors as second-rank tensors. In the frame of the local threefold rotation axis, the atomic form factor of all the B ions takes the form of
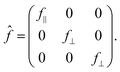 | (1) |
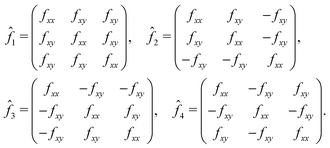 | (2) |
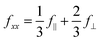 and
and 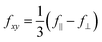 . The anisotropy of the B site, f‖ − f⊥, is encoded in the off-diagonal element fxy, which is usually negligible compared to the diagonal element fxx. At forbidden reflections, however, such as (002), the diagonal elements of the structure factor vanish, while the off-diagonal elements remain:
. The anisotropy of the B site, f‖ − f⊥, is encoded in the off-diagonal element fxy, which is usually negligible compared to the diagonal element fxx. At forbidden reflections, however, such as (002), the diagonal elements of the structure factor vanish, while the off-diagonal elements remain: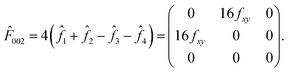 | (3) |
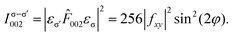 | (4) |
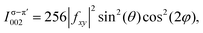 | (5) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10]) and is zero at φ = 0° and 90° (along [100] and [010]), whereas in the σ–π′ channel, the intensity peaks at φ = 0° and 90° and is zero at φ = 45° and 135° [Fig. 1(f)].
10]) and is zero at φ = 0° and 90° (along [100] and [010]), whereas in the σ–π′ channel, the intensity peaks at φ = 0° and 90° and is zero at φ = 45° and 135° [Fig. 1(f)].
Various REXS studies have demonstrated the ATS origin of the resonant forbidden (002) reflection in spinels by confirming the azimuthal angular and polarization dependence predicted by eqn (4) and (5).4–8 Little attention has been devoted to systematically tracking the evolution of these resonant forbidden reflections as a function of strain or growth conditions. A better understanding of how resonant forbidden reflections depend on material parameters may further enhance the utility of REXS as a quantitative probe of materials. Here, we investigate the resonant forbidden (002) reflection in a typical spinel oxide, LiV2O4. Unlike the case of the extensively studied Fe3O4, where Fe K-edge scattering is complicated by contributions from both the A and B sites, in LiV2O4, V K-edge scattering selectively probes the B sites, leading to a simpler interpretation. We have also developed procedures to grow LiV2O4 thin films on a variety of substrates and facets via pulsed laser deposition (PLD).21,22 We observed a resonant forbidden (002) reflection of ATS origin across all our films, but the energy dependence and integrated intensity of the (002) reflection show systematic changes depending on the substrate used. We explain these variations in terms of the strain state of the film and its impact on local crystalline anisotropy, as well as the differing degree of antiphase domains induced by the mismatch of the film and substrate unit cells.
2 Methods
Thin films of LiV2O4 were grown via PLD as previously described in ref. 21 and 22. The deposited films were as thin as 10–30 nm, in order to maintain a coherently strained state when grown on MgAl2O4(001) and MgO(001).REXS at the V K edge around 5.465 keV was performed at the bending magnet beamline MPI at the KIT light source KARA and the P09 beamline of DESY. Measurements at KARA were carried out in the vertical four-circle scattering mode. The beam was monochromatized by a sagittally focusing Si(111) double crystal monochromator, the sample was kept in He atmosphere at room temperature, and an Eiger 2D detector from Dectris was used without prior polarization analysis. At DESY, thin-film samples were mounted on the cold finger of a closed cycle cryostat (advanced research systems), allowing the samples to be pumped down to high vacuum to avoid ionization damage to the film. Measurements were otherwise performed at room temperature with the beamline incident energy tuned close to the V K absorption edge energy and with the beam focused down to a ∼80 × 200 μm2 (V × H) size. A pyrolitic graphite (001) crystal was used to analyze the polarization of the diffracted beam. The orientation Û![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) matrix was retrieved by aligning the (002) and (202) Bragg reflections of the substrate (or (004) and (404) in the case of MgAl2O4), and then the (004) reflection of the film was found relative to the substrate Û
matrix was retrieved by aligning the (002) and (202) Bragg reflections of the substrate (or (004) and (404) in the case of MgAl2O4), and then the (004) reflection of the film was found relative to the substrate Û![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) matrix. Azimuthal dependence was carried out by rotating the sample around the scattering wavevector; the azimuthal angle ψ was 0° when the [0
matrix. Azimuthal dependence was carried out by rotating the sample around the scattering wavevector; the azimuthal angle ψ was 0° when the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction was along the incident beam.
0] direction was along the incident beam.
Density functional theory (DFT) calculations of LiV2O4 were performed using the Vienna ab initio simulation package (VASP) package,23,24 which utilizes the projector augmented-wave method.25 The valence electrons used were Li 1s22s1, V 3s23p64s23d3, and O 2s22p4. We used the Perdew–Burke–Ernzerhof parametrization of the generalized gradient approximation.26 The sampling of the Brillouin zone was 10 × 10 × 10, the energy cutoff of the plane-wave basis was 700 eV, and ionic relaxation of internal atomic coordinates was performed with a force tolerance smaller than 1 meV Å−1.
REXS simulations of the resonant forbidden (002) reflection in LiV2O4 were performed using the finite difference method near edge structure (FDMNES) code, which is based on DFT and suitable to describe K-edge absorption.27
Atomic structures were visualized using the VESTA software.28
3 Results
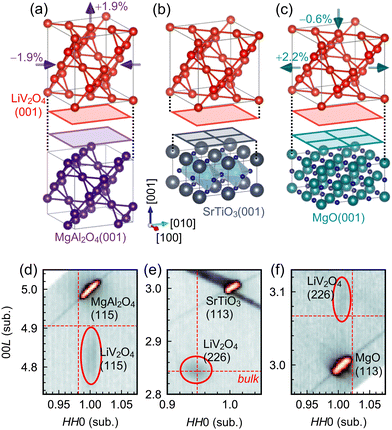
We focus on thin films of LiV2O4(001) prepared on three distinct substrates: MgAl2O4(001), SrTiO3(001), and MgO(001). The different lattice relationships between LiV2O4 and the substrates resulted in different strain states of the films [Fig. 2(a)–(c)]. MgAl2O4 has the same cubic spinel structure as LiV2O4, but with a lattice constant a of 8.085 Å that is −1.9% smaller than that of LiV2O4, a = 8.24 Å. We found that beneath a critical thickness of ∼15 nm, our thin films of LiV2O4/MgAl2O4(001) were coherently strained with in-plane lattice constants a and b compressed by −1.9% to match that of MgAl2O4, as seen in the reciprocal space map of Fig. 2(d). The out-of-plane lattice constant c is expanded due to the Poisson effect, typically by +1 to +2% [+1.9% for the film studied in this work, Fig. 2(d)], resulting in a tetragonal unit cell. SrTiO3 is a cubic perovskite whose lattice constant a = 3.905 Å (2a = 7.810 Å) is nearly half of that of LiV2O4; nevertheless, due to the large lattice mismatch of −5.2% and distinct lattice types, our thin films of LiV2O4/SrTiO3(001) were always relaxed with bulk lattice constant ∼8.24 Å [Fig. 2(e)]. MgO is a cubic rock salt whose lattice constant a = 4.212 Å (2a = 8.424 Å) is also close to half of that of LiV2O4. The lattice mismatch of +2.2% is small enough that below a critical thickness of ∼40 nm, our thin films of LiV2O4/MgO(001) were coherently strained with in-plane lattice constants a and b expanded by +2.2% to match that of MgO [Fig. 2(f)]. The out-of-plane lattice constant c is concomitantly contracted by typically −0.5 to −1.5% [−0.6% for the film studied in this work, Fig. 2(f)], resulting again in a tetragonal unit cell. The different strain states of the films (compressive or tensile in the (001) plane), their different symmetries (cubic or tetragonal), and the different epitaxial relationships (one or two substrate lattice constants per film lattice constant) all provide different microscopic parameters for our present REXS study.As shown in Fig. 3(a)–(c), we observed a resonant forbidden (002) reflection near the V K edge in LiV2O4 films deposited on all three substrates. Scans along 00L in reciprocal space in the σ–σ′ channel reveal a peak around L = 2 when the photon energy is tuned to 5.487 keV and the azimuthal angle is set to ψ = 45°. This (002) peak disappears either when the photon energy is tuned away from resonance, e.g., at 5.467 keV [Fig. 3(b)], or when the azimuthal angle is set to 0° [Fig. 3(a)–(c)]. The (002) peak is more difficult to see for the film on SrTiO3 due to a strong background from a nearby (001) reflection of the substrate, but is nevertheless clear when we compare scans on and off the resonant energy at ψ = 45° (Fig. 3(b); inset shows on-resonant scan subtracted by off-resonant scan).
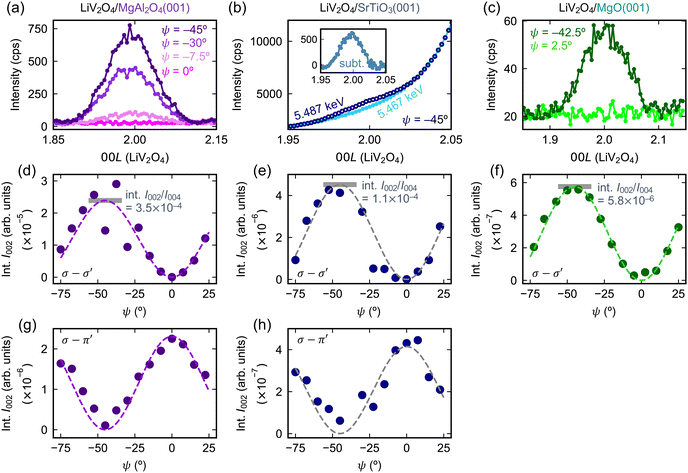 | ||
| Fig. 3 (a)–(c) Resonant forbidden (002) reflections at the V K edge in LiV2O4 thin films on various substrates. The photon energy used is 5.487 keV unless otherwise noted, and the polarization channel is σ–σ′. The intensity is reported in counts per second (cps). In the case of LiV2O4/SrTiO3 (b), the LiV2O4(002) reflection is more difficult to observe, because of a large background tail from a nearby substrate reflection, SrTiO3(001). The inset of (b) has the same axes as the main panel and shows the subtraction (subt.) of the data in the main panel. (d)–(h) Azimuthal dependence of the integrated intensity (int. I) of the resonant forbidden (002) reflections in the σ–σ′ and σ–π′ channels. The dotted lines are fits to eqn (4) in (d)–(f) and eqn (5) in (g) and (h). The horizontal gray bars in (d)–(f) label the maxima extracted from the fits, normalized by the intensity of the non-resonant (004) reflection. | ||
For the films on each of the substrates, we further tracked the azimuthal angular and polarization dependence of the (002) reflection [Fig. 3(d)–(h)]. To make meaningful comparisons, we compute the integrated intensity, which is the area under the (002) peak in the L scans, after normalizing by various beam parameters and the film thickness. The integrated intensity in the σ–σ′ channel obeys a sin2(2ψ) dependence, while the integrated intensity in the σ–π′ channel obeys a cos2(2ψ) dependence. (In the case of LiV2O4/MgO(001), the signal-to-noise ratio in the σ–π′ channel was too small to perform a proper analysis, and hence we only show the analysis in the σ–σ′ channel.) These functional forms are in agreement with predictions of ATS scattering of LiV2O4 both in the cubic phase on SrTiO3 with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m [eqn (4) and (5)], as well as the tetragonal phase on MgAl2O4 and MgO, presumably with space group I41/amd (see ESI† for derivation). We thus confirm a resonant forbidden (002) reflection of ATS origin in LiV2O4 thin films on MgAl2O4(001), SrTiO3(001), and MgO(001). While the azimuthal angular dependence of the (002) integrated intensity remains the same across all three films, their overall amplitudes differ greatly. When normalized by the intensity of the regular LiV2O4(004) Bragg reflection, the maximum integrated intensity of the LiV2O4(002) reflection at ψ = 45° decreases by a factor of three from LiV2O4/MgAl2O4 to LiV2O4/SrTiO3, then by another factor of 20 from LiV2O4/SrTiO3 to LiV2O4/MgO [Fig. 3(d)–(f)].
m [eqn (4) and (5)], as well as the tetragonal phase on MgAl2O4 and MgO, presumably with space group I41/amd (see ESI† for derivation). We thus confirm a resonant forbidden (002) reflection of ATS origin in LiV2O4 thin films on MgAl2O4(001), SrTiO3(001), and MgO(001). While the azimuthal angular dependence of the (002) integrated intensity remains the same across all three films, their overall amplitudes differ greatly. When normalized by the intensity of the regular LiV2O4(004) Bragg reflection, the maximum integrated intensity of the LiV2O4(002) reflection at ψ = 45° decreases by a factor of three from LiV2O4/MgAl2O4 to LiV2O4/SrTiO3, then by another factor of 20 from LiV2O4/SrTiO3 to LiV2O4/MgO [Fig. 3(d)–(f)].
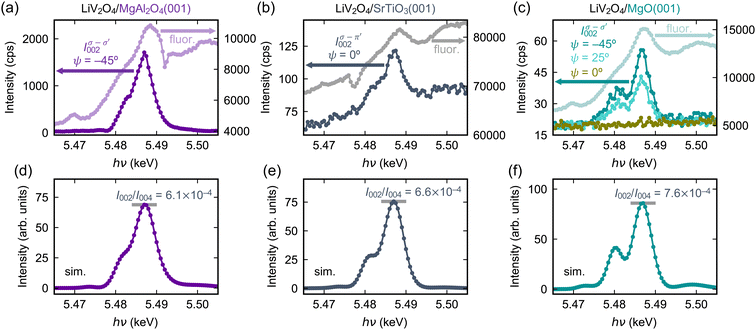
Fig. 4(a)–(c) show the anomalous energy dependence of the resonant forbidden (002) reflections from 5.465 to 5.505 keV. In the LiV2O4/MgAl2O4 film, the spectrum comprises a primary peak centered at 5.487 keV and a kink around 5.483 keV. As we proceed to the films on SrTiO3 and MgO, it becomes more evident that the kink is a secondary peak that gains additional spectral weight and splits off from the primary peak. In the LiV2O4/MgO film, the primary peak at 5.487 keV and the secondary peak at 5.482 keV are clearly separated. We confirm that the secondary peak around 5.482 eV has the same azimuthal angular dependence predicted by ATS scattering as the primary peak [Fig. 4(c)] and does not arise from a distinct microscopic origin (e.g., charge or magnetic order, refer to ref. 29). Instead, the double-peak structure reflects the complicated energy dependence of the V atomic form factor tensor in the local environment of the strained film, as well as a small phase difference due to the different c-axis lattice constants of the films.10,30
We performed REXS simulations to better elucidate the microscopic basis of the anomalous energy dependence of the LiV2O4(002) reflection and its variation on different substrates. For the structural models, we simply adopted the experimental lattice constants of LiV2O4 on the three different substrates (Fig. 2), which fix the internal V and Li positions, then used ionic relaxation within DFT to estimate the internal O positions. For each film, we computed the energy-dependent matrix elements fxx(E) and fxy(E) of the atomic form factor tensor. From eqn (4), I002 is then simply proportional to |fxy(E)|2. At a qualitative level, the simulations reproduce the split-peak structure that becomes more prominent when proceeding from LiV2O4/MgAl2O4(001) to LiV2O4/SrTiO3(001) to LiV2O4/MgO(001) [Fig. 4(d)–(f)]. This qualitative agreement confirms that the anomalous energy dependence of the (002) reflection is mostly structural in origin: under the different strain states, there are small changes to the local anisotropy of the V-ion sites due to changes in the V–O and V–V distances and angles. These small changes are sensitively encoded in the off-diagonal element fxy, which is proportional to the difference f‖ − f⊥, and whose squared magnitude determines the intensity of the resonant forbidden (002) reflection.
The REXS simulations demonstrate that the strain state of the film alone, which results in changes of the local V-site anisotropy, is able to qualitatively explain the anomalous energy dependence of the resonant forbidden (002) reflection in LiV2O4 on different substrates. These simulations, however, do not reproduce the large substrate dependence that we see in the integrated intensities of the (002) reflection, normalized by the intensity of the allowed (004) reflection. The simulations predict that I002/I004 increases moderately by about 25% from the strained film on MgAl2O4 to the oppositely strained film on MgO. The experimental data shows instead that the integrated I002 normalized by I004 decreases by a factor of ∼60 from the strained film on MgAl2O4 to the oppositely strained film on MgO. Some microscopic factors in the film beyond simply a strained unit cell must be at play. We suspect that such a large variation does not arise from the atomic form factors ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) themselves, but from differences in the structure factor
themselves, but from differences in the structure factor 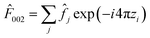 that arise from differences in the atomic positions {rj} when structural domains are present.
that arise from differences in the atomic positions {rj} when structural domains are present.
We hypothesize that the integrated intensities of the (002) reflection are modulated by the differing amounts of antiphase domain boundaries in the films on the various substrates. Antiphase domain boundaries represent the dominant defects in spinels and govern key properties with technological significance in spinels. In magnetite, for example, antiphase domain boundaries induce antiferromagnetic coupling between ferromagnetic domains, which alters the spin-transport properties.14 Antiphase domain boundaries also play a role in strain transmission,31 as well as in the capacity degradation of potential spinel battery cathodes after repeated electrochemical cycling.32
Antiphase domain boundaries are particularly amplified in heteroepitaxial thin films. When spinel LiV2O4 (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) is deposited on perovskite SrTiO3(001) (space group Pm
m) is deposited on perovskite SrTiO3(001) (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) or rock-salt MgO(001) (space group Fm
m) or rock-salt MgO(001) (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), there is both a reduction in translational symmetry from a ≈ 4 Å to a ≈ 8 Å, as well as a reduction in point-group symmetries. The fourfold rotation axes along a/b/c in Pm
m), there is both a reduction in translational symmetry from a ≈ 4 Å to a ≈ 8 Å, as well as a reduction in point-group symmetries. The fourfold rotation axes along a/b/c in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m are replaced by 41 screw axes along a/b/c in Fd
m are replaced by 41 screw axes along a/b/c in Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. This mismatch in translational and rotational symmetries allow LiV2O4 to nucleate at different sites and with different orientations that are equivalent with respect to the SrTiO3(001) or MgO(001) substrates, but that lead to antiphase boundaries in the film once the domains coalesce. There are seven such kinds of antiphase boundaries in spinel compounds, with Burgers vectors 1/4[110], 1/4[1
m. This mismatch in translational and rotational symmetries allow LiV2O4 to nucleate at different sites and with different orientations that are equivalent with respect to the SrTiO3(001) or MgO(001) substrates, but that lead to antiphase boundaries in the film once the domains coalesce. There are seven such kinds of antiphase boundaries in spinel compounds, with Burgers vectors 1/4[110], 1/4[1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0], 1/4[101], 1/4[10
0], 1/4[101], 1/4[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], 1/4[011], 1/4[01
], 1/4[011], 1/4[01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], and 1/2[100].33 Numerous reports of epitaxial thin films of spinel oxides, including Fe3O4,31,33–36 NiFe2O4,37 and CoCr2O4,38 have confirmed that the density of antiphase boundaries is significantly larger on substrates such as SrTiO3 and MgO with higher symmetry, than on spinel substrates such as MgAl2O4. The antiphase domain boundaries facilitate the transmission of epitaxial strain from the substrate and explain why spinel films deposited on MgO, for example, can be coherently strained up to much larger critical thicknesses compared to films deposited on MgAl2O4.31,36 The typical domain sizes for spinel thin films on MgO range from 5 to 40 nm.34
], and 1/2[100].33 Numerous reports of epitaxial thin films of spinel oxides, including Fe3O4,31,33–36 NiFe2O4,37 and CoCr2O4,38 have confirmed that the density of antiphase boundaries is significantly larger on substrates such as SrTiO3 and MgO with higher symmetry, than on spinel substrates such as MgAl2O4. The antiphase domain boundaries facilitate the transmission of epitaxial strain from the substrate and explain why spinel films deposited on MgO, for example, can be coherently strained up to much larger critical thicknesses compared to films deposited on MgAl2O4.31,36 The typical domain sizes for spinel thin films on MgO range from 5 to 40 nm.34
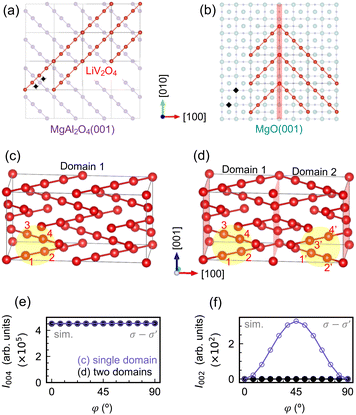
We focus our discussion on 1/4[101]- and 1/4[011]-type antiphase boundaries, which have been estimated to dominate ∼60% of the antiphase boundaries in a spinel Fe3O4/MgO(001) thin film.33 These kinds of shifts involve an out-of-plane, [001] component to the Burgers vector and result in B-ion chains that run orthogonally in the same plane. As shown in Fig. 5(a) and (b), such domains arise naturally on the MgO(001) surface (or the SrTiO3(001) surface), but not on the MgAl2O4(001) surface. The MgAl2O4(001) surface has twofold symmetry, and if the Al-ion chains run along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] direction, then the V-ion chains of the nucleation layer of LiV2O4 should run along [110] according to the spinel structure with its 41 screw axis [Fig. 5(a)]. The MgO(001) or SrTiO3(001) surfaces have fourfold symmetry, so the V-ion chains of the nucleation layer of LiV2O4 can run equally well along the [110] and [
10] direction, then the V-ion chains of the nucleation layer of LiV2O4 should run along [110] according to the spinel structure with its 41 screw axis [Fig. 5(a)]. The MgO(001) or SrTiO3(001) surfaces have fourfold symmetry, so the V-ion chains of the nucleation layer of LiV2O4 can run equally well along the [110] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] directions, leading to domains of orthogonal V-ion chains [Fig. 5(b)].
10] directions, leading to domains of orthogonal V-ion chains [Fig. 5(b)].
When two such orthogonal domains are present, the (002) reflection becomes reduced. Back in the case of a single domain [Fig. 1(e)], the appearance of a resonant forbidden (002) reflection in the σ–σ′ channel relied on the fact that at φ = 45°, the photon polarization vector is perpendicular to the [110]-oriented B-ion chains in the z = 0 and 0.5 planes, but parallel to the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10]-oriented B-ion chains in the z = 0.25 planes, leading to different scattering amplitudes that do not completely cancel. If, however, there is a neighboring domain with [
10]-oriented B-ion chains in the z = 0.25 planes, leading to different scattering amplitudes that do not completely cancel. If, however, there is a neighboring domain with [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10]-oriented B-ion chains in the z = 0 and 0.5 planes and [110]-oriented B-ion chains in the z = 0.25 planes, and these scattering amplitudes can be summed coherently with those of the first domain, then they cancel. For two orthogonal domains with equal volume and basis atoms labeled 1–4 and 1′–4′, respectively [Fig. 5(d)], the structure factor is given by
10]-oriented B-ion chains in the z = 0 and 0.5 planes and [110]-oriented B-ion chains in the z = 0.25 planes, and these scattering amplitudes can be summed coherently with those of the first domain, then they cancel. For two orthogonal domains with equal volume and basis atoms labeled 1–4 and 1′–4′, respectively [Fig. 5(d)], the structure factor is given by
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 002 = 4( 002 = 4(![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1 + 1 + ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2 − 2 − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 3 − 3 − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 4) + 4( 4) + 4(![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1′ + 1′ + ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2′ − 2′ − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 3′ − 3′ − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 4′), 4′), | (6) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1′ =
1′ = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 3,
3, ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2′ =
2′ = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 4,
4, ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 3′ =
3′ = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 1, and
1, and ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 4′ =
4′ = ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) 2 by symmetry. Then
2 by symmetry. Then ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 002 is simply zero. Fig. 5(e) and (f) show REXS simulations for a 2 × 1 × 1 supercell of LiV2O4 with a single domain [Fig. 5(c)] and a 2 × 1 × 1 supercell of LiV2O4 composed of two orthogonal domains of equal volume [Fig. 5(d)]. The allowed (004) Bragg reflections have nearly identical intensities. The resonant forbidden (002) reflections, on the other hand, show the predicted ATS behavior for the single-domain supercell, but is extinguished in the double-domain supercell with equal domain sizes.
002 is simply zero. Fig. 5(e) and (f) show REXS simulations for a 2 × 1 × 1 supercell of LiV2O4 with a single domain [Fig. 5(c)] and a 2 × 1 × 1 supercell of LiV2O4 composed of two orthogonal domains of equal volume [Fig. 5(d)]. The allowed (004) Bragg reflections have nearly identical intensities. The resonant forbidden (002) reflections, on the other hand, show the predicted ATS behavior for the single-domain supercell, but is extinguished in the double-domain supercell with equal domain sizes.
We speculate that such antiphase domains provide a possible microscopic mechanism for the large variation of the integrated I002 normalized by I004. In LiV2O4/MgAl2O4, due to the identical symmetries of the unit cells, we expect the scattering intensity to originate primarily from a single film domain, leading to a sizeable resonant forbidden (002) reflection. In LiV2O4/MgO, due to the mismatched symmetries of the unit cells, we expect a high density of antiphase domain boundaries to strongly reduce the integrated I002/I004 by a factor of 60 compared to that in LiV2O4/MgAl2O4. In LiV2O4/SrTiO3, although antiphase domain boundaries are also expected, in reality, the film is relaxed due to the large lattice mismatch of −5.2%. The relaxation results in a larger mosaic spread of the film, as evidenced by its rocking curve whose full width at half maximum is an order of magnitude larger than those of the strained films (see ESI†). The enhanced mosaicity decreases the effective volume of the film that scatters X-rays coherently. The integrated I002/I004 for LiV2O4/SrTiO3 is therefore only a factor of three smaller than that of LiV2O4/MgAl2O4, even though antiphase domains are expected in the former, because the volume of coherent scattering is also strongly reduced by the large mosaicity, such that the X-rays predominantly probe a single domain.
4 Conclusions
We have performed REXS at the V K edge on a series of epitaxial LiV2O4 films deposited on MgAl2O4(001), SrTiO3(001), and MgO(001) and consistently observed a resonant forbidden (002) reflection of ATS origin. The anomalous energy dependence of the (002) reflection shows a systematic dependence on the strain state of the films, while the integrated intensity of the (002) reflection decreases by more than an order of magnitude in the film on MgO compared to the film on MgAl2O4. We hypothesize that this large decrease may be due to the much greater proliferation of antiphase domains in thin films on MgO, which have different translational and point-group symmetries than spinel LiV2O4. We hope that future investigations with electron microscopy may directly confirm the link between antiphase domains and the integrated intensity of resonant forbidden reflections, which would further establish the utility of REXS as a diagnostic probe of spinel microstructure. Unlike electron microscopy, REXS could open the door to non-destructive, in situ, and operando monitoring of antiphase domains during epitaxial growth, post-growth annealing, or electrochemical processes.Author contributions
R. O., M. K., and D. H. performed experiments with support from P. W. and S. F. R. O. and D. H. analyzed the data with input and interpretation from P. W., S. F., T. P., and H. T. D. H. wrote the manuscript with feedback from all authors.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge E. Benckiser for discussions, as well as F. Adams, M. Dueller, U. Niemann, K. Pflaum, S. Prill-Diemer, and B. Stuhlhofer for technical support. The KIT Institute for Beam Physics and Technology (IBPT) is acknowledged for the operation of the storage ring Karlsruhe Research Accelerator (KARA), and for provision of beamtime at the KIT light source. Open Access funding provided by the Max Planck Society.Notes and references
- J. Kokubun and V. E. Dmitrienko, Eur. Phys. J.-Spec. Top., 2012, 208, 39–52 CrossRef CAS
.
- T. A. W. Beale, G. Beutier, S. R. Bland, A. Bombardi, L. Bouchenoire, O. Bunău, S. Di Matteo, J. Fernández-Rodrguez, J. E. Hamann-Borrero, J. Herrero-Martn, V. L. R. Jacques, R. D. Johnson, A. Juhin, T. Matsumura, C. Mazzoli, A. M. Mulders, H. Nakao, J. Okamoto, S. Partzsch, A. J. Princep, V. Scagnoli, J. Strempfer, C. Vecchini, Y. Wakabayashi, H. C. Walker, D. Wermeille and Y. Yamasaki, Eur. Phys. J.-Spec. Top., 2012, 208, 89–98 CrossRef CAS
.
- L. Paolasini and F. de Bergevin, C. R. Phys., 2008, 9, 550–569 CrossRef CAS
.
- K. Hagiwara, M. Kanazawa, K. Horie, J. Kokubun and K. Ishida, J. Phys. Soc. Jpn., 1999, 68, 1592–1597 CrossRef CAS
.
- J. García, G. Subías, M. G. Proietti, H. Renevier, Y. Joly, J. L. Hodeau, J. Blasco, M. C. Sánchez and J. F. Bérar, Phys. Rev. Lett., 2000, 85, 578–581 CrossRef PubMed
.
- J. García, G. Subías, M. G. Proietti, J. Blasco, H. Renevier, J. L. Hodeau and Y. Joly, Phys. Rev. B, 2001, 63, 054110 CrossRef
.
- M. Kanazawa, K. Hagiwara, J. Kokubun and K. Ishida, J. Phys. Soc. Jpn., 2002, 71, 1765–1770 CrossRef CAS
.
- G. Subías, J. Garcia, M. G. Proietti, J. Blasco, H. Renevier, J. L. Hodeau and M. C. Sánchez, Phys. Rev. B, 2004, 70, 155105 CrossRef
.
- R. J. Goff, J. P. Wright, J. P. Attfield and P. G. Radaelli, J. Condens. Matter Phys., 2005, 17, 7633 CrossRef CAS
.
- Y. Joly, J. E. Lorenzo, E. Nazarenko, J.-L. Hodeau, D. Mannix and C. Marin, Phys. Rev. B, 2008, 78, 134110 CrossRef
.
- S. Grenier, A. Bailly, A. Y. Ramos, M. De Santis, Y. Joly, J. E. Lorenzo, S. Garaudée, M. Frericks, S. Arnaud, N. Blanc and N. Boudet, Phys. Rev. B, 2018, 97, 104403 CrossRef CAS
.
-
H. Takagi and S. Niitaka, in Introduction to Frustrated Magnetism: Materials, Experiments, Theory, ed. C. Lacroix, P. Mendels and F. Mila, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 155–175 Search PubMed
.
- A. Sundaresan and N. V. Ter-Oganessian, J. Appl. Phys., 2021, 129, 060901 CrossRef CAS
.
- W. Eerenstein, T. T. M. Palstra, S. S. Saxena and T. Hibma, Phys. Rev. Lett., 2002, 88, 247204 CrossRef CAS PubMed
.
- N. Fontaiña-Troitiño, M. A. Ramos-Docampo, M. Testa-Anta, B. Rodríguez-González, M. Bañobre-López, L. Bocher, K. P. McKenna and V. Salgueiriño, J. Mater. Chem. C, 2018, 6, 12800–12807 RSC
.
- D. Liu, W. Zhu, J. Trottier, C. Gagnon, F. Barray, A. Guerfi, A. Mauger, H. Groult, C. M. Julien, J. B. Goodenough and K. Zaghib, RSC Adv., 2014, 4, 154–167 RSC
.
- J. M. Gonçalves, D. P. Rocha, M. N. T. Silva, P. R. Martins, E. Nossol, L. Angnes, C. S. Rout and R. A. A. Munoz, J. Mater. Chem. C, 2021, 9, 7852–7887 RSC
.
- G. Yuan, H. Zhang, Y. Cheng, Y. Zhong, Q. Zhuo and X. Sun, J. Mater. Chem. C, 2021, 9, 14278–14285 RSC
.
- D. H. Templeton and L. K. Templeton, Acta Crystallogr., Sect. A, 1980, 36, 237–241 CrossRef
.
- V. E. Dmitrienko, Acta Crystallogr., Sect. A, 1983, 39, 29–35 CrossRef
.
- T. F. Schweizer, U. Niemann, X. Que, Q. He, L. Zhou, M. Kim, H. Takagi and D. Huang, APL Mater., 2023, 11, 021109 CrossRef CAS
.
- U. Niemann, Y.-M. Wu, R. Oka, D. Hirai, Y. Wang, Y. E. Suyolcu, M. Kim, P. A. van Aken and H. Takagi, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2215722120 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- O. Bunău and Y. Joly, J. Condens. Matter Phys., 2009, 21, 345501 CrossRef
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- C. Donnerer, M. C. Rahn, M. M. Sala, J. G. Vale, D. Pincini, J. Strempfer, M. Krisch, D. Prabhakaran, A. T. Boothroyd and D. F. McMorrow, Phys. Rev. Lett., 2016, 117, 037201 CrossRef CAS PubMed
.
- Y. Lu, A. Frano, M. Bluschke, M. Hepting, S. Macke, J. Strempfer, P. Wochner, G. Cristiani, G. Logvenov, H.-U. Habermeier, M. W. Haverkort, B. Keimer and E. Benckiser, Phys. Rev. B, 2016, 93, 165121 CrossRef
.
- S. K. Arora, R. G. S. Sofin, I. V. Shvets and M. Luysberg, J. Appl. Phys., 2006, 100, 073908 CrossRef
.
- S. Li, Z. Yao, J. Zheng, M. Fu, J. Cen, S. Hwang, H. Jin, A. Orlov, L. Gu, S. Wang, Z. Chen and D. Su, Angew. Chem., 2020, 59, 22092–22099 CrossRef CAS PubMed
.
- A. Ikeuchi, S. Hiura, T. Mizuno, E. Kaji, A. Subagyo and K. Sueoka, Jpn. J. Appl. Phys., 2012, 51, 08KB02 CrossRef
.
- W. Eerenstein, T. T. M. Palstra, T. Hibma and S. Celotto, Phys. Rev. B, 2002, 66, 201101 CrossRef
.
- J. G. Zheng, G. E. Sterbinsky, J. Cheng and B. W. Wessels, J. Vac. Sci. Technol., B, 2007, 25, 1520–1523 CrossRef CAS
.
- M. Luysberg, R. G. S. Sofin, S. K. Arora and I. V. Shvets, Phys. Rev. B, 2009, 80, 024111 CrossRef
.
- R. Datta, S. Kanuri, S. V. Karthik, D. Mazumdar, J. X. Ma and A. Gupta, Appl. Phys. Lett., 2010, 97, 071907 CrossRef
.
- R. Guzman, J. Heuver, S. Matzen, C. Magén and B. Noheda, Phys. Rev. B, 2017, 96, 104105 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02239d |
| ‡ Present address: Department of Physics, Chung-Ang University, Dongjak District, Seoul, South Korea. |
| This journal is © The Royal Society of Chemistry 2024 |