Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring the influence of (n − 1)d subvalence correlation and of spin–orbit coupling on chalcogen bonding†
Nisha
Mehta‡
 * and
Jan M. L.
Martin
* and
Jan M. L.
Martin

Department of Molecular Chemistry and Materials Science, Weizmann Institute of Science, 7610001 Rehovot, Israel. E-mail: nisha.mehta@weizmann.ac.il
First published on 31st July 2024
Abstract
This article presents a comprehensive computational investigation into chalcogen bonding interactions, focusing specifically on elucidating the role of subvalence (n − 1)d and (n − 1)sp correlation. The incorporation of inner-shell (n − 1)d correlation leads to a decrease in interaction energies for chalcogen-bonded systems (at least those studied herein), contradicting the observations regarding halogen bonding documented by Kesharwani et al. in J. Phys. Chem. A, 2018, 122 (8), 2184–2197. The significance of (n − 1)sp subvalence correlation appears to be lower by an order of magnitude. Notably, among the various components of interaction energies computed at the PNO-LCCSD(T) or DF-CCSD levels, we identify the PNO-LMP2 or DF-MP2 component of the (n − 1)d correlation as predominant. Furthermore, we delve into the impact of second-order spin–orbit coupling (SOC2) on these interactions. The SOC2 effects appear to be less significant than the (n − 1)d correlation; however, they remain non-trivial, particularly for Te complexes. For the Se complexes, SOC2 is much less important. Generally, SOC2 stabilizes monomers more than dimers, resulting in reduced binding of the latter. Notably, at equilibrium and stretched geometries, SOC2 and (n − 1)d destabilize the complex; however, at compressed geometries, they exhibit opposing effects, with (n − 1)d becoming stabilizing.
1 Introduction
Non-covalent interactions exert a crucial influence on the physical and chemical properties of diverse systems.1,2 They are pivotal in processes such as protein folding, ligand interactions, packing and stacking arrangements, organocatalysis, supramolecular chemistry, and conformational stability, underscoring their significance across a spectrum of scientific disciplines.3,4 A molecule featuring a chalcogen atom, such as sulfur, selenium, or tellurium, can partake in a multitude of non-covalent interactions, exemplified by phenomena such as chalcogen bonding, electrostatic interactions, and hydrogen bonding. Chalcogen bonding is a type of non-covalent interaction that involves the interactions between a chalcogen atom (chiefly S, Se, or Te) and a Lewis base or electron-rich region in the neighboring molecule. In chalcogen bonding, a chalcogen atom functions as an electrophile, while the interacting partner contributes electron density to facilitate the interaction. These interactions exhibit a pronounced directional character. The importance of chalcogen bonding interactions lies in their role as a unique and versatile class of noncovalent interactions, influencing molecular recognition, supramolecular assembly, and crystal engineering, with potential applications in drug design, materials science, and catalysis.5–17Numerous systems engage in chalcogen bonding via the σ-hole; nonetheless, an alternative avenue involves the π-hole. This distinctive π-hole constitutes a positively charged domain, positioned orthogonally to a planar π-framework. This positive region demonstrates an affinity for interacting with electron donors. Illustrative instances encompass interactions like SO3⋯H2O,18–20 SO3⋯NH3,21–23 (SO3)n⋯H2CO,24,25 (SO3)n⋯CO,26 and (SO3)n⋯(CO)n,26 where n = 1,2.
Computational methodologies, such as ab initio calculations, play a pivotal role in the examination of chalcogen bonding interactions. It enables precise predictions of molecular structures, energetics, and electronic properties, yielding invaluable insights that might pose challenges or prove unattainable through experimental means. Furthermore, the results can function as a reference point for refining less expensive computational approaches, like DFT and force field methods. Nonetheless, to conduct a thorough benchmark study, it is imperative to accumulate statistics from a sufficiently extensive array of calculations. Illustrative examples of such comprehensive datasets include the Gn test sets,27–30 database 2015B,31 MGCDB84 (Main Group Chemistry Data Base, 84 subsets) of the Berkeley group,32 and the Grimme and Goerigk groups’ GMTKN5533 dataset (general main-group thermochemistry, kinetics, and noncovalent interactions, 55 problem sets), as well as the latter's predecessors GMTKN2434 and GMTKN30.35 These extensive databases encompass a diverse array of benchmark sets, including directional non-covalent interactions such as hydrogen and halogen bonding. While prior research extensively explored halogen bonding interactions, as detailed in the references, it is noteworthy that the aforementioned datasets do not encompass complexes representing chalcogen bonding interactions. To address this gap, one of us and coworkers previously developed the CHAL336 benchmark36 comprising 336 chalcogen-bonded dimers, hitherto the largest and most accurate of its kind.
As we delve into the intricacies of chalcogen bonding, our focus narrows down to a crucial and often overlooked aspect—the importance of subvalence (n − 1)d and (n − 1)sp correlation contributions to chalcogen bonding interactions. For other types of noncovalent interactions, especially involving lighter elements, inner-shell correlation is routinely neglected—this is easy to justify for elements like O and even S, where the core-valence gaps are 19.4 and 5.8 Hartree, respectively. For Se and Te, however, the outer-core (n − 1)d orbitals lie just 1.8 and 1.3 Hartree, respectively, below the valence shell—even smaller than in the adjacent halogens Br and I, for which it has previously been shown37 that (n − 1)d correlation contributes quite significantly to the interaction energy, particularly at shorter distances.
However, if we include core-valence effects, it behooves us to also consider whether other contributions could not be of similar importance. What comes to mind in particular is spin–orbit coupling (SOC), a quantum phenomenon resulting from the interaction between an electron's spin and the magnetic field generated by its orbital motion around the nucleus. SOC can exert a significant influence on the electronic and magnetic properties of materials, particularly those containing heavy elements with large atomic numbers. Closed-shell systems are not subject to first-order SOC, but they may be stabilized by second-order SOC (SOC2: see, e.g.,38–41). For instance, De Jong and coworkers42 found for HBr, Br2, HI, and I2 2nd order SOC stabilizations of {0.1, 0.4, 0.5, 2.0} kcal mol−1, respectively. An experimental manifestation of SOC2 is the zero-field splitting (ZFS) in the X3Σ− ground states of chalcogen diatomics: see, e.g., Table 6 in ref. 43, where one finds ZFS of 23.5 cm−1 for S2, 510 cm−1 for Se2, and 1975 cm−1 for Te2. (That is, 0.067, 1.458, and 5.647 kcal mol−1, respectively—note a rough Z4 dependence on the atomic number Z as conjectured in ref. 44 and noted, in a solid state physics context, in ref. 45). As such numbers are actually in the same energetic range as the subvalence (outer-core) correlation effects we are considering here, we ought to at least attempt to gauge the importance of SOC2 for chalcogen bonding interactions, and compare its importance with that of outer-core correlation.
2 Computational details
We have selected TeO3⋯TeHF, SeO3⋯SeHF, and SO3⋯SHF as exemplars of chalcogen bonding interactions involving Te, Se, and S, respectively. In this study, the reference geometries for TeO3⋯TeHF, SeO3⋯SeHF, and SO3⋯SHF were acquired from ref. 36 and employed without additional optimization. The original 1.0re structure had undergone optimization using the PW6B9546-D3(BJ)47 method with a def2-TZVPD48–50 basis set. In our current study, we determined the remaining structures through stretching and compressing the intermonomer distance (with frozen monomer geometries) by scaling factors of {0.80, 0.85, 0.90, 0.95, 1.0, 1.05, 1.10, 1.25, 1.50, 2.0} using an in-house Python script. The XYZ coordinates for all 30 structures can be found in the ESI.† Initially, we included compressed distances of 0.80re and 0.85re; however, we subsequently opted to omit them due to the strong intermonomer repulsion at such compressed geometries. Consequently, the statistics presented in this manuscript pertain to distances of {0.90, 0.95, 1.0, 1.05, 1.10, 1.25, 1.50, 2.0}, totaling 24 dimers. In response to one of the reviewer's requests, we have also included TeHF⋯NH3, SeHF⋯NH3, and SHF⋯NH3 in our study. The geometries of these molecules were optimized using the PW6B9546/def2-TZVPP48,49 level of theory with ORCA 5.0.251–53 for the optimization process. Additionally, we obtained stretched and compressed intermonomer distances (while keeping the monomer geometries fixed) by applying scaling factors of {0.90, 0.95, 1.0, 1.05, 1.10, 1.25, 1.50, 2.0} through the aforementioned Python script. The corresponding XYZ coordinates are provided in the ESI.†The computations were conducted on the “ChemFarm” HPC cluster of the Faculty of Chemistry at the Weizmann Institute of Science. All ab initio calculations, both canonical and localized, were performed using MOLPRO 2023.2.54 Specifically, we employed a combination of Dunning correlation-consistent cc-pVnZ (where n = D, T, Q, 5) basis sets55 for hydrogen atoms, along with their corresponding augmented counterparts, aug-cc-pVnZ,56 for non-hydrogen atoms other than the chalcogens sulfur, for which we employed aug-cc-pWCVnZ,57,58 and selenium and tellurium, for which we utilized aug-cc-pWCVnZ-PP.48,59,60 (In this context, we would like to mention ref. 61 and references therein, which recommended the incorporation of aug-cc-pWCVnZ basis sets for the accurate treatment of core-electron correlation.)
Our canonical calculations were limited to the density fitting CCSD (coupled cluster with iterative singles and doubles62) level as implemented in MOLPRO. For the higher CCSD(T) level,63 we employed localized orbital CCSD(T) approximations, and specifically the PNO-LCCSD(T) method (pair natural orbital localized coupled cluster, see ref. 64 for a review), and using the DomOpt = Normal, Tight, and vTight threshold combination as detailed in the MOLPRO 2024 online manual65—which for Tight differ slightly from the original values given in Ma and Werner.66
Basis set extrapolation was carried out by means of the two-point extrapolation formula EL = E∞ + B/Lα, where L denotes the maximum angular momentum present within the basis set and α represents the exponent associated with the level of theory and basis set pair. Equivalently,67 this can be written in the Schwenke68 form E∞ = EL + AL(EL − EL−1), if the Schwenke extrapolation coefficient 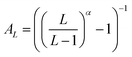 . (For a discussion of the equivalence relations between the various two-point extrapolation formulas, see ref. 67).
. (For a discussion of the equivalence relations between the various two-point extrapolation formulas, see ref. 67).
For the HF, MP2, CCSD, and (T), our {T,Q}Z Schwenke coefficients are 0.415, 0.915, 0.700, and 0.730, respectively, taken from ref. 67 and 69. Likewise, for the {Q,5}Z extrapolation, the corresponding values are 0.528, 1.208, 0.930, and 0.810. It should be noted that we employed identical extrapolation exponents for both the localized and canonical methods, as they should converge to the same result.
Spin–orbit coupling calculations were performed at the STEOM-CCSD70 level as implemented in the ORCA software package (version 5.0.2).51–53 The zeroth order regular approximation (ZORA) method was used to account for scalar relativistic effects.71 The aug-cc-pVTZ-DK basis set58,72–74 was employed, in conjunction with the auxiliary basis sets SARC/J,75–79 and def2-TZVPP/C80,81. Spin–orbit integrals were evaluated within the RI-SOMF(1X) approximation.82 In addition, we also computed spin–orbit coupling calculations at the CAM-B3LYP83-/aug-cc-pVQZ-DK level using the time-dependent density functional theory (TD-DFT) module implemented in the ORCA software package.
In addition to the Boys–Bernardi counterpoise corrections84 and the original “raw” (uncorrected) values, we also employ the mean of both (referred to as “half-CP”), a practice rationalized by Sherrill et al.85 and by Brauer et al.86
Finally, symmetry-adapted perturbation theory (SAPT, see ref. 87 for a review) calculations were performed employing the SAPT module88 within the PSI4 software framework.89
3 Results and discussion
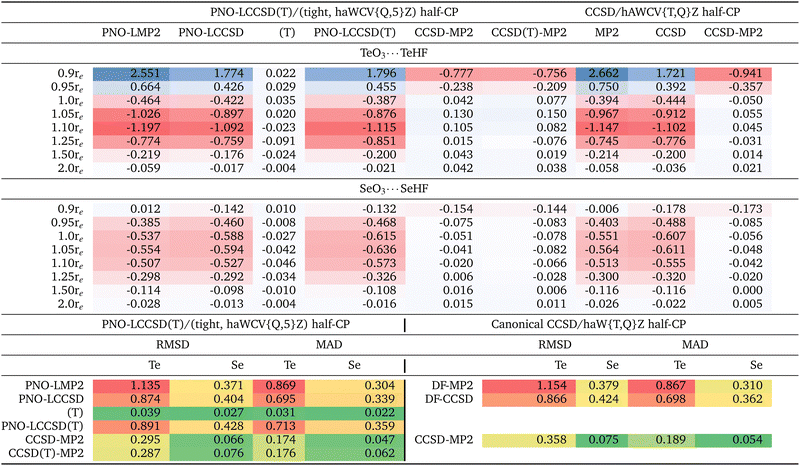
The complete list of the 24 chalcogen-bonded systems, together with our best values for the interaction energies obtained in the present work, is outlined in the final two columns of Table 3. It is crucial to note that throughout this manuscript, positive interaction energy or BE values signify dimer stabilization, as we have reported the negative of the difference between the complex and monomer energies. Due to hardware limitations, we were unable to compute interaction energies utilizing the haWCV5Z basis set at the canonical CCSD level, nor could we incorporate (T). Therefore, our canonical calculations were limited to the DF-CCSD/haWCV{T,Q}Z level. However, we were able to conduct computations using the 5Z-sized basis set through the localized PNO-LCCSD(T) scheme. We have selected the PNO-LCCSD(T) approach, opting for the (Tight, {Q,5}Z) half-CP as our optimal reference level. Localized methods such as PNO-LCCSD(T) (tight, {Q,5}Z) serves as a suitable alternative when canonical references are not feasible, as recommended in ref. 90–93. Both methods converge to the same values at the complete basis set limit. Although we will delve into this more thoroughly in the following section, it is crucial to note that our reference level (i.e., PNO-LCCSD(T) (Tight, {Q,5}Z) half-CP exhibits an RMSD of just 0.046 kcal mol−1 when compared to both the raw and full-CP counterparts (Table 1). Needless to say, at the true CBS limit, the difference between raw and CP-corrected values should be zero: a significant discrepancy between raw and CP in a CBS extrapolation suggests that the underlying calculations are inadequate or that the extrapolation procedure is problematic or both.| (A) | (B) | |||||
|---|---|---|---|---|---|---|
| Te | Se | S | All | Te | Se | |
| HF | 0.012 | 0.010 | 0.006 | 0.010 | ||
| PNO-LMP2 | 0.027 | 0.018 | 0.026 | 0.024 | 0.027 | 0.005 |
| PNO-LCCSD | 0.055 | 0.038 | 0.006 | 0.039 | 0.017 | 0.002 |
| (T) | 0.011 | 0.007 | 0.002 | 0.007 | 0.003 | 0.001 |
| PNO-LCCSD(T) | 0.065 | 0.044 | 0.007 | 0.046 | 0.020 | 0.003 |
| CCSD-MP2 | 0.029 | 0.023 | 0.025 | 0.026 | 0.010 | 0.003 |
| CCSD(T)-MP2 | 0.040 | 0.029 | 0.026 | 0.032 | 0.007 | 0.002 |
We performed three distinct sets of computations: (i) solely considering valence electrons, (ii) including valence and (n − 1)d electrons, and (iii) encompassing valence, (n − 1)d, and (n − 1)sp electrons. Unless otherwise specified, the statistical analyses presented in subsequent section pertains to ‘valence + (n − 1)d electrons’.
3.1 Some observations on the counterpoise corrections for the chalcogen bonding interactions
First we wish to establish how basis set superposition error (BSSE) behaves for different components of the interaction energy (SCF, MP2 correlation, and post-MP2 correction) and obtain interaction energies with basis sets large enough that BSSE has been reduced to insignificance. It has been argued numerous time in the literature (perhaps the first time by Helgaker and coworkers94) that BEraw and BECP tend to converge to the CBS limit from opposite directions: hence, BEhalf-CP = (BEraw + BEfull-CP)/2 naturally suggests itself as the optimal choice (see ref. 85, 86 and references therein). When observing smaller RMSDs for CP-uncorrected results, this is mainly due to error compensation between BSSE (which causes overbinding) and intrinsic basis set insufficiency (IBSI, which leads to underbinding).86 In such cases, this suggests the need for larger basis sets. It has been shown in the past (e.g., ref. 69 and 85) that even a 5Z-sized basis set may still be too far from CBS for an MP2 or coupled cluster calculation for its BSSE to outweigh its IBSI; hence, applying half-CP correction on top of {Q,5}Z extrapolation appears to be more appropriate.Thus, we observed a slower-than-usual convergence of basis sets for the SCF component. Although no systematic trend is evident, Table S1 (ESI†) suggest that basis set convergence is slower for sulfur-based complexes, followed by tellurium and selenium.
Let us next consider the MP2 correlation component. At the PNO-LMP2 (Tight, {Q,5}Z) level, the RMSD of half-CP with both CP-corrected and uncorrected interaction energies is just 0.024 kcal mol−1. {T,Q}Z extrapolation seems to yield lower RMSDs than 5Z. As an example, 5Z yields RMSD of 0.496 kcal mol−1, in comparison to just 0.073 kcal mol−1 for {T,Q}Z, this is even the case for post-MP2 corrections as well, which we will be discussing next. It appears that {T,Q}Z extrapolation may potentially yields superior results compared to utilizing the 6Z basis set. For example, in a very recent study on basis set extrapolations,95 it has been shown that for the W4-17 thermochemical benchmark,96 the RMSD computed for BSSEs at the CCSD/haVnZ + d level are {3.94, 1.74, 0.77, 0.31} kcal mol−1 for n = {T,Q,5,6}, in contrast to 0.27 kcal mol−1 for haV{T,Q}Z and 0.13 kcal mol−1 for haV{Q,5}Z.
We observed an increase in RMSDs upon incorporating counterpoise correction. Sorting by RMSD may suggest that opting for the “raw” data is optimal for the majority of basis sets. For instance, even for a 5Z-sized basis set, the RMSD increases from 0.326 kcal mol−1 to 0.496 and 0.667 kcal mol−1 upon incorporating half and full-CP corrections, respectively. However, this does not imply that one should avoid using counterpoise correction. Rather, as explained at length by Sherrill and coworkers85 for orbital-based calculations, and by Brauer et al.86 for explicitly correlated ones, such ‘right trends for the wrong reason’ reflect that ‘counterpoise-uncorrected’ interaction energies suffer from error compensation between BSSE and IBSI. In such cases, larger basis sets are indicated.
Furthermore, canonical DF-MP2 calculations using the haWCV{T,Q}Z extrapolation with half-counterpoise correction yield an RMSD of only 0.059 kcal mol−1 from the localized reference level (Table S1 in ESI†). This suggests that both our localized and canonical outcomes are converging towards the same basis set limit, affirming that any observations made with the localized scheme are not merely artifacts of its usage.
It is noteworthy that the CCSD-MP2 term exhibits a more rapid basis set convergence compared to the MP2 term discussed earlier (refer to Table 1 and Table S1, ESI†). Interestingly, this finding contradicts the trend observed for atomization energies, as documented by Ranasinghe and Petersson.97
At the {T,Q}Z/Tight level, the RMSD for half-CP is just 0.046 kcal mol−1, slightly larger than for full-CP (0.036 kcal mol−1) but lower than for uncorrected results (0.080 kcal mol−1). RMSD values at the canonical DF-CCSD – DF-MP2/haWCV{T,Q}Z are equally small (0.124, 0.079 and 0.042 kcal mol−1, respectively, for the full-CP, half-CP and ‘raw’ results).
What about the CCSD(T)-MP2 component? At the reference level [PNO-LCCSD(T) – PNO-LMP2/(tight, haWCV{Q,5}Z) half-CP], the discrepancy between half-CP values and CP-corrected and uncorrected interaction energies is merely 0.032 kcal mol−1 RMSD—comparable in magnitude to what we observed for the CCSD-MP2 (i.e., PNO-LCCSD – PNO-LMP2/(tight, haWCV{Q,5}Z) half-CP)) component. While it is customary in noncovalent interactions to generally consider CCSD(T)-MP2 together without further separation, in this study, it may be worthwhile to delve into the (T) component separately. This is particularly relevant for the upcoming section, where we will explore that the incorporation of subvalence (n − 1)d electrons—central to the focus of this manuscrip—may not significantly impact the (T) component. It's worth noting that the basis set convergence of the (T) component is faster compared to MP2 and CCSD-MP2 components. Uncorrected and counterpoise-corrected (T)/haWCV{Q,5}Z results are practically identical, with an RMS difference of only 0.007 kcal mol−1. (T)/{T,Q}Z extrapolation with tight settings and half-CP yields RMSD of 0.015 kcal mol−1. Once more, for most basis sets without CBS extrapolation, counterpoise corrections seem to be disadvantageous.
In summary, for chalcogen bonding interactions, CP correction generally worsens the statistical outcomes even with basis sets as large as 5Z—owing to error cancellation between basis set superposition error and intrinsic basis set insufficiency, highlighting the necessity of employing large basis sets, particularly for the MP2 component, when studying such interactions. It seems that employing CBS extrapolation and applying CP correction atop it represents the best strategy. Furthermore, {T,Q}Z extrapolation surpasses the performance of the 5Z basis set.
3.2 Effect of (n − 1)d and (n − 1)sp subvalence electron correlation
To examine core-valence correlation contributions, we conducted three sets of calculations for a given level of theory: (i) valence electrons only, (ii) valence + (n − 1)d electrons, and (iii) valence + (n − 1)d + (n − 1)sp electrons. The interaction energy contributions calculated are provided in Table 2 and ESI.†At the reference level [i.e., PNO-LCCSD(T)/(tight, hAWCV{Q,5}Z) half-CP], the inclusion of (n − 1)d subvalence correlation destabilizes the TeO3⋯TeHF complex by 0.386 kcal mol−1. As the TeO3⋯TeHF distance is increased, this destabilization effect intensifies, reaching a maximum at 1.10re, where (n − 1)d subvalence correlation contributes 1.119 kcal mol−1 to the destabilization. Beyond this point, the impact of (n − 1)d subvalence correlation diminishes, with a contribution of only 0.021 kcal mol−1 at 2.0re, still contributing to the overall decrease in interaction energy. For the SeO3⋯SeHF complex, the maximum destabilization effect is observed at 1.05re, with a value of 0.636 kcal mol−1. The RMSD values between the ‘valence only’ and ‘valence + (n − 1)d’ calculations are 0.891 kcal mol−1 for Te complexes and 0.428 kcal mol−1 for Se complexes.
Furthermore, the incorporation of (n − 1)sp correlation effects in Te complexes slightly increases the destabilization. The RMSD values between ‘valence + (n − 1)d’ and ‘valence + (n − 1)spd’ are 0.067 kcal mol−1 and 0.191 kcal mol−1 for Te and Se complexes, respectively, indicating that the impact of (n − 1)sp subvalence correlation is an order of magnitude lower compared to the effects observed for (n − 1)d subvalence correlation.
Before we delve into more detail on the effect of (n − 1)d inner shell correlation, we first should explore its basis set convergence, as shown in Table S4 in the ESI.† A similar table for (n − 1)sp is also provided in the ESI.† Te complexes exhibit significantly slower basis set convergence for the (n − 1)d inner shell correlation component compared to Se complexes, as discussed above. While exploring how BSSE behaves for the different components of the (n − 1)d contribution to the total interaction energy (MP2 and post MP2-correction), we again noticed that for all tripleZ–5Z basis sets, CP correction mostly degrades the statistics. However, for CBS extrapolated values (where the lion's share of basis set errors is already taken care of), CP correction does help. Once again, CP-uncorrected data benefits from error cancellation between BSSE and IBSI as their effects are in opposite directions. Furthermore, the (T) component of the (n − 1)d correlation displays the most rapid basis set convergence.
Table 2 presents the (n − 1)d component of the total interaction energies calculated at the localized PNO-LCCSD(T) and canonical DF-CCSD/haWCV{T,Q}Z levels for all 24 systems studied herein. (The corresponding table for (n − 1)sp can be found in the ESI†). Among different components of PNO-LCCSD(T) (or DF-CCSD), PNO-LMP2 (or DF-MP2) contributes the lion's share. The RMSD between valence and valence + subvalence (n − 1)d for PNO-LMP2 is 1.135 kcal mol−1. This discrepancy is not an artifact of the localized scheme, as we also obtained an RMSD of 1.154 kcal mol−1 at the MP2/haWCV{T,Q}Z level. The CCSD-MP2 component displays around one-fourth of the RMSD observed for MP2. Furthermore, the (T) component of the (n − 1)d correlation is extremely small, measuring only 0.039 kcal mol−1. These findings are crucial, as they might prove useful in future work. Keeping the calculations including (n − 1)d correlation down to the MP2 level leads to substantial savings in CPU time and memory/mass storage overhead.
Furthermore, as discussed earlier in this section, (n − 1)d effects are repulsive for both equilibrium and stretched geometries, which is somewhat surprising but could be attributed to the systems explored in this study. As expected, these effects gradually diminish for stretched geometries and effectively reduce to very small values at 2.0re. However, for compressed geometries, (n − 1)d correlation effects are attractive for Te complexes.
Conducting a similar examination on the (n − 1)sp subvalence correlation reveals that in the case of Te-complexes, the (n − 1)sp component of (T) is significantly larger than what was observed for (n − 1)d (0.109 versus 0.040 kcal mol−1), and consistently exhibits a repulsive nature. Therefore, although the (n − 1)sp subvalence component appears to be an order of magnitude smaller than the (n − 1)d contribution in the total PNO-LCCSD(T) interaction energies, the PNO-LMP2 and (T) corrections operate in opposite directions, resulting in error cancellation at the PNO-LCCSD(T) level. Thus, it is imperative to incorporate (n − 1)sp subvalence correction as well, particularly when our calculations are confined to the MP2 level.
3.3 Spin–orbit coupling
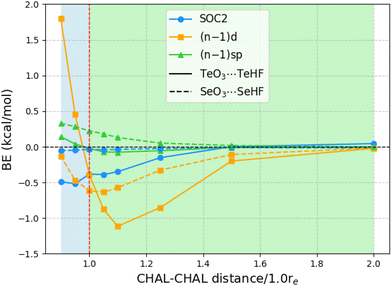
The above observations concerning the importance of subvalence correlation might lead the reader to wonder whether, for such heavy elements as Te, second-order spin–orbit coupling (SOC2) might not be of comparable importance. (As all species considered here are closed-shell singlets, there is no first-order spin–orbit contribution.) We computed SOC2 for each of the 24 chalcogen-bonded dimers using STEOM-CCSD in ORCA, with the aug-cc-pVTZ-DK basis set.Fig. 1 illustrates the SOC2-induced stabilization of the ground state in relation to the binding energies of all 24 systems at the STEOM-CCSD/aug-cc-pVTZ-DK level. The binding energies in this scenario are calculated as the negative of the difference between the energy of the complex and the energy when the monomers are at a distance where SOC2 effects are negligible (at a sufficiently long distance SOC2 effects become negligible). Additionally, the plot depicts the magnitude of inner-shell subvalence (n − 1)d and (n − 1)sp correlation contributions, as discussed in the preceding section, at the PNO-LCCSD(T)(tight, haWCV{Q,5}Z) half-CP level. Here, again, a negative value indicates destabilization effects. For TeO3⋯TeHF complexes, at equilibrium separation, both SOC2 and the inner-shell subvalence (n − 1)d contribute to the destabilization of the dimer, with SOC2 and (n − 1)d having the same magnitude of around −0.4 kcal mol−1.
Upon compression of the dimer, SOC2 continues to contribute approximately −0.5 kcal mol−1, but the inner-shell subvalence (n − 1)d begins to stabilize the TeO3⋯TeHF dimer, resulting in opposing corrective effects. Conversely, upon stretching the TeO3⋯TeHF, SOC2 remains constant up to a distance of 1.10re, but the subvalence (n − 1)d destabilizes by 1.119 kcal mol−1. As the Te–Te distance is further extended, both effects diminish. For instance, at a distance of 1.5re, the SOC2 effects become negligible, although the contribution of (n − 1)d remains slightly significant at −0.2 kcal mol−1.
For the Se complexes, SOC2 effects are much less significant, consistent with the apparent ∝Z4 proportionality of SOC2. (By way of illustration: already in 1998, Runeberg and Pyykkö found that the SOC2 stabilizations of Xe2 and Rn2 are 0.7 and 4.5 meV, respectively—a ratio of 6.4 ≈ (86/54)4. Similarly, Feller et al. found SOC2 stabilizations of 0.4 and 2.0 kcal mol−1, respectively, for Br2 and I2 diatomics, consistent with (53/35)4 ≈ 5.3.) For example, at equilibrium distances, SOC2 destabilizes the dimer by only 0.035 kcal mol−1, whereas incorporating (n − 1)d subvalence electrons has an effect of 0.615 kcal mol−1 towards destabilization. As we extend the Se–Se distances, both SOC2 and subvalence (n − 1)d contributions converge to zero. The effect of subvalence (n − 1)sp remains negligible throughout.
In order to rule out the possibility that the SOC2 we observed above is not a cumulative effect from the two chalcogens in ChO3⋯ChHF, as one reviewer suggested, we also explored a simpler NH3⋯ChHF system. The computed values are reported in ESI.† For NH3⋯TeHF, the SOC2 value is −0.754 kcal mol−1. Upon compression, the SOC2 continues to destabilize; for instance, the value is −1.045 kcal mol−1 for 0.90re. When stretching NH3⋯TeHF, the value remains nearly the same, and as expected, SOC2 diminishes to −0.011 kcal mol−1 for 2.0re.
| NDF2 | CSPI | DEBC | Hobza ratio | %HF | (A) | (B) | |
|---|---|---|---|---|---|---|---|
| BE (kcal mol−1) | BE (kcal mol−1) | ||||||
| TeO3⋯TeHF | |||||||
| 0.90re | −402.048 | −88.398 | 1.000 | 0.38 | 100.51 | 23.221 | 21.145 |
| 0.95re | 34.805 | 8.424 | 0.993 | 0.39 | 96.55 | 30.523 | 29.366 |
| 1.0re | 11.801 | 3.146 | 0.953 | 0.40 | 92.59 | 31.278 | 30.936 |
| 1.05re | 6.238 | 1.837 | 0.878 | 0.42 | 88.74 | 28.525 | 28.784 |
| 1.10re | 4.151 | 1.355 | 0.805 | 0.44 | 85.41 | 24.285 | 24.848 |
| 1.25re | 2.581 | 1.098 | 0.739 | 0.51 | 80.05 | 12.701 | 12.955 |
| 1.50re | 2.210 | 1.037 | 0.720 | 0.64 | 80.86 | 5.137 | 5.279 |
| 2.0re | 4.442 | 1.910 | 0.886 | 0.57 | 93.16 | 1.282 | 1.325 |
| SeO3⋯SeHF | |||||||
| 0.90re | 4.308 | 1.095 | 0.738 | 0.27 | 21.51 | 8.844 | 9.513 |
| 0.95re | 3.323 | 0.946 | 0.687 | 0.30 | 50.90 | 12.075 | 13.018 |
| 1.0re | 2.617 | 0.833 | 0.640 | 0.33 | 57.72 | 12.618 | 13.634 |
| 1.05re | 2.132 | 0.754 | 0.602 | 0.37 | 60.15 | 11.887 | 12.846 |
| 1.10re | 1.798 | 0.698 | 0.572 | 0.40 | 61.32 | 10.670 | 11.356 |
| 1.25re | 1.263 | 0.588 | 0.507 | 0.54 | 63.90 | 7.033 | 7.492 |
| 1.50re | 0.993 | 0.476 | 0.430 | 0.74 | 69.85 | 3.321 | 3.577 |
| 2.0re | 1.026 | 0.462 | 0.420 | 0.72 | 78.85 | 0.727 | 0.776 |
| SO3⋯SHF | |||||||
| 0.90re | 1.647 | 0.437 | 0.401 | 0.29 | −5.56 | 7.897 | 9.328 |
| 0.95re | 1.267 | 0.392 | 0.365 | 0.31 | 20.56 | 9.431 | 10.756 |
| 1.0re | 0.988 | 0.356 | 0.335 | 0.34 | 31.95 | 9.762 | 10.965 |
| 1.05re | 0.791 | 0.329 | 0.312 | 0.37 | 38.80 | 9.456 | 10.528 |
| 1.10re | 0.654 | 0.309 | 0.295 | 0.41 | 43.79 | 8.821 | 9.745 |
| 1.25re | 0.449 | 0.271 | 0.261 | 0.52 | 54.30 | 6.376 | 7.004 |
| 1.50re | 0.401 | 0.254 | 0.247 | 0.66 | 65.34 | 3.149 | 3.349 |
| 2.0re | 0.516 | 0.320 | 0.305 | 0.60 | 75.98 | 0.669 | 0.720 |
For NH3⋯SeHF, the SOC2 effects are an order of magnitude smaller at −0.085 kcal mol−1. This value remains nearly the same when compressing or stretching the dimer; for instance, it is −0.141 kcal mol−1 for 0.90re and −0.068 kcal mol−1 for 1.10re.
Thus, it's clear that the observed SOC2 effects are not simply due to a cumulative effect from the two chalcogens.
SOC2 values computed using the SOC-TD-DFT code in ORCA at the all-electron CAM-B3LYP/aug-cc-pVQZ-DK level are reported in the ESI.†
3.4 Nature of non-covalent chalcogen interactions
Finally, we investigate the nature of non-covalent interactions present in all 24 systems considered in this manuscript. Symmetry-Adapted Perturbation Theory (SAPT, see ref. 87 for a review) provides a systematic framework for breaking down the total interaction energy into distinct components, thus clarifying the nature of intermolecular forces. Following the notation of ref. 69 and 88 at the two least expensive levels of SAPT, namely SAPT0 and SAPT2, the interaction energy can be partitioned as follows: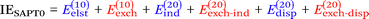 | (1) |
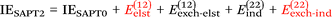 | (2) |
Before delving into our results, let us consider various indices that have been developed to identify the nature of non-covalent interactions. The Hobza dispersion/electrostatic ratio98 uses the information from the above equations: D/E ≥ 1.7 is deemed dispersion-dominant, D/E ≤ 0.59 (i.e., 1/1.7) electrostatic-dominant, and the range in between ‘mixed-influence’.
One of us has proposed alternative indices (see ref. 69) that only entail MP2 calculations and do not necessitate SAPT computations. The first of these approaches is the correlation spin polarization index (CSPI), which serves as an indicator of the nature of non-covalent interactions.
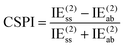 | (3) |
In systems where the interaction energy is primarily governed by dispersion forces, CSPI tends to approach zero. However, in systems where non-dispersion factors contribute to the correlation portion of the interaction energy, CSPI will deviate significantly from zero.
Nevertheless, in the case of nearly dissociated dimers, the absolute values of IEaa and IEab become so small that the CSPI may change sign. To address this issue, the authors have also introduced the DEBC index (dispersion–electrostatic balance in correlation).
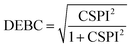 | (4) |
DEBC spans a scale from 0, indicating a system dominated purely by dispersive forces, to 1, indicating a system governed solely by non-dispersive interactions. This should be considered in tandem with %HF (percentage of Hartree–Fock in the interaction energy), which is defined as follows:
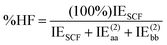 | (5) |
The %HF value tends towards 100% in systems where binding primarily results from pure electrostatic effects such as dipole–dipole interactions.
Returning now to the 24 chalcogen bonded systems investigated in this paper, Table 3 displays the NDF2, CSPI, DEBC, Hobza ratio (dispersion/electrostatic), and %HF for all 24 chalcogen bonded dimers. Additionally, interaction energies computed using PNO-LCCSD(T)/(tight, haWCV{Q,5}Z) half-CP and DF-CCSD/hAWCV{T,Q}Z half-CP are included in the last two columns.
At equilibrium distances, the Hobza ratios for the TeO3⋯TeHF, SeO3⋯SeHF, and SO3⋯SHF complexes are 0.40, 0.33, and 0.34, respectively. These values suggest that the interactions lean towards the electrostatic-dominated end of the spectrum, albeit to a lesser extent than a purely hydrogen-bonded complex like the acetic acid dimer, for which the value is around 0.5, as reported in Table 16 of the ref. 69. %HF also indicates that Te complexes are dominated by electrostatic effects, followed by Se and S, a trend consistent with CSPI and DEBC analyses.
Moreover, in all three complexes, even the stretched geometries (e.g.; 2.0re) persist within the electrostatic realm (more towards the ‘mixed-influence’ region) as indicated by the Hobza ratios of 0.57, 0.72, 0.60, respectively, for the Te, Se and S complexes. The respective %HF values are 93%, 79%, and 76% respectively.
Therefore, although definitive conclusions regarding the nature of NCIs investigated in this study are challenging to draw, it is evident that dispersion effects are minimal across all 24 complexes examined.
4 Conclusions
Our computational investigation into chalcogen bonding interactions has led us to conclude the following:1. The inclusion of inner-shell (n − 1)d subvalence correlation destabilizes chalcogen dimers by nontrivial amounts—a trend opposite to that observed for halogen bonding interactions in ref. 37. (At highly compressed geometries, however, subvalence (n − 1)d correlation begins to stabilize the complex.) Among the various interaction energies components computed at the PNO-LCCSD(T) or DF-CCSD levels, the PNO-LMP2 or DF-MP2 component of the (n − 1)d correlation constitutes the lion's share, which could prove useful in future investigations. Keeping the (n − 1)d correlation treatment down to the MP2 level affords significant savings in CPU time and memory/storage overhead.
2. The effect of the lower (n − 1)sp subvalence correlation is notably less pronounced. The PNO-LMP2 and (T) components exert opposing influences, leading to error cancellation at the PNO-LCCSD(T) level. Therefore, if one is limited to MP2 level calculations, it is essential to also include (n − 1)sp subvalence correlation.
3. The SOC2 effects appear to be less significant than the (n − 1)d correlation; however, they remain non-trivial, particularly for Te complexes. For the Se complexes, SOC2 effects are much less significant, consistent with the approximate ∝Z4 proportionality of SOC2. SOC2 stabilizes the monomer more than the dimer (as the dimer orbitals are separated further and hence the denominator in the interaction is reduced), and as a result destabilizes the dimers. At equilibrium and stretched geometries, SOC2 and (n − 1)d destabilize the complex in tandem; at compressed geometries, however, they work in opposite directions as (n − 1)d becomes stabilizing there.
4. We observe that all three complexes, TeO3⋯TeHF, SeO3⋯SeHF, and SO3⋯SHF, tend towards the electrostatic-dominated end of the spectrum at shorter, but enter a mixed-influence regime at longer, intermonomer separations.
5. Employing complete basis set (CBS) extrapolation along with CP correction appears to be the most effective strategy. Interestingly, {T,Q}Z extrapolation outperforms the 5Z basis set, highlighting its potential superiority in these analyses. Additionally, we observe a slower-than-usual convergence of basis sets for the SCF component.
Data availability
All data supporting the findings of this study are included within the article and its ESI.†Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
Work on this paper was supported by the Israel Science Foundation (grant 1969/20) and by a research grant from the Artificial Intelligence and Smart Materials Research Fund (in memory of Dr Uriel Arnon), Israel. Nisha Mehta would like to acknowledge the Feinberg Graduate School for a Sir Charles Clore Postdoctoral Fellowship as well as Dean of the Faculty and Weizmann Postdoctoral Excellence fellowships. Nisha Mehta acknowledges the School of Chemistry, The University of Melbourne, for the Visiting Academic appointment. Nisha Mehta would like to extend her heartfelt thanks to her friend, Dr Marcos Casanova-Páez, for introducing her to STEOM-CCSD in ORCA.Notes and references
- K. E. Riley, M. Pito
![[n with combining breve]](https://www.rsc.org/images/entities/char_006e_0306.gif) ák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS.
ák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063 CrossRef CAS. - J.
![[R with combining breve]](https://www.rsc.org/images/entities/char_0052_0306.gif) ezáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071 CrossRef.
ezáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071 CrossRef. - K. E. Riley and P. Hobza, Acc. Chem. Res., 2013, 46, 927–936 CrossRef CAS.
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CAS.
- F. T. Burling and B. M. Goldstein, J. Am. Chem. Soc., 1992, 114, 2313–2320 CrossRef CAS.
- J. C. Taylor and G. D. Markham, J. Biol. Chem., 1999, 274, 32909–32914 CrossRef CAS.
- M. Iwaoka, S. Takemoto, M. Okada and S. Tomoda, Chem. Lett., 2001, 132–133 CrossRef CAS.
- M. Iwaoka, S. Takemoto and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 10613–10620 CrossRef CAS PubMed.
- M. Iwaoka, S. Takemoto, M. Okada and S. Tomoda, Bull. Chem. Soc. Jpn., 2002, 75, 1611–1625 CrossRef CAS.
- M. H. Coonan, I. E. Craven, M. R. Hesling, G. L. Ritchie and M. A. Spackman, J. Phys. Chem., 1992, 96, 7301–7307 CrossRef CAS.
- M. Iwaoka and S. Tomoda, J. Am. Chem. Soc., 1996, 118, 8077–8084 CrossRef CAS.
- V. I. Minkin and R. M. Minyaev, Chem. Rev., 2001, 101, 1247–1266 CrossRef CAS PubMed.
- P. Sanz, M. Yáñez and O. Mó, Chem. – Eur. J., 2002, 8, 3999–4007 CrossRef CAS.
- S. Hayashi and W. Nakanishi, Bull. Chem. Soc. Jpn., 2008, 81, 1605–1615 CrossRef CAS.
- G. Sánchez-Sanz, I. Alkorta and J. Elguero, Mol. Phys., 2011, 109, 2543–2552 CrossRef.
- G. Sánchez-Sanz, C. Trujillo, I. Alkorta and J. Elguero, ChemPhysChem, 2012, 13, 496–503 CrossRef.
- M. D. Esrafili and F. Mohammadian-Sabet, Chem. Phys. Lett., 2015, 628, 71–75 CrossRef CAS.
- V. Bondybey and J. English, J. Mol. Spectrosc., 1985, 109, 221–228 CrossRef CAS.
- L. J. Larson, M. Kuno and F.-M. Tao, J. Chem. Phys., 2000, 112, 8830–8838 CrossRef CAS.
- T. Loerting and K. R. Liedl, J. Phys. Chem. A, 2001, 105, 5137–5145 CrossRef CAS.
- Y. Mo and J. Gao, J. Phys. Chem. A, 2001, 105, 6530–6536 CrossRef CAS.
- G. Merino, V. I. Bakhmutov and A. Vela, J. Phys. Chem. A, 2002, 106, 8491–8494 CrossRef CAS.
- M. Pszona, K. Haupa, A. Bil, K. Mierzwicki, Z. Szewczuk and Z. Mielke, J. Mass Spectrom., 2015, 50, 127–135 CrossRef CAS PubMed.
- L. M. Azofra, I. Alkorta and S. Scheiner, Phys. Chem. Chem. Phys., 2014, 16, 18974–18981 RSC.
- L. M. Azofra, I. Alkorta and S. Scheiner, in Noncovalent interactions in dimers and trimers of SO3 and CO, ed. M. F. Ruiz-Lopez and F. J. Olivares del Valle, Springer Berlin Heidelberg, Berlin, Heidelberg, 2016, pp. 159–166 Search PubMed.
- L. M. Azofra, I. Alkorta and S. Scheiner, Theor. Chem. Acc., 2014, 133, 1586 Search PubMed.
- L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221–7230 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2005, 123, 124107 CrossRef PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126 CrossRef CAS.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS.
- N. Mehta, T. Fellowes, J. M. White and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 2783–2806 CrossRef CAS PubMed.
- M. K. Kesharwani, D. Manna, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2018, 122, 2184–2197 CrossRef CAS PubMed.
- P. Schwerdtfeger, L. v Szentpály, K. Vogel, H. Silberbach, H. Stoll and H. Preuss, J. Chem. Phys., 1986, 84, 1606–1612 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- L. Visscher and K. G. Dyall, J. Chem. Phys., 1996, 104, 9040–9046 CrossRef CAS.
- L. Visscher, J. Styszyñski and W. C. Nieuwpoort, J. Chem. Phys., 1996, 105, 1987–1994 CrossRef CAS.
- D. Feller, K. A. Peterson, W. A. de Jong and D. A. Dixon, J. Chem. Phys., 2003, 118, 3510–3522 CrossRef CAS.
- J.-B. Rota, S. Knecht, T. Fleig, D. Ganyushin, T. Saue, F. Neese and H. Bolvin, J. Chem. Phys., 2011, 135, 114106 CrossRef.
- A. Karton, P. R. Taylor and J. M. L. Martin, J. Chem. Phys., 2007, 127, 064104 CrossRef PubMed.
- M. Kurpas, P. E. Faria Jr, M. Gmitra and J. Fabian, Phys. Rev. B, 2019, 100, 125422 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS.
- ORCA – an ab initio, density functional and semiempirical program package, V. 5.0.2, F. Neese, MPI für Chemische Energiekonversion, Mülheim a. d. Ruhr (Germany).
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al. , J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- T. Schwabe, J. Phys. Chem. A, 2013, 117, 2879–2883 CrossRef CAS PubMed.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- Q. Ma and H.-J. Werner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1371 Search PubMed.
- See the MOLPRO online documentation at page https://www.molpro.net/manual/doku.php?id=local_correlation_methods_with_pair_natural_orbitals_pnos.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2019, 15, 1044–1052 CrossRef CAS PubMed.
- J. M. L. Martin, AIP Conf. Proc., 2018, 2040, 020008 CrossRef.
- D. W. Schwenke, J. Chem. Phys., 2005, 122, 014107 CrossRef PubMed.
- B. Brauer, M. K. Kesharwani, S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2016, 18, 20905–20925 RSC.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS.
- D. H. Bross and K. A. Peterson, Theor. Chem. Acc., 2014, 133, 1434 Search PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- D. A. Pantazis and F. Neese, Theor. Chem. Acc., 2012, 131, 1292 Search PubMed.
- C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- L. A. Burns, M. S. Marshall and C. D. Sherrill, J. Chem. Theory Comput., 2014, 10, 49–57 CrossRef CAS.
- B. Brauer, M. K. Kesharwani and J. M. L. Martin, J. Chem. Theory Comput., 2014, 10, 3791–3799 CrossRef CAS PubMed.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272 CAS.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. D. Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. OBrien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2019, 15, 1044–1052 CrossRef CAS PubMed.
- G. Santra, E. Semidalas, N. Mehta, A. Karton and J. M. L. Martin, Phys. Chem. Chem. Phys., 2022, 24, 25555–25570 RSC.
- P. R. Nagy, L. Gyevi-Nagy, B. D. Lörincz and M. Kállay, Mol. Phys., 2023, 121, e2109526 CrossRef.
- H.-J. Werner and A. Hansen, J. Chem. Theory Comput., 2023, 19, 7007–7030 CrossRef CAS.
- A. Halkier, H. Koch, P. Jørgensen, O. Christiansen, I. M. B. Nielsen and T. Helgaker, Theor. Chem. Acc., 1997, 97, 150–157 Search PubMed.
- V. Fishman, E. Semidalas and J. M. L. Martin, J. Phys. Chem. A, 2024 Search PubMed , http://arxiv.org/abs/2405.04658, revised.
- A. Karton, N. Sylvetsky and J. M. L. Martin, J. Comput. Chem., 2017, 38, 2063–2075 CrossRef CAS.
- D. S. Ranasinghe and G. A. Petersson, J. Chem. Phys., 2013, 138, 144104 CrossRef PubMed.
- J. Rezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Spreadsheet containing RMSD at various levels of theory, results of SAPT and other NCI indices; Cartesian coordinates (in.xyz format) of all structures; interaction energies at various levels of theory (in.txt format). See DOI: https://doi.org/10.1039/d4cp01877j |
| ‡ Present address: School of Chemistry, The University of Melbourne, VIC 3010, Australia. |
| This journal is © the Owner Societies 2025 |