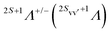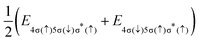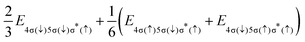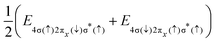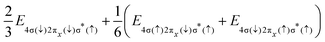Open Access Article
Open Access ArticleAb initio Auger spectrum of the ultrafast dissociating 2p3/2−1σ* resonance in HCl†
Mateja
Hrast
 *ab,
Marko
Ljubotina
*ab,
Marko
Ljubotina
 b and
Matjaž
Žitnik
*ac
b and
Matjaž
Žitnik
*ac
aJožef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia. E-mail: matjaz.zitnik@ijs.si
bInstitute of Science and Technology Austria (ISTA), Am Campus 1, 3400 Klosterneuburg, Austria. E-mail: mateja.hrast@ist.ac.at
cFaculty of Mathematics and Physics, University of Ljubljana, Jadranska 31, 1000 Ljubljana, Slovenia
First published on 10th December 2024
Abstract
We present an ab initio theoretical method to calculate the resonant Auger spectrum in the presence of ultrafast dissociation. The method is demonstrated by deriving the L-VV resonant Auger spectrum mediated by the 2p3/2−1σ* resonance in HCl, where the electronic Auger decay and nuclear dissociation occur on the same time scale. The Auger decay rates are calculated within the one-center approximation and are shown to vary significantly with the inter-nuclear distance. A quantum-mechanical description of dissociation is effectuated by propagating the corresponding Franck–Condon factors. The calculated profiles of Auger spectral lines resemble those of atomic Auger decay but here the characteristic tails extend towards lower electron kinetic energies, which reflect specific features of the potential energy curves. The presented method can describe the resonant Auger spectrum for an arbitrary speed of dissociation and simplifies to known approximations in the limiting cases.
1 Introduction
The concept of ultrafast dissociation (UFD) was first proposed in 1986 by Morin and Nenner in the analysis of their experimental results on the HBr molecule.1 They concluded that the Auger decay of the 3d hole in a molecule, resonantly excited to an anti-bonding state, mostly occurs after the neutral dissociation of HBr has taken place, as the observed electron spectrum was similar to that emitted by the 3d hole in atomic Br. Atomic lines, demonstrating dissociation on a time scale shorter than Auger decay, were later found in the spectra of other molecules, as well, typically upon excitation of an electron from an inner to an antibonding molecular orbital.2–7Despite the abundance of experimental data,8–17 the competition between UFD and Auger decay still lacks theoretical description, which would thoroughly follow the UFD driven changes of electronic decay from the molecular to purely atomic environment. Due to numerous degrees of freedom, the molecular Auger spectra are rather complex with different overlapping features, which makes theoretical modelling of even the simplest molecules challenging. While calculations of the electronic structure of the molecular ground state and valence-excited states are now performed routinely, accurate methods to describe the asymptotically free Auger electron wave in a true molecular potential have only emerged recently.18–21
In a recent work, Kokkonen et al.4 studied UFD in chloromethanes with a 2p vacancy on chlorine. Clear experimental evidence of UFD was found in the lightest species CH3Cl, while no clear UFD signal was observed in the heaviest CCl4, although the initial dynamics within the Franck–Condon region is similar for both.22 A simple Mulliken analysis showed that the charge redistribution triggered by dissociation is faster in heavier chloromethanes and may affect the electronic wavefunctions significantly during the dissociation. However, this analysis alone is insufficient to directly explain the difference between the observed 2p3/2−1σ* resonant Auger (RA) spectra of different chloromethanes. Clearly, Auger rate calculations that account for the variation of the electronic molecular states during dissociation are required to explain the observation.
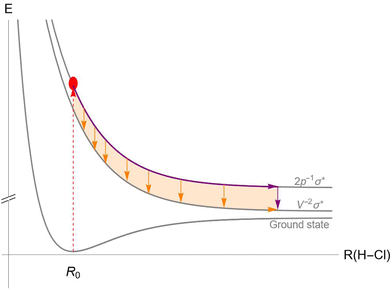
An example of the competition between UFD and Auger decay in the HCl molecule is illustrated in Fig. 1. After exciting an electron from the 2p core orbital of the chlorine atom to the antibonding LUMO σ* (red dashed arrow), the molecule finds itself in an ultrafast dissociating state, represented by the top potential energy curve (PEC). As the system travels along the PEC, Auger decay can occur at any point during the dissociation (orange arrows) or later in the separated atoms (purple arrow), placing the molecule (or in the separated case, the chlorine atom) in the ionized state with two vacancies in the valence shell. Unlike in fluorescence decay, PECs of the initial and final states of the Auger decay are never parallel, so the energy difference between the PECs varies with inter-nuclear distance, and the corresponding Auger spectral line is non-trivially broadened.
This exact process had already been extensively studied experimentally2,6,23–27 but the only attempt that we are aware of to model the mixed molecular-atomic nature of Auger lineshapes is that of Kukk et al.28 (later reproduced by Menzel et al.3). They used a simple exponential interpolation through potential energy points from ref. 29. The Auger line shapes were generated using a Monte-Carlo procedure, assuming a vibrational ground state and relying on a semi-classical description of dissociation along the PEC of the 2p−1σ* state, based on the experimentally known parameters. While they have assigned the Auger kinetic energy at the moment of emission to the difference in the corresponding PECs, they have assumed the Auger decay rate to be independent of the inter-nuclear distance. Their work was later used by Kivimäki et al. to fit the angular-dependent experimental spectra.24 They used a combination of a pseudo-Voigt profile for the atomic peak and a symmetric Gaussian for the molecular tail, which adequately described the measured spectra.
There are other existing approaches to treat the UFD and Auger decay simultaneously, however, they rely on different simplifications, which are not valid for the decay of the Cl 2p hole. For example, Goldsztejn et al.30 treated the 1s photoionization and excitation in HCl. They derived quantum-mechanical expressions for the Auger cross-section within the Franck–Condon region. However, their approach is only applicable for small deviations from the ground state geometry, which is sufficient to describe the K-LL Auger decay, which occurs on about 8 times shorter time scale than the decay of the Cl 2p hole.31 Another approach was suggested and applied to the HF molecule by Pahl et al.,32 where only the nuclear wave-function was propagated in time, while the electronic part was assumed to be independent of the nuclear coordinates. However, the recent work of Kokkonen et al.4 shows that the electronic part must play an important role in the case of the L-VV Auger decay of the 2p vacancy in chloromethanes. Inhester et al.33 combined a model of classically-propagating nuclei with an explicit integration of coupled Schrödinger equations to describe the electron continuum wavefunction at different molecular geometries. Their model was recently used to describe the measured Auger spectra of water.14,17 The most recent theoretical approach by Tenorio et al.34 employed a combination of a restricted-active-space perturbation theory and molecular dynamics simulations to describe the effect of UFD in ozone. Their nuclear dynamics calculation is based on a statistical description of the initial geometry and adiabatic propagation in small time steps. Although the works of Inhester et al. and Tenorio et al. accurately capture the main features of the measured Auger spectra, we show in this work that a quantum-mechanical description of nuclear dynamics is needed to model specifically asymmetric line-shapes produced by UFD.
Several theoretical studies have also been performed to describe the non-resonant Auger decay following 2p photoionization of HCl. The most recent is that by Kivilompolo et al.,9 who performed a non-relativistic ab initio calculation of the Auger electron spectra in several chlorine-containing molecules. They used a Hartree–Fock based method, the one-center approximation (which has been successfully applied to the HCl molecule before35,36) and also included configuration interaction and lifetime vibrational interference. However, their treatment of dissociation of the 2p−1 molecular ion was derived solely from the shape of the PEC near the equilibrium distance, because the dissociation is slower than in the 2p−1σ* case.
This paper presents a relatively simple and robust, ab initio approach for calculating the Auger spectrum of an ultrafast dissociating molecular state that follows the evolution of the molecular state all along the potential energy curve. First, a quantum-chemical calculation of PECs for all molecular states is required. Next, the one-center method37 is employed to project the evolving molecular orbitals onto the atom with a localized core hole, which gives the largest contribution to the Auger decay rate. These projections are then expanded in the atomic orbitals of the atom with the core–hole. Assuming frozen spectator orbitals at different stages of dissociation, the expressions for the Auger decay rates reduce to a sum of atomic-like terms, which are relatively simply evaluated. The quantum-mechanical approach of Gelmukhanov and Ågren38 is adapted to our case to treat nuclear dynamics. Partial amplitudes are derived in terms of Franck–Condon factors using a quasiclassical propagator. To obtain the spectral lines, the contributions are integrated over the energy range of each final state, which generates the characteristic shape for a given Auger transition. Finally, the spectral lines of all final states are summed into the total Auger spectrum. To illustrate the method we present the calculation of the resonant Auger electron spectrum of the 2p → σ* excitation in the HCl molecule.
This paper is organized as follows. In Section 2, we present the method of calculation, including the calculation of the PECs in Section 2.1, the calculation of the Auger decay rates in Section 2.2, while Section 2.3 presents the treatment of nuclear dynamics of the molecule, which undergoes Auger decay at the same time. This gives the total Auger electron spectrum, which is presented and discussed in Section 3, including a comparison with the experimental spectrum. Finally, Section 4 gives the conclusions and suggests possible improvements in the presented method.
2 Method
2.1 Potential energy curves
To account for the Auger decay which can occur throughout the dissociation process the PECs up to large inter-nuclear distances are required for all the states involved in the RA decay. A method to calculate accurate PECs up to large inter-nuclear distances with extensive configuration mixing was presented by Pradhan et al.,29 who reported PECs for the lowest 12 states of the HCl+ ion. To obtain reasonably good PECs for the remaining states we have limited the description of molecular states to linear combinations of single-configuration electronic states with different spin projections. StoBe deMon implementation of the density functional theory (DFT) method based on the Kohn–Sham equations39 was used to calculate molecular orbitals. The PD86 PBE non-local exchange–correlation functional of Perdew and Wang40,41 was used. A flexible augmented correlation consistent polarised valence quadruple zeta basis set AugccPVQZ42 with two additional diffuse s, p, and d functions was used on the chlorine atom, while the ii_iglo43 basis set was used on the hydrogen atom. The energy convergence threshold for the self-consistent field procedure was 10−7 a.u., the grid consisted of 70 and 50 radial points on chlorine and hydrogen atoms, respectively, and 26 angular points per radial shell.The initial state 2p−1σ* of the Auger decay is known to submit to a strong spin–orbit coupling, as well as to the molecular field splitting.36 To account for both effects, we calculated the PECs of the 2px,y,z−1σ* states and applied the method proposed by Gel'mukhanov44 at each point of the PEC. The method treats spin–orbit coupling of the 2p core hole only and the Hamiltonian in the molecular basis is directly diagonalized to simultaneously account for the molecular field splitting. Our results at the equilibrium geometry agree with those of Aksela et al.23 and the expected splitting of the 2p3/2 and 2p1/2 atomic lines is verified in the dissociation limit. This work focuses on the calculation of the Auger spectrum emitted from the lowest 2p3/2−1σ* electronic state of HCl in the presence of a fast neutral dissociation.
The final states of the Auger process v−1v′−1σ*, with the two valence shell vacancies v and v′ in either 4σ, 5σ or 2π molecular orbitals, and a spectator electron in the σ* orbital, are given in Table 1. For some of the states, PECs are reported in ref. 29, while others were calculated from linear combinations of single-configuration states, which satisfy the spin, angular momentum and symmetry requirements of true molecular states. Even though these wavefunctions can be very complicated, the final state energies are straightforwardly expressed in terms of energies for electronic configurations with different distributions of spin projections (see column 4 of Table 1).
Although DFT produces PECs of reasonably accurate shapes, we find that in our implementation the energy differences between the asymptotic states are not entirely reliable. To improve this, we assign each molecular state its dissociation limit using the Wigner–Witmer rules.45 As indicated in the last column of Table 1, the limits correspond to excited states of the Cl+ ion with two 3s and/or 3p vacancies. Our PECs are shifted vertically to match the energy differences of the corresponding atomic states, taken from ref. 46, in the dissociation limit. The resulting PECs are shown in Fig. 2.
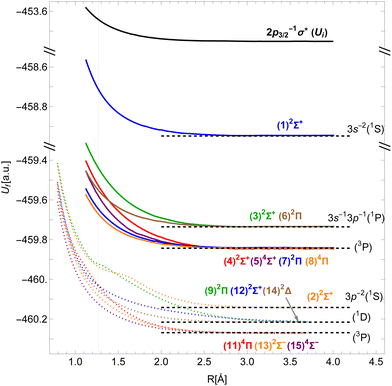 | ||
| Fig. 2 Potential energy curves of the 2p3/2−1σ* state in HCl (black) and of the v−1v′−1σ* states of the HCl+ molecular ion (colors; dotted curves taken from Pradhan et al.29). Horizontal dashed lines denote the energies of the Cl+ ionic states. The vertical line shows the equilibrium inter-nuclear distance of HCl. | ||
The shape of the initial state's PEC governs the dynamics of dissociation, as discussed in Section 2.3. The differences between the initial and final states' PECs at different inter-nuclear distances correspond to the kinetic energies of the Auger electron.
2.2 Auger transition rates
The Auger transition rate from an initial state Ψi with the energy Ei to a final state Ψf of the molecular ion plus a continuum electron ψε with the respective energies Ef and ε in atomic units is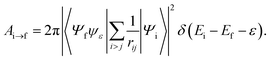 | (1) |
The initial state Ψi is the 2p−1σ* electronic state of HCl with total spin S′ and projection MS′, antisymmetrized with respect to the exchange of any two electrons.
The final state Ψf consists of a pair of vacancies vv′ in the valence shell and an electron in the σ* orbital, coupled to total spin S, its projection MS, and projection Λ of the orbital angular momentum on the molecular axis. The unpaired vv′ electrons are coupled to a spin Svv′ with a projection MSvv′, and the same orbital angular momentum projection Λ. Within the one-center approximation (see below) the free Auger electron with spin projection msε is approximated by the sum of partial waves
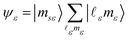 | (2) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ε = 3 were included in our calculations.
ε = 3 were included in our calculations.
The sum in eqn (1) runs over all electron pairs and rij = |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j| denotes the inter-electronic distance. We are interested in the Auger rate (1) averaged over the initial spin S′, spin projection MS′ and the projection m of the orbital angular momentum of the core–hole, as well as summed over the final spin projections MS and msε. Furthermore, we take into account that Auger transitions conserve total spin and its projection, as well as the projection of the total orbital angular momentum. Then the averaged Auger decay rate integrated over the electron emission angle can be written as:
j| denotes the inter-electronic distance. We are interested in the Auger rate (1) averaged over the initial spin S′, spin projection MS′ and the projection m of the orbital angular momentum of the core–hole, as well as summed over the final spin projections MS and msε. Furthermore, we take into account that Auger transitions conserve total spin and its projection, as well as the projection of the total orbital angular momentum. Then the averaged Auger decay rate integrated over the electron emission angle can be written as:
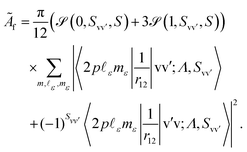 | (3) |
The two matrix elements in eqn (3) are the direct and exchange two-electron integrals of the given pairs of spin–orbitals (often denoted Jvv′ and Kvv′), and the spin factor ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is given by
is given by
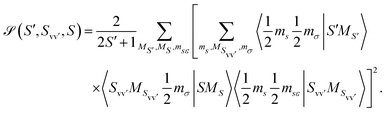 | (4) |
To calculate the two-electron integrals from eqn (3) we employ the one-center method,37 which only retains the terms in the molecular orbital expansion that are centered on the same atom as the core–hole. This has proven successful for a well-localized core–hole, since the largest contributions to the decay rate integral come from the vicinity of the core–hole. Furthermore, in the vicinity of the core–hole the molecular orbitals can be well described by a linear combination of atomic orbitals centered on the atom containing the hole. If the expansion coefficients Cvi (i runs over the atomic orbitals) of the valence orbitals v are known, the work of Chelkowska and Larkins35 gives the necessary data to calculate the sums in eqn (3). As the molecular orbitals evolve during the dissociation, the corresponding coefficients Cvi, also evolve, which we have determined as a function of inter-nuclear distance using the least squares method. The atomic orbitals of Cl were calculated by the Hartree–Fock method using the ATSP atomic structure calculation package.47 The two 2π molecular orbitals were found to directly correspond to the 2px and 2py orbitals of Cl throughout dissociation. The 4σ and 5σ molecular orbitals have contributions of both 3s and 3pz atomic orbitals at the equilibrium distance and change into pure 3s and 3pz respectively in the atomic limit. Consequently, their 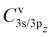 coefficients depend on the inter-nuclear distance, as shown in Fig. 3.
coefficients depend on the inter-nuclear distance, as shown in Fig. 3.
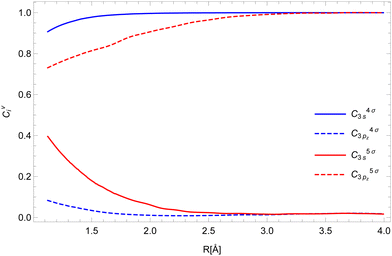 | ||
| Fig. 3 The expansion coefficients Cvi of the valence shell v into atomic orbitals i for the 4σ (blue) and 5σ (red) orbitals. | ||
This expansion allowed for a straightforward application of the  non-resonant rates from Chelkowska and Larkins35 (see eqn (7) therein) in the calculation of the resonant Auger rates. Using atomic orbitals and continuum waves calculated ab initio with the atomic code GRASP2K,48 we have reevaluated the Slater integrals Rk between the four radial parts of the atomic orbitals participating in the Auger decay. We found good agreement with the values from Table II of Chelkowska and Larkins.35
non-resonant rates from Chelkowska and Larkins35 (see eqn (7) therein) in the calculation of the resonant Auger rates. Using atomic orbitals and continuum waves calculated ab initio with the atomic code GRASP2K,48 we have reevaluated the Slater integrals Rk between the four radial parts of the atomic orbitals participating in the Auger decay. We found good agreement with the values from Table II of Chelkowska and Larkins.35
Our results for the Auger decay rates to the v−1v′−1σ* final states as a function of inter-nuclear distance are presented in Fig. 4. As the expansion into atomic orbitals in principle depends on inter-nuclear distance, so does the Auger rate, though each final state is affected differently. Those without 4σ or 5σ vacancies exhibit constant rates in our model (dashed lines). The strongest effect can be seen for the states with two 5σ vacancies and 5σ−12π−1 configurations. States with a 4σ vacancy experience a smaller change of the rate because this vacancy is more localized. For all final states the calculation shows an enhancement in the probability for the Auger transition at a larger inter-nuclear distance. The relative change of the rate from the equilibrium position to the separated atoms limit can be up to 100% which makes previous assumptions about a constant Auger rate questionable.28
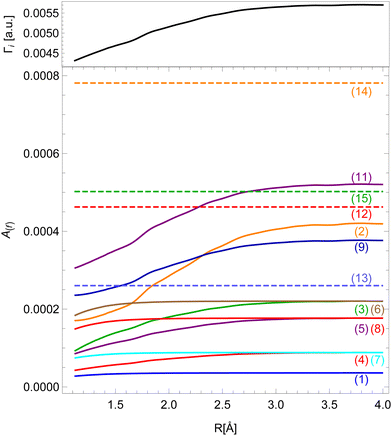 | ||
| Fig. 4 Dependence of Auger decay rates on the inter-nuclear distance for different final states (colors, see Table 1) and the total decay rate Γi (black). | ||
Even though the transition rates calculated by the method described above are averaged over the orbital angular momentum of the core–hole m, we may approximately assign the resulting spectrum to the resonant Auger spectrum of the 2p3/2−1σ* initial state. The sum of the transition rates into all final states gives the total decay rate Γi of the initial state, which is shown on top of Fig. 4.
Finally, we note that while all other final states dissociate into a chlorine ion and a neutral hydrogen in the ground state, the (10)2Π final state dissociates into neutral chlorine and the hydrogen ion, which means the decay must occur via the inter-Coulombic decay (ICD) channel and cannot be described by the one-center method. Therefore this work does not consider the contribution of the (10)2Π state to the Auger spectrum.
2.3 Nuclear dynamics
Within the Born–Oppenheimer approximation, the molecular wavefunction is split into the electronic (ψ) and nuclear part (χ). Treating the resonant Auger decay as a two-step process, photoexcitation by a photon with energy ω and Auger decay by ejecting an electron with energy ε, the scattering amplitude into final state f is given by38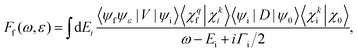 | (5) |
The dipole matrix element Di0 = 〈ψi|D|ψ0〉 in (5) has a constant value for all final states and can be set to 1, when calculating only the spectral shape. The absolute squares of the Coulomb matrix elements |Vfi|2 = |〈ψfψε|V|ψi〉|2 are approximated by Ãf/2π. As the averaged Auger rates are real and non-zero at all inter-nuclear distances we can, up to a sign globally, estimate
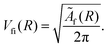 | (6) |
The matrix elements 〈χqf|χki〉 and 〈χki|χ0〉 in eqn (5) are the so-called continuum–continuum (cc) and bound–continuum (bc) Franck–Condon (FC) factors.49 They are evaluated using the ground state of the harmonic oscillator to represent the nuclear wavefunction of the ground state χ0, and for the initial and final states, χki and χqf, the numerical solutions of the Schrödinger equation with the corresponding PEC are employed. The latter are evaluated at the equilibrium energy Ei = Ui(R0) for the initial state, while the final state energy depends also on the kinetic energy of the Auger electron, Ef = Ei − ε. The corresponding wave vectors are then given by 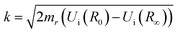 and
and 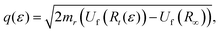 respectively, where Rt is the classical turning point for a molecular state with energy Ef on the final state's potential.
respectively, where Rt is the classical turning point for a molecular state with energy Ef on the final state's potential.
The solutions for χi and χf for a given energy come in pairs, where χA behaves as a sine wave in the R → ∞ limit and χB as a cosine (see Fig. 5). As the dissociation is described by an outgoing rather than a standing wave, the two solutions must be combined to obtain the nuclear wavefunction of the initial state
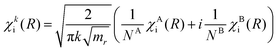 | (7) |
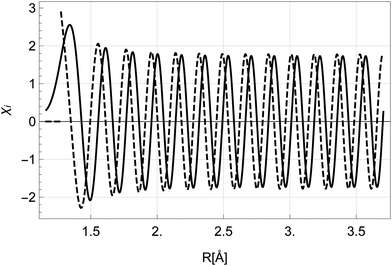 | ||
| Fig. 5 The nuclear wavefunctions χAi (full) and χBi (dashed) with energy Ei = Ui(R0) in the initial state. The function χBi diverges at R < R0 and is set to 0 in the classically forbidden region. | ||
Let us now return to eqn (5). We expand the amplitude to the double integral over R and R′ > R to get
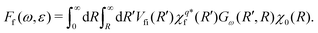 | (8) |
To evaluate the Green's function propagator Gω(R′, R), Gelmukhanov and Ågren38 assume a semi-classical approximation of χki and derive the expression
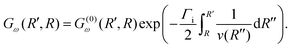 | (9) |
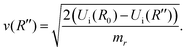 | (10) |
Instead of using the semi-classical approximation as in the work of Gelmukhanov and Ågren,38 we use the numerical eigenfunction χki (see eqn (7)), to estimate the prefactor 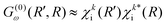 . In addition, we modify the exponential factor in (9) to account for the R-dependence of the decay rate Γi, taking it under the integral over R′′. Finally, the expression for the RA amplitude becomes
. In addition, we modify the exponential factor in (9) to account for the R-dependence of the decay rate Γi, taking it under the integral over R′′. Finally, the expression for the RA amplitude becomes
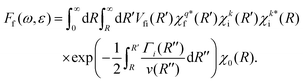 | (11) |
Expression (11) matches the results of Gelmukhanov and Ågren38 for all limiting cases they consider. Note that the Γi, we refer to in our work, signifies the full-width-at-half-maximum (FWHM) of the natural lifetime broadening of the initial state, which is twice larger than the half-width (HWHM) value used by Gelmukhanov and Ågren.38
3 Results and discussion
The expression for the total resonant Auger cross-section is given by the Fermi golden rule as ref. 50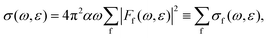 | (12) |
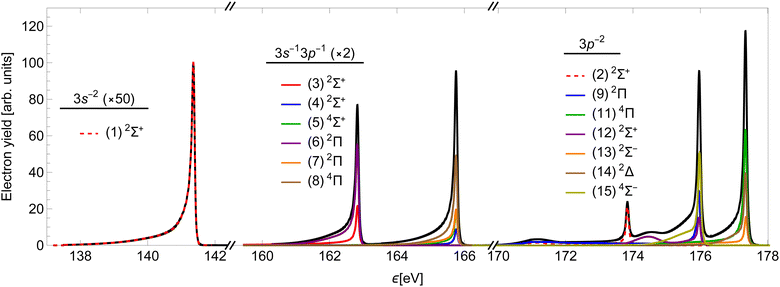
Using the method presented in Section 2, we calculated the partial cross-sections σf and summed them into the total Auger spectrum of the 2p3/2−1σ* state of HCl (see Fig. 6). The spectrum consists of three distinct groups of lines: the one at the lowest ε corresponds to the final states, which dissociate to the 3s−2 states of Cl+, the middle to the 3s−13p−1 states and the highest to the 3p−2 states.
The two high-energy parts of the spectrum can be compared to the experimental result of ref. 51, which measured the corresponding Auger spectrum integrated over the emission angle of the Auger electron (Fig. 7). Our calculation fails to capture the relative intensities of the experimental peaks, mostly due to neglecting the effect of spin–orbit (SO) coupling of final states, which would split the right-most 3P peak into three components. The SO interaction splits the peaks without changing the total yield. We verify that the ratio of the total area for the three states converging to 3P with respect to the total area of the peaks converging to 1D in our calculation is reasonably close to that in the experiment. Despite this, we see that our calculation quite accurately reproduces the asymmetric lineshapes in the high-energy part of the spectrum (a) and even some details in the molecular tails. We note specifically the additional peaks at around 175 eV and 178 eV, which are produced by the smaller slope of the PECs (2), (9) and (12) right above the equilibrium R. The lower of the two is slightly wider than in the experiment, which could be caused by small inaccuracies in the PECs. There is an additional feature at around 180 eV, which is not reproduced in our calculation. It probably stems from the predissociation of the vibrational states in the A2σ+ potential, which is caused by the SO interaction with the dissociative 5σ−12π−14Π final state.29 The low-energy part of the spectrum in panel (b) is over-estimated by our calculation. This indicates a different level of accuracy achieved in the low- and high-energy parts of the spectrum. In the former, the line shapes are also not reproduced well, which is probably a consequence of using less accurate PECs.
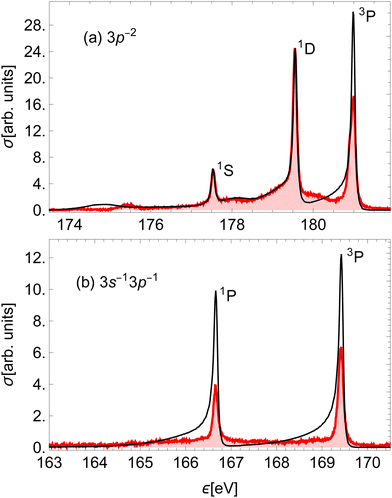 | ||
| Fig. 7 Comparison of the (a) high-energy and (b) low-energy part of the calculated Auger electron spectrum (black) to the experimental result on HCl51 (red). The calculated peaks were moved horizontally to match the corresponding experimental peaks and scaled to the (highest) 1D experimental peak. Each peak is denoted by the Cl+ final state in the dissociation limit. | ||
To illustrate the significance of the varying decay rate, we compare in Fig. 8 the spectral line of the state (2)2Σ+ to the spectral line of the same state calculated with constant partial decay rates, fixed at the value in the atomic limit. At small inter-nuclear distances the total rate Γi, as well as the partial decay rates Ãf, are larger in this case than in reality. This affects the relative intensity of the molecular tail compared to the high-energy atomic peak, in particular overestimating the intensity of the molecular tail.
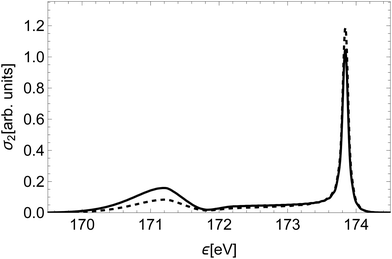 | ||
| Fig. 8 Comparison of the spectral line of the state (2)2Σ+ (dashed) to the spectral line of the same state calculated with constant decay rates, fixed at the value of R∞ (full). | ||
Furthermore, we compare our quantum-mechanical treatment of nuclear dynamics to a classical approach. The latter assumes a classical dissociation dynamics based on the slope of the initial state's PEC, a smearing of the initial position based on the ground vibration state of a harmonic oscillator and a Loretzian broadening by Γi(R) (similar to that of Kukk et al.28). Fig. 9 shows a striking difference between the spectral line for the state (14) obtained with the classical and quantum models. The high-energy peaks have a similar shape and width, while the low-energy part is highly over-estimated by the classical model.
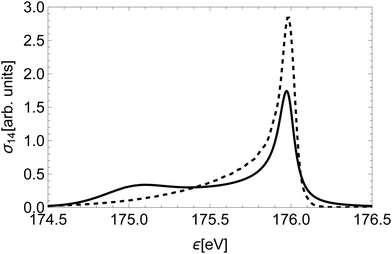 | ||
| Fig. 9 The Auger spectral line of state (14)2Δ calculated in a classical approximation (full) and the quantum-mechanical treatment of Section 2.3 (dashed). | ||
This discrepancy stems from the fact that in the region of the low kinetic energies the nuclear part of the amplitude is significantly suppressed, while in the classical model of decay dynamics the system spends a significant amount of time in this region.
4 Conclusions
We have calculated the resonant Auger electron spectrum of the 2p3/2−1σ* state of HCl, which undergoes ultra-fast dissociation on the same time-scale. Comparison to available experimental results shows very good agreement in the shape of spectral lines, which validates the proposed approximations for calculating such spectra. This is, to our knowledge, the first ab initio method that considers the variation of Auger rates during all stages of molecular dissociation, and proves the importance of this effect in describing the RA spectrum.The quantum-mechanical description of nuclear dynamics was shown to significantly affect the shapes of the spectral lines. Considering the dependence of transition rates on the nuclear distance has further improved the shape of the low-energy tails. The total Auger rate was seen to sensitively depend on the exact values of the radial integrals Rk. On the other hand, the shape of the total spectrum is not that sensitive to these parameters. The shape of the final states' PECs in the molecular region strongly affects the shapes of the molecular tails, while the position of the atomic peak crucially depends on the corresponding dissociation limit.
Our approach works for the 2p−1σ* resonance of the HCl molecule but can also be directly applied to other molecular systems with a localized core–hole, even when the usual approximations, presented in ref. 38, are not applicable. For the results of Section 2.2 to be valid, the shapes of the spectator orbitals should not change significantly during the decay. On the other hand, the change of the participating valence orbitals in the vicinity of the core–hole is reflected in the variation of decay rates with the inter-nuclear distance. In larger molecules the orbital of a weakly bound inner-valence hole may receive more significant contributions from the neighbouring atoms than in HCl, which challenges the validity of the one-center approximation. For very large molecules the approximation of the continuum state by partial waves (see eqn (2)) is no longer valid, since the potential in which the Auger electron moves is largely distorted by other atoms and the core–hole state becomes delocalized.
The main features of the developed theory could also be applied to a participator decay, if final states populated by such decay were dissociative. However, in the presented case of the 2p−1σ* resonance in the HCl molecule the probability for participator decay to both accessible states (X2Π and A2Σ+ from ref. 29) is suppressed, and our calculation of spectator rates quite accurately reproduces the measured spectrum.
To improve the description of the final states, one could consider their L–S coupling, which should particularly improve the shape of the 3P atomic peak, as the dissociation limit in fact splits into three different channels by their total angular momenta J = 0, 1, and 2. Previous studies show that the distribution of intensities among these three peaks doesn't obey the statistical ratio known from atomic physics. To model this theoretically one should therefore consider the dissociation of molecular states as an interference between three possible channels. A method for this had been proposed by Lee, Williams and Freed,52 who applied it to the OH molecule.
To improve the Auger decay rates within the one-center approximation, a more refined calculation could avoid averaging over the 2p orbitals of the initial state and explicitly consider the transition from either the 2p3/2−1σ* state or one of the higher LS-split states. Ultimately, one would like to abandon the one-center approximation and consider a truly molecular Auger electron continuum.
Data availability
Data for this article, including potential energy curves, Auger decay rates and spectral lines, are available at ZENODO at https://doi.org/10.5281/zenodo.13833475.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is based upon work from COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). This work was financially supported by the Slovenian Research Agency in the framework of research program P1-0112 Studies of Atoms, Molecules and Structures by Photons and Particles. Part of this work was financed by the European Research Council (ERC) through the Starting Grant No. 801770 (ANGULON). The authors acknowledge P. Lablanquie, H. Iwayama, F. Penent, K. Soejima and E. Shigemasa for sharing their unpublished experimental spectra on HCl.References
- P. Morin and I. Nenner, Phys. Rev. Lett., 1986, 56, 1913–1916 CrossRef CAS PubMed.
- H. Aksela, S. Aksela, M. Ala-Korpela, O.-P. Sairanen, M. Hotokka, G. Bancroft, K. Tan and J. Tulkki, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6000–6005 CrossRef CAS PubMed.
- A. Menzel, B. Langer, J. Viefhaus, S. Whitfield and U. Becker, Chem. Phys. Lett., 1996, 258, 265–270 CrossRef CAS.
- E. Kokkonen, K. Jänkälä, M. Patanen, W. Cao, M. Hrast, K. Bučar, M. Žitnik and M. Huttula, J. Chem. Phys., 2018, 148, 174301 CrossRef CAS PubMed.
- D. L. Hansen, J. Cotter, G. R. Fisher, K. T. Leung, R. Martin, P. Neill, R. C. C. Perera, M. Simon, Y. Uehara, B. Vanderford, S. B. Whitfield and D. W. Lindle, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2629–2647 CrossRef CAS.
- H. Aksela, S. Aksela, O.-P. Sairanen, A. Kivimäki, G. M. Bancroft and K. H. Tan, Phys. Scr., 1992, 1992, 122 CrossRef.
- E. Pahl, L. Cederbaum, H.-D. Meyer and F. Tarantelli, Phys. Rev. Lett., 1998, 80, 1865–1868 CrossRef CAS.
- A. F. Lago, J. Z. Dávalos, U. Kerdpin and A. S. Schlachter, J. Chem. Phys., 2006, 110, 13717–13723 CrossRef CAS PubMed.
- M. Kivilompolo, A. Kivimäki, H. Aksela, M. Huttula, S. Aksela and R. F. Fink, J. Chem. Phys., 2000, 113, 662–675 CrossRef CAS.
- H. Sann, T. Havermeier, C. Müller, H.-K. Kim, F. Trinter, M. Waitz, J. Voigtsberger, F. Sturm, T. Bauer, R. Wallauer, D. Schneider, M. Weller, C. Goihl, J. Tross, K. Cole, J. Wu, M. S. Schöffler, H. Schmidt-Böcking, T. Jahnke, M. Simon and R. Dörner, Phys. Rev. Lett., 2016, 117, 243002 CrossRef CAS PubMed.
- N. Boudjemia, K. Jänkälä, R. Püttner, T. Marchenko, O. Travnikova, R. Guillemin, L. Journel, I. Ismail, D. Koulentianos, S. Kosugi, Y. Azuma, M. Patanen, M. Huttula, D. Céolin, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2020, 22, 26806–26818 RSC.
- O. Travnikova, T. Marchenko, G. Goldsztejn, K. Jänkälä, N. Sisourat, S. Carniato, R. Guillemin, L. Journel, D. Céolin, R. Püttner, H. Iwayama, E. Shigemasa, M. N. Piancastelli and M. Simon, Phys. Rev. Lett., 2016, 116, 213001 CrossRef PubMed.
- O. Travnikova, E. Kukk, F. Hosseini, S. Granroth, E. Itälä, T. Marchenko, R. Guillemin, I. Ismail, R. Moussaoui, L. Journel, J. Bozek, R. Püttner, P. Krasnov, V. Kimberg, F. Gel'mukhanov, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2022, 24, 5842–5854 RSC.
- T. Marchenko, L. Inhester, G. Goldsztejn, O. Travnikova, L. Journel, R. Guillemin, I. Ismail, D. Koulentianos, D. Céolin, R. Püttner, M. N. Piancastelli and M. Simon, Phys. Rev. A, 2018, 98, 063403 CrossRef CAS.
- T. Jahnke, R. Guillemin, L. Inhester, S.-K. Son, G. Kastirke, M. Ilchen, J. Rist, D. Trabert, N. Melzer, N. Anders, T. Mazza, R. Boll, A. De Fanis, V. Music, T. Weber, M. Weller, S. Eckart, K. Fehre, S. Grundmann, A. Hartung, M. Hofmann, C. Janke, M. Kircher, G. Nalin, A. Pier, J. Siebert, N. Strenger, I. Vela-Perez, T. M. Baumann, P. Grychtol, J. Montano, Y. Ovcharenko, N. Rennhack, D. E. Rivas, R. Wagner, P. Ziolkowski, P. Schmidt, T. Marchenko, O. Travnikova, L. Journel, I. Ismail, E. Kukk, J. Niskanen, F. Trinter, C. Vozzi, M. Devetta, S. Stagira, M. Gisselbrecht, A. L. Jäger, X. Li, Y. Malakar, M. Martins, R. Feifel, L. P. H. Schmidt, A. Czasch, G. Sansone, D. Rolles, A. Rudenko, R. Moshammer, R. Dörner, M. Meyer, T. Pfeifer, M. S. Schöffler, R. Santra, M. Simon and M. N. Piancastelli, Phys. Rev. X, 2021, 11, 041044 CAS.
- H. J. Thompson, O. Plekan, M. Bonanomi, N. Pal, F. Allum, A. D. Brynes, M. Coreno, S. Coriani, M. B. Danailov, P. Decleva, A. Demidovich, M. Devetta, D. Faccialà, R. Feifel, R. Forbes, C. Grazioli, D. M. P. Holland, P. Piseri, K. C. Prince, D. Rolles, M. S. Schuurman, A. Simoncig, R. J. Squibb, B. N. C. Tenorio, C. Vozzi, M. Zangrando, C. Callegari, R. S. Minns and M. D. Fraia, J. Phys. B: At., Mol. Opt. Phys., 2024, 57, 215602 CrossRef CAS.
- I. Ismail, L. Inhester, T. Marchenko, F. Trinter, A. Verma, A. De Fanis, A. Ferté, D. E. Rivas, D. Peng, D. Koulentianos, E. Kukk, F. Penent, G. Doumy, G. Sansone, J. D. Bozek, K. Li, L. Young, M. Ilchen, M. N. Piancastelli, M. Meyer, N. Velasquez, O. Travnikova, R. Boll, R. Guillemin, R. Dörner, R. Taeb, S. Dold, S. Carniato, T. M. Baumann, T. Mazza, Y. Ovcharenko, R. Püttner and M. Simon, Phys. Rev. A, 2024, 110, 013108 CrossRef CAS.
- G. Grell and S. I. Bokarev, J. Chem. Phys., 2020, 152, 074108 CrossRef CAS PubMed.
- W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084124 CrossRef CAS PubMed.
- B. N. C. Tenorio, T. A. Voß, S. I. Bokarev, P. Decleva and S. Coriani, J. Chem. Theory Comput., 2022, 18, 4387–4407 CrossRef CAS PubMed.
- N. K. Jayadev, W. Skomorowski and A. I. Krylov, J. Phys. Chem. Lett., 2023, 14, 8612–8619 CrossRef CAS PubMed.
- R. Bohinc, M. Žitnik, K. Bučar, M. Kavčič, L. Journel, R. Guillemin, T. Marchenko, M. Simon and W. Cao, J. Chem. Phys., 2013, 139, 134302 CrossRef CAS PubMed.
- H. Aksela, E. Kukk, S. Aksela, O. P. Sairanen, A. Kivimaki, E. Nommiste, A. Ausmees, S. J. Osborne and S. Svensson, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 4259 CrossRef CAS.
- A. Kivimäki, E. Kukk, J. Karvonen, J. Mursu, E. Nõmmiste, H. Aksela and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 2724–2730 CrossRef.
- E. Kukk, J. Electron Spectrosc. Relat. Phenom., 2002, 127, 43–51 CrossRef CAS.
- E. Sokell, A. Wills, M. Wiedenhoeft, X. Feng, D. Rolles and N. Berrah, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 1535 CrossRef CAS.
- P. Lablanquie, H. Iwayama, F. Penent, K. Soejima and E. Shigemasa, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 96–100 CrossRef CAS.
- E. Kukk, H. Aksela, O. Sairanen, S. Aksela, A. Kivimäki, E. Nõmmiste, A. Ausmees, A. Kikas, S. J. Osborne and S. Svensson, J. Chem. Phys., 1996, 104, 4475–4480 CrossRef CAS.
- A. D. Pradhan, K. P. Kirby and A. Dalgarno, J. Chem. Phys., 1991, 95, 9009–9023 CrossRef CAS.
- G. Goldsztejn, R. Guillemin, T. Marchenko, O. Travnikova, D. Céolin, L. Journel, M. Simon, M. N. Piancastelli and R. Püttner, Phys. Chem. Chem. Phys., 2022, 24, 6590–6604 RSC.
- M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307 CrossRef CAS.
- E. Pahl, L. S. Cederbaum, H.-D. Meyer and F. Tarantelli, Phys. Rev. Lett., 1998, 80, 1865–1868 CrossRef CAS.
- L. Inhester, C. F. Burmeister, G. Groenhof and H. Grubmüller, J. Chem. Phys., 2012, 136, 144304 CrossRef CAS PubMed.
- B. N. C. Tenorio, K. B. Møller, P. Decleva and S. Coriani, Phys. Chem. Chem. Phys., 2022, 24, 28150–28163 RSC.
- E. Z. Chelkowska and F. P. Larkins, At. Data Nucl. Data Tables, 1991, 49, 121–206 CrossRef CAS.
- R. F. Fink, M. Kivilompolo, H. Aksela and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 1988–2000 CrossRef CAS.
- H. Siegbahn, L. Asplund and P. Kelfve, Chem. Phys. Lett., 1975, 35, 330–335 CrossRef CAS.
- F. Gelmukhanov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 379–393 CrossRef CAS PubMed.
- K. Hermann, L. G. M. Pettersson, M. E. Casida, C. Daul, A. Goursot, A. Koester, E. Proynov, A. St-Amant, D. R. Salahub, V. Carravetta, H. Duarte, C. Friedrich, N. Godbout, M. Gruber, J. Guan, C. Jamorski, M. Leboeuf, M. Leetmaa, M. Nyberg, S. Patchkovskii, L. Pedocchi, F. Sim, L. Triguero and A. Vela, StoBe-deMon version 3.3, 2014 Search PubMed.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. E. Woon, J. Dunning and H. Thom, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- S. Huzinaga, J. Chem. Phys., 1965, 42, 1293–1302 CrossRef.
- F. Gel'mukhanov, H. Ågren, S. Svensson, H. Aksela and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 53, 1379–1387 CrossRef PubMed.
- L. D. Landau and L. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory, Butterworth-Heinemann, 3rd edn, 1981, vol. 3 Search PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database, 2022, https://cccbdb.nist.gov/, [Online; accessed 27. 4. 2023].
- C. Froese-Fischer, Computational Atomic Structure: An MCHF Approach, 1st edn, 1997 Search PubMed.
- P. Jönsson, X. He, C. F. Fischer and I. P. Grant, Comput. Phys. Commun., 2007, 177, 597–622 CrossRef.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, Oxford University Press, 3rd edn, 1996 Search PubMed.
- F. Gel'mukhanov and H. Ågren, Phys. Rep., 1999, 312, 87–330 CrossRef.
- P. Lablanquie, private communication, 2023 Search PubMed.
- S. Lee, C. J. Williams and K. F. Freed, Chem. Phys. Lett., 1986, 130, 271–277 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Derivation of the Auger decay rates. See DOI: https://doi.org/10.1039/d4cp03727h |
| This journal is © the Owner Societies 2025 |