GOCIA: a grand canonical global optimizer for clusters, interfaces, and adsorbates
Zisheng
Zhang
 *abc,
Winston
Gee
*abc,
Winston
Gee
 a,
Robert H.
Lavroff
a,
Robert H.
Lavroff
 a and
Anastassia N.
Alexandrova
a and
Anastassia N.
Alexandrova
 *a
*a
aDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095-1569, USA. E-mail: ana@chem.ucla.edu
bSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, Stanford, California 94305, USA. E-mail: zishengz@stanford.edu
cSUNCAT Center for Interface Science and Catalysis, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
First published on 9th December 2024
Abstract
Restructuring of surfaces and interfaces plays a key role in the activation and/or deactivation of a wide spectrum of heterogeneous catalysts and functional materials. The statistical ensemble representation can provide unique atomistic insights into this fluxional and metastable realm, but constructing the ensemble is very challenging, especially for the systems with off-stoichiometric reconstruction and varying coverage of mixed adsorbates. Here, we report GOCIA, a versatile global optimizer for exploring the chemical space of these systems. It features the grand canonical genetic algorithm (GCGA), which bases the target function on the grand potential and evolves across the compositional space, as well as many useful functionalities, with implementation details explained. GOCIA has been applied to various systems in catalysis, from clusters to surfaces and from thermal to electrocatalysis.
1 Introduction
Understanding the catalyst's surface structure under reaction conditions is crucial for deciphering the reaction mechanism and further design or optimization. In the recent decade, with the development of in situ and operando characterization techniques, many common thermal and electrocatalysts have been found to undergo highly non-trivial restructurings during operation.1 Moreover, the “restructuring” is oftentimes not a single well-defined transformation but a collective phenomena which involves multiple coexisting catalyst states, pathways, time scales, and intricate interplay with adsorbates and environments.2Molecular dynamics (MD) based methods, when combined with enhanced sampling techniques3 and/or machine learning interatomic potentials,4,5 have become a powerful tool to model many dynamical behaviors in catalysis. However, they typically focus on the potential energy landscape of a fixed-composition system and hence are often insufficient for exploring the chemical space of off-stoichiometric restructuring systems with a fluctuating composition and without any well-defined collective variable.
Another approach is to revise the representation of a catalyst as a statistical ensemble of catalyst states instead of a single or a few selected structures.6,7 By extending to a grand canonical (GC) ensemble representation, all reaction-relevant global minimum (GM) and local minimum (LM) catalyst states with varying geometry and composition (including both the surface itself and adsorbate/adatom coverage) can be included in the representation, with their individual contributions to reactivity or spectroscopic signals properly evaluated.8 By probing the response of GC free energetics of the states to external factors (i.e., reaction conditions), the ensemble becomes condition-dependent in nature and can be used to understand and predict structural evolution during operation9 or to better simulate properties or spectra by ensemble averaging.10
Despite the simplicity of the ensemble representation theory, obtaining such an ensemble – including the ab initio thermodynamics of all relevant surface phases – is rather computationally challenging.11 The difficulty lies in exponentially growing chemical space of off-stoichiometric restructuring versus the system size and number of elements. Indeed, constructing a realistic ensemble requires inclusion of all relevant states, which means searching extensively the global and local minima on the potential energy surface (PES), for all relevant stoichiometries. Note that the global optimization minima search at the density functional theory (DFT) level, even for small clusters with a fixed composition, is highly nontrivial.12,13
A recently emerging family of GO techniques is to directly use the grand canonical free energy (Ω, also named grand potential), which is a function of the system's composition at a given set of chemical potentials, as the target function of the minima search. This allows for GC global optimization, in which the stoichiometry is also treated as a set of discrete variables to optimize. In this way, we do not need to extensively sample each possible stoichiometry in a grid-search fashion, but can efficiently sample into relevant stoichiometries on the grand canonical free energy surface (FES) and produce a distribution of stoichiometries in the resultant states. Due to the discrete nature of the compositional degrees of freedom, the fluctuating system size (not on a single PES), and the unavailability of analytical Hessians in plane-wave electronic structure codes, it is not straightforward to adapt many global optimization algorithms that are previously successful for canonical minima search of clusters and crystal structures,14–18 for ab intio GC global optimization of surface systems under periodic boundary conditions (PBC). In recent years, there have been some successful applications of GC treatments to cluster or surface systems, within algorithms such as GC basin hopping (BH),19,20 GC Monte Carlo (MC),21 and the GC genetic algorithm (GA).22,23 However, in the context of PBC surface systems and ab initio minima searches, the available algorithms are usually tailored for a specific set of systems or components, considering either cluster isomerization, surface reconstruction, or adsorbate configurations, but not all of them. A derivative-free and PBC-compatible GC global optimizer that addresses all mentioned aspects of interfacial complexities has been lacking.
This article is aimed to introduce our recent efforts in developing a global optimizer of clusters, interfaces, and adsorbates (GOCIA)24 – a versatile Python package featuring GC global optimization of off-stoichiometric restructuring surface systems at the ab initio level – with a detailed dissection of its components, and to showcase its previous successful applications, applicability, and a roadmap to future developments.
2 Overview of features
GOCIA is built to achieve efficient global optimization of periodic systems and can handle internally many nuances that come under the periodic boundary conditions such as overlapping of boundary atoms and breaking of polyatomic fragments.The main feature of GOCIA is the grand canonical genetic algorithm (GCGA) which can efficiently explore the relevant regions in the chemical space of varying compositions, by using grand canonical free energy as the search target, and it eliminates the need for grid search for every possible composition. Built on the basis of a gradient-embedded GA,12,13 the GCGA can achieve extremely efficient exploration of geometric and compositional space, as compared to MD- or Monte Carlo (MC)-based approaches, and yield a GC ensemble of exclusively minima states.
GOCIA was initially built to handle amorphous layers without directional or well-defined bonding modes, where every atom in the sampling region was allowed to form any type of bond (as individual adatoms). A recent update enabled our implementation of the GCGA to handle the coverage of polyatomic and mixed adsorbates while maintaining their intactness, which is rather relevant to study the reaction intermediate-relevant surface phenomenon and the complex interplay between surface atoms and multiple types of surface species.
The random structure generator of GOCIA, whose primary role is to make the initial population for the GCGA, can also work as a good one-shot sampler for smaller systems such as smaller subnanometer clusters supported on surfaces and adsorbate configurations at low coverage.25
GOCIA also provides a toolkit and a streamlined workflow for grand canonical density functional theory (GCDFT) calculations using the surface charging approach. This is useful for sampling of electrified interfaces, such as those used in electrocatalysis.
Every mentioned component of GOCIA is highly versatile and can be customized to meet a broadness of needs in the areas of catalysis, materials science, surface science, and so on.
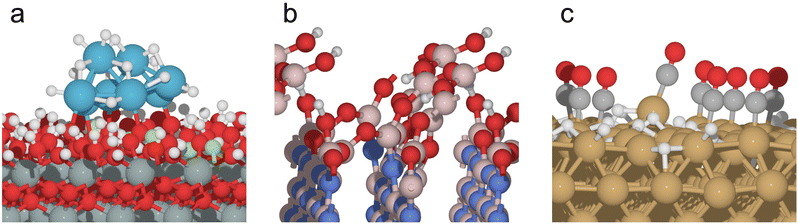
GOCIA has been applied to study the structure, reactivity, and spectroscopy of many surface systems ranging from clusters to amorphous over-layers and to reconstruction of crystalline metal electrodes, in thermal- and electro-catalysis.26 A few representative systems shown in Fig. 1a–c are: fluorine-doped tin oxide (FTO) supported Ptn (n = 1–8) clusters under varying H coverage during the electrochemical hydrogen evolution reaction (HER);10 partial boron oxide/hydroxide over-layer formed on hexagonal boron nitride (hBN) under conditions of oxidative dehydrogenation of propane (ODHP);27,28 restructuring of crystalline Cu facets induced by H and CO coverage under CO2 reduction reaction (CO2RR) conditions.29 Other notable applications include restructuring of Cu under acidic HER conditions,9,30 metal–support contact angle of small nanoparticles (NPs),25 and the structure of amorphous nickel oxide/hydroxide on the Pt surface.31
3 Code architectures
3.1 The interface class
Central to GOCIA is the interface class which is a representation of the system of study.The interface class is based on the atom class (from the ASE module32) with some additional structure-related metadata as is illustrated in Fig. 2. There are two atomistic parts within an interface object, a constrained region and a relaxed region. The constrained region is usually the bottom few layers of the slab and can mimic the behaviour of the bulk. The relaxed region is the part of the surface that can interact with the external environment but cannot change its own composition, usually the top few layers of the slab or supported surface species such as subnanometer clusters or adatoms.
The user would also need to define a rectangular sampling box (by the coordinates of its vertices) which intersects with the top few layers of the relaxed region. Compositional changes are only allowed within the sampling box.
In the case of sampling polyatomic adsorbates, one would also need to supply a list of atomic indices for each adsorbate, so that GOCIA can keep track of the connectivity and make sure that every adsorbate is intact during the local and global optimizations, with a similar practice to ref. 13.
A number of useful functions are built-in under the interface class for easy access, modification, and geometric analysis of each individual component.
3.2 Data structure
During the global optimization, a large number of structures are generated, and each must be fully optimized to a local minimum before it can be added to the ensemble. GOCIA will make a dedicated sub-directory to each structure, so that the local optimization jobs would be performed in separate sub-directories and not the interfere with each other. After a local optimization job finishes, the results will be updated to the project database file in the main directory.The project database file (a SQL database in the ASE format) stores all optimized structures along with their metadata (calculator, energy, magnetic moments, fragment lists, labels, population information, etc.), to allow for easy query and manipulation.
All structures in a global optimization search share the same definition of the constrained region, the relaxed region, and the sampling box. These information are stored in a substrate.vasp file (it can be in any format that supports periodic structures with constraints) which is one of the required input files.
The other variables needed to set up a global optimization run, such as the dictionary of chemical potentials, control parameters of GA, and paths/commands to initiate software, can be provided as a separate input.py file in the main directory or included in the main “manager” script (vide infra).
3.3 Parallel scheme
The overall parallelization efficiency of the global optimization depends on two factors. (i) The scaling performance of the local optimization calculation: for most electronic structure codes, the scaling performance versus the number of nodes is rather poor, and the optimal parallelism setting is usually within 20 nodes per instance.33 (ii) The population updating of the GA: to avoid too drastic a change of the population, it is more beneficial to add new structures to the population one-by-one or in small batches (similar to the population size), instead of in large batches.Depending on the job requirements and queuing policy of the high performance computer (HPC), GOCIA users can choose from two different workflows: (i) if the HPC allows submission of a large number of small jobs from a single user: submit a manager job of long wall time, as a single-core process on the login node or interactive session (the manager sleeps periodically and is not resource intensive at all). The manager job will automatically make and submit many worker jobs, each performing a series of local optimization calculations on a structure to which the worker is assigned. The manager will check the queue constantly and resubmit a new worker job if an old one has finished (Fig. 3a). (ii) If the HPC strongly encourages large jobs by measures such as limiting the wall time of smaller jobs: use the multiprocessing module of Python to maintain a pool of many worker processes. The main script will automatically spawn a new worker process to the idle nodes whenever an old one has finished. This should be submitted as a single large bundled job (Fig. 3b).
3.4 Extensibility
GOCIA currently supports VASP the best, covering all functionalities described in this article. In principle, GOCIA can interface with any code via the ASE Calculator class to perform the core functionalities. It is noted that, although the ASE calculator class interface is easy to use, it comes with some compromise in computational efficiency (charge density and/or wave function IO or re-initialization from the use of a Python wrapper per force call) and some advanced functionalities (GCDFT). A workaround is to define the calculator such that it runs a local optimization internally using the code's own optimizer, and then GOCIA calls it for a single point, which conserves the conveniences of using the ASE calculator class while suffering no bottleneck. Since GC global optimization is a highly computationally intensive task, we plan to ultimately make an individual optimized interface for each popular plane-wave electronic structure and semi-empirical methods.4 Grand canonical genetic algorithm
Before going into the details of the GCGA, we first discuss the challenges in exploring the off-stoichiometric restructuring. In the context of thermal and electro-catalytic surfaces, we assume that the system is always in the electronic ground state for a given set of nuclear positions. Finding the stable and metastable structures of a certain stoichiometry is then equal to locating the global minimum and local minimum of the ground state potential energy surface (PES) defined by a non-convex function, E(r), where r is the atomic coordinate. For a system containing N atoms, there are 3N variables, spanning a vast high-dimensional space. Moreover, there is no analytical expression of E(r) due to its quantum mechanical nature, and all values (energy) and gradients (forces) need to be computed numerically for ab initio methods, which is extremely resource-intensive.Abstraction, such as treating surface adsorption configurations as lattices or graphs, and describing adsorbate coverages in a mean-field manner, could help reduce the dimensionality of the problem. However, these abstraction will only hold when the surface itself is relatively rigid regardless of the adsorbate/adatoms on it. In other words, the coupling between surface species coverage/configuration and the arrangement of surface atoms is negligible. This might be actually the case for some systems, but it is quite dangerous to assume so universally, with the growing collection of reports on non-trivial restructurings of surfaces and clusters.34 For the latter, there exists no shortcut.
The picture further complicates when we allow the composition to vary—the system becomes a collection of many constant-composition potential energy hyper-surfaces, each with different dependence on external factors/conditions. Let us consider a system where the number of X and Y atoms, nX and nY, can vary. In the discrete compositional space, each grid point defined by (nX,nY) entails a full PES.
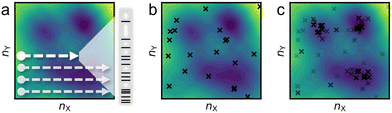
The most straightforward approach to explore this chemical space is the grid search (Fig. 4a)—performing a canonical global optimization on the corresponding constant-composition PES of each (nX,nY). This approach would in theory yields the most uniform sampling distribution over the whole chemical space; however, it is extremely inefficient as the vast majority of the (nX,nY) grids are in the irrelevant regime to the ambient or operating conditions of the catalyst. In addition, the compositional space is infinite, and the initial definition of the grid (i.e., the upper and lower bounds) is arbitrary.
Stochastic sampling into random compositional grids, using techniques such as the bond length distribution algorithm (BLDA),35 can provide a bird's-eye view of the GC free energy landscape at a very low cost (Fig. 4b). For smaller systems, the one-shot stochastic samples may sometime suffice as a (sub-)ensemble.36 However, for larger systems, it is as inefficient as the grid search approach because, again, the majority of the compositional space is catalytically irrelevant.
To steer the search towards the relevant regions in the compositional space, one can adopt the GC free energy Ω, within the GC ensemble (μVT), as the basis of the target function. The composition is then treated as an additional set of variables to optimize. In a typical iterative GC global optimization search, the initial stochastic samples inform the searcher about the “promising” regions, and the search direction is adaptively updated throughout the search to sample denser and denser into the relevant minima regions (Fig. 4c). We illustrate the power of the GCGA with the example of amorphous non-stoichiometric BxOyHz over-layer on borides (Fig. 1b). The GCGA, even if starting from a bad initial guess of compositions, can evolve self-adaptively and progressively toward the final GM region and discover many low-lying regions along the way (Fig. 5a). As a result, the GCGA significantly outperforms BLDA in sampling both GM and low-lying LMs for this complex ternary B–O–H system (Fig. 5b).
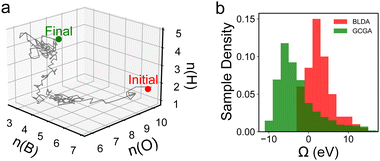 | ||
| Fig. 5 Results from ref. 27 showing (a) the progressive evolution of the population across the B–O–H compositional space and (b) the comparison between the GCGA and BLDA in sampling low Ω structures. | ||
4.1 Calculation of the grand canonical free energy
Now we introduce the calculation of the main thermodynamic metric used in GC global optimization, GC free energy Ω. In the context of off-stoichiometric surface restructuring under a certain reaction condition, we divide the atoms into two groups: group A includes species (blue spheres in Fig. 2) that the system can freely exchange with the reservoir, such as adatoms and adsorbates and group B are atoms in the substrate (relaxed and constrained regions in Fig. 2). The whole system is labeled as AB. The number of atoms in group B is constant, while those in the group A can fluctuate. The GC free energy of a certain AB configuration with respect to the group A species can then be written as: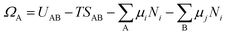 | (1) |
 as the electronic energy of a bare surface slab, EB.
as the electronic energy of a bare surface slab, EB.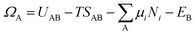 | (2) |
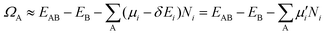 | (3) |
μ is a function of reaction conditions such as temperature, partial pressure, concentration, pH, and electrode potential. For example, the corrected chemical potential of H,  , can be expressed as follows:
, can be expressed as follows:
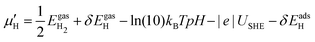 | (4) |
 is the electronic energy of an optimized gas phase H2 molecule. δEgas can be obtained from vibrational analysis of the gas phase H2 molecule and thermochemistry calculations. The pH effect is incorporated using the Nernst equation, and the electrode potential effect is included using the computational hydrogen electrode model. δEadsH can be obtained from vibrational analysis and thermochemistry calculations on one or a set of relevant H adsorption configurations.
is the electronic energy of an optimized gas phase H2 molecule. δEgas can be obtained from vibrational analysis of the gas phase H2 molecule and thermochemistry calculations. The pH effect is incorporated using the Nernst equation, and the electrode potential effect is included using the computational hydrogen electrode model. δEadsH can be obtained from vibrational analysis and thermochemistry calculations on one or a set of relevant H adsorption configurations.
It is noted that the calculation of μ for some elements or species can be less straightforward for a lack of appropriate reference state and/or the limitation of the electronic structure method. The calculated μ can be off by up to a few hundred meV from the realistic condition, and in some cases, one may only be able to estimate a relevant range of μ for a specific species. In these cases, it is advised to perform multiple searches at various μ values in the relevant range, so as to gain a broader distribution of stoichiometry. If there are prior experimental information on the surface composition or adsorbate coverage, one may also vary the μ on a sub-ensemble (from one-shot sampling or an unfinished search) and probe the response of the GM stoichiometry by using the ensemble analysis functions provided by GOCIA (vide infra). This will help narrow down the μ window relevant to the experiment.
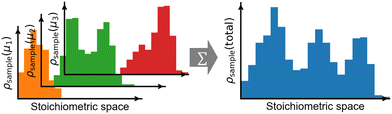
Each GC global optimization run would yield likely a multi-modal distribution of stoichiometries (Fig. 6, left panel). The number of modes and the width of the distribution can be highly system dependent, so it is recommended to always check the stoichiometric distribution in the final ensemble merged from multiple searches—they should ideally join and have a more or less uniform density over the stoichiometric space of interest (Fig. 6, right panel). If there is any discontinuity, then more sampling is deserved at its corresponding μ values. After sufficient sampling, the final merged ensemble can be used for further analysis at any μ within the interpolated range among the sampled μ values.
4.2 Initialization: random structure generation
To build the initial population for the GA search (Fig. 7), one would perform a random structure generation starting from a base surface which reflects the surface structure in a clean and fresh state, usually a major facet or a putative GM configuration, depending on the availability of prior knowledge of the system. It is strongly recommended to randomly perturb the base surface (using the rattle function of the interface class) to impregnate sufficient geometric diversity into the initial population. The optimal magnitude of the perturbation can be system dependent: usually one would use a small magnitude for more rigid and ordered systems and a large magnitude for softer and more amorphous systems.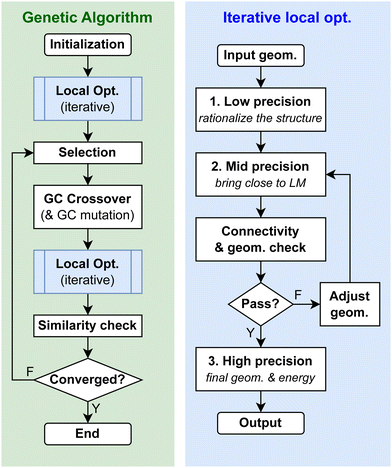 | ||
| Fig. 7 The workflow of the GCGA evolution process and the iterative multi-stage local optimization process implemented in GOCIA. | ||
GOCIA offers three types of structure generation methods to construct the over-layer or place adsorbates on the base surface: (i) growth sampling: it first randomly selects an existing atom from the relaxed region. A random unit vector will be generated to be the direction of the “growth”. The adatom/adsorbate is then aligned to the “growth” direction and placed along it, with the selected surface atom as the starting point. The distance between the adatom/adsorbate and the selected surface atom is then sampled from the bond length distribution algorithm (BLDA),35 based on the covalent bond radii of the two atoms that should form the surface-adsorbate bond. This methods can generate new structures with the most reasonable interatomic distances with high efficiency, but it may fail for some corner cases where the growth direction is ambiguous, such as the interface between a large cluster and the surface, or when the surface is already quite crowded with adsorbates. (ii) Box sampling: it directly makes attempts to place adatoms/adsorbates into the sampling box with random positions and orientations. Since it is less dependent on the surface structure, it works well on cases with irregular shapes and morphology, non-directional and multi-center bonds, and very crowded surfaces. It should be noted that this method can also be used to generate molecular packing structures, such as the micro-solvation slab,37 by applying connectivity constraints and expanding the sampling box. (iii) Graph sampling: this method constructs a connectivity graph of the top surface layer, and then identify the atop, bridge, and hollow sites using the NetworkX module.38 Adsorbates are then added to the identified sites with random rotations. It should be noted that this method expects well-defined lattices and works the best for exploring adsorption on unrestructured surfaces or just to enrich the initial population.
In all three methods, the interatomic distances of attempted geometry are checked to avoid bad contacts. The user may also opt to check the similarity of a new structure with already generated structures to prevent duplicates in the very beginning. GOCIA also offers many user-defined constraints such as bonds that must (or must not) form, upper and lower limits of the coordination number, and whether the added adatom/adsorbate can incorporate into the relaxed region or must stay above. If multiple types of adatoms/adsorbates are to be added, the list can be randomly shuffled before addition to prevent biases from the original ordering. The process iterates until all adatoms/adsorbates have been added to the sampling box while satisfying all geometric and connectivity constraints.
It should be noted that although the GA is not very sensitive to the initial population, the number of sample evaluations before locating the GM or, in other words, the success rate to locate the GM within a certain number of sample evaluations, can depend on the initialization. If some knowledge of the structure is available, starting from a close enough putative structure can save a lot of node-hours. But even without any prior knowledge, the GCGA can still evolve to the ground truth structure if the initial population is diverse enough, although at a higher cost.9
If the user wishes to more extensively sample the LMs, it is recommended to run multiple GCGA searches with different initial populations in terms of geometry and composition. Hereby, the multiple searches would start from different regions in the chemical space and the sample along different paths on its way to the GM.
4.3 Pre-optimization and iterative local optimization
It is essential to locally optimize each sample for a successful global optimization and construction of a physically meaningful final ensemble.12,13,39,40 In GOCIA, every generated sample, either from random initialization or crossover and mutation, is locally optimized to a minimum before it can be accepted.To ensure an aggressive and progressive sampling, which underlies extensive and delocalized exploration of the chemical space, oftentimes one would allow some unphysical connectivity or interatomic distances to form in the random structure generation. For electronic structure calculators, this may cause slow-down (or even failure) of the self-consistent field (SCF) cycle or force convergence to the initial steps in the local optimization.
A remedy to this problem is to perform a pre-optimization at a lower level of theory before the structure is fed to the electronic structure calculator. GOCIA currently supports Hookean and Lennard-Jones potential as the calculator for the preoptimization. Any code for the geometric adjustment can be interfaced to GOCIA as the pre-optimizer via the ASE calculator class.
To reduce the overall computational expense, we adopt a multi-stage local optimization strategy (Fig. 7), where each stage has a different level of precision and convergence criteria, from computationally cheaper to more expensive. In this way, we can rationalize the structure in earlier and cheaper stages and bring the structure closer to its local optimum, before the final stage of higher precision for production. The flowchart illustrates a 3-stage scheme, but the user may reduce or increase the number of stages if needed.
Since electronic structure calculators do not intrinsically constrain connectivity (bonds are determined quantum mechanically), some unwanted motifs or bonds may form during the local optimizations. GOCIA also offers an iterative local optimization scheme which checks the geometry for undesired connectivity after each stage. If any unwanted substructure is detected, GOCIA would modify the structure to meet the constraint and call for another multi-stage local optimization. This again goes iteratively until convergence of the connectivity (Fig. 7, right). Currently, GOCIA supports the following connectivity constraints: (1) make sure where is no desorbed species that is not connected to the slab, (2) remove any atom that is outside the sampling region, (3) force all adsorbates to directly form bonds with the surface, (4) remove fragments that are not intact, (5) prevent bonds between fragments, and (6) remove atoms that are not involved in a specific type of bonds. Each connectivity constrained can be switched on and off or modified easily. Users can also define their own constraints (geometric or compositional) inside the worker script to archive the unwanted structure, terminate the job, or modify the structure and send it back for re-optimization. This iterative local optimization scheme is one of the main features of GOCIA enabling investigation of a complex adsorption system, and it can be easily interfaced with other GC global optimizers.
4.4 Grand canonical crossover, mutation, and selection
The crossover, mutation, and selection process largely follow the original genetic algorithm proposed by ref. 41 and the gradient-embedded genetic algorithm proposed by ref. 12. Here, we only highlight a few notable GC modifications and additions in Fig. 8. | ||
| Fig. 8 Crossover of two parent structures to produce a child structure, with an illustration of possible mutation operations. | ||
In the GC crossover process, the parent structures are split-and-spliced along the same cutting plane. In the case of any bad atomic contact, the one whose center is closer to the cutting plane would be preserved, while the farther one would be removed. As a result, the composition of the child structure can be naturally different from its parents (analogous to chromosomes). In the case of polyatomic adsorbate, the bridle atom (via which the adsorbate is supposed to bind to the substrate) is viewed as the center of the adsorbate.
In the GC mutation process, GOCIA offers the following operators: (i) adding an atom/fragment, (ii) deleting an atom/fragment, (iii) moving a random atom/fragment to a random empty site, (iv) rattling the surface atoms along random vectors drawn from a normal distribution, (v) translating the buffer slab along a x or y axis by a fraction of the cell length, and (vi) permuting a random fraction of the buffer slab. If an offspring is too similar to its parent, its mutation rate is increased to 100% to avoid recalculating the same structure.
In the selection process, an over-mating penalty factor of 1 + (Nmate)−3/4 is multiplied to the grand canonical free energy-based fitness factor. Here, Nmate is the mating counts, and it penalizes the candidates that have mated too many times to diversify the population. Similarity checks against the current population are performed before adding any new candidate to remove duplicates. Adopted mutation operations include: upon the addition of each offspring to the population, the candidate with the lowest fitness is archived to maintain the population size.
We note that the theoretical framework of GC ensemble representation and many of the features of GOCIA presented herein (Sections 4.1–4.6) are universal and not confined to usage with GA. We chose GA to be the weight lifter in our past works due to: (i) its well-benchmarked capability in locating GM for a wide spectrum of systems with little hyper-parameter tuning,42 (ii) its algorithmic simplicity and hence high extensibility and customizability, (iii) GA naturally handles variable-length configurations (analogous to chromosomes) which well suits the GC ensemble sampling tasks, (iv) it avoids the use of Hessians which is very expensive to compute numerically with ab initio methods, and (v) it allows for “unphysical” structural operations (Fig. 8) to take very aggressive leaps across chemical space instead of small local steps bound by finite temperature criteria and inertia. We are open for other more sophisticated alternatives to GA, but, for now, our focus is on improving the GC capabilities, by designing new target functions and mutation operations, within the GA scheme.
4.5 Filtering and sorting the ensemble
It is important to avoid or prevent duplicate structures during the global optimization or final analysis of the ensemble. GOCIA adopts an adapted version of the similarity checker proposed by ref. 42, which considers both energetic and structural aspects. This method assesses geometric similarity by comparing sorted lists of interatomic distances, enabling it to identify symmetrically equivalent duplicates without the need of a predefined number of unique clusters in the data set.After duplicate removal, the unique structures in the ensemble would be sorted by GC free energy and written to a new database which contains all essential metadata from the search. The database file can be used for statistical analysis or computing ensemble-average properties. GOCIA would also report an oversampling ratio which reflects how extensively the chemical space has been sampled. A low oversampling ratio suggests that the sampling is far from extensive, while a high oversampling ratio often means that the search is extensive enough.
The evolution trajectory of a GCGA run, although bearing no physical meaning in a strict sense, contains many useful information. GOCIA offers scripts for tracking the progress of the GCGA by plotting Ω versus the number of samples on-the-fly. It can easily visualize the key new GM's in the search history and if there is a good sign of convergence. It can also inform if there is any sign of significantly restructuring, usually characterized by an apparent dive of the population's Ω to a much lower value and remains there, without the need to inspect each structure in the trajectory.
GOCIA also stores the inheritance information of each candidate in the database. To be specific, the identity of each candidate's parents and the type of mutation (if any) that it went through. GOCIA offers scripts that can track the lineage of any candidate and plot its family tree. This can inform putative pathways via which the restructured GM may arise from pristine structures, and which mutation operations are the most effective for the system of study.
4.6 Ensemble analysis and beyond
The filtered and sorted ensemble of unique minima structures well covers the GM and relevant LMs to a specific condition defined by the chosen μ. By merging multiple ensembles from searches at different sets of μ (followed by filtering and sorting again), a more complete GC ensemble is yielded and can be used to study the system's behaviors at all interpolated μ values among the sampled ones.GOCIA offers a GCE class for ab initio thermodynamic analysis of the GC ensemble database. But before anything, an important thing to check is the distribution of stoichiometries. The GCE class offer functions that can cluster the minima into separate groups of the same stoichiometry. By plotting statistical histograms, one can learn about the density (counts) of samples for each stoichiometry, which informs whether the samples cover a continuous range in the chemical space which is the prerequisite for further analysis with interpolated μ values. By calculating the structural similarity metric (the same as in Section 4.5) with respect to a few reference structures, one can also group the samples by their restructuring patterns and check their sampling density.
Within each group, it is straight forward to extract the low-energy local minima (LELMs) as a relevant sub-ensemble, which can be used for further refinement at a higher level of theory or with additional treatments such as solvation and GCDFT. A recommended energy cutoff relative to the GM of each group is 10 kBT; however, one should always check if the relative energies of the LELMs would reorder at a different level of theory, and there may be a need to use a higher cutoff.
The GCE class offers functions for the easy calculation of Ω and Boltzmann population, p, of any states within the ensemble at a specific μ or a series of μ values (Fig. 9a–c) by:
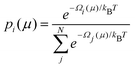 | (5) |
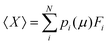 | (6) |
In the cases where the Boltzmann statistics fail, the ensemble can still serve as an ab initio thermodynamics database for kinetics simulations, as it well covers the relevant LELMs. The combination of global optimization and quasi-kinetic MC simulation has been used to study the off-equilibrium structural evolution such as Ostwald ripening of sub-nano clusters36 and surface roughening of Cu electrodes during the CO2 RR.29
5 Grand canonical density functional theory
GOCIA also supports GCDFT calculations using the surface charging approach.43 Specifically, the potential-dependent grand canonical electronic free energy, Ωel(ϕ), of a charged electrode/electrolyte interface at a constant potential (i.e., a constant μe), is approximated by an effective capacitor model with a constant capacitance: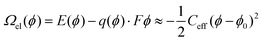 | (7) |
We can then replace the electronic energy terms (EAB and EB in eqn (3)) with the resulted Ωel(ϕ). In this way, we can eventually obtain the potential-dependent total GC free energy, Ωtot, with respect to all adatoms/adsorbates as well as electrons:
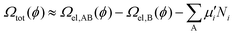 | (8) |
5.1 Slab symmetrization
Symmetrized slabs are recommended for constant-potential calculations. GOCIA can construct a symmetrized slab using mirror and center symmetry operations from an asymmetric slab. This operation only requires a few structural parameters and can be easily applied to a large number of structures within the same ensemble. The user can also make customized operations that combine multiple symmetry operations and atom addition/removal for slabs with unusual stacking or chirality.5.2 Automated surface charging workflow
GOCIA provides a wrapper for easy surface charging calculations. The user only needs to provide a list of numbers of fractional electrons that needs to be added/removed from the system, and GOCIA would calculate the corresponding Nel and make the input files. A separate job sub-directory will be made for each Nel, and it again can be run in a serial or parallel way. After jobs corresponding to all Nel values converge, GOCIA can automatically parse the output files, extract the key results, and then fit and report the Ωel–ϕ relationship. After all GCDFT calculations converge, GOCIA can extract the fitting parameters and write them into the database file for further data query and analysis (similar to Section 4.5).We note that the described treatment relies on many assumptions including (i) a constant interfacial capacitance, (ii) no dramatic potential-dependent geometric changes, (iii) the minima structures are obtained under constant-charge conditions, and the electronic degree of freedom is added a posteriori. A rigorous GCDFT treatment would require all samples to be locally optimized under constant-potential conditions, which is technically doable37,45–48 but computationally too expensive for a very large number of samples in a typical GC global optimization. Our a posteriori approach has been a successful compromise for metallic systems with simple adsorbates such as H and CO.9,10,29 For surfaces with high polarity and larger flexible adsorbates,49 the constant-potential treatment may be necessary during the search, and we are working on making it more affordable.
6 Comments and perspectives
We would like to note that GOCIA is not a black box, but rather an open toolbox with many tunable parts and options. The user should be prepared to make customization according to the nature of the system of study, especially the specifics of each individual component. Otherwise, the sampling could wander off to unwanted FES regions due to a very unreasonable initial distribution, or get stranded for a long time in a local FES region due to insufficient diversity, and waste a lot of computational resources.Future developments of the GOCIA would include: (i) varying the chemical potentials (corresponding to reaction conditions) during the search. The “scan rate” can be adaptive and depend on how extensive the local chemical potential regime has been sampled. This can be useful in identifying the critical conditions where there is a switch in thermodynamic GM. (ii) Symmetry-based operations and substructure representations, which may accelerate the convergence for some systems where the bonding is more directional and coordination patterns, are more well-defined.17 (iii) Motif-based operations, which can keep track of energetically favorable structural motifs during the search and include them in later structure generation steps, similar to ref. 13 but covering periodic and multi-component cases. (iv) Sampling of explicit solvation layers. Some key goals are determining electrolyte hydration structures and building micro-solvation models for surface species in a more adaptive and efficient way. (v) Metrics for the extensiveness of LM exploration. Two promising options are conformational entropy50 and similarity descriptors checked against the search trajectory. They can serve as additional target functions to control exploitation (finding GM) versus exploration (discover new LMs). (vi) Incorporating Hessian-based techniques into GC schemes, such as sparse methods for efficient harmonic vibrational density calculations.19,51,52 They can boost the search efficiency when the calculators support analytical Hessians. (vii) Including the electronic degree of freedom in the GC search for electrochemical systems. This is paramount for surfaces with high polarity and/or flexible adsorbates whose geometry responds dramatically to varying potentials.
Machine learning (ML) models, especially the interatomic potentials, have undergone impressive development over the recent decade.53–56 However, in our opinion, there are still two obstacles in applying them to global optimizations. (i) Overall cost: the computational cost for generating the training data for making a good model that well covers the corner cases would be comparable to, if not larger than, that of a direct global optimization approach. (ii) Force accuracy: unlike the case of MD, global optimizations require very accurate forces (at a magnitude of a few meV Å−1) to ensure that the final ensemble contains only minima states and exclude saddle points or other structures on flat local regions of the PES. (iii) Differentiability and description of non-local effects: we look forward to further advances in ML model architectures that can enable more accurate force predictions and new features to surpass the limitations discussed before. At this time, GOCIA would still serve as an excellent generator of diverse and off-equilibrium training datasets – or it can be incorporated as an on-the-fly component into active learning workflows.
7 Conclusions
Herein, we report GOCIA, an open-source Python package for general-purpose global optimization of various off-stoichiometric restructuring systems. GOCIA has proven versatile, efficient, and successful in a wide range of applications involving adatoms, clusters, crystalline surfaces, amorphous over-layers, and/or adsorbate coverage.This manuscript covers the main features of GOCIA, with detailed descriptions of its code structure and the grand canonical genetic algorithm. The relevant theories are explained, and other key functionalities are introduced.
GOCIA is a highly versatile and extendable code, and it can be potentially customized to study many other systems beyond heterogeneous catalysis, such as plasma chemistry, metallurgy, batteries, environmental chemistry, surface molecular assemblies, and other functional materials. GOCIA is an ongoing effort and is open to comments and contributions from researchers in all aforementioned areas, and we hope to continue the development and implementation of community-needed features in the future.
Author contributions
Zisheng Zhang: conceptualization, investigation, methodology, software, supervision, visualization, writing – original draft, and writing – review and editing; Winston Gee: methodology, software, and writing – review and editing; Robert H. Lavroff: software and writing – review and editing; Anastassia N. Alexandrova: conceptualization, supervision, and writing – review and editing.Data availability
The software described in this manuscript is open-sourced and freely available at https://github.com/zishengz/gocia.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation CBET grant 2103116 and the U.S. Department of Energy, Office of Science, Basic Energy Science Program, grant DE-SC0020125 and DE-SC0019152. ZZ was supported previously by the Edwin W. Pauley Fellowship and Dissertation Year Award at UCLA and currently by the Stanford Energy Fellowship at the Stanford Precourt Institute for Energy. The computational resource used for the development and application of GOCIA includes: Hoffman2 the UCLA-shared cluster; Cori and Perlmutter of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract DE-AC02-05CH11231 and Theta of the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program at the Argonne Leadership Computing Facility, a U.S. Department of Energy Office of Science User Facility operated under Contract DE-AC02-06CH11357.Notes and references
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef.
- R. H. Lavroff, H. W. Morgan, Z. Zhang, P. Poths and A. N. Alexandrova, Chem. Sci., 2022, 13, 8003–8016 RSC.
- G. Piccini, M.-S. Lee, S. F. Yuk, D. Zhang, G. Collinge, L. Kollias, M.-T. Nguyen, V.-A. Glezakou and R. Rousseau, Catal. Sci. Technol., 2022, 12, 12–37 RSC.
- J.-C. Liu, L. Luo, H. Xiao, J. Zhu, Y. He and J. Li, J. Am. Chem. Soc., 2022, 144, 20601–20609 CrossRef PubMed.
- J. S. Lim, J. Vandermause, M. A. Van Spronsen, A. Musaelian, Y. Xie, L. Sun, C. R. OConnor, T. Egle, N. Molinari and J. Florian, et al. , J. Am. Chem. Soc., 2020, 142, 15907–15916 CrossRef PubMed.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef.
- B. Zandkarimi and A. N. Alexandrova, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1420 Search PubMed.
- Z. Zhang, E. Jimenez-Izal, I. Hermans and A. N. Alexandrova, J. Phys. Chem. Lett., 2018, 10, 20–25 CrossRef PubMed.
- Z. Zhang, Z. Wei, P. Sautet and A. N. Alexandrova, J. Am. Chem. Soc., 2022, 144, 19284–19293 CrossRef.
- Z. Zhang, T. Masubuchi, P. Sautet, S. L. Anderson and A. N. Alexandrova, Angew. Chem., 2023, 135, e202218210 CrossRef.
- T. Lee and A. Soon, Nat. Catal., 2024, 7, 4–6 CrossRef.
- A. N. Alexandrova and A. I. Boldyrev, J. Chem. Theory Comput., 2005, 1, 566–580 CrossRef PubMed.
- A. N. Alexandrova, J. Phys. Chem. A, 2010, 114, 12591–12599 CrossRef PubMed.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys.”, 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef.
- A. Banerjee, D. Jasrasaria, S. P. Niblett and D. J. Wales, J. Phys. Chem. A, 2021, 125, 3776–3784 CrossRef PubMed.
- F. Calvo, D. Schebarchov and D. Wales, J. Chem. Theory Comput., 2016, 12, 902–909 CrossRef.
- G. Sun, A. N. Alexandrova and P. Sautet, ACS Catal., 2020, 10, 5309–5317 CrossRef.
- R. B. Wexler, T. Qiu and A. M. Rappe, J. Phys. Chem. C, 2019, 123, 2321–2328 CrossRef.
- G. Sun, A. N. Alexandrova and P. Sautet, J. Chem. Phys., 2019, 151, 194703 CrossRef.
- B. C. Revard, W. W. Tipton, A. Yesypenko and R. G. Hennig, Phys. Rev. B, 2016, 93, 054117 CrossRef.
- Z. Zhang, GOCIA: Global Optimizer for Clusters, Interfaces, and Adsorbates, https://github.com/zishengz/gocia.
- A. Salcedo, D. Zengel, F. Maurer, M. Casapu, J.-D. Grunwaldt, C. Michel and D. Loffreda, Small, 2023, 19, 2300945 CrossRef.
- Z. Zhang, PhD thesis, University of California, Los Angeles, 2024.
- Z. Zhang, I. Hermans and A. N. Alexandrova, J. Am. Chem. Soc., 2023, 145, 17265–17273 CrossRef PubMed.
- M. C. Cendejas, O. A. Paredes Mellone, U. Kurumbail, Z. Zhang, J. H. Jansen, F. Ibrahim, S. Dong, J. Vinson, A. N. Alexandrova and D. Sokaras, et al. , J. Am. Chem. Soc., 2023, 145, 25686–25694 CrossRef.
- Z. Zhang, W. Gee, P. Sautet and A. N. Alexandrova, J. Am. Chem. Soc., 2024, 146, 16119–16127 CrossRef PubMed.
- D. Cheng, Z. Wei, Z. Zhang, P. Broekmann, A. N. Alexandrova and P. Sautet, Angew. Chem., 2023, 135, e202218575 CrossRef.
- C. Wan, Z. Zhang, J. Dong, M. Xu, H. Pu, D. Baumann, Z. Lin, S. Wang, J. Huang and A. H. Shah, et al. , Nat. Mater., 2023, 22, 1022–1029 CrossRef PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- F. Wende, M. Marsman, Z. Zhao and J. Kim, International Workshop on OpenMP, 2017.
- J. Zhang and V.-A. Glezakou, Int. J. Quantum Chem., 2021, 121, e26553 CrossRef.
- H. Zhai and A. N. Alexandrova, J. Chem. Theory Comput., 2016, 12, 6213–6226 CrossRef.
- B. Zandkarimi, P. Poths and A. N. Alexandrova, Angew. Chem., 2021, 133, 12080–12089 CrossRef.
- A. H. Shah, Z. Zhang, Z. Huang, S. Wang, G. Zhong, C. Wan, A. N. Alexandrova, Y. Huang and X. Duan, Nat. Catal., 2022, 5, 923–933 CrossRef.
- A. Hagberg, P. J. Swart and D. A. Schult, Exploring network structure, dynamics, and function using NetworkX, Los alamos national laboratory (lanl), los alamos, nm (united states) technical report, 2008.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef PubMed.
- R. L. Johnston, Dalton Trans., 2003, 4193–4207 RSC.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef PubMed.
- L. B. Vilhelmsen and B. Hammer, J. Chem. Phys., 2014, 141, 044711 CrossRef.
- S. N. Steinmann and P. Sautet, J. Phys. Chem. C, 2016, 120, 5619–5623 CrossRef.
- K. Mathew, V. S. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef.
- Z. Xia and H. Xiao, J. Chem. Theory Comput., 2023, 19, 5168–5175 CrossRef.
- G. Kastlunger, P. Lindgren and A. A. Peterson, J. Phys. Chem. C, 2018, 122, 12771–12781 CrossRef.
- S. Islam, F. Khezeli, S. Ringe and C. Plaisance, J. Chem. Phys., 2023, 159, 234117 CrossRef.
- S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, J. Am. Chem. Soc., 2023, 145, 25352–25356 CrossRef PubMed.
- Z. Zhang, B. Zandkarimi, J. Munarriz, C. E. Dickerson and A. N. Alexandrova, ChemCatChem, 2022, 14, e202200345 CrossRef.
- P. Pracht and S. Grimme, Chem. Sci., 2021, 12, 6551–6568 RSC.
- K. Sutherland-Cash, D. Wales and D. Chakrabarti, Chem. Phys. Lett., 2015, 625, 1–4 CrossRef.
- K. H. Sutherland-Cash, R. G. Mantell and D. J. Wales, Chem. Phys. Lett., 2017, 685, 288–293 CrossRef.
- D. Tang, R. Ketkaew and S. Luber, Chem. – Eur. J., 2024, 30, e202401148 CrossRef PubMed.
- K. Wan, J. He and X. Shi, Adv. Mater., 2024, 36, 2305758 Search PubMed.
- S. Bae, D. Shin, H. Kim, J. W. Han and J. M. Lee, J. Chem. Theory Comput., 2024, 20, 2284–2296 CrossRef PubMed.
- H. Jung, L. Sauerland, S. Stocker, K. Reuter and J. T. Margraf, npj Comput. Mater., 2023, 9, 114 CrossRef.
| This journal is © the Owner Societies 2025 |