Open Access Article
Open Access ArticleUnusual variability of isomers in copper(II) complexes with 1,8-bis(2-hydroxybenzyl)-cyclam†
Milan
Maďar
 a,
Jan
Faltejsek
a,
Jan
Faltejsek
 ab,
Hana
Bušková
bc,
Lucie
Koláčná
ab,
Hana
Bušková
bc,
Lucie
Koláčná
 d,
Adam
Jaroš
d,
Adam
Jaroš
 b,
Jan
Kotek
b,
Jan
Kotek
 a,
Michal
Straka
a,
Michal
Straka
 b,
Vojtěch
Kubíček
b,
Vojtěch
Kubíček
 *a and
Jiří
Ludvík
*a and
Jiří
Ludvík
 d
d
aDepartment of Inorganic Chemistry, Faculty of Science, Charles University, Hlavova 8, 128 40 Prague 2, Czech Republic. E-mail: kubicek@natur.cuni.cz
bCzech Academy of Sciences, Institute of Organic Chemistry and Biochemistry, Flemingovo náměstí 542/2, 160 00 Prague 6, Czech Republic
cDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University, Hlavova 8, 128 40 Prague 2, Czech Republic
dCzech Academy of Sciences, J. Heyrovsky Institute of Physical Chemistry, Dolejškova 2155/3, 182 23 Prague 8, Czech Republic
First published on 2nd January 2025
Abstract
Copper isotopes and their complexes are intensively studied due to their high potential for applications in radiodiagnosis and radiotherapy. Here, we study the CuII complex of 1,8-bis(2-hydroxybenzyl)-cyclam (H2L), which forms an unexpected variety of isomers differing in the mutual orientation of the substituents on the cyclam nitrogen atoms, the protonation of the phenolate pendant, and the ligand denticity. The interconversion of the isomers is rather slow, which made the isolation, identification and investigation of some of the individual species possible. The most stable and the most common form is the hexacoordinated trans-III isomer. However, several other forms were also observed in solution in the course of HPLC, UV-VIS and electrochemical measurements. The isomers present in solution were identified by comparison with the solid-state structures solved by X-ray diffraction analysis on single crystals and with the help of theoretical calculations. The phenolate pendant is coordinated both in the protonated and deprotonated state; however, the coordination in the axial position of the hexacoordinated trans-III complex is weak, especially in its protonated state. Conversely, the CuII ion is pentacoordinated in the cis-V isomer with only one phenolate strongly coordinated in the basal plane of the distorted tetragonal pyramid. The computational data showed that the phenolate groups might form strong intraligand hydrogen bonds competitive with the metal-phenolate bonds, stabilizing the structure of the complex. In addition, theoretical calculations revealed that several geometries are energetically close to the optimal one, which indicates possible dynamic behaviour of the complex in solution.
1. Introduction
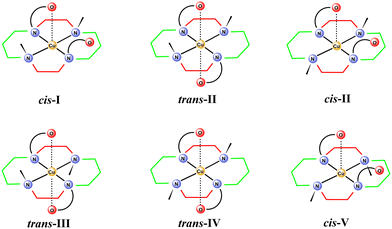
Tetraazamacrocyclic ligands are broadly used as metal ion complexing agents due to the high stability and significant inertness of their complexes. Among them, 1,4,8,11-tetraazacyclotetradecane (cyclam) is the first choice ligand for the complexation of first-row transition metal ions. Cyclam complexes have found applications in various fields, such as medical imaging and therapy, CO2 reduction, hydrogen production, and catalysis. Significant attention has been given to the copper complexes because the copper isotopes show high potential for both diagnostic and therapeutic applications in nuclear medicine. 67Cu is a promising therapeutic isotope, 64Cu has been studied for diagnostic purposes in positron emission tomography (PET) as well as in single-photon emission computed tomography (SPECT), and 61Cu and 62Cu are PET isotopes.1–4 The Cu isotopes cannot be administered to patients in the form of salts due to nonspecific deposition of CuII ions in tissues. Therefore, various ligand systems have been studied as carriers, whose role is delivering the isotope to the target tissue. Cyclam derivatives are among the most studied ligands, as their CuII complexes typically show high thermodynamic stability, high kinetic inertness, and high selectivity over ZnII and NiII ions, which are typical impurities in copper radioisotope solutions.1–4The CuII complexes of cyclam derivatives are specific due to the formation of isomers showing a relatively slow interconversion (up to weeks at room temperature). The isomers differ in the mutual orientation of the substituents on the cyclam nitrogen atoms (Fig. 1)5–7 and, consequently, in colour, stability, redox properties, etc. The isomers are labelled with roman numbers I–V and prefixes that indicate the position of the additional substituents in the coordination sphere: cis- and trans- for hexacoordinated and pc- for pentacoordinated complexes. However, in this paper, we use the prefixes cis- and trans- to describe the mutual position of the two pendant arms with respect to the macrocycle plane, as it makes the discussion easier to follow.
There are some studies reporting details about the formation of several isomers, mostly those undergoing a very slow interconversion.8,9 However, the isomerism is often completely neglected in biomedically aimed studies of CuII complexes with cyclam derivatives. In addition, our recent results indicate the presence of various isomers during the process of complexation,9 which is important for the understanding of the complexation mechanism and for the biomedical properties of the complexes (biodistribution, pharmacokinetics, etc.). The isomerism of CuII complexes with cyclam derivatives is typically studied by UV-VIS spectrometry. There are also works reporting EPR measurements and DFT calculations.10–13 Despite the stability of the isomers, their formation and mutual interconversion is not very understood.
Macrocyclic molecules used in radiomedicine are commonly modified with the coordinating pendant arms attached to the nitrogen atoms. The role of the pendant arms is to increase the thermodynamic stability and kinetic inertness, and to accelerate complex formation. The most common pendant arm used is acetate; however, other pendant arms bearing, e.g., phosphonates, amines, pyridines, alcohols etc., are also used to modify ligand selectivity, complex stability, inertness, hydrophilicity, biodistribution, or pharmacokinetics.
ortho-Methylphenol is a pendant arm that is typically used in ligands designed for the complexation of “hard” metal ions (according to hard–soft acid–base theory), as its deprotonation yields a phenolate anion, which is a “hard” donor. However, phenolate-bearing ligands might also be applicable for the complexation of CuII and other ions with intermediate hardness. Moreover, phenol derivatives bearing additional reactive groups are suitable for subsequent coupling to biomolecules, which serve as vectors for targeted imaging or therapy. The advantage of phenolate derivatives is that the attachment of an additional group to the benzene ring does not introduce a chiral centre, as opposed to the modification of a macrocycle backbone or a methylene group in the acetate pendant arms.
Owing to these advantages, increasing attention has been devoted to cyclam derivatives bearing phenolate pendant arms. The first derivative, 1,8-bis(methylphenol)cyclam (H2L in Fig. 2), and its CuII complex, were reported by Brechbiel in 2001.14 Its CuII complex is hexacoordinated and adopts the trans-III conformation. Later, ligands bearing methylated and t-butylated phenols (compound a in Fig. 2), were studied as the complexing agents for large metal ions (lanthanides, uranyl).15–19 The metals are hexacoordinated and the ligands adopt the cis-I conformation in the reported complexes. Another group of bis(methylphenol)-based ligands bears an additional formyl group in position 3 of the phenol ring (compound b in Fig. 2).20–24 These ligands allow coordination of two metal ions, the first one in the macrocyclic cavity and the second by the formyl group, while the phenolate acts as a bridge between the two metal ions. The reported CoIII complex is hexacoordinated with the cis-V conformation.24 The NiII complex of analogous ligands bearing only one phenol pendant arm (compound c in Fig. 2) is pentacoordinated and the cyclam ring adopts the cis-V conformation.25 In comparison, the ligand bearing two methylquinol groups (compound d in Fig. 2) forms an MnII hexacoordinated complex with trans-III geometry.26
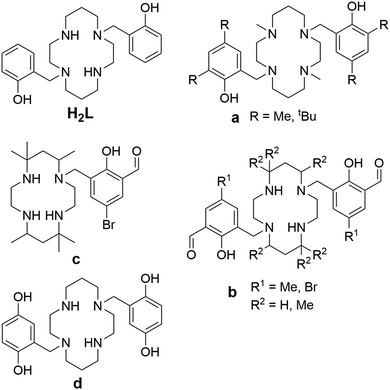 | ||
| Fig. 2 The studied ligand H2L and other previously reported cyclam-based ligands featuring phenolic pendant arms (a–d). | ||
Recently, we have reported an electrochemical study of the CuII complexes with 1,8-disubstituted hexadentate cyclam ligands, including 1,8-bis(methylphenol)cyclam (H2L), and we have observed the presence of several isomers in the solution,27 although only the trans-III isomer was previously reported in the literature.14 Thus, to identify and isolate individual isomers, to describe the conditions and rate of their interconversion and, thus, to better understand the coordination properties of H2L, we investigated CuII complexes in detail. Here, we report a combined electrochemical, spectrometric and chromatographic study of the solution behaviour, accompanied by isolation, solid-state structures and theoretical calculations of the observed isomers, showing the variability of the coordination modes of H2L.
2. Results and discussion
2.1 Syntheses and separation of the complexes
The complexes were synthesized by mixing the ligand and a CuII salt in solution. When the complexation reaction was carried out in a methanol–chloroform (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture, pure trans-III isomer was formed (according to HPLC), which crystallized from the reaction mixture as the structure IIIC (due to the number of analogous structures, they are denoted by the Roman number indicating isomerism of the macrocycle, and the letter in superscript indicates the individual solid-state structure, see Fig. S3–S10†).
1) mixture, pure trans-III isomer was formed (according to HPLC), which crystallized from the reaction mixture as the structure IIIC (due to the number of analogous structures, they are denoted by the Roman number indicating isomerism of the macrocycle, and the letter in superscript indicates the individual solid-state structure, see Fig. S3–S10†).
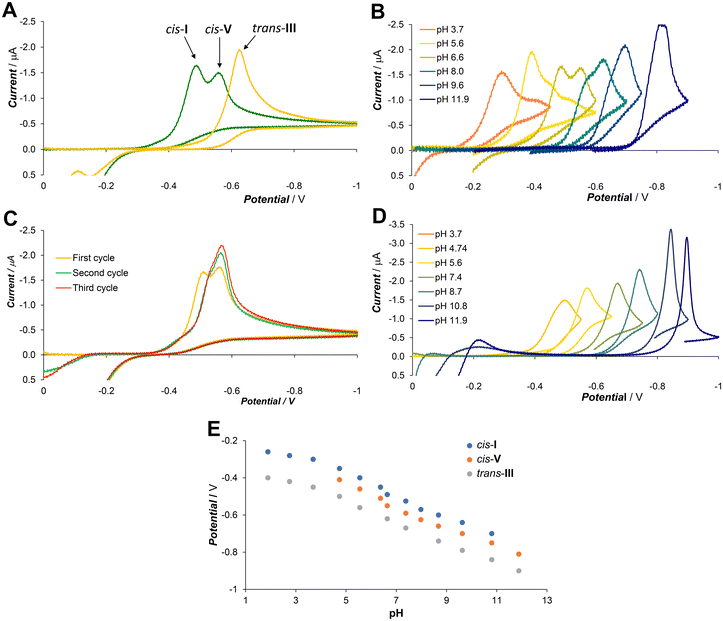
Mixing of the ligand and the CuII salt in aqueous solution, followed by a pH adjustment with alkali–metal hydroxide or ammonia led to significant colour changes – violet in acidic, blue in neutral and green in alkaline solution. The colour change was most likely associated with the deprotonation of the phenol group; however, HPLC analysis showed the presence of multiple species in solution (Fig. 3A). The chromatogram of the complex solution at pH 4 showed one dominant peak at 7.8 min, which we ascribed to the cis-I isomer (see the following discussion and section 2.4). Subsequent alkalization up to pH 4 led to the gradual formation of another species, which was manifested by the appearance of a new peak at 8.3 min, which was identified as the cis-V isomer by comparison with an X-ray analysed standard (see section 2.3). The two species were in thermodynamic equilibrium, with the ratio of the peak areas 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at pH 10, and they were separated by FLASH chromatography.
1 at pH 10, and they were separated by FLASH chromatography.
To get information on the rate of the spontaneous interconversion, the separated cis-I and cis-V isomers were incubated at 25 °C in solutions with pH 4 or 8 and the reaction was monitored by UV-VIS spectroscopy (Fig. S1†). The isomerization half-times were t1/2 ∼ 2 h at pH 4 and 15 min and at pH 8, and the resulting spectra were identical for experiments starting from both pure isomers proving that they reach the same thermodynamic equilibrium.
The compound eluted at 7.8 min could not be unambiguously identified by X-ray diffraction, because the HPLC-purified material could be isolated only in the microcrystalline form. However, it is not the trans-III isomer that was prepared in further experiments (see below) and shows different UV-VIS spectra. Thus, it is one of the remaining possibilities, cis-I, cis-II, trans-II or trans-IV. As this unidentified isomer exists in equilibrium with the cis-V isomer, and one might expect that inversion on the coordinated secondary amino group is much faster than that of the tertiary amine, isomer cis-I or cis-II could be proposed. We suggest that isomer cis-I is more probable as it was reported as the low temperature kinetic product formed by cyclam-1,8-diphosphonate.8 Moreover, despite the fact that two dominant peaks were observed using HPLC, it should be mentioned that other minor peaks were observed and that the peak at 7.8 min shows significant asymmetry, which indicates the presence of some less abundant isomers being in a slow interconversion. Thus, we cannot exclude that the cis-II isomer is also present in the solution.
Crystallization from the solutions containing the mixture of complexes formed at room temperature or separated isomers yielded single-crystals of complexes VA, VB and IIIF (see section 2.3). Isolation of the trans-III isomer is somewhat surprising as it was not observed in HPLC chromatograms of the reaction mixture after complexation and it requires heating to be formed (see below). However, its crystallization could be explained by slow formation even at room temperature during the long-term crystallization experiments combined with preferential crystallization due to the high symmetry and low solubility of the trans-III complex.
Heating the cis-I or cis-V isomers or their mixture at 90 °C led to the formation of the trans-III isomer, which was identified by comparison with an X-ray analysed standard (see section 2.3). This isomer is present as the dominant one in the studied pH range of 4–10 as proved by the HPLC analysis (peak at 7.7 min in Fig. 3B) and cyclic voltammetry (see section 2.2). Despite its HPLC retention time being similar to that of the low-temperature isomers, the spectral and electrochemical data clearly indicate the different structure of this isomer. The formation half-time of the trans-III isomer is t1/2 ∼ 73 min at pH 4 and 12 min at pH 8 at 90 °C (Fig. S2†). This process is significantly slower than the mutual interconversion of the cis-I and cis-V isomers. Crystallization from solution containing the trans-III isomer yielded single-crystals of complexes IIIA, IIIB, IIID and IIIE (see section 2.3).
2.2 Electrochemistry
Cyclic voltammetry at a hanging mercury drop was employed as a “dynamic” method, which can reveal reversibility of the system, stability of the first intermediate, the presence of other possible intermediates and/or different products and their retrograde redox reactions. The mercury drop method was selected because it provided significantly better sensitivity and reproducibility than measurement with glassy carbon or platinum electrodes.The general CV and DC-polarography study of the Cu–L system was reported recently together with other ligands.27 Free ligand H2L is not redox active in the studied potential range. The initial complexation experiments were performed at pH 6.6 employing excess ligand to assure full complexation. The CuII ions are reduced in a single two electron step (Fig. 4A) consisting of one-electron reduction followed by CuI complex dissociation and reduction of the free CuI ion.
The copper amalgam formed was reoxidised at weakly negative potentials (0 to −0.2 V) and the CuII ion was immediately recomplexed by the excess ligand (all potentials are reported vs. SCE). The reduction of the complexes was significantly shifted to a more negative potential compared to the free CuII aqua ion due to the stabilization by the strong ligand binding. The solution prepared by mixing the ligand and the CuII ions at room temperature showed at pH 6.6 two dominant peaks at −0.49 V and −0.56 V, indicating the equilibrium of two major isomers. The intensity of both peaks changed with the pH (Fig. 4B), and they correspond well to HPLC data. The less negative peak (assigned to the cis-I isomer, see discussion above) dominated at low pH, both peaks were almost equal at neutral pH, and the more negative one (the cis-V isomer) dominated at high pH. However, in the second and ongoing scans, the peak at the more negative potential dominated (Fig. 4C). This could be explained by the fact that the reoxidized copper was complexed by the excess ligand leading firstly to the cis-V isomer, which is the first kinetic product that, consequently, isomerized partially to the cis-I isomer.
Overnight heating at 90 °C led quantitatively to the trans-III isomer, which was reduced at a more negative potential (−0.63 V at pH 6.6) than the cis-I and cis-V isomers. The single peak of trans-III was observed throughout the whole studied pH range (Fig. 4D). The reduction potential of all observed isomers changes with pH, while their relative difference does not change (Fig. 4E).
2.3 Solid-state structures of the ligand and complexes
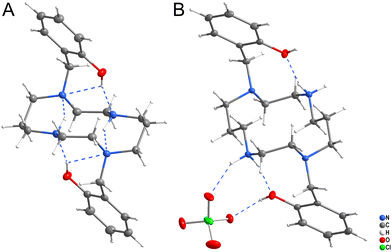
Two crystal structures of ligand H2L were determined (Fig. 5). Crystallization from neutral solution led to the material of composition H2L, in which both protons were localized on the phenol groups. The structure is stabilized by strong intramolecular hydrogen bonds (Fig. 5A and Table S1†), as the phenol groups form hydrogen bonds to the nitrogen atoms N1 and N4 and additional hydrogen bonds were formed between the secondary and tertiary amino groups.Crystallization of the solution acidified with HClO4 to pH ∼ 2 yielded the material of composition (H4L)(ClO4)2. The ligand is tetraprotonated, with two protons bound to the phenol oxygen atoms and two to the secondary amino groups. The phenol and secondary amino groups are connected by intramolecular hydrogen bonds and they both form additional hydrogen bonds to the perchlorate anion (Fig. 5B and Table S2†).
Eight X-ray structures of [Cu(L)] complexes differing in the ring isomerism, in protonation and/or in solvate molecules, were determined. Coordination bond lengths and angles, parameters of the crystal structures and parameters of hydrogen bonds are listed in Tables S3–S13.†
Complexes IIIA and IIIB (Fig. S3 and S4†) of composition trans-[Cu(L)]·2MeOH and trans-[Cu(L)]·2H2O, respectively, contain one independent complex molecule of similar geometry (Fig. 6A). The macrocycle adopts the trans-III conformation and the CuII ion is hexacoordinated in a tetragonally-bipyramidal coordination sphere. The axial coordination is weak, as the deprotonated phenolate anions are very distant (IIIA: dCu–O = 2.369 Å; IIIB: dCu–O = 2.462 Å). The solvate molecules (methanol in complex IIIA and water in complex IIIB) are bound through hydrogen bonds to the phenolate oxygen atoms and secondary cyclam amino groups.
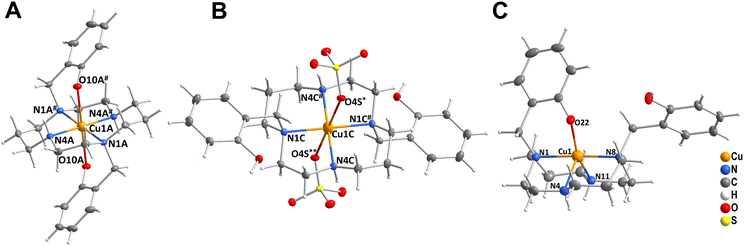 | ||
| Fig. 6 The geometry of the trans-III-[Cu(L)] unit in compound IIIA (A), trans-[Cu(H2L)](SO4)2 unit in compound IIIF (B), and [Cu(HL)]+ unit in compound VB (C). | ||
Complexes IIIC, IIID and IIIE of composition trans-[Cu(H2L)]Cl2, trans-[Cu(HL)]Cl·H2O and trans-[Cu(H2L)](CF3COO)2, respectively (Fig. S5–S7†) show similar coordination motifs with the trans-III macrocycle conformation (Fig. 6A) and a tetragonally-bipyramidal coordination sphere. However, the ligand is mono- or di-protonated on the phenol groups and, thus, its interaction is even weaker when compared to the previous compounds. The axial distances are longer than those in complexes IIIA and IIIB (IIIC: dCu–O = 2.526 Å; IIID: 2.491 Å; IIIE: 2.521 Å). The complex positive charge is compensated by either chloride or highly disordered trifluoroacetate anions. The geometry of the diprotonated complex is similar to that reported previously for the diacetate of the diprotonated complex [Cu(H2L)](OAc)2·2H2O, which has an even longer Cu–O distance (dCu–O = 2.652).14
Crystals IIIF of composition trans-[Cu(H2L)][Cu(H2L)(SO4)2]·6MeOH·2H2O contain two independent complex molecules, both featuring a hexacoordinated metal ion with the coordination sphere of a tetragonal bipyramid, the trans-III macrocycle conformation and all phenol groups protonated. The coordination motif of the first complex molecule is almost identical to that found in complexes IIIC and IIIE (Fig. 6A) – both protonated phenol pendant arms are weakly coordinated in the axial position (dCu–O = 2.524 Å). In contrast, the ligand in the second complex molecule is coordinated only through the nitrogen atoms. Phenol groups are not coordinated and axial positions are occupied by sulphate anions (Fig. 6B). The sulphate anions interconnect the two complex molecules forming hydrogen bonds to the coordinated phenol hydroxyl groups (Fig. S8†). Additional hydrogen bonds are formed between methanol molecules of crystallization and secondary macrocycle amino groups.
Complex molecules found in the crystal structures of compounds VA and VB of composition cis-[Cu(HL)]2SO4·6MeOH and cis-[Cu(HL)](CF3CO2), respectively (Fig. S9 and S10†), have very similar geometries (Fig. 6C). The CuII ion is pentacoordinated by four cyclam nitrogen atoms and one deprotonated phenolate oxygen atom. The macrocycle adopts conformation cis-V. The coordination spheres of complexes VA and VB are close to a tetragonal pyramid with the apical position occupied by the secondary amino group (N4). In both structures, all coordination bond lengths are in the range 1.9–2.2 Å. The non-coordinated phenol group is protonated. Positive charges of the complexes are compensated by the sulphate and trifluoroacetate ions, respectively. Complex VA crystallized as a solvate with methanol. All methanol molecules, and sulphate and trifluoroacetate anions were found to be disordered.
2.4. Theoretical calculations
Theoretical calculations were performed to support and rationalize the experimental observations, in particular to reveal which isomers are present in solution as well as to understand the isomerism of the studied complexes and the coordination properties of the phenolate pendant arm in solution. For clarity and readability of the following section, we limit the information on various computational details to a minimum. All details on the computational protocols and levels of theory are collected in the Methods section.| Isomer | Relative energy [kcal mol−1] | ||
|---|---|---|---|
| [Cu(H2L)]2+ | [Cu(HL)]+ | [Cu(L)] | |
| a ΔG values were calculated using the COSMO-RS protocol, see Methods, and are given relative to the trans-III isomer for each of the protonated states separately (each column). | |||
| cis-I | 4.55 | 6.19 | 12.04 |
| cis-II | 11.33 | 8.36 | 10.24 |
| trans-II | 6.25 | 5.89 | 4.71 |
| trans-III | 0.00 | 0.00 | 0.00 |
| trans-IV | 11.82 | 10.91 | 12.26 |
| cis-V | 5.18 | 7.48 | 18.68 |
The calculated relative ΔG energies (Table 1) show that the trans-III isomer is the most stable one in all protonation states, followed by cis-I, cis-V, and trans-II, which are by ∼3–19 kcal mol−1 less stable, depending on the protonation state. The small energy differences indicate that these isomers may also be present in solution.
The calculated structures are shown in Fig. 7, S14, and S15.† Two interesting features should be mentioned here. First, the pendant arms may form intramolecular hydrogen bonds, as seen, e.g. in Fig. 7 for the monoprotonated cis-I, cis-II, and cis-V isomers. Second, possible intra-ligand hydrogen bonds between the phenolate oxygen and NH group may be formed as well. This is discussed in more detail in section 2.4.3.
 | ||
| Fig. 7 Calculated optimized structures of the monoprotonated isomers in a model with two explicit water molecules. For relative ΔG energies, see Table 1. | ||
However, the comparison of other calculated results (Table S18†) with the experimental data (Fig. 4) is not straightforward. The experimental potentials gradually change with pH and cannot be simply separated into contributions of the differently protonated species, because the more protonated (i.e. more positively charged) species are typically reduced preferentially.
The experimental potentials of individual isomers follow the same order along the whole studied pH range and their mutual differences are more or less constant. Thus, the reduction potentials relative to the most stable trans-III isomer were compared with the theoretically predicted relative values, as shown in Table 2.
| Isomer | Calculated ΔEa [V] | Experimental ΔEa [V] | ||
|---|---|---|---|---|
| [Cu(H2L)]2+ | [Cu(HL)]+ | [CuL] | [Cu(HnL)]n+ | |
| a All values are relative to those of the trans-III isomer. | ||||
| cis-I | 0.12 | −0.09 | 0.05 | 0.14–0.15 |
| cis-II | 0.10 | 0.27 | 0.22 | — |
| trans-II | 0.10 | 0.18 | 0.24 | — |
| trans-III | 0.00 | 0.00 | 0.00 | 0 |
| trans-IV | 0.21 | 0.33 | 0.31 | — |
| cis-V | 0.03 | −0.05 | 0.13 | 0.08–0.09 |
For the diprotonated and deprotonated forms, the results obtained for the two isomers identified by X-ray diffraction are in agreement with the experimental data – the trans-III potential is the most negative while cis-V is slightly less negative. However, unambiguous assignment of the third major isomer observed in the cyclic voltammograms is difficult. From the set of possible isomers, we can exclude the trans-IV isomer, which has the highest redox potential. However, the calculated potentials of the remaining isomers are close to each other and the potential order is quite sensitive towards the protonation state of the isomers.
For the monoprotonated form, the theoretically predicted values change and the cis-I and cis-V potentials are slightly more negative than that of trans-III. This shows a high sensitivity of the calculated potentials towards protonation of the complex and the presence of intramolecular hydrogen bonds (see below). This is also closely related to the fact that the calculated potentials change with the solvent model used, i.e. with the explicit water molecules included (Table S18†).
Although the third isomer cannot be unambiguously identified, we expect that this is the cis-I isomer, because the cis-I isomer is the second (after trans-III) most common one reported for analogous CuII complexes with cyclam derivatives. In addition, the cis-I isomer was previously identified by X-ray diffraction analysis in the system with cyclam-1,8-diphosphonate and it shows similar electrochemical behavior.8,27
| Isomer | Cu–O coordination bond | NH–O hydrogen bond | OH–O hydrogen bond | |||||
|---|---|---|---|---|---|---|---|---|
| Pendant 1 | Pendant 2 | |||||||
| DICu–O | d Cu–O | DICu–O | d Cu–O | DINH–O | d N–O | DIO–H/H–O | d O–O | |
| a Identical hydrogen bonds were found for both phenolate-secondary amine pairs in this isomer. In all other isomers, regardless of protonation, the strength of the hydrogen bond in the second phenolate-secondary amine pair is negligible. | ||||||||
| cis-I [CuL] | 0.09 | 3.3 | 0.33 | 2.1 | 0.23 | 2.7 | — | — |
| cis-I [Cu(HL)]+ | 0.27 | 2.3 | 0.15 | 3.0 | 0.01 | 3.2 | 0.32/0.21 | 2.6 |
| cis-I [Cu(H2L)]2+ | 0.08 | 3.3 | 0.33 | 2.4 | 0.20 | 3.0 | 0.34/0.19 | 2.7 |
| trans-III [CuL] | 0.05 | 3.4 | 0.32 | 2.3 | 0.26 | 2.6 | — | — |
| trans-III [Cu(HL)]+ | 0.01 | 5.0 | 0.32 | 2.3 | 0.01 | 4.2 | — | — |
| trans-III [Cu(H2L)]2+ | 0.25 | 2.6 | 0.25 | 2.6 | 0.19a | 3.0 | — | — |
| cis-V [CuL] | 0.37 | 2.0 | 0.25 | 2.6 | — | — | — | — |
| cis-V [Cu(HL)]+ | 0.41 | 2.1 | 0.01 | 4.1 | — | — | 0.30/0.20 | 2.6 |
| cis-V [Cu(H2L)]2+ | 0.37 | 2.2 | 0.01 | 4.2 | — | — | 0.34/0.22 | 2.6 |
The cis and trans isomers prefer different coordination geometries around the metal. Nitrogen atoms in the trans isomers are mostly arranged in a square planar fashion around the CuII ion, which is located in the centre of the plane that they form. Oxygen atoms are then coordinated only weakly with long Cu–O distances (2.4–2.6 Å), both in the protonated and the deprotonated forms. The calculated individual structures are shown in Fig. 8. In the calculated structure of the fully deprotonated trans-III isomer, one pendant phenolate coordinates (DICu–O = 0.32) to the central CuII ion while the other forms a stable hydrogen bond to the secondary amine of the macrocyclic ring. In the mono-protonated trans-III isomer, the protonated phenolate is semi-coordinated, whereas the deprotonated one coordinates similarly as in the deprotonated form (DICu–O = 0.32). Complete protonation of the trans-III isomer leads to the formation of a fully symmetric structure. Both protonated phenolate pendants are coordinated and their DICu–O = 0.25 is somewhat lower than that found for coordination of the deprotonated pendant.
 | ||
| Fig. 8 Calculated optimized structures of the trans-III isomer in all studied protonation states with two explicit water molecules. Relative ΔG energies are shown in Table 1, and selected bond distances in Table 3. | ||
The pentacoordinated asymmetric structure of the deprotonated trans-III isomer is somewhat surprising as all solid-state structures of the complexes are hexacoordinated and symmetric. Thus, we subjected the trans-III isomer to computational scans of the distance between the uncoordinated pendant arm's oxygen atom and the central copper atom (Fig. 9). The scan started with the energetically lowest pentacoordinated structure. When the uncoordinated phenolate oxygen atom is pushed towards the CuII center, forming the hexacoordinated structure, there is only a mild rise in energy by 1.1 kcal mol−1. However, a true energetic minimum could not be located here. Further bond shortening of the Cu–O distance leads to decoordination of the other phenolate pendant at the opposite side of the macrocyclic plane, which eventually forms a hydrogen bond with the secondary amine group of the cyclam skeleton, and the resulting structure minimizes to a system identical to the initial one. The comparable energies of the starting pentacoordinated system and the intermediate hexacoordinated one result from the low phenolate coordination bonding energy, which is comparable to the energy of the intra-ligand pendant-O⋯H–N hydrogen bonds. This is also documented by the comparable delocalization indexes of the coordination and hydrogen bonds, 0.32 and 0.26, respectively (Table 3).
The cis-I and cis-V isomers behave differently than the trans-III isomer. Most importantly, the cis-complexes are typically penta-coordinated (except for their fully deprotonated forms) with the coordination polyhedron, whose shape is half way between the square pyramid and trigonal bipyramid geometry (Fig. S16 and S17†). In the protonated form, the Cu–O distance is typically long (2.3–2.8 Å) with low DIs close to zero. The protonated cis-isomers are also energetically less favoured, see Table 1. As soon as the first pendant deprotonates, it coordinates strongly in the basal or equatorial plane with a short Cu–O bond length of 2.0–2.3 Å and higher DICu–O ∼ 0.3–0.4. The calculated structures of the protonated cis-isomers mostly contain a strong intramolecular hydrogen bond between the non-coordinated and coordinated phenol/ate. The cis-V isomer energy scan as a function of Cu–O distance (Fig. S18†) shows that hexacoordination is energetically significantly disfavoured here.
The deprotonated form of the cis-I isomer maintains pentacoordination (Fig. S16†). However, the energy scan (Fig. S19†) shows that the hexacoordinated form is energetically very close (<1 kcal mol−1). In contrast, the second pendant in the deprotonated cis-V isomer is semicoordinated, primarily because the formation of the competing hydrogen interaction with the secondary amine groups of the macrocyclic ring is not possible here, as the hydrogen atoms point in the opposite direction of the macrocyclic ring plane.
3. Conclusions
Surprising isomeric variability of the CuII complex with 1,8-bis(methylphenol)cyclam was found and studied in detail using X-ray diffractometry, and theoretical calculations supported by electrochemistry, UV-vis spectra and HPLC analysis. Several isomers differing in their mutual orientation of the substituents on the cyclam nitrogen atoms were found in solution and in the solid state. The solid-state structures as well as the theoretical calculations showed that the phenolate pendant arm can be coordinated in both the protonated and the deprotonated forms. The coordination of phenolate was found to be weak when bound in the axial position of the square-bipyramidal coordination sphere of the trans-III isomer, which is the most stable one thermodynamically. In contrast, coordination of the deprotonated phenolate in the equatorial position of isomer cis-V is a stronger one. The theoretical calculations revealed high phenol/ate ability to form hydrogen bonds among themselves and even with the NH moiety of the chelate itself. Intermolecular hydrogen bonds were found in the solid state, whereas intramolecular hydrogen bonds were predicted for complexes in solution. In a crystal, the weak phenol/ate coordination allows for its replacement in the coordination sphere by water molecules or by coordinating anions. This finding is crucial for the application of phenolate pendant arms in the design of copper chelators. Whereas the commonly used acetate pendants almost always coordinate to the metal ion, if the number of pendant arms matches the coordination number of the metal ion, the weak coordination of the phenol/ate, the cleavage of the corresponding coordination bond and replacement with other coordinating species must be considered.Theoretical calculations showed that the implicit solvent model provides a good insight but may not be suitable for a full and accurate description of the studied systems, as they form strong intramolecular hydrogen bonds, and the explicit water molecules should be included in the model for obtaining reliable results. The calculations revealed that the Gibbs energies of the pentacoordinated and hexacoordinated forms in the deprotonated systems are comparable and thus both forms may exist simultaneously in the solution being in a fast exchange, because the energy barriers between the coordinated and hydrogen-bonded phenolate are negligible (<1 kcal mol−1). In addition, the dynamic behaviour of the complex in the solution might be further influenced by additional weak interactions with the solvent and various ions and molecules present in the solution.
4. Methods and experimental
4.1. General
All commercially available starting materials were used without further purification. 1,8-Bis(methylphenol)cyclam was synthesized according to the published procedure.144.2. HPLC
The analyses were carried out on a Waters ACQUITY QDa spectrometer (MS: electrospray ionization at atmospheric pressure, m/z 100–1250; UV-Vis: λ = 210–800 nm diode array) equipped with an RP column (XBridge BEH C18 2.5 μm, 3.0 × 100 mm) using a mixture of 1 ‰ TFA in H2O and 1 ‰ TFA in acetonitrile (MeCN) according to this gradient: 0.0 min 0% MeCN, 2.0 min 0% MeCN, 13.0 min 60% MeCN, 13.1 min 0% MeCN, 15.0 min 0% MeCN.4.3. FLASH chromatography
The separations were performed on an ECOM ECS28P0X (UV-Vis Diode array detector λ = 200–800 nm) with stationary phase: SiO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NORMASIL 60 (40–63 μm) VWR chemicals. The stationary phase was used in reusable empty columns and after purification it was discarded. Reverse phase chromatography was done using 40 g columns prefilled with C18 stationary phase (YMC-Dispopack AT, ODS-25, Lot: 13578). The universal gradient of MeCN in H2O (using 1 ‰ of TFA as a modifier is specified in every experimental procedure separately) with a flow of 50 ml min−1 was used: 0.0 min 0% MeCN, 2.0 min 0% MeCN, 7.0 min 100% MeCN, 10.0 min 100% MeCN. After each use, the column was also washed with 150 ml of MeOH and equilibrated with 100 ml of H2O.
NORMASIL 60 (40–63 μm) VWR chemicals. The stationary phase was used in reusable empty columns and after purification it was discarded. Reverse phase chromatography was done using 40 g columns prefilled with C18 stationary phase (YMC-Dispopack AT, ODS-25, Lot: 13578). The universal gradient of MeCN in H2O (using 1 ‰ of TFA as a modifier is specified in every experimental procedure separately) with a flow of 50 ml min−1 was used: 0.0 min 0% MeCN, 2.0 min 0% MeCN, 7.0 min 100% MeCN, 10.0 min 100% MeCN. After each use, the column was also washed with 150 ml of MeOH and equilibrated with 100 ml of H2O.
4.4. Syntheses of the complexes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) and the mixture was separated by FLASH chromatography (SiO2) using an ethanol–ammonium hydroxide mixture (5
1 w%) and the mixture was separated by FLASH chromatography (SiO2) using an ethanol–ammonium hydroxide mixture (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) as a mobile phase. The complex was isolated as the first fraction of chromatography after evaporation (yield 25 mg). The solids were dissolved in water–methanol (50
1 w%) as a mobile phase. The complex was isolated as the first fraction of chromatography after evaporation (yield 25 mg). The solids were dissolved in water–methanol (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 w%) solution and violet crystals suitable for X-Ray diffraction were obtained by slow evaporation after one week. Elem. anal.: calcd C 54.58, H 7.63, N 10.61, Cu 12.03; found C 54.77, H 7.62, N 10.64, Cu 12.07.
50 w%) solution and violet crystals suitable for X-Ray diffraction were obtained by slow evaporation after one week. Elem. anal.: calcd C 54.58, H 7.63, N 10.61, Cu 12.03; found C 54.77, H 7.62, N 10.64, Cu 12.07.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) chloroform mixture (1
chloroform mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 50 ml). The solution was filtered immediately. Pink crystals suitable for X-Ray diffraction were obtained by slow evaporation of the solvents over several days. Elem. anal.: calcd C 52.70, H 6.63, N 10.24, Cu 11.62; found C 52.77, H 6.84, N 10.27, Cu 11.64.
1, 50 ml). The solution was filtered immediately. Pink crystals suitable for X-Ray diffraction were obtained by slow evaporation of the solvents over several days. Elem. anal.: calcd C 52.70, H 6.63, N 10.24, Cu 11.62; found C 52.77, H 6.84, N 10.27, Cu 11.64.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) and the mixture was separated by FLASH chromatography (SiO2; the commercial sorbent typically contains traces of sulphate anions) using an ethanol–ammonium hydroxide mixture (5
1 w%) and the mixture was separated by FLASH chromatography (SiO2; the commercial sorbent typically contains traces of sulphate anions) using an ethanol–ammonium hydroxide mixture (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) as the mobile phase. The complex was isolated as the third fraction of chromatography after evaporation (yield 23 mg). Solids were dissolved in methanol and violet crystals suitable for X-Ray diffraction were obtained after two days by slow evaporation. Elem. anal.: calcd C 47.25, H 7.34, N 8.16, Cu 9.26; found C 47.44, H 7.33, N 8.20, Cu 9.30.
1 w%) as the mobile phase. The complex was isolated as the third fraction of chromatography after evaporation (yield 23 mg). Solids were dissolved in methanol and violet crystals suitable for X-Ray diffraction were obtained after two days by slow evaporation. Elem. anal.: calcd C 47.25, H 7.34, N 8.16, Cu 9.26; found C 47.44, H 7.33, N 8.20, Cu 9.30.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) and the mixture was separated by FLASH chromatography (SiO2; the commercial sorbent typically contains traces of sulphate anions) using an ethanol–ammonium hydroxide mixture (5
1 w%) and the mixture was separated by FLASH chromatography (SiO2; the commercial sorbent typically contains traces of sulphate anions) using an ethanol–ammonium hydroxide mixture (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w%) as the mobile phase. The complex was isolated as the second fraction of chromatography after evaporation (yield 47 mg). Solids were dissolved in methanol and violet crystals suitable for X-Ray diffraction were obtained after two days by slow evaporation. Elem. anal.: calcd C 52.97, H 7.45, N 9.41, Cu 10.68; found C 53.05, H 7.42, N 9.46, Cu 10.73.
1 w%) as the mobile phase. The complex was isolated as the second fraction of chromatography after evaporation (yield 47 mg). Solids were dissolved in methanol and violet crystals suitable for X-Ray diffraction were obtained after two days by slow evaporation. Elem. anal.: calcd C 52.97, H 7.45, N 9.41, Cu 10.68; found C 53.05, H 7.42, N 9.46, Cu 10.73.
4.5. X-ray diffraction study
Diffraction data of most of the structures were collected at 120 K (Cryostream Cooler, Oxford Cryosystem) on a Bruker D8 VENTURE Kappa Duo PHOTON100 diffractometer with an IμS micro-focus-sealed tube using Mo-Kα (λ = 0.71073 Å) radiation. Data were analysed using the SAINT (Bruker AXS Inc.) software package and subsequently corrected for absorption effects using the numerical method (SADABS). The structures were solved using direct methods (SHELXT2014)28 and refined with full-matrix least-squares techniques (SHELXL2014).29In general, all non-hydrogen atoms were refined anisotropically. All hydrogen atoms were found in the difference density map. However, the hydrogen atoms bound to the carbon atoms were fixed in theoretical positions using Ueq(H) = 1.2Ueq(C) to keep the number of refined parameters low and only hydrogen atoms bound to oxygen atoms were fully refined, if possible. Details on refinement of individual crystal structures are given in the ESI† and an overview of the experimental data is compiled in Table S13.†
4.6. UV-VIS
UV-VIS spectra were measured on a Specord 50 Plus (Analytic Jena) spectrometer in a quartz-glass cell with an optical path of 1 cm. Solutions were prepared by mixing ligand and metal solutions. pH was maintained with acetate buffer (c = 0.4 M, pH = 4) and HEPES buffer (c = 0.4 M, pH = 8) or adjusted with NaOH solution. The measurements were performed at cM = cL = 4 mM.Isomerisation rate constants and corresponding half-times were calculated from the absorbance at the maximum of the corresponding band according to the first order kinetic equation (eqn (1)):
| A = A0·e−kt. | (1) |
4.7. Cyclic voltammetry
The solutions were prepared from the freshly prepared stock solutions of the complexes. All voltametric measurements were performed in a three-electrode setup in an undivided electrochemical cell using a hanging mercury drop electrode (HMDE). The saturated calomel reference electrode (SCE) was separated by a salt bridge filled with buffer, and platinum foil served as an auxiliary electrode. The CVs were recorded at the scan rates of 0.1–1.0 V s−1 using variable potential ranges and rates. Cyclic voltammetry was carried out using a Static mercury drop electrode SMDE 1 (Laboratorní přístroje Praha, CZ) and Autolab potentiostat PGSTAT 101 (Metrohm, Switzerland). Argon was used as an inert gas to remove oxygen from the studied solutions.4.8. Theoretical methods
 | ||
| Scheme 1 Computational protocol used in evaluation of Gibbs energies, protonation constants and redox potentials. | ||
The initial geometries were obtained from crystal structures applying the Crest program30 with the xTB 6.5.0, GFN2-xTB semiempirical method31 and analytical linearized Poisson-Boltzmann implicit water. We constrained the dihedral angles including nitrogen atoms to stop the metadynamics engine from flipping the isomers. This provided a set of lowest conformers for each of the studied isomers and protonation states. Because of known problematic energy ordering of the conformers obtained from CREST using the GFN2-xTB energies, we recalculated the energies of several lowest conformers for each isomer and protonation state at the DFT BP86-D3 level using the def2-TZVP basis set, in water, using the COSMO-RS32 solvent model.
The lowest isomers were then optimized using the GGA BP86 functional,33,34 Grimme's D3-BJ (Becke–Johnson) dispersion correction,35,36 and a def2-TZVP37 basis set, as implemented in the TURBOMOLE 7.6 code.38–40 We optimized the structures of all considered isomers in different protonation states and calculated their Gibbs energies at ambient temperature.
For investigation of systems with explicitly assigned water molecules, we drew a series of estimated structures (always at least eight of them) with potential locations of the water molecule(s) in the specified conformation. These estimates were then subjected to optimization at the same level as mentioned above, and the geometry with the lowest energy in the set was taken as the final one and used for the calculations of enthalpies, redox potentials and pKA values, see below.
Gtotal = Eel + ΔGSOLV + EZPE + pV − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(qtransqrotqvib) ln(qtransqrotqvib) | (2) |
In our modified protocol, the EZPE (zero-point energy) and the pV and RT terms in eqn (2) were calculated with the THERMO42 utility using the harmonic vibration analysis obtained with the Aoforce43 module of TURBOMOLE for the gas-phase optimized BP86/def2-TZVP geometries. Both the solvent optimized and gas-phase optimized BP86/def2-TZVP geometries were used for BP86/def2-TZVPD44 single-point calculation of Eel (electronic energy) and for a BP86/def2-TZVPD COSMO calculation with dielectric constant ε = infinity, which is needed by the COSMO-RS program to produce ΔGSOLV, see Scheme 1 on the right.
The reduction potential was calculated as a one-electron reduction reaction from eqn (3),
| E[V] = 27.21(Gox[Hartree] − Gred[Hartree]) − EO (SCE)[V] | (3) |
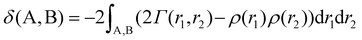 | (4) |
In eq. (4) the ρ(r) and Γ(r1 and r2) are one- and two-electron densities, respectively, and the integrations are performed through one or two individual atomic basins.
Additionally, consideration was given to the percentage value of the average number of electrons from the donor atom (oxygen) shared with the electron density acceptor (i.e., the copper cation or hydrogen). This value can be precisely expressed as the percentage share of half of the delocalization index to the total average number of electrons localized at the donor atom (oxygen).
Author contributions
All authors contributed to the study conception and design and participated in the manuscript writing. Milan Maďar: the shared first author, was responsible for the synthesis of the ligand and complexes and experimental data acquisition and, curation and interpretation. Jan Faltejsek: the shared first author, was responsible for theoretical calculations. Hana Bušková and Adam Jaroš participated in theoretical calculations. Lucie Koláčná was responsible for the electrochemical measurements and data curation. Jan Kotek was responsible for the X-ray analysis. Michal Straka (theoretical calculations), Vojtěch Kubíček (synthesis, spectral measurements and diffraction data) and Jiří Ludvík (electrochemistry) were responsible for supervision and funding of the project, interpretation of the data and finalization of the manuscript. All authors read and approved the final manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr I. Císařová (Charles University) for performing the X-ray diffraction measurements. The project is supported by the Grant Agency of the Czech Republic (21-23261S). The students M. M. and J. F. are grateful to the Grant Agency of Charles University (Grants 1368120 and 184624). J. L. and L. K. acknowledge the institutional support RVO 61388955.References
- T. J. Wadas, E. H. Wong, G. R. Weisman and C. J. Anderson, Chem. Rev., 2010, 110, 2858 CrossRef CAS PubMed.
- M. T. Ma and P. S. Donnelly, Curr. Top. Med. Chem., 2011, 11, 500 CrossRef CAS PubMed.
- E. W. Price and C. Orvig, Chem. Soc. Rev., 2014, 43, 260 RSC.
- T. W. Price, J. Greenman and G. J. Stasiuk, Dalton Trans., 2016, 45, 15702 RSC.
- B. Bosnich, C. K. Poon and M. L. Tobe, Inorg. Chem., 1965, 4, 1102 CrossRef CAS.
- M. Meyer, V. Dahaoui-Gindrey, C. Lecomte and R. Guilard, Coord. Chem. Rev., 1998, 178–180, 1313 CrossRef CAS.
- X. Liang and P. J. Sadler, Chem. Soc. Rev., 2004, 33, 246–266 RSC.
- J. Kotek, P. Lubal, P. Hermann, I. Císařová, I. Lukeš, T. Godula, I. Svobodová, P. Táborský and J. Havel, Chem. – Eur. J., 2003, 9, 233 CrossRef CAS PubMed.
- T. David, V. Kubíček, O. Gutten, P. Lubal, J. Kotek, H.-J. Pietzsch, L. Rulíšek and P. Hermann, Inorg. Chem., 2015, 54, 11751 CrossRef CAS PubMed.
- N. Camus, N. Le Bris, S. Nuryyeva, M. Chessé, D. Esteban-Gómez, C. Platas-Iglesias, R. Tripier and M. Elhabiri, Dalton Trans., 2017, 46, 11479 RSC.
- Y. Shi, G. Stella, J.-M. Chu and Y. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202211450 CrossRef CAS PubMed.
- J. S. Derrick, Y. Kim, H. Tak, K. Park, J. Cho, S. H. Kim and M. H. Lim, Dalton Trans., 2017, 46, 13166 RSC.
- M. M. Le Roy, S. Héry, N. Saffon-Merceron, C. Platas-Iglesias, T. Troadec and R. Tripier, Inorg. Chem., 2023, 62, 8112 CrossRef CAS PubMed.
- H. Luo, R. D. Rogers and M. W. Brechbiel, Can. J. Chem., 2001, 79, 1105 CrossRef CAS.
- L. Maria, I. C. Santos, L. G. Alves, J. Marçalo and A. M. Martins, J. Organomet. Chem., 2013, 728, 57 CrossRef CAS.
- L. Maria, M. Soares, I. C. Santos, V. R. Sousa, E. Mora, J. Marçalo and K. V. Luzyanin, Dalton Trans., 2016, 45, 3778 RSC.
- L. Maria, N. A. G. Bandeira, J. Marçalo, I. C. Santos, A. S. D. Ferreira and J. R. Ascenso, Inorg. Chem., 2022, 61, 346 CrossRef CAS PubMed.
- L. Maria, I. C. Santos, V. R. Sousa and J. Marçalo, Inorg. Chem., 2015, 54, 9115 CrossRef CAS PubMed.
- L. Maria, V. R. Sousa, I. C. Santos, E. Mora and J. Marçalo, Polyhedron, 2016, 119, 277 CrossRef CAS.
- N. Sengottuvelan, D. Saravanakumar, V. Narayanan, M. Kandaswamy, K. Chinnakali and G. Senthilkumar, Bull. Chem. Soc. Jpn., 2004, 77, 1153 CrossRef CAS.
- S. Sreedaran, K. Shanmuga Bharathi, A. Kalilur Rahiman, K. Rajesh, G. Nirmala and V. Narayanan, J. Coord. Chem., 2008, 61, 3594 CrossRef CAS.
- S. Sreedaran, K. Shanmuga Bharathi, A. Kalilur Rahiman, K. Rajesh, G. Nirmala, L. Jagadish, V. Kaviyarasan and V. Narayanan, Polyhedron, 2008, 27, 1867 CrossRef CAS.
- S. Sreedaran, K. Shanmuga Bharathi, A. Kalilur Rahiman, L. Jagadish, V. Kaviyarasan and V. Narayanan, Polyhedron, 2008, 27, 2931 CrossRef CAS.
- M. Sethupathi, B. Thulasinathan, N. Sengottuvelan, K. Ponnuchamy, F. Perdih, A. Alagarsamy and M. Karthikeyan, ACS Omega, 2022, 7, 669 CrossRef CAS PubMed.
- N. Sengottuvelan, D. Saravanakumar and M. Kandaswamy, Inorg. Chem. Commun., 2005, 8, 297 CrossRef CAS.
- S. Karbalaei, E. Knecht, A. Franke, A. Zahl, A. C. Saunders, P. R. Pokkuluri, R. J. Beyers, I. Ivanović-Burmazović and C. R. Goldsmith, Inorg. Chem., 2021, 60, 8368 CrossRef CAS PubMed.
- L. Koláčná, M. Maďar, V. Kubíček and J. Ludvík, ChemElectroChem, 2024, e202300 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A:Found. Adv., 2015, 71, 3 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C:Struct. Chem., 2015, 71, 3 Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652 CrossRef CAS PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 34, 8822 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- S. Grimme, J. Anthony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
- D. Bím, L. Rulíšek and M. Srnec, J. Phys. Chem. Lett., 2016, 7, 7 CrossRef PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955 CrossRef CAS PubMed.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2004, 384, 103 CrossRef CAS.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990 Search PubMed.
- T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, 2019 Search PubMed.
- X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: UV-VIS study: isomerisation kinetics; X-ray diffraction study: figures and tables with structural parameters and crystallographic data; theoretical calculations: optimized structures, predicted energies, interatomic distances, reduction potentials and Gibbs free energies. CCDC 2392211–2392220. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt03166k |
| This journal is © The Royal Society of Chemistry 2025 |