Advancing electrochemical N₂ reduction: interfacial electrolyte effects and operando computational approaches

Abstract

The electrochemical N₂ reduction reaction (eNRR) is a promising pathway for clean and sustainable production of ammonia, a compound essential for global industry. The challenges of the eNRR lie in the complexity of the electrode–electrolyte interface (EEI). While advances have been made in tuning the electrolyte compositions, the understanding of underlying atomic-level mechanisms remains limited. Operando computational techniques are emerging as instrumental tools to address relevant issues. In this review, we highlight a path forward by summarizing the recent advances in engineering strategies for direct-eNRR, including cations, organic solvents, ionic liquids; and for indirect-NRR with the incorporation of lithium-mediators. Additionally, we summarized relevant computational techniques that can investigate the interfacial dynamic properties associated with electrolyte modifications within N₂ reduction. By promoting the application of these computational methodologies, this review contributes to the ongoing efforts towards the realization of highly efficient electrochemical N₂ reduction.

---

Broader context

This review highlights the critical role of electrolyte engineering in enhancing the efficiency of the electrocatalytic nitrogen reduction reaction (eNRR) for green ammonia (NH₃) synthesis from N₂. The electrolyte can significantly influence the reaction by affecting how reactants interact with the catalyst, stabilizing key intermediates, and optimizing the overall reaction environment. The review explores various electrolyte engineering strategies, including the use of organic solvents, ionic liquids, and modifications of alkali cations, which have shown promise in improving NH₃ synthesis efficiency. However, despite experimental advancements, finding the ideal electrolyte composition remains a major challenge. Computational techniques, including density functional theory (DFT) and classical force field-based molecular dynamics (MD), microkinetic modelling (MKM), and machine learning (ML), are essential for overcoming challenges in electrolyte optimization for eNRR. These methods provide atomic-level insights into electrolyte behaviour and allow for fine-tuning compositions to enhance catalytic performance. By combining these computation tools, researchers can fine-tune electrolyte compositions and accelerate the discovery of more efficient systems. Computational techniques are vital for providing more insights and overcoming current challenges in electrolyte engineering for eNRR, therefore advancing sustainable ammonia synthesis at an industrial scale.

1. Introduction

Ammonia (NH₃) is a carbon-free energy carrier and is essential in agriculture and food industries. More than 95% of NH₃ production relies on the traditional Haber–Bosch process that is energy intensive with significant greenhouse gas (i.e. CO₂) emission because of intensive processing conditions such as temperature of 400–600 °C and pressure of 20–40 MPa.¹ In contrast, electro-driven chemical reactions offer a promising alternative for sustainable, carbon-free green NH₃ synthesis (gNH₃s), leveraging the growing availability of renewable energy sources.

Among the other nitrogen fixation pathways such as nitrate and nitrite reduction, electrochemical N₂ reduction reaction (eNRR) offers distinct advantages.^2–5 Firstly, eNRR relies on atmospheric N₂, an abundant and readily available feedstock, whereas nitrate and nitrite sources are limited and would require additional sourcing. Additionally, eNRR offers a more streamlined reaction process, converting N₂ directly to NH₃ under mild conditions without requiring complex intermediates, whereas nitrate and nitrite reduction involve multistep reactions that challenge selectivity and control. eNRR can also be powered by renewable energy sources, lowering the environmental footprint and making it more sustainable compared to the environmental risks of using nitrate or nitrite as primary feedstocks. However, further development is necessary to achieve cost and efficiency competitiveness with the traditional Haber–Bosch process. Currently, there still persist significant hurdles in achieving efficient NH₃ production.⁶

Importantly, electrochemical N₂ reduction performance depends significantly on properties and characteristics of the electrode–electrolyte interface (EEI), which can be tuned via either, engineering of the electrode, or the electrolyte. A number of methods are reported to improve eNRR performance via regulating electrocatalytic material surfaces including, metal doping,^7–9 alloying,^10,11 defect engineering,^12–14 and nanoscale structuring.^15–22 Particularly, in recent years, transition-metal complexes have emerged as promising catalysts for eNRR due to their tuneable and coordination environments, which suggested to be capable of stabilizing key N₂ intermediates.^23–26 These studies underscore the potential of transition-metal complexes as state-of-the-art catalysts for eNRR, offering tailored active sites and ligand environments that significantly contribute to enhanced N₂ reduction performance. Nevertheless, the strong competition from the hydrogen evolution reaction (HER) and the limited accessibility of interfacial N₂ molecules result in sluggish kinetics for NH₃ synthesis, posing challenges for industrial upscaling. Promising results for electrochemical N₂ reduction have been reported by screening and tuning electrolyte compositions to create eNRR-favored interfacial microenvironments.^27,28 However, a comprehensive understanding of the electrolyte's role remains limited, highlighting the need for deeper insights and guidelines to construct highly active and selective electrochemical systems. These include cations, solvent types, ionic liquids, and using mediators such as lithium. Among the use of these electrolyte contents, we provide an overview of two distinct reaction strategies for electrochemical N₂ reduction, including (1) direct electrocatalytic N₂ reduction reaction, direct-eNRR, where N₂ is catalyzed/reduced directly on the electrode surface;²⁹ and (2) indirect/mediated electrochemical N₂ reduction using lithium, known as Li-NRR.

Computational techniques, especially density functional theory (DFT), are being widely used in material science and focus on describing physical properties i.e. electronic structure, from the computation of the ground-state energy for electrocatalyst materials and establishing the structure–activity relationship to identify the optimal catalysts for direct-eNRR.^30,31 However, the dynamic mechanisms when electrolyte are considered remain unclear. Emerging computational techniques that incorporate the timescale and/or realistic electrochemical conditions (i.e. electrode potential and pH) are needed to establish understanding of the electrochemical EEI. Therefore, further design based on integration of material regulation and electrolyte engineering appears practical for realization of gNH₃s.

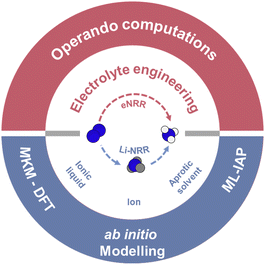
Here we report a critical assessment of advances in electrolyte engineering beginning with an overview of both direct-eNRR and indirect Li-NRR. For direct-eNRR, we assess interfacial electrolyte compositions including the effect of, cation, solvent type, and ionic liquid on electrocatalytic N₂ reduction. For Li-NRR, the fundamental changes in electrolyte composition focusing on lithium salt as anions and various proton sources are summarized. Based on these phenomena, we outline computations that could investigate electrolytes performance within eNRR including, first-principles integration for realistic conditions and kinetic modelling (mean field – microkinetic modelling and kinetic Monte Carlo simulation), ab initio modelling incorporated with explicit solvent molecules and machine learning-interatomic potential (ML-IAPs) for extended simulation time-scales. We provide a perspective on future computational contributions to this field and the likely outcomes in establishing interfacial dynamics for eNRR. We conclude that electrolyte engineering is important to advancing sustainable global gNH₃s via electrochemical reduction of N₂. Findings will benefit researchers and manufacturers in guiding computations for electrolyte engineering (Fig. 1).

Fig. 1 Scheme of electrolyte engineering for both direct electrocatalytic NRR (top panel) and lithium-mediated NRR (bottom panel), and associated operando computation techniques.

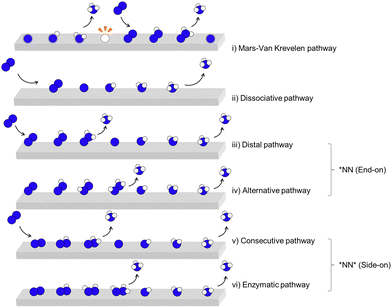
2. Mechanisms for NRR

A critical step in reducing N₂ to NH₃ is breaking the highly stable N≡N triple bond, a practical challenge evidenced by high negative electron affinity of N₂ molecule of −1.8 eV and significant ionization potential of 15.06 V.³² There are two pathways for N₂ reduction to activate the N≡N bonds, (1) a conventional electrocatalytic process in an electrochemical interface encompassing electrode and electrolyte, defined as the direct strategy, (2) mediated process on electro-induced lithium/lithium-based decomposition, defined as the indirect strategy.

2.1 Mechanism for direct electrocatalytic N₂ reduction

Direct eNRR on catalysts surface involves six proton-coupled electron transfers for every two NH₃ molecules production (eqn (1)).

N_2(g) + 6H⁺ + 6e⁻ ↔ 2NH_3(g) (1)

The reaction mechanism is classified into six general pathways as depicted in Fig. 2, (i)–(vi). Abghoui et al.^33–39 reported that the Mars–van Krevelen (MvK) mechanism (i) is significantly advantageous for electrochemical synthesis of NH₃ in transition metal nitrides (TMNs) compared with dissociative and associative mechanisms (Section 2.1.2). The MvK mechanism involves reduction of lattice N atoms present in the surface of the TMN, resulting in formation of NH₃ molecules and the generation of N vacancies. These vacancies are then filled with gaseous N₂, ensuring the continuation of the eNRR.

Fig. 2 Direct electrocatalytic N₂ reduction. Electrocatalytic NRR reduction pathways, (i) Mars–van Krevelen (MvK), (ii) dissociative (iii) distal and (iv) alternative pathway initiated with *NN end-on adsorption, (v) consecutive and (vi) enzymatic initiated with *NN side-on adsorption.

The difference between the dissociative pathway (ii) and associative pathway (iii)–(vi) is how the N≡N triple bond is cleaved. In the dissociative pathway, the nitrogen molecule is initially adsorbed onto the catalyst surface, where the N≡N triple bond is cleaved, resulting in two nitrogen atoms that are subsequently hydrogenated to form NH₃. However, such bond cleavage requires a significant energy input due to the strength of the N≡N bond, making the dissociative pathway challenging under ambient conditions. This dissociative mechanism, though energetically demanding, is characteristic of the Haber–Bosch process,¹² which operates at high temperatures and pressures to overcome the energy barrier associated with N≡N cleavage. Catalysts such as iron (Fe), ruthenium (Ru), and molybdenum (Mo) based material are commonly used for ammonia production via Haber–Bosch process. Among these, specific catalytic sites, including Fe C7 and Ru B5, have been identified as particularly active, facilitating N₂ dissociation more energetically favorably.⁴⁰

In contrast, the associative pathway is generally considered the most common mechanism for direct electrocatalytic N₂ reduction reaction under ambient conditions, especially in aqueous electrochemical environments. In this pathway, the dissolved N₂ molecule adsorbs onto the electrode surface without immediately breaking the N≡N bond. It undergoes a series of continuous hydrogenation steps primarily from H₂O molecules, forming intermediates such as N₂H, N₂H₂, and eventually NH₃. The first NH₃ molecule desorbs concurrently with N–N bond cleavage, allowing for efficient ammonia production at lower energy requirements compared to the dissociative pathway. This associative mechanism can be further classified into four distinct sub-pathways based on the orientation of configurations: (iii) distal, and (iv) alternative pathways; and start from the side-on configuration; (v) consecutive pathway, and (vi) enzymatic pathway. Various electrocatalysts have shown promise in facilitating these pathways for direct-eNRR, including transition metals (TMs) and their derivatives, such as metal oxides, nitrides, and sulphides, etc.²⁹ Additionally, metal-free catalysts like nitrogen- or boron-doped carbon materials and metal–organic frameworks (MOFs) exhibit notable reductive activity. These catalysts offer diverse electronic structures and active sites that can stabilize N₂ adsorption and promote hydrogenation, thus enhancing direct-eNRR efficiency under ambient conditions.

Compared to the lithium-mediated NRR that's going to be introduced in the next session, the mechanism of direct eNRR offers unique advantages, particularly through its adaptable and streamlined design. Operating without complex intermediates, direct eNRR allows for simpler reaction pathways that facilitate efficient nitrogen reduction at lower energy costs. Its flexibility in electrolyte composition enables targeted tuning to optimize performance for nitrogen reduction. With these benefits, direct eNRR provides a straightforward, efficient solution well-suited to decentralized and on-site ammonia production, offering a sustainable approach that complements renewable energy applications for nitrogen fixation.

2.2 Mechanism for Li-NRR

Li-NRR (lithium mediated nitrogen reduction reaction) is established via introducing lithium salt to the non-aqueous electrolyte where lithium ions are mediators for N₂ reduction under highly reducing potential (−3.04 V versus standard hydrogen electrode, SHE).⁴¹ This method is extensively reported and initially by Fichtner et al.⁴² in the 1930s, and later in the 1990s by Tsuneto et al.^43,44 A fundamental component in Li-NRR electrolyte is lithium salt, proton sources (HA), and solvent (typically, tetrahydrofuran-THF). The reaction mechanism for Li-NRR involves the steps shown in eqn (2)–(4).^45–47 The steps involve (1) electro-deposition of Li⁺ from a Li-salt in solution, (2) dissociation of N₂ on the deposited metallic Li, and (3) protonation of activated nitrogen molecule(s) from a proton carrier (HA), which is capable of undergoing a deprotonation–reprotonation cycle.

Li⁺ + e⁻ ↔ Li (s) (2)

N₂ ↔ 2*N (3)

*N + 3AH ↔ 3A⁻ + NH₃ (4)

For Li-NRR the lithium plating is essential because it enables subsequent reactions. Based on how nitrogens are split and whether protonation is a chemical or electrocatalytical process, there are four possible mechanisms.⁴⁸ In addition, a fifth mechanism exists, if the different proton shuttle mechanism are considered, as shown in Fig. 3.⁴⁹ These five mechanisms can be classified as those without involvement of SEI (Fig. 3a) and those with SEI, formation (Fig. 3b).

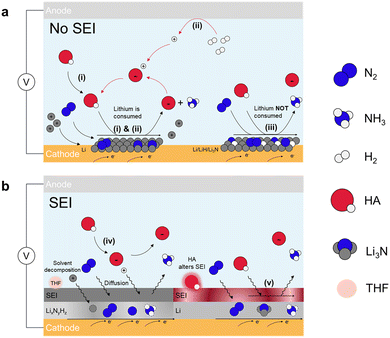Fig. 3 Indirect Li-NRR. Schematic for lithium-mediated NRR with (a) no SEI formed and (b) SEI formed. Five potential mechanisms are summarized.⁴⁸ These include lithium cycling with (i) proton source from the electrolyte⁵⁰ and (ii) proton shuttle model in which proton is from H₂ oxidation.⁴⁹ (iii) Electro-driven Li-NRR where lithium only provides the electron.⁴⁶ SEI diffusion model for (iv) non-reactive SEI,⁴⁷ and (v) adjusted permeable SEI layer through HA.⁵¹

Pathways (i) and (ii) exhibit the same mechanism of N₂ splitting where N₂ molecules undergo spontaneous dissociation and chemically react with the electrodeposited Li to form Li₃N because of the strong electron donating ability of Li metal. The key differences between these two pathways lie in the proton source and the sustainability of the processes. In pathway (i), the proton source is ethanol. After ethanol donates a proton to the activated nitrogen (Li₃N), the deprotonated ethanol remains, leading to its consumption and making the process less sustainable.^46,50 In pathway (ii), the proton comes from H₂ inserted at the anode side that undergoes the electrocatalytic oxidation process (HOR), offering a sustainable approach towards NH₃ production. These two pathways are reported to follow CC model (chemical nitrogen splitting and chemical protonation) as they can proceed even if current is off.⁵² In pathway (iii), a key difference from the previous pathways is that lithium is electrodeposited but not returned to the solution, leading to excessive lithium buildup. This causes competing reactions, such as hydrogen evolution reaction (HER), which undermine the overall efficiency of the reaction. The pathway also involves the formation of multiple lithium-based components due to the high reactivity of metallic lithium, including Li, Li₃N and LiH. About the reaction mechanism, on the layer of lithium-contained species, N₂ is electrocatalytically dissociated and receives protons from the electrolyte to form NH₃. DFT studies show that intermediates exhibit the capability of producing NH₃ in the order of Li > Li₃N > LiH.⁴⁶ These three pathways operate without a solid electrolyte interphase (SEI), making the selectivity and activity for NH₃ formation largely dependent on lithium electrodeposition, as shown in Fig. 3a.^53–56

Beyond the pathways (i)–(iii), two other pathways for Li-NRR exist that involves the formation of solid electrolyte interphase (SEI). The SEI is a passivation layer that forms on the electrode surface, much like in traditional Li-ion batteries, where it develops from the decomposition of non-aqueous electrolytes under highly reductive potentials. This layer serves to protect the negative electrode by preventing further decomposition of the electrolyte. In the context of Li-NRR, the SEI plays a similar role, determining the stability and efficiency of nitrogen reduction, particularly in pathways (iv) and (v) as depicted in Fig. 3b. Once the SEI is formed, it facilitates the diffusion of reactants (N₂, H⁺, and Li⁺) and products (NH₃) through it during the reduction process.⁵⁷ The major difference between pathway (v) and (iv) is that in pathway (v), the proton sources participate in SEI formation and can alter its permeability, depending on the main products formed from the interaction between the proton sources and active lithium.⁵¹ The rate at which these species diffuse through the SEI directly influences the overall performance of the reaction. The permeability of the SEI, influenced by the proton sources involved in its formation, is key to its effectiveness. Therefore, understanding how the SEI forms and functions, as well as modifying its physical and chemical properties, is crucial for enhancing the stability, efficiency, and long-term performance of the Li-NRR process.

The Li-NRR mechanism utilizes lithium's high reactivity to address the inherent difficulty of breaking the strong N≡N bond, which allows nitrogen reduction to proceed efficiently, largely under ambient temperatures and pressures.⁵³ Furthermore, Li-NRR benefits from excellent selectivity, with minimal competing side reactions, such as hydrogen evolution, which can otherwise reduce efficiency. This high selectivity contributes to improved faradaic efficiency, as more input energy is directed specifically toward ammonia formation, decreasing the need for post-reaction product separation and purification. Together, these attributes make Li-NRR a highly promising method for ammonia synthesis, offering a novel approach to activate the exceptionally stable N₂ molecule and providing a viable alternative to traditional nitrogen fixation processes that are often energy-intensive and resource-demanding.

2.3 Competing hydrogen evolution reaction (HER)

HER occurs on the cathode with only two proton-coupled electron transfer, as shown in eqn (5)–(7). It is a dominating competing reaction in direct eNRR. HER has an equilibrium potential close to NH₃ production, therefore leads to sluggish kinetics for eNRR and corresponding low current efficiency and yield for NH₃. HER exists in both direct eNRR and (Section 2.1) and Li-NRR pathway (iii), because of the high reactivity of electrodeposited-lithium metal, providing facile electron transfer to the surface proton and forming H₂.

Volmer: H⁺ + e⁻ + * ↔ *H (5)

Heyrovsky: H⁺ + e⁻ + *H ↔ H_2(g) (6)

Tafel: *H + *H ↔ H_2(g) (7)

3. Electrolyte engineering for direct electrocatalytic NRR

The general mechanism for direct-eNRR for NH₃ synthesis requires a sequence of proton and electron transfers. At the EEI, while electrocatalysts facilitates electron transfer to N₂, the electrolyte component plays multiple roles, including transporting reactants (N₂) and products (NH₃) and influencing the transfer rate of proton sources i.e. H₂O. Electrolyte engineering is especially effective in addressing the challenge that the equilibrium potentials of eNRR and HER are close to each other, making it crucial to regulate the electrolyte for selective nitrogen reduction while minimizing competing hydrogen evolution. The reported approaches of electrolyte engineering for direct eNRR include cations, solvents including organic solvents and ionic liquids. Each of these methods plays a distinct role in influencing the overall efficiency and selectivity of eNRR, as presented in the following sections. Overall, a summary of the direct electrocatalytic NRR process of different metal active sites with employing various electrolytes is tabulated in Table 1.

Table 1 Summary of electrochemical performance metrics for various electrocatalysts with their respective electrolytes in the direct electrocatalytic NRR

Electrode	Electrolyte type	Electrolyte	NH3 yield^a (nmol s^−1)	FE (%)
a Units for ammonia yield rate converted to nmol s^−1 with respect to the catalytic area (cm^−2) or mass (mg^−1).
N-doped carbon nanospikes^18	SIW	0.25 M LiClO4 (NaClO4/KClO4)	1.59 ± 0.12 cm^−2	11.56 ± 0.85
Ag triangular nanoplates^58	SIW	0.1 M KOH (LiOH/NaOH)	0.954 mg^−1	25
Cu^59	SIW	0.32 M KOH (LiOH/NaOH/RbOH/CsOH)	0.86 cm^−2	18 ± 3
Cu^56	WIS	5 M LiClO4	19.7 ± 3.9 × 10^−2 cmGSA^−2	12
Rh1/MnO2^60	WIS	9 M K2SO4	4.43 mg^−1	73.3
TiO2/Au^61	WIS	20 M LiTFSI	0.33 cm^−2	37.2
Carbon^62	WIS	10 M LiCl	(9.5 ± 0.4) × 10^−1 cm^−2	71 ± 1.9
WSe2−x^63	WIS	12 M LiClO4	2.96 mg^−1	62.5
Ni^64	Organic solvent	0.1 M LiCl/EDA + 0.05 M H2SO4	3.58 × 10^−2 cm^−2	17.2
Ni^65	Organic solvent	2-Propanol/H2O (9 : 1, v/v)	1.54 × 10^−1 cm^−2	0.89
FeOOH/CNTs^66	Organic solvent	Methanol/H2O (0.16 vol%)	4.28 ± 0.12 mg^−1	75.9 ± 4.1
OV-rich α-Fe2O3^67	Ionic liquid	n-Octylammonium formate	0.52 mg^−1	6.63
Nano-Fe^68	Ionic liquid	[P6,6,6,14][F6P]	0.1690 cm^−2	20
α-Fe@Fe3O4^69	Ionic liquid	[C4mpyr][eFAP] + 1H,1H,5H-octafluoropentyl-1,1,2,2-tetrafluoro- ethyl ether (FPEE)	3.71 × 10^−4 cm^−2	32
Fe^70	Ionic liquid	[P6,6,6,14][eFAP]	4.730 × 10^−3 cm^−2	60

---

3.1 Cation effect

Cations on a charged electrode surface accumulate and form the electrochemical double layer (EDL) that is essential for electrocatalytic reaction kinetics. These cations affect the interfacial potential, electric field, pH, and geometric microenvironment, leading to significant chemical interactions with adsorbed intermediates, affecting overall electrocatalytic performance.^71,72 In particular, the presence of cations reduces proton donor ability due to solvation and steric effects, which slows down HER kinetics while increasing the selectivity for NH₃ formation. For direct eNRR, the concentration of cations introduced to the electrolyte plays an important role in affecting the dynamics of the EEI. Depending on the salt concentration, salt-based aqueous electrolytes can be categorized into two types: (1) low-concentrated salt (salt-in-water, SIW) electrolyte and (2) high-concentrated salt (water-in-salt, WIS, salt concentration exceeds 5 M) electrolyte.⁷³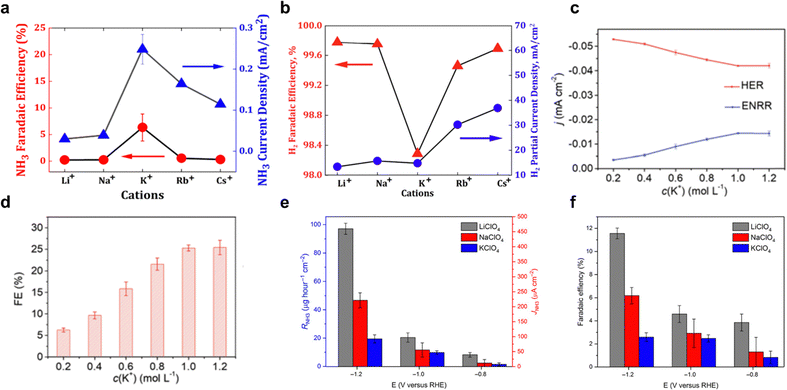

3.1.1 Salt-in-water (SIW) electrolyte. The impact of cations, particularly alkali metal cations (AM⁺), in low-concentration SIW electrolytes on the direct eNRR is significant and multifaceted. The interactions between hydrated AM⁺ cations, such as Li⁺, Na⁺, K⁺ and Cs⁺, and the electrode at the EEI are primarily non-covalent, rather than the covalent and electrostatic interactions.⁷⁴ These dynamic non-covalent interactions between hydrated AM⁺ and reaction intermediates is important in understanding how the cation affect redox reaction activity. The physical and chemical properties of these hydrated cations, such as ionic radii, hydration energy, and their ability to stabilize reaction intermediates, play a crucial role in enhancing proton-coupled electron transfer (PCET) and electrochemical performance of eNRR.⁷⁵ Among these cations, Li⁺ and K⁺ have been identified as particularly effective in improving the selectivity and activity of eNRR, as will be discussed in the following paragraphs. Potassium ions K⁺ have been shown to stabilize key reaction intermediates and increase the concentration of water molecules in the hydration shell, leading to enhanced nitrogen reduction performance (Fig. 4a and b).⁵⁹ Specifically, studies involving bismuth nanocrystals (BiNCs) with K⁺-containing electrolyte have reported a high selectivity (FE) of 66%, and a current density of 4.2 mA cm⁻² at −0.6 V vs. RHE.⁷⁵ In addition, experimental findings show eNRR performance are enhanced with increasing salt concentration(s) (Fig. 4c and d).^56,58 Similarly, lithium ions (Li⁺) in low-concentration aqueous electrolytes exhibit significant electrocatalytic reactivity, particularly on electrodes with sharp-tip features. This improved reactivity is attributed to the strongest solvent effect of Li⁺ amongst all AM⁺.^{18,56,76–79} For example, the N-doped carbon nanospike (CNS) electrode developed by Song et al.¹⁸ and the β-FeOOH nanorods developed by Zhu et al.⁷⁸ both demonstrated boosted FE, NH₃ production and partial current density in the presence of low concentrated Li⁺, compared to Na⁺ and K⁺ (Fig. 4e and f). The observed enhanced in performance is largely due to the increased concentration of N₂ within the Stern layer, which resulted from an intensified electric field at sharp spikes on the electrode.¹⁸ This intensified electric field, driven by the strong solvation effect of Li⁺, enhances the adsorption and accumulation of dissolved N₂ molecules at the electrode surface. Consequently, the concentration of N₂ at the electrode surface becomes significantly higher than in the bulk electrolyte, thereby improving overall efficiency of nitrogen reduction. Furthermore, the formation of dehydrated cation layer surrounding the tip suppresses HER, which further promotes overall eNRR performance.⁸⁰

Fig. 4 Salt-in-water electrolyte. Faradaic efficiency (FE) and current density for (a) NH₃, (b) H₂. Reproduced with permission.⁵⁹ Copyright 2020, American Chemical Society. (c) Effective current density, and (d) FE for eNRR and HER on AgTPs in electrolyte with different potassium cations concentrations. Reproduced with permission.⁵⁸ copyright 2019, Royal Society of Chemistry. Electrolyte counterion effect of Li⁺ (grey-colour), Na⁺ (red), and K⁺ (blue) upon (e) formation rate and partial current density and (f) FE, which shows the order of Li⁺ > Na⁺ > K⁺. Reproduced with permission.⁸⁰ Copyright 2018, American Association for the Advancement of Science.

Despite these promising outcomes, there remains limited understanding of how cation affects the morphology of the EEI and eNRR dynamics. This knowledge gap highlights the need for further research to better understand how cations in SIW electrolyte could promote eNRR processes.

3.1.2 Water-in-salt (WIS) electrolyte. Water-in-salt (WIS) electrolytes, characterized by their ultra-high salt concentration, present a distinct advantage over traditional SIW electrolytes in enhancing eNRR performance. Unlike SIW, where water is the dominant component, WIS electrolytes contain a much higher concentration of salt, typically exceeding 5 M. This leads to a significantly lower number of water molecules available to solvate ions, which effectively reduces water activity and mitigates the occurrence of water hydrolysis.⁷³

The reduced water activity in WIS electrolytes plays a crucial role in enhancing eNRR performance. By lowering the availability of active water molecules, these electrolytes increase the concentration of nitrogens at the electrode interface, thereby improving nitrogen delivery to the catalytic sites and boosting selectivity by suppressing competing reactions such as HER.^56,58 As reported by Song et al.,¹⁸ the smaller cation induces a stronger electric field that contributes to an enriched N₂ concentration at the interface, resulting in the ‘salting-out’ effect that, similarly, enriches the interfacial N₂ concentration because of N₂ precipitation, reported by Wang et al.⁶² This effect is accompanied by a disruption of the hydrogen bond network and an increased density of immobilized water molecules around the solute ions. As a result, the efficiency of these water molecules as proton sources and solvents decreases, thereby boosting the performance of eNRR. For example, a superior eNRR was achieved using 10 M LiCl as WIS electrolyte, which resulted in a faradaic efficiency (FE) of 71 ± 1.9% and NH₃ yield of 9.5 ± 0.4 × 10⁻¹⁰ M s⁻¹ cm⁻² at −0.3 V vs. RHE (Fig. 5a and b). However, it is important to note that further increasing the salt concentration does not necessarily lead to improved eNRR performance, as the protonation step may be impeded by a deficiency of active H₂O molecules, as suggested by Liu et al.⁶¹

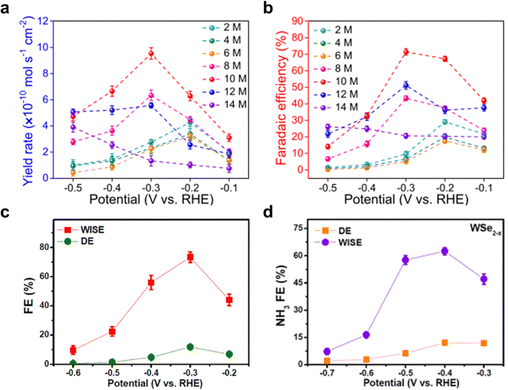Fig. 5 Water-in-salt electrolyte. (a) Yield rate and (b) corresponding NH₃ faradaic efficiency in different salt concentrations (from 2 to 14 M). Reproduced with permission.⁶² Copyright 2021, Springer. The NH₃ formation FE over (c) Rh₁/MnO₂, reproduced with permission,⁶⁰ copyright 2022, Elsevier and (d) Se-vacancy-rich (WSe_2−x) in both dilute electrolytes (DEs) and WISEs at selected potential. Reproduced with permission,⁶³ Copyright 2022, American Chemical Society.

Employing WIS electrolyte has reportedly been used and integrated with catalyst engineering including for e.g. vacancy, doping,^56,60,61,63 to enhance its potential and applications. For example, Shen et al.^60,63 demonstrated that using Rh₁/MnO₂ and WSe_2−x electrodes in combination with a WIS electrolyte, resulted in highly significant FE of 73.3% and 62.5%, respectively (Fig. 5c and d). This remarkable selectivity performance is attributed to the synergistic effect arising from accumulation of delocalized electrons at vacancy sites or single atom doping sites, coupled with the rigid solvation sheaths formed in WIS environment. These factors collectively improve the transportation and activation kinetics of nitrogen while inhibiting proton mobility, leading to enhanced efficiency in the electrochemical N₂ reduction.

3.2 Solvent effect

Non-aqueous solvents, including organic solvents and ionic liquids (ILs), enhance N₂ solubility and improve eNRR performance compared to aqueous electrolytes. Organic solvents improve N₂ solubility and reduce HER kinetics, but can form by-products. Mixing organic solvents with water balances solubility and stability, significantly improving NH₃ production. ILs provide high conductivity and stability, also improve N₂ solubility, especially when they are fluorinated. Combining ILs with aprotic solvents could further enhance N₂ solubility and suppresses HER, leading to higher NH₃ production and efficiency.

3.2.1 Organic solvent. To address low N₂ solubility in aqueous electrolytes, non-aqueous organic solvents (HA) have been introduced as they offer greater N₂ solubility, increasing the availability of N₂ molecules for eNRR.⁸¹ Additionally, because of structural polarity, the distorted hydrogen bond network causes higher kinetic barriers for HER which in turnenhances eNRR selectivity. However, the reduction of organic solvents, particularly when these solvents are present in high concentration, can be problematic. For example, Kim et al.⁶⁵ reportedly compared two types of electrolytes, (1) a mixture of 2-propanol and water (9 : 1, v/v) and (2) pure de-ionized water, Fig. 6a. It was found that the mixed solvent significantly boosted FE for eNRR, exhibiting a 7 to 8-fold increase compared to pure water. However, despite this, FE remained relatively low (<1%) due to instability arising from alkoxides formation during 2-propanol reduction. To address this, LiCl was used as a supporting salt with ethylenediamine (EDA) as the electrolyte for NH₃ synthesis (Fig. 6b), resulting in an overall FE of 17.2%. Therefore, pure organic solvents as electrolyte are not optimal because of the formation of non-sustainable by-products. A mixture of organic solvents with sustainable proton sources such as H₂O, has reportedly emerged as a solution.⁶⁴ This addresses low N₂ solubility in aqueous solutions whilst maintaining overall stability. By combining organic solvents with water, it appears possible to leverage the benefits of both types of solvents, leading to a more sustainable electrochemical process. Ren et al.⁶⁶ employed alcohol-water system (i.e., methanol, ethanol, n-propanol, n-butanol, dimethyl sulfoxide, and pure water) for electrolyte in eNRR, and reported a volcano-like relationship between the selected alcohols and their proton-donating ability. Amongst these, volumetric content of H₂O in 0.16% in methanol–water electrolyte exhibited a record high eNRR FE of 75.9 ± 4.1% and NH₃ yield of 262.5 ± 7.3 mg h⁻¹ mg⁻¹ on catalyst FeOOH/CNTs, an 8-fold increase compared with conventional aqueous electrolytes, Fig. 6c and d. In addition, the electrode potential for optimal eNRR is more negative with methanol–water electrolyte, providing a high degree of control of activity and selectivity for NH₃ production. The synergistic effect of boosting N₂ solubility and reducing HER kinetics leads to an expanded electrochemical potential window. This broadened range provides greater flexibility in fine-tuning the selectivity of the reaction, whilst concurrently preserving the efficiency of NH₃ production. Moreover, the use of organic solvents has also been reported to offer advantages through the phenomenon of molecular crowding, as investigated by Guo et al. in their study which employed hydrophilic ploy(ethylene glycol) PEG400.⁸² The addition of PEG promoted the overall eNRR performances in both acidic and alkaline electrolytes, as shown in Fig. 6e and f. In particular, a maximum ammonia faradaic efficiency (FE) of 32.13% and a yield of 1.07 μM cm⁻² h⁻¹ were achieved in PEG-containing acidic electrolytes. This enhancement is attributed to the suppression of the Heyrovsky step in the HER, resulting from the sluggish proton diffusion caused by strong hydrogen-bonding interactions between electronegative oxygen atom in PEG and hydrogen atom in H₃O⁺/H₂O. This interaction effectively limits proton mobility, thereby favouring the nitrogen reduction reaction over competing HER processes.

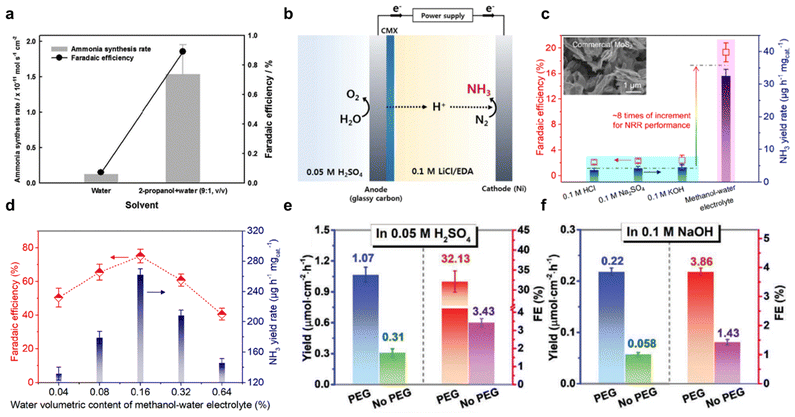Fig. 6 Solvent effect. (a) Effect of electrolyte medium of water or 2-propanol on NH₃ synthesis rate and FE. Reproduced with permission.⁶⁵ Copyright 2016, The Electrochemical Society. (b) Schematic for ethylenediamine (EDA)-based NH₃ synthesis. Reproduced with permission.⁶⁴ Copyright 2016, The Electrochemical Society. (c) Comparison of NRR performance achieved by commercial MoS₂ in aqueous electrolytes and methanol–water electrolyte. The inset is the scanning electron micrograph image of used commercial MoS₂. (d) NRR FE and NH₃ yield rate over FeOOH/CNTs at the applied potential of −1.2 V vs. Ag/AgCl for 2 h in methanol–water electrolytes with water volumetric content of 0.04, 0.08, 0.16, 0.32, and 0.64%, respectively. Reproduced with permission.⁶⁶ Copyright 2021, American Chemical Society. NH₃ yield and FE of TiO₂ nanoarray electrode in (e) 0.05 M H₂SO₄, and (f) 0.1 M NaOH electrolyte with/without 20 wt% poly(ethylene glycol) PEG400. Reproduced with permission.⁸² Copyright 2021, Wiley-VCH.

3.2.2 Ionic liquids solvent. Ionic-liquids (ILs) also emerged as a promising electrolyte component for the direct eNRR selection due to their unique properties, such as high conductivity, high thermal and chemical stability, low volatility, and a wide electrochemical window.⁸³ Applications of ILs began in 2016, with some studies reporting high N₂ solubility and conversion efficiency for NH₃ production.

Many studies have been conducted to investigate the solubility of gases in various ILs.^84–89 Kang et al.⁹⁰ reported synthesis of a series of phosphonium-based ILs with highly fluorinated anions. It was found that fluorine content is important to dissolving more N₂. A binary system consisting of an IL and a fluorinated solvent mixture reportedly exhibits capability to dissolve a greater quantity of N₂ molecules.⁹¹ Three fluorinated solvents were included in this work, namely trifluorotoluene (TFT), 1H,1H,2H-heptafluorocyclopentane (HFCP), and 1H,1H,5H-octafluoropentyl 1,1,2,2-tetrafluoroethyl ether (FPEE), in combination with the ionic liquid 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl)trifluorophosphate [C₄mpyr][eFAP]. There was an increasing N₂ solubility with increasing volume fraction of fluorinated solvent, being advantageous for eNRR. Therefore, based on the recent progress, two types of non-aqueous solvents are summarised which are pure IL, and IL – organic solvent-based mixtures.

The first application of ILs as electrolyte in electrocatalytic N₂ reduction was reported in 2016.⁹² A gas diffusion electrode coated with Cp₂TiCl₂-supported hydrophobic IL, specifically 1-butyl-1-methylpyrrolidinium tris(pentafluoroethyl)tri fluorophosphate ([C₉H₂₀N][(C₂F₅)₃PF₃]), was used in a solid polymer electrolysis (SPE) cell for NH₃ production. For this configuration, the NH₃ yield per Cp₂TiCl₂ and current efficiency achieved are 27% and 0.2%, respectively. Inspired by this work, Zhou et al. in 2017 further advanced the use of IL.⁷⁰ They employed [P_6,6,6,14][eFAP] as the electrolyte, which has high N₂ solubility, and achieved a conversion efficiency of up to 60% for NH₃ using nanostructured iron-based catalysts. However, the production of NH₃ remained low, at 10⁻¹² M s⁻¹ cm⁻², due to the high viscosity of IL, which limited N₂ mass transfer (Fig. 7a and b).

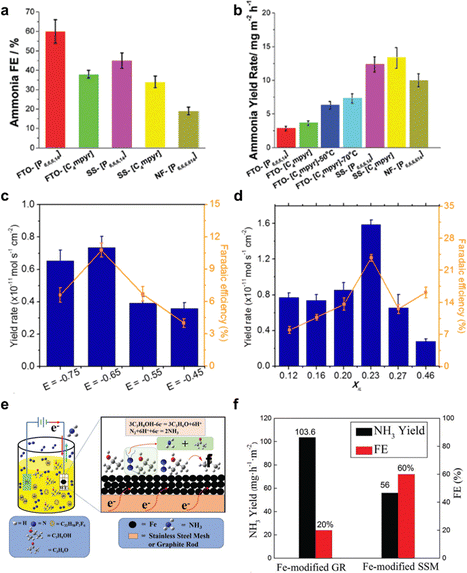Fig. 7 eNRR performance using ionic liquid. (a) Faradaic efficiency and (b) NH₃ production rate for electro-reduction of selected N₂-saturated ionic liquids on selected electrodes at a constant potential −0.8 V vs. NHE. Findings for FTO and SS substrate are based on a 3 h experiment. Reproduced with permission.⁷⁰ Copyright 2017, Royal Society of Chemistry. (c) Potential dependence of NH₃ yield and FE (%) at IL mole fraction X_IL = 0.16. (d) Constant potential electrolysis at −0.65 V vs. NHE in selected mixed electrolytes. Reproduced with permission.⁶⁹ Copyright 2018, American Chemical Society. (e) Schematic for the one-step electrocatalytic synthesis of NH₃ and acetone in ionic liquids. (f) NH₃ yield and faradaic efficiency in this work, using Fe-modified graphene and Fe-modified stainless steel as electrode. Reproduced with permission.⁶⁸ Copyright 2021, Royal Society of Chemistry.

Recent advancements in eNRR have demonstrated the benefits of combining ionic liquids with other components to enhance eNRR performance. Suryanto et al.⁹³ explored a mixture of an aprotic fluorinated solvent and ionic liquid mixture FPEE-[C₄mpyr][eFAP] as electrolyte.⁹¹ This combination significantly boosted eNRR selectivity and activity when α-Fe nanorods were used as the electrode under ambient conditions. The optimized electrolyte mixture, with a mole fraction (X_IL) of 0.23, achieved the highest ammonia yield (approximately 2.35 × 10⁻¹¹ M s⁻¹ cm_GSA⁻²) and efficiency (32%), at −0.65 V vs. NHE (Fig. 7c and d).

Building on the advantages of these combinations, Zhang et al.⁶⁸ reported a one-step electrochemical synthesis of NH₃ from N₂ in an ionic liquid using a nano-Fe catalyst in an electrolyte that combines ionic liquid and isopropanol. Isopropanol also serves as the proton source to limit proton supply, which not only enhanced nitrogen solubility but also suppressed the competitive HER. This innovative combination resulted in a high ammonia production efficiency of 60% and a production rate of 13.06 mg m⁻² h⁻¹ (Fig. 7e and f).

4. Electrolyte engineering for indirect Li-NRR

In Li-NRR, non-aqueous electrolytes were used, and lithium ions are introduced into the electrolyte as mediators for N₂ reduction and might form part of the electrode surface. This is quite distinct to direct eNRR, where the electrode material does not directly participate in N₂ reduction. Therefore, the overall electrochemical activity and selectivity is largely depend on the physical and chemical property of the electro-induced lithium or lithium-based deposition, along with the corresponding SEI formation.^46–48,51 There are two main reasons for the use of electrolyte in Li-NRR, which are providing sources of Li⁺ and H⁺. THF is extensively reported as the solvent for Li-NRR, capable of dissolving significant amounts of N₂.⁹⁴ A common electrolyte system for Li-NRR is a mixture of Li-salt/THF/HA. The resemblance of metallic Li to the SEI layer in traditional Li-ion⁶¹ batteries is hypothesized to significantly impact the overall performance of Li-NRR.⁹⁵ Therefore, regulating the chemical and physical property of SEI by varying electrolyte components can effectively improve Li-NRR for sustainable NH₃ production.⁴⁸ Here, we summarize the effect on the selection of various Li-salt with different anions (Section 4.1) and how proton sources impact Li-NRR (Section 4.2). A summary of the indirect Li-NRR process using various electrolytes is tabulated in Table 2.

Table 2 Summary of electrochemical performances metrics for various electrode materials with corresponding electrolytes and reaction conditions of indirect electrochemical Li-NRR

Electrode	Electrolyte	Reaction conditions	NH3 yield^a (nmol s^−1)	FE (%)
a Units for ammonia yield rate converted to nmol s^−1 with respect to the catalytic area (cm^−2) or mass (mg^−1). b Room temperature. c Averaged ammonia yield rate; stabilized yield rate after 24 h of operation is given 150 ± 8 cm^−2.
Ni^96	THF/LiNTf2/ethanol	15 bar, RT^b	223 ± 8 cm^−2 (ave.)^c	∼100
Ni^97	THF/LiNTf2/ethanol	15 bar, RT	530 ± 20 cm^−2	98 ± 2
Ni^97	THF/LiNTf2/iso-propanol	15 bar, RT	430 ± 20 cm^−2	96 ± 1
Mo^98	THF/LiClO/ethanol	20 bar, RT	10.8 ± 0.2 cm^−2	78 ± 1.3
Stainless steel cloth (SSC)^99	THF/LiBF4/PhOLi	1 bar, RT	—	72 ± 3
SSC^100	Diethylene glycol dimethyl ether/LiBF4/EtOH	1 bar, RT	—	64 ± 1
SSC^101	THF/LiBF4/ethanol	1 bar, RT	—	61 ± 1
Cu^57	THF/LiBF4/ethanol	20 bar, RT	2500 ± 100 cm^−2	71 ± 3
Cu^49	THF/LiBF4/tris(pentafluoroethyl)trifluorophosphate	20 bar, RT	53 ± 1 cm^−2	69 ± 1

---

4.1 Anion effect

The selection of anions in the electrolyte significantly influences the performance and efficiency of the Li-NRR process. Common anions used in Li-NRR include perchlorate (ClO₄⁻), tetrafluoroborate (BF₄⁻), and triflate (OTf⁻). Several experiments have explored the effects of these Li-salts on Li-NRR performance.^48,50,102 For instance, Li et al. performed a theoretical investigation for screening lithium salts;⁵⁷ demonstrating through first-principle studies that fluorine-based electrolyte like LiHF₂ and LiF, shows slower Li⁺ conductivity but higher surface mobility, which collectively led to a relatively stable phase of the enriched-SEI layer. Based on these theoretical insights, a high selectivity and NH₃ production rate was reported using LiBF₄ as the electrolyte, achieving approximately 71 ± 3% FE and 2.5 ± 0.1 μM s⁻¹ cm_geo⁻² at a current density of 1 A cm_geo⁻² (Fig. 8a and b). Fig. 8c shows that the thinnest SEI layer was formed with LiBF₄, resulting in less NH₃ accumulated within the SEI compared with other lithium salts, but with higher selectivity.⁹⁵ Additionally, Fu et al.¹⁰³ assessed various lithium salts in a continuous-flow reactor, which was coupled with hydrogen oxidation at the anode. Among the investigated lithium salts (BOB⁻, PF₆⁻, ClO₄⁻, TFSI⁻, and BF₄⁻), LiBF₄ offered superior performance with a FE of up to 61% (Fig. 8d). This enhanced performance was attributed to the formation of a compact SEI layer. Their study also highlighted two critical principles for designing effective lithium salts for Li-NRR: ensuring reductive stability by avoiding anions with carbonyl or carboxyl groups, which could be reduced by metallic lithium, and addressing electrolyte poisoning due to polymerization. Moreover, Du et al.⁹⁶ investigated the use of concentrated salt with bis(trifluoromethylsulfonyl)imide (NTf₂⁻) and bis(fluorosulfonyl)imide (FSI⁻) anions for Li-NRR. These anions were found to be highly stable under lithium-reduction conditions and supported rapid lithium electro-deposition rates. Superior Li-NRR performance was achieved with an NH₃ production rate of 150 ± 20 nM s⁻¹ cm⁻² and a current efficiency of 99%, using 2 M LiNTf₂ in THF/ethanol with a Ni wire electrode at a fixed potential of −0.55 V vs. Li/Li⁺. The study revealed that a concentrated LiNTf₂ electrolyte resulted in the greatest FE and NH₃ production compared to LiFSI and other common electrolytes (Fig. 8e). LiNTf₂ electrolyte reportedly creates a compact SEI layer that resulted in the superior FE. Further investigations showed that varying the concentration of LiNTf₂ from 0.1 M to 3 M indicated that the optimal NH₃ production rate occur between 1.5 M–2.0 M, as shown in Fig. 8f. These findings from the studies on Li-NRR provide valuable evidence of the practicality and effectiveness of different lithium salts in advancing gNH₃ production.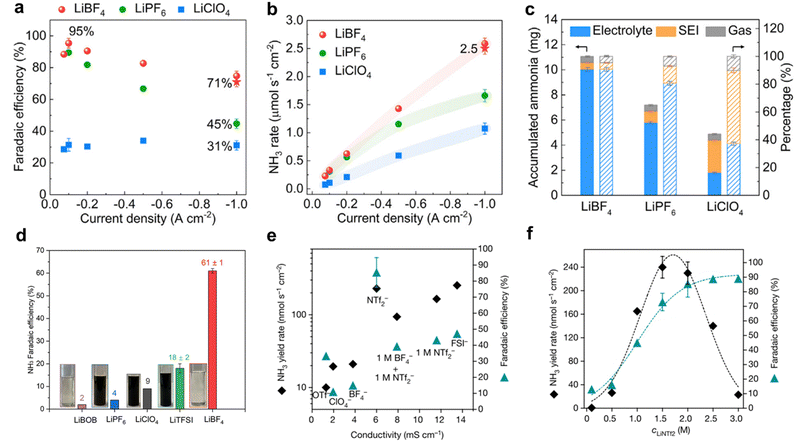

Fig. 8 Lithium salt effect. (a) Faradaic efficiency and (b) NH₃ production of porous Cu electrode using differing lithium salts at current density from −0.075 to −1.0 A cm_geo⁻². (c) Accumulated NH₃ amount in electrolyte, SEI, and gas phase using different lithium salts at a current density of −1.0 A cm_geo⁻². Reproduced from permission.⁹⁵ Copyright 2022, Elsevier. (d) Faradaic efficiencies of different lithium salts at 1 M and, 0.5 M for LiBOB. Reproduced with permission.¹⁰³ Copyright 2024, American Chemical Society. (e) NRR faradaic efficiency and NH₃ yield rate plotted against conductivity for different electrolytes at 2 M, a mixed 1 M LiNTf₂ + 1 M LiBF₄ system and 1 M LiNTf₂. (f) Comparison of the Li-NRR faradaic efficiency with NH₃ yield rate as a function of LiNTf₂ concentration. Reproduced with permission.⁹⁶ Copyright 2022 Springer.

4.2 Proton sources

The selection of proton source is crucial for Li-NRR, not only it drives the protonation of Li₃N, but also take part in the formation of SEI that has significant impact on the long-term reductive stability and the corresponding NH₃ formation activity and selectivity. Ethanol (EtOH) is the earliest reported and has been the most extensively studied in Li-NRR electrochemical system, whereas the precise reasons for itswidespread use and effectiveness still remain unclear.⁴³ Du et al.⁹⁷ reported that it is irreversibly consumed due to THF oxidation, forming by-products of 2-ethoxytetrahydorfuran and pentanal diethyl acetal (Fig. 9a and b). In addition, the reduced metallic lithium is highly electrochemically and chemically unstable and forms lithium ethoxide (CH₃LiO) with ethanol.^50,94 Therefore, an increasing concentration of ethanol as proton source can lead to its consumption due to the interaction of Li, and further leads to the unstable electrochemical system. A major issue related to this is the sacrificial solvent mechanism, where protons are not produced from sustainable sources such as H₂O or H₂, thereby limiting the practical industrial application. Other types of alcohols have also been reported and shown some promising results, such as 1-butanol, iso-propanol, and etc.^51,97,99 Iso-propanol has been proposed as an alternative proton source, showing similar high Li-NRR reaction metrics (Fig. 9c) without undergoing THF degradation.⁹⁷ Additionally, Lazouski et al.⁵¹ and Krishnamurthy et al.¹⁰⁴ reported the effect of chemical nature of proton donor via solvatochromic Kamlet–Taft parameters, reflecting the hydrogen bond donating (α) and accepting (β) capabilities. Findings showed that linear aliphatic alcohols exhibited the highest number of highly active proton donor groups for Li-NRR. Among the proton donors tested, including the commonly used ethanol, 1-butanol exhibited the greatest NH₃ selectivity. Additionally, the NH₃ FE exhibited a peak in response to concentration at 0.25 M, showing a correlation between NH₃ FE and SEI permeability, which in turn effects relative mass-transfer coefficients for N₂ and H₂ through SEI. Optimal selection of both the lithium salt and proton carrier plays a synergistic role in enhancing Li-NRR performances. In addition to sacrificial proton source, a “proton shuttle” mechanism also exists, reported by Suryanto et al.,⁴⁹ as shown in Fig. 3a for pathway (ii). Such a non-sacrificial proton mechanism, involving using proton source that can reversibly donate and accept protons without being consumed in the reaction. For example, phosphonium-based cations such as trihexyltetradecylphosphonium ([P_6,6,6,14]⁺)⁷⁰ have been shown to undergo reversible deprotonation, forming a stable ylide structure, confirmed through ³¹P nuclear magnetic resonance (NMR) and mass spectrometry. This provides a foundation for undergoing a complete cycle of protonation–deprotonation, for highly stable Li-NRR operations with minimal oxidation or reduction of the proton source. Consequently, such proton shuttle mechanism has led to highly stable long-term Li-NRR, achieving a constant NH₃ formation rate of 53.7 ± 0.4 nM s⁻¹ cm⁻², and a constant current density of 22.5 mA cm⁻² in one-compartment cell reactor, with a mean FE of 69%. However, a limitation of the proton shuttle mechanism is the limited mass-transfer in the batch cell reactors.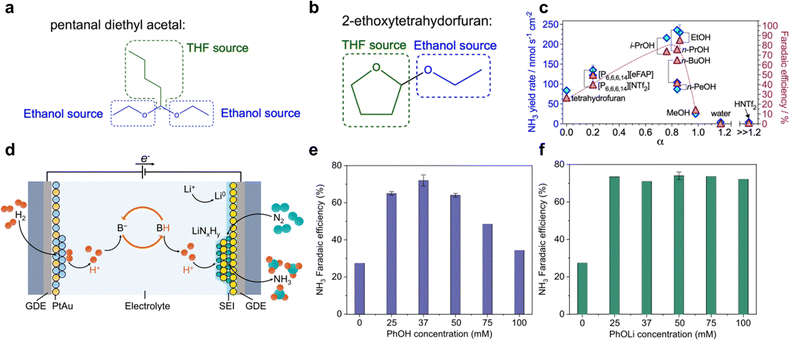

Fig. 9 Proton source effect. Most plausible side products (a) 2-ethoxytetrahydrofuran and (b) pentanal diethyl acetal with ethanol and tetrahydrofuran sources highlighted with, respectively, blue and green colour. (c) NH₃ yield rate and Li-NRR FE plotted against Kamlet–Taft hydrogen bond donation parameter for the proton carrier (except NH₄NTf₂) added at 0.1 M concentration (except for the tetrahydrofuran data, which represent a solution with no additional proton carrier). Reproduced with permission.⁹⁷ Copyright 2023, Royal Society of Chemistry. (d) Schematic proton-shuttling process for lithium-mediated ammonia synthesis in a continuous-flow electrolyzer. Faradaic efficiency changed with varying (e) phenol, and (f) lithium phenoxide concentrations. Reproduced with permission.⁹⁹ Copyright 2024 Springer.

More recently, an innovative approach for continuous NH₃ production has emerged by incorporating the hydrogen oxidation reaction (HOR) at the anode of continues-flow electrolyser, which generates renewable H⁺ on the go (Fig. 9d).^99,101 In this design, EtOH is initially employed to provide protons and form NH₃. The resulting ethoxide EtO⁻ acts as a proton shuttle mediator, which can combine with D₂ (isotope-labelled deuterium) for further protonation. This is confirmed by the ND_x (x = 1, 2, and 3) products through operando mass spectrometry tests. This setup achieved a FE for ammonia production of up to 61 ± 1% with an energy efficiency of 13 ± 1%, demonstrating the potential for highly stable continuous-flow electrochemical synthesis of ammonia by Li-NRR.

In addition, this research also raises the question of whether EtOH could be replaced by with other proton carriers. Further investigation revealed that while EtOH plays a crucial role in SEI formation, H⁺ generated from the anode can be shuttled with other species, even without EtOH.¹⁰⁵ Experiments conducted by Fu et al. found that phenol (PhOH) exhibited the highest FE of 72 ± 3% in the Li-NRR process, attributed to the highly-stable deprotonated PhO⁻ (Fig. 9e).⁹⁹ Interestingly, protons in proton sources (HA) were found to be non-essential for ammonia formation, as demonstrated by the use of PhOLi (Fig. 9f), which achieved a FE of 74 ± 2%. Moving forward, understanding the mechanistic aspects of the proton shuttle mechanism is crucial for engineering electrolytes that can achieve high NH₃ activity and selectivity in Li-NRR, ultimately contributing to the practical development of green ammonia synthesis (gNH₃s).

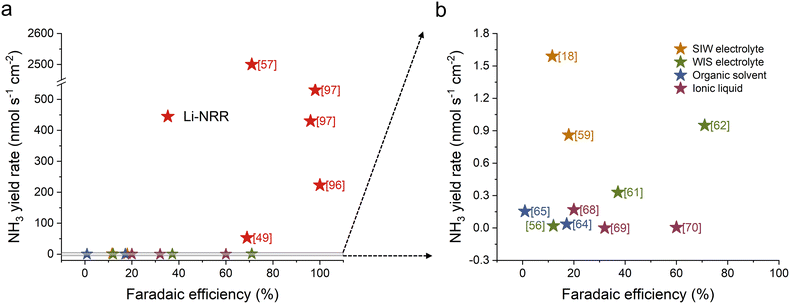
Additionally, Fig. 10 compares ammonia yield rate and faradaic efficiency for both direct eNRR and Li-NRR, offering a clearer perspective on various electrolyte engineering strategies. As shown in Fig. 10a, Li-NRR generally exhibits higher NH₃ selectivity and activity compared to direct eNRR in most experimental studies. Fig. 10b provides an enlarged view of different electrolyte engineering approaches in direct eNRR, highlighting the challenge of simultaneously achieving both high activity and selectivity.

Fig. 10 Experimental results from the literature showing faradaic efficiency (%) versus NH₃ yield rate (nmol s⁻¹ cm⁻²). (a) Comparison of N₂ reduction performance for both direct eNRR and Li-NRR mechanisms. (b) Enlarged view comparing N₂ reduction in the direct eNRR mechanism through various electrolyte engineering approaches.

5. Computational techniques for electrolyte modelling: dynamic and kinetic mechanism

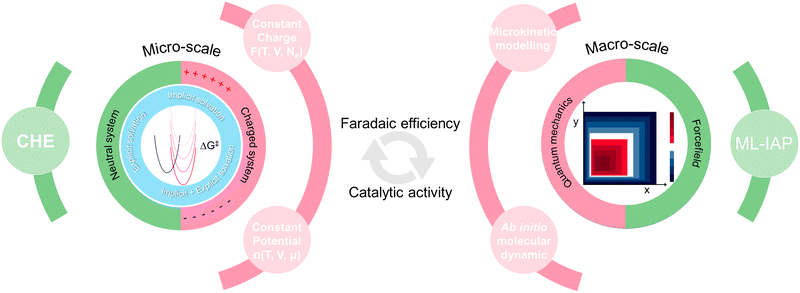
Although electrolyte engineering can significantly enhance eNRR reductive performance, the underlying mechanism(s) are still not fully understood. Therefore, computation techniques will become powerful tools to reveal the reaction mechanisms and establish guidelines for electrolyte design. Modelling electrolytes requires consideration for both solvation and electrode potential effects, which impacts reaction intermediates, electrodes, and electrolytes. To model the solvation effect, there are three methods to consider this in calculations, in the order of increasing computation costs: (1) implicit solvation model, giving the dielectric and ionic response of electrolyte by creating a solvation cavity definition which treats the interface as a dielectric continuum; (2) explicit solvation model, which builds electrolyte components into the modelling process, and (3) hybrid implicit plus explicit solvation models, which combines the consideration in points (1) and (2), as depicted in Fig. 11.

Fig. 11 Schematic illustration of computation techniques for electrolyte engineering, spanning from microscopic descriptors employing quantum-level based calculations that include solvation and electrode potential effects, to macroscopic kinetic strategies, bridging the gap for practical electrochemical performances.

When treating electrode potential in simulations, the simplest and most common approach is the computational hydrogen electrode (CHE). This method accounts for electrode potential (U) by adding a constant term (−eU) to the free energy calculations for neutral system.^101,106,107 While CHE has been widely accepted and used in the past, it has limitations when it comes to capturing the detailed effects of specific electrode conditions on the reaction.

To improve upon the limitations of the simplified CHE model, more advanced methods have been developed to simulate reactions under specific electrode potentials. These methods often involve introducing additional electrons into the system to alter the work function, thereby adjusting the electrode potential. In such cases, the computation unit cell will need to be neutralized to avoid artificial electrostatic interactions.¹⁰⁸ This can be achieved through solvation models and specific approaches, such as constructing a uniform counter-charge background or placing a counter-charged explicit electrolyte/electrode system, which results in a realistic region of decaying electrostatic potentials.^109,110 With these method in place, the system could accommodate an additional number of electrons (N_e). When the charge of a system is held constant, this approach is referred to as the constant-charge method.¹⁰⁸ Alternatively, the charge of a system can be varied to maintain a constant electrode potential, known as the constant-potential method, where the electron's chemical potential (μ) of the system is kept in constant. In this approach, the surface potential is determined relative to the vacuum state for the work function, while the number of electrons is adjusted within the system in a self-consistent manner.^111,112 The key difference between the constant charge and constant potential methods lie in whether electron exchange with an external source is allowed, which enables the potential to remain constant throughout the calculation. These advanced techniques enable us to conduct simulations not only for material design but also for capturing interfacial dynamics, which is crucial for advancing electrolyte design modelling in complex scenarios.

In the following sections, we present a comprehensive summary of electrolyte modelling approaches. We begin with constant electrode potential (CEP) with static first-principles calculations (Section 5.1.1). We then explore its application in macroscopic kinetic computations, including mean-field microkinetic modelling (MF-MKM) (Section 5.1.2), and kinetic Monte Carol simulation (kMC) (Section 5.1.3). Beyond this hybrid approach based on static calculation, we also discuss quantum mechanical molecular dynamics simulations, which employ fully explicit solvent and electrolyte molecules through an ab initio modelling approach (Section 5.2). While this method provides the most accurate depiction of solvation and electrification effects, it is limited by short time scales and high computational costs. To overcome these challenges, we also examine the use of machine learning-interatomic potentials (ML-IAPs) generated from DFT calculations, which extend molecular dynamics simulations to longer time scales while maintaining quantum mechanical accuracy (Section 5.3).

5.1 Microkinetic modelling of first-principle based computations

5.1.1 Constant electrode potential (CEP) method. The electrode potential (U) plays a significant role in governing the surface processes on electrocatalysts, influencing the kinetics of eNRR compared with HER. In realistic electrochemical systems, catalyst surface changes quite dynamically, both in terms of the structure and the electronic states. Early methods addressed these surface charge changes through post-processing techniques, including the CHE model and the constant-charge method. The CHE model, as reported by Nørskov et al.,¹⁰⁷ handles the potential-dependent energy barriers by postprocessing based on single barrier calculations under neutral charged conditions. In the constant-charge scheme, the total charge of the system remains fixed, electron transfer occurring only between the species within the system. In both approaches, the potential effect is only included indirectly, without considering the changes in the Fermi energy level of the system. This leads to discrepancies between simulated models and real operating systems under constant potential.

The constant electrode potential (CEP) method was then developed to address the dynamic potential/charge variations in catalyst surface and simulate the realistic electrocatalytic N₂ reduction kinetics.^28,113 In the CEP model, the Fermi energy level or μ is pre-set and remains consistent at all time. Computationally, this method relies on the implicit solvation model such that the electrode–electrolyte interface is treated as polarizable continuum model, where the electronic and continuum ionic charge are distributed via linear Poisson–Boltzmann model (LPB) or non-linear Poisson¹¹⁴ – Boltzmann model (NLPB), providing the fundamental treatment of the electrified system.¹¹⁵ Alternative methods are also available, such as the self-consistent continuum solvation (SCCS) model, where the ionic charge is distributed on a Gaussian-shaped plane.¹¹⁶ The LPB model is available through software such as VASPsol,^117,118 implemented in the most widely used plane wave DFT code – Vienna Ab Initio Simulation Package (VASP). In addition, Mathew et al.¹¹⁸ developed the charge-asymmetric nonlocally determined local-electric (CANDLE) solvation model to determine asymmetrically charged solvents that was implemented in JDFTx code.¹¹⁹ Non-local cavity definition is used in the solvation model and prevented the possible “solvent leakage”.¹²⁰ Most recently, Plaisance et al.¹²¹ developed “VASPsol++” solvation model based on the origin framework of VASPsol code that is implemented in VASP,⁹³ capturing a non-local cavity and dielectric responses that is closer to the realistic electrochemical operating condition, which characterized a non-linear double hump shape of the differential capacitance curve.¹²²

These computational codes provide a foundational base for simulating charged surface under applied electrode potentials. By incorporating ionic screening and a self-consistent field cycle, the number of electrons (N_e) can be determined and adjusted through an external charge flux (also known as the reference electrode), which operates in a self-consistent manner. This approach enables the exchange and optimization of N_e needed to maintain the equivalent Fermi energy in the grand canonical ensemble. Consequently, the overall charge of the system varies self consistently, establishing a constant potential framework instead of a constant charge. Liu's team developed a constant-potential model for ab initio molecular dynamics (AIMD) simulation, and implemented it into VASP.^123–127 This model, referred to as the constant-potential hybrid-solvation dynamic model (CP-HS-DM), incorporates both explicit and implicit solvation models enabled by VASPsol. In this model, the ionic charge compensates the net electronic charges, maintaining the overall charge neutrality of the unit cell, while the Fermi level evolves according to the grand-canonical distribution at the target electrode potential. Specifically, the external electrochemical potential (U) is adjusted by computing the work function (Φ) through variations in N_e, which are required to achieve equivalent Fermi energy in the grand-canonical states, with reference to the standard hydrogen electrode (SHE):

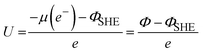where Φ and Φ_SHE are the work function of, respectively, the simulating system and SHE (ranging from 4.43–4.85 eV from experimental results).¹²⁸ The free energy in the grand canonical state is computed from:

Ω = E_tot + ΦN_e (9)

This foundation sets the stage for further advancements in microkinetic modelling strategies such as the MF-MKM and kMC, enabling more detailed and accurate predictions of electrochemical processes through time via engineering electrolyte and enhancing our understanding of complex catalytic systems.

5.1.2 Mean-field microkinetic modelling (MF-MKM). MF-MKM was developed in the late 20th century and has been widely employed in heterogeneous electrocatalysis due to its computational efficiency.^129–136 It focuses on prediction for a simplified overall process by neglecting the distribution of the active sites and adsorbates on the electrode surfaces. The general formulation of MF-MKM utilizes parameters for all reaction intermediates, including thermodynamic inputs for adsorption energies and kinetic inputs for activation energies of rate-limiting steps. The reaction network is constructed by formulating reaction rate equations with appropriate boundary conditions, which are then represented as a series of ordinary differential equations (ODEs). By solving these ODEs under site balancing at steady-state, the surface coverage of all adsorbed species and the overall rate can be determined and used to obtain the Tafel slope and the exchange current density (i₀) for a particular operating condition.¹³⁵

In the past, MF-MKM has been used to develop efficient electrocatalyst materials. For an eNRR example, Singstock et al.¹³⁷ assessed the mechanism on Fe–S–Mo surface which exhibited good N₂ reduction.¹³⁸ The computation of the effect of a realistic solvated environment was achieved via grand-canonical density functional theory (GC-DFT) using a hybrid solvation model (implicit + explicit). The GC-based nudged elastic band (NEB), combined with MF-MKM analysis showed good agreement with experimental results, as shown in Fig. 12a and b. This approach is instrumental in identifying effective electrocatalysts by modelling the kinetic performance in a realistic electrocatalytic environment. In addition to the material design, it is important to incorporate the electrolyte effect such as the cation effect, mass transfer, and local pH values. By using such method, Choi et al.¹³⁹ resolved the discrepancy between experiment and theoretical computation for potential- and pH-dependent competition of NRR/HER. A cross-over potential was found between the N₂ adsorption and H adsorption (Volmer-step) on Fe–N–C catalysts, leading to a different surface coverage for each species, which resulted in varied yield rates and FE. Such advanced techniques have achieved a similar experimental value (pH and electrode potential) for the maximum NH₃ yield rate and selectivity (Fig. 12c–e). In addition, our recent work has provided atomic-level insight into the critical role of interfacial N₂ concentration by employing MF-MKM combined with first-principle calculations.¹⁴⁰ It is suggested that the sluggish N₂ reductive activity cannot be addressed by merely regulating the electrode potential or material design alone. Instead, optimal eNRR conditions should ensure both strong N₂ activation by the electrocatalysts and a high N₂ availability at EEI, which can be improved through targeted electrolyte engineering strategies.

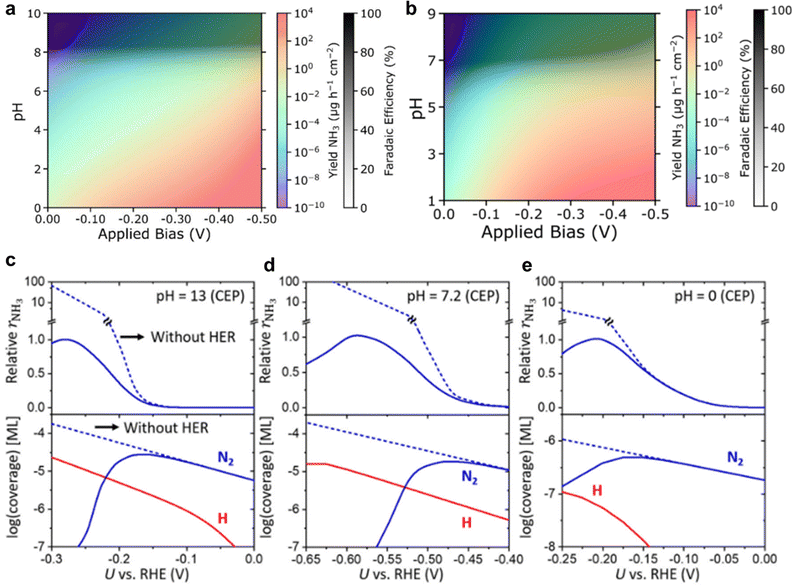Fig. 12 Microkinetic modelling for eNRR. Heatmap for NH₃ yield (coloured shading) and NRR FE (black and white shading) as pH and applied bias are varied in NRR microkinetic model with employing (a) CHE model, and (b) CEP model for Fe₂Mo₆S₈. Reproduced with permission.¹³⁷ Copyright 2022, American Chemical Society. MKM findings using CEP model at three pH, (c) 13, (d) 7.2 and (e) 0. The relative r_NH3 is determined via dividing r_NH3 by its maximum value. Dashed lines represent MKM without HER. r_NH3 and coverage are shown in the upper and lower panels, respectively. Reproduced with permission.¹³⁹ Copyright 2021 Springer.

MF-MKM approach can be widely used for eNRR, including Li-NRR mechanism. Andersen et al.⁴⁷ were the first established a simple microkinetic modelling model for Li-NRR. In this model, the diffusion of Li⁺, H⁺ and N₂ molecules are explicitly considered and assumed to be the rate-limiting steps. Consequently, the selectivity for NH₃ and H₂ formation at steady state can be predicted and presented as function of diffusion rates of Li⁺, H⁺, and N₂. The concentrations of H⁺ and N₂ significantly contribute to the high selectivity of Li⁺ deposition and NH₃ formation, which can be improved by employing gas diffusion electrode. In addition, the MF-MKM investigation revealed that the diffusion rates play a crucial role in forming the SEI layer, further determining the overall electrochemical performance.

5.1.3 Kinetic Monte Carlo (kMC) simulation. Due to the necessity of understanding the dynamic interplay between elementary processes and the interfacial environment, there is an increasing demand for spatial-dependent modelling that can handle larger atomistic systems and for longer simulation times. This approach allows for a more accurate representation of the complex interactions occurring at the interface, capturing the spatial variations and temporal dynamics that are crucial for a deeper understanding of heterogeneous electrocatalytic processes. The kMC approach uses statistical algorithms to determine the probability of an event i.e. elementary reactions including, adsorption, desorption and diffusion, from discrete-time scale arrays of femtoseconds to seconds.^{27,135,136,141,142} Interfacial dynamic variations corresponding to multiple reaction intermediates cannot be assessed through zero-dimensional MF-MKM.¹⁴³ In kMC simulation for every event, each state transition jump in a system follows a stochastic Markov process¹⁴² where the probability of state transition from state i to state j at a certain time t, p_ij(t), is independent of the preceding history (<t), and is expressed as an exponential distribution rate constant with respect to unit time, k_ij, given by eqn (10):

p_ij(t) = k_ij exp(−k_ijt) (10)

Developments have been reported for different Monte Carlo algorithm^141,144,145e.g. Ising model,¹⁴⁶ lattice-gas model¹⁴⁷ and Potts model.^148,149 It is capable of explicitly accommodating spatial inhomogeneity arising from site types and incorporate spatial correlations resulting from lateral interactions among adsorbates.¹⁴³ Therefore, providing an accurate electrochemical prediction at a microscopic level and guiding the design strategy of both active electrocatalyst and electrolyte is achievable in the future. Additional reports use the DFT-kMC method in electrocatalysis include, CO oxidation, NO reduction and oxidation and ethylene hydrogenation. Lee et al.¹⁵⁰ combined DFT-kMC analysis to establish the best performing NRR electrocatalyst amongst different Ru-based novel bimetallic catalysts, RuTi, RuV₂, Ru₃W, RuZn₃ and RuZr. Thermodynamic and electronic structure was determined via DFT computation and used for sequential kMC simulations that simulated kinetic performance i.e. turnover frequency TOF, Fig. 13a, and coverages, Fig. 13b, for the reaction pathway of NRR and HER, together with time evolution for different intermediates. The computation results demonstrated high eNRR electrocatalytic performance of these Ru-based bimetallic material of RuV₂(110).

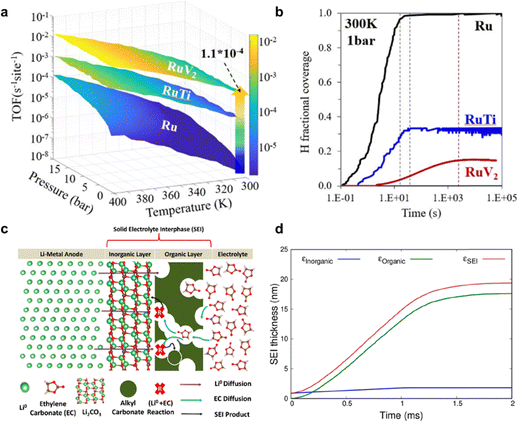Fig. 13 kMC simulation for eNRR. (a) TOF value for eNRR on Ru(001) and bimetallic catalysts RuTi(110) and, RuV₂(110) as a function of temperature, pressure and time. (b) H coverage change over time on Ru(001) and bimetallic Ru-based catalysts under mild conditions of 300 K and 1 bar. Reproduced with permission.¹⁵⁰ Copyright 2022, American Chemical Society. (c) Schematic for electrode/electrolyte interface and where SEI growth reactions are expected to occur. (d) Evolution of SEI layer thickness with time following the ethylene carbonate decomposition reaction over Li₂CO₃(001). Reproduced with permission.¹⁵¹ Copyright 2022, American Chemical Society.

In addition to modelling the reaction process, kMC simulation could also be used to model dynamic phenomena including formation of the SEI^27,151–153 and ion diffusion.¹⁴³ The understanding about SEI formation is important because its presence and characteristics significantly impact long-term stability. Although no specific example exists for eNRR, there are relevant studies in Li-metal battery field. To be specific, the SEI formation is a consequence of electrolyte reduction involving organic and inorganic layer, as shown in Fig. 13c. Initially, the formed SEI layer on the electrode surfaces acts as a protective barrier, preventing further reduction of the electrolyte during initial stages. However, SEI layer growth results in capacity loss and leads to the poor battery performance in a single cycle.¹⁵¹ Furthermore, kMC is capable of simulating evolution of the SEI layer thickness with time, as shown in Fig. 13d.¹⁵¹ Similarly, in the context of the Li-NRR electrochemical reaction, the presence and characteristics of the SEI layer on the electrode surface play a crucial role in determining the long-term stability and efficiency of the reaction. Understanding the SEI layer growth through modelling methods can enable the tuning of its growth behaviour, thereby enhancing Li-NRR performance. This makes it a focus area for improving the durability and effectiveness of these systems, and the understanding of this behaviour can benefit from kMC modelling.

5.2 Ab initio modelling: explicit solvation model

Molecular dynamic (MD) simulation is also a crucial computation strategy for electrolyte modelling with explicit solvent. It allows configuration of the realistic electrochemical reaction microenvironment, thus serving as a better bridge between computation and experiment.^154,155 Within MD, there are mainly three categories: classic molecular dynamics (cMD); ab initio molecular dynamics (AIMD); machine learning based molecular dynamics (MLMD). In cMD simulations, particle motion is based on the empirical force fields in the form of classical mechanics equations. However, the accuracy of cMD in describing bond formation and breaking during electrocatalytic reactions at the EEI is limited, as it does not fully represent the electronic polarization behaviour in interactions between the electrolyte and electrode.¹⁵⁶ Hence, in this section, we focus on the AIMD approach, and MLMD approach in the later section.

There are two type of AIMD simulation methods: Born–Oppenheimer MD (BOMD) and Car–Parrinello MD (CPMD).¹⁵⁷ Every MD step is quantum mechanically calculated by solving the Schrödinger equation based on adiabatic approximation (or BO approximation), which separates the wave function and Hamiltonian of the nucleus. In AIMD simulations, the solvent or electrolyte is explicitly modelled, revealing the interfacial microenvironment or EDL when an external potential is applied. This approach provides simulation trajectories at a quantum mechanical level, effectively capturing the interfacial structural dynamics.^158–161 Factors including, the coordination number (Fig. 14a), hydrogen bonding net (Fig. 14b), water orientation (Fig. 14c) and EDL structures, making significant impact on the reaction energetic. Combining the sampling techniques (metadynamics and thermodynamic integration) with (constrained) AIMD modelling strategy, the free energy differences between two states can be obtained.^162–165 Whilst this method has been developed and applied in theoretical study of electrocatalytic processes including HER and carbon dioxide reduction reaction (CO₂RR), application to electrochemical nitrogen reduction reaction (eNRR) is limited.

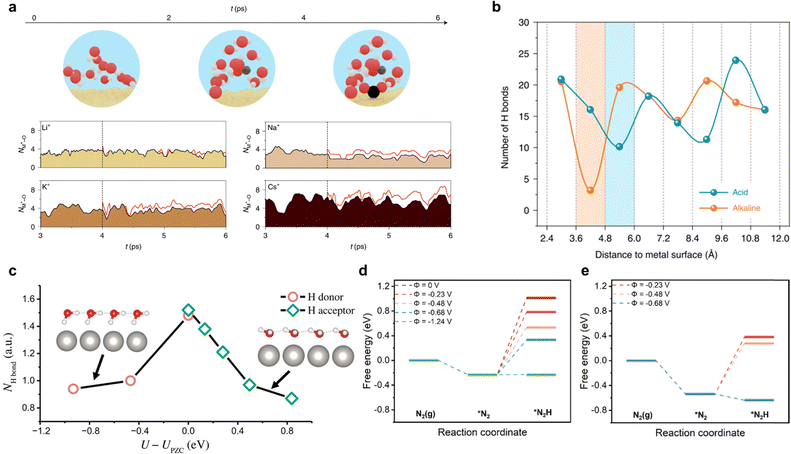Fig. 14 Ab initio modelling of electrochemical reactions including eNRR. (a) Cation coordination with CO₂. Cation–oxygen bond length evolution with the presence of various cations by AIMD simulations at 300 K. Reproduced with permission.¹⁶⁶ Copyright 2021 Springer. (b) Statistical distribution of the number of H bonds along the Pt(111) electrode surface in normal direction. Shaded areas represent gap zones of interfacial water and H-bond networks. Reproduced with permission.¹⁶⁷ Copyright 2022 Springer. (c) Number of hydrogen bond donors and acceptors of interface water molecules on Pt(111) catalyst as a function of potential. A hydrogen bond is defined when the O–O distance is <3.5 Å and the O–O–H angle is <35°. Insets show the structural models of interface water at negative and positive potentials a.u., arbitrary units. Reproduced with permission.¹⁶⁸ Copyright 2020, American Association for the Advancement of Science. Comparison of free energy for the first protonation of N₂ with variation in electrode potential: (d) CHE model and (e) thermodynamic integration with full explicit solvent model (right). Reproduced with permission.¹⁶⁹ Copyright 2022, American Chemical Society.

Incorporating realistic aqueous environments and varying electrode potentials in AIMD simulations significantly enhances the accuracy of modelling electrochemical interfaces for eNRR. Qian et al.¹⁶⁹ reported an AIMD simulation and considered the effect of electrode potential and aqueous environment and on Fe–N₄ solid–liquid interface/EEI. The aqueous environment was simulated by including the explicit water molecules (ca. 141), whilst the electrode potential was modified via varying the number of H₃O⁺ in the system. Constrained AIMD (c-AIMD) simulation and thermodynamic integration was applied to analyse the free energy profiles of N₂ adsorption and its proton transfer. The free energy diagram for the hydrogenation of *N₂ was determined by comparing the explicit solvent model and the CHE-based model, Fig. 14d and e. It was found that the explicit solvent model predicted a lower potential for the exothermic conversion of *N₂ than the CHE-based model. Computed findings were in good agreement with experiment,¹³⁹ evidencing accuracy and consistency of the modelling method, and establishing the significance of incorporating realistic aqueous environment and accounting for electrode potential. More recently, Mao et al.¹⁷⁰ explored the role of alkali ions in modulating the activity and selectivity of NRR on Fe electrode via AIMD approach and evidenced by experiments. Four promotion effects of alkali cations on advancing NRR kinetics were identified: (i) N≡N bond cleavage; (ii) intermediate stabilization; (iii) HER suppression; and (iv) charge redistribution on the interface. Additionally, among the selected alkali ions (Li⁺, Na⁺, and K⁺), the Li⁺ solvation shell mediates the NRR kinetics by receiving the lowest *NNH formation energy barrier −0.50 eV at constant potential condition U = −0.3 V vs. RHE. For Li-NRR, several detailed DFT studies have been conducted to assist experimental procedures. These include, computing the formation free energy of possible Li-contained compounds at selected voltage, modelling the free-energy barrier for surface mobility⁹⁵ and determining the free energy diagram for N₂ reduction intermediates on possible formed Li-contained SEI.⁴⁶ Maniscalco et al.¹⁷¹ simulated the first step of Li-NRR via CPMD to show a new, unexplored mechanism, namely, nitrogen adsorption into the lithium bulk, nitrogen–hydrogen reaction and oxygen reactivity with the lithium surface. Hydrogen activation facilitated ready reaction with molecular nitrogen driven by the low density of lithium and the formation of oxide and nitride structures. Because of the complexity of the electrochemical environment of Li-NRR, the future optimal method for scale-up is likely in in modelling the potential electrolyte reduction, SEI formation and simulating the EDL on the electrified interface.^27,152,155 With AIMD, it is difficult to maintain a constant electrode potential during computation because the potential/charges on the electrode are affected by the dipole variations on the EEI, thereby affecting the reaction rates, such limitation is reportedly obviated for HER and ORR,^28,123,125 however there are no reports for eNRR.

Theoretically, AIMD can simulate all elements in the periodic table and provides accurate insights into bond cleavage and formation, charge transfer, and polarization effects. However, for electrolyte modelling, AIMD approach can be computationally expensive because it requires a significant number of energetically favourable solvent arrangements within a larger simulation cell to accurately describe dynamics within the EDL, which confines the overall simulation to a short time frame. Progress towards developing more affordable methods to accurately capture solvent and electrolyte dynamics is essential. Machine-learning techniques may play a crucial role in this effort, and will be discussed in the following section.

5.3 Machine learning-interatomic potentials (ML-IAP): extended time scale with ab initio accuracy

To address limitations of computational resources and constraints of atomic size and time length scale, development of machine learning-interatomic potential (ML-IAP) enables extended simulation time and atomic size scale together with ab initio accuracy.^161,172 ML-IAPs represents the potential-energy surfaces (PES) by fitting large data sets from DFT-based computations via machine learning. A first step is to construct a set of data containing the energies and atomic forces corresponding to individual points on the PES. The structural inputs, e.g. atomic coordinates, are transformed onto suitable machine learning numerical descriptors e.g. atom centered symmetry functions, bispectrum of the neighbour density and Coulomb matrix after ‘training’ with equivalent atomic configurations such as permutation, translation and rotation(s). The goal of training is to optimize the parameters of a ‘smooth’ PES that best describes the structural input data for high-dimensional system. The ML-IAPs therefore is derived through selected machined-learned regressions to improve scalability of simulation model size and time span. Selected ML-IAPs reported include, neural network potential (NNP),¹⁷³ spectral neighbour analysis potential (SNAP),¹⁷⁴ Gaussian approximation potential (GAP),¹⁷⁵ smooth overlap atomistic potential (SOAP)¹⁷⁶ and deep-potential (DP).¹⁷⁷

At present, there are limited reports applying machine learning framework models to develop efficient and accurate MLPs for complex multiphase such as the interfacial solid–liquid system. Specifically, Schran et al.¹⁷⁸ reported six complex aqueous systems i.e. F⁻–H₂O, SO₄²⁻–H₂O, CNT–H₂O, BNNT–H₂O, MoS₂–H₂O and TiO₂–H₂O through AIMD-driven active learning protocols relying on neural network potentials (Behler–Parrinello NNPs). This method reportedly gave high-accurate performance of >90% in reference to AIMD findings. These outcomes are derived from an array of features including, radial distribution functions (RDFs), vibrational density of states (VDOS) and the root mean square error (RMSE) of the force. A Behler–Parrinello NNPs, based active learning training workflow¹⁷⁹ was used to characterize the pressure–temperature dependent behaviour of a single layer of water molecules within a graphene-like channel from a first-principle based understanding,¹⁸⁰ to give insight into possible future development of nano-scaled materials and electrolyte design. However, there appears to be limited reports on the application of MLPs on N₂ reductive process, which highlights a promising area for future research and development.

6. Conclusion and perspective

In this review, we explored two pathways for green NH₃ synthesis: the conventional direct electrocatalytic NRR and the novel indirect Li-NRR. Both pathways have shown significant progress through electrolyte engineering approaches based on experimental results. To scale electrochemical ammonia synthesis for industrial viability, specific performance targets must be achieved. According to the US Department of Energy's REFUEL program (2016),¹⁸¹ practical electrochemical NH₃ production requires high production rates of current density above 300 mA cm⁻². Additionally, the Coulombic or faradaic efficiency should exceed 90%, dedicating the majority of the current to ammonia synthesis and minimizing side reactions such as hydrogen evolution. An energy efficiency of at least 60% is also required to ensure a substantial portion of electrical energy is directly converted into ammonia. Achieving these benchmarks would allow electrochemical methods to compete with the traditional thermochemical Haber–Bosch process.

For direct eNRR, these methods include modifying alkali cations and concentrations in SIW and WIS electrolytes, utilizing organic solvents, and employing ionic-liquid-based electrolytes. Developing an optimal interfacial microenvironment is key to enhancing the electrocatalytic performance of the N₂ reduction process. For Li-NRR, higher NH₃ FE and yield rates have been reported by regulating lithium salts and proton sources. However, a deeper understanding is required to explore the formation of the SEI in relation to electrolyte compositions and its impact on the long-term stability of continuous NH₃ synthesis. To achieve these, computational techniques offer a quantitative theoretical framework to understand interfacial dynamics at the atomic level, providing insights to fine-tune electrolyte compositions and enhance eNRR performances. For practical green NH₃ synthesis (gNH₃s), future developments in both reaction pathways are necessary.

For direct eNRR, future theoretical computations will need to incorporate both the electrode potential and solvation effect. Present understanding of the impact of electrolytes is insufficient, including ions, organic solvents, and ILs, as well as corresponding interfacial dynamics such as EDL structure, cation concentration, and local pH, on the electrified interface in electrocatalytic NRR. A judicious combination of first-principles-based microkinetic modelling, and ab initio modelling, together with advanced in situ/operando characterisations including, in situ Raman spectroscopy, in situ XRD and FTIR spectroscopy will therefore be needed to establish interfacial electrocatalytic dynamics and atomic-level understanding of eNRR.

For indirect Li-NRR, experimental results have achieved highly selective NH₃ formation at the laboratory scale. However, high energy efficiency remains a significant challenge.¹⁸² One major reason is that the reduction of Li⁺ requires a very negative electrode potential of up to −3.04 V vs. SHE. Similarly, other metals such as calcium and magnesium have demonstrated the feasibility of mediated-NRR processes, but they also require high reduction potentials, with standard reduction potentials of −2.87 V and −2.37 V vs. SHE, respectively.^183–185 It is important to explore other active metals or metal alloys to provide a strong foundation for mediating NRR under potential to achieve higher energy efficiency.¹⁸⁶

Moreover, with the development of proton-shuttle mechanisms and reactor designs employing HOR to avoid the proton sacrificial phenomenon, the long-term stability of the electrochemical process has significantly improved. However, solvent degradation and volatility remain an issue in THF-based electrochemical systems, exploring alternative electrolyte solvents is needed for future development of gNH₃s. Recent publications have aimed at assessing optimal solvents based on their conductivity, side reactions, and NH₃ FE.^100,187,188 For instance, compared to the cyclic ether-based solvents, chain-ether-based solvent is reported to exhibit higher stability in Li-NRR electrochemical system, attributed to the more complete solvation of conductive ions.¹⁸⁸ 300 h of stable operation is achieved employing diethylene glycol dimethyl ether by Li et al.¹⁰⁰ Although significant progress has been made, the ultimate goal of industrial implementation to replace the Haber–Bosch (H–B) process still faces several challenges, including achieving higher energy efficiency, ensuring long-term stability, and addressing issues such as solvent decomposition in electrochemical systems.

To summarize, it is recognized that electrolytes significantly impact the electrochemical performance of NRR in both reaction pathways. To accelerate progress, advanced computation techniques incorporated with MD – based approach are efficient tools for exploring the underlying interfacial dynamics brought by the electrolyte contents. However, challenge still exists in accessing long time scales while maintaining quantum-level accuracy when employing full explicit solvation models. Machine learning interatomic potential-based forcefield simulations may be key to advancing electrolyte engineering by enabling longer simulation times and larger system sizes while maintaining ab initio accuracy.

Author contributions

L. J. conceptualized and contributed to writing – original draft. X. B. and X. Z. reviewed and contributed to conceptualizing and discussion. K. D. reviewed and contributed to writing the MS. Y. J. conceptualization, reviewing and supervision.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge the financial support from Australian Research Council (ARC) Centre of Excellent project through CE230100032.

Notes and references

1. J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639.
2. S. Paul, S. Sarkar, A. Adalder, S. Kapse, R. Thapa and U. K. Ghorai, ACS Sustainable Chem. Eng., 2023, 11, 6191–6200.
3. S. Sarkar, A. Adalder, S. Paul, S. Kapse, R. Thapa and U. K. Ghorai, Appl. Catal., B, 2024, 343, 123580.
4. R. Daiyan, T. Tran-Phu, P. Kumar, K. Iputera, Z. Tong, J. Leverett, M. H. A. Khan, A. Asghar Esmailpour, A. Jalili, M. Lim, A. Tricoli, R. S. Liu, X. Lu, E. Lovell and R. Amal, Energy Environ. Sci., 2021, 14, 3588–3598.
5. A. Adalder, S. Paul, N. Barman, A. Bera, S. Sarkar, N. Mukherjee, R. Thapa and U. K. Ghorai, ACS Catal., 2023, 13, 13516–13527.
6. X. Fu, J. Zhang and Y. Kang, Chem Catal., 2022, 2, 2590–2613.
7. T. Wu, H. Zhao, X. Zhu, Z. Xing, Q. Liu, T. Liu, S. Gao, S. Lu, G. Chen, A. M. Asiri, Y. Zhang and X. Sun, Adv. Mater., 2020, 32, 2000299.
8. T. Wu, X. Zhu, Z. Xing, S. Mou, C. Li, Y. Qiao, Q. Liu, Y. Luo, X. Shi, Y. Zhang and X. Sun, Angew. Chem., Int. Ed., 2019, 58, 18449–18453.
9. H. M. Xu, H. R. Zhu, C. J. Huang, Z. J. Zhang, T. Y. Shuai, Q. N. Zhan and G. R. Li, Sci. China: Chem., 2024, 67, 1137–1160.
10. Z. H. Xue, S. N. Zhang, Y. X. Lin, H. Su, G. Y. Zhai, J. T. Han, Q. Y. Yu, X. H. Li, M. Antonietti and J. S. Chen, J. Am. Chem. Soc., 2019, 141, 14976–14980.
11. C. Kim, J. Y. Song, C. Choi, J. P. Ha, W. Lee, Y. T. Nam, D. M. Lee, G. Kim, I. Gereige, W. Bin Jung, H. Lee, Y. Jung, H. Jeong and H. T. Jung, Adv. Mater., 2022, 34, 2205270.
12. C. Yang, Y. Zhu, J. Liu, Y. Qin, H. Wang, H. Liu, Y. Chen, Z. Zhang and W. Hu, Nano Energy, 2020, 77, 105126.
13. W. Peng, M. Luo, X. Xu, K. Jiang, M. Peng, D. Chen, T. S. Chan and Y. Tan, Adv. Energy Mater., 2020, 10, 1–9.
14. Y. Wang, M. M. Shi, D. Bao, F. L. Meng, Q. Zhang, Y. T. Zhou, K. H. Liu, Y. Zhang, J. Z. Wang, Z. W. Chen, D. P. Liu, Z. Jiang, M. Luo, L. Gu, Q. H. Zhang, X. Z. Cao, Y. Yao, M. H. Shao, Y. Zhang, X. B. Zhang, J. G. Chen, J. M. Yan and Q. Jiang, Angew. Chem., Int. Ed., 2019, 58, 9464–9469.
15. L. Chen, C. Tang, Y. Jiao and S. Z. Qiao, ChemSusChem, 2021, 14, 671–678.
16. L. Chen, C. Tang, K. Davey, Y. Zheng, Y. Jiao and S.-Z. Qiao, Chem. Sci., 2021, 12, 8079–8087.
17. Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086.
18. Y. Song, D. Johnson, R. Peng, D. K. Hensley, P. V. Bonnesen, L. Liang, J. Huang, F. Yang, F. Zhang, R. Qiao, A. P. Baddorf, T. J. Tschaplinski, N. L. Engle, M. C. Hatzell, Z. Wu, D. A. Cullen, H. M. Meyer, B. G. Sumpter and A. J. Rondinone, Sci. Adv., 2018, 4, 1700336.
19. Y. Yang, S. Wang, H. Wen, T. Ye, J. Chen, C. Li and M. Du, Angew. Chem., Int. Ed., 2019, 58, 15362–15366.
20. P. Liu, Z. Huang, S. Yang, J. Du, Y. Zhang, R. Cao, C. Chen, L. Li, T. Chen, G. Wang, D. Rao, X. Zheng and X. Hong, ACS Catal., 2022, 12, 8139–8146.
21. X.-Y. Zhang, I. V. Zatovsky, J.-M. Cao and X.-L. Wu, Tungsten, 2024, 6, 657–662.
22. L.-W. Chen, Y.-C. Hao, J. Li, L. Hu, Y. Guo, S. Li, D. Liu, Z. Zhu, S.-Q. Wu, H.-Z. Huang, A.-X. Yin, B. Wang and Y.-W. Zhang, Sci. China: Chem., 2022, 65, 2188–2196.
23. U. K. Ghorai, S. Paul, B. Ghorai, A. Adalder, S. Kapse, R. Thapa, A. Nagendra and A. Gain, ACS Nano, 2021, 15, 5230–5239.
24. A. Biswas, N. Barman, A. Nambron, R. Thapa, K. Sudarshan and R. S. Dey, Mater. Horiz., 2024, 11, 2217–2229.
25. S. Murmu, S. Paul, S. Kapse, R. Thapa, S. Chattopadhyay, N. Abharana, S. N. Jha, D. Bhattacharyya and U. K. Ghorai, J. Mater. Chem. A, 2021, 9, 14477–14484.
26. S. Paul, S. Sarkar, D. Dolui, D. Sarkar, M. Robert and U. K. Ghorai, Dalton Trans., 2023, 52, 15360–15364.
27. J. W. Abbott and F. Hanke, J. Chem. Theory Comput., 2022, 18, 925–934.
28. X. Zhao, Z. H. Levell, S. Yu and Y. Liu, Chem. Rev., 2022, 122, 10675–10709.
29. G. Qing, R. Ghazfar, S. T. Jackowski, F. Habibzadeh, M. M. Ashtiani, C.-P. Chen, M. R. Smith and T. W. Hamann, Chem. Rev., 2020, 120, 5437–5516.
30. Y. Yang, J. Wang, Y. Shu, Y. Ji, H. Dong and Y. Li, Phys. Chem. Chem. Phys., 2022, 24, 8591–8603.
31. X. Zhang, K. Ren, Y. Liu, Z. Gu, Z. Huang, S. Zheng, X. Wang, J. Guo, I. V. Zatovsky, J. Cao and X. Wu, Acta Phys.-Chim. Sin., 2023, 40, 2307057.
32. C. G. Zhan, J. A. Nichols and D. A. Dixon, J. Phys. Chem. A, 2003, 107, 4184–4195.
33. Y. Abghoui, A. L. Garden, J. G. Howalt, T. Vegge and E. Skúlason, ACS Catal., 2016, 6, 635–646.
34. Y. Abghoui and E. Skúlason, Catal. Today, 2017, 286, 78–84.
35. Y. Abghoui and E. Skúlason, Catal. Today, 2017, 286, 69–77.
36. Y. Abghoui and E. Skúlason, J. Phys. Chem. C, 2017, 121, 24036–24045.
37. Y. Abghoui and E. Skúlason, J. Phys. Chem. C, 2017, 121, 6141–6151.
38. Y. Abghoui, A. L. Garden, V. F. Hlynsson, S. Björgvinsdóttir, H. Ólafsdóttir and E. Skúlason, Phys. Chem. Chem. Phys., 2015, 17, 4909–4918.
39. X. Yang, J. Nash, J. Anibal, M. Dunwell, S. Kattel, E. Stavitski, K. Attenkofer, J. G. Chen, Y. Yan and B. Xu, J. Am. Chem. Soc., 2018, 140, 13387–13391.
40. K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Christensen and J. K. Nørskov, Science, 2005, 307, 555–558.
41. W. Chang, A. Jain, F. Rezaie and K. Manthiram, Nat. Catal., 2024, 7, 231–241.
42. F. Fichter, P.-L. Girard and H. Erlenmeyer, Helv. Chim. Acta, 1930, 13, 1228–1236.
43. A. Tsuneto, A. Kudo and T. Sakata, Chem. Lett., 1993, 851–854.
44. A. Tsuneto, A. Kudo and T. Sakata, J. Electroanal. Chem., 1994, 367, 183–188.
45. J. M. McEnaney, A. R. Singh, J. A. Schwalbe, J. Kibsgaard, J. C. Lin, M. Cargnello, T. F. Jaramillo and J. K. Nørskov, Energy Environ. Sci., 2017, 10, 1621–1630.
46. J. A. Schwalbe, M. J. Statt, C. Chosy, A. R. Singh, B. A. Rohr, A. C. Nielander, S. Z. Andersen, J. M. McEnaney, J. G. Baker, T. F. Jaramillo, J. K. Norskov and M. Cargnello, ChemElectroChem, 2020, 7, 1542–1549.
47. S. Z. Andersen, M. J. Statt, V. J. Bukas, S. G. Shapel, J. B. Pedersen, K. Krempl, M. Saccoccio, D. Chakraborty, J. Kibsgaard, P. C. K. Vesborg, J. Nørskov and I. Chorkendorff, Energy Environ. Sci., 2020, 13, 4291–4300.
48. X. Cai, C. Fu, H. Iriawan, F. Yang, A. Wu, L. Luo, S. Shen, G. Wei, Y. Shao-Horn and J. Zhang, iScience, 2021, 24, 103105.
49. B. H. R. Suryanto, K. Matuszek, J. Choi, R. Y. Hodgetts, H. L. Du, J. M. Bakker, C. S. M. Kang, P. V. Cherepanov, A. N. Simonov and D. R. MacFarlane, Science, 2021, 372, 1187–1191.
50. N. Lazouski, Z. J. Schiffer, K. Williams and K. Manthiram, Joule, 2019, 3, 1127–1139.
51. N. Lazouski, K. J. Steinberg, M. L. Gala, D. Krishnamurthy, V. Viswanathan and K. Manthiram, ACS Catal., 2022, 12, 5197–5208.
52. T. Wang, Y. Zhang, B. Huang, B. Cai, R. R. Rao, L. Giordano, S. G. Sun and Y. Shao-Horn, Nat. Catal., 2021, 4, 753–762.
53. M. Spry, O. Westhead, R. Tort, B. Moss, Y. Katayama, M.-M. Titirici, I. E. L. Stephens and A. Bagger, ACS Energy Lett., 2023, 8, 1230–1235.
54. R. Tort, O. Westhead, M. Spry, B. J. V. Davies, M. P. Ryan, M. M. Titirici and I. E. L. Stephens, ACS Energy Lett., 2023, 1003–1009.
55. L. Gao, Y. Cao, C. Wang, X. Yu, W. Li, Y. Zhou, B. Wang, Y. Yao, C. Wu, W. Luo and Z. Zou, Angew. Chem., Int. Ed., 2021, 133, 5317–5321.
56. A. Guha, S. Narayanaru, N. M. Kaley, D. Krishna Rao, J. Mondal and T. N. Narayanan, Mater. Today Commun., 2019, 21, 100700.
57. S. Li, Y. Zhou, K. Li, M. Saccoccio, R. Sažinas, S. Z. Andersen, J. B. Pedersen, X. Fu, V. Shadravan, D. Chakraborty, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Joule, 2022, 6, 2083–2101.
58. W. Y. Gao, Y. C. Hao, X. Su, L. W. Chen, T. A. Bu, N. Zhang, Z. L. Yu, Z. Zhu and A. X. Yin, Chem. Commun., 2019, 55, 10705–10708.
59. N. C. Kani, A. Prajapati, B. A. Collins, J. D. Goodpaster and M. R. Singh, ACS Catal., 2020, 10, 14592–14603.
60. P. Shen, X. Li, Y. Luo, N. Zhang, X. Zhao and K. Chu, Appl. Catal., B, 2022, 316, 121651.
61. M. Liu, S. Zhang, M. Chen and L. Wu, Appl. Catal., B, 2022, 319, 121925.
62. M. Wang, S. Liu, H. Ji, T. Yang, T. Qian and C. Yan, Nat. Commun., 2021, 12, 3198.
63. P. Shen, X. Li, Y. Luo, Y. Guo, X. Zhao and K. Chu, ACS Nano, 2022, 16, 7915–7925.
64. K. Kim, C. Yoo, J. Kim, H. C. Yoon and J. Han, J. Electrochem. Soc., 2016, 163, F1523–F1526.
65. K. Kim, N. Lee, C.-Y. Yoo, J.-N. Kim, H. C. Yoon and J.-I. Han, J. Electrochem. Soc., 2016, 163, F610–F612.
66. Y. Ren, C. Yu, X. Han, X. Tan, Q. Wei, W. Li, Y. Han, L. Yang and J. Qiu, ACS Energy Lett., 2021, 6, 3844–3850.
67. C. Zhang, S. Liu, T. Chen, Z. Li and J. Hao, Chem. Commun., 2019, 55, 7370–7373.
68. Q. Zhang, Y. Zhao, L. Yu, X. Zhang, Y. Bei and B. Tang, Green Chem., 2021, 23, 7685–7691.
69. B. H. R. Suryanto, C. S. M. Kang, D. Wang, C. Xiao, F. Zhou, L. Miguel Azofra, L. Cavallo, X. Zhang and D. R. MacFarlane, ACS Energy Lett., 2018, 3, 1219–1224.
70. F. Zhou, L. M. Azofra, M. Ali, M. Kar, A. N. Simonov, C. McDonnell-Worth, C. Sun, X. Zhang and D. R. MacFarlane, Energy Environ. Sci., 2017, 10, 2516–2520.
71. M. M. Waegele, C. M. Gunathunge, J. Li and X. Li, J. Chem. Phys., 2019, 151, 160902.
72. B. Deng, M. Huang, X. Zhao, S. Mou and F. Dong, ACS Catal., 2022, 12, 331–362.
73. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943.
74. D. Strmcnik, K. Kodama, D. Van Der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Marković, Nat. Chem., 2009, 1, 466–472.
75. Y.-C. Hao, Y. Guo, L.-W. Chen, M. Shu, X.-Y. Wang, T.-A. Bu, W.-Y. Gao, N. Zhang, X. Su, X. Feng, J.-W. Zhou, B. Wang, C.-W. Hu, A.-X. Yin, R. Si, Y.-W. Zhang and C.-H. Yan, Nat. Catal., 2019, 2, 448–456.
76. Y. Liu, M. Han, Q. Xiong, S. Zhang, C. Zhao, W. Gong, G. Wang, H. Zhang and H. Zhao, Adv. Energy Mater., 2019, 9, 1–9.
77. G. F. Chen, X. Cao, S. Wu, X. Zeng, L. X. Ding, M. Zhu and H. Wang, J. Am. Chem. Soc., 2017, 139, 9771–9774.
78. X. Zhu, Z. Liu, Q. Liu, Y. Luo, X. Shi, A. M. Asiri, Y. Wu and X. Sun, Chem. Commun., 2018, 54, 11332–11335.
79. X. Sun, P. Wang, K. Davey, Y. Zheng and S. Z. Qiao, Small, 2023, 19, 1–7.
80. Y. Song, D. Johnson, R. Peng, D. K. Hensley, P. V. Bonnesen, L. Liang, J. Huang, F. Yang, F. Zhang, R. Qiao, A. P. Baddorf, T. J. Tschaplinski, N. L. Engle, M. C. Hatzell, Z. Wu, D. A. Cullen, H. M. Meyer, B. G. Sumpter and A. J. Rondinone, Sci. Adv., 2018, 4, 1–9.
81. C. B. Kretschmer, J. Nowakowska and R. Wiebe, Ind. Eng. Chem., 1946, 38, 506–509.
82. Y. Guo, J. Gu, R. Zhang, S. Zhang, Z. Li, Y. Zhao, Z. Huang, J. Fan, Z. Chen and C. Zhi, Adv. Energy Mater., 2021, 11, 2101699.
83. Y. Tian, Y. Liu, H. Wang, L. Liu and W. Hu, ACS Sustainable Chem. Eng., 2022, 10, 4345–4358.
84. J. C. Thermodynamics, S. Stevanovic and M. F. C. Gomes, J. Chem. Thermodyn., 2013, 59, 65–71.
85. J. L. Anderson, J. K. Dixon and J. F. Brennecke, Acc. Chem. Res., 2007, 40, 1208–1216.
86. D. Almantariotis, T. Gefflaut, A. A. H. Pádua, J. Y. Coxam and M. F. Costa Gomes, J. Phys. Chem. B, 2010, 114, 3608–3617.
87. J. E. Bara, T. K. Carlisle, C. J. Gabriel, D. Camper, A. Finotello, D. L. Gin and R. D. Noble, Ind. Eng. Chem. Res., 2009, 48, 2739–2751.
88. P. Scovazzo, D. Camper, J. Kieft, J. Poshusta, C. Koval and R. Noble, Ind. Eng. Chem. Res., 2004, 43, 6855–6860.
89. D. Almantariotis, A. S. Pensado, H. Q. N. Gunaratne, C. Hardacre, A. A. H. Pádua, J. Y. Coxam and M. F. Costa Gomes, J. Phys. Chem. A, 2017, 121, 426–436.
90. C. S. M. Kang, X. Zhang and D. R. Macfarlane, J. Phys. Chem. C, 2018, 122, 24550–24558.
91. C. S. M. Kang, X. Zhang and D. R. MacFarlane, J. Phys. Chem. C, 2019, 123, 21376–21385.
92. A. Katayama, T. Inomata, T. Ozawa and H. Masuda, Electrochem. Commun., 2016, 67, 6–10.
93. B. H. R. Suryanto, C. S. M. Kang, D. Wang, C. Xiao, F. Zhou, L. M. Azofra, L. Cavallo, X. Zhang and D. R. MacFarlane, ACS Energy Lett., 2018, 3, 1219–1224.
94. G. R. Zhuang, K. Wang, Y. Chen and P. N. Ross, J. Vac. Sci. Technol., A, 1998, 16, 3041–3045.
95. S. Li, Y. Zhou, K. Li, M. Saccoccio, R. Sažinas, S. Z. Andersen, J. B. Pedersen, X. Fu, V. Shadravan, D. Chakraborty, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Joule, 2022, 6, 2083–2101.
96. H.-L. Du, M. Chatti, R. Y. Hodgetts, P. V. Cherepanov, C. K. Nguyen, K. Matuszek, D. R. MacFarlane and A. N. Simonov, Nature, 2022, 609, 722–727.
97. H. L. Du, K. Matuszek, R. Y. Hodgetts, K. Ngoc Dinh, P. V. Cherepanov, J. M. Bakker, D. R. MacFarlane and A. N. Simonov, Energy Environ. Sci., 2023, 1082–1090.
98. K. Li, S. Z. Andersen, M. J. Statt, M. Saccoccio, V. J. Bukas, K. Krempl, R. Sažinas, J. B. Pedersen, V. Shadravan, Y. Zhou, D. Chakraborty, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Science, 2021, 374, 1593–1597.
99. X. Fu, A. Xu, J. B. Pedersen, S. Li, R. Sažinas, Y. Zhou, S. Z. Andersen, M. Saccoccio, N. H. Deissler, J. B. V. Mygind, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Nat. Commun., 2024, 15, 2417.
100. S. Li, Y. Zhou, X. Fu, J. B. Pedersen, M. Saccoccio, S. Z. Andersen, K. Enemark-Rasmussen, P. J. Kempen, C. D. Damsgaard, A. Xu, R. Sažinas, J. B. V. Mygind, N. H. Deissler, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Nature, 2024, 629, 92–97.
101. X. Fu, J. B. Pedersen, Y. Zhou, M. Saccoccio, S. Li, R. Sažinas, K. Li, S. Z. Andersen, A. Xu, N. H. Deissler, J. B. V. Mygind, C. Wei, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov and I. Chorkendorff, Science, 2023, 379, 707–712.
102. N. Lazouski, M. Chung, K. Williams, M. L. Gala and K. Manthiram, Nat. Catal., 2020, 3, 463–469.
103. X. Fu, S. Li, N. H. Deissler, J. B. V. Mygind, J. Kibsgaard and I. Chorkendorff, ACS Energy Lett., 2024, 3790–3795.
104. D. Krishnamurthy, N. Lazouski, M. L. Gala, K. Manthiram and V. Viswanathan, ACS Cent. Sci., 2021, 7, 2073–2082.
105. J. Bjarke Valbæk Mygind, J. B. Pedersen, K. Li, N. H. Deissler, M. Saccoccio, X. Fu, S. Li, R. Sažinas, S. Z. Andersen, K. Enemark-Rasmussen, P. C. K. Vesborg, J. Doganli-Kibsgaard and I. Chorkendorff, ChemSusChem, 2023, 16, 1–9.
106. R. Y. Hodgetts, H. L. Du, T. D. Nguyen, D. Macfarlane and A. N. Simonov, ACS Catal., 2022, 12, 5231–5246.
107. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
108. U. Benedikt, W. B. Schneider and A. A. Auer, Phys. Chem. Chem. Phys., 2013, 15, 2712.
109. K. Schwarz and R. Sundararaman, Surf. Sci. Rep., 2020, 75, 100492.
110. A. Y. Lozovoi, A. Alavi, J. Kohanoff and R. M. Lynden-Bell, J. Chem. Phys., 2001, 115, 1661–1669.
111. C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402.
112. A. Y. Lozovoi and A. Alavi, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245416.
113. J. A. Gauthier, S. Ringe, C. F. Dickens, A. J. Garza, A. T. Bell, M. Head-Gordon, J. K. Nørskov and K. Chan, ACS Catal., 2019, 9, 920–931.
114. D. Gunceler, K. Letchworth-Weaver, R. Sundararaman, K. A. Schwarz and T. A. Arias, Modell. Simul. Mater. Sci. Eng., 2013, 21, 074005.
115. S. Ringe, N. G. Hörmann, H. Oberhofer and K. Reuter, Chem. Rev., 2022, 122, 10777–10820.
116. O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 234117.
117. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 0–8.
118. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101.
119. R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler, Y. Ozhabes and T. A. Arias, SoftwareX, 2017, 6, 278–284.
120. O. Andreussi, N. G. Hörmann, F. Nattino, G. Fisicaro, S. Goedecker and N. Marzari, J. Chem. Theory Comput., 2019, 15, 1996–2009.
121. S. M. R. Islam, F. Khezeli, S. Ringe and C. Plaisance, J. Chem. Phys., 2023, 159, 234117.
122. R. Sundararaman, K. Letchworth-Weaver and K. A. Schwarz, J. Chem. Phys., 2018, 148, 144105.
123. X. Zhao and Y. Liu, J. Am. Chem. Soc., 2021, 143, 9423–9428.
124. Z. Levell, J. Le, S. Yu, R. Wang, S. Ethirajan, R. Rana, A. Kulkarni, J. Resasco, D. Lu, J. Cheng and Y. Liu, Chem. Rev., 2024, 124, 8620–8656.
125. X. Bai, X. Zhao, Y. Zhang, C. Ling, Y. Zhou, J. Wang and Y. Liu, J. Am. Chem. Soc., 2022, 144, 17140–17148.
126. X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777.
127. S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, J. Am. Chem. Soc., 2023, 145, 25352–25356.
128. E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
129. A. H. Motagamwala, M. R. Ball and J. A. Dumesic, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 413–450.
130. J. Chen, M. Jia, P. Hu and H. Wang, J. Comput. Chem., 2021, 42, 379–391.
131. E. D. Hermes, A. N. Janes and J. R. Schmidt, J. Chem. Phys., 2019, 151, 014112.
132. A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807.
133. I. A. W. Filot, R. A. Van Santen and E. J. M. Hensen, Angew. Chem., Int. Ed., 2014, 53, 12746–12750.
134. A. Bajpai, K. Frey and W. F. Schneider, Langmuir, 2020, 36, 465–474.
135. A. H. Motagamwala and J. A. Dumesic, Chem. Rev., 2021, 121, 1049–1076.
136. B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048.
137. N. R. Singstock and C. B. Musgrave, J. Am. Chem. Soc., 2022, 144, 12800–12806.
138. K. Lu, F. Xia, B. Li, Y. Liu, I. B. Abdul Razak, S. Gao, J. Kaelin, D. E. Brown and Y. Cheng, ACS Nano, 2021, 15, 16887–16895.
139. C. Choi, G. H. Gu, J. Noh, H. S. Park and Y. Jung, Nat. Commun., 2021, 12, 4353.
140. L. Jiang, X. Bai, X. Zhi and Y. Jiao, Adv. Energy Mater., 2024, 14, 1–11.
141. M. Pineda and M. Stamatakis, J. Chem. Phys., 2022, 156, 120902.
142. M. Andersen, C. Panosetti and K. Reuter, Front. Chem., 2019, 7, 1–24.
143. J. Li, I. Maresi, Y. Lum and J. W. Ager, J. Chem. Phys., 2021, 155, 164701.
144. T. P. Schulze, J. Comput. Phys., 2008, 227, 2455–2462.
145. A. F. Voter, Radiat. Eff. Solids, 2007, 1–23.
146. R. Harris and M. Grant, J. Phys. A: Gen. Phys., 1990, 23, 2–7.
147. M. Biehl, Multiscale Model. Ep. Growth, 2005, pp. 3–18.
148. D. Raabe, Acta Mater., 2000, 48, 1617–1628.
149. W. E. Frazier, S. Hu and V. V. Joshi, Comput. Mater. Sci., 2020, 185, 109945.
150. C. H. Lee, S. Pahari, N. Sitapure, M. A. Barteau and J. S. I. Kwon, ACS Catal., 2022, 12, 15609–15617.
151. M. Bin Jassar, C. Michel, S. Abada, T. De Bruin, S. Tant, C. Nieto-Draghi and S. N. Steinmann, ACS Appl. Energy Mater., 2023, 6, 6934–6945.
152. Q. Wu, M. T. McDowell and Y. Qi, J. Am. Chem. Soc., 2023, 145, 2473–2484.
153. A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15.
154. G. Fan, W. Xu, J. Li, Y. Ni, M. Yu, F. Liu and F. Cheng, J. Phys. Chem. C, 2022, 126, 13629–13639.
155. S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003.
156. E. Cea-Klapp, J. M. Míguez, P. Gómez-Álvarez, F. J. Blas, H. Quinteros-Lama and J. M. Garrido, Phys. Chem. Chem. Phys., 2020, 22, 27121–27133.
157. N. Yao, X. Chen, Z. H. Fu and Q. Zhang, Chem. Rev., 2022, 122, 10970–11021.
158. J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Phys. Rev. Lett., 2017, 119, 1–6.
159. S. Surendralal, M. Todorova and J. Neugebauer, Phys. Rev. Lett., 2021, 126, 166802.
160. X. Y. Li, A. Chen, X. H. Yang, J. X. Zhu, J. B. Le and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 7299–7304.
161. J. B. Le, X. H. Yang, Y. B. Zhuang, M. Jia and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 8924–8931.
162. J. Cheng, X. Liu, J. VandeVondele, M. Sulpizi and M. Sprik, Acc. Chem. Res., 2014, 47, 3522–3529.
163. Encyclopedia of Applied and Computational Mathematics, ed. B. Engquist, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015.
164. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
165. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601.
166. M. C. O. Monteiro, F. Dattila, B. Hagedoorn, R. García-Muelas, N. López and M. T. M. Koper, Nat. Catal., 2021, 4, 654–662.
167. P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Nat. Catal., 2022, 5, 900–911.
168. J. B. Le, Q. Y. Fan, J. Q. Li and J. Cheng, Sci. Adv., 2020, 6, 1–8.
169. S.-J. Qian, H. Cao, J.-W. Chen, J.-C. Chen, Y.-G. Wang and J. Li, ACS Catal., 2022, 12, 11530–11540.
170. X. Mao, X. Bai, G. Wu, Q. Qin, A. P. O’Mullane, Y. Jiao and A. Du, J. Am. Chem. Soc., 2024, 146, 18743–18752.
171. D. Maniscalco, D. A. Rudolph, E. Nadimi and I. Frank, Nitrogen, 2022, 3, 404–413.
172. T. Mueller, A. Hernandez and C. Wang, J. Chem. Phys., 2020, 152, 050902.
173. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 1–4.
174. A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330.
175. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 1–4.
176. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–16.
177. T. Wen, L. Zhang, H. Wang, E. Winan and D. J. Srolovitz, Mater. Futures, 2022, 1, 022601.
178. C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–8.
179. V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512–516.
180. B. Lin, J. Jiang, X. C. Zeng and L. Li, Nat. Commun., 2023, 14, 4110.
181. G. Soloveichik, ARPA-e, 2016, pp. 1–16. https://arpa-e.energy.gov/?q=arpa-e-programs/refuel.
182. D. Jin, A. Chen and B. L. Lin, J. Am. Chem. Soc., 2024, 146, 10–13.
183. X. Fu, V. A. Niemann, Y. Zhou, S. Li, K. Zhang, J. B. Pedersen, M. Saccoccio, S. Z. Andersen, K. Enemark-Rasmussen, P. Benedek, A. Xu, N. H. Deissler, J. B. V. Mygind, A. C. Nielander, J. Kibsgaard, P. C. K. Vesborg, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Nat. Mater., 2024, 23, 101–107.
184. M. Krebsz, R. Y. Hodgetts, S. Johnston, C. K. Nguyen, Y. Hora, D. R. MacFarlane and A. N. Simonov, Energy Environ. Sci., 2024, 17, 4481–4487.
185. J. Gallagher, Nat. Energy, 2024, 9, 627.
186. Y. Chen, C. Ye, N. Zhang, J. Liu, H. Li, K. Davey and S. Z. Qiao, Mater. Today, 2024, 73, 260–274.
187. X. Cai and J. Zhang, Nat. Energy, 2024, 9, 629–630.
188. X. Cai, X. Li, J. You, F. Yang, Z. Shadike, S. Qin, L. Luo, Y. Guo, X. Yan, S. Shen, G. Wei, Z. J. Xu and J. Zhang, J. Am. Chem. Soc., 2023, 145, 25716–25725.

---