Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tracking Li atoms in real-time with ultra-fast NMR simulations†
Angela F.
Harper
 *a,
Tabea
Huss
*a,
Tabea
Huss
 a,
Simone S.
Köcher
a,
Simone S.
Köcher
 ab and
Christoph
Scheurer
a
ab and
Christoph
Scheurer
a
aFritz-Haber Institute of the Max Planck Society, Berlin, Germany. E-mail: harper@fhi.mpg.de
bInstitut für Energie und Klimaforschung (IEK-9), Forschungszentrum Jülich GmbH, Jülich, Germany
First published on 3rd May 2024
Abstract
We present for the first time a multiscale machine learning approach to jointly simulate atomic structure and dynamics with the corresponding solid state Nuclear Magnetic Resonance (ssNMR) observables. We study the use-case of spin-alignment echo (SAE) NMR for exploring Li-ion diffusion within the solid state electrolyte material Li3PS4 (LPS) by calculating quadrupolar frequencies of 7Li. SAE NMR probes long-range dynamics down to microsecond-timescale hopping processes. Therefore only a few machine learning force field schemes are able to capture the time- and length scales required for accurate comparison with experimental results. By using a new class of machine learning interatomic potentials, known as ultra-fast potentials (UFPs), we are able to efficiently access timescales beyond the microsecond regime. In tandem, we have developed a machine learning model for predicting the full 7Li electric field gradient (EFG) tensors in LPS. By combining the long timescale trajectories from the UFP with our model for 7Li EFG tensors, we are able to extract the autocorrelation function (ACF) for 7Li quadrupolar frequencies during Li diffusion. We extract the decay constants from the ACF for both crystalline β-LPS and amorphous LPS, and find that the predicted Li hopping rates are on the same order of magnitude as those predicted from the Li dynamics. This demonstrates the potential for machine learning to finally make predictions on experimentally relevant timescales and temperatures, and opens a new avenue of NMR crystallography: using machine learning dynamical NMR simulations for accessing polycrystalline and glass ceramic materials.
I. Introduction
Probing dynamical effects is particularly important for energy materials, in which mobile ions drive the device functionality. The mobility of species and structural features such as disorder and defects are closely interwoven, and often are the critical factors for determining device performance. In order to establish a correlation between structure and dynamics, various experimental ssNMR methods can be employed.1,2 One such method is SAE NMR, which is commonly used to study Li dynamics operando within solid-state Li-ion battery materials.3–6 SAE probes the quadrupolar interaction of the EFG tensor at the 7Li nucleus (spin I = 3/2) with its local surrounding environment in order to observe the motion of Li-ions hopping between various sites in a material.Combining static experimental ssNMR spectra with first principles density functional theory (DFT) is already an established method for elucidating structure in crystalline and amorphous battery materials.7–11 Within the literature on NMR crystallography for battery materials, there is a primary focus on calculating chemical shielding (CSA) tensors,8,12–15 as quadrupolar interactions are only a secondary effect, observed for nuclei with I > 1/2. However, there are also many DFT calculated quadrupolar parameters derived from EFG tensors, used in NMR crystallography for common quadrupolar nuclei found in battery materials, such as 7Li, 17O, and 27Al.10,16–21 While the calculation of static EFG tensors using DFT is a straightforward approach, a technique such as SAE requires computational methods that are capable of following dynamic processes over both long length and timescales. Studying these dynamics is of course impossible with DFT calculated ssNMR tensors (both CSA and EFG tensors), due to the computational constraints associated with the fact that DFT typically scales as 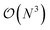 . Even recent applications of machine learning to NMR have been limited to static use-cases,22 incapable of capturing dynamical or time-dependent effects. A classical approach using the Sternheimer approximation has proven successful for tracking ion motion in liquid electrolytes, where the fast ion motion reduces the requirements for computing NMR observables to picosecond timescales.23 However, for slower ion motion (relative to the liquid state), this approach is not feasible, and therefore cannot be applied to study solid-state Li-ion motion, which requires simulations on the order of microseconds.
. Even recent applications of machine learning to NMR have been limited to static use-cases,22 incapable of capturing dynamical or time-dependent effects. A classical approach using the Sternheimer approximation has proven successful for tracking ion motion in liquid electrolytes, where the fast ion motion reduces the requirements for computing NMR observables to picosecond timescales.23 However, for slower ion motion (relative to the liquid state), this approach is not feasible, and therefore cannot be applied to study solid-state Li-ion motion, which requires simulations on the order of microseconds.
Fortunately, the recent introduction of machine learning inter-atomic potentials (MLIPs) has enabled simulations of such long-timescale processes within reasonable computational time and at sufficient fidelity for complex materials.24–26 The first generation of MLIPs achieved speedups of three orders of magnitude over DFT, making nanosecond simulations possible in many cases.27–29 Even more recently, a set of ultra-fast machine learning potentials (UFPs) was introduced27 which provides a speedup of nearly five orders of magnitude over DFT, while maintaining the same accuracy as some of the most accurate MLIPs such as the Gaussian Approximation Potential (GAP).28 With the UFP, it is now possible to routinely simulate up to the microsecond timescale almost at DFT accuracy.30–33
By using the UFP combined with a machine learning model for EFG tensors, we can now extend the capabilities of NMR crystallography to make dynamical simulations on microsecond timescales a reality. Using this UFP+ML-EFG model, we will demonstrate how to calculate the relevant ACF of quadrupolar precession frequencies for SAE experiments in the fast ion conductor Li3PS4 (LPS). LPS is the ideal system to study dynamic Li processes as it has both a crystalline (β-LPS) and amorphous (am-LPS) phase which are Li-ion conducting with predicted Li hopping mechanisms in the 105 to 107 s−1 range.34,35 We finally show that SAE would be highly sensitive to understanding Li-ion motion in these materials on the micro-structural level, and therefore propose to use this method in combination with experimental SAE to further study the intermediate glass-ceramic LPS materials which are known to have large amounts of disorder.36
II. Methods
A. SAE NMR and the EFG tensor
SAE NMR is a probe of the change in the quadrupolar precession frequency (ωQ) over time for a specific nucleus with a spin I > 1/2, such as 7Li, which has a nuclear spin of I = 3/2. For the nucleus of a single Li atom, ωQ is extracted from the EFG tensor V, which describes the interaction between the quadrupole of the nucleus and its surrounding electric field. The EFG tensor is the second positional derivative of the electric field V around the nucleus,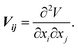 | (1) |
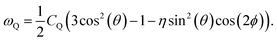 | (2) |
To generate an echo experimentally, which is proportional to the ωQ(t), a Jeener–Broekaert pulse-sequence is used,38,39 and the resulting 〈ACFωQ〉, measures the phase of ωQ(t = 0) with ωQ(t = tm) where tm is the mixing time used in the pulse sequence. In the case of I = 3/2,3
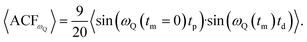 | (3) |
| 〈ACFωQ〉 ∝ 〈ωQ(tm = 0)·ωQ(tm)〉. | (4) |
The 〈ACFωQ〉 measures the probability of finding a Li-ion at time t = tm in a position with an equivalent ωQ as it had at time t = 0. Thus, in materials in which the Li atoms visit sites with different ωQ, the 〈ACFωQ〉 in eqn (4) typically behaves as a decaying exponential function and one can extract the decay time τSAE directly using a stretched exponential form of the Lipari–Szabo relation,3,41
| 〈ACFωQ〉 = b2 + (1 − b2)·exp(−(tm/τSAE)γ). | (5) |
DFT simulations access the limit of {tp, td} → 0, as in eqn (4) and (5), and neglect any experimental dead time, hence allowing us to naturally simulate a non-ensemble averaged ACFωQ for site specific trajectories within a molecular dynamics (MD) simulation. We can therefore target processes which are faster than the lower limit of what is possible in experimental SAE, as the experiment is limited by the lower bound on the order of 10 μs, defined by td and tp as well as the inverse of the quadrupolar interaction.40,43 It is therefore possible to extract an atomistic ACFωQ from an MD simulation as long as one can calculate the EFG tensors for all Li atoms across every snapshot of the simulation. A single snapshot of the MD simulation with ωQ and CQ calculated for each individual atomic site from DFT is the equivalent of the 0 K temperature limit, in which all motion in the system is frozen and all ions remain in their initial site. Under realistic room temperature experimental conditions for SAE, the quadrupolar observables are averaged (![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) Q and
Q and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q), not only over the fast timescale hopping events which are masked in experiment but also over thermal effects and different Li sites.
Q), not only over the fast timescale hopping events which are masked in experiment but also over thermal effects and different Li sites.
B. Ultra-fast potentials
Studying timescales relevant for spin alignment measurements necessitates an efficient methodology for the evaluation of energies and forces to drive molecular dynamics over microsecond timescales. Xie et al. have recently introduced a new interatomic potential, matching the accuracy of established MLIPs but boosting the speed by one or two orders of magnitude, such that it is comparable with the computational efficiency of classical force-fields.27 The architecture uses a local representation of atomic environments as established by fundamental work using SOAP and Behler–Parrinello symmetry functions.44,45The energy of the system is expanded as a sum of 2-body and 3-body contributions using cubic B-splines, which combine the beneficial properties of smoothness and differentiability with the advantage of a compact support. Hence, the number of basis functions that need to be evaluated in every energy computation step is strongly limited, as a maximum of four functions can be non-zero in every segment. The low number of basis functions directly relates to a high computational efficiency.27
The UFP is trained using the active learning procedure shown in the workflow in Fig. 1A. The initial dataset is an existing set of LPS structures which was used to train a GAP28 for LPS.31 The UFP is trained and iteratively improved by adding structures of β- and am-LPS to the training set. Structures are drawn from UFP-MD simulations, where the UFP used for each iteration is the most recent UFP obtained during the training workflow. This active learning cycle of training, UFP-MD simulation, and model evaluation is repeated iteratively until convergence of the UFP energy and force errors is achieved. Finally, the converged energy and forces over a withheld test set are displayed in Fig. 1B (3.1 meV per atom and 109.9 meV Å−1, respectively). These are comparable with the corresponding errors for the GAP for LPS.31 In addition to the iterative training procedure used to create a robust dataset, the hyperparameters specific to the UFP model were also optimized. Details are given in the ESI Table 1.†
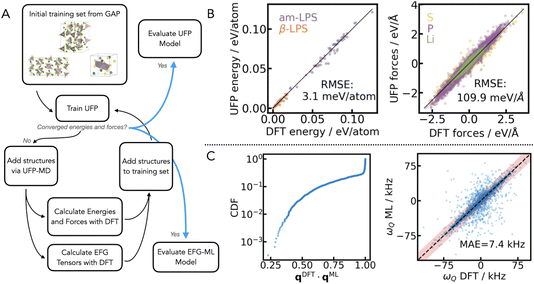 | ||
| Fig. 1 Workflow of the UFP+ML-EFG training. The left panel shows the active learning workflow (A) starting from a set of structures used to train a GAP28 for LPS31 to the final training of the UFP (B) and ML-EFG model (C). The UFP has an RMSE in the energies of 3.1 meV per atom and forces of 109.9 meV Å−1. The ML-EFG model is assessed both by the quality of the relative orientation of the tensors and the MAE in ωQ. C shows the combined distribution function (CDF) of the quaternion scalar product between the DFT and ML quaternions, qDFT·qML. This indicates that the majority of tensors are oriented in the same direction comparing DFT to ML. The ML-EFG model has an error of 7.4 kHz on ωQ, where the experimental sensitivity of 7Li SAE (10 kHz) is shown shaded in red. | ||
C. An ML model for EFG tensors
The Symmetry Adapted Gaussian Process Regression (SA-GPR) machine learning framework, combines covariant atomic descriptors with symmetry adapted kernels in order to learn tensors of any dimension with Gaussian process regression.46 We have previously shown that by using tensorial learning via the SA-GPR framework, we are able to predict quadrupolar frequencies (ωQ) for the 7Li nucleus within the experimental sensitivity of SAE NMR.47 We couple the workflow for tensorial learning to the active learning procedure used for training the UFP, as shown in Fig. 1A, in order to train a model for predicting the 7Li EFG tensors of β- and am-LPS. The final set of structures from the active learning procedure for the UFP is used as the training set for validating the ML-EFG model.The final set of DFT computed 7Li EFG tensors over structures of Li3PS4 contains 166 diverse structures from the LPS UFP model, which have a total of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 Li environments. The EFG tensor for each atom is calculated for all the structures using the plane-wave pseudopotential DFT code CASTEP v22.48,49 The hyperparameters for the SA-GPR descriptor are optimized as described in the ESI,† using a 5-fold cross validation procedure with a test set, which is withheld from training. The resulting mean absolute error (MAE) for the test set in ωQ is 7.4 kHz, and the correlation plot is shown in Fig. 1C. It is important to note that the density of points of ωQ within the red bar is high, and thus this representation highlights the outliers as they are clearer to distinguish from the majority.
448 Li environments. The EFG tensor for each atom is calculated for all the structures using the plane-wave pseudopotential DFT code CASTEP v22.48,49 The hyperparameters for the SA-GPR descriptor are optimized as described in the ESI,† using a 5-fold cross validation procedure with a test set, which is withheld from training. The resulting mean absolute error (MAE) for the test set in ωQ is 7.4 kHz, and the correlation plot is shown in Fig. 1C. It is important to note that the density of points of ωQ within the red bar is high, and thus this representation highlights the outliers as they are clearer to distinguish from the majority.
In addition to evaluating the MAE in ωQ, it is also important to validate how well the ML-EFG model predicts the orientation of the 7Li EFG tensors. Besides magnitude (CQ) and shape (η), the 〈ACFωQ〉 is a sensitive measure of the orientation of one tensor at a time tm relative to another at t0. We use the unit quaternion q to uniquely define the orientation of each tensor.47,50 The unit quaternion is a superior metric for determining orientation over Euler angles, as it is independent of the choice of reference system. Therefore, in Fig. 1C, we show the cumulative distribution function (CDF) of the scalar product between the DFT calculated and ML-EFG predicted quaternions, qDFT·qML. A scalar product of 1 indicates perfect alignment, and from Fig. 1C, we see that around 75% of the predicted EFG tensors are well aligned with their DFT reference (qDFT·qML ≥ 0.9). This is an important factor as it will reduce the noise in the 〈ACFωQ〉, eqn (4).
We finally test the ML-EFG model for size extensivity, because the system sizes included in the training set are between 200 and 256 atoms per unit cell, due to DFT performance considerations, while our target structures for β-LPS and am-LPS are 384 and 576 atoms, respectively. Therefore, we calculated the EFG tensors using DFT for two structures of β- and am-LPS each, extracted from the final 1 μs UFP simulations, and predicted the 7Li EFG tensors for these four structures using the ML-EFG model (see ESI Fig. S2†). The accuracy of the ωQ parameter for these four larger models is 9.2 kHz, which is below the experimentally known sensitivity of 7Li SAE experiments of about 10 kHz. Thus, we can say with confidence that our model will have reasonable accuracy on the larger system sizes used in the final 1 μs UFP simulations.
III. Results
A. Microsecond simulations with UFPs
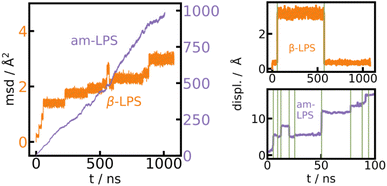
In addition to the low energy and force errors of the UFP shown in Fig. 1, it is also important to validate the behavior of the UFP relative to high quality first principles methods. Therefore, we compare the structural models generated using the UFP with literature models generated from ab initio molecular dynamics (AIMD). The radial distribution function (RDF) for β-LPS and am-LPS in a 300 K, 1 μs simulation with the UFP is shown in the ESI, Fig. S5,† in comparison with two literature references for the RDF of β- and am-LPS from AIMD.51,52 The UFP simulated RDFs for both β- and am-LPS show excellent agreement with AIMD. We also compare the UFP with the established method of Turbo-GAP53 for β-LPS and am-LPS using the mean square displacement (MSD) at 500 K (see Fig. S6 in the ESI†). We reach a perfect agreement for the am-LPS and a deviation of a factor of five for the β-LPS. The deviation can be explained with a much higher sensitivity of the MSD on the barrier height and density in the crystalline material and could potentially be improved by extending the dataset with additional nudged elastic band calculations over Li hopping events.Furthermore, we can extract the average hopping rate of Li-ions by discretizing the MSD of all independent single ion trajectories (details of the discretization procedure are given in the ESI†) (Fig. 2). From the discretized trajectories, we calculate Li hopping rates of 2.57 × 105 s−1 for β-LPS and 7.0 × 107 s−1 for am-LPS. Our results of significantly faster ion diffusion in am-LPS than in the crystalline β-LPS phase are in line with our previous findings and experimental reports.31,54,55
Finally, as a result of using the UFP, we are able to simulate dynamics at 300 K for 1 μs. To the best of our knowledge, simulations of this length have not yet been executed using MLIPs. Typical simulation times with MLIPs are on the order of nanoseconds, reaching 100 ns at most.56 Additionally, most previous studies use higher temperatures in their MD runs,31,57,58 which induces an extrapolation error in their property prediction at room temperature. With an established methodology like the Turbo-GAP, a 1 μs MD simulation would require on the order of 1 million CPUh. With an acceleration factor of 25 over TurboGAP, the UFP-MD for LPS on the other hand was computationally feasible in a couple of weeks (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPUh on a single compute node).
000 CPUh on a single compute node).
B. ACF for quadrupolar frequencies
Using the UFP+ML-EFG model, we obtain the 〈ACFωQ〉 over a 1 μs simulation at 300 K run using the UFP for both β- and am-LPS, as shown in Fig. 3. The 〈ACFωQ〉 is averaged over all Li atoms in each system, and normalized to [0,1].Firstly, and perhaps most importantly, we are simulating an infinite, pristine, single crystal, by imposing periodic boundary conditions over the unit cell of β-LPS. Because SAE can only distinguish between sites with an inequivalent average local EFG,3 if Li hopping events only occur between sites with equivalent average EFGs (![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q(t1) =
Q(t1) = ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q(t2)), the 〈ACFωQ〉 will not exhibit the characteristic exponential decay. While this would usually be associated with vanishing mobility (which is not the case in β-LPS as shown in Fig. 2 left), it can also be due to insensitivity of SAE with respect to motion between equivalent
Q(t2)), the 〈ACFωQ〉 will not exhibit the characteristic exponential decay. While this would usually be associated with vanishing mobility (which is not the case in β-LPS as shown in Fig. 2 left), it can also be due to insensitivity of SAE with respect to motion between equivalent ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q. Thus, if there are a few sets of mutually inequivalent sites with similar
Q. Thus, if there are a few sets of mutually inequivalent sites with similar ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q one would obtain a partially averaged
Q one would obtain a partially averaged ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q,43 which is the weighted average between the
Q,43 which is the weighted average between the ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q for each of these sites. A single crystal, therefore, will always be such a case, because all of the sites have the same predominant orientation throughout the simulation. A slow decay, beyond the microsecond timescale, would be dominated in a polycrystalline material by Li motion across grain boundaries of differently oriented crystalline grains. In this case, the τSAE decay could be modeled as a function of the Li diffusion coefficient and grain size distribution.
Q for each of these sites. A single crystal, therefore, will always be such a case, because all of the sites have the same predominant orientation throughout the simulation. A slow decay, beyond the microsecond timescale, would be dominated in a polycrystalline material by Li motion across grain boundaries of differently oriented crystalline grains. In this case, the τSAE decay could be modeled as a function of the Li diffusion coefficient and grain size distribution.
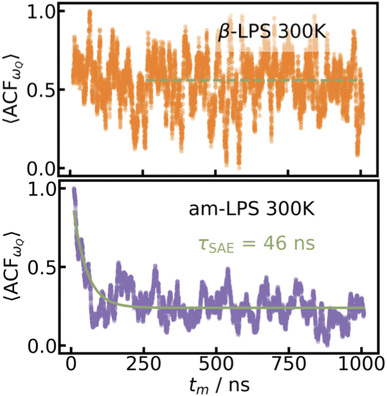 | ||
| Fig. 3 〈ACFωQ〉 for β-LPS and am-LPS. The 〈ACFωQ〉 given by eqn (4) calculated over a 1 μs UFP-MD simulation at 300 K for 144 Li atoms in single-crystalline β-LPS (top, orange) and 216 Li atoms in am-LPS (bottom, purple). A decay time, τSAE = 46 ns, can be extracted from the am-LPS 〈ACFωQ〉. | ||
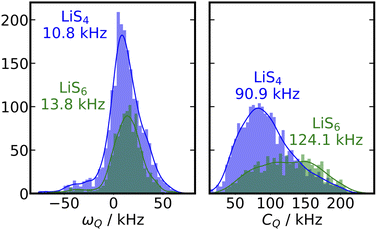
Secondly, in this particular example of β-LPS, there are only two crystallographically inequivalent Li sites, a tetrahedral LiS4 site and an octahedral LiS6 site, which possess almost identical local ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q. We can show this by looking at a distribution of the DFT calculated ωQ values of all the crystalline β-LPS structures included in the training set for our ML-EFG model, shown in the left panel of Fig. 4. The distributions are fairly narrow and the average
Q. We can show this by looking at a distribution of the DFT calculated ωQ values of all the crystalline β-LPS structures included in the training set for our ML-EFG model, shown in the left panel of Fig. 4. The distributions are fairly narrow and the average ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q for LiS4 is 10.8 kHz, and for LiS6
Q for LiS4 is 10.8 kHz, and for LiS6![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q is 13.8 kHz, a difference of less than 4 kHz. A close look at the first 250 ns of the β-LPS 〈ACFωQ〉 suggests that there is a small initial decay due to the inverse jump rate between LiS4 and LiS6 sites, which is undetectable due to both the signal-to-noise ratio of the 〈ACFωQ〉 as a result of the overlap in ωQ between the sites, as well as the low number of Li sites (144 total) in the β-LPS unit cell. This could likely be resolved in the model with a larger sampling of trajectories, but is not relevant for the observable quantities in the SAE experiment, where one would observe the residual, partially averaged coupling, shown in green in Fig. 3.
Q is 13.8 kHz, a difference of less than 4 kHz. A close look at the first 250 ns of the β-LPS 〈ACFωQ〉 suggests that there is a small initial decay due to the inverse jump rate between LiS4 and LiS6 sites, which is undetectable due to both the signal-to-noise ratio of the 〈ACFωQ〉 as a result of the overlap in ωQ between the sites, as well as the low number of Li sites (144 total) in the β-LPS unit cell. This could likely be resolved in the model with a larger sampling of trajectories, but is not relevant for the observable quantities in the SAE experiment, where one would observe the residual, partially averaged coupling, shown in green in Fig. 3.
To highlight the intricate relationship between tensor shape and orientation in β-LPS that leads to the very similar and narrow ωQ distributions displayed in Fig. 4 (left) we also compute a theoretical autocorrelation function 〈ACFCQ〉 of the orientation-independent coupling constant, CQ, experienced by the Li ions during their motion through the crystalline model in the MD simulation. We note that this is not a directly accessible quantity in the SAE experiment.59 We compute this 〈ACFCQ〉 in a similar fashion to that for ωQ given in eqn (4),
| 〈ACFCQ〉 ∝ 〈CQ(tm = 0)·CQ(tm)〉, | (6) |
A histogram of all of the individual atomistic CQ values calculated using DFT on the β-LPS training set is shown in Fig. 4, right panel. The spread of CQ values for the LiS6 sites is much wider than that for LiS4, and their averages are able to be discriminated (a 30 kHz difference). LiS6 sites have an average ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) Q of 124.1 kHz, whereas LiS4 sites have an
Q of 124.1 kHz, whereas LiS4 sites have an ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) Q of 90.9 kHz. Thus while
Q of 90.9 kHz. Thus while ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q cannot be used to distinguish these two sites, their
Q cannot be used to distinguish these two sites, their ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) Q values could be a good target to understand the local structure in ideal single crystal β-LPS.
Q values could be a good target to understand the local structure in ideal single crystal β-LPS.
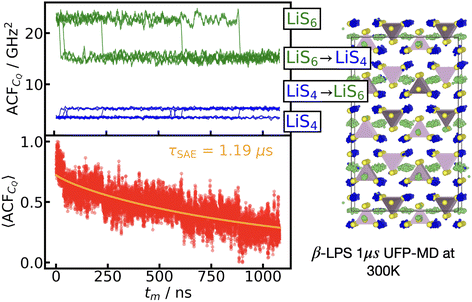
Using the UFP-MD, we are able to track single-atom trajectories across the simulation, and therefore can calculate a single-atom ACFCQ, for each site in the β-LPS crystalline structure. In order to understand how the 〈ACFCQ〉 behaves, we separate the individual single atom ACFCQ, by the Li sites at time t = 0. In Fig. 5, we plot both the individual ACFCQ and 〈ACFCQ〉, where the individual ACFCQ are colored by the site in which the Li atom started at time t = 0. The 〈ACFCQ〉 average is calculated over the 13 Li ions that experience a hop to a different site (either LiS4 → LiS6 or vice versa) during the 1 μs simulation, to reduce the noise in the 〈ACFCQ〉. We show that averaging over only the sites which hop is a reasonable assumption to make by comparing these results to a 1 μs simulation at 350 K, shown in the ESI Fig. S3,† in which 102 Li atoms hop during the simulation, and there is better averaging over more sites.
From the top panel in Fig. 5, we can clearly distinguish the individual ACFCQ for LiS6 sites (green), LiS4 sites (blue), and hopping events between the sites, as there is a steep rise (or drop) in the ACFCQ at each hopping event. Taking the average over all 13 Li sites, the 〈ACFCQ〉 does exhibit an exponential decay. Fitting the 〈ACFCQ〉 in Fig. 5 to eqn (5), we find a decay time of τ = 1.19 μs, or a Li hopping rate of 8.41 × 105 s−1. This is on the same order of magnitude as the Li hopping rate extracted from the MSD, 2.57 × 105 s−1. Additionally, by removing the orientation dependence, and averaging over only the hopping sites, we achieve better signal to noise ratio, and can more clearly distinguish the small initial decay at (tm < 50 ns).
Previous work on Li hopping in LPS using a 100 ps AIMD simulation of am-LPS with 48 Li atoms at 600 K, predicts Li hopping rates in the range of 1011 s−1.60 Their method for determining a Li hopping event involved tracking the escape time for Li atoms to leave a 3 Å radius surrounding the nearest polyanion and fitting this escape mechanism to an exponential decay function. Given the short timescale of the simulation, they were only able to access hopping events with residence times shorter than 100 ps (1010 s−1). As the shortest τSAE = 46 ns, for real ion hops in am-LPS, this requires a simulation of at least several nanoseconds at 300 K considering the signal-to-noise ratio in the simulation to accurately estimate the hopping rate. This highlights the importance of simulating both at room temperature and for a sufficiently long simulation time, in order to achieve convergence of the Li dynamics and observe the correct motion of Li atoms within LPS. Similar inaccuracies from simple extrapolation to ambient conditions are expected for any material with broad and complex distributions of migration barriers that become progressively accessible upon temperature increase.
IV. Discussion
This study pioneers the application of the latest generation of machine learning techniques to directly predict dynamical ssNMR observables at microsecond timescales from atomistic simulations. It is important to stress that an ssNMR calculation with DFT accuracy on the μs timescale would not be possible without leveraging machine learning to predict the EFG tensors. Calculating EFG tensors for the 576 atom am-LPS unit cell over a 1 μs simulation would cost roughly 22.5 million CPUh, with snapshots taken every 100 ps. The same prediction made using the ML-EFG model uses 500 CPUh. This is a factor of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 speedup over DFT-calculated EFG tensors. Therefore, this is, to the best of our knowledge, the first dynamical ssNMR calculation performed at DFT level accuracy, and on an experimentally relevant timescale.
000 speedup over DFT-calculated EFG tensors. Therefore, this is, to the best of our knowledge, the first dynamical ssNMR calculation performed at DFT level accuracy, and on an experimentally relevant timescale.
By integrating first-principles methodologies, it ensures consistent multi-scaling between NMR calculations derived from DFT and predictions applied to large-scale structures. Unlike AIMD studies on Li-ion conduction and diffusivity, where high temperatures are necessary in order to promote ion motion and gather enough statistics, we are able to simulate LPS at 300 K, which is the relevant temperature for comparison with realistic experimental solid state electrolyte systems.
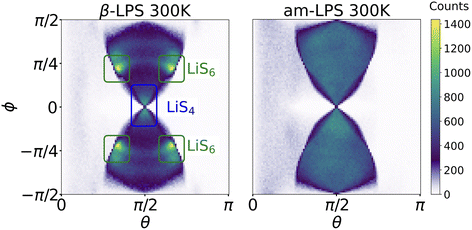
By calculating 〈ACFωQ〉 in both β- and am-LPS, we find that the decay time for Li in am-LPS at 300 K is on the order of 46 ns, while the 〈ACFωQ〉 of single-crystalline β-LPS exhibits no characteristic exponential decay, and instead oscillates about an average value of 〈ACFωQ〉. By considering the orientations of the EFG tensors during the simulations in both β-LPS and am-LPS we can see more clearly the differences in behavior of the EFG tensor in these two materials. Fig. 6 shows a 2D histogram of all of the accessed angles during the full 1 μs simulation at 300 K for β- and am-LPS. In the β-LPS histogram (Fig. 6 left), the majority of the angles (θ, ϕ) are clustered around either (π/2, 0) for LiS4 tetrahedra or (π/2 ± π/6, ±π/4) for LiS6. On the other hand, there are no clear preferred values of (θ, ϕ) for am-LPS, indicating that the Li atoms experience a wide array of environments during the 1 μs simulation. The large spread in angular distribution in the am-LPS case is what leads to the characteristic rapid decay shown in Fig. 3, as the Li ions visit sites with all possible orientations during the full simulation, leading to loss of correlation, which is normally characteristic of SAE in glasses or polymers.23,61 Once Li atoms are in a single crystalline grain, this orientational memory loss is no longer possible, and we see slow, or nonexistent decay as in β-LPS.
We assessed the two limits of overall microstructure in the LPS fast ion conductors. The β-LPS crystal represents an infinitely large, fully uniform single crystal of LPS, as depicted in orange in Fig. 7. As such, all the ωQ values in both LiS4 and LiS6 sites have the same predominant value (c.f.Fig. 4 left), which does not vary throughout the simulation, even during Li hopping events. In addition, the mean ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) Q for LiS4 and LiS6 are only 4 kHz apart, and the spread of the individual atomic ωQ for LiS6 is entirely contained within the distribution for LiS4, as presented in Fig. 4. Therefore, we would expect a vanishingly small decay of 〈ACFωQ〉 for single crystal β-LPS, in which only those two sites are accessible, and then observe a residual, partially averaged coupling throughout. However in a polycrystalline material, shown in green in Fig. 7, where LiS4 and LiS6 sites are oriented along different crystal axes in neighboring grain boundaries, we are no longer limited by the predominant orientation of the ideal single crystal. In this case, we would expect lower τSAE, and a better sensitivity to inter-grain Li-ion motion for SAE.
Q for LiS4 and LiS6 are only 4 kHz apart, and the spread of the individual atomic ωQ for LiS6 is entirely contained within the distribution for LiS4, as presented in Fig. 4. Therefore, we would expect a vanishingly small decay of 〈ACFωQ〉 for single crystal β-LPS, in which only those two sites are accessible, and then observe a residual, partially averaged coupling throughout. However in a polycrystalline material, shown in green in Fig. 7, where LiS4 and LiS6 sites are oriented along different crystal axes in neighboring grain boundaries, we are no longer limited by the predominant orientation of the ideal single crystal. In this case, we would expect lower τSAE, and a better sensitivity to inter-grain Li-ion motion for SAE.
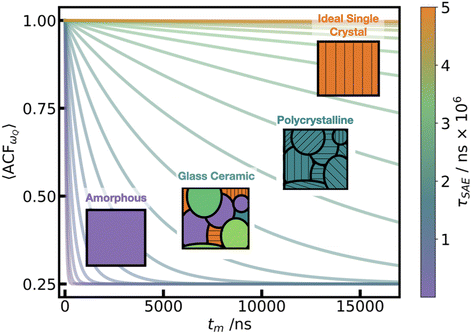 | ||
| Fig. 7 Schematic of range of crystalline to amorphous τSAE. The plot shows a range of decay functions, eqn (5), with τSAE from 50 ns to 5 million ns. The inset figures show schematics of the expected microscale structure at each of these varying decay rates, with black lines in the glass ceramic and polycrystalline denoting different grains. | ||
At the other extreme, we consider the bulk am-LPS, represented by the unstructured purple square in Fig. 7, and find that 〈ACFωQ〉 decays rapidly over a period of 46 ns. In the homogeneous amorphous regime, we can see that as the amorphous PS4 backbone changes across the simulation, Li atoms experience continually changing electronic environments, and thus we can think of the Li atoms moving in a “glass-like” ensemble of sites embedded in PS4 environments. At a 46 ns decay rate, τSAE is outside of the range detectable by a real SAE experiment which would, at best, yield a small residual coupling b2 > 0 (see eqn (5)). In a fast ion conductor, we expect this rapid decay of the 〈ACFωQ〉, however this is the first time we are able to accurately quantify the rate of this decay in an amorphous material, highlighting the importance of this UFP+ML-EFG approach.
These two regimes (single crystal and fully amorphous), which are straightforward to simulate, are not representative of the realistic microstructure in glass-ceramic LPS electrolytes.36 All of the glass ceramic materials that are critical for building the next generation of all solid state batteries such as LISCION, LIPON, LGPS, and LPS62 lie within this range between fully amorphous to fully crystalline Li-ion conductors with hypothetical τSAE decay constants schematically depicted in Fig. 7. That is, they are a mixture of glassy regions and crystalline regions (depicted as the glass ceramic and polycrystalline in Fig. 7), in which the Li-ion conductivity across grain boundaries is often the determining factor for the quality of these super-ionic conductors. In these cases, we propose that SAE will provide a unique grain-boundary sensitive technique for understanding Li-ion diffusion, as the intra-grain diffusion will be at either the amorphous or crystalline limit, and therefore undetectable with SAE.
Experimentally, the Granwehr group has observed τSAE ≈ 30–50 ms (ref. 63) in a polycrystalline sample of β-LPS, which is well above the intra-grain decay rates we have predicted here. This can likely be rationalized by sufficiently fast (τ ≤ 1 μs) intra-grain diffusion leading to partially averaged coupling tensors, combined with long timescale inter-grain diffusion processes between the polycrystalline grains (τSAE ≈ ms). However, determining the rates and mechanisms of these processes which combine to give an experimental decay rate in the ms time scale, requires dynamical NMR crystallography and analysis techniques that allow one to unfold the various timescales and effective partially averaged interaction tensors contained in the measured data.59 From this point onward, we now have the capability to make such an approach, by combining dynamical ssNMR with data analysis and simulations to interpret the unfolded data in terms of atomistic processes.
Beyond suggesting further work on grain-boundary simulations, we demonstrate the potential to access Li-ion motion even in single crystals, by deriving 〈ACFCQ〉 and calculating a corresponding τ, which does exhibit a decay at 300 K for β-LPS. Furthermore, we show that the Li hopping rate predicted by τ−1 from 〈ACFCQ〉 is comparable with that calculated from the β-LPS MSD.
We are just at the beginning of this new era of NMR crystallography in which we are able to accurately model dynamical processes at the same temperatures and timescales as experiment. This workflow combining UFPs and experimental observables is a baseline on which the next generation of machine learning for materials methods can be based. We are now one step closer to bridging the gap between theory and experiment, and can tackle more dynamic operando calculations, which were previously computationally infeasible.
Author contributions
Angela F. Harper: data curation, formal analysis, investigation, methodology, visualization, project administration, writing – original draft, writing – review and editing; Tabea Huss: data curation, formal analysis, investigation, visualization, writing – original draft; Simone S. Köcher: conceptualization, supervision, writing – review and editing; Christoph Scheurer: conceptualization, supervision, funding acquisition, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
All the authors would like to thank Prof. Dr Josef Granwehr for scientific exchange and discussions regarding experimental SAE. All computational resources were provided by the Max Planck Computing and Data Facility (MPCDF). AFH would like to acknowledge the support of the Alexander von Humboldt Foundation. TH acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the cluster of excellence EXC 2089: e-conversion. CS acknowledges funding by the Bundesministerium für Bildung und Forschung (BMBF) within the project AdamBatt2 (FKZ 03XP0558D). Open Access funding provided by the Max Planck Society.References
- K. Märker, C. Xu and C. P. Grey, Operando NMR of NMC811/graphite lithium-ion batteries: structure, dynamics, and lithium metal deposition, J. Am. Chem. Soc., 2020, 142, 17447 CrossRef PubMed.
- M. Gombotz and H. M. R. Wilkening, Fast Li ion dynamics in the mechanosynthesized nanostructured form of the solid electrolyte Li3YBr6, ACS Sustainable Chem. Eng., 2021, 9, 743 CrossRef CAS.
- M. Wilkening and P. Heitjans, From micro to macro: Access to long-range Li+ diffusion parameters in solids via microscopic 6,7Li spin-alignment echo NMR spectroscopy, ChemPhysChem, 2012, 13, 53 CrossRef CAS.
- C. Yu, S. Ganapathy, E. R. H. v. Eck, H. Wang, S. Basak, Z. Li and M. Wagemaker, Accessing the bottleneck in all-solid state batteries, lithium-ion transport over the solid-electrolyte-electrode interface, Nat. Commun., 2017, 8, 1086 CrossRef.
- K. Hogrefe, N. Minafra, W. G. Zeier and H. M. R. Wilkening, Tracking ions the direct way: long-range Li+ dynamics in the thio-LISICON family Li4MCh4 (M = Sn, Ge; Ch = S, Se) as probed by 7Li NMR relaxometry and 7Li spin-alignment echo NMR, J. Phys. Chem. C, 2021, 125, 2306 CrossRef CAS.
- B. Gadermaier, K. Hogrefe, P. Heitjans and H. M. R. Wilkening, Direct assessment of ultralow Li+ jump rates in single crystalline Li3N by evolution-time-resolved 7Li spin-alignment echo NMR, Eur. J. Inorg. Chem., 2021, 2021, 1028 CrossRef CAS.
- S. E. Ashbrook and D. M. Dawson, Exploiting periodic first-principles calculations in NMR spectroscopy of disordered solids, Acc. Chem. Res., 2013, 46, 1964 CrossRef CAS PubMed.
- S. E. Ashbrook and D. McKay, Combining solid-state NMR spectroscopy with first-principles calculations–a guide to NMR crystallography, Chem. Commun., 2016, 52, 7186 RSC.
- C. Szczuka, B. Karasulu, M. F. Groh, F. N. Sayed, T. J. Sherman, J. D. Bocarsly, S. Vema, S. Menkin, S. P. Emge and A. J. Morris, et al., Forced disorder in the solid solution Li3P–Li2S: a new class of fully reduced solid electrolytes for lithium metal anodes, J. Am. Chem. Soc., 2022, 144, 16350 CrossRef CAS PubMed.
- A. F. Harper, S. P. Emge, P. C. Magusin, C. P. Grey and A. J. Morris, Modelling amorphous materials via a joint solid-state NMR and X-ray absorption spectroscopy and DFT approach: application to alumina, Chem. Sci., 2023, 14, 1155 RSC.
- A. F. Harper, M. L. Evans, J. P. Darby, B. Karasulu, C. P. Koçer, J. R. Nelson and A. J. Morris, Ab initio structure prediction methods for battery materials: A review of recent computational efforts to predict the atomic level structure and bonding in materials for rechargeable batteries, Johnson Matthey Technol. Rev., 2020, 64, 103 CrossRef CAS.
- J. E. Frerichs, J. Koppe, S. Engelbert, L. Heletta, G. Brunklaus, M. Winter, G. K. Madsen and M. R. Hansen, 119Sn and 7Li solid-state NMR of the binary Li–Sn intermetallics: structural fingerprinting and impact on the isotropic 119Sn shift via DFT calculations, Chem. Mater., 2021, 33, 3499 CrossRef CAS.
- I. G. Shenderovich, Experimentally established 15N NMR absolute shielding scale for theoretical calculations, J. Phys. Chem. A, 2023, 127, 5547 CrossRef CAS.
- E. Chaloupecká, V. Tyrpekl, K. Bártová, Y. Nishiyama and M. Dračínskỳ, NMR crystallography of amino acids, Solid State Nucl. Magn. Reson., 2024, 130, 101921 CrossRef PubMed.
- S. S. Köcher, P. Schleker, M. Graf, R.-A. Eichel, K. Reuter, J. Granwehr and C. Scheurer, Chemical shift reference scale for Li solid state NMR derived by first-principles DFT calculations, J. Magn. Reson., 2018, 297, 33 CrossRef.
- S. E. Ashbrook and S. Sneddon, New methods and applications in solid-state NMR spectroscopy of quadrupolar nuclei, J. Am. Chem. Soc., 2014, 136, 15440 CrossRef CAS PubMed.
- M. M. Islam and T. Bredow, Lithium diffusion pathways in β-Li2TiO3: a theoretical study, J. Phys. Chem. C, 2016, 120, 7061 CrossRef CAS.
- M. T. Dunstan, J. M. Griffin, F. Blanc, M. Leskes and C. P. Grey, Ion dynamics in Li2CO3 studied by solid-state NMR and first-principles calculations, J. Phys. Chem. C, 2015, 119, 24255 CrossRef CAS.
- O. E. Zeman, I. L. Moudrakovski, C. Hartmann, S. Indris and T. Bräuniger, Local electronic structure in AlN studied by single-crystal 27Al and 14N NMR and DFT calculations, Molecules, 2020, 25, 469 CrossRef CAS PubMed.
- E. N. Bassey, P. J. Reeves, I. D. Seymour and C. P. Grey, 17O NMR spectroscopy in lithium-ion battery cathode materials: challenges and interpretation, J. Am. Chem. Soc., 2022, 144, 18714 CrossRef CAS PubMed.
- I. D. Seymour, D. S. Middlemiss, D. M. Halat, N. M. Trease, A. J. Pell and C. P. Grey, Characterizing oxygen local environments in paramagnetic battery materials via 17O NMR and DFT calculations, J. Am. Chem. Soc., 2016, 138, 9405 CrossRef CAS.
- M. C. Venetos, M. Wen and K. A. Persson, Machine learning full NMR chemical shift tensors of silicon oxides with equivariant graph neural networks, J. Phys. Chem. A, 2023, 127, 2388 CrossRef CAS.
- I. Chubak, L. Alon, E. V. Silletta, G. Madelin, A. Jerschow and B. Rotenberg, Quadrupolar 23Na+ NMR relaxation as a probe of subpicosecond collective dynamics in aqueous electrolyte solutions, Nat. Commun., 2023, 14, 84 CrossRef CAS PubMed.
- V. L. Deringer, M. A. Caro and G. Csányi, Machine learning interatomic potentials as emerging tools for materials science, Adv. Mater., 2019, 31, 1902765 CrossRef CAS.
- T. W. Ko and S. P. Ong, Recent advances and outstanding challenges for machine learning interatomic potentials, Nat. Comput. Sci., 2023, 3, 998 CrossRef CAS.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 2453 CrossRef CAS.
- S. R. Xie, M. Rupp and R. G. Hennig, Ultra-fast interpretable machine-learning potentials, npj Comput. Mater., 2023, 9, 162 CrossRef.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Mace: Higher order equivariant message passing neural networks for fast and accurate force fields, in Advances in Neural Information Processing Systems, ed. S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, Curran Associates, Inc., 2022, vol. 35, pp. 11423–11436 Search PubMed.
- G. Sivaraman, A. N. Krishnamoorthy, M. Baur, C. Holm, M. Stan, G. Csányi, C. Benmore and Á. Vázquez-Mayagoitia, Machine-learned interatomic potentials by active learning: amorphous and liquid hafnium dioxide, npj Comput. Mater., 2020, 6, 104 CrossRef CAS.
- C. G. Staacke, T. Huss, J. T. Margraf, K. Reuter and C. Scheurer, Tackling structural complexity in Li2S-P2S5 solid-state electrolytes using machine learning potentials, Nanomaterials, 2022, 12, 2950 CrossRef CAS.
- J. Zhao, J. Byggmästar, H. He, K. Nordlund, F. Djurabekova and M. Hua, Complex Ga2O3 polymorphs explored by accurate and general-purpose machine-learning interatomic potentials, npj Comput. Mater., 2023, 9, 159 CrossRef CAS.
- L. C. Erhard, J. Rohrer, K. Albe and V. L. Deringer, Modelling atomic and nanoscale structure in the silicon–oxygen system through active machine learning, Nat. Commun., 2024, 15, 1927 CrossRef CAS PubMed.
- H. Stöffler, T. Zinkevich, M. Yavuz, A. Senyshyn, J. Kulisch, P. Hartmann, T. Adermann, S. Randau, F. H. Richter and J. Janek, et al., Li+-ion dynamics in β-Li3PS4 observed by NMR: local hopping and long-range transport, J. Phys. Chem. C, 2018, 122, 15954 CrossRef.
- H. Stöffler, T. Zinkevich, M. Yavuz, A.-L. Hansen, M. Knapp, J. Bednarcik, S. Randau, F. H. Richter, J. Janek and H. Ehrenberg, et al., Amorphous versus crystalline Li3PS4: local structural changes during synthesis and Li ion mobility, J. Phys. Chem. C, 2019, 123, 10280 CrossRef.
- H. Tsukasaki, S. Mori, H. Morimoto, A. Hayashi and M. Tatsumisago, Direct observation of a non-crystalline state of Li2S–P2S5 solid electrolytes, Sci. Rep., 2017, 7, 4142 CrossRef PubMed.
- P. P. Man, Quadrupole couplings in nuclear magnetic resonance, general, Encyclopedia of Analytical Chemistry, 2000, vol. 10, DOI:10.1002/9780470027318.a6111.
- J. Jeener and P. Broekaert, Nuclear magnetic resonance in solids: thermodynamic effects of a pair of rf pulses, Phys. Rev., 1967, 157, 232 CrossRef CAS.
- R. Böhmer, Multiple-time correlation functions in spin-3/2 solid-state NMR spectroscopy, J. Magn. Reson., 2000, 147, 78 CrossRef PubMed.
- R. Böhmer, K. Jeffrey and M. Vogel, Solid-state Li NMR with applications to the translational dynamics in ion conductors, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87 CrossRef.
- G. Lipari and A. Szabo, Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. theory and range of validity, J. Am. Chem. Soc., 1982, 104, 4546 CrossRef CAS.
- J. C. Mauro and Y. Z. Mauro, On the Prony series representation of stretched exponential relaxation, Phys. A, 2018, 506, 75 CrossRef.
- M. F. Graf, H. Tempel, S. S. Köcher, R. Schierholz, C. Scheurer, H. Kungl, R.-A. Eichel and J. Granwehr, Observing different modes of mobility in lithium titanate spinel by nuclear magnetic resonance, RSC Adv., 2017, 7, 25276 RSC.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Symmetry-adapted machine learning for tensorial properties of atomistic systems, Phys. Rev. Lett., 2018, 120, 036002 CrossRef CAS PubMed.
- A. F. Harper, S. Köcher, K. Reuter and C. Scheurer, Performance metrics for tensorial learning: prediction of Li4Ti5O12 nuclear magnetic resonance observables at experimental accuracy, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-j0kp2.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567 CrossRef CAS.
- C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- S. W. Shepperd, Quaternion from rotation matrix, J. Guid. Control Dyn., 1978, 1, 223 CrossRef.
- M. Sadowski and K. Albe, Computational study of crystalline and glassy lithium thiophosphates: Structure, thermodynamic stability and transport properties, J. Power Sources, 2020, 478, 229041 CrossRef CAS.
- J. G. Smith and D. J. Siegel, Low-temperature paddlewheel effect in glassy solid electrolytes, Nat. Commun., 2020, 11, 1483, DOI:10.1038/s41467-020-15245-5.
- M. A. Caro, Optimizing many-body atomic descriptors for enhanced computationalperformance of machine learning based interatomic potentials, Phys. Rev. B, 2019, 100, 024112 CrossRef CAS.
- C. Dietrich, R. Koerver, M. W. Gaultois, G. Kieslich, G. Cibin, J. Janek and W. G. Zeier, Spectroscopic characterization of lithium thiophosphates by XPS and XAS – a model to help monitor interfacial reactions in all-solid-state batteries, Phys. Chem. Chem. Phys., 2018, 20, 20088 RSC.
- M. Taches, J. Malugani, R. Mercier and G. Robert, Ionic conductivity of and phase transition in lithium thiophosphate Li3PS4, Solid State Ionics, 1984, 14, 181 CrossRef.
- K. Shimizu, P. Bahuguna, S. Mori, A. Hayashi and S. Watanabe, Enhanced ionic conductivity through crystallization of glass-Li3PS4 by machine learning molecular dynamics simulations, J. Phys. Chem. C, 2024, 128(24), 10139–10145 CrossRef CAS.
- L. Gigli, D. Tisi, F. Grasselli and M. Ceriotti, Mechanism of charge transport in lithium thiophosphate, Chem. Mater., 2024, 36, 1482 CrossRef CAS PubMed.
- J.-S. Kim, W. D. Jung, J.-W. Son, J.-H. Lee, B.-K. Kim, K.-Y. Chung, H.-G. Jung and H. Kim, Atomistic assessments of lithium-ion conduction behavior in glass–ceramic lithium thiophosphates, ACS Appl. Mater. Interfaces, 2019, 11, 13 CrossRef CAS PubMed.
- J. Granwehr and P. J. Roberts, Inverse Laplace Transform of Multidimensional Relaxation Data Without Non-Negativity Constraint, J. Chem. Theory Comput., 2012, 8, 3473 CrossRef CAS.
- B. Lee, K. Jun, B. Ouyang and G. Ceder, Weak correlation between the polyanion environment and ionic conductivity in amorphous Li–P–S superionic conductors, Chem. Mater., 2023, 35, 891 CrossRef CAS.
- M. Wilkening, A. Kuhn and P. Heitjans, Atomic-scale measurement of ultraslow Li motions in glassy LiAlSi2O6 by two-time 6Li spin-alignment echo NMR correlation spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054303 CrossRef.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Design principles for solid-state lithium superionic conductors, Nat. Mater., 2015, 14, 1026 CrossRef CAS.
- J. Granwehr, personal communication, 2024.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00074a |
| This journal is © The Royal Society of Chemistry 2025 |