Organic NMR crystallography: enabling progress for applications to pharmaceuticals and plant cell walls

Abstract

The application of NMR crystallography to organic molecules is exemplified by two case studies. For the tosylate salt of the active pharmaceutical ingredient, Ritlectinib, solid-state NMR spectra are presented at a ¹H Larmor frequency of 1 GHz and a magic-angle spinning (MAS) frequency of 60 kHz. Specifically, ¹⁴N–¹H heteronuclear multiple-quantum coherence (HMQC) and ¹H–¹H double-quantum (DQ) single-quantum (SQ) correlation experiments are powerful probes of hydrogen bonding interactions. A full assignment of the ¹H, ¹³C and ¹⁴N/¹⁵N chemical shifts is achieved using also ¹H–¹³C cross polarization (CP) HETCOR spectra together with gauge-including projector augmented wave (GIPAW) DFT calculation for the geometry-optimised X-ray diffraction crystal structure that is reported here (CCDC 2352028). In addition, GIPAW calculations are presented for the ¹³C chemical shifts in the two polymorphs of cellulose for which diffraction structures are available. For both case studies, a focus is on the discrepancy between experiment and GIPAW calculation.

---

Introduction

Built upon the DFT gauge-including projector augmented wave (GIPAW) method,^1–3 the value of NMR crystallography for analysis of solid-state structures of organic molecules is being increasingly recognised. This paper aims to take stock of where the field is today, notably considering that experimental solid-state NMR can now readily access magnetic fields corresponding to a ¹H Larmor frequency of at least 1 GHz and magic-angle spinning (MAS) frequencies of at least 60 kHz. The paper identifies current challenges and points to new approaches under consideration. The focus is on applications to pharmaceuticals,⁴ but suitability for aiding in the interpretation of solid-state NMR spectra of plant cell walls⁵ is also considered.

For the calculation of chemical shieldings for the spin I = 1/2 nuclei ¹H and ¹³C, there is an extensive literature that the collaborative computational project for NMR crystallography (CCP-NC) database⁶ based on the .magres format⁷ is endeavouring to bring into one place. From this extensive literature, it is well established that the discrepancy with respect to experiment is usually within 1% of the chemical shift range, i.e., within ∼0.2 ppm and ∼2 ppm for ¹H and ¹³C chemical shifts, respectively.^3,8,9

That said, there are challenges. It is known that the gradient of a plot of experimental isotropic chemical shift against GIPAW calculated absolute shielding deviates from minus one,¹⁰ and there is disagreement in the community as to how referencing should be carried out. It is to be noted that this referencing problem is circumvented by a recently published method that considers differences in calculated chemical shielding between solution and the solid state. Such a difference does not require referencing, and an evaluation of correlation with respect to the corresponding change in experimental chemical shift between solution and solid enables the differentiation of solid-state form.^11,12 We also note that larger discrepancies between experiment and GIPAW calculation have been systematically observed for specific chemical groups, notably for OH⋯O ¹H and N=C–N ¹³C chemical shifts.¹³ Moreover, there remains the challenge that GIPAW calculation at an effective temperature of 0 K does not reproduce the known temperature dependence of hydrogen-bonded ¹H chemical shifts.^14–17 An important quadrupolar (I ≥ 1) nucleus for studying hydrogen bonding interactions in organic solids is ¹⁴N for which ¹H detection is important;^18–22 DFT calculation is valuable for prediction of the electric field gradients that determines the quadrupolar parameters that affect the solid-state NMR spectra.

A review of applications of NMR crystallography to pharmaceutical molecules

As one of the fathers of the field of NMR crystallography, alongside Francis Taulelle,²³ Robin Harris focused on applications to small and moderately sized organic molecules, notably, pharmaceuticals.^24,25 Early applications of the GIPAW method were, with Chris Pickard, Francesco Mauri and Jonathan Yates, for the calculation of ¹H, ¹³C and ¹⁹F chemical shifts in the pharmaceutical flurbiprofen, presented with MAS NMR spectra,²⁶ and, together with Lyndon Emsley, for the calculation of ¹³C chemical shifts for testosterone for the two distinct molecules in the asymmetric unit cell, presented with two-dimensional ¹³C refocused INADEQUATE MAS NMR spectra.²⁷

Applications to pharmaceuticals up to 2018 are referred to in the comprehensive review of NMR crystallography of organic solids by Hodgkinson;⁹ here, we refer to some specific highlights. The added value of an NMR crystallography approach for quantifying intermolecular interactions, notably hydrogen bonding, was demonstrated by calculations of the change in chemical shift between a GIPAW calculation for the full crystal structure and an isolated molecule for phenylphosponic acid by Gervais et al.,²⁸ for maltose anomers by Yates et al.,²⁹ and by Bradley et al. for the pharmaceutical indomethacin.³⁰ A significant advance was the coupling of NMR crystallography with crystal structure prediction (CSP) by Emsley and Day and co-workers, whereby, as demonstrated for thymol, best agreement to the putative CSP structures was obtained via determining the root mean squared error (RMSE) between experimental and GIPAW calculated ¹H and ¹³C chemical shifts.³¹ The importance of NMR crystallography to the pharmaceutical industry is demonstrated by a growing number of publications in collaboration with scientists from pharmaceutical companies, for example to sibenadet polymorphs with AstraZeneca³² and to cimetidine and tenoxicam with GlaxoSmithKline,³³ both in 2012. The potential to incorporate dispersion correction into DFT calculations in the DFT-D approach was demonstrated by Dudenko et al. for indomethacin in 2013.³⁴ As an alternative to the GIPAW planewave method, Beran and co-workers have advocated for a fragment-based approach that permits the use of hybrid functionals such as PBE0.^35–38 A major advance whose significance is ever increasing was the development in 2018 by Ceriotti, Emsley and co-workers of the Shift-ML method for predicting chemical shifts by applying machine learning based on a training set of GIPAW calculated chemical shifts.³⁹

Focusing on the last five years since 2019, there have been a range of impressive applications of NMR crystallography and methodological advances. Combining NMR crystallography, including two-dimensional ¹H–¹³C and ¹H–¹⁵N HETCOR MAS NMR spectra, with electron diffraction, Guzman-Afonso et al. have identified the hydrogen bonding network in form B of the pharmaceutical cimetidine.⁴⁰ Bartova et al. have combined calculation with experiment, notably ¹⁴N–¹H two-dimensional MAS NMR spectra, to study tautomerism in azo dyes, focusing on hydrogen bonding interactions.⁴¹ Scarperi et al. have used NMR crystallography to study the pharmaceutical carbimazole, presenting ¹H double-quantum (DQ) and ¹H–¹³C heteronuclear correlation MAS NMR spectra.⁴² Dudek et al. have used NMR crystallography with ¹H DQ MAS NMR spectra to probe the co-crystal landscape when an AB binary system (barbituric acid : thiobarbituric acid) is perturbed by a crystalline synthon C (1-hydroxy-4,5-dimethyl-imidazole 3-oxide) in a ball mill.⁴³ Dudek and co-workers and Pawlak et al. have also combined NMR crystallography with CSP for co-crystals of the antibiotic linezolid⁴⁴ and for the pharmaceutical teriflunomide.⁴⁵ Mathew et al. have presented an NMR crystallography study of the pharmaceutical sitagliptin phosphate monohydrate including ¹³C–¹³C and ¹³C–¹⁵N MAS NMR correlation spectra recorded at natural abundance using dynamic nuclear polarisation.⁴⁶ Brouwer and Mikolajewski have recently presented GIPAW calculations along with ¹H DQ and ¹H–¹³C heteronuclear correlation MAS NMR spectra for glucose, to identify trends in the ¹H chemical shift with hydrogen bonding parameters,⁴⁷ noting that Shen et al. have presented GIPAW calculations to complement ¹⁷O MAS NMR experiments for the same sugar molecule.⁴⁸ Chierotti and co-workers have combined experiment such as ¹H DQ and ¹H–¹³C heteronuclear correlation as well as ¹⁴N–¹H MAS NMR spectra, and GIPAW calculation to study co-crystals of the pharmaceutical ethionamide,⁴⁹ probe tautomerism in the pharmaceutical mebanazole,⁵⁰ identify zwitterions, in combination with CSP, in isomers of pyridine dicarboxylic acid,⁵¹ and to analyse leucopterin, the white pigment in butterfly wings, including a ¹H DQ MAS spectrum at 1 GHz.⁵² Working together with scientists at AstraZeneca and Pfizer, Brown and co-workers have presented NMR crystallography studies of a range of pharmaceutical molecules.^4,33,53–56

Together with Dracinsky, Hodgkinson has advocated for bringing together of molecular dynamics and nuclear quantum effects in the path-integral molecular dynamics (PIMD) approach.⁵⁷ This proves important for predicting salt or co-crystal formation corresponding to the transfer or not of a proton, as evidenced by the ¹H chemical shift.^58,59 Dracinsky has investigated geometry optimisation and GIPAW NMR calculation using the hybrid functional B3LYP or the meta-GGA functional rSCAN⁶⁰ and observed improved agreement compared to experiment for ¹H and ¹³C chemical shifts.⁶¹ This analysis has been extended to NMR crystallography of amino acids.⁶² Recently, building upon the use of a molecular correction term with a hybrid density functional,⁶³ Iuliucci et al. have compared the agreement compared to experiment for computationally more expensive double hybrid or Moller–Plesset perturbation theory (MP2), with no advantage for the test set of ¹³C and ¹⁵N chemical shifts being observed.⁶⁴ Schurko and co-workers have investigated how hybrid density functionals can improve agreement with respect to experiment for the ¹³C chemical shielding tensor for the pharmaceutical cimetidine.⁶⁵ Recently Holmes et al. have compared the agreement to experiment for the ¹³C chemical shielding tensor for five nitrogen-dense compounds when employing the hybrid functional PBE0 or the double-hybrid functional PBE0-DH.⁶⁶ Emsley and co-workers have published a series of impressive papers that make use of the ShiftML resource. Bayesian statistical theory has been integrated into the use of NMR chemical shifts,^67,68 and to enhance crystal structure prediction protocols.^69,70 Chemical-shift dependent interaction maps based on ShiftML have been presented.⁷¹ Working with scientists at AstraZeneca, structural insight has been derived for amorphous pharmaceuticals.^72,73

Experimental and computational details

Solid-state NMR

Experiments were performed using a Bruker Avance III, a Bruker Avance II+, and a Bruker NEO spectrometer operating at a ¹H Larmor frequency of 500.0 MHz, 600.0 MHz, and 1000.0 MHz, respectively, corresponding to a ¹³C Larmor frequency of 125.8 MHz, 150.9 MHz, and 251.5 MHz, respectively. ¹⁴N–¹H experiments were performed at a ¹H Larmor frequency of 600 MHz and a ¹⁴N Larmor frequency of 43.4 MHz. A 1.3 mm HXY probe at 60 kHz MAS and a 4 mm HXY probe at 12.5 kHz MAS, both in double resonance mode, were utilised. The ¹H 90° pulse duration was 2.5 μs corresponding to a ¹H nutation frequency of 100 kHz. SPINAL-64 ¹H heteronuclear decoupling⁷⁴ was employed during the acquisition of a ¹³C or ¹⁵N FID. In all 2D experiments, States-TPPI was used to obtain sign-discrimination in F₁. A recycle delay of 12 s was used.

¹H–¹³C 1D Cross-Polarisation (CP) MAS NMR and 2D CP Heteronuclear Correlation (HETCOR) MAS NMR at 600 MHz and 1 GHz. For CP at 12.5 kHz MAS, CP was achieved using a ramp (70–100%).⁷⁵ The nutation frequencies for ¹H and ¹³C, respectively, during CP were approximately 100 kHz and 80 kHz at 600 MHz and 12.5 kHz MAS and 50 kHz and 10 kHz at 1 GHz and 60 kHz MAS. The SPINAL-64 pulse duration was 5.1 μs at 12.5 kHz MAS and 45.8 μs at 60 kHz MAS. The phase cycling employed was as follows: ¹H 90° pulse (90° 270°), ¹³C CP contact pulse (2{0°} 2{180°} 2{90°} 2{270°}), receiver (0° 180° 180° 0° 90° 270° 270° 90°).

For HETCOR at 1 GHz and 60 kHz MAS, no homonuclear ¹H decoupling was applied in t₁. 1 GHz spectra were recorded with low-power ¹³C rf. irradiation during CP at an irradiation frequency of 50 ppm or 120 ppm. Here, 32 transients were co-added for each of the 128 (¹³C at 120 ppm) or 192 (¹³C at 50 ppm) t₁ FIDs using a t₁ increment of 50 μs, resulting in an experimental time of 14 or 21 hours.

¹H–¹⁵N 1D Cross-Polarisation (CP) MAS NMR. CP was achieved using a ramp on ¹H (50–100%),⁷⁵ with the same phase cycling as for the ¹H–¹³C experiments. The nutation frequencies for ¹H and ¹⁵N during CP were 70 kHz and 25 kHz. The SPINAL-64 pulse duration was 5.3 μs at a ¹H nutation frequency of 100 kHz.

Fast MAS (60 kHz) ¹H–¹H 2D NMR Experiments at 600 MHz and 1 GHz. ¹H–¹H double quantum (DQ) spectra with one rotor period of BaBa recoupling^76,77 were acquired using a rotor-synchronised t₁ increment of 16.67 μs. In both cases, 48 transients were co-added for each of the 128 t₁ FIDs, corresponding to an experimental time of 21 hours. A 16-step phase cycle was implemented, with Δp = ±2 selected during DQ excitation (4 steps) and Δp = −1 on the z-filter 90° pulse (4 steps), where p is the coherence order. The phase cycling employed was as follows: ¹H BABA pulses (0° 90° 180° 270°), ¹H 90° (z-filter) (4 {0°} 4{90°} 4{180°} 4{270°}), receiver (0° 180° 0° 180° 90° 270° 90° 270° 180° 0° 180° 0° 270° 90° 270° 90°).

2D ¹⁴N–¹H heteronuclear multiple-quantum coherence (HMQC)^18–22 MAS (60 kHz) NMR experiments. These were acquired with 8 rotor periods (133.6 μs), 16 rotor periods (267.2 μs) and 24 rotor periods (400.8 μs) of phase-inverted R³ recoupling with +x −x phase inversion for every rotor period of the n = 2 (ν₁ = 2ν_R) rotary resonance recoupling pulses.^{19,22,78–81} The ¹⁴N pulses were both of duration 11 μs. A rotor-synchronised t₁ increment of 16.67 μs was used. The experiments were obtained with 32 coadded transients for each of the 256 t₁ FIDs, corresponding to 27 hours experimental time. A 4-step nested phase cycle was used to select changes in the coherence order Δp = ±1 on the first ¹H pulse (2 steps) and Δp = ±1 on the last ¹⁴N pulse (2 steps).

Referencing. The ¹³C and ¹H chemical shifts were referenced with respect to tetramethylsilane (TMS) using L-alanine at natural abundance as the secondary reference. The CH₃ group of L-alanine is referenced at 1.1 ppm for the ¹H methyl resonance and 177.8 ppm for the ¹³C carboxylate resonance. This corresponds to adamantane at 1.85 ppm for ¹H⁸² and 38.5 ppm for ¹³C.⁸³ The ¹⁴N shifts were referenced with respect to saturated NH₄Cl aqueous solution using β-aspartyl-L-alanine at natural abundance, whereby the NH resonance is at −284 ppm at a ¹H Larmor frequency of 600 MHz, corresponding to liquid CH₃NO₂ at 0 ppm.^21,84 The ¹⁵N chemical shifts are also referenced to liquid CH₃NO₂ at 0 ppm.⁸⁵ For equivalence to the chemical shift scale frequently used in protein ¹⁵N NMR, where the alternative IUPAC reference (see Appendix 1 of ref. 86) is liquid ammonia at 50 °C, it is necessary to add 379.5 ppm to the given values.⁸⁷ The accuracy of the experimental shifts is within ±0.2, ±0.1 and ±5 for ¹H, ¹³C and ¹⁵N, and ¹⁴N, respectively.

GIPAW calculations

Density functional theory (DFT) calculations were performed using CASTEP⁸⁸ version 19.1 for 1 and version 20.1 or 22.1 for the cellulose polymorphs. For the full crystal, geometry optimisation with fixed unit cell parameters followed by magnetic shielding calculations to determine the NMR parameters were completed. Distances stated in this paper are for the geometry optimised crystal structure. The Perdew–Burke–Ernzerhof (PBE) exchange correlation functional,⁸⁹ a plane-wave basis set with ultrasoft pseudopotentials and a plane-wave cut-off energy of 800 eV were implemented. The calculations for the cellulose polymorphs were repeated using the regularised version of the SCAN functional,⁹⁰ rSCAN.⁶⁰ A maximum Monkhorst–Pack grid spacing of 2π × 0.1 Å⁻¹ or 2π × 0.05 Å⁻¹ was used. The GIPAW^1,2 method was used to calculate the NMR parameters: calculated isotropic chemical shifts were determined from the calculated chemical shieldings according to δ_{iso_calc} = σ_ref − σ_calc. It is noted that it is common practice to calculate a specific reference shielding for each system (see, e.g., Table S8 of ref. 39), though average values over a range of compounds are also available.³⁸ For 1, ¹³C, different reference shieldings were used for high- and low-ppm chemical shifts:⁹¹ 172 ppm for >45 ppm and 175 ppm for <45 ppm. For 2, the reference shieldings for the different calculations are stated in the results Table 5. For ¹H and ¹⁵N, a reference shielding of 31 ppm and −160 ppm was used, respectively.

Case study 1: the active pharmaceutical ingredient Ritlectinib tosylate

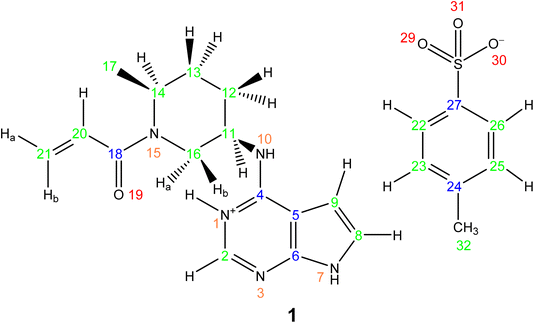
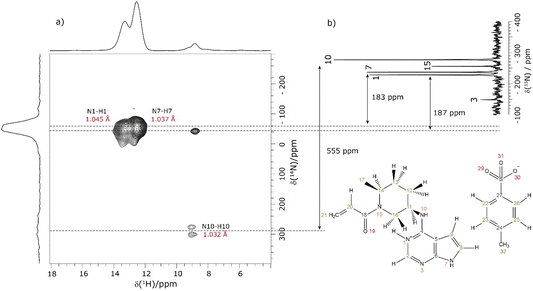
This section showcases current state-of-the-art experimental solid-state NMR for the application of NMR crystallography to moderately sized active pharmaceutical ingredients (APIs). The API, Ritlecitinib,⁹² functions as a selective and irreversible JAK3 inhibitor for irritable bowel disease with additional studies in progress for further uses as a treatment for alopecia areata⁹³ and Crohn's disease.⁹⁴ The irreversible binding is covalent in nature to a specific cysteine residue (Cys-909) within the JAK3 protein.⁹⁵ The original synthesis for the molecule, Ritlectinib, was described by Thorarensen et al.⁹⁶ In this work, the API is considered in its tosylate salt form, 1 (see Scheme 1).⁹⁷

Scheme 1

NMR crystallography is particularly well suited to the probing of intermolecular hydrogen bonding that is a key driver of the specific crystal packing adopted in the solid state. Advantage is taken of the marked sensitivity of the ¹H chemical shift and also the ¹⁴N/¹⁵N chemical shift and the ¹⁴N quadrupolar interaction to hydrogen bonding.^22,33,98,99 This is illustrated for 1 in Fig. 1 that presents a two-dimensional ¹⁴N–¹H HMQC^18–22 (Fig. 1a) and a ¹H–¹⁵N cross polarization (CP) (Fig. 1b) MAS NMR spectrum. Note that there are two NMR-active nuclei for nitrogen, ¹⁴N and ¹⁵N, with natural abundances of 99.6% and 0.4%, respectively, whereby the ¹⁵N nucleus has spin I = 1/2, while the ¹⁴N nucleus has spin I = 1. The NMR spectra of nuclei with I ≥ 1 are affected by strong quadrupolar interactions between the electric quadrupole moment of the nucleus and the surrounding electric field gradient.

Fig. 1 (a) A ¹⁴N–¹H (600 MHz) HMQC MAS (60 kHz) NMR spectrum with skyline projections of 1 recorded with 16 rotor periods of phase-inverted R³ recoupling, τ_RCPL = 267.2 μs. (b) Comparison to a 1D ¹H (500 MHz)–¹⁵N CP (3.5 ms) MAS (12.5 kHz) NMR spectrum of 1 acquired with 10 240 co-added transients. The arrows indicate the difference between the ¹⁴N shift and the ¹⁵N chemical shifts for N1, N7 and N10.

In Fig. 1a, intense ¹⁴N–¹H correlation peaks are observed at a ¹H chemical shift of 12.8 and 13.6 ppm for a ¹⁴N shift of −45 and −40 ppm, respectively, that are assigned (see below discussion) to the N7–H7 and N1–H1 directly bonded pairs of dipolar-coupled nuclei. As illustrated in Fig. 1 by the double-headed arrows, this corresponds to a change as compared to the ¹⁵N chemical shifts observed in Fig. 1b of 187 and 183 ppm, respectively. This difference arises because the ¹⁴N shift is the sum of the isotropic chemical shift (that to a good approximation is the same for ¹⁴N and ¹⁵N) and the isotropic second-order quadrupolar shift whose magnitude depends on the strength of the quadrupolar interaction (and is also inversely proportional to the B₀ magnetic field).²¹ The assignment of the observed peaks is made on the basis of a DFT calculation using the GIPAW method as implemented within the CASTEP program. By taking as input a DFT geometry-optimised crystal structure of 1, the GIPAW calculation yields the chemical shielding and the electric field gradient for each nucleus both of which depend on the electronic environment. Table 1 lists the experimental and GIPAW calculated ¹⁴N and ¹⁵N NMR parameters for 1. It is observed that the experimental quadrupolar product is very similar for N1 and N7 at 2.6 and 2.5 MHz, respectively, which is ∼20% bigger than the calculated magnitudes of 2.2 and 2.1 MHz, respectively.

Table 1 Experimentally determined ¹⁵N chemical shifts and ¹⁴N shifts (at a ¹⁴N Larmor frequency of 43.3 MHz) of 1 from Fig. 1, along with the GIPAW calculated parameters

Atom no.	δ(^15N)exp^a (ppm)	δ(^15N)calc^b (ppm)	δ(^14N)exp^c (ppm)	δ ^Qiso(^14N)exp^d (ppm)	P Qexp ^e (MHz)	P Qcalc ^f (MHz)
a ^15N isotropic chemical shift values as taken from the ^1H–^15N CP MAS spectrum presented in Fig. 1b. b δ iso = σref − σiso, where σref = −160 ppm. c Centre of gravity of the ^14N peaks extracted from the ^14N–^1H HMQC spectrum presented in Fig. 1a. Here, the error is estimated to be within ±5 ppm. d δ ^Qiso(^14N)exp = δ(^14N)exp − δ(^15N)exp. e P Qexp is calculated from δ^Qiso(^14N)exp using the equation: δ^Qiso = (3/40)(PQ/v0)^2 × 10^6, where 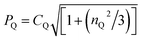.^19,21,100 Note that the sign of PQ cannot be determined experimentally. f DFT calculation for the geometry-optimised crystal structure of 1 (CCDC 2352028).
1	−228.3	−227.2	−45	183	2.6	−2.2
3	−148.8	−147.5	—	—	—	−4.0
7	−237.1	−227.3	−40	187	2.5	−2.1
10	−277.1	−278.3	278	555	3.8	−3.8
15	−256.1	−249.3	—	—	—	−4.2

---

Lower intensity peaks are also observed at a ¹H chemical shift of 9.2 ppm that corresponds to the H10 atom that is directly bonded to the N10. The peak at a ¹⁴N shift of −40 ppm corresponds to a longer range N⋯H proximity between N1 and H2 that is bonded to the neighbouring atom in the six-membered aromatic ring. The observation of this correlation peak enables the assignment of the N1–H1 cross peak, that is not possible based on the GIPAW calculation of the nitrogen chemical shift. Note that the calculated values of N1 and N7 are within 0.1 ppm, whereas the experimental ¹⁵N chemical shifts differ by 8.8 ppm (see Table 1). A low intensity N10–H10 correlation peak is observed at a ¹⁴N shift of 278 ppm. In this context, note that the quadrupolar coupling constant is significantly bigger for N10 (see Table 1) and that the intensity in such spectra depends on the choice of pulse duration for the two ¹⁴N pulses, with the optimum value dependent on the quadrupolar coupling constant.¹⁰¹ No cross peaks are observed for the N3 and N15 sites for which there is not a directly attached hydrogen atom. Peak intensity in a ¹⁴N–¹H HMQC MAS NMR spectrum depends on the recoupling of ¹⁴N–¹H dipolar couplings, here using the phase-inverted R³ method.^{19,22,78–81} Fig. S3 in the ESI† compares the ¹⁴N–¹H HMQC MAS NMR spectrum in Fig. 1a to two other spectra recorded with different durations of R³ recoupling of the ¹⁴N–¹H dipolar couplings.

Considering the ¹H–¹⁵N CP MAS NMR spectrum in Fig. 1b, note that in a CP MAS spectrum, the peak intensity depends on the transfer of transverse magnetisation from ¹H to ¹⁵N during the CP contact time. The build-up of CP signal as a function of the contact time depends on the ¹H–¹⁵N dipolar couplings that also determine the loss of signal due to T_1ρ relaxation during the ¹H spin-lock pulse. Hence different build-up behaviour is observed for the protonated and non-protonated nitrogen resonances, i.e., CP MAS spectra are not quantitative. In Fig. 1b, while the non-protonated N3 and N15 resonances are observed, it is evident that they have lower intensity than that is observed for the protonated N1, N7 and N10 resonances.

Table 2 lists the hydrogen bond parameters, namely the N⋯O and H⋯O distances as well as the NHO angles for the three intermolecular NH⋯O hydrogen bonds formed between the three NH moieties and oxygen atoms of the tosylate anion (see also Fig. 2). Note that the H⋯O distances are the similar (1.71 and 1.74 Å) for the N1–H1⋯O31 and the N1–H7⋯O31 hydrogen bonds formed by NH groups on two different API molecules with the same acceptor oxygen atom of one tosylate anion. Table 2 also compares the experimental and GIPAW calculated ¹H chemical shifts for the three NH groups in 1. The NH GIPAW calculated ¹H chemical shifts are at least 0.7 ppm higher than the experimental ¹H chemical shifts. This is a consequence of the well-established temperature dependence of such hydrogen-bonded ¹H chemical shifts in both solution^102–105 and solid-state NMR,^14–17 whereby the ¹H chemical shift increases upon decreasing temperature, i.e., if the experimental measurement could be performed at close to 0 K, better agreement to the GIPAW calculation that corresponds to 0 K would be expected. In this regard, further note that the GIPAW calculated ¹H chemical shift is higher for H7 than for H1 (14.7 as compared to 14.3 ppm), while, experimentally, H1 has the higher ¹H chemical shift, noting the above discussion of the assignment based on the cross peak to N10 observed in Fig. 1a.

Table 2 Hydrogen bonding distances and angles from the geometry-optimised crystal structure of 1 (CCDC 2352028, see Fig. 2) and experimental and GIPAW calculated ¹H NMR chemical shifts for the NH protons

Atom 1	Atom 2	Atom 3	Distance [N⋯O] (Å)	Distance [H⋯O] (Å)	Angle [NHO] (°)	Expt. δ(^1H) (ppm)	Calc. δ(^1H) (ppm)
N10	H10	O29	2.85	1.84	166.2	9.2	9.9
N1	H1	O31	2.73	1.71	164.6	13.6	14.3
N7	H7	O31	2.78	1.74	176.0	12.8	14.7

---

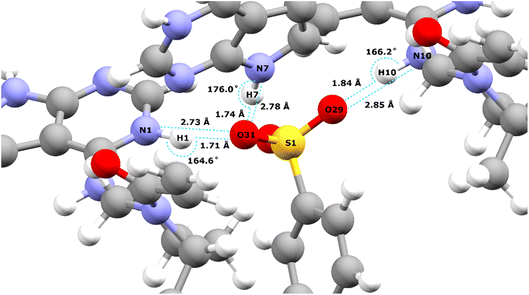Fig. 2 Intermolecular NH⋯O hydrogen bonds in the DFT (CASTEP) geometry optimised crystal structure of 1 (CCDC 2352028) between the oxygen atoms of the tosylate salt and the three NH protons of the API free base (see Table 2 for the hydrogen bond distances and angles).

In an NMR crystallography study of a pharmaceutical, further insight is obtained by carrying out a ¹H–¹H double-quantum (DQ) single-quantum (SQ) homonuclear correlation MAS NMR experiment, as presented for 1 in Fig. 3 that was recorded at a ¹H Larmor frequency of 1 GHz. The creation of DQ coherence between two ¹H spins relies on a dipolar coupling between the two spins, with the dipolar coupling having an inverse cubed dependence on the internuclear distance: the presence or absence of DQ correlation peaks is indicative of the close proximity, typically up to 3.5 Å, or not of two hydrogen atoms.^98,106,107

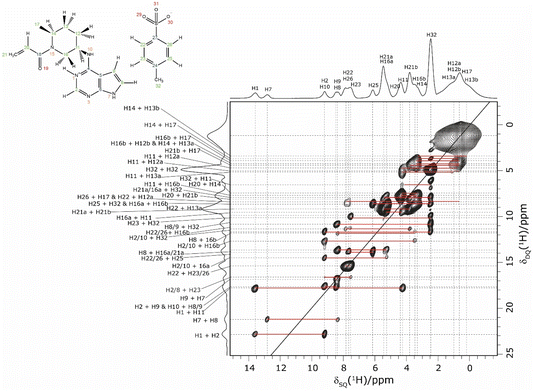Fig. 3 A ¹H (1 GHz) DQ–SQ 2D MAS (60 kHz) NMR spectrum of 1 with skyline projections recorded with one rotor period of BaBa recoupling. The base contour level is at 4% of the maximum peak height.

Consider the two highest ppm ¹H resonances at 12.8 and 13.6 ppm corresponding to the H7 and H1 NH, for which strong ¹⁴N–¹H correlation peaks were observed in Fig. 1. For the H7 SQ ¹H resonance, there is one pair of DQ peaks at 12.8 + 8.4 = 21.2 ppm, while for the H1 SQ ¹H resonance, there are two pairs of DQ peaks at 13.6 + 9.2 = 22.8 ppm and at 13.6 + 4.2 = 17.8 ppm. On the basis of the GIPAW calculation of ¹H chemical shifts for the geometry optimised crystal structure of 1, these are assigned to intramolecular H–H proximities (see Table 3) of the NH H7 to the CH H8 neighbour in the same aromatic ring (at 8.4 ppm) and between the NH H1 and the CH H2 neighbour in the same aromatic ring (at 9.2 ppm) and between the NH H1 and the CH H11 of the adjacent ring (at 4.2 ppm).

Table 3 H–H proximities^a (<3.5 Å) in 1 corresponding to experimentally observed ¹H DQ frequencies as seen in Fig. 3

Proton 1	δ SQ1 (ppm)	Proton 2	δ SQ2 (ppm)	δ DQ (ppm)	Separation (Å)
a The proximities were extracted from the DFT geometry-optimised (CASTEP) crystal structure of 1 (CCDC 2352028). Note that intra-CH3 and intra-CH2 H–H proximities for atoms 12, 13 and 17 that correspond to the broad peak at ∼1 + ∼1 = ∼2 ppm are not listed.
13b (CH3)	0.2	14 (CH)	3.3	3.5	2.49
17 (CH3)	0.6	14 (CH)	3.3	3.9	2.47, 2.47, 3.07
17 (CH3)	0.6	16b (CH2)	3.5	4.1	2.42, 3.31
12b (CH2)	0.7	16b (CH2)	3.5	4.2	2.65
13a (CH2)	1.0	14 (CH)	3.3	4.3	2.36
17 (CH3)	0.6	21b (CH2)	3.8	4.4	2.47, 2.70
32 (CH3)	2.4	32 (CH3)	2.4	4.8	1.78, 1.78
12a (CH2)	0.7	11 (CH)	4.3	5.0	2.50
12b (CH2)	0.7	11 (CH)	4.3	5.0	3.07
13a (CH2)	1.0	11 (CH)	4.3	5.3	2.49
32 (CH3)	2.4	11 (CH)	4.3	6.7	2.97
16b (CH2)	3.5	11 (CH)	4.3	7.8	3.05
14 (CH)	3.3	20 (CH)	4.4	7.7	1.88
32 (CH3)	2.4	16a (CH2)	5.3	7.7	3.21, 2.80, 2.64
32 (CH3)	2.4	21a (CH2)	5.4	7.8	3.16
21b (CH2)	3.8	20 (CH)	4.4	8.2	2.43
17 (CH3)	0.6	26 (CH)	7.6	8.2	2.77
32 (CH3)	2.4	25 (CH)	6.2	8.6	2.53, 3.00
12a (CH2)	0.7	22 (CH)	7.8	8.5	3.09
13a (CH2)	1.0	22 (CH)	7.8	8.8	2.93
16b (CH2)	3.5	16a (CH2)	5.3	8.8	1.77
21b (CH2)	3.8	21a (CH2)	5.4	9.2	1.87
11 (CH)	4.3	16a (CH2)	5.3	9.6	2.43
32 (CH3)	2.4	23 (CH)	7.5	9.9	2.45, 3.31
32 (CH3)	2.4	8 (CH)	8.4	10.8	2.90, 2.69
32 (CH3)	2.4	9 (CH)	8.5	10.9	3.02, 2.96
26 (CH)	7.6	16b (CH2)	3.5	11.1	2.70
32 (CH3)	2.4	2 (CH)	9.2	11.6	2.63, 3.17
32 (CH3)	2.4	10 (NH)	9.2	11.6	3.20, 3.34
16b (CH2)	3.5	8 (CH)	8.4	11.9	2.63
16b (CH2)	3.5	10 (NH)	9.2	12.7	2.31
11 (CH)	4.3	10 (NH)	9.2	13.5	2.95
16a (CH2)	5.3	8 (CH)	8.4	13.7	2.17
25 (CH)	6.2	26 (CH)	7.6	13.8	2.48
21a (CH2)	5.4	8 (CH)	8.4	13.8	3.43
25 (CH)	6.2	22 (CH)	7.8	14.0	2.71
16a (CH2)	5.3	2 (CH)	9.2	14.5	2.90
16a (CH2)	5.3	10 (NH)	9.2	14.5	2.71
23 (CH)	7.5	22 (CH)	7.8	15.3	2.49
26 (CH)	7.6	22 (CH)	7.8	15.4	2.71
8 (CH)	8.4	9 (CH)	8.5	16.9	2.70
9 (CH)	8.5	10 (NH)	9.2	17.7	2.56
9 (CH)	8.5	2 (CH)	9.2	17.7	3.18
11 (CH)	4.3	1 (NH)	13.6	17.9	2.13
8 (CH)	8.4	7 (NH)	12.8	21.2	2.51
2 (CH)	9.2	1 (NH)	13.6	22.8	2.25

---

The assignment of the CH ¹H resonances is aided by the two-dimensional ¹H–¹³C heteronuclear correlation (HETCOR) solid-state NMR spectra of 1 presented in Fig. 4b and c. These spectra were recorded using a pulse sequence whereby CP was employed to transfer magnetisation from ¹H to ¹³C via¹³C–¹H heteronuclear dipolar couplings. Note that, for this experimental implementation at 60 kHz MAS and a ¹H Larmor frequency of 1 GHz, a low ¹³C nutation frequency of 10 kHz was applied during CP such that the presented spectra had to be separately recorded for the high-ppm (aromatic) and low-ppm (aliphatic) regions, as presented in Fig. 4b and c, respectively. Fig. 4 additionally presents in Fig. 4a a one-dimensional ¹H (600 MHz)–¹³C CP MAS (12.5 kHz) NMR spectrum of 1 that was recorded with a CP contact time of 2 ms. Asterisks in Fig. 4a denote spinning sidebands that are observed at 83 ppm (corresponding to 12.5 kHz at the ¹³C Larmor frequency of 150.9 MHz) away from the centreband for carbonyl, aromatic and alkene ¹³C resonances that exhibit large chemical shift anisotropies.

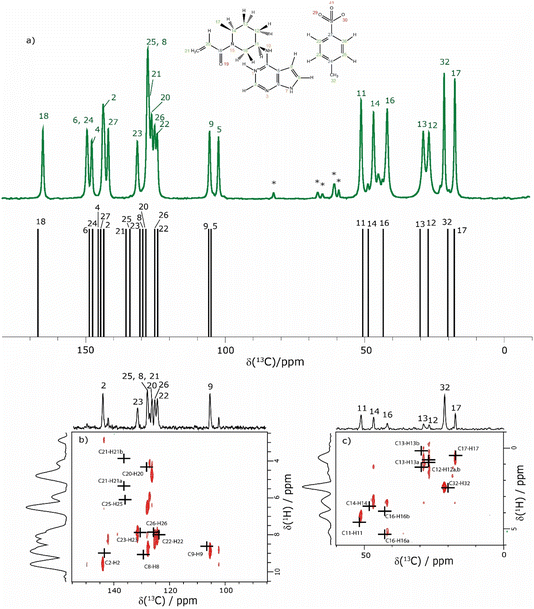Fig. 4 (a) A 1D ¹H (600 MHz)–¹³C CP (2 ms) MAS (12.5 kHz) NMR spectrum (top) of 1 acquired with 2048 co-added transients. The asterisks denote spinning sidebands. The stick spectrum (bottom) represents the GIPAW calculated ¹³C chemical shifts for the DFT (CASTEP) geometry-optimised structure of 1 (CCDC 2352028, see Table 4). (b) and (c) Two-dimensional ¹H (1 GHz)–¹³C CP (500 μs) HETCOR MAS (60 kHz) NMR spectra with skyline projections for the aromatic and aliphatic regions, respectively. Here, the low-power ¹³C irradiation during CP was at an irradiation frequency of (b) 120 ppm and (c) 50 ppm. The black crosses in (b) and (c) represent the GIPAW calculated chemical shifts for the directly bonded CH connectivities up to 1.1 Å. The base contour level is at 17% and 14% of the maximum peak height for (b) and (c), respectively.

The CP contact time was 2 ms for the one-dimensional ¹H–¹³C CP MAS (12.5 kHz) NMR spectrum in Fig. 4a and 500 μs for the 2D ¹H–¹³C CP-HETCOR MAS NMR spectra in Fig. 4b and c. As discussed above for the ¹H–¹⁵N CP MAS NMR spectrum in Fig. 1b, solid-state NMR spectra recorded using CP are not quantitative in that the peak intensities in the ¹H–¹³C CP MAS NMR spectrum depend on the transfer of transverse magnetisation from ¹H to ¹³C during the CP contact time. For the CP contact time of 500 μs as used to record the CP-HETCOR MAS NMR spectra, resonances are predominantly observed in Fig. 4b and c for the protonated CH, CH₂ and CH₃ resonances. By comparison, for the CP contact time of 2 ms as used to record the one-dimensional CP MAS NMR spectrum in Fig. 4a, similar intensity is observed for the protonated and non-protonated resonances.

In Fig. 4, the results of the GIPAW calculation for the DFT (CASTEP) geometry-optimised crystal structure of 1 are represented by a stick spectrum in Fig. 4a for the calculated ¹³C chemical shifts and by black crosses in Fig. 4b and c for the calculated ¹H and ¹³C chemical shifts for the CH, CH₂ and CH₃ moieties. Table 4 lists the assigned experimental and GIPAW calculated ¹H and ¹³C chemical shifts for 1. For the aliphatic resonances, i.e., those with a ¹³C chemical shift below 55 ppm, there is good agreement between solid-state NMR experiment and GIPAW calculation: for ¹³C, the biggest discrepancy compared to experiment is for C14 at 2.0 ppm, while for ¹H, the biggest discrepancy is 0.4 ppm for H16b (see Fig. 4a and c and Table 4). For the high ppm (>100 ppm) ¹³C resonances, the ¹H–¹³C CP-HETCOR MAS NMR spectrum in Fig. 4b enables the distinguishing of protonated and non-protonated carbon atoms for which the ¹³C chemical shifts are similar, namely the C9 CH at 105.6 ppm from the C5 C at 102.3 ppm, as well as the C2 CH at 143.6 ppm from the C27 C at 141.8 ppm. Specifically, high intensity C9–H9 and C2–H2 cross peaks are observed for the directly bonded pairs of ¹³C and ¹H at (105.6 ppm, 8.5 ppm) and (143.6 ppm, 9.2 ppm), respectively. By comparison, only weak intensity cross peaks are observed for proximities between the non-protonated C5 C at 102.3 ppm with H9 (at 8.5 ppm) that is attached to the neighbouring C9 atom of the 5-membered ring, and between the non-protonated tosylate C27 C at 141.8 ppm with H22 (at 7.8 ppm) and H26 (at 7.6 ppm) that are attached to the neighbouring C22 and C26 atoms of the phenyl ring.

Table 4 Experimental solid-state and GIPAW calculated ¹H and ¹³C NMR chemical shifts (in ppm) for 1

Atom no.	Solution-state^a		Solid-state		GIPAW calculated^b
	^1H	^13C	^1H	^13C	^1H	^13C
a Solution-state data was measured in DMSO. (Brackets indicate chemical shifts for the trans rotamer around the amine bond.) b GIPAW calculated values for the geometry-optimised crystal structure of 1 (CCDC 2352028). A reference shielding value of 172.0 ppm was used for all ^13C atoms above 45 ppm, whilst for the ^13C atoms below 45 ppm, a reference shielding value of 175.0 ppm was used.^91 In the case of ^1H, a reference value of 31 ppm was used. c In the case of the methyl groups, an average value is reported for the ^1H GIPAW calculated chemical shifts.
1 (NH^+)	13.44	—	13.6	—	14.3	—
2 (CH)	8.39	142.7	9.2	143.6	9.0	143.6
4 (C)	—	149.9	—	147.9	—	145.8
5 (C)	—	101.7	—	102.3	—	105.6
6 (C)	—	145.0	—	149.5	—	148.4
7 (NH)	12.67	—	12.8	—	14.7	—
8 (CH)	7.44	124.4	8.4	127.9	9.1	129.7
9 (CH)	6.93	101.5	8.5	105.6	8.6	106.6
10 (NH)	9.19	—	9.2	—	9.9	—
11 (CH)	3.97 (4.00)	48.2 (48.9)	4.3	51.0	4.6	51.1
12 (CH2)	1.96–1.80	24.7	0.7	26.6	0.9, 0.7	27.4
13 (CH2)	1.80–1.61	28.8 (27.8)	1.0, 0.2	28.7	1.2, 0.2	29.8
14 (CH)	4.41 (4.81)	46.6 (42.3)	3.3	46.5	3.6	48.5
16 (CH2)	4.54, 2.80 (4.11, 3.14)	39.3 (43.3)	5.3, 3.5	41.6	5.3, 3.9	42.9
17 (CH3)	1.23 (1.16)	16.4 (14.9)	0.6	17.3	0.5^c	17.4
18 (C=O)	—	165.0 (164.5)	—	165.4	—	166.5
20 (CH)	6.85	128.9 (128.7)	4.4	126.1	4.3	128.0
21 (CH2)	6.12, 5.72 (6.12, 5.87)	127.2 (127.4)	5.4, 3.8	127.5	5.4, 3.8	136.5
22 (CH)	7.49	125.4	7.8	124.3	8.0	124.1
23 (CH)	7.12	128.0	7.5	131.6	7.8	131.1
24 (C)	—	145.4	—	149.6	—	147.8
25 (CH)	7.12	128.0	6.2	127.9	6.1	135.8
26 (CH)	7.49	125.4	7.6	125.3	7.8	125.6
27 (C)	—	137.6	—	141.8	—	144.8
32 (CH3)	2.29	20.7	2.4	21.3	2.5^c	20.0

---

The most crowded part of the ¹H–¹³C CP-HETCOR MAS NMR spectrum in Fig. 4b is between ¹³C chemical shifts of 120 and 140 ppm corresponding to aromatic CH and alkene CH and CH₂ resonances. Moreover, this is where the greatest discrepancy between experiment and GIPAW calculation is observed. Considering ¹H chemical shifts below 6.5 ppm, four cross peaks are expected for the C25–H25 tosylate pair and the C20–H20, C21–H21a and C21–H21b alkene pairs. In Fig. 4b, experimental cross peaks are observed for ¹³C chemical shifts between 126.1 ppm and 127.9 ppm for ¹H chemical shifts below 6.5 ppm, while the GIPAW calculated ¹³C chemical shifts are 128.0, 136.5 and 135.8 ppm for C20, C21 and C25, respectively. For the assignment in Table 4, there is a discrepancy of 9.0 and 7.9 ppm for C21 and C25. The biggest discrepancy for ¹H is for the C8 CH, where the experimental and GIPAW calculated ¹H chemical shifts are 8.4 and 9.1 ppm, respectively.

Table 4 lists both solution (DMSO) and solid-state NMR chemical shifts for 1. The differences between experimental solution- and solid-state NMR ¹³C chemical shifts are mostly within ±2 ppm, as was the case for the discrepancy between most experimental solid-state and GIPAW calculated ¹³C chemical shifts discussed above. The biggest difference between solid-state and solution ¹³C chemical shifts is 4.5 ppm for C6. Greater variation as compared to the much smaller range of chemical shifts (∼20 ppm for ¹H compared to ∼200 ppm for ¹³C) is observed for the ¹H chemical shifts, noting the greater sensitivity of the ¹H chemical shift to the solid-state packing, e.g., ring currents from the aromatic groups. Variations of more than 1 ppm are observed for the H9 CH and the H20 CH with solution and solid-state ¹H chemical shifts of 6.93 ppm and 8.5 ppm for H9 and 6.85 ppm and 4.4 ppm for H20.

Returning to the ¹H–¹H DQ–SQ MAS NMR spectrum of 1 that was presented in Fig. 3, it is evident that the assignment of the ¹H SQ resonances in Fig. 3 follows from the assignment of the CH correlation peaks in the ¹H–¹³C CP-HETCOR MAS NMR spectra that were presented in Fig. 4b and c. This is further shown in Fig. 5 that presents the ¹H–¹³C CP-HETCOR MAS NMR spectra (top) with the ¹H–¹H DQ–SQ MAS NMR spectra (bottom), whereby the HETCOR spectra have been rotated through 90° such that there is a common horizontal ¹H SQ chemical axis.

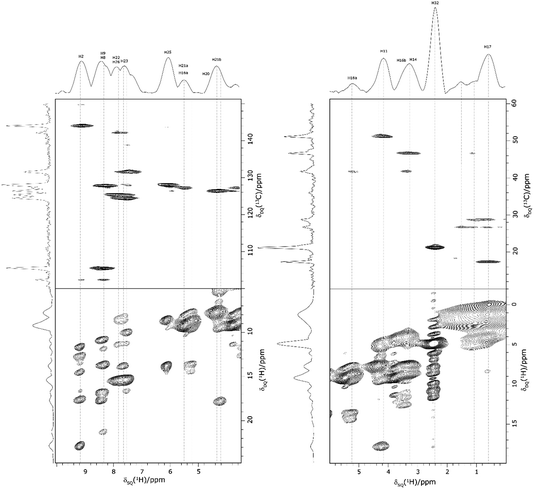Fig. 5 2D MAS (60 kHz) NMR spectra with skyline projections of 1 recorded at 1 GHz. Top: ¹H–¹³C CP HETCOR spectra for the high (left) and low (right) ppm regions repeated from Fig. 4b and c, respectively. Bottom: Corresponding regions of the ¹H–¹H DQ–SQ spectrum repeated from Fig. 3. Note that the ¹H–¹³C CP HETCOR spectra have been rotated through 90° so as to achieve the alignment of the ¹H SQ axis as horizontal for both sets of spectra.

Case study 2: cellulose polymorphs

In ref. 5, Simmons et al. employed GIPAW calculation of ¹³C NMR chemical shifts for 10 residue DFT-optimised molecular dynamics generated xylan structures to confirm that changes observed experimentally for the ¹³C NMR chemical shifts for xylan are sensitive to the adoption of a two- and three-fold screw. As shown in Table 1 of ref. 5, agreement between experiment and GIPAW calculation for the change in ¹³C NMR chemical shift varied from within 0.8 ppm to within 3.4 ppm. In the context also of the observation of six different glucose environments with distinct ¹³C NMR chemical shifts that are common to the cellulose in a range of plants (poplar wood, spruce wood and grasses), it is interesting to consider, in Table 5, the discrepancy between experiment and GIPAW calculation for the two cellulose polymorphs for which crystal structures are available, cellulose Iα and cellulose Iβ.^108,109 Note that in both cases there are two distinct molecules in the asymmetric unit cell. Specifically, in cellulose Iα, the two distinct molecules are neighbouring molecules within the same chain, whereas, in cellulose Iβ, the two distinct molecules correspond to separate chains, called centre and origin. Table 5 presents calculated ¹³C NMR chemical shifts for three different calculation approaches and compares the GIPAW calculations to experimental ¹³C NMR chemical shifts reported by Brouwer and Mikolajewski.^110,111 Two calculations using the PBE functional are presented: one with an incompletely converged geometry optimisation (as in the submitted article made available ahead of the discussion meeting) and one with converged geometries. In addition, results are presented for a calculation using the meta-GGA rSCAN for both the geometry optimisation and the GIPAW NMR calculation. It is evident that better agreement to experiment is observed when using rSCAN with both reduced RMSD and maximum difference. We note that GIPAW calculations of mono- and disaccharides have also been reported by Yates et al. for maltose,²⁹ by Brouwer et al. for glucose¹¹² and by Kibalchenko et al. for galactose,¹¹³ while quantum-chemical calculations have been presented for fragments of the cellulose structures by Wang et al.¹¹⁴

Table 5 Comparison of GIPAW calculated ¹³C NMR chemical shifts (in ppm) for cellulose polymorphs to experiment

	Cellulose Iα				Cellulose Iβ
	GIPAW^a			Expt^b	GIPAW^a			Expt^b
	PBE (not conv.)	PBE (conv.)	rSCAN		PBE (not conv.)	PBE (conv.)	rSCAN
a The crystal structures for cellulose Iβ (JINROO05, 792796)^108 and cellulose Iβ (JINROO01, 810 597)^109 were used as starting points for geometry optimisation. b Experimental values are taken from Brouwer and Mikolajewski.^110,111 with C1 chemical shifts switched for cellulose Iβ^115 Assignment to unit 1 and unit 2 is based on the relative change in the C1 and C5 ^13C chemical shift c δ calc. = σref − σcalc. d The ^13C chemical shift with the maximum discrepancy between experiment and GIPAW calculation is indicated in underlined bold.
Unit 1	C7–C12				C1, C3, …
C1	107.6	108.2	105.4	105.6	106.6	108.2	105.6	104.4
C2	74.0	74.4	74.8	72.2	73.3	72.8	73.5	71.7
C3	74.4	74.8	75.5	74.6	73.2	72.0	73.4	75.3
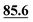
C4	87.3	86.1		89.4	87.9	90.2	89.4	88.4
C5	70.8	71.8	72.7	73.1	71.0	69.4	70.6	71.4
C6	65.3	65.0	65.5	65.7	64.4	64.0	64.9	66.0
Unit 2	C1–C6				C13, C15, …
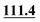
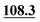
C1	107.6	106.9	104.2	105.5	108.7			106.1
C2	75.4	74.1	74.4	71.2	70.7	70.5	71.4	71.7
C3	75.1	74.0	74.5	75.1	75.3	74.1	75.1	74.4
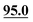
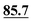
C4	93.6		93.7	90.3		88.1	87.4	89.2
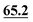
C5		66.9	68.0	71.3	74.5	71.2	72.2	72.9
C6	63.3	64.0	65.0	65.8	65.3	64.5	65.2	65.2
σ ref ^c	168.1	168.1	178.5		168.1	168.7	178.0
RMSD	2.8	2.6	2.2		1.8	2.5	1.3
Max. diff.^d	6.1	4.7	3.8		3.5	5.3	2.1

---

Summary and outlook

This article has presented two case studies of the application of NMR crystallography of organic molecules to two important research areas, namely pharmaceuticals and plant cell walls. Building upon 20 years of literature applications, these two case studies showcase the great value of DFT calculation using the GIPAW method, in complementing experimental solid-state NMR. While agreement with experiment is good, indeed remarkably good given the inherent approximations of DFT, the discrepancy that typically corresponds to 1% of the chemical shift range for ¹H and ¹³C is nevertheless restrictive, for example in seeking to provide evidence for different structural models for plant cell walls where there are only subtle changes in chemical shift. There is thus much motivation for continued innovation in the field of NMR crystallography.

Data availability

The calculated and experimental data for this study are provided as a supporting data set from WRAP, the Warwick Research Archive Portal at http://wrap.warwick.ac.uk/188293.

Conflicts of interest

Some of the authors are employees of Pfizer, and compound 1 is a Pfizer pharmaceutical.

Acknowledgements

ZR and JL thank the Engineering and Physical Sciences Research Council (EPSRC) and Pfizer (ZR) and the University of Warwick and Bruker (JL) for PhD funding. APB acknowledges support from the CASTEP-USER project, funded by EPSRC (EP/W030438/1). The UK High-Field Solid-State NMR Facility used in this research was funded by EPSRC and BBSRC (EP/T015063/1) and, for the 1 GHz instrument, EP/R029946/1. We acknowledge the X-ray diffraction and the Scientific Computing Research Technology Platform at the University of Warwick for the PXRD experiment and for cellulose CASTEP calculations, respectively. Helpful discussions with Anjali Menakath, Ben Tatman and Mohammed Rahman at the University of Warwick are acknowledged.

References

1. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
2. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
3. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733.
4. Z. Rehman, W. T. Franks, B. Nguyen, H. F. Schmidt, G. Scrivens and S. P. Brown, J. Pharm. Sci., 2023, 112, 1915.
5. T. J. Simmons, J. C. Mortimer, O. D. Bernardinelli, A. C. Poppler, S. P. Brown, E. R. Deazevedo, R. Dupree and P. Dupree, Nat. Commun., 2016, 7, 13902.
6. https://www.ccpnc.ac.uk/database/ .
7. S. Sturniolo, T. F. G. Green, R. M. Hanson, M. Zilka, K. Refson, P. Hodgkinson, S. P. Brown and J. R. Yates, Solid State Nucl. Magn. Reson., 2016, 78, 64.
8. R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174.
9. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10.
10. G. N. M. Reddy, D. S. Cook, D. Iuga, R. I. Walton, A. Marsh and S. P. Brown, Solid State Nucl. Magn. Reson., 2015, 65, 41.
11. H. Blade, C. D. Blundell, S. P. Brown, J. Carson, H. R. W. Dannatt, L. P. Hughes and A. K. Menakath, J. Phys. Chem. A, 2020, 124, 8959.
12. M. Rahman, H. R. W. Dannatt, C. D. Blundell, L. P. Hughes, H. Blade, J. Carson, B. P. Tatman, S. T. Johnston and S. P. Brown, J. Phys. Chem. A, 2024, 128, 1793.
13. E. K. Corlett, H. Blade, L. P. Hughes, P. J. Sidebottom, D. Walker, R. I. Walton and S. P. Brown, Solid State Nucl. Magn. Reson., 2020, 108, 101662.
14. S. K. Mann, M. K. Devgan, W. T. Franks, S. Huband, C. L. Chan, J. Griffith, D. Pugh, N. J. Brooks, T. Welton, T. N. Pham, L. L. McQueen, J. R. Lewandowski and S. P. Brown, J. Phys. Chem. B, 2020, 124, 4975.
15. C. J. Pickard, E. Salager, G. Pintacuda, B. Elena and L. Emsley, J. Am. Chem. Soc., 2007, 129, 8932.
16. J. N. Dumez and C. J. Pickard, J. Chem. Phys., 2009, 130, 104701.
17. A. L. Webber, B. Elena, J. M. Griffin, J. R. Yates, T. N. Pham, F. Mauri, C. J. Pickard, A. M. Gil, R. Stein, A. Lesage, L. Emsley and S. P. Brown, Phys. Chem. Chem. Phys., 2010, 12, 6970.
18. S. Cavadini, S. Antonijevic, A. Lupulescu and G. Bodenhausen, J. Magn. Reson., 2006, 182, 168.
19. Z. H. Gan, J. P. Amoureux and J. Trebosc, Chem. Phys. Lett., 2007, 435, 163.
20. S. Cavadini, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 56, 46.
21. A. S. Tatton, J. P. Bradley, D. Iuga and S. P. Brown, Z. Phys. Chem., 2012, 226, 1187.
22. B. Tatman, H. Modha and S. P. Brown, J. Magn. Reson., 2023, 352, 107459.
23. F. Taulelle, Solid State Sci., 2004, 6, 1053.
24. R. K. Harris, Solid State Sci., 2004, 6, 1025.
25. R. K. Harris, Analyst, 2006, 131, 351.
26. J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402.
27. R. K. Harris, S. A. Joyce, C. J. Pickard, S. Cadars and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 137.
28. C. Gervais, M. Profeta, V. Lafond, C. Bonhomme, T. Azais, H. Mutin, C. J. Pickard, F. Mauri and F. Babonneau, Magn. Reson. Chem., 2004, 42, 445.
29. J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Amado, A. M. Gil and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 10216.
30. J. P. Bradley, S. P. Velaga, O. N. Antzutkin and S. P. Brown, Cryst. Growth Des., 2011, 11, 3463.
31. E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, J. Am. Chem. Soc., 2010, 132, 2564.
32. J. P. Bradley, C. J. Pickard, J. C. Burley, D. R. Martin, L. P. Hughes, S. D. Cosgrove and S. P. Brown, J. Pharm. Sci., 2012, 101, 1821.
33. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, CrystEngComm, 2012, 14, 2654.
34. D. V. Dudenko, J. R. Yates, K. D. M. Harris and S. P. Brown, CrystEngComm, 2013, 15, 8797.
35. J. D. Hartman, S. Monaco, B. Schatschneider and G. J. O. Beran, J. Chem. Phys., 2015, 143, 102809.
36. G. J. O. Beran, J. D. Hartman and Y. N. Heit, Acc. Chem. Res., 2016, 49, 2501.
37. J. D. Hartman, G. M. Day and G. J. O. Beran, Cryst. Growth Des., 2016, 16, 6479.
38. J. D. Hartman, R. A. Kudla, G. M. Day, L. J. Mueller and G. J. O. Beran, Phys. Chem. Chem. Phys., 2016, 18, 21686.
39. F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 4501.
40. C. Guzman-Afonso, Y. L. Hong, H. Colaux, H. Iijima, A. Saitow, T. Fukumura, Y. Aoyama, S. Motoki, T. Oikawa, T. Yamazaki, K. Yonekura and Y. Nishiyama, Nat. Commun., 2019, 10, 3537.
41. K. Bartova, I. Cisarova, A. Lycka and M. Dracinsky, Dyes Pigm., 2020, 178, 108342.
42. A. Scarperi, G. Barcaro, A. Pajzderska, F. Martini, E. Carignani and M. Geppi, Molecules, 2021, 26, 4577.
43. M. K. Dudek, J. Sniechowska, A. Wroblewska, S. Kazmierski and M. J. Potrzebowski, Chem.–Eur. J., 2020, 26, 13264.
44. M. Khalaji, P. Paluch, M. J. Potrzebowski and M. K. Dudek, Solid State Nucl. Magn. Reson., 2022, 121, 101813.
45. T. Pawlak, I. Sudgen, G. Bujacz, D. Iuga, S. P. Brown and M. J. Potrzebowski, Cryst. Growth Des., 2021, 21, 3328.
46. R. Mathew, I. V. Sergeyev, F. Aussenac, L. Gkoura, M. Rosay and M. Baias, Solid State Nucl. Magn. Reson., 2022, 119, 101794.
47. D. H. Brouwer and J. G. Mikolajewski, Solid State Nucl. Magn. Reson., 2023, 123, 101848.
48. J. H. Shen, V. Terskikh, J. Struppe, A. Hassan, M. Monette, I. Hung, Z. H. Gan, A. Brinkmann and G. Wu, Chem. Sci., 2022, 13, 2591.
49. D. Bernasconi, S. Bordignon, F. Rossi, E. Priola, C. Nervi, R. Gobetto, D. Voinovich, D. Hasa, N. T. Duong, Y. Nishiyama and M. R. Chierotti, Cryst. Growth Des., 2020, 20, 906.
50. F. Bravetti, S. Bordignon, E. Alig, D. Eisenbeil, L. Fink, C. Nervi, R. Gobetto, M. U. Schmidt and M. R. Chierotti, Chem.–Eur. J., 2022, 28, e202103589.
51. F. Bravetti, R. E. Russo, S. Bordignon, A. Gallo, F. Rossi, C. Nervi, R. Gobetto and M. R. Chierotti, Molecules, 2023, 28, 1876.
52. F. Bravetti, L. Tapmeyer, K. Skorodumov, E. Alig, S. Habermehl, R. Huhn, S. Bordignon, A. Gallo, C. Nervi, M. R. Chierotti and M. U. Schmidt, IUCrJ, 2023, 10, 448.
53. P. M. J. Szell, S. P. Brown, L. P. Hughes, H. Blade and S. O. N. Lill, Chem. Commun., 2020, 56, 14039.
54. P. M. J. Szell, J. R. Lewandowski, H. Blade, L. P. Hughes, S. O. N. Lill and S. P. Brown, CrystEngComm, 2021, 23, 6859.
55. A. J. Al-Ani, P. M. J. Szell, Z. Rehman, H. Blade, H. P. Wheatcroft, L. P. Hughes, S. P. Brown and C. C. Wilson, Cryst. Growth Des., 2022, 22, 4696.
56. P. M. J. Szell, Z. Rehman, B. Tatman, L. P. Hughes, H. Blade and S. P. Brown, ChemPhysChem, 2023, 24, 8.
57. M. Dracinsky, J. Vicha, K. Bartova and P. Hodgkinson, ChemPhysChem, 2020, 21, 2075.
58. J. Blahut, J. R. Stocek, M. Sala and M. Dracinsky, J. Magn. Reson., 2022, 345, 107334.
59. J. R. Stocek, O. Socha, I. Cisarova, T. Slanina and M. Dracinsky, J. Am. Chem. Soc., 2022, 144, 7111.
60. A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101.
61. M. Dracinsky, Molecules, 2021, 26, 3857.
62. T. V. Chaloupecka E, K. Bártová, Y. Nishiyama and M. Dracínský, Solid State Nucl. Magn. Reson., 2024, 130, 101921.
63. M. Dracinsky, P. Unzueta and G. J. O. Beran, Phys. Chem. Chem. Phys., 2019, 21, 14992.
64. R. J. Iuliucci, J. D. Hartman and G. J. O. Beran, J. Phys. Chem. A, 2023, 127, 2846.
65. S. T. Holmes, O. G. Engl, M. N. Srnec, J. D. Madura, R. Quinones, J. K. Harper, R. W. Schurko and R. J. Iuliucci, J. Phys. Chem. A, 2020, 124, 3109.
66. S. T. Holmes, C. M. Boley, A. Dewicki, Z. T. Gardner, C. S. Vojvodin, R. J. Iuliucci and R. W. Schurko, Magn. Reson. Chem., 2024, 62, 179.
67. E. A. Engel, A. Anelli, A. Hofstetter, F. Paruzzo, L. Emsley and M. Ceriotti, Phys. Chem. Chem. Phys., 2019, 21, 23385.
68. M. Cordova, M. Balodis, B. S. de Almeida, M. Ceriotti and L. Emsley, Sci. Adv., 2021, 7, eabk2341.
69. M. Balodis, M. Cordova, A. Hofstetter, G. M. Day and L. Emsley, J. Am. Chem. Soc., 2022, 144, 7215.
70. M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter, M. Ceriotti and L. Emsley, J. Phys. Chem. C, 2022, 126, 16710.
71. M. Cordova and L. Emsley, J. Am. Chem. Soc., 2023, 145, 16109.
72. M. Cordova, M. Balodis, A. Hofstetter, F. Paruzzo, S. O. N. Lill, E. S. E. Eriksson, P. Berruyer, B. S. de Almeida, M. J. Quayle, S. T. Norberg, A. S. Ankarberg, S. Schantz and L. Emsley, Nat. Commun., 2021, 12, 2964.
73. M. Cordova, P. Moutzouri, S. O. N. Lill, A. Cousen, M. Kearns, S. T. Norberg, A. S. Ankarberg, J. McCabe, A. C. Pinon, S. Schantz and L. Emsley, Nat. Commun., 2023, 14, 5138.
74. B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97.
75. G. Metz, X. L. Wu and S. O. Smith, J. Magn. Reson., Ser. A, 1994, 110, 219.
76. W. Sommer, J. Gottwald, D. E. Demco and H. W. Spiess, J. Magn. Reson., Ser. A, 1995, 113, 131.
77. I. Schnell, A. Lupulescu, S. Hafner, D. E. Demco and H. W. Spiess, J. Magn. Reson., 1998, 133, 61.
78. D. P. Raleigh, M. H. Levitt and R. G. Griffin, Chem. Phys. Lett., 1988, 146, 71.
79. P. R. Costa, J. D. Gross, M. Hong and R. G. Griffin, Chem. Phys. Lett., 1997, 280, 95.
80. S. J. Huang, S. B. Liu and J. C. C. Chan, Solid State Nucl. Magn. Reson., 2009, 36, 110.
81. A. L. Webber, S. Masiero, S. Pieraccini, J. C. Burley, A. S. Tatton, D. Iuga, T. N. Pham, G. P. Spada and S. P. Brown, J. Am. Chem. Soc., 2011, 133, 19777.
82. S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1991, 64, 685.
83. C. R. Morcombe and K. W. Zilm, J. Magn. Reson., 2003, 162, 479.
84. E. K. Corlett, H. Blade, L. P. Hughes, P. J. Sidebottom, D. Walker, R. I. Walton and S. P. Brown, CrystEngComm, 2019, 21, 3502.
85. S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1991, 64, 688.
86. R. K. Harris, E. D. Becker, S. M. C. De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Pure Appl. Chem., 2008, 80, 59.
87. G. E. Martin and C. E. Hadden, J. Nat. Prod., 2000, 63, 543.
88. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallog., 2005, 220, 567.
89. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
90. J. W. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
91. A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, J. Phys. Chem. A, 2010, 114, 10435.
92. M. F. Brown, A. Casimiro-Garcia, Y. Che, J. W. Coe, M. E. Flanagan, A. M. Gilbert, M. M. Hayward, J. D. Langille, J. I. Montgomery, J.-B. Telliez, A. Thorarensen and R. J. Unwalla, Pyrrolo[2,3-d]pyrimidinyl, pyrrolo[2,3-b]pyrazinyl and pyrrolo[2,3-d]pyridinyl acrylamides, WO2015083028A1, 2015, https://patents.google.com/patent/WO2015083028A1/en?oq=WO2015%2f083028.
93. H. A. Ramírez-Marín and A. Tosti, Drug Des., Dev. Ther., 2022, 16, 363.
94. F. D'Amico, G. Fiorino, F. Furfaro, M. Allocca and S. Danese, Expert Opin. Invest. Drugs, 2018, 27, 595.
95. H. Xu, M. I. Jesson, U. I. Seneyiratne, T. H. Lin, M. N. Shari, L. Xue, C. Nguyen, R. A. Everley, J. I. Trujillo, D. S. Johnson, G. R. Point, A. Thorarensen, L. Kilty and J. B. Telliez, ACS Chem. Biol., 2019, 14, 1235.
96. A. Thorarensen, M. E. Dowty, M. E. Banker, B. Juba, J. Jussif, T. Lin, F. Vincent, R. M. Czerwinski, A. Casimiro-Garcia, R. Unwalla, J. I. Trujillo, S. Liang, P. Balbo, Y. Che, A. M. Gilbert, M. F. Brown, M. Hayward, J. Montgomery, L. Leung, X. Yang, S. Soucy, M. Hegen, J. Coe, J. Langille, F. Vajdos, J. Chrencik and J. B. Telliez, J. Med. Chem., 2017, 60, 1971.
97. B. M. Samas, Y. Tao, D. J. Critcher, D. S. B. Daniels, K. P. Girard, G. S. Goeken and P. R. Rose, Pyrrolo[2,3-d]pyrimidine tosylate salt, crystalline form thereof and manufacturing process and intermediates thereto, US Pat., US20210387989A1, 2021, https://patents.google.com/patent/US20210387989A1/en.
98. S. P. Brown, Solid State Nucl. Magn. Reson., 2012, 41, 1.
99. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Iuga, A. J. Edwards and S. P. Brown, Mol. Pharmaceutics, 2013, 10, 999.
100. A. Samoson, Chem. Phys. Lett., 1985, 119, 29.
101. A. G. M. Rankin, J. Trébosc, P. Paluch, O. Lafon and J. P. Amoureux, J. Magn. Reson., 2019, 303, 28.
102. U. Liddel and N. F. Ramsey, J. Chem. Phys., 1951, 19, 1608.
103. J. T. Arnold and M. E. Packard, J. Chem. Phys., 1951, 19, 1608.
104. N. Muller and R. C. Reiter, J. Chem. Phys., 1965, 42, 3265.
105. M. Garcia-Viloca, R. Gelabert, A. González-Lafont, M. Moreno and J. M. Lluch, J. Am. Chem. Soc., 1998, 120, 10203.
106. S. P. Brown, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 199.
107. J. P. Bradley, C. Tripon, C. Filip and S. P. Brown, Phys. Chem. Chem. Phys., 2009, 11, 6941.
108. Y. Nishiyama, J. Sugiyama, H. Chanzy and P. Langan, J. Am. Chem. Soc., 2003, 125, 14300.
109. Y. Nishiyama, P. Langan and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074.
110. D. H. Brouwer and J. G. Mikolajewski, Cellulose, 2023, 30, 4827.
111. D. H. Brouwer and J. G. Mikolajewski, Cellulose, 2023, 30, 11341.
112. D. H. Brouwer, K. P. Langendoen and Q. Ferrant, Can. J. Chem., 2011, 89, 737.
113. M. Kibalchenko, D. Lee, L. M. Shao, M. C. Payne, J. J. Titman and J. R. Yates, Chem. Phys. Lett., 2010, 498, 270.
114. T. Wang, H. Yang, J. D. Kubicki and M. Hong, Biomacromolecules, 2016, 17, 2210.
115. R. Cresswell, P. K. Deralia, Y. Yoshimi, S. P. Brown, R. Dupree and P. Dupree, 2024, https://biorxiv.org/cgi/content/short/2024.08.24.609305v1.

---

Footnote

† Electronic supplementary information (ESI) available: Single-crystal X-ray diffraction of 1 (CCDC 2352028) details; powder X-ray diffraction of 1; additional solid-state NMR spectra of 1. CCDC 2352028. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4fd00088a

---