Open Access Article
Open Access ArticleCharacterization of ephedrine HCl and pseudoephedrine HCl using quadrupolar NMR crystallography guided crystal structure prediction†
Carl H.
Fleischer
III
 ab,
Sean T.
Holmes
ab,
Sean T.
Holmes
 ab,
Kirill
Levin
ab,
Kirill
Levin
 c,
Stanislav L.
Veinberg
c and
Robert W.
Schurko
c,
Stanislav L.
Veinberg
c and
Robert W.
Schurko
 *ab
*ab
aDepartment of Chemistry & Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: rschurko@fsu.edu
bNational High Magnetic Field Laboratory, Tallahassee, FL 32310, USA
cDepartment of Chemistry & Biochemistry, University of Windsor, Windsor, ON N9B 3P4, Canada
First published on 24th June 2024
Abstract
Quadrupolar NMR crystallography guided crystal structure prediction (QNMRX-CSP) is a nascent protocol for predicting, solving, and refining crystal structures. QNMRX-CSP employs a combination of solid-state NMR data from quadrupolar nuclides (i.e., nuclear spin >1/2), static lattice energies and electric field gradient (EFG) tensors from dispersion-corrected density functional theory (DFT-D2*) calculations, and powder X-ray diffraction (PXRD) data; however, it has so far been applied only to organic HCl salts with small and rigid organic components, using 35Cl EFG tensor data for both structural refinement and validation. Herein, QNMRX-CSP is extended to ephedrine HCl (Eph) and pseudoephedrine HCl (Pse), which are diastereomeric compounds that feature distinct space groups and organic components that are larger and more flexible. A series of benchmarking calculations are used to generate structural models that are validated against experimental data, and to explore the impacts of the: (i) starting structural models (i.e., geometry-optimized fragments based on either a known crystal structure or an isolated gas-phase molecule) and (ii) selection of unit cell parameters and space groups. Finally, we use QNMRX-CSP to predict the structure of Pse in the dosage form Sudafed® using only 35Cl SSNMR data as experimental input. This proof-of-concept work suggests the possibility of employing QNMRX-CSP to solve the structures of organic HCl salts in dosage forms – something which is often beyond the capabilities of conventional, diffraction-based characterization methods.
1. Introduction
Advances in theory and computational power have enabled the rise of crystal structure prediction (CSP) methods for the discovery of new materials and refinement of their solid-state structures,1–7 including active pharmaceutical ingredients (APIs),8–11 metal–organic frameworks,12,13 and organic semi-conductors.14–16 There are numerous commercial and open-access CSP software packages available,17–23 many of which are used in combination with experimental data and/or other computational methods. For the CSP of organic compounds, the Cambridge Crystallographic Data Center24 (CCDC) has run six CSP “blind tests” (a seventh is currently underway), where participants are tasked with predicting the crystal structures of various organic molecules, ranging from those with small organic components to intricate multicomponent cocrystals.25–30 Limitations of CSP methods include, but are not limited to: (i) the need for advanced algorithms for searching the complex structure spaces,4,31 especially for systems that have high molecular weights, high flexibility,32,33 and/or multiple independent molecules,34 all of which increase the computational cost; and (ii) the difficulties in the ranking the relative energies of candidate structures.35–37NMR crystallography (NMRX), which utilizes a combination of solid-state NMR (SSNMR), quantum chemical computations, and in some cases, powder X-ray diffraction (PXRD) data, is widely used for the prediction, refinement, and validation of structures,38–42 and has emerged as a means of improving CSP methods.1–7 Notably, NMRX-CSP can greatly decrease the computational costs associated with CSP methods, while also providing metrics for validation of structural models (i.e., via comparison of experimentally measured and computationally derived NMR parameters and crystallographic data).43–48 While PXRD provides invaluable information on long-range order, the space group, and the unit cell parameters,49,50 SSNMR adds information on local atomic environments through chemical shifts,51–53 interatomic proximities through dipolar couplings,54–56 and confirmation of the number of asymmetric units.57 These data reduce the search space of computational methods, which refine candidate crystal structures, determine relative energy rankings, and calculate NMR interactions for comparison with experiment.35,36,58
To date, the vast majority of NMRX-CSP studies on organic systems rely upon the comparisons of experimental and calculated 1H and 13C chemical shifts;39–42,51–53 however, given the ubiquity of elements with quadrupolar nuclei in organic solids (i.e., spin I > 1/2, including 14N, 17O, 23Na, and 35Cl), it seems their exploitation would be of great benefit. The quadrupolar interaction, which is the interaction between the nuclear quadrupole moment and the electric field gradients (EFGs) at the nuclear origin, can be directly measured from SSNMR spectra of quadrupolar nuclides, in the form of the quadrupolar coupling constant, CQ, and asymmetry parameter, ηQ (see Table 1 for definitions). The EFGs, which are described by symmetric, second-rank tensors, are exquisitely sensitive to their local electronic environments, as well as longer-range electrostatic interactions that often do not have significant influences on chemical shifts. The EFG tensor principal components and their orientations in the molecular/crystal frame depend only upon the ground-state electron density; as such, first principles calculations of EFG tensors are very efficient in comparison to those of chemical shielding.60,61 Despite these advantages, the use of quadrupolar nuclei in NMRX-CSP studies is limited to date, with a few reports of 14N–1H correlation experiments and/or 13C–14N residual dipolar couplings to determine the proximities of these atom pairs.62–64 We suspect that the two main reasons that quadrupolar guided NMRX-CSP has largely gone underutilized are: (i) the acquisition of high quality SSNMR spectra of quadrupolar nuclides has traditionally been regarded as challenging and outside of the interest of many practitioners of advanced SSNMR methods; and (ii) there have been issues with calculations of EFG tensors in organic solids that match well with experiment.60,61,65,66 Fortunately, the former issue has largely been resolved, with a wide range of hardware and pulse sequences available to the end user for the investigation of quadrupoles; however, the latter issue has only recently been addressed by including reparametrized semi-empirical dispersion corrections in geometry optimizations.67,68
| C Q (MHz)c |
η
Q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
δ iso (ppm)d | Ω (ppm)d |
κ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
α (°)e | β (°)e | γ (°)e | ||
|---|---|---|---|---|---|---|---|---|---|
| a Theoretical EFG tensor parameters were obtained from calculations on XRD-derived structural models that were refined at the RPBE-D2* level. b The experimental uncertainties in the last digit for each value are indicated in parentheses. c The principal components of the EFG tensors are defined such that |V33| ≥ |V22| ≥ |V11|. The quadrupolar coupling constant and asymmetry parameter are given by CQ = eQV33/h, and ηQ = (V11 − V22)/V33, respectively. The sign of CQ cannot be determined from the experimental 35Cl spectra. d The principal components of the chemical shift tensors are defined using the frequency-ordered convention, with δ11 ≥ δ22 ≥ δ33. The isotropic chemical shift, span, and skew are given by δiso = (δ11 + δ22 + δ33)/3, Ω = δ11 − δ33, and κ = 3(δ22 − δiso)/Ω, respectively. e The Euler angles α, β, and γ define the relative orientation of the EFG and chemical shift tensors using the ZY′Z′′ convention for rotation. f Calculated 35Cl magnetic shielding constants were converted to the chemical shift scale through a separate calculation on a geometry optimized structural model of L-histidine HCl·H2O (based on a structure from the CSD, code HSTCM01) for which the experimental chemical shift is set to 34.5 ppm (see ref. 59). | |||||||||
| Eph | Exp. | 1.23(2) | 0.43(3) | 43(1) | 65(5) | −0.7(1) | 22(5) | 50(5) | 2(20) |
| Calc. | 1.110 | 0.44 | 42 | 65 | −0.13 | 237 | 62 | 78 | |
| Pse | Exp. | 2.20(2) | 0.85(3) | 41(1) | 70(10) | 0.3(2) | 30(30) | 30(5) | 150(30) |
| Calc. | −2.774 | 0.45 | 36 | 74 | 0.89 | 128 | 83 | 237 | |
Our group has recently developed a quadrupolar guided NMR crystallographic crystal structure prediction (QNMRX-CSP) protocol for the prediction, validation, and refinement of structures of organic HCl salts using the comparison of experimental and calculated 35Cl EFG tensors.69 In this initial work, QNMRX-CSP was benchmarked using five HCl salts and successfully used in two blind tests, all of which have known crystal structures featuring small unit cells and simple, rigid organic molecules. The ultimate objective of QNMRX-CSP is to predict and refine high-quality crystal structures, starting only with a molecular formula and 35Cl EFG tensor data (and in some cases, PXRD data).
In this work, we extend QNMRX-CSP benchmarking calculations to organic HCl salts featuring larger unit cells and organic molecules of increased conformational complexity. Specifically, we investigate solid forms of (1R,2S)-(−)-ephedrine HCl (Eph) and (1S,2S)-(+)-pseudoephedrine HCl (Pse), which have different space groups and unit cell parameters (N. B.; it is emphasized that these are not enantiomorphs),70,71 as well as 35Cl SSNMR data that were acquired in our laboratory. Four aspects of QNMRX-CSP benchmarking are considered, featuring different starting points and conditions, with the objective of obtaining structural candidates that agree well with the known crystal structures. The final aspect involves applying QNMRX-CSP to predict the structure of Pse in the dosage form Sudafed®, using only 35Cl SSNMR data of this solid form. Finally, we discuss the expansion of QNMRX-CSP to incorporate other quadrupolar nuclides (e.g., 14N, 17O), as well as tandem operation with conventional NMRX-CSP methods featuring 13C and 15N chemical shifts; this may enable applications to molecules of greater size and complexity, and possibly the characterization of microcrystalline forms of APIs in dosage forms that undergo structural changes, including hydration, disproportionation, amorphization, and phase changes due to tableting.
2. Methods
2.1 Chemicals
Ephedrine HCl, pseudoephedrine HCl (Scheme 1), and Sudafed® Sinus Congestion 30 mg Nasal Decongestant (Sudafed®), which contains 19.5 wt% Pse, were purchased and ground with a pestle to be used in all subsequent experiments.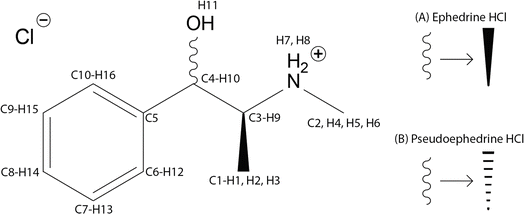 | ||
| Scheme 1 Molecular diagrams and atomic numbering for (1R,2S)-(−)-ephedrine HCl (A) and (1S,2S)-(+)-pseudoephedrine HCl (B). | ||
2.2 Powder X-ray diffraction
PXRD patterns of Eph and Pse were acquired with a Proto AXRD benchtop X-ray diffractometer operating with Bragg–Brentano geometry and featuring a Cu Kα radiation source and a Proto DECTRIS hybrid pixel detector. The X-ray tube voltage and amperage were 30 kV and 20 mA, respectively. Diffraction patterns were acquired with a detector scanning 2θ from 5° to 40° with a step size of 0.015° and a dwell time of 4 s. The PXRD pattern of Sudafed® was acquired using a Rigaku Miniflex X-ray diffractometer operating with Bragg–Brentano geometry and featuring a Cu Kα radiation source and a D/tex Ultra 250 1D silicon strip detector. The X-ray tube voltage and amperage were 40 kV and 15 mA, respectively. Diffraction patterns were acquired with a detector scanning 2θ from 2.5° to 50° with a step size of 0.03° and at a rate of 0.5° min−1.2.3 Solid-state NMR spectroscopy
2.4 Computational details
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 and CASTEP
84 and CASTEP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 and (ii) CASTEP Data Manager (developed in our laboratory) is used to automate QNMRX-CSP.69 CASTEP Data Manager takes advantage of a standalone academic version of CASTEP 2020 and is available at https://github.com/rschurko.
85 and (ii) CASTEP Data Manager (developed in our laboratory) is used to automate QNMRX-CSP.69 CASTEP Data Manager takes advantage of a standalone academic version of CASTEP 2020 and is available at https://github.com/rschurko.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 is used to explore the conformational space of Eph and Pse. Polymorph requires the specification of a space group, motion groups, and atomic charges. In this context, motion groups are defined as a geometry optimized organic cation and a Cl− anion, with Hirshfeld charges assigned to each atom. Subsequently, these inputs are used in the Polymorph routine, which employs a four-step approach to generate a maximum of 10
84 is used to explore the conformational space of Eph and Pse. Polymorph requires the specification of a space group, motion groups, and atomic charges. In this context, motion groups are defined as a geometry optimized organic cation and a Cl− anion, with Hirshfeld charges assigned to each atom. Subsequently, these inputs are used in the Polymorph routine, which employs a four-step approach to generate a maximum of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidate crystal structures per trial, where a trial is defined as one complete iteration of the four-step Polymorph routine—this includes the following steps: (i) packing, (ii) clustering, (iii) force-field geometry optimization, and (iv) clustering. Packing uses a Monte Carlo simulated annealing algorithm to generate the candidate crystal structures with a maximum and minimum temperature of 1.5 × 105 K and 300 K, heating and cooling factors of 0.025 and 0.0005, and a minimum move factor of 1.0 × 10−10. Clustering removes duplicate structures that are generated during the packing step based on a radial distribution cutoff of 7.0 Å, a tolerance of 0.13, and 140 bins. Dreiding force-field86 geometry optimizations are used to refine the candidate structure and calculate their static lattice energies. Convergence for the force-field geometry optimization is reached after a maximum change in energy of 2 × 10−5 kcal mol−1, in force of 10−3 kcal mol−1 Å−1, in stress of 10−3 GPa, and in atomic displacement of 10−5 Å. Candidate structures are clustered again to remove any duplicate structures following force-field geometry optimization. A final round of clustering is performed following all trials of Polymorph.
000 candidate crystal structures per trial, where a trial is defined as one complete iteration of the four-step Polymorph routine—this includes the following steps: (i) packing, (ii) clustering, (iii) force-field geometry optimization, and (iv) clustering. Packing uses a Monte Carlo simulated annealing algorithm to generate the candidate crystal structures with a maximum and minimum temperature of 1.5 × 105 K and 300 K, heating and cooling factors of 0.025 and 0.0005, and a minimum move factor of 1.0 × 10−10. Clustering removes duplicate structures that are generated during the packing step based on a radial distribution cutoff of 7.0 Å, a tolerance of 0.13, and 140 bins. Dreiding force-field86 geometry optimizations are used to refine the candidate structure and calculate their static lattice energies. Convergence for the force-field geometry optimization is reached after a maximum change in energy of 2 × 10−5 kcal mol−1, in force of 10−3 kcal mol−1 Å−1, in stress of 10−3 GPa, and in atomic displacement of 10−5 Å. Candidate structures are clustered again to remove any duplicate structures following force-field geometry optimization. A final round of clustering is performed following all trials of Polymorph.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 is used to conduct plane-wave DFT-D2*
85 is used to conduct plane-wave DFT-D2*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68 geometry optimizations and subsequent calculations of NMR interaction tensors. Three types of geometry optimizations are used: (i) truncated, (ii) convergent, and (iii) full volume convergent. All optimizations use the RPBE functional with a plane-wave energy cutoff of 800 eV, ultrasoft pseudopotentials generated on-the-fly,87 the zeroth-order regular approximation,88 and a k-point spacing of 0.05 Å−1. The three approaches differ in the implementation of the low memory BFGS scheme,89 where for truncated geometry optimizations the maximum BFGS cycle is set to 5, whereas the convergent and full volume convergent geometry optimizations are refined until the convergence thresholds. The convergence thresholds are set to be reached after a maximum change in energy of 5 × 10−6 eV per atom, in displacement of 5 × 10−4 Å, and a maximum force of 10−2 eV Å−1. Full volume convergent calculations have the added convergence threshold of a maximum stress tolerance of 0.02 GPa and use a fixed basis quality with soft compressibility. A nuclear quadrupole moment of Q(35Cl) = −8.112 fm2 is used for the calculation of the 35Cl EFG tensors.90
68 geometry optimizations and subsequent calculations of NMR interaction tensors. Three types of geometry optimizations are used: (i) truncated, (ii) convergent, and (iii) full volume convergent. All optimizations use the RPBE functional with a plane-wave energy cutoff of 800 eV, ultrasoft pseudopotentials generated on-the-fly,87 the zeroth-order regular approximation,88 and a k-point spacing of 0.05 Å−1. The three approaches differ in the implementation of the low memory BFGS scheme,89 where for truncated geometry optimizations the maximum BFGS cycle is set to 5, whereas the convergent and full volume convergent geometry optimizations are refined until the convergence thresholds. The convergence thresholds are set to be reached after a maximum change in energy of 5 × 10−6 eV per atom, in displacement of 5 × 10−4 Å, and a maximum force of 10−2 eV Å−1. Full volume convergent calculations have the added convergence threshold of a maximum stress tolerance of 0.02 GPa and use a fixed basis quality with soft compressibility. A nuclear quadrupole moment of Q(35Cl) = −8.112 fm2 is used for the calculation of the 35Cl EFG tensors.90
2.5 Metrics for assessing candidate structures
| (i) Elow ≤ Elat ≤ 0.865 × Elow |
In M3, candidate structural models are retained if they have an Elat that is less than or equal to a cutoff static lattice energy, Ecutoff, such that:
| (ii) Elat − Elow ≤ Ecutoff |
| Δkk = |Vcalckk − Vexpkk| |
2.6 Structural validation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 blind tests have set thresholds of RMSDs ≤ 0.80 Å and R-factors ≤ 10% as acceptable.92–95
24 blind tests have set thresholds of RMSDs ≤ 0.80 Å and R-factors ≤ 10% as acceptable.92–95
where F0 is the calculated signal amplitude of the convergent geometry optimized crystal structures and Fc is the calculated signal amplitude of the candidate structure.
3. Research and discussion
3.1 Characterization with powder X-ray diffraction and solid-state NMR spectroscopy
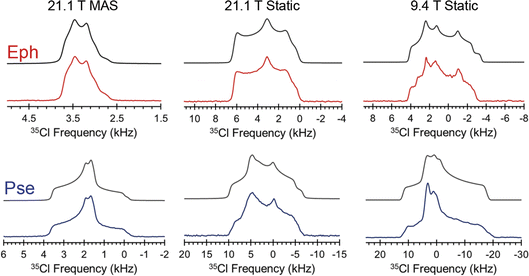
The Cl− ion environments of Eph and Pse each feature three H⋯Cl hydrogen bonds (i.e., r(H⋯Cl) ≲ 2.6 Å)98 involving one alcohol and two charged secondary amine moieties (Fig. 3 and Table 2). In Eph, the three hydrogen bonds are classified as short contacts (i.e., r(H⋯Cl) ≲ 2.2 Å), which are those hydrogen bonds having the highest impact on the 35Cl EFG tensors.99–102 From the large number of 35Cl EFG tensors that have been measured and calculated for organic HCl salts, it is well known that the presence of one or two short contacts typically results in sizeable magnitudes of CQ (e.g., from 6.0 to 10.5 MHz);81,99,100,103–118 however, in the case of Eph, the magnitude of CQ is small (1.23 MHz).
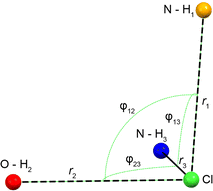 | ||
| Fig. 3 Schematic of the H⋯Cl hydrogen bond network for the DFT-D2* refined crystal structures of Eph and Pse. From shortest to longest, r1, r2, and r3 correspond to the H⋯Cl bond lengths with secondary amine, alcohol, and another secondary amine moiety, respectively. Angles φij describe the interbond angles. Values are shown in Table 2. | ||
| r 1 (Å)a | r 2 (Å)a | r 3 (Å)a | φ 12 (°)a | φ 13 (°)a | φ 23 (°)a | Avg. φ | |
|---|---|---|---|---|---|---|---|
| a For definitions of geometrical parameters, see Fig. 3. b Structure 24-317 is one of the six structures predicted by QNMRX-CSP; see Section 3.2.3 for relevant discussion. | |||||||
| Eph | 2.184 | 2.210 | 2.212 | 82.68 | 83.90 | 79.37 | 81.98 |
| Pse | 2.142 | 2.214 | 2.358 | 95.44 | 91.68 | 77.87 | 88.33 |
| 24-317b | 2.159 | 2.198 | 2.263 | 90.06 | 88.66 | 84.21 | 87.64 |
In order to understand the origins of this small CQ value in Eph, the local geometry of the Cl− ion is considered. There are clear guidelines for predicting arrangements of point charges that result in zero EFGs at any point in space;119 for instance, these have been applied by Bryce and co-workers in computational models of a ClH43− ion, where the magnitudes of CQ and ηQ are observed to change as a function of distortion away from tetrahedral symmetry.81 The most well-known examples include the placement of N equal point charges at the N vertices of polyhedra, like tetrahedra, cubes, and octahedra, which yields zero EFGs at a point S0 at their centers (i.e., the centroid). Interestingly, no EFGs occur at S0 if N/2 equal point charges are positioned at N/2 vertices such that none are related by inversion through S0. The ClH3− “fragment” in Eph has a trigonal pyramidal arrangement, with all the H⋯Cl⋯H bond angles, ∠(HClH), near 90°; hence, its geometry resembles this latter configuration, with the hydrogen atoms arranged approximately near the three orthogonal vertices of a fictitious cube. However, since the symmetry is not perfectly cubic, there are non-zero EFGs, accounting in part for the small magnitude of CQ.
A similar hydrogen bonding arrangement is observed for Pse; however, one of the H⋯Cl− hydrogen bonds in the ClH3− fragment involving a secondary amine group is significantly longer than the other two short contacts. This likely accounts for the CQ = 2.20 MHz, which is larger than that of Eph.
3.2 QNMRX-CSP
QNMRX-CSP was designed to predict the crystal structures of small organic HCl salts.69 This method is comprised of three modules, each of which features distinct steps and metrics (a flowchart depicting this protocol is shown in Scheme S1†). The functions of the three modules are as follows: Module 1 (M1) selects molecular fragments that correspond to “chemically sensible” arrangements of atoms defined in terms of their individual conformations, followed by the assignment of motion groups and atomic Hirshfeld charges. Module 2 (M2) generates thousands of unique candidate structures, which exhibit distinct unit cells and packing arrangements (see Section 2.4). Finally, Module 3 (M3) refines the structural models through plane-wave DFT-D2* geometry optimizations and comparison of calculated and experimental 35Cl EFG tensors. Steps are actions in each module applied to candidate structures (vide infra). Metrics are parameters used to retain the best candidate structures, which include unit cell parameters (a, b, c, α, β, and γ), static lattice energies (Elat, along with Elow and Ecutoff), and 35Cl EFG distances (ΓEFG) (see Section 2.5 for definitions). Candidate structures are validated via comparison to convergent geometry-optimized structural models based on known crystal structures (Eph: OPT-EPHECL02, and Pse: OPT-PEPHCL) by calculating R-factors (of PXRD patterns) and atomic position RMSDs; those with values falling below the thresholds described in Section 2.5 are considered valid structural models.In the ensuing sections, we describe the use of QNMRX-CSP for benchmarking calculations on Eph and Pse (Table 3), including calculations using: (i) fragments obtained from a geometry optimized structural model based on a known crystal structure as a starting point (Section 3.2.1); (ii) geometry optimized fragments based on isolated, gas-phase molecules as a starting point (Section 3.2.2); (iii) fragments from (i) above for Pse, but with the space group, unit cell parameters, and 35Cl quadrupolar parameters for Eph (and vice versa, Section 3.2.3); and (iv) fragments from (ii), but only with 35Cl quadrupolar parameters (XRD data is absent, Section 3.2.4). The purposes of (iii) and (iv) are to explore the outcome of QNMRX-CSP calculations when experimental data is limited or unavailable, with the hope of developing general applications to de novo crystal structure predictions.
| Section # | Origin of motion group | PXRD | SSNMR | ||
|---|---|---|---|---|---|
| Known crystal structure | Isolated molecule | Unit cell parameters | Space group | 35Cl EFGs | |
| 3.2.1 | ✓ | — | ✓ | ✓ | ✓ |
| 3.2.2 | — | ✓ | ✓ | ✓ | ✓ |
| 3.2.3 | ✓ | — | ✓ | ✓ | ✓ |
| 3.2.4 | — | ✓ | — | — | ✓ |
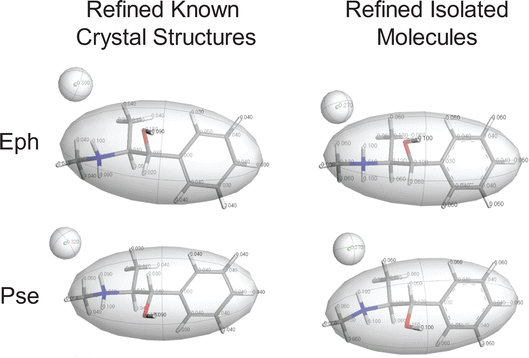
| QNMRX-CSP protocol | Known crystal structuresa | Refined isolated moleculeb | ||||
|---|---|---|---|---|---|---|
| Initial | Retained | Initial | Retained | |||
| a The starting point for these calculations were geometry optimized structures based on a known crystal structure. b The starting point for these calculations were geometry optimized structures based on isolated, gas-phase molecules. | ||||||
| Eph | ||||||
| M2: ± 20% UCPs; Elow ≤ 13.5% | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889 889 |
→ | 702 | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673 673 |
→ | 901 |
| M3 Step 1: ΓEFG ≤ 0.70 MHz; Elat ≤ 135 kJ mol−1 | 702 | → | 25 | 901 | → | 9 |
| M3 Step 2: ΓEFG ≤ 0.49 MHz; Elat ≤ 50 kJ mol−1 | 25 | → | 19 | 9 | → | 9 |
| M3 Step 3: ΓEFG ≤ 0.49 MHz; Elat ≤ 1 kJ mol−1 | 19 | → | 6 | 9 | → | 1 |
| Pse | ||||||
| M2: ± 20% UCPs; Elow ≤ 13.5% | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 718 |
→ | 242 | 177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
→ | 922 |
| M3 Step 1: ΓEFG ≤ 0.70 MHz; Elat ≤ 135 kJ mol−1 | 242 | → | 4 | 922 | → | 22 |
| M3 Step 2: ΓEFG ≤ 0.49 MHz; Elat ≤ 50 kJ mol−1 | 4 | → | 3 | 22 | → | 10 |
| M3 Step 3: ΓEFG ≤ 0.49 MHz; Elat ≤ 1 kJ mol−1 | 3 | → | 2 | 10 | → | 1 |
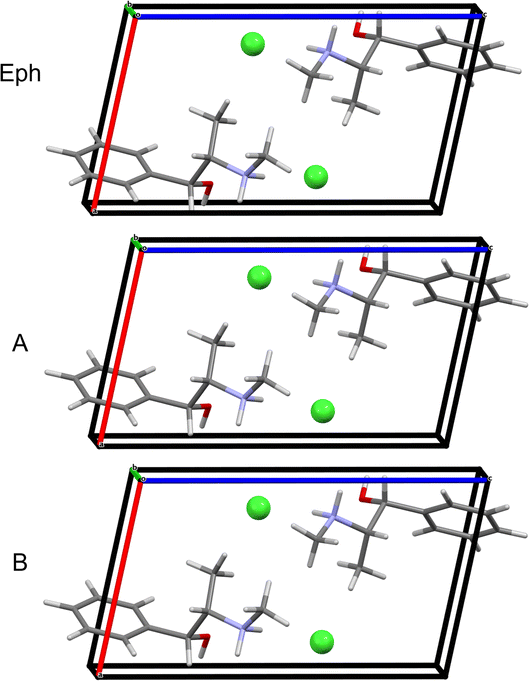
The starting point is Module 1 (M1): (i) in M1 Step 1, the crystal structure of Eph (EPHECL02) is obtained from the CCDC; (ii) in M1 Step 2, a convergent geometry optimization is conducted to refine the atomic coordinates; (iii) in M1 Step 3, Hirshfeld charges (Table S5†), as determined from population analysis, are assigned to the atoms; and (iv) in M1 Step 4, the organic cation and chloride anion are assigned as motion groups (Fig. 4).
In Module 2 (M2), the motion groups from M1 are used in the four-step Polymorph routine (see Section 2.4), which consists of packing, clustering, force-field geometry optimization, and clustering, leading to thousands of candidate structures. This routine is repeated 10 times (each iteration is defined as a trial, meaning that there are 10 trials), after which a final clustering of candidate structures is performed, leading to 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889 candidates. The best candidate structures are retained using the unit cell parameters and energy metrics (unit cell parameters within ±20% of the experimental values, and the bottom 13.5% of the Elat; see Section 2.5 for explanations), retaining 702 structures.
889 candidates. The best candidate structures are retained using the unit cell parameters and energy metrics (unit cell parameters within ±20% of the experimental values, and the bottom 13.5% of the Elat; see Section 2.5 for explanations), retaining 702 structures.
Module 3 (M3) consists of four steps: (i) in M3 Step 1, truncated geometry optimizations (i.e., those that are halted after five BFGS iterations, see Section 2.5) are conducted on the candidate structures followed by application of energy and EFG distance metrics (Ecutoff = 135 kJ mol−1 and ΓEFG ≤ 0.70 MHz), resulting in 25 candidate structures being retained; (ii) in M3 Step 2, convergent geometry optimizations are conducted on the candidate structures, leading to the retention of 19 structures using energy and EFG distance metrics (Ecutoff = 135 kJ mol−1 and ΓEFG ≤ 0.49 MHz); (iii) in M3 Step 3, the unit cell parameters of the candidate structures are adjusted to match those of EPHECL02 and subsequent convergent geometry optimizations are conducted, followed by the application of energy and EFG distance metrics (Ecutoff = 1 kJ mol−1 and ΓEFG ≤ 0.49 MHz), which retains 6 candidate structures; and (iv) in M3 Step 4, the final 6 structures are assessed for validation (Fig. 5A and Table 5). In this case, only 1 structure has RMSDs and R-factors that are below the CCDC thresholds (see Section 2.6), though the other 5 candidate structures exhibit similar packing motifs (Fig. S3† and Table 5) but fail structural validation.
| Motion groupa | Structural model | Γ EFG (MHz) | E lat (kJ mol−1) | R (%) | RMSD (Å) | |
|---|---|---|---|---|---|---|
| a The starting point for each motion group was either a known crystal structure (OPT-EPHECL02 or OPT-PEPHCL), or a refined isolated molecule. b Structural models that failed validation because of poor agreement with PXRD. | ||||||
| Eph | OPT-EPHECL02 | 5-98 | 0.102 | 0.000 | 2.26 | 0.026 |
| OPT-EPHECL02 | 3-12b | 0.086 | 0.008 | 17.75 | 0.169 | |
| OPT-EPHECL02 | 3-2b | 0.092 | 0.019 | 18.03 | 0.174 | |
| OPT-EPHECL02 | 6-11b | 0.085 | 0.023 | 17.97 | 0.167 | |
| OPT-EPHECL02 | 5-3b | 0.087 | 0.030 | 17.97 | 0.173 | |
| OPT-EPHECL02 | 5-7b | 0.070 | 0.082 | 18.22 | 0.174 | |
| Isolated molecule | 10-1 | 0.113 | 0.000 | 2.33 | 0.027 | |
| Pse | OPT-PEPHCL | 5-307 | 0.387 | 0.000 | 1.19 | 0.011 |
| OPT-PEPHCL | 8-117 | 0.393 | 0.029 | 1.94 | 0.014 | |
| Isolated molecule | 44-278 | 0.408 | 0.000 | 1.56 | 0.013 | |
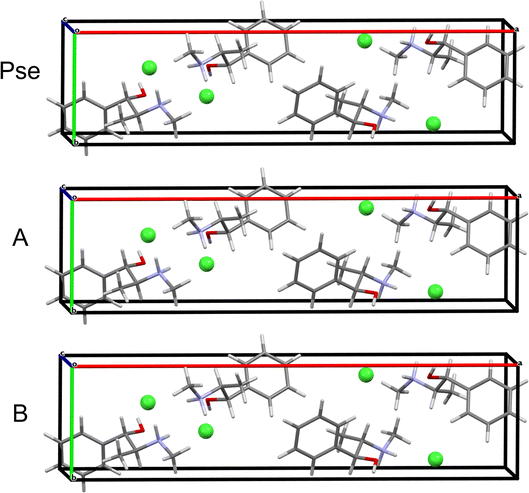
QNMRX-CSP is similarly applied to predict the structure of Pse starting from the PEPHCL structure, resulting in 2 candidate structures (Fig. 6A and Table 5). Both candidate structures have RMSDs and R-factors well below the CCDC thresholds.
QNMRX-CSP is similarly applied to Pse; however, a total of 50 trials of the Polymorph routine are necessary, resulting in 1 structure passing validation in M3 Step 4 (Fig. 6B and Table 5). Comparison of the isolated organic fragments from each of the predicted candidate structures for Eph and Pse to their respective gas-phase refined organic fragments is achieved with the RMSDs; here, the RMSDs of the Eph organic fragments are higher than those of Pse (0.233 Å and 0.073 Å, respectively).
| QNMRX-CSP protocol | Initial | Retained | |
|---|---|---|---|
| Pse molecular fragments and Eph metrics | |||
| M2: ± 20% UCPs; Elow ≤ 13.5% | 505![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 475 |
→ | 2993 |
| M3 Step 1: ΓEFG ≤ 0.70 MHz; Elat ≤ 135 kJ mol−1 | 2993 | → | 3 |
| M3 Step 2: ΓEFG ≤ 0.49 MHz; Elat ≤ 50 kJ mol−1 | 3 | → | 0 |
| M3 Step 3: ΓEFG ≤ 0.49 MHz; Elat ≤ 1 kJ mol−1 | 0 | → | 0 |
| Eph molecular fragments and Pse metrics | |||
| M2: ± 20% UCPs; Elow ≤ 13.5% | 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
→ | 795 |
| M3 Step 1: ΓEFG ≤ 0.70 MHz; Elat ≤ 135 kJ mol−1 | 795 | → | 74 |
| M3 Step 2: ΓEFG ≤ 0.49 MHz; Elat ≤ 50 kJ mol−1 | 74 | → | 57 |
| M3 Step 3: ΓEFG ≤ 0.49 MHz; Elat ≤ 1 kJ mol−1 | 57 | → | 6 |
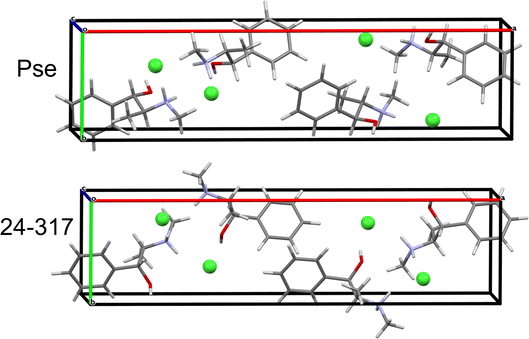
QNMRX-CSP was similarly applied to the Eph cation (OPT-EPHECL02) and Cl− anion in the P212121 space group of Pse. After only 30 trials in M2, 6 structures were passed to M3 Step 4 for validation. In comparison to OPT-PEPHCL, all 6 structures have RMSDs and R-factors above the CCDC threshold (Fig. 7 and Table 7). The 6 structures each feature three H⋯Cl hydrogen bonds (one alcohol and two secondary amine moieties, Fig. 3 and Table 2), similar to the Cl− environment of Pse (vide supra). This might indicate that Eph has a theoretical polymorph with a structure in the P212121 space group with 35Cl EFG tensors similar to those of Pse, though this is beyond the scope of the current study.
| Structural model | Γ EFG (MHz) | E lat (kJ mol−1) | R (%) | RMSD (Å) |
|---|---|---|---|---|
| 24-317 | 0.481 | 0.000 | 95.87 | 0.776 |
| 14-129 | 0.283 | 0.010 | 88.14 | 0.787 |
| 17-119 | 0.282 | 0.029 | 87.90 | 0.788 |
| 19-89 | 0.283 | 0.193 | 86.26 | 0.787 |
| 14-92 | 0.271 | 0.251 | 86.21 | 0.785 |
| 24-152 | 0.287 | 0.357 | 88.32 | 0.788 |
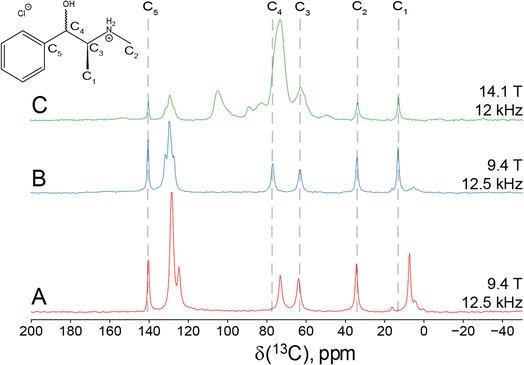
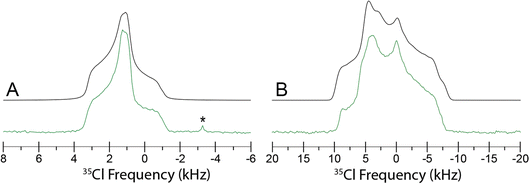
Since Eph and Pse are readily differentiated by their distinct 35Cl CT patterns, it is possible to use 35Cl SSNMR to determine which, if either, solid form is present in Sudafed®. The 35Cl{1H} MAS and static NMR spectra of Sudafed® at 18.8 T (Fig. 8) have powder patterns matching that of bulk Pse, confirming its presence. In addition, there is a small peak ca. −41.1 ppm that indicates the presence of NaCl, which is not detected in the PXRD pattern (Fig. S4†). The 13C spectrum of Sudafed® (Fig. 1C) features peaks corresponding to excipients in the range of ca. 60–110 ppm; however, the outer peaks match well with those in the spectrum of bulk Pse. The PXRD pattern of Sudafed® (Fig. S1C†) also clearly indicates the presence of Pse, based on comparison to its simulated PXRD pattern. However, indexing the PXRD data to obtain information on the space group and unit cell parameters is nontrivial due to the interfering signals from the excipients.
There are several considerations for using QNMRX-CSP in the absence of XRD data: (i) the choice of space group(s) that should be searched using the Polymorph routine (M2); (ii) determination of valid unit cell parameters for selecting candidate structures (M2); and (iii) the choice of unit cell parameters that should be used in the last stages of structural refinement (M3). To address the first consideration, the CCDC database was data mined to determine the number of crystal structures with the following criteria: (i) C, H, O, N, and Cl atoms only; (ii) the Cl atom is an anion; and (iii) Z′ = 1. We identified 4713 structures meeting these criteria, whose space groups were ranked according to their frequency. Five space groups (i.e., P21/c, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , P212121, P21, and Pna21) with Z ≤ 4 account for 81.4% of structures (Table S6†). Herein, the Polymorph routine is applied only to structural models in these five space groups to limit the computational cost. To address the second consideration, the 1000 candidate structures with the lowest energies resulting from 10 trials of the Polymorph routine are retained, regardless of the predicted unit cell parameters (i.e., structural models are retained based only on relative energies). Finally, the third consideration is addressed by conducting a full volume convergent geometry optimization (Section 2.4) to refine the unit cell parameters and atomic coordinates of the candidate structures, as opposed to adjusting the former to match those of the indexed PXRD pattern.
, P212121, P21, and Pna21) with Z ≤ 4 account for 81.4% of structures (Table S6†). Herein, the Polymorph routine is applied only to structural models in these five space groups to limit the computational cost. To address the second consideration, the 1000 candidate structures with the lowest energies resulting from 10 trials of the Polymorph routine are retained, regardless of the predicted unit cell parameters (i.e., structural models are retained based only on relative energies). Finally, the third consideration is addressed by conducting a full volume convergent geometry optimization (Section 2.4) to refine the unit cell parameters and atomic coordinates of the candidate structures, as opposed to adjusting the former to match those of the indexed PXRD pattern.
With these considerations in mind, QNMRX-CSP was performed to predict the structure of Pse in Sudafed® (Table 8) using only 35Cl quadrupolar parameters. Starting with the refined gas-phase motion group of Pse described in Section 3.2.2, 10 trials of the Polymorph routine were conducted for each of the five space groups. The 1000 candidate structures with the lowest static lattice energies in each space group were retained and clustered to remove duplicates. The remaining candidate structures were subjected to truncated geometry optimizations, followed by retention of structures using only the EFG distance metric (i.e., ΓEFG ≤ 0.70 MHz). This resulted in the elimination of all candidate structures with the space groups P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , P21, and Pna21. Convergent geometry optimization and application of the second EFG distance metric (i.e., ΓEFG ≤ 0.49 MHz) led to the retention of 6 structural models, all in the P212121 space group. Final volume convergent geometry optimizations resulted in 6 candidate structures that were retained for structural validation.
, P21, and Pna21. Convergent geometry optimization and application of the second EFG distance metric (i.e., ΓEFG ≤ 0.49 MHz) led to the retention of 6 structural models, all in the P212121 space group. Final volume convergent geometry optimizations resulted in 6 candidate structures that were retained for structural validation.
| P21/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P212121 | P21 | Pna21 | |
|---|---|---|---|---|---|
| a Initial number of structures obtained from 10 trials of Monte Carlo simulated annealing. b Number of structures following clustering. c Remaining structures following truncated geometry optimization and application of the 35Cl EFG distance with a cut-off of 0.70 MHz. d Remaining structures following convergent geometry optimization and application of the 35Cl EFG distance with a cut-off of 0.49 MHz. e Remaining structures following full volume convergent geometry optimization and application of the 35Cl EFG distance with a cut-off of 0.49 MHz. f Number of candidate structures matching the refined crystal structure of Pse (CSD code PEPHCL). | |||||
| MC-SAa | 1000 | 1000 | 1000 | 1000 | 1000 |
| Clusterb | 362 | 314 | 190 | 190 | 190 |
| TGOc | 1 | 0 | 6 | 0 | 0 |
| CGEd | 0 | 0 | 6 | 0 | 0 |
| UCP CGEe | 0 | 0 | 6 | 0 | 0 |
| Validationf | 0 | 0 | 6 | 0 | 0 |
The final structural models have similar packing motifs and unit cell volumes (Fig. 9) with RMSDs below the CCDC threshold (Table 9). However, they have unit cell volumes that are overestimated relative to that of the known crystal structure by ca. 1.2–1.5%, which leads to poor agreement between their simulated PXRD patterns and that of the known crystal structure (Fig. S5†). This is not unexpected, as full volume convergent DFT-D2* geometry optimizations tend to overestimate unit cell volumes.68
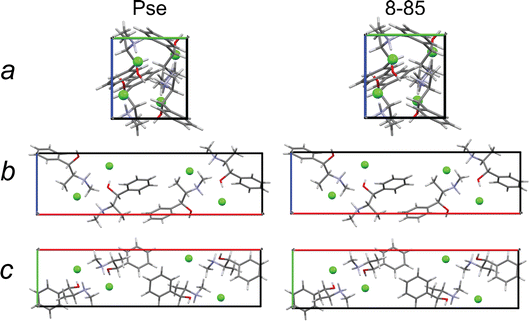 | ||
| Fig. 9 A view along each crystallographic axis for a crystal structure of Pse obtained by QNMRX-CSP, 8-85, and the convergent geometry optimized crystal structure of Pse. | ||
| 35Cl EFG dist. (MHz) | Energy diff. (kJ mol−1) | Volume (Å3) | Volume diff. (%) | RMSD (Å) | R (%) | |
|---|---|---|---|---|---|---|
| PEPHCL | — | — | 1124.871 | — | — | — |
| 2-75 | 0.233 | 0 | 1138.202 | 1.19 | 0.073 | 89.61 |
| 7-62 | 0.204 | 0.029 | 1141.548 | 1.48 | 0.078 | 94.63 |
| 8-91 | 0.207 | 0.048 | 1139.949 | 1.34 | 0.076 | 94.54 |
| 8-71 | 0.191 | 0.067 | 1141.009 | 1.43 | 0.079 | 97.00 |
| 8-86 | 0.182 | 0.077 | 1140.464 | 1.39 | 0.080 | 91.70 |
| 8-85 | 0.202 | 0.096 | 1141.099 | 1.44 | 0.080 | 97.80 |
4. Conclusions
Herein, QNMRX-CSP has been extended to systems featuring crystal structures of greater complexity than those investigated to date (i.e., higher molecular weights, greater conformational flexibility in the organic components, and larger unit cells). First, it was demonstrated that 35Cl SSNMR spectra of Eph and Pse provide distinct spectral fingerprints for each crystalline phase, with the 35Cl EFG tensors lending insight into the distinct hydrogen bonding arrangements of the Cl− ions. Second, QNMRX-CSP benchmarking calculations were conducted for structural models of Eph and Pse. Two sets of calculations with different geometry-optimized organic fragments as starting points (i.e., one from the known crystal structure and the other from the gas phase) were carried out, yielding structural models in good agreement with known structures, featuring RMSDs ≤ 0.80 Å and R-factor ≤ 10%, which are below recommended CCDC thresholds.92–95 Third, QNMRX-CSP benchmarking calculations were conducted using a geometry-optimized motion group of Pse packed into unit cells of the space group of Eph, where the unit cell parameters and 35Cl EFG tensors of Eph were used to retain the best candidate structures (and vice versa). In both cases, it was found that no viable candidate structures emerged. Finally, using only the 35Cl EFG tensors determined from the 35Cl SSNMR spectra of a sample of Sudafed®, we confirmed that Pse is the solid form therein, and conducted QNMRX-CSP benchmarking calculations that yield candidate structural models that passed most metrics, with the exception of the R-factors – this is due to small overestimations of the unit cell volumes in the DFT-D2* calculations.QNMRX-CSP, while still in the early stages of development, shows much promise; however, it still faces challenges, many of which can lead to future extensions of the protocol. As systems grow in complexity, the use of other quadrupolar nuclides (i.e., 14N and 17O) could prove useful for predicting the best structural models – their involvement in both covalent and hydrogen bonds would provide different perspectives on structure. The tandem use of QNMRX-CSP with methods employing either first principles calculations of chemical shielding or rapid prediction of chemical shifts could also be beneficial (i.e., 1H, 13C, and 15N). For instance, determination of the best starting fragments with the aid of DFT calculations of chemical shifts would be relatively inexpensive, since these could serve to limit the number of possible molecular conformations.43,120,121 Conversely, the use of artificial intelligence methods (e.g., ShiftML![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122,123) could be advantageous for filtering candidate structures. This increased efficiency could lead in several directions. First, it may be possible to predict previously unknown polymorphs, subject to modification of the metrics for choosing candidate structures (e.g., multiple NMR interaction tensors with benchmarked cutoff values). Second, this would permit an exploration of an increased number of space groups (as opposed to the five discussed herein) and a more extensive conformational space. Finally, difficulties related to geometry optimizations remain. We currently use the DFT-D2* method, which is known to slightly overestimate unit cell volumes. It is possible that higher-order dispersion corrections (e.g., DFT-D3 or DFT-D3/BJ)124–126 can be reparametrized for organic solids in a similar manner to DFT-D2 – this would greatly benefit from the increased efficiency in calculations described above. These considerations can open doors for the discovery of new solid forms, including polymorphs, and perhaps even solvates and hydrates – all of which are relevant for de novo CSP of APIs in situ in complex dosage forms.
122,123) could be advantageous for filtering candidate structures. This increased efficiency could lead in several directions. First, it may be possible to predict previously unknown polymorphs, subject to modification of the metrics for choosing candidate structures (e.g., multiple NMR interaction tensors with benchmarked cutoff values). Second, this would permit an exploration of an increased number of space groups (as opposed to the five discussed herein) and a more extensive conformational space. Finally, difficulties related to geometry optimizations remain. We currently use the DFT-D2* method, which is known to slightly overestimate unit cell volumes. It is possible that higher-order dispersion corrections (e.g., DFT-D3 or DFT-D3/BJ)124–126 can be reparametrized for organic solids in a similar manner to DFT-D2 – this would greatly benefit from the increased efficiency in calculations described above. These considerations can open doors for the discovery of new solid forms, including polymorphs, and perhaps even solvates and hydrates – all of which are relevant for de novo CSP of APIs in situ in complex dosage forms.
Data availability
The CASTEP data manager (CDM), an executable application developed in-house, is available on the web from https://github.com/rschurko. Additional data are available in the ESI.†Author contributions
C. H. Fleischer III and S. T. Veinberg acquired the PXRD data. C. H. Fleischer III, S. T. Holmes, K. Levin, and S. L. Veinberg participated in the acquisition of the SSNMR data. C. H. Fleischer III conducted QNMRX-CSP. C. H. Fleischer III, S. L. Holmes, and R. W. Schurko contributed to the writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for research support from The Florida State University and the National High Magnetic Field Laboratory (NHMFL), which is funded by the National Science Foundation Cooperative Agreement (DMR-1644779, DMR-2128556) and by the State of Florida. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0022310, covering expenses related to postdoctoral wages. We also thank Genentech and the Natural Sciences and Engineering Research Council of Canada (NSERC, RGPIN-2016_06642 Discovery Grant) for funding the early stages of this research. We thank Dr Victor Terskikh for acquiring 35Cl SSNMR spectra at 21.1 T at the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a National Research Facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Quebec, the National Research Council of Canada, and Bruker BioSpin (https://www.nmr900.ca).References
- S. M. Woodley and R. Catlow, Crystal Structure Prediction from First Principles, Nat. Mater., 2008, 7, 937–946, DOI:10.1038/nmat2321.
- G. M. Day, Current Approaches to Predicting Molecular Organic Crystal Structures, Crystallogr. Rev., 2011, 17, 3–52, DOI:10.1080/0889311X.2010.517526.
- S. L. Price, Predicting Crystal Structures of Organic Compounds, Chem. Soc. Rev., 2014, 43, 2098–2111, 10.1039/c3cs60279f.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Structure Prediction Drives Materials Discovery, Nat. Rev. Mater., 2019, 4, 331–348, DOI:10.1038/s41578-019-0101-8.
- D. H. Bowskill, I. J. Sugden, S. Konstantinopoulos, C. S. Adjiman and C. C. Pantelides, Crystal Structure Prediction Methods for Organic Molecules: State of the Art, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 593–623, DOI:10.1146/annurev-chembioeng-060718-030256.
- Y. Wang, J. Lv, P. Gao and Y. Ma, Crystal Structure Prediction via Efficient Sampling of the Potential Energy Surface, Acc. Chem. Res., 2022, 55, 2068–2076, DOI:10.1021/acs.accounts.2c00243.
- G. J. O. Beran, Frontiers of Molecular Crystal Structure Prediction for Pharmaceuticals and Functional Organic Materials, Chem. Sci., 2023, 14, 13290–13312, 10.1039/d3sc03903j.
- M. Baias, C. M. Widdifield, J. N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Powder Crystallography of Pharmaceutical Materials by Combined Crystal Structure Prediction and Solid-State 1H NMR Spectroscopy, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080, 10.1039/c3cp41095a.
- M. A. Neumann, J. Van De Streek, F. P. A. Fabbiani, P. Hidber and O. Grassmann, Combined Crystal Structure Prediction and High-Pressure Crystallization in Rational Pharmaceutical Polymorph Screening, Nat. Commun., 2015, 6, 7793, DOI:10.1038/ncomms8793.
- L. M. Leblanc and E. R. Johnson, Crystal-Energy Landscapes of Active Pharmaceutical Ingredients Using Composite Approaches, CrystEngComm, 2019, 21, 5995–6009, 10.1039/c9ce00895k.
- G. Sun, Y. Jin, S. Li, Z. Yang, B. Shi, C. Chang and Y. A. Abramov, Virtual Coformer Screening by Crystal Structure Predictions: Crucial Role of Crystallinity in Pharmaceutical Cocrystallization, J. Phys. Chem. Lett., 2020, 11, 8832–8838, DOI:10.1021/acs.jpclett.0c02371.
- J. P. Darby, M. Arhangelskis, A. D. Katsenis, J. M. Marrett, T. Friščić and A. J. Morris, Ab Initio Prediction of Metal-Organic Framework Structures, Chem. Mater., 2020, 32, 5835–5844, DOI:10.1021/acs.chemmater.0c01737.
- Y. Xu, J. M. Marrett, H. M. Titi, J. P. Darby, A. J. Morris, T. Friščić and M. Arhangelskis, Experimentally Validated Ab Initio Crystal Structure Prediction of Novel Metal-Organic Framework Materials, J. Am. Chem. Soc., 2023, 145, 3515–3525, DOI:10.1021/jacs.2c12095.
- A. N. Sokolov, S. Atahan-Evrenk, R. Mondal, H. B. Akkerman, R. S. Sánchez-Carrera, S. Granados-Focil, J. Schrier, S. C. B. Mannsfeld, A. P. Zoombelt, Z. Bao and A. Aspuru-Guzik, From Computational Discovery to Experimental Characterization of a High Hole Mobility Organic Crystal, Nat. Commun., 2011, 2, 437, DOI:10.1038/ncomms1451.
- C. Y. Cheng, J. E. Campbell and G. M. Day, Evolutionary Chemical Space Exploration for Functional Materials: Computational Organic Semiconductor Discovery, Chem. Sci., 2020, 11, 4922–4933, 10.1039/d0sc00554a.
- J. A. Schmidt, J. A. Weatherby, I. J. Sugden, A. Santana-Bonilla, F. Salerno, M. J. Fuchter, E. R. Johnson, J. Nelson and K. E. Jelfs, Computational Screening of Chiral Organic Semiconductors: Exploring Side-Group Functionalization and Assembly to Optimize Charge Transport, Cryst. Growth Des., 2021, 21, 5036–5049, DOI:10.1021/acs.cgd.1c00473.
- J. D. Gale, GULP: A Computer Program for the Symmetry-Adapted Simulation of Solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637, 10.1039/a606455h.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—Evolutionary Crystal Structure Prediction, Comput. Phys. Commun., 2006, 175, 713–720, DOI:10.1016/j.cpc.2006.07.020.
- D. C. Lonie and E. Zurek, XtalOpt: An Open-Source Evolutionary Algorithm for Crystal Structure Prediction, Comput. Phys. Commun., 2011, 182, 372–387, DOI:10.1016/j.cpc.2010.07.048.
- C. J. Pickard and R. J. Needs, Ab Initio Random Structure Searching, J. Phys.: Condens. Matter, 2011, 23, 053201, DOI:10.1088/0953-8984/23/5/053201.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A Method for Crystal Structure Prediction, Comput. Phys. Commun., 2012, 183, 2063–2070, DOI:10.1016/j.cpc.2012.05.008.
- T. Yamashita, S. Kanehira, N. Sato, H. Kino, K. Terayama, H. Sawahata, T. Sato, F. Utsuno, K. Tsuda, T. Miyake and T. Oguchi, CrySPY: A Crystal Structure Prediction Tool Accelerated by Machine Learning, Sci. Technol. Adv. Mater.: Methods, 2021, 1, 87–97, DOI:10.1080/27660400.2021.1943171.
- J. Wang, H. Gao, Y. Han, C. Ding, S. Pan, Y. Wang, Q. Jia, H. T. Wang, D. Xing and J. Sun, MAGUS: Machine Learning and Graph Theory Assisted Universal Structure Searcher, Natl. Sci. Rev., 2023, 10, nwad128, DOI:10.1093/nsr/nwad128.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179, DOI:10.1107/S2052520616003954.
- J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, A Test of Crystal Structure Prediction of Small Organic Molecules, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714, DOI:10.1107/S0108768100004584.
- W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Dzyabchenko, P. Erk, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, J. P. M. Lommerse, W. T. M. Mooij, S. L. Price, H. Scheraga, B. Schweizer, M. U. Schmidt, B. P. van Eijck, P. Verwer and D. E. Williams, Crystal Structure Prediction of Small Organic Molecules: A Second Blind Test, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 647–661, DOI:10.1107/S0108768102005669.
- G. M. Day, W. D. S. Motherwell, H. L. Ammon, S. X. M. Boerrigter, R. G. Della Valle, E. Venuti, A. Dzyabchenko, J. D. Dunitz, B. Schweizer, B. P. Van Eijck, P. Erk, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, F. J. J. Leusen, C. Liang, C. C. Pantelides, P. G. Karamertzanis, S. L. Price, T. C. Lewis, H. Nowell, A. Torrisi, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt and P. Verwer, A Third Blind Test of Crystal Structure Prediction, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 511–527, DOI:10.1107/S0108768105016563.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Significant Progress in Predicting the Crystal Structures of Small Organic Molecules – a Report on the Fourth Blind Test, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125, DOI:10.1107/S0108768109004066.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Towards Crystal Structure Prediction of Complex Organic Compounds – a Report on the Fifth Blind Test, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551, DOI:10.1107/S0108768111042868.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Report on the Sixth Blind Test of Organic Crystal Structure Prediction Methods, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459, DOI:10.1107/S2052520616007447.
- Ş. Atahan-Evrenk and A. Aspuru-Guzik, Prediction and Calculation of Crystal Structures: Methods and Applications, Topics in Current Chemistry, ed. Atahan-Evrenk, S. and Aspuru-Guzik, A., Springer International Publishing, Cham, 2014, vol. 345, DOI:10.1007/978-3-319-05774-3.
- D. E. Braun, J. A. McMahon, R. M. Bhardwaj, J. Nyman, M. A. Neumann, J. Van De Streek and S. M. Reutzel-Edens, Inconvenient Truths about Solid Form Landscapes Revealed in the Polymorphs and Hydrates of Gandotinib, Cryst. Growth Des., 2019, 19, 2947–2962, DOI:10.1021/acs.cgd.9b00162.
- M. K. Dudek and K. Drużbicki, Along the Road to Crystal Structure Prediction (CSP) of Pharmaceutical-like Molecules, CrystEngComm, 2022, 24, 1665–1678, 10.1039/d1ce01564h.
- Y. A. Abramov, L. Iuzzolino, Y. Jin, G. York, C.-H. Chen, C. S. Shultz, Z. Yang, C. Chang, B. Shi, T. Zhou, C. Greenwell, S. Sekharan and A. Y. Lee, Cocrystal Synthesis through Crystal Structure Prediction, Mol. Pharmaceutics, 2023, 20, 3380–3392, DOI:10.1021/acs.molpharmaceut.2c01098.
- G. M. Day, J. Chisholm, N. Shan, W. D. S. Motherwell and W. Jones, An Assessment of Lattice Energy Minimization for the Prediction of Molecular Organic Crystal Structures, Cryst. Growth Des., 2004, 4, 1327–1340, DOI:10.1021/cg0498148.
- J. Nyman and G. M. Day, Static and Lattice Vibrational Energy Differences between Polymorphs, CrystEngComm, 2015, 17, 5154–5165, 10.1039/c5ce00045a.
- C. R. Taylor and G. M. Day, Evaluating the Energetic Driving Force for Cocrystal Formation, Cryst. Growth Des., 2018, 18, 892–904, DOI:10.1021/acs.cgd.7b01375.
- C. Martineau, J. Senker and F. Taulelle, NMR Crystallography, in Annual Reports on NMR Spectroscopy, ed. Harris, R. K., Wasylishen, R. E. and Duer, M. J., John Wiley & Sons Ltd, New York, NY, 2014, vol. 82, pp. 1–57, DOI:10.1016/B978-0-12-800184-4.00001-1.
- S. E. Ashbrook and D. McKay, Combining Solid-State NMR Spectroscopy with First-Principles Calculations – a Guide to NMR Crystallography, Chem. Commun., 2016, 52, 7186–7204, 10.1039/C6CC02542K.
- D. L. Bryce, NMR Crystallography: Structure and Properties of Materials from Solid-State Nuclear Magnetic Resonance Observables, IUCrJ, 2017, 4, 350–359, DOI:10.1107/S2052252517006042.
- P. Hodgkinson, NMR Crystallography of Molecular Organics, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53, DOI:10.1016/j.pnmrs.2020.03.001.
- K. D. M. Harris, NMR Crystallography as a Vital Tool in Assisting Crystal Structure Determination from Powder XRD Data, Crystals, 2022, 12, 1277, DOI:10.3390/cryst12091277.
- J. K. Harper and D. M. Grant, Enhancing Crystal-Structure Prediction with NMR Tensor Data, Cryst. Growth Des., 2006, 6, 2315–2321, DOI:10.1021/cg060244g.
- E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Powder Crystallography by Combined Crystal Structure Prediction and High-Resolution1H Solid-State NMR Spectroscopy, J. Am. Chem. Soc., 2010, 132, 2564–2566, DOI:10.1021/ja909449k.
- M. Baias, J. N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, De Novo Determination of the Crystal Structure of a Large Drug Molecule by Crystal Structure Prediction-Based Powder NMR Crystallography, J. Am. Chem. Soc., 2013, 135, 17501–17507, DOI:10.1021/ja4088874.
- A. Hofstetter, M. Balodis, F. M. Paruzzo, C. M. Widdifield, G. Stevanato, A. C. Pinon, P. J. Bygrave, G. M. Day and L. Emsley, Rapid Structure Determination of Molecular Solids Using Chemical Shifts Directed by Unambiguous Prior Constraints, J. Am. Chem. Soc., 2019, 141, 16624–16634, DOI:10.1021/jacs.9b03908.
- M. K. Dudek, P. Paluch, J. Śniechowska, K. P. Nartowski, G. M. Day and M. J. Potrzebowski, Crystal Structure Determination of an Elusive Methanol Solvate-Hydrate of Catechin Using Crystal Structure Prediction and NMR Crystallography, CrystEngComm, 2020, 22, 4969–4981, 10.1039/d0ce00452a.
- T. Pawlak, I. Sudgen, G. Bujacz, D. Iuga, S. P. Brown and M. J. Potrzebowski, Synergy of Solid-State NMR, Single-Crystal X-Ray Diffraction, and Crystal Structure Prediction Methods: A Case Study of Teriflunomide (TFM), Cryst. Growth Des., 2021, 21, 3328–3343, DOI:10.1021/acs.cgd.1c00123.
- M. M. Woolfson, An Introduction to X-Ray Crystallography, Cambridge University Press, 2nd edn, 1997 Search PubMed.
- K. Shankland, An Overview of Powder X-Ray Diffraction and its Relevance to Pharmaceutical Crystal Structures, 2016, pp. 293–314, DOI:10.1007/978-1-4939-4029-5_8.
- R. K. Harris, S. Cadars, L. Emsley, J. R. Yates, C. J. Pickard, R. K. R. Jetti and U. J. Griesser, NMR Crystallography of Oxybuprocaine Hydrochloride, Modification II, Phys. Chem. Chem. Phys., 2007, 9, 360–368, 10.1039/b614318k.
- J. K. Harper, R. Iuliucci, M. Gruber and K. Kalakewich, Refining Crystal Structures with Experimental 13C NMR Shift Tensors and Lattice-Including Electronic Structure Methods, CrystEngComm, 2013, 15, 8693–8704, 10.1039/c3ce40108a.
- C. M. Widdifield, J. D. Farrell, J. C. Cole, J. A. K. Howard and P. Hodgkinson, Resolving Alternative Organic Crystal Structures Using Density Functional Theory and NMR Chemical Shifts, Chem. Sci., 2020, 11, 2987–2992, 10.1039/c9sc04964a.
- M. R. Chierotti and R. Gobetto, NMR Crystallography: The Use of Dipolar Interactions in Polymorph and Co-Crystal Investigation, CrystEngComm, 2013, 15, 8599–8612, 10.1039/c3ce41026a.
- P. Thureau, S. Sturniolo, M. Zilka, F. Ziarelli, S. Viel, J. R. Yates and G. Mollica, Reducing the Computational Cost of NMR Crystallography of Organic Powders at Natural Isotopic Abundance with the Help of 13C-13C Dipolar Couplings, Magn. Reson. Chem., 2019, 57, 256–264, DOI:10.1002/mrc.4848.
- J. Struppe, C. M. Quinn, S. Sarkar, A. M. Gronenborn and T. Polenova, Ultrafast 1H MAS NMR Crystallography for Natural Abundance Pharmaceutical Compounds, Mol. Pharmaceutics, 2020, 17, 674–682, DOI:10.1021/acs.molpharmaceut.9b01157.
- A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, NMR Crystallography of Campho[2,3-c]Pyrazole (Z’ = 6): Combining High-Resolution 1H-13C Solid-State MAS NMR Spectroscopy and GIPAW Chemical-Shift Calculations, J. Phys. Chem. A, 2010, 114, 10435–10442, DOI:10.1021/jp104901j.
- S. L. Price, Computed Crystal Energy Landscapes for Understanding and Predicting Organic Crystal Structures and Polymorphism, Acc. Chem. Res., 2009, 42, 117–126, DOI:10.1021/ar800147t.
- O. Socha, P. Hodgkinson, C. M. Widdifield, J. R. Yates and M. Dračínský, Exploring Systematic Discrepancies in DFT Calculations of Chlorine Nuclear Quadrupole Couplings, J. Phys. Chem. A, 2017, 121, 4103–4113, DOI:10.1021/acs.jpca.7b02810.
- A. J. Vega, Quadrupolar Nuclei in Solids, in Encyclopedia of Magnetic Resonance, ed. Grant, D. M. and Harris, R. K., John Wiley & Sons, Ltd, Chichester, UK, 2007, pp. 3869–3888, DOI:10.1002/9780470034590.emrstm0431.
- J. Autschbach, S. Zheng and R. W. Schurko, Analysis of Electric Field Gradient Tensors at Quadrupolar Nuclei in Common Structural Motifs, Concepts Magn. Reson., 2010, 36A, 84–126, DOI:10.1002/cmr.a.20155.
- F. Bravetti, R. E. Russo, S. Bordignon, A. Gallo, F. Rossi, C. Nervi, R. Gobetto and M. R. Chierotti, Zwitterionic or Not? Fast and Reliable Structure Determination by Combining Crystal Structure Prediction and Solid-State NMR, Molecules, 2023, 28, 1876, DOI:10.3390/molecules28041876.
- C. M. Widdifield, S. O. Nilsson Lill, A. Broo, M. Lindkvist, A. Pettersen, A. Svensk Ankarberg, P. Aldred, S. Schantz and L. Emsley, Does Z ′ Equal 1 or 2? Enhanced Powder NMR Crystallography Verification of a Disordered Room Temperature Crystal Structure of a P38 Inhibitor for Chronic Obstructive Pulmonary Disease, Phys. Chem. Chem. Phys., 2017, 19, 16650–16661, 10.1039/c7cp02349a.
- M. Khalaji, P. Paluch, M. J. Potrzebowski and M. K. Dudek, Narrowing down the Conformational Space with Solid-State NMR in Crystal Structure Prediction of Linezolid Cocrystals, Solid State Nucl. Magn. Reson., 2022, 121, 101813, DOI:10.1016/j.ssnmr.2022.101813.
- R. P. Chapman and D. L. Bryce, Application of Multinuclear Magnetic Resonance and Gauge-Including Projector-Augmented-Wave Calculations to the Study of Solid Group 13 Chlorides, Phys. Chem. Chem. Phys., 2009, 11, 6987, 10.1039/b906627f.
- T. Charpentier, The PAW/GIPAW Approach for Computing NMR Parameters: A New Dimension Added to NMR Study of Solids, Solid State Nucl. Magn. Reson., 2011, 40, 1–20, DOI:10.1016/j.ssnmr.2011.04.006.
- S. T. Holmes and R. W. Schurko, Refining Crystal Structures with Quadrupolar NMR and Dispersion-Corrected Density Functional Theory, J. Phys. Chem. C, 2018, 122, 1809–1820, DOI:10.1021/acs.jpcc.7b12314.
- S. T. Holmes, C. S. Vojvodin and R. W. Schurko, Dispersion-Corrected DFT Methods for Applications in Nuclear Magnetic Resonance Crystallography, J. Phys. Chem. A, 2020, 124, 10312–10323, DOI:10.1021/acs.jpca.0c06372.
- A. A. Peach, C. H. I. Fleischer, K. Levin, S. T. Holmes, J. E. Sanchez and R. W. Schurko, Quadrupolar NMR Crystallography Guided Crystal Structure Prediction (QNMRX-CSP), CrystEngComm, 2024, 26, 4782 RSC.
- E. A. Collier, R. J. Davey, S. N. Black and R. J. Roberts, 17 Salts of Ephedrine: Crystal Structures and Packing Analysis, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 498–505, DOI:10.1107/S0108768106012018.
- M. Mathew and G. J. Palenik, The Crystal and Molecular Structures of (+)-Pseudoephedrine and (+)-Pseudoephedrine Hydrochloride, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1016–1022, DOI:10.1107/S0567740877005287.
- A. Pines, M. G. Gibby and J. S. Waugh, Proton-Enhanced NMR of Dilute Spins in Solids, J. Chem. Phys., 1973, 59, 569–590, DOI:10.1063/1.1680061.
- O. Peersen, X. L. Wu, I. Kustanovich and S. O. Smith, Variable-Amplitude Cross-Polarization MAS NMR, J. Magn. Reson., Ser. A, 1993, 104, 334–339, DOI:10.1006/jmra.1993.1231.
- G. Metz, X. L. Wu and S. O. Smith, Ramped-Amplitude Cross Polarization in Magic Angle Spinning NMR, J. Magn. Reson., Ser. A, 1994, 110, 219–227, DOI:10.1006/jmra.1994.1208.
- J. Schaefer and E. O. Stejskal, Carbon-13 Nuclear Magnetic Resonance of Polymers Spinning at the Magic Angle, J. Am. Chem. Soc., 1976, 98, 1031–1032, DOI:10.1021/ja00420a036.
- A. Pines, M. G. Gibby and J. S. Waugh, Proton-Enhanced Nuclear Induction Spectroscopy 13C Chemical Shielding Anisotropy in Some Organic Solids, Chem. Phys. Lett., 1972, 15, 373–376, DOI:10.1016/0009-2614(72)80191-X.
- R. E. Taylor, 13C CP/MAS: Application to Glycine, Concepts Magn. Reson., 2004, 22A, 79–89, DOI:10.1002/cmr.a.20015.
- P. Bertani, J. Raya and B. Bechinger, 15N Chemical Shift Referencing in Solid State NMR, Solid State Nucl. Magn. Reson., 2014, 61–62, 15–18, DOI:10.1016/j.ssnmr.2014.03.003.
- E. L. Hahn, Spin Echoes, Phys. Rev., 1950, 80, 580–594, DOI:10.1103/PhysRev.80.580.
- J. C. C. Chan, Spin Echoes in Half-Integer Quadrupole Systems, Concepts Magn. Reson., 1999, 11, 363–377, DOI:10.1002/(SICI)1099-0534(1999)11:6<363::AID-CMR2>3.0.CO;2-A.
- D. L. Bryce and G. D. Sward, Chlorine-35/37 NMR Spectroscopy of Solid Amino Acid Hydrochlorides: Refinement of Hydrogen-Bonded Proton Positions Using Experiment and Theory, J. Phys. Chem. B, 2006, 110, 26461–26470, DOI:10.1021/jp065878c.
- S. G. J. van Meerten, W. M. J. Franssen and A. P. M. Kentgens, SsNake: A Cross-Platform Open-Source NMR Data Processing and Fitting Application, J. Magn. Reson., 2019, 301, 56–66, DOI:10.1016/j.jmr.2019.02.006.
- K. Eichele, WSOLIDS1: Solid-State NMR Simulated (Version 1.21.7), Universität Tübingen, 2021 Search PubMed.
- R. L. C. Akkermans, N. A. Spenley and S. H. Robertson, Monte Carlo Methods in Materials Studio, Mol. Simul., 2013, 39, 1153–1164, DOI:10.1080/08927022.2013.843775.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr.–Cryst. Mater., 2005, 220, 567–570, DOI:10.1524/zkri.220.5.567.65075.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: A Generic Force Field for Molecular Simulations, J. Phys. Chem., 1990, 94, 8897–8909, DOI:10.1021/j100389a010.
- J. R. Yates, C. J. Pickard and F. Mauri, Calculation of NMR Chemical Shifts for Extended Systems Using Ultrasoft Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401, DOI:10.1103/PhysRevB.76.024401.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, The Zero-Order Regular Approximation for Relativistic Effects: The Effect of Spin–Orbit Coupling in Closed Shell Molecules, J. Chem. Phys., 1996, 105, 6505–6516, DOI:10.1063/1.472460.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, Relaxation of Crystals with the Quasi-Newton Method, J. Comput. Phys., 1997, 131, 233–240, DOI:10.1006/jcph.1996.5612.
- P. Pyykkö, Year-2017 Nuclear Quadrupole Moments, Mol. Phys., 2018, 116, 1328–1338, DOI:10.1080/00268976.2018.1426131.
- D. W. Alderman, M. H. Sherwood and D. M. Grant, Comparing, Modeling, and Assigning Chemical-Shift Tensors in the Cartesian, Irreducible Spherical, and Icosahedral Representations, J. Magn. Reson., Ser. A, 1993, 101, 188–197, DOI:10.1006/jmra.1993.1029.
- D. E. McREE, Computational Techniques, in Practical Protein Crystallography, Elsevier, 1999, p. 91, DOI:10.1016/B978-012486052-0/50005-1.
- J.-M. Rondeau and H. Schreuder, Protein Crystallography and Drug Discovery, in The Practice of Medicinal Chemistry, Elsevier, 2015, pp. 511–537, DOI:10.1016/B978-0-12-417205-0.00022-5.
- F. H. Allen, The Cambridge Structural Database: A Quarter of a Million Crystal Structures and Rising, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388, DOI:10.1107/S0108768102003890.
- G. Barr, W. Dong, C. J. Gilmore, A. Kern, A. Parkin and C. C. Wilson, Using the Cambridge Structural Database to Validate Powder Structures, Z. Kristallogr., Suppl., 2007, 2007, 209–214, DOI:10.1524/zkri.2007.2007.suppl_26.209.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, Mercury 4.0 : From Visualization to Analysis, Design and Prediction, J. Appl. Crystallogr., 2020, 53, 226–235, DOI:10.1107/S1600576719014092.
- G. S. H. Lee, R. C. Taylor, M. Dawson, G. S. K. Kannangara and M. A. Wilson, High-Resolution Solid State 13C Nuclear Magnetic Resonance Spectra of 3,4-Methylenedioxyamphetamine Hydrochloride and Related Compounds and Their Mixtures with Lactose, Solid State Nucl. Magn. Reson., 2000, 16, 225–237, DOI:10.1016/S0926-2040(00)00071-0.
- G. Desiraju and T. Steiner, The Weak Hydrogen Bond, Oxford University Press, Oxford, England, 2001, vol. 9, DOI:10.1093/acprof:oso/9780198509707.001.0001.
- M. Hildebrand, H. Hamaed, A. M. Namespetra, J. M. Donohue, R. Fu, I. Hung, Z. Gan and R. W. Schurko, 35Cl Solid-State NMR of HCl Salts of Active Pharmaceutical Ingredients: Structural Prediction, Spectral Fingerprinting and Polymorph Recognition, CrystEngComm, 2014, 16, 7334–7356, 10.1039/c4ce00544a.
- H. Hamaed, J. M. Pawlowski, B. F. T. Cooper, R. Fu, S. H. Eichhorn and R. W. Schurko, Application of Solid-State 35Cl NMR to the Structural Characterization of Hydrochloride Pharmaceuticals and Their Polymorphs, J. Am. Chem. Soc., 2008, 130, 11056–11065, DOI:10.1021/ja802486q.
- S. T. Holmes, C. S. Vojvodin, N. Veinberg, E. M. Iacobelli, D. A. Hirsh and R. W. Schurko, Hydrates of Active Pharmaceutical Ingredients: A 35Cl and 2H Solid-State NMR and DFT Study, Solid State Nucl. Magn. Reson., 2022, 122, 101837, DOI:10.1016/j.ssnmr.2022.101837.
- C. S. Vojvodin, S. T. Holmes, L. K. Watanabe, J. M. Rawson and R. W. Schurko, Multi-Component Crystals Containing Urea: Mechanochemical Synthesis and Characterization by 35 Cl Solid-State NMR Spectroscopy and DFT Calculations, CrystEngComm, 2022, 24, 2626–2641, 10.1039/D1CE01610E.
- A. M. Namespetra, D. A. Hirsh, M. P. Hildebrand, A. R. Sandre, H. Hamaed, J. M. Rawson and R. W. Schurko, 35Cl Solid-State NMR Spectroscopy of HCl Pharmaceuticals and Their Polymorphs in Bulk and Dosage Forms, CrystEngComm, 2016, 18, 6213–6232, 10.1039/C6CE01069E.
- M. K. Pandey, H. Kato, Y. Ishii and Y. Nishiyama, Two-Dimensional Proton-Detected 35Cl/1H Correlation Solid-State NMR Experiment under Fast Magic Angle Sample Spinning: Application to Pharmaceutical Compounds, Phys. Chem. Chem. Phys., 2016, 18, 6209–6216, 10.1039/c5cp06042g.
- A. A. Peach, D. A. Hirsh, S. T. Holmes and R. W. Schurko, Mechanochemical Syntheses and 35Cl Solid-State NMR Characterization of Fluoxetine HCl Cocrystals, CrystEngComm, 2018, 20, 2780–2792, 10.1039/c8ce00378e.
- D. A. Hirsh, S. T. Holmes, P. Chakravarty, A. A. Peach, A. G. Dipasquale, K. Nagapudi and R. W. Schurko, In Situ Characterization of Waters of Hydration in a Variable-Hydrate Active Pharmaceutical Ingredient Using 35Cl Solid-State NMR and X-Ray Diffraction, Cryst. Growth Des., 2019, 19, 7349–7362, DOI:10.1021/acs.cgd.9b01218.
- A. V. Wijesekara, A. Venkatesh, B. J. Lampkin, B. VanVeller, J. W. Lubach, K. Nagapudi, I. Hung, P. L. Gor’kov, Z. Gan and A. J. Rossini, Fast Acquisition of Proton-Detected HETCOR Solid-State NMR Spectra of Quadrupolar Nuclei and Rapid Measurement of NH Bond Lengths by Frequency Selective HMQC and RESPDOR Pulse Sequences, Chem.–Eur. J., 2020, 26, 7881–7888, DOI:10.1002/chem.202000390.
- D. Iuga, E. K. Corlett and S. P. Brown, 35Cl–1H Heteronuclear Correlation Magic-Angle Spinning Nuclear Magnetic Resonance Experiments for Probing Pharmaceutical Salts, Magn. Reson. Chem., 2021, 59, 1089–1100, DOI:10.1002/mrc.5188.
- S. T. Holmes, J. M. Hook and R. W. Schurko, Nutraceuticals in Bulk and Dosage Forms: Analysis by 35Cl and 14N Solid-State NMR and DFT Calculations, Mol. Pharmaceutics, 2022, 19, 440–455, DOI:10.1021/acs.molpharmaceut.1c00708.
- L. M. Abdulla, A. A. Peach, S. T. Holmes, Z. T. Dowdell, L. K. Watanabe, E. M. Iacobelli, D. A. Hirsh, J. M. Rawson and R. W. Schurko, Synthesis and Characterization of Xylazine Hydrochloride Polymorphs, Hydrates, and Cocrystals: A 35Cl Solid-State NMR and DFT Study, Cryst. Growth Des., 2023, 23, 3412–3426, DOI:10.1021/acs.cgd.2c01539.
- P. M. J. Szell, Z. Rehman, B. P. Tatman, L. P. Hughes, H. Blade and S. P. Brown, Exploring the Potential of Multinuclear Solid-State 1H, 13C, and 35Cl Magnetic Resonance To Characterize Static and Dynamic Disorder in Pharmaceutical Hydrochlorides, ChemPhysChem, 2023, 24, e202200558, DOI:10.1002/cphc.202200558.
- D. L. Bryce, M. Gee and R. E. Wasylishen, High-Field Chlorine NMR Spectroscopy of Solid Organic Hydrochloride Salts: A Sensitive Probe of Hydrogen Bonding Environment, J. Phys. Chem. A, 2001, 105, 10413–10421, DOI:10.1021/jp011962a.
- T. Azäs, C. Bonhomme and M. E. Smith, 35Cl Quadrupolar Constants Obtained by Solid-State NMR: Study of Chlorinated Al-O-P Clusters, Involving OH ⋯ Cl Hydrogen Bonds, Solid State Nucl. Magn. Reson., 2003, 23, 14–27, DOI:10.1016/S0926-2040(02)00012-7.
- C. Gervais, R. Dupree, K. J. Pike, C. Bonhomme, M. Profeta, C. J. Pickard and F. Mauri, Combined First-Principles Computational and Experimental Multinuclear Solid-State NMR Investigation of Amino Acids, J. Phys. Chem. A, 2005, 109, 6960–6969, DOI:10.1021/jp0513925.
- R. P. Chapman and D. L. Bryce, A High-Field Solid-State 35/37Cl NMR and Quantum Chemical Investigation of the Chlorine Quadrupolar and Chemical Shift Tensors in Amino Acid Hydrochlorides, Phys. Chem. Chem. Phys., 2007, 9, 6219–6230, 10.1039/b712688c.
- G. H. Penner, R. Webber and L. A. O'Dell, A Multinuclear NMR and Quantum Chemical Study of Solid Trimethylammonium Chloride, Can. J. Chem., 2011, 89, 1036–1046, DOI:10.1139/v11-034.
- F. G. Vogt, G. R. Williams and R. C. B. Copley, Solid-State NMR Analysis of a Boron-Containing Pharmaceutical Hydrochloride Salt, J. Pharm. Sci., 2013, 102, 3705–3716, DOI:10.1002/jps.23679.
- F. G. Vogt, G. R. Williams, M. Strohmeier, M. N. Johnson and R. C. B. Copley, Solid-State NMR Analysis of a Complex Crystalline Phase of Ronacaleret Hydrochloride, J. Phys. Chem. B, 2014, 118, 10266–10284, DOI:10.1021/jp505061j.
- J. W. Akitt and W. S. McDonald, Arrangements of Ligands Giving Low Electric Field Gradients, J. Magn. Reson., 1984, 58, 401–412, DOI:10.1016/0022-2364(84)90144-6.
- J. K. Harper, A. E. Mulgrew, J. Y. Li, D. H. Barich, G. A. Strobel and D. M. Grant, Characterization of Stereochemistry and Molecular Conformation Using Solid-State NMR Tensors, J. Am. Chem. Soc., 2001, 123, 9837–9842, DOI:10.1021/ja010997l.
- J. K. Harper, D. H. Barich, J. Z. Hu, G. A. Strobel and D. M. Grant, Stereochemical Analysis by Solid-State NMR: Structural Predictions in Ambuic Acid, J. Org. Chem., 2003, 68, 4609–4614, DOI:10.1021/jo020377i.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Chemical Shifts in Molecular Solids by Machine Learning, Nat. Commun., 2018, 9, 4501, DOI:10.1038/s41467-018-06972-x.
- M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter, M. Ceriotti and L. Emsley, A Machine Learning Model of Chemical Shifts for Chemically and Structurally Diverse Molecular Solids, J. Phys. Chem. C, 2022, 126, 16710–16720, DOI:10.1021/acs.jpcc.2c03854.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 Dispersion Coefficient Model, J. Chem. Phys., 2017, 147, 7, DOI:10.1063/1.4993215.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00089g |
| This journal is © The Royal Society of Chemistry 2025 |