Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Large property models: a new generative machine-learning formulation for molecules
Tianfan
Jin
a,
Veerupaksh
Singla
 a,
Hsuan-Hao
Hsu
a and
Brett M.
Savoie
a,
Hsuan-Hao
Hsu
a and
Brett M.
Savoie
 *b
*b
aDavidson School of Chemical Engineering, Purdue University, West Lafayette, Indiana, USA
bDepartment of Chemical and Biomolecular Engineering, The University of Notre Dame, Notre Dame, Indiana, USA. E-mail: bsavoie2@nd.edu
First published on 27th September 2024
Abstract
Generative models for the inverse design of molecules with particular properties have been heavily hyped, but have yet to demonstrate significant gains over machine-learning-augmented expert intuition. A major challenge of such models is their limited accuracy in predicting molecules with targeted properties in the data-scarce regime, which is the regime typical of the prized outliers that it is hoped inverse models will discover. For example, activity data for a drug target or stability data for a material may only number in the tens to hundreds of samples, which is insufficient to learn an accurate and reasonably general property-to-structure inverse mapping from scratch. We’ve hypothesized that the property-to-structure mapping becomes unique when a sufficient number of properties are supplied to the models during training. This hypothesis has several important corollaries if true. It would imply that data-scarce properties can be completely determined using a set of more accessible molecular properties. It would also imply that a generative model trained on multiple properties would exhibit an accuracy phase transition after achieving a sufficient size—a process analogous to what has been observed in the context of large language models. To interrogate these behaviors, we have built the first transformers trained on the property-to-molecular-graph task, which we dub “large property models” (LPMs). A key ingredient is supplementing these models during training with relatively basic but abundant chemical property data. The motivation for the large-property-model paradigm, the model architectures, and case studies are presented here.
1 Introduction
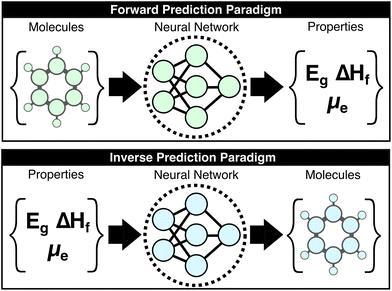
Machine-learning (ML) research in the chemical sciences has produced a panoply of models that generally increase the accuracy and reduce the computational cost of predicting molecular properties. As these methods mature, solving the so-called “forward-problem” of predicting the properties of a given chemical structure is becoming routine when the requisite data is available; however, the “inverse-problem” of finding an optimal set of chemical structures under functional constraints is more directly relevant to molecular design and remains unsolved (Fig. 1).1–15 This work introduces the concept of the “large property model” (LPM), which represents a direct solution to the inverse problem by leveraging property scaling to make the property-to-molecular-graph mapping learnable. The core question that is explored here is whether the inverse mapping of molecular properties to molecular structures is possible when provided a sufficient number of properties per molecule. The presented LPM implementation and benchmarks support an affirmative answer to this question, which opens a new paradigm for generative chemical models.Deep generative models try to directly solve the inverse problem by learning the conditional probability, P(molecule|properties), then sampling this distribution with respect to targeted properties to yield exemplary structures. The hope is that a model of this distribution, f(properties) = P(molecules), that is provided sufficient examples of molecules with different property combinations would be able to generate non-trivial structures for unseen property combinations. The popular examples of language models—where the corresponding task is to learn P(next token|context)—image generators—P(image|caption)—and music generators—P(waveform|description)—have become ubiquitous over the past several years.12,14,16–20 As anyone who has experimented with these can attest, they also demonstrate that non-trivial interpolations can emerge from such models as they are scaled up. Despite ample forerunners to developing analogous generative models for molecule generation, none have yet to significantly outperform expert intuition or forward-prediction workflows (e.g., for screening molecular libraries and their derivatives using ML-augmented filters).21
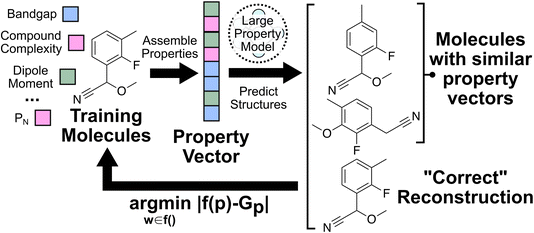
Several problems have been identified with deep generative chemical models, including the high frequency of invalid structures, false positives, and high data intensity, which rules out applications to prized but data-scarce properties.16,21–36 The structures generated by generative chemical models can also fail in more subtle ways—they may match targeted properties, but they aren’t stable, can’t be synthesized, aren’t soluble, are too expensive, or any number of other things that experts subconsciously normalize over when trying to design a molecule.21,22,26,37,38 We hypothesize that the origin of this poor performance is fundamentally due to the paucity of general chemical information utilized during training contemporary generative chemical models. For instance, although large numbers of chemical structures are typically utilized (>100k), only a small number of properties are supplied, which leaves these models with the unrealistic task of trying to learn chemistry from scratch while simultaneously generating application-relevant molecules. The motivating idea for LPMs may be glibly expressed as teaching generative models general chemistry before teaching them to predict PhD-level properties.
In conventional formulations, generative chemical models are trained to learn a conditional distribution P(G|p0), where p0 is some property of interest (e.g., bandgap, toxicity, binding affinity, etc.), and G is the molecular graph typically expressed using a grammar-like SMILES or SELFIES.39,40 However, every molecule has many more properties than just the sought after p0. For example, every molecule has a heat of formation, an electric dipole moment, a vibrational spectrum, and so-forth. So in practice, when one samples P(G|p0), one is also necessarily sampling the larger conditional distribution P(G|p0, p1, p2, …, pN), where {p0, p1, p2, …, pN} constitutes some “complete” set of properties that represent a basis set for uniquely specifying G. Thus, a user that is querying P(G|p0) is asking for a set of molecules conditioned on a host of implicit properties. In common terms, the user querying P(G|p0) is asking “give me a molecule with p0 but sample the rest of the unspecified properties from a reasonable physical distribution.” The limited exposure to these implicit properties helps explain why generative models often generate what seem to be unphysical structures when sampling the edge of the observed property distribution.3,4,41 In light of this, it should be advantageous to train the model to explicitly learn the full conditional distribution P(G|p0, p1, p2, …, pN) from examples with a complete set of properties supplied, rather than try to indirectly learn the conditional distribution by only viewing examples of P(G|p0), with the other properties implicit in the graph but not directly represented.
The conditional distribution P(G|p0) is typically learned indirectly, using architectures based on autoencoders with auxiliary prediction tasks or adversarial architectures.24,42–44 In contrast, the most straightforward formulation would be to learn the property-to-molecule mapping, f(p) = P(G), directly:
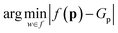 | (1) |
(1) The reconstruction accuracy of the model should monotonically increase with the number of independent properties supplied during training (i.e., the length of p).
(2) Including off-target properties in training may still improve the performance of sampling useful molecules with on-target property values.
(3) A finite number of properties are necessary to uniquely specify a molecule of a given size.
(4) A finite number of properties are necessary to uniquely predict every additional molecular property.
(5) The complexity of the conditional distribution P(G|p) decreases as the length of p increases, terminating in a delta function about a single molecule.
Others implications can be imagined. Not all of these will be directly explored in the following case studies, but these might serve as a basis for further discussion.
2 Methods
2.1 Data
The current study uses a set of 1.3 M molecules taken from Pubchem. These molecules were curated to have up to 14 heavy atoms and include the elements CHONFCl. For each of these species, Auto3D was used to generate a geometry, and 23 properties were calculated for each structure using either GFN2-xTB, as implemented in the xtb package, or directly parsed from PubChem.45,46 The complete set of properties are as follows, based on whether it was generated from xtb or parsed from PubChem: (xtb) dipole moment, total energy, total enthalpy, total free energy, HOMO–LUMO gap, heat capacity at constant pressure, standard entropy, vertical ionization potential, vertical electron affinity, global electrophilicity index, max/min/avg electrostatic potential, free energies of solvation in octanol and water, total solvent accessible surface areas in octanol and water, and quadrupole moment; (Pubchem) compound complexity, number of H-bond acceptors and donors, log(P), and topological polar surface area. In combination, this led to a total of 23 properties that were used as inputs to the LPMs during training and evaluation.It is beyond the scope of a Faraday Discussions article to fully excavate all the details of how these properties were calculated and their accuracy. For the purposes of training and evaluating the LPMs, we will take these properties as ground-truth labels. However, the training splits (https://www.doi.org/10.6084/m9.figshare.26380666), raw property data (https://www.doi.org/10.6084/m9.figshare.26380918), and model checkpoints (https://www.doi.org/10.6084/m9.figshare.26380837) have been deposited on figshare.
A set of 80 trivial properties were also calculated for each molecule that we refer to as “constraints”, because these are properties that the user will often know in advance and would like to apply as a design constraint. For example, setting the number of fluorines to zero or limiting the size of the molecule is easy owing to the explicit inclusion of these constraints during training. The training constraints include the number of atoms of each element and boolean true/false flags for a list of common functional groups. These constraints are concatenated with property vectors after embedding and prior to the attention layers. For the purpose of the following discussion, when we refer to “property vectors”, we are referring to the catenated tensor associated with the separately embedded constraints and properties.
2.2 Architecture
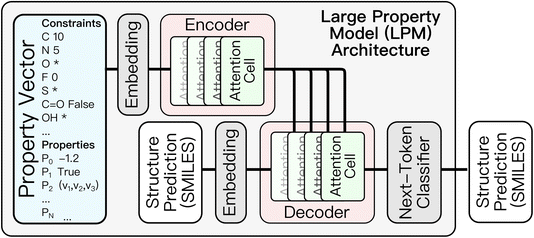
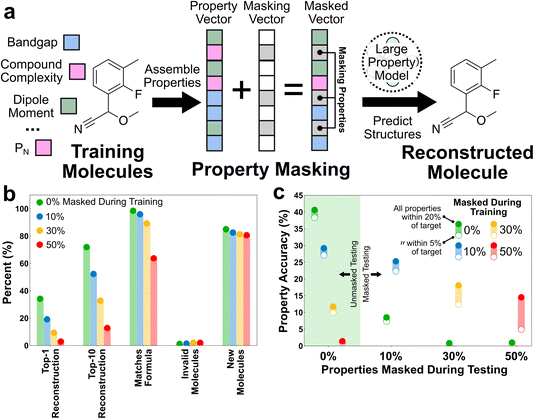
A multimodal transformer architecture was designed and implemented here for the property-to-graph problem (Fig. 3). The architecture consists of a property encoder with self-attention cells and a graph decoder with masked cross-attention that uses the encoded property vector in the decoding. The transformer is multimodal in that it accepts different classes of properties, each with their own encoding. In particular, all class properties (here, these are only associated with constraints) are embedded using a property-specific word embedding, and all scalar properties are encoded separately, each with a property-specific linear layer. After embedding, the property information occupies a [101, demb] tensor, where demb is the embedding dimension that is equal to 256 for all of the models discussed here. The embedded property tensor is transformed by a series of four eight-headed self-attention cells into a tensor of the same size that is used as the key and value inputs in the cross-attention blocks of the graph decoder.The graph decoder is constructed as a next-token SMILES predictor that begins with a “start” token. The decoding occurs recursively until the decoder predicts an “end” token or the decoded string reaches the maximum length. The input to the decoder is tokenized and embedded into a [dwin, demb] tensor based on a SMILES vocabulary with dvocab tokens, where dwin is the maximum length of the context window that is equal to 35 for all of the models discussed here. Sinusoidal positional embedding is added to the decoder embedding to capture the positional context (this isn’t required in the property encoder because we desire it to be positionally invariant). The embedded [dwin, demb] tensor is then transformed through four eight-headed cross-attention cells where the key and value inputs are supplied by the encoder output. Finally, the output of the decoder is projected to a [dwin, dvocab] tensor during training with a dense layer and a softmax to predict the probability of the next SMILES token. During inference, the final projection is to a [1, dvocab] tensor because it is performed in a token-by-token fashion.
2.3 Training and evaluation
The models were trained and tested using fixed 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 training
10 training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) validation
validation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) testing splits assigned randomly from the 1.3 M molecule dataset. The models were trained on next-token prediction using masked cross-attention in the decoder, a cross-entropy loss, dropout for the dense layers in each attention cell, the Adam optimizer with learning rate 2
testing splits assigned randomly from the 1.3 M molecule dataset. The models were trained on next-token prediction using masked cross-attention in the decoder, a cross-entropy loss, dropout for the dense layers in each attention cell, the Adam optimizer with learning rate 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000−0.5 × demb−0.5, and a patience of 30 epochs evaluated on the validation set to conclude training. The 1.05 M training samples of property/graph pairs were randomly sampled in batches of 100 for training. All numerical properties were min–max [0, 100] normalized with respect to the training distribution. Training until termination by patience took between 54–106 epochs for the models trained here.
000−0.5 × demb−0.5, and a patience of 30 epochs evaluated on the validation set to conclude training. The 1.05 M training samples of property/graph pairs were randomly sampled in batches of 100 for training. All numerical properties were min–max [0, 100] normalized with respect to the training distribution. Training until termination by patience took between 54–106 epochs for the models trained here.
A subset of the models were trained under conditions where a fraction of the inputted properties were masked. Masking was incorporated using a special token for class-based inputs and the mean value across the training set for scalar inputs. Both constrained properties and real properties were masked.
During structure inference, a beam search was implemented to decode the top-n structures predicted by each model to be consistent with the supplied property vector.47–49 For a beam size of 1, the beam search is simply a greedy decoding. For a beam size of n, next-token prediction occurs for the n most probable decodings that occur after each cycle.
3 Results and discussion
3.1 Property space
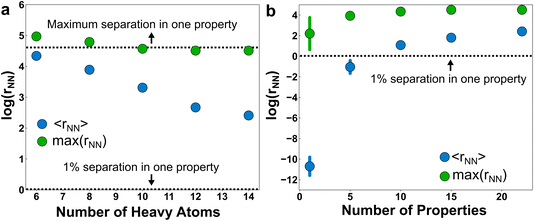
The inverse problem is challenging because there is a one-to-many mapping between any individual property and many molecular structures. However, with a sufficient number of properties, the relationship between property vectors and molecules should approach one-to-one. Between the two extremes, the density of molecules in property space should monotonically decrease as more properties are considered.How many properties does it take to uniquely specify a chemical structure? To sketch an answer to this question, 22 properties from the dataset (all xtb-calculated properties, except the quadrupole moment, plus the number of h-bond donors and acceptors from Pubchem) were used to specify a position in property space for all 1.3 M molecules and calculate the nearest-neighbor separations in various scenarios (Fig. 4). The theoretical maximum separation between a pair of molecules in property space grows as 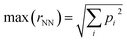 , where the summation runs over all properties and pi is the range of the property. All properties were percent normalized between [0, 100] and the natural log of the percentage normalized separation was used for the y-axes. Under these conditions, the maximum log(rNN) values are ∼4.6 and 6.2 for 1-dimensional and 22-dimensional property spaces, respectively.
, where the summation runs over all properties and pi is the range of the property. All properties were percent normalized between [0, 100] and the natural log of the percentage normalized separation was used for the y-axes. Under these conditions, the maximum log(rNN) values are ∼4.6 and 6.2 for 1-dimensional and 22-dimensional property spaces, respectively.
Unsurprisingly, the mean separation between molecules, 〈rNN〉, decreases as molecules are added to the property space (Fig. 4a). For example, if the molecular scope was limited to diatomics, then a single property—say, electric dipole moment—would probably be sufficient to uniquely identify the species. But as the number of heavy atoms (HAs) in the molecules grows (and correspondingly the number of molecules in the space), the number of properties required to uniquely specify the chemical graph also grows. Nevertheless, the molecules remain unusually clustered in property space. For example, a 22-dimensional volume with sides of 100 containing 1.3 M molecules has a number density of 1.3 × 10−38. This corresponds to an average nearest-neighbor separation of 66 (∼4.2 on natural log scale) for an ideal gas of 22-dimensional spheres occupying the same volume. The ∼5× larger ideal gas separation than 〈rNN〉 for the full dataset (i.e., the 14-HA case) is evidence of significant clustering in property space of these molecules. It isn’t clear if this clustering is intrinsic to the physically relevant space of chemistry or if this clustering merely reflects the limits of PubChem curation and synthetic biases. Regardless, the existence of this relatively low-dimensional manifold is consistent with the hypothesis that a relatively small set of physical properties may usefully span molecular space.
Although they are clustered, the molecules are still distinguishable from one another when provided a sufficient number of properties (Fig. 4b). If we use a 1% difference in at least one property as a measure of distinctiveness, then the molecules are on average distinguishable in the full 22-dimensional property space. But as the dimensionality of the property space shrinks, many of the molecules become indistinguishable by this measure. It isn’t until approximately 10 properties that the molecules are distinct on average (i.e., exhibiting an effective separation of 1% from another molecule in property space). We hypothesized that the choice of properties would play a major role in distinguishing molecules, with more orthogonal properties producing property spaces with larger effective separations. To test this, we estimated the standard deviations in separations upon resampling subsets of the properties at random and calculating the molecular separations in the resulting property spaces. Somewhat surprisingly, the uncertainty with respect to property selection becomes effectively zero after moving into a 10-dimensional property space or larger. This is indirect support of the motivating hypothesis that property redundancy emerges from a sufficient basis set of physical properties.
3.2 LPM performance
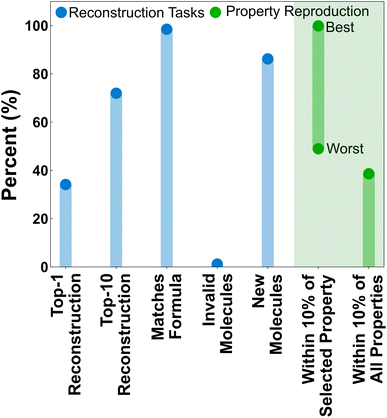
The feasibility of the property-to-graph task was first evaluated by training a LPM model without property masking and evaluating its performance in several graph reconstruction and property prediction tasks (Fig. 5). We consider it informative to distinguish between the LPM performance in reproducing the exact molecules associated with particular property vectors (i.e., the reconstruction tasks shown in blue), and reproducing molecules that exhibit consistent property vectors with the inputs (i.e., the property reproduction tasks shown in green). Using the property vectors as inputs, the LPM predicts an exact match of the testing-set molecule associated with the inputted property vector ∼35% of the time. The testing-set molecule is within the top-10 structures ∼75% of the time. Structural isomers of the testing-set molecules are also commonly predicted within the top-10. The LPM has an even stronger ability to match formula constraints, with the formula reconstruction accuracy approaching 100% for the testing set. Invalid top-1 predictions from the LPM (i.e., SMILES strings that do not correspond to valid Lewis structures) are also negligible. It is notable that no extra effort or architectural innovations were applied to filter invalid SMILES. This common problem of generative models simply resolved itself through scale and training on the property-to-graph task.Less than 100% accuracy in the top-1 reconstruction task is not necessarily a bad thing, given that the most direct application of the LPM is to generate new molecules. Additionally, the clustering of molecules in property space (Fig. 4) suggests that multiple molecules are likely to exist with similar property profiles to the property vectors being used here for inference. Indeed, ∼90% of the top-1 predicted molecules are new (i.e., contained neither within the training nor validation splits). But how well do the generated molecules actually reproduce the property vectors that were used during inference? To assess this, the properties of the top-1 predicted structures were calculated according to the same protocol as the training data and the statistics for reproducing individual properties and all properties were calculated (Fig. 5, green). Not all properties are equally easy to reproduce. The most easily satisfied property was total energy, which was reproduced in ∼99.87% of the top-1 predictions, and the hardest individual property to reproduce was average electrostatic potential, which was only reproduced in ∼49% of the top-1 predictions. Remarkably, over 40% of the top-1 predicted structures reproduced all 22 properties within 10% of the requested value.
3.3 Masking case-studies
In an authentic generative scenario, the user may only desire to explicitly specify a small number of properties. The current LPMs accept up to 21 properties. Rather than specifying all 21 properties, the user might only wish to specify one property and have the other 20 properties be conditionally sampled by the model. Can the LPMs be trained to perform inference on a subset of properties?To test this we implemented a simple masking strategy that consisted of keeping a fixed set of input properties and constraints but randomly masking subsets of the inputs during training (Fig. 6a). Masking was implemented by replacing scalar properties with the mean value from the training dataset and replacing categorical properties with a special masking token. The rationale for this strategy was that it would force the model to rely on a broader set of relationships between the properties because the available information was not fixed from inference to inference. Moreover, the relationships used by the LPM for inference would have to be dynamic in the masking scenario, because the inputs being masked were randomly selected from sample to sample. Conversely, this training strategy would make conditional inference easy for the user, as any unknown properties could simply be masked during inference.
Four LPMs were trained and tested under conditions with varying levels of property masking (Fig. 6b). The 0% masking LPM is the same as that used in Fig. 5, but the other LPMs were newly trained for this case study. All LPM architectures were held fixed and no attempt was made to fine-tune the architecture to improve performance in the masking scenario. Masking has a monotonic adverse effect on LPM performance in the structure reconstruction tasks (Fig. 6b). Masking a fraction of properties is the same as reducing the property space from the perspective of information, and so it makes sense that the confidence in predicting a specific graph goes down as more properties are masked. Notably, the top-1 accuracy nearly falls to zero for the 50% masking case, which approximately matches the 10-property threshold that we identified in the Fig. 4b discussion as being necessary for practically distinguishing molecules within the training distribution. It is also notable that masking has a negligible effect on the prediction of invalid molecules and new molecules. This is consistent with all of these LPMs being trained in property spaces that are sufficiently informative to learn both the grammar and interpolation of the training distribution of molecules.
Masking was envisioned to help in predicting molecules with targeted properties subject to limited off-target property information. Thus, although masking is expected to hurt reconstruction accuracy, it should help property prediction accuracy in property-scarce scenarios. To test this, the LPMs trained in the varying masking scenarios were tested for property reproduction in both unmasked and masked scenarios (Fig. 6c). During these tests, the full testing set of property vectors were used with the specified percentage of inputs masked. The properties of the resulting top-1 predictions were then characterized and compared with the unmasked portions of the inputted property vectors. The accuracy is reported as the percentage of the top-1 predictions that exhibit all properties (i.e., excluding constraints) within a specified percentage (either 5% or 20%) of the unmasked inputted values. The 0% masking LPM was used as a baseline and tested under all masking scenarios. Each masked LPM was tested under the same masking conditions as its training and also the 0% masking scenario. Note that these tests are quite expensive because the properties of all new molecules must be characterized to evaluate the accuracy of the predictions; this is the only reason why all combinations of masked training and masked testing were not performed.
Several notable behaviors emerge from this case study. First, the performance of the LPM trained without masking rapidly deteriorates in circumstances where it only has access to a subset of properties. In contrast, the masked LPMs all outperform the unmasked LPM in masked testing scenarios. This largely validates the hypothesis that masking forces the LPMs to learn a more dynamic set of property relationships, whereas the unmasked LPM relies on a fixed set of relationships that produce very poor results subject to incomplete information. Second, the LPMs trained with masking can still perform useful inference in the unmasked scenario. In particular, the LPM trained with 30% masking shows a small reduction in property accuracy in the unmasked scenario, while the LPM trained with 10% masking actually performs better in the unmasked scenario. Because the accuracy is only evaluated on the unmasked properties, this latter result unequivocally shows that some of the properties possess mutual information, such that their joint specification increases their individual accuracy. Finally, the difference between the “all properties within 20% of target” and “all properties within 5% of target” accuracy measures increases with the masking level of evaluation, regardless of the masking level during training. We interpret this as additional evidence of the mutual information amongst the properties. As the number of properties available for inference shrinks, so do the accuracy and confidence of the properties associated with the predicted molecules.
4 Conclusions
Our initial experiments with LPMs suggest that the property-to-molecular-structure mapping becomes directly learnable using a relatively low-dimensional property space. The finitude of property space has the corollaries that (1) a minimal basis set of properties exists with respect to which other properties are derivative, (2) that even seemingly unrelated properties can possess mutual information, and (3) that the conditional chemical structure distribution becomes simpler as more properties are explicitly specified. These corollaries suggest the practical possibility of making effective few-shot generative models by pretraining on property-rich conditional property to graph distributions and fine tuning on a small number of specific examples. These and many other implications of LPM performance should be interrogated.Several things have also been intentionally left out of this study: we haven’t tested the LPMs in extrapolative scenarios; we haven’t tested the scaling behavior of the LPMs with respect to training data; we haven’t tested the scaling behavior of the LPMs beyond a small set of possible properties; we haven’t tested the transferability of LPMs to data-scarce or other unseen properties; we haven’t explored self-supervised training tasks beyond masking; we haven’t fine-tuned the architecture for performance. These and many other things are extensions of the ideas described here and will have to wait for future communications.
Data availability
Figshare repositories have been created for the training, testing, and validation sets (https://www.doi.org/10.6084/m9.figshare.26380666), for the model checkpoints (https://www.doi.org/10.6084/m9.figshare.26380837), and for the raw property data (https://www.doi.org/10.6084/m9.figshare.26380918).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible by the National Science Foundation (NSF) Division of Chemical, Bioengineering, Environmental, and Transport Systems (CBET) through support provided by the Electrochemical Systems Program (grant number: 2045887-CBET, Program Manager: Dr Carol Read).References
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, Analyzing learned molecular representations for property prediction, J. Chem. Inf. Model., 2019, 59(8), 3370–3388 CrossRef CAS PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A graph-convolutional neural network model for the prediction of chemical reactivity, Chem. Sci., 2019, 10(2), 370–377 RSC.
- N. C. Iovanac and B. M. Savoie, Improved chemical prediction from scarce data sets via latent space enrichment, J. Phys. Chem. A, 2019, 123(19), 4295–4302 CrossRef CAS.
- N. C. Iovanac, R. MacKnight and B. M. Savoie, Actively searching: inverse design of novel molecules with simultaneously optimized properties, J. Phys. Chem. A, 2022, 126(2), 333–340 CrossRef CAS.
- S. Boobier, D. R. J. Hose, A. J. Blacker and B. N. Nguyen, Machine learning with physicochemical relationships: solubility prediction in organic solvents and water, Nat. Commun., 2020, 11(1), 5753 CrossRef CAS PubMed.
- G. A. Pinheiro, J. Mucelini, M. D. Soares, R. C. Prati, J. L. F. Da Silva and M. G. Quiles, Machine learning prediction of nine molecular properties based on the smiles representation of the qm9 quantum-chemistry dataset, J. Phys. Chem. A, 2020, 124(47), 9854–9866 CrossRef CAS.
- K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Machine learning meets mechanistic modelling for accurate prediction of experimental activation energies, Chem. Sci., 2021, 12(3), 1163–1175 RSC.
- S. Tian, N. I. Arshad, D. Toghraie, S. Ali Eftekhari and M. Hekmatifar, Using perceptron feed-forward artificial neural network (ann) for predicting the thermal conductivity of graphene oxide-al2o3/water-ethylene glycol hybrid nanofluid, Case Stud. Therm. Eng., 2021, 26, 101055 CrossRef.
- K. Atz, F. Grisoni and G. Schneider, Geometric deep learning on molecular representations, Nat. Mach. Intell., 2021, 3(12), 1023–1032 CrossRef.
- X. Fang, L. Liu, J. Lei, D. He, S. Zhang, J. Zhou, F. Wang, H. Wu and H. Wang, Geometry-enhanced molecular representation learning for property prediction, Nat. Mach. Intell., 2022, 4(2), 127–134 CrossRef.
- A. D. McNaughton, R. P. Joshi, C. R. Knutson, A. Fnu, K. J. Luebke, J. P. Malerich, P. B. Madrid and N. Kumar, Machine learning models for predicting molecular uv–vis spectra with quantum mechanical properties, J. Chem. Inf. Model., 2023, 63(5), 1462–1471 CrossRef CAS PubMed.
- J. Pan, Large language model for molecular chemistry, Nat. Comput. Sci., 2023, 3(1), 5 CrossRef PubMed.
- E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, Chemprop: A machine learning package for chemical property prediction, J. Chem. Inf. Model., 2024, 64(1), 9–17 CrossRef CAS PubMed.
- P. Liu, Y. Ren, J. Tao and Z. Ren, Git-mol: A multi-modal large language model for molecular science with graph, image, and text, Comput. Biol. Med., 2024, 171, 108073 CrossRef CAS.
- R. Barrett and J. Westermayr, Reinforcement learning for traversing chemical structure space: Optimizing transition states and minimum energy paths of molecules, J. Phys. Chem. Lett., 2024, 15(1), 349–356 CrossRef CAS PubMed.
- D. Flam-Shepherd, K. Zhu and A. Aspuru-Guzik, Language models can learn complex molecular distributions, Nat. Commun., 2022, 13, 3293 CrossRef CAS PubMed.
- K. Maik Jablonka, Q. Ai, A. Al-Feghali, S. Badhwar, J. D. Bocarsly, A. M. Bran, S. Bringuier, L. C. Brinson, K. Choudhary and D. Circi, et al., 14 examples of how llms can transform materials science and chemistry: a reflection on a large language model hackathon, Digital Discovery, 2023, 2(5), 1233–1250 RSC.
- N. Yoshikawa, M. Skreta, K. Darvish, S. Arellano-Rubach, Z. Ji, L. B. Kristensen, A. Zou Li, Y. Zhao, H. Xu and A. Kuramshin, et al., Large language models for chemistry robotics, Auton. Robots, 2023, 47(8), 1057–1086 CrossRef.
- T. Guo, B. Nan, Z. Liang, Z. Guo, N. Chawla, O. Wiest and X. Zhang, et al., What can large language models do in chemistry? a comprehensive benchmark on eight tasks, Adv. Neural Inf. Process. Syst., 2023, 36, 59662–59688 Search PubMed.
- Q. Ai, F. Meng, J. Shi, B. Pelkie and C. W. Coley, Extracting structured data from organic synthesis procedures using a fine-tuned large language model, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-979fz.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Generative models for molecular discovery: Recent advances and challenges, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12(5), e1608 CrossRef.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: generative models for matter engineering, Science, 2018, 361(6400), 360–365 CrossRef CAS.
- S. Kang and K. Cho, Conditional molecular design with deep generative models, J. Chem. Inf. Model., 2019, 59(1), 43–52 CrossRef CAS.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, Automatic chemical design using a data-driven continuous representation of molecules, ACS Cent. Sci., 2018, 4(2), 268–276 CrossRef.
- J. Zhang, R. Mercado, O. Engkvist and H. Chen, Comparative study of deep generative models on chemical space coverage, J. Chem. Inf. Model., 2021, 61(6), 2572–2581 CrossRef CAS PubMed.
- T. Sousa, J. Correia, V. Pereira and M. Rocha, Generative deep learning for targeted compound design, J. Chem. Inf. Model., 2021, 61(11), 5343–5361 CrossRef CAS.
- R. J. L. Townshend, S. Eismann, A. M. Watkins, R. Rangan, M. Karelina, R. Das and R. O. Dror, Geometric deep learning of rna structure, Science, 2021, 373(6558), 1047–1051 CrossRef CAS.
- R. Chowdhury, N. Bouatta, S. Biswas, C. Floristean, A. Kharkar, K. Roy, C. Rochereau, G. Ahdritz, J. Zhang and G. M. Church, et al., Single-sequence protein structure prediction using a language model and deep learning, Nat. Biotechnol., 2022, 40(11), 1617–1623 CrossRef CAS PubMed.
- Y. Yoshikai, T. Mizuno, S. Nemoto and H. Kusuhara, A Novel Molecule Generative Model of Vae Combined with Transformer for Unseen Structure Generation, arXiv, 2024, preprint, arXiv:2402.11950, DOI:10.48550/arXiv.2402.11950.
- X. Luo, Z. Wang, P. Gao, J. Lv, Y. Wang, C. Chen and Y. Ma, Deep Learning Generative Model for Crystal Structure Prediction, 2024, preprint, arXiv:2403.10846, DOI:10.48550/arXiv.2403.10846.
- T. Yue, L. Tao, V. Varshney and Y. Li, Benchmarking study of deep generative models for inverse polymer design, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-gzq4r.
- K. Choudhary, AtomGPT: Atomistic Generative Pretrained Transformer for Forward and Inverse Materials Design, J. Phys. Chem. Lett., 2024, 15, 6909–6917 CrossRef CAS PubMed.
- S. Mal, G. Seal and P. Sen, Maggen: A graph-aided deep generative model for inverse design of permanent magnets, J. Phys. Chem. Lett., 2024, 15(12), 3221–3228 CrossRef CAS.
- Y.-S. Lin, Structure prediction of cyclic peptides via molecular dynamics and machine learning, Biophys. J., 2024, 123(3), 296a CrossRef.
- G. Crocioni, D. L. Bodor, C. Baakman, F. M. Parizi, D.-T. Rademaker, G. Ramakrishnan, S. A. van der Burg, D. F. Marzella, J. Mc Teixeira and L. C. Xue, Deeprank2: Mining 3d protein structures with geometric deep learning, J. Open Source Softw., 2024, 9(94), 5983 CrossRef.
- A. H. Cheng, A. Lo, S. Miret, B. H. Pate and A. Aspuru-Guzik, Determining 3d structure from molecular formula and isotopologue rotational spectra in natural abundance with reflection-equivariant diffusion, J. Chem. Phys., 2024, 160(12), 124115 CrossRef CAS.
- P. Renz, D. Van Rompaey, J. Kurt Wegner, S. Hochreiter and G. Klambauer, On failure modes in molecule generation and optimization, Drug Discovery Today: Technol., 2019, 32–33, 55–63 CrossRef.
- T. Ciepliński, T. Danel, S. Podlewska and S. Jastrzebski, Generative models should at least be able to design molecules that dock well: a new benchmark, J. Chem. Inf. Model., 2023, 63(11), 3238–3247 CrossRef PubMed.
- D. Weininger, Smiles, a chemical language and information system. 1. introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28(1), 31–36 CrossRef CAS.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Self-referencing embedded strings (SELFIES): A 100% robust molecular string representation, Mach. Learn.: Sci. Technol., 2020, 1(4), 045024 Search PubMed.
- N. C. Iovanac and B. M. Savoie, Improving the generative performance of chemical autoencoders through transfer learning, Mach. Learn.: Sci. Technol., 2020, 1(4), 045010 Search PubMed.
- R. Pollice, G. d. P. Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-D’Addario, A. K. Nigam, C. T. Ser and Z. Yao, et al., Data-driven strategies for accelerated materials design, Acc. Chem. Res., 2021, 54(4), 849–860 CrossRef CAS PubMed.
- M. Aldeghi and C. W. Coley, A focus on simulation and machine learning as complementary tools for chemical space navigation, Chem. Sci., 2022, 13(28), 8221–8223 RSC.
- D. M. Anstine and O. Isayev, Generative models as an emerging paradigm in the chemical sciences, J. Am. Chem. Soc., 2023, 145(16), 8736–8750 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, Gfn2-xtb—an accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671 CrossRef CAS PubMed.
- Z. Liu, T. Zubatiuk, A. Roitberg and O. Isayev, Auto3d: Automatic generation of the low-energy 3d structures with ani neural network potentials, J. Chem. Inf. Model., 2022, 62(22), 5373–5382 CrossRef CAS.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Attention is all you need, Adv. Neural Inf. Process. Syst., 2017, 30, 6000–6010 Search PubMed.
- R. Winter, F. Montanari, F. Noé and D.-A. Clevert, Learning continuous and data-driven molecular descriptors by translating equivalent chemical representations, Chem. Sci., 2019, 10(6), 1692–1701 RSC.
- M. Moret, M. Helmstädter, F. Grisoni, G. Schneider and D. Merk, Beam search for automated design and scoring of novel ror ligands with machine intelligence, Angew. Chem., Int. Ed., 2021, 60(35), 19477–19482 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |