Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate predictions of chemical shifts with the rSCAN and r2SCAN mGGA exchange–correlation functionals†
Jonathan R.
Yates
 a and
Albert P.
Bartók
a and
Albert P.
Bartók
 b
b
aDepartment of Materials, University of Oxford, Oxford OX1 3PH, UK. E-mail: jonathan.yates@materials.ox.ac.uk
bDepartment of Physics and Warwick Centre for Predictive Modelling, School of Engineering, University of Warwick, Coventry CV4 7AL, UK. E-mail: Albert.Bartok-Partay@warwick.ac.uk
First published on 25th July 2024
Abstract
We benchmark the rSCAN and r2SCAN exchange–correlation functionals by comparing the Nuclear Magnetic Resonance (NMR) magnetic shieldings predicted by Density Functional Theory (DFT) to experimentally observed chemical shifts of halide and oxide inorganic compounds. Significant improvement in accuracy is achieved compared to the Generalised Gradient Approximation (GGA) at a marginally higher computational cost. When using rSCAN or r2SCAN, the correlation coefficient between computationally predicted and experimental values approaches the theoretically expected value of −1 while reducing the deviation, allowing more accurate and reliable spectrum assignments of complex compounds in experimental investigations.
1 Introduction
The ability of NMR crystallography to address problems in structural chemistry is intrinsically linked to the availability of accurate approaches to predict NMR parameters; the more accurately we can predict NMR parameters the wider the range of materials problems that can be confidently addressed. Sources of errors and inaccuracies in calculations of NMR parameters can be numeric in origin: an incomplete basis-set, inaccurate pseudopotentials, and other forms of underconvergent parameters. Such issues can be controlled by careful validation studies. Physical approximations are another source of error, these include: the choice of simulation cell when studying defects, methods (if any) to account for thermal and zero-point motion, the effects of special relativity (heavy atom effects), and, in the case of calculations based on DFT, the choice of exchange–correlation functional. In this article we wish to focus on the last of these approximations: the choice of exchange–correlation functional.Perdew’s ‘Jacob’s Ladder’ classification of exchange–correlation functionals1 starts at the non-interacting Hartree world. The first three rungs of the ladder are the semi-local functionals: the local density approximation (LDA), the generalised gradient approximation (GGA) and the meta generalised gradient approximation (mGGA). These depend on the charge density, increasing order derivatives of the charge and the kinetic energy density. These quantities are readily available in most implementations of Kohn–Sham DFT, at a low computational cost. Higher rungs on the ladder depend additionally on Hartree–Fock-like contributions – so-called non-local functionals.
The PBE GGA functional2 has been widely used for the prediction of NMR parameters in solids. PBE is computationally efficient in solid-state DFT codes, and gives generally good accuracy for NMR parameters (for examples see the two comprehensive reviews on applications of the GIPAW approach3,4). The use of non-local functionals is expected to result in more accurate NMR parameter predictions. However, non-local functionals are challenging to use with solid-state codes due to the high computational cost of the non-local exchange. In recent years a number of approaches have been developed to use expensive, but very accurate quantum chemistry techniques, locally on the region of interest, whilst accounting for the electrostatics of the solid-state. These include cluster approaches,5 embedding schemes6 and correction (or extrapolation) approaches.7,8 All provide a route to using non-local functionals and indeed also more sophisticated quantum chemistry techniques in solid-state calculations.
While solid-state calculations of NMR parameters using the PBE functional have been widely used, there is one notable failing: the accurate prediction of 19F chemical shifts and halide shifts more generally. This was first noted in a study by Zheng et al.9 and shortly after by Griffin and co-workers.10 Both studies found that while there was a linear agreement between calculated magnetic shieldings and experimental chemical shifts, the line of best fit deviated significantly from the expected theoretical value of −1. A careful study by Sadoc11 eliminated the use of pseudopotentials as a source of this error, confirming that the PBE functional was responsible for the discrepancy. They also highlighted that fluorine atoms bonded to atoms such Ca, Sc and La with 3d or 4f localized empty orbitals are subject to an additional error. This can be corrected by adjusting the level of the d states in the metal ion pseudopotential.12 Despite these problems the PBE functional has been used to assign experimental 19F spectra, with authors using a calibration curve to convert between magnetic shielding and chemical shift.10,11,13
Laskowski et al.14 examined the origins of the 19F chemical shift using all-electron calculations within the Wien2K software package.15 In a further study16 they extended their work to O, Cl, Br, showing that all elements have PBE predicted shieldings with slopes which differ from the theoretical value of −1. These could not be corrected in a universal way by adding Hubbard “+U” corrections to the neighbouring metal atoms. Non-local functionals also did not solve the issue, unless the proportion of Fock-exchange was adjusted in a empirical manner. Intriguingly, the Becke–Johnson (BJ) potential gave slopes closest to the ideal value of −1. We have also found a similar result for 19F using the planewave pseudopotential approach with BJ potential.17 The BJ exchange–correlation potential can be regarded as potential-only mGGA. The use of this class of effective potentials is somewhat limited, due to the fact that there is no corresponding functional defined, therefore neither the total energy, nor its derivatives, the forces are available. As a result, the BJ potential may not be used to carry out geometry optimisation of atomic structures. However, the good agreement raises the question of whether true mGGA functionals will give similarly good agreement with experiment.
mGGA functionals were originally proposed in the 1980s. However, difficulties in constructing a universally accurate mGGA functional meant that their use was limited to specific classes of molecules, materials or certain properties. This changed with the introduction of the Strongly Constrained and Appropriately Normed (SCAN) mGGA functional in 2015.18 SCAN satisfies all 17 of the known, theoretically derived, physical constraints on such an exchange–correlation functional. It gives an improved description of the electronic structure for a wide range of systems, such as liquid water and ice,19 semiconductor materials20 and metal oxides.21 However, the SCAN functional poses numerical challenges to practical calculations. Specifically, the form of iso-orbital indicator used in SCAN and other mGGA functionals introduces numerical instabilities into calculations. These are especially magnified in the case of plane-wave basis sets. To address this issue we introduced22 a regularised version of the SCAN functional (rSCAN). This functional mostly preserves the accuracy of the original SCAN functional, with a stability comparable to the widely used PBE functional. rSCAN does break one of the constraints of the original SCAN functional, which results in formation energies which are poorer with rSCAN than the original SCAN.23 However, rSCAN does preserve SCAN’s potential energy surface and so the two functionals are expected to result in identical structural properties.24 To address the loss of desirable attributes due to the regularisation process, the original authors of SCAN proposed a third functional, r2SCAN, designed to preserve all of SCAN’s constraints, whilst being numerically more stable than SCAN.25 In this paper we assess the accuracy of the rSCAN and r2SCAN mGGA exchange–correlation functionals in predicting chemical shifts for a range of inorganic compounds.
2 Methods
We use the same set of oxide and halide compounds as ref. 16. The starting structures for all compounds were taken from the ICSD. We performed a full geometry optimisation of the structures, including the atomic positions and the cell parameters. Calculations of the NMR magnetic shielding tensors used the GIPAW approach.26,27 Calculations were performed using a pre-release copy of version 25 of the CASTEP plane-wave pseudopotential code. All calculations used ultrasoft pseudopotentials, 800 eV planewave cut-off energy, a fine-grid, four times more dense than that of the plane-wave basis, for the calculation of the density and local potential terms and a 0.03 Å−1 minimum k-point spacing for the sampling of the Brillouin zone. All calculations were carried out using a consistent choice of functional – i.e. the rSCAN reported shieldings were computed using atomic geometries optimised with rSCAN pseudopotentials generated with rSCAN. We give further details on the construction of the pseudopotentials below. The conversion between magnetic shielding σ and chemical shift δ is given by| δ = σref − σ | (1) |
2.1 Pseudopotentials
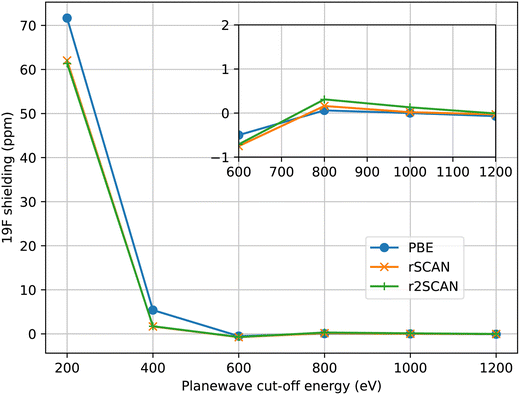
For all calculations we have aimed to use ultrasoft pseudopotentials that were generated from all-electron atomic calculations using a consistent choice of functional. When the PBE functional was used for the planewave calculation, PBE was used to generate the pseudopotential. With the mGGA functionals, rSCAN and r2SCAN, we used pseudopotentials generated with RSCAN, due to minor instabilities observed in the r2SCAN pseudopotential generation which affected a few atomic species. While the instabilities can be eliminated by adjusting the pseudopotential parameters, this process requires extensive validation which is out of the scope of this work. The mGGA potentials were constructed following the procedure we outlined in ref. 17. All pseudopotentials were generated using the CASTEP’s default C19 set of pseudopotential definitions. This means that the same parameters (e.g. cut-off radius, number of non-local projectors) were used in the pseudopotential construction, independent of functional employed.In Fig. 1 we show the convergence of 19F isotropic magnetic shielding as a function of the size of the plane-wave basis set in MgF2. All three functionals converge at a similar rate, indicating a similar numerical stability overall. r2SCAN is slightly slower to converge than rSCAN, which is slower than PBE; however, the differences are rather small. We find that we can use the same basis set to give converged magnetic shieldings for both the GGA and mGGA calculations.
3 Results
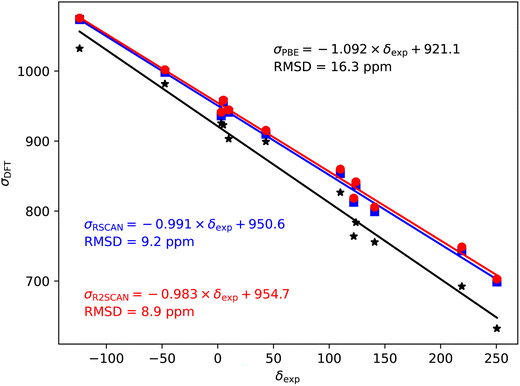
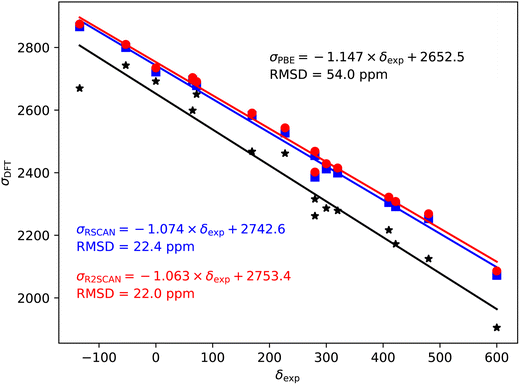
Fig. 2–5 show the magnetic shielding calculated with the PBE, rSCAN and r2SCAN functionals plotted against the experimental chemical shifts. For each functional we fit a line of the form σDFT = −mδexp + c. The fitted equations are shown in the figures together with the root mean square deviation (RMSD) from the fitted line.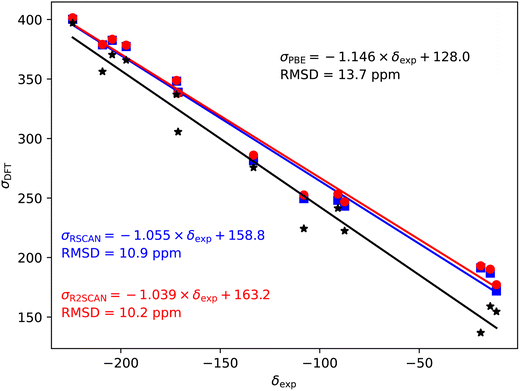 | ||
| Fig. 2 19F magnetic shieldings, σ, calculated with the PBE (black), rSCAN (blue) and r2SCAN (red) functionals vs. experimental chemical shifts, δ. For each functional the line of best fit is given. | ||
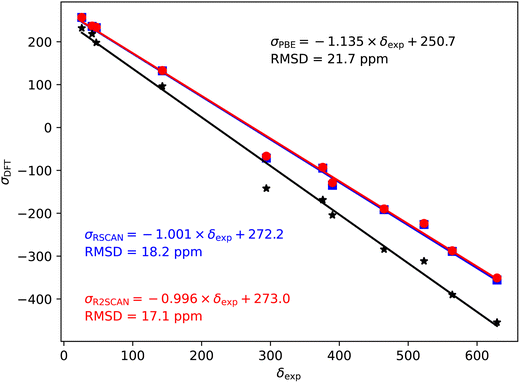 | ||
| Fig. 3 17O magnetic shieldings, σ, calculated with the PBE (black), rSCAN (blue) and r2SCAN (red) functionals vs. experimental chemical shifts, δ. For each functional the line of best fit is given. | ||
The 19F shieldings are shown in Fig. 2. The slope fit is significantly overestimated by the PBE results (−1.146). Both the rSCAN and r2SCAN functionals give a slope that is much closer to −1. The r2SCAN results also reduce the RMSD from the fitted line.
In the case of the 17O magnetic shielding predictions, the PBE slope (−1.135) is again over-estimated, when compared to experimental values in Fig. 3. The rSCAN and r2SCAN functionals show a marked improvement while improving the correlation of the predicted and measured values.
The 35/37Cl magnetic shieldings also give an overestimate of the slope with PBE; however, the slope (−1.092) is smaller than for the other nuclei studied here, Fig. 4. Again, rSCAN and r2SCAN improve both the slope and the correlation of the predictions.
79/81Br also shows a significant over-estimate of the slope of predicted magnetic shieldings with PBE (−1.147). This is reduced in the rSCAN and r2SCAN predicted shieldings, however, the slopes are still somewhat larger than −1; −1.074 for rSCAN and −1.063 for r2SCAN. The two mGGA functions do however, give a significantly improved correlation between calculation and experiment.
In Table 1 we summarise the calculated magnetic shieldings. We also convert the shieldings into chemical shifts for direct comparison with experimental values. To do the conversions we apply eqn (1) using reference shieldings obtained by fitting a straight line with gradient of −1 to the calculated shielding and experimental chemical shift. In Table 1 we report the root mean square errors (RMSE) between the calculated and experimental chemical shift for each functional. The RMSEs reported in Table 1 are larger than the deviations given in the figures as the latter allow for a slope which deviates from the ideal −1. The rSCAN and r2SCAN functionals give RMSEs which are approximately half the size of the PBE errors. The largest errors are for the Ca compounds CaF, CaO, CaCl2, CaBr2. While the SCAN family of functionals provides an overall improvement in the calculated magnetic shieldings it is evident they do not provide the correct physical description to solve the issues with the unoccupied Ca d orbitals highlighted in ref. 11 and 12. In ref. 11 the authors used a Ca pseudopotential with the d states shifted in energy. We find that a shift of this magnitude overcompensates for the error. However, a smaller shift of 1.25 eV produces magnetic shieldings for all four compounds that are in significantly closer agreement with experiment. This reduces the RMSE for all elements, and most significantly for 17O. The use of a smaller energy shift is consistent with DFT+U calculations which have found that the SCAN family of functionals need smaller values of the Hubbard U term than PBE.21
| σ-PBE | σ-rSCAN | σ-r2SCAN | δ-PBE | δ-rSCAN | δ-r2SCAN | δ-Exp. | |
|---|---|---|---|---|---|---|---|
| Fluorides | |||||||
| LiF | 370.4 | 382.5 | 383.4 | −224.0 | −216.7 | −215.2 | −204.3 |
| NaF | 397.1 | 400.2 | 401.5 | −250.6 | −234.4 | −233.4 | −224.2 |
| KF | 275.6 | 281.3 | 286.0 | −129.1 | −115.5 | −117.9 | −133.3 |
| RbF | 241.4 | 248.1 | 253.4 | −95.0 | −82.3 | −85.2 | −90.9 |
| CsF | 154.5 | 171.9 | 177.2 | −8.1 | −6.1 | −9.0 | −11.2 |
| MgF2 | 365.9 | 377.3 | 378.5 | −219.5 | −211.5 | −210.3 | −197.3 |
| CaF2 | 224.3 | 249.5 (266.6) | 252.6 | −77.8 | −83.7 (−100.8) | −84.4 | −108 |
| SrF2 | 222.4 | 243.2 | 246.8 | −76.0 | −77.4 | −78.7 | −87.5 |
| BaF2 | 159.0 | 186.9 | 190.2 | −12.6 | −21.1 | −22.0 | −14.3 |
| AlF3 | 337.0 | 348.2 | 348.8 | −190.6 | −182.4 | −180.7 | −172 |
| Ga3 | 305.6 | 338.9 | 338.1 | −159.2 | −173.1 | −170.0 | −171.2 |
| InF3 | 356.2 | 378.7 | 379.1 | −209.8 | −212.9 | −210.9 | −209.2 |
| TlF | 136.8 | 191.3 | 193.0 | 9.7 | −25.5 | −24.8 | −19.1 |
| RMS error | 17.5 | 11.7 (9.8) | 10.6 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Oxides | |||||||
| BeO | 231.9 | 256.7 | 256.9 | −24.0 | 15.3 | 17.5 | 26 |
| MgO | 197.9 | 233.0 | 233.8 | 10.0 | 39.0 | 40.6 | 47 |
| SrO | −204.4 | −134.9 | −128.6 | 412.3 | 406.9 | 403.0 | 390 |
| BaO | −454.5 | −355.6 | −350.8 | 662.4 | 627.7 | 625.3 | 629 |
| SrTiO3 | −284.2 | −191.5 | −189.8 | 492.1 | 463.6 | 464.2 | 465 |
| CaO | −142.0 | −71.4 (−24.55) | −66.8 | 350.0 | 343.4 (296.6) | 341.2 | 294 |
| SiO2 | 218.5 | 235.8 | 236.8 | −10.5 | 36.2 | 37.6 | 41 |
| BaZrO3 | −168.7 | −94.8 | −92.8 | 376.6 | 366.8 | 367.2 | 376 |
| BaSnO3 | 96.4 | 132.3 | 133.0 | 111.5 | 139.7 | 141.4 | 143 |
| BaTiO3 (1) | −390.1 | −289.0 | −287.4 | 598.1 | 561.0 | 561.8 | 564 |
| BaTiO3 (2) | −311.6 | −226.3 | −223.7 | 519.5 | 498.3 | 498.1 | 523 |
| RMS error | 35.9 | 18.2 (10.5) | 17.2 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Chlorides | |||||||
| LiCl | 922.9 | 955.5 | 958.4 | −8.4 | −4.3 | −2.6 | 5 |
| NaCl | 981.7 | 998.2 | 1001.8 | −67.1 | −47.0 | −45.9 | −47.4 |
| KCl | 925.5 | 936.1 | 941.4 | −10.9 | 15.1 | 14.4 | 3.1 |
| AgCl | 903.1 | 941.2 | 944.5 | 11.4 | 10.0 | 11.3 | 9.8 |
| CsCl | 826.6 | 853.6 | 859.8 | 88.0 | 97.6 | 96.0 | 110 |
| RbCl | 899.2 | 909.9 | 915.3 | 15.4 | 41.4 | 40.5 | 43.2 |
| CuCl | 1032.2 | 1073.6 | 1075.7 | −117.7 | −122.4 | −119.8 | −124 |
| TlCl | 632.2 | 698.7 | 702.9 | 282.4 | 252.6 | 253.0 | 250.5 |
| CaCl2 | 763.9 | 812.6 (842.7) | 818.4 | 150.7 | 138.6 (108.5) | 137.5 | 122 |
| BaCl2 (1) | 783.6 | 836.9 | 841.6 | 131.0 | 114.3 | 114.2 | 124 |
| BaCl2 (2) | 692.2 | 743.2 | 748.6 | 222.3 | 208.0 | 207.2 | 219 |
| SrCl2 | 755.6 | 799.1 | 805.7 | 159.0 | 152.2 | 150.2 | 140.8 |
| RMS error | 18.9 | 9.2 (8.8) | 9.0 | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Bromides | |||||||
| KBr | 2692.0 | 2721.9 | 2734.9 | −73.2 | 3.7 | 4.1 | 0 |
| LiBr | 2598.7 | 2695.8 | 2703.8 | 20.1 | 29.8 | 35.1 | 64.7 |
| NaBr | 2742.7 | 2800.1 | 2809.8 | −124.0 | −74.5 | −70.8 | −52.9 |
| RbBr | 2650.3 | 2678.4 | 2691.0 | −31.5 | 47.2 | 47.9 | 71.7 |
| CsBr | 2461.5 | 2526.9 | 2543.2 | 157.2 | 198.7 | 195.8 | 227.4 |
| AgBr | 2467.6 | 2582.6 | 2590.3 | 151.1 | 143.0 | 148.6 | 169.3 |
| CaBr2 | 2261.8 | 2385.9 (2455.5) | 2401.9 | 357.0 | 339.7 (270.1) | 337.1 | 280 |
| SrBr2 (1) | 2172.0 | 2291.5 | 2308.0 | 446.8 | 434.1 | 431.0 | 422 |
| SrBr2 (2) | 2216.7 | 2304.8 | 2321.8 | 402.1 | 420.8 | 417.2 | 410 |
| SrBr2 (3) | 2278.8 | 2399.0 | 2414.9 | 340.0 | 326.6 | 324.0 | 320 |
| SrBr2 (4) | 2286.3 | 2412.1 | 2428.7 | 332.4 | 313.5 | 310.3 | 300 |
| BaBr2 (1) | 2315.5 | 2454.7 | 2468.4 | 303.3 | 270.9 | 270.6 | 280 |
| BaBr2 (2) | 2124.9 | 2253.1 | 2268.7 | 493.9 | 472.5 | 470.3 | 480 |
| TlBr | 1904.9 | 2072.2 | 2086.1 | 713.8 | 653.4 | 652.9 | 600 |
| CuBr | 2669.6 | 2866.5 | 2874.9 | −50.8 | −140.9 | −136.0 | −134.1 |
| RMS error | 61.6 | 27.0 (22.2) | 25.4 | ||||
3.1 Computational cost
For calculations that involve iterative minimisation (e.g. the ground-state energy, geometry optimisation, magnetic shielding tensors) the total computational time depends on both the number of operations required per iteration, and the number of iterations required for convergence. In our experience the number of steps required for convergence is typically very close for the PBE and rSCAN functionals. This applies to the calculation of the electronic ground-state, the optimisation of the geometry and the calculation of the magnetic shielding tensors. The difference in computational cost between PBE and rSCAN arises from the additional operations needed to apply the mGGA potential. The application of the mGGA potential takes approximately four times as many operations as a GGA potential. The impact of these additional operations on the overall run-time depends on the size of system studied. The cost of using mGGA functionals will be greatest in calculations in which the application of the local potential dominates – this is typically the case for systems with small numbers of atoms, or those in which the Fast Fourier Transform is distributed over a very large number of cores. In many other cases the cost difference between mGGA and GGA calculations will be much smaller – e.g. for large atoms counts the application of the non-local pseudopotential dominates the computational costs, and this is independent of functional choice. To give some indicative numbers for the calculation of NMR shielding tensors: for a 6 atom cell of MgF2 run on a single core of an Apple M1 the time for rSCAN was 2.0 times a PBE calculation with otherwise equivalent settings. For a 256 atom cell of GeSe run on 512 cores of an AMD EPYC 7742, 2.25 GHz system the time for rSCAN was 1.25 times a PBE calculation.4 Conclusions
We have shown that the regularised versions of the SCAN mGGA functional give chemical shifts in good agreement with experiment. rSCAN and r2SCAN have significantly lower RMSEs than the widely used PBE functional, with only a modest increase in computational cost. However, rSCAN and r2SCAN do not correct the errors present in calcium containing compounds. These can be corrected through the use of an empirically adjusted pseudopotential. Such compounds remain an interesting test case for the development of new exchange–correlation functionals.Data availability
All of the relaxed crystal structures and calculated magnetic shielding tensors are available in the supplementary information.†Author contributions
Both authors contributed equally to all aspects of this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Both authors acknowledge support from the Collaborative Computational Project for NMR Crystallography (CCP-NC), the UKCP Consortium and the CASTEP-USER grant. All three sources of funding were provided by the Engineering and Physical Sciences Research Council (EPSRC) under grant numbers EP/M022501/1, EP/P022561/1 and EP/W030438/1, respectively. We acknowledge computational resources provided by Scientific Computing Research Technology Platform of the University of Warwick and the EPSRC-funded HPCMidlands+ consortium (Grant No. EP/T022108/1).Notes and references
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20 CrossRef CAS PubMed.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS.
- S. T. Holmes, R. J. Iuliucci, K. T. Mueller and C. Dybowski, J. Chem. Theory Comput., 2015, 11, 5229–5241 CrossRef CAS PubMed.
- J. D. Hartman, A. Balaji and G. J. O. Beran, J. Chem. Theory Comput., 2017, 13, 6043–6051 CrossRef CAS PubMed.
- T. Nakajima, Chem. Phys. Lett., 2017, 677, 99–106 CrossRef CAS.
- M. Dračínský, P. Unzueta and G. J. O. Beran, Phys. Chem. Chem. Phys., 2019, 21, 14992–15000 RSC.
- A. Zheng, S.-B. Liu and F. Deng, J. Phys. Chem. C, 2009, 113, 15018–15023 CrossRef CAS.
- J. M. Griffin, J. R. Yates, A. J. Berry, S. Wimperis and S. E. Ashbrook, J. Am. Chem. Soc., 2010, 132, 15651–15660 CrossRef CAS.
- A. Sadoc, M. Body, C. Legein, M. Biswal, F. Fayon, X. Rocquefelte and F. Boucher, Phys. Chem. Chem. Phys., 2011, 13, 18539–18550 RSC.
- M. Profeta, M. Benoit, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2004, 126, 12628–12635 CrossRef CAS PubMed.
- A. Sadoc, M. Biswal, M. Body, C. Legein, F. Boucher, D. Massiot and F. Fayon, Solid State Nucl. Magn. Reson., 2014, 59–60, 1–7 CrossRef CAS PubMed.
- R. Laskowski and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245117 CrossRef.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS.
- R. Laskowski, P. Blaha and F. Tran, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195130 CrossRef.
- A. P. Bartók and J. R. Yates, Phys. Rev. B, 2019, 99, 235103 CrossRef.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- M. Chen, H.-Y. Ko, R. C. Remsing, M. F. Calegari Andrade, B. Santra, Z. Sun, A. Selloni, R. Car, M. L. Klein, J. P. Perdew and X. Wu, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10846 CrossRef CAS.
- R. C. Remsing, M. L. Klein and J. Sun, Phys. Rev. B, 2017, 96, 831 CrossRef.
- G. S. Gautam and E. A. Carter, Phys. Rev. Mater., 2018, 2, 095401 CrossRef.
- A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 150, 161101 CrossRef PubMed.
- D. Mejía-Rodríguez and S. B. Trickey, J. Chem. Phys., 2019, 151, 207101 CrossRef.
- A. P. Bartók and J. R. Yates, J. Chem. Phys., 2019, 151, 207102 CrossRef.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Archive of magres files containing calculated magnetic shielding tensors. See DOI: https://doi.org/10.1039/d4fd00142g |
| This journal is © The Royal Society of Chemistry 2025 |