Concluding remarks: Faraday Discussion on NMR crystallography

Abstract

This Faraday Discussion explored the field of NMR crystallography, and considered recent developments in experimental and theoretical approaches, new advances in machine learning and in the generation and handling of large amounts of data. Applications to a wide range of disordered, amorphous and dynamic systems demonstrated the range and quality of information available from this approach and the challenges that are faced in exploiting automation and developing best practice. In these closing remarks I will reflect on the discussions on the current state of the art, questions about what we want from these studies, how accurate we need results to be, how we best generate models for complex materials and what machine learning approaches can offer. These remarks close with thoughts about the future direction of the field, who will be carrying out this type of research, how they might be doing it and what their focus will be, along with likely possible challenges and opportunities.

---

Introduction: where were we and where are we?

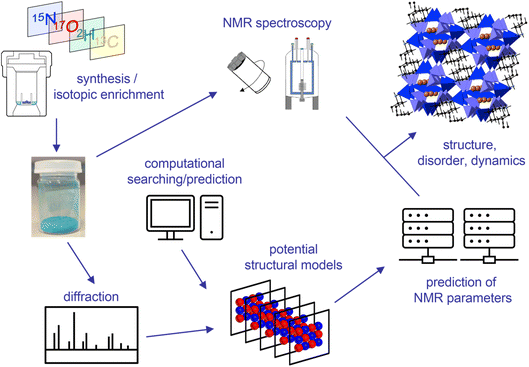
The structural characterisation of a solid is the first step in understanding the structure–property relationships that govern the application (and ultimately the design) of functional materials. Solid-state NMR spectroscopy, with its ability to provide element-specific measurements of the atomic-scale environment, has emerged as a key complementary tool to widely used diffraction-based approaches, particularly for materials that exhibit disorder or dynamics, providing insight in the study of energy materials, pharmaceuticals, biomolecules, porous solids, ceramics, polymers and glasses.^1,2 As outlined in the opening lecture of this Faraday Discussion, given by Lyndon Emsley (https://doi.org/10.1039/D4FD00151F), quantum-chemical calculations have long been used in NMR spectroscopy, although early work was focussed on molecular systems and liquid-state measurements.^3,4 The key challenge when applying these approaches to solids is the high level of accuracy required to capture the small changes in the NMR parameters that reveal the arrangement of atoms or molecules in three-dimensional space, enabling differentiation between very similar structural arrangements that ultimately may have different physical and chemical properties. The prediction of NMR parameters in the solid state was revolutionised in 2001 with the introduction of periodic planewave approaches based on Density Functional Theory (DFT), such as the gauge-including projector augmented wave (GIPAW⁵) approach, which exploited the inherent translational symmetry of an extended solid and avoided the need to approximate such systems as large molecules or clusters.

Early attention in this field focussed on evaluating the accuracy of the computational approaches used, comparing experimental measurements with calculated parameters for well characterised systems.^6–12 Calculations were used to confirm experimental results, particularly when there was some ambiguity or uncertainty involved, and to predict parameters that could be more difficult to measure, such as anisotropic shielding or quadrupolar coupling. In some cases, such predictions then guided the experimental measurements that were subsequently made.^6–12 The focus in most cases, however, was on the interpretation and assignment of the NMR spectrum itself, with NMR parameters usually predicted for one or two fairly simple models. Over the last two decades (and as highlighted by many of the papers presented at this Faraday Discussion), there has been a reversal of this process with NMR experiments and calculations used alongside each other, often with equal billing, to provide insight into the local structure, disorder, dynamics and chemical reactivity of a solid material.^6–12 A typical example of an “NMR crystallography” approach is summarised in Fig. 1, and shows the synthesis of the material of interest with isotopic enrichment where needed, and the acquisition of a range of multinuclear and multidimensional NMR spectra. A set of potential structural models are then generated, sometimes using automated searching methods, but perhaps more usually exploiting information from diffraction (either for the material itself or for related materials in the literature). The NMR parameters predicted (typically, but not exclusively, using DFT) can then be compared to experimental measurements to gain insight into the arrangement(s) of atoms and molecules that are of relevance in the material under study. It is clear from Fig. 1 that a typical NMR crystallographic study may involve the use of many different experimental and computational approaches, and a wide range of expertise is often required. This Faraday Discussion considered the current state-of-the-art in both experiment and computation, the challenges in integrating these successfully and the progress that would be needed to alleviate difficulties in the future (https://doi.org/10.1039/D4FD00079J, https://doi.org/10.1039/D4FD00106K, https://doi.org/10.1039/D4FD00123K, https://doi.org/10.1039/D4FD00114A, https://doi.org/10.1039/D4FD00072B, https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00075G, https://doi.org/10.1039/D4FD00128A, https://doi.org/10.1039/D4FD00142G). Papers discussed applications to materials including pharmaceuticals (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00088A, https://doi.org/10.1039/D4FD00089G, https://doi.org/10.1039/D4FD00097H), cellulose (https://doi.org/10.1039/D4FD00088A), energy materials (https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00074A), porous solids (https://doi.org/10.1039/D4FD00082J, https://doi.org/10.1039/D4FD00100A), glasses (https://doi.org/10.1039/D4FD00129J), hydrogels (https://doi.org/10.1039/D4FD00081A), biomaterials (https://doi.org/10.1039/D4FD00108G) and ceramics (https://doi.org/10.1039/D4FD00103F), demonstrating the range and the complexity of systems that can be studied and the new information they provide. This Faraday Discussion highlighted the potential of these techniques to provide structural and chemical insight, with atomic-level detail, into the materials that will shape our future.

Fig. 1 Schematic showing a typical NMR crystallography workflow.

Discussion: what do we want from these studies?

The ultimate aim of most applied NMR crystallography is to determine “the structure” of the material under study. For some solids this corresponds to a unique arrangement of atoms or molecules, which can conveniently be described by a set of crystallographic parameters (i.e., the size and shape of a unit cell, the symmetry elements present and the coordinates of unique atoms). This is often most easily visualised pictorially, enabling a rapid and easy assessment of how atoms are bonded/coordinated, and how molecules or structural units are joined on a longer lengthscale. It has been suggested that the human brain processes images much faster than text, and research shows that people are more likely to remember information presented in the form of pictures,^13,14 making this type of pictorial representation of structure a highly desirable output.

For disordered materials, however, multiple atomic and molecular arrangements may contribute. What is really meant by “the structure” for complex solids, and how do we best present the structural information obtained using NMR crystallography? The structure produced for disordered materials using Bragg diffraction is an average picture, averaged over both space and time.^15,16 Although this can remain a valuable approach, enabling a large volume of complicated information to be conveyed in a simple way, for materials exhibiting high levels and different types of disorder this quickly becomes a challenge. As an example, Fig. 2a shows the structural model for GaPO-34A (a new gallophosphate framework^17,19) determined using single-crystal X-ray diffraction. This looks a reasonable structure solution, with pores and channels that contain the methylimidazolium structure directing agent (SDA) and the addition of F⁻ and OH⁻ anions to the framework for charge balance. However, NMR crystallography reveals this is a highly disordered material,¹⁷ with 1/6 of the anion sites vacant, leading to subsequent variation in the position of the surrounding framework atoms. There is also F⁻/OH⁻ disorder across the remaining 5 anion sites, which is not captured in the model. There are three possible positions for the SDA (with refined occupancies of 50%, 33% and 17%), but the position of the N within the ring is not defined by diffraction, leading to two possible orientations in each case. However, ⁷¹Ga NMR spectra show evidence for microsecond timescale dynamics of the SDA, suggesting dynamic, rather than static, disorder. The structure shows only five- and six-coordinate Ga species, but the NMR spectrum reveals four-, five- and six-coordinate Ga is present (with intensity ratios of ∼2.5 : ∼1 : ∼2.5), suggesting there is also some fractional occupancy of the water attached to the framework. It could be argued that the picture in Fig. 2a is at best incomplete, but perhaps at worst is incorrect, inaccurate or misleading, raising the general question of when a pictorial representation of a structure, although highly desirable, is not sufficiently useful to be the final aim.

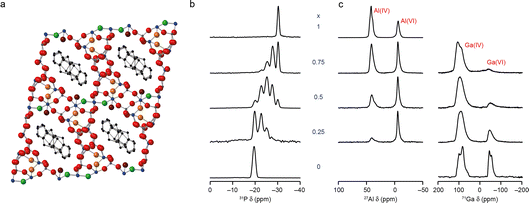Fig. 2 (a) Schematic showing the crystal structure of as-made GaPO-34A(mimHF), determined by single-crystal diffraction viewed down the a axis (blue = Ga, dark grey = P, black = C, green = F, red = O, maroon = O in H₂O and orange = O in OH). (b) ³¹P (20.0 T, 50 kHz) MAS NMR spectra of calcined Al_xGa_1−xPO₄-34 and (c) ²⁷Al (9.4 T, 14 kHz) and ⁷¹Ga (20.0 T, 55 kHz) MAS NMR spectra of as-made Al_xGa_1−xPO₄-34. Adapted from ref. 17 and 18 with permission.

NMR spectroscopy is sensitive to the local structure, with the isotropic chemical shift in particular determined by the number, type and arrangement of neighbouring and next nearest neighbouring atoms. For more complex structures there is the question, therefore, of whether it could be sufficient just to understand the local structure. As considered in the context of an amorphous drug (https://doi.org/10.1039/D4FD00078A) in this Faraday Discussion, if we can determine the detailed atomic-scale environment for different elements at different sites within the structure, do we really need to understand the long-range distribution of structural units or motifs? The answer to this question may well depend on the system under study and the application of interest, and whether this depends on the neighbouring environment or on more general bulk properties. It should also be noted that while such an approach may be the best (or the only) option for highly disordered or amorphous materials, probing only the local structure can in some cases obscure long-range ordering effects. As an example, in our recent work on new mixed-metal phosphate frameworks (or AlGaPOs),¹⁸ the ³¹P MAS NMR spectra of calcined AlGaPO-34 were consistent with a random distribution of the cations within the framework (as shown in Fig. 2b). However, in the as-made form of the material ²⁷Al, ⁷¹Ga MAS NMR spectra clearly showed a strong preference for Al and Ga to occupy the octahedral and tetrahedral sites, respectively (as shown in Fig. 2c), leading to long-range cation ordering to which the ³¹P NMR spectrum of the calcined material is not sensitive.

In many cases, multiple structural models may be of relevance to the material under study and the question of how to display this structural information clearly and concisely becomes even more challenging. For molecular systems, and as shown in this Faraday Discussion (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00078A), an ensemble of conformations and arrangements can often be superimposed in a useful pictorial representation, clearly showing the aspects of the structure that are retained or varied between models. It is perhaps much more challenging to see how this can be achieved for many inorganic systems, where hundreds (or even thousands) of possible atomic arrangements may be of interest, and that number of structural pictures would not be useful or easy to overlay or quickly interpret (https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00108G). A similar, but slightly different, problem is encountered for systems where the model can be extremely large (e.g., amorphous solids or glasses (https://doi.org/10.1039/D4FD00106K, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00129J)) or for those displaying considerable dynamic behaviour, where the local structure may differ over distance or in time (https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00082J, https://doi.org/10.1039/D4FD00108G, https://doi.org/10.1039/d4fd00103f). It may be useful to highlight specific local or long-range arrangements (i.e., those with particularly relevant ordering or clustering of atoms or interesting H-bonding motifs), and note the effect upon the NMR parameters of interest (https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00088A, https://doi.org/10.1039/D4FD00089G, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00108G). However, in such cases it can also be desirable to change the desired “output” of the study, and plot the variation in local geometric parameters, such as bond distances or torsion angles (https://doi.org/10.1039/D4FD00078A), that are present within a set of models, map the cation distribution (https://doi.org/10.1039/D4FD00106K), or simulate the experimental (diffraction, pdf or NMR) data that would result from an ensemble of structures (https://doi.org/10.1039/D4FD00106K, https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00082J, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J, https://doi.org/10.1039/D4FD00108G). Ultimately, the way that we can, or choose to, present the information obtained from NMR crystallographic studies will vary with the system considered and the problem being addressed, with bespoke solutions developed that can highlight the key information and insight that has been obtained.

Discussion: how accurate do we need to be?

The accuracy with which structures, conformations, relative energies and NMR parameters can be determined is intrinsically linked to the unambiguous identification of the correct structure from a set of possible models, or to good matches with experimental data (subsequently enabling insight into local structure, disorder or dynamics). Although there are a number of parameters and approximations that determine this accuracy and can provide potential sources of error if not chosen correctly, for DFT calculations the choice of the exchange–correlation functional is perhaps one of the most important. A widely used representation is the “Jacob’s ladder”²⁰ of functional classification, where ascending the ladder increases (in principle at least) the accuracy of the results obtained, bringing the researcher closer to the ultimate aim of the “heaven of chemical accuracy”. Building from the non-interacting Hartree world, rungs 1–3 are semi-local functionals, while higher rungs employ additional Hartree–Fock based contributions, leading to hybrid (rung 4) and double hybrid (rung 5) functionals. As discussed at the Faraday Discussion (https://doi.org/10.1039/D4FD00072B, https://doi.org/10.1039/D4FD00142G), including these additional terms is computationally expensive, particularly in the planewave formalism, and the most popular approaches for periodic calculations use GGA (rung 2) functionals (often Perdew–Burke–Ernzerhof (PBE)²¹), owing to their computational efficiency and accuracy across a wide range of systems.^6–12 These are often supplemented by the use of semi-empirical dispersion correction (SEDC) schemes to provide a better description of long-range interactions, often resulting in better agreement with experimental data from both diffraction and NMR spectroscopy.^6–12,22,23 The Faraday Discussion (https://doi.org/10.1039/D4FD00072B, https://doi.org/10.1039/D4FD00142G) considered possible approaches for ascending Jacob’s ladder, and improving the accuracy of the calculations used within a periodic approach (as opposed to e.g., cluster- or fragment-based methods that had previously been employed to allow the use of the more accurate functionals²⁴). The improvement in accuracy of the calculated isotropic chemical shift on moving to a meta GGA functional (rSCAN/r²SCAN), with only a small increase in computational cost (factor ∼1.25 to 2), was shown for a set of oxide and halide inorganic compounds (https://doi.org/10.1039/D4FD00142G), where the gradients of plots comparing experimental and computational data were significantly closer to the ideal value of 1. Other work explored if using hybrid functionals for geometry optimisation produced better agreement with experiment (https://doi.org/10.1039/D4FD00072B). It was shown (for ¹³C/¹⁵N NMR of molecular crystals) that the improvement when using hybrid functionals results primarily from that gained in the calculation of chemical shifts, rather than any significant improvement in the crystal geometry. However, and perhaps surprisingly, double-hybrid functionals gave little systematic improvement, highlighting the complexity of the area, and it was suggested that the most cost-effective approach may be the hybrid-level calculation of chemical shifts for structures optimised using GGA functionals.

Another barrier to moving up Jacob’s ladder is likely to be the transferability of the approaches developed, with many higher functionals requiring some empirical fitting. The aim is that the time and cost spent on the development, optimisation and testing of new functionals leads to improvements across a wide range of systems. It may be that this will be easier in organic systems, where despite the multitude of possible structures a more limited set of nuclei (e.g., H, C, N and O) and more similar local bonding are typically present. Inorganic materials are likely to present a greater practical and philosophical challenge, with a much wider range of nuclei present (some lighter and some much heavier), a greater variety of local environments, more varied chemical bonding, and in most cases relatively little experimental information available in the literature against which comparisons can be made.^1,2,6–8 Ultimately, these issues seem likely to limit the development of more sophisticated functionals for these systems, or the practical choices that can realistically be made when solving real-world problems.

Although perhaps the natural tendency of experimentalists is to question the accuracy of the theoretical approaches employed (and to use a match to the experimental data as the only measure of “success”), a legitimate question from a theorist concerns the accuracy, and particularly the reproducibility, of the experimental parameters that are measured. The ease with which values can be determined, and the errors to which they are subjected, depends not only on the parameter in question, but also on the nucleus for which measurements are made and the other interactions present within the system (including e.g., large ¹H/¹H dipolar couplings (https://doi.org/10.1039/D4FD00076E)).^1,2 Isotropic shielding is usually much easier to measure than the anisotropic shielding (where the number of spinning sidebands has a significant impact on the accuracy of the answer²⁵). However, for quadrupolar (I > 1/2) nuclei²⁶ the presence of the second-order quadrupolar broadening, the subsequent overlap of spectral signals and the more sophisticated experiments needed to obtain high resolution, typically results in more significant errors in every parameter (even those easy to measure for spin I = 1/2 nuclei). The presence of disorder and dynamics not only complicates the experimental analysis, but can, particularly in the case of the latter, lead to significant errors or completely incorrect values if these are not appropriately taken into account.^1,2 As considered in a number of sessions at this Faraday Discussion, experimental studies usually do a reasonable job of estimating the uncertainty associated with e.g., the fitting of an NMR spectrum (i.e., the precision of a measurement) and often also provide some insight into the repeatability of replicate analyses. However, many studies don’t attempt to quantify or discuss the absolute experimental errors and the reproducibility of results between duplicate experiments. How different will results be if they are acquired by different people, on different instruments, at different magnetic fields or with different MAS rates? How important is the control of temperature, the type/power of decoupling used, the quality of the shimming or even the choice of (secondary) reference material? While many experimentalists have an intuitive “feeling” for this under the stated conditions of the measurement, the meeting discussed the advantages of quantifying this more directly and more systematically, which may become increasingly important as more effort and cost is devoted to theoretical improvements.

In addition to difficulties associated with experimental NMR measurements and analysis, the synthesis of complex materials itself poses significant challenges. Small changes in the conditions of a reaction, the scale at which it is carried out, or even in something as simple as the exact glassware or autoclaves used, can lead to differences in the materials produced, as also demonstrated for a number of systems in the Faraday Discussion (https://doi.org/10.1039/D4FD00079J, https://doi.org/10.1039/D4FD00123K, https://doi.org/10.1039/D4FD00081A). For disordered/amorphous materials, it could be argued that these changes result in truly different materials, and that the variation in conditions provides a route to control the atomic arrangements and the corresponding material properties.^15,16 However, in other cases, attempts to reproduce the synthesis of a specific material can lead to solids that appear identical by many bulk characterisation techniques, but have different physical and chemical properties, resulting from differences in crystallite size and shape, surface structure or hydration level, or in the nature, level and distribution of defects or impurities. Understanding such structural detail is likely to become increasingly important in the future, with growing recognition of the importance of these effects in determining the properties and reactivity of a solid. NMR spectroscopy (through e.g., magnetisation transfer, selective isotopic enrichment and surface sensitive experiments) offers an ideal approach for providing such atomic-level detail,^1,2 and it is likely that the focus of related computational work will also shift towards this aspect in the future. Much greater detail will be required to describe the synthesis of a solid, exactly how it was post-synthetically treated and even how (and for how long) it was stored, for true controlled materials design to be achieved. The increasing interest in the repeatability and reproducibility of results, discussed in various sessions at the Faraday Discussion, is reflected in recent publications,^27–29 the ongoing drive for publication of open data and the growing numbers of community science initiatives to test synthetic and analytical approaches (e.g., ref. 30–32), and it now seems the time for the NMR crystallography community to also take on this challenge.

Discussion: how should we generate structural models?

One of the most challenging steps in the NMR crystallography workflow shown in Fig. 1, particularly for less experienced researchers, is the generation and identification of suitable structural models, which often requires more sophisticated computational approaches and specialist expertise. The aim is to generate models that are chemically and energetically relevant, with limited structural and chemical bias, in a cost-effective and time-efficient manner – a non-trivial task! For disordered and amorphous materials, models need to be sufficiently large and realistic to capture the key structural variations (and be representative, therefore, of the entire material), but need to exploit order where possible, ensuring calculations can remain tractable and solutions can perhaps be related to some type of simple chemical picture, as discussed above.

Even for well-ordered systems the generation of “good” models requires some choices to be made, e.g., around geometry optimisation when diffraction-based data is available. There are questions over whether to vary the position of all atoms or only of light atoms (e.g., ¹H, which may have simply been placed rather than refined), and whether to fix the experimentally determined unit cell parameters (as these are supposedly “known” values and may avoid the cell expansion that can often be seen with GGA-based functionals).^6–12 The decisions taken (as considered in the Faraday Discussion (https://doi.org/10.1039/D4FD00072B, https://doi.org/10.1039/D4FD00075G, https://doi.org/10.1039/D4FD00128A, https://doi.org/10.1039/D4FD00142G, https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00088A, https://doi.org/10.1039/D4FD00089G, https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00108G, https://doi.org/10.1039/D4FD00103F)) may depend on the type of system (i.e., whether a molecular or an extended solid and whether there is any structural flexibility, as in some porous solids^6,7), the type of functional used and the inclusion (or otherwise) of a SEDC scheme, as well as on the nature and quality of the diffraction measurements and the temperature at which these were made. The use of hybrid functionals for the optimisation of molecular solids was shown in the meeting to slightly reduce the bond length error distributions, although this gain was suggested not, perhaps, to justify the additional cost (https://doi.org/10.1039/D4FD00072B). Although different choices were made for different studies, it is clear that good geometry optimisation is intrinsically linked to the prediction of accurate NMR parameters. As an example, Fig. 3 shows ⁸⁹Y MAS NMR spectra simulated using the NMR parameters calculated using DFT for an ensemble of structural models of a Y₂Sn_xTi_2−xO₇ ceramic with varying atomic arrangements.^33,34 In Fig. 3a, the 279 models were optimised with the VASP code (PBE+U, E_cut = 520 eV, k-sampling of the gamma point) prior to NMR calculations carried out using CASTEP. In Fig. 3b, the models were further optimised using CASTEP (PBE, E_cut = 816 eV, k-point spacing = 0.04 2π Å⁻¹) prior to the calculation of the NMR parameters. The two approaches have resulted in quite different ⁸⁹Y MAS NMR spectra; those in Fig. 3a appearing more idealised (as can be seen from the deconvolution in Fig. 3d), while those in Fig. 3b show more complex, overlapped lineshapes, with a wider range of isotropic chemical shifts for the same type of local environment, but are in better agreement with the experimental lineshape.^33,34

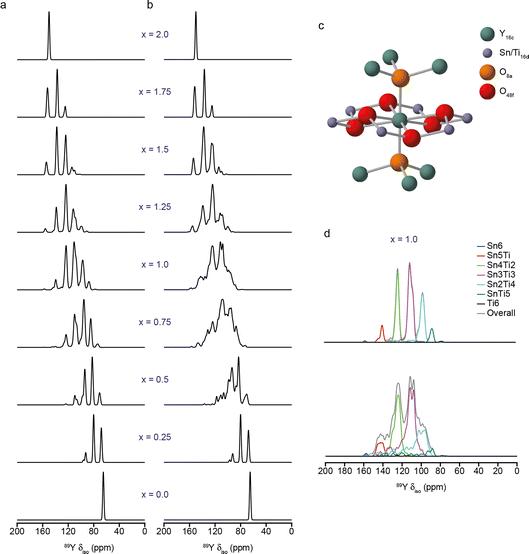Fig. 3 (a and b) Simulated (using DFT-calculated parameters) ⁸⁹Y MAS NMR of models of Y₂Sn_xTi_2−xO₇ with varying atomic arrangements. In (a), models were optimised using VASP (PBE+U, E_cut = 520 eV, k-sampling of the gamma point), while in (b) a second optimisation using CASTEP (PBE, E_cut = 816 eV, k-point spacing = 0.04 2π Å⁻¹) was employed prior to the calculation of the NMR parameters. (c) Schematic showing the local structure around the pyrochlore A (16c) site, including six next nearest neighbour B (16d) sites that may be occupied by Sn or Ti. (d) Deconvolution of simulated spectra from (a) and (b) for x = 1, showing the contributions from species with different numbers of Sn and Ti next nearest neighbours. Adapted from ref. 33 and 34.

As materials become more complex, the computational challenge increases, and one approach to ensuring this remains feasible on a reasonable timescale with reasonable computational resources is to simplify the models used, restricting the focus to the local environment and the impact that such changes have on the NMR parameters. For molecular solids this could involve considering only a single molecule or small cluster of molecules. For extended systems an “embedded cluster” approach is often used, where the periodic nature of the system is maintained (avoiding the breaking and termination of dangling bonds) and only the type or position of the neighbouring or next nearest neighbouring atoms are varied. These are clearly cost-efficient and simple options, but only consider a limited chemical and structural space (retaining significant bias in the final models). They have, however, been shown to be particularly useful for the assignment of spectral signals where changes in the local structure have the greatest effect, but provide less insight into “the structure” of a complex material as a whole.^6–12

If the effect of long-range changes on the NMR parameters are required, if energetics and thermodynamic parameters are to be calculated, or if less is known about the structure, multiple structural models will need to be generated. Papers in the Faraday Discussion exploited a number of ways to do this, including generating a simple subset of possible models by swapping the nature or positions of atoms (https://doi.org/10.1039/D4FD00072B, https://doi.org/10.1039/D4FD00077C, https://doi.org/10.1039/D4FD00103F). It may, however, be preferable to consider generating (as in the example above in Fig. 3) a complete set of unique atomic configurations (so-called ensemble modelling) using automated codes such as Site Occupancy Disorder (SOD) or Supercell,^35,36 within a unit cell or supercell, proving greater structural variation. The ability of these methods to provide information on the relative energies and configurational entropies of all models also allows the determination of thermodynamic parameters, the simulation of complete NMR spectra and their variation with temperature.

If less is known about the possible structure one option is to use crystal structure prediction (CSP) techniques.^37–39 As shown in the Faraday Discussion (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00089G) this has been particularly successful for molecular solids (e.g., pharmaceuticals, drugs and solvates), where the chemical connectivity is fully (or almost fully) known but the conformation and packing is undetermined. For extended (typically inorganic) solids complete randomisation of the atomic positions is usually unfeasible, but efficiency can be improved by fixing the absolute or relative positions of atoms or groups that are unambiguously determined, or by constraining exactly where substitutions can be made. Although this clearly increases bias, the compromise with computational cost is usually necessary. There is also (as shown in this Faraday Discussion (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J, https://doi.org/10.1039/D4FD00108G)) an increasing use of molecular dynamics (MD) to generate structural models particularly for systems that lack significant long-range order, such as glasses, although the differences in glass models predicted using classical MD and ab initio MD was noted (https://doi.org/10.1039/D4FD00129J). The use of MD enables the rapid generation of large sets of potential structures for which NMR parameters can be predicted, NMR spectra can be simulated and/or correlations between different parameters (e.g., C_Q and δ_iso) or between one parameter and the local geometry can be determined (https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00129J).

When compared to the simpler models discussed above, it is clear that more sophisticated approaches explore a greater range of chemical and structural space, with less (or at least more controllable) bias, but that they can be costly, with time and effort expended on parameter space that is simply not relevant for the material of interest. When the “the best model” or “the best set of models” needs to be established there is also the question of how these can be chosen or how their probability of being correct/present is determined. A number of papers (https://doi.org/10.1039/D4FD00106K, https://doi.org/10.1039/D4FD00114A, https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00089G, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J) presented in the Faraday Discussion discussed ways in which this can be achieved, from simply ranking on the basis of energies, measuring the match to experimental data (from diffraction or spectroscopy), or considering how frequently structural motifs are generated. For any comparison to experiment it is necessary (i) to have an unambiguous spectral assignment and (ii) to define a benchmark against which “good/likely” or “bad/unlikely” models can be evaluated. In the first case, this can be achieved by minimising specific errors between calculated and experimental parameters, creating probability maps using multiple nuclei, or exploiting a range of more complex two-dimensional experiments that can confirm (or disprove) more tentative suggestions (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00088A, https://doi.org/10.1039/D4FD00089G, https://doi.org/10.1039/D4FD00097H). These approaches have been shown to work well for molecular solids (using ¹³C NMR and, more recently, ¹H NMR (https://doi.org/10.1039/D4FD00076E)), but a range of practical and philosophical challenges remain for the vast range of inorganic materials, with a single protocol likely to remain largely unfeasible. When defining a benchmark for comparison to experimental data, the simplest approach is to compare the RMSE for an entire structure to the expected uncertainties of experimental data (determined for a set of related of model compounds (https://doi.org/10.1039/D4FD00151F)). However, work at the Faraday Discussion also described more formal measures of confidence, using a range of approaches based on Bayes analysis (https://doi.org/10.1039/D4FD00106K, https://doi.org/10.1039/D4FD00114A, https://doi.org/10.1039/D4FD00151F).

Additional challenges are present when generating models to provide insight into dynamics, and the effect that this has on the NMR spectrum. These challenges vary with the nature of the species moving, and the type and timescale of the motion. The approach used for model generation will also depend on what is already known, or can be reasonably assumed, about the structure. The advantages of different approaches were discussed (https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00082J, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00108G), including the use of MD to predict rapid motion directly, manual modification of atomic positions in a series of static calculations to model slower motions and mesoscopic modelling of long-range diffusion. The use of machine learned potentials in MD (see below) also allowed motion on longer (microsecond) timescales to be studied (https://doi.org/10.1039/D4FD00074A). The effect of any dynamics on the NMR spectrum will depend not just on the motion itself (and the variation in the NMR parameters in which it results) but on its relation to the NMR timescale, which is determined by the nucleus studied, the interactions that affect the lineshape seen and the magnetic field at which measurements are made. As an example, Fig. 4 shows the predicted effect of ¹H motion on two different types of high-resolution ¹⁷O NMR spectra of clinohumite (a magnesium silicate mineral of relevance to water storage in the inner Earth).⁴⁰ The same microsecond timescale exchange between H1 and H2 has different effects on the ¹⁷O spectrum acquired using MQMAS in Fig. 4b (where the motion is “fast” compared to the millisecond timescale to which second-order quadrupolar broadening is sensitive, and so complete averaging of the NMR parameters is seen), and on that acquired using STMAS (where the motion is now on the “intermediate” timescale owing to the presence of first-order quadrupolar broadening in the satellite transitions, and leads to differential line broadening for different sites).⁴⁰ A number of papers in the Faraday Discussion (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00100A) also demonstrated the use of MD ensembles to model vibrational averaging on the spectrum.

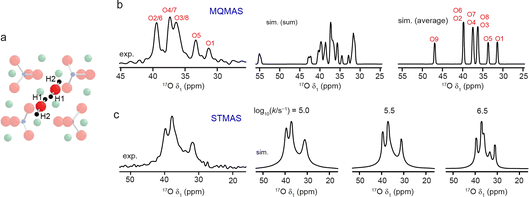Fig. 4 (a) Schematic showing H1 and H2 positions in clinohumite (each of which is 50% occupied). (b) Experimental ¹⁷O (9.4 T, 8 kHz) isotropic MQMAS NMR spectrum of clinohumite, along with spectra (simulated using DFT-calculated parameters) assuming no dynamics (summed) and fast dynamics (averaged). (c) Experimental ¹⁷O (9.4 T, 8 kHz) isotropic STMAS NMR spectrum of clinohumite, along with spectra simulated (using the DFT-calculated parameters) assuming ¹H exchange between H1 and H2 with the rate constants shown. Adapted from ref. 40.

Although a number of innovative and sophisticated approaches have been demonstrated to tackle the challenges of generating a sufficient number of structural models of good quality and relevance, for the less experienced researcher this step in the NMR crystallographic process can often be a bottleneck, limiting the progress that can be made and the timescale on which it is achieved. Considering how best to address this problem, for both experienced and less specialist users, will have to be a future focus for the community.

Discussion: is machine learning the future?

The recent rise of artificial intelligence has sparked significant interest in both the scientific community and the popular media, with this new technology apparently having the potential to simultaneously save and doom humanity. In the physical and life sciences the potential of machine learning (ML) to transform the way in which large amounts of data are generated, handled and analysed, and to automate experimental and computational work, promises a step change for materials discovery and characterisation.^41,42 In this Faraday Discussion a number of papers described the use of ML in various steps of the NMR crystallography process shown in Fig. 1, exploring its advantages and limitations, and exploiting its benefits for specific applications (https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00128A, https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J).

The use of ML to calculate interaction tensors, thereby bypassing costly and lengthy quantum-chemical calculations, was demonstrated in the Faraday Discussion for the study of crystalline and amorphous pharmaceuticals (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H), energy materials (https://doi.org/10.1039/D4FD00074A), oxides (https://doi.org/10.1039/D4FD00128A), zeolites (https://doi.org/10.1039/D4FD00100A) and glasses (https://doi.org/10.1039/D4FD00129J), with accuracies at a similar level to DFT. As for most ML applications, debate continues over the necessary size and quality of the training dataset. For solution-phase NMR spectroscopy, ML models can be trained on large experimental databases, allowing direct and rapid prediction of experimental parameters. However, in solids no sufficiently large experimental resources exist, and ML models are instead trained on databases built using DFT methods. A number of papers in the Faraday Discussion exploited ShiftML/ShiftML2 (databases of calculated chemical shifts for molecular solids, trained on DFT data for structures from the Cambridge Structural Database),⁴³ incorporating this into an automated and transferable workflow for the study of pharmaceuticals (https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00076E, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H). However, for the inorganic systems studied bespoke training was carried out (https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00128A, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J), using DFT calculations on a smaller set of related model systems, before the ML potentials were applied to a larger set of structures, in many cases generated using MD.

Although good agreement with the DFT-generated training data was seen in the work described above, enabling rapid consideration of a much larger set of structural models, there remains the questions of how accurate we need results to be (with training on DFT-generated data only ever being as good as the underlying DFT methods, as discussed above) and how well environments that are less closely related to the training data can be predicted. The scope of any training data may well be fairly opaque to an end user, and the uncertainty associated with a prediction (or its variability between different environments) may not be clear. The importance of the precision of a prediction will likely vary with the problem in question, i.e., whether a conclusion relies on extremely small or absolute differences in NMR parameters that need to be accurately assessed (in which case higher-level DFT calculations on a small number of models may be preferred), or whether a significantly larger amount of information on multiple structural models is of more use (even if the uncertainty associated with each is greater). The general transferability of any ML learned model also remains a question, particularly for inorganic solids where greater structural and chemical variation is common. DFT calculations often have known inaccuracies or challenges for particular nuclei or when particular nuclei are present, making it less clear whether a model trained on a series of simple compounds from a database can be applied to a complex, disordered material which may contain elements, environments and defect motifs that are well outside of the scope of the training data.

As the availability of data (and the accuracy of DFT methods) increases such problems and concerns may diminish, although the ultimate dream would perhaps be to be able to train ML models directly on experimental data, thereby bypassing the challenges and inaccuracies of DFT calculations altogether. However, the community may also need to give some thought to the creation and curation of such external databases – who can deposit data? Is the quality of that data checked? Is metadata required to describe the choices made (e.g., in the codes used, functionals, dispersion corrections or the parameters for a geometry optimisation)? Is a bigger database with a more varied set of structures generated by different approaches better than multiple databases with more internally consistent but much smaller sets of data? Does an end user need to see the database content at any point or just use the resulting ML model? Can researchers choose to include/exclude particular data from any models developed? The sharing and combining of data (be it computational or even in the future experimental) generates interesting and important questions about responsible research, ethics, the transparency of research and its reproducibility that have not yet received the more formal consideration that is likely to be required in the future.

Whatever the concerns, barriers or challenges, it is clear that ML prediction of interaction tensors has the ability to save considerable amounts of time, and in some cases transform the science that can be carried out. A significantly larger number of models can be considered for structure solution or when modelling disorder, and much larger systems can be studied much more rapidly than when using DFT calculations. Even for more challenging inorganic systems (where questions of training data scope and transferability are perhaps more pertinent) the ability to actively learn on part of an ensemble of structures generated for a particular application may still lead to transformative time savings, even for a bespoke study.

It was also clear from this Faraday Discussion that the use of ML to generate potentials that can be used in MD (https://doi.org/10.1039/D4FD00074A, https://doi.org/10.1039/D4FD00151F, https://doi.org/10.1039/D4FD00078A, https://doi.org/10.1039/D4FD00097H, https://doi.org/10.1039/D4FD00100A, https://doi.org/10.1039/D4FD00129J) may lead to a step change in the timescales that can be routinely probed using this approach, coming closer to the microsecond and millisecond timescales that are often of interest to experimentalists. These potentials will also enable much larger systems to be studied using MD (of particular interest for more disordered or amorphous materials) and will enable multiple runs to be carried out, thereby giving a much better insight into the effects of temperature. Given the use of MD, as described above, to not only follow dynamics directly but to generate a wider range of less biased structural models, there will be additional advantages and benefits in this area too, enabling multiple, larger and more complete sets of models/conformations to be generated, and a wider range of defect/intermediate structures to be considered. The effects of including vibrational averaging when determining parameters or in spectral simulations may also become much more routine.

Whatever your views, worries or concerns about artificial intelligence more generally, ML is the most significant change that NMR crystallography has seen in the last two decades. It remains to be seen how big a difference it will make, e.g., where it will be used routinely, where it will make the biggest impact and how it will be affected by coming developments, but it will undoubtedly play an important role in the future of the field.

Conclusions: where are we going?

It is clear from this Faraday Discussion that it is an exciting time for the field of NMR crystallography, with rapid progress made in many areas over the last few years. Although the meeting discussed recent experimental and theoretical advances, the breadth and complexity of the systems to which these techniques were applied suggests that the audience for this set of papers will not just be specialist practitioners, but researchers across the physical, chemical, materials and life sciences with problems regarding structure or reactivity to solve. When considering the answers to some of the questions posed above, therefore, we need to consider what this wider audience need or would like to have, what they want to know, how they would like answers presented, how quickly they need results and how accurate they need these to be. We need also to think about how we as a community will work with a wider and more diverse set of researchers in the future. Modern scientific research is often carried out using a “team science” approach,^44,45 bringing together multiple researchers with specialist expertise to address a problem from different perspectives using complementary methods. However, we may also want to broaden and widen our field, enabling researchers in other fields to become “NMR crystallographers” themselves and employ some or all of the workflow in Fig. 1 in their own work. The future for these two routes may well look different, with more specialist and bespoke solutions providing defined contributions to a larger project required in the first, while the second will need the development of more general and robust methods, perhaps with higher levels of automation, easy-to-use interfaces/programs and freely available tools designed to organise, analyse and visualise large amounts of data without assuming individuals have the specialist knowledge (or indeed to the time to dedicate) to develop these themselves. In either approach, however, the community will need to consider how new developments are communicated or incorporated, how best practice can be shared and how data can be made more widely available.

What will we be doing in this future research? While there will always be a place for using computation to interpret and assign complex NMR spectra, for applying NMR crystallographic approaches to characterise existing materials, and for experimental measurement of disorder, dynamics and reactivity, the future may well demand more focus on predictive approaches. It is likely this will involve predicting not only the most likely or viable structures, but also predicting the properties of materials with different atomic arrangements or disorder, providing key insights that, after subsequent experimental investigation, will help address the structure–property–application relationship which underpins the design (rather than simply the characterisation) of future functional materials which are both efficient and sustainable. The detailed insight NMR crystallography can provide into both the local and average structure has the potential to ensure it is a key contributor to this difficult, but increasingly necessary, aim.

There will, of course, be significant, ongoing and new challenges to address, including the drive for greater accuracy, the study of larger systems and studies over longer timescales, although we have seen in this Faraday Discussion ways in which we might begin to tackle some of these. The increasing drive for automation and the growing need to combine information from multiple experimental techniques will lead both to challenges and to new opportunities. The ability to calculate (with good accuracy) chemical shielding, quadrupolar and J coupling tensors is now standard within a periodic approach, but paramagnetic interactions still pose problems. While solutions can be found to predict these on a case-by-case basis particularly in molecular systems (see e.g., (https://doi.org/10.1039/D4FD00077C) and ref. 46–48), implementing this routinely within a periodic framework is non-trivial. There is also likely to be a move away from simply characterising bulk structure in the future, with growing recognition of the roles that the surface structure, grain boundaries and interfaces, and the type, level and distribution of defects play in determining the properties (and reactivity) of a solid. The sensitivity of NMR spectroscopy to local structure, and the ability to selectively study individual atoms, surfaces or components of a system using techniques including isotopic enrichment, magnetisation transfer or dynamic nuclear polarisation,¹ will make this an increasingly popular approach when atomic-level insight is vital. There is growing interest in following reactions and syntheses experimentally, as was reflected in the in situ and operando NMR experiments shown in this Faraday Discussion (https://doi.org/10.1039/D4FD00079J, https://doi.org/10.1039/D4FD00077C), and it seems likely that computational approaches will also need to expand further in this direction. This may be by direct modelling of synthesis or chemical reactions (if sufficient accuracy, timescales and time resolution is possible) or through rapid and easy generation of models to allow the defects, intermediates and metastable species present in the materials and reactions studied experimentally to be identified. Sharing of best practice and new advances is key to the development and impact of the field, but this Faraday Discussion has highlighted the range of systems studied and problems addressed, showing that any “one size fits all” automated approach is still a while away and might never be feasible for all systems. However, it is abundantly clear that NMR crystallography has an enormous amount to offer in tackling the scientific, societal, health and industrial challenges that the world faces and will play a key role in future scientific research.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. B. Reif, S. E. Ashbrook, L. Emsley and M. Hong, Nat. Rev. Methods Primers, 2021, 1, 2.
2. R. F. Moran, D. M. Dawson and S. E. Ashbrook, Int. Rev. Phys. Chem., 2017, 36, 39–115.
3. J. C. Facelli, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 58, 176–201.
4. Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Buehl and V. G. Malkin, Wiley-VCH, Weinheim, 2004.
5. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
6. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates and F. Mauri, Chem. Rev., 2012, 112, 5733–5779.
7. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204.
8. D. L. Bryce, IUCrJ, 2017, 4, 350–359.
9. T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20.
10. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
11. S. A. Southern and D. L. Bryce, Annu. Rep. NMR Spectrosc., 2021, 102, 1–80.
12. Modern NMR Crystallography: Concepts and Applications, ed. D. Bryce, New Developments in NMR Book Series, Royal Society of Chemistry, 2024, in press.
13. A. Yadav, M. M. Phillips, M. A. Lundeberg, M. J. Koehler, K. Hilden and K. H. Dirkin, J. Comput. High Educ., 2011, 23, 15–37.
14. A. Paivio and K. Caspo, Cogn. Psychol., 1973, 5, 176–206.
15. A. Simonov and A. L. Goodwin, Nat. Rev. Chem., 2020, 4, 657–673.
16. A. L. Goodwin, Nat. Commun., 2019, 10, 10–13.
17. S. E. Ashbrook, D. M. Dawson, Z. Gan, J. E. Hooper, I. Hung, L. E. Macfarlane, D. McKay, L. K. McLeod and R. I. Walton, Inorg. Chem., 2020, 59, 11616–11626.
18. L. K. Broom, G. J. Clarkson, N. Guillou, J. E. Hooper, D. M. Dawson, C. C. Tang, S. E. Ashbrook and R. I. Walton, Dalton Trans., 2017, 46, 16895–16904.
19. D. M. Dawson, J. A. Clayton, T. H. D. Marshall, N. Guillou, R. I. Walton and S. E. Ashbrook, Chem. Sci., 2024, 15, 4374–4385.
20. J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
22. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
23. S. Sneddon, D. M. Dawson, C. J. Pickard and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2014, 16, 2660–2673.
24. J. D. Hartman, S. Monaco, B. Schatschneider and G. J. O. Beran, J. Chem. Phys., 2015, 143, 102809.
25. P. Hodgkinson and L. Emsley, J. Chem. Phys., 1997, 107, 4808–4816.
26. S. Sneddon and S. E. Ashbrook, J. Am. Chem. Soc., 2014, 136, 15440–15456.
27. R. Ciriminna, G. Angellotti, G. Li Petri and M. Pagliaro, Heliyon, 2024, 10, e33658.
28. M. Baker, Nature, 2016, 533, 452–454.
29. R. G. Bergman and R. L. Danheiser, Angew. Chem., 2016, 128, 12736–12737.
30. H. L. B. Boström, S. Emmerling, F. Heck, C. Koschnick, A. J. Jones, M. J. Cliffe, R. Al Natour, M. Bonneau, V. Guillerm, O. Shekhah, M. Eddaoudi, J. Lopez-Cabrelles, S. Furukawa, M. Romero-Angel, C. Martí-Gastaldo, M. Yan, A. J. Morris, I. Romero-Muñiz, Y. Xiong, A. E. Platero-Prats, J. Roth, W. L. Queen, K. S. Mertin, D. E. Schier, N. R. Champness, H. H.-M. Yeung and B. V. Lotsch, Adv. Mater., 2023, 15, 2304832.
31. J. W. M. Osterrieth, et al. , Adv. Mater., 2022, 34, 2201502.
32. IZA Synthesis Commission, http://www.iza-online.org/synthesis/default.htm.
33. R. F. Moran, PhD thesis, University of St Andrews, 2019.
34. R. F. Moran, D. McKay, P. C. Tornstrom, A. Aziz, A. Fernandes, R. Grau-Crespo and S. E. Ashbrook, J. Am. Chem. Soc., 2019, 141, 17838–17846.
35. R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. De Leeuw, J. Phys.: Condens.Matter, 2007, 19, 256201.
36. K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminf., 2016, 8, 17.
37. S. M. Woodley, G. M. Day and R. Catlow, Philos. Trans. R. Soc., A, 2020, 378, 20190600.
38. C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
39. G. J. O. Beran, Chem. Sci., 2023, 14, 13290–13312.
40. J. M. Griffin, S. Wimperis, A. J. Berry, C. J. Pickard and S. E. Ashbrook, J. Phys. Chem. C, 2009, 113, 465–471.
41. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Muller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
42. J. Liu and J. E. Hein, Nat. Synth., 2023, 2, 464–466.
43. M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter, M. Ceriotti and L. Emsley, J. Phys. Chem. C, 2022, 126, 16710–16720.
44. G. R. Lotrecchiano, L. M. Bennett and Y. Vovides, Hum. Soc. Sci. Commun., 2023, 10, 810.
45. H. B. Love, B. K. Fosdick, J. E. Cross, M. Suter, D. Egan, E. Tofany and E. R. Fisher, Hum. Soc. Sci. Commun., 2022, 9, 371.
46. A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271.
47. D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Chem. Mater., 2013, 25, 1723–1734.
48. Z. Ke, D. M. Dawson, S. E. Ashbrook and M. Buehl, Chem. Sci., 2022, 13, 2674–2685.

---