Concluding remarks: Faraday Discussion on data-driven discovery in the chemical sciences

Abstract

This Faraday Discussion was the first to focus on the increasingly central role of big data, machine learning, and artificial intelligence in the chemical sciences. The aim was to critically discuss these topics, and to explore the question of how data can enable new discoveries in chemistry, both now and in the future. The programme spanned computational and experimental work, and encompassed emerging topics such as natural language processing, machine-learned potentials, optimization strategies, and robotics and self-driving laboratories. Here I provide some brief introductory comments on the history of this field, along with some personal views on the discussion topics covered, concluding with three future challenges for this area.

---

1. A (very) brief history of data-driven discovery in the chemical sciences

It is difficult to write a coherent history of data-driven discovery in the chemical sciences. In a sense, all discoveries are “data-driven”—Archimedes would have subscribed to this—but the specific focus of this Faraday Discussion was the role of big data, machine learning, and artificial intelligence (AI). Even this narrower definition of data-driven discovery resists a single, definitive history: like rivers, few ideas have a single source. However, there are some antecedents to these modern methods that are worth mentioning. This short discussion is by no means comprehensive.

In organic chemistry, the Hammett equation¹ relates reaction rates and equilibrium constants to simple substituent and reaction rate parameters. This is an early example of a data-driven framework that was an important precursor to later regression models, such as quantitative structure–activity relationship (QSAR)² and quantitative structure–property relationship (QSPR)³ approaches. It also heralded the development of more advanced and generalisable molecular descriptors,^4,5 which are a key enabler for the chemical sciences, and were much discussed at this meeting.

Recently, the production of large amounts of computational data to drive discovery has outpaced our ability to acquire large experimental datasets in the chemical sciences, even though the automation of experimental chemistry is an older topic. The concept of laboratory automation goes back to at least 1875,⁶ and it has been widely adopted in the pharmaceutical industry.^7,8 However, like data-driven computational studies, chemistry automation has undergone a revolution recently with the creation of self-driving laboratories and closed-loop autonomous experiments. A unifying theme between data-driven computational and experimental discovery strategies is the advent of machine learning and AI. It is an exciting time to be working in this fast-moving area. Indeed, I am writing these concluding remarks just after the award of the 2024 Nobel Prize in Chemistry to David Baker, Demis Hassabis and John Jumper for computational protein design⁹ and protein structure prediction,^10,11 an accomplishment that was driven by computation, well-curated experimental ‘big data’, and AI.

2. Data-driven discovery, 2024

2.1. Spiers Memorial Lecture

The meeting was opened by Alan Aspuru-Guzik, who gave the Spiers Memorial Lecture (https://doi.org/10.1039/d4fd00153b). He gave a broad and rousing talk, covering functional taxonomies for machine leaning (ML) in chemistry, generative models and inverse design, and robotics. An overarching hierarchy for ML in chemistry was suggested, starting with data (Fig. 1). ‘Data’ was exemplified by a project involving asynchronous cloud-based delocalized closed-loop discovery, where multiple groups worldwide collaborated to discovery high-performing organic laser emitters, synchronized by a central AI entity.¹² ‘Representation’ was exemplified by self-referencing embedded strings (SELFIES),¹³ along with a warning about a potential ‘bitter lesson’ in this field; that is, the risk of embedding knowledge into AI approaches, only to be quickly superseded by more generalized, scaled computational methods. Large language models were given as an example. ‘Evaluation’, meaning benchmarking, was exemplified with the Tartarus benchmarking platform,¹⁴ with specific examples in organic light emitting diode (OLED) research. The lecture concluded with the question of whether it is possible to produce a robot-embodied ‘AI scientist’, with the example of the Organa platform developed recently in Toronto.¹⁵ This lecture set a great scene for what turned out to be a fantastic meeting.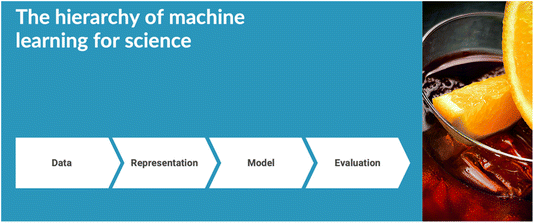

Fig. 1 Hierarchy of machine learning for science, as suggested by Alán Aspuru-Guzik. Watch out for the “bitter lesson”!

2.2. Session 1: discovering chemical structure

This session comprised six papers spanning inorganic and organic systems, and “chemical structure” encompassed both molecules and extended crystalline solids, with a strong flavour of crystal structure prediction. The session was chaired by Graeme Day and Janine George.

Chris Pickard opened the session with a discussion of ‘hot random search and datum-derived structures’, focussing on ab initio random searching (AIRSS). His paper (https://doi.org/10.1039/d4fd00134f) showed how long computational anneals—performed between direct structural relaxation and enabled by ephemeral data-derived potentials (EDDPs)¹⁶—can be incorporated into AIRSS to bias the sampling of challenging systems towards low-energy configurations. This method can tackle solid-state crystals with varying levels of complexity, ranging from molecular H₂ and NH₃, up to ionic lattices such as Mg₂IrH₆, and pyrope garnet structures (Fig. 2). These first-principles, theory-driven, random structure searching methods can identify novel arrangements of matter and inspire new experimental science, and surprisingly complex structures can emerge from small groups of atomic building blocks. An exciting enabler for these computationally demanding methods is the rise of EDDPs and other machine-learned interatomic potentials (MLIPs), which can massively accelerate traditional structure searches.

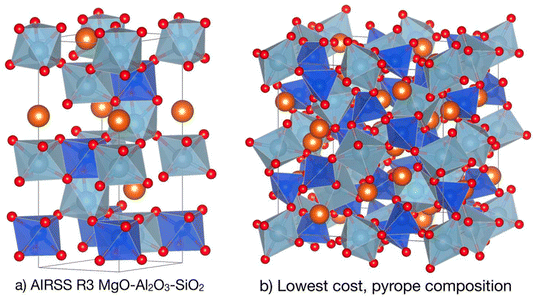Fig. 2 Generation of pyrope garnet structure. (a) The conventional cell of the R3 symmetry AIRSS-generated structure for a single formula unit of MgO–Al₂O₃–SiO₂ at 10 GPa. (b) The lowest predicted cost structure in the pyrope Mg₃Al₂(SiO₄)₃ composition, which is identical to the experimental 180-atom conventional cell garnet structure. Reproduced from https://doi.org/10.1039/d4fd00134f.

The next paper was by Chris Collins, who described the integration of machine learning with the heuristic crystal structure prediction code, FUSE¹⁷ (https://doi.org/10.1039/d4fd00094c). This work used a generative machine-learning model to produce the starting population of crystal structures for a heuristic algorithm, as demonstrated in the paper with eight known compounds with reported crystal structures (Fig. 3) and three hypothetical compounds. When comparing only the structure generators, the mean speedup across the whole suite of tests is a factor of 2.2 times faster with generative methods, albeit with slowdown in some cases. This occurs when the generative models create a population of starting structures that is far from the density functional theory (DFT) local minimum.

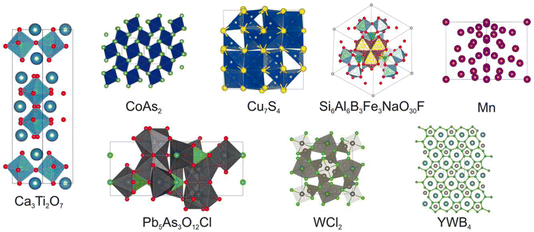Fig. 3 The reported crystal structures of the eight known compounds tested in https://doi.org/10.1039/d4fd00094c.

Next, Brett Savoie discussed “large property models” (LPMs) as a new generative machine-learning formulation for molecules (https://doi.org/10.1039/d4fd00113c). This ‘inverse design’ approach (Fig. 4, left) used a set of 1.3 M molecules taken from Pubchem, for which a range of properties was computed, such as dipole moment, total enthalpy, HOMO–LUMO gap, and other properties. For the purposes of this evaluation, these computed properties were taken as the ground truth labels. A multimodal transformer architecture was designed and implemented for this property-to-graph inverse design problem. The graph decoder was constructed as a next-token SMILES predictor that begins with a “start” token, and the decoding occurs recursively until the decoder predicts an “end” token or the decoded string reaches the maximum length.

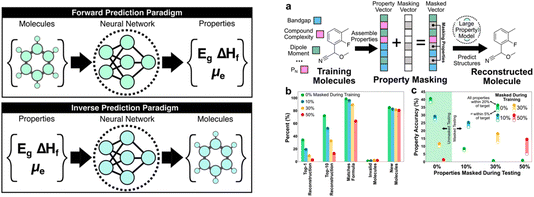Fig. 4 Comparison of forward and inverse prediction paradigms (left) and a property masking case study (right), reproduced from https://doi.org/10.1039/d4fd00113c.

Initial experiments with LPMs suggest that the property-to-molecular-structure mapping becomes directly learnable using a relatively low-dimensional property space, although several questions remain, such as transferability of LPMs to data-scarce or other unseen properties. Related studies have fine-tuned LLMs, such as GPT-3, using large structure/computed property datasets in a forward-predictive fashion.¹⁸

Venkat Kapil described the data-efficient fine-tuning of foundational models for first-principles thermodynamic property predictions (https://doi.org/10.1039/d4fd00107a). This is a challenging area, because reliable predictions require a tolerance of 4.2 kJ mol⁻¹ for absolute sublimation enthalpies and an even tighter tolerance of less than 1 kJ mol⁻¹ for relative sublimation enthalpies, and the computational cost is high. In this context, machine-learning potentials—here, the multi-atomic cluster expansion (MACE) architecture¹⁹—provide an avenue for first principles accuracy modelling of molecular crystals at finite temperature. Training a MACE model by fine-tuning the parameters of the pre-trained MACE-MP-0 model, as opposed to training it from scratch, resulted in improved accuracy and data efficiency. Only 50 to 100 training structures sampled for a given T, P condition were needed to achieve sub-kJ mol⁻¹ and sub 1% agreement on the average energy and density, respectively, against a reference DFT NPT ensemble. The authors suggest future developments to increase data efficiency to apply these methods to more complex molecular crystals, or compounds with multiple polymorphs.

Next, Takuya Taniguchi gave a paper on knowledge distillation of neural network potentials (NNPs) for molecular crystals (https://doi.org/10.1039/d4fd00090k). The study investigated strategies to improve the accuracy of a pre-trained NNP for organic molecular crystals by distilling knowledge from a teacher model (Fig. 5). The most effective knowledge transfer was achieved when fine-tuning using only soft targets, that is, the teacher model's inference values. Knowledge distillation was shown to be an effective technique for improving the performance of models in predicting the properties of organic molecular crystals, as exemplified in a proof-of-concept study focusing on elastic properties. The student model, which learned the knowledge of the teacher model PFP, improved its volume reproducibility to an accuracy close to that of the teacher model.

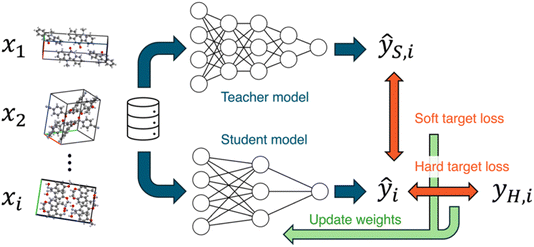Fig. 5 Knowledge distillation of neural networks. In this work, the teacher and student models were the two neural network potentials, PreFerred Potential (PFP) and Crystal Hamiltonian Graph Network (CHGNet), respectively. Reproduced from https://doi.org/10.1039/d4fd00090k.

Closing Session 1 was a paper by Veronika Jurásková, who presented studies on modelling ligand exchange in metal complexes with machine-learning potentials (https://doi.org/10.1039/d4fd00140k). This paper introduced a strategy to train machine-learning potentials, also using MACE,¹⁹ for metal–ligand complexes in explicit solvents. Taking the structure and ligand exchange dynamics of Mg²⁺ in water and Pd²⁺ in acetonitrile as two illustrative model systems, the metal ion–solvent radial distribution functions were in excellent agreement with experimental data, confirming the capacity of MACE to capture the structure of the polarised solvent shells around the cations.

Taken together, the papers in Session 1 made a convincing case for the power of machine-learned interatomic potentials across a range of areas in the chemical sciences, showing that these approaches are valuable for inorganic and organic solids alike. They also gave an exciting glimpse of the growing power of generative methods, both to speed up heuristic inorganic materials structure searches (https://doi.org/10.1039/d4fd00094c) and to produce candidate molecules with target properties (https://doi.org/10.1039/d4fd00113c).

2.3. Session 2: discovering structure–property correlations

Session 2 comprised seven papers and was chaired by Nadine Schneider and Fernanda Duarte. The papers spanned accessible web-based interfaces for Bayesian optimisation (https://doi.org/10.1039/d4fd00109e), ML models for peptide function (https://doi.org/10.1039/d4fd00099d), machined-learned tensors for predicting anisotropy (https://doi.org/10.1039/d4fd00096j), natural language processing for curating large computational databases (https://doi.org/10.1039/d4fd00087k), the importance of considering noise in ML from datasets (https://doi.org/10.1039/d4fd00091a), “prediction rigidities” for assessing ML model robustness (https://doi.org/10.1039/d4fd00101j), and data analysis of complex thermochemical networks using active thermochemical tables (https://doi.org/10.1039/d4fd00110a).

Kim Jelfs opened this session with a paper on Web-BO (https://doi.org/10.1039/d4fd00109e), a new graphical user interface (GUI)-based Bayesian optimization service, aiming to improve the accessibility of data-driven optimisation tools in chemistry; see: https://suprashare.rcs.ic.ac.uk/web-bo/

Bayesian optimization (BO), among a range of other algorithms,²⁰ has shown great promise recently for data-driven chemical sciences, both for experimental^21–23 and computational applications (e.g., see https://doi.org/10.1039/10.1039/d4fd00094c, discussed above, and https://doi.org/10.1039/d4fd00099d, the paper discussed next). BO outperforms more traditional factorial design of experiments for high-dimensional, multivariate experimental space. However, the entry barrier for the average chemist to use BO in their research is relatively high. Web-BO, a modular platform that is easily integrated into existing electronic lab notebook (ELN) frameworks, aims to bridge that gap (Fig. 6). It can be used as a standalone database and optimiser for chemical tasks. No coding experience is necessary to work with Web-BO and to apply BO algorithms to chemical optimisation tasks. In its first iteration, Web-BO uses the Merck platform, BayBE, for its back-end functionality.²⁴ The paper exemplified the use of Web-BO with the optimization of a palladium-catalysed coupling reaction.^25,26 Web-BO looks like an exciting resource for the chemistry community and it should draw more research groups into using optimisation approaches in the future.

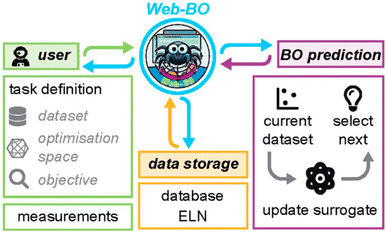Fig. 6 Summary of the Web-BO interface and functionality, reproduced from https://doi.org/10.1039/d4fd00109e.

Next, Arya Changriarath Sivadasan presented a paper on sequence determinants of protein phase separation and recognition by protein phase-separated condensates through molecular dynamics and active learning (https://doi.org/10.1039/d4fd00099d). Quantitative molecular dynamics simulations and derived free-energy values can capture how a sequence encodes the chemical and biological properties of a protein. But these calculations are computationally demanding, even after reducing the representation by coarse-graining, presenting an opportunity for active learning strategies.²⁷ This paper, too, employed a BO framework (Fig. 7).

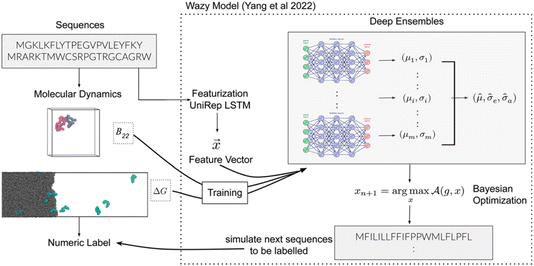Fig. 7 Schematic overview of the active learning framework for predicting peptides using Bayesian optimisation (BO) and molecular dynamics (MD) simulations, reproduced from https://doi.org/10.1039/d4fd00099d.

While modelling sequence–property relationships is a difficult challenge, this paper showed that it is possible to train neural network models with molecular dynamics simulations to design disordered proteins to self-interact and phase separate and to bind to phase-separated condensates. The key is to use appropriate featurisation from pre-trained sequence models,^27–29 coupled with BO for sampling the candidates most useful for training a protein design.

Alex Ganose's paper focused on the discovery of highly anisotropic dielectric crystals using equivariant graph neural networks (https://doi.org/10.1039/d4fd00096j). The basic idea was to use computed dielectric tensors to predict anisotropy in solids,^30,31 but again—a recurrent theme in this meeting—the DFT methods are expensive: up to hundreds of CPU hours per structure at the time of writing. Also, DFT scales cubically with the number of atoms, so the simulation of large cells becomes impractical. The paper used the latest approaches in equivariant graph neural networks to develop a model that can predict the full dielectric tensor of crystals. The resulting model—AnisoNet—was trained on the Materials Project dataset of ca. 6700 dielectric tensors, achieving state-of-the-art accuracy in scalar dielectric prediction in addition to capturing the directional response (Fig. 8). Importantly, AnisoNet is configured so that it predictions will always be consistent with the input structure symmetry, therefore eliminating unphysical tensors such as anisotropy for cubic materials.

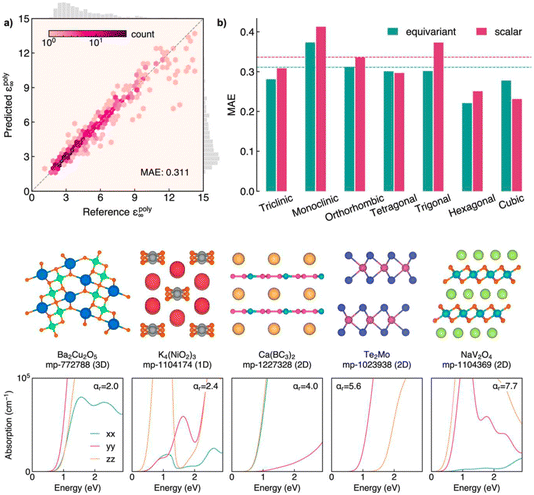Fig. 8 Upper panels: performance of AnisoNet in predicting the polycrystalline dielectric constant on the Materials Project dielectric test set. Lower panels: crystal structures and optical absorption spectra for a selection of highly anisotropic materials identified by screening using AnisoNet. Both figures are reproduced from https://doi.org/10.1039/d4fd00096j.

This paper also highlighted a future challenge, discussed further in Section 3, below: to date, most property-prediction machine-learning models have focused on scalar targets, such as the 13 properties listed in the MatBench dataset.³² Understanding of tensorial properties is important for assessing technological function, and will become more important as data-driven approaches progress beyond predicting bulk properties towards understanding the impact of interfaces, surfaces, defects and mesoscale properties.

Heather Kulik's paper focussed on leveraging natural language processing to curate computational databases for transition-metal complexes (https://doi.org/10.1039/d4fd00087k). The breadth of transition-metal chemical space covered by databases such as the Cambridge Structural Database and the derived computational database, tmQM³³ (86 665 datasets), is not conducive to application-specific modelling and the development of structure–property relationships. More broadly, this is a problem that will grow exponentially as we develop more ‘big data’ resources in chemical sciences—it raises the significant problem of how to interact with, understand and exploit such data. For example, how do we link such data with target functions and applications? This paper exploited both supervised and unsupervised natural language processing (NLP) techniques to link experimentally synthesized compounds in the tmQM database to their respective applications. This allowed the authors to curate four distinct datasets: (i) tmCAT for catalysis, (ii) tmPHOTO for photophysical activity, (iii) tmBIO for biological relevance, and (iv) tmSCO for magnetism. Analyzing the chemical substructures within each dataset reveals common chemical motifs in each of the designated applications (see Fig. 9 for a catalysis example).

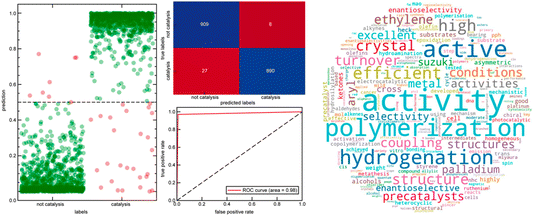Fig. 9 Left: prediction probability (left), confusion matrix (top right) and receiver operating characteristic curve (bottom right) of the catalysis classifier on the set-aside test set. Right: word cloud of the 300 most important features of a catalysis random forest classifier scaled by the feature importance score, not including direct catalysis keywords. Reproduced from https://doi.org/10.1039/d4fd00087k.

Within the tmCAT dataset (Fig. 9), analysis of common electronic and geometric descriptors revealed that commonly used descriptors fail to distinguish between catalytic and non-catalytic sets. However, the analysis of the coordination geometry of catalytically relevant complexes showed that geometries with open metal sites were enhanced in the tmCAT set. This study has potential implications for essentially any large dataset where structural or other descriptors can be correlated with computed or measured function—the authors mention metal–organic frameworks³⁴ in their conclusions, but this is just one example of many. This work complements earlier studies by Cole³⁵ and, in my view, these tools and their successors will be an essential component for the long-term success of data-driven strategies in the chemical sciences. Without such tools, we will simply drown in information.

Next up was Daniel Crusius with the potentially contentious title “Are we fitting data or noise? Analysing the predictive power of commonly used datasets in drug-, materials-, and molecular-discovery” (https://doi.org/10.1039/d4fd00091a). Experimental errors can be considerable in chemical sciences, and the authors of this paper identify an important challenge—sparse, noisy data—that is central to data-driven approaches. This has only rarely been considered quantitatively. In this study, the authors analysed commonly used ML datasets for regression and classification from drug discovery, molecular discovery, and materials discovery. They then derived maximum and realistic performance bounds for 9 such datasets by introducing noise based on estimated or actual experimental errors. Comparison of the estimated performance bounds to the reported performance of leading ML models in the literature showed that 4 out of 9 of the ML models had reached or surpassed dataset performance limitations and, thus, might potentially be fitting noise (Fig. 10).

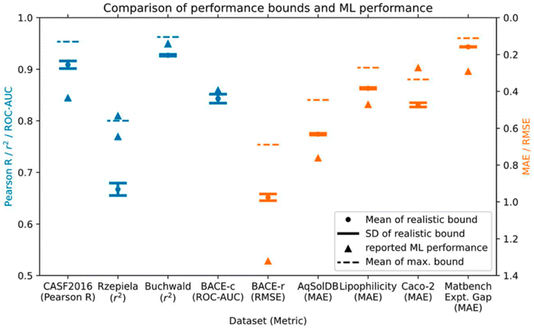Fig. 10 Performance bounds for 9 different datasets compared to reported ML performance from the literature. The authors suggest that the reported ML model performances for the BACE classification dataset (BACE-c), the Caco-2, and the Rzepiela datasets seem unrealistically high, given the estimated experimental error. Reproduced from https://doi.org/10.1039/d4fd00091a.

The authors highlight that datasets with computational endpoints are often used in materials science applications, and that such datasets do not have experimental noise, and are thus a promising path forward if experimental data is scarce. While computational datasets may not have ‘noise’ in the experimental sense, they do always have finite errors, and this may not always be systematic. As such, I would suggest that similar considerations also hold for machine learning from computational datasets. Moreover, as discussed in the paper above by Ganose (https://doi.org/10.1039/d4fd00096j), bulk property predictions might (and frequently will) fail to capture experimental factors such as surface effects and defects. Care must therefore be taken if blending experimental datasets with computational datasets (e.g., derived from ‘perfect’, idealized crystalline materials) for the purposes of machine learning. A well-known example is the metal–organic framework MOF-5, which has shown reported experimental surface areas over a huge range of 260–4400 m² g⁻¹.³⁶ It is known that defects, impurities, and interpenetration³⁷ can contribute to surface area in MOFs and in other frameworks, so it is not necessarily reasonable to assume that the highest experimental surface area represents the perfect, idealised MOF-5 crystal. What, then, is the experimental ‘ground truth’ surface area for MOF-5? These variations in surface area are not necessarily “errors”, as such, although the scope for measurement errors is also substantial. Even for reproducible syntheses with robust, error-free measurements, small changes in synthesis conditions can create large changes in measured properties. For example, the production of catenated or non-catenated forms of a MOF might switch abruptly with very small changes to solvent conditions or temperature, and the properties of the products will be totally different. Similar effects are well known for the solid-state syntheses of metal oxides and of battery materials, where properties can be dominated by interfaces, grain boundaries, and defects, which can be highly sensitive to the precise reaction conditions. This is a huge challenge for both machine-learning models and (particularly) for the interpretation of large literature-derived databases, linking back to Kulik's paper, above (https://doi.org/10.1039/d4fd00087k).

Next, Sanggyu Chong presented a paper on prediction rigidities^38,39 for data-driven chemistry (https://doi.org/10.1039/d4fd00101j), which are a family of metrics derived from the loss function that can be used to understand the robustness of ML model predictions, thus connecting thematically to the previous paper. Prediction rigidities are derived from a constrained loss formulation to quantify the degree of sensitivity, or “rigidity”, of a ML model when the value of one prediction is perturbed away from that obtained from the unconstrained model. Specifically, this was applied to regression models. From a practical perspective, they allow for an understanding of how stable the ML model predictions are with respect to changes in the model architecture or dataset makeup. This is a generalizable idea in ML, but the authors exemplify it here for atomistic ML models. Such metrics will be needed in the future to improve the interpretability and transferability of data-driven techniques.

The final paper in Session 2 was presented by Branko Ruscic on the data analysis of complex thermochemical networks using active thermochemical tables, focusing on the case of glycine chemistry (https://doi.org/10.1039/d4fd00110a). In truth, this paper was quite far from my expertise—the reader is referred to the paper—but in essence, this is another data mining approach (enhanced by additional in-house calculations from the authors), and hence relates thematically to the paper by Kulik, above (https://doi.org/10.1039/d4fd00087k).

2.4. Session 3: discovering trends in big data

Session 3 comprised five papers and was chaired by Philippe Schwaller and Janine George. The session spanned encoder–decoder models for organic reaction prediction pretrained solely on language data (https://doi.org/10.1039/d4fd00104d), organic crystal structure prediction ‘at scale’ (https://doi.org/10.1039/d4fd00105b), optical materials discovery and design with federated databases and machine learning (https://doi.org/10.1039/d4fd00092g), the fundamental question “How big is big data?” (https://doi.org/10.1039/d4fd00102h), and how to make the InChI (International Chemical Identifier) standard FAIR and sustainable while moving to inorganics (https://doi.org/10.1039/d4fd00145a).

Jiayun Pang open the session with her paper on pre-trained language models for chemistry (https://doi.org/10.1039/d4fd00104d). Molecular structure representations, such as SMILES and SELFIES,¹³ bear similarity to language sequences, making it possible to adopt transformer-based⁴⁰ NLP algorithms to process and analyse molecules in a similar fashion as used to process and analyse text. Here, the authors explored this for organic reaction prediction tasks (Fig. 11). The approach involved three models: the original T5 model,⁴¹ the FlanT5 model,^42,43 and the ByT5 model.⁴⁴ The preliminary results indicate that although FlanT5 and ByT5 are pretrained only on language tasks, they provide a solid foundation for fine-tuning in reaction prediction, even though the USPTO_500_MT dataset covered only general organic reactions and contained limited stereochemical information.⁴⁵

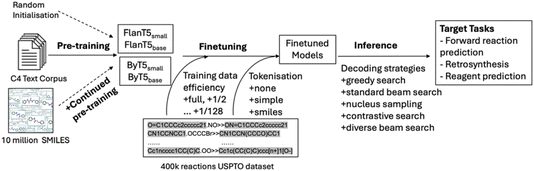Fig. 11 Workflow for pretraining, fine-tuning and inference, reproduced from https://doi.org/10.1039/d4fd00104d.

Christopher Taylor's paper focused on predictive crystallography at scale, specifically presenting crystal structure prediction (CSP) landscapes for a set of for more than 1000 small, rigid organic molecules (https://doi.org/10.1039/d4fd00105b). A sub-set of these is shown in Fig. 12 (left). Continuing the trend in the meeting for machine-learned energy models (e.g., https://doi.org/10.1039/d4fd00107a and https://doi.org/10.1039/d4fd00090k, above), the authors trained an initial model on 7950 selected crystal structures from ca. 85% of the CSP landscapes (up to 9 crystal structures per landscape), randomly selected from within 8 kJ mol⁻¹ of the global energy minimum of each landscape, corresponding to just under 5% of the crystal structures (166 395 structures in total) within this energy range. Following initial training, active learning was applied to identify crystal structures from the training landscapes with highest uncertainty in the lattice energy correction (see the paper for details). The performance of the resulting model on the test set shows remarkably low error, returning a mean average error (MAE) of just 0.93 kJ mol⁻¹. Re-optimisation with a trained MACE model yielded considerable improvements in the geometric agreement of predicted structures with experiment (Fig. 12, lower) and of their energy ranking on the CSP landscapes. While the methods are ultimately quite different, there are conceptual similarities with the FUSE study (https://doi.org/10.1039/d4fd00094c), discussed above, for accelerating inorganic structure prediction.

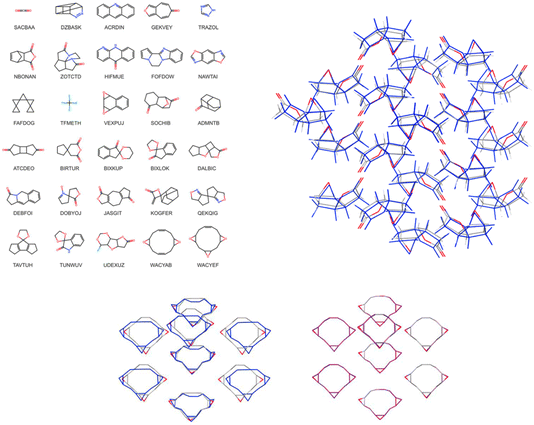Fig. 12 Left: molecular diagrams and crystal structure CSD reference codes for (top three rows) a random selection of the 1007 molecules included in the large-scale CSP study. The bottom three rows show molecules in the set with the largest differences between in-crystal and optimised molecular geometries; the CSP landscapes for these molecules were re-optimised using a transferrable MACE model. Right: overlay of 30-molecule clusters from the X-ray determined crystal structure (atoms coloured by element, CSD reference code SIBJIX) with the matching prediction (blue). Lower: overlay of the experimentally determined crystal structure (atoms coloured by element, CSD reference code WACYEF) with: (left) the matching structure from the force field (FIT + DMA) CSP (blue); and (right) the matching CSP structure after re-optimisation with the transferable MACE model (purple). Reproduced from https://doi.org/10.1039/d4fd00105b.

To my knowledge, this is the largest CSP dataset produced to date. It is exciting for many reasons, for one because the generalization and broadening of these methods could lead to the more routine use of CSP for materials design,^46,47 where the calculation of lattice energy landscapes is currently rate-limiting, even using force-field approaches. Numerous challenges remain. For one thing, chemical space for organics is very diverse, and the inclusion of a broader training set of molecules, such as charged salts and flexible molecules, would be needed to make this ML method more general. This paper points the way, however, and the use of transferable ML energy models seems like the logical next progression for this field, at least in the absence of a step-change in theory and/or computational hardware architectures.

Next up was Matthew Evans, presenting his paper on optical materials discovery using federated databases and machine learning (https://doi.org/10.1039/d4fd00092g). The paper presented a framework to search for materials with a strong linear optical response, that is, high-refractive-index materials, which have multiple practical uses and are also a good starting point in the search for more exotic nonlinear optical properties. Yet again (c.f., previous paper and https://doi.org/10.1039/d4fd00096j in Session 2), the computational design barrier is the high computational cost of first-principles simulations, which makes inexpensive machine-learned proxies an attractive filter prior to more expensive calculations.^48,49

Notwithstanding that GGA-based DFT typically underestimates band gaps in an uncontrolled and unsystematic way, which will be reflected in an overestimation of the refractive index, it is impressive that this method can produce both known and unsynthesized targets in this way (Fig. 13).

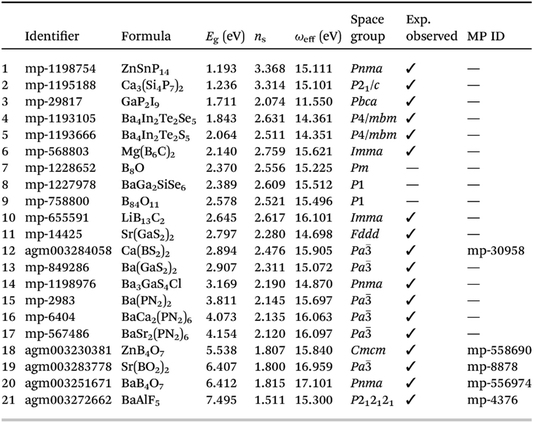Fig. 13 Table showing list of most promising materials identified by screening with respect to Herfindahl–Hirschman indices (related to constituent element availability), synthesisability, and quality as a high refractive index compound, sorted by ascending band gap, reproduced from https://doi.org/10.1039/d4fd00092g. Of these 21 compounds, 18 have been observed before experimentally.

Claudia Draxl posed the big question in her paper, “How big is big data?” (https://doi.org/10.1039/d4fd00102h). This is a crucial topic for the chemical sciences, where experimental data tends to be sparse (unlike, say, social media data) and often noisy (see https://doi.org/10.1039/d4fd00091a, above), while computational data can be larger (e.g., https://doi.org/10.1039/d4fd00104d) but also subject to systematic or non-systematic errors, as discussed in the previous paper. As such, the “bigness” of data encompasses not only data volume, but also data quality. This fascinating paper posed the question: “What does big mean in the realm of materials science data?”

A key conclusion of the paper was that there is a lack of interoperability between two large computational materials datasets, the Materials Project⁵⁰ and AFLOW.⁵¹ In short, it seems that the AFLOW and MP datasets turn out to sample the underlying material space differently, since the MP materials appear biased towards lower formation energies (Fig. 14). The conclusion was that these two databases are not “big” enough in the sense that they are not diverse enough to be able to make predictions across a wider range of diversity. The paper also evaluated infrastructure requirements for big data in the chemical sciences, including direct cost estimates for training on specific datasets using today's Amazon Web Service prices.

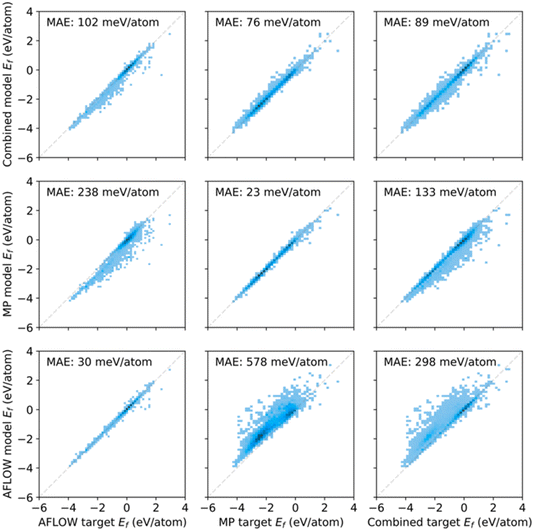Fig. 14 Predicted versus calculated (target) formation energies for AFLOW and MP data, as well as the combined dataset. The bottom row (left column) shows the model trained (evaluated) on the AFLOW data, the middle row (middle column) the MP data, and the top row (right column) the combined data. The lower performance for training with the combined data was ascribed to differences in computational details, such as Brillouin-zone (BZ) sampling, basis-set cutoff, convergence criteria, etc. Reproduced from (https://doi.org/10.1039/d4fd00102h).

Closing this session was a paper presented by Gerd Blanke concerning the new v1.07 release of the InChI (International Chemical Identifier) standard (https://doi.org/10.1039/d4fd00145a), which is a cornerstone of chemical informatics. For the new v1.07 release, the code was analyzed and the major steps documented, and more than 3000 bugs and security issues, as well as nearly 60 Google OSS-Fuzz issues, were fixed. These improvements help InChI to play a key role in making data FAIR (Findable, Accessible, Interoperable, and Reusable) in the realm of chemical sciences.

2.5. Session 4: discovering synthesis targets

There were five papers in Session 4, covering topics such as uncertainty analysis of neural-fingerprint models (https://doi.org/10.1039/d4fd00095a), retrosynthesis algorithms (https://doi.org/10.1039/d4fd00093e), filters in material screening pipelines for synthesizable inorganic materials (https://doi.org/10.1039/d4fd00120f), mapping inorganic crystal space (https://doi.org/10.1039/d4fd00063c), and machine-learned materials synthesis insights from text-mined literature recipes (https://doi.org/10.1039/d4fd00112e). This session was chaired by Phillippe Schwaller and Volker Derringer.

The first paper was presented by Miriam Mathea (https://doi.org/10.1039/d4fd00095a). The paper focused on a key problem for ML-led chemical discovery – that is, evaluating the reliability of ML predictions for single unknown compounds. Global prediction errors, such as mean average error (MAE), are useful for assessing the overall reliability of models. However, models often perform markedly better for some compounds than others. The large-scale CSP study discussed above (https://doi.org/10.1039/d4fd00105b) gave examples of this. For the synthetic chemist, the attempted synthesis of a predicted hypothetical compound may be a large endeavour, which could easily consume a year or more of a researcher's time. As such, experimentalists may be more interested in local information on the reliability of a single prediction than average errors, or overall methodology statistics. This study explored the uncertainty estimates of neural fingerprint-based models by comparing pure graph neural networks (GNN) to classical machine-learning algorithms combined with neural fingerprints. The authors investigated the advantage of extracting the neural fingerprint from the GNN and integrating it into a method known for producing better-calibrated probability estimates.

Specifically, the learned molecular representation from Chemprop^52,53 was used as input for machine-learning techniques that naturally output better-calibrated probabilities than deep neural networks while retaining classification performance. The results of the investigation demonstrate that when neural fingerprints are used in conjunction with classical machine-learning methods, there is a slight decrease in prediction performance compared to the native Chemprop model. However, these models provide significantly improved uncertainty estimates. I can see significant advantages in such a trade-off: for example, an experimental research group might want to choose five target compounds with a predicted band gap in the range of 2.0–2.2 eV, with high confidence of them all falling in that range, rather than being able to predict band gaps with higher accuracy across a broader energy range.

The next paper was presented by Marwin Segler on the topic of re-evaluating retrosynthesis algorithms within the Syntheseus framework (https://doi.org/10.1039/d4fd00093e).

The paper tackled two key problems in creating metrics for single- and multi-step retrosynthesis. First, it is not clear how metrics used when benchmarking single-step and multi-step synthesis planning algorithms in isolation should be interpreted in the context of an end-to-end retrosynthesis pipeline. Second, model comparison and metrics have hitherto been inconsistent. The goal was to specify best practices for evaluating retrosynthesis algorithms, which were codified in a python package called Syntheseus (Fig. 15). This study highlights several pitfalls and best practices, and details how Syntheseus can address these.

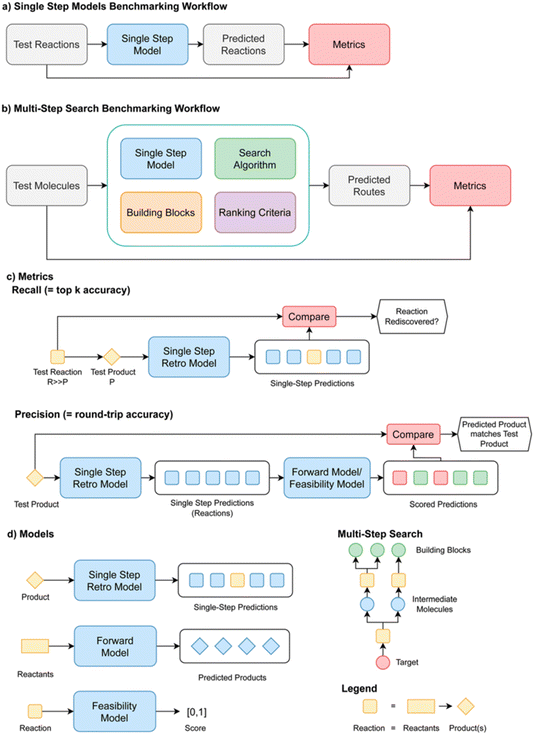Fig. 15 Benchmarking workflows and metrics for retrosynthesis algorithms in Syntheseus, reproduced from https://doi.org/10.1039/d4fd00093e.

The next paper presented by Basita Das focused on embedding human knowledge in material screening pipelines as filters to identify novel synthesizable inorganic materials (https://doi.org/10.1039/d4fd00120f). Arguably, the generative design of inorganic crystalline materials is no longer a bottleneck, since there are now huge databases of hypothetical compounds. Most of these, however, will prove to be unsynthesizable. How then does one weed out the bad ones? One answer is accurate lattice energy calculations, but these are still expensive and require acceleration (https://doi.org/10.1039/d4fd00105b, above), and even then, it is not always the case that thermodynamic products are formed in experiments. For example, kinetic, metastable polymorphs are commonplace.

A different approach is to apply a set of downselection filters^54,55 to a synthetic database to identify candidate compounds that satisfy certain chemical rules embedded in the filter (see also next paper, https://doi.org/10.1039/d4fd00063c). In this paper (https://doi.org/10.1039/d4fd00120f), the authors developed a 6-filter pipeline that reduced a library of >100 000 hypothetical perovskite-inspired to a mere 27 that were deemed likely to be synthesizable – that is, 0.027% of the total library (Fig. 16, upper). There are multiple ways that such sub-sets might be visualized, but a very appealing one that is familiar to solid-state chemists is a ternary phase diagram (Fig. 16, lower). This is a powerful strategy, and the potential transferability to other inorganic structure families is clear. An interesting question is whether there are analogues for other materials, such as organic crystals. Certainly, several of the filters do not translate so well, such as electronegativity balance, oxidation state frequency filters, and so forth. I can, however, see some parallels that might be used in organic CSP, such as filters for the propensity to form cocrystals (where computational tools already exist) or space group frequency statistics (see e.g., paper https://doi.org/10.1039/d4fd00105b from Session 3, and specifically Fig. 3 in that paper). In the conclusions of this paper, the authors also posit a range of other possible filters, such as “manufacturability” framed as a multi-factor descriptor that embeds domain knowledge such as precursor solubility, thermal budget, materials availability, and supply-chain resilience, among other factors. Such general concepts are surely transferable outside of the domain of inorganic solids, for example into areas such as pharmaceutical synthesis.

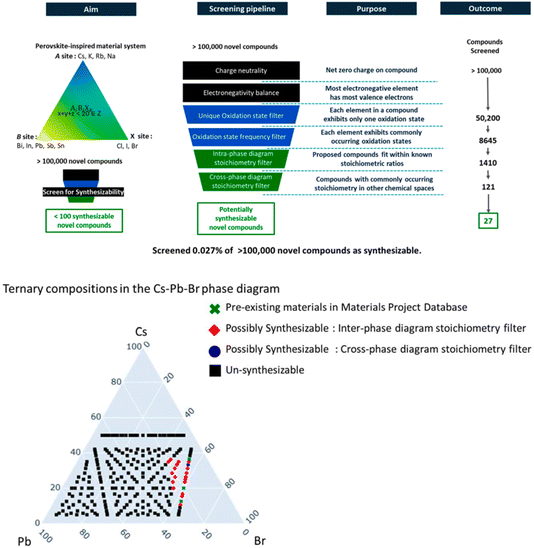Fig. 16 Upper: screening pipeline formed from stitching together chemical rules and human intuition-driven filters to explore the ternary phase diagrams of “perovskite-inspired” materials. Lower: ternary phase diagram of Cs–Pb–Br. A total of 235 charge-neutral compounds were identified in this phase diagram, out of which 3 compounds, CsPbBr₃, CsPb₂Br₅ and Cs₄PbBr₆ (green crosses) were previously reported in the Materials Project Database. Out of all 235 compounds, only one new compound, Cs₃PbBr₅ (marked in blue) was identified as synthesizable by the complete pipeline of filters. Reproduced from (https://doi.org/10.1039/d4fd00120f).

The penultimate paper in this session was presented by Aron Walsh (https://doi.org/10.1039/d4fd00063c). This study enumerated binary, ternary, and quaternary element and species combinations to produce an extensive library of over 10¹⁰ (!) stoichiometric inorganic compositions. The unique combinations were vectorised using compositional embedding vectors⁵⁶ drawn from a variety of published machine-learning models. Dimensionality-reduction techniques were employed to present a two-dimensional representation of inorganic crystal chemical space, which was labelled according to whether the combinations pass standard chemical filters (c.f., previous paper) and if they appear in known materials databases.

This lecture started with a fascinating conundrum: the number of possible unique combinations for binary, ternary, and quaternary inorganic compounds grows exponentially (column 2, Fig. 17), and yet binary compounds dominate both known experimental databases. Higher-order compounds are also, proportionately, underrepresented in computational databases such as the Materials Project (Fig. 17). Why is this? One possible answer is that complex compounds have an inherent thermodynamic tendency to disproportionate into simpler compounds. A more sociological answer is that both experimentalists and computationalists have focused more on simpler compounds because of the “untameable” complexity—both are the result of human-led searches, and to some extent, we have mostly found the things that we were looking for. Probably, both factors are at play, but whatever the reason, the statistics in Fig. 17 suggest that more complex, higher-order compounds are relatively scarce, which hints at unexplored territories in materials science, particularly for ternary and quaternary compounds.

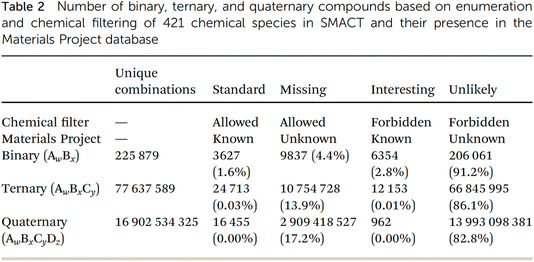Fig. 17 Statistics arising from the Semiconducting Materials from Analogy and Chemical Theory (SMACT) code⁵⁷ compared with the Materials Project database, reproduced from https://doi.org/10.1039/d4fd00063c.

This analysis suggests that lots of possible compounds are missing, but raises the question of where exactly to look for them. This is a challenging problem, but visualising embedded vectors through the lens of the applied filters (Fig. 18) allows the identification of areas of chemical space with distinctive characteristics, which might in turn prompt specific energy-based searches (e.g., https://doi.org/10.1039/d4fd00094c) or function-based searches (e.g., https://doi.org/10.1039/d4fd00096j) in the future. This is an elegant and powerful way to look for ‘white space’ in materials science in the future, and it could also be combined with additional filters of the type discussed in the previous paper, above (https://doi.org/10.1039/d4fd00120f).

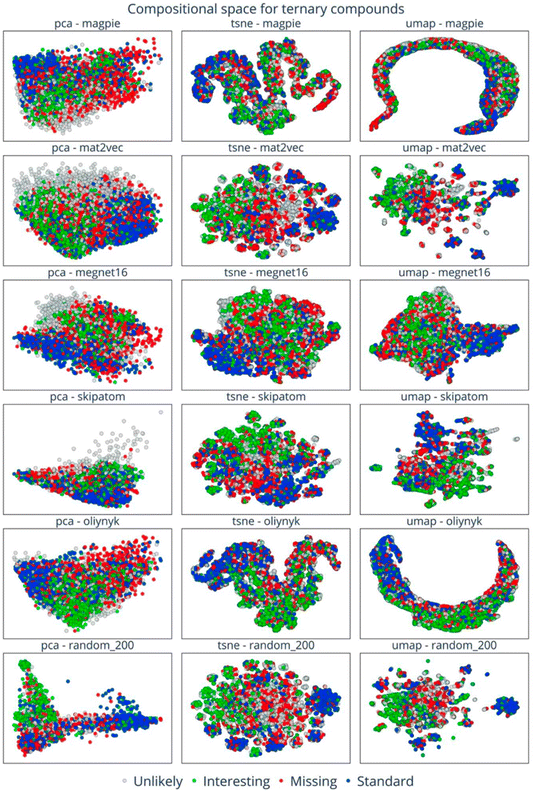Fig. 18 Visualisation of embedding vectors for the space of quaternary compounds with six element embeddings across PCA, t-SNE, and UMAP dimension-reduction methods. The data points are colour-coded to indicate the four categories of composition: standard (blue), missing (red), interesting (green), and unlikely (grey). Reproduced from https://doi.org/10.1039/d4fd00063c.

Wenhao Sun closed Session 4 with a critical reflection on attempts to machine-learn materials synthesis insights from text-mined literature recipes (https://doi.org/10.1039/d4fd00112e).^58–60 Between 2016 and 2019, the presenter participated in efforts to text-mine 31 782 solid-state synthesis recipes and 35 675 solution-based synthesis recipes from the literature. The slightly dispiriting conclusion was that these datasets do not satisfy the “4 Vs” of data science—that is: volume, variety, veracity and velocity. For this reason, the author suggested that machine-learned regression or classification models built from such datasets will have limited utility in guiding the predictive synthesis of novel materials. On the other hand, these large datasets provided the opportunity to identify anomalous synthesis recipes, which in fact did inspire new hypotheses on how materials form, which were later validated by experiment.

3. Future challenges and opportunities

This was an excellent meeting that covered a diverse but ultimately coherent range of topics. A nice characteristic of the meeting was that most presenters were candid, pointing out the limitations of their methods, and what we cannot currently do with data-driven techniques in the chemical sciences—the final paper in Session 4 was an excellent example of this (https://doi.org/10.1039/d4fd00112e). Following this spirit, I suggest below three areas of challenge and, hence, of opportunity, following Alán Aspuru-Guzik's rally cry to work on problems that have not been solved before.

3.1. Mesoscale descriptors

There was much discussion in this meeting about various types of descriptors, but ultimately these mostly fell into three classes: molecular structure descriptors, crystal structure descriptors, and bulk property descriptors. As pointed out by Ganose (https://doi.org/10.1039/d4fd00096j), data-driven approaches will need to progress beyond predicting bulk properties and ‘perfect’ molecules and crystals, towards understanding the impact of interfaces, surfaces, defects and mesoscale properties. There was almost no discussion of mesoscale descriptors at this meeting. Indeed, to my knowledge, this topic has barely been explored in the context of data-driven chemical sciences, even though mesoscale effects and defects can totally dominate performance in materials such as heterogenous catalysts, batteries, and porous solids. A quick survey of the literature (Web of Science, 25-10-2024) found little research in this domain; for example, a search for “molecular descriptor*” gave 7479 hits, while “mesoscale descriptor*” gave 2 hits (both about oceanography, not chemistry), while “nanoscale descriptor*” and “coarse grain descriptor*” gave no hits at all.

The reasons for this are perhaps clear. Mesoscale effects such as particle size, surface structure, and grain boundaries are at best expensive to calculate: often, they are essentially impossible to predict a priori. Mesoscale descriptors can be garnered by experiment, for example by measuring particle size for heterogeneous catalysts, but the obvious disadvantage is that these experimental descriptor measurements might well be more difficult and time consuming than the measurement of the catalytic activity itself. As such, data-driven approaches using experimental descriptors might not accelerate materials discovery processes; indeed, they could slow it down, unless the descriptor measurements are much more facile than measuring the desired property of interest.

In fact, we have one example in heterogenous photocatalysis⁶¹ where we combined computed bulk property descriptors (electron affinity, ionization potential, optical gap) with the experimentally measured descriptor of catalyst dispersibility, which was effectively a proxy for surface hydrophilicity and particle size. The variation in photocatalytic activity across a library of 170 catalysts did not correlate strongly with any single physical descriptor, but a machine-learning model involving the four separate descriptors (three computed and one measured) described up to 68% of the variation in the catalytic activity. The limitations of such experimental descriptors are obvious: they are not forward predictive, in the sense that we cannot (yet) predict particle size and hydrophilicity for an unknown candidate catalyst (although the latter, hydrophilicity, might be more computationally tractable). Moreover, 32% of the variance in catalytic activity is not accounted for by the ML model, even with this additional experimental descriptor. This is unsurprising: for example, defects can affect catalytic activity, and we had no descriptor for that in this study. A related example, discussed above, is the metal–organic framework, MOF-5, which can show reported experimental surface areas over a huge range of 260–4400 m² g⁻¹,³⁶ even though the surface area descriptor for ‘perfect’ crystalline MOF-5 yields a single number.

The way forward here is not totally clear, but it is an area that must be addressed. This is particularly important for data-driven materials chemistry, where mesoscale effects abound. In the absence of a radical change in computing technology, and the ability to do full atomistic mesoscale simulations, I suggest that the best approach for now might be to use (necessarily) approximate computed mesoscale descriptors, which may serve to better guide material selection workflows, provided that the approximation is not so great that we end up fitting computational “noise” (https://doi.org/10.1039/d4fd00091a). For high dimensional experimental searches, multiple descriptors, even if very approximate (see 3.2), might translate to a real cumulative benefit—but they do need to be shown to be better than nothing!

This strategy is more tractable for some problems than for others. Defects, for example, can be greatly influenced by small changes to reaction conditions, but are hard to predict a priori. Likewise, to predict average particle size, let alone particle size distributions, would require a sufficiently precise model of nucleation and growth, which is still challenging outside of simple model systems. By contrast, Monte Carlo simulations of crystal growth have become relatively affordable for some materials,⁶² although this requires some prior knowledge of certain thermodynamic parameters. Such platforms, if scaled, might provide a basis for computed mesoscale descriptors. An alternative approach is to simply give up on data-driven methods for properties that cannot be pre-estimated by computation, even approximately, and to brute force the experimental search of such mesoscale areas of chemical space using robots,²² but this in turn necessitates fast, robust, autonomous robotic platforms.

3.2. Chemical abstractions and pseudomaterials

Apart from the papers on literature mining, most of the discussion at this meeting involved atomistic data. That is, the molecular descriptors and crystal descriptors were based on atomic information, and properties were calculated from atomistic models. Leaving aside the question of the mesoscale (3.1), this raises the question of computational cost, both for forward and inverse design approaches (Fig. 4, above, https://doi.org/10.1039/d4fd00113c). That is, we might be limited by the cost of calculating properties for large numbers of materials at the atomistic level, whether using forward or inverse design approaches.

In my view, an underexplored area of research is to use greater levels of chemical abstraction. A beautiful example of this was given by Kaija and Wilmer,⁶³ who pioneered the use of “pseudomaterials”. Their first study focused on the search for porous materials to store methane, and they posed the question of what is the maximum methane storage capacity that might be attained in any porous solid. To explore this, they calculated high-pressure methane adsorption in 600 000 randomly generated porous crystals, or “pseudomaterials” (Fig. 19, left), using grand canonical Monte Carlo (GCMC) simulations. These pseudomaterials were periodic configurations of Lennard-Jones spheres whose coordinates in space, along with corresponding well depths and radii, were all chosen at random. GCMC simulations were then performed for pressures of 35 and 65 bar at a temperature of 298 K, and these simulations are much cheaper than for fully atomistic representations. Despite this high level of abstraction—there were no atoms in the simulations—these fast calculations predicted a potential ‘upper bound’ for methane storage in real porous solids (<300 v/v STP) that agreed with prior experimental observations. That is, this could constitute a general limit to methane storage in any porous solid imaginable that is imposed by the inherent thermodynamics of gas sorption processes.

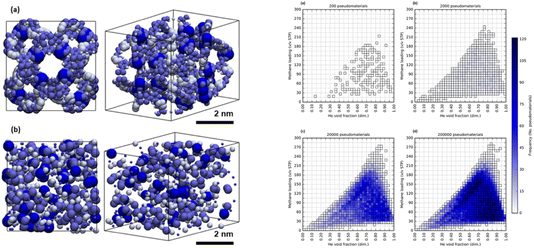Fig. 19 Left: renderings of (a) a synthesizable MOF, NU-125, and (b) a randomly generated configuration of LJ spheres, or “pseudomaterial”. Right: 2D histograms for samples of (a) 200, (b) 2000, (c) 20 000, and (d) 200 000 pseudomaterials from a library of 300 000 pseudomaterials. The predictions converge on a CH₄ capacity (<300 v/v STP) that might be a physical ‘upper bound’ for methane storage in porous solids. Reproduced from ref. 63.

This is a fascinating and potentially generalizable idea, although of course not all physical properties can be described by Lennard-Jones spheres. It is interesting to speculate how we might create similarly inexpensive abstractions, or “pseduomaterials”, for other properties, such as electronic structure in solids.

3.3. Emergent complexity

Ultimately, there are some chemical systems that defy current data-driven design approaches. Nature abounds with such examples, like photosystem II. These complex, multicomponent structures are not currently designable using bottom-up simulations, neither with forward nor inverse design approaches. One promising strategy here might be to calculate useful descriptors that are available for the sub-components of the assemblies, and then to use robotics and optimization strategies, underpinned by those descriptors, to discover the higher-order structures. Again, this approach hinges on speed, robustness, and flexibility of the automated platforms. This is an exciting goal for self-driving laboratories—that is, to discover materials with useful emergent functions that simply could not have been designed from the atoms up. A similar challenge exists for retrosynthesis: currently, I am not aware of any retrosynthetic schemes designed using AI that might not in principle have been arrived at by a trained synthetic organic chemist, but this is a worthy goal for the future.

Data availability

There are no unpublished new data in this paper; it is a meeting summary.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author thanks the Royal Society for a Research Professorship (RSRP\S2\232003). I am also very grateful to the Leverhulme Trust for supporting the Leverhulme Research Centre for Functional Materials Design, which has allowed us to investigate new approaches to data-driven materials design since 2016.

References

1. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103.
2. C. Hansch, Drug Dev. Res., 1981, 1, 267–309.
3. L. B. Kier and L. H. Hall, Pharm. Res., 1990, 7, 801–807.
4. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
5. L. B. Kier and L. H. Hall, Molecular Connectivity in Chemistry and Drug Research, ISBN: 9780124065604, 1976.
6. K. Olsen, JALA, 2012, 17, 469–480.
7. J. C. Reader, Curr. Top. Med. Chem., 2004, 4, 671–686.
8. C. Bernlind and C. Urbaniczky, Org. Process Res. Dev., 2009, 13, 1059–1067.
9. B. Kuhlman, G. Dantas, G. C. Ireton, G. Varani, B. L. Stoddart and D. Baker, Science, 2003, 302, 1364–1368.
10. J. Jumper, et al. , Nature, 2021, 596, 583–589.
11. https://www.nobelprize.org/prizes/chemistry/2024/summary/ .
12. F. Strieth-Kalthoff, et al. , Science, 2024, 384, eadk9227.
13. M. Krenn, F. Häse, A. K. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn.; Sci. Tech., 2020, 1, 045024.
14. A. Nigam, R. Pollice, G. Tom, K. Jorner, J. Willes, L. Thiede, A. Kundaje and A. Aspuru-Guzik, NeurIPS, 2023.
15. K. Darvish, M. Skreta, Y. Zhao, N. Yoshikawa, S. Som, M. Bogdanovic, Y. Cao, H. Hao, H. Xu, A. Aspuru-Guzik, A. Garg and F. Shkurti, arXiv, 2024, preprint, arXiv:2401.06949v1 DOI:10.48550/arXiv.2401.06949.
16. P. T. Salzbrenner, S. H. Joo, L. J. Conway, P. I. Cooke, B. Zhu, M. P. Matraszek, W. C. Witt and C. J. Pickard, J. Chem. Phys., 2023, 159, 144801.
17. C. Collins, G. R. Darling and M. J. Rosseinsky, Faraday Discuss., 2018, 211, 117–131.
18. Z. Xie, X. Evangelopoulos, Ö. Omar, A. Troisi, A. I. Cooper and L. Chen, Chem. Sci., 2024, 15, 500–510.
19. I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436.
20. C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126.
21. F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145.
22. B. Burger, et al. , Nature, 2020, 583, 237.
23. B. J. Shields, J. Stevens, J. Li, M. Parasam, F. Damani, J. I. M. Alvaro, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89.
24. M. Fitzner, A. Šošić, A. Hopp and A. Lee, BayBE, https://github.com/emdgroup/baybe/.
25. B. J. Reizman, Y.-M. Wang, S. L. Buchwald and K. F. Jensen, React. Chem. Eng., 2016, 1, 658–666.
26. K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem.: Methods, 2021, 1, 116–122.
27. Z. Yang, K. A. Milas and A. D. White, bioRxiv, 2022, preprint,  DOI:10.1101/2022.08.05.502972.
28. E. C. Alley, G. Khimulya, S. Biswas, M. AlQuraishi and G. M. Church, Nat. Methods, 2019, 16, 1315–1322.
29. Z. Lin, H. Akin, R. Rao, B. Hie, Z. Zhu, W. Lu, N. Smetanin, R. Verkuil, O. Kabeli, Y. Shmueli, A. dos Santos Costa, M. Fazel-Zarandi, T. Sercu, S. Candido and A. Rives, Science, 2023, 379, 1123–1130.
30. K. Lejaeghere, et al. , Science, 2016, 351, aad3000.
31. I. Petousis, D. Mrdjenovich, E. Ballouz, M. Liu, D. Winston, W. Chen, T. Graf, T. D. Schladt, K. A. Persson and F. B. Prinz, Sci. Data, 2017, 4, 160134.
32. A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 1.
33. D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135–6146.
34. S. Park, B. Kim, S. Choi, P. G. Boyd, B. Smit and J. Kim, J. Chem. Inf. Model., 2018, 58, 244–251.
35. M. C. Swain and J. M. Cole, J. Chem. Inf. Model., 2016, 56, 1894–1904.
36. K. K. Gangu, S. Maddila and S. B. Jonnalagadda, RSC Adv., 2022, 12, 14282–14298.
37. J. Hafizovic, M. Bjørgen, U. Olsbye, P. D. C. Dietzel, S. Bordiga, C. Prestipino, C. Lamberti and K. P. Lillerud, J. Am. Chem. Soc., 2007, 129, 3612–3620.
38. S. Chong, F. Grasselli, C. Ben Mahmoud, J. D. Morrow, V. L. Deringer and M. Ceriotti, J. Chem. Theory Comput., 2023, 19, 8020–8031.
39. F. Bigi, S. Chong, M. Ceriotti and F. Grasselli, arXiv, 2024, preprint, arXiv:2403.02251,  DOI:10.48550/arXiv.2403.02251.
40. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. u. Kaiser and I. Polosukhin, Adv. Neural Inf. Process. Syst., 2017, 5998–6008.
41. C. Raffel, N. Shazeer, A. Roberts, K. Lee, S. Narang, M. Matena, Y. Zhou, W. Li and P. J. Liu, J. Mach. Learn. Res., 2020, 21, 1–67.
42. H. W. Chung, et al., CoRR, abs/2210.11416, 2022.
43. S. Longpre, L. Hou, T. Vu, A. Webson, H. W. Chung, Y. Tay, D. Zhou, Q. V. Le, B. Zoph, J. Wei and A. Roberts, International Conference on Machine Learning, ICML 2023, Honolulu, Hawaii, USA, 2023, pp. 22631–22648.
44. L. Xue, A. Barua, N. Constant, R. Al-Rfou, S. Narang, M. Kale, A. Roberts and C. Raffel, Trans. Assoc. Comput. Linguist., 2022, 10, 291–306.
45. G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Nat. Commun., 2020, 11, 4874.
46. G. M. Day and A. I. Cooper, Adv. Mater., 2018, 30, 1704944.
47. M. O'Shaughnessy, J. Glover, R. Hafizi, M. Bahri, R. Clowes, S. Y. Chong, S. P. Argent, G. M. Day and A. I. Cooper, Nature, 2024, 630, 102.
48. P. J. M. A. Carriço, M. Ferreira, T. F. T. Cerqueira, F. Nogueira and P. Borlido, Phys. Rev. Mater., 2024, 8, 015201.
49. J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. L. Marques, Sci. Adv., 2021, 7, eabi7948.
50. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
51. C. E. Calderon, et al. , Comput. Mater. Sci., 2015, 108, 233–238.
52. K. Yang, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388.
53. E. Heid, K. P. Greenman, Y. Chung, S.-C. Li, D. E. Graff, F. H. Vermeire, H. Wu, W. H. Green and C. J. McGill, J. Chem. Inf. Model., 2024, 64, 9–17.
54. D. W. Davies, K. T. Butler, O. Isayev and A. Walsh, Faraday Discuss., 2018, 211, 553–568.
55. K. Pal, Y. Xia, J. Shen, J. He, Y. Luo, M. G. Kanatzidis and C. Wolverton, npj Comput. Mater., 2021, 7, 1.
56. D. W. Davies, K. T. Butler, A. J. Jackson, A. Morris, J. M. Frost, J. M. Skelton and A. Walsh, Chem, 2016, 1, 617–627.
57. D. W. Davies, K. T. Butler, A. J. Jackson, J. M. Skelton, K. Morita and A. Walsh, J. Open Source Softw., 2019, 4, 1361.
58. O. Kononova, et al. , Sci. Data, 2019, 6, 203.
59. H. Huo, et al. , npj Comput. Mater., 2019, 5, 62.
60. T. He, et al. , Chem. Mater., 2020, 32, 7861–7873.
61. Y. Bai, L. Wibraham, B. J. Slater, M. A. Zwijenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063–9071.
62. M. W. Anderson, et al. , Nature, 2017, 544, 456–459.
63. A. R. Kaija and C. E. Wilmer, J. Phys. Chem. Lett., 2018, 9, 4275–4281.

---