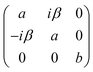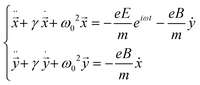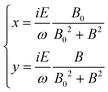Strong and reciprocal magneto-phonon effects in a 2D antiferromagnetic semiconductor FePSe₃

Abstract

Magnon–phonon coupling and spin–phonon interaction, both of which are interplays between phonons and magnetism, provide a new way to manipulate phonons. Two-dimensional (2D) magnetic systems are anisotropic in their magnetic order and may have magnons carrying spin angular momentum. According to recent reports, angular momentum can be transferred by the interaction of magnons and phonons. Here, focusing on two additional features in the Raman spectra at low frequencies that appear below the Néel temperature, we report that we can control the interplay between spin and lattice vibration and the energy of phonons coupled with magnons by changing the excitation laser power in the 2D antiferromagnetic FePSe₃ which shows magnon–phonon coupling in the absence of an external magnetic field. On the other hand, in high frequency of Raman spectra, another spin–phonon Raman scattering was observed for FePSe₃. Our results show that an out-of-plane magnetic field can control phonons and induce a Raman scattering rotation of the A_g mode. In this work, we provide a method of local heating to regulate the phonons coupled with magnons and reveal a spin–phonon phenomenon in antiferromagnetic materials.

---

1. Introduction

The discovery of two-dimensional (2D) magnetic materials such as CrI₃ ¹ and Cr₂Ge₂Te₆ ² in 2017 marked a significant milestone in condensed matter physics. These materials exhibit long-range magnetic order even when reduced to a single atomic layer. According to the Mermin–Wagner theorem,³ thermal fluctuations in a 2D isotropic Heisenberg model would destroy any long-range magnetic order, preventing spontaneous magnetization. However, the magnetic anisotropy observed in materials like CrI₃ and Cr₂Ge₂Te₆ compensates for the impact of thermal fluctuations, thus allowing for the stabilization of long-range magnetic order in two dimensions. The emergence of 2D van der Waals (vdWs) magnetic materials and the ability to engineer their unique electronic and magnetic properties^4–6 have tuned multiple physical effects, such as giant magnetoresistance (GMR)⁷ and tunnel magnetoresistance (TMR),⁸ enabling the 2D magnetic materials to serve as a promising platform for specific applications in spintronics and magnetic storage.

Magnonics, as a distinct field from spintronics focusing on the study of high-frequency information propagation and processing with the manipulation of spin waves (magnons), has gained significant traction with the advent and rapid development of 2D magnetic materials and spin dynamics.^9–12 Thus, magnons have been observed in several materials such as CrI₃,^13,14 MnBi₂Te₄ ¹⁵ and MnPS₃ ¹⁶ and have attracted increasing attention due to the fact that magnons can offer lower energy consumption and have shorter wavelengths than the charge-based devices,^10,17 which can lead to more compact and miniaturized devices. However, the current generation of magnons exhibit inefficiency due to its dependence on the conversion of uncontrollable thermal energy.^18–21

The interplay between the spin and lattice further enriches the field of 2D magnonics with the participation of phonons which can propagate a long distance in materials, reducing energy dissipation and processing information more efficiently. As a dynamic form of spin–lattice interactions, the magnon–phonon coupling, which provides precise control of magnons, has arisen particular interest.^22–25 Moreover, previous research projects have demonstrated that the energy of magnons in antiferromagnetic materials (AFM) more coincides with phonons than in ferromagnetic materials (FM), due to the inherent high frequencies (two orders of magnitude higher than ferromagnetic materials) exhibited by AFM.^26–29 MPX₃ (where M = Fe, Cr, Co, Mn, Ni and X = S or Se),^30,31 one of the families of typical AFM, has shown great potential in the research of magnon–phonon coupling.^23,32 A strong magnon–phonon coupling has been directly discovered in FePS₃ at high magnetic fields by Raman spectroscopy.³³ Thin FePSe₃ makes the magnon and phonon couple at 0 T as a reality.³⁴ This allows MPX₃ to be ideal platforms for coupling of magnons and phonons. Effective control and management of phonons and magnons are significant challenges in contemporary physics and materials science. Electric fields, magnetic fields, and strain are commonly employed to regulate phonons. But in many cases, the propagation of magnons and phonons in magnonic devices requires the maintenance of global magnetic order. Local control of magnon–phonon coupling allows for the localized tuning of magnon properties without affecting the overall magnetic order. Consequently, for thin 2D vdWs materials, laser-induced local thermal modulation may be an effective approach for their device applications.³⁵ However, phonons exhibit low sensitivity to temperature, making it difficult to achieve precise control through temperature manipulation. Moreover, phonons related to magnetic order are more susceptible to the influence of magnetic fields than phonons that are unrelated to magnetism. So far, another interaction between spins and phonons which can manipulate pure phonons under a magnetic field in the absence of magnons and induce Raman scattering rotation has also been observed in 2D non-magnetic MoS₂,³⁶ InSe³⁷ and magnetic material CrBr₃.³⁸ Furthermore, the nonreciprocal change of polarized Raman intensity was also found in the magnetic material CrI₃.³⁹ These research findings provide new insights and application directions for the fundamental properties of phonons and their role in magnetic materials. However, how this spin–phonon interaction behaves in AFM is still unclear.

In this article, we report the spatially localized control of spin fluctuation by local laser heating to modulate magnon–phonon coupling and the energy of phonons coupled with magnons in the irradiated region without altering the global magnetic order, combined with Raman spectroscopy of 2D AFM FePSe₃. Our result also unambiguously demonstrates the existence of two degenerate phonon modes in this material by laser heating at 0 T and 6 T; these two phonons have opposite angular momentum and selectively interact with the spin-up and spin-down magnons. Besides, we observed spin–phonon interaction which induces a giant reciprocal rotation in FePSe₃ of the A_g mode at a high frequency in Raman spectra. The intensities of XX and XY polarization configurations show significant changes when the out-of-plane magnetic field is applied. The direction of polarization is counterclockwise when a positive magnetic field is applied, while the direction of polarization becomes clockwise when a negative magnetic field is applied.

2. Results and discussion

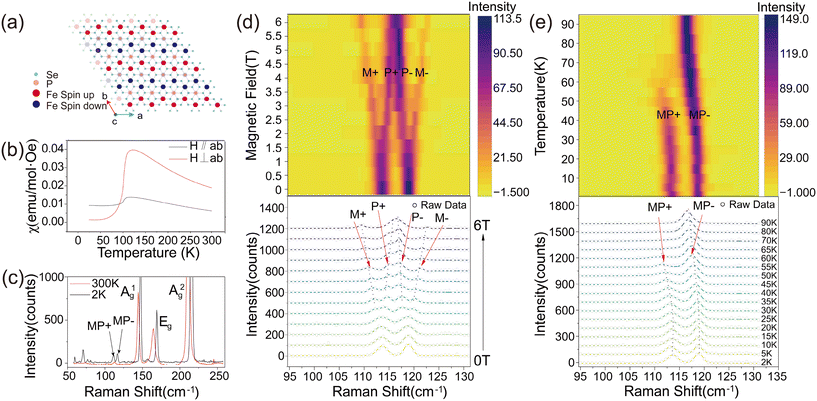
Transition metal phosphorus trichalcogenides (MPX₃, where M = Fe, Mn, Ni, and X = S, Se) are a family of van der Waals antiferromagnetic semiconductors,^30,31 whose monolayer counterparts present intralayer antiferromagnetism. Among them, FePSe₃ is promising for spintronics and magnonics due to its combination of antiferromagnetism and narrower band gap (∼1.3 eV). Its crystal structure belongs to the trigonal R3̄ space group and the top view is illustrated in Fig. 1a. At its magnetic ground state, the Fe atoms in a monolayer FePSe₃ lattice form a 2D hexagonal spin lattice, containing a zigzag antiferromagnetic (AFM) order.⁴⁰ The magnetic moments at Fe sites alternate between spin-up and spin-down configurations along the Z-axis on adjacent chains. As corroborated by the temperature-dependent magnetic susceptibility curve presented in Fig. 1b, the change of perpendicular (H⊥ab) magnetic susceptibility is much larger than that of parallel (H∥ab), pointing to a signature of strong magnetic anisotropy of the whole system in FePSe₃ that is consistent with its well-known Ising type magnetic order, which is out of plane.

Fig. 1 (a) Top-view of the FePSe₃ crystal structure and its magnetic ordering. (b) The magnetic susceptibility of FePSe₃. (c) Comparative Raman spectra of few-layer FePSe₃ at 300 K and 2 K. MP indicates the magnon–phonon coupled mode, where MP+ (MP−) refers to the coupling between spin-up (spin-down) magnons and phonons. (d) Raman intensity mapping and the corresponding spectra of FePSe₃ at 2 K as a function of magnetic field. M denotes the magnon peak, with M+ (M−) representing spin-up (spin-down) magnons. The two degenerate phonon modes, labeled as P, undergo splitting under magnon interactions. The resulting non-degenerate phonons coupled to spin-up (spin-down) magnons are denoted as P+ (P−). (e) Temperature dependence of Raman modes of low-energy magnon–phonon (MP) branches in few-layer FePSe₃, measured from 2 K to 90 K at a zero magnetic field.

Fig. 1c exhibits the Raman spectra of a few-layer FePSe₃ flake (about 25 nm, as shown in Fig. S1†) on a 280 nm SiO₂/Si substrate at 300 K and 2 K. The main Raman modes at higher frequencies (>120 cm⁻¹) primarily arise from the vibrations of the [P₂Se₆]⁴⁻ units and thus indicate blueshift with decreasing temperature. The Raman features emerging at lower frequencies (∼75 cm⁻¹ and 117 cm⁻¹) have been attributed to the vibrations of Fe²⁺ ions which turn into Raman-active modes after the phase transition from paramagnetic to AFM states.^41,42 Interestingly, the Raman mode at 117 cm⁻¹ “splits” into two modes upon the AFM transition. Some recent works claimed that these two additional features in Fig. 1c are the magnon–phonon coupling modes which are designated as MP, with MP+ (MP−) specifically indicating the coupling between phonon and spin-up (spin-down) magnon. By increasing external magnetic fields along the out-of-plane direction, the two MP modes split into four peaks (M+, P+, P− and M+), as shown in Fig. 1d. The M+ (blue up triangles) and M− (purple down triangles) show Zeeman splitting at higher magnetic fields (>1.5 T) with a g-factor of −0.71 and 0.66 cm⁻¹/T, respectively (shown in Fig. S2†), verifying their magnon essence. Meanwhile, the P+ and P− depart from M+ and M−, respectively, and merge into one peak whose peak position is no longer dependent on the fields. Fig. 1d presents the temperature-dependent Raman spectra of FePSe₃ at 0 T. At a low temperature range (<30 K), MP+ and MP− show negligible temperature dependence. As the temperature exceeds 30 K, a dramatic red shift takes place for both peaks. In the high temperature range (>60 K), the MP+ mode disappears completely, while the “MP−” mode is restored independent of temperature.

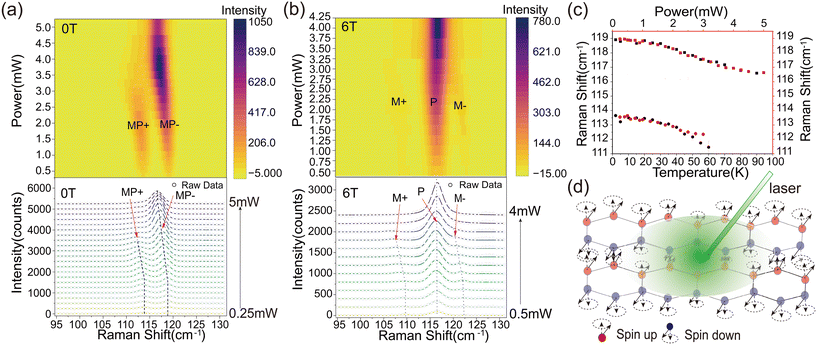
In FePSe₃, the phonon vibrational frequency and magnon precession frequency are coincidently in resonance, in stark contrast to FePS₃, where the magnon needs high magnetic fields driven by the Zeeman shift to reach resonance energy with the adjacent phonon. They could be very close or even overlay if strong coupling between the two quasiparticles does not exist. The temperature- and field-dependent evolution of MP+ and MP− both verify the existence of strongly coupled magnon–phonon at zero field. The increase in temperature globally changes the magnetic fluctuations, magnon and phonon populations, leading to the energy shift and change of coupling strength. To modify and detect the strong coupling locally, we performed power-dependent Raman scattering measurements on a few-layer FePSe₃ flake.

The evolution of the Raman spectra with varying laser power from 0.25 mW to 5 mW at 0 T is depicted in Fig. 2a. At mild laser powers (e.g., <1 mW), the MP+ and MP− branches (energy and peak intensity) are negligibly modified. As the laser power exceeds 1 mW, the peak positions of MP+ and MP− begin to exhibit an obvious redshift, from 113.8 and 118.9 cm⁻¹ to 111.4 and 116.9 cm⁻¹, respectively. At higher laser power (>3 mW), the MP+ branch vanishes as its signal intensity significantly decreases, while the MP− branch “merges” into the phonon mode labeled as “P”. The energy redshift of MP− saturates when laser power increases to ∼4.5 mW. Interestingly, the laser-power dependence (Fig. 2a) and the temperature dependence (Fig. 1e) of the Raman spectral energy position match very well at 0 T, implying that the sample is locally heated by the laser power. In this manner, the power-dependent Raman spectra of FePSe₃ at 6 T (Fig. 2b) experience similar temperature modification. The dotted lines in Fig. 2a and 1e represent the red shift of the Raman peaks, which are plotted versus laser power (red traces and axis) and temperature (black traces and axis) in Fig. 2c. By mirroring the two sets of traces, the temperature of the laser spot is accurately evaluated.

Fig. 2 (a) and (b) The laser power dependence Raman spectra of low-energy magnon–phonon (MP) branches in few-layer FePSe₃ at 0 T and 6 T, respectively. (c) The position of a Raman peak as a function of laser power and temperature at 0 T. Circles denote MP+ and squares denote MP−, with black indicating temperature-dependent parameters and red representing power-dependent parameters. (d) Schematic diagram of local tuning of magnon properties by laser heating.

In general, phonons and magnons are subject to Bose–Einstein statistics but operate in different energy regimes. The energy required to excite phonons is typically higher than that for magnons, making phonons less sensitive to temperature. As laser power increases, the high-wavenumber Raman peaks of FePSe₃ (as shown in Fig. S3†) remain unchanged, while the low-wavenumber MP+ and MP− peaks redshift predominantly. Since MP+ and MP− contain strongly coupled magnons and phonons, their sensitivity to temperature can be attributed to the contribution from either the low-wavenumber phonons or the magnons. According to the field-dependent Raman spectra (Fig. 1d), the magnons and phonons are completely decoupled at high magnetic fields (e.g., 6 T). Therefore, at 6 T, by increasing the laser power, the magnons and phonons are modified separately which fit well with temperature-dependent Raman spectra (Fig. S4b†). At this point, the magnons (M+ and M− branches) exhibit a redshift, while the phonon (P) barely changes in frequency (Fig. S4a†). This indicates that the low-wavenumber phonon is nearly independent of temperature and the redshift of MP+ and MP− mainly originate from the frequency change of magnons. It also unambiguously proves that the strong coupling at 0 T arises from a pair of degenerate phonons and two branches of antiferromagnetic magnons. Circularly polarized Raman spectroscopy in Fig. S8† shows the chirality of the two branches. The left- and right-handed chirality of lattice vibration selectively interacts with the spin-up and spin-down magnons, topologically protecting the strong coupling.³⁴ In addition, the laser power can locally decouple the magnon and phonon, thus adding an important controlling knob to the potential magnonic devices based on FePSe₃, and it is the interaction between magnons and phonons that modulates the phonon energy under local heating.

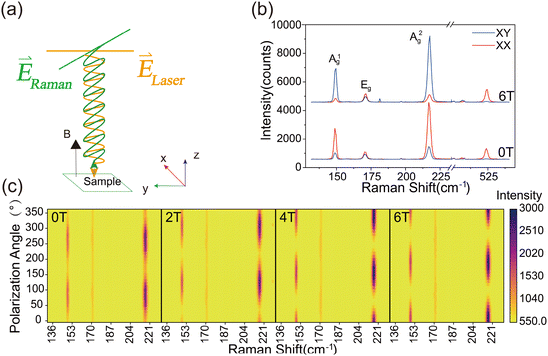
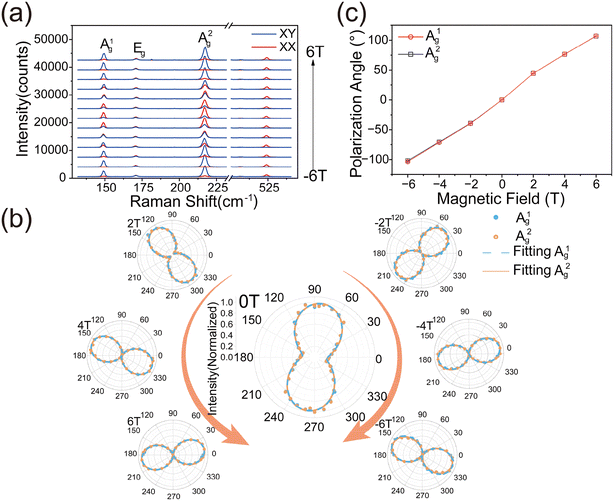
Besides the magnon–phonon strong coupling at low frequencies, the magneto-Raman effects of the high frequency phonons also show prominent field dependence. The Raman spectrum of phonons at 149.6 cm⁻¹ and 217.5 cm⁻¹ with A_g symmetry exhibit an apparent anisotropic polarization dependence behavior and show a marked twofold rotational symmetry. In contrast, the phonon at 171.5 cm⁻¹ with E_g symmetry is not sensitive to the polarization configuration, indicating that the in-plane E_g vibration mode is isotropic (Fig. S4†). Fig. 3a shows the experimental diagram of polarization Raman spectroscopy. The linear polarized incident light is directed vertically to the surface of the sample FePSe₃ and the Raman scattering is also normal to the surface, with the magnetic field applied along the z-axis. Fig. 3b shows the Raman spectrum of the Raman scattering parallel to the incident light (XX) and perpendicular to the incident light (XY), under the out-of-plane magnetic field at 0 T and 6 T, respectively. The relative Raman intensities of the XX and XY polarization configurations measured for the A_g modes change significantly with the magnitude of the applied magnetic field, while the intensity of the E_g mode remains unchanged and is found to be independent of the magnetic field. In contrast to FePSe₃, the scattering polarization of silicon also shows no dependence on the magnetic field, although a twofold anisotropic pattern is also observed, as shown in Fig. S5 and S6.† Therefore, this indicates that the observed phenomenon specifically occurs in the out-of-plane A_g mode phonons in 2D AFM FePSe₃ in the presence of the magnetic field. To further elucidate the effect of the magnetic field on the polarization Raman intensity of the A_g modes, angle-dependent maps of linear polarization Raman scattering of FePSe₃ are presented in Fig. 3c, with the magnetic field varying from 0 T to 6 T. The results show that the polarization direction of the two A_g modes rotates significantly with increasing magnetic field strength, while the intensity of the E_g mode remains constant. Additionally, the polarization axes of the A_g¹ and A_g² modes exhibit identical directions and angles of rotation under the same magnetic field. This spin–phonon optical phenomenon has previously been reported in the non-magnetic 2D material MoS₂.⁴³ As illustrated schematically in Fig. 3a, under an out-of-plane magnetic field, there is an angular deviation between the Raman scattering and the incident light. This phenomenon can be attributed to the Lorentz force acting on the local d-orbital electrons involved in the Raman scattering process, induced by the external magnetic field.

Fig. 3 (a) Experimental diagram of polarization Raman scattering. The polarization of the incident laser is along the y-axis while the scattering laser has an angle along the y axis with the magnetic field. (b) The parallel and perpendicular polarization A_g¹, E_g and A_g² Raman modes of FePSe₃ and Si with magnetic fields at 0 T and 6 T. (c) The 2D maps of the linear polarization Raman spectra of FePSe₃ with magnetic fields at 0 T, 2 T, 4 T, and 6 T, respectively.

To further verify this phenomenon, we measured the Raman scattering under the opposite magnetic field. The XX and XY polarization configurations of the Raman spectrum with the magnetic field from −6 T to 6 T are shown in Fig. 4a. The A_g mode intensity of XX polarization decreases with the magnetic field increasing from 0 T to 5 T and reaches the minimum at 5 T, then increasing with the field over 5 T, while XY configurations exhibit antiparallel behavior. Meanwhile, the negative magnetic field exhibits the same tendency. Additionally, the Raman scattering intensity of the A_g¹ and A_g² modes as a function of polarization angle under magnetic fields from −6 T to 6 T has also been measured, as shown in Fig. 4c. The polarization axis is parallel to the direction of the incident polarized light at 0 T. The rotation direction of the polarization axis reverses when the direction of the magnetic field is reversed. When a positive magnetic field is applied, the direction of polarization is counterclockwise, while the direction of polarization changes clockwise when a negative magnetic field is applied. More obviously, the rotation angle is remarkably giant, as shown in Fig. 4b and c. The polarization axis is rotated from −107° to 102° as the magnetic field varies from −6 T to +6 T and the absolute values of polarization rotation angles are equal in the positive and negative magnetic field, shown in Fig. 4b, which is different from the magnetic material CrI₃.³⁸ The frequency, line width, and peak shape of the Raman spectrum do not change, indicating that the magnetic field has no effect on the lattice structure.

Fig. 4 (a) The parallel and perpendicular polarization Raman spectra of FePSe₃ and Si with the magnetic field varying from −6 T to 6 T. (b) The linear polarization Raman spectrum of FePSe₃ with the magnetic field varying from −6 T to 6 T. (c) The rotation angle of polar Raman.

This phenomenon can be explained by the fact that when the FePSe₃ transfers from the non-magnetic to the antiferromagnetic case, the time-reversal symmetry is broken, which can induce an antisymmetric component in the Raman tensors.

When there is no magnetic field applied, the Raman tensor of FePSe₃ in the antiferromagnetic state is

When the magnetic field is applied normally to the sample surface, the Lorentz force will induce the motion of electrons in plane, and this changes the electronic susceptibility α(B) and modifies the Raman tensor elements. The magnetic field dependence α(B) can be derived by considering the Lorentz force. In a 2D case, the kinetic equations for electrons driven by a magnetic field can be written as

Thus,

Then, we can get the electronic susceptibility:

where ; when the applied magnetic field is close to the value B₀, it has the greatest effect on the Raman intensity. So, the Raman tensor of A_g now can be written as

The intensity of Raman scattering is given by

Therefore, , ; so, the intensity of XX and XY is influenced by the magnetic field, resulting in a transfer of Raman intensity between the two orthogonal polarization configurations. As for the reciprocal phenomenon, compared with ferromagnetic materials, the magnetic moments of antiferromagnetic materials are equal under positive and negative magnetic fields, resulting in the Lorentz force being consistent under positive and negative magnetic fields.

These newly observed phenomena exhibit signals several times stronger than traditional magneto-optical effects, such as the Kerr and Faraday effects, providing a new method for magneto-optical characterization. Moreover, using magnetic fields instead of other external fields to control the polarization of Raman modes is of great significance, as it offers a new way to manipulate phonons that are unrelated to magnetism. This control not only deepens the understanding of interactions between spins, phonons, and photons but also significantly expands the application scope and design freedom of magnonic devices, playing a very important role in the application of magnonics.

3. Conclusions

In summary, we unambiguously prove the magnon–phonon strong coupling in FePSe₃ at 0 T by combining field- and power-dependent Raman spectroscopy. The laser power can locally excite the spin fluctuation (the amplitude of spin precession), and the population and energy of the AFM magnon are consequently changed, thus modulating the magnon–phonon coupling and phonon energy, thereby adding an important controlling knob to the potential magnonic devices based on FePSe₃. A giant reciprocal spin–phonon interaction was observed. Through time symmetry breaking and Lorentz force on the local d-orbital electrons, the polarization axis of the A_g Raman mode can be dramatically rotated by an external out-of-plane magnetic field perpendicular to the basal plane. In contrast to the 2D ferromagnetic materials, the rotation of the Raman tensor in FePSe₃ is reciprocal and symmetric to positive and negative magnetic fields, which is due to the antiferromagntic orders. Our result demonstrates the 2D antiferromagnet FePSe₃ as a unique platform for spintronics and magnons both at zero and high fields.

4. Methods

4.1 Sample preparation

The FePSe₃ single crystal was grown using chemical vapor transport (CVT) reactions in a vacuum-sealed quartz tube with I₂ as the transport agent. Fe, P and Se powders were loaded on one side of the sealed tube with accurate stoichiometric proportions. The tube was then placed in a tube furnace, aligned to the middle of two heating zones. In two weeks, the source and empty ends of the tube were set at 750 and 650 °C, the temperature gradient driving the transport and reaction of chemical vapors, making nucleation and crystal growth happen at the low temperature end. After growth, millimeter sized crystals with a flake appearance were obtained. Few-layer FePSe₃ flakes were obtained from the FePSe₃ crystal synthesized by CVT via mechanical exfoliation by using polydimethysiloxane (PDMS), and transferred onto the Si substrates with a layer of 280 nm SiO₂. All the measurements were performed in a helium environment at a low temperature and the sample was very stable.

4.2 Magneto-Raman measurement

The Raman measurements were recorded using a WITec Alpha 300R confocal Raman microscope, based on a closed-cycle helium cryostat (attoDRY2100, attocube) with base temperatures down to 1.8 K and a superconducting magnet (the maximum out of plane magnetic field was up to ±9 T and the in-plane magnetic field was ±3 T). The 532 nm linear polarized laser was focused perpendicular to the surface of the sample through a 69.94× objective lens (numerical aperture = 0.82) for the Raman measurement at a low temperature and magnetic field. The maximum power was kept below 5 mW to avoid damage to the sample. The Raman signals were first collected using a photonic crystal fiber and then coupled into the spectrometer with 1800 g mm⁻¹ grating. The polarization-resolved Raman spectra were obtained by rotating the polarization of the analyzer, which was placed before the photonic crystal fiber.

Author contributions

Y.S. and B.L. contributed equally to this work. Y.S., B.L., S.L., and T.Y. conceived the project and designed the experiments. Y.S., B.L., S.A.X., and H.Y.L. prepared the samples and conducted the experimental measurements. C.K.G. performed the theoretical calculations. Y.S. and B.L. analyzed the data and wrote the manuscript with input from all coauthors. S.L. and T.Y. supervised the whole project.

Data availability

The datasets generated and analyzed in this study are available from the corresponding author on reasonable request. All relevant data supporting the findings of this study are included within the article and its ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by the National Key Research and Development Program of China (No. 2021YFA1200800) and the Start-up Funds of Wuhan University.

References

1. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
2. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
3. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136.
4. X. Cheng, Z. Cheng, C. Wang, M. Li, P. Gu, S. Yang, Y. Li, K. Watanabe, T. Taniguchi, W. Ji and L. Dai, Nat. Commun., 2021, 12, 6874.
5. Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. Zhang, Nature, 2018, 563, 94–99.
6. Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J.-H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782.
7. Y. Tian and S. Yan, Sci. China:Phys., Mech. Astron., 2013, 56, 2–14.
8. Z. Wang, I. Gutiérrez-Lezama, N. Ubrig, M. Kroner, M. Gibertini, T. Taniguchi, K. Watanabe, A. Imamoğlu, E. Giannini and A. F. Morpurgo, Nat. Commun., 2018, 9, 2516.
9. A. Barman, G. Gubbiotti, S. Ladak, A. O. Adeyeye, M. Krawczyk, J. Gräfe, C. Adelmann, S. Cotofana, A. Naeemi, V. I. Vasyuchka, B. Hillebrands, S. A. Nikitov, H. Yu, D. Grundler, A. V. Sadovnikov, A. A. Grachev, S. E. Sheshukova, J.-Y. Duquesne, M. Marangolo, G. Csaba, W. Porod, V. E. Demidov, S. Urazhdin, S. O. Demokritov, E. Albisetti, D. Petti, R. Bertacco, H. Schultheiss, V. V. Kruglyak, V. D. Poimanov, S. Sahoo, J. Sinha, H. Yang, M. Münzenberg, T. Moriyama, S. Mizukami, P. Landeros, R. A. Gallardo, G. Carlotti, J.-V. Kim, R. L. Stamps, R. E. Camley, B. Rana, Y. Otani, W. Yu, T. Yu, G. E. W. Bauer, C. Back, G. S. Uhrig, O. V. Dobrovolskiy, B. Budinska, H. Qin, S. Van Dijken, A. V. Chumak, A. Khitun, D. E. Nikonov, I. A. Young, B. W. Zingsem and M. Winklhofer, J. Phys.: Condens. Matter, 2021, 33, 413001.
10. S. Neusser and D. Grundler, Adv. Mater., 2009, 21, 2927–2932.
11. P. Pirro, V. I. Vasyuchka, A. A. Serga and B. Hillebrands, Nat. Rev. Mater., 2021, 6, 1114–1135.
12. B. Flebus, D. Grundler, B. Rana, Y. Otani, I. Barsukov, A. Barman, G. Gubbiotti, P. Landeros, J. Akerman, U. Ebels, P. Pirro, V. E. Demidov, K. Schultheiss, G. Csaba, Q. Wang, F. Ciubotaru, D. E. Nikonov, P. Che, R. Hertel, T. Ono, D. Afanasiev, J. Mentink, T. Rasing, B. Hillebrands, S. V. Kusminskiy, W. Zhang, C. R. Du, A. Finco, T. Van Der Sar, Y. K. Luo, Y. Shiota, J. Sklenar, T. Yu and J. Rao, J. Phys.: Condens. Matter, 2024, 36, 363501.
13. J. Cenker, B. Huang, N. Suri, P. Thijssen, A. Miller, T. Song, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Xiao and X. Xu, Nat. Phys., 2021, 17, 20–25.
14. A. McCreary, T. T. Mai, F. G. Utermohlen, J. R. Simpson, K. F. Garrity, X. Feng, D. Shcherbakov, Y. Zhu, J. Hu, D. Weber, K. Watanabe, T. Taniguchi, J. E. Goldberger, Z. Mao, C. N. Lau, Y. Lu, N. Trivedi, R. Valdés Aguilar and A. R. Hight Walker, Nat. Commun., 2020, 11, 3879.
15. D. Lujan, J. Choe, M. Rodriguez-Vega, Z. Ye, A. Leonardo, T. N. Nunley, L.-J. Chang, S.-F. Lee, J. Yan, G. A. Fiete, R. He and X. Li, Nat. Commun., 2022, 13, 2527.
16. W. Xing, L. Qiu, X. Wang, Y. Yao, Y. Ma, R. Cai, S. Jia, X. C. Xie and W. Han, Phys. Rev. X, 2019, 9, 011026.
17. A. V. Chumak, V. I. Vasyuchka, A. A. Serga and B. Hillebrands, Nat. Phys, 2015, 11, 453–461.
18. Y. Wang, D. Zhu, Y. Yang, K. Lee, R. Mishra, G. Go, S.-H. Oh, D.-H. Kim, K. Cai, E. Liu, S. D. Pollard, S. Shi, J. Lee, K. L. Teo, Y. Wu, K.-J. Lee and H. Yang, Science, 2019, 366, 1125–1128.
19. J. Han, P. Zhang, J. T. Hou, S. A. Siddiqui and L. Liu, Science, 2019, 366, 1121–1125.
20. W. Xing, L. Qiu, X. Wang, Y. Yao, Y. Ma, R. Cai, S. Jia, X. C. Xie and W. Han, Phys. Rev. X, 2019, 9, 011026.
21. H. Fulara, M. Zahedinejad, R. Khymyn, A. A. Awad, S. Muralidhar, M. Dvornik and J. Åkerman, Sci. Adv., 2019, 5, eaax8467.
22. D. A. Bozhko, V. I. Vasyuchka, A. V. Chumak and A. A. Serga, Low Temp. Phys., 2020, 46, 383–399.
23. T. T. Mai, K. F. Garrity, A. McCreary, J. Argo, J. R. Simpson, V. Doan-Nguyen, R. V. Aguilar and A. R. H. Walker, Sci. Adv., 2021, 7, eabj3106.
24. K. Wang, J. He, M. Zhang, H. Wang and G. Zhang, Nanotechnology, 2020, 31, 435705.
25. D. Lançon, H. C. Walker, E. Ressouche, B. Ouladdiaf, K. C. Rule, G. J. McIntyre, T. J. Hicks, H. M. Rønnow and A. R. Wildes, Phys. Rev. B, 2016, 94, 214407.
26. T. Jungwirth, X. Marti, P. Wadley and J. Wunderlich, Nat. Nanotechnol., 2016, 11, 231–241.
27. S. M. Rezende, A. Azevedo and R. L. Rodríguez-Suárez, J. Appl. Phys., 2019, 126, 151101.
28. J. R. Hortensius, D. Afanasiev, M. Matthiesen, R. Leenders, R. Citro, A. V. Kimel, R. V. Mikhaylovskiy, B. A. Ivanov and A. D. Caviglia, Nat. Phys., 2021, 17, 1001–1006.
29. M. A. Weiss, A. Herbst, J. Schlegel, T. Dannegger, M. Evers, A. Donges, M. Nakajima, A. Leitenstorfer, S. T. B. Goennenwein, U. Nowak and T. Kurihara, Nat. Commun., 2023, 14, 7651.
30. K. Du, X. Wang, Y. Liu, P. Hu, M. I. B. Utama, C. K. Gan, Q. Xiong and C. Kloc, ACS Nano, 2016, 10, 1738–1743.
31. R. Samal, G. Sanyal, B. Chakraborty and C. S. Rout, J. Mater. Chem. A, 2021, 9, 2560–2591.
32. D. J. Gillard, D. Wolverson, O. M. Hutchings and A. I. Tartakovskii, npj 2D Mater. Appl., 2024, 8, 6.
33. S. Liu, A. Granados del Águila, D. Bhowmick, C. K. Gan, T. Thu Ha Do, M. A. Prosnikov, D. Sedmidubský, Z. Sofer, P. C. M. Christianen, P. Sengupta and Q. Xiong, Phys. Rev. Lett., 2021, 127, 097401.
34. J. Cui, E. V. Boström, M. Ozerov, F. Wu, Q. Jiang, J.-H. Chu, C. Li, F. Liu, X. Xu, A. Rubio and Q. Zhang, Nat. Commun., 2023, 14, 3396.
35. F. Català, F. Marsà, M. Montes-Usategui, A. Farré and E. Martín-Badosa, Sci. Rep., 2017, 7, 16052.
36. J. Ji, A. Zhang, J. Fan, Y. Li, X. Wang, J. Zhang, E. W. Plummer and Q. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2349–2353.
37. W. Fu, X. Zhao, K. Wang, Z. Chen, K. Leng, D. Fu, P. Song, H. Wang, L. Deng, S. J. Pennycook, G. Zhang, B. Peng and K. P. Loh, Nano Lett., 2020, 20, 5330–5338.
38. T. Yin, K. A. Ulman, S. Liu, A. Granados Del Águila, Y. Huang, L. Zhang, M. Serra, D. Sedmidubsky, Z. Sofer, S. Y. Quek and Q. Xiong, Adv. Mater., 2021, 33, 2101618.
39. Z. Liu, K. Guo, G. Hu, Z. Shi, Y. Li, L. Zhang, H. Chen, L. Zhang, P. Zhou, H. Lu, M.-L. Lin, S. Liu, Y. Cheng, X. L. Liu, J. Xie, L. Bi, P.-H. Tan, L. Deng, C.-W. Qiu and B. Peng, Sci. Adv., 2020, 6, eabc7628.
40. A. Wiedenmann, J. Rossat-Mignod, A. Louisy, R. Brec and J. Rouxel, Solid State Commun., 1981, 40, 1067–1072.
41. Q. Xie, S. Hu, C. Hu, Q. Sheng, L. Chen, J. Zheng, W. Wang, L. Ma and G. Cheng, Appl. Phys. Lett., 2023, 122, 161901.
42. D. Jana, P. Kapuscinski, A. Pawbake, A. Papavasileiou, Z. Sofer, I. Breslavetz, M. Orlita, M. Potemski and C. Faugeras, Phys. Rev. B, 2023, 108, 144415.
43. Y. Wan, X. Cheng, Y. Li, L. Dai and E. Kan, RSC Adv., 2021, 11, 4035–4041.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04743e

‡ These authors contributed equally to this work.

---