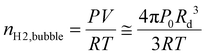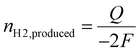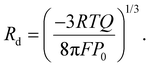Combined effects of electrode morphology and electrolyte composition on single H₂ gas bubble detachment during hydrogen evolution reaction

Abstract

During the hydrogen evolution reaction, H₂ gas bubbles form on the electrode surface, significantly affecting electrochemical processes, particularly at high current densities. While promoting bubble detachment has been shown to enhance the current density, the mechanisms governing gas bubble detachment at the electrochemical interface remain poorly understood. In this study, we investigated the interplay between electrode surface morphology and electrolyte composition on single H₂ gas bubble detachment during hydrogen evolution reaction (HER). Using well-defined Pt microelectrodes as model systems, we systematically modify and enhance their surface roughness through mechanical polishing to investigate these effects in detail. By modulating the Marangoni effect through variations in electrolyte composition and applied potential, we identified two distinct detachment behaviours. When the Marangoni force acts towards the electrodes, H₂ gas bubbles are positioned closer to the electrode surface and exhibit roughness-dependent detachment, with smaller bubbles detaching earlier on rougher surfaces. Conversely, when the Marangoni force is directed away from the electrode, H₂ gas bubbles are located farther from the electrode surface and show roughness-independent detachment sizes. These findings highlight the importance of considering both electrode and electrolyte effects to optimize gas bubble detachment during electrochemical reactions.

---

Sunghak Park

Sunghak Park is an Assistant Professor in the Department of Future Energy Engineering at Sungkyunkwan University, Republic of Korea. He received his Ph.D. in Materials Science and Engineering from Seoul National University in 2019. He subsequently conducted postdoctoral research at Seoul National University (2019–2021) and at the Leiden Institute of Chemistry, Leiden University (2021–2024). His research focuses on understanding and controlling various dynamic phenomena at (photo)electrochemical interfaces, including gas bubble evolution during electrochemical reactions.

Introduction

Hydrogen, produced via water electrolysis using renewable electricity, is expected to play a crucial role in achieving a sustainable energy system by enabling surplus renewable electricity storage, decarbonizing sectors that are difficult to electrify, and replacing fossil fuels as feedstock in chemical and fuel production industries.^1,2 For efficient water electrolysis, extensive research has been conducted to better understand and optimize the electrode/electrolyte interface, where the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) take place.^3–8 However, under high current density conditions, which are typical for practical water electrolyser operations, the interface becomes more complex due to the inevitable formation of gas bubbles. The evolution of these gas bubbles—through nucleation, growth, coalescence, and detachment—could significantly affect the energy conversion efficiency of water electrolysis. This occurs through several mechanisms, including altering concentration fields, blocking the active surface area of electrocatalysts, increasing solution resistance, and inducing convective flow.^9,10 Moreover, gas bubble evolution has been suggested to affect electrode stability, either through inducing mechanical stress or by increasing local current density.^11,12

While a comprehensive understanding on how to accurately predict and control the impacts of gas bubble evolution on electrochemical responses has not yet been achieved, recent studies have shown that promoting faster gas bubble detachment can improve efficiency and increase current density.^13,14 Gas bubble detachment is a complex phenomenon influenced by a range of forces. When external fields such as convective flow, magnetic, or acoustic fields are applied, additional forces can be exerted to enhance gas bubble detachment and improve efficiency.¹⁵ In the absence of such external forces, the detachment of a single gas bubble is primarily governed by the balance between buoyancy and surface tension at the triple-phase boundary, as described by the Fritz model for spreading bubbles.¹⁶ The Fritz model along with the corresponding result for pinned bubbles^17,18 has provided a rationale for recent efforts to enhance gas bubble detachment without additional energy input by reducing pinning forces, achieved through engineering electrode surface properties such as wettability, hydrophilicity, and hydrophobicity.^19–21

Beyond capillarity, recent studies on single gas bubble evolution using disk-type microelectrodes have highlighted the crucial role of additional forces acting on gas bubbles generated during electrochemical reactions.^22–24 For instance, electrostatic interactions between charged gas bubbles and polarized electrodes may become important, potentially explaining the oscillatory motion observed in single H₂ gas bubbles under large overpotentials.²⁵ Another influential force, arising from solutal or thermal Marangoni flow²⁶—a convective flow along the bubble/electrolyte interface driven by surface tension gradients due to concentration or temperature gradients—has been experimentally validated.²⁷ As a result of this convective flow, gas bubbles experience an additional hydrodynamic force known as the Marangoni force. Given that surface tension is inherently dependent on various factors such as temperature, pressure, and concentration, the specific origin of the Marangoni force can vary depending on the electrochemical conditions. A temperature gradient caused by intense ohmic heating near the electrode surface region at high current densities has been identified as one source of these surface tension gradients during hydrogen evolution reaction, a phenomenon called thermal Marangoni effect.^28,29 Furthermore, our groups have shown that variation in electrolyte composition and concentration could manipulate gas bubble detachment,^30,31 which can be rationalized by the Marangoni force driven by ion concentration gradient, referred to as the solutal Marangoni effect.³² Recent simulations support these findings by providing detailed indication of the relative importance of thermal and solutal Marangoni effects under specific electrochemical conditions.^33,34

In this study, we expand previous findings by investigating how variations in electrode surface morphology and electrolyte composition affect gas bubble behaviour at the electrochemical interface. Our initial observation revealed that gas bubble detachment from a freshly polished electrode surface was inconsistent, likely due to inconsistent contact of the bubble with contamination on Pt. We found that an electrochemical pretreatment involving potential cycling between oxidative and reductive potentials could provide a well-defined clean surface with consistent gas bubble evolution. Using this pretreatment, we further studied gas bubble evolution on electrodes with varied surface morphologies. Our results reveal that the detachment size depends on surface roughness, correlating with the direction of the Marangoni force. Specifically, when the Marangoni force is directed toward the electrode, gas bubbles detach more quickly and at smaller sizes on rougher surfaces compared to smoother ones, indicating roughness-dependent detachment size. Conversely, when the Marangoni force is directed away from the electrode, detachment size remains the same regardless of surface roughness, indicating roughness-independent behaviour in these conditions. These findings highlight the importance of a comprehensive understanding of both electrolyte and electrode effects at the electrochemical interface for optimizing gas bubble detachment. Relying solely on either electrode or electrolyte properties may not be sufficient; instead, the combined influence of both is essential for achieving optimal gas bubble detachment.

Results and discussion

For accurately studying single H₂ gas bubble evolution, establishing an appropriate surface preparation protocol is essential. To achieve this, we first focus on how to achieve reproducible electrochemical oscillations during hydrogen evolution reaction in H₂SO₄, providing insights on the H₂ gas bubble evolution. Previous studies using 100 μm-sized microelectrodes in H₂SO₄ have shown that single H₂ gas bubbles periodically evolve from the electrode surface.^30,35–38 This process induces periodic oscillations in the current during chronoamperometry and in the potential during chronopotentiometry, with each oscillation peak corresponding to the moment of bubble detachment (ESI Fig. S1†). By analysing the oscillation period in either chronoamperometry or chronopotentiometry, the time required for bubble detachment (i.e., the period of the bubble evolution, T) of a single gas bubble can be determined under the given conditions.

For example, Fig. 1a illustrates a complete evolution cycle of such a single H₂ bubble produced at −1.3 V_RHE (vs. Reversible Hydrogen Electrode, RHE) in 1 M H₂SO₄, represented by the electrochemical current response and corresponding snapshots of the bubble. Note that the observations described here similarly also apply at less negative potentials.³⁰ Following the departure of the preceding bubble at time t = 0, the current is high initially, which is attributed to an increased availability of the electrode surface and a reduction in the obstruction of current pathway. This triggers the nucleation of numerous nano- and micrometer-sized gas bubbles on the electrode surface, which quickly coalesce to form a single larger bubble. Previous studies have demonstrated that H₂ bubble might reside atop a “carpet” of microbubbles, meaning that it is not necessarily in direct contact with the electrode surface. Consequently, bubble growth occurs not only via gas diffusion¹⁸ but also through intensive coalescence with this bed of tiny precursors.^13,25,30

Fig. 1 (a) The current vs. dimensionless time (t/T), supplemented with the snapshots of the H₂ bubble at different stages of its evolution (correspondingly marked by hexagon symbols). t/T = 0 marks the bubble nucleation and t/T = 1 denotes the bubble detachment. T is the period of the bubble evolution. The red inset zooms into the bubble's bottom region, highlighting the microbubble carpet sandwiched between the primary bubble and the electrode surface. Black scale bar represents 200 μm, and white scale bar within the inset is 50 μm. (b) An example of measuring the thickness of microbubbles’ carpet, δ, (for details see Experimental section). The experiments correspond to a rougher surface (mechanically polished with sandpaper) at −1.3 V_RHE in 1 M H₂SO₄.

As the bubble grows, the electrochemical current gradually reduces, eventually attaining a minimum value (approximately at t/T = 0.5 in Fig. 1a). This decline is attributed to the increasing size of the bubble and its position relative to the electrode surface, which is influenced by the carpet thickness δ (shown in Fig. 1b). The δ, calculated as the distance between the bubble base and the electrode surface, has been previously observed to vary throughout the bubble evolution (see also Fig. 6c and d) in response to varying force balance.^25,30,39 Although the bubble continues to grow, the electrochemical current begins to rise again after approximately t/T = 0.5. This behavior results from the interplay between the carpet thickness and the bubble size, both of which affect the current path and available electrode surface area, and consequently, the ohmic resistance.^9,40 At t/T = 1, the bubble departs, reaching a critical radius R_d where upward forces such as buoyancy (F_b) overcome downward forces like Marangoni (F_M) and electric (F_e) forces. This departure event causes a sharp increase in the electrochemical current, marking the beginning of the next evolution cycle. For additional details such as the radius (R) over time, also in 1 M HCl, we refer to ESI Fig. S2.†

Furthermore, because the size of the H₂ gas bubble significantly exceeds that of the electrode, nearly all the generated H₂ gas is captured by the bubble rather than diffusing into the bulk electrolyte.^30,35 Under these conditions, the detachment radius of the single H₂ gas bubble can be estimated by calculating the accumulated charge during each oscillation and applying Faraday's law. Further details of the oscillation analysis can be found in the Experimental section.

Fig. 2a displays the oscillation of the electrochemical current recorded in H₂SO₄ at −0.32 V_RHE using an electrode surface prepared by mechanical polishing. Despite holding the potential at a fixed value, the oscillations were unstable, with fluctuating amplitude, period, and shape across successive periods. This instability indicates irreproducible single gas bubble evolution on the electrode surface between different cycles, likely influenced by surface debris or contaminations introduced during electrode preparation. To assess the condition of the Pt microelectrode surface, a blank voltammogram was measured in H₂SO₄ (Fig. 2b).⁴¹ The light blue curves show no distinct hydrogen peaks at 0.125 V_RHE and 0.270 V_RHE, which are characteristic of the (110) and (100) step sites of a clean polycrystalline Pt surface, respectively.^42,43

Fig. 2 This figure demonstrates the effect of the electrochemical pretreatment on reproducible electrochemical oscillation: (a) chronoamperometry curve of a 100 μm Pt disk microelectrode without electrochemical pretreatment (measurement condition: 0.5 M H₂SO₄, −0.32 V_RHE). (b) Cyclic voltammogram during electrochemical pretreatment (pretreatment condition: potential cycling between 0.05 to 1.35 V_RHE, 30 cycles at scan rate of 1 V s⁻¹). (c) Chronoamperometry curves after electrochemical pretreatment (measurement condition: 0.5 M H₂SO₄, −0.32 V_RHE). Each trial was performed on different days using the same electrode and procedure. (d) Period of electrochemical oscillation in (c).

Subjecting the Pt microelectrode to oxidation–reduction potential cycling, a common pretreatment method for cleaning a Pt surface, resulted in well-defined blank voltammogram, with clearly visible hydrogen peaks at 0.125 V_RHE and 0.270 V_RHE (dark blue curved in Fig. 2b). Following this pretreatment, stable, reliable, and reproducible oscillations were observed during chronoamperometry at a fixed potential (Fig. 2c), indicating consistent single H₂ gas bubble evolution on the electrode surface after electrochemical pretreatment. Furthermore, highly reproducible oscillation data were consistently obtained when the same Pt microelectrode was used after undergoing the electrochemical pretreatment steps (Fig. 2c and d).

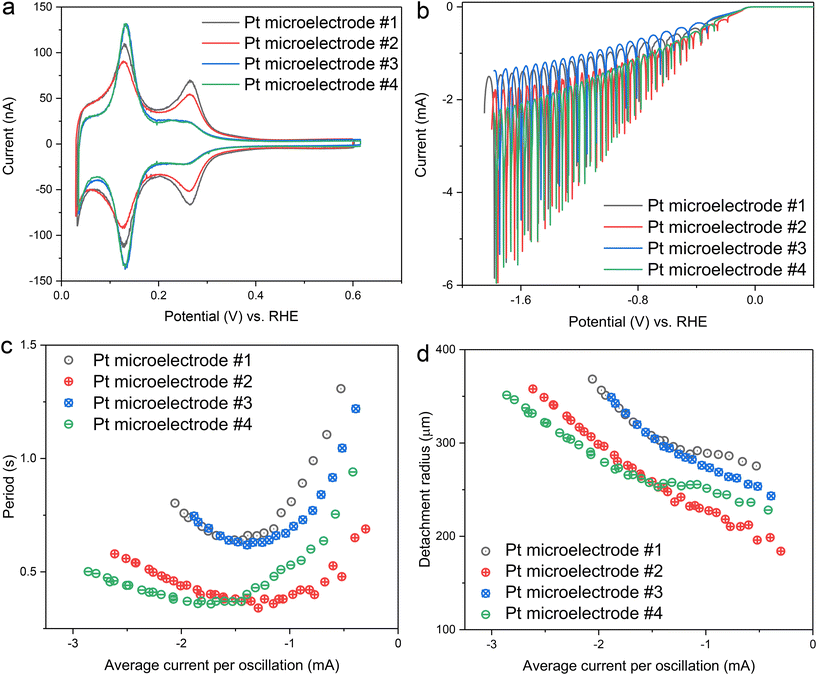
In the next step, the reproducibility of the oscillation was further evaluated by preparing four different Pt microelectrodes. After the potential cycling pretreatment, all four electrodes displayed clear blank voltammograms, though with varying ratios between different hydrogen adsorption/desorption peaks (Fig. 3a). Based on the ratio of the hydrogen peaks corresponding to the (110) and (100) step sites, the electrodes were grouped into two categories: electrodes #1 and #2 exhibited both (110) and (100) hydrogen peaks, while electrodes #3 and #4 showed one strong hydrogen peak, corresponding to the (110) step site. These variations in peak ratios suggest differences in surface texture among the electrodes, likely caused by the non-homogeneous texture of the original Pt wire used to prepare the Pt microelectrodes. Despite the differences in surface texture, no significant influence on H₂ gas bubble evolution was observed in H₂SO₄ (Fig. 3b). All electrodes exhibited clear oscillation over a wide potential range, regardless of their surface characteristics. The trends in period and detachment radius were also consistent across all electrodes: as the magnitude of average current (or overpotential) increased, the period followed a V-shaped curve, while the detachment radius kept increasing (Fig. 3c and d).

Fig. 3 Reproducibility of electrochemical oscillation from different Pt microelectrodes. (a) Blank voltammograms of each Pt microelectrode, highlighting hydrogen adsorption/desorption peaks at a scan rate of 0.5 V s⁻¹ after pretreatment. (b) Linear sweep voltammograms of each Pt microelectrode, recorded at a scan rate of 0.1 V s⁻¹ to capture oscillatory features during the sweep. (c) Period of a single H₂ gas bubble evolution, obtained from the oscillations shown in (b). (d) Detachment radius of a single H₂ gas bubble, derived from electrochemical oscillations in (b).

According to previous studies, the V-shaped behaviour of the period can be explained by two distinct origins of the surface tension gradient that govern the Marangoni effect.³¹ At low current conditions, the surface tension gradient is primarily determined by ion concentration gradients, leading to the dominance of solutal Marangoni forces. Since H₂SO₄ has a positive surface tension increment,⁴⁴ the resulting solutal Marangoni force is directed toward the electrode. At high current conditions, the temperature gradient becomes the dominant factor, resulting in the dominance of thermal Marangoni forces, which also act toward the electrode due to the higher temperature near the electrode surface. Although both solutal and thermal Marangoni forces act in the same direction in the case of H₂SO₄, their dependence on current differs, leading to distinct relationships: in the solutal-dominant regime, the period is inversely proportional to the current, while in the thermal-dominant regime, the period scales linearly with the current (see the ESI of Park et al.³¹). Notably, the attained minimum of the period in Fig. 3c, where these two competing factors are comparable, occurs at similar currents of approximately −1.5 mA for all electrodes. This implies consistent transition behaviour between the two regimes, independent of surface texture.

Although the general trends in period and detachment radius were consistent across all electrodes, the absolute values varied between them. Considering that the origin of the Marangoni force—ion concentration and temperature gradients—is primarily influenced by the current, the deviations observed between different electrodes under the same current conditions suggest the involvement of additional forces other than the Marangoni force. Possible contributors to these additional forces include pinning forces at the triple-phase boundary (adhesion forces),⁴⁵ an apparent force arising from the bubble-bubble coalescence, and an electrical force³⁹ (ESI Fig. S3†). While the exact origin of these additional forces cannot be identified at this moment, they appear to be more sensitive to differences between electrodes, such as scratches or slightly different morphologies, rather than surface texture difference. For example, electrode #3 and #4 exhibited nearly identical blank voltammograms, yet their detachment period and radius values were notably different.

To further investigate how surface morphology affects the detachment of single H₂ gas bubbles, we prepared two extreme morphologies of electrode surfaces using different polishing procedures (Fig. 4a). A smoother surface was prepared by polishing the electrode with diamond polishing suspensions of decreasing particle size (smallest particle size: 0.05 μm). As shown in Fig. 4b and c, a symmetrical, circular bright region is clearly visible, confirming the ideal disk-shaped geometry of the Pt microelectrode. AFM measurements further confirmed the smoothness of the electrode surface, with a root mean square (RMS) roughness of 9.6 nm (Fig. 4d and ESI Fig. S4†). Several fine lines visible in both the SEM and AFM images are scratches introduced during the polishing process. In contrast, a rougher surface was achieved by polishing the electrode with SiC sandpaper (average particle size: 10.3 μm), followed by the same electrochemical pretreatment. The effect of sandpaper polishing is evident in the SEM images (Fig. 4e and f), which reveal a much rougher surface with multiple valleys of varying heights and orientations. AFM measurements confirm the roughness, showing an RMS roughness of 186 nm. Furthermore, the roughness factor—defined as the ratio between the electrochemically active surface area and the geometrical surface area—was determined from hydrogen desorption peaks.^46,47 The rougher surface exhibits a higher roughness factor (4.7) compared to the smoother surface (1.4), further supporting the differences in surface morphology between the two electrodes (ESI Fig. S5†).

Fig. 4 Surface morphology characterization of microelectrodes with smoother and rougher surfaces. (a) Schematic illustration of the preparation procedure for smoother and rougher surfaces. The smoother surface was achieved by polishing with diamond paste (particle size: 0.05 μm), while the rougher surface was prepared by polishing with SiC sandpaper (average particle size: 10.3 μm). Both surfaces underwent the same electrochemical pretreatment after polishing. (b and c) Scanning Electron Microscopy (SEM) images of the smoother surface. (d) AFM height image (50 μm × 50 μm) of the smoother surface. (e and f) SEM images of the rougher surface. (g) AFM height image (50 μm × 50 μm) of the rougher surface. Scale bars in SEM images are 10 μm. Note that the height scale in d and g are different.

The effect of surface roughness on the evolution of single H₂ gas bubble was investigated using linear sweep voltammetry in two different electrolytes: 1 M H₂SO₄ and 1 M HCl. Both electrolytes exhibit high microbubble coalescence efficiency but differ in surface tension increment (H₂SO₄: 0.44 mN m⁻¹ mol⁻¹ L and HCl: −0.27 mN m⁻¹ mol⁻¹ L⁻¹).⁴⁴ The opposite signs of these surface tension increments result in the solutal Marangoni forces acting in opposite directions on H₂ gas bubbles in each electrolyte. This contrast therefore provides an ideal system for modulating the solutal Marangoni effect while maintaining the evolution of individual H₂ gas bubbles. A comparison of the two surface morphologies revealed that the rougher surface exhibited a larger HER current, which is attributed to its larger surface area and distinct bubble-electrode geometry (further discussion will be provided in the context of Fig. 6). Specifically, the minimum point of each oscillation (indicated by dashed lines in Fig. 5a and d) is higher for the rougher surface, resulting in a higher average current per oscillation for the rougher surface in both electrolytes (ESI Fig. S6†).

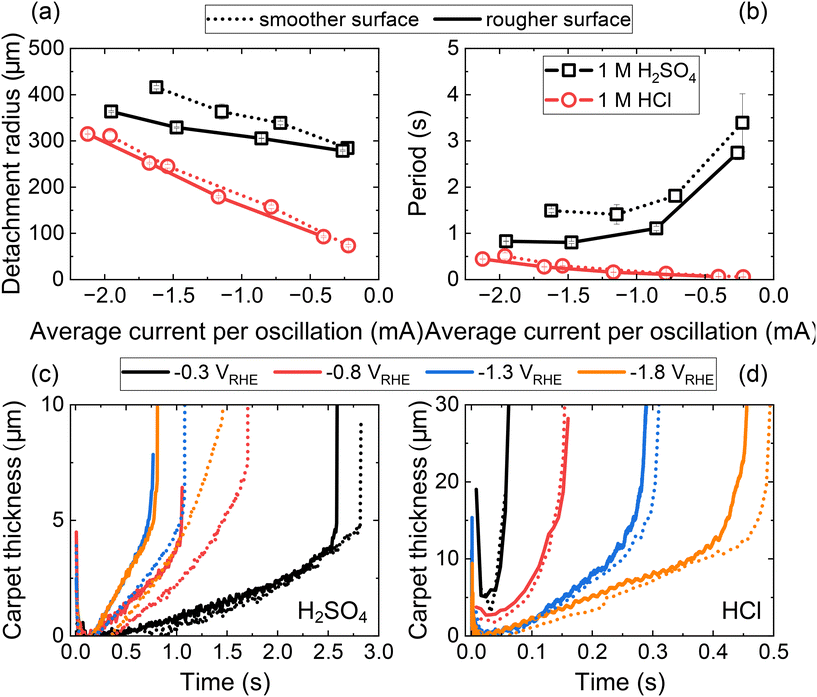
Fig. 5 Roughness effects on single H₂ gas bubble detachment in 1 M H₂SO₄ and 1 M HCl. (a) Linear sweep voltammograms in 1 M H₂SO₄. (b and c) Period (b) and detachment radius (c) of single H₂ gas bubbles in 1 M H₂SO₄, analyzed from oscillations in a. (d) Linear sweep voltammograms in 1 M HCl. (e and f) Period (e) and detachment radius (f) of single H₂ gas bubbles in 1 M HCl, analyzed from oscillations in d. (g and h) Period (g) and detachment radius (h) obtained from oscillation analysis via chronoamperometry in 1 M HCl using two different electrodes with different surface conditions. Raw electrochemical oscillation data can be found in ESI Fig. S7.† The yellow and blue areas in the figures serve as visual guides to distinguish between two different regimes: where the Marangoni force is directed toward the electrode (yellow) and away from the electrode (blue), respectively.

Fig. 6 Detailed bubble evolution during chronoamperometry. Detachment radius (a) and period (b) as a function of average current per oscillation. Carpet thickness (c and d) throughout the bubble evolution for 1 M H₂SO₄ and 1 M HCl, respectively. The dotted curves mark the smoother surfaces, while the solid curves correspond to the rougher surfaces.

In H₂SO₄, the periods for both the smoother and the rougher surfaces exhibited a V-shaped curve (Fig. 5b) as a function of the average current per oscillation. Across the entire parameter range studied, faster detachment was observed from the rougher surface. The period is determined by both the detachment size of the gas bubble and the rate of gas bubble growth, which is determined by the average current per oscillation. Analysis of the detachment radius further revealed that the faster detachment on the rougher surface was attributable not only to an increased average current, hence faster reaction and hydrogen generation, but also to a smaller detachment radius on the rougher surface (Fig. 5c). This reduced detachment radius suggests the retaining force acting on the H₂ gas bubble in H₂SO₄ is diminished on the rougher surface, facilitating the earlier detachment. As discussed later, the additional retaining force on the smoother surfaces is primarily attributed to a pinning force at the bubble/electrode contact area.

In the case of HCl electrolyte, the period decreased monotonically with the (absolute) HER current (Fig. 5e). The absence of an inversely correlating region in this electrolyte can be explained by the direction of the solutal Marangoni force, which is directed away from the electrode due to a negative surface tension increment.⁴⁴ This results in faster detachment in a low current region compared to the case of H₂SO₄, leading to a continuously decreasing period as the overpotential or current decreases. In relation to surface morphology, the slope of the detachment period curve was smaller for the rougher surface, indicating faster detachment from the rougher surface, consistent with the result from H₂SO₄.

However, the detachment radius in HCl showed a trend distinct from that observed in H₂SO₄. At lower average current levels, the detachment radius was the same for both smoother and rougher surfaces, with roughness-dependent behaviour (smaller detachment size for the rougher surface) appearing only at higher current conditions (Fig. 5f). This trend was further clarified by oscillation analysis from chronoamperometry, which provides average values for the period and detachment radius at each potential or current level (Fig. 5g, h and ESI Fig. S7†). It is noteworthy that the detachment radius obtained from both surface morphologies and two separate electrodes matched at low current, highlighting a roughness-independent behaviour in this regime. The similar detachment size across smoother and rougher surfaces indicates the reduction or absence of roughness-sensitive retaining forces under these specific conditions.

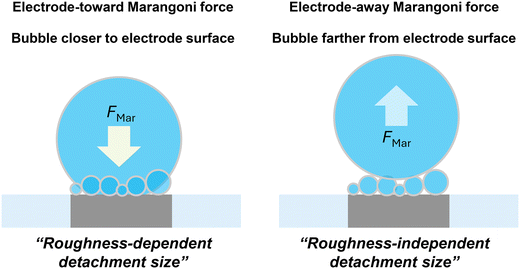
These observations provide a notable correlation between the detachment radius and the direction of Marangoni force. In H₂SO₄, the solutal and thermal effects align, resulting in a Marangoni force directed toward the electrode across all current regions. In contrast, for HCl, the direction of the Marangoni force would gradually shift away from the electrode toward the electrode as the current increases and the dominant Marangoni effect transitions from solutal to thermal. Previously, we estimated the boundary conditions (potentials and currents) between these competing effects by comparing surface tension change ratios associated with temperature and ion concentration variations. In 1 M HCl, the boundary condition was identified around −1 mA.³⁰ Using this boundary condition, we provided a visual representation in Fig. 5, where regions with a Marangoni force directed toward the electrode are highlighted in yellow, and regions with a force directed away from the electrode are marked in blue. As illustrated in Fig. 5c, f and h, the detachment radius depends on surface roughness when the resultant Marangoni force is directed towards the electrode (yellow region). However, when the Marangoni force is directed away from the electrode (blue region), the detachment radius becomes independent of surface roughness.

To further examine the geometry of a single H₂ gas bubble during HER, specifically its size and position relative to the electrode surface, an additional set of chronoamperometric measurements was conducted at various potentials using two new microelectrodes in parallel with image recording using a high-speed shadowgraphy system, see Fig. 1 and 6 and ESI Fig. S2.† Note that each of the two electrodes has been exclusively used for the measurements in either 1 M H₂SO₄ or 1 M HCl. Furthermore, each of the two electrodes was first polished using the diamond polishing suspensions (down to 0.05 μm) to perform measurements on smoother surface and then re-polished with a SiC sandpaper (10.3 μm) to perform measurements on rougher surface.

Fig. 6 documents the detachment radius (a) and period (b) of the bubble as a function of average current per oscillation in 1 M H₂SO₄ (black line) and 1 M HCl (red line). Fig. 6c and d document the thickness of the carpet (see Fig. 1b for definition), as a function of time in 1 M H₂SO₄ (c) and 1 M HCl (d), and for various potentials. The dotted curves represent measurements for the smoother surfaces, while the solid curves correspond to the rougher surfaces. Additional details, including the time-dependent current, the average current per oscillation as a function of potential, the time-dependent radii of single bubbles and the carpet thickness as a function of bubble radius are provided in the ESI Fig. S8, S9 and S10.†

Similar to Fig. 5, the average current per oscillation is consistently higher across the studied potential range for the rougher surface compared to the smoother surface (see ESI Fig. S8†). This observation holds true for both 1 M H₂SO₄ and 1 M HCl. The trends in bubble detachment size (Fig. 6a) and period (Fig. 6b) also align with those observed in Fig. 5. Specifically, for 1 M H₂SO₄ in Fig. 6a and b, both the bubble detachment size and period are consistently larger for the smoother surface across the entire range of average current studied. In contrast, for 1 M HCl, these characteristics are comparable in the lower range of average current (blue region in Fig. 5) but become larger for the smoother surface at higher average currents (yellow region in Fig. 5).

The higher electrochemical current observed for the rougher surface compared to the smoother surface can be attributed to differences in the geometry of the bubble-electrode system, specifically to differences in the carpet of microbubbles (Fig. 6c and d) that separate the bubble base from the electrode surface. In the case of 1 M H₂SO₄ (Fig. 6c) at −0.3 V_RHE, the similarity in δ for both surfaces results in comparable current and detachment size (see ESI Fig. S8† and Fig. 6a). However, as the overpotential increases, the difference in δ between bubbles generated on rougher (larger δ) and smoother (smaller δ) surfaces leads to a significant increase in current (e.g., at −0.8 V_RHE, −1.3 V_RHE, and −1.8 V_RHE). ESI Fig. S10† documents the carpet thickness δ as a function of bubble radius and applied potential. A similar trend is observed for 1 M HCl, although values of δ from smoother and rougher surfaces are more alike in this case. Note, however, that imaging limitations, such as slight defocusing of the bubble contour, inaccuracies in detecting the position of electrode and bubble base, or image analysis errors, could potentially introduce discrepancies of a few pixels (1 pixel ≈ 1 μm).

The carpet thickness is governed by the balance of forces acting on the growing bubble. In the case of 1 M H₂SO₄, this balance can be thought of a competition between upward buoyancy (F_b), and downward forces, such as the Marangoni (F_M) and electric (F_e) forces. The apparent downward force arising from bubble-carpet coalescence has been demonstrated to be negligible (see ESI in Bashkatov et al.¹³). Both F_M and F_e have been shown to depend non-linearly on δ.^25,36,39 Therefore, as the buoyancy force continues to grow with increasing bubble size, the system adjusts dynamically shifting the equilibrium position to a larger δ (see ESI Fig. S10† for a δ vs. R dependence). This leads to an increase in the current,²⁵ which in turn affects the downward forces.

However, this process has a limit. F_M and F_e reach their maximum magnitudes at a critical bubble carpet thickness δ, beyond which they begin to decrease as δ increases further.^25,36,39 When the buoyancy force exceeds the combined downward forces, the equilibrium can no longer be maintained, resulting in bubble departure from the electrode surface at R_d. Further complexity arises from the solutal and thermal Marangoni effects, which may act in opposite directions—as seen in the case of 1 M HCl—and both dependent on the current.

To strengthen the point, Bashkatov et al.³⁶ reported that dynamic changes in the applied potential further influence δ. When the potential increases [decreases] during bubble evolution, the stronger [weaker] downward forces bring the bubble closer to [farther from] the electrode, leading to a thinner [thicker] bubble carpet thickness δ according to the new equilibrium position. Bashkatov et al.³⁶ also reported that the critical δ depends on the applied potential (or current). When the potential is interrupted (set to the level of open circuit potential, OCP), the bubble departs from the electrode rapidly.

The trend observed in Fig. 6c and d, comparing δ between 1 M H₂SO₄ and 1 M HCl, aligns with the above discussion on the δ-dependence of the force balance. In 1 M HCl, the carpet thickness is approximately 2–3 times larger. This difference can be attributed to the opposing directions of the solutal and thermal components of the total Marangoni force. In 1 M HCl, the upward solutal Marangoni force counteracts and weakens the downward thermal Marangoni force or even becomes dominant at lower potentials/currents (blue region in Fig. 5e–h). In contrast, in 1 M H₂SO₄, both solutal and thermal components act in the same downward direction. Consequently, the net downward force is smaller in 1 M HCl, allowing for a thicker carpet and smaller departure size. This leads to larger currents and a significantly shorter bubble evolution period (Fig. 6b). Overall, the quantitative relationship between carpet thickness, electrochemical current, and Marangoni forces remains complex and non-trivial, and its detailed analysis is beyond the scope of the present manuscript.

A closer examination of the region around the bubble base and the smoother electrode in 1 M H₂SO₄ reveals the formation of a neck connecting the bubble to the electrode, as shown in Fig. 7a. This indicates that the large single bubble partially blocks the electrode. Due to limitations in resolution, the small observation area, and the continuous formation of microbubbles, the neck can only be resolved shortly before bubble detachment. Fig. 7b further demonstrates that the bubble remains attached to the electrode surface even after the potential is interrupted, i.e. set to a level of OCP. This behavior is consistently observed across all potentials studied for the smoother surface. In contrast, the bubble detaches rapidly following a potential interruption for the rougher surface in 1 M H₂SO₄ and both surfaces in 1 M HCl. Additionally, no neck formation was observed throughout the bubble evolution in these three cases (due to its substantially smaller size or absence).

Fig. 7 Necking process of the bubble base attached to the smoother surface in 1 M H₂SO₄. Images shortly before bubble detachment (a) and shortly after potential interruption, i.e. setting to the open circuit potential (OCP) (b). The potential interruption is performed at a random instant of time. The black scale bars are 200 μm and the white scale bars inside the insets are 50 μm.

The formation of the neck in 1 M H₂SO₄ may sufficiently explain the observed differences in detachment radius and period between rougher and smoother surfaces seen in Fig. 5b, c and 6a, b. The bubble-electrode contact is characterized by a contact radius r_c (see inset in Fig. 7b) and modifies the force balance by introducing an additional downward pinning force, F_p = 2πr_cσ sin θ, and an upward pressure correction force, 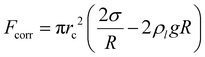. Here σ denotes the surface tension, ρ_l – the liquid density and g – the gravitational acceleration. Given the imaging limitations (including poor focus in the neck region) discussed above, we cautiously estimate that the bubble is pinned with a constant contact radius between 3 μm and 5 μm. Since the bubble radius significantly exceeds the contact radius, F_corr can be neglected, leaving the force balance between upward F_b and downward pinning force F_p, Marangoni force F_M, and electric force F_e.

In cases where the reaction ceases, as for example in Fig. 7b, F_M and F_e are effectively zero. Therefore, the force balance is between F_b and F_s only. For instance, considering a bubble with R = 290 μm produced at −0.8 V_RHE in Fig. 7b, the buoyancy force can be estimated as . Here Δρ = ρ_l − ρ_g ≈ ρ_l is the density difference between the liquid (ρ_l) and gas (ρ_g). This suggests that the pinning force holding the bubble on the electrode surface, even after the potential interruption, must be at least of the same magnitude.

For a pinned, growing bubble, the contact angle θ at the gas–solid-electrolyte interface evolves, reaching at most 90° during the bubble detachment at the pinch-off stage.⁴⁸ Furthermore, since bubble growth in Fig. 7b is interrupted prior to detachment, the contact angle is expected to remain well below 90°. Assuming θ = 30°, 45° or 60° the contact radii can be estimated via F_b = F_p, yielding r_c ≈ 5 μm, 3 μm or 2.5 μm, respectively. This estimation aligns closely with a previously estimated contact radius (r_c ≈ 3–5 μm).

We now address the observed differences in the detachment radius between the smoother and rougher surfaces in 1 M H₂SO₄. For rougher surfaces, we assume that neck formation is either absent or significantly smaller than for smoother electrodes. Using the average detachment radii from ESI Fig. S8† at −0.8 V_RHE for the smoother (R_d = 339 μm) and for the rougher (R_d = 305 μm) surfaces, the corresponding buoyancy forces are estimated as F_b = 1.60 μN and F_b = 1.17 μN, respectively. Assuming all other downward forces remain identical, the difference (0.43 μN) can be attributed to F_p.

To estimate the pinning force F_p, we arbitrarily select r_c = 3 μm and θ = 90°, yielding F_p = 1.36 μN for a bubble on the smoother surface. The comparison demonstrates qualitative agreement, though a quantitative discrepancy remains: F_p is approximately three times larger than the difference in buoyancy forces (0.43 μN). The quantitative differences may arise from inaccurate estimates of r_c and θ, leading to an overestimation of F_p. For example, if the contact line advances (moves inward) before detachment, the contact angle at detachment might be smaller, for example θ ≈ 70°.¹⁸ Further discrepancies likely come from variations in other downward forces between the smoother and rougher surfaces. Consistent with the numerical simulations, F_e and F_M may be smaller when the bubble grows closer to the electrode surface.^36,39 For example, Bashkatov et al.³⁶ (also see Hossain et al.³⁹) estimated a Marangoni-associated hydrodynamic force of F_h ≈ 0.40 μN at δ ≈ 2 μm and F_h ≈ 0.70 μN at δ ≈ 8 μm for a bubble with similar R = 304 μm but at a larger potential of −3 V_Ptwire. The electric force has been reported to be of similar^25,39 magnitude. Given these error sources, the estimate gives a reasonable magnitude of F_p.

Finally, it appears possible that the contact patch, setting F_p, might vary with the applied potential. At higher potentials or currents, larger downward forces press the bubble more strongly against the electrode, possibly enhancing the bubble-electrode contact. Previous studies have demonstrated that an H₂ bubble produced in 1 M H₂SO₄, but at a much higher potential, can become fully attached to the microelectrode, covering its surface almost entirely.⁴⁹ Therefore, the increasing difference in detachment diameters at higher potentials, as seen in ESI Fig. S8,† may be attributed to the geometry of the neck. Overall, the observed contact radius in 1 M H₂SO₄ suggests that the pinning force constitutes an important roughness-sensitive retaining force.

Building on the earlier discussion on the direction of the total Marangoni force (sum of thermal- and solutal Marangoni effects), acting upward at lower potentials and downward at higher potentials in the case of 1 M HCl we could further elaborate on the two distinct regimes observed in Fig. 5, marked by blue and yellow regions. At lower currents or potentials, the Marangoni force acts upward, making bubble attachment to the electrode surface less likely. In this regime, the pinning force only plays a minor role (if any) in the force balance, resulting in similar bubble sizes on both smoother and rougher surfaces. However, upon exceeding a threshold current or potential, the Marangoni force acts downward, thus the bubble might stick to the electrode surface (although we were not able to resolve it) and finally cause the roughness dependent detachment features observed.

Fig. 8 summarizes the detachment characteristics and bubble locations. Under the conditions where Marangoni force is directed toward electrode surface, single H₂ gas bubbles are typically located closer to the electrode surface and their detachment is strongly influenced by surface roughness. This roughness-dependent detachment is likely due to variations in pinning forces under different surface conditions. In contrast, when the Marangoni force is directed away from the electrode surface, single H₂ gas bubbles are positioned farther from the electrode surface and exhibit a roughness-independent detachment radius. These findings highlight the importance of considering both electrode and electrolyte properties when optimizing H₂ gas bubble detachment. Depending on the direction of the Marangoni effects, gas bubble locations and consequently the force balance determining gas bubble detachment can vary significantly.

Fig. 8 Schematic illustration of our hypothesis regarding the configuration of H₂ gas bubble under varying Marangoni effects. When the Marangoni force is directed toward the electrode, a single H₂ gas bubble is positioned closer to the electrode surface. In this case, an additional retaining force—sensitive to surface roughness—acting on the bubble is more pronounced, resulting in roughness-dependent detachment radius. Conversely, when the Marangoni force is directed away from the electrode, a single gas bubble is located farther from the electrode surface. In this case, the additional retaining force might be minimal or negligible, resulting in roughness-independent detachment radius.

Conclusions

In this work, we investigated the impact of electrode surface cleanliness and morphology on the detachment of single H₂ gas bubbles during the hydrogen evolution reaction in different electrolytes using a Pt microelectrode. We found that reproducible single H₂ gas bubble evolution is achieved on a well-defined Pt surface, which can be obtained through electrochemical pretreatment involving cycling between oxidating and reductive potentials. Furthermore, we observed that the effect of surface roughness on bubble detachment depends on the direction of the Marangoni force acting on the bubbles. When the Marangoni force is directed toward the electrode, the single H₂ gas bubble remains closer to the electrode surface. In this configuration, the gas bubble detaches at a smaller size on rougher surfaces compared to smoother surfaces, likely due to roughness-sensitive additional retaining force, such as pinning forces at the triple-phase boundary. Conversely, when the Marangoni force is directed away from the electrode, the single H₂ gas bubble is positioned farther from the electrode surface. In this configuration, the detachment size is independent of surface roughness, likely due to minimal additional retaining forces. These results highlight the importance of considering both electrode surface properties and electrolyte effects, particularly the Marangoni effect, for optimizing gas bubble detachment thus enhancing the efficiency of water electrolysis.

Experimental

Chemicals

All chemicals were used without further purification process. The electrolytes were prepared from H₂SO₄ (96%, Suprapur, Merck), HCl (30%, Suprapur, Merck), and Milli-Q water (≥18.2 MΩ cm, TOC < 5 ppb).

Microelectrode preparation and characterization

The Pt microelectrode was fabricated by sealing Pt wire (100 μm diameter, 99.99%, Goodfellow) within a soda-lime glass capillary (1.4 mm outer diameter, 1.12 mm inner diameter, Hilgenberg) via flame annealing. For electrodes with a smoother surface, the Pt microelectrode was polished mechanically using diamond polishing suspensions of decreasing particle size (3.0, 1.0, 0.25, 0.05 μm, Buehler) on a micropolishing cloth. For electrodes with a rougher surface, mechanical polishing was performed with SiC sandpaper (P2000, Starcke).

The surface morphology of the prepared Pt microelectrode was characterized using scanning electron microscopy (Apreo, Thermo Fisher Scientific) with an acceleration voltage of 2 kV and an electron beam current of 13 pA. The surface roughness was further characterized by atomic force microscopy (AFM, JPK NanoWizard 4) using soft tapping mode cantilevers with a spring constant of 2 N m⁻¹ and resonance frequency of 70 kHz. All measurements were performed in air at ambient temperature and humidity and the data was analysed using the JPK Data Processing software. AFM images (50 μm × 50 μm) of the smoother surface were taken at 1 Hz and the rougher surface were taken at 0.075 Hz.

Electrochemical characterization

Electrochemical experiments were conducted in a homemade PEEK cell with a transparent glass window on the side (ESI Fig. S11†). The electrochemical cell was cleaned by soaking it in a permanganate solution (0.5 M H₂SO₄, 1 g L⁻¹ KMnO₄). Prior to use, the cell was rinsed thoroughly with Milli-Q water, immersed in diluted piranha solution to remove manganese oxide residues. Afterward, the cells were rinsed again and boiled in Milli-Q water five times.

Linear sweep voltammetry and chronoamperometry were performed in a three-electrode setup using a Bio-Logic SP300 potentiostat, with a platinum wire (99.9%, MaTeck) as the counter electrode and a leakless Ag/AgCl (ET072-1, eDAQ) as the reference electrode. Before electrochemical measurements, the polished electrode underwent electrochemical pretreatment, cycling 30 times between reductive and oxidative potentials from 0.05 and 1.35 V (vs. RHE) at a scan rate of 1 V s⁻¹ in Ar-purged H₂SO₄.

The electrochemically active surface area of the prepared Pt microelectrode was determined from the charge of the hydrogen desorption peak in blank voltammogram obtained from H₂SO₄ electrolyte (210 μC cm⁻²).^46,47 The total charge for hydrogen desorption was obtained by integrating the current from 0.05 to 0.6 V (vs. RHE) after subtraction of the double layer current. The roughness factor was calculated by dividing electrochemically active surface area by the geometrical surface area (100 μm diameter disk type microelectrode: 7.854 × 10⁻⁵ cm²).

Electrochemical oscillation analysis

To gain insights into individual single H₂ gas bubble behaviours, electrochemical oscillations observed during linear sweep voltammetry or chronoamperometry were analyzed. Previous studies have shown a correlation between single H₂ gas bubble evolution and electrochemical oscillation using synchronized bubble shadowgraph and electrochemical measurements.^30,35 The detachment period, defined as the time required for a single H₂ gas bubble to detach from the electrode surface, corresponds to the oscillation period.

For the detachment radius, we combined Faraday's law with the ideal gas equation.

From the ideal gas equation:

where n_H2,bubble, R, T, P, P₀, V, and R_d represent the moles of H₂ in the gas bubble, the gas constant, the temperature, the pressure, the atmospheric pressure, the detachment volume, and the detachment radius of the H₂ gas bubble, respectively. Under our experimental conditions, contributions from the hydrostatic (∼0.004P₀ for 4 cm electrolyte height) and the Laplace pressure (∼0.032P₀ for 100 μm R_d) can be safely neglected when accounting for pressure.

At the same time, the amount of H₂ gas produced during one oscillation cycle can be described using Faraday's law:

where n_H2,produced, Q, and F denote the moles of produced H₂, the total charge during one oscillation cycle, and the Faraday constant, respectively.

Since the diameter of a single H₂ gas bubble is generally much larger than that of the microelectrode, we can reasonably assume that all generated H₂ gas molecules are captured by the single H₂ gas bubble, a condition validated for microelectrode studies:^30,35

n_H2,bubble = n_H2,produced.

Rearranging the equations, we obtain the following expression, which enables the estimation of R_d from the electrochemical oscillation data:

To further validate our approach, we additionally compared the estimated detachment radius obtained from oscillation data with that determined through image analysis (ESI Fig. S12†). As shown in ESI Fig. S12,† this comparison supports our approach.

Image analysis

To examine the geometry of the H₂ bubble throughout its evolution, an additional set of chronoamperometric measurements was conducted in parallel with image recording using a shadowgraphy system. The experiments have been performed using a three-electrode electrochemical cell, closely resembling that used in earlier studies.^13,25,27 The microelectrode (∅ 100 μm, Pt) was inserted horizontally facing upward in the base of a cuboid glass cuvette possessing four transparent sides and with dimensions of 10 × 10 × 40 mm³. The system was completed by the reference electrode (Ag/AgCl) and a counter electrode (∅ 0.5 mm Pt wire) both inserted vertically from the top. The electrochemical cell was controlled by a potentiostat (BioLogic, VSP-300) at a constant potential of −0.3 to −1.8 V (vs. RHE). The current was recorded with a sampling rate of 1 kHz over a period of 30 s. The optically transparent cell allows the visualization of the bubble dynamics using a shadowgraphy system. It consists of LED illumination (SCHOTT, KL 2500) with a microscope, connected to a high-speed camera (Photron, FASTCAM NOVA S16), providing a spatial resolution of 996 pix per mm. Image recording was performed at either 60 or 125 Hz.

The bubble radius was determined using a standard image processing routine based on the Canny edge detection method followed by circle fitting in MATLAB R2022b, as illustrated in Fig. 1b. The carpet thickness, δ, was calculated as the distance between the bubble bottom and the electrode surface. To improve precision, a separate circle was fitted to a smaller section of the bubble edge (detected via the Canny edge method) near the electrode, rather than using the initially fitted circle obtained during radius calculation. The bottom point of this newly fitted circle served as the reference for calculating δ. For further details, we refer to the ESI in Bashkatov et al.²⁵

Author contributions

Sunghak Park: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, visualization, writing – original draft, writing – review & editing; Aleksandr Bashkatov: conceptualization, data curation, formal analysis, investigation, methodology, project administration, visualization, writing – original draft, writing – review & editing; Jordy J. J. Eggebeen: investigation, data curation, writing – review & editing; Siyoung Lee: investigation, validation, writing – review & editing; Detlef Lohse: funding acquisition, project administration, resources, supervision, writing – review & editing; Dominik Krug: conceptualization, formal analysis, funding acquisition, project administration, resources, supervision, writing – review & editing; Marc T. M. Koper: conceptualization, formal analysis, funding acquisition, project administration, resources, supervision, writing – review & editing.

Data availability

Data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

S. P. acknowledges the support by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science and ICT (RS-2025-00518899). J. J. J. E. and M. T. M. K. received funding from the European Research Council through ERC Advanced Grant “FRUMKIN” no.101019998. D. L. and D. K. received funding from the Advanced Research Center Chemical Building Blocks Consortium (ARC CBBC), under the project of New Chemistry for a Sustainable Future (project number 2021.038.C.UT.14) and from the European Research Council (ERC) (BU- PACT grant agreement number 950111).

References

1. J. A. Turner, Sustainable hydrogen production, Science, 2004, 305, 972–974.
2. S. Van Renssen, The hydrogen solution?, Nat. Clim. Change, 2020, 10, 799–801.
3. N. Dubouis and A. Grimaud, The hydrogen evolution reaction: from material to interfacial descriptors, Chem. Sci., 2019, 10, 9165–9181.
4. T. E. Jones, D. Teschner and S. Piccinin, Toward realistic models of the electrocatalytic oxygen evolution reaction, Chem. Rev., 2024, 124, 9136–9223.
5. T. S. Jacobs, et al., Luminescence thermometry probes local heat effects at the platinum electrode surface during alkaline water electrolysis, ACS Energy Lett., 2024, 9, 3335–3341.
6. I. Ledezma-Yanez, et al., Interfacial water reorganization as a pH-dependent descriptor of the hydrogen evolution rate on platinum electrodes, Nat. Energy, 2017, 2, 1–7.
7. A. J. Shih, et al., Water electrolysis, Nat. Rev. Methods Primers, 2022, 2, 84.
8. M. Chatenet, et al., Water electrolysis: from textbook knowledge to the latest scientific strategies and industrial developments, Chem. Soc. Rev., 2022, 51, 4583–4762.
9. A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. F. Rivas, Influence of bubbles on the energy conversion efficiency of electrochemical reactors, Joule, 2020, 4, 555–579.
10. P. A. Kempler, R. H. Coridan and L. Luo, Gas evolution in water electrolysis, Chem. Rev., 2024, 124, 10964–11007.
11. A. R. Zeradjanin, P. Narangoda, I. Spanos, J. Masa and R. Schlögl, How to minimise destabilising effect of gas bubbles on water splitting electrocatalysts?, Curr. Opin. Electrochem., 2021, 30, 100797.
12. N. Todoroki, K. Nagasawa, H. Enjoji and S. Mitsushima, Suppression of catalyst layer detachment by interfacial microstructural modulation of the NiCo2O4/Ni oxygen evolution electrode for renewable energy-powered alkaline water electrolysis, ACS Appl. Mater. Interfaces, 2023, 15, 24399–24407.
13. A. Bashkatov, et al., Performance enhancement of electrocatalytic hydrogen evolution through coalescence-induced bubble dynamics, J. Am. Chem. Soc., 2024, 146, 10177–10186.
14. S. Yuan, et al., Bubble evolution and transport in PEM water electrolysis: mechanism, impact, and management, Prog. Energy Combust. Sci., 2023, 96, 101075.
15. G. F. Swiegers, et al., The prospects of developing a highly energy-efficient water electrolyser by eliminating or mitigating bubble effects, Sustainable Energy Fuels, 2021, 5, 1280–1310.
16. W. Fritz, Berechnung des maximalvolumes von dampfblasen, Phys. Z., 1935, 36, 379–384.
17. A. K. Chesters, Modes of bubble growth in the slow-formation regime of nucleate pool boiling, Int. J. Multiphase Flow, 1978, 4, 279–302.
18. Ç. Demirkır, J. A. Wood, D. Lohse and D. Krug, Life beyond fritz: on the detachment of electrolytic bubbles, Langmuir, 2024, 40, 20474–20484.
19. W. Xu, Z. Lu, X. Sun, L. Jiang and X. Duan, Superwetting electrodes for gas-involving electrocatalysis, Acc. Chem. Res., 2018, 51, 1590–1598.
20. R. Iwata, et al., Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting, Joule, 2021, 5, 887–900.
21. J. Ryu and D. W. Lee, Tailoring hydrophilic and hydrophobic microenvironment for gas-liquid-solid triphase electrochemical reactions, J. Mater. Chem. A, 2024, 12, 10012–10043.
22. S. A. Guelcher, Y. E. Solomentsev, P. J. Sides and J. L. Anderson, Thermocapillary phenomena and bubble coalescence during electrolytic gas evolution, J. Electrochem. Soc., 1998, 145, 1848.
23. S. D. Lubetkin, The fundamentals of bubble evolution, Chem. Soc. Rev., 1995, 24, 243–250.
24. J. Park, et al., Insights into bubble dynamics in water splitting, ACS Energy Lett., 2025, 10, 212–237.
25. A. Bashkatov, S. S. Hossain, X. Yang, G. Mutschke and K. Eckert, Oscillating hydrogen bubbles at pt microelectrodes, Phys. Rev. Lett., 2019, 123, 214503.
26. L. E. Scriven and C. V. Sternling, The marangoni effects, Nature, 1960, 187, 186–188.
27. X. Yang, D. Baczyzmalski, C. Cierpka, G. Mutschke and K. Eckert, Marangoni convection at electrogenerated hydrogen bubbles, Phys. Chem. Chem. Phys., 2018, 20, 11542–11548.
28. J. Massing, et al., Thermocapillary convection during hydrogen evolution at microelectrodes, Electrochim. Acta, 2019, 297, 929–940.
29. S. S. Hossain, G. Mutschke, A. Bashkatov and K. Eckert, The thermocapillary effect on gas bubbles growing on electrodes of different sizes, Electrochim. Acta, 2020, 353, 136461.
30. S. Park, et al., Solutal marangoni effect determines bubble dynamics during electrocatalytic hydrogen evolution, Nat. Chem., 2023, 15, 1532–1540.
31. S. Park, D. Lohse, D. Krug and M. T. M. Koper, Electrolyte design for the manipulation of gas bubble detachment during hydrogen evolution reaction, Electrochim. Acta, 2024, 485, 144084.
32. D. Lohse and X. Zhang, Physicochemical hydrodynamics of droplets out of equilibrium, Nat. Rev. Phys., 2020, 2, 426–443.
33. A. M. Meulenbroek, A. W. Vreman and N. G. Deen, Competing marangoni effects form a stagnant cap on the interface of a hydrogen bubble attached to a microelectrode, Electrochim. Acta, 2021, 385, 138298.
34. A. M. Meulenbroek, N. G. Deen and A. W. Vreman, Marangoni forces on electrolytic bubbles on microelectrodes, Electrochim. Acta, 2024, 144510.
35. X. Yang, F. Karnbach, M. Uhlemann, S. Odenbach and K. Eckert, Dynamics of single hydrogen bubbles at a platinum microelectrode, Langmuir, 2015, 31, 8184–8193.
36. A. Bashkatov, et al., On the growth regimes of hydrogen bubbles at microelectrodes, Phys. Chem. Chem. Phys., 2022, 24, 26738–26752.
37. P. Kristof and M. Pritzker, Effect of electrolyte composition on the dynamics of hydrogen gas bubble evolution at copper microelectrodes, J. Appl. Electrochem., 1997, 27, 255–265.
38. D. Fernández, P. Maurer, M. Martine, J. M. D. Coey and M. E. Möbius, Bubble formation at a gas-evolving microelectrode, Langmuir, 2014, 30, 13065–13074.
39. S. S. Hossain, A. Bashkatov, X. Yang, G. Mutschke and K. Eckert, Force balance of hydrogen bubbles growing and oscillating on a microelectrode, Phys. Rev. E, 2022, 106, 035105.
40. X. Lu, et al., Evolution of hydrogen bubbles on a microelectrode driven by constant currents and its impact on potential response, Chem. Eng. J., 2024, 500, 156890.
41. V. Climent and J. M. Feliu, Thirty years of platinum single crystal electrochemistry, J. Solid State Electrochem., 2011, 15, 1297–1315.
42. V. Climent and J. Feliu, Single crystal electrochemistry as an in situ analytical characterization tool, Annu. Rev. Anal. Chem., 2020, 13, 201–222.
43. O. Diaz-Morales, T. J. P. Hersbach, C. Badan, A. C. Garcia and M. T. M. Koper, Hydrogen adsorption on nano-structured platinum electrodes, Faraday Discuss., 2018, 210, 301–315.
44. P. K. Weissenborn and R. J. Pugh, Surface tension of aqueous solutions of electrolytes: relationship with ion hydration, oxygen solubility, and bubble coalescence, J. Colloid Interface Sci., 1996, 184, 550–563.
45. C. Demirkir, et al., To jump or not to jump: adhesion and viscous dissipation dictate the detachment of coalescing wall-attached bubbles, in Manuscript in Preparation, 2025, https://arxiv.org/abs/2501.05532.
46. L. Jacobse, S. J. Raaijman and M. T. M. Koper, The reactivity of platinum microelectrodes, Phys. Chem. Chem. Phys., 2016, 18, 28451–28457.
47. Q.-S. Chen, J. Solla-Gullón, S.-G. Sun and J. M. Feliu, The potential of zero total charge of Pt nanoparticles and polycrystalline electrodes with different surface structure: the role of anion adsorption in fundamental electrocatalysis, Electrochim. Acta, 2010, 55, 7982–7994.
48. A. K. Chesters, An analytical solution for the profile and volume of a small drop or bubble symmetrical about a vertical axis, J. Fluid Mech., 1977, 81, 609–624.
49. Y. Han, A. Bashkatov, M. Huang, K. Eckert and G. Mutschke, Impact of tracer particles on the electrolytic growth of hydrogen bubbles, Phys. Fluids, 2024, 36, 012107.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5nr00234f

---