Mechanism and modelling of thermally initiated RAFT step-growth polymerization†
Samantha Marie
Clouthier
 ,
Joji
Tanaka
,
Joji
Tanaka
 * and
Wei
You
* and
Wei
You
 *
*
Department of Chemistry, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3290, USA. E-mail: joji@email.unc.edu; wyou@unc.edu
First published on 5th December 2024
Abstract
Here we report the modelling of thermally initiated RAFT step-growth polymerization kinetics of maleimide and acrylate monomers with bifunctional RAFT agents bearing tertiary carboxyalkyl-stabilized fragmentable R groups. By analytically solving the governing equations of our model, derived from the proposed mechanism, we demonstrate that the kinetics of these polymerizations follows first order with respect to monomer concentration. Furthermore, the obtained apparent rate constant (kapp) values indicate that acrylate monomers polymerize at slower rates compared to maleimide monomers during thermally initiated RAFT step-growth polymerization.
Reversible addition–fragmentation chain transfer (RAFT) is a controlled radical polymerization (CRP) technique mediated by chain transfer agents (CTAs or RAFT agents) that proceeds by a degenerative chain transfer mechanism.1–6 Although RAFT polymerizations are considered advantageous due to their user-friendly nature, high functional group tolerance, and ability to polymerize a wide range of monomer classes, they are predominantly limited to all-carbon backbones.3 Step-growth polymerizations on the other hand involve the reaction of two functional groups to form polymers in a stepwise manner. As such, a wide range of backbone functionalities can be incorporated into the monomers utilized for polymerization. However, step-growth polymerizations often require harsh conditions to achieve sufficient monomer conversion and afford high molecular-weight polymers,7 which limits the functionalities that can be incorporated into the backbone.
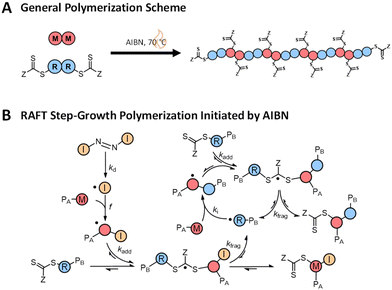
RAFT step-growth polymerization combines the beneficial characteristics of RAFT polymerization, like the user-friendly nature and high functional group tolerance, with the versatility in backbone functionality of step-growth polymerization, giving access to highly functional polymer backbones (Scheme 1A).8–13 As such, RAFT step-growth polymerization provides a route to functional polymer backbones with foreseeable applications, from drug delivery to chemical recycling.13,14
 | ||
| Scheme 1 (A) General RAFT step-growth polymerization scheme. (B) Thermally initiated RAFT step-growth mechanism. | ||
RAFT step-growth typically employs bifunctional reagents for both the monomer and CTA and proceeds through a single-unit monomer insertion (SUMI) mechanism (Scheme 1). The basics of the RAFT–SUMI mechanism and kinetics have been explored in previous investigations, including the effect of monomers15–17 and initiation methods.18 As shown below, RAFT step-growth traditionally proceeds by the thermal decomposition of an exogenous azo-initiator to generate the radicals used in the RAFT step-growth cycle, similar to thiol–ene step-growth polymerization (Scheme 1B).19–21 The RAFT step-growth cycle can be broken down into three steps: (1) monomer addition to a CTA-derived R˙ radical to generate a monomer (or backbone)-derived M˙ radical (ki, Scheme 1B), (2) RAFT agent addition to the M˙ radical to generate a chain transfer intermediate radical adduct CTA˙ (kadd, Scheme 1B), and (3) fragmentation of CTA˙ to regenerate the CTA-derived R˙ radical (kfrag, Scheme 1B). The driving forces for the polymerization to proceed via step-growth rather than chain-growth are low homopropagation (kp), high ki and a high chain transfer equilibrium described by the ratio of forward and reverse chain transfer constant coefficients (Ctr/C−tr).13
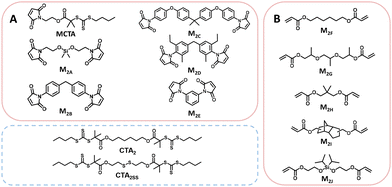
Thermally initiated RAFT step-growth has been demonstrated with both maleimide (MCTA–M2E, Scheme 2A) and acrylate (M2F–M2J, Scheme 2B) monomers with bifunctional RAFT agents that bear tertiary carboxyalkyl R groups (MCTA, CTA2, and CTA2SS) (Scheme 2).8–10 Thus far, the kinetics of RAFT step-growth polymerizations has been treated as pseudo-first-order reactions without considering the rate-limiting steps.8–10 Here, we investigate the mechanism of thermally initiated RAFT step-growth of maleimide and acrylate monomers through kinetic modelling, where we consider rate-limiting steps of the RAFT step-growth cycle and subsequently fit experimental data following our kinetic models to obtain apparent rate constants (kapp).
To aid in the interpretation of the observed polymerization kinetics for thermally initiated RAFT step-growth, we have developed a model based on the key steps in the mechanism. The model is based on the proposed mechanism (Scheme 1B) involving 5 species: the monomer (M), the RAFT agent (CTA), and three radical species generated by the cycle (backbone radical (M˙), RAFT agent radical (R˙), and RAFT step-growth adduct radical (CTA˙)). From these species, we defined governing equations for the model (eqn (1)–(5)), where eqn (1) and (2) describe the consumption of monomer groups through the monomer addition to R˙ and the consumption of the RAFT agent by addition to M˙, respectively. Eqn (1) and (2) assume that the consumption of the monomer or RAFT agent groups by initiation is negligible. Additionally, eqn (3)–(5) describe the concentrations of the three radical species in the RAFT step-growth cycle, accounting for initiation (in the case of eqn (3)), termination, and generation and consumption throughout the RAFT step-growth cycle. For simplification, the reverse chain transfer process in the RAFT step-growth cycle is not considered. This is a reasonable assumption, particularly for examples where the CTA bears a more radically stabilized fragmentable group (R˙) relative to monomer derived radical species (M˙).
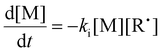 | (1) |
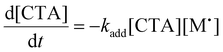 | (2) |
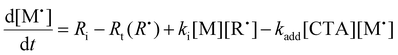 | (3) |
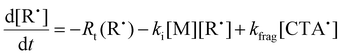 | (4) |
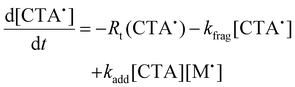 | (5) |
The initiation rate (Ri) accounted for in eqn (3) is defined by eqn (6), where f is the initiation efficiency of monomer addition to the initiator radical (I˙), kd is the decomposition rate of the initiator, and [I] is the concentration of initiator species. Notably, defining Ri in this manner has limitations at high monomer conversion due to the assumption of a constant value for f. Because of radical side reactions, a value of f = 1 is not recommended; rather, a value of f = 0.65 has been recommended and adopted for azo-initiators.13,22 Nevertheless, initiator efficiency (f) is expected to fall at high monomer conversion (when the monomer concentration becomes a limiting factor). Rates of termination (Rt(M˙), Rt(R˙), and Rt(CTA˙)) by a variety of radical–radical combination events are highlighted in eqn (7)–(9). Notably, all termination events by radical–radical combinations are assumed to be equally likely; thus, termination-related rate constants (kt1, kt2, kt3, kt4, kt5, and kt6) are all equal and can be further simplified by a general termination kinetic parameter (kt). Furthermore, eqn (7)–(9) can be summed together to give a general rate of termination (Rt) (eqn (10)).
| Ri = 2fkd[I] | (6) |
| Rt(M˙) = 2kt1[M˙]2 + kt2[M˙][R˙] + kt3[M˙][CTA˙] | (7) |
| Rt(R˙) = kt2[M˙][R˙] + 2kt4[R˙]2 + kt5[R˙][CTA˙] | (8) |
| Rt(CTA˙) = kt3[M˙][CTA˙] + kt5[R˙][CTA˙] + 2kt6[CTA˙]2 | (9) |
| Rt = Rt(M˙) + Rt(R˙) + Rt(CTA˙) | (10) |
The rate of polymerization (Rp) can be analytically solved using eqn (1)–(10). The consumption rates of the monomer and RAFT agent can be assumed to be equal, and therefore, eqn (1) and (2) can be set equal. Furthermore, the steady-state approximation can be adopted, allowing eqn (3)–(5) to be set equal to zero, giving eqn (11) as the overall rate expression (see the ESI† for a more detailed derivation of eqn (11)).
Eqn (11) can be simplified by establishing various limiting cases between the three kinetic parameters of the RAFT step-growth cycle (kfrag, ki, and kadd). In case 1, the fragmentation of the RAFT step-growth radical adduct is established as the rate-limiting step (kadd, ki ≫ kfrag), which gives eqn (12) and establishes RAFT step-growth as a zeroth-order reaction. Case 2 assumes that the monomer addition to the R˙ species is the rate-limiting step (kadd, kfrag ≫ ki), simplifying the Rp term to eqn (13), where the reaction order is first order with respect to monomer concentration. Additionally, case 3 can be
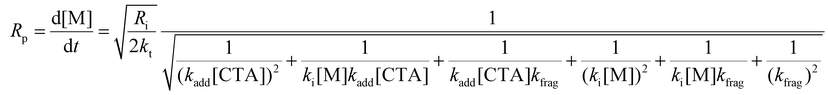 | (11) |
Case 1: kadd, ki ≫ kfrag
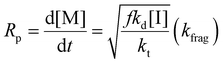 | (12) |
Case 2: kadd, kfrag ≫ ki
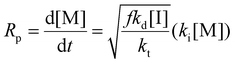 | (13) |
Case 3: kfrag, ki ≫ kadd
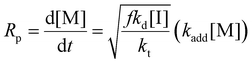 | (14) |
Case 4: kfrag ≈ kadd ≈ ki
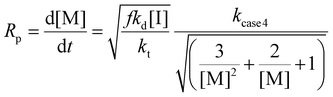 | (15) |
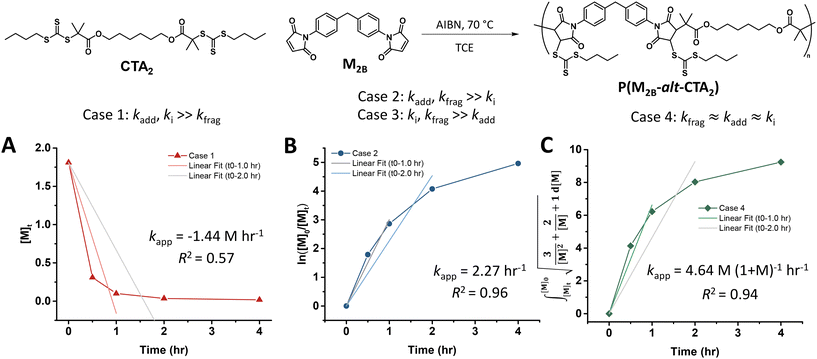
Experimental polymerization data for maleimide and acrylate monomers (Scheme 2) can be fit using the model predictions established for cases 1–4. As a result, experimental data of RAFT step-growth polymerization of CTA2 and N,N′-(1,4-phenylene)dimaleimide, M2B (Scheme 2),9 were plotted according to each of the 4 cases established previously with linear regressions applied from 0 to 1.0 hours and 0 to 2.0 hours (Fig. 1, Table S1†). It is important to note that rate orders often change as a reaction progresses due to shifts in the rate-limiting step or the influence of competing reactions. While the rate fittings presented here focus on the initial stages of polymerization, the later stages are arguably more critical for step-growth polymerizations, as high monomer conversions are essential to achieve high molecular weights. Nevertheless, determining the rate order and apparent rate constants (kapp) for RAFT step-growth polymerization provides valuable quantitative insights, particularly when comparing the two reported monomer classes. Additionally, it should be acknowledged that 1H-NMR analysis at high monomer conversions (p > 98%) may be prone to errors.
Fitting the data according to case 1 (kadd, ki ≫ kfrag) where a zeroth-order relation with respect to monomer concentration is predicted gives poor fits (kapp is 1.44 M h−1 and R2 < 0.6, where kapp is defined in eqn (S10)†) (Fig. 1A, Table S1†). Furthermore, both cases 2 and 3 (kadd, kfrag ≫ ki and ki, kfrag ≫ kadd, respectively) give a first-order relation with respect to monomer concentration, and therefore, fitting with a first-order plot cannot distinguish the two cases. Nevertheless, the polymerization data appear to follow first-order kinetics (kapp = 2.27 h−1 and R2 = 0.96, where kapp for cases 2 and 3 are defined by eqn (S11) and (S12),† respectively) (Fig. 1B, Table S1†). Notably, the polymerization plateaus after 2.0 hours, which is likely a result of the efficiency factor, f, falling at high monomer conversion.22 Additionally, this plateau in the kinetics at high monomer conversion could be attributed to an increasing occurrence of retardation (vide infra). Lastly, case 4 (kfrag ≈ kadd ≈ ki) was also fitted, giving a kapp value of 4.64 M (1 + M)−1 h−1 and an R2 value of 0.94, where kapp for case 4 is defined in eqn (S13)† (Fig. 1C, Table S1†).
Similarly, the polymerization data for monomer 1,6-hexanediol diacrylate, M2F, with CTA2 (Scheme 2),10 can be plotted according to the same 4 cases as before with linear regressions from 0 to 4.0 hours (Fig. S1, Table S2†), where again cases 2 and 3 give the best fit (kapp = 0.98 h−1R2 = 1.00) compared to cases 1 and 4 (where kapp = −0.29 M h−1 and 1.87 M (1 + M)−1 h−1 and R2 = 0.82 and 1.00, respectively). Notably, the polymerization kinetics for RAFT step-growth of acrylates does not demonstrate a plateau at high monomer conversion as observed in the case of maleimides (Fig. 1), possibly indicating that the monomer addition to the initiator radical (which is accounted for by f) is less rate-limiting for acrylates than for maleimides.
As observed, cases 2 and 3 yield the best linear fit for the experimental data; however, this alone does not distinguish between the two cases. Additionally, fitting case 4 results in only slightly lower R2 values compared to cases 2 and 3, making it difficult to differentiate between these cases based solely on model fitting. Nonetheless, due to the reactive nature of trithiocarbonate, it is unlikely for kadd to be rate limiting (as assumed by case 3). Furthermore, Tanaka et al. recently classified the selectivity of various RAFT–SUMI monomer and RAFT agent pairs, categorizing maleimide and acrylate monomers with RAFT agents bearing tertiary carboxyalkyl fragmentation to be driven by the chain transfer equilibrium. Thus we can assume that the kinetics of these monomer classes can be classified under case 2, where monomer addition to the R˙ radical, defined by ki, is rate-limiting.13 Therefore, we will use case 2 (eqn (13)) to model the kinetics of the monomers defined in this text (Scheme 2), where apparent rate constants (kapp) can be defined using eqn (S11).†
Although these fits use only 3 to 5 data points, we emphasize that this is sufficient to estimate kapp values, which is further demonstrated with model polymerizations of M2B and M2F with CTA2, where more kinetic data points are taken, demonstrating little difference in the obtained kapp values (Fig. S2–S4, Tables S3–S5†).
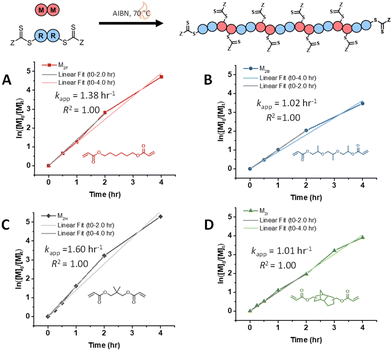
Previously, Tanaka et al. varied monomer concentration for AB RAFT step-growth using the monomer MCTA (Scheme 2).8 Conditions for maintaining both initiator concentration constant ([AIBN]0 = 0.05 M) and initiator-to-RAFT agent ratio constant ([MCTA]0/[AIBN]0 = 20) were investigated and fitted to determine kapp values (Tables S6 and S7, Fig. S5 and S6†). Similarly, Archer et al. investigated the dependence of monomer concentration for A2 + B2 RAFT step-growth of diacrylates by varying monomer concentration of M2F polymerized with CTA2, while maintaining either initiator concentration constant ([AIBN]0 = 0.05 M) or initiator-to-RAFT agent ratio constant ([CTA]0/[AIBN]0 = 40) (Fig. S7 and S8, Tables S8 and S9†).10 Keeping the initial initiator concentration constant for both maleimides and acrylates displayed slight variation in kapp values. However, varying initiator concentration by a factor of 2 demonstrated significant changes in kapp values equivalent to 21/2, which is in accordance with eqn (11), where Rp is dependent on [I]1/2. These findings of Rp depending on initiator concentration (rather than on the ratio of CTA to initiator) differs from traditional RAFT chain-growth polymerization kinetics, where the kinetics are dependent on the CTA-to-initiator ratio as modelled by the intermediate radical termination (IRT) model.23 This lack of retardation in RAFT step-growth polymerization is likely attributable to the rapid fragmentation of the R-group from the RAFT agent. However, as the reaction progresses, it is important to consider that the RAFT process may begin to compete with chain transfer involving the polymer backbone CTA. This competition could lead to an increased occurrence of degenerative chain transfer (or equivalent fragmentation), ultimately resulting in retardation.
Furthermore, various maleimide monomers polymerized with CTA2 (M2A, M2B, M2C, M2D, and M2E) were fitted according to case 2 to determine kapp (Fig. 1B and 2, Tables S1 and S10†).8,9 Monomers M2A and M2B when polymerized demonstrate kapp values of approximately 2.0 h−1. Interestingly, the polymerization of bis(3-ethyl-5-methyl-4-maleimidophenyl)methane (M2C) with CTA2 displayed a slower rate compared to M2A and M2B (kapp = 0.53 h−1), which is consistent with the literature, where N-aromatic maleimides with alkyl ortho-substituents show reduced polymerization rates.24 Additionally, the polymerization of 2,2-bis[4-(4-maleimidophenoxy)phenyl]propane (M2D) with CTA2 showed an increase in polymerization rate (kapp = 2.68 h−1), suggesting that O-phenyl substituents para to the maleimide ring increase polymerization rate and monomer reactivity. Lastly, 4,4-substituted phenylene bismaleimide (M2E), where the maleimide units are attached to the same phenyl ring, gave rate constants (kapp) of approximately 1.5 h−1.
 | ||
| Fig. 2 Kinetic analysis of RAFT step-growth for maleimide monomers with CTA2: (A) M2A, (B) M2C, (C) M2D, and (D) M2E. | ||
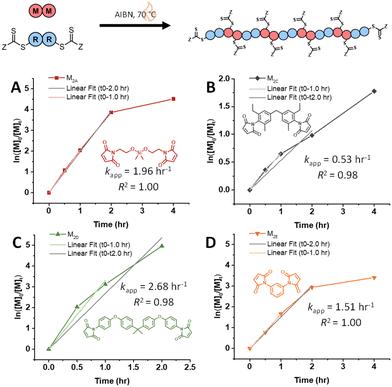
Next, RAFT step-growth polymerizations of various acrylate monomers ((M2F, tripropylene glycol diacrylate (M2G), neopentyl glycol diacrylate (M2H), and tricyclo[5.2.1.02,6]decanedimethanol diacrylate (M2I)) with CTA2 were fitted using the model derived from case 2, and kapp values were obtained (Fig. 3, Table S11†). Generally, monomers M2F, M2G, M2H, and M2I show kapp values around 1.00 h−1 (Fig. 3, Table S11†). Notably, acrylate monomers demonstrate lower kapp values compared to maleimide monomers (kapp = 1.0 h−1 and 2.0 h−1, respectively), suggesting that acrylate monomers demonstrate slower addition to the CTA-derived R˙ radical compared to maleimide monomers (Fig. 2 and 3). Similar trends in kapp values for maleimide monomers and acrylate monomers are seen when investigating RAFT–SUMI kinetics of model monomers N-ethyl maleimide (MA) and butyl acrylate (BA) with the monofunctional RAFT agent BDMAT, where kapp = 0.973 h−1 and 0.58 h−1, respectively (Fig. S9 and S10, Table S12†).8,10
 | ||
| Fig. 3 Kinetic analysis of RAFT step-growth for diacrylate monomers with CTA2: (A) M2F, (B) M2G, (C) M2H, and (D) M2I. | ||
Lastly, we compared the rate of polymerization for monomers M2B, M2F, and M2J polymerized with the disulfide-tethered bifunctional RAFT agent, CTA2SS (Fig. S11, Table S13†).10,25,26 The polymerization rate for CTA2SS with M2B and M2F does not drastically change (kapp ∼ 2.0 h−1, kapp ∼ 1.0 h−1, respectively), suggesting that the disulfide bond tethering the bifunctional RAFT agent does not affect the rate as the R˙ radical is identical for CTA2 and CTA2SS. Interestingly, the silyl ether-tethered diacrylate monomer (M2J) when polymerized under RAFT step-growth with CTA2SS shows a reduced rate (kapp = 0.69 h−1), possibly suggesting reduced monomer reactivity.
In summary, thermally initiated RAFT step-growth polymerization kinetics of maleimide and acrylate monomers with bifunctional RAFT agents with tertiary carboxyalkyl stabilized fragmentations have been successfully modelled. By analytically solving the governing equations for these polymerizations, we determined that the kinetics follows first-order behavior with respect to monomer concentration. This is attributed to the rate-limiting step for the investigated monomer classes being monomer addition to the R˙ species from RAFT agent fragmentation, characterized by the kinetic parameter ki. Furthermore, after modelling the polymerization for a variety of maleimide and acrylate monomers, it was found that acrylate monomers exhibit lower kapp values compared to maleimides, which is likely due to slower monomer addition to the R˙ species for acrylates compared to maleimides. Additionally, we demonstrate the [I]1/2 dependence of Rp through fitting polymerizations conducted with varied monomer and initiator concentrations for both acrylates and maleimides.
Author contributions
The manuscript was written through contributions from all authors.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare the following competing financial interest(s): J. T. and W. Y. are named inventors on a patent application owned by UNC-Chapel Hill (PCT/US2022/042087) which laid the foundation for this work. Dr You is also a co-founder of Delgen Biosciences, a startup company that has licensed this UNC patent application.Acknowledgements
This work was financially supported by the National Science Foundation (NSF) under Award CHE-2108670. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. (NSF DGE-2439854). The Bruker AVANCE III Nanobay 400 MHz NMR Spectrometer was funded by NSF under Grant No. CHE-0922858, and the Bruker NEO 600 MHz NMR spectrometer was funded by NSF under Grant No. CHE-1828183. The authors thank Dr Marc A. ter Horst from University of North Carolina's Department of Chemistry NMR Core Laboratory for the use of the NMR spectrometers.References
- S. Perrier, Macromolecules, 2017, 50, 7433–7447 CrossRef.
- J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562 CrossRef.
- C. L. Moad and G. Moad, Chem. Teach. Int., 2021, 3, 3–17 CrossRef.
- N. Corrigan, K. Jung, G. Moad, C. J. Hawker, K. Matyjaszewski and C. Boyer, Prog. Polym. Sci., 2020, 111, 101311 CrossRef.
- J. Zhang, B. Farias-Mancilla, I. Kulai, S. Hoeppener, B. Lonetti, S. Prevost, J. Ulbrich, M. Destarac, O. Colombani, U. S. Schubert, C. Guerrero-Sanchez and S. Harrisson, Angew. Chem., Int. Ed., 2021, 60, 4925–4930 CrossRef.
- Y. Zhang, Y. Tang, J. Zhang and S. Harrisson, ACS Macro Lett., 2021, 10, 1346–1352 CrossRef.
- L. Billiet, D. Fournier and F. Du Prez, Polymer, 2009, 50, 3877–3886 CrossRef.
- J. Tanaka, N. E. Archer, M. J. Grant and W. You, J. Am. Chem. Soc., 2021, 143, 15918–15923 CrossRef PubMed.
- P. Boeck, N. Archer, J. Tanaka and W. You, Polym. Chem., 2022, 13, 2589–2594 RSC.
- N. E. Archer, P. T. Boeck, Y. Ajirniar, J. Tanaka and W. You, ACS Macro Lett., 2022, 11, 1079–1084 CrossRef.
- S. M. Clouthier, J. Tanaka and W. You, Polym. Chem., 2022, 13, 6114–6119 RSC.
- P. T. Boeck, J. Tanaka, W. You, B. S. Sumerlin and A. S. Veige, Polym. Chem., 2023, 14, 2592–2598 RSC.
- J. Tanaka, J. Li, S. M. Clouthier and W. You, Chem. Commun., 2023, 59, 8168–8198 RSC.
- R. Wei, T. Tiso, J. Bertling, K. O'Connor, L. M. Blank and U. T. Bornscheuer, Nat. Catal., 2020, 3, 867–871 CrossRef.
- R. Liu, L. Zhang, Z. Huang and J. Xu, Polym. Chem., 2020, 11, 4557–4567 RSC.
- S. Houshyar, D. J. Keddie, G. Moad, R. J. Mulder, S. Saubern and J. Tsanaktsidis, Polym. Chem., 2012, 3, 1879–1889 RSC.
- J. Xu, Macromolecules, 2019, 52, 9068–9093 CrossRef.
- L. Zhang, R. Liu, Z. Huang and J. Xu, Polym. Chem., 2021, 12, 581–593 RSC.
- N. B. Cramer, T. Davies, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 4631–4636 CrossRef.
- N. B. Cramer, S. K. Reddy, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 7964–7969 CrossRef.
- S. K. Reddy, N. B. Cramer and C. N. Bowman, Macromolecules, 2006, 39, 3673–3680 CrossRef.
- G. Moad, Prog. Polym. Sci., 2019, 88, 130–188 CrossRef.
- K. G. E. Bradford, L. M. Petit, R. Whitfield, A. Anastasaki, C. Barner-Kowollik and D. Konkolewicz, J. Am. Chem. Soc., 2021, 143, 17769–17777 CrossRef.
- A. Matsumoto, T. Kubota and T. Otsu, Macromolecules, 1990, 23, 4508–4513 CrossRef.
- O. R. Courtney, S. M. Clouthier, S. Perrier, J. Tanaka and W. You, ACS Macro Lett., 2023, 12, 1306–1310 CrossRef.
- S. M. Clouthier, J. Li, J. Tanaka and W. You, Polym. Chem., 2024, 15, 17–21 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4py01188k |
| This journal is © The Royal Society of Chemistry 2025 |