Open Access Article
Open Access ArticleBest-of-both-worlds computational approaches to difficult-to-model dissociation reactions on metal surfaces
Geert-Jan
Kroes
 * and
Jörg
Meyer
* and
Jörg
Meyer

Leiden Institute of Chemistry, Gorlaeus Laboratories, P. O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: g.j.kroes@chem.leidenuniv.nl
First published on 5th November 2024
Abstract
The accurate modeling of dissociative chemisorption of molecules on metal surfaces presents an exciting scientific challenge to theorists, and is practically relevant to modeling heterogeneously catalyzed reactive processes in computational catalysis. The first important scientific challenge in the field is that accurate barriers for dissociative chemisorption are not yet available from first principles methods. For systems that are not prone to charge transfer (for which the difference between the work function of the surface and the electron affinity of the molecule is larger than 7 eV) this problem can be circumvented: chemically accurate barrier heights can be extracted with a semi-empirical version of density functional theory (DFT). However, a second important challenge is posed by systems that are prone to (full or partial) electron transfer from the surface to the molecule. For these systems the Born–Oppenheimer approximation breaks down, and currently no method of established accuracy exists for modeling the resulting effect of non-adiabatic energy dissipation on the dissociative chemisorption reaction. Because two problems exist for this class of reactions, a semi-empirical approach to computing barrier heights, which would demand that computed and experimental dissociative chemisorption probabilities match, is unlikely to work. This Perspective presents a vision on how these two problems may be solved. We suggest an approach in which parameterized density functionals are used as in the previous semi-empirical approach to DFT, but in which the parameters are based on calculations with first principles electronic structure methods. We also suggest that the diffusion Monte-Carlo (DMC) and the random phase approximation (RPA) probably are the best two first principles electronic structure methods to pursue in the framework of the approach that we call first-principles based DFT (FPB-DFT) – providing DMC and the RPA with a steppingstone towards benchmarking and future applications in computational catalysis. Probably the FPB density functional is best based on screened hybrid exchange in combination with non-local van der Waals correlation. We also propose a new electronic friction method called scattering potential friction (SPF) that could combine the advantages and avoid the disadvantages of the two main existing electronic friction approaches for describing non-adiabatic effects: by extracting an electronic scattering potential from a DFT calculation for the full molecule–metal surface system, it might be possible to compute friction coefficients from scattering phase shifts in a computationally convenient and robust fashion. Combining the FPB-DFT and SPF methods may eventually result in barrier heights of chemical accuracy for the difficult-to-model class of systems that are prone to charge transfer. This should also enable the construction of a representative database of barrier heights for dissociative chemisorption on metal surfaces. Such a database would allow testing new density functionals, or, more generally, new electronic structure approaches on a class of reactions that is of huge importance to the chemical industry. Additionally, the difficult-to-model sub-class of systems we focus on is essential to sustainable chemistry and important for a sustainable future. Adding the database envisaged to large databases already existing but mostly addressing gas phase chemistry will enable testing density functionals that have a claim to universality, i.e., to be good for all chemical systems of importance. We also make a suggestion for how to develop such a generally applicable functional, which should have the correct asymptotic dependence of the exchange contribution to the energy in both the gas phase and the metal. Finally we suggest some improvements in the representation of potential energy surfaces and in dynamics methods that would help with the validation of the proposed methods.
1. Introduction
The production of most chemicals involves heterogeneous catalysis at some stage.1 Heterogeneously catalyzed processes usually involve a sequence of elementary reactions on surfaces, and often these surfaces are of metal particles. An important class of elementary reactions is formed by dissociative chemisorption reactions, in which a bond in the molecule breaks and both resulting fragments bond to the surface. Such reactions are interesting for both practical and scientific reasons.Minimum barrier heights (Eb) (or transition states, TSs) for dissociative chemisorption (DC) are not just important for this specific reaction alone. Heterogeneously catalysed reactions consist of a sequence of elementary reaction steps. Among these sequences barriers to DC reactions often control the rate (we should actually say: the “turn-over-frequency”) of an entire heterogeneously catalysed process.2,3 Important examples are steam reforming for hydrogen production4 and production of ammonia to make fertilizer.5,6 The accuracy with which these Eb (TSs) can be calculated has an important impact on computational heterogeneous catalysis.7,8 With the present accuracy one can predict trends in heterogeneous catalysis using transition metals (TMs), and, with reasonable accuracy, which catalysts should be good for producing specific chemicals.8,9 But theory is not yet very accurate for turn-over-frequencies of entire heterogeneously catalysed processes, as illustrated by errors in the computed rate of ammonia production still being as large as 1–2 orders of magnitude.8,10 This poses a major problem to the accurate calculation of these rates, and the catalysis literature has emphasized the need for higher accuracy than afforded now by current density functionals (DFs) for achieving predictive power.11 It is hard to overemphasize the importance of this. Catalysis is “the single most important and pervasive interdisciplinary technology in the chemical industry”, it has been a “key enabling technology” for most of the societal challenges in Horizon 2020, and with the production of artificial fertilizers HC makes it possible to feed a world population of 7 billion humans.12 Improvements in catalysts can reduce the energy demand of the chemical industry by at least 20–40%.12
The study of how molecules react at or, more generally, scatter from metal surfaces is also to a large extent curiosity driven. The study of these processes is the subject of the field of molecule–surface reaction dynamics.13–19 Instead of reacting a molecule may also scatter back to the gas phase, possibly changing its vibrational and/or rotational state. These outcomes all depend on e.g. the molecule's incident translational energy, its initial rovibrational state, the surface temperature (Ts), and, crucially, on how the molecule interacts with the surface.13 Whether or not the molecule will react will of course depend on the barrier height to reaction but, just like for gas phase reactions,20–25 the accurate prediction of barriers for DC reactions on metals comes with major challenges.13,26–28 The latter reactions have been addressed mostly with density functional theory (DFT), which is perhaps not surprising: these reactions take place in complex systems containing many electrons to be modelled, and with more than 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 papers published annually DFT is probably the most important electronic structure method for complex systems.29 What is surprising, though, is that far more databases with benchmark data are available for testing new electronic structure methods on gas phase reaction barriers23–25,30 than on dissociative-chemisorption-on-metals barriers.31,32 Given the large practical importance of the latter category of reactions, one might expect the opposite. As will become clear from the below, this has to do with the fact that accurate quantum chemical calculations are much more challenging to carry out for molecules interacting with metal surfaces than for molecules interacting with one another in the gas phase. Before we dive into explaining this, let us first explain what the present state-of-the-art is in the former area of applications.
000 papers published annually DFT is probably the most important electronic structure method for complex systems.29 What is surprising, though, is that far more databases with benchmark data are available for testing new electronic structure methods on gas phase reaction barriers23–25,30 than on dissociative-chemisorption-on-metals barriers.31,32 Given the large practical importance of the latter category of reactions, one might expect the opposite. As will become clear from the below, this has to do with the fact that accurate quantum chemical calculations are much more challenging to carry out for molecules interacting with metal surfaces than for molecules interacting with one another in the gas phase. Before we dive into explaining this, let us first explain what the present state-of-the-art is in the former area of applications.
To determine barrier heights (Eb) for DC on metals, in the present state-of-the-art a semi-empirical electronic structure approach, called specific reaction parameter DFT (hence: SRP-DFT),13,33–35 is taken. Here one takes a judiciously chosen13,36 density functional (DF) with a single adjustable parameter. This parameter is then fitted so that calculations based on the adjusted DF and using a suitable dynamics model and method reproduce DC probabilities that are measured as a function of translational incidence energy in supersonic molecular beam experiments. In Surface Science DC probabilities are also called by the shorter name “sticking probabilities” and denoted by the symbol S0, as we will often do from now on. Even though only one parameter, which correlates with Eb, in the DF is tweaked in SRP-DFT, the approach yields DFs that are generally capable of reproducing S0 curves over large ranges of energies. The reason is that standard DFT, though not capable of predicting Eb for a DC-on-metal system accurately, is capable of yielding quite a good description of the variation of the barrier height with the system's configuration (e.g., the molecule's orientation and impact site on the surface, for a diatomic molecule).37,38 According to the so-called hole model39 this should be a sufficient condition for theory to be able to compute accurate S0, although in practice it is also necessary to choose a dynamical model and method capable of accurately describing dynamical effects.13,40 Using the SRP-DFT approach, it has been possible to extract Eb for 14 systems in which a molecule dissociatively chemisorbs on a metal surface, which has led to a database that can be used to test existing and new DFs on their accuracy for DC for these systems.32
So far, in the SRP-DFT approach the exchange part of the exchange–correlation functional of DFT has been based on the generalized gradient approximation (GGA).20 Unfortunately, this approach breaks down for systems that are characterized by the charge transfer energy E(CT) being smaller than 7 eV.41 Here, E(CT) is defined as the work function of the metal surface minus the electron affinity of the incident molecule. In systems with E(CT) < 7 eV the metal easily lets go of an electron (low work function) and/or the molecule is eager to accept it (a positive electron affinity implies a high affinity for electrons). As a result such systems are prone to (partial) electron transfer from the surface to the molecule. GGA functionals perform poorly for systems affected by charge transfer.42 Such breakdown is illustrated for an individual system in Fig. 1, for HCl + Au(111), which has E(CT) = 5.8 eV. Even using about the most repulsive GGA DF still compatible with a good description of the metal (RPBE48), the measured DC probability is overestimated, suggesting that Eb is underestimated with the RPBE DF. This holds true even though RPBE typically overestimates Eb for systems with E(CT) ≥ 7 eV.32 Recent work49 has suggested that the difference might be due to the calculations using a higher “coverage” than the experiments, which were done in the zero-coverage limit.43 We believe that this is not correct: in the recent experiments, “coverage” refers to pre-coverage by Cl.49 In the calculations,43 “coverage” refers to the density of the incident HCl beam. AIMD calculations found little difference between sticking probabilities employing a (3 × 3) surface unit cell and a (2 × 2) surface unit cell (HCl “coverages” of 1/9 and 1/4, respectively).45 This result implies that the (2 × 2) dynamics calculations should already be useable in comparisons with experiments in the zero-coverage limit.
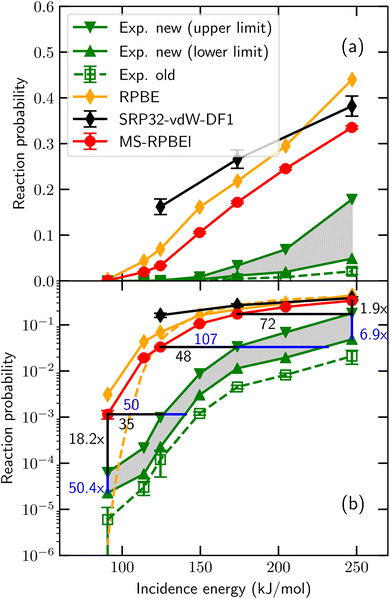 | ||
| Fig. 1 Sticking probabilities computed43 for HCl + Au(111) with the MS-RPBEl meta-GGA DF,43 the RPBE GGA DF,44 and the SRP32-vdW1 DF featuring semi-local exchange and non-local correlation45 are compared to experimental results, for normal incidence. The open green squares are the experimental sticking probabilities first published,46 while the upper base and lower base triangles represent upper and lower bounds to the experimental S0 obtained from an improved analysis of the experiments.43 Panel (a) uses a linear and panel (b) a logarithmic scale for S0. In panel (b) results of QCT44 (orange diamonds connected by solid orange line) as well as of QD47 (orange dashed lines) calculations using the RPBE DF are presented. Figure taken from ref. 43 (https://doi.org/10.1021/acs.jpcc.0c03756). Further permission requests to be directed to the ACS. | ||
As illustrated by Fig. 2, similar observations as for HCl + Au(111) have been made for other systems with, as a rule of thumb, E(CT) < 7 eV,41 such as O2 + Al(111)51,52 and Cu(111),53 H2O + Ni(111),54 and NH3 + Ru(0001).55,56 By the phrase “rule of thumb” we mean to say that E(CT) 7 eV can be taken as an approximate number for the value of E(CT) that determines whether a GGA likely breaks down according to the empirical evidence presented in Fig. 2 and ref. 41. In line with this trend,41 RPBE-DFT calculations underestimated the barrier height computed for H2 + Mg(0001) with diffusion Monte-Carlo,57 which is an accurate stochastic first-principles-based electronic structure method.58 As also illustrated by Fig. 2 for systems with E(CT) > 7 eV it has been possible to model the DC on metals with chemical accuracy using GGA density functionals.
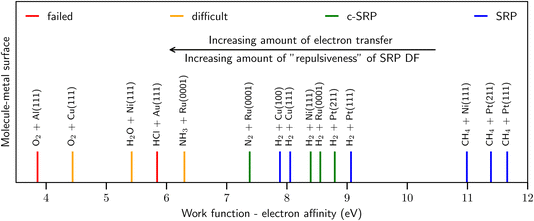 | ||
| Fig. 2 Correlation of the ability of DFs based on GGA-exchange with E(CT), i.e., the difference between the work function of the metal surface and the electron affinity of the incoming molecule50 (shown with vertical lines). The blue and green lines represent systems for which it was possible to derive a SRP DF. The red lines represent systems for which the use of the repulsive RPBE GGA DF leads to overestimating computed S0, while the orange lines indicate systems for which computed results strongly suggest that this is the case. See Fig. 70 of ref. 13 for how the work functions of the surfaces and the electron affinities of the molecules were obtained. Figure taken from ref. 41 (https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02452). Further permission requests to be directed to the ACS. | ||
As noted in ref. 41 and in the caption of Fig. 2 the evidence for GGA-breakdown for E(CT) < 7 eV is solid for some systems (indicated with red in Fig. 2) while still subject to some uncertainty for other systems (indicated with orange in Fig. 2). For instance, in quantum dynamics calculations on D2O + Ni(111) making approximations to parallel translational motion of the molecule and the surface vibrations and based on a RPBE48 GGA potential energy surface, the RPBE results overestimated experimental sticking probabilities for the 2ν3 state, while they underestimated the measured values for the 1ν3 state at low average incidence energies (see Fig. 6 of ref. 54). It is not clear which comparison should be given precedence: the experimental probabilities are larger for the 2ν3 state (at values up to about 10−2 instead of values up to about 10−3 for the 1ν3 state), suggesting that the comparison should be the most important for the higher excited vibrational state. On the other hand errors in the shape of the PES, which could also occur for a GGA functional, might make it harder to accurately describe the reactivity of higher excited vibrational states with theory. In conclusion, the “border” of 7 eV should not be interpreted strictly, but rather as a rule of thumb. More accurate dynamical calculations (i.e., using less dynamical approximations) may be required than was possible in 2016 (ref. 54) to determine whether RPBE fails for D2O + Ni(111), for which E(CT) ≈ 5.4 eV. Note that an accurate comparison cannot be based on experimental “laser-off” results and theoretical results for the vibrational ground state, as an appropriate inclusion of excited vibrational states would lead to a theoretical laser-off reactivity that should be much higher than the theoretical result for the ground vibrational state only.54,59
A similar problem as discussed above for systems with E(CT) < 7 eV is observed when modeling experiments on vibrationally inelastic scattering, especially if the incident molecule is initially in a highly excited vibrational state. Vibrationally inelastic scattering, in which the molecule's vibrational state changes in an otherwise non-reactive molecule–surface collision, might be thought to lie in the realm of physics rather than chemistry. The process is however intimately related to DC, as changes in the bond length of the incident molecule are implicated in both processes and thus probe the barrier region of the potential energy surface (PES) of the system. This interrelatedness is also illustrated in Fig. 3, which compares computational with experimental results for vibrationally inelastic scattering of NO from Au(111), for which E(CT) = 5.3 eV.63 In Fig. 3, the calculations labeled BOMD, MDEF(LDFA), MDEF(ODF) used a PES that allowed for DC, i.e., bond stretching can result in reaction.64 In contrast, the calculations labeled MDEF and IESH used a PES that did not allow reaction.65 Clearly the use of these two different PESs leads to different results, but Fig. 3 also illustrates another problem for systems with E(CT) < 7 eV. As mentioned earlier, in these systems the metal tends to easily let go of an electron (low work function) and the molecule is eager to accept it (again, a positive electron affinity implies a high affinity for electrons). This implies that the system is prone to non-adiabatic effects related to electron–hole pair (ehp) excitation, as also illustrated in Fig. 4.15 In Fig. 3 the acronyms used are telltale of how these non-adiabatic effects are described. “MDEF” stands for molecular dynamics calculations describing ehp excitation in a weak coupling approximation using “electronic friction” (EF).66 “IESH” calculations used the independent electron surface hopping (IESH) method, which allows for strong coupling between two diabatic electronic states of the molecule–metal system (i.e., neutral-metal and anion–metal) with ehp excited states superimposed.67,68 In spite of the improvements made to the PES,64Fig. 3 therefore also illustrates how the present state-of-the-art theory dealing with non-adiabatic effects falls short in describing the chemical physics problem of vibrationally inelastic scattering of NO from Au(111).
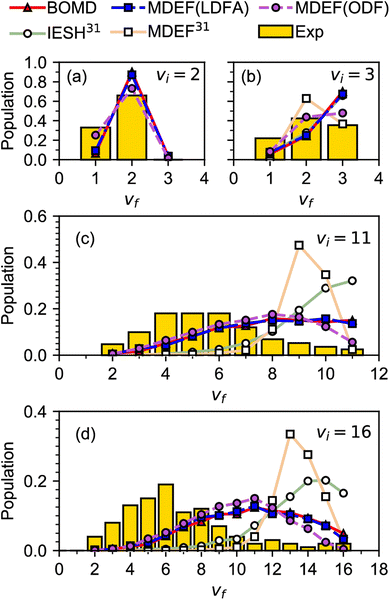 | ||
| Fig. 3 Experimental60–62 relative probabilities for scattering of NO from Au(111) in its initial vibrational state vi to the final vibrational state vf are compared with calculations63 using different dynamical models and potential energy surfaces. Results are given for (a) vi = 2, (b) vi = 3, (c) vi = 11, and (d) vi = 16. The reference in the legend corresponds to the reference with that number in ref. 63. The relevant details are discussed in the text, for other details see ref. 63. Figure taken from ref. 63 (https://doi.org/10.1021/jacsau.0c00066). Further permission requests to be directed to the ACS. | ||
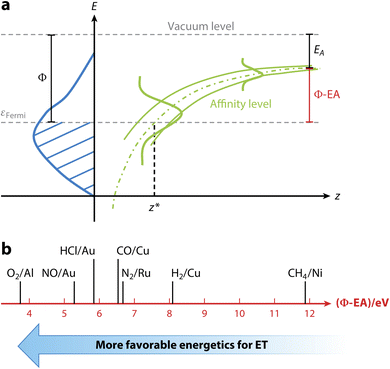 | ||
| Fig. 4 Correlation of E(CT) with non-adiabatic effects. (a) Non-adiabatic effects are governed by E(CT), i.e., the difference of the work function of the surface, here indicated with the symbol Φ, and the electron affinity of the molecule, EA, as indicated. The energy needed to transfer an electron from the surface to the molecule can be diminished by the image–charge interaction, which stabilizes the indicated anion affinity level of the approaching molecule. If needed the remaining energy required for full electron transfer can come from e.g. the incident translational and vibrational energy of the impinging molecule. (b) E(CT) as an indicator of how likely non-adiabatic effects are. Systems to the left (small E(CT)) are more prone to ehp excitation than systems to the right. For details see ref. 15. Used with permission of Annual Reviews of Physical Chemistry, from [The Dynamics of Molecular Interactions and Chemical Reactions at Metal Surfaces: Testing the Foundations of Theory, K. Golibrzuch, N. Bartels, D. J. Auerbach, and A. M. Wodtke, vol. 66, pp. 399–425, 2015]; permission conveyed through Copyright Clearance Center, Inc. | ||
The problem with describing electronically non-adiabatic effects can be illustrated for DC of N2 on Ru(0001),69 for which E(CT) at 7.4 eV actually somewhat exceeds 7 eV, as illustrated in Fig. 5. As in Fig. 2 “LDFA and “ODF” label two different EF methods that can be used to describe ehp excitation; below we will outline their differences and describe them in some detail. The point made by Fig. 5 is that the computed S0, which are shown on a log scale, depend dramatically on which of the two EF methods (LDFA or ODF) is used. Specifically, the S0 curves computed with molecular dynamics with electronic friction (MDEF) using the LDFA and the ODF are removed from one another in incidence energy by more than 2 kcal mol−1 (1 kcal mol−1 ≈ 0.043 eV). This is problematic because at present it is unclear if any on the two EF methods is capable of accurately describing the effect of ehp excitation on DC on metals.
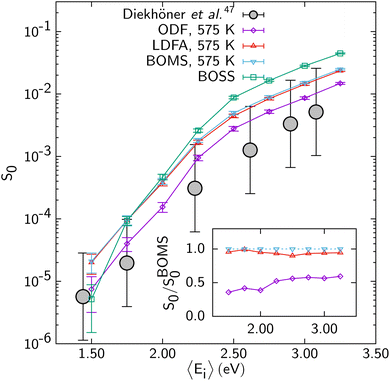 | ||
| Fig. 5 S 0 computed for N2 + Ru(0001) with MDEF and the RPBE DF using the Born–Oppenheimer static surface (BOSS) model,70 the Born–Oppenheimer moving surface (BOMS) model,70 and the non-Born–Oppenheimer moving surface (NBOMS) model with the LDFA and the ODF approximations69 are shown as a function of Ei. Experimental results are also shown. Figure taken from ref. 69 (https://pubs.acs.org/doi/10.1021/acs.jpclett.9b00523). Further permission requests to be directed to the ACS. | ||
The above observations lead to the following clear conclusion for systems with E(CT) < 7 eV: given the uncertainties surrounding the accuracy of the present methods developed to describe non-adiabatic effects, an approach to deriving the PES with a semi-empirical DF based on reproducing measured sticking probabilities alone is clearly doomed to fail (see below). In the present state-of-the-art the choice of the semi-empirical DF is likely to depend on what method is used to describe non-adiabatic effects, which are strong for E(CT) < 7 eV (Fig. 4). At the same time, as will be discussed below first principles electronic structure methods with demonstrated chemical accuracy for dissociative-chemisorption-on-metal systems in general are not yet available, and the workhorse method (DFT-GGA) fails for systems with E(CT) < 7 eV (Fig. 2). Therefore, a risk exists for such systems that if agreement with experiment is achieved the agreement might be achieved “for the wrong reason”, i.e., due to cancellation of errors resulting from errors in both the PES and in the method used to describe non-adiabatic effects. In any case for such systems a semi-empirical approach is bound to go south if GGA-DFT is used, in which case “delocalization” errors are expected in the DFT due to (partial) charge transfer,42 which additionally causes strong non-adiabatic effects15 that we do not yet know how to model accurately.69 In other words, when E(CT) < 7 eV it never rains but it pours.
At this point it is good to stop for a moment and to also emphasize the practical importance of systems for which E(CT) < 7 eV. It will be clear that these systems will often involve molecules with a high affinity for electrons, including oxygen containing molecules like O2, methanol, and CO2. It is hard to overemphasize the practical importance of these systems. The oxygen reduction reaction is crucial to clean energy conversion in fuel cells, and the chemistry of O2 is of tremendous overall importance.71 Methanol and related compounds such as dimethyl ether and oxy-methylene ethers, which can be produced from CO2,72 are considered to be important clean energy fuels in the future.12 In short, many of the systems that pose the challenges discussed above are also crucial to sustainable chemistry, and it is therefore also practically important to address these challenges.
As discussed below, the greatest challenge is to come up with an accurate electronic structure approach that is ultimately based on first principles, and which can be used for predictive purposes. As emphasized elsewhere37 such a method is also preferred in general for other reasons: standing in the way of semi-empirical approaches, experiments might yield conflicting results, they may not be well documented, or they may simply be absent for the system of interest.13 More accurate PESs will also be needed if the field studying collisions of molecules with metal surfaces is ever to match the field studying gas phase molecular collisions for level of detail and accuracy.73 And once it will be possible to accurately compute PESs it will also be possible to test different methods for dealing with non-adiabatic effects more rigorously than now feasible for systems with E(CT) smaller than or approximately equal to 7 eV. Developing improved methods for dealing with such non-adiabatic effects also represents a very important challenge, which can already be addressed now. Finally, a number of challenges is related to how dynamics calculations need to be performed to validate new theories through comparison of computed observables with experiments.
All of the challenges described above will be addressed below. For this we will first address the state-of-the-art in electronic structure theory (Section 2.1). Next, we will consider theories dealing with electronically non-adiabatic effects in scattering of molecules from metal surfaces (Section 2.2). After that we will briefly consider methods needed to compute sticking probabilities with dynamics, including methods for PES construction (Section 2.3). Next, we will sketch a vision of how to proceed with improvements. Improvements in electronic structure theory and in methods for dealing with non-adiabatic effects will be addressed in Sections 3.1 and 3.2. Improvements in the representation of PESs and in dynamics calculations will be briefly discussed in Sections 3.3. Section 3.4 deals with the validation of the new methods through comparison with experiments. We end with summary conclusions (Section 4).
2. The state-of-the-art in modeling dissociative chemisorption on metals
2.1 State-of-the-art electronic structure theory
Present theoretical research on DC of molecules on metal surfaces usually bases itself on electronic structure calculations performed with DFT, using DFs at the GGA rung of Jacob's ladder,20 and in some cases employing DFs at the meta-GGA rung,20 both of which belong to the group of semi-local functionals. GGA and meta-GGA DFs are called semi-local because they evaluate the exchange–correlation energy density at a point in space as a function of that electronic density and its derivatives.74 In some cases GGA correlation or meta-GGA correlation is replaced with a non-local correlation functional. For this typically the vdW-DF1 (ref. 75) or vdW-DF2 (ref. 76) correlation functionals are combined with GGA exchange, or the rVV10 (ref. 77) correlation functional is combined with meta-GGA exchange. The problem usually encountered with such functionals is illustrated for strictly semi-local functionals (i.e., also using semi-local correlation) in Fig. 6. This figure shows results of dynamical calculations of the probability of sticking in the benchmark system H2 + Cu(111)79 with comparison to experiment.78 According to the hole model,39 which states that for a given incidence energy the sticking probability should equal the proportion of geometries (impact site and molecular orientation) for which the molecule's energy exceeds the geometry's barrier height, agreement between theory and experiment of S0 would signal the accurate calculation of barriers. As will be clear from Fig. 6 the accurate computation of barriers is accomplished with none of the GGA (PBE80 and RPBE48) and meta-GGA (TPSS,82 revTPSS,83 and SCAN81) standard functionals tested. We also use Fig. 6 to reiterate a point already alluded to implicitly above: barrier heights are not observables. Their validation requires dynamics calculations of measured S0 as illustrated with Fig. 6.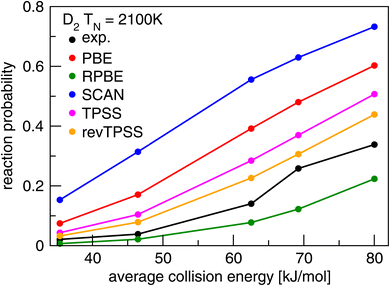 | ||
| Fig. 6 Values of S0 measured78 in molecular beam experiments for D2 + Cu(111) are compared to computed79 values using PESs based on DFT calculations using the GGA PBE80 and RPBE48 DFs, and the meta-GGA SCAN,81 TPSS,82 and rev-TPSS83 DFs. Figure taken from ref. 79 (https://doi.org/10.1021/acs.jpca.9b02914). Further permission requests to be directed to the ACS. | ||
As alluded to in the Introduction the type of standard functionals discussed above can be combined in a semi-empirical way to model a particular (“easy-to-model”, E(CT > 7 eV) class of systems with chemical accuracy. A generic form of a parameterizable exchange–correlation functional that can be used for this is
| EXC = xEX1 + (1 − x)EX2 + EC | (1) |
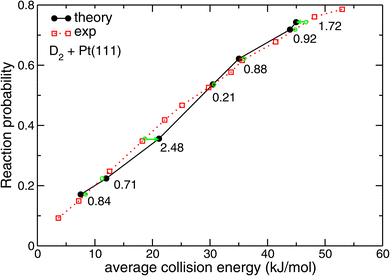 | ||
| Fig. 7 Reaction probabilities computed86 with SRP-DFT for D2 + Pt(111) are compared with experimental values.87 The green symbols indicate at which interpolated collision energies measured sticking probabilities would be obtained for values equal to those computed with theory. The numbers indicate the distance (in kJ mol−1) of the corresponding points on the interpolated experimental curve to the points computed with dynamics along the collision energy axis. Reprinted from E. N. Ghassemi, M. Wijzenbroek, M. F. Somers, and G. J. Kroes, Chemically accurate simulation of dissociative chemisorption of D2 on Pt(111), Chem. Phys. Lett., 2017, 683, 329–335, licensed under CC-BY 4.0. | ||
With the SRP-DFT procedure a database (called SBH17) has been constructed presenting accurate barrier heights for DC in 17 molecule–metal surface systems, and this database has been used to benchmark the performance of 14 density functionals.32 We show results for a selection of these functionals (2 GGAs, 2 meta-GGAs, and 2 combinations of GGA exchange with non-local van der Waals correlation) in Table 1. Notable conclusions from Table 1 are that the best performing DF was the general purpose PBE80 GGA density functional, and that the MS2 “made-simple” DF88 was the best performing meta-GGA DF, perhaps because it was explicitly constructed to do well for metals as well as molecules. Importantly, the RPBE48 and BEEF-vdW2 (ref. 89) functionals do not perform so well on barriers of easy-to-model systems. The performance of these functionals on barriers has been overrated due to systematic errors made with computing barrier heights in an earlier study that resulted in the SBH10 database.31 In this SBH10 study activation energies computed with DFT were compared with reference values of classical barrier heights for 9 of the 10 systems selected.31 There are two systematic differences between how the reference values of classical barrier heights and the values of the activation energies have been computed:31 (i) the activation energies contain zero-point energy corrections for the reactants and the transition state (barrier geometry), whereas the classical barrier heights do not. (ii) In the calculations of the activation energies the surface atoms were allowed to relax in the presence of the dissociating molecule in the transition state.31 This was not allowed in the SRP-DFT calculations of the reference values of classical barrier heights.32 The reason is that, so far, SRP-DFT has been built on the comparison with sticking experiments using supersonic molecular beams, and in the underlying dynamics of DC the surface atoms do not have time to relax to the full minimum barrier geometry (in which the surface atoms would be relaxed).13 This is because the surface atoms usually do not have time to respond to the (fast) incoming molecule in a supersonic molecular beam experiment.
| Functional | Type of DF | MAE | r MAE | MSE | r MSE |
|---|---|---|---|---|---|
| PBE | GGA | 2.38 | 1 | −1.34 | 5 |
| RPBE | GGA | 5.26 | 13 | 5.26 | 13 |
| PBEα57-vdW-DF2 | GGA + vdW | 2.86 | 4 | −0.92 | 3 |
| BEEF-vdW-DF2 | GGA + vdW | 4.40 | 10 | 4.40 | 10 |
| MS2 | Meta-GGA | 2.70 | 3 | −1.71 | 6 |
| SCAN | Meta-GGA | 3.23 | 7 | −2.42 | 8 |
Fig. 8 illustrates both a reason for why the SRP procedure based on semi-local exchange DFs works so well for easy-to-model systems (E(CT) > 7 eV), and why it will usually fail for systems that are difficult-to-model (for which, as a rule of thumb, E(CT) > 7 eV). Fig. 8 presents results58 for an easy-to-model system (H2 + Cu(111), E(CT) = 8.1 eV) and a system that turned out to be difficult-to-model (H2 + Al(110), E(CT) = 7.2 eV). For H2 + Cu(111) barrier heights computed with GGAs, meta-GGAs, and functionals containing GGA exchange and non-local correlation scatter around the semi-empirical SRP-DFT value. It thus makes sense that appropriately mixing such functionals according to eqn (1) allows an experiment on sticking of H2 on Cu(111) to be reproduced. For H2 + Al(110), on the other hand, none of these functionals, including the more repulsive ones, overestimates the semi-empirical value of the barrier height.58 It is for the same reason that DC of HCl on Au(111) has, so far, not been well described (see Fig. 1): the functionals used up to now all contained semi-local exchange and therefore underestimated barrier heights resulting in overestimated computed S0. Clearly, for difficult-to-model systems an approach that is more generally applicable than combining semi-local exchange with semi-local or non-local correlation from DFT is needed.
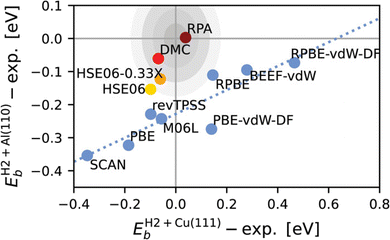 | ||
| Fig. 8 Lowest reaction barrier heights for H2 + Al(110) vs. those for H2 + Cu(111), both taken relative to the best semi-empirical values, as obtained with DFs including semi-local exchange (i.e., not including exact exchange, indicated by blue symbols), with screened hybrid DFs (yellow and orange symbols), with diffusion Monte-Carlo (red symbol) and with the RPA (maroon symbol). The concentric gray shaded ellipses indicate areas that would be circles in an equal-distanced representation, with radii of 1 (darkest grey), 2, 3, and 4 (lightest gray) kcal mol−1 respectively. For details see ref. 58. Figure reprinted from B. Oudot, K. Doblhoff-Dier, Journal of Chemical Physics, vol. 161, Article ID 054708, 2024; licensed under a Creative Commons Attribution (CC-BY) license. | ||
For gas phase reactions semi-local functionals systematically underestimate barrier heights.20–25 This has variously been attributed to self-interaction errors and delocalization errors,20–22,42 where the latter may be considered an overarching term encompassing self-interaction error.42 To improve the description of gas phase barriers a successful strategy has been to use hybrid functionals, which are on the fourth rung of the DFT ladder20 and admix exact exchange (EXX, also called Hartree–Fock exchange) with semi-local exchange.23–25 In this endeavor, it has often paid off to use a somewhat higher fraction of exact exchange than used in hybrid functionals for general purposes.23,42,90,91 When dealing with metals it is important to screen the EXX at long distances between the electrons, to avoid a collapse of the density of states of the electrons at the Fermi-level.92 For DC of O2 on Al(111), which is an infamously difficult-to-model system, it has recently been shown41 that sticking probabilities can be obtained with a much higher accuracy than possible with semi-local DFs if a screened hybrid DF with an increased fraction of EXX (HSE03-1/3X)41,93,94 is used, as shown in Fig. 9. While it is yet to be demonstrated that screened hybrids also perform systematically better for easy-to-model systems, it is encouraging to see that the very similar screened hybrid HSE06-1/3X58,97 outperformed all GGAs and meta-GGAs tested on the two H2 + Al(110) and Cu(111) systems (see also Fig. 8). The observation to the contrary in tests on the SBH10 database31 can most likely58 be attributed to the incorrect comparison of computed activation energies with reference values of classical barrier heights, as detailed before. While calculations using hybrid functionals are expensive even with screened hybrids, it is also encouraging to note that at least for O2 + Al(111) the use of a non-self-consistent approach using GGA densities (HSE03-1/3X) was quite successful.98 We note that electronically adiabatic dynamics calculations were used to compare dynamics results based on the HSE03-1/3X PES with experiment, thus neglecting ehp excitation. The reasons that we expect this approximation to be accurate for O2 + Al(111) is that good agreement with experiment was also obtained with adiabatic dynamics calculations using an accurate PES based on embedded correlated wave function theory95 (see also Fig. 9), and that we expect the friction coefficients that would be computed at the barrier geometries for O2 + Al(111) to be small, as the metal electron densities should be small at these geometries, which occur far from the surface.41,95
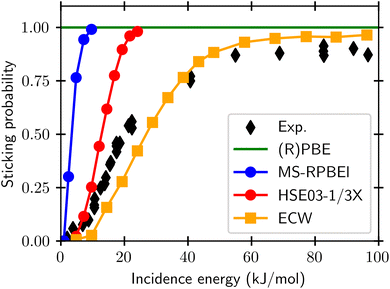 | ||
| Fig. 9 Sticking probabilities computed with the GGA PBE and RPBE DFs,51,52 the meta-GGA MS-RPBEl DF,41 the screened hybrid HSE03-1/3X DF,41 and with embedded correlated wave function theory95 are compared with experimental results, for sticking of O2 on Al(111).96 Figure taken from ref. 41 (https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02452). Further permission requests to be directed to the ACS. | ||
Recently two papers28,58 appeared in which the random phase approximation99–101 in a DFT framework employing the adiabatic-connection fluctuation-dissipation theorem (ACFDT-RPA,102 henceforth simply RPA), which may be considered a fifth-rung density functional,20 was used in periodic calculations. The results look very promising: agreement to within chemical accuracy was obtained for H2 + Cu(111)28,58 and for H2 + Al(110)58 (see also Fig. 8). Here one has to keep in mind that the method has only been tested on barriers for two dissociative-chemisorption-on-metals reactions thus far. For the BH76 database of gas phase reaction barriers the RPA (MAE = 2.3 kcal mol−1 (ref. 103)) was outperformed13 by diffusion Monte-Carlo (MAE = 1.2 kcal mol−1 (ref. 104, and 105)). The reliable application of RPA to energy differences like barrier heights relies on quite substantial error cancellation,20 but this can work quite well in applications to solids.20,106 The RPA may be viewed as a double hybrid functional and recently another double hybrid functional (XYG3)107 was tested on H2 + Cu(111) with very promising results108 using a cluster-based approach, as will be discussed further below.
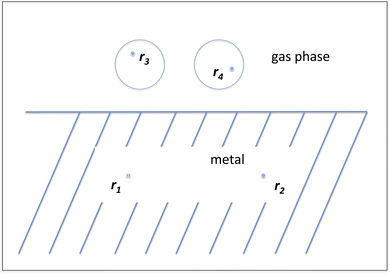
Before moving on to electronic structure methods other than DFT it is good to sketch a fundamental problem that exists in DFT for describing reactions of molecules on metal surfaces. Benchmark studies show that for gas phase reactions density functionals exist that exhibit an accuracy for barrier heights of about 2 kcal mol (ref. 23, and 24) To our knowledge, the best DF developed so far23 is a range separated hybrid DF109 in which the percentage of exact exchange is maximum at long range (for large distances between the points r3 and r4 in Fig. 10). However, for molecule–metal surface systems there is a principal problem: metals are best described with screened hybrid DFs,93 with the amount of exact exchange becoming zero at long range (for large distances between r1 and r2 in Fig. 10). In contrast, in the gas phase the fraction of exact exchange would ideally be 1 at long range to correctly describe the required 1/R behavior of the exchange–correlation potential in the gas phase.110,111 A DF incorporating the correct long-range behavior in the gas and the metal would move us a step closer to a universally accurate DF. A possible route to meeting this challenge will be sketched in Section 3.
Diffusion Monte-Carlo (DMC) is a stochastic first principles method.112 It has been applied to DC on metals27,37,38,57,113 and to water addition to CO on Pt(111).114 For cases where the minimum barrier to DC on a metal could be compared to experiment (H2 + Cu(111)27 and Al(110)37) results close to chemical accuracy were achieved (errors of about 1.5 kcal mol−1). The barrier computed for H2 dissociation above a bridge site on Pt(111) agreed with a semi-empirical SRP-DFT value to 0.8 kcal mol;113 this comparison is less direct because the bridge site is not the minimum barrier geometry for this system. Agreement with the activation barrier for water addition to CO on Pt(111) (better than 1 kJ mol−1)114 was even more excellent, but perhaps fortuitously so. Comparison of DMC to DFT calculations using standard functionals (with only semi-local exchange) showed that, while generally inaccurate at predicting absolute barrier heights, such functionals are remarkably accurate at predicting how the barrier height varies with the geometry of the barrier in reduced dimensionality.38 This observation helps with explaining why, with tuning of just one parameter in a functional with semi-local exchange, SRP-DFT is usually capable of accurately describing both the threshold and the slope of measured sticking curves.13,37
For the calculation of gas phase reaction barrier heights, the CCSD(T)115 method represents the gold standard. Calculations on physisorption of small molecules on semi-conductor116 and insulator117,118 surfaces have been done with the CCSD(T) method, using periodic boundary conditions117,118 and embedded cluster formalisms.116,118 These calculations are quite accurate (sub-chemical accuracy). Periodic CCSD(T) calculations of the barrier height for DC of H2 on Si(100) were consistent with the experimental lower bound of Eb,119 but to our knowledge it has not yet been possible to perform CCSD(T) calculations on molecules interacting with metal surfaces. Zhang and Grüneis have recently reviewed and presented an outlook for the application of coupled cluster methods in the field of materials science, including a discussion of surface chemistry.120
CCSD(T) but also other ab initio many-electron wave function methods are currently too computationally expensive for periodic calculations on DC on metals. However, they may be applied in an embedded cluster fashion (“embedded correlated wave function theory”, ECW), using density functional embedding.121 While this leads to a formally exact theory,121 in practice a limiting factor is the size of the cluster that can be treated with ab initio theory, as the convergence of the results depends critically on the size of the cluster that can be handled.26,28 Nonetheless accurate results can be obtained with this approach. Dynamics calculations based on an embedded CASPT2 (ref. 122 and 123) PES were in semi-quantitative agreement with experiments on sticking of O2 on Al(111),95 although agreement to within chemical accuracy was not yet achieved (see also Fig. 9). However, embedded CASPT2 calculations failed for H2 + Cu(111), which at the time was not recognized because the comparison to experiment was not made in an appropriate way:124 it was based on an erroneous fit of the activation energy as a function of temperature125 instead of a direct comparison to the semi-empirical barrier height.33 On the other hand embedded NEVPT2 (ref. 126) calculations agreed with the semi-empirical barrier height for H2 + Cu(111) to within chemical accuracy,28 and there is reason to believe that NEVPT2 should be more robust than CASPT2.124 In the same way as used for correlated wave function theory density functional embedding can also be used with RPA for the cluster, which provided semi-quantitative agreement with the semi-empirical barrier height for H2 + Cu(111) at far less computational expense than more accurate periodic RPA calculations.28 A problem with validation of results may be that calculations in which the molecule is centered on different clusters for different adsorption geometries in different ways might be needed, while using these calculations to construct a PES in a consistent manner may then not be obvious.
Another approach in which clusters are employed to allow the use of correlated wave function methods is the ONIOM approach.127 In this approach the ab initio result for the molecule interacting with the metal cluster is corrected with the difference of a periodic and a cluster DFT calculation for the same adsorption geometry. Sautet and co-workers128 applied this approach to H2 dissociation on Cu(100) at a barrier geometry in reduced dimensionality (this was not the full-dimensional minimum barrier geometry). Good agreement with a semi-empirical SRP-DFT result was obtained with the use of MRCI-Q (i.e., multi-reference CI129 with Davidson correction130) but not with a CCSD(T)115 treatment of the cluster, which seems suspect. Araujo et al.131 have used the ONIOM approach employing a global hybrid (i.e., M06) density functional91 for the cluster, while using a dispersion corrected DFT functional (PBE-D3 (ref. 80, 132 and 133)) to correct for finite-size effects. One might argue that in such a set-up a hybrid functional is used that is screened in a primitive way, with the screening length determined by the cluster size. Results131 were obtained that were in excellent agreement with accurate semi-empirical reference values of minimum barrier heights for five systems contained in the SBH10 (ref. 31) and SBH17 (ref. 32) databases. However, the reference values were, for 4 of the 5 systems studied, classical barrier heights obtained with the surface held static at the geometry appropriate for the vacuum–solid interface. Because Araujo et al.131 computed activation energies (i.e., zero-point vibration energy corrected barrier heights, allowing the surface atoms to relax in the calculations on the transition state), the agreement that was achieved is rather meaningless.37 Xu and coworkers108 have made this important distinction when benchmarking the performance of the doubly hybrid functional XYG3 (ref. 107) for H2 dissociation on Cu(111) using an ONIOM-based approach including a systematic convergence test with respect to cluster size. It is very encouraging that they have obtained remarkably good agreement (to within chemical accuracy) with the semi-empirical SRP-DFT result.108
In summary, the state-of-the-art for calculating classical barrier heights for DC on metals is as follows. DFT with functionals using semi-local exchange yields a mean absolute error ≥2.4 kcal mol−1 for easy-to-model systems. These functionals tend to be accurate for the variation of the barrier height with system geometry. As a result, tuning such functionals to obtain agreement with experimental sticking curves (SRP-DFT) has facilitated the construction of a database (SBH17) with chemically accurate reference values of classical barriers for easy-to-model systems. However, functionals with semi-local exchange systematically underestimate barrier heights for difficult-to-model systems. Calculations on O2 + Al(111) offer hope that screened hybrid functionals are more accurate for these systems. Limited evidence for two H2-metal systems (H2 + Cu(111) and Al(110)) offers hope that this increased accuracy holds for molecule–metal surface systems in general. Evidence for these two systems suggests that the most accurate approaches currently available are periodic DMC and periodic RPA. Correlated wave function theory with density functional embedding is accurate in principle but problems with the convergence of the size of the cluster treated with the high-level method may stand in the way of achieving chemical accuracy. This cluster size convergence problem does not occur for calculations on H2 + Cu(111) with the doubly hybrid functional XYG3 based on the ONIOM approach.108 Periodic calculations with these functionals and without embedding can hopefully confirm this very encouraging trend.
2.2 State-of-the-art in describing electronically non-adiabatic effects in molecules scattering from metal surfaces
In periodic solids the electrons form a continuum of states (bands). In metals, the highest band with electrons in it, the conduction band, is only partly filled. With unoccupied states readily available at practically zero excitation energy, it follows that collisions with molecules can (or actually, will134,135) at least cause transitions in which electrons are excited from states below the metal's Fermi level to states above the Fermi level. This process is called electron–hole pair (ehp) excitation, and it breaks the Born–Oppenheimer approximation. Globally speaking, two cases can be distinguished.136 In the first case scattering takes place without changes in the electronic state of the molecule scattered back to the gas phase, or, in case of reaction, with the electronic state of the system staying close to the electronic ground state of the full system. In the second case, the molecule scattered back to the gas phase has changed its electronic state, or it has done so temporarily when it interacted with the metal, or immediately after reaction the electronic state of the system is not close to that of the ground state of the full system. Loosely speaking the first case might be thought of as a case of weak coupling136 between the nuclear and electronic degrees of freedom, while in the second case there is strong coupling136 between the two. Below we will focus on the first case but we will also say something about the second case. We will restrict ourselves to methods that have been applied to actual chemical/physical systems, although excellent work (e.g. ref. 137–139) has been presented concerning methods that have been applied to limiting case model systems, which models in future may also be applied to real life systems.Systems with weak coupling may be dealt with using electronic friction (EF) methods.66,140 In the words of Dou and Subotnik,141 “EF represents the first order correction to the Born–Oppenheimer approximation in the presence of a manifold of fast electronic states”, i.e., those of the perturbed metal. As a result, atoms moving close to a metal surface “experience a drag in the presence of a manifold of electronic states”.141 The EF method may be seen as an extreme type mean field Ehrenfest method, in which the electronic ground state potential replaces the potential averaged over (multiple) ehp states. In MDEF, the energy dissipation to the electrons directly affects the nuclear motion. Time-dependent perturbation theory can be used to derive electronic friction theory, which can be cast in a generalized Langevin form for the nuclear equations of motion.66 Friction coefficients mediate the energy flow to the electrons through friction forces, and through fluctuation forces that depend on temperature. EF theory invokes the Markov approximation, thereby assuming short (i.e., zero) decoherence times.136,142
Basically two types of EF methods exist. In orbital dependent friction (ODF)66,143–146 the elements of the EF tensor (i.e., the friction coefficients) are written as
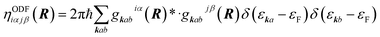 | (2) |
ODF coefficients generally yield anisotropic friction tensors that may depend strongly on the molecular coordinates. In performing ODF calculations one has to take special care that the computed friction coefficients are well converged with respect to a number of parameters in the underlying electronic structure calculations.147 For computationally convenient evaluation in dynamics, friction tensors can be fitted using symmetry adapted neural network techniques.148
An advantage of the ODF method already mentioned above is that it takes into account the electronic structure of the molecule and the metal. However, the ODF method also has several disadvantages. ODF is based on linear response theory, which means that non-adiabatic perturbations are taken into account only up to first order, which further emphasizes the character of the method as a “weak coupling” approximation.66,149 Periodic DFT calculations of ODF tensors (i.e., the computation of the friction coefficients in eqn (2)) for an isolated molecule interacting with a surface are typically based on inter-band transitions only, combined with a broadening of the δ-functions present in eqn (2) during Brillouin zone integration. This leads to a non-physical dependence of the resulting friction coefficients on broadening parameters,69,150–152 which represents a conceptual shortcoming. In practice the problem has been handled pragmatically by performing calculations with varying broadening parameters. Often one can show that the results are rather insensitive to these widths, within a range of widths that includes the broadening parameter used in the actual calculations.146,153 Nonetheless this is not a wholly satisfactory state-of-affairs. ODF has also been shown to yield unphysically large friction in the region of the doublet-singlet spin transition for H-atoms incident on a non-magnetic metal surface (Cu(111)).154 Because techniques were lacking for the efficient evaluation of eqn (2), until recently ODF coefficients were only computed for and used in low-dimensional scattering calculations155–158 However, recently 6D friction tensors have become available for and have been used in dynamics simulations on DC of diatomic molecules on metals (e.g., H2 + Ag(111)152,153 and Cu(111),146 and N2 + Ru(0001)69).
The local density friction approximation (LDFA) is the second state-of-the-art EF technique currently in use. The LDFA maps the friction problem onto single atoms embedded as impurity in a homogeneous electron gas (HEG) via the electron density of the pristine, unperturbed surface at the points where each atom in a molecule resides.159 The HEG, or jellium, is a simple model for bulk metals with nearly free electrons in which the nuclei of the metal atoms have been smeared out as a constant background. The scattering of jellium electrons at an atom embedded therein has been calculated at the level of the local density approximation (LDA)160 and more recently also at the generalized gradient approximation161 to DFT by self-consistently solving the Kohn–Sham equations, using spherical symmetry and atomic units
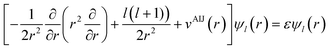 | (3) |
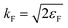 and angular momentum l, described by radial wave functions ψl(r) scatter from this potential, which results in the well-known phase shift expression for asymptotically large distances r = R161
and angular momentum l, described by radial wave functions ψl(r) scatter from this potential, which results in the well-known phase shift expression for asymptotically large distances r = R161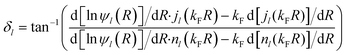 | (4) |
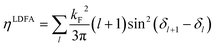 | (5) |
LDFA friction coefficients rely on the independent atom approximation (IAA): they are isotropically dependent on the Cartesian coordinates of each atom in the molecule.159 Thus, a disadvantage of the LDFA method is that the effect of the full ES of the molecule is not taken into account.162
Eqn (2) and (5) can be used to compute friction forces that are linearly proportional to the atom's velocity and the friction coefficients defined in these equations. The LDFA rests on a firm theoretical basis when applied to atoms scattering from metals.163 The approach based on eqn (5) and the friction force derived from it have been shown to correspond to the exact low velocity limit of an atom moving through jellium as obtained with time-dependent density functional theory.164 The LDFA has been applied to many DC systems69,146,152,153,165,166 and much of the work prior to 2017 has been reviewed by Alducin et al.19
As discussed also in ref. 13, calculations with the LDFA by itself suggest that ehp excitation can usually be neglected when computing DC probabilities, with energy shifts between adiabatic and non-adiabatic sticking curves usually smaller than 1 kcal mol−1. Comparisons now available for H2-metal systems (H2 + Cu(111)146 and Ag(111)152,153) also suggest that for these systems it hardly matters whether ODF or the LDFA is used to compute EF coefficients. The only system for which a large difference has been found between sticking probabilities computed with the LDFA and ODF is the already mentioned N2 + Ru(0001) system (see Fig. 5).69 Much of the above observations can be explained from the size of the friction coefficients for the systems discussed, the differences between LDFA and ODF values (Fig. 11), and the regime of velocities relevant to the sticking. For instance, the ODF friction coefficients for N2 + Ru(0001) are roughly an order of magnitude larger than those for H2 + Cu(111) (Fig. 11). Also, for N2 + Ru(0001) the friction coefficients for motion towards the surface as well as for the molecular vibration are much larger with ODF than in the LDFA. The same is not true for H2 + Cu(111). Even though N2 is much heavier than H2, their velocities do not differ much in the regimes relevant to reaction (up to about 0.5 eV for H2 + Cu(111),146 and 4 eV for N2 + Ru(0001)69). The much larger ODF friction coefficients for both degrees of freedom for the latter system then make the difference, explaining both why ODF friction has a large effect, and why this effect is much larger than obtained with the LDFA. These results also suggest caution in interpreting the older LDFA results: the N2 + Ru(0001) results of Fig. 5 convincingly show that a small effect of LDFA friction on sticking is no guarantee whatsoever for a small effect of ODF on sticking (see Fig. 5). This latter observation makes research on the accuracy of these two EF theories, and efforts aimed at developing a better theory all the more relevant.
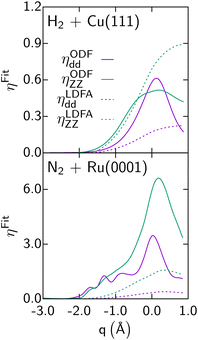 | ||
| Fig. 11 Diagonal elements of the friction tensor, ηqq(in m eV ps Å−2), are shown as a function of q (d is the bond distance of the molecule, Z the distance of the molecule's center of mass to the surface) for the LDFA and the ODF approximations, as computed for H2 + Cu(111)146 and N2 + Ru(0001).69 Data taken from ref. 146 and 69. This figure has been reproduced from ref. 13 with permission from the Royal Society of Chemistry, copyright 2021. | ||
The IESH method has originally been developed for the strong coupling regime, where EF approaches are not expected to work.167 Perhaps the most prominent example is multi-quantum vibrational relaxation of initially highly vibrationally excited NO scattering from Au(111) (see Fig. 3d). The IESH method uses a discretized version of the Newns–Anderson model, in which electrons do not interact.67,68,167 In these one-electron states the modeled electrons can be present in states below and above the Fermi level in the conduction band of the metal, and in the affinity level, i.e., the extra orbital of the molecule to which a metal electron can move to make a state in which the anion of the molecule interacts with the metal (a π* orbital in NO). The method can thus be used to simulate a system in which (partial) electron transfer from the surface to the molecule occurs. The Ne electrons included in the model can be in the lowest M one-electron states; then the system is in the ground state. Alternatively, one or more electrons can be excited to higher-lying one-electron states. The motion of the nuclei is treated with the QCT method subject to the forces related to the PES for the electronic state the system is in at any given time. The time-dependent Schrödinger equation (TDSE) for the electrons is integrated simultaneously. The effect of the NA couplings (between the neutral molecule–surface state and the anion–surface state, and through ehp excitation) is taken into account using the fewest switches surface hopping method.168
Important inputs to the IESH calculations are the PESs for the diabatic neutral molecule–metal and anion–metal states, and the coupling potential. In the approach used mostly so far65 they have been obtained from the adiabatic ground state PES, the Bader charge of the molecule, and the change of the electronic energy of the system upon application of a small electric field. Meng and Jiang169 have recently described a pragmatic approach in which two diabatic PESs are computed with constrained DFT (CDFT170,171), constraining both the surface and the molecule to be neutral in one case, and putting an extra electron on the impinging molecule in the other case. Hereby they used that with CDFT the number of electrons on the molecule can be set equal to the number appropriate for either the neutral molecule or the anion, thereby obtaining the appropriate corresponding diabatic energy.170,171 CDFT can also be used to derive the coupling potential,171 but for this Meng and Jiang instead followed the original approach of Tully and co-workers.65 Diabatic PESs and couplings were analyzed to arrive at qualitative predictions regarding vibrational relaxation of NO and CO scattered from Au(111) and Ag(111).169 The revPBE DF172 was used in the calculations on NO + Au(111) and Ag(111), and the vdW-DF1 DF75 (featuring revPBE exchange but replacing PBE with vdW-DF1 correlation) for CO + Au(111) and Ag(111).
Very recently Jiang and co-workers173 have used their CDFT approach to construct high-dimensional neural network PESs for CO + Au(111). They have used their approach to study vibrationally inelastic scattering of initially highly vibrationally excited CO (in v = 17) from Au(111). As can be seen in Fig. 12 their IESH calculations173 built on CDFT potentials yields results in quite good agreement with the original experiments.174 However, the improvement over dynamics calculations using the same PES but making the Born–Oppenheimer approximation (“BOMD”) is not unequivocal. For example, while the BOMD results overestimate the survival probabilities of CO(v = 17), the IESH results tend to underestimate these quantities. The improvement achieved with IESH for vibrational de-excitation from v = 2 to v = 1 is however unambiguous (Fig. 4a of ref. 173, results not shown here). Nonetheless one should keep in mind that reproducing similar results for NO scattering from Au(111) (as in Fig. 3) should put higher demands on the approach to compute PESs, as the charge transfer energy of NO + Au(111) (5.3 eV) is far lower than that of CO + Au(111) (6.9 eV).
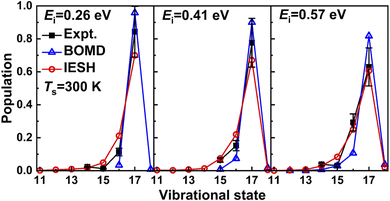 | ||
| Fig. 12 Measured174 relative probabilities for scattering of CO from Au(111) in its initial vibrational state vi = 17 to the final vibrational state vf (on the x-axis) are compared with calculations173 using the IESH method. For details see the text. Taken from ref. 173. Reprinted figure with permission from [G. Meng, J. Gardner, N. Hertl, W. Dou, R. J. Maurer and B. Jiang, Physical Review Letters, 133, 036203, 2024]. Copyright (2024) by the American Physical Society. | ||
2.3 State-of-the-art tools for dynamics
Dynamics calculations can be used to calculate observables such as sticking probabilities and probabilities for vibrationally and/or rotationally inelastic and/or diffractive scattering.13 The hole model39 teaches us that agreement of computed with measured sticking probabilities indicates that the barrier heights obtained with the electronic structure method used are accurate.13,40 This is the case if direct dynamics or an accurately fitted PES is used, and if an accurate dynamical model and method is selected to compute the sticking probabilities. Good agreement of dynamics calculations with experiment for more detailed dynamical observables, such as rotationally inelastic scattering probabilities or diffraction probabilities, indicates a very high quality of the underlying electronic structure method and possibly the method used to fit the PES, as such computed observables are highly sensitive to details of the PES used.175The fitting of a PES can be avoided if one can afford the computational resources to run direct dynamics calculations (ab initio molecular dynamics (AIMD)176,177 or density functional molecular dynamics (DFMD)34), which uses (quasi-)classical trajectories. This approach will work for the calculation of probabilities that are not too small (currently, >10−3), as the inherent statistical error in the computed probability p is equal to 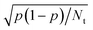 , where Nt is the number of trajectories run. Otherwise, it is best to first compute electronic structure data and fit a PES to these data. Fitting PESs can now be done accurately with the corrugation reducing procedure178 for diatomic molecules interacting with static surfaces, using permutationally invariant polynomials combined with neural network methods for diatomic and polyatomic molecules interacting with static surfaces,179,180 or using a high-dimensional neural network method70,181,182 for molecules interacting with mobile surfaces, in which the surface atoms are allowed to move. In general, fitting an accurate PES to electronic structure data does not represent a bottleneck to the accurate calculation of observables. However, efficiency may be an issue if there is high computational expense associated with either the electronic structure calculations (cost per data point) or the dynamics calculations (number of trajectories needed).
, where Nt is the number of trajectories run. Otherwise, it is best to first compute electronic structure data and fit a PES to these data. Fitting PESs can now be done accurately with the corrugation reducing procedure178 for diatomic molecules interacting with static surfaces, using permutationally invariant polynomials combined with neural network methods for diatomic and polyatomic molecules interacting with static surfaces,179,180 or using a high-dimensional neural network method70,181,182 for molecules interacting with mobile surfaces, in which the surface atoms are allowed to move. In general, fitting an accurate PES to electronic structure data does not represent a bottleneck to the accurate calculation of observables. However, efficiency may be an issue if there is high computational expense associated with either the electronic structure calculations (cost per data point) or the dynamics calculations (number of trajectories needed).
The choice of the dynamical model requires care. As a rule of thumb, for accurate sticking probabilities surface atom motion needs to be modeled if the impinging molecule is heavier than D2, or the surface temperature is high (Ts ≫ 300 K).13 In another rule of thumb, it is advisable to attempt to model electronically non-adiabatic effects if E(CT) is smaller than or close to 7 eV (ref. 69) and/or the impinging molecule is in a highly excited vibrational state.15,183,184 The role of both dissipative mechanisms can now be studied with MDEF calculations if a high-dimensional neural network PES is available,44,69,185 or with ab initio molecular dynamics with electronic friction (AIMDEF).186,187 As noted above, the accuracy likely depends on the type of EF implemented, but it is not yet clear which approach is most accurate. Strong non-adiabatic effects can be modeled with the independent electron surface hopping (IESH) method68 using classical dynamics and, essentially, the fewest switches surface hopping algorithm,168 and this can now be done while also including surface motion accurately.173
The quasi-classical trajectory (QCT) method is, perhaps surprisingly, usually very accurate for modeling activated DC of diatomic molecules as measured in supersonic molecular beam experiments, even for H2.165 This is because188 these experiments imply a high degree of averaging over rovibrational states, and, especially for highly activated dissociation, in experiments at low incidence energies sticking often takes place through the (classically allowed) reaction of vibrationally excited molecules.189,190 Also for this reason tunneling usually does not play a very large role.191 However, in DC of polyatomic molecules intramolecular vibrational relaxation may cause problems for the QCT method, especially for molecules incident in vibrationally excited states and/or at high nozzle temperatures.192 These problems may be avoided by e.g. restricting simulations to cases where a molecule containing H-atoms is partially deuterated with only the one remaining XH-stretch vibration pre-excited, or by keeping the nozzle-temperature low.35,192,193 In the simulation of state-to-state scattering experiments special attention has to be paid to the algorithm to assign final states.194–197 With the use of particular Gaussian binning methods for assigning final states and a method called adiabatic correction it is also possible to obtain QCT sticking probabilities in good agreement with quantum dynamics results for non-activated sticking, as shown by Bonnet and co-workers for H2 + Pd(111).196
Quantum dynamical simulations of DC of diatomic molecules have usually been performed with the time-dependent wave packet method,198–201 the application of which is fairly routine by now if the molecule contains at least one H-atom. However, TDWP calculations on reaction of heavy diatomic molecules on static surfaces can still be difficult to obtain converged results for, and are rather rare.202 In the largest DC problem to which the TDWP method was applied while simulating motion in all molecular degrees of freedom without approximations, H2O reacts on Cu(111)203 and Ni(100).204 Calculations with the TDWP method on DC of polyatomic molecules often invoke reduced dimensionality approximations.54,205,206 In TDWP calculations usually the static surface approximation is invoked, but reliable approximations have been developed to take into account the effect of surface atom motion or surface temperature on sticking on metal surfaces in an a posteriori fashion.207–209
The DC of polyatomic molecules, like CH4, H2O, and CO2, on metals has often been studied with a reaction path Hamiltonian (RPH) method.210,211 While approximate, a large advantage of this method is that the effect of all the molecular vibrations can be modeled for such small-sized polyatomic molecules. While approximations are usually needed to the molecular rotations and translational motion parallel to the surface, guidelines on successful strategies are available.205,212–215 An already mentioned a posteriori method207,208 can be used to accurately216,217 treat the effect of surface temperature. Under conditions in which quasi-classical mechanics should be accurate RPH calculations agreed well with full-dimensional DFMD calculations, where all calculations were based on the same density functional.191,214 However, it has been suggested that under conditions at which the system may swerve from the minimum energy reaction path (e.g. at high incidence energies) the RPH method may become less accurate.192
A fairly new approach to incorporating quantum effects in molecular dynamics simulations is non-equilibrium ring polymer molecular dynamics (NE-RPMD).218 Strictly speaking RPMD is only valid under specific conditions not found in real systems,219 and just like the QCT method it therefore needs to be tested on systems to establish under which conditions it is valid. Comparisons to quantum dynamics results for e.g. H2 + Cu(111),220 D2O + Ni(111),220 and H2 + Co(0001)221 show that NE-RPMD performs much better than the QCT method in the tunneling regime, probably also because NE-RPMD is capable of avoiding artificial energy leakage. However, the method did not perform as well as QCT for H2 + Cu(111)220 at intermediate collision energies, and slightly overestimated reaction in H2 + Co(0001) at high incidence energies.221 A comparison to quantum dynamics results for H2 + Pd(111)221 shows that NE-RPMD may not work for non-activated dissociation if the dynamics is affected by quantum resonances. An advantage of NE-RPMD is that its use avoids artificial intramolecular vibrational redistribution (IVR), making it a much better method than QCT for describing DC of CH4 on Pt(111).192 The ordinary RPMD method applicable in the canonical regime performed rather well at reproducing accurately measured experimental rate constants for DC of H2 on Pt(111).222 This finding was significant because the calculations222 were based on a SRP density functional fitted to supersonic molecular beam experiments,86 which should therefore yield a chemically accurate description of the H2–Pt(111) interaction.13 NE-RPMD has also been used to study scattering of H-atoms from graphene,223 hydrogen spillover from a Pt atom embedded in Cu(111),224 and NO desorption from Pd(111) under thermal conditions.225
3. The way forward
It is clear that the largest challenges exist for systems characterized by E(CT) < 7 eV. Therefore, these are the systems to tackle. To be practical, it is good to pick systems that have already been studied experimentally, because especially in the beginning it will be necessary to validate computed results through comparisons with experiments. Systems with E(CT) < 7 eV for which accurate results for activated sticking are available from supersonic molecular beam experiments include O2 + Al(111),96,226 Ag(110),227–229 Cu(111),230,231 and Cu(100),232–234 HCl + Au(111)43 and Cu(111),235 D2O + Ni(111),59 CO2 + Cu(110),236 and NO + Cu(111).237,238 There are thus plenty of systems to study. Experimental results for state-to-state scattering are also available for HCl + Au(111)239,240 and for NO + Cu(111).237,238 As will be discussed below the availability of experiments on sticking and state-to-state scattering has special advantages in the situation where uncertainties exist concerning the electronic structure method as well as the method to treat non-adiabatic energy dissipation.3.1 Electronic structure
As mentioned before the greatest challenge is to come up with an electronic structure method that is accurate and ultimately based on first principles as well as efficient at computing PESs. For this we suggest to use parameterized density functionals (similar to eqn (1)) as before, but now to base the choice of functional on a few calculations with an accurate, first principles-based (FPB) electronic structure method for judiciously chosen (barrier) geometries. Thereby FPB-DFs are still specific to a particular system, but they do provide a steppingstone towards broader testing of the underlying first principles electronic structure methods. An approach that uses the diffusion Monte-Carlo method to generate the first principles results (quantum Monte-Carlo based DFT, QMC-DFT) was recently tested successfully on the DC of H2 on Al(110).37 The proof-of-concept calculation provided a sticking curve that was displaced from the measured sticking curve241 along the incidence–energy axis by only 1.4 kcal mol−1, suggesting the barriers in the PES to be accurate to within this number (see Fig. 13). For this system E(CT) = 7.2 eV, and a semi-local exchange functional could be used that was a weighted average of the exchange parts of the PBE80 and RPBE48 GGA DFs, while vdW-DF2 (ref. 76) correlation was employed. The QMC-DFT approach was called a best-of-both-worlds approach37 because it combined the accuracy of DMC (for the few calculations “nailing the PES” to first principles results) with the efficiency of DFT for computing a whole PES. Just like the SRP-DFT approach, QMC-DFT works because standard DFT is already quite good at describing the variation of the barrier height with system geometry,37,38 so the only thing that needs to be done is to fit the parameter in the DF to the first principles result for the minimum barrier height.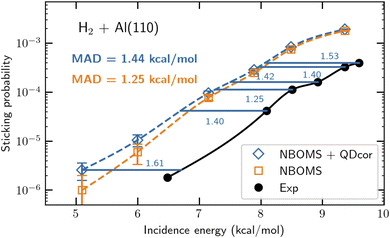 | ||
| Fig. 13 Computed37 and measured241,242S0 for H2 + Al(110). S0 computed with the NBOMS model, and as computed with the NBOMS model but also corrected for quantum dynamical effects, are compared to experimental values. The blue horizontal lines and numbers (kcal mol−1) indicate the energy distance between the measured S0 and the S0 computed with the NBOMS model corrected for nuclear quantum effects. Figure taken from ref. 37 (https://doi.org/10.1021/acs.jpclett.3c02972). Further permission requests to be directed to the ACS. | ||
The QMC-DFT approach is yet to be tested on systems with values of E(CT) less than 7 eV. For reasons discussed above, we anticipate that the density functional of eqn (1) will have to be modified to include exact exchange (EXX). Based on the research on O2 + Al(111)41 discussed above such a DF should combine screened hybrid exchange with van der Waals correlation. To reiterate, measured S0 for O2 + Al(111) could be reproduced semi-quantitatively with the HSE03-1/3X DF,41 which is the screened hybrid HSE03 DF93,94 with the maximal fraction of EXX, a, increased to 1/3 (see Fig. 9). Increasing a further and adding van der Waals correlation should broaden the computed S0 curve,41 increasing the agreement with the experiments41 and a similar approach is likely to work for other systems with E(CT) < 7 eV. An even better approach will probably be to use one of two recent screened hybrid van der Waals DFs, called vdW-DF-ahcx243 and vdW-DF2-ahbr,244 which were designed to not only give a good description of metals but also to make the exchange and correlation parts of the functional compatible. The parameter a (and/or the screening range parameter243,244) can be tuned to achieve agreement with QMC. If these DFs243,244 do not work for a specific system, this may not present a problem: there are sufficient other conceivable combinations of screened hybrid111,245 and van der Waals DFs77,246 to try. We also believe that the balance that can be struck between the need to correct for the self-interaction error and the need to describe static correlation by tuning a will not depend much on the geometry of the barriers relevant to the systems we will investigate. Should this not be so then a way to correct for this exists (see below).
We believe that DMC (as primed with a variational Monte-Carlo calculation using a single Kohn–Sham DFT determinant as input27,37) is, of the first principles methods already tested, likely the most successful. However, the available evidence28,58,108 suggests that the RPA99–102 method and the double hybrid functional XYG3 (ref. 107) should also be tried. In this respect a more general name for the approach than QMC-DFT could be first principles-based DFT (FPB-DFT), on the understanding, of course, that essentially all DFs are based on first principles via LDA correlation. Should it be possible to extend CCSD(T)115 from molecules interacting with semi-conductor surfaces119 to molecule–metal surface interactions, then naturally CCSD(T) can also be applied within an FPB-DFT approach. The same goes for the ECW method of Carter and co-workers,28,121 which would be especially worthwhile if the embedded cluster can be made large enough for convergence in combination with a highly accurate correlated wave function method. In all cases the principle would be the same: the accuracy would come from fitting a mixing coefficient in a density functional of an appropriate form to accurate first principles results for well-chosen geometries, and the resulting density functional would then allow the efficient computation of a full PES.
Coming back to DMC, one may attempt to improve DMC over the single-determinant version tested so far. The main sources of error in a DMC calculation are the fixed-node approximation (the quality of the DMC solution depends somewhat on the quality of the trial wave function through the nodes it inherits from it) and the locality approximation, which arises from the need to use pseudo-potentials to keep the costs of the calculation at bay. Attempts to achieve chemical accuracy (errors <1 kcal mol−1, chemical accuracy) would probably need to reduce the fixed node error using a multi-determinant approach or approaches equivalent to it and based on geminals.247,248 A multi-determinant approach one could try would use charge constrained DFT170,171 to compute diabatic DFT wave functions for the neutral system and the system with one electron transferred to the molecule,169 using that the two Slater determinants used need not be orthogonal.249 For systems containing 5d metals like HCl + Au(111) it may be necessary to use a new type of more accurate pseudo-potential, but procedures to obtain these250,251 or more general procedures to reduce the locality error252 are available. It may also be possible to reduce the statistical error in the Eb computed with DMC using approaches aimed at reducing time step error.253 In other words, there are systematic ways of improving the quality of the DMC calculations used to pin the barrier height in QMC-DFT.
In Section 2.1 we have already sketched a fundamental problem existing with the treatment of molecule–metal surface reactions using DFT, also referring to Fig. 10. It would be nice to have a generally applicable DF (i.e., not one specific to only one or a few particular systems, like a SRP-DF13 or a FPB-DF) available with a guaranteed accuracy of ≈ 2 kcal mol−1 for barrier heights for DC of molecules on metal surfaces. As sketched above, for our system of interest in the gas phase the DF would ideally behave as a range separated hybrid DF109 in which the percentage of exact exchange is maximum at long range (for large distances between r3 and r4 in Fig. 10). However, in the metal the DF should behave as a screened hybrid DF,93 with the amount of exact exchange becoming zero at long range (for large distances between r1 and r2 in Fig. 10). One way to accomplish this would be to develop a “true made-simple hybrid DF”.254,255 To understand this class of DFs we draw an analogy with “made-simple” meta-GGA DFs.79,88 In these DFs, in each point of space an optimal mixture of two GGA exchange DFs is determined from an inhomogeneity parameter α that depends on the local kinetic energy density τ.88 The value of α is used to determine whether the τ computed at a point in space corresponds to metallic or covalent bonding.88,256 Extension of this idea to hybrid DFs implies that the percentage of exact exchange assigned to each pair of points in the double integral over space should depend on the values of α at both points, leading to what we call a true made-simple hybrid DF (which differs from the made-simple hybrid DF introduced in ref. 88). It should also be possible to use the values of other parameters256 at these points.257
To arrive at a true-made simple hybrid functional, in evaluating EXX in the integral over the two points r and r′ one would like the contribution to the exchange made by these points to depend on where they are in Fig. 10. For this we first note that the expression for a global hybrid DF reads:
| Exc,gh = aEx,gh + (1 − a)Ex,sl + Ec | (6) |
| Fx,int(s,α) = Fx,1(p) + f(α)[Fx,0(p) − Fx,1(p)] | (7) |
Sun et al. then went on to define what they called a MS hybrid DF.88 However, instead of making a a function of f(α), which might have seemed the logical choice, they merely used f(α) to define the gradient enhancement factor in eqn (7), and then fitted a to a database, this way defining a global hybrid DF, which they called MGGA_MS2h, and which had a = 0.09.88 We would not expect this DF to perform well for barrier heights for DC on metals in general, because a DF with this low a value of a would not be expected to work well for systems with E(CT) < 7 eV.
Instead, one might attempt to develop a true MS hybrid DF of the form
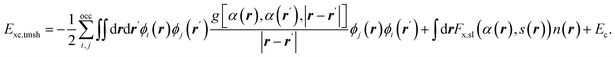 | (8) |
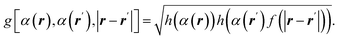 | (9) |
For h(α) one could try an expression that is proportional to the f(α) used in the MS meta-GGAs, which approaches zero in metals, where it will thus appropriately suppress EXX. With the scheme outlined, in the integral over r and r′ the contribution to the exchange made by these points would depend on where they are in Fig. 10, as needed. We sketch just the basic ingredients the method might have here. The true MS hybrid DFs bear a similarity to the local hybrid DFs discussed in ref. 257, which use a local mixing function in the first term on the rhs of eqn (8); one might be able to take inspiration and guidance from this work, for instance, concerning the use of a so-called calibration function one will need, which was omitted by Borlido et al.255 Clearly, work will be needed on g, and on the relationship between g and Fx,sl. As noted by Borlido et al.255 it should also be possible to use off-diagonal mixing in the second term on the rhs of eqn (8), which would however imply the use of a non-local exchange DF instead of the semi-local DF used in this term.259
An alternative approach one might also pursue would be to develop a general purpose DF through machine learning. This might simply be a follow-up version of the DM21 local hybrid DF, for which code and learned network weights are publicly available,260 which should then also be trained on e.g. reaction barrier heights for DC on metals and adsorption of molecules on metals. Such a DF would be a local hybrid DF, as the exchange energy density is already an ingredient of DM21. It might also be possible to develop a machine learned DF in the spirit of the made simple hybrid DF approach by providing the integrand of the first integral in eqn (8) on a two-dimensional grid of points (r, r′) to be used as an additional “feature”260 in the training of the underlying neural network.
3.2 Non-adiabatic effects
As discussed above the ODF and LDFA EF methods both have their specific advantages and disadvantages for describing non-adiabatic effects on reaction. To combine their advantages while avoiding their disadvantages, a new scheme we call scattering potential friction (SPF) could work as follows. As discussed before, the LDFA scheme relates the atom-in-jellium model and the “real surface system” via the electron density in the bare metal. Instead, the SPF scheme would extract an electronic scattering potential from a DFT slab calculation that includes the full molecule–surface interaction, unlike the one obtained self-consistently in the atom-in-jellium model. This Kohn–Sham effective potential along a particular direction, vslab(r), would be based on the same DF as used in the calculations of the PES and describes the perturbation of the jellium. The latter would be a good approximation in particular for free-electron-like metals like Al and (somewhat less so) the noble metals Cu, Ag, Au and Ni that form part of the systems mentioned above as systems of interest for which experiments are available. If a spherically symmetrized description within a certain cut-off (muffin-tin approximation) along different directions is appropriate, phase shifts and thus scattering potential friction coefficients could be obtained analogously to eqn (3)–(5). In fact, analytical expressions have already been obtained for the anisotropic friction tensor of a diatomic molecule based on non-overlapping spherical potentials (muffin-tin approximation, eqn (C11)–(C17) of ref. 261). However, at the time (in 1975)261 scattering phase shifts could not yet be calculated; this was first done numerically by Puska and Nieminen in 1983.160 In the spirit of ref. 261 one could fit vslab(r) to a muffin-tin form and use this to calculate the concomitant phase shifts to obtain the anisotropy and the corrugation of the friction coefficients, which can then also be compared with ODF results. Like in the LDFA, spin-polarization can be easily included in the SPF formalism, and it avoids the computational complications of ODF described above.As noted above EF methods are not expected to be sufficient for describing the case of strong coupling, e.g. when a scattering molecule temporarily picks up an electron from the surface while strongly interacting with it. It is not yet well known under what conditions electronic friction theories break down and a strong coupling method like the IESH method should be used. This should not only depend on the value of E(CT), but also on the degree of vibrational excitation of the molecule, as stretched molecule tend to take up an electron more easily,183,262 which is an additional reason that non-adiabatic effects are especially strong for multi-quantum vibrational relaxation.183 Important inputs to the IESH calculations are the PESs for the diabatic neutral molecule–metal and anion–metal states, and the coupling potential. As noted, in the approach used mostly so far65 they are obtained from an adiabatic ground state PES, the Bader charge of the molecule, and the change of the electronic energy of the system upon application of a small electric field. In an improved implementation these three quantities would all be computed with a FPB-DF fitted to first principles energies for the adiabatic ground state. As noted one can also use a pragmatic approach169,173 in which the two diabatic PESs are computed with CDFT.170,171 Again, an improved implementation would use a FPB-DF fitted to first principles energies for the adiabatic ground state in the CDFT calculations. Rather than using Bader charges to derive the coupling potentials as has been done so far in the CDFT approach,169,173 CDFT can also be used to derive the coupling potential using “CDFT-couplings” (i.e., eqn (51) of ref. 171) directly, and this might be a further improvement.
3.3 PES representation and dynamics
Several approaches can be used to best represent the first principles-based results. This concerns the representation of the first principles results through the FPB density functional, as well as making an accurate fit of FPB-DFT data. In the simplest approach, one can simply fit the PES for the molecule interacting with the mobile surface using e.g. the Behler–Parinello high-dimensional neural network (BP-HDNN) method discussed above,181,263 which uses atomic neural networks to enforce the symmetries of the system.263 Improvements can likely be made with a divide-and-conquer approach of Smits and Somers264 in which the full potential describing the molecule interacting with the surface is written as| Vfull(r,q) = VSS(r,qid) + Vdist(q) + Vcoup(r,q). | (10) |
The divide-and-conquer approach described above has an added advantage if it is difficult to represent accurate first principles results for differing barrier geometries with the use of a FPB density functional based on a single parameter, e.g., the parameter describing the maximum allowed EXX a. This can be mended37 by allowing a to vary with impact site (X,Y) and the azimuthal orientation angle ϕ describing the molecule's orientation relative to the surface. This can be done by expanding a in a few (2–4) expansion functions of X, Y and ϕ that are totally symmetric under the plane group267 of the system, just like it is possible to fit a molecule-rigid surface PES using such expansion functions.268 An internally consistent procedure can be obtained by allowing this variation in the DFT calculations needed to fit VSS(r,qid) and Vcoup(r,q) only. The potential describing the metal can be based on calculations using the average of a(X,Y,ϕ) over X, Y and ϕ, or the (EAM) fit already mentioned above could be used for Vdist(q). In either case a fully consistent description of the metal would be obtained. Finally, in the future it will probably be possible to derive a true first principles quality PES by adding a high-dimensional neural network (HDNN) PES based on the difference between say a thousand first principles energies and a FPB-DFT PES. This is in the spirit of the Δ-machine learning approach recently used to obtain a CCSD(T) level PES for MD simulations of liquid water,269 and it may already be possible to obtain DMC-quality PESs in this manner for a few selected systems of interest.
Of the systems of interest mentioned above for which experiments exist, accurate results can be obtained with the QCT method if the projectile is a diatomic molecule. For a system like D2O + Ni(111)59 we speculate that it might now be possible to perform TDWP calculations for the molecule interacting with the static surface, and to incorporate a posteriori corrections for the effect of surface temperature as described above in Section 2. The system incorporates nine molecular degrees of freedom. Assuming that the expense of the computation will increase by a factor of  for each degree of freedom by replacing H with D, the expense of the calculation should increase relative to that performed 8 years ago for H2O + Cu(111)220 by about a factor 24.5. Assuming Moore's law to hold and using that the H2O + Cu(111)220 calculation was done 8 years ago, a full-dimensional TDWP calculation of D2O on Ni(111) should then be possible in the year of writing (2024), ensuring that the latter system can be modeled with high accuracy. A system like CO2 + Cu(110)236 is likely best modeled with NE-RPMD to ensure that artificial IVR between the CO stretch vibrations is avoided.192 In any case, as discussed in the previous section NE-RPMD needs more testing on systems to learn for which systems and under which conditions this method is reliable and improves significantly over QCT. A good alternative may be to use the RPH method for CO2 + Cu(110)236 and use an a posteriori method to incorporate surface temperature. An advantage of the NE-RPMD method is that it is possible to also incorporate surface atom motion in a more direct way.192 It is also possible to incorporate electronic friction in RPMD for thermal rates,270,271 which suggests that the same can be done for NE-RPMD, which might enable an upgraded version of MDEF with some nuclear quantum effects, like tunneling and avoidance of artificial IVR, described.
for each degree of freedom by replacing H with D, the expense of the calculation should increase relative to that performed 8 years ago for H2O + Cu(111)220 by about a factor 24.5. Assuming Moore's law to hold and using that the H2O + Cu(111)220 calculation was done 8 years ago, a full-dimensional TDWP calculation of D2O on Ni(111) should then be possible in the year of writing (2024), ensuring that the latter system can be modeled with high accuracy. A system like CO2 + Cu(110)236 is likely best modeled with NE-RPMD to ensure that artificial IVR between the CO stretch vibrations is avoided.192 In any case, as discussed in the previous section NE-RPMD needs more testing on systems to learn for which systems and under which conditions this method is reliable and improves significantly over QCT. A good alternative may be to use the RPH method for CO2 + Cu(110)236 and use an a posteriori method to incorporate surface temperature. An advantage of the NE-RPMD method is that it is possible to also incorporate surface atom motion in a more direct way.192 It is also possible to incorporate electronic friction in RPMD for thermal rates,270,271 which suggests that the same can be done for NE-RPMD, which might enable an upgraded version of MDEF with some nuclear quantum effects, like tunneling and avoidance of artificial IVR, described.
3.4 Validation and experiments
The validation of the FPB-DFT electronic structure approach in combination with the new SPF method to deal with non-adiabatic effects will require considerable care. We suggest that several systems be tackled to avoid a situation where good agreement is obtained for 1 or 2 systems for the wrong reasons, i.e., through error cancellation. The problem is that we are dealing with a situation where the ground state electronic structure method is not yet validated for systems with E(CT) < 7 eV. Specifically, DMC and RPA and the double hybrid functional XYG3 have been shown to be accurate for two systems with E(CT) > 7 eV, but we do not yet know how well they will perform for systems with E(CT) < 7 eV, and at the same time one would try to evaluate the accuracy of the new SPF method, or of another method for dealing with non-adiabatic effects. Probably the best strategy would be to test the FPB-DFT method using one specific first principles method in a systematic way on several systems, in combination with SPF, ODF, and the LDFA. If the FPB-DFT method combined with a specific EF method consistently yields the best results for all or the majority of the systems, this would constitute strong evidence for the accuracy of both the first principles electronic structure method and the particular EF method used.The availability of experiments on both sticking and state-to-state scattering, and especially on vibrationally inelastic scattering, would be especially useful for validation of a method for describing non-adiabatic effects. The reason is as follows. Energy dissipation through, for instance, ehp excitation affects sticking and state-to-state scattering in a fundamentally different way. Whether or not a molecule undergoes DC is only affected by ehp excitation on the way to the barrier; once the molecule is over the barrier, its fate is decided (it will stick). The opposite is true for scattering: the size of e.g. state-to-state vibrationally inelastic scattering probabilities is affected by ehp excitation on the way to the barrier as well as on the way back to the gas phase. In the past this idea has been used to establish that DC of H2 on metal surfaces is unlikely to be affected much by ehp excitation, as results for both reaction and diffractive scattering in H2 + Pt(111) could be reproduced with an adiabatic approach using one and the same PES.262 We anticipate that it could be quite useful to have accurate and detailed experiments on both sticking and vibrationally inelastic scattering available on systems like HCl + Cu(111)235 and NO + Cu(111),237,238 as the dissociation barrier is not so high for these systems. The HCl + Au(111) system will be quite useful to work on even though the dissociation barrier is high, as experiments are available for both sticking43 and scattering.239,240 For NO on Au(111) a wealth of detailed experiments is available on scattering,60–62,272 making this system quite useful for benchmarking, even though it might be too inert for sticking measurements. For NO + Cu(111)237,238 some results are already available, but the accuracy of the sticking results is not so clear and not so much results are available on the vibrationally inelastic scattering yet.
We propose that barrier heights for systems with E(CT) < 7 eV, once validated and established to be accurate, are added to the systems in the SBH17 database,32 which now mostly incorporates systems with E(CT) > 7 eV (16 out of 17). The new database thus obtained would be a representative database of barriers for DC on metal surfaces. To develop a database of appropriate size, statistical methods (i.e., “least absolute shrinkage and selection operator”273 and “stepwise regression”274) can be employed as also used by Morgante and Peverati275 to reduce their large ACCDB database (8656 unique datapoints) to a much smaller database (ASCDB, 200 unique datapoints). Adding the thus obtained database to existing databases of chemical and other properties of interest,23,25,30,276–279 which mostly address gas phase systems, could provide considerable assistance with benchmarking density functionals that aim to be “universal”, i.e., for any system of interest to chemists and physicists. The existing large databases23,25,30,276–279 do contain barriers for gas phase reactions, but none of them contain barrier heights for molecule–metal surface reactions.
So far we have simply assumed that experimental data for sticking coefficients would always come from supersonic molecular beam experiments, which measure sticking probabilities at fairly well defined hyperthermal collision energies. There is also a good reason for this. Such molecular beam experiments are able to probe the reactivity on well-defined Miller index surfaces, making these experiments suitable for validation.280 In contrast, until recently, in the usual kinetics experiments performed under thermal conditions highly activated reactions often took place at ill-defined defects like steps, kinks, or vacancies.281,282 This makes these older experiments unsuitable for validation purposes, because the geometry for which the barrier height needs to be computed is not clear.280
As nicely discussed and summarized by Jiang and co-workers,225 this situation has now changed thanks to recent experiments by Kitsopoulos, Wodtke, and Auerbach and co-workers. They have measured thermal rates for a number of reactions using a new combination of techniques, involving velocity-resolved kinetic traces determined with ion-imaging. Such experiments have addressed how steps affect CO desorption from Pt(111),283 CO desorption from Pd(111) and Pt(111),284 CO oxidation on Pt(111) and the stepped Pt(332) surface,285,286 thermal CO desorption from and CO oxidation on Pd(332),287 NH3 desorption from Pt(111) and Pt(332),288 thermal H-atom recombination on Pt(111) and Pt(332),289 and thermal recombination of HD on Pd(111) and Pd(332).290 In these experiments strategies have been employed to isolate the effects defects might have on reaction rates on macroscopic low index surfaces. For instance, rates were measured on both low index and stepped surfaces, and the assumption was made that the defect sites on the macroscopic low index surface exhibit a similar reactivity as the step sites on the stepped surface. As a result, these experiments likely offer a good testing ground to kinetics methods computing rates based on DFT modeling of the system. Inspired by these new experimental developments, new computational kinetics methods are being developed for predicting rates.222,225,289 The CO2 + Pd, the CO2 + Pt and the NH3 + Pt systems all have E(CT) < 7 eV, so the experiments on these systems are all potentially useful for testing FPB-DFT as formulated here, using appropriate computational kinetics methods for validation.
4. Summary and outlook
Dissociative chemisorption reactions on metal surfaces are of interest for both practical and scientific reasons. The barriers of these reactions are often important to the accurate modeling of heterogeneously catalyzed processes, but first principles methods capable of computing these barriers with chemical accuracy have not yet been established. Presently the molecule–metal surface interaction, which governs the molecule's reaction on as well as its state-to-state scattering from surfaces, is mostly studied with DFT. With present-day density functionals this method is not yet accurate enough, and few databases exist for testing DFT on DC barriers.In the present state-of-the-art a semi-empirical version of DFT is used (SRP-DFT), in which a parameter in a functional with GGA exchange is fitted to reproduce sticking probabilities measured in a supersonic molecular beam experiments. Using this approach chemically accurate barriers have been extracted for a number of systems and collected in a database than can be used for testing electronic structure methods (SBH17). Unfortunately, this approach breaks down for systems affected by charge transfer, i.e., for which, as a rule of thumb, the difference between the surface's work function and the molecule's electron affinity (i.e., E(CT)) is less than 7 eV. Comparison to experiments shows that with the present approach, which is based on PESs computed with functionals containing semi-local exchange, sticking is overestimated, and vibrationally inelastic scattering is not described accurately. These systems are also prone to electronically non-adiabatic effects like electron–hole pair excitations, for which the accuracy of existing methods is difficult if not impossible to benchmark separately.
Because there are two sources of uncertainty in computing sticking probabilities for systems with E(CT) < 7 eV, a semi-empirical approach for adjusting the functional to only reproduce measured sticking probabilities cannot be expected to work. This is unfortunate because these systems are quite important to sustainable chemistry. To address the problem described above, this Perspective has first summarized the present state-of-the-art in electronic structure theory for molecules interacting with metal surfaces, in the description of non-adiabatic effects in these systems, and in extracting computed observables for comparison with experiments through fitting of PESs and dynamics calculations. After that a vision has been sketched on how to make progress in these areas so as to eventually achieve accurate theoretical predictions for systems that are often of high practical relevance to sustainable chemistry.
Concerning electronic structure theory, a problem with DFT using standard semi-local functionals (GGAs or meta-GGAs) is that such functionals are usually inaccurate for predicting sticking curves. This implies that they are inaccurate for barrier heights to DC on metals. For systems with E(CT) > 7 eV this can be addressed by constructing system-specific parameterized functionals, which mix semi-local exchange functionals and use either semi-local or non-local but efficient-to-evaluate correlation functionals. In this semi-empirical approach, the mixing parameter is varied until sticking probabilities measured in supersonic molecular beam experiments are reproduced. For these systems this approach works because the minimum barrier height can be straddled with functionals containing semi-local exchange, and because standard functionals are capable of describing how the barrier height to sticking varies with system geometry.
The semi-empirical approach described above does not work for systems with E(CT) < 7 eV because functionals using semi-local exchange systematically underestimate barrier heights for these systems. Calculations on an infamous system with E(CT) < 7 eV, i.e., O2 + Al(111), suggest that this problem may be resolved by using screened hybrid density functionals. We have also noted a fundamental DFT problem with describing molecules interacting with metals: at long range the fraction of exact exchange should be maximum in the gas phase, while it should be minimum (exact exchange should be screened) in the metal.
Two first principles, or non-empirical, methods have recently been demonstrated to show promise of predictive accuracy for barrier heights in two benchmark systems. Diffusion Monte-Carlo achieved an accuracy of about 1.5 kcal mol−1 for H2 + Cu(111) and Al(110). The RPA method showed chemical accuracy for both systems (errors <1 kcal mol−1). Because results are only available for two systems at this stage, it cannot yet be said which method will be best; DMC worked better than the RPA for a database with 76 barrier heights for gas phase reactions.
An application of the CCSD(T) method, which has been called the gold standard for computing gas phase barriers, to DC on metals has not yet been demonstrated. Like other ab initio many electron-wave function methods (or correlated wave function methods), CCSD(T) is currently computationally too expensive for periodic calculations on DC on metals. However, such methods show promise when applied in an embedded cluster fashion, using density functional embedding. But the accuracy of this embedded correlated wave function approach is not yet as high as achieved with the RPA and DMC methods. Another cluster-based approach, the ONIOM method, has shown very promising results when carefully monitoring the convergence with respect to cluster size and combined with a doubly hybrid functional. Like the RPA, the latter makes the PES depend on unoccupied states and thus comes at a computational price that appears to be unavoidable when high accuracy is needed.
Systems in which a molecule approaches a metal surface are always prone to electron–hole pair excitation due to molecular motion, an electronically non-adiabatic effect breaking the Born–Oppenheimer approximation. If the coupling between molecular motion and the electrons in the metal is weak, this can be addressed with electronic friction theory. Friction tensors can be incorporated in a generalized Langevin form for the nuclear equations of motion. Two EF methods currently exist. The ODF method takes the electronic structure of the molecule and the metal surface into account. Problems of the ODF method are that it exhibits a non-physical dependence on the broadening parameters needed to compute friction coefficients from electron–phonon coupling matrix elements, and that its use may lead to unphysically large friction in regions where a spin transition of an impinging atom or molecule occurs. Going beyond the Markov approximation that is currently applied to coarse grain the effect of the electron on the nuclear dynamics could be a way forward. The LDFA method does not exhibit these problems, and has been shown to be reliable for atoms scattering from metals. However, the LDFA method does not include effects related to the electronic structure of the molecule and of the metal other than the mere perturbation of an atom embedded in (bulk) jellium. Neither of these two methods has at present been proven to be universally more accurate for describing non-adiabatic effects on DC on metal surfaces. In fact, they give quite different results for at least one benchmark system, i.e., N2 + Ru(0001).
Cases in which the coupling between molecular motion and the metal electrons is strong, for instance when the molecule is able to (temporarily) pick up a partial charge from the metal in what is not the system's electronic ground state, cannot be described by electronic friction methods. Such cases can be described with the IESH method, in which the motion of the neutral molecule on the metal surface is coupled to states in which the molecule is an anion or the metal electron is excited to a virtual metal level. In the present state-of-the-art the two molecule–metal surface states are computed with CDFT, and the coupling potentials with a model involving Bader charges and the change of energy of the charged system in an imposed electric field.
Concerning dynamics to compute observables like sticking coefficients and scattering probabilities, the fitting of a PES can be avoided in direct dynamics calculations. This is feasible only if the electronic structure approach is computationally efficient and if the probabilities to be computed are large enough that they can be computed with high enough statistical accuracy using a limited number of classical trajectories. Otherwise a divide-and-conquer approach needs to be used in which electronic structure data are computed first and next fitted to a PES, after which calculations using an appropriate dynamical model and method need to be performed. For PES fitting accurate methods are now available, and this stage does usually not present bottlenecks if enough electronic structure data are available for making an accurate fit.
In the dynamical model, a rule of thumb is that surface atom motion has to be modeled for molecules heavier than D2, and/or for surface temperatures considerably higher than room temperature. It is advisable to attempt to model non-adiabatic effects for systems for with E(CT) < 7 eV. Both (nuclear and electronic) dissipative degrees of freedom can be modeled computing forces on the fly with AIMDEF or with a pre-computed PES using MDEF.
Of the dynamics methods, the QCT method is usually highly accurate at describing activated sticking in supersonic molecular beam experiments. The QCT method may also yield accurate results for sticking if improved methods are used for assigning final states of scattered molecules and the so-called adiabatic correction is applied. In specific cases (low nozzle temperature, or the vibrationally excited state involves the highest frequency vibration of the molecule isolated from other vibrations) the QCT method may also yield accurate results for sticking of polyatomic molecules.
Concerning quantum dynamics, the TDWP method is a very accurate method that has been applied to DC of diatomic molecules and of the H2O molecule. The computational expense of the method is currently too high to treat sticking of bigger molecules. Sticking of intermediately sized molecules can be modeled quantum dynamically with the reaction path Hamiltonian method. With both the TDWP and the RPH method it is possible to rather accurately describe the effects of surface temperature using post-processing methods. Researchers are also starting to explore the accuracy of non-equilibrium ring polymer molecular dynamics, which can describe sticking in the tunneling regime more accurately than QCT. The use of NE-RPMD avoids artificial intra-molecular vibrational relaxation in the molecule on the way to the surface, which is a known problem with the QCT method. However, NE-RPMD is not more accurate than QCT under all conditions, and more research is needed to establish empirically under which conditions and for which systems NE-RPMD improves over the QCT method.
Coming to the way forward, it is clear that the greatest challenges exist for systems with E(CT) < 7 eV. A number of systems have been identified for which accurate results are available from supersonic molecular beam experiments, or for which accurate rates are available from thermal experiments using new techniques (velocity-resolved kinetic traces determined with ion imaging). Calculations with the new approaches suggested in this Perspective can model these systems for validation.
The greatest challenge likely lies with the electronic structure approach for the electronic ground state. As a steppingstone for testing first principles-based methods, we suggest to use system-specific parameterized density functionals as before, but now to base the parameters in these functionals on calculations with accurate first principles methods, like DMC or the RPA method (FPB-DFT), for judiciously chosen geometries. Systematic ways of diminishing the fixed-node and the locality errors in DMC exist. It will probably be best to use a parameterized density functional with exchange taken from a screened hybrid functional, combined with one of the Chalmers–Rutgers van de Waals correlation functionals. Judicious choices exist for the combination of these, and the maximum fraction of exchange and/or the range parameter in the functional can be tuned to fit to the first principles result.
The next great challenge is to come up with an EF method that combines the advantages and avoids the pitfalls of the two existing methods, the LDFA and the ODF methods. With the new (SPF) approach, we suggest to focus on extracting an electronic scattering potential (as a Kohn–Sham effective potential) from a DFT calculation for the full molecule–metal surface system. The method would use analytical expressions that were already derived, but at a time when it was not yet possible to evaluate them numerically on computers. Improvements of the IESH approach have also been discussed and consist of using a FPB density functional in the CDFT calculations, and actual CDFT couplings for the non-adiabatic coupling potentials.
For fitting PESs we suggest using the high-dimensional neural network potential approach of Behler and Parinello, or more recently developed machine learning techniques with different descriptor representations. Improvements can likely be made by splitting the molecule–surface interaction up in three components. In this way, if needed one might also correct for errors in fitting the density functional to first principles results at different geometries, by allowing the fitting parameter to vary according to the full symmetry of the molecule–metal surface system. It may also be possible to upgrade PESs obtained with FPB-DFT to an actual first principles PES. This can likely be done using a Δ-machine learning approach in which, for a limited number of judiciously chosen points, an added neural network potential is fit to the difference between first principles and fitted FPB-DFT results.
We have also provided some discussion on how some of the experimental results we suggest to model can be best addressed with available dynamics methods. For instance, we suggest that the D2O + Ni(111) system can now be tackled with the TDWP method, and that calculations on CO2 + Cu(110) can be done with NE-RPMD, and/or the RPH method.
Furthermore, we have discussed ways of validating the new computational approaches with comparisons to experiments. We have argued that systems for which experimental sticking and vibrational state-to-state scattering results exist will be especially useful to validating approaches for electronically non-adiabatic scattering. The reason is that these two processes are affected by non-adiabatic energy dissipation in fundamentally different ways.
Once accurate barrier heights are available for systems with E(CT) < 7 eV, these should be added to results that are already available for systems with E(CT) > 7 eV in the SBH17 database. This way, the first representative (i.e., including systems with no restrictions on E(CT)) database for barrier heights to DC on metal surfaces would be obtained. This database would be quite useful to computational heterogeneous catalysis. Adding this database to existing large databases containing results for mostly gas phase systems should also be very useful, as it should clearly be desirable to be able to test whether new electronic structure approaches work for both types of systems. Such a database would also be useful to testing a new “true made simple hybrid density functional”, which would incorporate the correct limiting behavior of long-range exact exchange in both the gas phase and the metal. We anticipate that such a functional should be a local hybrid, using diagnostics based on the kinetic energy density to determine where the electrons are in the system to more accurately evaluate the exchange interaction between them. We also anticipate that with the right training machine-learning based density functionals incorporating exchange energy densities might be successful at exhibiting the right long-range behavior of exchange in both parts of molecule–metal surface systems.
In summary, a clear route can be envisaged to an improved modeling of molecule–metal surface systems that are prone to charge transfer, many of which are likely important to sustainable chemistry. As always, the devil will be in the details and, as always, it will be fun coming up with the solutions with well thought out fundamental research. We anticipate this to be a vibrant direction of research that can provide wonderful challenges to researchers for decades to come before they can declare “problem solved” and go on their way to solve the next great problem.
Author contributions
G. J. K. wrote the outline of the manuscript. Both G. J. K. and J. M. contributed to the writing of the original draft of the manuscript, the review of the manuscript, and the editing of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We are grateful to Prof. Bin Jiang for providing us with an electronic copy of Fig. 12. Part of the work presented here was supported financially by the ERC (with the ERC-ADG-2013 grant no. 338580) and by NWO (through CW-TOP grants no. 715.011.000 and 715.017.001) and through several grants of computer time by NWO-NCF and NWO-EW.References
- R. Noyori, Nat. Chem., 2009, 1, 5–6 CrossRef CAS PubMed.
- C. A. Wolcott, A. J. Medford, F. Studt and C. T. Campbell, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- M. K. Sabbe, M. F. Reyniers and K. Reuter, Catal. Sci. Technol., 2012, 2, 2010–2024 RSC.
- R. D. Beck, P. Maroni, D. C. Papageorgopoulos, T. T. Dang, M. P. Schmid and T. R. Rizzo, Science, 2003, 302, 98–100 CrossRef CAS.
- G. Ertl, J. Vac. Sci. Technol., A, 1983, 1, 1247–1253 CrossRef CAS.
- K. Honkala, A. Hellman, I. N. Remediakis, A. Logadottir, A. Carlsson, S. Dahl, C. H. Cristensen and J. K. Nørskov, Science, 2005, 307, 555–558 CrossRef CAS.
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- B. W. J. Chen, L. Xu and M. Mavrikakis, Chem. Rev., 2021, 121, 1007–1048 CrossRef CAS PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Nørskov, Science, 2014, 345, 197–200 CrossRef CAS.
- J. K. Nørskov, F. Abild-Petersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U.S.A., 2011, 108, 937–943 CrossRef PubMed.
- S. Perathoner, G. Centi, S. Gross and E. M. J. Hensen, Science and technology roadmap on catalysis for Europa: A path to create a sustainable future, https://www.euchems.eu/wp-content/uploads/2016/07/160729-Science-and-Technology-Roadmap-on-Catalysis-for-Europe-2016.pdf.
- G. J. Kroes, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048 RSC.
- B. Jiang and H. Guo, J. Chem. Phys., 2019, 150, 180901 CrossRef.
- K. Golibrzuch, N. Bartels, D. J. Auerbach and A. M. Wodtke, Annu. Rev. Phys. Chem., 2015, 66, 399–425 CrossRef CAS.
- D. Farías and R. Miranda, Prog. Surf. Sci., 2011, 86, 222–254 CrossRef.
- H. Chadwick and R. D. Beck, Annu. Rev. Phys. Chem., 2017, 68, 39–61 CrossRef CAS PubMed.
- D. J. Auerbach, J. C. Tully and A. M. Wodtke, Nat. Sci., 2021, 1, e10005 CrossRef CAS.
- M. Alducin, R. Diéz Muiño and J. I. Juaristi, Prog. Surf. Sci., 2017, 92, 317–340 CrossRef CAS.
- J. P. Perdew, MRS Bull., 2013, 38, 743–750 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. T. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- E. Sim, S. Song, S. Vuckovic and K. Burke, J. Am. Chem. Soc., 2022, 144, 6625–6639 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- R. Peverati and D. G. Truhlar, Philos. Trans. R. Soc., A, 2014, 372, 20120476 CrossRef.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32214 RSC.
- F. Libisch, C. Huang, P. L. Liao, M. Pavone and E. A. Carter, Phys. Rev. Lett., 2012, 109, 198303 CrossRef PubMed.
- K. Doblhoff-Dier, J. Meyer, P. E. Hoggan and G. J. Kroes, J. Chem. Theory Comput., 2017, 13, 3208–3219 CrossRef CAS PubMed.
- Z. Y. Wei, J. M. P. Martirez and E. A. Carter, J. Chem. Phys., 2023, 159, 194108 CrossRef CAS.
- A. Pribram-Jones, D. A. Gross and K. Burke, Annu. Rev. Phys. Chem., 2015, 66, 283–304 CrossRef CAS.
- P. Morgante and R. Peverati, J. Comput. Chem., 2019, 40, 839–848 CrossRef CAS PubMed.
- S. Mallikarjun Sharada, T. Bligaard, A. C. Luntz, G. J. Kroes and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 19807–19815 CrossRef CAS.
- T. Tchakoua, N. Gerrits, E. W. F. Smeets and G. J. Kroes, J. Chem. Theory Comput., 2023, 19, 245–270 CrossRef CAS PubMed.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G. J. Kroes, Science, 2009, 326, 832–834 CrossRef.
- F. Nattino, D. Migliorini, G. J. Kroes, E. Dombrowski, E. A. High, D. R. Killelea and A. L. Utz, J. Phys. Chem. Lett., 2016, 7, 2402–2406 CrossRef CAS PubMed.
- D. Migliorini, H. Chadwick, F. Nattino, A. Gutiérrez-Gonzalez, E. Dombrowski, E. A. High, H. Guo, A. L. Utz, B. Jackson, R. D. Beck and G. J. Kroes, J. Phys. Chem. Lett., 2017, 8, 4177–4182 CrossRef CAS.
- T. Tchakoua, T. Jansen, Y. van Nies, R. F. A. van den Elshout, B. A. B. van Boxmeer, S. P. Poort, M. G. Ackermans, G. S. Beltrão, S. A. Hildebrand, S. E. J. Beekman, T. van der Drift, S. Kaart, A. Santic, E. E. Spuijbroeck, N. Gerrits, M. F. Somers and G. J. Kroes, J. Phys. Chem. A, 2023, 127, 10481–10498 CrossRef CAS PubMed.
- A. D. Powell, N. Gerrits, T. Tchakoua, M. F. Somers, H. F. Busnengo, J. Meyer, G. J. Kroes and K. Doblhoff-Dier, J. Phys. Chem. Lett., 2024, 15, 307–315 CrossRef CAS PubMed.
- A. D. Powell, G. J. Kroes and K. Doblhoff-Dier, J. Chem. Phys., 2020, 153, 224701 CrossRef CAS.
- M. Karikorpi, S. Holloway, N. Henriksen and J. K. Nørskov, Surf. Sci., 1987, 179, L41–L48 CrossRef CAS.
- A. Salin, J. Chem. Phys., 2006, 124, 104704 CrossRef CAS.
- N. Gerrits, E. W. F. Smeets, S. Vuckovic, A. D. Powell, K. Doblhoff-Dier and G. J. Kroes, J. Phys. Chem. Lett., 2020, 11, 10552–10560 CrossRef CAS PubMed.
- K. R. Bryenton, A. A. Adeleke, S. G. Dale and E. R. Johnson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 13, e1631 Search PubMed.
- N. Gerrits, J. Geweke, E. W. F. Smeets, J. Voss, A. M. Wodtke and G. J. Kroes, J. Phys. Chem. C, 2020, 124, 15944–15960 CrossRef CAS.
- Q. H. Liu, X. Y. Zhou, L. S. Zhou, Y. L. Zhang, X. Luo, J. Guo and B. Jiang, J. Phys. Chem. C, 2018, 122, 1761–1769 CrossRef CAS.
- G. Füchsel, X. Y. Zhou, B. Jiang, J. I. Juaristi, M. Alducin, H. Guo and G. J. Kroes, J. Phys. Chem. C, 2019, 123, 2287–2299 CrossRef PubMed.
- P. R. Shirhatti, J. Geweke, C. Steinsiek, C. Bartels, I. Rahinov, D. J. Auerbach and A. M. Wodtke, J. Phys. Chem. Lett., 2016, 7, 1346–1350 CrossRef CAS.
- T. H. Liu, B. N. Fu and D. H. Zhang, J. Chem. Phys., 2017, 140, 164706 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- Q. Shen, L. Zhu, J. Wu, W. Dong, X. Wang, T. Wang, B. Jiang and X. M. Yang, Chin. J. Chem. Phys., 2024, 37, 490–496 CrossRef CAS.
- N. Gerrits, E. W. F. Smeets, S. Vuckovic, A. D. Powell, K. Doblhoff-Dier and G. J. Kroes, J. Phys. Chem. Lett., 2020, 11, 10552–10560 CrossRef CAS.
- J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2005, 94, 036104 CrossRef.
- J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421 CrossRef.
- M. Ramos, C. Díaz, A. E. Martínez, H. F. Busnengo and F. Martín, Phys. Chem. Chem. Phys., 2017, 19, 10217–10221 RSC.
- B. Jiang and H. Guo, Phys. Chem. Chem. Phys., 2016, 18, 21817–21824 RSC.
- X. X. Hu, M. Yang, D. Q. Xi and H. Guo, J. Chem. Phys., 2018, 149, 044703 CrossRef.
- N. Gerrits and G. J. Kroes, J. Phys. Chem. C, 2019, 123, 28291–28300 Search PubMed.
- M. Pozzo and D. Alfè, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245313 CrossRef.
- B. Oudot and K. Doblhoff-Dier, J. Chem. Phys., 2024, 161, 054708 CrossRef CAS PubMed.
- P. M. Hundt, B. Jiang, M. E. van Reijzen, H. Guo and R. D. Beck, Science, 2014, 344, 504–507 CrossRef CAS PubMed.
- Y. Huang, A. M. Wodtke, H. Hou, C. T. Rettner and D. J. Auerbach, Phys. Rev. Lett., 2000, 84, 2985–2988 CrossRef CAS PubMed.
- K. Golibrzuch, P. R. Shirhatti, I. Rahinov, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Chem. Phys., 2014, 140, 044701 CrossRef PubMed.
- N. Bartels, B. C. Krüger, D. J. Auerbach, A. M. Wodtke and T. Schäfer, Angew. Chem., Int. Ed., 2014, 53, 13690–13694 CrossRef CAS PubMed.
- C. L. Box, Y. L. Zhang, R. R. Yin, B. Jiang and R. J. Maurer, JACS Au, 2021, 1, 164–173 CrossRef CAS PubMed.
- R. R. Yin, Y. L. Zhang and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 5969–5974 CrossRef CAS PubMed.
- S. Roy, N. Shenvi and J. C. Tully, J. Chem. Phys., 2009, 130, 174716 CrossRef.
- M. Head-Gordon and J. C. Tully, J. Chem. Phys., 1995, 103, 10137–10145 CrossRef CAS.
- N. Shenvi, S. Roy and J. C. Tully, Science, 2009, 326, 829–832 CrossRef CAS PubMed.
- N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107 CrossRef PubMed.
- P. Spiering, K. Shakouri, J. Behler, G. J. Kroes and J. Meyer, J. Phys. Chem. Lett., 2019, 10, 2957–2962 CrossRef CAS PubMed.
- K. Shakouri, J. Behler, J. Meyer and G. J. Kroes, J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS.
- M. M. Montemore, M. A. van Spronsen, R. J. Madix and C. M. Friend, Chem. Rev., 2017, 118, 2816–2862 CrossRef.
- A. Morales-Garcia, F. Viñes, J. R. B. Gomes and F. Illas, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2021, 11, e1530 CrossRef CAS.
- D. H. Zhang and H. Guo, Annu. Rev. Phys. Chem., 2016, 67, 135–158 CrossRef CAS PubMed.
- T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Chem. Theory Comput., 2008, 4, 1254–1262 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Lee, É. D. Murray, L. Z. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 CrossRef.
- H. A. Michelsen, C. T. Rettner, D. J. Auerbach and R. N. Zare, J. Chem. Phys., 1993, 98, 8294–8307 CrossRef CAS.
- E. W. F. Smeets, J. Voss and G. J. Kroes, J. Phys. Chem. A, 2019, 123, 5395–5406 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. W. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. W. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. L. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- E. W. F. Smeets and G. J. Kroes, J. Phys. Chem. C, 2021, 125, 8993–9010 CrossRef CAS.
- E. N. Ghassemi, M. Wijzenbroek, M. F. Somers and G. J. Kroes, Chem. Phys. Lett., 2017, 683, 329–335 CrossRef.
- A. C. Luntz, J. K. Brown and M. D. Williams, J. Chem. Phys., 1990, 93, 5240–5246 CrossRef CAS.
- J. W. Sun, R. Haunschild, B. Xiao, I. W. Bulik, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2013, 138, 044113 CrossRef.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811–4815 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- W. W. Gao, T. A. Abtew, T. Cai, Y. Y. Sun, S. B. Zhang and P. H. Zhang, Solid State Commun., 2016, 234–235, 10–13 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- R. R. Yin, Y. L. Zhang, F. Libisch, E. A. Carter, H. Guo and B. Jiang, J. Phys. Chem. Lett., 2018, 9, 3271–3277 CrossRef CAS.
- L. Österlund, I. Zoric and B. Kasemo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15452–15455 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- R. A. B. van Bree, N. Gerrits and G. J. Kroes, Faraday Discuss., 2024, 251, 361–381 RSC.
- D. Bohm and D. Pines, Phys. Rev., 1951, 82, 625–634 CrossRef CAS.
- D. Pines and D. Bohm, Phys. Rev., 1952, 85, 338–353 CrossRef CAS.
- D. Bohm and D. Pines, Phys. Rev., 1953, 92, 609–625 CrossRef CAS.
- D. C. Langreth and J. P. Perdew, Phys. Rev. B: Solid State, 1977, 15, 2884–2901 CrossRef.
- J. Paier, X. Ren, P. Rinke, G. E. Scuseria, A. Grüneis, G. Kresse and M. Scheffler, New J. Phys., 2012, 14, 043002 CrossRef.
- X. J. Zhou and F. Wang, J. Comput. Chem., 2017, 38, 798–806 CrossRef CAS.
- K. Krongchon, B. Busemeyer and L. K. Wagner, J. Chem. Phys., 2017, 146, 124129 CrossRef PubMed.
- J. Harl, L. Schimka and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115126 CrossRef.
- Y. Zhang, X. Xu and W. A. G. III, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 4963–4968 CrossRef CAS.
- Z. Chen, Z. Liu and X. Xu, Nat. Commun., 2023, 14, 936 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- C.-O. Almbladh and U. von Barth, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3231–3244 CrossRef CAS PubMed.
- T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Chem. Phys., 2007, 127, 221103 CrossRef.
- B. M. Austin, D. Y. Zubarev and W. A. Lester, Jr., Chem. Rev., 2012, 112, 263–288 CrossRef CAS PubMed.
- P. E. Hoggan, Adv. Quantum Chem., 2018, 76, 271–278 CrossRef CAS.
- R. O. Sharma, T. T. Rantala and P. E. Hoggan, J. Phys. Chem. C, 2020, 124, 26232–26240 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Headgordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207–4212 CrossRef CAS PubMed.
- H. Z. Ye and T. C. Berkelbach, Faraday Discuss., 2024, 254, 628–640 RSC.
- B. X. Shi, A. Zen, V. Kapil, P. R. Nagy, A. Grüneis and A. Michaelides, J. Am. Chem. Soc., 2023, 145, 25372–25381 CrossRef CAS PubMed.
- T. Tsatsoulis, S. Sakong, A. Groß and A. Grüneis, J. Chem. Phys., 2018, 149, 244105 CrossRef PubMed.
- I. Y. Zhang and A. Grüneis, Front. Mater., 2019, 6, 123 CrossRef.
- F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775 CrossRef CAS PubMed.
- K. Andersson, P. Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- P. Celani and H. J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- Q. Zhao, X. Zhang, J. M. P. Martirez and E. A. Carter, J. Chem. Theory Comput., 2020, 16, 7078–7088 CrossRef CAS.
- C. T. Rettner, H. A. Michelsen and D. J. Auerbach, J. Chem. Phys., 1995, 102, 4625–4641 CrossRef CAS.
- C. Angeli, R. Cirimaglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- K. Morokuma, Bull. Korean Chem. Soc., 2003, 24, 797–801 CrossRef CAS.
- F. Göltl, C. Houriez, M. Guitou, G. Chambaud and P. Sautet, J. Phys. Chem. C, 2014, 118, 5374–5382 CrossRef.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- R. B. Araujo, G. L. S. Rodrigues, E. Campos dos Santos and L. G. M. Petterson, Nat. Commun., 2022, 13, 6853 CrossRef CAS PubMed.
- S. Grimme, J. Anthony, S. Ehrlich and K. Goerigk, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Allouche, J. Comput. Chem., 2012, 32, 174–182 CrossRef PubMed.
- E. Hasselbrink, Science, 2009, 326, 809–810 CrossRef CAS.
- E. Müller-Hartmann, T. V. Ramakrishnan and G. Toulouse, Phys. Rev. B: Solid State, 1971, 3, 1102–1119 CrossRef.
- S. P. Rittmeyer, V. J. Bukas and K. Reuter, Adv. Phys.: X, 2018, 3, 1381574 Search PubMed.
- I. G. Ryabinkin and A. F. Izmaylov, J. Phys. Chem. Lett., 2017, 8, 440–444 CrossRef CAS PubMed.
- Z. Jin and J. E. Subotnik, J. Chem. Theory Comput., 2021, 17, 614–626 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 2024, 160, 124708 CrossRef CAS PubMed.
- Y. Li and G. Wahnström, Phys. Rev. Lett., 1992, 68, 3444–3447 CrossRef CAS.
- W. Dou and J. E. Subotnik, J. Chem. Phys., 2018, 148, 230901 CrossRef PubMed.
- S. P. Rittmeyer, J. Meyer and K. Reuter, Phys. Rev. Lett., 2017, 119, 176808 CrossRef.
- B. Hellsing and M. Persson, Phys. Scr., 1984, 29, 360–371 CrossRef CAS.
- M. Askerka, R. J. Maurer, V. S. Batista and J. C. Tully, Phys. Rev. Lett., 2016, 116, 217601 CrossRef PubMed.
- R. J. Maurer, M. Askerka, V. S. Batista and J. C. Tully, Phys. Rev. B, 2016, 94, 115432 CrossRef.
- P. Spiering and J. Meyer, J. Phys. Chem. Lett., 2018, 9, 1803–1808 Search PubMed.
- C. L. Box, W. G. Stark and R. J. Maurer, Electron. Struct., 2023, 5, 035005 Search PubMed.
- Y. L. Zhang, R. J. Maurer and B. Jiang, J. Phys. Chem. C, 2020, 124, 186–195 Search PubMed.
- M. Persson and B. Hellsing, Phys. Rev. Lett., 1982, 49, 662–665 Search PubMed.
- J. R. Trail, M. C. Graham and D. M. Bird, Comput. Phys. Commun., 2001, 137, 163–173 Search PubMed.
- D. Novko, M. Alducin, M. Blanco-Rey and J. I. Juaristi, Phys. Rev. B, 2016, 94, 224306 Search PubMed.
- Y. L. Zhang, R. J. Maurer, H. Guo and B. Jiang, Chem. Sci., 2019, 10, 1089–1097 RSC.
- R. J. Maurer, B. Jiang, H. Guo and J. C. Tully, Phys. Rev. Lett., 2017, 118, 256001 Search PubMed.
- J. R. Trail, D. M. Bird, M. Persson and S. Holloway, J. Chem. Phys., 2003, 119, 4539–4549 CAS.
- J. R. Trail, M. C. Graham, D. M. Bird, M. Persson and S. Holloway, Phys. Rev. Lett., 2002, 88, 166802 Search PubMed.
- A. C. Luntz and M. Persson, J. Chem. Phys., 2005, 123, 074704 Search PubMed.
- A. C. Luntz, M. Persson and G. O. Sitz, J. Chem. Phys., 2006, 124, 091101 Search PubMed.
- G. Füchsel, T. Klamroth, S. Monturet and P. Saalfrank, Phys. Chem. Chem. Phys., 2011, 13, 8659–8670 Search PubMed.
- J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102 CAS.
- M. J. Puska and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 6121–6128 CAS.
- N. Gerrits, J. I. Juaristi and J. Meyer, Phys. Rev. B, 2020, 102, 155130 CrossRef CAS.
- A. C. Luntz, I. Makkonen, M. Persson, S. Holloway, D. M. Bird and M. S. Mizielinski, Phys. Rev. Lett., 2009, 102, 109601 CrossRef CAS.
- P. M. Echenique, R. M. Nieminen and R. H. Ritchie, Solid State Commun., 1981, 37, 779–781 CrossRef CAS.
- A. Salin, A. Arnau, P. M. Echenique and E. Zaremba, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 2537–2548 CrossRef CAS.
- E. W. F. Smeets, G. Füchsel and G. J. Kroes, J. Phys. Chem. C, 2019, 123, 23049–23063 CrossRef CAS.
- E. N. Ghassemi, E. W. F. Smeets, M. F. Somers, G. J. Kroes, I. M. N. Groot, L. B. F. Juurlink and G. Füchsel, J. Phys. Chem. C, 2019, 123, 2973–2986 Search PubMed.
- S. Roy, N. Shenvi and J. C. Tully, J. Phys. Chem. C, 2009, 113, 16311–16320 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- G. Meng and B. Jiang, J. Chem. Phys., 2022, 157, 214103 CrossRef CAS PubMed.
- Q. Wu and T. Van Voorhis, J. Chem. Theory Comput., 2006, 2, 765–774 CrossRef CAS PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2011, 112, 321–370 CrossRef.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- G. Meng, J. Gardner, N. Hertl, W. Dou, R. J. Maurer and B. Jiang, Phys. Rev. Lett., 2024, 133, 036203 CrossRef CAS PubMed.
- R. J. V. Wagner, N. Henning, B. C. Krüger, G. B. Park, J. Altschaffel, A. Kandratsenka, A. M. Wodtke and T. Schafer, J. Phys. Chem. Lett., 2017, 8, 4887–4892 CrossRef CAS.
- C. Díaz, R. A. Olsen, H. F. Busnengo and G. J. Kroes, J. Phys. Chem. C, 2010, 114, 11192–11201 CrossRef.
- A. Groß and A. Dianat, Phys. Rev. Lett., 2007, 98, 206107 CrossRef.
- X. Y. Zhou, B. Kolb, X. Luo, H. Guo and B. Jiang, J. Phys. Chem. C, 2017, 121, 5594–5602 CrossRef CAS.
- H. F. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651 CrossRef CAS.
- B. Jiang and H. Guo, J. Chem. Phys., 2014, 141, 034109 CrossRef.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- Y. L. Zhang, C. Hu and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 4962–4967 CrossRef CAS.
- Y. H. Huang, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 2000, 290, 111–114 CrossRef CAS.
- A. M. Wodtke, D. Matsiev and D. J. Auerbach, Prog. Surf. Sci., 2008, 83, 167–214 CrossRef CAS.
- K. Shakouri, J. Behler, J. Meyer and G. J. Kroes, J. Phys. Chem. C, 2018, 122, 23470–23480 CrossRef CAS.
- M. Blanco-Rey, J. I. Juaristi, R. Díez Muiño, H. F. Busnengo, G. J. Kroes and M. Alducin, Phys. Rev. Lett., 2014, 112, 103203 CrossRef CAS.
- P. Saalfrank, J. I. Juaristi, M. Alducin, M. Blanco-Rey and R. Diéz Muiño, J. Chem. Phys., 2014, 141, 234702 CrossRef.
- R. N. Porter and L. M. Raff, in Dynamics of Molecular Collisions, Part B, ed. W. H. Miller, Plenum, New York, 1976, pp. 1–52 Search PubMed.
- E. N. Ghassemi, M. Somers and G. J. Kroes, J. Phys. Chem. C, 2018, 122, 22939–22952 CrossRef.
- T. Tchakoua, A. D. Powell, N. Gerrits, M. F. Somers, K. Doblhoff-Dier, H. F. Busnengo and G. J. Kroes, J. Phys. Chem. C, 2023, 127, 5395–5407 Search PubMed.
- F. Nattino, H. Ueta, H. Chadwick, M. E. van Reijzen, R. D. Beck, B. Jackson, M. C. van Hemert and G. J. Kroes, J. Phys. Chem. Lett., 2014, 5, 1294–1299 CrossRef CAS PubMed.
- N. Gerrits, B. Jackson and A. Bogaerts, J. Phys. Chem. Lett., 2024, 15, 2566–2572 CrossRef CAS PubMed.
- F. Nattino, D. Migliorini, M. Bonfanti and G. J. Kroes, J. Chem. Phys., 2016, 144, 044702 CrossRef PubMed.
- L. Bonnet and J. C. Rayez, Chem. Phys. Lett., 1997, 277, 183–190 CrossRef CAS.
- L. Bonnet, Int. Rev. Phys. Chem., 2013, 32, 171–228 Search PubMed.
- A. Rodríguez-Fernández, L. Bonnet, C. Crespos, P. Larrégaray and R. Diéz Muiño, J. Phys. Chem. Lett., 2019, 10, 7629–7635 CrossRef.
- L. Zhang, J. Chen and B. Jiang, J. Phys. Chem. C, 2021, 125, 4995–5005 CrossRef CAS.
- G. J. Kroes, E. J. Baerends and R. C. Mowrey, Phys. Rev. Lett., 1997, 78, 3583–3586 CrossRef CAS.
- J. Q. Dai and J. C. Light, J. Chem. Phys., 1997, 107, 1676–1679 CrossRef CAS.
- T. H. Liu, B. N. Fu and D. H. Zhang, J. Chem. Phys., 2013, 139, 184705 CrossRef PubMed.
- G. J. Kroes and C. Díaz, Chem. Soc. Rev., 2016, 45, 3658–3700 RSC.
- H. Shi, T. H. Liu, Y. Fu, X. Lu, B. Fu and D. H. Zhang, J. Phys. Chem. C, 2021, 125, 23105–23114 CrossRef CAS.
- Z. J. Zhang, T. H. Liu, B. N. Fu, X. M. Yang and D. H. Zhang, Nat. Commun., 2016, 7, 11953 CrossRef CAS.
- T. H. Liu, J. Chen, Z. J. Zhang, X. J. Shen, B. N. Fu and D. H. Zhang, J. Chem. Phys., 2018, 148, 144705 CrossRef.
- X. J. Shen, Z. J. Zhang and D. H. Zhang, J. Chem. Phys., 2016, 144, 101101 CrossRef.
- X. J. Shen, Z. J. Zhang and D. H. Zhang, J. Chem. Phys., 2017, 147, 024702 CrossRef PubMed.
- A. K. Tiwari, S. Nave and B. Jackson, Phys. Rev. Lett., 2009, 103, 253201 CrossRef PubMed.
- A. K. Tiwari, S. Nave and B. Jackson, J. Chem. Phys., 2010, 132, 134702 CrossRef.
- X. J. Shen, Z. J. Zhang and D. H. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 25499–25504 RSC.
- B. Jackson and S. Nave, J. Chem. Phys., 2011, 135, 114701 CrossRef PubMed.
- S. Nave and B. Jackson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 233408 CrossRef.
- H. Chadwick, H. Guo, A. Gutiérrez-González, J. P. Menzel, B. Jackson and R. D. Beck, J. Chem. Phys., 2018, 148, 014701 CrossRef.
- H. Guo, J. P. Menzel and B. Jackson, J. Chem. Phys., 2018, 149, 244704 CrossRef PubMed.
- H. Guo and B. Jackson, J. Chem. Phys., 2016, 144, 184709 CrossRef.
- B. Jackson, F. Nattino and G. J. Kroes, J. Chem. Phys., 2014, 141, 054102 CrossRef.
- V. L. Campbell, N. Chen, H. Guo, B. Jackson and A. L. Utz, J. Phys. Chem. A, 2015, 119, 12434–12441 CrossRef CAS PubMed.
- H. Guo, A. Farjamnia and B. Jackson, J. Phys. Chem. Lett., 2016, 7, 4576–4584 CrossRef CAS.
- R. Welsch, K. Song, Q. Shi, S. C. Althorpe and T. F. Miller III, J. Chem. Phys., 2016, 145, 204118 CrossRef.
- S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller III, Annu. Rev. Phys. Chem., 2013, 64, 387–413 CrossRef CAS.
- Q. H. Liu, L. Zhang, Y. Li and B. Jiang, J. Phys. Chem. Lett., 2019, 10, 7475–7481 CrossRef CAS.
- C. Li, Q. Liu, L. Zhang, Y. Li and B. Jiang, Mol. Phys., 2021, 120, e1941367 CrossRef.
- L. Zhang, J. Zuo, Y. V. Suleimanov and H. Guo, J. Phys. Chem. Lett., 2023, 14, 7118–7125 CrossRef CAS.
- H. Y. Jiang, M. Kammler, F. Z. Ding, Y. Dorenkamp, F. R. Manby, A. M. Wodtke, T. F. Miller III, A. Kandratsenka and O. Bünermann, Science, 2019, 364, 379–382 CrossRef CAS.
- K. Gu, C. Li, S. Lin and H. Guo, J. Phys. Chem. C, 2022, 126, 17093–17101 CrossRef CAS.
- C. Li, Y. Li and B. Jiang, Chem. Sci., 2023, 14, 5087–5098 RSC.
- M. Kurahashi and Y. Yamauchi, Phys. Rev. Lett., 2013, 110, 246102 CrossRef PubMed.
- L. Vattuone, M. Rocca, C. Boragno and U. Valbusa, J. Chem. Phys., 1994, 101, 713–725 CrossRef CAS.
- A. Raukema, D. A. Butler and A. W. Kleyn, J. Phys.: Condens. Matter, 1996, 8, 2247–2263 CrossRef CAS.
- M. Kurahashi, J. Chem. Phys., 2019, 151, 084702 CrossRef.
- M. Minniti, D. Farías, P. Perna and R. Miranda, J. Chem. Phys., 2012, 137, 074706 CrossRef CAS.
- D. Y. Zhang, C. Jansen, A. W. Kleyn and L. B. F. Juurlink, Phys. Chem. Chem. Phys., 2023, 25, 14862–14868 RSC.
- J. Hall, O. Saksager and I. Chorkendorff, Chem. Phys. Lett., 1993, 216, 413–417 CrossRef CAS.
- M. Yata and H. Rouch, Appl. Phys. Lett., 1999, 75, 1021–1023 CrossRef CAS.
- P. Junell, M. Ahonen, M. Hirsimäki and M. Valden, Surf. Rev. Lett., 2004, 11, 457–461 CrossRef CAS.
- Q. Shen, J. Wu, F. Zhou, Y. Song, W. Dong, X. Wang, T. Wang and X. M. Yang, Rev. Sci. Instrum., 2022, 93, 013201 CrossRef CAS PubMed.
- S. K. Singh and P. R. Shirhatti, J. Chem. Phys., 2024, 160, 024702 CrossRef CAS.
- H. Hou, Y. Huang, S. J. Gulding, C. T. Rettner, D. J. Auerbach and A. M. Wodtke, Science, 1999, 284, 1647–1650 CrossRef CAS.
- H. Hou, C. T. Rettner, D. J. Auerbach, Y. Huang, S. J. Gulding and A. M. Wodtke, Faraday Discuss., 1999, 113, 181–199 RSC.
- R. Cooper, I. Rahinov, C. Yuan, X. M. Yang, D. J. Auerbach and A. M. Wodtke, J. Vac. Sci. Technol., A, 2009, 27, 907–912 CrossRef CAS.
- J. Geweke, P. R. Shirhatti, I. Rahinov, C. Bartels and A. M. Wodtke, J. Chem. Phys., 2016, 145, 054709 CrossRef.
- H. F. Berger and K. D. Rendulic, Surf. Sci., 1991, 253, 325–333 CrossRef CAS.
- H. F. Berger, PhD thesis, Technische Universität Graz, 1992.
- V. Shukla, Y. Jiao, C. Frostenson and P. Hyldgaard, J. Phys.: Condens.Matter, 2022, 34, 025902 CrossRef CAS.
- V. Shukla, Y. Jiao, J.-H. Lee, E. Schröder, J. B. Neaton and P. Hyldgaard, Phys. Rev. X, 2022, 12, 041003 CAS.
- J. W. Song, K. Yamashita and K. Hirao, J. Chem. Phys., 2011, 135, 071103 CrossRef.
- D. Chakraborty, K. Berland and T. Thonhauser, J. Chem. Theory Comput., 2020, 16, 5893–5911 CrossRef CAS.
- A. Raghav, R. Maezono, K. Hongo, S. Sorella and K. Nakano, J. Chem. Theory Comput., 2023, 19, 2222–2229 CrossRef CAS PubMed.
- K. Nakano, S. Sorella, D. Alfè and A. Zen, J. Chem. Theory Comput., 2024, 20, 4591–4604 CrossRef CAS.
- S. Pathak and L. K. Wagner, J. Chem. Phys., 2018, 149, 234104 CrossRef.
- J. T. Krogel and F. A. Reboredo, J. Chem. Phys., 2020, 153, 104111 CrossRef CAS.
- T. Ichibha, Y. Nikaido, M. C. Bennett, J. T. Krogel, K. Hongo, R. Maezono and F. A. Reboredo, J. Chem. Phys., 2023, 159, 164114 CrossRef CAS.
- A. Zen, J. G. Brandenburg, A. Michaelides and D. Alfè, J. Chem. Phys., 2019, 151, 134105 CrossRef.
- T. A. Anderson and C. J. Umrigar, J. Chem. Phys., 2021, 154, 214110 CrossRef CAS.
- J. P. Perdew, V. N. Staroverov, J. Tao and G. E. Scuseria, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 052513 CrossRef.
- P. Borlido, M. A. L. Marques and S. Botti, J. Chem. Theory Comput., 2018, 14, 939–947 CrossRef CAS.
- J. W. Sun, B. Xiao, Y. Fang, R. Haunschild, P. Hao, A. Ruzsinszky, G. I. Csonka, G. E. Scuseria and J. P. Perdew, Phys. Rev. Lett., 2013, 111, 106401 CrossRef PubMed.
- M. M. Maier, A. V. Arbuznikov and M. Kaupp, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1378 Search PubMed.
- J. W. Sun, B. Xiao and A. Ruzsinszky, J. Chem. Phys., 2012, 137, 051101 CrossRef PubMed.
- A. V. Krukau, G. E. Scuseria, J. P. Perdew and A. Savin, J. Chem. Phys., 2008, 129, 124103 CrossRef PubMed.
- J. Kirkpatrick, B. McMorrow, D. H. P. Turban, A. L. Gaunt, J. S. Spencer, A. G. D. G. Matthews, A. Obika, L. Thiry, M. Fortunato, D. Pfau, L. Román Castellanos, S. Petersen, A. W. R. Nelson, P. Kohli, P. Mori-Sánchez, D. Hassabis and A. J. Cohen, Science, 2021, 374, 1385–1389 CrossRef CAS.
- E. G. d'Agliano, P. Kumar, W. Schaich and H. Suhl, Phys. Rev. B: Solid State, 1975, 11, 2122–2143 CrossRef.
- P. Nieto, E. Pijper, D. Barredo, G. Laurent, R. A. Olsen, E. J. Baerends, G. J. Kroes and D. Farías, Science, 2006, 312, 86–89 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef.
- B. Smits and M. F. Somers, J. Chem. Phys., 2021, 154, 074710 CrossRef CAS.
- J. Meyer and K. Reuter, Angew. Chem., Int. Ed., 2014, 53, 4721–4724 CrossRef CAS PubMed.
- H. W. Sheng, M. J. Kramer, A. Cadien, T. Fujita and M. W. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134118 CrossRef.
- T. J. Frankcombe, M. A. Collins and D. H. Zhang, J. Chem. Phys., 2012, 137, 144701 CrossRef.
- G. J. Kroes, J. G. Snijders and R. C. Mowrey, J. Chem. Phys., 1995, 103, 5121–5136 CrossRef CAS.
- J. Daru, H. Forbert, J. Behler and D. Marx, Phys. Rev. Lett., 2022, 129, 226001 CrossRef CAS.
- Y. Litman, E. S. Pós, C. L. Box, R. Martinazzo, R. J. Maurer and M. Rossi, J. Chem. Phys., 2022, 156, 194106 CrossRef CAS.
- Y. Litman, E. S. Pós, C. L. Box, R. Martinazzo, R. J. Maurer and M. Rossi, J. Chem. Phys., 2022, 156, 194107 CrossRef CAS.
- R. Cooper, Z. S. Li, K. Golibrzuch, C. Bartels, I. Rahinov, D. J. Auerbach and A. M. Wodtke, J. Chem. Phys., 2012, 137, 064705 CrossRef PubMed.
- R. Tibshirani, J. Roy. Stat. Soc. B, 1996, 58, 267–288 CrossRef.
- M. A. Efroymson, Multiple regression analysis, Mathematical methods for digital computers, Wiley, New York, 1960 Search PubMed.
- P. Morgante and R. Peverati, Phys. Chem. Chem. Phys., 2019, 21, 19092–19103 RSC.
- M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993 CrossRef CAS.
- H. S. Yu, W. J. Zhang, P. Verma, X. He and D. G. Truhlar, Phys. Chem. Chem. Phys., 2015, 17, 12146–12160 RSC.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS PubMed.
- S. Dahl, A. Logadottir, R. C. Egeberg, J. H. Larsen, I. Chorkendorff, E. Törnqvist and J. K. Nørskov, Phys. Rev. Lett., 1999, 83, 1814–1817 CrossRef.
- T. Zambelli, J. Wintterlin, J. Trost and G. Ertl, Science, 1996, 273, 1688–1690 CrossRef CAS.
- K. Golibrzuch, P. R. Shirhatti, J. Geweke, J. Werdecker, A. Kandratsenka, D. J. Auerbach, A. M. Wodtke and C. Bartels, J. Am. Chem. Soc., 2015, 137, 1465–1475 CrossRef CAS PubMed.
- D. J. Harding, J. Neugebohren, H. Hahn, D. J. Auerbach, T. N. Kitsopoulos and A. M. Wodtke, J. Chem. Phys., 2017, 147, 013139 CrossRef.
- J. Neugebohren, D. Borodin, H. W. Hahn, J. Altschäffel, A. Kandratsenka, D. J. Auerbach, C. T. Campbell, D. Schwarzer, D. J. Harding, A. M. Wodtke and T. N. Kitsopoulos, Nature, 2018, 558, 280–283 CrossRef CAS PubMed.
- G. B. Park, T. N. Kitsopoulos, D. Borodin, K. Golibrzuch, J. Neugebohren, D. J. Auerbach, C. T. Campbell and A. M. Wodtke, Nat. Rev. Chem., 2019, 3, 723–732 CrossRef.
- D. Borodin, K. Golibrzuch, M. Schwarzer, J. Fingerhut, G. Skoulatakis, D. Schwarzer, T. Seelemann, T. N. Kitsopoulos and A. M. Wodtke, ACS Catal., 2020, 10, 14056–14066 CrossRef CAS PubMed.
- D. Borodin, I. Rahinov, O. Galparsoro, J. Fingerhut, M. Schwarzer, K. Golibrzuch, G. Skoulatakis, D. J. Auerbach, A. Kandratsenka, D. Schwarzer, T. N. Kitsopoulos and A. M. Wodtke, J. Am. Chem. Soc., 2021, 143, 18305–18316 CrossRef CAS.
- D. Borodin, N. Hertl, G. B. Park, M. Schwarzer, J. Fingerhut, Y. Q. Wang, J. X. Zuo, F. Nitz, G. Skoulatakis, A. Kandratsenka, D. J. Auerbach, D. Schwarzer, H. Guo, T. N. Kitsopoulos and A. M. Wodtke, Science, 2022, 377, 394–398 CrossRef CAS PubMed.
- M. Schwarzer, N. Hertl, F. Nitz, D. Borodin, J. Fingerhut, T. N. Kitsopoulos and A. M. Wodtke, J. Phys. Chem. C, 2022, 126, 14500–14508 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2025 |