Understanding polymer–colloid gels: a solvent perspective using low-field NMR†
Léo
Hervéou‡
ab,
Gauthier
Legrand‡
b,
Thibaut
Divoux
 b and
Guilhem P.
Baeza§
b and
Guilhem P.
Baeza§
 *a
*a
aINSA Lyon, UCBL, CNRS, MATEIS, UMR5510, 69621, Villeurbanne, France. E-mail: guilhem.baeza@insa-lyon.fr
bENSL, CNRS, Laboratoire de physique, F-69342 Lyon, France
First published on 6th November 2024
Abstract
The present work emphasizes the relevance of low-field NMR relaxometry to investigate colloid-polymer hydrogels by probing water dynamics across a wide range of formulations between 10 °C and 80 °C. By examining the temperature dependence of the transverse relaxation time T2, we demonstrate a clear link between the NMR response and the rheological behavior of the hydrogels. In particular, we show that NMR relaxometry targeting the solvent provides reliable insights into the hydrogel microstructure and allows the detection of phase transitions and aging processes. Our findings suggest that this solvent-focused technique could greatly benefit the soft matter community, complementing other experimental methods in the study of gels.
Hydrogels represent a fascinating class of versatile materials originally consisting of a low fraction of hydrosoluble polymer forming a 3D percolated network in water.1 Important progress regarding their structural design has been made in the last few decades, notably leading to the emergence of double-2–4 and hybrid-networks,5,6 respectively incorporating two (or more7) polymers and inorganic particles. These advanced materials exhibit enhanced mechanical properties, leading to widespread use in key sectors like the food industry,8,9 medical engineering,10–12 and energy.13,14 Among them, natural polymer-based hydrogels relying on networks of proteins, polyesters, or polysaccharides present the advantage of employing abundant, biocompatible, and (sometimes) edible polymers. Their amphiphilic nature, coupled with well-chosen inorganic particles, results in a rich phase diagram where mechanical properties can be easily selected from the formulation and the processing conditions.15–17 For example, we have recently demonstrated the dual nature of physical hydrogels made of the sodium salt of carboxymethylcellulose (CMC) and carbon black (CB) soot particles. Depending on their composition, CB–CMC hydrogels can either display a microstructure akin to a colloidal gel in which a percolated network of CB particles is stabilized by CMC, or a polymer gel in which a CMC matrix is physically cross-linked by CB particles.18
Besides, the amphiphilic character of natural polymer-based hydrogels makes them particularly thermo-sensitive, including within the narrow temperature window defined by water crystallization and vaporization (0 and 100 °C).19 In addition to irreversible chemical alteration, temperature changes can significantly impact chain conformation (e.g., protein denaturation)20, or strongly influence the gelation scenario, leading to major topological changes of the network.21 Such changes have been evidenced by multiple techniques, among which low-field (LF) NMR relaxometry was shown to yield precious insights regarding the microstructure of complex biological tissues22,23 and foodstuff.24–27 This technique, which is used to obtain information about the mobile protons of a sample, has also been recently coupled to rheometry offering time-resolved information on the sample microstructure under shear.28–31 In solid porous media, low-field NMR targets the solvent to compute the sample's pore size distribution.32 In contrast, in aqueous suspensions and hydrogels, where water is replaced by D2O to mask the contribution from the proton of the solvent, low-field NMR targets the dynamics of the dispersed phase alone.
Here, we take a mixed approach by conducting LF 1H-NMR experiments on CB–CMC hydrogels to monitor the dynamics of water, i.e., the solvent, over a wide range of compositions and temperatures. The use of the popular Carr–Purcell–Meiboom–Gill (CPMG) pulse routine33–35 allows us to measure the spin–spin (transverse) relaxation time T2, which, in the case of pure water is of several seconds.36 Our results clearly show that LF-NMR experiments targeting the solvent can effectively detect the sol–gel transition, thermally-induced phase transition, and physical aging. This makes it a promising and complementary technique to the traditional focus on the dispersed phase.
In the following, samples are denoted through the code “CMCX-CBY,” where X and Y represent the mass fraction (in wt%) of CB and CMC, respectively (see technical details in the Experimental section). Typical CPMG experiment outputs are presented in Fig. 1 for a low-density gel, i.e., a hydrogel of composition CMC0.01–CB2 where the transverse magnetization of hydrogen atoms (almost exclusively coming from water) I(t) decreases over a characteristic time T2 following the expression
I(t) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/T2), exp(−t/T2), | (1) |
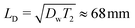 . This value is significantly larger than the mesh size of CMC gels determined from rheometry, which is approximately 50 nm (ref. 45) and comparable to the average diameter of CMC fringe micelles measured by neutron scattering, approximately 75 nm.46
. This value is significantly larger than the mesh size of CMC gels determined from rheometry, which is approximately 50 nm (ref. 45) and comparable to the average diameter of CMC fringe micelles measured by neutron scattering, approximately 75 nm.46
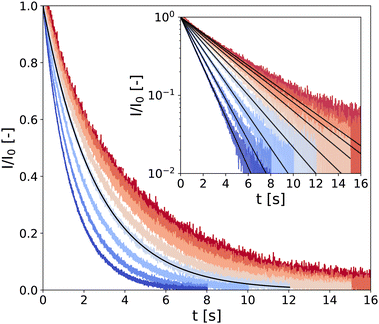 | ||
| Fig. 1 LF-NMR CPMG signal normalized by I0, the signal amplitude extrapolated at t = 0 s extracted from fitting the data with eqn (1) (black solid lines). Measurements are performed on a CMC0.01–CB2 hydrogel, every 10 °C between 10 °C and 80 °C (see color code from dark blue to red). Inset: Same data in semi-logarithmic representation. | ||
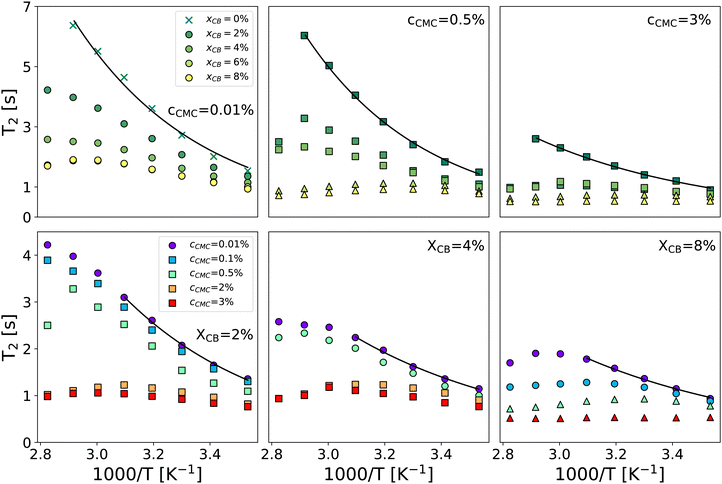
Fig. 2 gathers the times T2 measured across all samples investigated between 10 and 80 °C. The first row highlights the impact of CB content (xCB = 0–8 wt%) in three hydrogel matrices made of 0.01, 0.5, and 3 wt% of CMC, while the second row examines the impact of CMC concentration (cCMC = 0.01–3 wt%) for three CB contents 2, 4, and 8 wt%. At first glance, T2 generally decreases as the reciprocal temperature increases, reflecting the reduced mobility of water molecules. As expected, and consistent with our previous work on CMC hydrogels,46T2 in CB-free samples follows an Arrhenius dependence across the entire temperature range, expressed as:
T2 = T02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/RT) exp(−Ea/RT) | (2) |
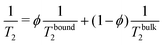 | (3) |
 | ||
| Fig. 2 Spin–spin relaxation time T2vs. reciprocal temperature for selected formulations varying xCB between 0 and 8 wt% for cCMC = 0.01, 0.5, and 3 wt% (top row, left to right) and varying cCMC between 0.01 and 3 wt% for xCB = 2, 4, and 8 wt% (bottom row, left to right). Solid lines are Arrhenius fits of data in the whole temperature range (top row) and the 283–323 K range (bottom row). Symbols refer to the rheological behavior: circle and cross: viscoelastic liquid, square: colloidal gel, and triangle: polymer gel (see the diagram in Fig. 3). | ||
Beyond the evolution of T2 with the temperature and the gel formulation, it is also worth noting that Ea, extracted from Arrhenius fits between 10 °C and 50 °C, clearly decreases as either cCMC or xCB increases. Its values range from ca. 19 kJ mol−1 in the most dilute samples (e.g., CMC0.01–, CMC0.1– and CMC-0.5–CB0), to nearly 0 kJ mol−1 in the densest hydrogel (CMC3–CB8), where T2 no longer seems to depend on temperature. Although it might be tempting to link these activation energies to effective binding energies determined in rheology,47 the interpretation in NMR is quite the opposite. Here, a low activation energy corresponds to high thermal stability in a material where water molecules move through a dense network with slow polymer dynamics.45 While a quantitative correlation between Ea and the network density/topology remains elusive, comparing these values with rheological properties allows us to build a remarkable phase diagram presented in Fig. 3. This diagram integrates (i) the sample rheological state – either viscoelastic liquid, polymer gel, or colloidal gel, as defined above in the introduction (data extracted from ref. 18) – and (ii) the Ea values measured from NMR experiments (see the color map). This dual analysis clearly illustrates the above-mentioned trend, showing that Ea decreases with increasing CB or CMC content, and highlights the excellent agreement between the two techniques in defining the polymer gel domain, which encompasses the densest materials (red zone). In addition, the highest Ea values (purple zone) are only observed in CB-free hydrogels, whereas nearly CMC-free gels display intermediate values (light green) across a wide range of xCB, indicating that the impact of CB and CMC on Ea is not equivalent. This observation supports the correlation between macroscopic rheological properties and local water diffusion: a CB-free liquid-like sample containing a relatively high fraction of (partly hydrophilic) CMC results in a lower impact on Ea than a gel made of a small fraction (e.g., 0.01 wt%) of CMC decorating a physically cross-linked network of (hydrophobic) CB particles. In other words, T2 is more sensitive to the presence of a 3D network (even if loose and made of strands that do not interact with water molecules) than to an increase in the concentration of a polymer that interacts favorably with water in solution. Although not directly comparable, this result aligns with observations in polymer melts, where T2 decreases with increasing cross-link density in a nearly identical chemical environment.48 The situation becomes more complex when moving away from the left- and bottom-axes of the diagram, where it appears that CMC and CB interact synergistically to influence Ea. This translates into the centro-symmetric color gradient originating from the CMC3–CB8 formulation (top-right corner of the diagram). In this region, which includes the densest viscoelastic liquids and colloidal gels, as well as all the polymer gels, Ea values progressively decrease as the material densifies, regardless of whether CB or CMC concentrations are increased. The transition from colloidal gel to viscoelastic liquid implies, in this case, a decrease of Ea (see e.g., xCB = 4 wt%), suggesting that favorable CMC–water interactions dominate the gelation process.
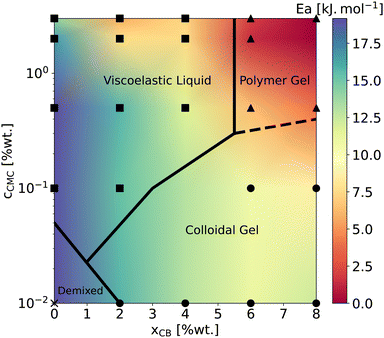 | ||
| Fig. 3 Phase diagram gathering rheological state determined at T = 22 °C extracted from ref. 18 and low-temperature apparent activation energies reported in Fig. 2. Symbols mark the sample formulations investigated in the present work. Squares, triangles, circles, and crosses correspond to viscoelastic liquids, polymer gels, colloidal gels, and a CB-free polymer solution, respectively. The color map is interpolated using the Gouraud shading from the matplotlib package (Python). Ea values are reported in ESI,† Section S2. | ||
Beyond the low-temperature regime mainly described by the phase diagram, a closer look at high-temperature data in Fig. 2 reveals a striking non-monotonic evolution of T2 in several formulations, particularly noticeable for xCB = 4 wt%. Overall, increasing the gel density systematically results in a progressive transition of T2(T) from (i) a monotonic Arrhenius profile, to (ii) a monotonic non-Arrhenius profile, and then to (iii) a non-monotonic profile (see e.g., the cCMC = 0.01% panel). While an Arrhenius profile is commonly expected from water molecules that steadily gain mobility with increasing temperature,49 a non-monotonic evolution here suggests a thermally induced modification of the network structure. Such a modification can be attributed to a change in the conformation of CMC polymers, which form a percolated network of increasing connectivity for higher temperatures, even in the absence of CB particles.45 This is further confirmed by CPMG experiments performed upon cooling, which show a perfect overlap of T2 during heating and cooling for samples with an Arrhenius profile, while revealing a significant decrease in T2 in the cooling branch for other profiles (see ESI,† Section S3). Interestingly, this hysteresis becomes more pronounced in samples with higher CB content, suggesting that denser colloid-polymer hydrogels exhibit a stronger tendency to age with changes in temperature. Although the low Ea values make it challenging to observe the non-monotonic trend of T2 in dense gels, this observation indicates that the rheological properties of these materials are likely to evolve in a complex manner upon heating.
In line with this reasoning, Fig. 4 shows the frequency dependence of the storage modulus of CMC3–CB8 measured on three different samples at 10 °C, 50 °C, and 70 °C. All three spectra exhibit a low-frequency plateau, which is linked to the topological density of the gel through entropic elasticity,50 and a high-frequency power-law evolution with an exponent α, corresponding to the relaxation modes of the network strands. As expected, increasing the temperature from 10 °C to 50 °C accelerates the strand relaxation dynamics and decreases the lifetime of attractive interactions (“stickers”),51 resulting in a significant decrease of G′ at both high- and low-frequencies. However, at 70 °C, the situation is more intriguing. Indeed, at this temperature, the plateau modulus increases significantly (by a factor of 4), and the power-law exponent α shifts from the Rouse-like value of 0.5 (observed for 10–50 °C) to 0.3, both of which unambiguously indicate a strong densification of the network, in good agreement with the aforementioned NMR results showing a decrease of T2. For completeness, we also confirm that the aging kinetics vary significantly with the temperature (see inset in Fig. 4), resulting in a rapid increase of G′ at 70 °C. This observation is in line with the non-monotonic onset of T2 observed in most formulations, from 1000/T ≈ 3.0 (i.e., T > 50 °C) in Fig. 2, which suggests a change in the network microstructure, and therefore different aging processes and dynamics.
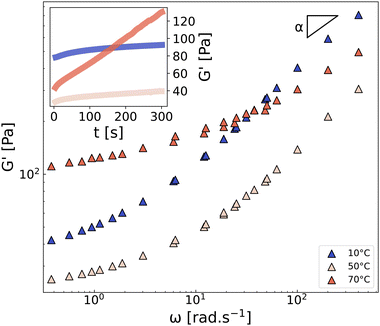 | ||
| Fig. 4 Frequency dependence of the storage modulus G′ of the CMC3–CB8 sample measured at 10, 50, and 70 °C for γ = 0.1%. The parameter α is the exponent characterizing the high-frequency power-law response G′ ∼ ωα. Inset: Time sweep measurement performed at ω = 2π rad s−1. See ESI,† Section S4 for G′′. | ||
To summarize, we have demonstrated that low-field NMR experiments that measure the spin–spin relaxation time T2 using the CPMG pulse sequence, are effective in probing the gelation and structural evolution of polymer–colloid hydrogels. Specifically, when using CMC, we observed a single and unstretched exponential decay of the transverse magnetization across all gel formulations and temperatures, indicating that water molecules are indistinguishable at the T2 timescale (4 s ± 3 s for all the samples). For T < 50 °C, T2(T) allows for extracting an apparent activation energy Ea, which can be directly compared to rheological data, offering an alternative perspective to study gelation. In the loosest networks, Ea is about 19 kJ mol−1, but it decreases to 0 kJ mol−1 in the densest networks, indicating a temperature-independent NMR response. On the other hand, for T > 50 °C, we observed significant network densification and accelerated aging, emphasizing the dominance of CB–CMC interactions over CMC–water and CMC–CMC interactions. These findings are supported by rheological experiments, establishing NMR relaxometry as a practical and valuable tool for systematically investigating hydrogels from the solvent point of view. Perspectives to improve this rheology-NMR dual approach will include systematic measurements of the spin–lattice relaxation time T1,52 which we expect to be much larger than T2 due to the exchange dynamics of water molecules. Pulse-field gradient NMR methods will also be considered to quantify the fraction and the diffusion coefficient of bound molecules in denser gels.53
Experimental section
Sample preparation
Samples are prepared by first dissolving sodium carboxymethylcellulose (NaCMC, Sigma Aldrich), Mw = 250 kg mol−1 and DS = 0.9 as specified by the manufacturer, (see ref. 45 for actual measured values) in deionized water (H2O). Stock solutions up to 5 wt% are prepared and stirred at room temperature for 48 h until homogeneous, before adding the carbon black (CB) particles (VXC72R, Cabot). Samples are placed in a sonicator bath for two rounds of 90 min separated by a period of 24 h under mechanical stirring. The samples are finally left at rest for another 24 h before being tested. The samples are characterized by their CMC concentration cCMC expressed in wt% of the stock solution (without CB) and their mass fraction of CB xCB, following ref. 54.LF-NMR
The 1H low-field NMR experiments were performed on a Bruker minispec mq20 spectrometer (“NF” electronics) operating at a resonance frequency of 20 MHz with 90° and 180° pulse lengths of 2.2 ms and 4.8 ms, respectively, and a dead time of 15 μs. A Car–Purcell–Meiboom–Gill (CPMG) echo train acquisition was used to measure data up to about three times the spin–spin relaxation time T2 of the gels. The echo-time was systematically set to 2τ = 2 ms. It was varied down to 2τ = 0.25 ms for a single sample (CMC2–CB2) at 10 °C and 80 °C showing no and little effect on the measurements of T2, respectively (see ESI,† Section S5). Measurements were performed by increasing the temperature in a step-wise manner from 10 °C to 80 °C every 10 °C with a BVT 3000 heater connected to a liquid nitrogen Dewar. Before each measurement, the temperature was left to stabilize for 10 min. For some samples, the experiments were then repeated from high to low temperatures to investigate aging effects (see ESI,† Section S3).Rheology
The rheological properties were measured with a cone-and-plate geometry (angle 2°, radius 20 mm and truncation 46 μm) connected to a strain-controlled rheometer (ARES G2, TA Instruments). The cone was smooth and the plate was sandblasted with a surface roughness of about 1 μm to prevent wall slip. For a given sample, each temperature was probed independently with a different loading and independent gap calibration. The three temperatures probed T = 10, 50, and 70 °C were maintained constant by a Peltier modulus placed under the bottom plate. The rheological protocol for linear viscoelastic characterization of the samples was divided into three consecutive steps: (i) a preshear at![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 for 3 min to erase the loading history and rejuvenate the sample;55–57 (ii) a recovery phase of 5 min during which we monitored the sample linear viscoelastic properties by applying small amplitude oscillations in the linear regime at a frequency ω = 2π rad s−1; (iii) a frequency sweep performed by mutliwave strain signals58 in the linear regime to span frequencies from ω = 0.30 to 420 rad s−1. The samples remained in the rheometer for 9 minutes, and no evidence of alternation due to evaporation was witnessed by visual inspection, even at the highest temperature.
= 500 s−1 for 3 min to erase the loading history and rejuvenate the sample;55–57 (ii) a recovery phase of 5 min during which we monitored the sample linear viscoelastic properties by applying small amplitude oscillations in the linear regime at a frequency ω = 2π rad s−1; (iii) a frequency sweep performed by mutliwave strain signals58 in the linear regime to span frequencies from ω = 0.30 to 420 rad s−1. The samples remained in the rheometer for 9 minutes, and no evidence of alternation due to evaporation was witnessed by visual inspection, even at the highest temperature.
Author contributions
CRediT: Léo Hervéou conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – review & editing; Gauthier Legrand conceptualization, investigation, validation, writing – review & editing; Thibaut Divoux conceptualization, methodology, project administration, resources, supervision, visualization, validation, writing – original draft, writing – review & editing; Guilhem P. Baeza conceptualization, methodology, project administration, resources, supervision, visualization, validation, writing – original draft, writing – review & editing.Data availability
Data for this article, including CPMG measurements I(t) for all the samples are available at https://www.researchgate.net/publication/384054735_Herveou_et_al_CPMG, DOI: https://doi.org/10.13140/RG.2.2.30502.33604.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All the authors warmly thank Carlos Fernandez-de-Albá (IMP, INSA-Lyon) and Cédric Lorthioir (LCMCP, Sorbonne University, Paris) for technical support and insightful discussions about low-field NMR experiments. This work was supported by the LABEX iMUST of the University of Lyon (ANR-10-LABX-0064), created within the “Plan France 2030” set up by the French government and managed by the French National Research Agency (ANR).Notes and references
- E. A. Appel, J. del Barrio, X. J. Loh and O. A. Scherman, Chem. Soc. Rev., 2012, 41, 6195–6214 RSC.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC.
- Q. Chen, H. Chen, L. Zhu and J. Zheng, J. Mater. Chem. B, 2015, 3, 3654–3676 RSC.
- X. Li and J. P. Gong, Nat. Rev. Mater., 2024, 1–19 Search PubMed.
- R. Messing and A. M. Schmidt, Polym. Chem., 2011, 2, 18–32 RSC.
- J. Li, W. R. Illeperuma, Z. Suo and J. J. Vlassak, ACS Macro Lett., 2014, 3, 520–523 CrossRef CAS PubMed.
- X. Li, C. Tang, D. Liu, Z. Yuan, H.-C. Hung, S. Luozhong, W. Gu, K. Wu and S. Jiang, Adv. Mater., 2021, 33, 2102479 CrossRef CAS PubMed.
- H. Zhang, F. Zhang and R. Yuan, Hydrogels based on natural polymers, Elsevier, 2020, pp. 357–410 Search PubMed.
- P. C. Nath, S. Debnath, K. Sridhar, B. S. Inbaraj, P. K. Nayak and M. Sharma, Gels, 2022, 9, 1 CrossRef PubMed.
- S. Rose, A. Prevoteau, P. Elzière, D. Hourdet, A. Marcellan and L. Leibler, Nature, 2014, 505, 382–385 CrossRef CAS.
- R. V. Ulijn, N. Bibi, V. Jayawarna, P. D. Thornton, S. J. Todd, R. J. Mart, A. M. Smith and J. E. Gough, Mater. Today, 2007, 10, 40–48 CrossRef CAS.
- L. L. Palmese, R. K. Thapa, M. O. Sullivan and K. L. Kiick, Curr. Opin. Chem. Eng., 2019, 24, 143–157 CrossRef PubMed.
- F. Zhao, J. Bae, X. Zhou, Y. Guo and G. Yu, Adv. Mater., 2018, 30, 1801796 CrossRef.
- Y. Shi, L. Peng and G. Yu, Nanoscale, 2015, 7, 12796–12806 RSC.
- P. Schexnailder and G. Schmidt, Colloid Polym. Sci., 2009, 287, 1–11 CrossRef CAS.
- H. Dehne, F. Hecht and A. Bausch, Soft Matter, 2017, 13, 4786–4790 RSC.
- C. Y. Anthony, A. A. Smith and E. A. Appel, Mol. Syst. Des. Eng., 2020, 5, 401–407 RSC.
- G. Legrand, S. Manneville, G. H. McKinley and T. Divoux, Macromolecules, 2023, 56, 2298–2308 CrossRef CAS.
- R. Moakes, A. Sullo and I. Norton, Food Hydrocoll., 2015, 45, 227–235 CrossRef CAS.
- C. Tanford, Adv. Protein Chem., 1968, 23, 121–282 CrossRef CAS.
- R. Fan, Y. Cheng, R. Wang, T. Zhang, H. Zhang, J. Li, S. Song and A. Zheng, Polymers, 2022, 14, 2379 CrossRef CAS PubMed.
- S. C. Deoni, Magn. Reson. Neuroimag., 2011, 65–108 CAS.
- C. Granziera and T. Sprenger, Brain Inflammation, Degeneration, and Plasticity in Multiple Sclerosis, in Brain Mapping, ed. A. W. Toga, Academic Press, Waltham, 2015, pp. 917–927 Search PubMed.
- T. Salomonsen, M. T. Sejersen, N. Viereck, R. Ipsen and S. B. Engelsen, Int. Dairy J., 2007, 17, 294–301 CrossRef CAS.
- N. Harbourne, J. C. Jacquier and D. ORiordan, Int. Dairy J., 2011, 21, 185–191 CrossRef CAS.
- E. Kirtil and M. H. Oztop, Food Eng. Rev., 2016, 8, 1–22 CrossRef.
- B. Ozel, S. S. Uguz, M. Kilercioglu, L. Grunin and M. H. Oztop, J. Food Process Eng., 2017, 40, e12465 CrossRef.
- K.-F. Ratzsch, C. Friedrich and M. Wilhelm, J. Rheol., 2017, 61, 905–917 CrossRef CAS.
- N. W. Radebe, K.-F. Ratzsch, C. O. Klein and M. Wilhelm, Rheol. Proc. Construct. Mater., 2020, 2, 256–265 Search PubMed.
- C. Fengler, J. Keller, K.-F. Ratzsch and M. Wilhelm, Adv. Sci., 2022, 9, 2104231 CrossRef CAS PubMed.
- Y. Xiong, Z. Xia, A. Lu and W. Chen, Anal. Chem., 2023, 95, 7545–7551 CrossRef CAS PubMed.
- B. Maillet, R. Sidi-Boulenouar and P. Coussot, Langmuir, 2022, 38, 15009–15025 CrossRef CAS PubMed.
- H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630 CrossRef CAS.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- R. W. Brown, Y.-C. N. Cheng, E. M. Haacke, M. R. Thompson and R. Venkatesan, Magnetic resonance imaging: physical principles and sequence design, John Wiley & Sons, 2014 Search PubMed.
- G. D. Fullerton, J. L. Potter and N. C. Dornbluth, Magn. Reson. Imaging, 1982, 1, 209–226 CrossRef CAS.
- D. Besghini, M. Mauri, P. Hashemi, M. Knarr, R. Adden, P. Mischnick and R. Simonutti, Macromolecules, 2023, 56, 4694–4704 CrossRef CAS.
- D. Capitani, V. Crescenzi, A. De Angelis and A. Segre, Macromolecules, 2001, 34, 4136–4144 CrossRef CAS.
- M. Abrami, G. Chiarappa, R. Farra, G. Grassi, P. Marizza and M. Grassi, ADMET DMPK, 2018, 6, 34–46 CrossRef.
- P. Y. Ghi, D. J. Hill and A. K. Whittaker, Biomacromolecules, 2002, 3, 991–997 CrossRef CAS PubMed.
- M. Kanekiyo, M. Kobayashi, I. Ando, H. Kurosu, T. Ishii and S. Amiya, J. Mol. Struct., 1998, 447, 49–59 CrossRef CAS.
- M. Abrami, I. DAgostino, G. Milcovich, S. Fiorentino, R. Farra, F. Asaro, R. Lapasin, G. Grassi and M. Grassi, Soft Matter, 2014, 10, 729–737 RSC.
- M. Abrami, F. Bignotti, F. Baldi, G. Spagnoli, A. Biasin, L. Grassi, G. Grassi and M. Grassi, Int. J. Pharm., 2023, 637, 122882 CrossRef CAS PubMed.
- J. H. Wang, J. Phys. Chem., 1965, 69, 4412 CrossRef CAS.
- G. Legrand, G. P. Baeza, S. Manneville and T. Divoux, arXiv, 2024, preprint, arXiv:2406.04453, DOI:10.48550/arXiv.2406.04453.
- G. Legrand, G. P. Baeza, M. Peyla, L. Porcar, C. Fernandez-de Alba, S. Manneville and T. Divoux, ACS Macro Lett., 2024, 13, 234–239 CrossRef CAS PubMed.
- G. P. Baeza, C. Dessi, S. Costanzo, D. Zhao, S. Gong, A. Alegria, R. H. Colby, M. Rubinstein, D. Vlassopoulos and S. K. Kumar, Nat. Commun., 2016, 7, 11368 CrossRef PubMed.
- V. Litvinov, W. Barendswaard and M. Van Duin, Rubber Chem. Technol., 1998, 71, 105–118 CrossRef CAS.
- M. Sattig, S. Reutter, F. Fujara, M. Werner, G. Buntkowsky and M. Vogel, Phys. Chem. Chem. Phys., 2014, 16, 19229–19240 RSC.
- L. R. G. Treloar, The physics of rubber elasticity, OUP Oxford, 1975.
- L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707 CrossRef CAS.
- C. D'Agostino, R. Liuzzi, L. F. Gladden and S. Guido, Soft Matter, 2017, 13, 2952–2961 RSC.
- C. DAgostino, V. Preziosi, G. Caiazza, M. V. Maiorino, E. Fridjonsson and S. Guido, Soft Matter, 2023, 19, 3104–3112 RSC.
- G. Legrand, S. Manneville, G. H. McKinley and T. Divoux, Macromolecules, 2023, 56, 2298–2308 CrossRef CAS.
- V. Viasnoff and F. Lequeux, Phys. Rev. Lett., 2002, 89, 065701 CrossRef.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- Y. M. Joshi and G. Petekidis, Rheol. Acta, 2018, 57, 521–549 CrossRef CAS.
- M. Mours and H. H. Winter, Rheol. Acta, 1994, 33, 385–397 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) T2 = f(cCMC) plots; (2) Ea values for all the samples; (3) cooling vs. heating T2 = f(1000/T) plots and Ea values for the whole set of samples; (4) corresponding viscous modulus of the elastic modulus plotted in Fig. 4; (5) CPMG experiments with various echo times. See DOI: https://doi.org/10.1039/d4sm01098a |
| ‡ These authors contributed equally to this work. |
| § Present address: Univ. Jean Monnet, Ingénierie des Matériaux Polymères, UMR 5223, 20 rue Annino, 42000 Saint-Etienne, France. |
| This journal is © The Royal Society of Chemistry 2025 |
